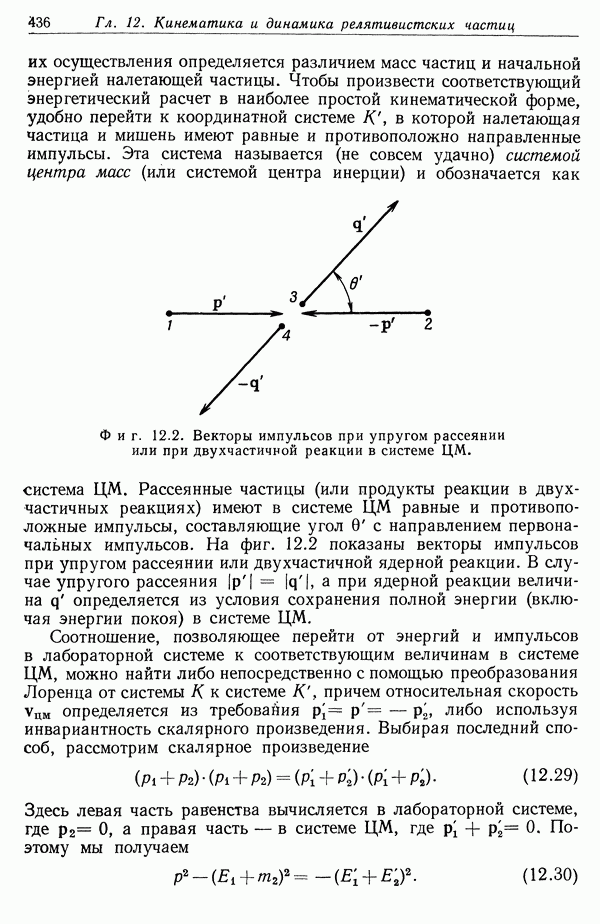
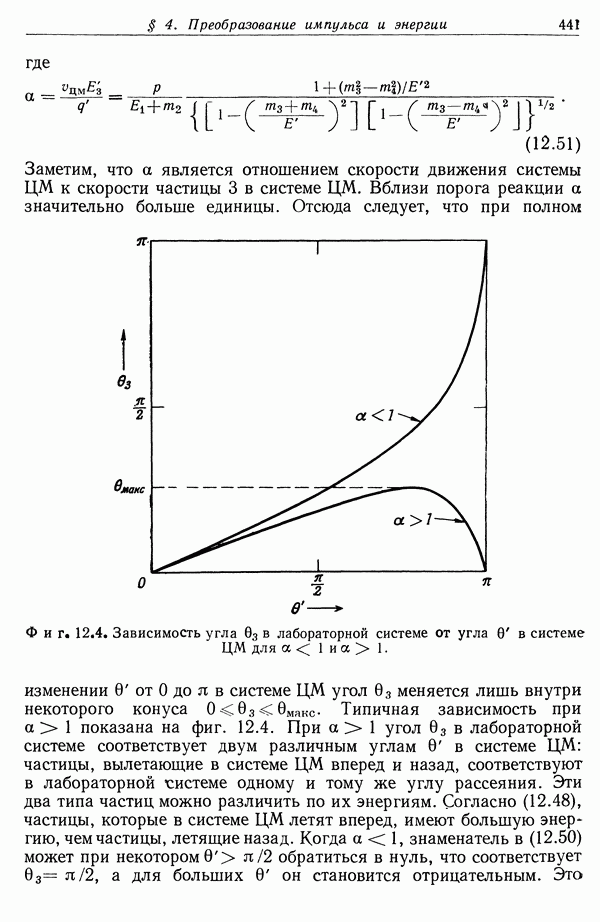
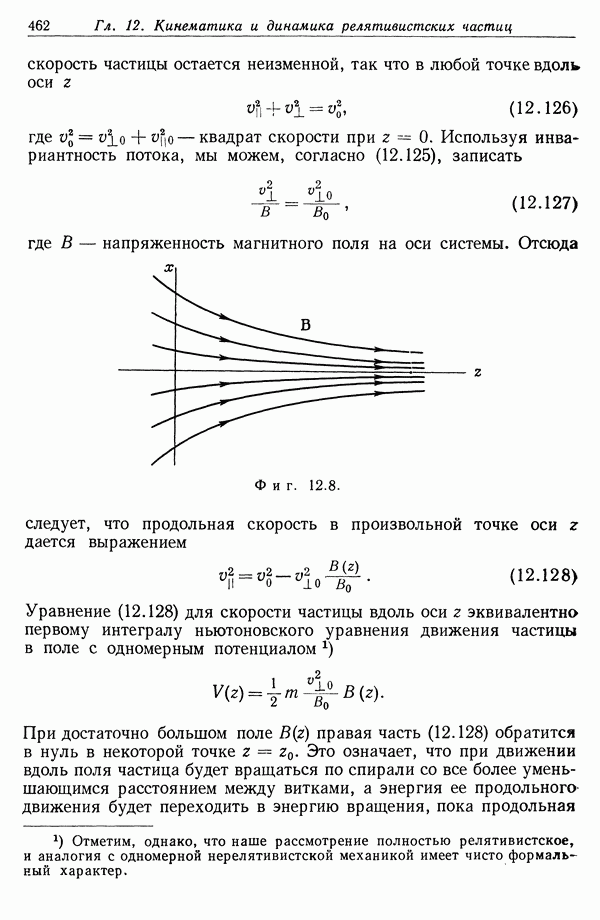
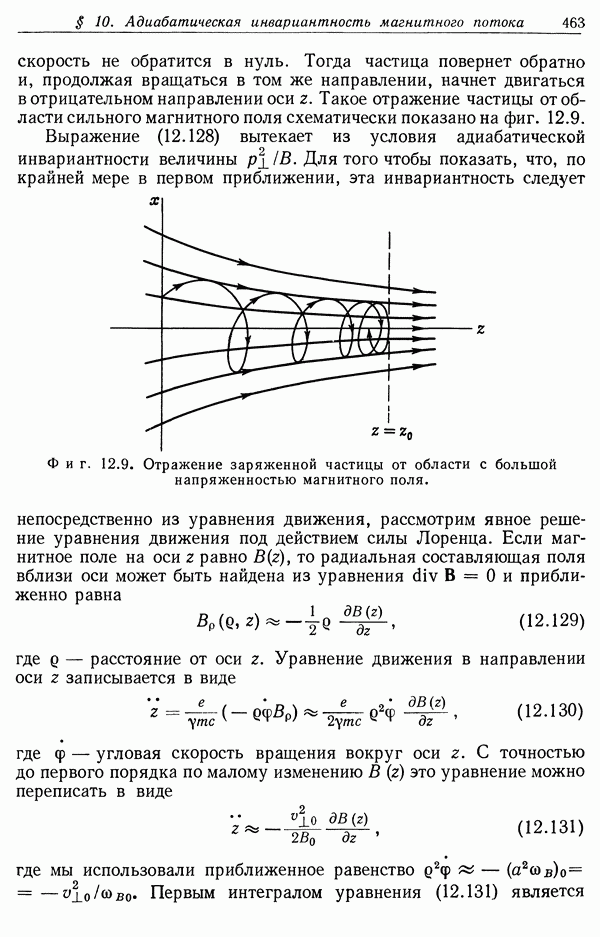
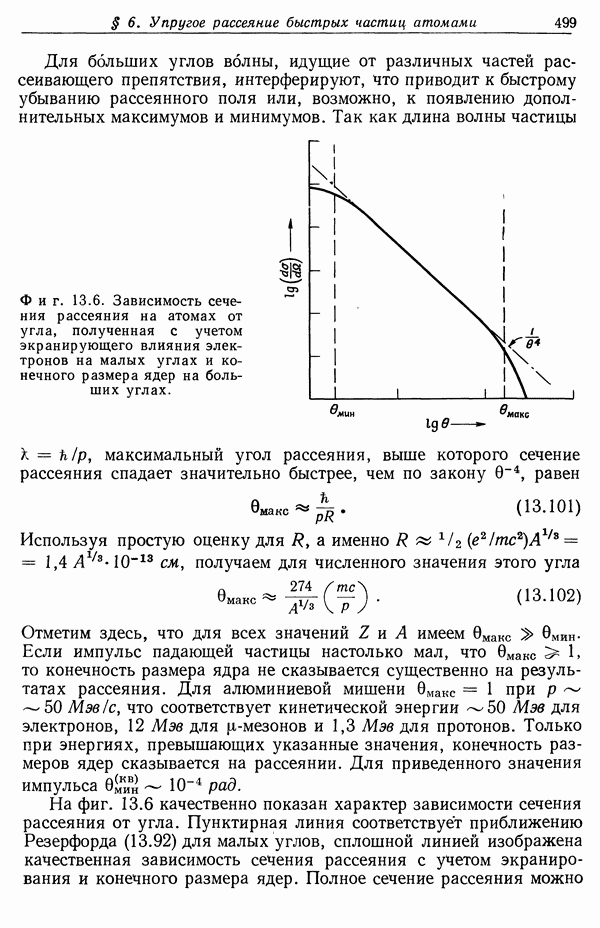
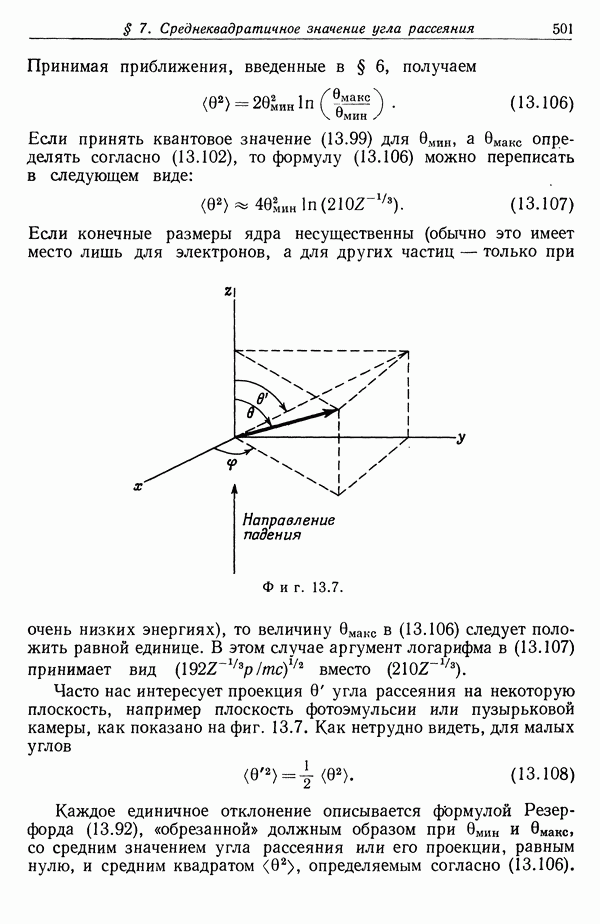
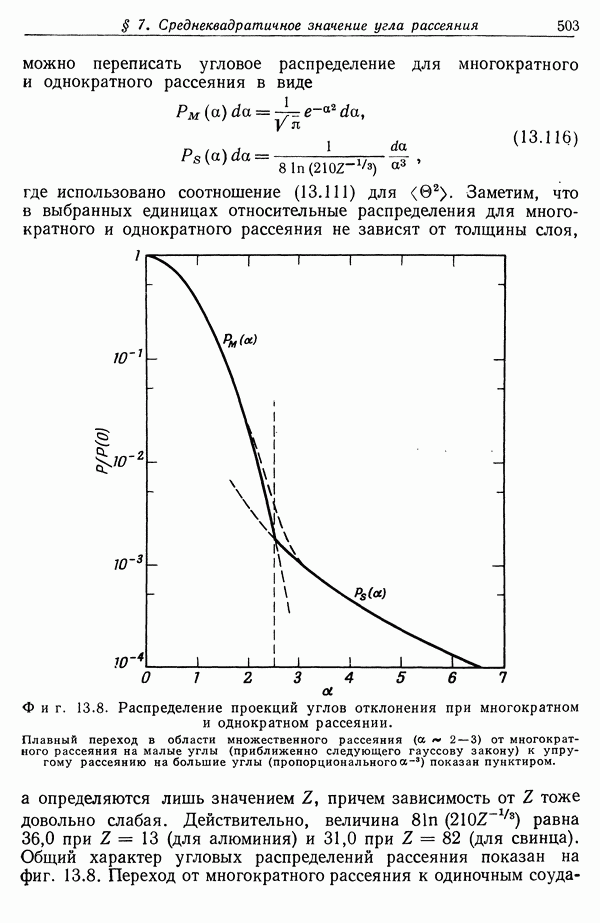
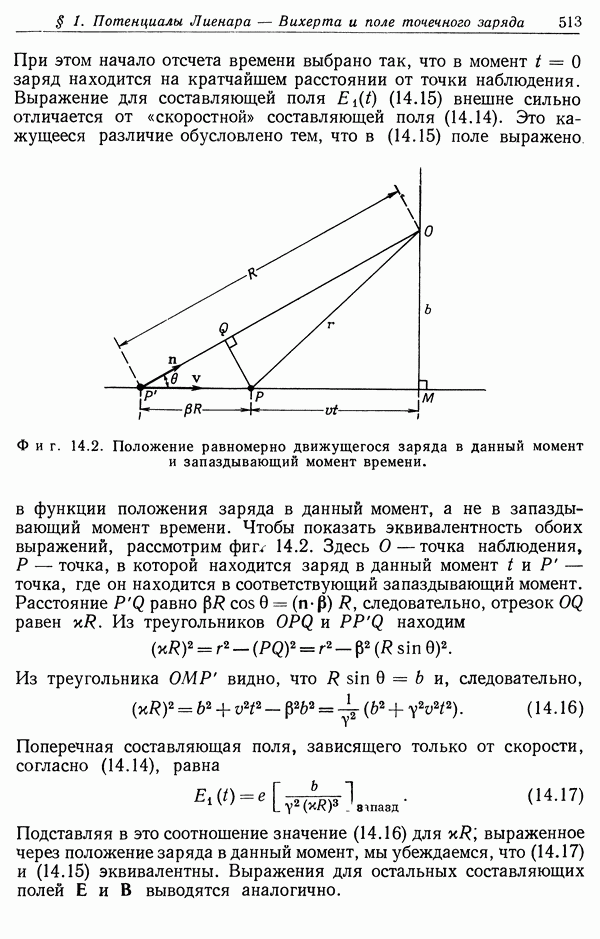
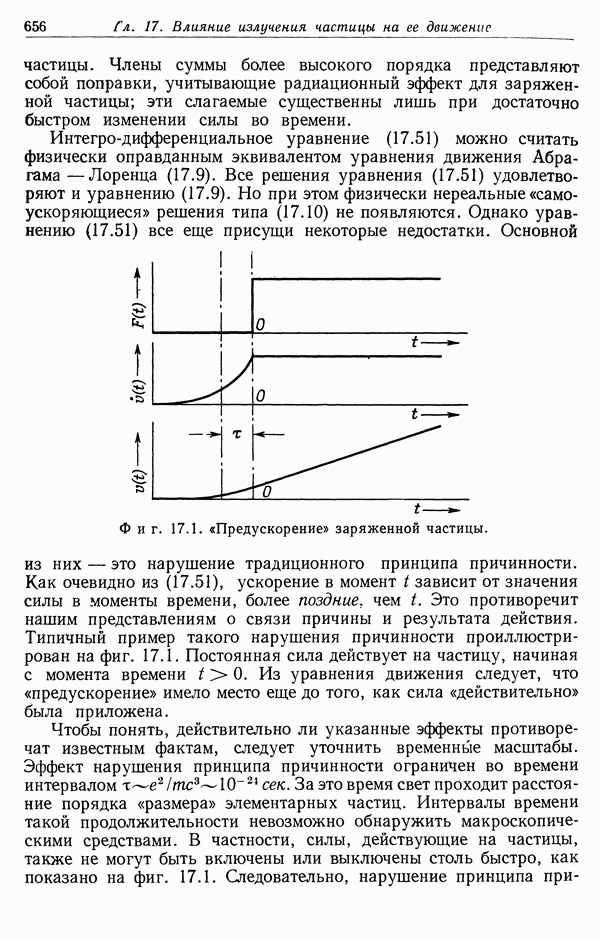
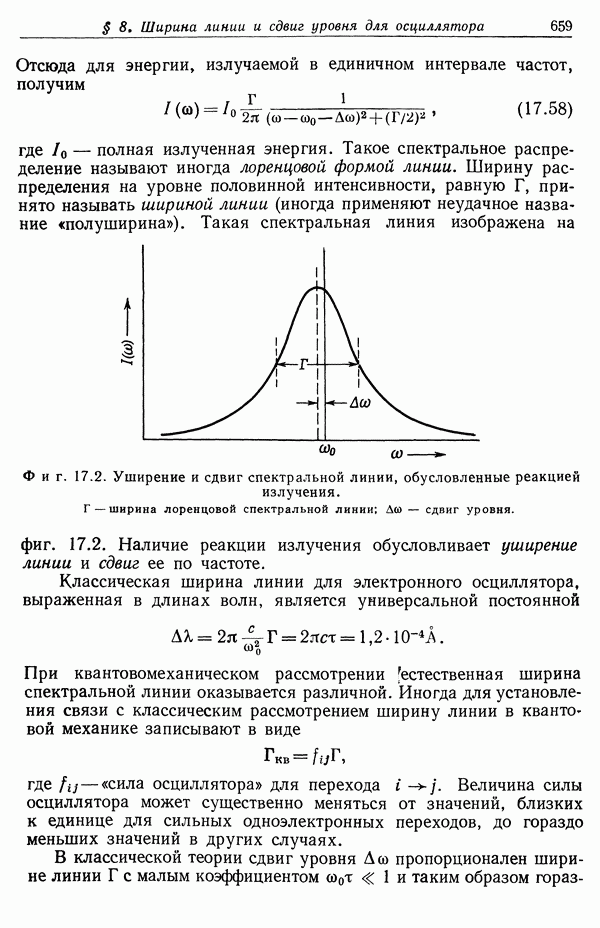
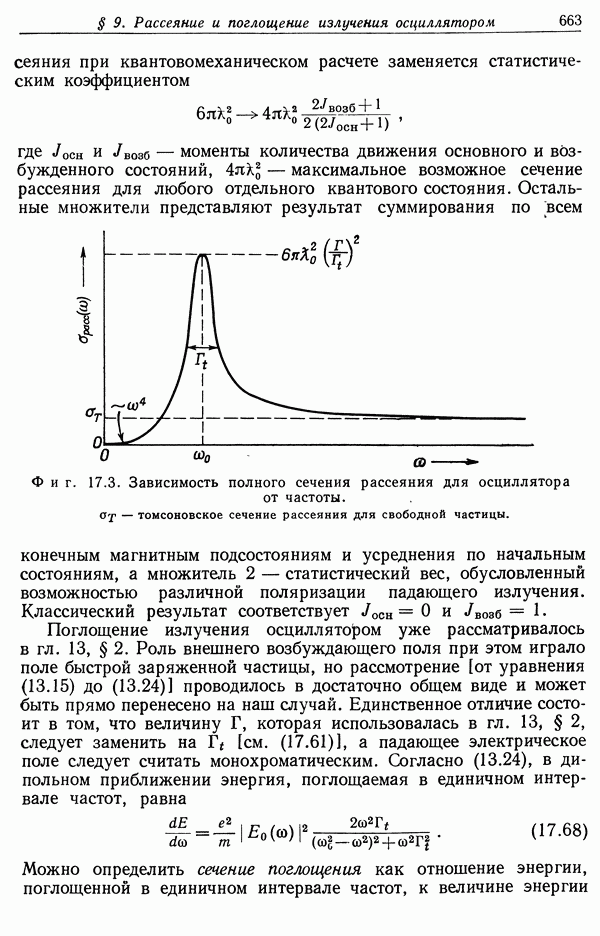
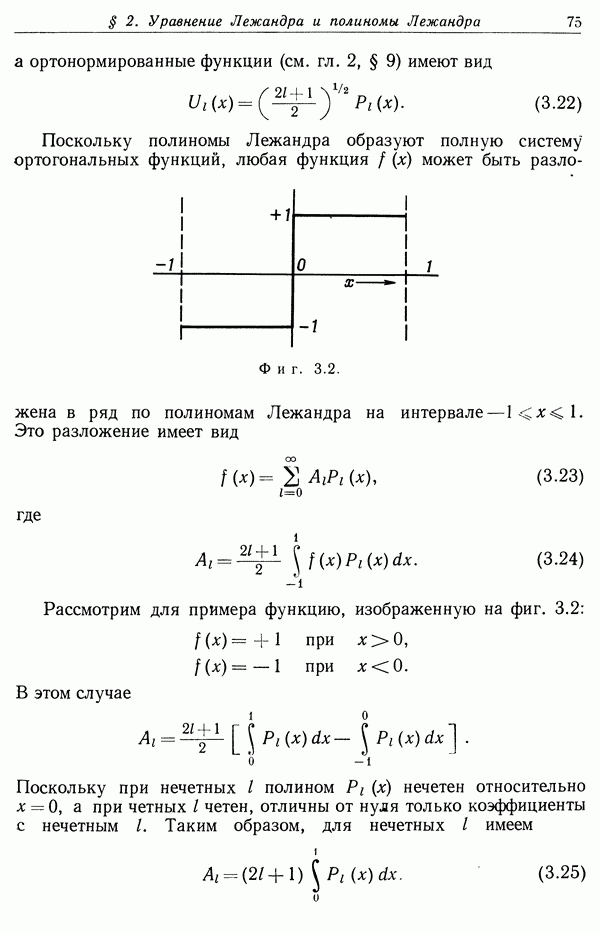| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
В этой главе основное внимание уделяется рассмотрению потенциала, обусловленного ограниченным распределением заряда, и дается его представление в виде разложения по мультиполям. В основном разложение проводится по сферическим гармоникам, но для нескольких первых мультиполей обсуждается их представление и в декартовых координатах. Затем вычисляется энергия мультиполя во внешнем электрическом поле. Путем рассмотрения поведения атомов в приложенном внешнем поле в сочетании с подходящей процедурой усреднения выводятся макроскопические уравнения электростатики. Затем описываются свойства диэлектриков, устанавливаются граничные условия для них и решаются некоторые типичные краевые задачи при наличии диэлектриков. На простых классических моделях иллюстрируются основные свойства диэлектриков: поляризуемость и диэлектрическая восприимчивость. В заключение рассматривается вопрос об электростатической энергии при наличии диэлектриков.
§ 1. Разложение по мультиполям
Ограниченное распределение заряда описывается плотностью заряда  отличной от нуля лишь внутри сферы радиусом R с центром в начале отсчета
отличной от нуля лишь внутри сферы радиусом R с центром в начале отсчета 
Потенциал вне сферы можно представить в виде разложения по сферическим гармоникам:

где вид постоянных коэффициентов выбран из соображения удобства при дальнейшем рассмотрении Выражение (4.1) называют обычно разложением по мультиполям; член, соответствующий  называется монополем, член с
называется монополем, член с  дипольным моментом и т. д. Смысл этих терминов станет ясным из дальнейшего. Задача состоит в том, чтобы выразить постоянные
дипольным моментом и т. д. Смысл этих терминов станет ясным из дальнейшего. Задача состоит в том, чтобы выразить постоянные  через функцию распределения плотности заряда
через функцию распределения плотности заряда  Искомое решение легко получается с помощью интегрального представления (1.17) для потенциала
Искомое решение легко получается с помощью интегрального представления (1.17) для потенциала

и разложения (3.70) для  Так как в данном случае нас интересует потенциал вне области, занятой распределением заряда, то следует положить
Так как в данном случае нас интересует потенциал вне области, занятой распределением заряда, то следует положить  При этом получаем
При этом получаем

Таким образом, коэффициенты в (4.1) оказываются равными

Эти коэффициенты называют мулыпипольными моментами. Для их физического истолкования выпишем в явном виде выражения нескольких первых моментов в декартовых координатах:

Здесь выписаны моменты лишь для  так как согласно
так как согласно  при действительной плотности заряда моменты с
при действительной плотности заряда моменты с  можно найти из соотношений
можно найти из соотношений

В выражениях (4.4)-(4.6) скаляр q определяет полный заряд, или момент нулевого порядка (монополь), вектор  есть электри ческий дипольный момент:
есть электри ческий дипольный момент:

a Q - составляющие тензора квадрупольного момента:

Мы видим, что  мультипольные коэффициенты (число которых равно
мультипольные коэффициенты (число которых равно  представляются линейной комбинацией декартовых составляющих соответствующих мультиполей. Предоставляем читателю в качестве упражнения провести вывод разложения для потенциала
представляются линейной комбинацией декартовых составляющих соответствующих мультиполей. Предоставляем читателю в качестве упражнения провести вывод разложения для потенциала  в декартовых координатах:
в декартовых координатах:

которое можно получить непосредственно, из разложения  в ряд Тейлора. Получение членов разложейия (4.10) выше квадрупольного оказывается гораздо более сложной задачей.
в ряд Тейлора. Получение членов разложейия (4.10) выше квадрупольного оказывается гораздо более сложной задачей.
Составляющие вектора напряженности электрического поля, обусловленного данным мультиполем, легче всего выразить в сферических координатах. Взятый со знаком минус градиент члена суммы (4.1), соответствующего фиксированным  , имеет следующие составляющие в сферической системе координат:
, имеет следующие составляющие в сферической системе координат:

Функции  можно представить как линейные комбинации других функций
можно представить как линейные комбинации других функций  однако соответствующие выражения не обладают достаточной наглядностью, и поэтому мы их не будем приводить. Векторное мультипольное поле лучше всего представлять с помощью векторных сферических гармоник, как это рассмотрено в гл. 16.
однако соответствующие выражения не обладают достаточной наглядностью, и поэтому мы их не будем приводить. Векторное мультипольное поле лучше всего представлять с помощью векторных сферических гармоник, как это рассмотрено в гл. 16.
Для диполя  , ориентированного вдоль оси z, составляющие поля (4.11) принимают простой вид:
, ориентированного вдоль оси z, составляющие поля (4.11) принимают простой вид:

Это поле можно записать в векторной форме, либо исходя из выражений (4.12), либо непосредственно вычисляя градиент от дипольного члена разложения в (4.10). Поле в точке  обусловленное диполем
обусловленное диполем  , расположенным в точке
, расположенным в точке  оказывается равным
оказывается равным

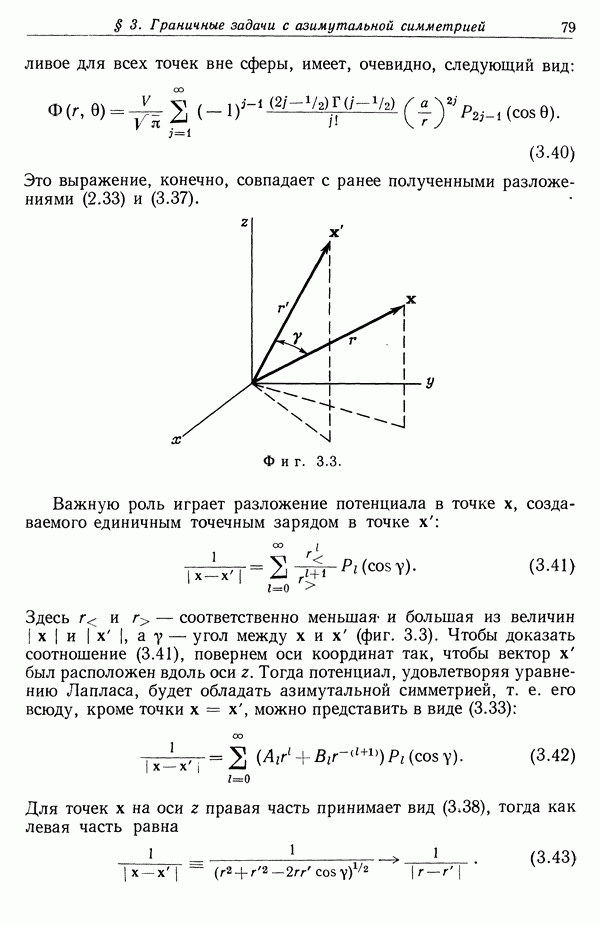
где  — единичный вектор, направленный из точки
— единичный вектор, направленный из точки  в точку
в точку 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
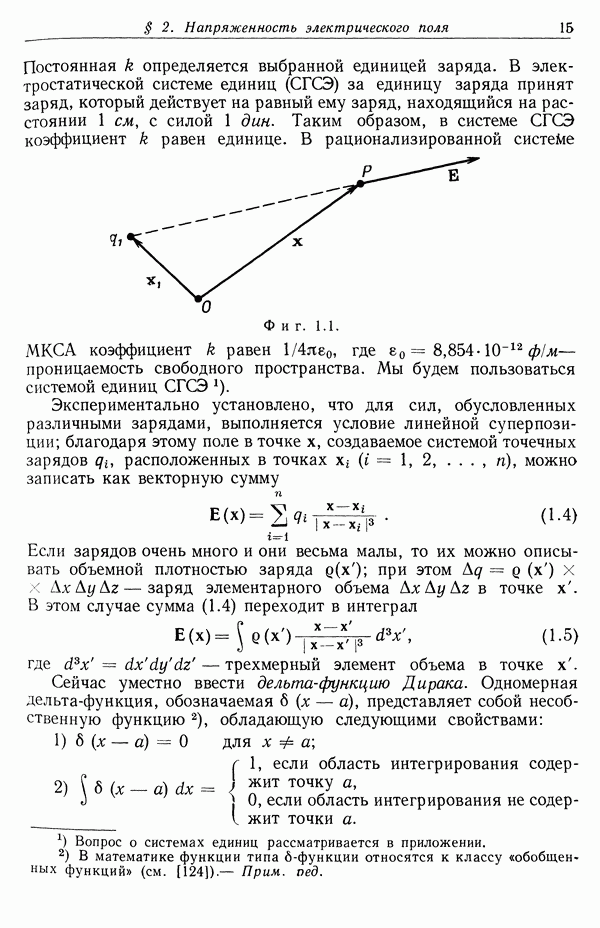
- § 2. Напряженность электрического поля
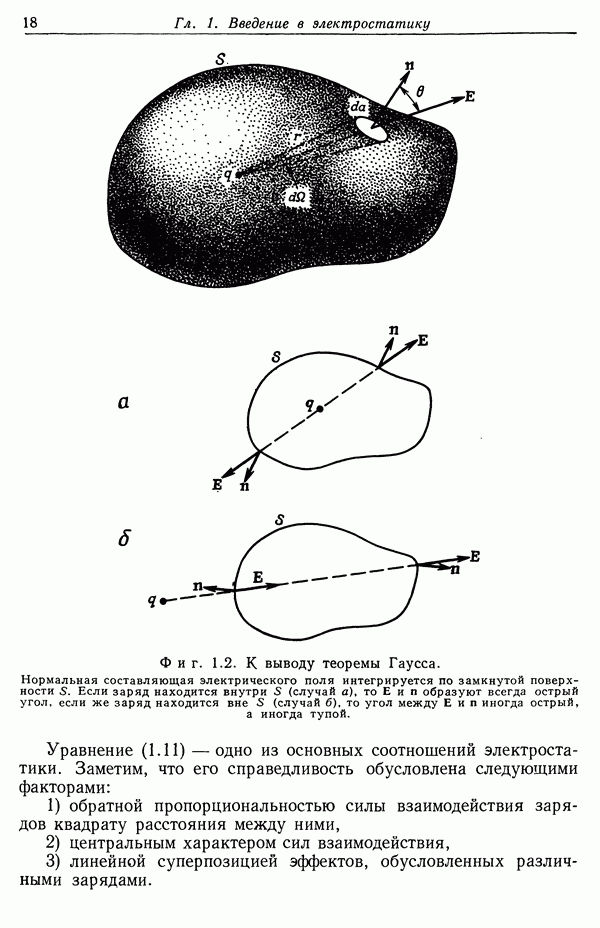
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
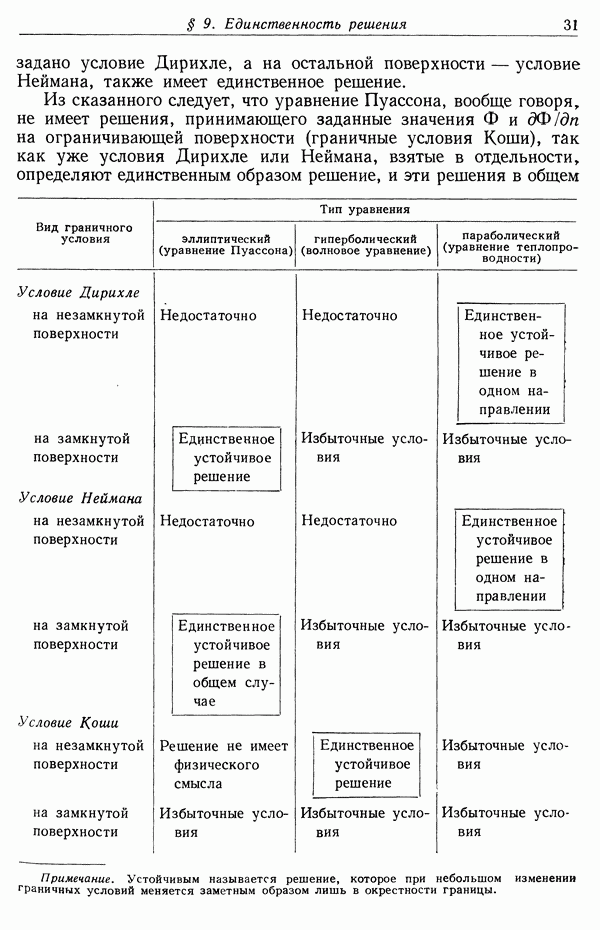
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
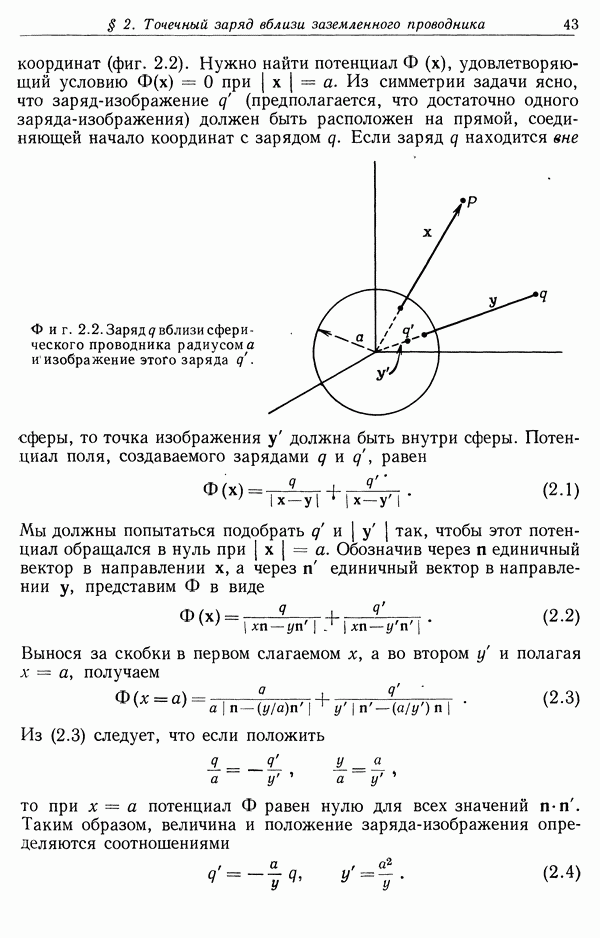
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
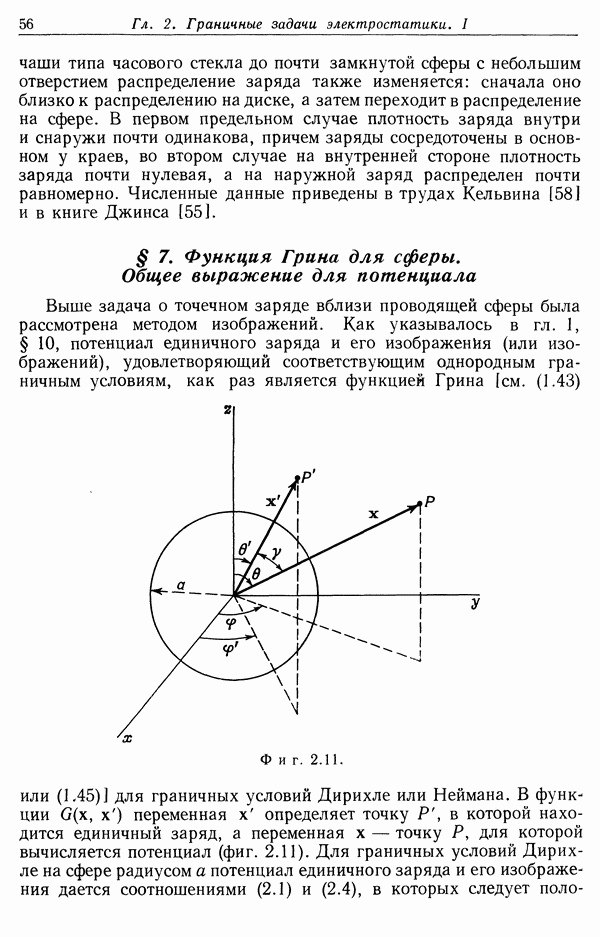
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
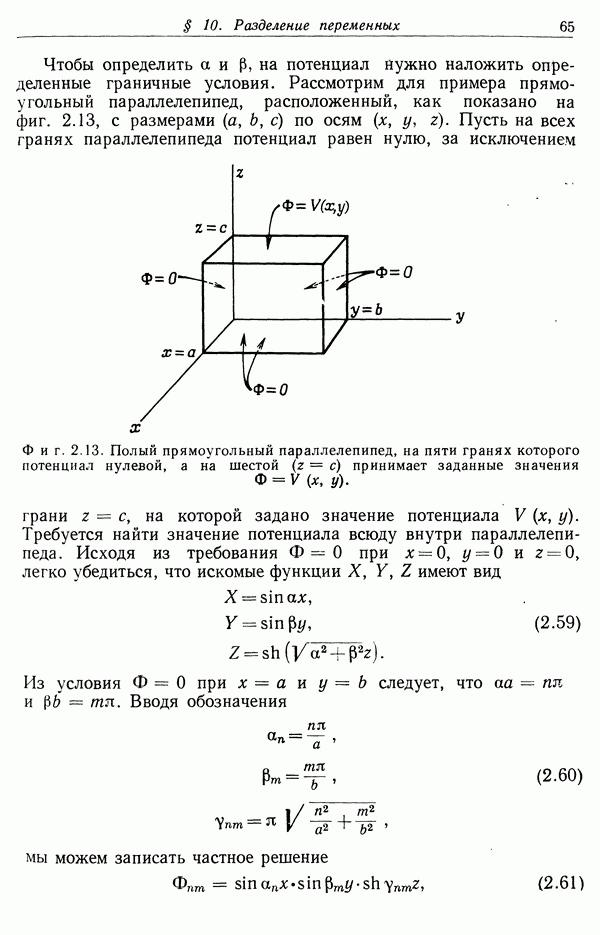
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
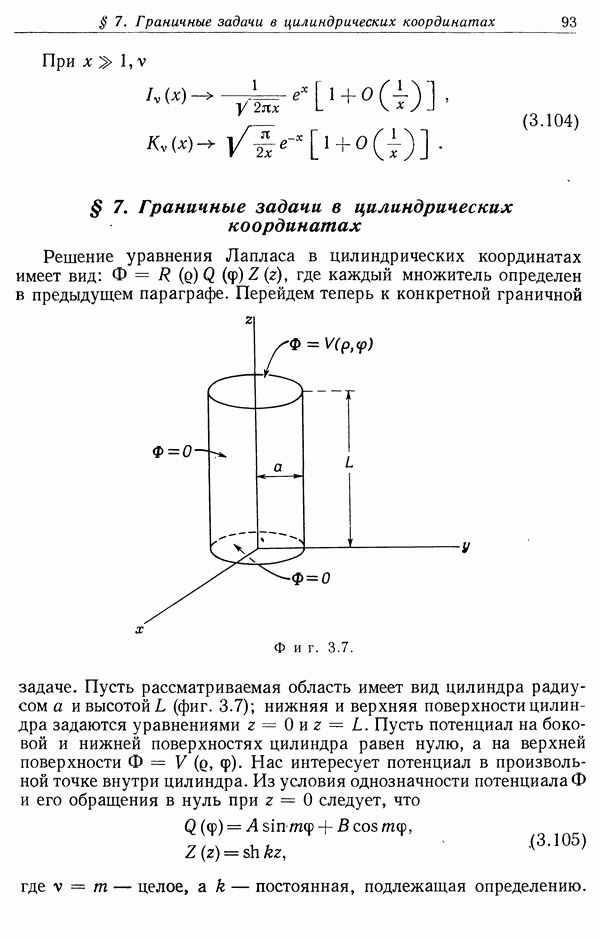
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 2. Линейная и круговая поляризация
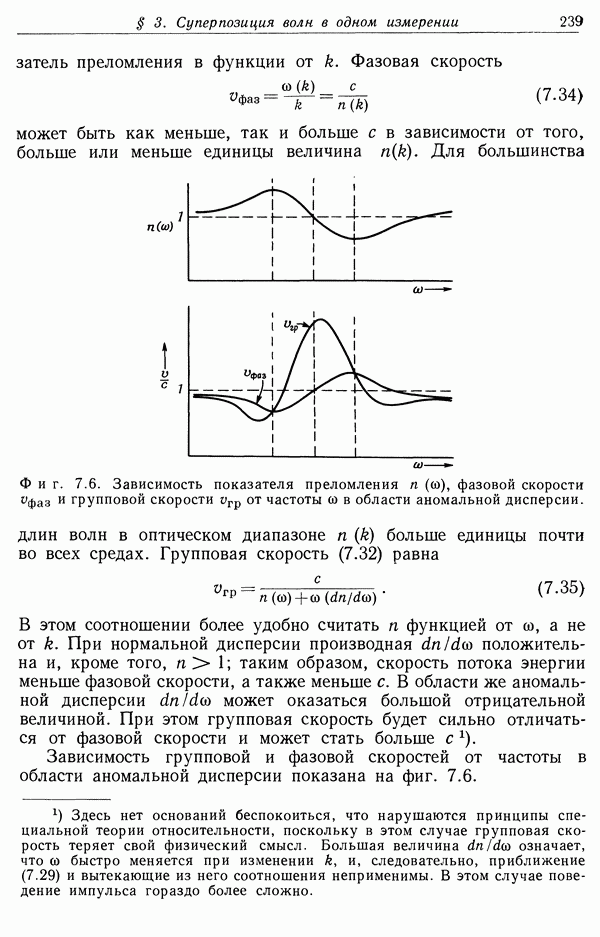
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
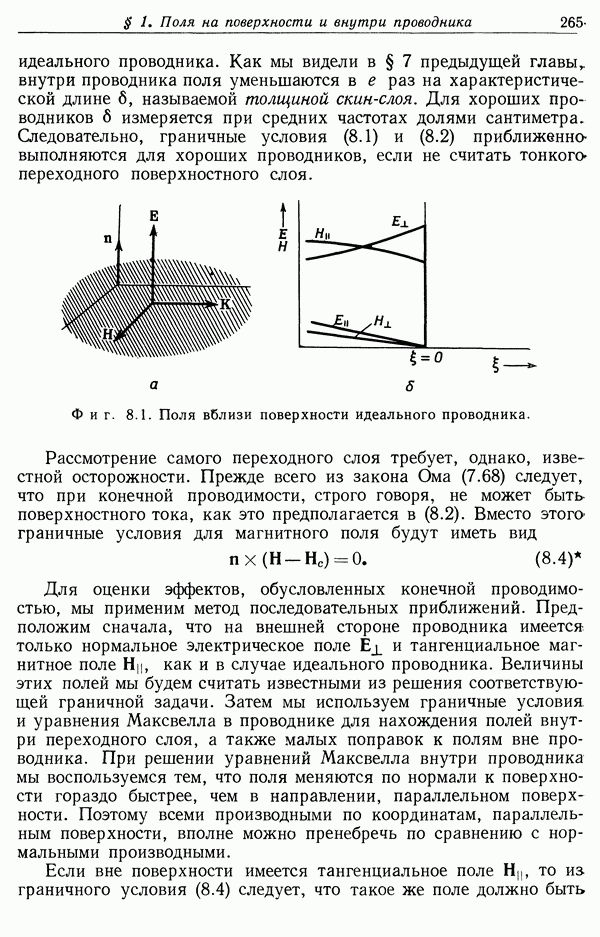
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
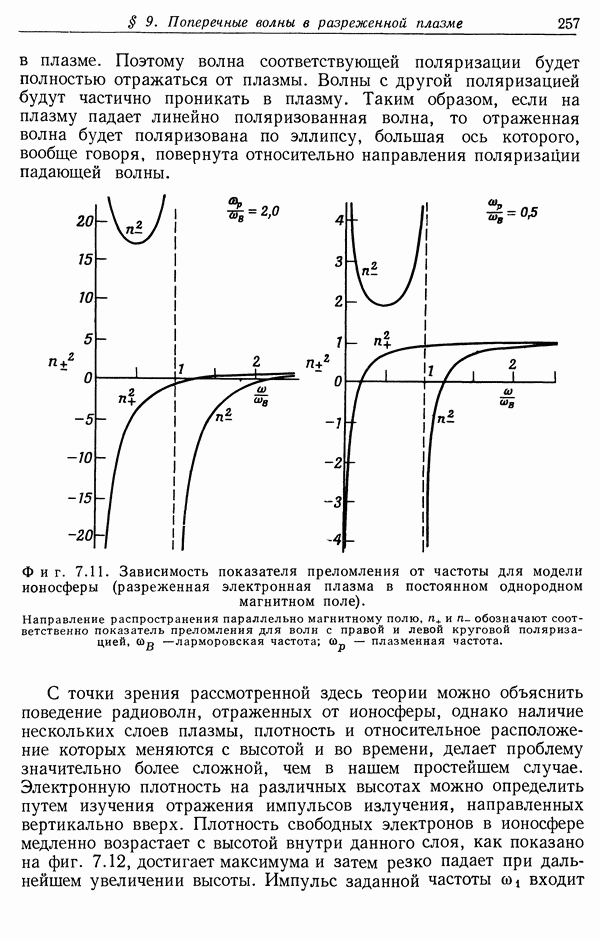
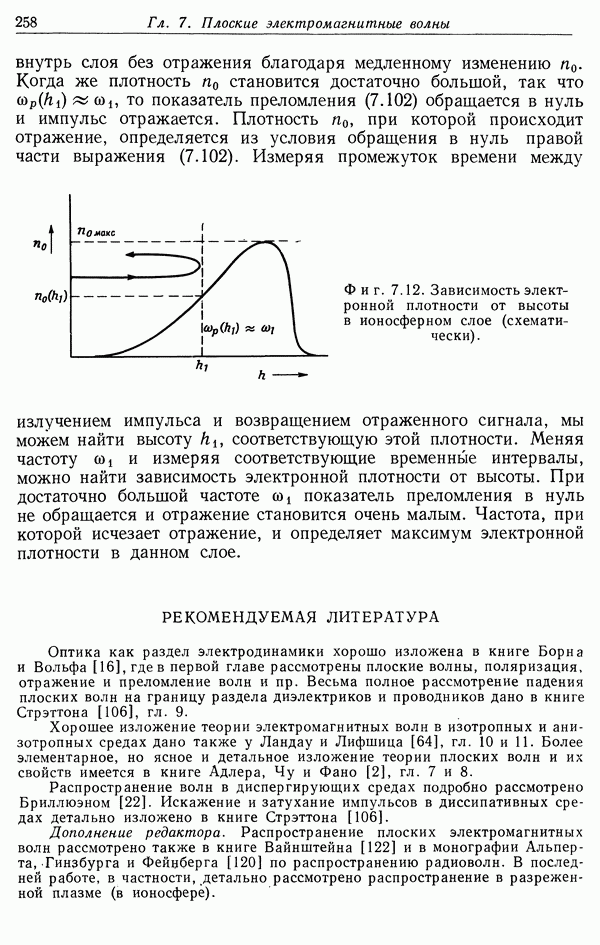
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
- § 7. Принцип Бабине для дополнительных экранов
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ