ЗАДАЧИ

14.1. Проверить непосредственным вычислением, что выражения для всех составляющих полей Е и В равномерно движущейся частицы, получающиеся из потенциалов Лиенара — Вихерта, совпадают с выражениями, найденными в тексте с помощью преобразований Лоренца. Использовать общий метод, описанный в конце § 1.

14.2. С помощью потенциалов Лиенара—Вихерта найти среднюю по времени мощность излучения в единицу телесного угла для нерелятивистской частицы с зарядом если:

а) частица совершает гармонические колебания вдоль оси z так, что ее мгновенное положение

б) частица движется с постоянной угловой частотой по окружности радиусом R, лежащей в плоскости

Построить график углового распределения излучения и определить полную мощность излучения в обоих случаях.

14.3. Нерелятивистская частица с зарядом массой и кинетической энергией претерпевает лобовое соударение с фиксированным центральным полем сил конечной протяженности. Силы являются отталкивающими и описываются потенциалом который превышает Е на близких расстояниях.

а) Показать, что полная излученная энергия определяется формулой

гдегмин — минимальное расстояние до центра сил, достигаемое при соударении.

б) Показать, что если взаимодействие описывается кулоновским потенциалом то полная излученная энергия равна

где — скорость заряда на бесконечности.

14.4. Частица с массой и зарядом q движется в плоскости, перпендикулярной однородному статическому магнитному полю В.

а) Вычислить полную энергию, излучаемую в единицу времени, выразив ее через заданные выше константы и отношение у полной энергии частицы к ее энергии покоя.

б) Показать, что если при частица имела полную энергию то в момент определяемый соотношением

она будет обладать полной энергией если

в) Найти кинетическую энергию частицы в момент t, если первоначально частица была нерелятивистской и имела кинетическую энергию при

г) Пусть частица, захваченная дипольным магнитным полем Земли, движется по спирали вдоль силовой линии. Где она будет больше излучать — вблизи экватора или вблизи точки поворота? Почему? Дать количественное обоснование.

14.5. Как и в задаче 14.2, п. заряд совершает простое гармоническое движение вдоль оси

а) Показать, что мгновенное значение мощности излучаемой в единицу телесного угла, равно

где

б) Произведя усреднение по времени, показать, что средние потери мощности в единицу телесного угла описываются соотношением

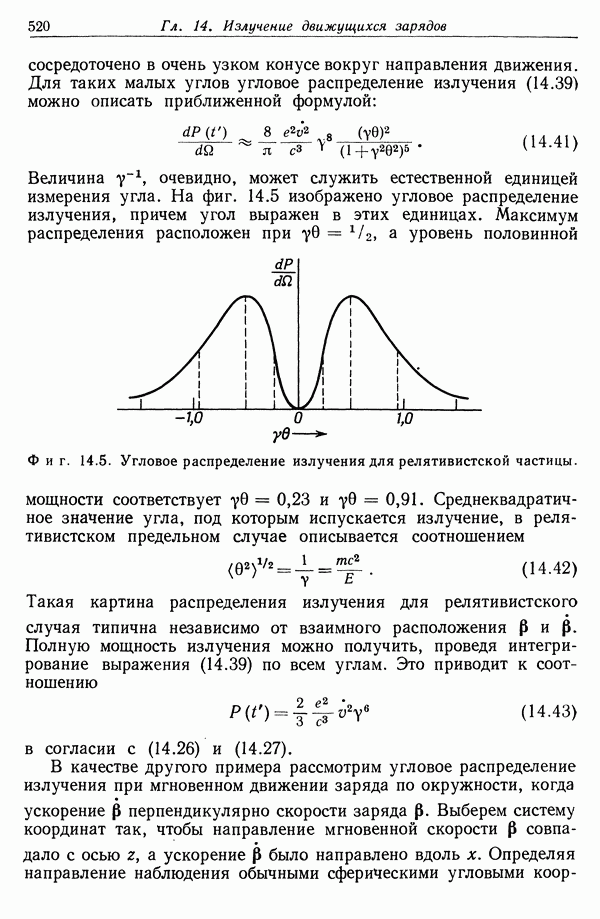
Построить схематический график углового распределения излучения для нерелятивистского и релятивистского движений.

14.6. Пусть излучающая частица совершает периодическое движение с периодом Т. С помощью формулы суммирования Пуассона или другим методом показать, что в этом случае непрерывный спектр излучаемых частот переходит в дискретный спектр, состоящий из частот, кратных основной частоте. Показать, что общее выражение для мощности излучения в единицу телесного угла на гармонике основной частоты имеет вид

14.7. а) Показать, что для простого гармонического движения заряда, рассмотренного в задаче 14.5, средняя мощность излучения в единицу телесного угла на гармонике равна

б) Показать, что в нерелятивистском предельном случае вся мощность излучается на основной гармонике и равна

где средний квадрат амплитуды колебаний.

14.8. Частица с зарядом движется с постоянной угловой частотой по окружности радиусом R, лежащей в плоскости

а) Показать, что точное выражение для углового распределения мощности излучения на гармонике имеет вид

где функция Бесселя порядка.

б) Считая движение нерелятивистским, получить приближенное выражение для Сопоставить с результатами задачи 14.2, п. «б».

в) Считая движение ультрарелятивистским, получить характеристики, приведенные в тексте для релятивистской частицы, движущейся по окружности (при этом полезно использовать формулы из книги Ватсона [114]).

14.9. Согласно принципу соответствия Бора, в предельном случае больших квантовых чисел классическое значение мощности излучения, на основной гармонике равно произведению энергии кванта на вероятность перехода (обратное среднее время жизни) между состояниями с главными квантовыми числами

а) Используя нерелятивистское приближение, показать, что для водородоподобного атома классическое выражение для вероятности перехода с круговой орбиты, характеризуемой главным квантовым числом на орбиту с квантовым числом имеет вид

б) Для водорода сравнить классическое значение времени жизни, найденное в п. «а», с точным квантовомеханическим значением для переходов .

14.10. При периодическом движении заряда излучение обладает дискретным спектром частот, кратных основной частоте движения. Значительное излучение на высших гармониках может иметь место либо из-за релятивистских эффектов (см. задачи 14.7 и 14.8) даже в случае, когда составляющие скорости строго синусоидальны, либо из-за того, что составляющие скорости меняются не синусоидально, хотя и периодически. Примером второго случая является нерелятивистское эллиптическое движение электрона в атоме водорода.

Орбита при этом может быть определена параметрическими уравнениями

где

— главная полуось эллипса, — эксцентриситет, угловая частота, — угол в плоскости орбиты. Параметры эллипса можно выразить через

энергию связи В и момент количества движения

а) Показать, что мощность излучения на гармонике равна

где — функция Бесселя порядка.

б) Показать, что для круговой орбиты полученный результат согласуется с решением задачи 14.8, п. «а».

14.11. Вместо одиночного заряда , движущегося с постоянной частотой по окружности радиусом R (см. задачу 14.8), рассмотреть движение системы N зарядов, относительные положения которых на окружности фиксирован

а) Показать, что мощность излучения на гармонике описывается соотношением

где — мощность излучения одного заряда (см. задачу 14.8, п. ), а

где - угловая координата заряда в момент

б) Показать, что при равномерном распределении зарядов по окружности излучение происходит лишь на гармониках, кратных а интенсивность излучения возрастает в раз по сравнению с излучением одиночного заряда. Дать качественное объяснение указанных фактов.

в) Показать без подробных вычислений, что при нерелятивистском движении полная мощность излучения зависит от N приблизительно как и, таким образом, в пределе при излучение отсутствует.

г) Аналогичным образом показать, что для релятивистских частиц зависимость мощности излучения от N определяется функцией при так что опять-таки в пределе излучение отсутствует.

д) Указать связь между результатами, полученными в п. «в» и «г», и известными излучательными свойствами стационарного тока в замкнутом контуре.

14.12. Рассмотреть в качестве идеализации постоянного тока в контуре систему из N идентичных зарядов q, движущихся по произвольному замкнутому пути с постоянной по величине скоростью v. Соседние заряды находятся на малом постоянном расстоянии А друг от друга.

Исходя из выражений Лиенара — Вихерта для полей каждой частицы и не накладывая никаких ограничений на величину скорости v, показать, что в пределе, когда , но , система не излучает, а электрическое и магнитное поля системы эквивалентны обычным статическим полям.

(Заметим, что в реальном контуре стационарные положительные ионы в проводнике создают электрическое поле, компенсирующее поле движущихся зарядов.)

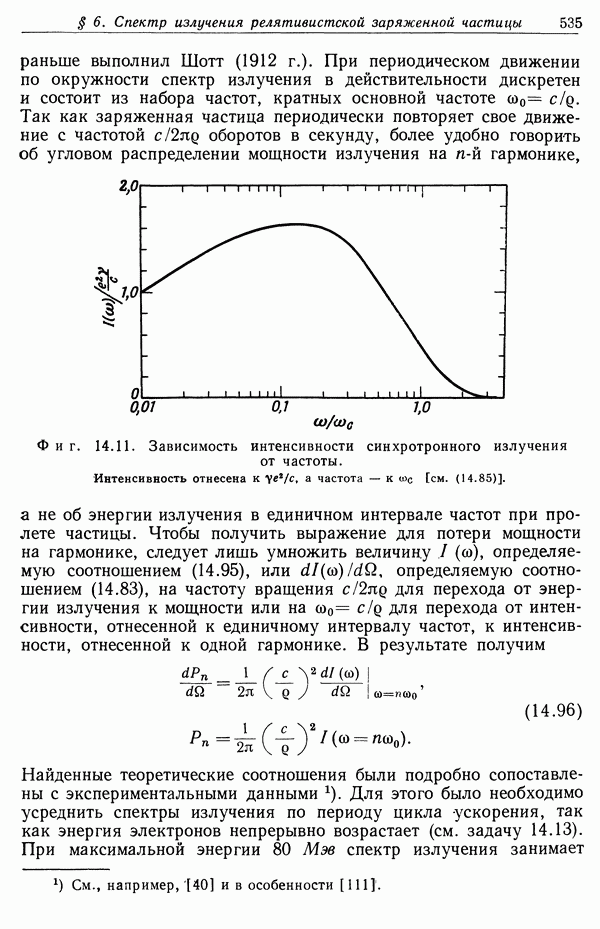
14.13. Пусть мгновенный спектр мощности излучения электрона в синхротроне описывается формулой

где

а) Показать, что если энергия электронов растет в течение одного цикла ускорения приблизительно линейно, то усредненный по циклу спектр мощности имеет вид

где

б) Найти предельные выражения для спектра мощности при

в) Пользуясь таблицами значений интеграла, входящего в приведенное выражение (он представляет собой неполную гамма-функцию), или с помощью графического интегрирования численно рассчитать спектр для . Построить график зависимости Р от и сравнить его с кривыми, приведенными в работе [40].

14.14. а) В рамках приближений, принятых в § 6 этой главы, показать, что при релятивистском движении частиц по траектории с мгновенным радиусом кривизны Q интенсивность излучения с правой и левой круговой поляризацией в единицу телесного угла в единичном интервале частот определяется выражением

б) Используя приведенное в п. выражение и формулы § 6, исследовать зависимость поляризации полного излучения от частоты и угла. В частности, определить степень поляризации: 1) на высоких частотах для всех значений углов; 2) на средних и низких сос) частотах для больших углов; 3) на средних и низких частотах для очень малых углов.

в) Провести сравнение с экспериментальными результатами, приведенными в работе [56].

14.15. Рассмотреть синхротронное излучение Крабовидной туманности. Электроны с энергиями до движутся в магнитном поле порядка гаусс.

а) Для гаусс вычислить радиус орбиты Q, основную частоту и критическую частоту .

б) Показать, что спектральное распределение мощности синхротронного излучения для релятивистских электронов с энергией Е в постоянном магнитном поле может быть представлено в виде

где — функция, равная единице при и быстро убывающая до нуля при [в задаче 14.13, например, а сос где -угол наклона спиральной траектории.

в) Показать, что при законе распределения электронов по энергии спектр мощности синхротронного излучения имеет вид

где

г) Наблюдения радиоизлучения и непрерывного оптического спектра Крабовидной туманности показывают, что в интервале частот от до постоянная . На более высоких частотах интенсивность спектральных компонент излучения быстро убывает с показателем а 1,5. Определить показатель степени в энергетическом спектре электронов и верхнюю границу спектра. Согласуется ли эта граничная энергия с данными, приведенными в п. «а»?

д) Используя решение задачи 14.4, п. «б», определить величину интервала времени, необходимого для того, чтобы энергия электронов уменьшилась от бесконечного значения до в поле гаусс. В каком отношении находится этот результат с известным временем жизни Крабовидной туманности?

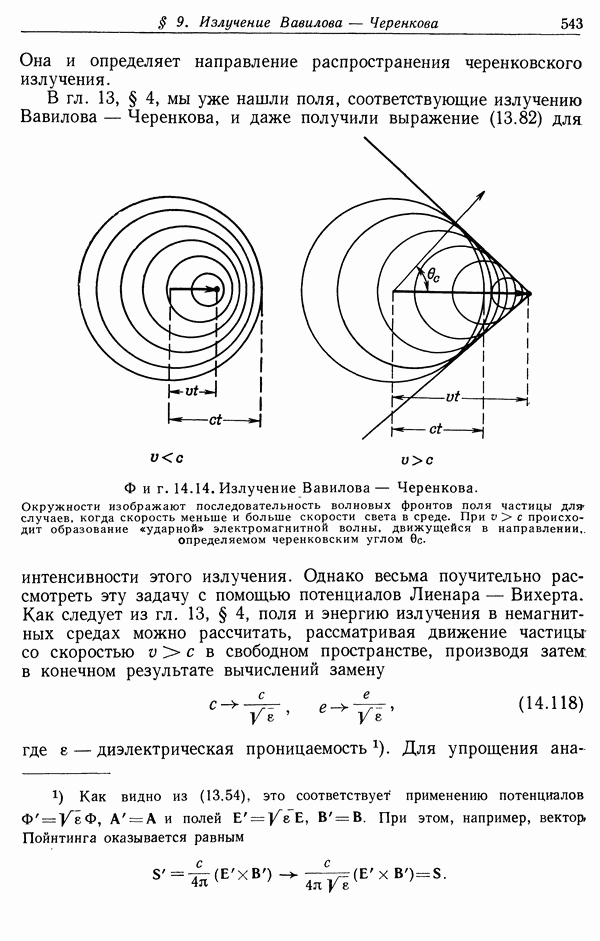
14.16. Считая, что показатель преломления плексигласа в области видимого света равен 1,50, вычислить угол, под которым испускается видимое черенковское излучение электронов и протонов в зависимости от их энергии, выраженной в Определить число квантов излучения с длиной волны в диапазоне от 4000 до 6000 А, излучаемых в плексигласе на пути 1 см электронами с энергией и протонами с энергиями