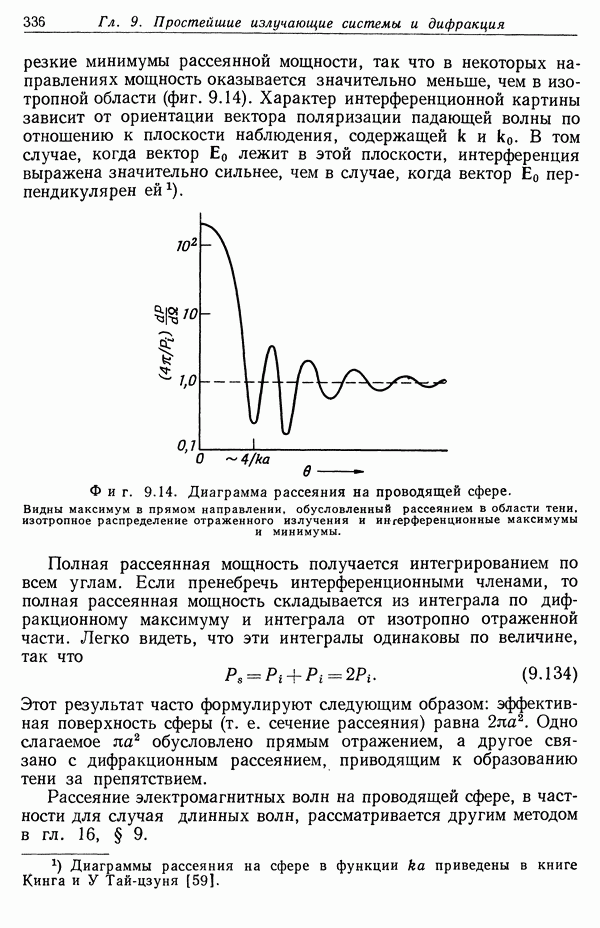
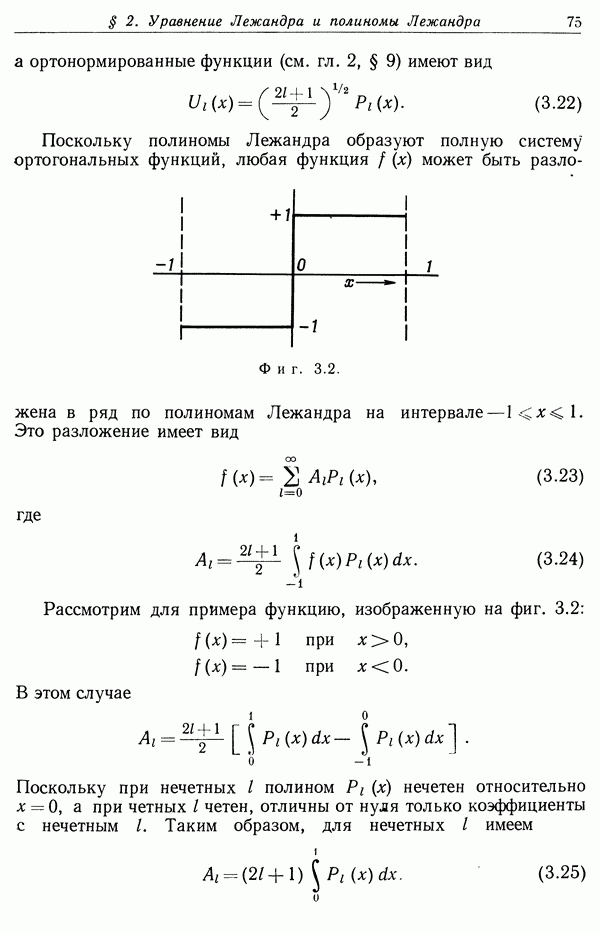| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
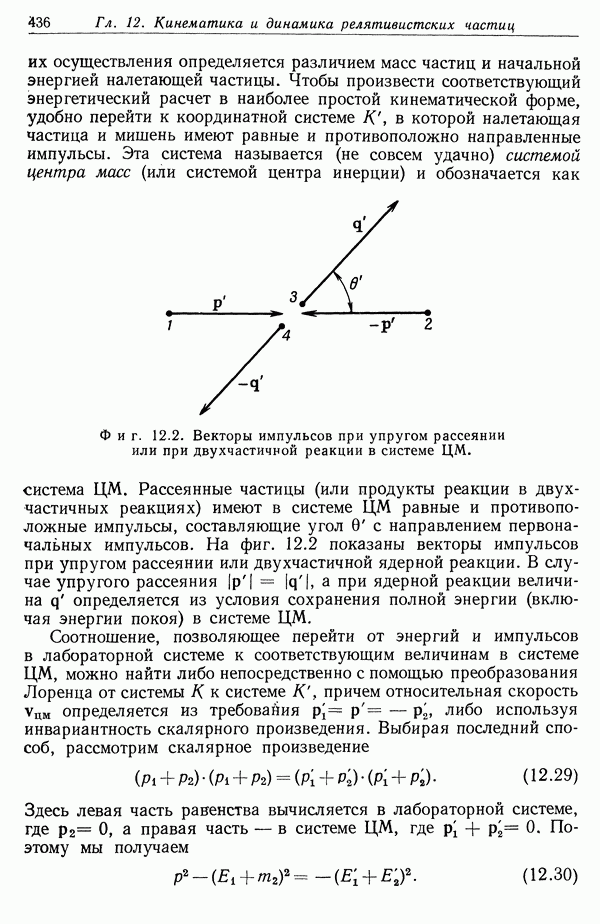
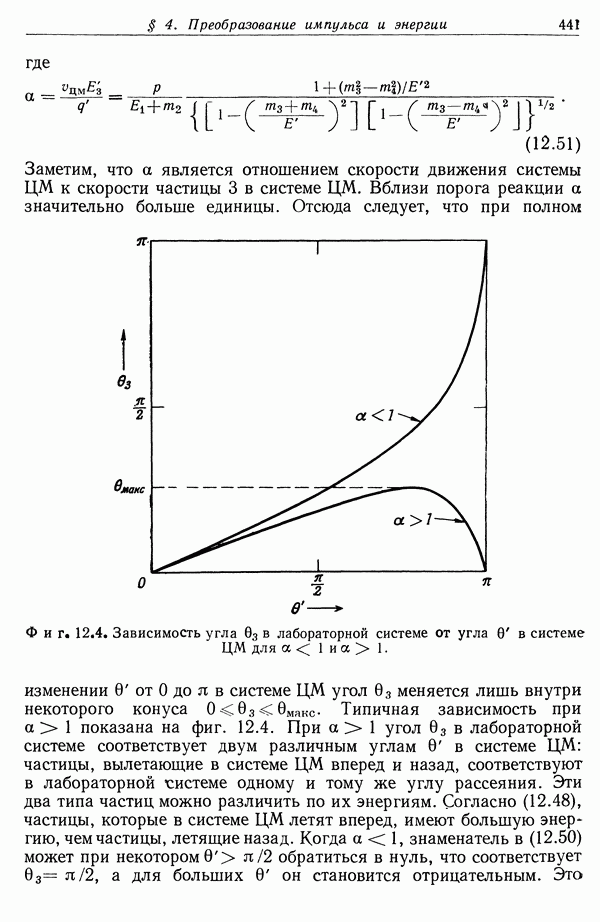
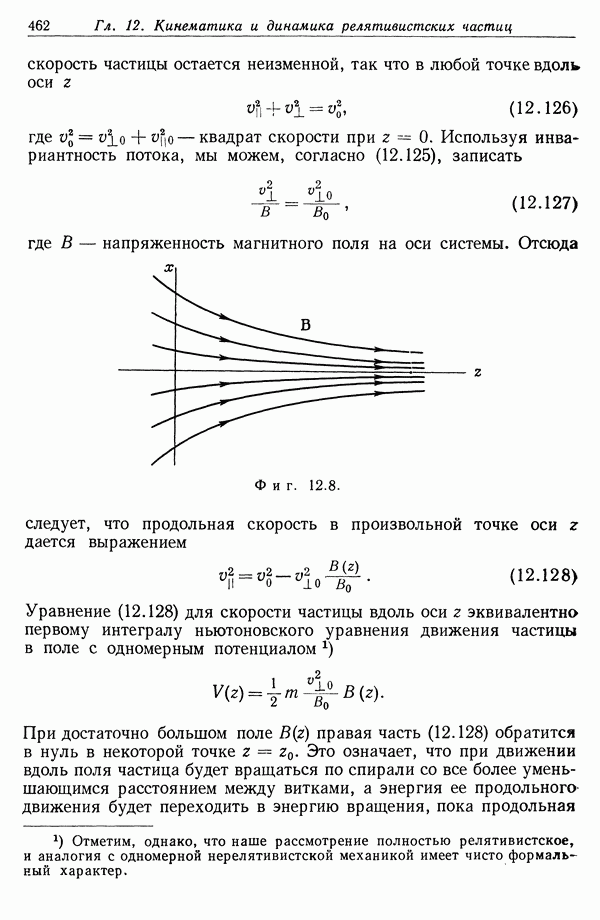
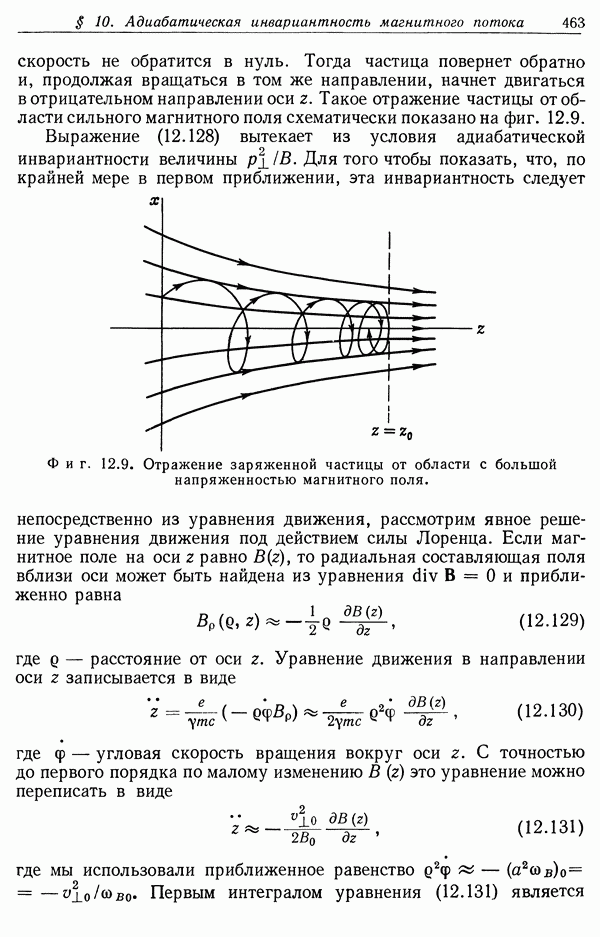
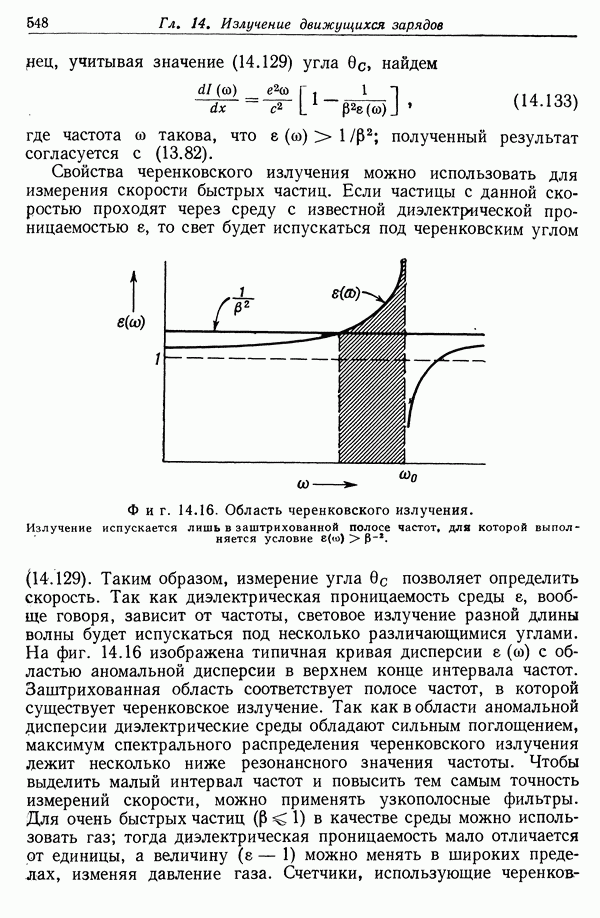
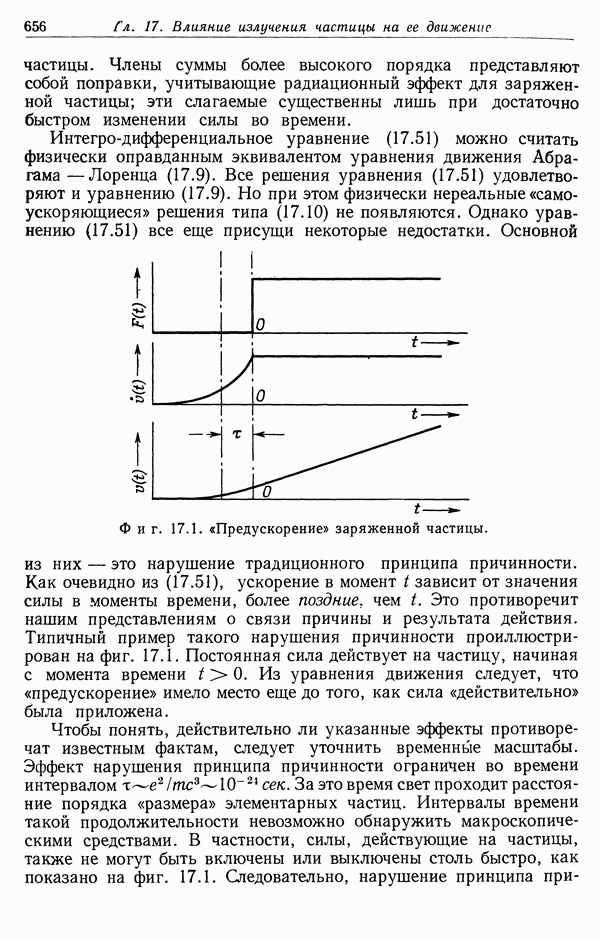
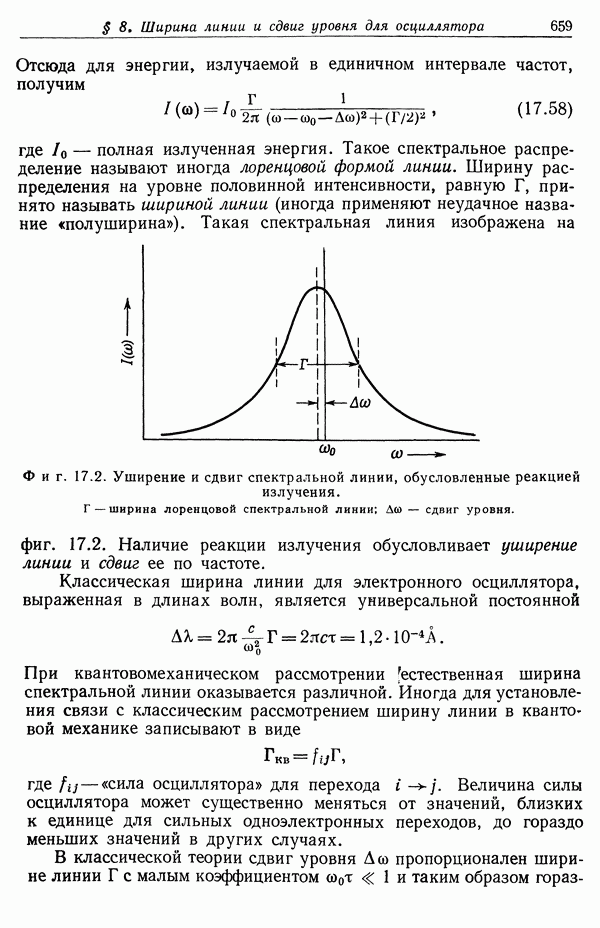
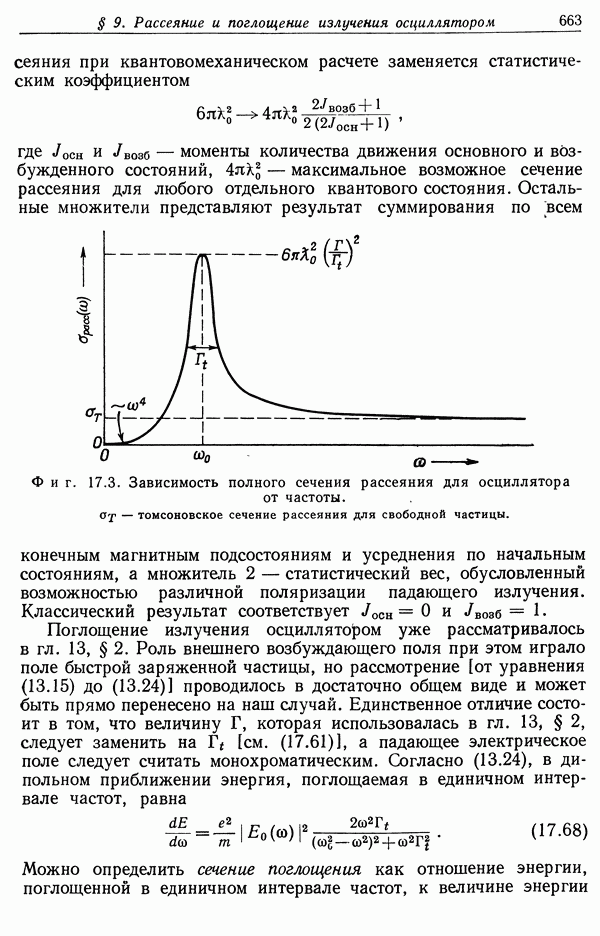
§ 6. Собственное время и световой конус
В предыдущих параграфах был рассмотрен ряд следствий специальной теории относительности и преобразований Лоренца. В следующих двух параграфах мы рассмотрим некоторые более формальные аспекты теории и введем ряд понятий и определений, весьма полезных при систематическом анализе физических явлений в специальной теории относительности.
При галилеевской относительности пространственные и временное координаты никак не связаны. Поэтому при преобразовании Галилея бесконечно малые элементы длины и интервалы времени порознь инвариантны
 (11.59)
(11.59)
Наоборот, при преобразовании Лоренца временные и пространственные координаты взаимосвязаны. Из (11.21) легко показать, что инвариантным элементом «длины» является величина
 (11.60)
(11.60)
Это приводит к понятию собственного времени, инвариантного относительно преобразований Лоренца. Рассмотрим систему, которую мы для определенности будем считать частицей, движущейся с мгновенной скоростью  относительно некоторой координатной системы
относительно некоторой координатной системы  . В системе координат
. В системе координат  которой частица в данный момент покоится, приращения координат и времени суть
которой частица в данный момент покоится, приращения координат и времени суть  . Отсюда получаем инвариантную длину (11.60):
. Отсюда получаем инвариантную длину (11.60):
 (11.61)
(11.61)
Это соотношение можно записать через скорость частицы 
 (11.62)
(11.62)
Соотношение (11.62) выражает рассмотренный выше эффект замедления времени. Однако более существенно то обстоятельство, что, как видно из вывода (11.62), время  , называемое собственным временем частицы, инвариантно относительно преобразования Лоренца. Важность этого понятия выяснится ниже, когда мы начнем рассматривать скорости изменения различных величин. Если некоторая величина ведет себя определенным образом при лоренцовском преобразовании, то ее производная по собственному времени вследствие инвариантности
, называемое собственным временем частицы, инвариантно относительно преобразования Лоренца. Важность этого понятия выяснится ниже, когда мы начнем рассматривать скорости изменения различных величин. Если некоторая величина ведет себя определенным образом при лоренцовском преобразовании, то ее производная по собственному времени вследствие инвариантности  ведет себя таким же образом. Производная же по обычному времени не имеет тех же трансформационных свойств, что сама величина. Из (11.62) следует, что интервал собственного времени
ведет себя таким же образом. Производная же по обычному времени не имеет тех же трансформационных свойств, что сама величина. Из (11.62) следует, что интервал собственного времени  — воспринимается в системе К как интервал времени
— воспринимается в системе К как интервал времени
 (11.63)
(11.63)
где  — соответствующие времена в системе К.
— соответствующие времена в системе К.
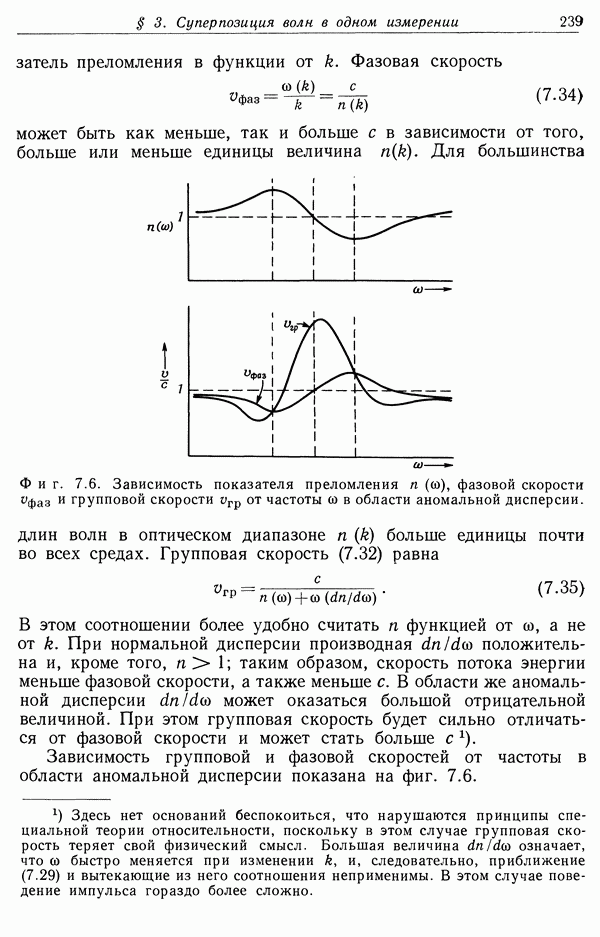
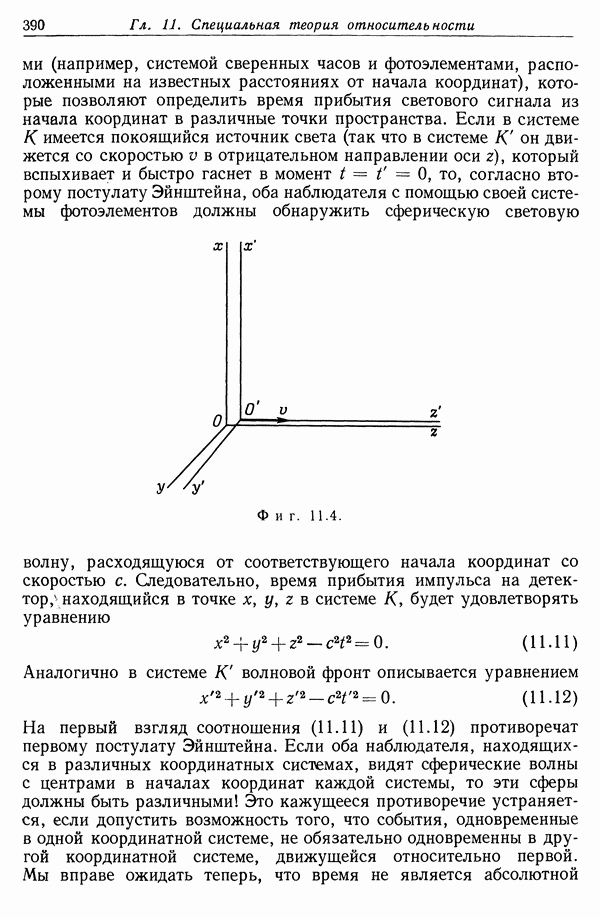
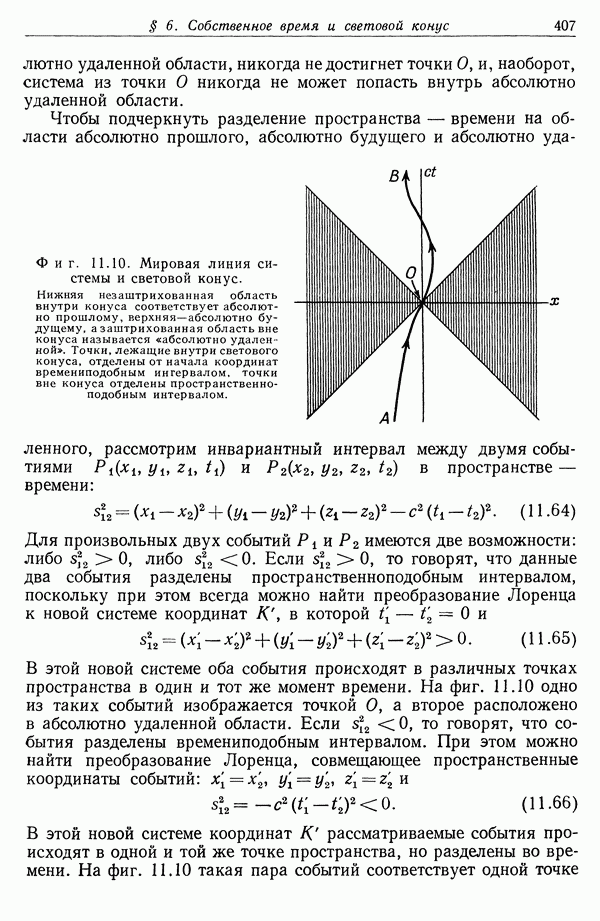
Другим плодотворным понятием в специальной теории относительности является понятие светового конуса и пространственноподобного и времениподобного интервалов между двумя событиями. Рассмотрим фиг. 11.10, на которой ось времени (ось  ) вертикальна, а пространственные оси перпендикулярны оси времени. Пусть в момент
) вертикальна, а пространственные оси перпендикулярны оси времени. Пусть в момент  некоторая физическая система, скажем частица, находится в начале координат. Поскольку скорость света является верхней границей для всех скоростей, то всю область пространства—времени можно разделить на три области «конусом», называемым световым конусом, поверхность которого определяется уравнением
некоторая физическая система, скажем частица, находится в начале координат. Поскольку скорость света является верхней границей для всех скоростей, то всю область пространства—времени можно разделить на три области «конусом», называемым световым конусом, поверхность которого определяется уравнением  Световой сигнал, испущенный при
Световой сигнал, испущенный при  из начала координат, будет распространяться вдоль линий, образующих на фиг. 11.10 угол 45° с осью времени. Но любая материальная система имеет скорость меньше с. Следовательно, с течением времени она может перемещаться лишь по пути (называемому ее мировой линией), расположенному внутри верхнего полу конуса, как, например, кривая ОВ. Так как пути систем лежат внутри верхнего полуконуса при
из начала координат, будет распространяться вдоль линий, образующих на фиг. 11.10 угол 45° с осью времени. Но любая материальная система имеет скорость меньше с. Следовательно, с течением времени она может перемещаться лишь по пути (называемому ее мировой линией), расположенному внутри верхнего полу конуса, как, например, кривая ОВ. Так как пути систем лежат внутри верхнего полуконуса при  то эта область называется областью абсолютно будущего. Аналогично область, лежащая внутри нижнего полуконуса, называется областью абсолютно прошлого. Физическая система может прийти в точку О только по пути типа АО, лежащему внутри нижнего полуконуса. Заштрихованная область вне светового конуса называется абсолютно удаленной областью. Система, находящаяся внутри абсолютно
то эта область называется областью абсолютно будущего. Аналогично область, лежащая внутри нижнего полуконуса, называется областью абсолютно прошлого. Физическая система может прийти в точку О только по пути типа АО, лежащему внутри нижнего полуконуса. Заштрихованная область вне светового конуса называется абсолютно удаленной областью. Система, находящаяся внутри абсолютно
удаленной области, никогда не достигнет точки О, и, наоборот, система из точки О никогда не может попасть внутрь абсолютно удаленной области.

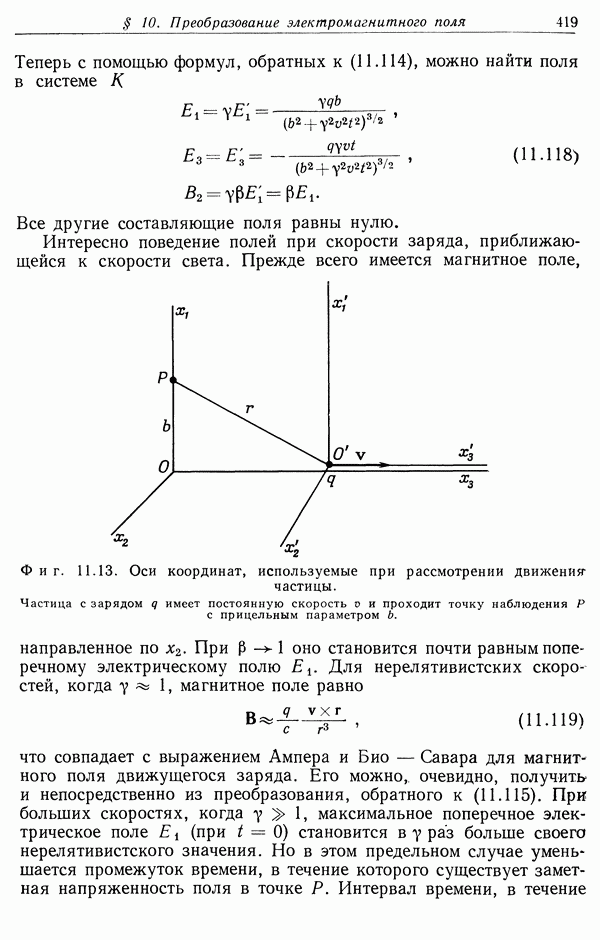
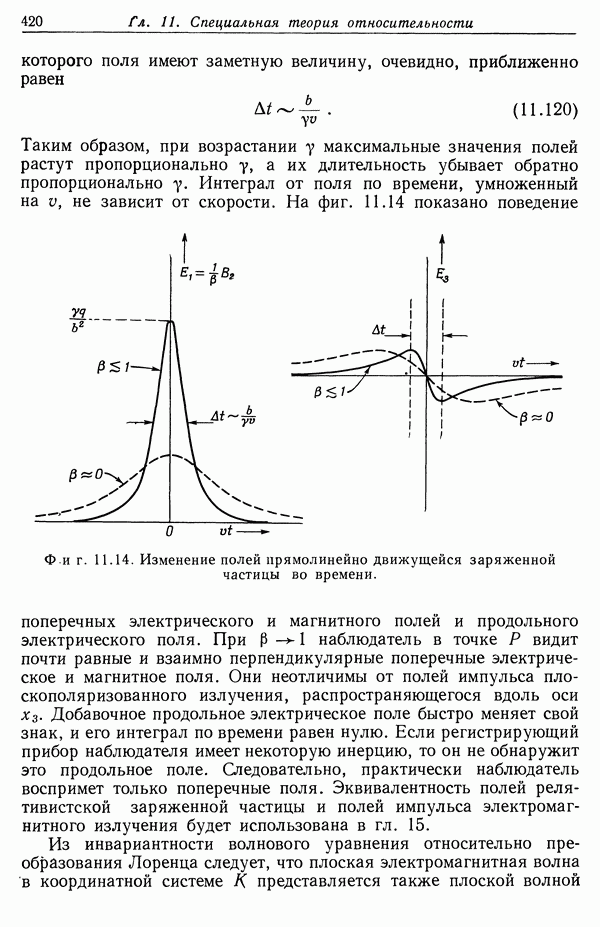
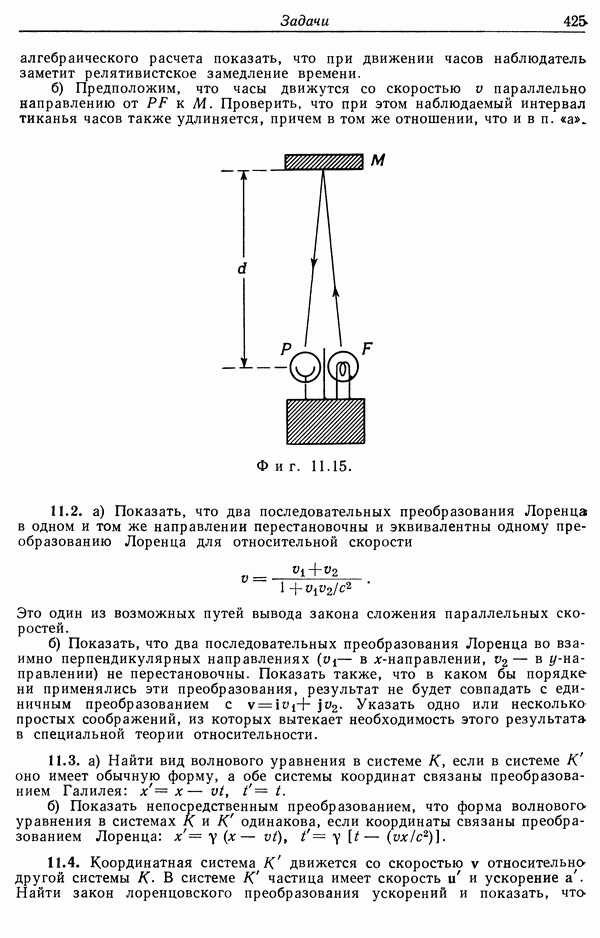
Фиг. 11.10. Мировая линия системы и световой конус. Нижняя незаштрихованная область внутри конуса соответствует абсолютно прошлому, верхняя — абсолютно будущему, а заштрихованная область вне конуса называется «абсолютно удаленной». Точки, лежащие внутри светового конуса, отделены от начала координат времениподобным интервалом, точки вне конуса отделены пространственноподобным интервалом.
Чтобы подчеркнуть разделение пространства — времени на области абсолютно прошлого, абсолютно будущего и абсолютно удаленного, рассмотрим инвариантный интервал между двумя событиями  в пространстве — времени:
в пространстве — времени:
 (11.64)
(11.64)
Для произвольных двух событий  имеются две возможности: либо
имеются две возможности: либо  либо
либо  Если
Если  то говорят, что данные два события разделены пространственноподобным интервалом, поскольку при этом всегда можно найти преобразование Лоренца к новой системе координат К, в которой
то говорят, что данные два события разделены пространственноподобным интервалом, поскольку при этом всегда можно найти преобразование Лоренца к новой системе координат К, в которой  и
и

В этой новой системе оба события происходят в различных точках пространства в один и тот же момент времени. На фиг. 11.10 одно из таких событий изображается точкой О, а второе расположено в абсолютно удаленной области. Если  то говорят, что события разделены времениподобным интервалом. При этом можно найти преобразование Лоренца, совмещающее пространственные координаты событий:
то говорят, что события разделены времениподобным интервалом. При этом можно найти преобразование Лоренца, совмещающее пространственные координаты событий: 
 (11.66)
(11.66)
В этой новой системе координат К рассматриваемые события происходят в одной и той же точке пространства, но разделены во времени. На фиг. 11.10 такая пара событий соответствует одной точке
в начале координат, а другой — расположенной в области абсолютно прошлого или абсолютно будущего.
Разделение интервалов между двумя событиями на два класса пространственноподобных и времениподобных инвариантно относительно преобразований Лоренца. Два события, разделенные пространственноподобным интервалом в одной системе координат, разделены пространственноподобным интервалом и во всех других системах координат. Это означает, что такие события не могут быть причинно связанными. Поскольку физическое взаимодействие распространяется из одной точки в другую со скоростью, не превышающей скорость света, то причинно связанными могут быть только события, разделенные времениподобным интервалом. На событие, которое произошло в начале координат на фиг. 11.10, могли повлиять лишь события, соответствующие точкам в области абсолютно прошлого.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
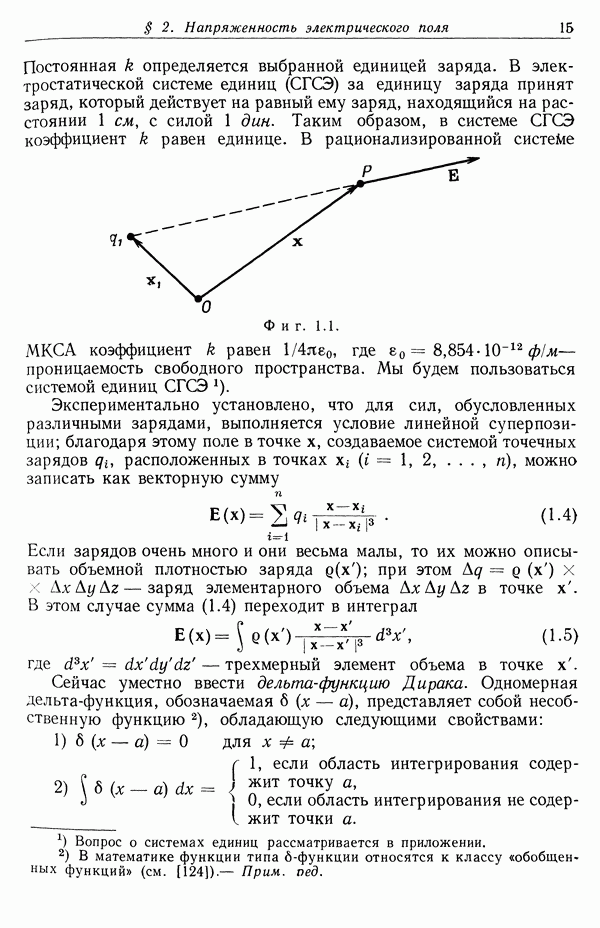
- § 2. Напряженность электрического поля
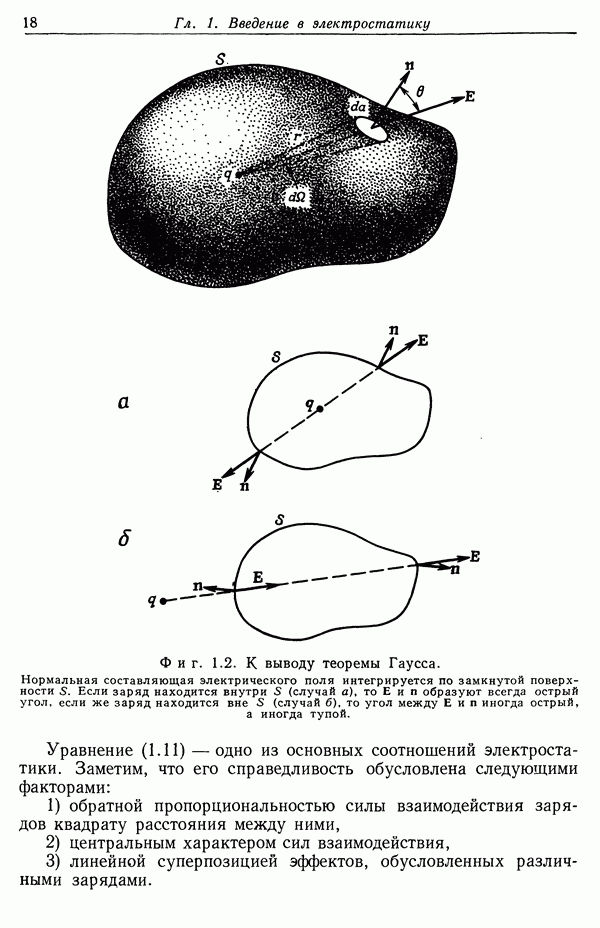
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
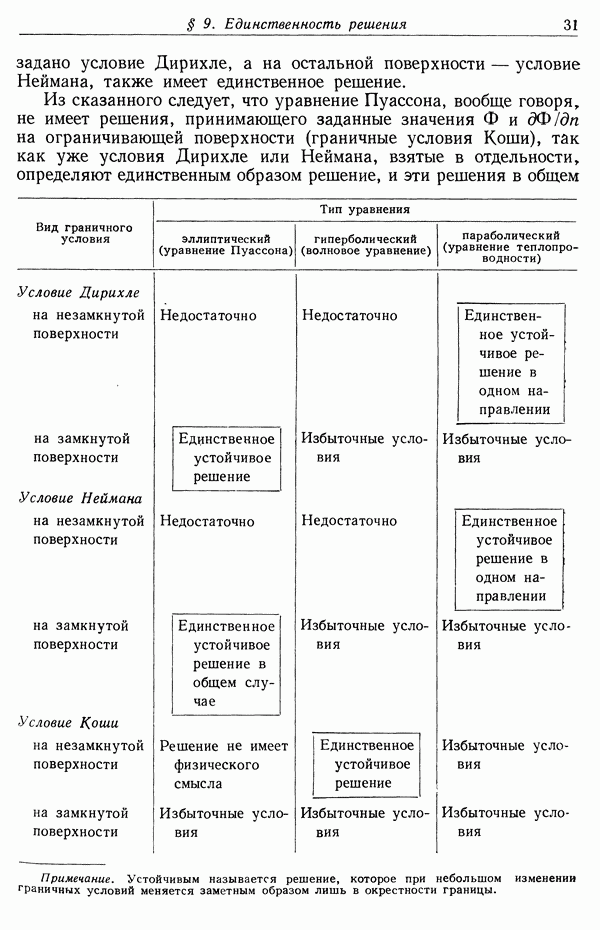
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
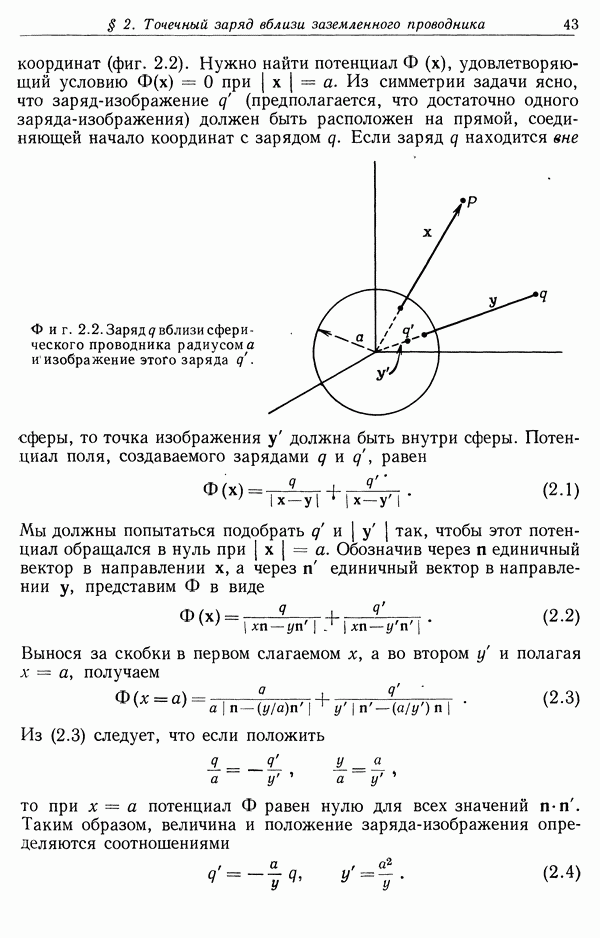
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
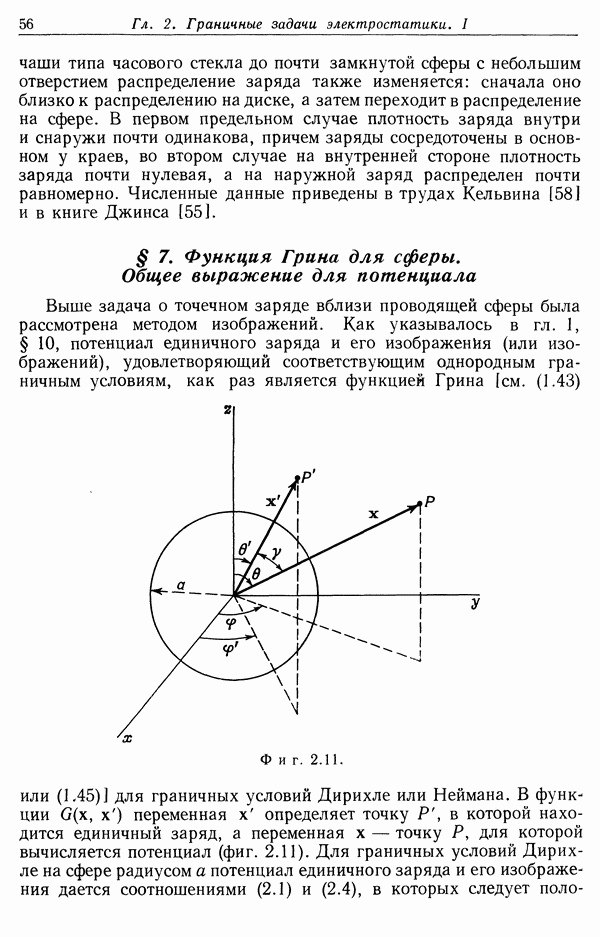
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
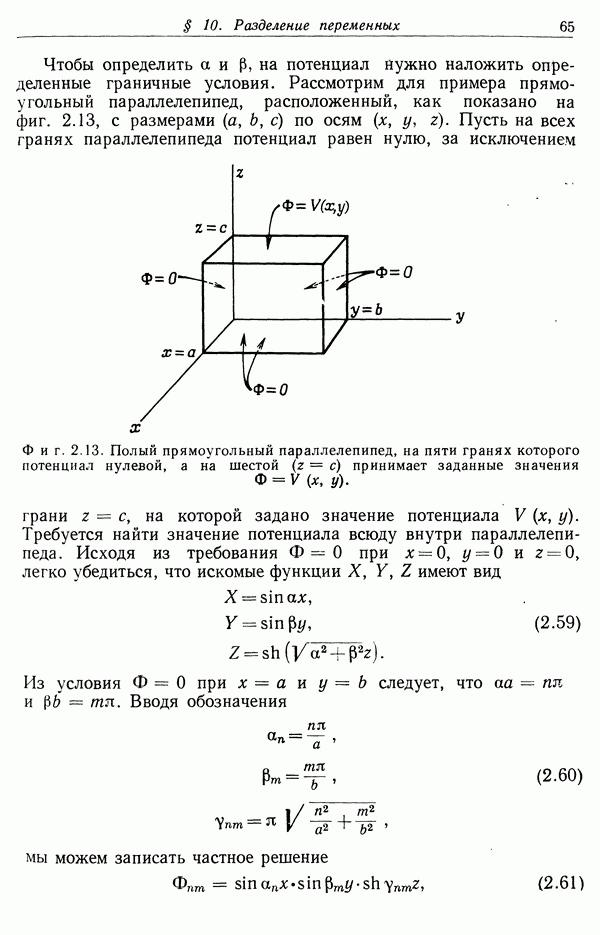
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
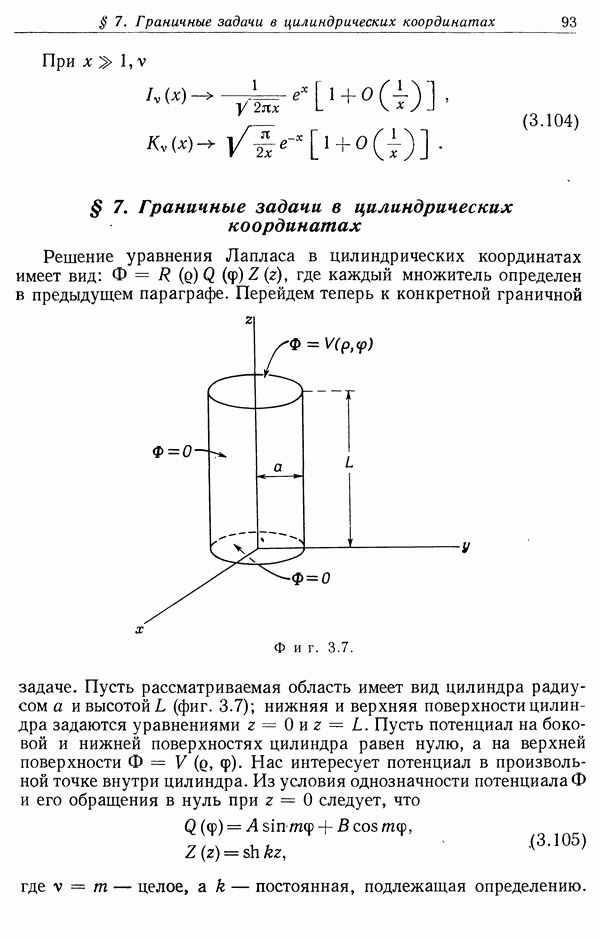
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
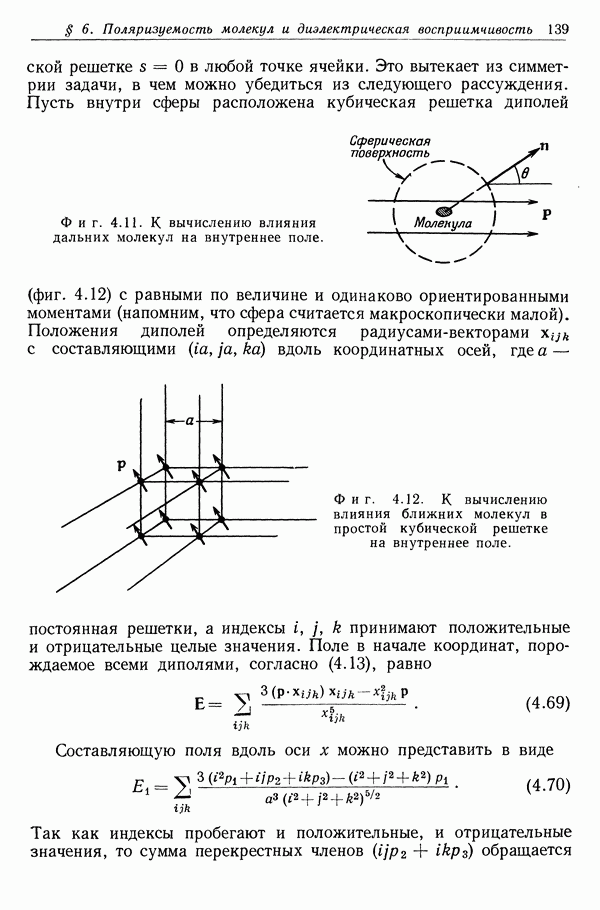
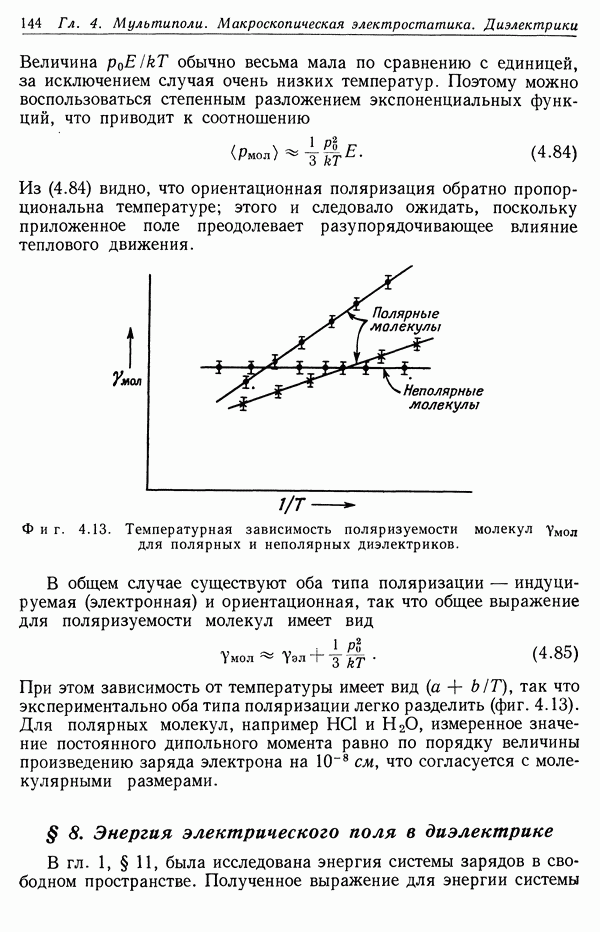
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
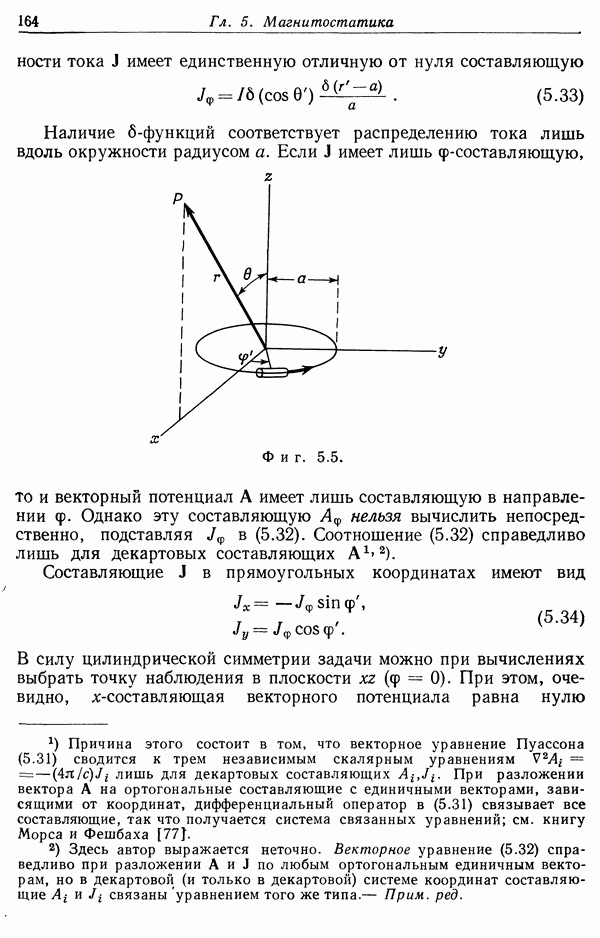
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
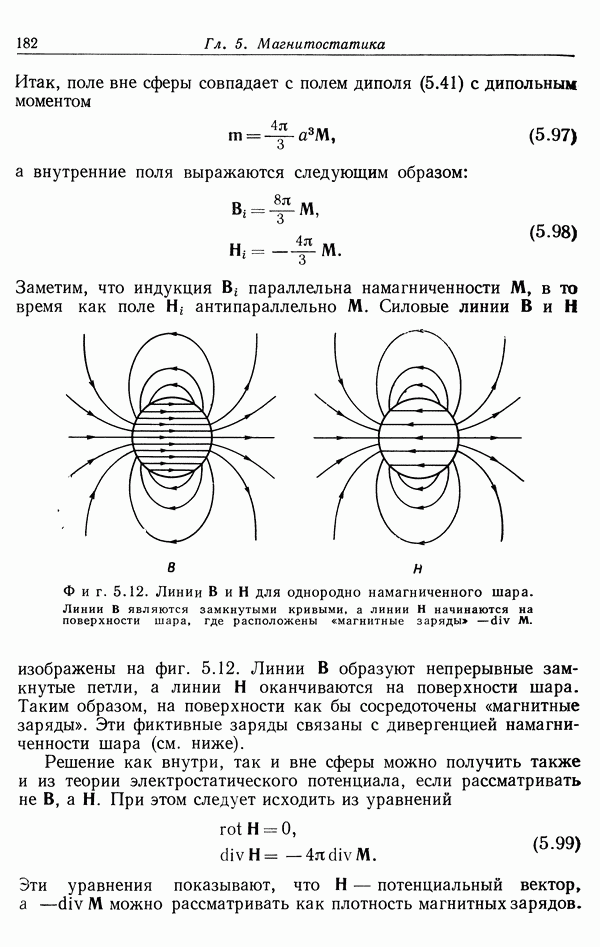
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
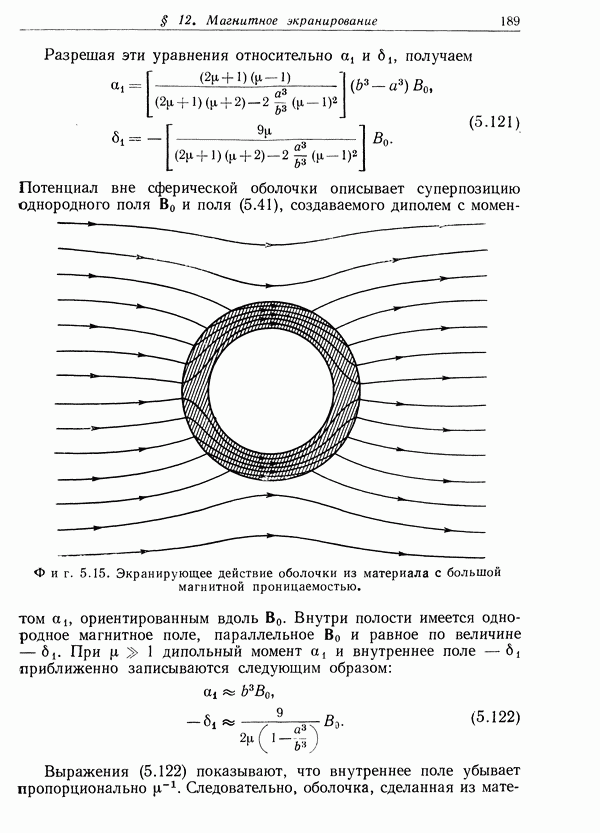
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
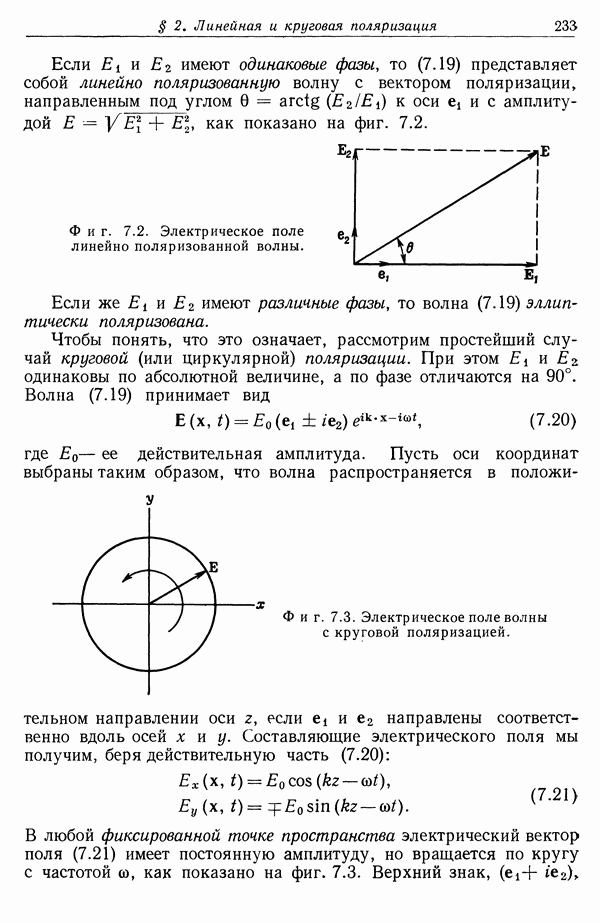
- § 2. Линейная и круговая поляризация
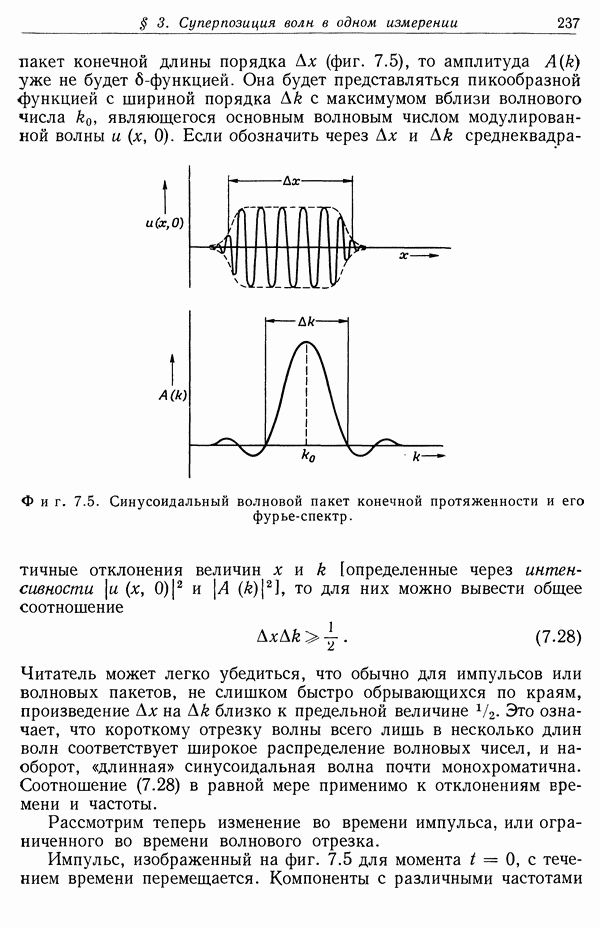
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
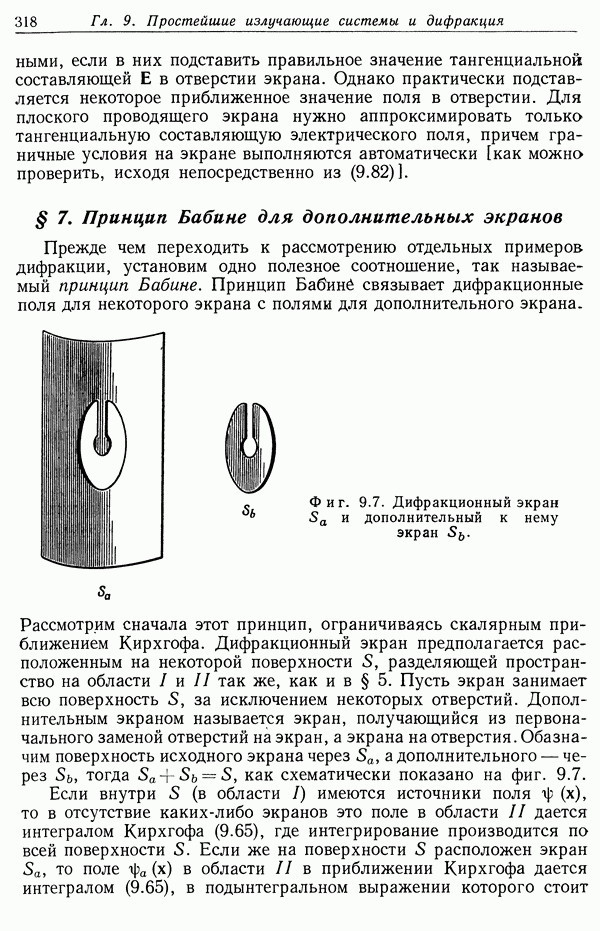
- § 7. Принцип Бабине для дополнительных экранов
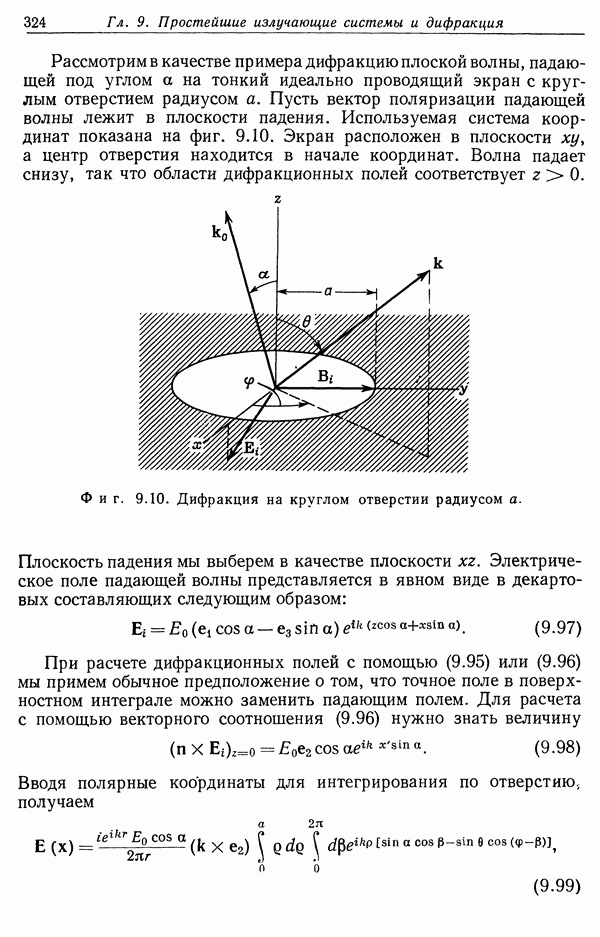
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
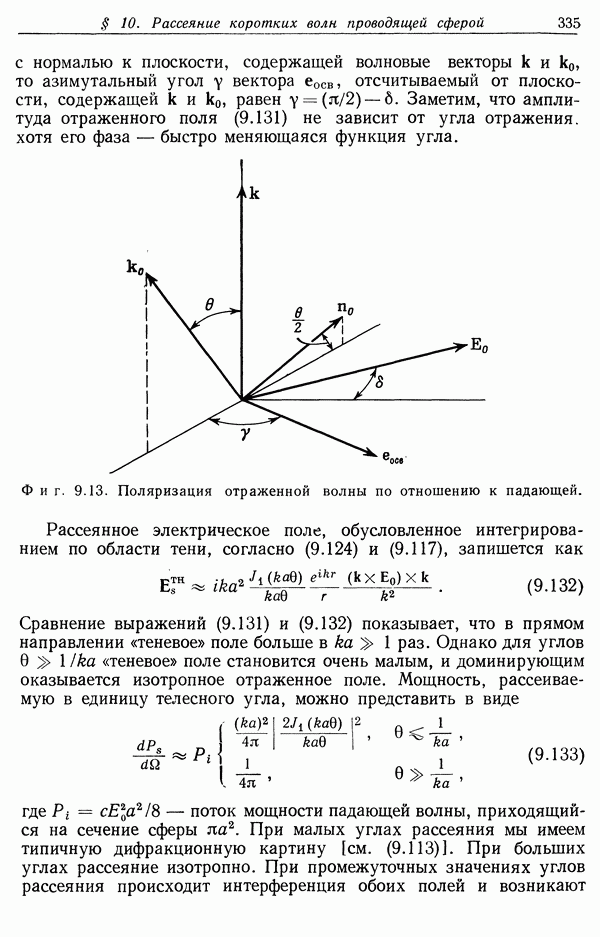
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
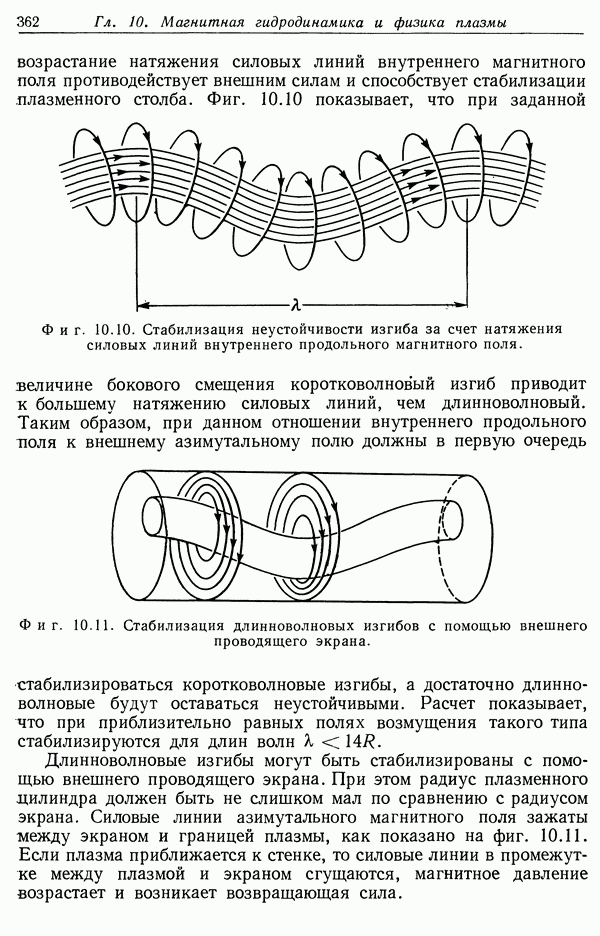
- § 7. Неустойчивости сжатого плазменного столба
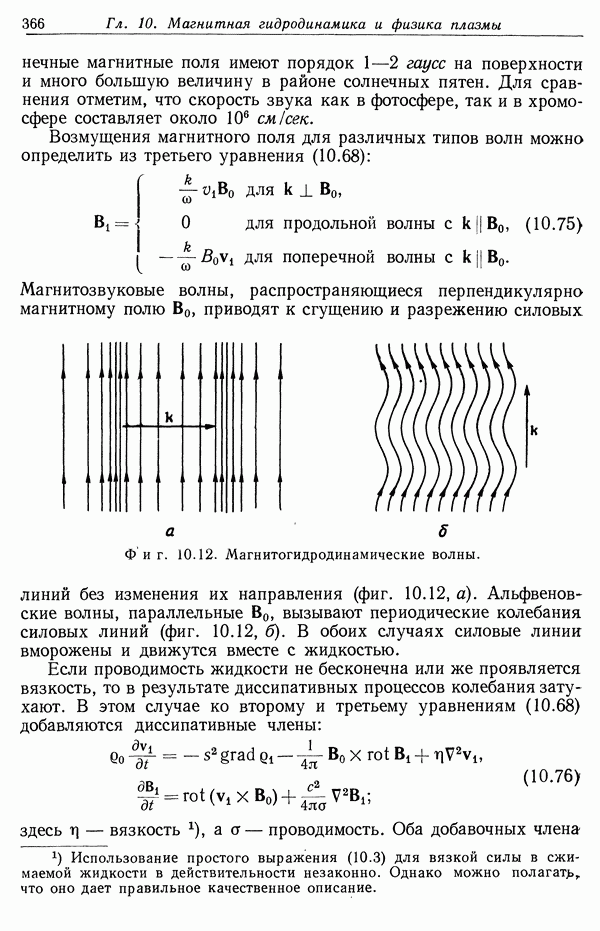
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
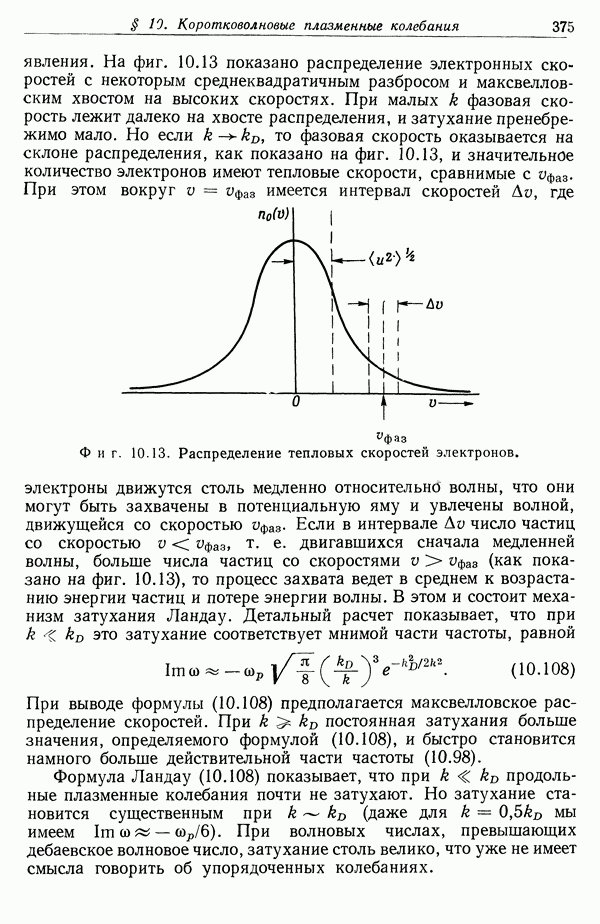
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
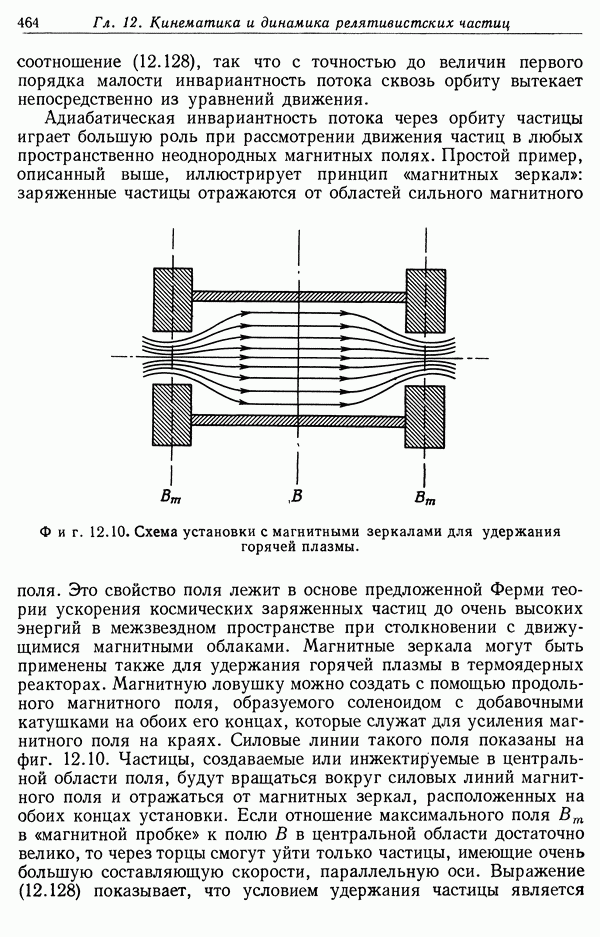
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
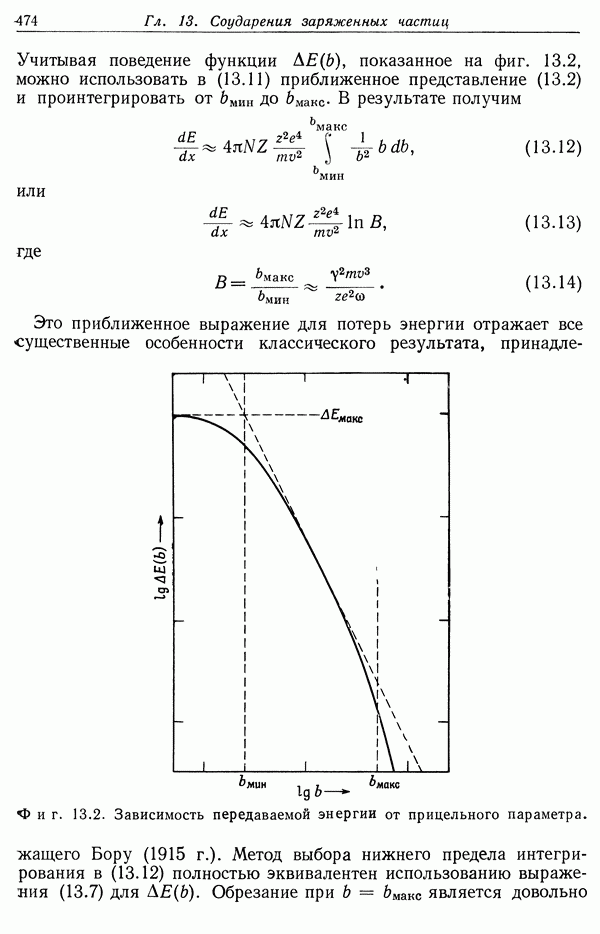
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
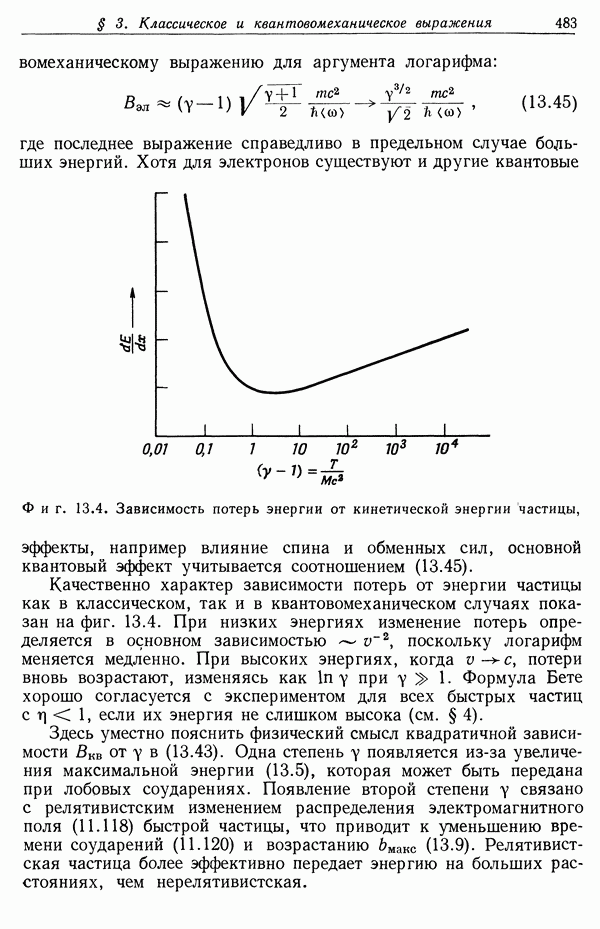
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
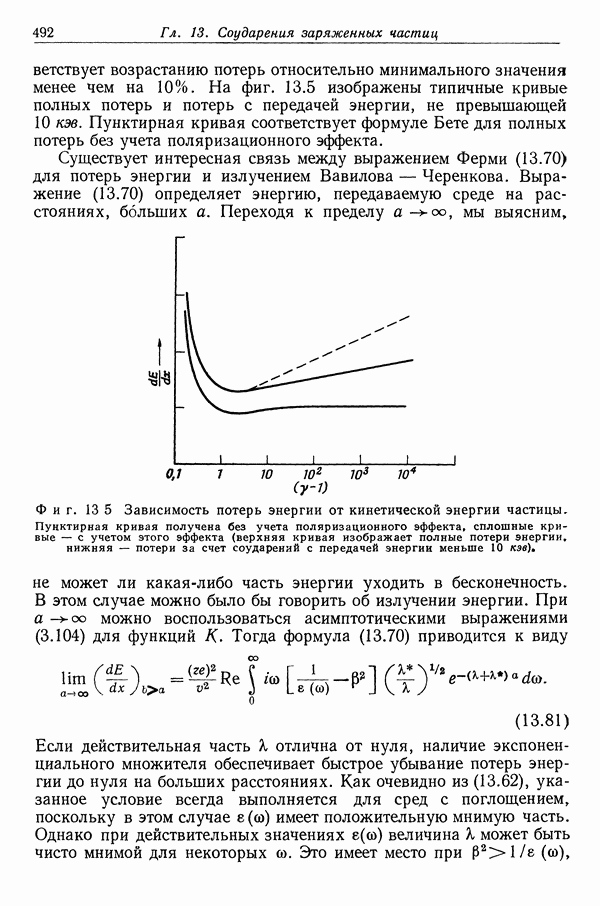
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
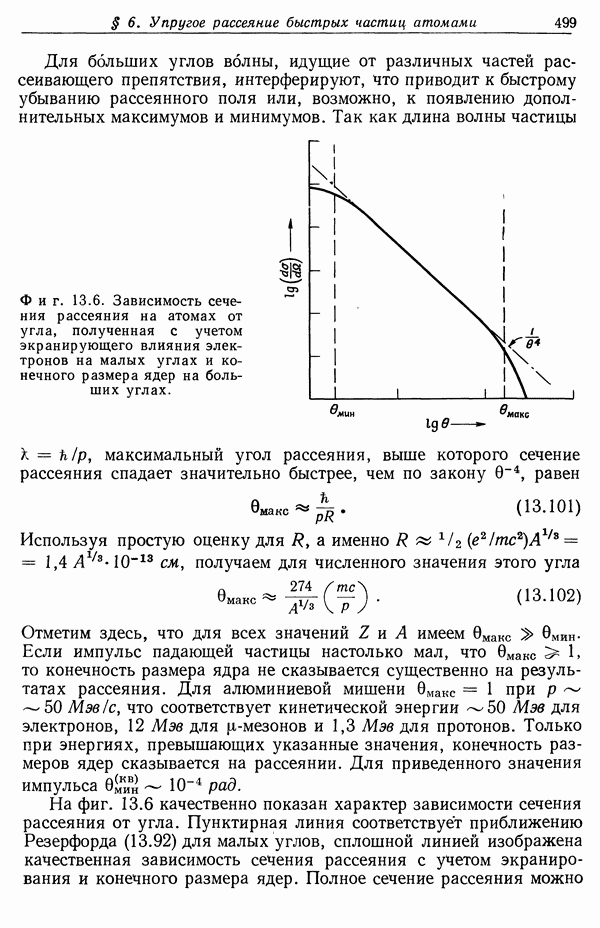
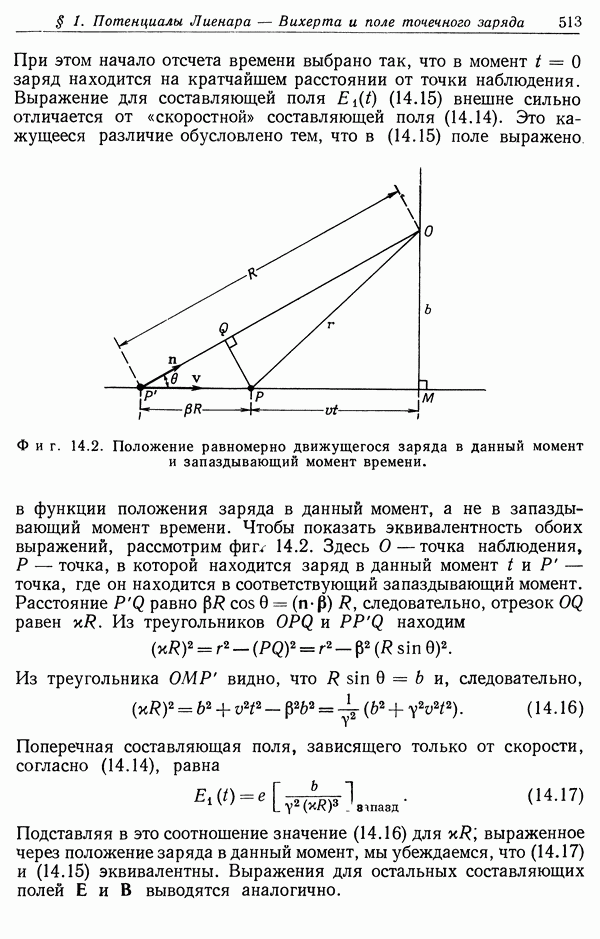
- § 6. Упругое рассеяние быстрых частиц атомами
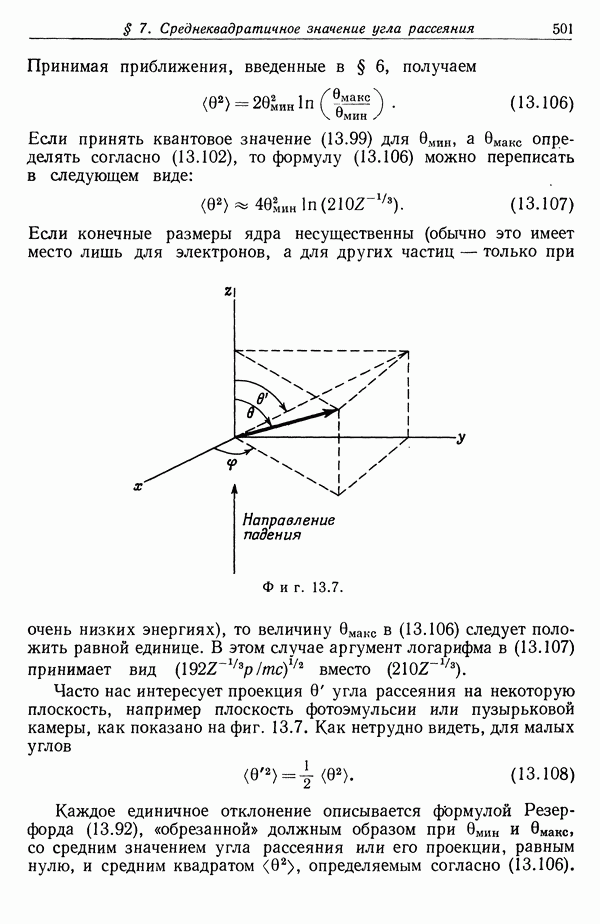
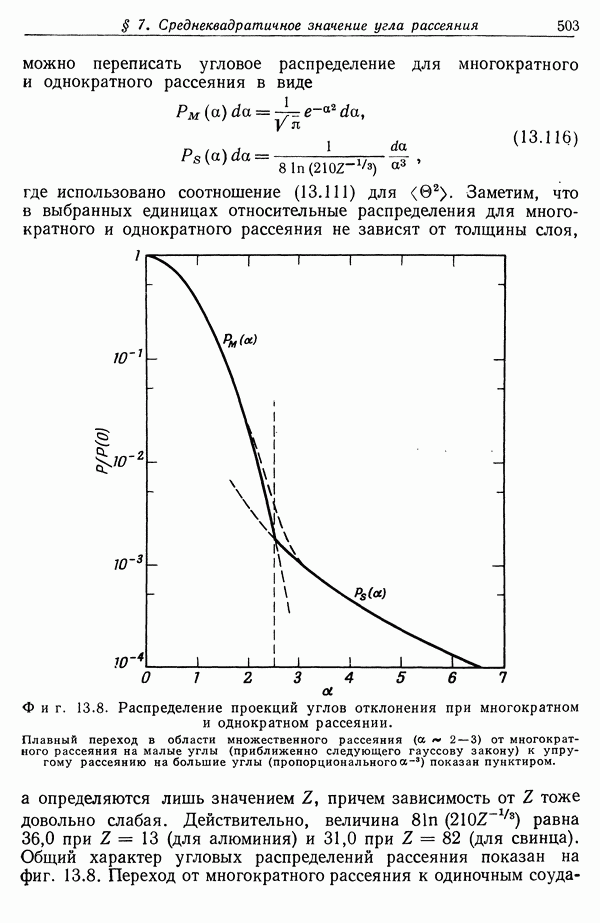
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
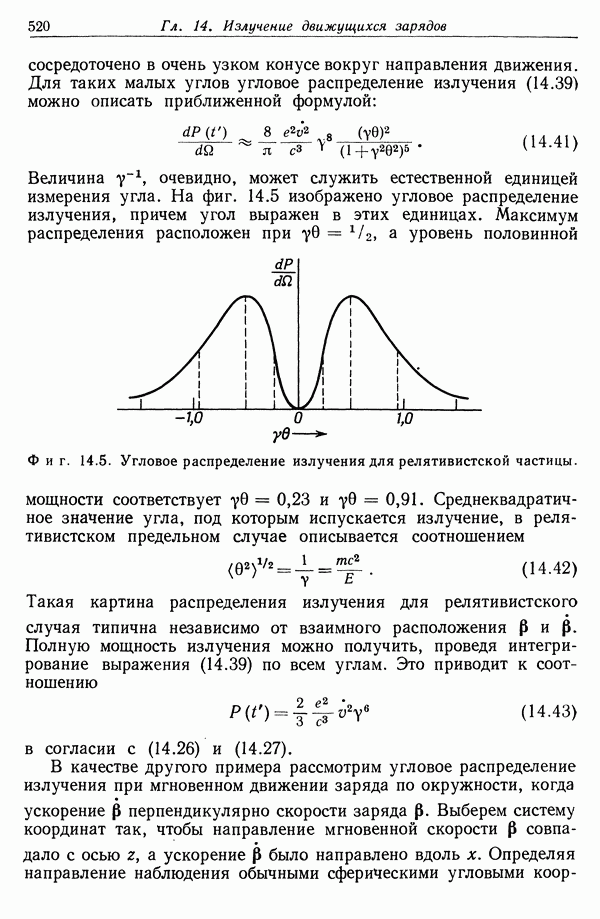
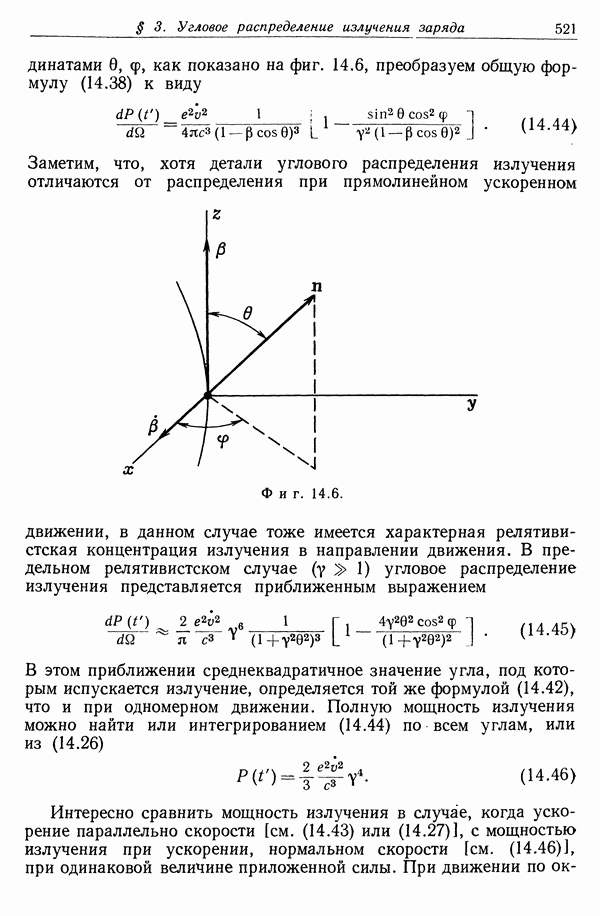
- § 3. Угловое распределение излучения ускоряемого заряда
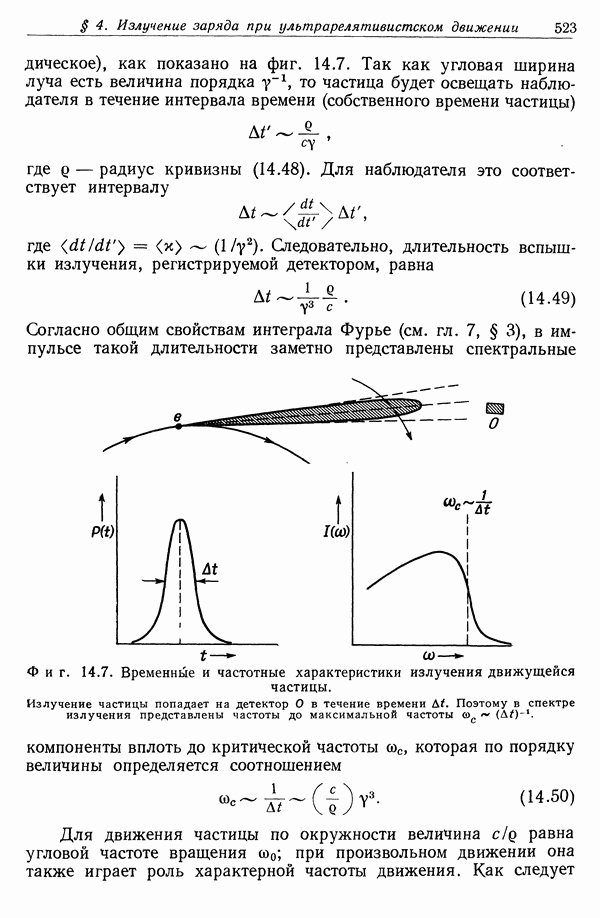
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
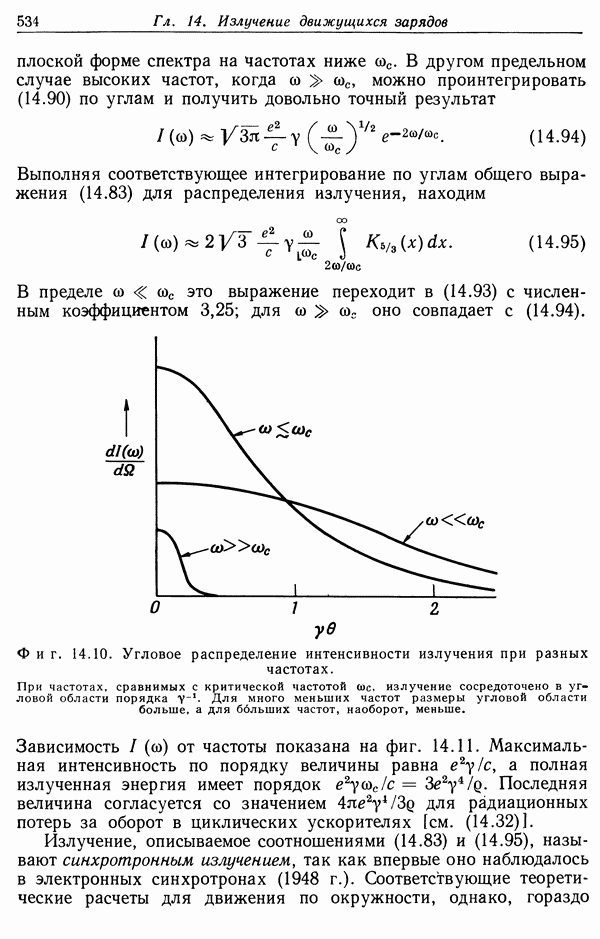
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
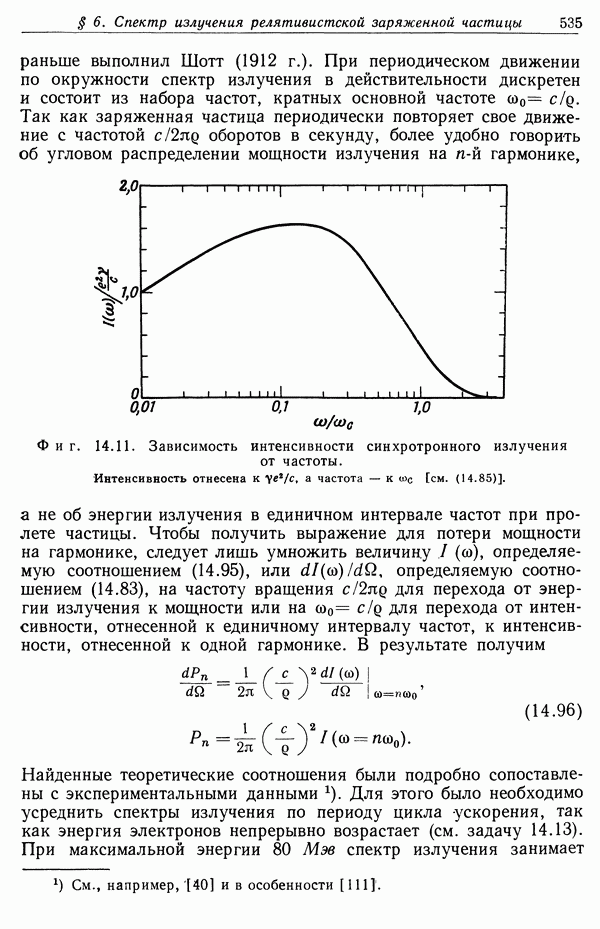
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
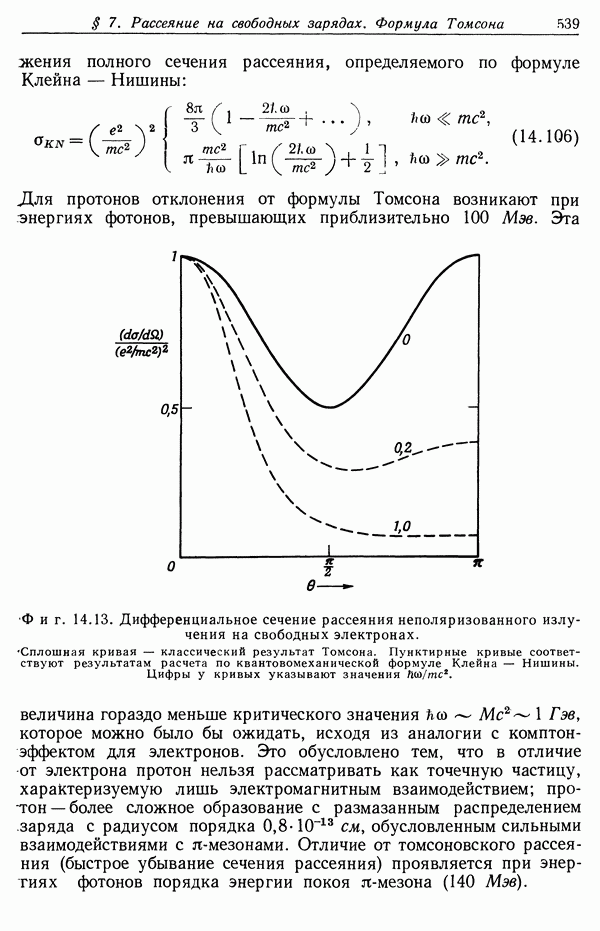
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
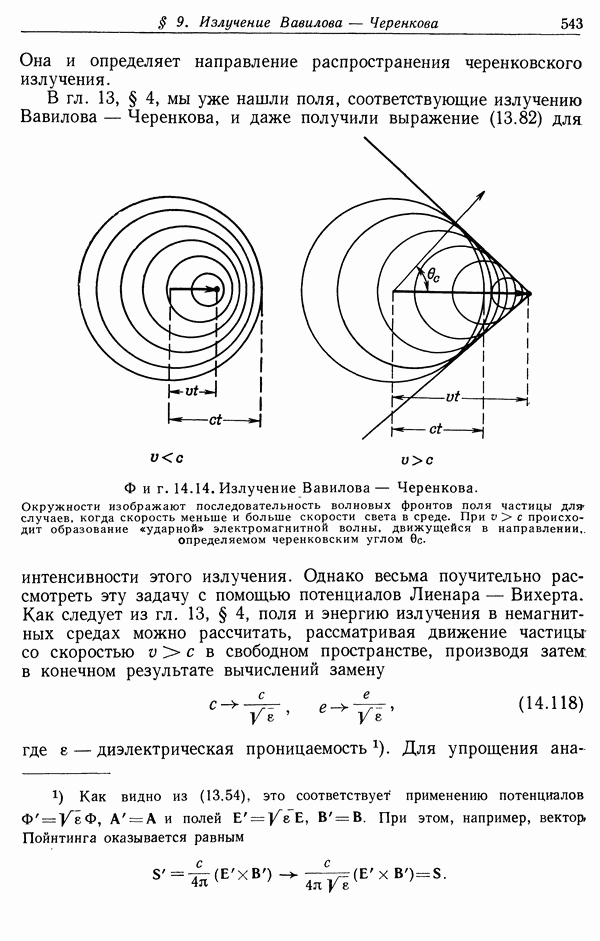
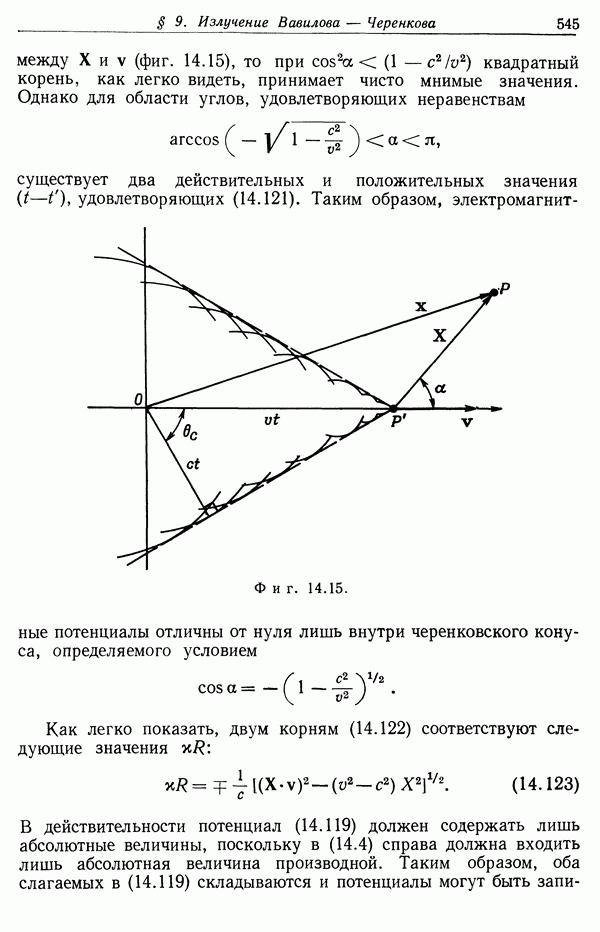
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ