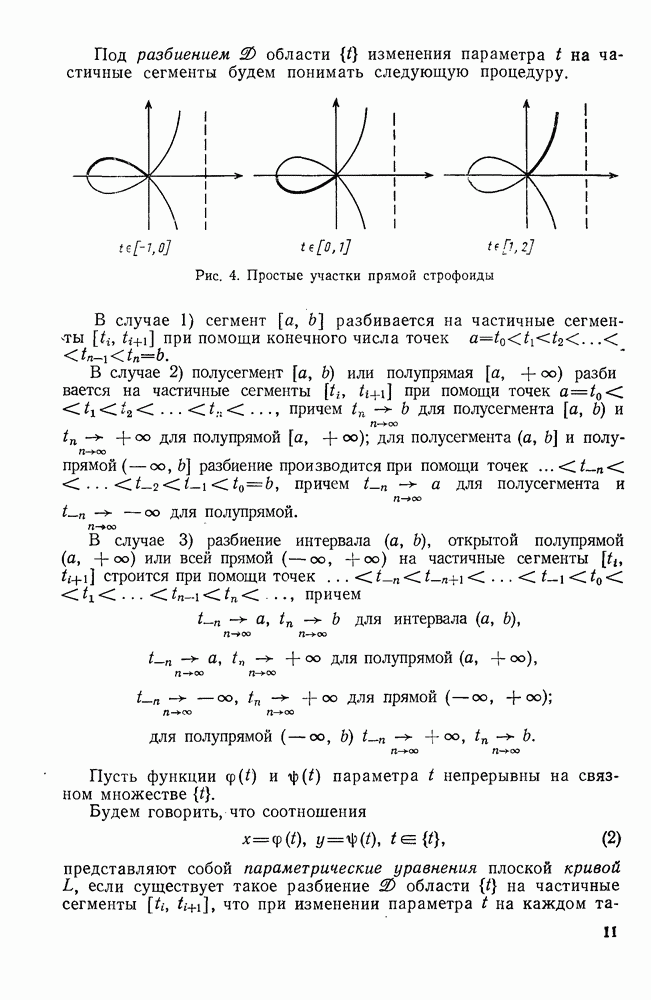
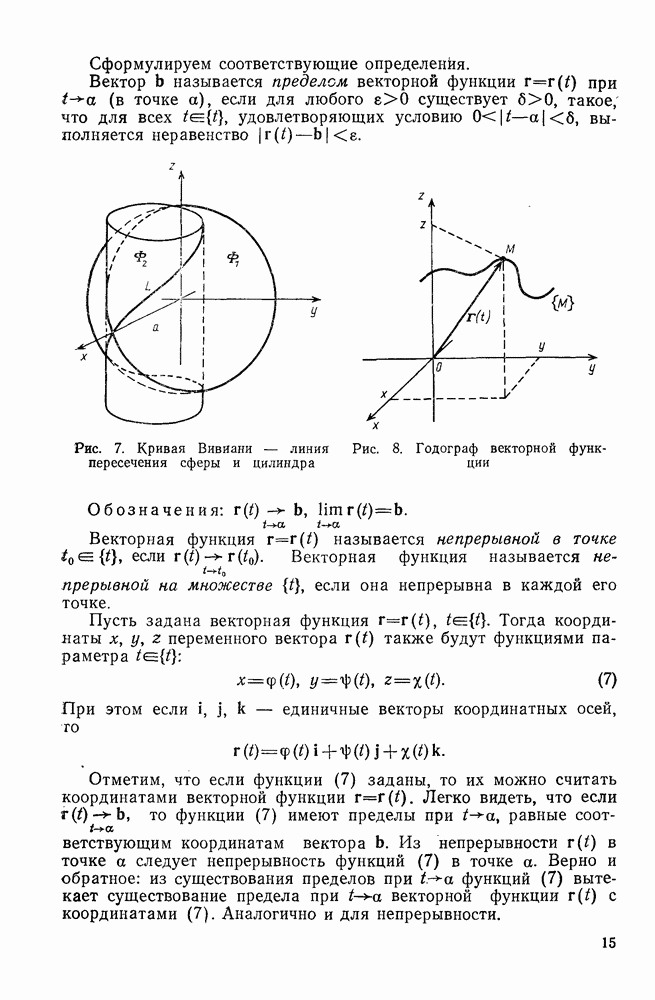
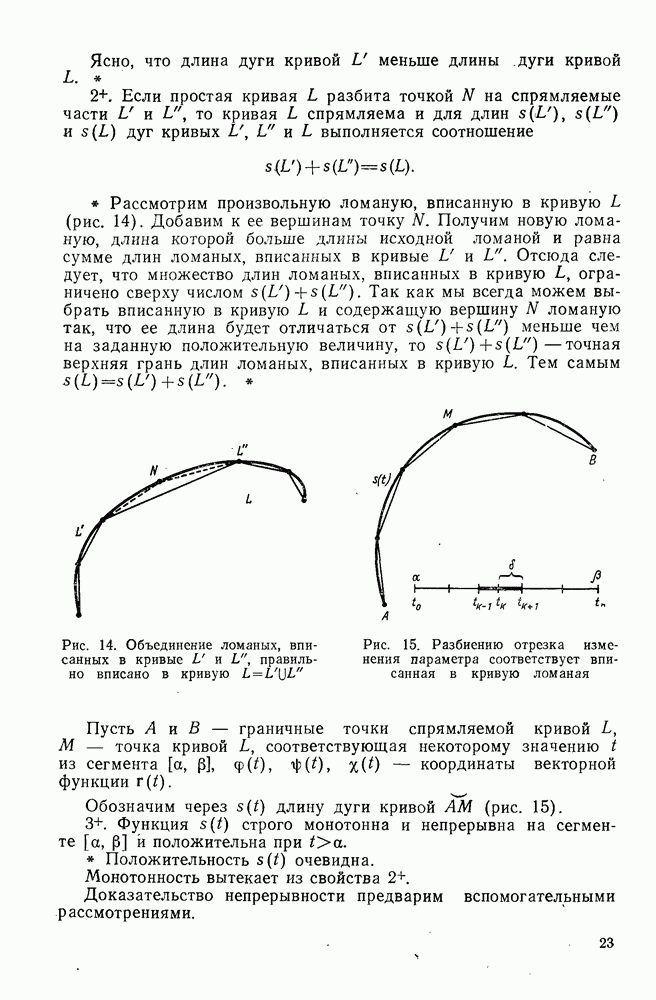
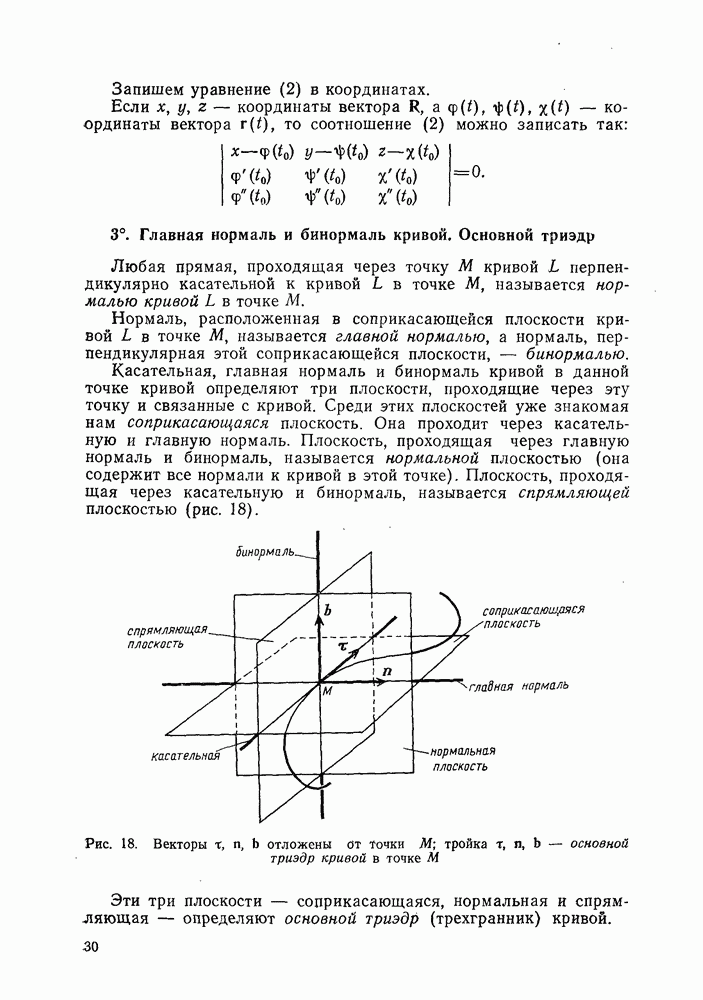
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
В конце прошлого и в начале нынешнего века  Гильберт занимался одним из важнейших вопросов естествознания — основаниями геометрии. Он детально исследовал проблему аксиоматического построения геометрии. Геометрия строилась им без обращения к каким-либо реальным объектам. Точки, прямые и плоскости не определялись, их свойства описывались аксиомами — исходными положениями, из которых логически выводились свойства различных геометрических фигур.
Гильберт занимался одним из важнейших вопросов естествознания — основаниями геометрии. Он детально исследовал проблему аксиоматического построения геометрии. Геометрия строилась им без обращения к каким-либо реальным объектам. Точки, прямые и плоскости не определялись, их свойства описывались аксиомами — исходными положениями, из которых логически выводились свойства различных геометрических фигур.
Известно, что планиметрия Евклида и сферическая геометрия представляют собой соответственно внутреннюю геометрию плоскостей и сфер евклидова пространства. Примеры поверхностей постоянной отрицательной кривизны — поверхности вращения, полученные  Миндингом, — не имэют на регулярных своих частях внутреннюю геометрию, совпадающую с геометрией частей плоскости Лобачевского, но имеют и особенности: ребра, острия и, главное, в целом не представляют полной плоскости Лобачевского. В 1901 г. Гильберт в работе «О поверхностях постоянной гауссовой кривизны» (Гильберт Д. Основания геометрии. М.; Л., ОГИЗ, 1948) рассмотрел вопрос о существовании в пространстве Е3 полной без особенностей плоскости Лобачевского и доказал, что в пространстве
Миндингом, — не имэют на регулярных своих частях внутреннюю геометрию, совпадающую с геометрией частей плоскости Лобачевского, но имеют и особенности: ребра, острия и, главное, в целом не представляют полной плоскости Лобачевского. В 1901 г. Гильберт в работе «О поверхностях постоянной гауссовой кривизны» (Гильберт Д. Основания геометрии. М.; Л., ОГИЗ, 1948) рассмотрел вопрос о существовании в пространстве Е3 полной без особенностей плоскости Лобачевского и доказал, что в пространстве  не существует полной и регулярной
не существует полной и регулярной
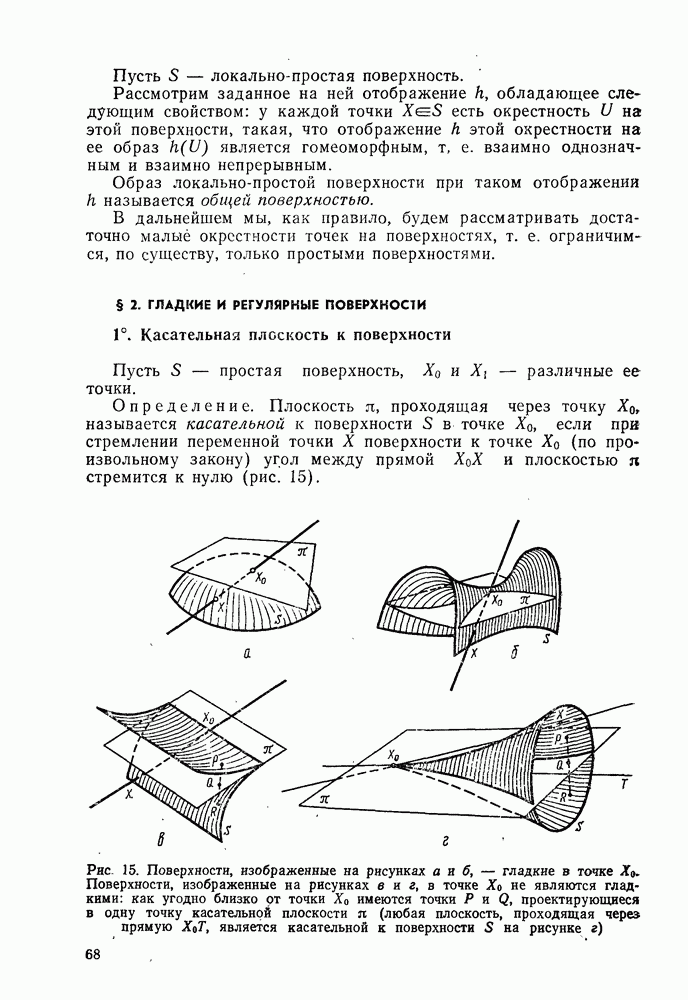
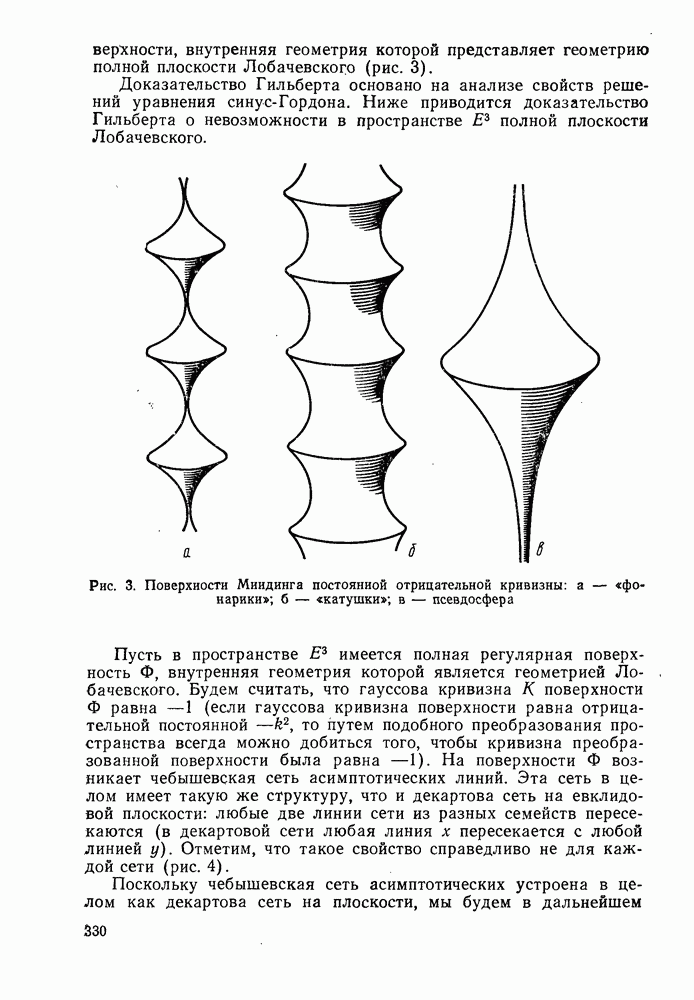
поверхности, внутренняя геометрия которой представляет геометрию полной плоскости Лобачевского (рис. 3).
Доказательство Гильберта основано на анализе свойств решений уравнения синус-Гордона. Ниже приводится доказательство Гильберта о невозможности в пространстве  полной плоскости Лобачевского.
полной плоскости Лобачевского.

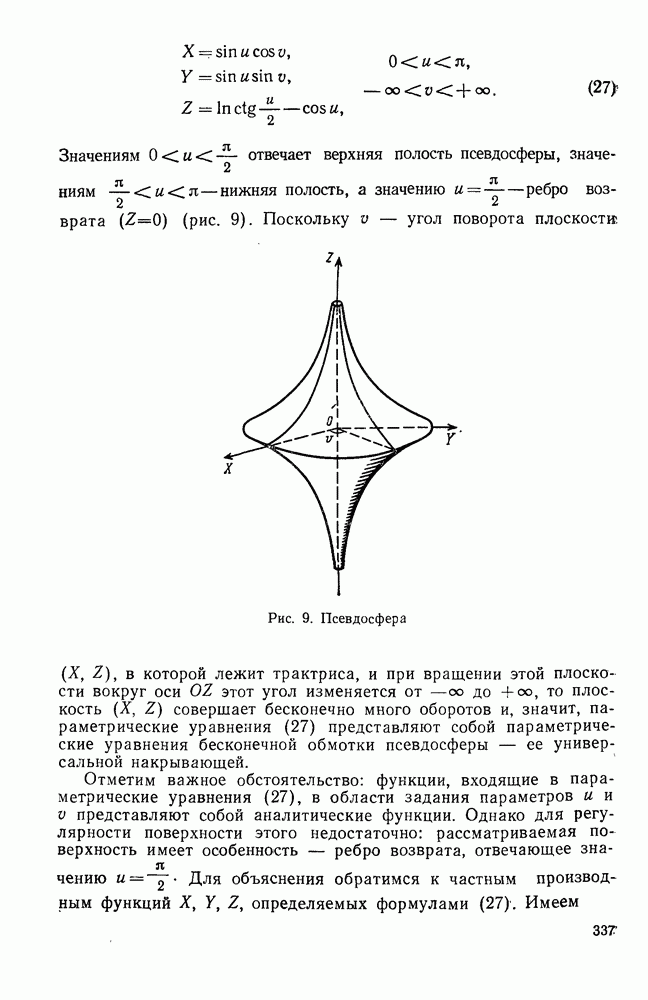
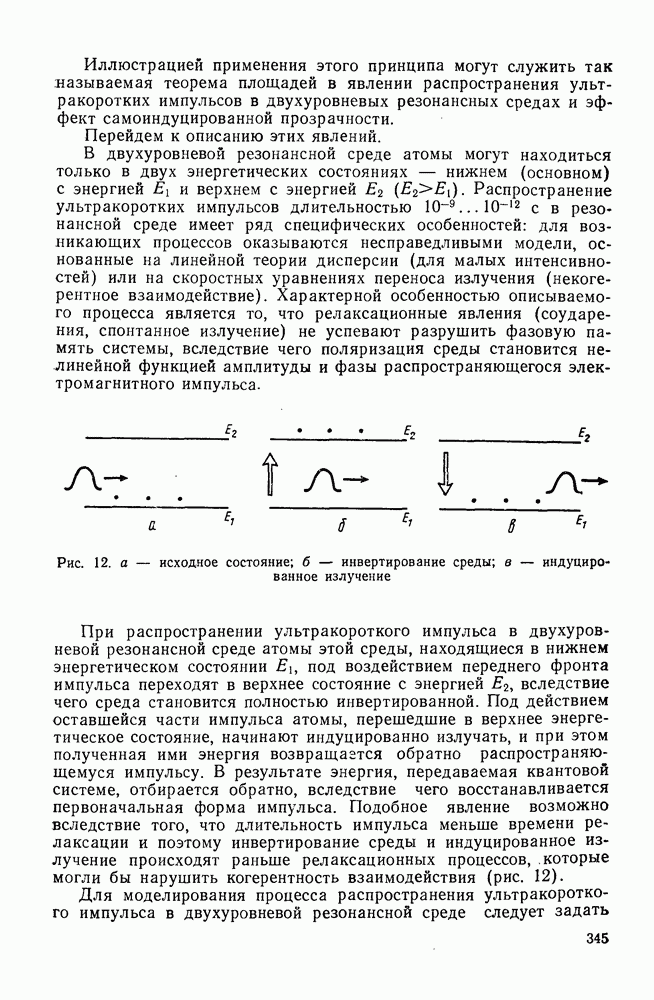
Рис. 3. Поверхности Миидинга постоянной отрицательной кривизны: а — «фонарики»; б - «катушки»; в — псевдосфера
Пусть в пространстве  имеется полная регулярная поверхность
имеется полная регулярная поверхность  внутренняя геометрия которой является геометрией
внутренняя геометрия которой является геометрией  бачевского. Будем считать, что гауссова кривизна К поверхности
бачевского. Будем считать, что гауссова кривизна К поверхности  равна —1 (если гауссова кривизна поверхности равна отрицательной постоянной
равна —1 (если гауссова кривизна поверхности равна отрицательной постоянной  то путем подобного преобразования пространства всегда можно добиться того, чтобы кривизна преобразованной поверхности была равна —1). На поверхности
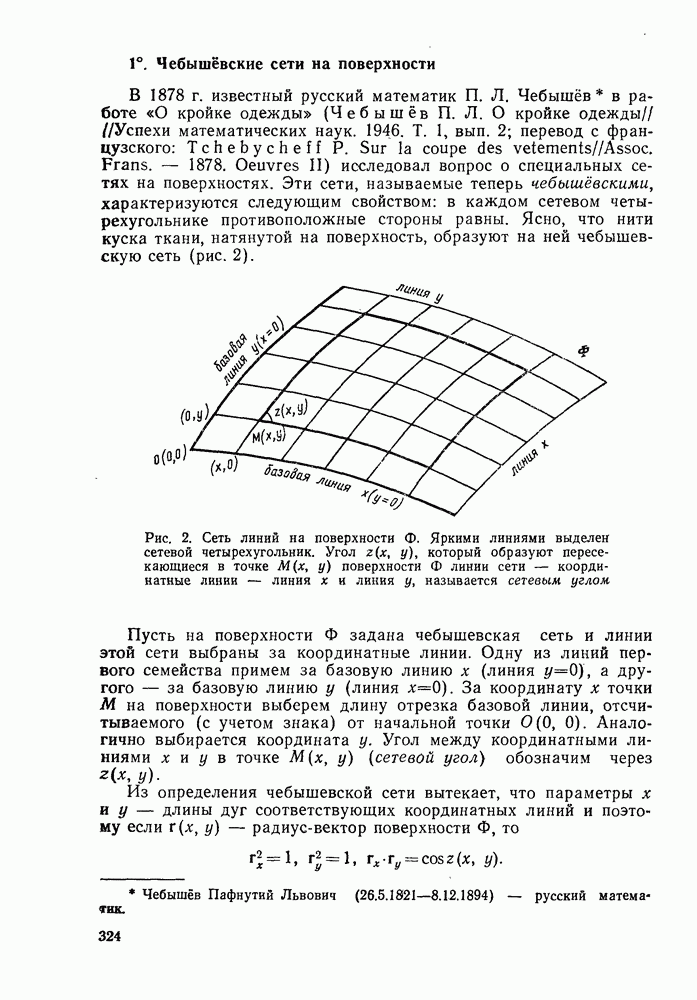
то путем подобного преобразования пространства всегда можно добиться того, чтобы кривизна преобразованной поверхности была равна —1). На поверхности  возникает чебышевская сеть асимптотических линий. Эта сеть в целом имеет такую же структуру, что и декартова сеть на евклидовой плоскости: любые две линии сети из разных семейств пересекаются (в декартовой сети любая линия х пересекается с любой линией
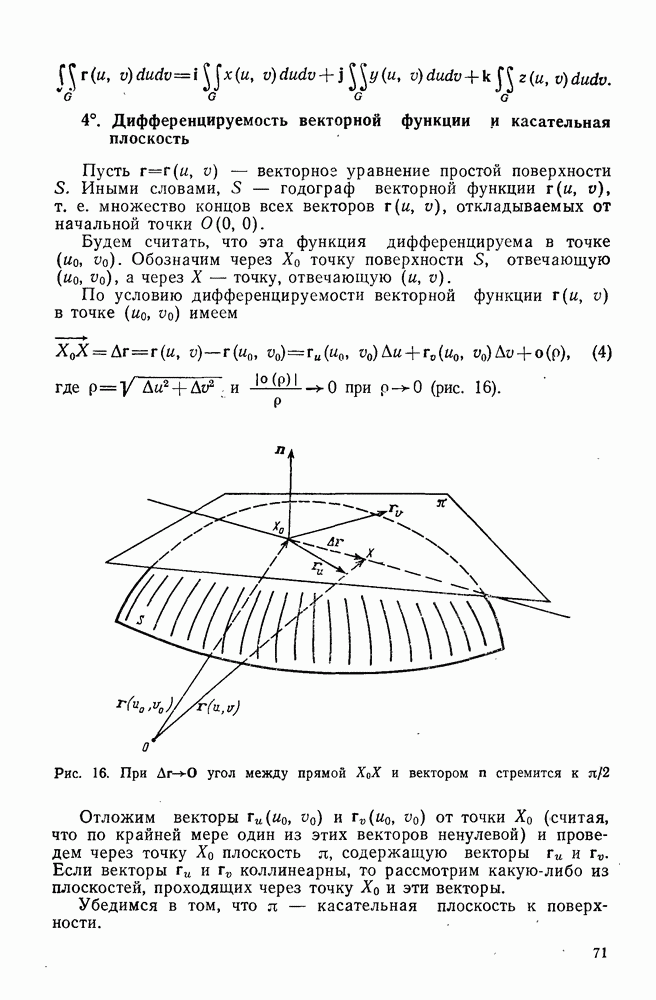
возникает чебышевская сеть асимптотических линий. Эта сеть в целом имеет такую же структуру, что и декартова сеть на евклидовой плоскости: любые две линии сети из разных семейств пересекаются (в декартовой сети любая линия х пересекается с любой линией  Отметим, что такое свойство справедливо не для каждой сети (рис. 4).
Отметим, что такое свойство справедливо не для каждой сети (рис. 4).
Поскольку чебышевская сеть асимптотических устроена в целом как декартова сеть на плоскости, мы будем в дальнейшем

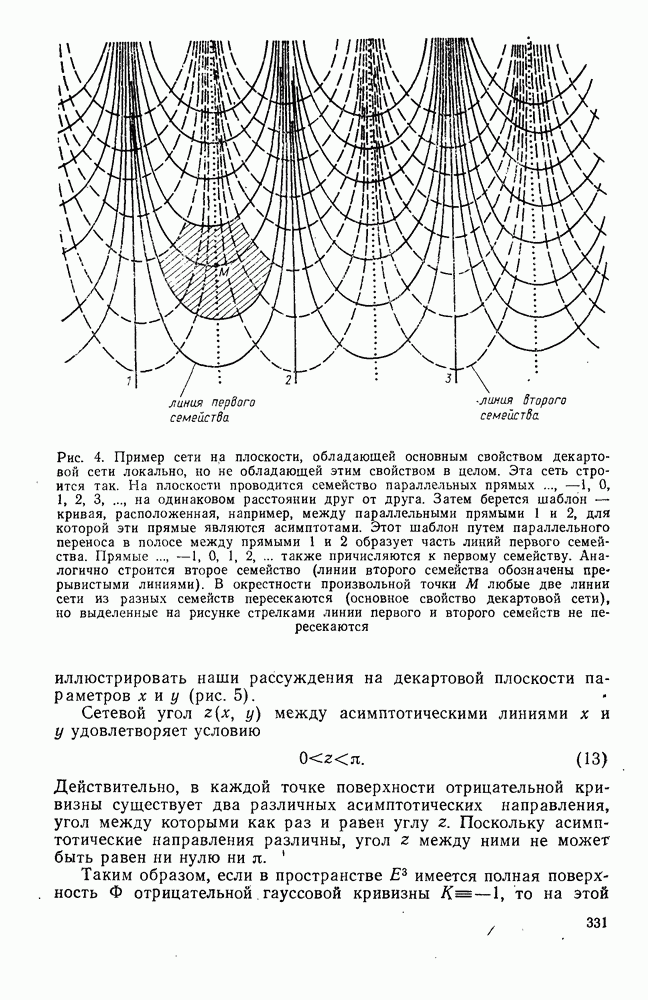
Рис. 4. Пример сети на плоскости, обладающей основным свойством декартовой сети локально, но не обладающей этим свойством в целом. Эта сеть строится так. На плоскости проводится семейство параллельных прямых —1, 0, 1, 2, 3, на одинаковом расстоянии друг от друга. Затем берется шаблон — кривая, расположенная, например, между параллельными прямыми 1 и 2, для которой эти прямые являются асимптотами. Этот шаблон путем параллельного переноса в полосе между прямыми 1 и 2 образует часть линий первого семейства. Прямые  также причисляются к первому семейству. Аналогично строится второе семейство (линии второго семейства обозначены прерывистыми линиями). В окрестности произвольной точки
также причисляются к первому семейству. Аналогично строится второе семейство (линии второго семейства обозначены прерывистыми линиями). В окрестности произвольной точки  любые две линии сети из разных семейств пересекаются (основное свойство декартовой сети), но выделенные на рисунке стрелками линии первого и второго семейств не пересекаются
любые две линии сети из разных семейств пересекаются (основное свойство декартовой сети), но выделенные на рисунке стрелками линии первого и второго семейств не пересекаются
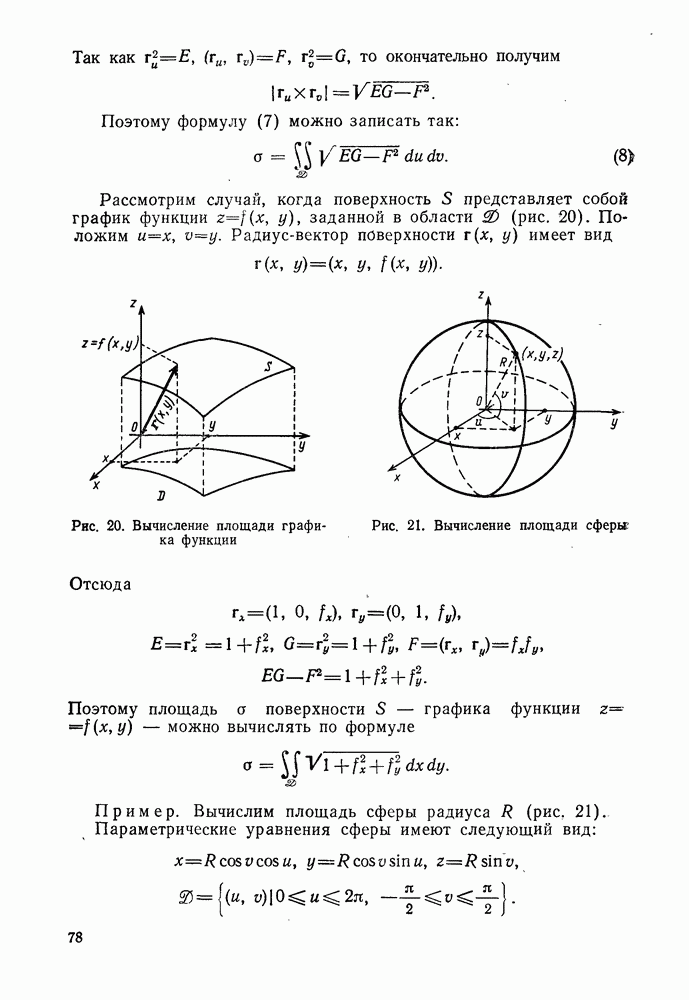
иллюстрировать наши рассуждения на декартовой плоскости параметров х и у (рис. 5).
Сетевой угол  между асимптотическими линиями х и у удовлетворяет условию
между асимптотическими линиями х и у удовлетворяет условию

Действительно, в каждой точке поверхности отрицательной кривизны существует два различных асимптотических направления, угол между которыми как раз и равен углу  Поскольку асимптотические направления различны, угол
Поскольку асимптотические направления различны, угол  между ними не может быть равен ни нулю ни
между ними не может быть равен ни нулю ни  .
.
Таким образом, если в пространстве  имеется полная поверхность
имеется полная поверхность  отрицательной гауссовой кривизны
отрицательной гауссовой кривизны  то на этой
то на этой
поверхности возникает чебышевская сеть асимптотических линий, устроенная в целом как декартова сеть на плоскости, причем сетевой угол  этой сети удовлетворяет уравнению синус-Гордона (1) и условию (13).
этой сети удовлетворяет уравнению синус-Гордона (1) и условию (13).

Рис. 5. Две любые линии 1-го и 2-го семейств чебышевской сети пересекаются. Из точек отрезка  базовой линии х проведем все линии 2-го семейства и на каждой из них отложим дугу одной и той же малой длины у. Концы отложенных отрезков образуют линию 1-го семейства, близкую к базовой и пересекающую произвольно выбранную линию 2-го семейства. Повторяя описанную процедуру достаточное число раз, дойдем до произвольной линии 1-го семейства. Тем самым произвольно выбранные линии из 1-го и 2-го семейств чебышевской сети пересекаются
базовой линии х проведем все линии 2-го семейства и на каждой из них отложим дугу одной и той же малой длины у. Концы отложенных отрезков образуют линию 1-го семейства, близкую к базовой и пересекающую произвольно выбранную линию 2-го семейства. Повторяя описанную процедуру достаточное число раз, дойдем до произвольной линии 1-го семейства. Тем самым произвольно выбранные линии из 1-го и 2-го семейств чебышевской сети пересекаются
Гильберт показал, что на всей плоскости параметров х и у не существует решения уравнения (1), удовлетворяющего условию (13). Это, очевидно, и доказывает невозможность в пространстве  полной плоскости Лобачевского.
полной плоскости Лобачевского.
Итак, предположим, что на всей плоскости  существует решение
существует решение  уравнения (1), удовлетворяющее условию (13).
уравнения (1), удовлетворяющее условию (13).
Частная производная  ибо из того, что
ибо из того, что  следовало бы
следовало бы  и далее в силу уравнения
и далее в силу уравнения  т. е. либо
т. е. либо  либо
либо  что противоречит условию (13).
что противоречит условию (13).
Без ограничения общности можно считать, что  (случай
(случай  рассматривается аналогично). Поэтому существует такое
рассматривается аналогично). Поэтому существует такое  что на отрезке
что на отрезке  (рис. 6)
(рис. 6)

Ясно, что


Рис. 6. Полуполоса  и полуполоса
и полуполоса 

Рис. 7. На участке  выполняется неравенство
выполняется неравенство 
Таким образом,

Согласно условию  на всей плоскости
на всей плоскости  в частности, в полуполосе
в частности, в полуполосе

Так как  то функция
то функция  монотонно возрастает при возрастании у в полуполосе
монотонно возрастает при возрастании у в полуполосе  самым вследствие неравенства (14) имеем
самым вследствие неравенства (14) имеем

Интегрируя неравенство (15) по х от нуля до а при любом фиксированном  получим
получим

После интегрирования неравенства (15) по х от 2а до За

С учетом условия  приходим к оценке
приходим к оценке

В полуполосе  является возрастающей функцией по
является возрастающей функцией по  ее производная положительна (см.
ее производная положительна (см.  Поэтому в полуполосе
Поэтому в полуполосе  выполняются соотношения
выполняются соотношения

Выберем а так, чтобы та было меньше  Тогда для значений
Тогда для значений  , удовлетворяющих условию (19), имеем (рис. 7)
, удовлетворяющих условию (19), имеем (рис. 7)

Отсюда и из уравнения (1) получаем, что для всех точек  полуполосы
полуполосы  справедливо неравенство
справедливо неравенство

Интегрируя это неравенство сначала по у от 0 до некоторого  а затем полученное неравенство по от а до 2а, приходим к соотношению
а затем полученное неравенство по от а до 2а, приходим к соотношению

Если взять

то из этого соотношения получается, что в некоторой точке  полуполосы
полуполосы  имеет место оценка
имеет место оценка

которая противоречит условию (13).
Утверждение Гильберта о невозможности в пространстве полной плоскости Лобачевского доказано.
Замечание. В самом начале проведенных рассуждений мы предположили, что в пространстве  существует полная регулярная поверхность, внутренняя геометрия которой является геометрией Лобачевского. Это предположение следует уточнить. Предварительно сделаем некоторые пояснения. Представим себе обычный бесконечный цилиндр в пространстве
существует полная регулярная поверхность, внутренняя геометрия которой является геометрией Лобачевского. Это предположение следует уточнить. Предварительно сделаем некоторые пояснения. Представим себе обычный бесконечный цилиндр в пространстве  Его можно рассматривать как поверхность, полученную склеиванием граничных прямых бесконечной полосы. Но этот же цилиндр можно рассматривать как евклидову плоскость, бесконечное число раз намотанную на цилиндр. При этом говорят, что евклидова плоскость является
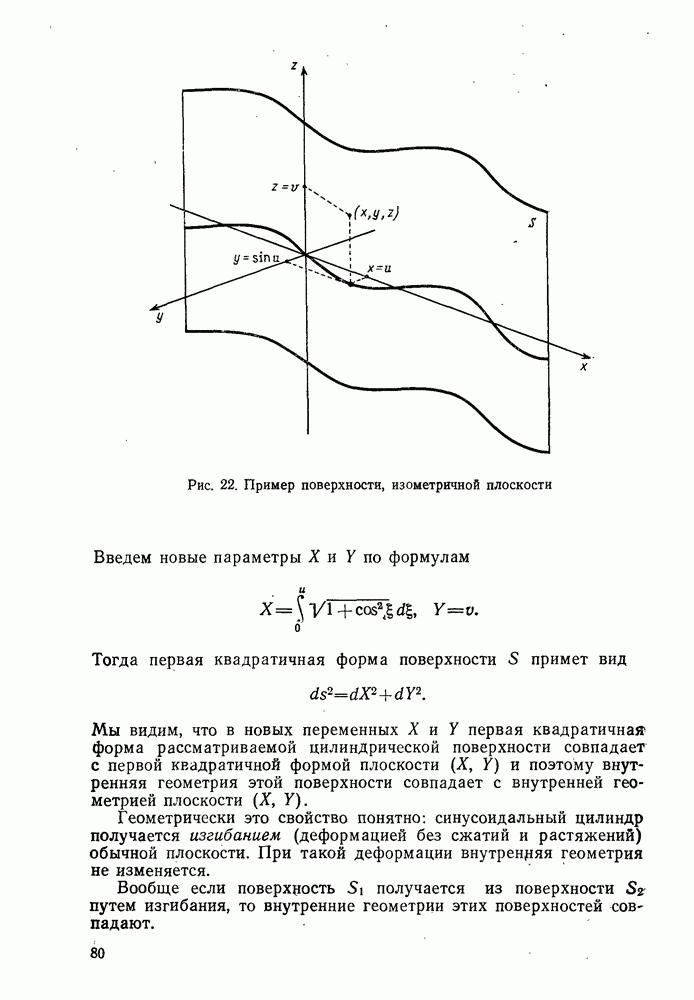
Его можно рассматривать как поверхность, полученную склеиванием граничных прямых бесконечной полосы. Но этот же цилиндр можно рассматривать как евклидову плоскость, бесконечное число раз намотанную на цилиндр. При этом говорят, что евклидова плоскость является

Рис. 8. а — бесконечная полоса на плоскости; б - цилиндр, полученный склеиванием граничных прямых; в - евклидова плоскость, бесконечное число раз намотанная на цилиндр
универсальной накрывающей цилиндра. Понятие универсальной накрывающей можно ввести для любой поверхности. В рассуждениях этого пункта имелась в виду именно универсальная накрывающая поверхности (рис. 8).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
- 2°. Простая поверхность
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
- 4°. Площадь поверхности
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
- § 5. ПОДМНОГООБРАЗИЯ
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
- 4°. Составные поверхности