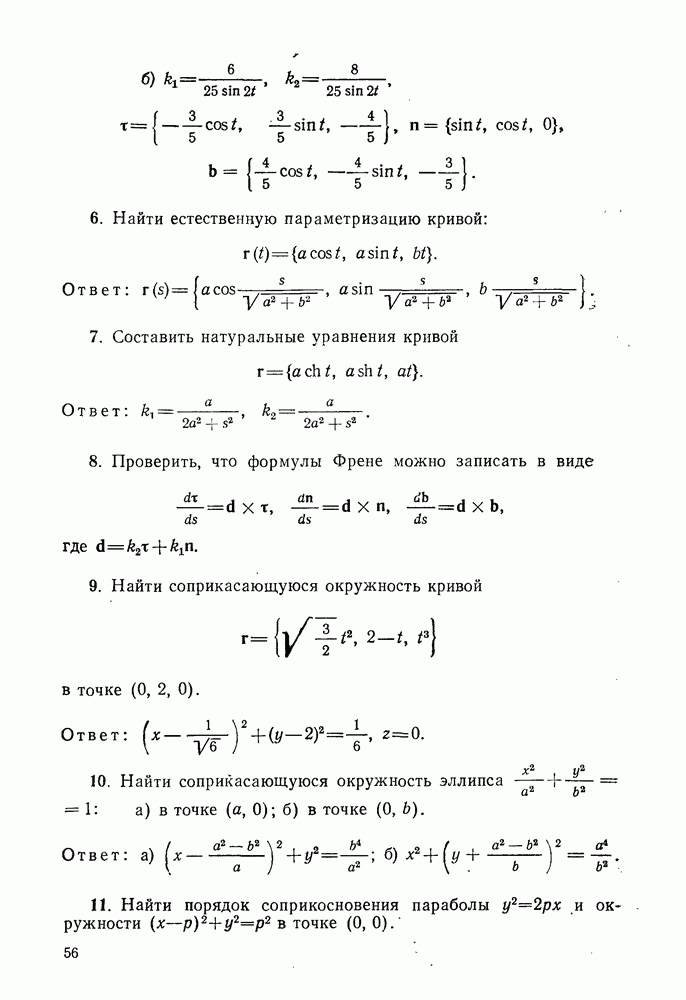| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3°. Теорема Бонне
Предположим выполненными следующие условия.
В некоторой односвязной открытой области  (рис. 46) на плоскости параметров
(рис. 46) на плоскости параметров  и
и  заданы две квадратичные формы:
заданы две квадратичные формы:

и

т. е. в каждой точке области  определены функции
определены функции


Рис. 46. Односвязная область изменения параметров 
Наложим на эти функции ряд ограничений.
1. Потребуем, чтобы всюду в области 3 первая из квадратичных форм

была положительно определенной.
2. Будем считать, что в каждой точке области 3 функции (21) — (22) связаны формулами Гаусса-Петерсона-Кодацци (19) — (20), при этом и сами функции и их производные, входящие в формулы (19) — (20), непрерывны всюду в области 3), Тогда имеет место следующее утверждение.
ТЕОРЕМА 4. Существует регулярная поверхность, для которой заданные формы (I) и (II) являются соответственно первой и второй квадратичными формами. Формами (I) и (II) эта поверхность определяется однозначно с точностью до положения в пространстве.
Тем самым утверждается, что при выполнении условий 1 и 2 в области  можно построить векторную функцию
можно построить векторную функцию

такую, что

и

где

Причем если  — произвольные векторы (векторы b и с неколлинеарны), то условиями
— произвольные векторы (векторы b и с неколлинеарны), то условиями

где  некоторая точка области 3, эта векторная функция определена однозначно.
некоторая точка области 3, эта векторная функция определена однозначно.
Существование. Прежде всего, пользуясь формулами (8)- (11) п. 1°, вычислим по коэффициентам  заданных квадратичных форм (I) и (II) коэффициенты
заданных квадратичных форм (I) и (II) коэффициенты 
Для решения поставленной задачи построим вспомогательную систему дифференциальных уравнений, линейных относительно неизвестных функций 


(несомненная связь уравнений системы (23) с деривационными формулами Вейнгартена (3) — (4) не случайна).
Построенная система (23) обладает следующим замечательным свойством: равенства

выполняются тождественно в силу уравнений (23).
Чтобы убедиться в этом, достаточно провести требуемые дифференцирования и, заменив появляющиеся в результате производные векторных функций  по формулам (23), воспользоваться формулами Гаусса-Петерсона-Кодацци (19) - (20).
по формулам (23), воспользоваться формулами Гаусса-Петерсона-Кодацци (19) - (20).
Тождественное выполнение равенств (24) означает, что для системы (23) соблюдены условия интегрируемости.
Из теории дифференциальных уравнений известно, что в этом случае система (23) имеет и притом единственное решение при заданных начальных значениях неизвестных функций.
Выберем три вектора  так, чтобы они образовывали правую тройку и в некоторой фиксированной точке
так, чтобы они образовывали правую тройку и в некоторой фиксированной точке  области 2) выполнялись равенства
области 2) выполнялись равенства

Пусть

— решение системы (23), удовлетворяющее выбранным начальным условиям

Так как для решения (26) системы (23) выполняется равенство

то найдется векторная функция

для которой

Эта векторая функция может быть вычислена, например, следующим образом:

(криволинейный интеграл берется вдоль гладкой кривой  целиком лежащей в области 2) и соединяющей точки
целиком лежащей в области 2) и соединяющей точки  и
и 
Покажем, что поверхность, задаваемая радиусом-вектором (28), имеет первую и вторую квадратичные формы, соответственно равные заданным формам

Чтобы убедиться в справедливости равенства

достаточно в силу соотношения (9) проверить, что

Преобразуем уравнения системы (23) к удобной для дальнейших рассмотрений форме.
Умножим их поочередно на векторы  и
и  . Из полученных при этом восемнадцати скалярных соотношений путем простейших преобразований приходим к двенадцати, которые можно рассматривать как систему дифференциальных уравнений для скалярных величин
. Из полученных при этом восемнадцати скалярных соотношений путем простейших преобразований приходим к двенадцати, которые можно рассматривать как систему дифференциальных уравнений для скалярных величин

Приведем часть из этих двенадцати уравнений:

Похожую структуру имеют и остальные восемь уравнений.
Непосредственной проверкой можно убедиться в том, что замена в уравнениях (31) величин (30) на

соответственно обратит каждое из уравнений (31) в тождество. Это относится и к восьми другим уравнениям.
Обратимся к соотношениям (25) и (27). Набор (32), как и набор (30), в точке  области 2) принимает значения
области 2) принимает значения

соответственно.
Из того, что наборы (30) и (32) имеют одинаковые начальные значения, в силу единственности решения системы (31) вытекает, что эти наборы совпадают тождественно:

Первое, второе и четвертое тождества (33) обеспечивают справедливость равенства (29).
Тем самым первая квадратичная форма поверхности с радиус-вектором (28) совпадает с формой (I).
Чтобы убедиться в совпадении второй квадратичной формы поверхности (28) с формой (II), обратимся к оставшимся тождествам (33):

Переписав их в несколько иной форме

видим, что вектор  является единичным вектором нормали поверхности (28). При этом в силу условий, наложенных на начальные значения
является единичным вектором нормали поверхности (28). При этом в силу условий, наложенных на начальные значения  тройка
тройка  правая и
правая и

Следовательно, коэффициенты второй квадратичной формы построенной поверхности равны соответственно

Умножая обе части каждого из первых четырех уравнений системы (23) скалярно на вектор  и принимая во внимание равенства (34), получаем, что
и принимая во внимание равенства (34), получаем, что

Это означает, что вторая квадратичная форма рассматриваемой поверхности (2) имеет вид

и тем самым совпадает с заданной формой (II).
На этом доказательство существования регулярной поверхности с заданными первой и второй квадратичными формами заканчивается.
Единственность. Покажем, что построенная выше поверхность единственна с точностью до положения в пространстве.
Пусть  — поверхности, заданные векторами
— поверхности, заданные векторами  у которых в соответствующих точках совпадают первые квадратичные формы и вторые квадратичные формы. Отметим на каждой из этих поверхностей по точке, отвечающей набору параметров и
у которых в соответствующих точках совпадают первые квадратичные формы и вторые квадратичные формы. Отметим на каждой из этих поверхностей по точке, отвечающей набору параметров и 

Параллельным переносом одной из поверхностей (если это необходимо) можно добиться совпадения отмеченных точек.
Считая, что точка  отвечающая набору параметров
отвечающая набору параметров  общая для обеих поверхностей, повернем одну из них так, чтобы в общей точке
общая для обеих поверхностей, повернем одну из них так, чтобы в общей точке  совпали единичные векторы нормалей к этим поверхностям. При этом, конечно, совпадут и касательные плоскости поверхностей в точке
совпали единичные векторы нормалей к этим поверхностям. При этом, конечно, совпадут и касательные плоскости поверхностей в точке 
Ясно, что проведенные действия не изменят квадратичных форм поверхности, перемещаемой в пространстве. Это обеспечивается тем, что при параллельном переносе поверхности и при ее повороте сохраняется взаимное расположение производных радиус-вектора и единичного вектора нормали.
Считая, что в общей точке поверхности  имеют общую нормаль, повернем одну из поверхностей вокруг этой нормали так, чтобы в точке
имеют общую нормаль, повернем одну из поверхностей вокруг этой нормали так, чтобы в точке  совпали направления соответствующих координатных линий поверхностей, скажем, линий
совпали направления соответствующих координатных линий поверхностей, скажем, линий  Тогда направления координатных линий
Тогда направления координатных линий  совпадут автоматически вследствие того, что углы между направлениями координатных линий определяются коэффициентами первой квадратичной формы и в точке
совпадут автоматически вследствие того, что углы между направлениями координатных линий определяются коэффициентами первой квадратичной формы и в точке  у обеих поверхностей они одинаковы.
у обеих поверхностей они одинаковы.
Пусть

радиус-векторы поверхностей  соответственно после описанных перемещений. Это означает, что в точке
соответственно после описанных перемещений. Это означает, что в точке  выполняются равенства
выполняются равенства

Обратимся к системе (23).
Каждый из наборов

и

является решением этой системы. Так как в силу условий (35) — (36)
эти решения совпадают в начальной точке  то вследствие единственности решения системы (23) они равны тождественно:
то вследствие единственности решения системы (23) они равны тождественно: 

Отсюда вытекает совпадение дифференциалов

и равенство

Полагая в нем  в силу условия (35) получим, что
в силу условия (35) получим, что
Следовательно,

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
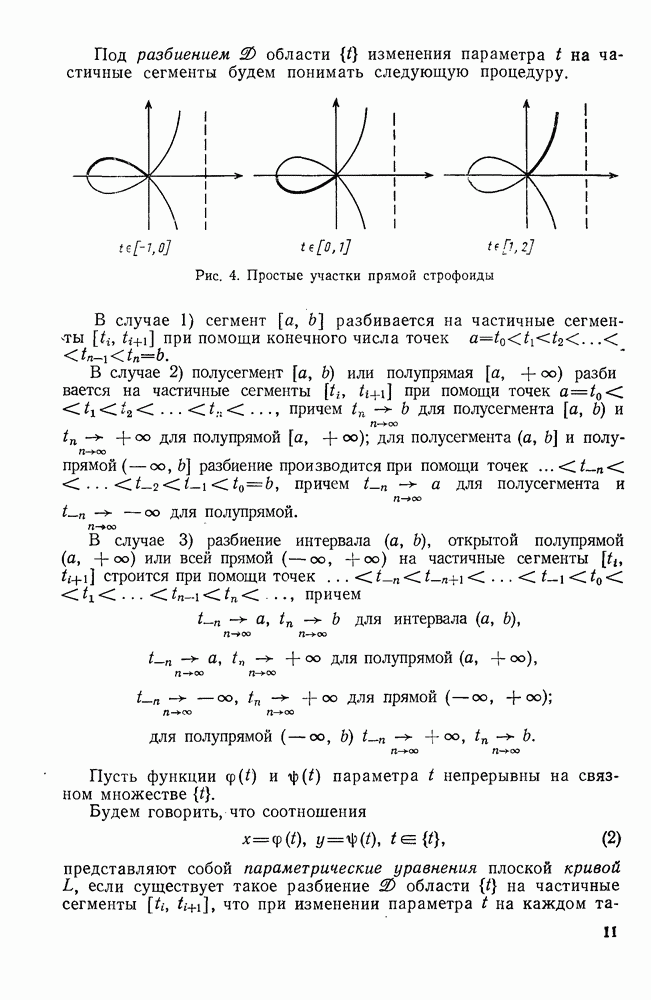
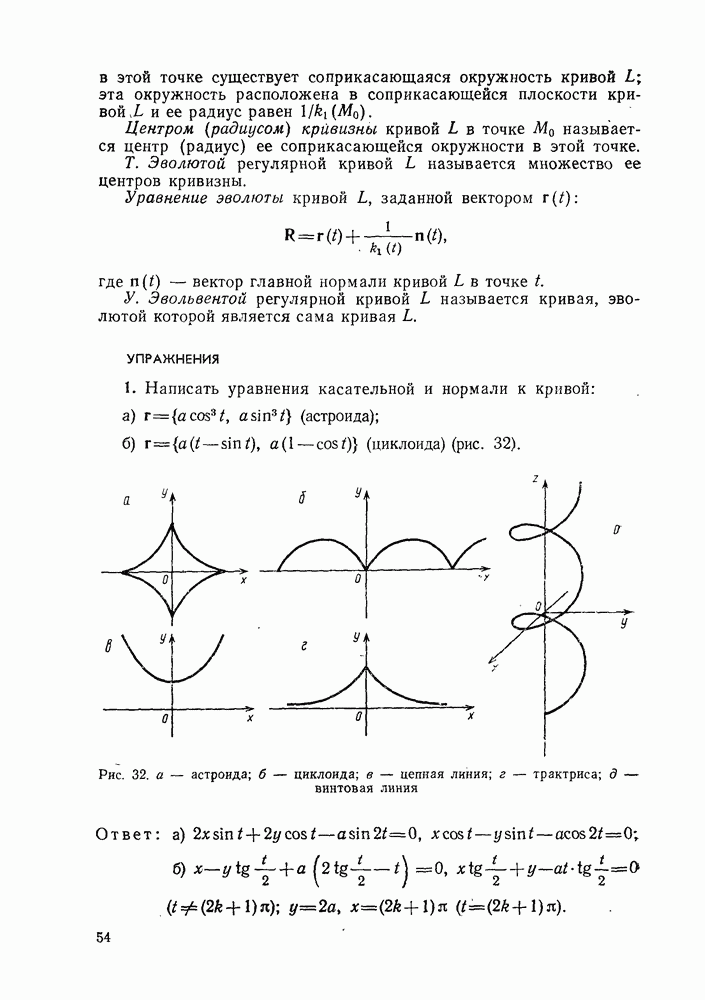
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
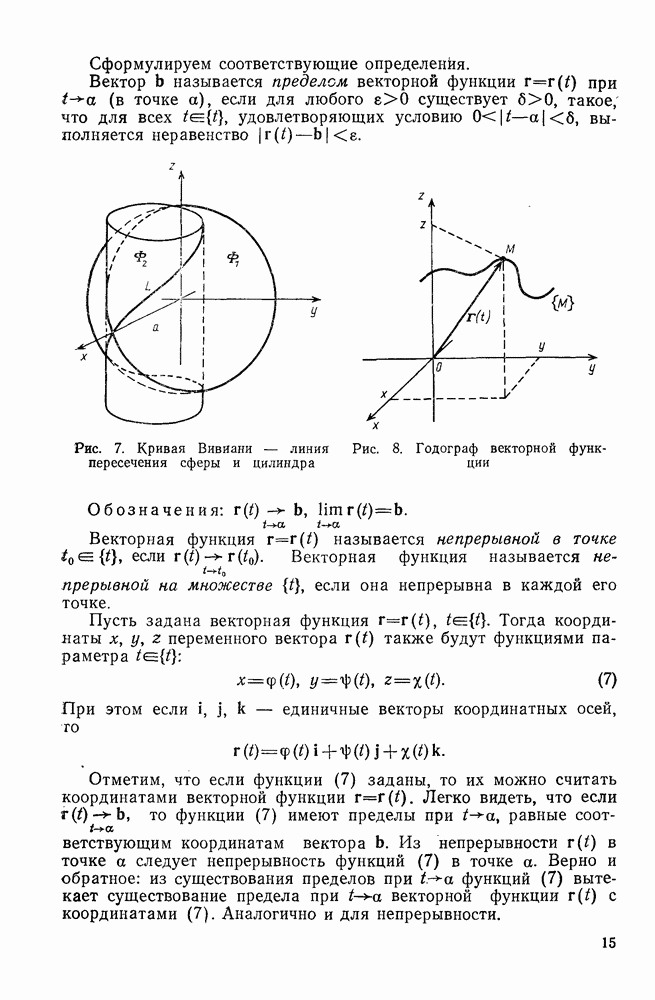
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
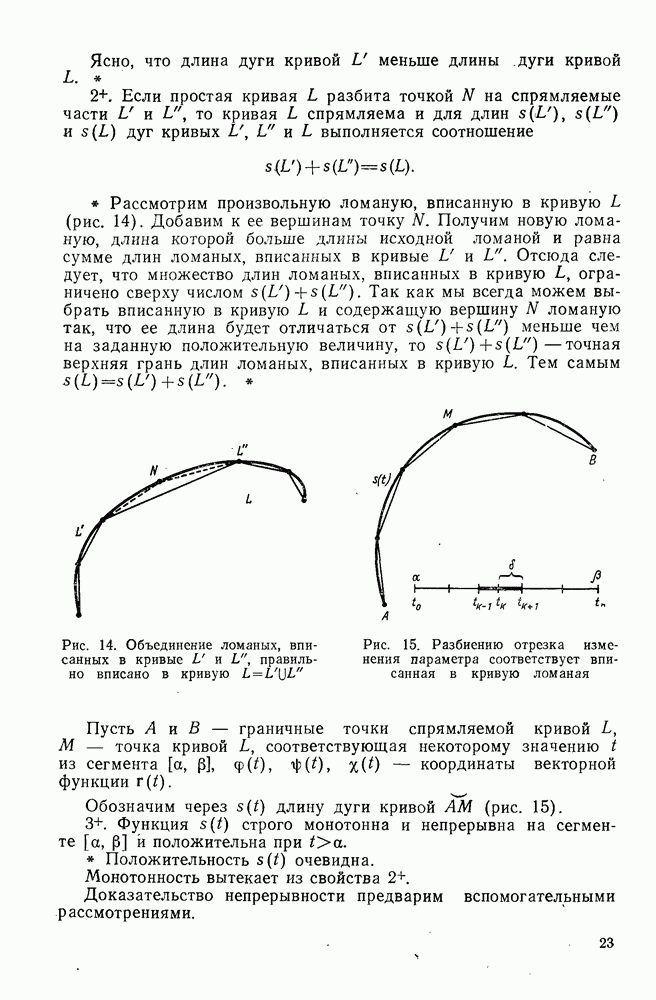
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
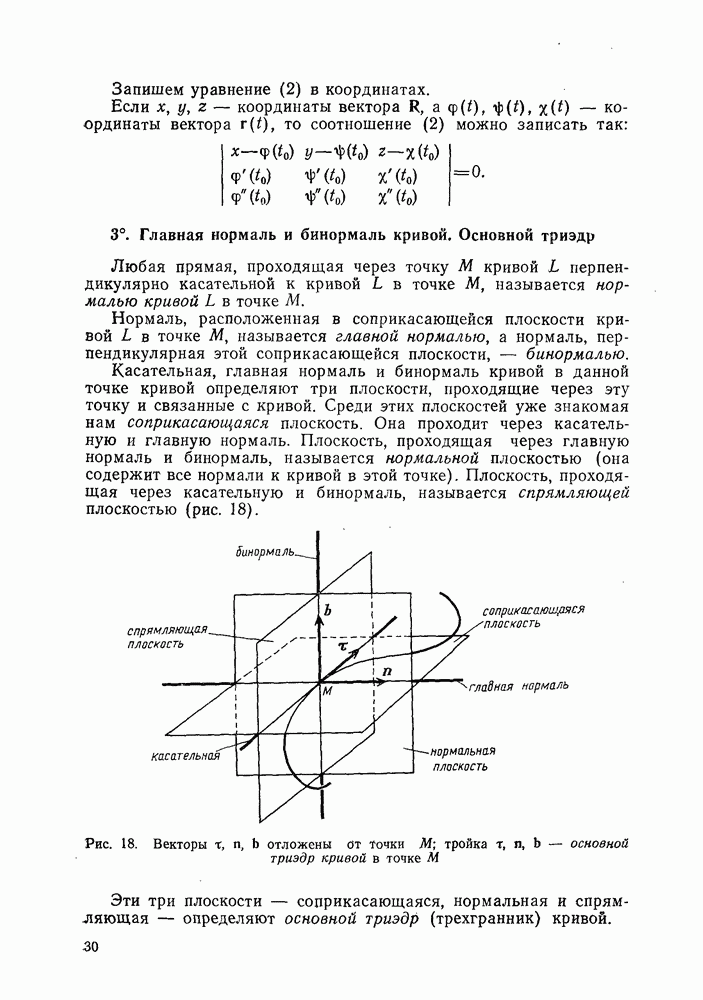
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
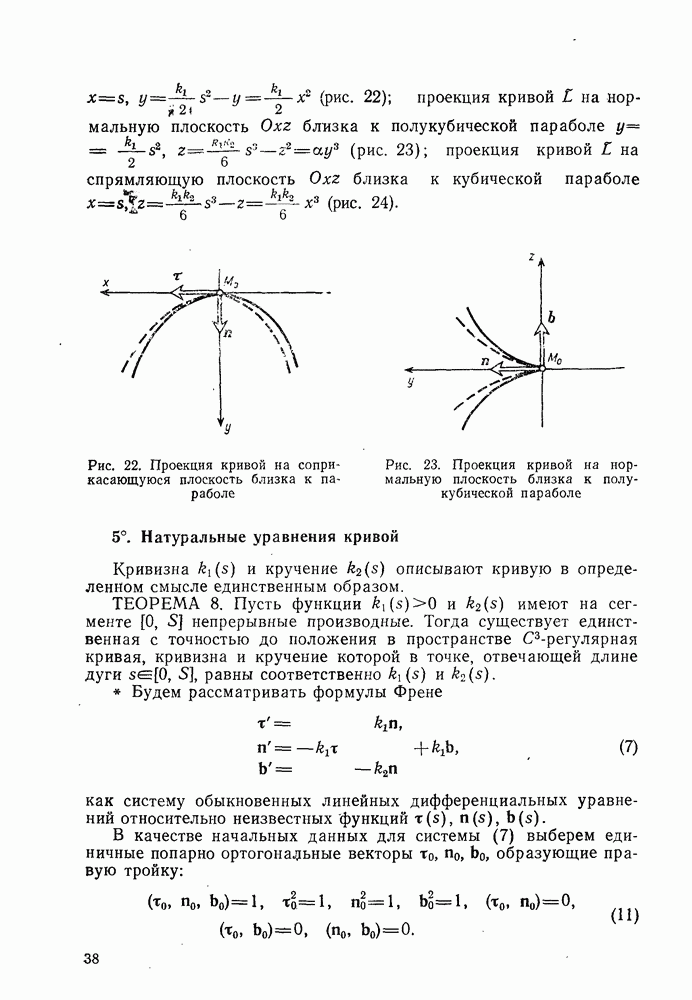
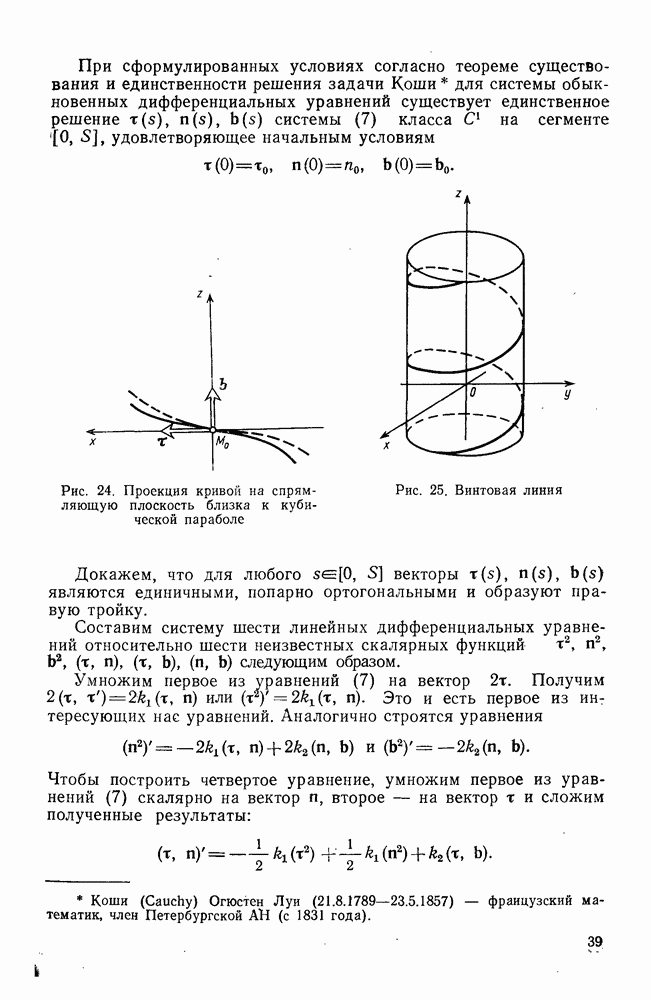
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
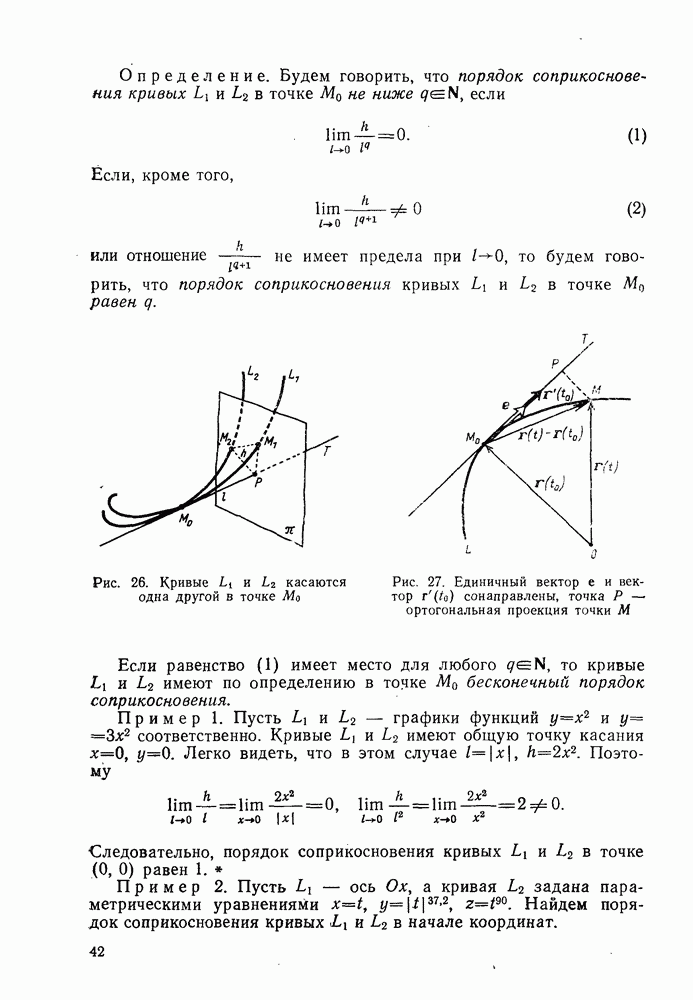
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
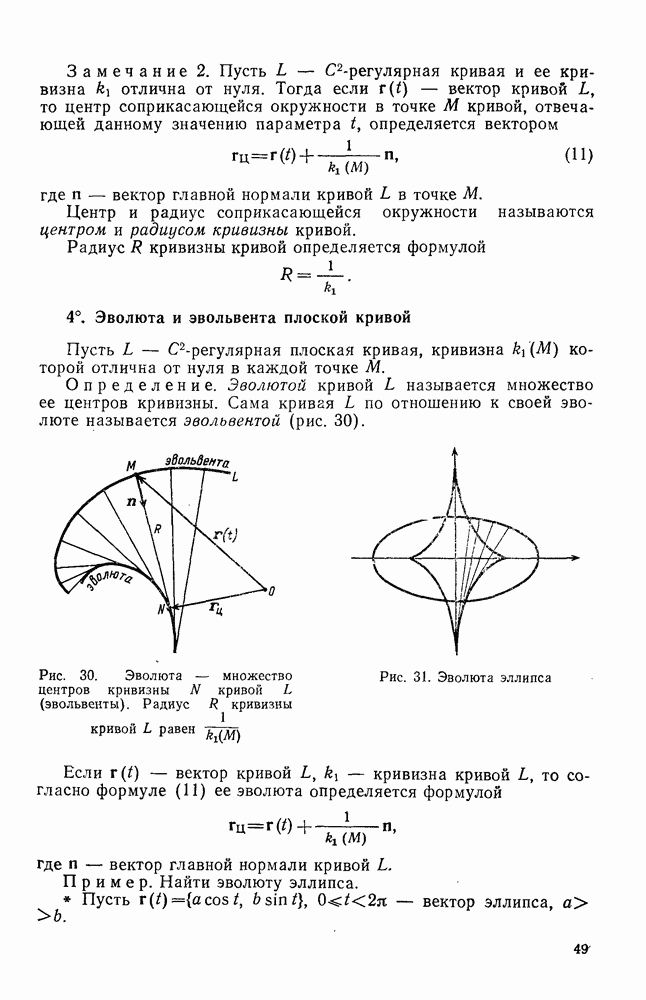
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
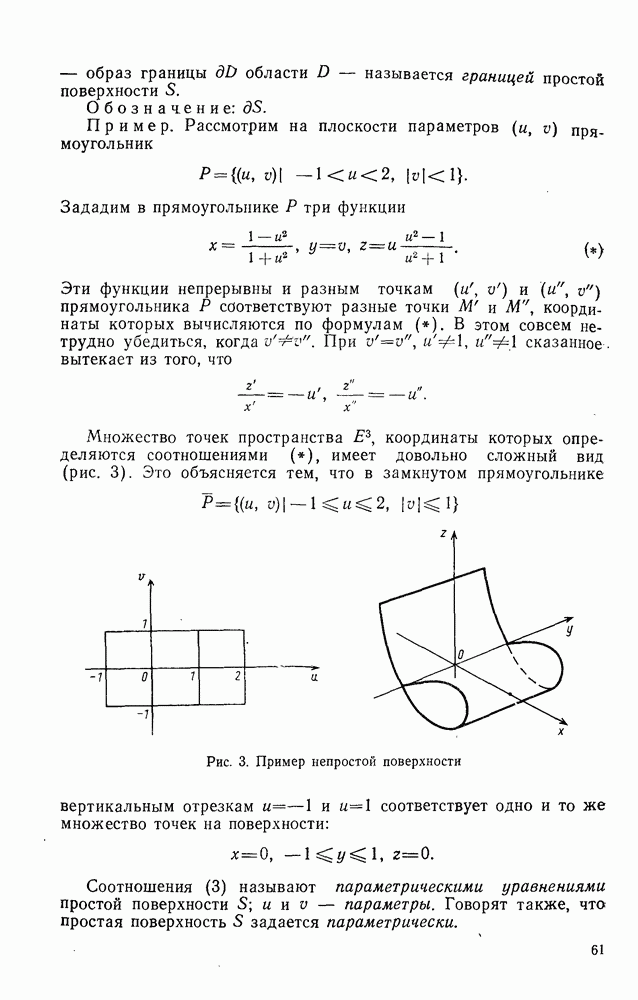
- 2°. Простая поверхность
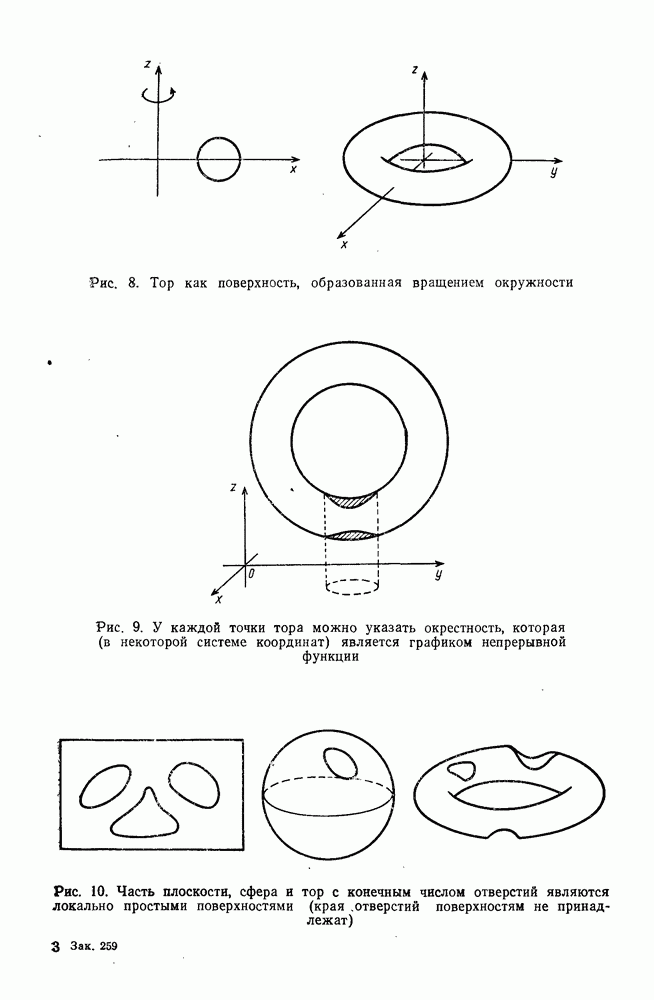
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
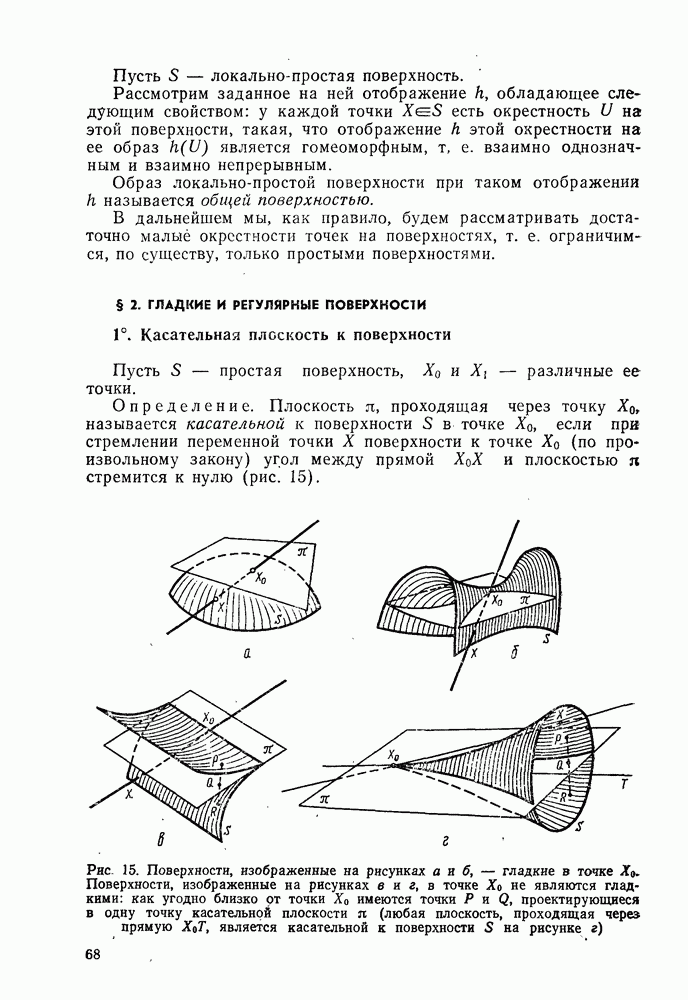
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
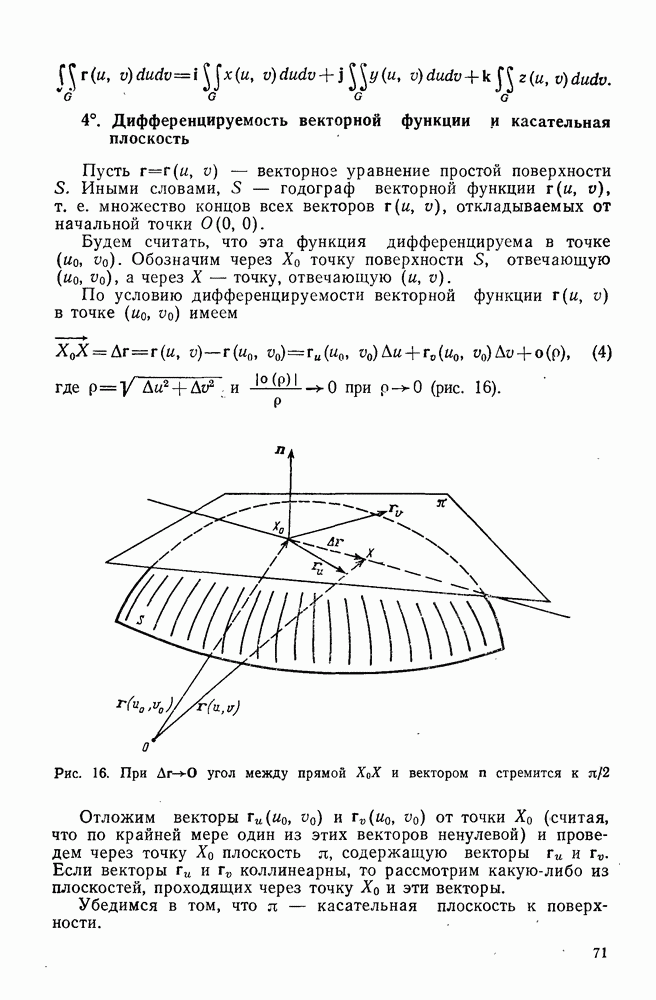
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
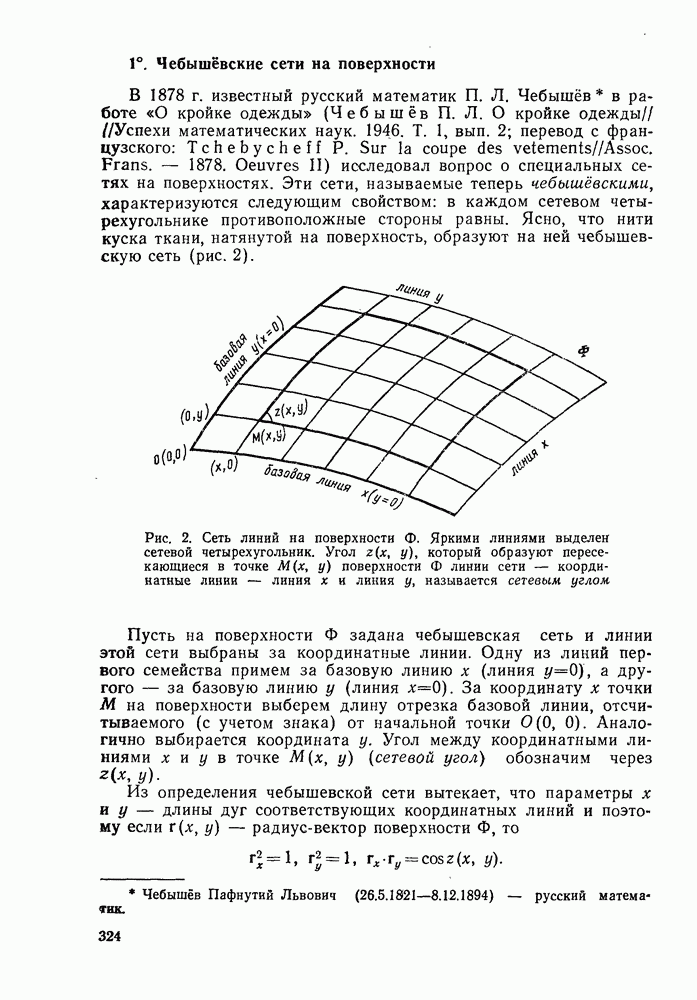
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
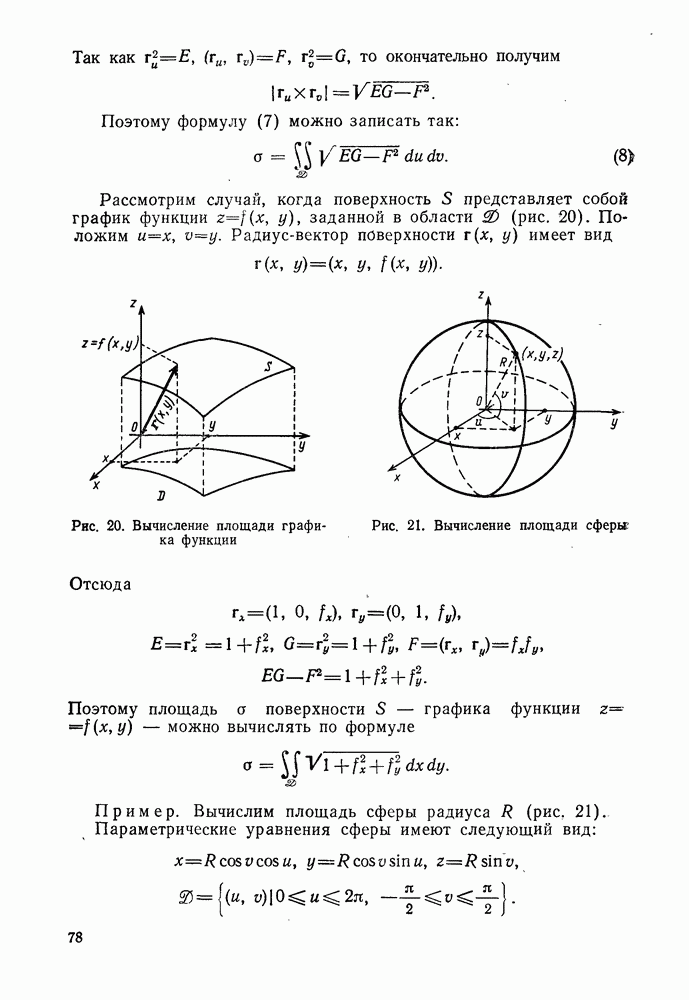
- 4°. Площадь поверхности
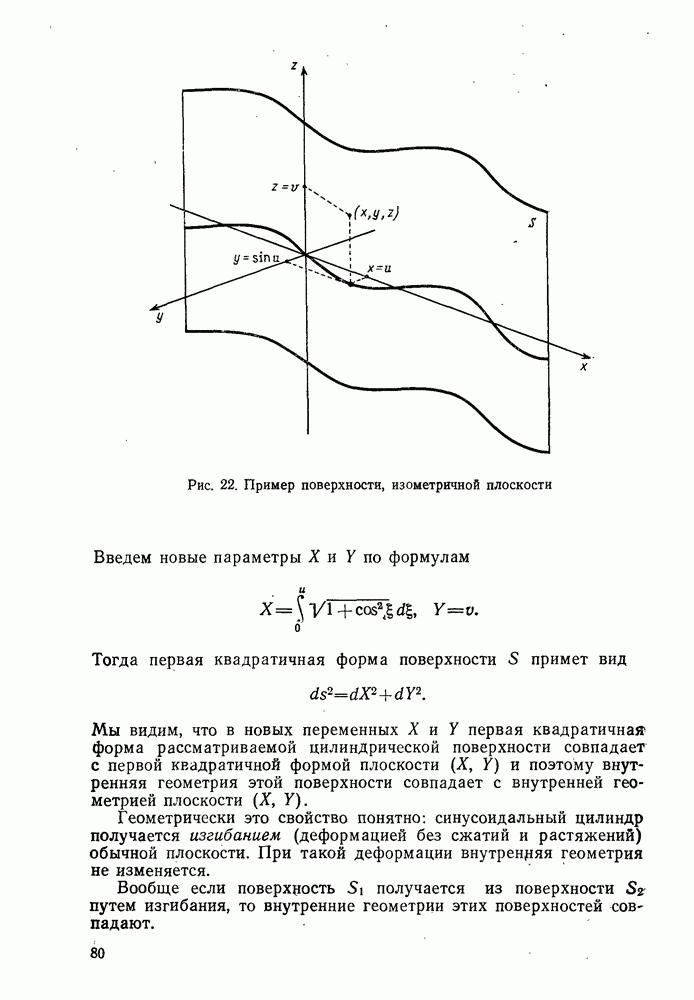
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
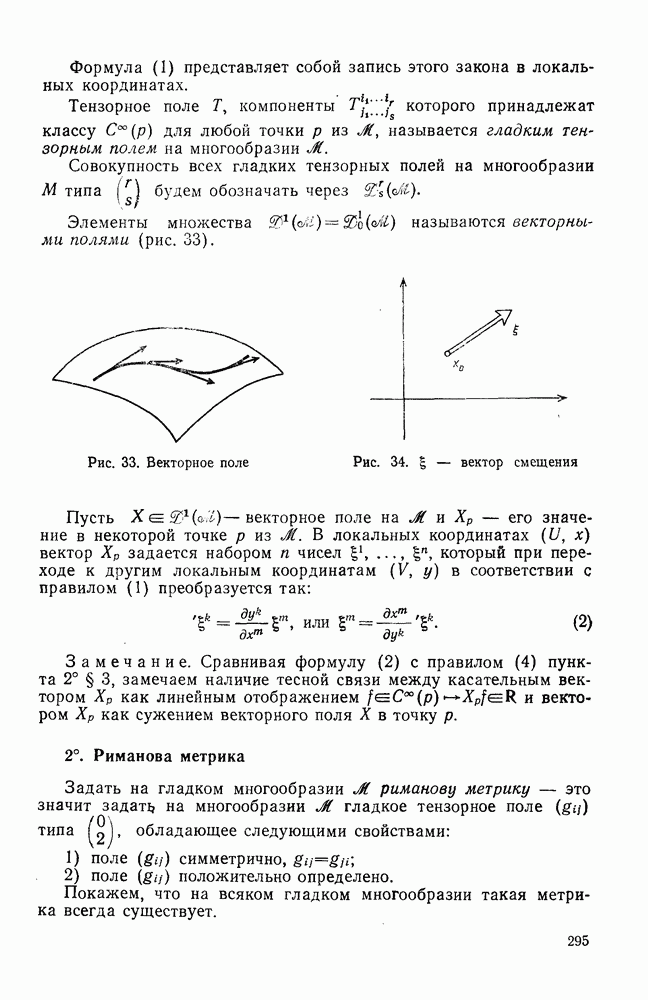
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
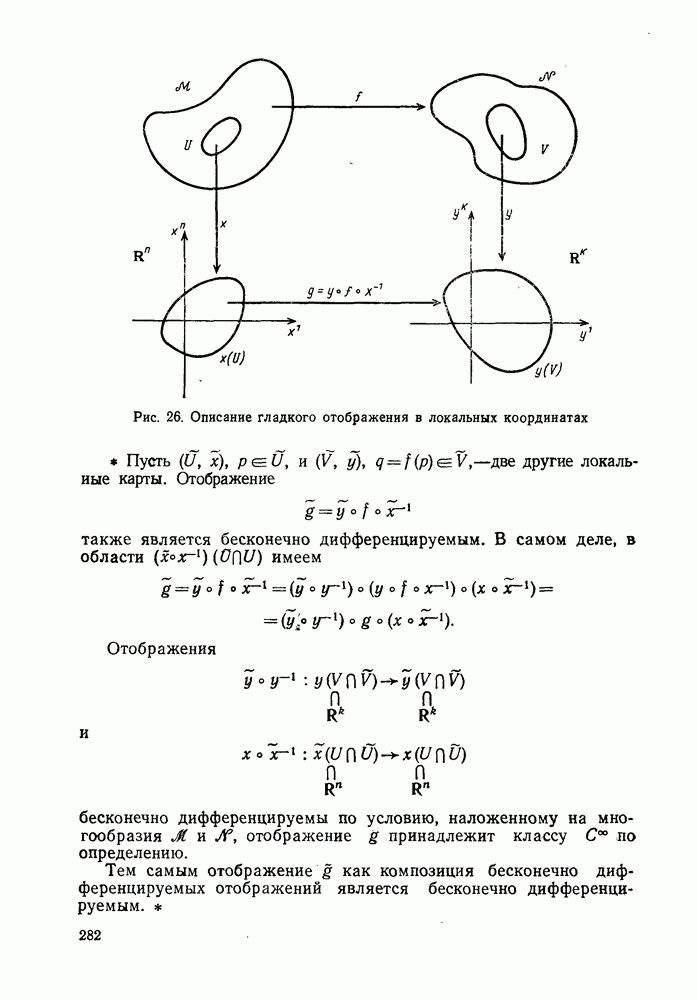
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
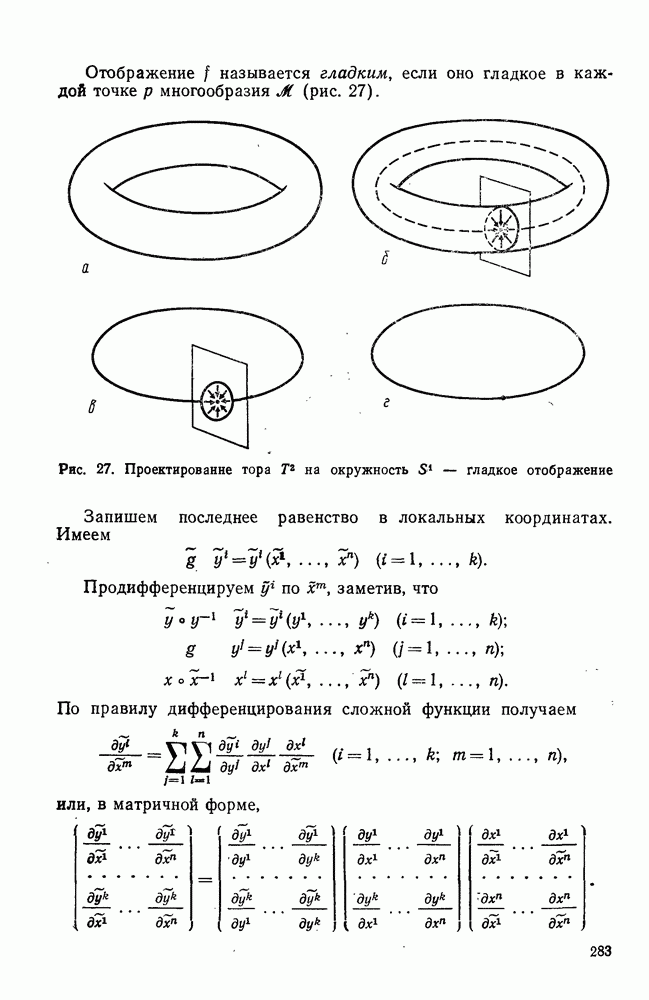
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
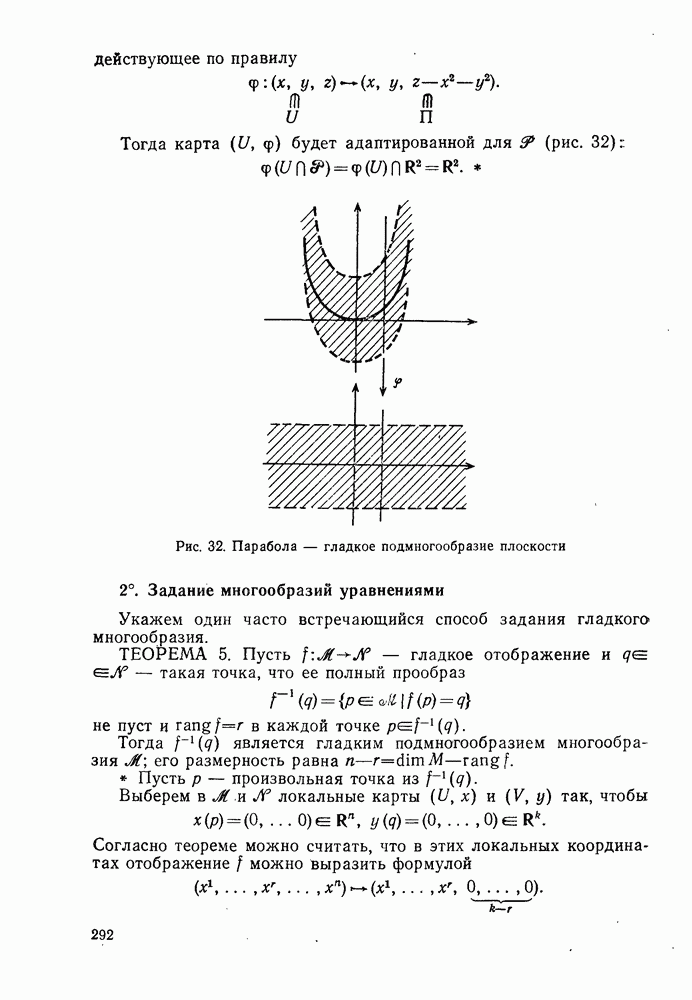
- § 5. ПОДМНОГООБРАЗИЯ
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
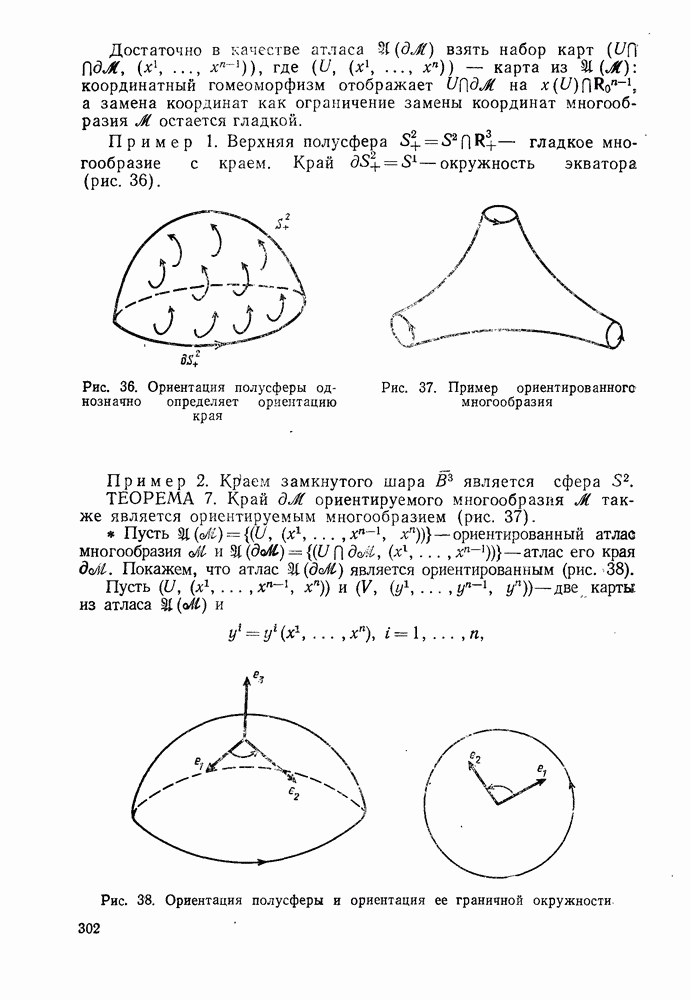
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
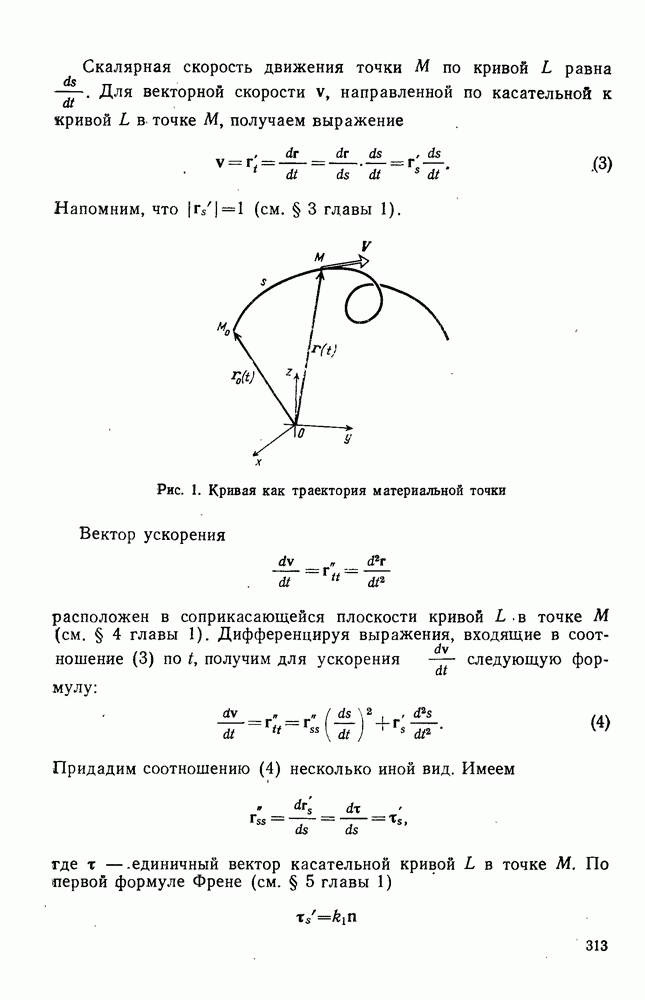
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
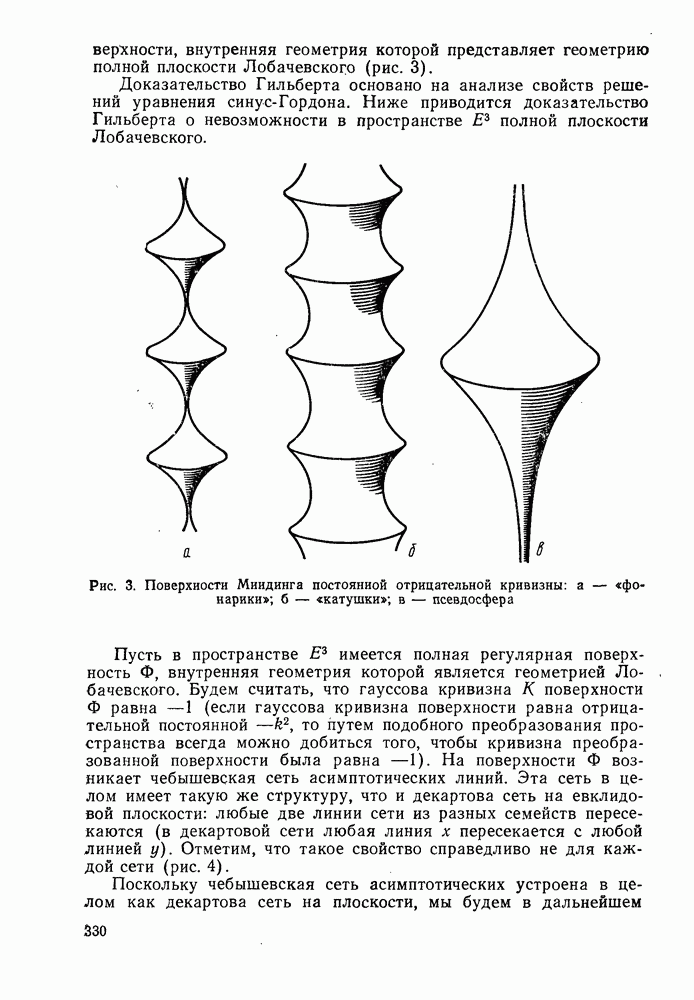
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
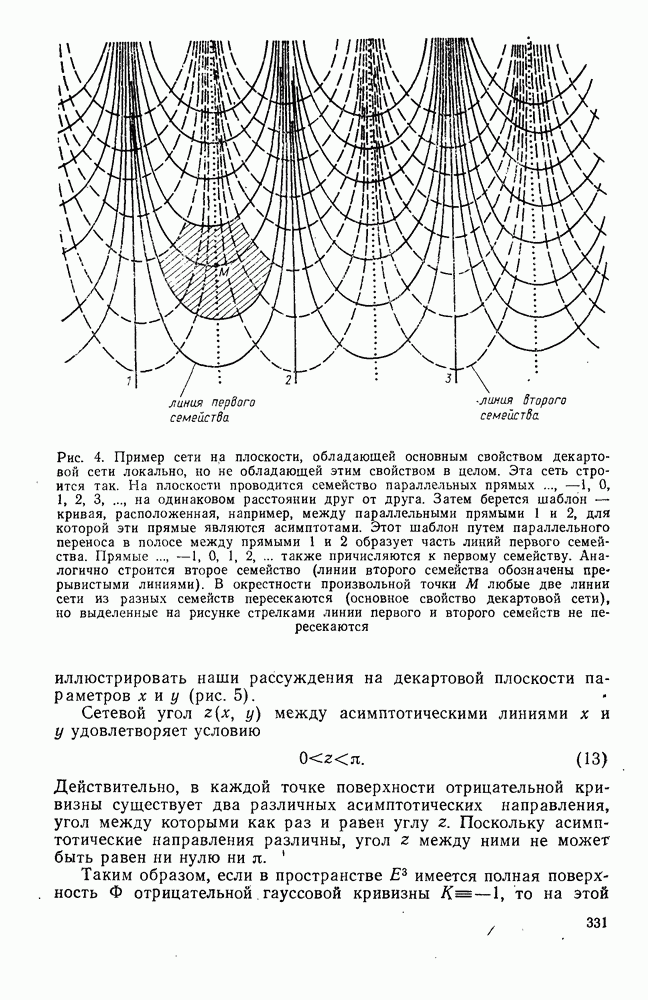
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
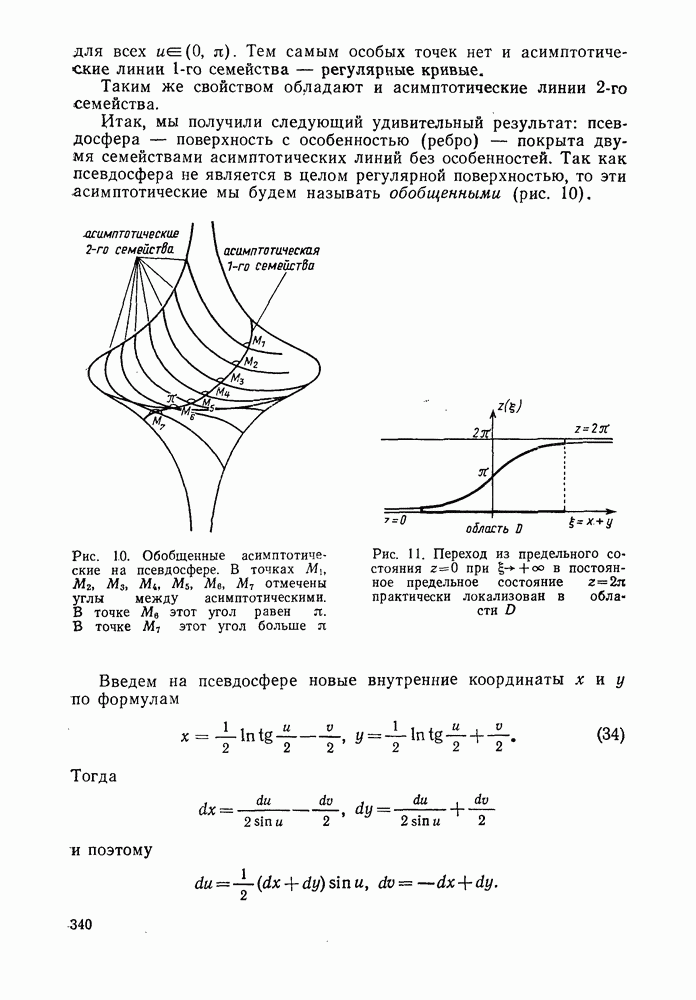
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
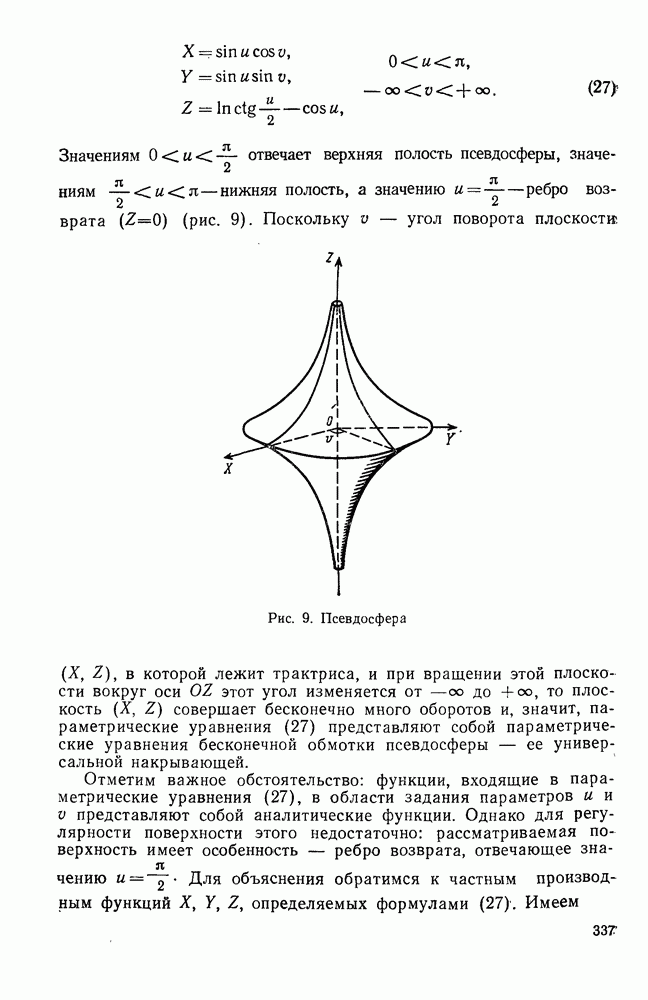
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
- 4°. Составные поверхности