| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
Предлагаемый ниже геометрический подход — физическая интерпретация поверхностей постоянной отрицательной кривизны, равной —1, предложенный А. Г. Поповым (см.: Попов А. Г. Геометрический подход в некоторых задачах, связанных с уравнением sin-Гордона: Автореф. канд. дис. М., 1988), будет рассмотрен на примере явления 1 приведенного перечня.
Основная идея заключается в следующем. Поверхности постоянной отрицательной кривизны, равной  используются в качестве фазовых поверхностей, описывающих эволюцию физического процесса, задаваемого уравнением синус-Гордона. Фазовая поверхность представляет собой аналог фазового пространства в классической механике — каждая точка фазовой поверхности полностью характеризует состояние исследуемых физических величин для соответствующих значений координат фазовой поверхности.
используются в качестве фазовых поверхностей, описывающих эволюцию физического процесса, задаваемого уравнением синус-Гордона. Фазовая поверхность представляет собой аналог фазового пространства в классической механике — каждая точка фазовой поверхности полностью характеризует состояние исследуемых физических величин для соответствующих значений координат фазовой поверхности.
Фазовую  отвечающую решению
отвечающую решению  уравнения синус-Гордона, обозначим через
уравнения синус-Гордона, обозначим через  Пусть
Пусть  область допустимых значений параметров х и у функции
область допустимых значений параметров х и у функции  Каждой точке
Каждой точке  отвечает точка
отвечает точка  При изменении параметров
При изменении параметров  связанных с изменением физического процесс
связанных с изменением физического процесс  меняется радиус-вектор
меняется радиус-вектор  поверхности
поверхности  описывая, вообще говоря, некоторую кривую
описывая, вообще говоря, некоторую кривую  фазовую траекторию
фазовую траекторию  Ясно, что
Ясно, что  определяет исследуемый процесс.
определяет исследуемый процесс.
Пусть  регулярная кривая, так что
регулярная кривая, так что  представляет собой достаточное число раз дифференцируемую функцию. Возможны следующие случаи:
представляет собой достаточное число раз дифференцируемую функцию. Возможны следующие случаи:
1)  , k - целое, т. е.
, k - целое, т. е.  располагается на регулярной части поверхности
располагается на регулярной части поверхности  ,
,
2)  , т. е.
, т. е.  совпадает с особенностью
совпадает с особенностью  (например, с ребром, как на псевдосфере).
(например, с ребром, как на псевдосфере).
Поповым сформулирован следующий принцип описания эволюции физической величины.
Пусть физическая величина  удовлетворяет уравнению синус-Гордона. Тогда в качестве фазовой поверхности для описания ее эволюции может быть использована соответствующая решению
удовлетворяет уравнению синус-Гордона. Тогда в качестве фазовой поверхности для описания ее эволюции может быть использована соответствующая решению  При этом выполняется следующее:
При этом выполняется следующее:

Иллюстрацией применения этого принципа могут служить так называемая теорема площадей в явлении распространения ультракоротких импульсов в двухуровневых резонансных средах и эффект самоиндуцированной прозрачности.
Перейдем к описанию этих явлений.
В двухуровневой резонансной среде атомы могут находиться только в двух энергетических состояниях — нижнем (основном) с энергией  и верхнем с энергией
и верхнем с энергией  Распространение ультракоротких импульсов длительностью
Распространение ультракоротких импульсов длительностью  с в резонансной среде имеет ряд специфических особенностей: для возникающих процессов оказываются несправедливыми модели, основанные на линейной теории дисперсии (для малых интенсивностей) или на скоростных уравнениях переноса излучения (некогерентное взаимодействие). Характерной особенностью описываемого процесса является то, что релаксационные явления (соударения, спонтанное излучение) не успевают разрушить фазовую память системы, вследствие чего поляризация среды становится нелинейной функцией амплитуды и фазы распространяющегося электромагнитного импульса.
с в резонансной среде имеет ряд специфических особенностей: для возникающих процессов оказываются несправедливыми модели, основанные на линейной теории дисперсии (для малых интенсивностей) или на скоростных уравнениях переноса излучения (некогерентное взаимодействие). Характерной особенностью описываемого процесса является то, что релаксационные явления (соударения, спонтанное излучение) не успевают разрушить фазовую память системы, вследствие чего поляризация среды становится нелинейной функцией амплитуды и фазы распространяющегося электромагнитного импульса.

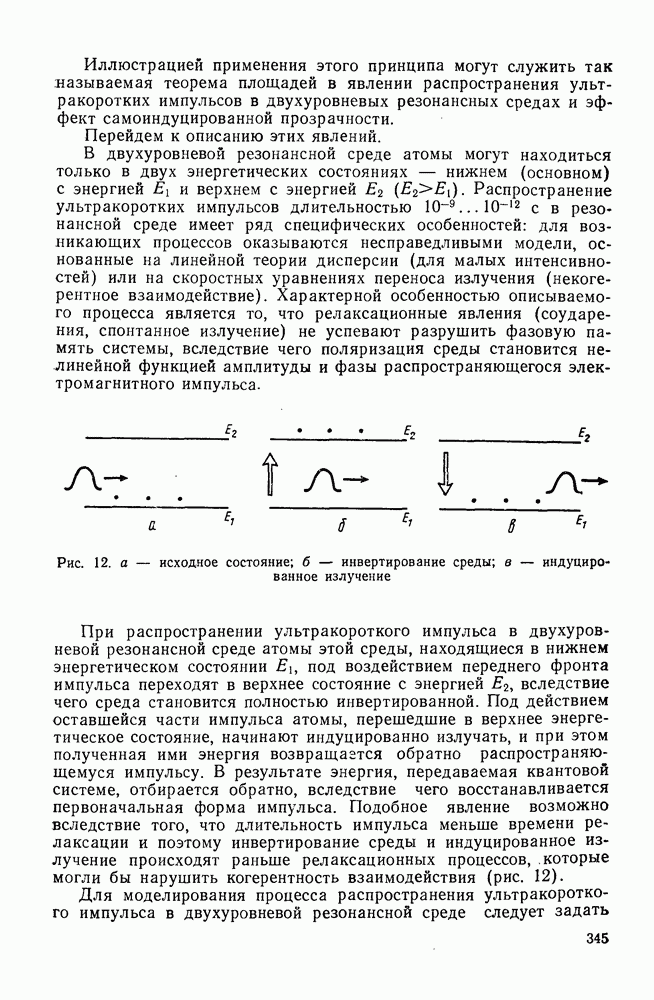
Рис. 12. а — исходное состояние; б - инвертирование среды; в — индуцированное излучение
При распространении ультракороткого импульса в двухуровневой резонансной среде атомы этой среды, находящиеся в нижнем энергетическом состоянии  под воздействием переднего фронта импульса переходят в верхнее состояние с энергией
под воздействием переднего фронта импульса переходят в верхнее состояние с энергией  вследствие чего среда становится полностью инвертированной. Под действием оставшейся части импульса атомы, перешедшие в верхнее энергетическое состояние, начинают индуцированно излучать, и при этом полученная ими энергия возвращается обратно распространяющемуся импульсу. В результате энергия, передаваемая квантовой системе, отбирается обратно, вследствие чего восстанавливается первоначальная форма импульса. Подобное явление возможно вследствие того, что длительность импульса меньше времени релаксации и поэтому инвертирование среды и индуцированное излучение происходят раньше релаксационных процессов, которые могли бы нарушить когерентность взаимодействия (рис. 12).
вследствие чего среда становится полностью инвертированной. Под действием оставшейся части импульса атомы, перешедшие в верхнее энергетическое состояние, начинают индуцированно излучать, и при этом полученная ими энергия возвращается обратно распространяющемуся импульсу. В результате энергия, передаваемая квантовой системе, отбирается обратно, вследствие чего восстанавливается первоначальная форма импульса. Подобное явление возможно вследствие того, что длительность импульса меньше времени релаксации и поэтому инвертирование среды и индуцированное излучение происходят раньше релаксационных процессов, которые могли бы нарушить когерентность взаимодействия (рис. 12).
Для моделирования процесса распространения ультракороткого импульса в двухуровневой резонансной среде следует задать
уравнения Максвелла для описания электромагнитного импульса и квантовый (двухуровневый) ансамбль атомов для описания среды.
Представим поле распространяющегося ультракороткого импульса как

где  координата, у — время,
координата, у — время,  — амплитуда,
— амплитуда,  фаза,
фаза,  — волновой вектор. Тогда дипольный момент системы можно записать в виде
— волновой вектор. Тогда дипольный момент системы можно записать в виде

где  реактивная составляющая (описывает вклад в дисперсию),
реактивная составляющая (описывает вклад в дисперсию),  активная составляющая (определяет вклад в поглощение света средой).
активная составляющая (определяет вклад в поглощение света средой).
Для рассматриваемой задачи система уравнений Максвелла приводится к эквивалентной системе

(см.: Полуэктов И. А., Попов Ю. М., Ройтберг В. С. Эффект самоиндуцированной прозрачности  ).
).
В уравнениях (42) приняты следующие обозначения:  разность заселенностей нижнего и верхнего энергетических состояний,
разность заселенностей нижнего и верхнего энергетических состояний,  частота перехода),
частота перехода),  число частиц в единице объема,
число частиц в единице объема,  нерезонансная часть коэффициента преломления.
нерезонансная часть коэффициента преломления.
В случае

система (42) допускает точное интегрирование. Условие (43) определяет так называемый случай отсутствия фазовой модуляции. Введем вектор

Это позволяет записать первые три уравнения системы (42) в следующем виде:

где  - вектор угловой скорости.
- вектор угловой скорости.
Поясним физический смысл вектора  . В отсутствие импульса атомы находятся в нижнем энергетическом состоянии
. В отсутствие импульса атомы находятся в нижнем энергетическом состоянии  . Полная инверсия соответствует повороту вектора
. Полная инверсия соответствует повороту вектора  на угол
на угол  . Пренебрежение релаксацией означает, что вращение вектора
. Пренебрежение релаксацией означает, что вращение вектора  заканчивается до того, как успевают сказаться релаксационные эффекты.
заканчивается до того, как успевают сказаться релаксационные эффекты.
В случае точного резонанса,  уравнение (44) легко интегрируется:
уравнение (44) легко интегрируется:

При этом угол поворота  определяется так:
определяется так:

Полный поворот равен

Величина  называется площадью импульса.
называется площадью импульса.
Четвертое уравнение системы (42) в случае  с учетом формул (45) заменой переменных
с учетом формул (45) заменой переменных

сводится к уравнению синус-Гордона

При подробном рассмотрении системы (42) относительно величины  выявляется следующая закономерность:
выявляется следующая закономерность:

определяющая изменение площади ультракороткого импульса (см.: Lamb G. L. jr. Analytical description of ultrashort optical pulse propogation in a resonant medium//Rev. Mod. Phys. 1971. V. 43, N 2. P. 99-124). Величина  коэффициент поглощения слабого монохроматического поля частоты
коэффициент поглощения слабого монохроматического поля частоты 
Из последней формулы нетрудно получить соотношение

выражающее содержание «теоремы площадей» (здесь  начальная площадь импульса).
начальная площадь импульса).
Из уравнения (48) вытекает, что если начальная площадь импульса  целое), то импульс должен распространяться в рассматриваемой среде без изменения площади. Такое явление получило название эффекта самоиндуцированной прозрачности. Если же начальная площадь Фото, как видно из формулы (49), площадь импульса стремится в процессе своей эволюции к стабильному значению
целое), то импульс должен распространяться в рассматриваемой среде без изменения площади. Такое явление получило название эффекта самоиндуцированной прозрачности. Если же начальная площадь Фото, как видно из формулы (49), площадь импульса стремится в процессе своей эволюции к стабильному значению 
Из соотношений (46), (47) видно, что при достаточно больших временах у функция  и площадь импульса
и площадь импульса  бесконечно близки. Поэтому для величины
бесконечно близки. Поэтому для величины  справедливы положения (40), (41) сформулированного принципа. При этом положение (41) соответствует эффекту самоиндуцированной прозрачности, а положение (40) качественно выражает «теорему площадей» (стремление площади импульса к значению, кратному
справедливы положения (40), (41) сформулированного принципа. При этом положение (41) соответствует эффекту самоиндуцированной прозрачности, а положение (40) качественно выражает «теорему площадей» (стремление площади импульса к значению, кратному  ).
).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
- 2°. Простая поверхность
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
- 4°. Площадь поверхности
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
- § 5. ПОДМНОГООБРАЗИЯ
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
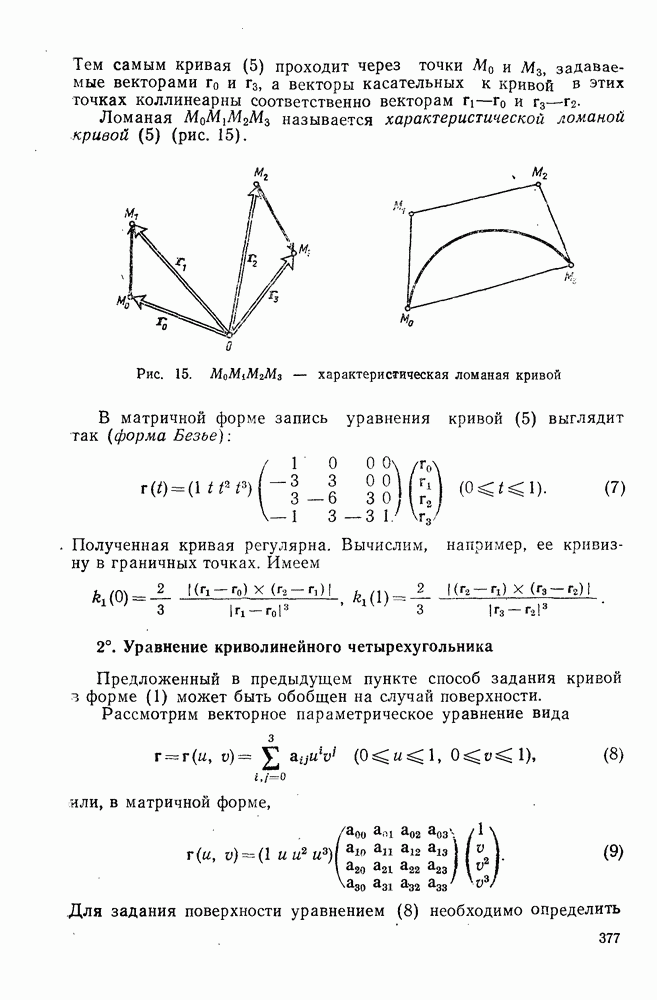
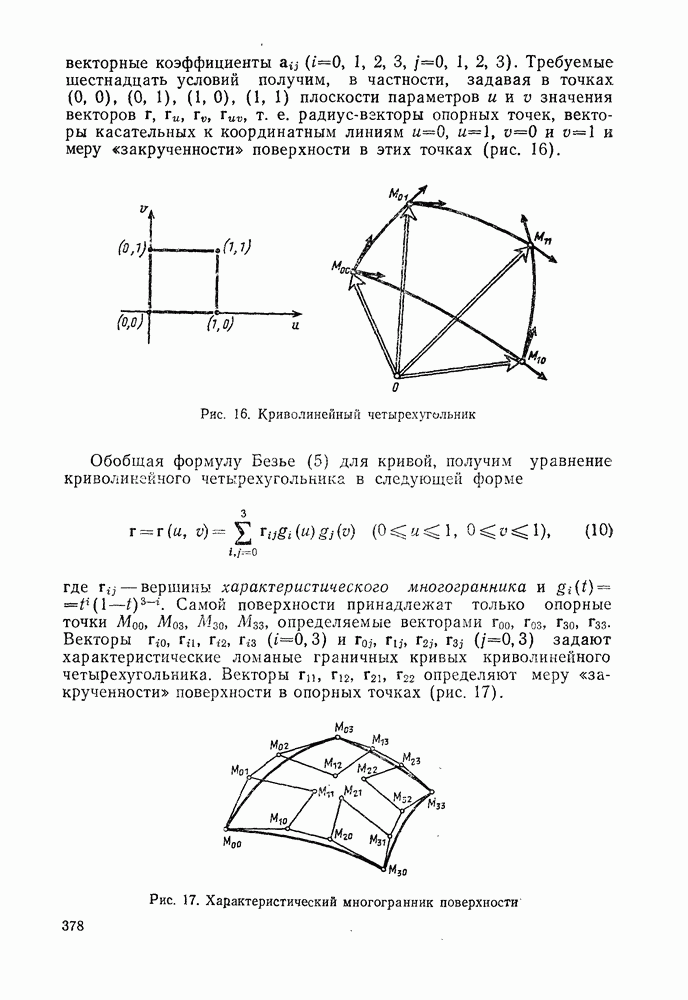
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
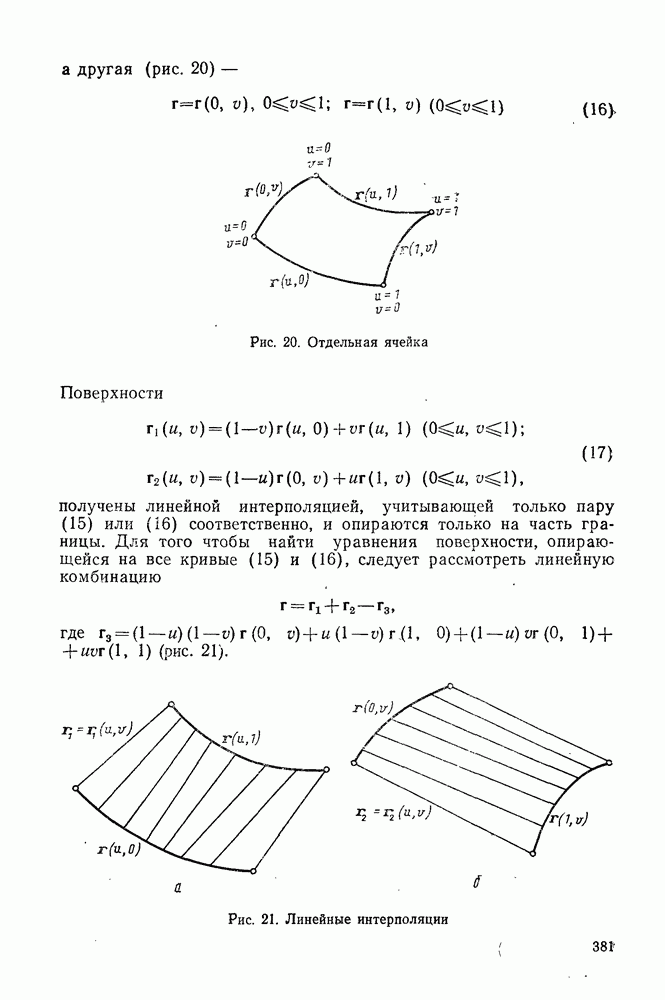
- 4°. Составные поверхности