| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
Пространство  называется пространством Минковского. В СТО это пространство рассматривается как пространство событий и представляет для физики особый интерес.
называется пространством Минковского. В СТО это пространство рассматривается как пространство событий и представляет для физики особый интерес.
Нумерация координат векторов в пространстве Минковского обычно начинается с нуля. Таким образом, согласно формуле (5), квадрат интервала  в пространстве
в пространстве  записывается так:
записывается так:

Ненулевой вектор х будем называть времениподобным, если  пространственноподобным, если
пространственноподобным, если  и изотропным, если
и изотропным, если 
Докажем следующее
УТВЕРЖДЕНИЕ. Множество концов всех времениподобных векторов, начала которых совпадают с произвольной фиксированной точкой псевдоевклидова пространства, образует конус.
Пусть  времениподобный вектор и
времениподобный вектор и  произвольное вещественное число. Если
произвольное вещественное число. Если  координаты вектора х, то
координаты вектора х, то  координаты вектора
координаты вектора  значит,
значит,

Поэтому вектор  также времениподобен:
также времениподобен:

Так как конус — это множество концов всех векторов  приведенных к общему началу
приведенных к общему началу  произвольный вектор из некоторого множества векторов пространства V), то утверждение доказано.
произвольный вектор из некоторого множества векторов пространства V), то утверждение доказано.
Совершенно аналогично устанавливается, что и множество всех концов пространственноподобных векторов с общим началом, и множество всех изотропных векторов образуют конусы.
Конус времениподобных векторов принято обозначать символом  (от англ. time - время), а конус пространственноподобных векторов — символом
(от англ. time - время), а конус пространственноподобных векторов — символом  (от англ. space - пространство).
(от англ. space - пространство).
В физике координата  отождествляется с выражением
отождествляется с выражением  где с — скорость света,
где с — скорость света,  временная переменная,
временная переменная,  называются пространственными переменными.
называются пространственными переменными.
Обратим внимание на структуру конуса  времениподобных векторов в пространстве Минковского. Этот конус распадается на две связные открытые компоненты
времениподобных векторов в пространстве Минковского. Этот конус распадается на две связные открытые компоненты  (конус будущего) и
(конус будущего) и  (конус прошлого). Конус
(конус прошлого). Конус  пространственноподобных векторов является связным множеством.
пространственноподобных векторов является связным множеством.
Остановимся на множествах  подробнее. Рассматривая вектор х как перемещение в пространстве
подробнее. Рассматривая вектор х как перемещение в пространстве  можно считать, что
можно считать, что
это перемещение характеризуется временным  и пространственным
и пространственным  перемещениями. Времениподобные векторы определяются условием
перемещениями. Времениподобные векторы определяются условием  Ясно, что в этом случае
Ясно, что в этом случае  Если при этом
Если при этом  то для перемещения х получается неравенство
то для перемещения х получается неравенство  Такое перемещение по определению принадлежит множеству
Такое перемещение по определению принадлежит множеству  и может рассматриваться как перемещение материальной частицы «в будущее». Если
и может рассматриваться как перемещение материальной частицы «в будущее». Если  то перемещение х принадлежит множеству
то перемещение х принадлежит множеству  и может рассматриваться как перемещение частицы «в прошлое» (в физике так интерпретируется движение античастиц).
и может рассматриваться как перемещение частицы «в прошлое» (в физике так интерпретируется движение античастиц).
Проведенные рассуждения объясняют наименования: конус будущего для множества  и конус прошлого для множества
и конус прошлого для множества 
Займемся теперь преобразованиями Лоренца в пространстве Минковского 
Пусть  базис, связанный с галилеевой системой координат в псевдоевклидовом пространстве з. В этом случае квадрат интервала
базис, связанный с галилеевой системой координат в псевдоевклидовом пространстве з. В этом случае квадрат интервала  имеет вид (6) и поэтому матрица
имеет вид (6) и поэтому матрица  метрического тензора пространства
метрического тензора пространства  запишется так:
запишется так:

Перейдем к новой галилеевой системе координат с базисом  и выясним условия, которым должны удовлетворять коэффициенты
и выясним условия, которым должны удовлетворять коэффициенты  матрицы В перехода от базиса
матрицы В перехода от базиса  к базису
к базису  Имеем
Имеем

Воспользуемся теперь тем обстоятельством, что матрица  метрического тензора в базисе
метрического тензора в базисе  также имеет вид (7). Так как
также имеет вид (7). Так как

то, полагая, например,  (напомним, что индексы
(напомним, что индексы  пробегают значения 0, 1, 2, 3) и обращаясь к матрице (7), приходим к соотношению
пробегают значения 0, 1, 2, 3) и обращаясь к матрице (7), приходим к соотношению

Аналогичным способом из соотношений (9) и (7) получаются еще две серии уравнений, связывающих коэффициенты  матрицы перехода от базиса
матрицы перехода от базиса  к базису
к базису 

Соотношения (10), (11) можно записать в матричной форме. Для этого наряду с матрицей  рассмотрим матрицу В, которая получается из матрицы В путем изменения знаков у элементов трех последних столбцов и последующего транспонирования. Тогда соотношения (10), (11) можно записать так:
рассмотрим матрицу В, которая получается из матрицы В путем изменения знаков у элементов трех последних столбцов и последующего транспонирования. Тогда соотношения (10), (11) можно записать так:

где  матрица (7). Полученная формула представляет собой аналог соответствующей формулы для матрицы С ортогонального преобразования евклидова пространства, записанной в ортонормированном базисе:
матрица (7). Полученная формула представляет собой аналог соответствующей формулы для матрицы С ортогонального преобразования евклидова пространства, записанной в ортонормированном базисе: 
Так как 

Обозначим через L совокупность всех общих преобразований Лоренца пространства Минковского и выделим из этих преобразований те, которые переводят каждый вектор из конуса будущего  в вектор, также принадлежащий
в вектор, также принадлежащий  Совокупность таких преобразований обычно называют преобразованиями Лоренца пространства
Совокупность таких преобразований обычно называют преобразованиями Лоренца пространства  и обозначают символом
и обозначают символом
Выделим еще два подмножества из класса общих преобразований Лоренца — так называемые собственные преобразования Лоренца  для которых
для которых  и несобственные преобразования Лоренца, для которых
и несобственные преобразования Лоренца, для которых 
Примером несобственного преобразования Лоренца является отражение относительно всех трех пространственных осей:

Пусть В — матрица произвольного несобственного преобразования,  матрица только что рассмотренного отражения. Ясно, что произведение произвольного несобственного преобразования Лоренца и отражения будет собственным преобразованием. Его матрица
матрица только что рассмотренного отражения. Ясно, что произведение произвольного несобственного преобразования Лоренца и отражения будет собственным преобразованием. Его матрица

Так как

то

Таким образом, всякое несобственное преобразование Лоренца является произведением некоторого собственного преобразования с матрицей В и отражения с матрицей 
Отметим еще один класс преобразований Лоренца

(пересечение подмножеств  и найдем те преобразования из этого класса, которые не изменяют координаты
и найдем те преобразования из этого класса, которые не изменяют координаты  Для этого достаточно описать преобразования двумерного
Для этого достаточно описать преобразования двумерного
псевдоевклидова подпространства с координатами  квадрат интервала длины в котором вычисляется по формуле
квадрат интервала длины в котором вычисляется по формуле 
Для рассматриваемого случая формулы (10), (11) запишутся так:

Полагая  найдем отсюда выражения для коэффициентов
найдем отсюда выражения для коэффициентов  матрицы В преобразования базисных векторов
матрицы В преобразования базисных векторов  в базисные векторы
в базисные векторы 

Знак в этих формулах выбирается из условия принадлежности преобразования классу 
Окончательные формулы преобразования координат имеют следующий вид:

Для выяснения физического смысла полученных формул перепишем их, полагая

Здесь, как обычно, с — скорость света в вакууме,  время, х, у, z - пространственные координаты. Итак,
время, х, у, z - пространственные координаты. Итак,

Физический смысл постоянной 
Допустим, что точка  в системе координат
в системе координат  неподвижна. Это означает, что время
неподвижна. Это означает, что время  изменяется, а пространственные координаты х, у, z неизменны. Как ведет себя точка
изменяется, а пространственные координаты х, у, z неизменны. Как ведет себя точка  относительно координатной системы
относительно координатной системы  Найдем дифференциалы соотношений (18). Так как
Найдем дифференциалы соотношений (18). Так как  то из формул (18) получим, что
то из формул (18) получим, что

Поэтому

Таким образом, всякая точка нзподвижная в системе координат  движется относительно системы координат
движется относительно системы координат  с постоянной скоростью
с постоянной скоростью  в направлении оси
в направлении оси  . С такой же скоростью движется и вся система (f, х, у, z) относительно системы (t, х, у, z).
. С такой же скоростью движется и вся система (f, х, у, z) относительно системы (t, х, у, z).
Итак,  где
где  скорость движения координатной системы
скорость движения координатной системы  . Так как скорость
. Так как скорость  любого движущегося тела меньше скорости света с, то
любого движущегося тела меньше скорости света с, то  Поэтому
Поэтому 
Заменяя в формулах  на
на  получим
получим

Формулы (19) называются формулами Лоренца. Они характеризуют переход от одной инерциальной системы координат  к другой инерциальной системе
к другой инерциальной системе  и широко используются в физике.
и широко используются в физике.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
- 2°. Простая поверхность
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
- 4°. Площадь поверхности
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
- § 5. ПОДМНОГООБРАЗИЯ
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
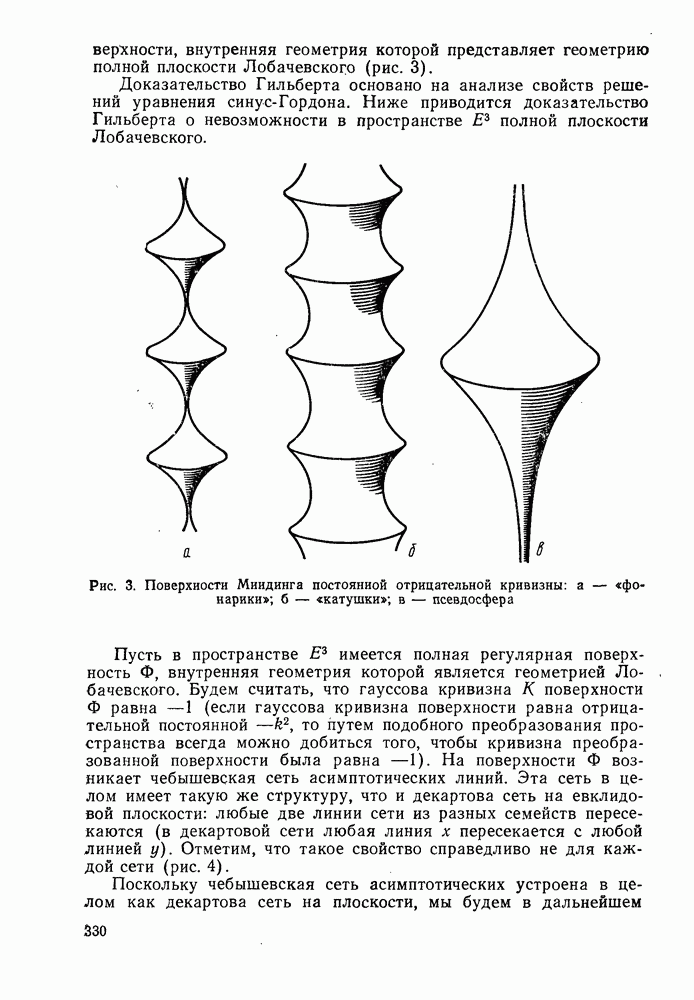
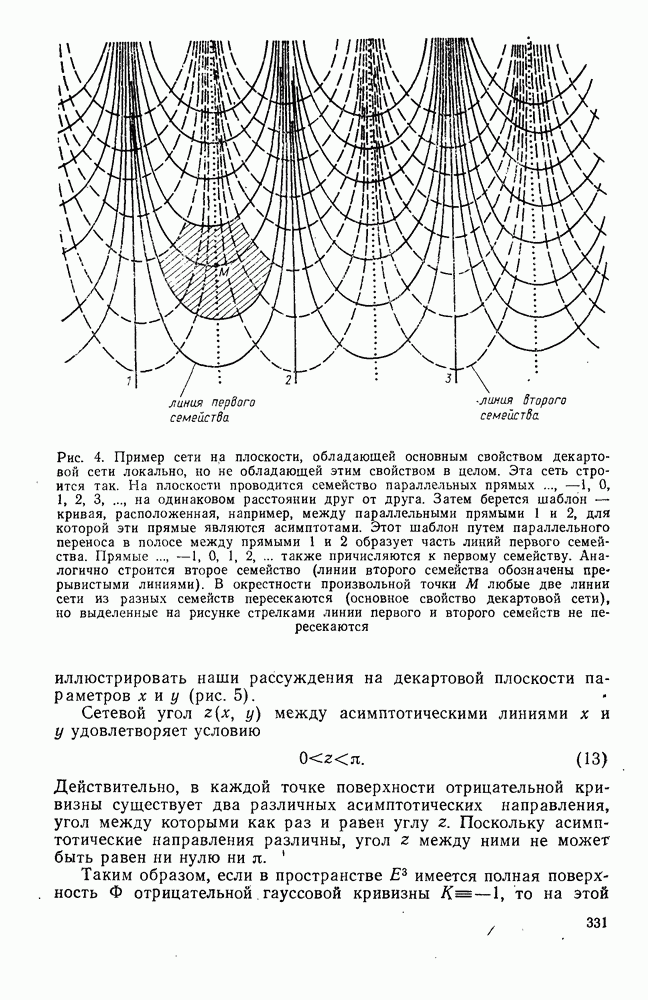
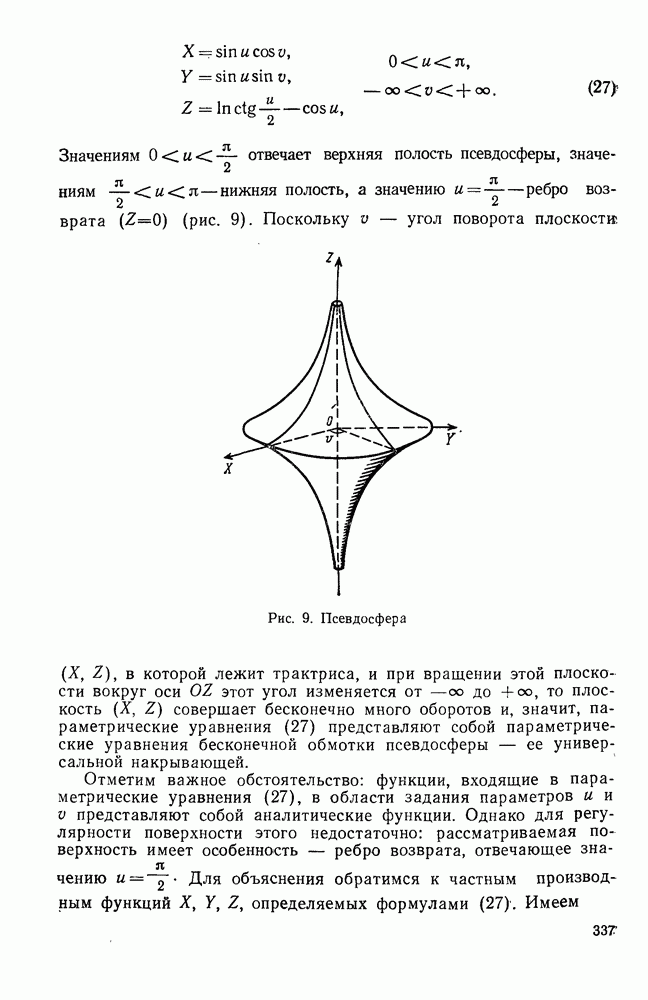
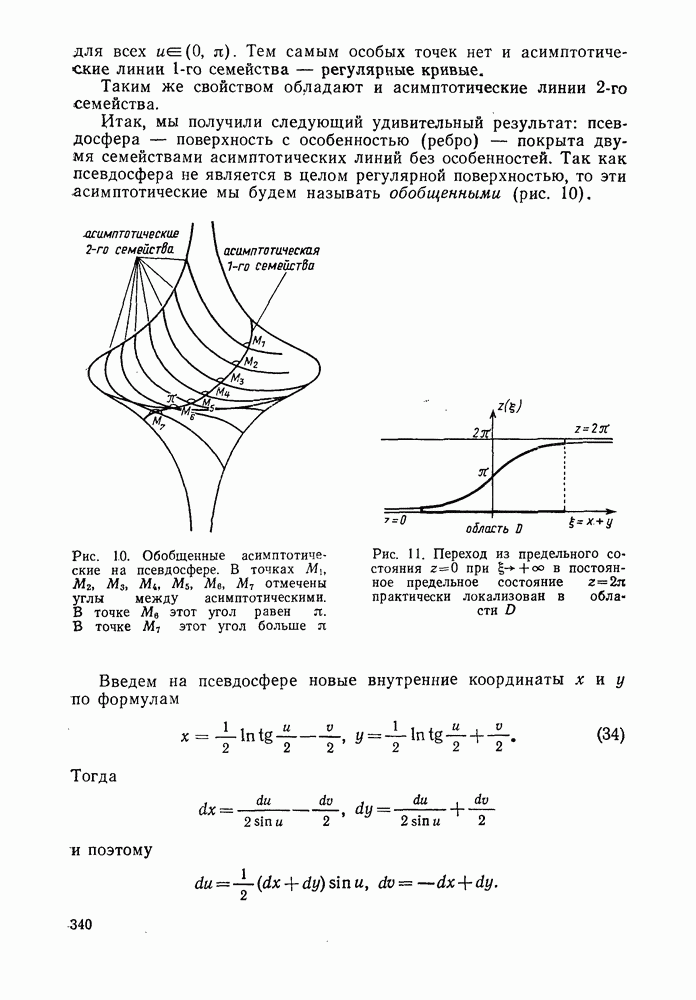
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
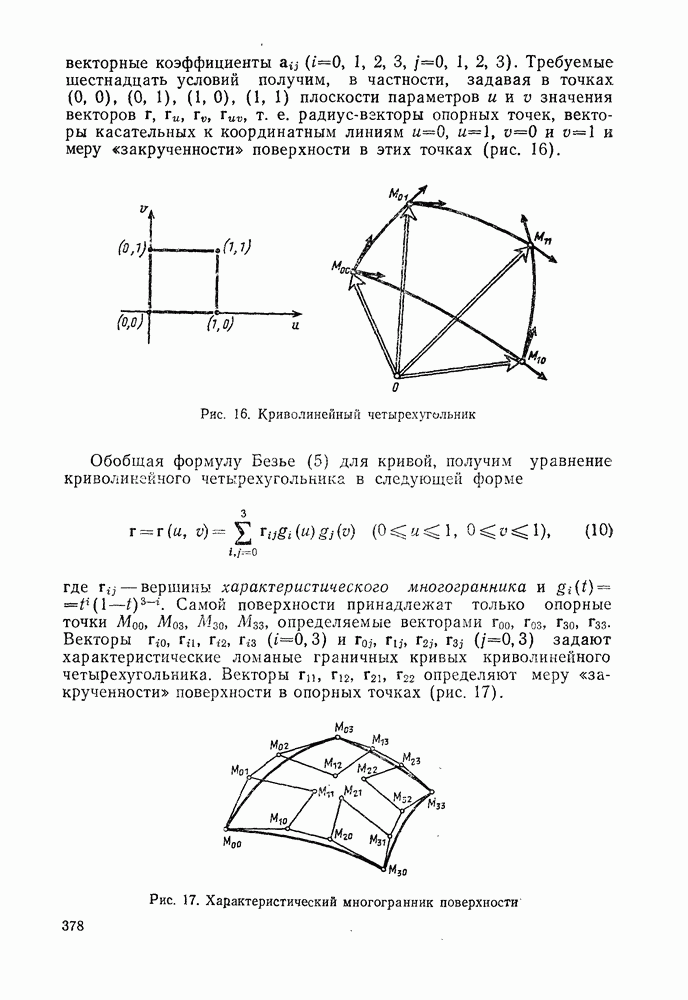
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
- 4°. Составные поверхности