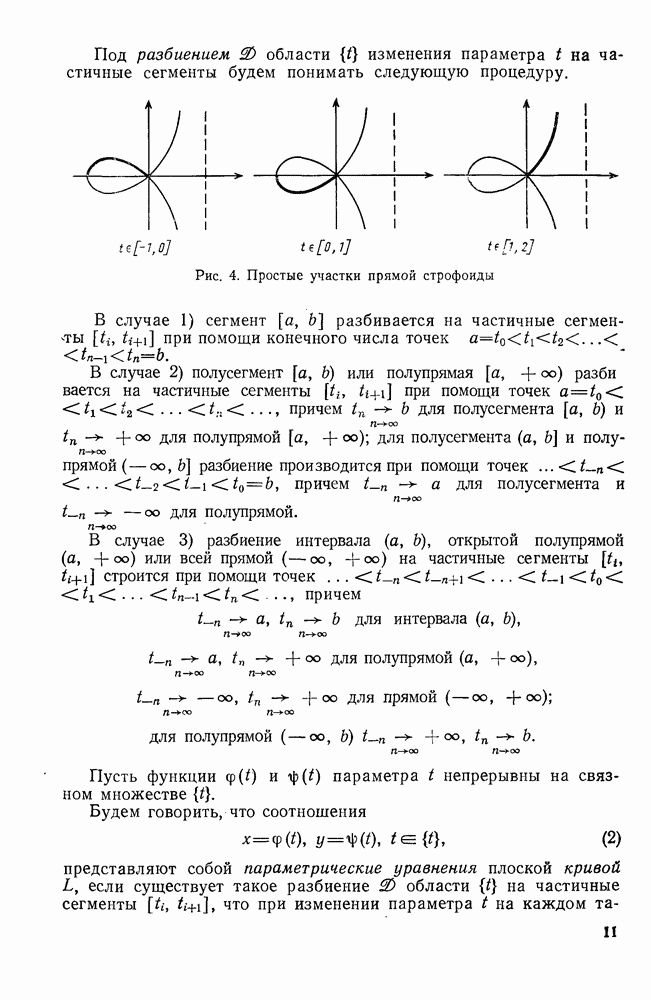
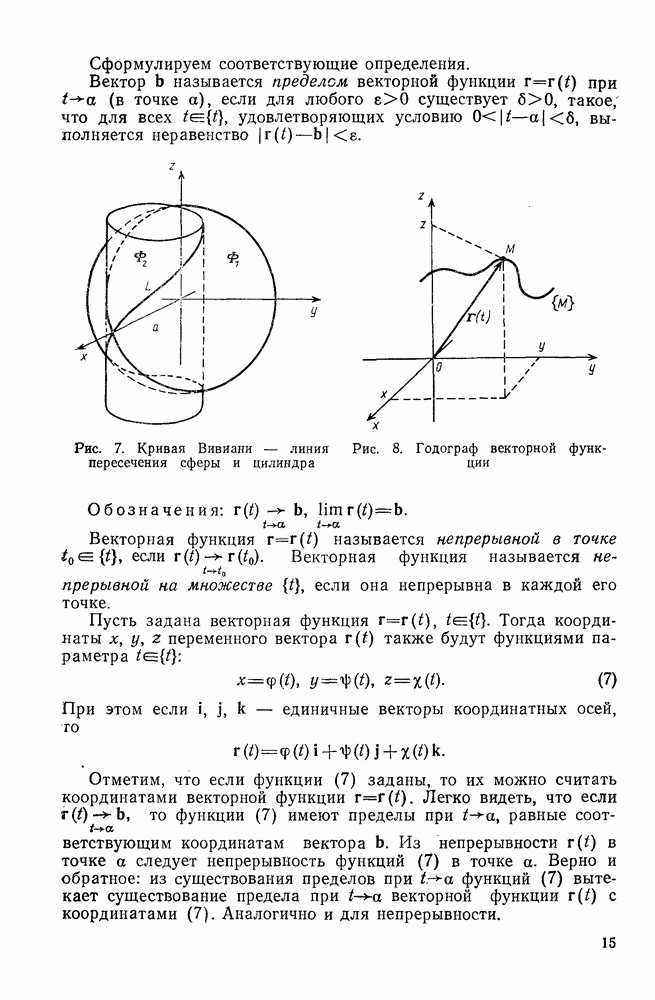
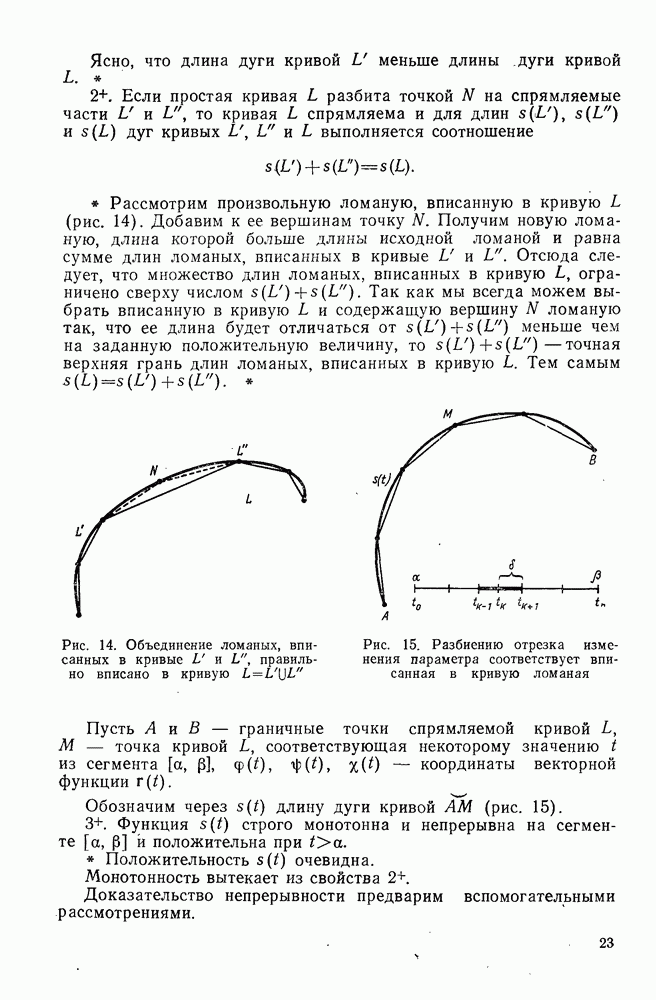
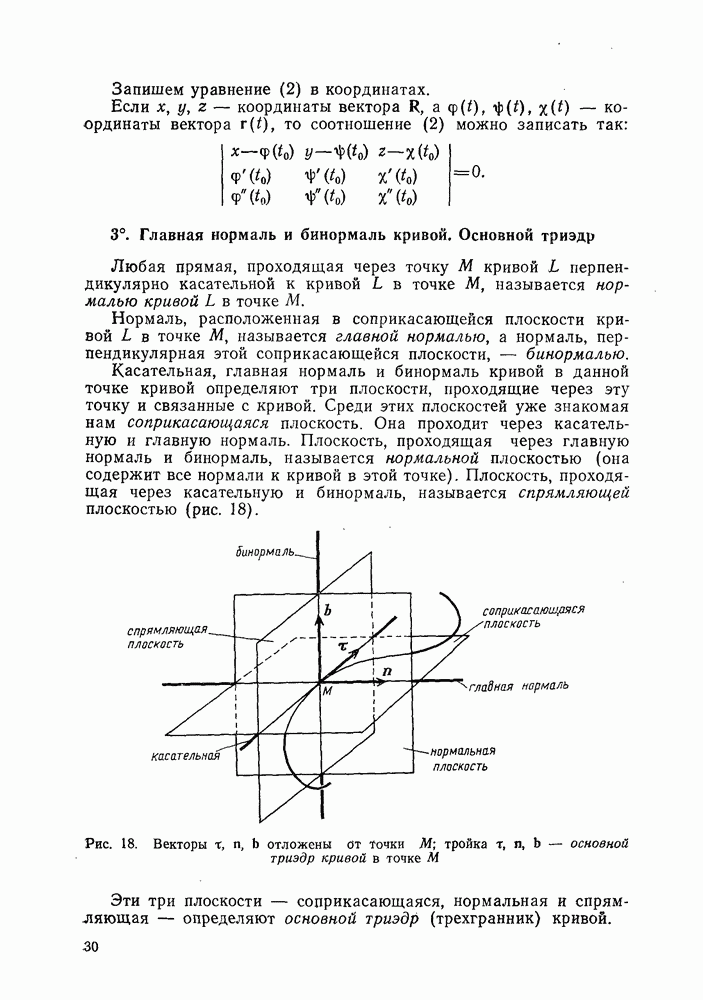
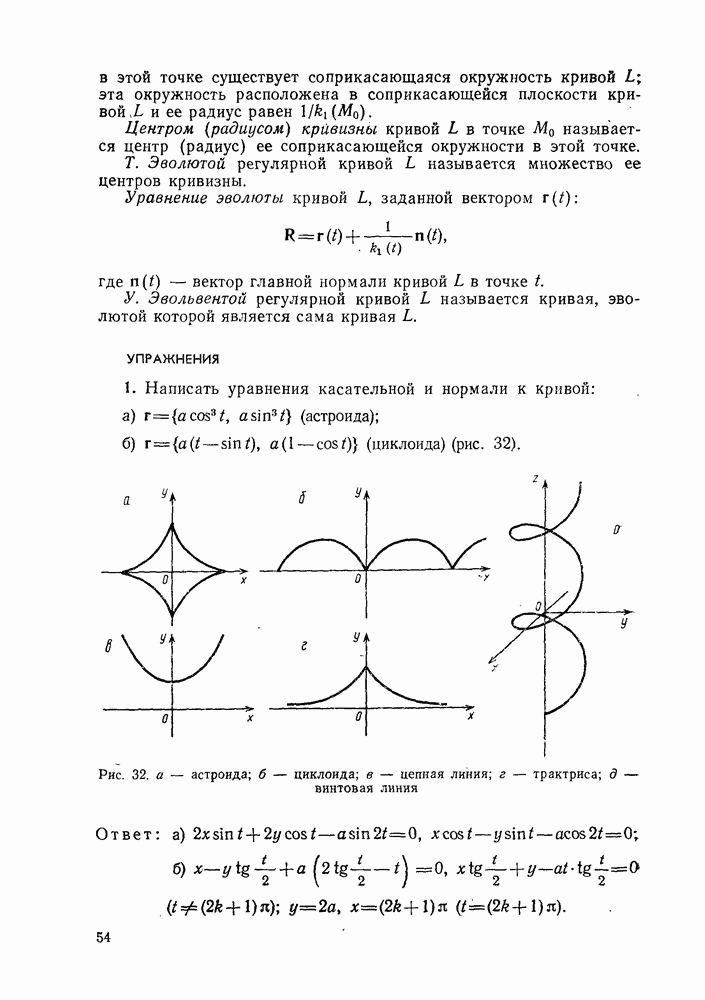
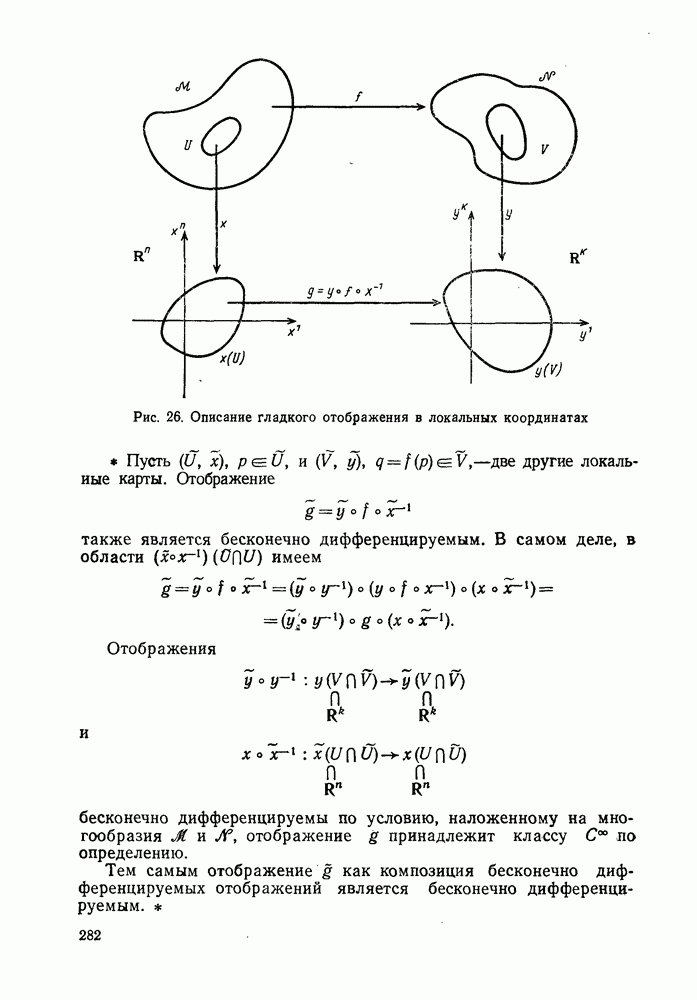
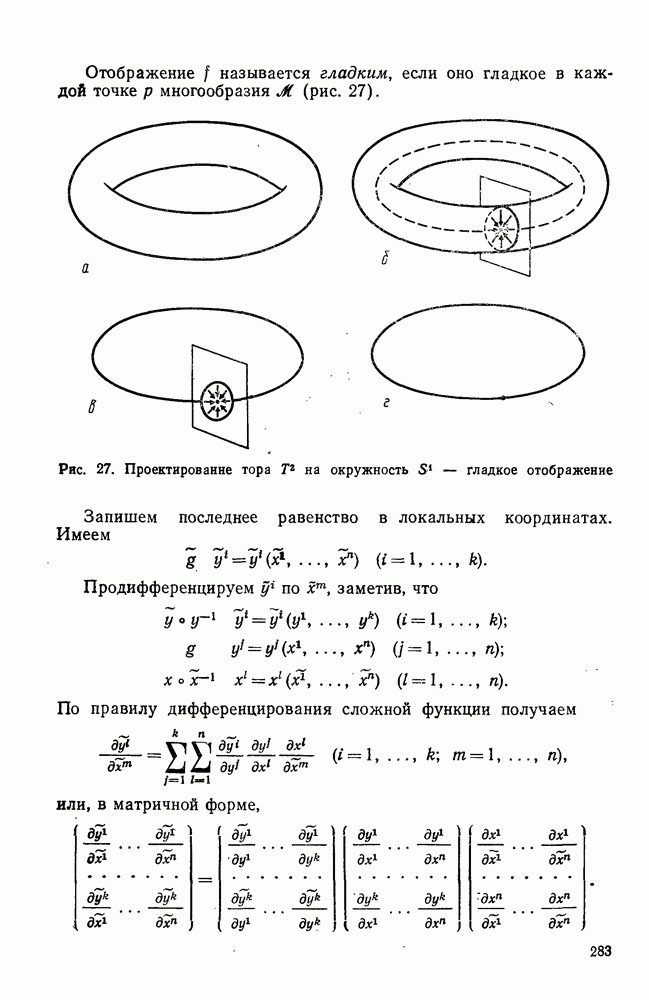
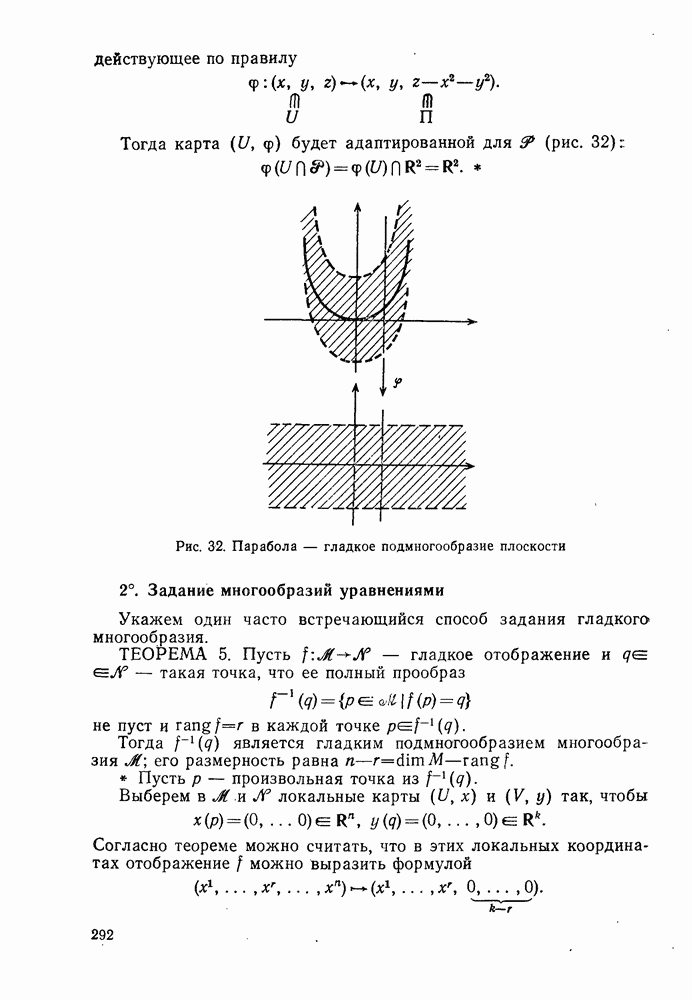
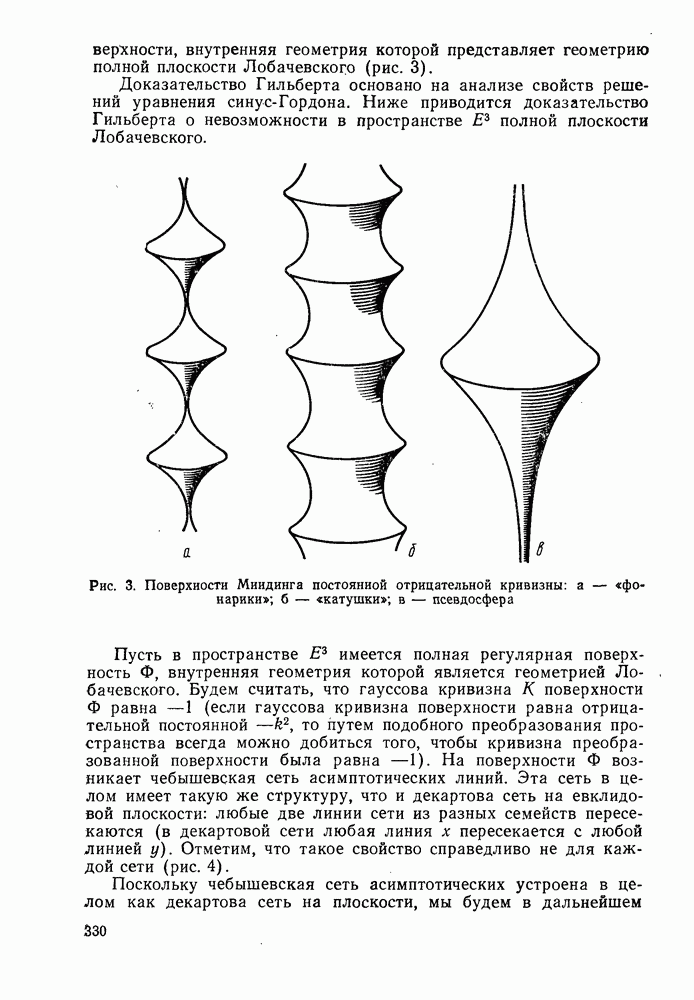
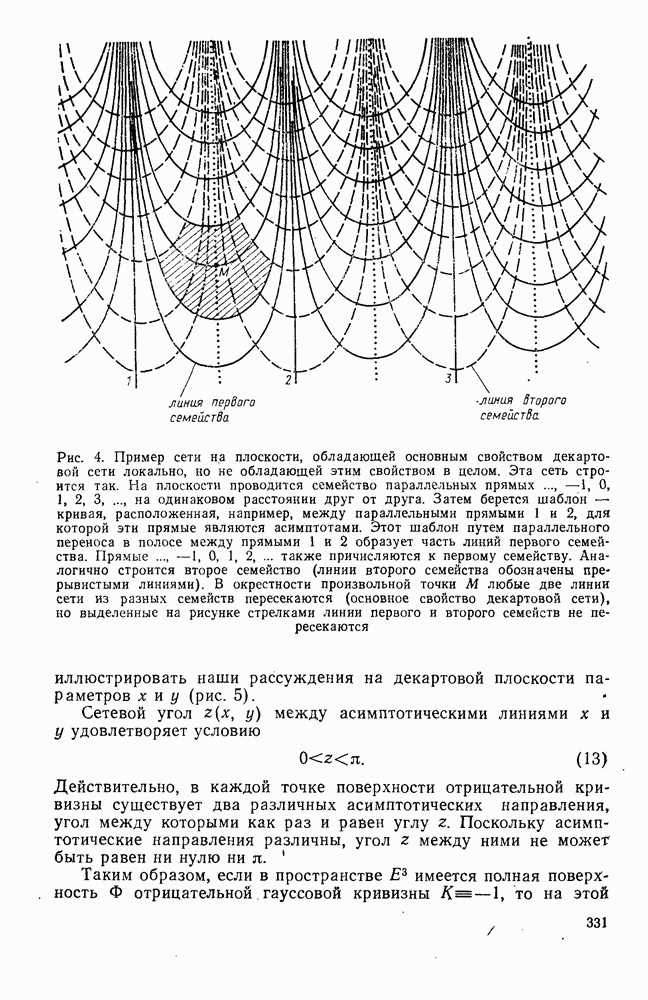
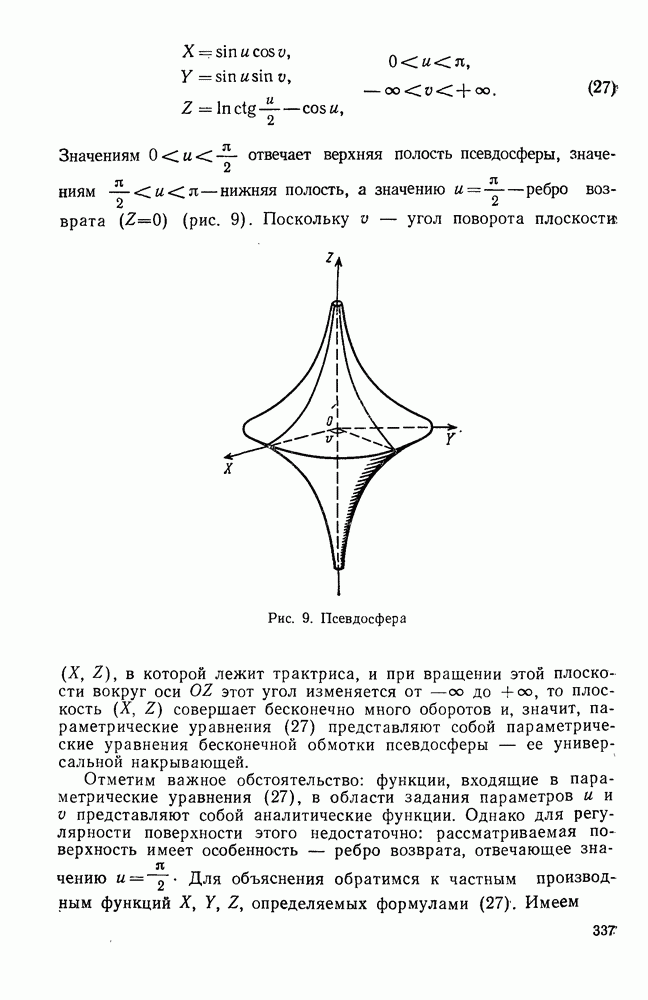
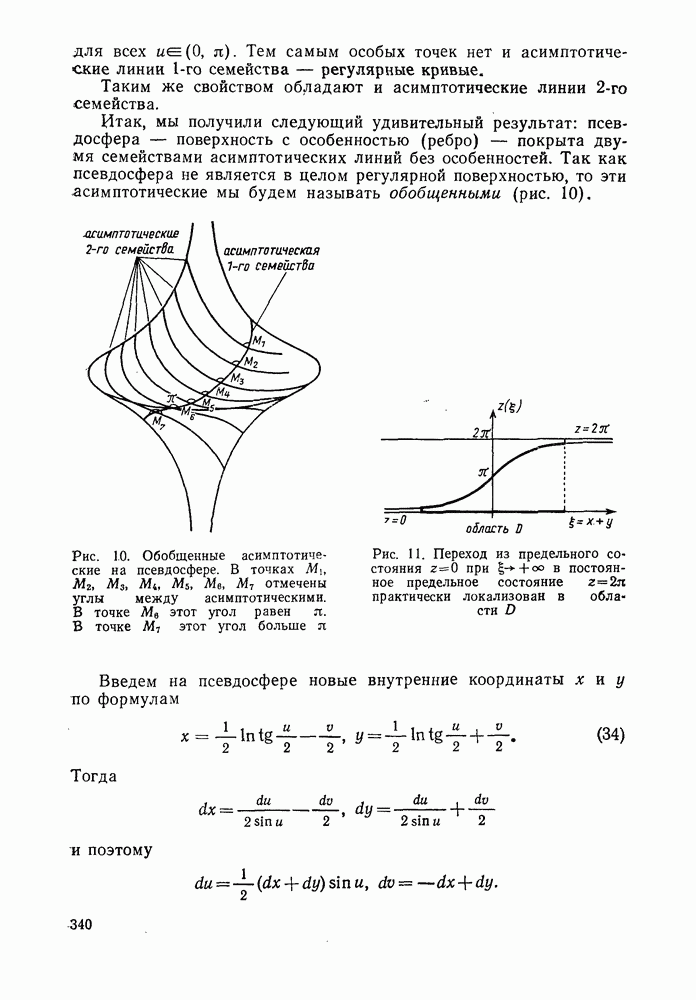
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
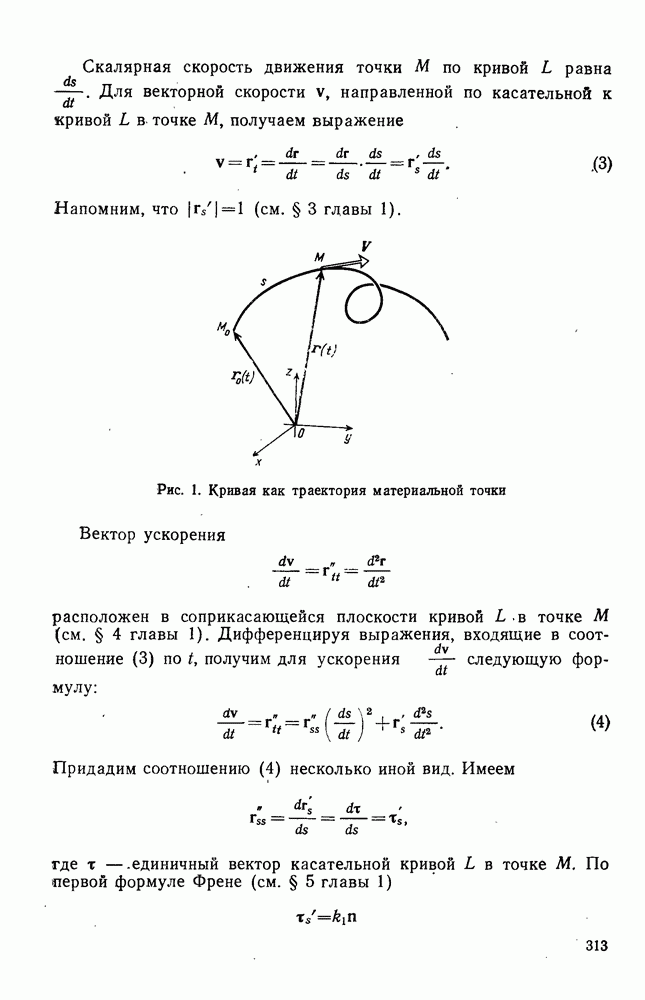
4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
В § 1 главы 4 мы уже говорили о понятии псевдориманова пространства. Напомним приведенные там рассуждения.
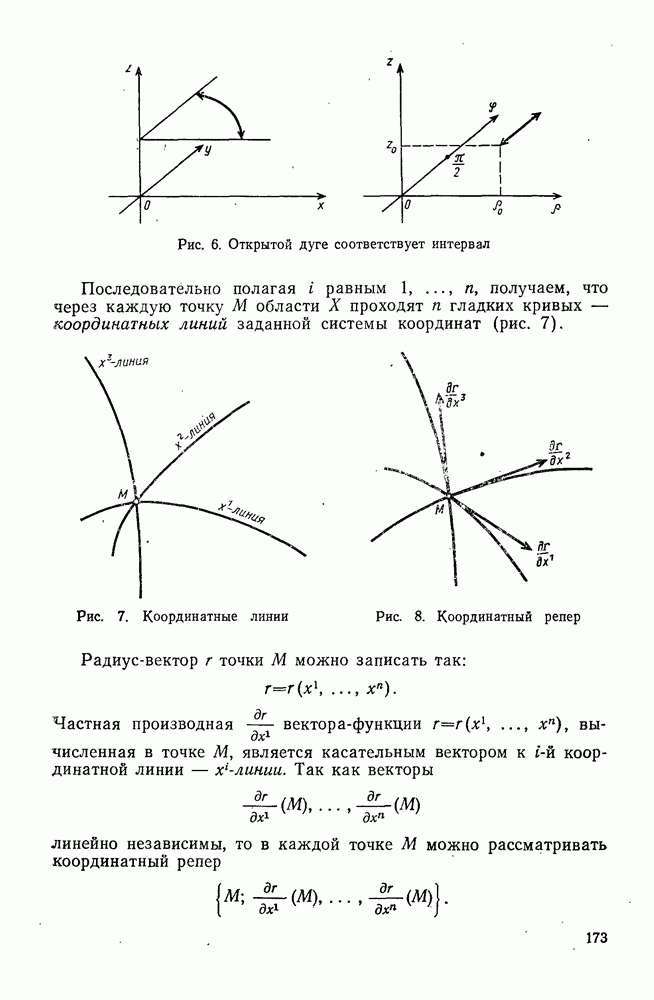
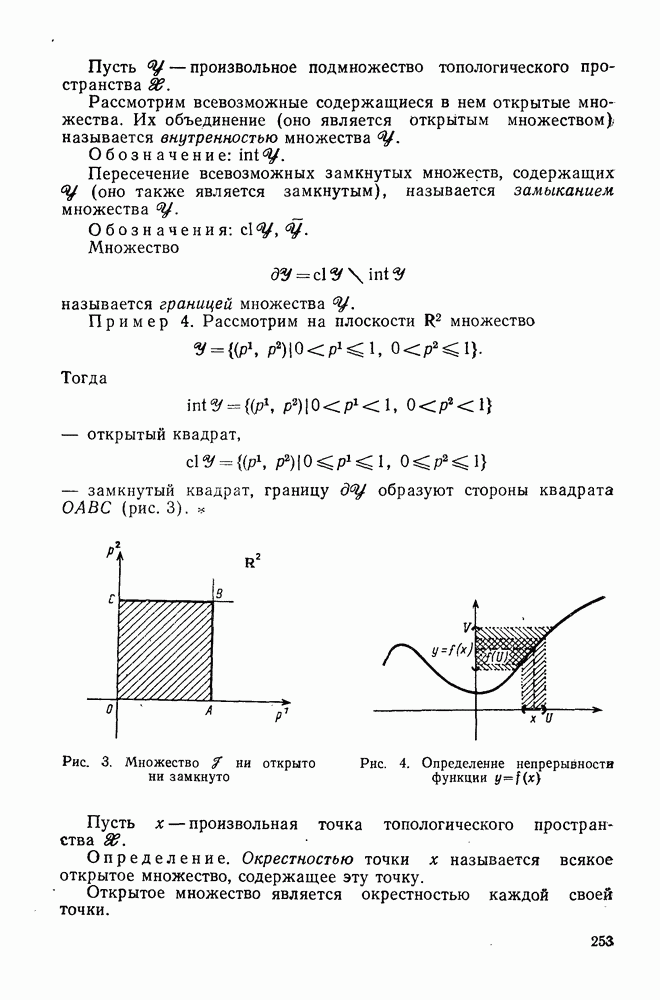
Пусть  открытое множество пространства
открытое множество пространства  На этом множестве
На этом множестве  задается поле симметричного тензора
задается поле симметричного тензора  При этом выполняются условия: квадратичная дифференциальная форма
При этом выполняются условия: квадратичная дифференциальная форма

в каждой точке множества 
1) невырождена;
2) имеет постоянную сигнатуру, т. е. нормальный вид квадратичной формы (20) не зависит от выбора точки из множества 
При помощи формы (20) введем на множестве  метрику, положив
метрику, положив

Выражение (21) для  называют линейным элементом, а тензор
называют линейным элементом, а тензор  метрическим тензором.
метрическим тензором.
Если форма (21) является положительно определенной, то говорят, что на множестве  введена риманова метрика; множество
введена риманова метрика; множество  в этом случае называется римановым пространством. Если же форма (21) является знакопеременной, то говорят, Что
в этом случае называется римановым пространством. Если же форма (21) является знакопеременной, то говорят, Что
на множестве  введена псевдориманова метрика и множества
введена псевдориманова метрика и множества  в этом случае называют псевдоримановым пространством.
в этом случае называют псевдоримановым пространством.
Римановы пространства рассматривались в главе 4. Там был построен аппарат для их изучения, были введены важные объекты и понятия. В этом пункте мы укажем, каким образом можно исследовать псевдоримановы пространства.
Исследование псевдоримановых пространств важно, в частно  потому, что они широко используются в общей теории относительности. Мы будем вести изложение по аналогии с построением теории римановых пространств.
потому, что они широко используются в общей теории относительности. Мы будем вести изложение по аналогии с построением теории римановых пространств.
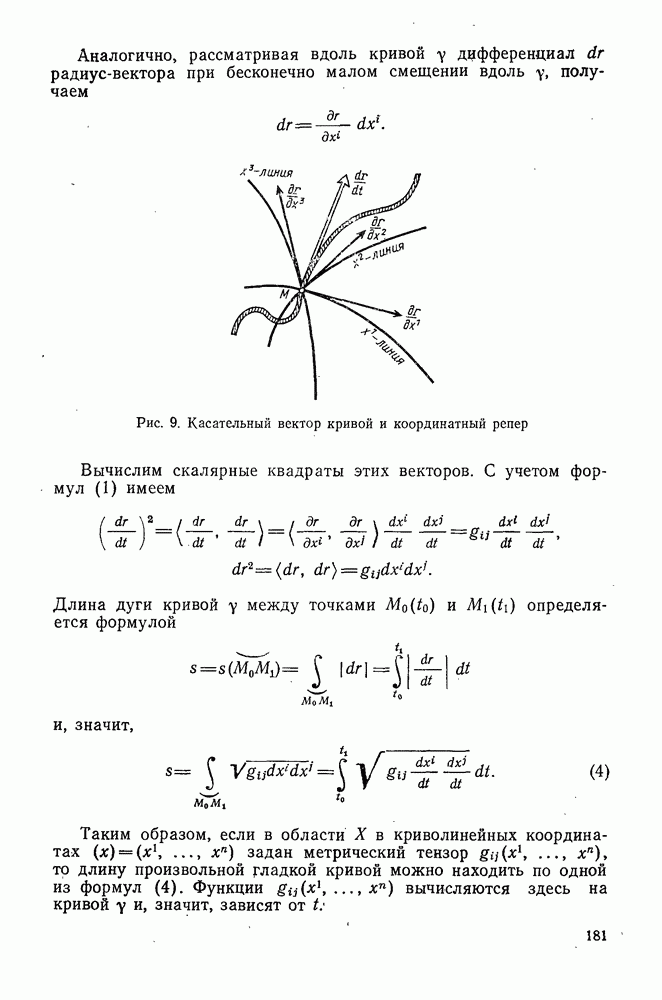
1. Касательное пространство. Разложим каждую компоненту метрического тензора  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  (здесь
(здесь  псевдориманово пространство: индекс
псевдориманово пространство: индекс  указывает его размерность, индексы
указывает его размерность, индексы  соответственно число положительных квадратов и число отрицательных квадратов в нормальном виде квадратичной формы
соответственно число положительных квадратов и число отрицательных квадратов в нормальном виде квадратичной формы  Имеем
Имеем

где 
Псевдоевклидово пространство  с линейным элементом
с линейным элементом

называется касательным псевдоевклидовым пространством в точке  псевдориманова пространства
псевдориманова пространства 
Формулы (21) — (23) позволяют записать линейный элемент  пространства
пространства  в следующем виде:
в следующем виде:

Из формулы (24) видно, что метрика  псевдориманова пространства
псевдориманова пространства  в окрестности точки
в окрестности точки  и метрика
и метрика  касательного псевдоевклидова пространства
касательного псевдоевклидова пространства  в окрестности этой же точки разнятся на малые первого порядка относительно
в окрестности этой же точки разнятся на малые первого порядка относительно 
Замечание. То, что линейный элемент (23) представляет собой метрику псевдоевклидова пространства  непосредственно вытекает из определения псевдрориманова пространства.
непосредственно вытекает из определения псевдрориманова пространства.
2. Преобразование координат в псевдоримановом и касательном псевдоевклидовом пространствах. Пусть точка  имеет нулевые координаты. Тогда линейный элемент
имеет нулевые координаты. Тогда линейный элемент  касательного пространства
касательного пространства  имеет следующий вид:
имеет следующий вид:

Некоторая окрестность точки  псевдориманова пространства
псевдориманова пространства  отображается взаимно однозначно на некоторую окрестность этой же точки касательного псевдоевклидова пространства
отображается взаимно однозначно на некоторую окрестность этой же точки касательного псевдоевклидова пространства  по правилу: точке
по правилу: точке  ставится в соответствие точка касательного пространства
ставится в соответствие точка касательного пространства  с координатами
с координатами 
Перейдем к новым координатам 

При этом преобразование координат произойдет и в касательном пространстве. Отметим, что в результате между окрестностью точки  в пространстве
в пространстве  и окрестностью этой же точки в пространстве
и окрестностью этой же точки в пространстве  устанавливается другое взаимно однозначное соответствие.
устанавливается другое взаимно однозначное соответствие.
Как преобразуются метрические тензоры пространств  Имеем
Имеем

Положим

Считая, что преобразование (26) переводит точку  в себя, т. е. что
в себя, т. е. что

формулу (27) можно записать в следующем виде:

или, короче,

При преобразовании координат (26) в касательном пространстве Епрл происходит линейное преобразование координат с матрицей 

Матрица не вырождена, так как

Правые части формул (29) — преобразований координат касательного пространства  представляют собой линейные члены в разложениях функций
представляют собой линейные члены в разложениях функций 

по формуле Тейлора:

3. Локально нормальные координаты в псевдоримановом пространстве
Определение. Координаты  в псевдоримановом пространстве называются нормальными в точке
в псевдоримановом пространстве называются нормальными в точке  , или локально нормальными, если
, или локально нормальными, если

и

Справедливо следующее утверждение:
В окрестности каждой точки псевдориманова пространства можно ввести координаты, нормальные в этой точке.
Доказательство сформулированного утверждения проводится в полной аналогии с доказательством теоремы о возможности введения в окрестности каждой точки риманова пространства координат, нормальных в этой точке (см. пункт 3° § 2 главы 4). Остановимся поэтому только на оснозных этапах доказательства.
Сначала обосновывается, что невырожденным линейным преобразованием координат вида (29) можно добиться того, что в точке  будут выполняться соотношения (30). Далее указывается такое преобразование координат, при котором сохраняются соотношения (30) и обеспечивается выполнение условий (31).
будут выполняться соотношения (30). Далее указывается такое преобразование координат, при котором сохраняются соотношения (30) и обеспечивается выполнение условий (31).
Отметим, что при завершении доказательства нужно воспользоваться формулами главы 3, приспособив их для рассматриваемого здесь случая.
Детали рассуждений оставляем читателю.
4. О тензоре кривизны (тензоре Римана-Кристоффеля) для псевдориманова пространства
Как было установлено выше, в окрестности данной точки  псевдориманова пространства
псевдориманова пространства  можно выбрать локально нормальные координаты так, что разложение метрического тензора по формуле Тейлора с центром в точке
можно выбрать локально нормальные координаты так, что разложение метрического тензора по формуле Тейлора с центром в точке  имеет вид
имеет вид

где

Напомним, что в случае риманова пространства было получено похожее выражение для компонент метрического тензора

и, главное, детально выяснена структура слагаемых 
Опуская подробности рассуждений (они вполне аналогичны тем, что былд проведены в § 2 главы 4), запишем окончательные выражения для компонент метрического тензора  пространства
пространства  в некоторой системе координат, нормальной в данной точке
в некоторой системе координат, нормальной в данной точке 

(здесь  координаты тензора Римана-Кристоффеля для данной точки
координаты тензора Римана-Кристоффеля для данной точки  и в указанной системе координат
и в указанной системе координат 
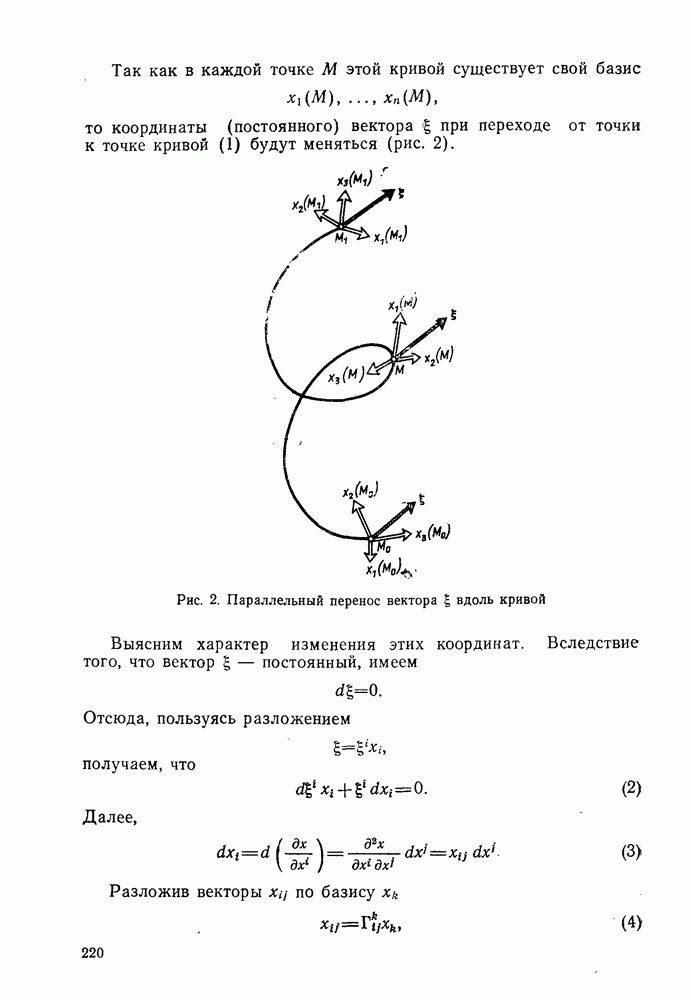
5. Параллельный перенос векторов в псевдоевклидовом пространстве
Пусть  -криволинейные координаты в псевдоевклидовом пространстве
-криволинейные координаты в псевдоевклидовом пространстве  Обозначим через х радиус-вектор точки
Обозначим через х радиус-вектор точки  с началом О. Векторы
с началом О. Векторы

образуют базис пространства  в точке
в точке 
Пусть постоянный вектор  переносится в пространстве
переносится в пространстве  параллельно (параллельный перенос в линейном пространстве
параллельно (параллельный перенос в линейном пространстве  снабженном вполне определенной метрикой, определяется обычно) по кривой
снабженном вполне определенной метрикой, определяется обычно) по кривой 

в каждой точке  кривой (34) есть базис
кривой (34) есть базис

Поэтому координаты (постоянного) вектора  будут меняться. В каждой точке кривой имеем
будут меняться. В каждой точке кривой имеем

Разлагая вектор  по базису
по базису 

с учетом формул (35) получим

Используя эти соотношения и одну из формул (35), найдем

Отсюда в силу линейной независимости векторов  имеем
имеем

Величины  входящие в формулу (36), уже знакомы нам. Это символы Кристоффеля 2-го рода (см. формулу (1) § 8 главы 3). Их называют также коэффициентами связности —
входящие в формулу (36), уже знакомы нам. Это символы Кристоффеля 2-го рода (см. формулу (1) § 8 главы 3). Их называют также коэффициентами связности —  связывают координаты
связывают координаты  вектора
вектора  в точке
в точке  с координатами
с координатами  этого вектора в близкой точке
этого вектора в близкой точке 
Соотношения (36) представляют собой систему обыкновенных дифференциальных уравнений, неизвестными в которых являются координаты  вектора
вектора  параллельно переносимого вдоль кривой (34). Интегрируя эту систему, получим координаты
параллельно переносимого вдоль кривой (34). Интегрируя эту систему, получим координаты  вектора
вектора  в произвольной точке
в произвольной точке  кривой (34) в базисе
кривой (34) в базисе 
Соотношения (36) называются уравнениями параллельного переноса вектора.
6. Векторы в псевдоримановом пространстве
Векторы в псевдоримановом пространстве вводятся в полной аналогии с введением векторов в римановом пространстве.
Пусть  псевдориманово пространство с метрическим тензором
псевдориманово пространство с метрическим тензором  некоторая его точка,
некоторая его точка,  касательное псевдоевклидово пространство в точке
касательное псевдоевклидово пространство в точке  с метрическим тензором
с метрическим тензором 
Пусть  базис в пространстве
базис в пространстве  связанный с координатами
связанный с координатами  Тогда по заданным в точке
Тогда по заданным в точке  числам
числам  определяется вектор
определяется вектор

в пространстве  Вектор
Вектор  мы будем называть вектором в псевдоримановом пространстве
мы будем называть вектором в псевдоримановом пространстве  в данной точке
в данной точке 
Перейдем в пространстве  к новым координатам
к новым координатам

Тогда базисные векторы  пространства
пространства  преобразуются по формулам
преобразуются по формулам

где  . Ясно, что
. Ясно, что

где 
Сравнивая выражения

и

получим формулы преобразования координат и вектора

Аналогично получаются и формулы

При помощи формул (39), (40) можно дать такое определение вектора в псевдоримановом пространстве:
вектором  в точке
в точке  псевдориманова пространства
псевдориманова пространства  называется упорядоченный набор
называется упорядоченный набор  чисел
чисел  координат вектора
координат вектора  преобразующийся при переходе от координатной системы
преобразующийся при переходе от координатной системы  к координатной системе
к координатной системе  по формулам (39), (40) в которых
по формулам (39), (40) в которых

7. Параллельный перенос векторов в псевдоримановом пространстве
Пусть точки  пространства
пространства  соединены кривой
соединены кривой  :
:

Пусть  вектор в точке
вектор в точке  пространства
пространства 
Уравнения

называются уравнениями параллельного переноса вектора  в псевдоримановом пространстве
в псевдоримановом пространстве 
Система (42) представляет собой систему обыкновенных дифференциальных уравнений, в которых неизвестными являются координаты  вектора параллельно переносимого вдоль
вектора параллельно переносимого вдоль
кривой (41), а символы Кристоффеля  вычисляются в точках этой кривой.
вычисляются в точках этой кривой.
8. Параллельный перенос тензоров
Дословно повторяя рассуждения пункта 4° § 3 главы 4, можно получить уравнения параллельного переноса тензоров в псевдоримановом пространстве.
Будем говорить, что тензор  переносится параллельно вдоль кривой L пространства
переносится параллельно вдоль кривой L пространства  если в каждой точке
если в каждой точке  кривой L его компоненты сохраняют постоянные значения относительно параллельно переносимого вдоль этой кривой базиса.
кривой L его компоненты сохраняют постоянные значения относительно параллельно переносимого вдоль этой кривой базиса.
Запишем общую формулу параллельного переноса тензора 

9. Абсолютный дифференциал и абсолютная производная Абсолютным (ковариантным) дифференциалом тензора  называется главная линейная часть приращения тензора
называется главная линейная часть приращения тензора  параллельно перенесенного в точку
параллельно перенесенного в точку  и тензора
и тензора  взятого в этой точке.
взятого в этой точке.
Например, для тензора типа формула для абсолютно  дифференциала имеет следующий вид:
дифференциала имеет следующий вид:

Мы не выписываем формулу для общего случая, отсылая читателя к пункту 5° § 3 главы 4. Там же читатель найдет формулы для вычисления абсолютной (ковариантной) производной тензора.
Отметим в заключение, что абсолютный дифференциал метрического тензора  псевдориманова пространства
псевдориманова пространства  равен нулю. Тем самым метрический тензор пространства
равен нулю. Тем самым метрический тензор пространства  образует в нем поле параллельных тензоров.
образует в нем поле параллельных тензоров.
10. Геодезические линии в псевдоримановом пространстве Геодезические линии в римановом пространстве были введены нами двумя способами — как линии постоянного направления и как экстремали функционала длины (кривые минимальной длины, соединяющие две заданные точки).
В случае псевдориманова пространства ввести геодезические как экстремали не представляется возможным. Для пояснения обратимся к частному случаю — псевдоевклидовой плоскости  Линейный элемент
Линейный элемент  плоскости
плоскости  задается формулой
задается формулой

Обратимся к координатной плоскости  считая, что на ней введена метрика (43). Тогда отрезки прямых, параллельных
считая, что на ней введена метрика (43). Тогда отрезки прямых, параллельных
биссектрисам координатных углов, имеют нулевую длину и поэтому любые две точки  этой плоскости можно соединить ломаной нулевой длины. Этот пример показывает, что вариационный подход к проблеме геодезических в случае псевдориманова пространства неосуществим (рис. 13).
этой плоскости можно соединить ломаной нулевой длины. Этот пример показывает, что вариационный подход к проблеме геодезических в случае псевдориманова пространства неосуществим (рис. 13).

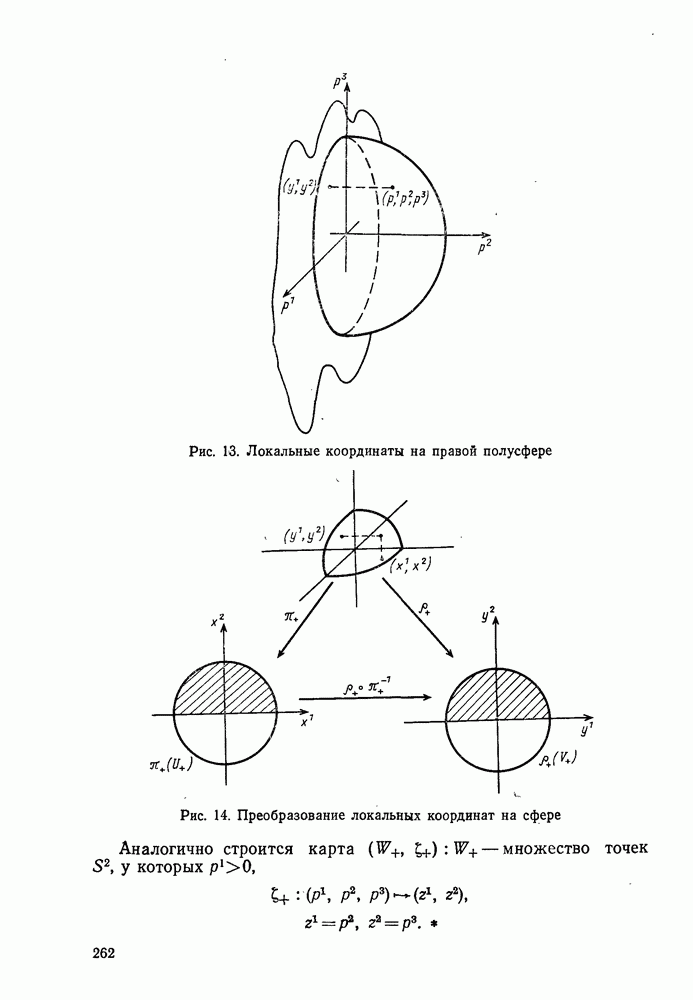
Рис. 13. Псевдоевклидова плоскость  с метрикой
с метрикой  Через каждую точку
Через каждую точку  проходят две прямые, параллельные биссектрисам координатных углов. Расстояние между любыми точками
проходят две прямые, параллельные биссектрисам координатных углов. Расстояние между любыми точками  на каждой из этих прямых равно нулю. Произвольно взятые точки
на каждой из этих прямых равно нулю. Произвольно взятые точки  можно соединить ломаной
можно соединить ломаной  длина которой равна нулю, — звенья этой ломаной параллельны биссектрисам координатных углов и имеют длины, равные нулю
длина которой равна нулю, — звенья этой ломаной параллельны биссектрисам координатных углов и имеют длины, равные нулю
Однако первый путь — введение геодезических как линий постоянного направления — дает нужный результат. При этом уравнения геодезических будут такими же, как и в случае римановз пространства.
Кривая L в псевдоримановом пространстве  называется геодезической линией, если любой вектор касательной к кривой L в какой-либо ее точке при параллельном переносе вдоль L остается вектором касательной этой кривой. Тем самым геодезическая линия — это линия постоянного направления.
называется геодезической линией, если любой вектор касательной к кривой L в какой-либо ее точке при параллельном переносе вдоль L остается вектором касательной этой кривой. Тем самым геодезическая линия — это линия постоянного направления.
Пусть  геодезическая в пространстве
геодезическая в пространстве  заданная параметрическими уравнениями
заданная параметрическими уравнениями

 вектор касательной к кривой L в точке
вектор касательной к кривой L в точке  Перенесем этот вектор параллельно вдоль кривой L в точку
Перенесем этот вектор параллельно вдоль кривой L в точку  отвечающую значению параметра
отвечающую значению параметра  из промежутка
из промежутка  и получим в точке
и получим в точке  вектор касательной
вектор касательной  Так как также вектор касательной к L в точке
Так как также вектор касательной к L в точке  и все векторы касательной к кривой L в точке М коллинеарны, то
и все векторы касательной к кривой L в точке М коллинеарны, то

Возникает естественный вопрос: нельзя ли выбрать на геодезической L новый параметр  так, чтобы вектор
так, чтобы вектор  в каждой ее точке получался параллельным переносом вектора
в каждой ее точке получался параллельным переносом вектора 
Покажем, что это возможно.
Параметр  введем при помощи соотношения
введем при помощи соотношения

т. е.

Отсюда и из формулы (44) получаем, что

Но  - вектор касательной к геодезической
- вектор касательной к геодезической  полученный параллельным переносом вдоль нее вектора Поэтому последнее равенство означает, что вектор касательной
полученный параллельным переносом вдоль нее вектора Поэтому последнее равенство означает, что вектор касательной  получается параллельным переносом вдоль геодезической L какого-то вектора касательной
получается параллельным переносом вдоль геодезической L какого-то вектора касательной 
Параметр  для которого векторы касательных - образуют вдоль геодезической поле параллельных векторов, называется каноническим. Ясно, что если
для которого векторы касательных - образуют вдоль геодезической поле параллельных векторов, называется каноническим. Ясно, что если  канонический параметр, то и
канонический параметр, то и  и В — постоянные числа) также является каноническим параметром.
и В — постоянные числа) также является каноническим параметром.
Итак, если геодезическая существует, то на ней можно выбрать в качестве параметра канонический параметр.
Справедливо следующее утверждение:
из каждой точки псевдориманова пространства по заданному в этой точке направлению исходит единственная геодезическая линия.
Пусть  параметрические уравнения геодезической и
параметрические уравнения геодезической и  каноническии параметр. Тогда вектор - вдоль искомой геодезической
каноническии параметр. Тогда вектор - вдоль искомой геодезической  неизвестные функции) переносится параллельно и, значит,
неизвестные функции) переносится параллельно и, значит,

Запишем последние соотношения в эквивалентной форме, поделив обе части на 

Соотношения (45) представляют собой систему обыкновенных дифференциальных уравнений, заданных в некоторой области изменения переменных  координат в пространстве
координат в пространстве  В этой области задан метрический тензор
В этой области задан метрический тензор  следовательно,
следовательно,  известные функции.
известные функции.
Соотношения (45) называются дифференциальными уравнениями геодезических.
По условию заданы точка  и направление b в этой точке. Пусть
и направление b в этой точке. Пусть  координаты точки
координаты точки  а
а  координаты вектора
координаты вектора 

Из теории обыкновенных дифференциальных уравнений известно, что система (45) при начальных данных (46) имеет единственное решение 
Итак, в псевдоримановом пространстве  определяется единственная геодезическая, исходящая из точки
определяется единственная геодезическая, исходящая из точки  в заданном направлении
в заданном направлении 
На этом мы завершаем изложение некоторых фактов теории псевдоримановых пространств. Они во многом похожи на римановы пространства. Но есть и существенные различия. Кое-где мы подчеркивали их. Главное отличие связано с измерением длин — в псевдоримановых пространствах имеются реальные кривые нулевой длины.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
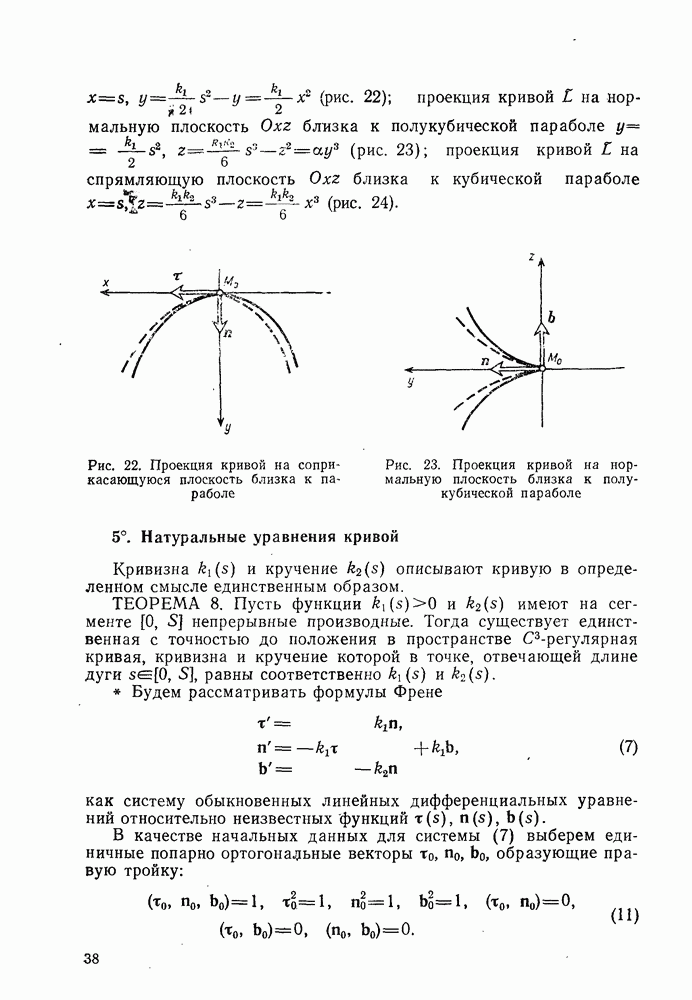
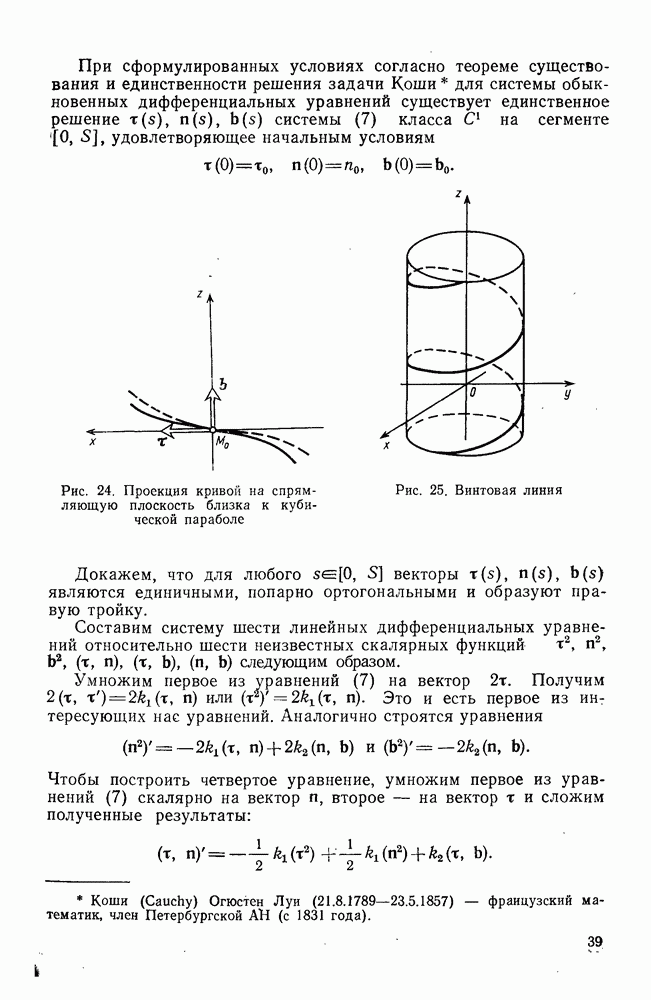
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
- 2°. Простая поверхность
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
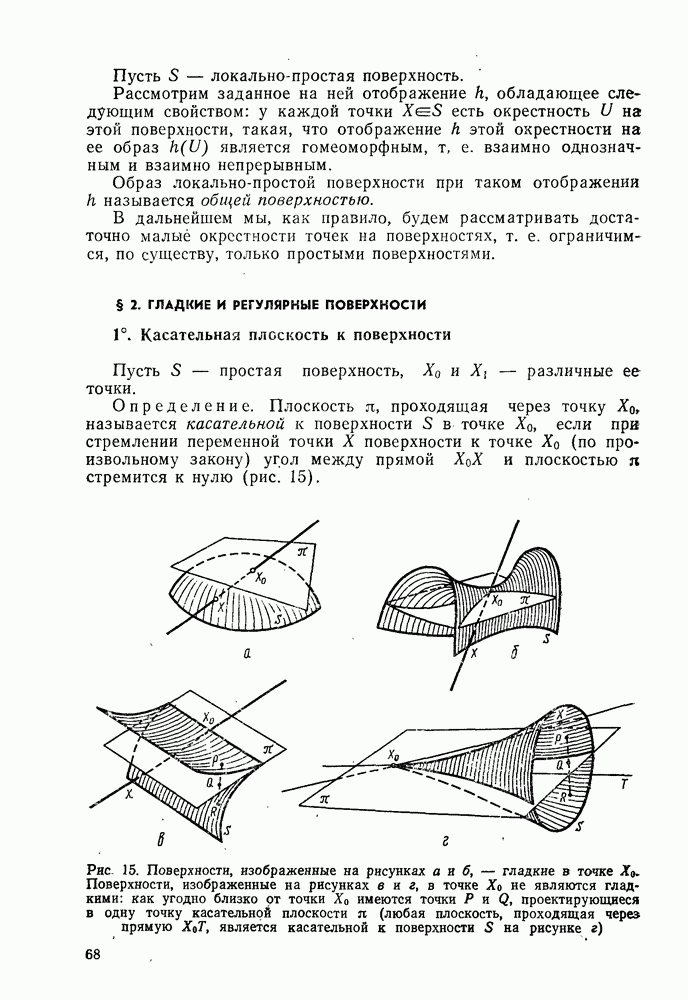
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
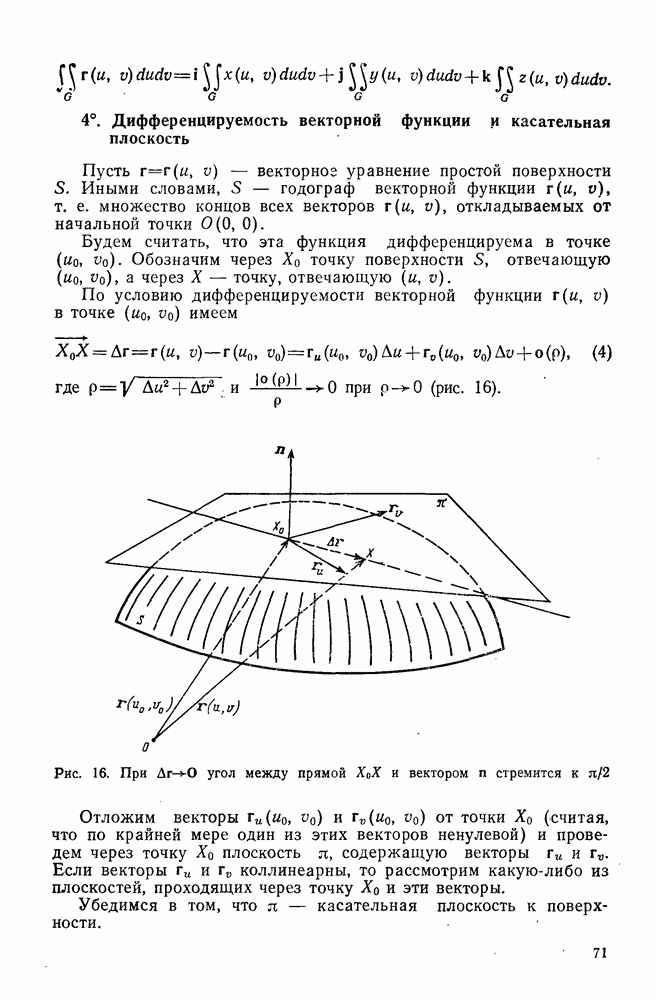
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
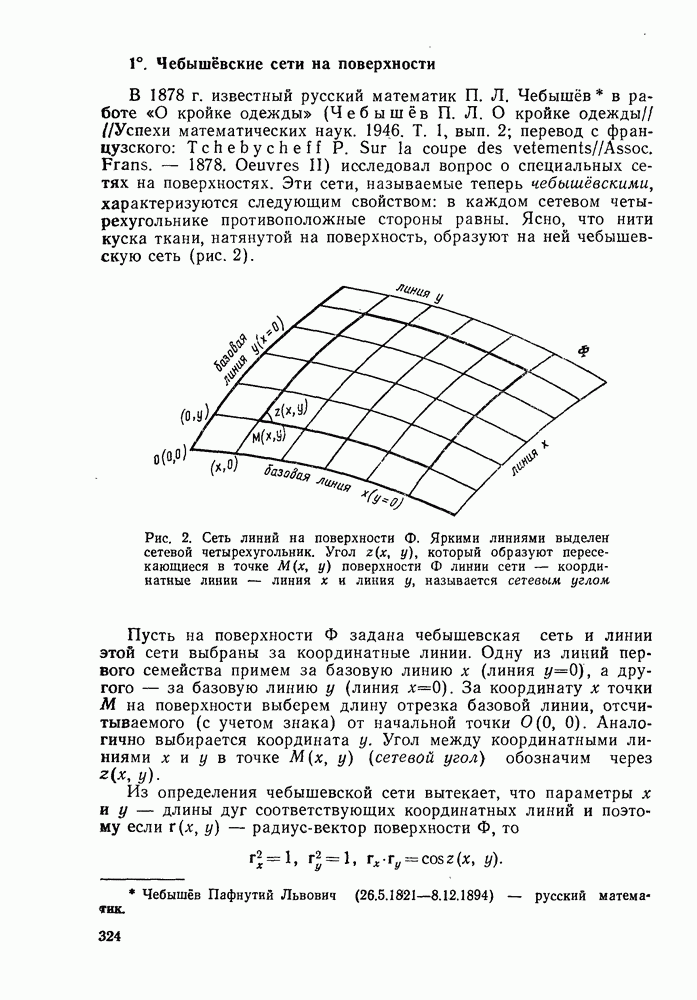
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
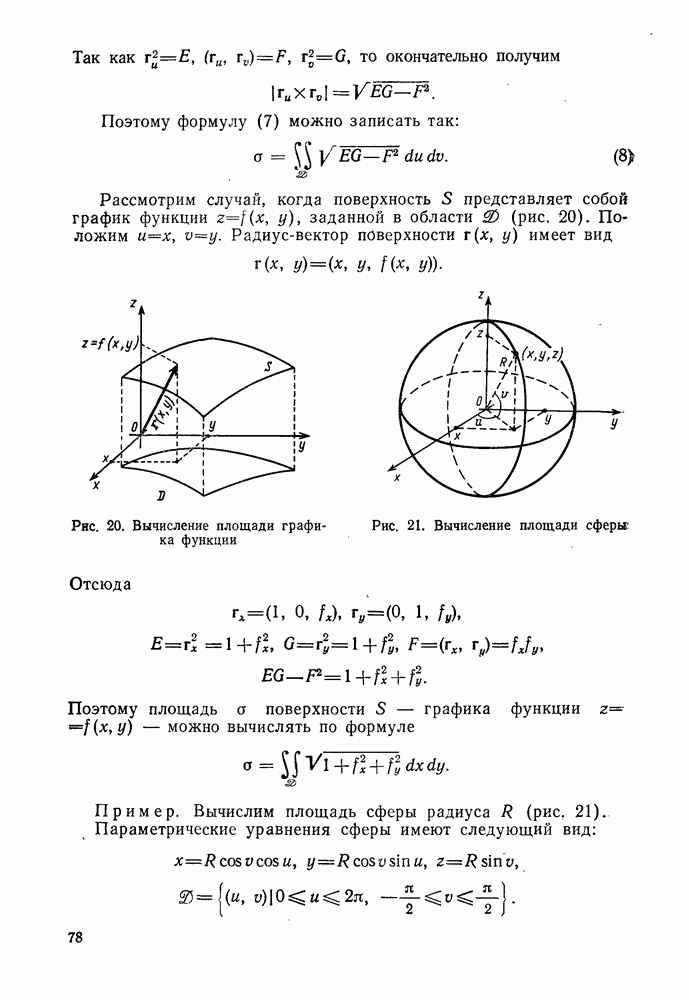
- 4°. Площадь поверхности
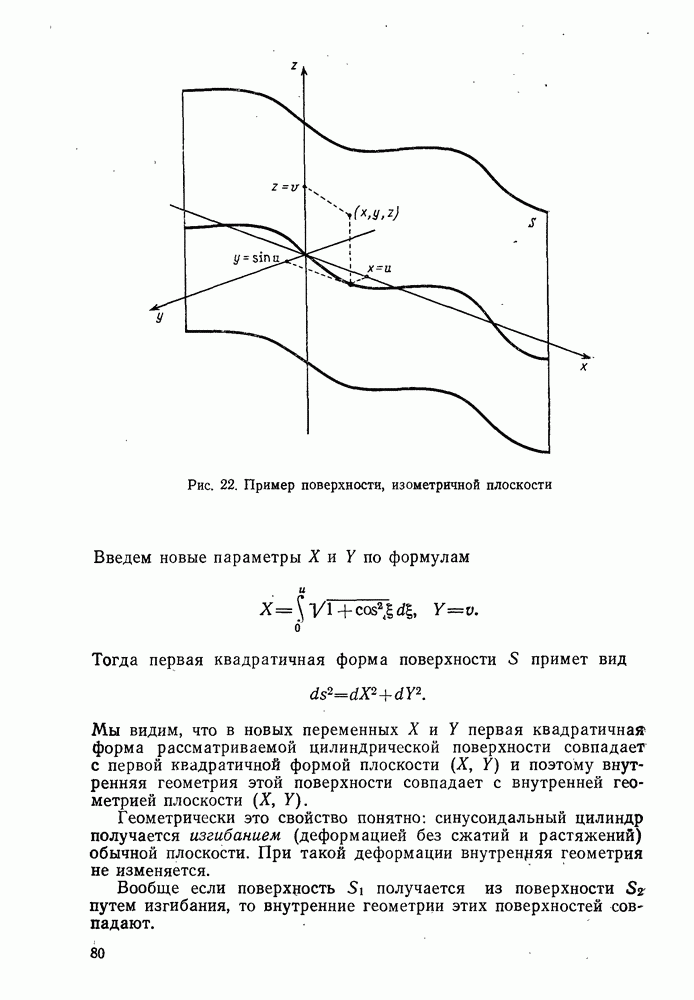
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
- § 5. ПОДМНОГООБРАЗИЯ
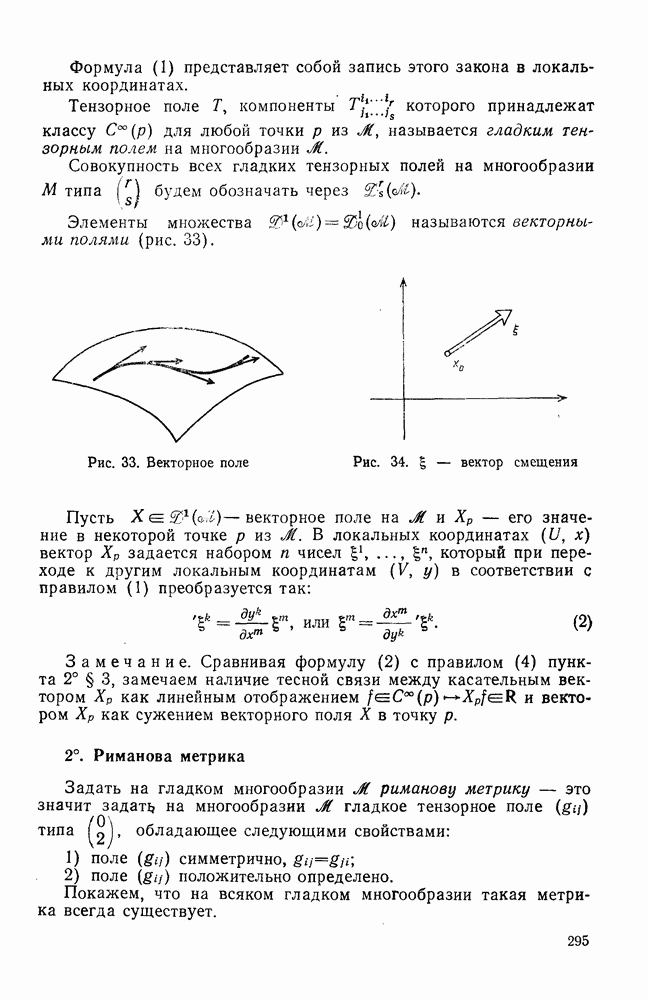
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
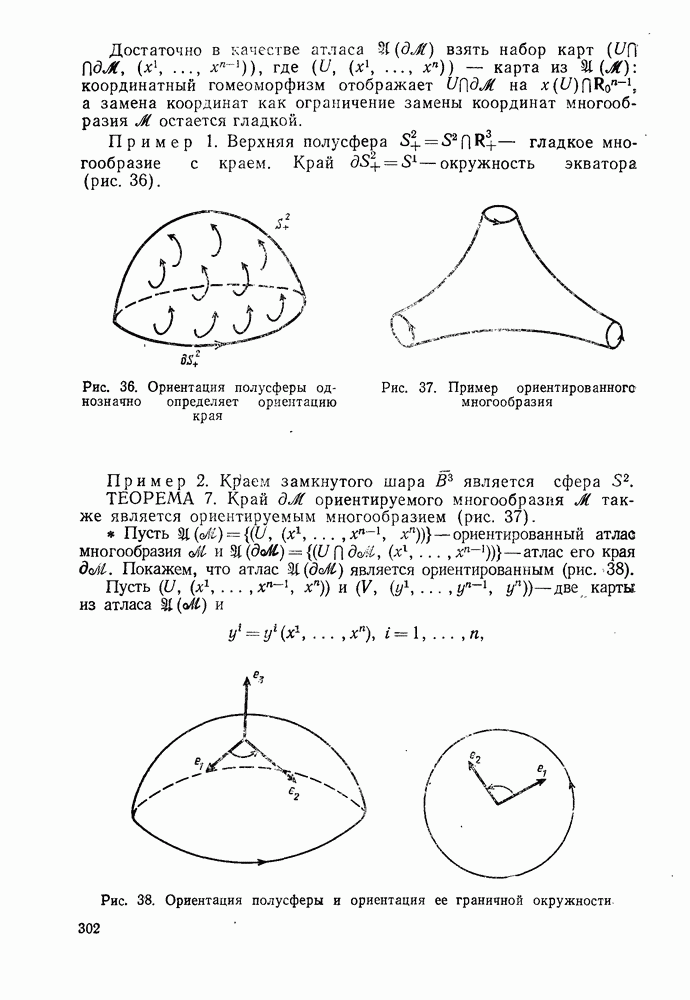
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
- 4°. Составные поверхности