| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. СИМВОЛЫ КРИСТОФФЕЛЯ
1°. Определение
Пусть в области X пространства  введена координатная система
введена координатная система 
Произвольная точка  области X определяется своим радиус-вектором
области X определяется своим радиус-вектором

В точке  естественно возникает репер
естественно возникает репер

Вычислим в точке  вторую производнук? ее радиус-вектора
вторую производнук? ее радиус-вектора

Ясно, что полученный вектор можно представить в виде линейной комбинации векторов

Легко видеть, что коэффициенты  в этом разложении симметричны:
в этом разложении симметричны:

В силу произвольности выбора точки  можно заключить, что соотношение (1) справедливо в любой точке области
можно заключить, что соотношение (1) справедливо в любой точке области 
Пусть  другая координатная система в области
другая координатная система в области  соответствующий координатный репер. Рассуждая как и выше, получаем, что
соответствующий координатный репер. Рассуждая как и выше, получаем, что

Найдем правило, по которому при переходе от координатной системы  к координатной системе
к координатной системе  по коэффициентам Т; можно вычислить коэффициенты
по коэффициентам Т; можно вычислить коэффициенты 
Продифференцируем векторную функцию

по  считая ее сложной функцией переменных
считая ее сложной функцией переменных  Имеем
Имеем

и, далее,

Преобразуем полученное выражение. Заменим в первой группе слагаемых каждый вектор  его выражением (1). Тогда, изменяя индекс суммирования во второй группе получим
его выражением (1). Тогда, изменяя индекс суммирования во второй группе получим

Так как

то окончательно имеем

Сравнивая последнее равенство с формулой (2), в силу единственности разложения вектора по базису получаем

Формула (4) представляет собой закон преобразования коэффициентов  В общем случае этот закон не является тензорным, так как вторая производная
В общем случае этот закон не является тензорным, так как вторая производная  необязательно равна нулю.
необязательно равна нулю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- ГЛАВА 1. ТЕОРИЯ КРИВЫХ
- § 1. ПОНЯТИЕ КРИВОЙ
- 2°. Плоские кривые, задаваемые параметрически
- 3°. Пространственные кривые
- 4°. Кривая как линия пересечения поверхностей
- 5°. Кривая как годограф векторной функции
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ КРИВЫЕ
- 2°. Гладкие кривые
- 3°. Дифференцирование и интегрирование векторных функций
- 4°. Достаточные условия гладкости кривой
- 5°. Регулярные кривые
- § 3. ДЛИНА ДУГИ КРИВОЙ
- 2°. Достаточные условия спрямляемости
- § 4. СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
- 1°. Определение соприкасающейся плоскости
- 2°. Достаточные условия существования соприкасающейся плоскости
- 3°. Главная нормаль и бинормаль кривой. Основной триэдр
- § 5. КРИВИЗНА И КРУЧЕНИЕ. ФОРМУЛЫ ФРЕНЕ
- 2°. Кручение кривой
- 3°. Формулы Френе
- 4°. Вид кривой вблизи данной точки
- 5°. Натуральные уравнения кривой
- § 6. СОПРИКОСНОВЕНИЕ КРИВЫХ
- 2°. Достаточные условия соприкосновения
- 3°. Соприкасающаяся окружность
- 4°. Эволюта и эвольвента плоской кривой
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 2. ТЕОРИЯ ПОВЕРХНОСТЕЙ
- § 1. ПОНЯТИЕ ПОВЕРХНОСТИ
- 1°. Плоские области
- 2°. Простая поверхность
- 3°. Локально простая поверхность
- 4°. Общая поверхность
- § 2. ГЛАДКИЕ И РЕГУЛЯРНЫЕ ПОВЕРХНОСТИ
- 1°. Касательная плоскость к поверхности
- 2°. Гладкие поверхности
- 3°. Дифференцирование и интегрирование векторных функций двух аргументов
- 4°. Дифференцируемость векторной функции и касательная плоскость
- 5°. Достаточные условия гладкости поверхности
- 6°. Регулярные поверхности
- § 3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. ИЗМЕРЕНИЯ НА ПОВЕРХНОСТИ
- 1°. Первая квадратичная форма поверхности
- 2°. Длина кривой на поверхности
- 3°. Угол между кривыми на поверхности
- 4°. Площадь поверхности
- 5°. Внутренняя геометрия поверхности. Изометричные поверхности
- § 4. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
- 1°. Определение второй квадратичной формы
- 2°. Классификация точек регулярной поверхности
- 3°. Кривизна кривой на поверхности
- 4°. Индикатриса Дюпена
- 5°. Главные кривизны
- 6°. Линии кривизны
- 7°. Формула Родрига
- 8°. Асимптотические направления
- 9°. Асимптотические линии
- 10°. Формула Эйлера
- 11°. Средняя и гауссова кривизны
- 12°. Поверхности вращения
- § 5. ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
- 2°. Основные уравнения теории поверхностей
- 3°. Теорема Бонне
- § 6. ВНУТРЕННЯЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ
- 1°. Геодезическая кривизна кривой на поверхности
- 2°. Геодезические линии
- 3°. Полугеодезические координатные системы
- 4°. Полугеодезические полярные координаты
- 5°. Экстремальные свойства геодезических
- 6°. Поверхности постоянной кривизны
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 3. ОСНОВЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ
- 1°. Определение тензора
- 2°. Корректность определения тензора
- 3°. Равенство тензоров
- § 2. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД ТЕНЗОРАМИ
- 1°. Определение алгебраических операций над тензорами
- 2°. Правило суммирования
- 3°. Теорема об алгебраических операциях над тензорами
- 4°. Операции над кососимметричными тензорами
- 5°. Внешние формы
- § 3. МЕТРИЧЕСКИЙ ТЕНЗОР
- 2°. Опускание и поднятие индексов
- Б. АФФИННОЕ (ТОЧЕЧНОЕ) ПРОСТРАНСТВО
- § 4. ТЕНЗОРЫ В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
- 2°. Аффинные координаты
- 3°. Тензоры в точечном пространстве
- § 5. ТЕНЗОРНОЕ ПОЛЕ
- § 6. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- 2°. Тензоры в криволинейных координатах
- 3°. О способе задания тензорного поля
- § 7. МЕТРИЧЕСКИЙ ТЕНЗОР В ТОЧЕЧНОМ ПРОСТРАНСТВЕ
- 2°. Длина дуги гладкой кривой
- 3°. Вычисление объема
- § 8. СИМВОЛЫ КРИСТОФФЕЛЯ
- 2°. Специальные системы координат
- 3°. Символы Кристоффеля 1-го и 2-го рода
- § 9. КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1°. Определение операции ковариантного дифференцирования
- 2°. Свойства операции ковариантного дифференцирования
- 3°. Тензор Римана-Крнстоффеля типа (1 3)
- 4°. Ковариантное дифференцирование и метрический тензор
- 5°. Тензор Римана-Кристоффеля типа (0 4)
- В. АРИФМЕТИЧЕСКОЕ (КООРДИНАТНОЕ) ПРОСТРАНСТВО
- § 10. ТЕНЗОРЫ В КООРДИНАТНОМ ПРОСТРАНСТВЕ
- 2°. Преобразования координат
- 3°. Понятие тензора
- 4°. Основные алгебраические операции над тензорами
- 5°. Метрический тензор в координатном пространстве
- 6°. Символы Кристоффеля и операция ковариантного дифференцирования
- 7°. Тензор Римана-Кристоффеля
- ГЛАВА 4. РИМАНОВА ГЕОМЕТРИЯ
- 2°. Примеры римановых пространств
- § 2. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О РИМАНОВОЙ ГЕОМЕТРИИ
- 2°. Преобразование координат в римановом и касательном пространствах
- 3°. Локально нормальные координаты
- 4°. Каноническое разложение метрического тензора
- § 3. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВЕКТОРОВ И ТЕНЗОРОВ
- 2°. Векторы в римановом пространстве
- 3°. Параллельный перенос векторов в римановом пространстве
- 4°. Параллельный перенос тензоров
- 5°. Абсолютный дифференциал и абсолютная производная
- 6°. Техника абсолютного дифференцирования
- 7°. Еще раз о параллельном переносе тензоров
- 8°. Параллельный перенос некоторых важных тензоров
- § 4. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Геодезические как экстремали
- § 5. СПЕЦИАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ В РИМАНОВОМ ПРОСТРАНСТВЕ
- 2°. Полугеодезические координаты
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
- ГЛАВА 5. ГЛАДКИЕ МНОГООБРАЗИЯ
- § 1. НЕКОТОРЫЕ ПОНЯТИЯ ТОПОЛОГИИ
- 1°. Топология координатного пространства
- 2°. Топологическое пространство
- 3°, Топологическое подпространство
- 4°. Непрерывное отображение. Гомеоморфизм
- 5°. Топологическое произведение
- 6°. Связность
- 7°. Отделимость
- 8°. Компактность
- 9°. Топологическое многообразие
- § 2. ГЛАДКИЕ МНОГООБРАЗИЯ
- 2°. Гладкие функции
- 3°. Разбиение единицы
- 4°. Произведение гладких многообразий
- § 3. КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- 1°. Касательный вектор
- 2°. Касательное пространство
- § 4. ГЛАДКИЕ ОТОБРАЖЕНИЯ
- 1°. Гладкое отображение. Диффеоморфизм
- 2°. Дифференциал гладкого отображения
- 3°. Ранг гладкого отображения
- § 5. ПОДМНОГООБРАЗИЯ
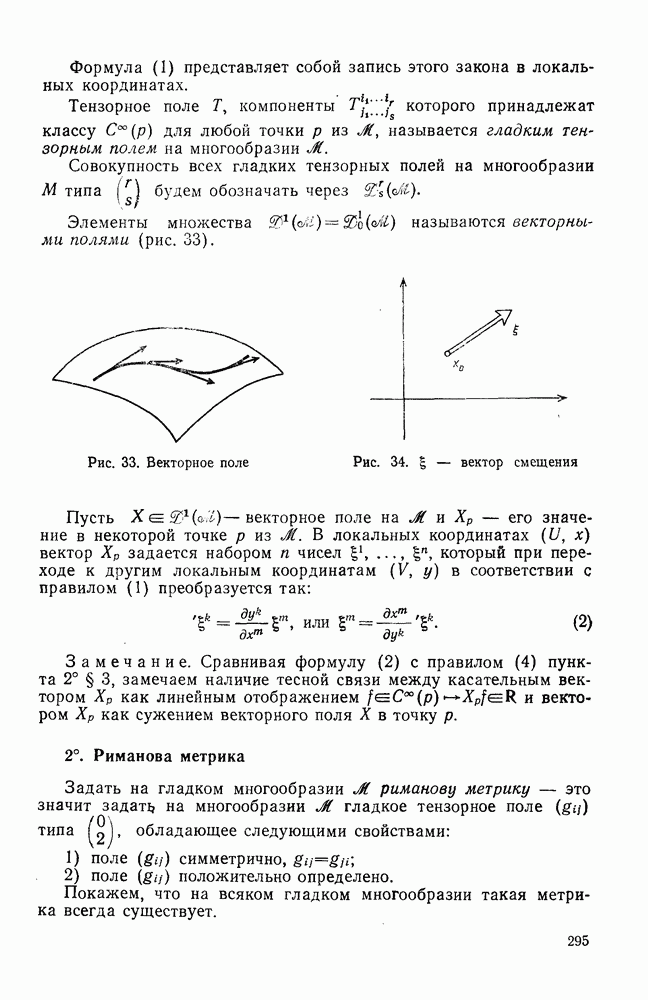
- § 6. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
- 2°. Риманова метрика
- 3°. Внешние дифференциальные формы на многообразии
- § 7. ИНТЕГРИРОВАНИЕ ПО МНОГООБРАЗИЮ
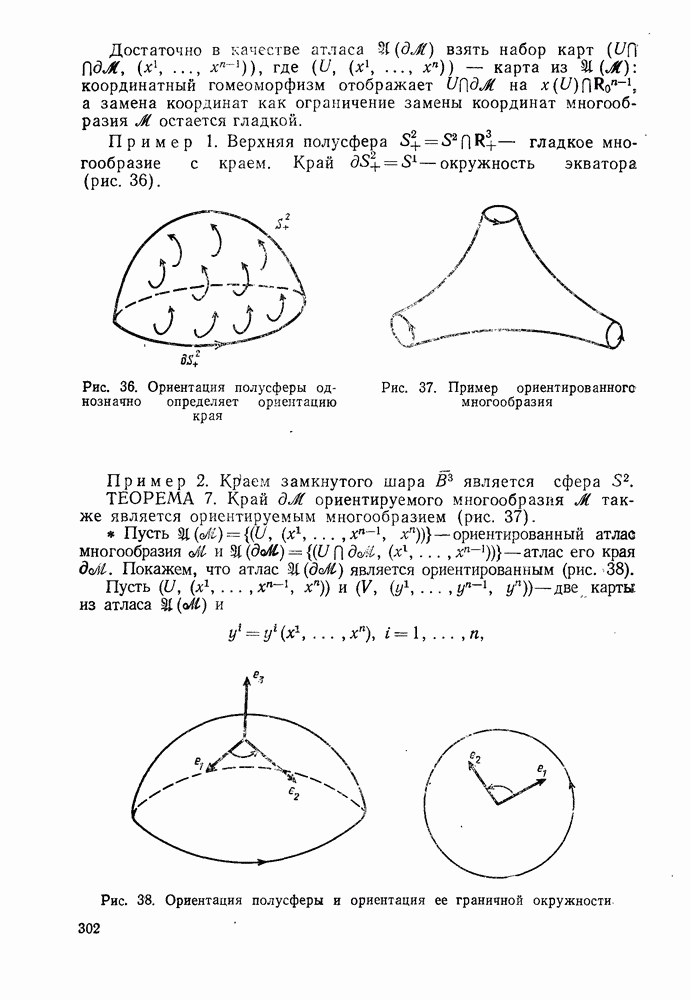
- 2°. Многообразие с краем
- 3°. Интеграл от дифференциальной формы по гладкому многообразию
- 4°. Формула Стокса
- СВОДКА ОСНОВНЫХ ПОНЯТИЙ, ФОРМУЛ, ФАКТОВ
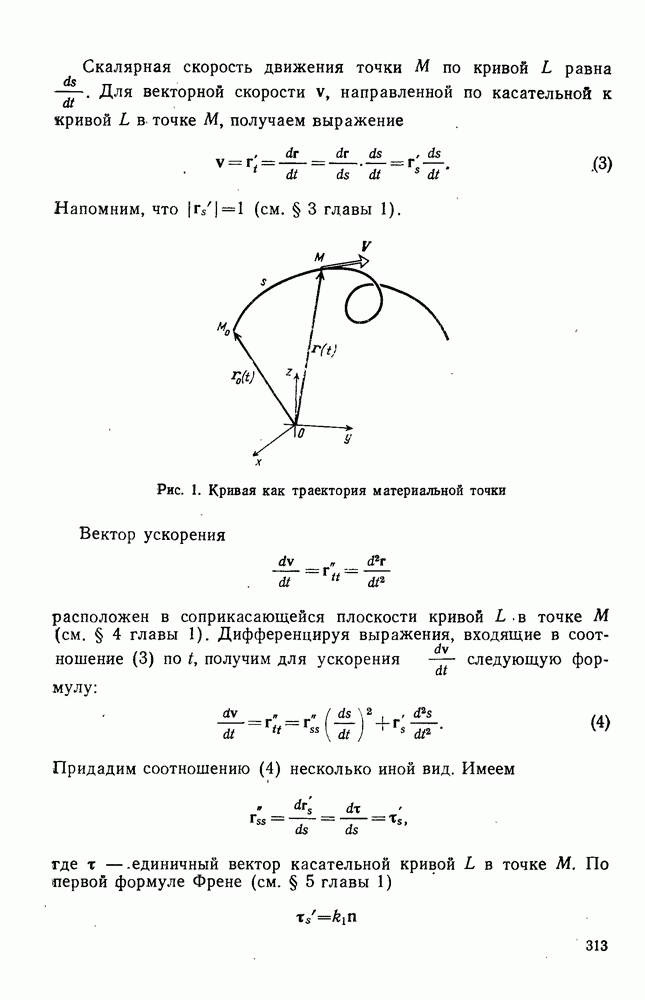
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
- 2°. Движение точки в поле сил
- 3°. Движение точки в параллельном поле сил
- 4°. Движение точки в центральном поле сил
- 5°. Движение в поле сил тяготения
- 6°. Движение заряженной частицы в электромагнитном поле
- 7°. Движение заряженной частицы в постоянном электромагнитном поле
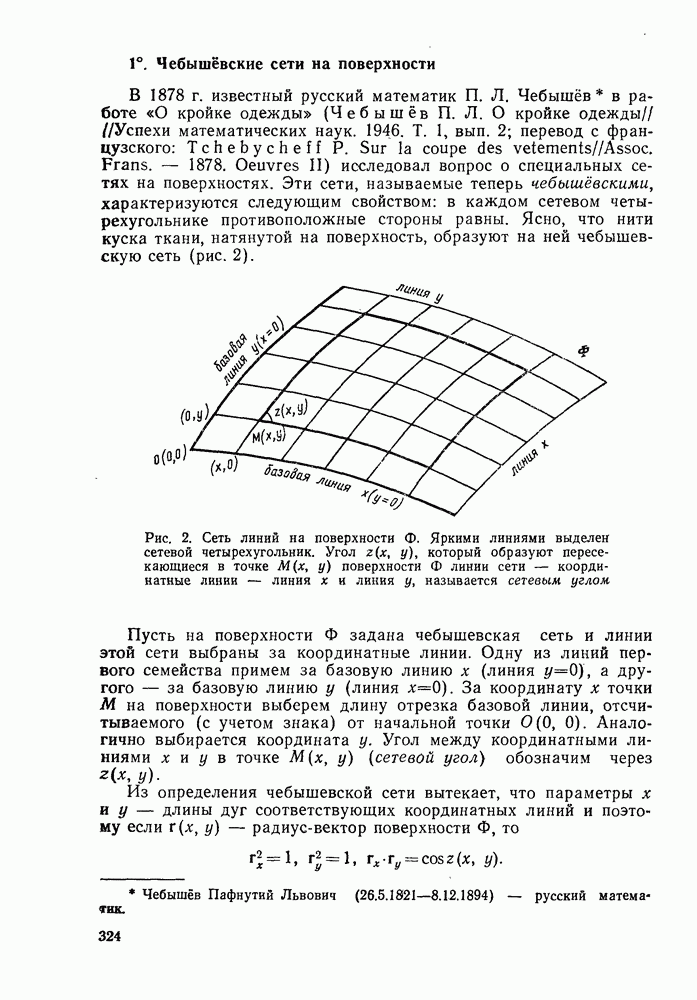
- § 2. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ
- 2°. Изометрические погружения плоскости Лобачевского в евклидово пространство Е3
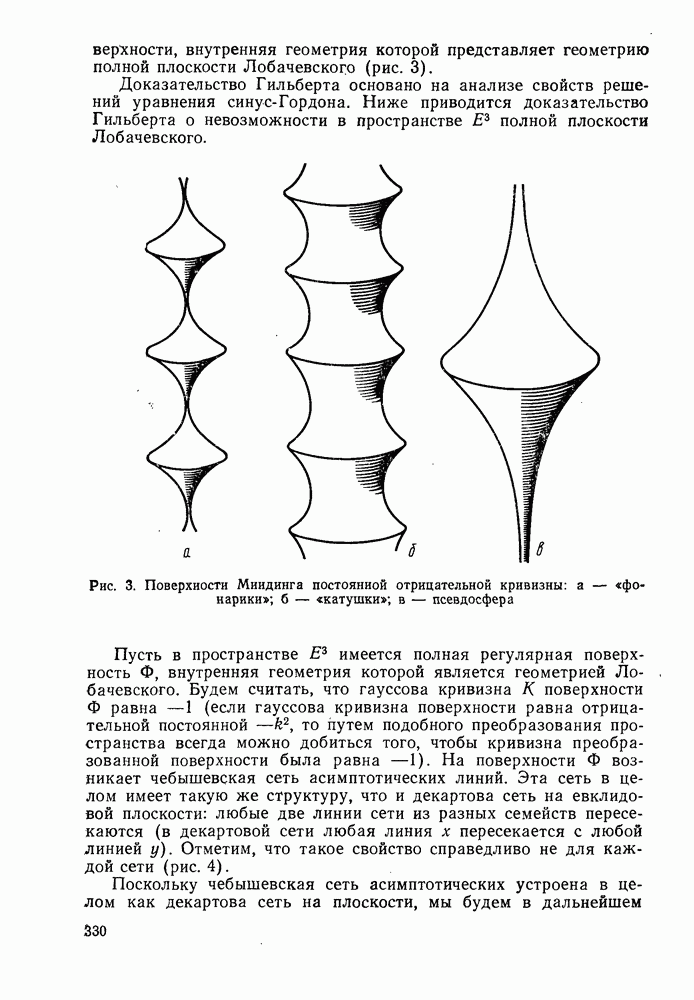
- 3°. Доказательство теоремы Гильберта о невозможности в евклидовом пространстве Е3 полной плоскости Лобачевского
- 4°. Доказательство существования регулярного решения уравнения синус-Гордона на всей плоскости
- 5°. Геометрическая интерпретация произвольных решений уравнения синус-Гордона
- 6°. Понятие солитонных решений дифференциальных уравнений
- 7°. Физическая интерпретация поверхностей постоянной отрицательной кривизны
- § 3. ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОЙ АЛГЕБРЫ И ВЕКТОРНОГО АНАЛИЗА В ТЕНЗОРНЫХ ОБОЗНАЧЕНИЯХ
- 2°. Операции опускания и поднятия индексов
- 3°. Ортонормированные базисы в пространстве En
- 4°. Дискриминантный тензор
- 5°. Ориентированный объем
- 6°. Векторное произведение
- 7°. Двойное векторное произведение
- 8°. Расходимость вектора
- 9°. Оператор Бельтрами — Лапласа
- 10°. Оператор Бельтрами — Лапласа в криволинейных координатах
- § 4. ПСЕВДОЕВКЛМДОВО И ПСЕВДОРИМАНОВО ПРОСТРАНСТВА
- 2°. Галилеевы координаты. Преобразования Лоренца
- 3°. Пространство Минковского. Преобразования Лоренца в пространстве Минковского
- 4°. Псевдориманово пространство. Метрический тензор псевдориманова пространства
- § 5. ПРОЕКТИРОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 2°. Уравнение криволинейного четырехугольника
- 3°. Составные кривые
- 4°. Составные поверхности