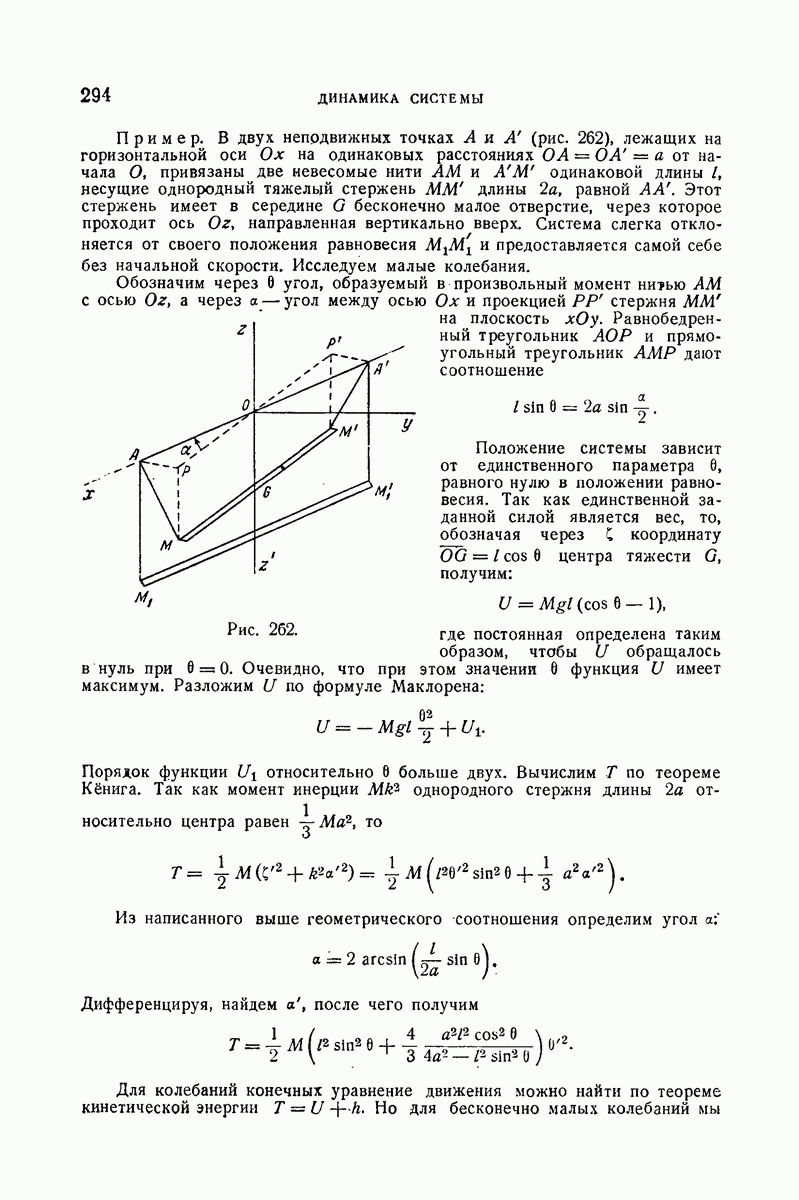
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
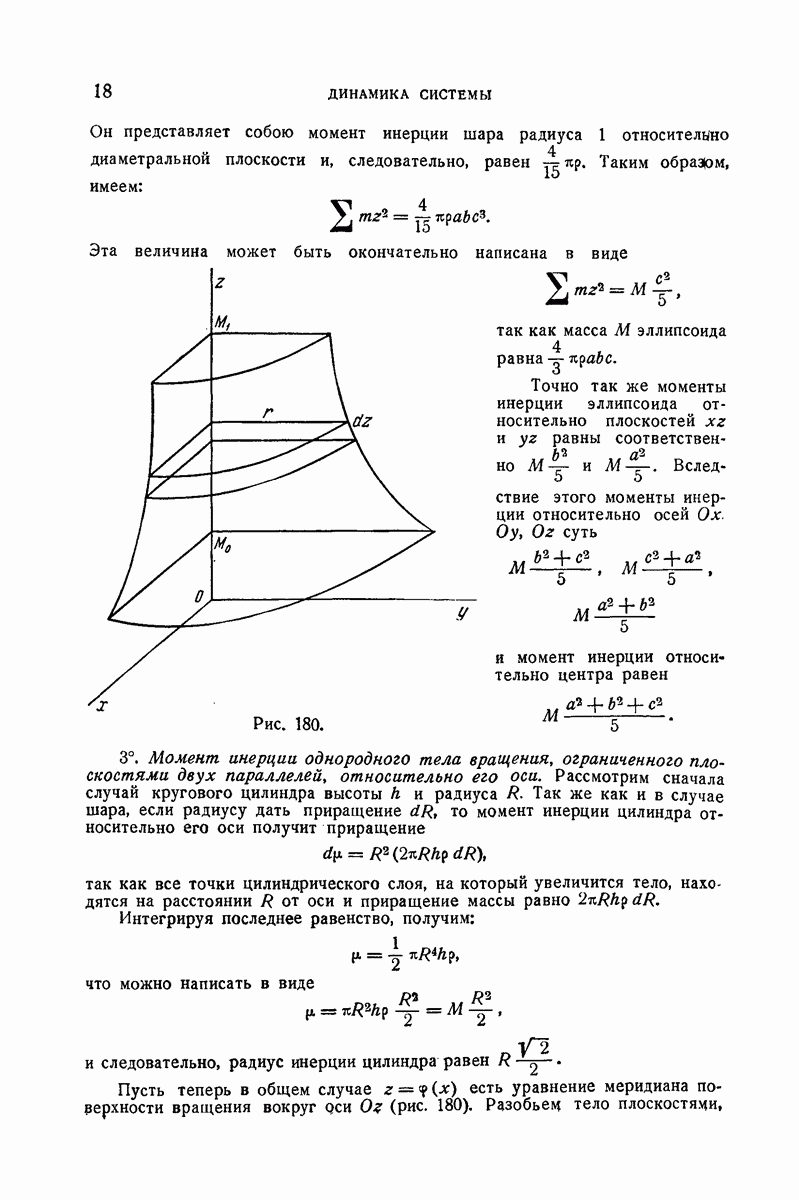
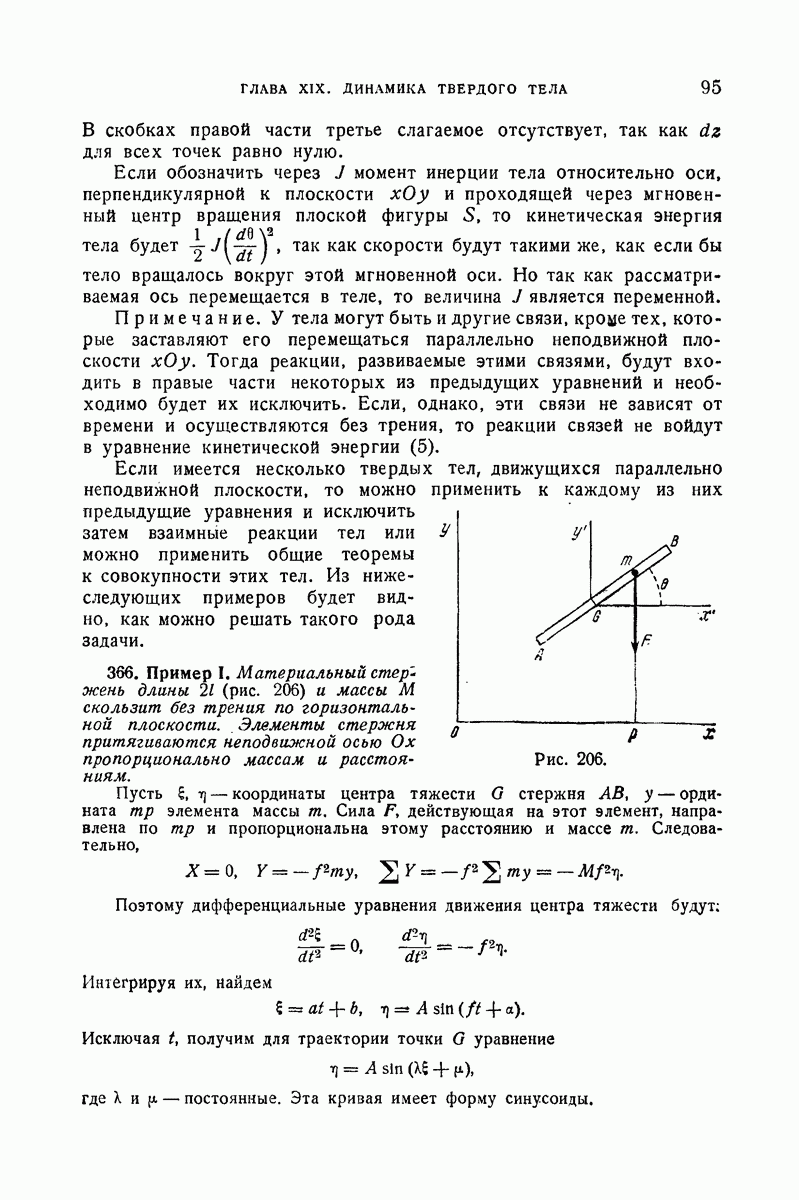
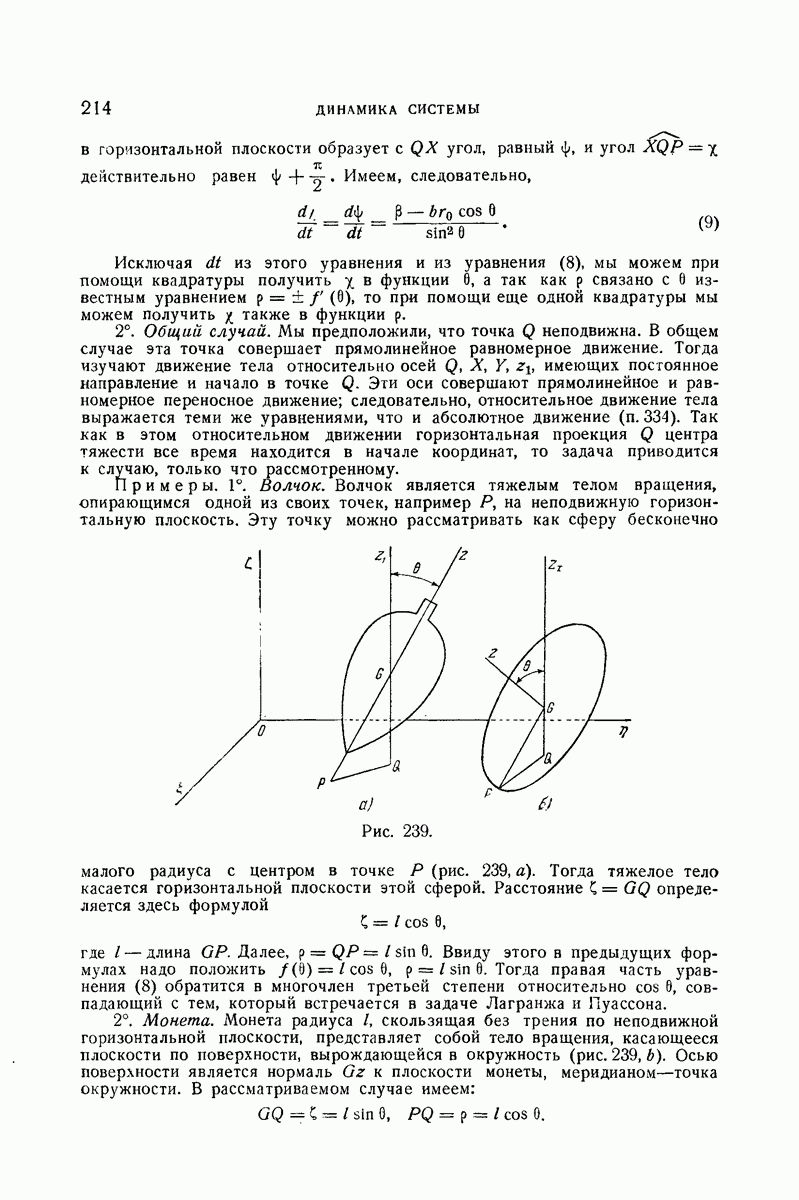
333. Примеры.
1°. Концы материальной однородной прямой  (рис. 186) массы от и длины 2а могут скользить без трения по горизонтальной окружности радиуса
(рис. 186) массы от и длины 2а могут скользить без трения по горизонтальной окружности радиуса  Насекомое той же массы
Насекомое той же массы  помещено в середине прямой, предполагаемой неподвижной. В момент
помещено в середине прямой, предполагаемой неподвижной. В момент  насекомое начинает двигаться вдоль прямой
насекомое начинает двигаться вдоль прямой  от С к В, пробегая в равные промежутки времени равные отрезки этой прямой. Найти движение системы и вычислить угол, на который повернется прямая от своего исходного положения, когда насекомое достигнет конца В.
от С к В, пробегая в равные промежутки времени равные отрезки этой прямой. Найти движение системы и вычислить угол, на который повернется прямая от своего исходного положения, когда насекомое достигнет конца В.
[Обозначить через  угол, который образует с неподвижной осью радиус-вектор, соединяющий середину С прямой с центром О, через
угол, который образует с неподвижной осью радиус-вектор, соединяющий середину С прямой с центром О, через  — расстояние
— расстояние  от насекомого М до точки С, причем
от насекомого М до точки С, причем  (v — постоянная)] (Лиценциатская, июль 1891).
(v — постоянная)] (Лиценциатская, июль 1891).

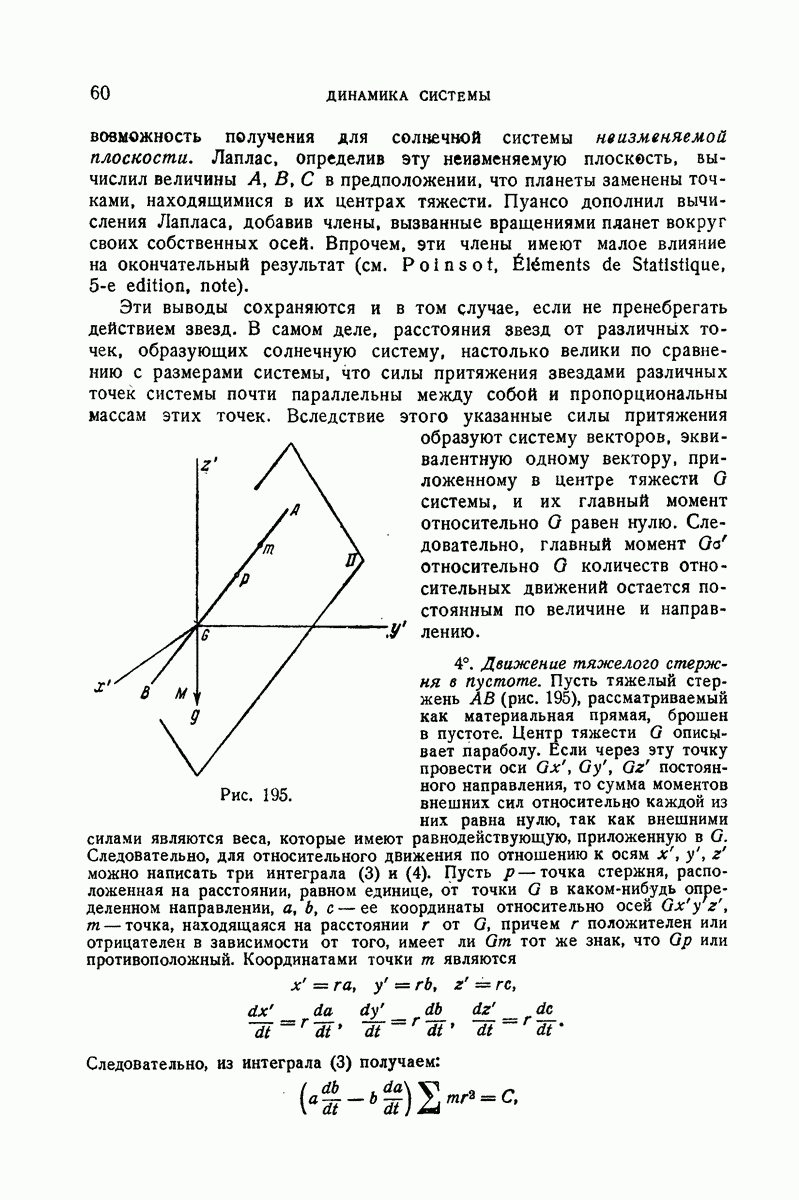
Рис. 186.
Внешние силы, приложенные к системе, образованной прямой и насекомым, суть: 1° вес; 2° нормальные реакции окружности на концы А и В прямой. Моменты всех этих сил относительно вертикали  равны нулю, так как силы веса параллельны оси
равны нулю, так как силы веса параллельны оси  а нормальные реакции лежат в плоскостях. нормальных к окружности в точках А и В и, следовательно, содержащих
а нормальные реакции лежат в плоскостях. нормальных к окружности в точках А и В и, следовательно, содержащих  Сумма моментов количеств движения относительно
Сумма моментов количеств движения относительно  является поэтому постоянной и поскольку она была вначале равна нулю, так как прямая и насекомое были неподвижны, то она останется равной нулю постоянно. Вычислим эту сумму, которая состоит:
является поэтому постоянной и поскольку она была вначале равна нулю, так как прямая и насекомое были неподвижны, то она останется равной нулю постоянно. Вычислим эту сумму, которая состоит:
а) из суммы моментов количеств движения всех точек прямой относительно  так как эта прямая является твердым телом, вращающимся вокруг
так как эта прямая является твердым телом, вращающимся вокруг  с угловой скоростью
с угловой скоростью  то эта сумма равна
то эта сумма равна  где
где  — момент инерции прямой относительно
— момент инерции прямой относительно 
б) из момента количества движения насекомого М; так как полярные координаты насекомого М суть  то этот момент равен
то этот момент равен  Имеем, следовательно,
Имеем, следовательно,

Но из прямоугольного треугольника  непосредственно находим:
непосредственно находим:

Подставляя в предыдущее уравнение, после приведения получим: 

где  - значение
- значение  в момент
в момент  Остальные уравнения, написанные выше, определяют
Остальные уравнения, написанные выше, определяют  и а в функции
и а в функции  Когда насекомое достигает точки В, имеем
Когда насекомое достигает точки В, имеем  откуда находим искомое значение
откуда находим искомое значение 
Определим значение  Если через
Если через  обозначить линейную плотность (массу единицы длины) и через
обозначить линейную плотность (массу единицы длины) и через  расстояние от элемента
расстояние от элемента  до центра, то момент инерции прямой
до центра, то момент инерции прямой  относительно ее центра тяжести С равен величине
относительно ее центра тяжести С равен величине

Момент инерции  относительно оси
относительно оси  или относительно точки О равен (п. 317)
или относительно точки О равен (п. 317)

Следовательно,

Если в какой-нибудь момент времени насекомое остановится на прямой, то и вся система остановится, так как в противном случае сумма моментов количеств движения не будет равна нулю.
2°. Листок бумаги положен на совершенно гладкую горизонтальную плоскость, по которой он может скользить без трения. Одна точка О этого листка неподвижна, так что листок может только вращаться вокруг точки О, оставаясь на плоскости. Так, например, получится, если листок приколот в точке О булавкой к горизонтальной плоскости. На листке начерчена окружность радиуса а, проходящая через О (рис. 187, I и II).
Бумага была вначале в покое и на нее, в точке А, диаметрально противоположной точке О окружности было положено без начальной скорости насекомое.

Рис. 187.
В момент  насекомое начало двигаться по окружности с постоянной относительно бумаги скоростью V. Найти движение системы (Rоuth (Раус), Rigid dynamics).
насекомое начало двигаться по окружности с постоянной относительно бумаги скоростью V. Найти движение системы (Rоuth (Раус), Rigid dynamics).
Выберем в плоскости в качестве неподвижных осей ось  совпадающую с начальным положением диаметра О А (положение
совпадающую с начальным положением диаметра О А (положение  и ось
и ось  к ней перпендикулярную. Внешние силы, приложенные к системе (бумага и насекомое), суть силы веса, нормальные реакции плоскости и реакция иглы на бумагу в точке О. Моменты всех этих сил относительно оси
к ней перпендикулярную. Внешние силы, приложенные к системе (бумага и насекомое), суть силы веса, нормальные реакции плоскости и реакция иглы на бумагу в точке О. Моменты всех этих сил относительно оси  перпендикулярной к плоскости
перпендикулярной к плоскости  в точке О, равны нулю. Следовательно, сумма моментов количеств движения относительно оси
в точке О, равны нулю. Следовательно, сумма моментов количеств движения относительно оси  постоянна. Теорема
постоянна. Теорема
площадей применима к движению системы в плоскости  и так как система была вначале в покое, то постоянная площадей равна нулю. Таким образом:
и так как система была вначале в покое, то постоянная площадей равна нулю. Таким образом:

Если насекомое вращается в каком-нибудь направлении вокруг точки О, то бумага должна поворачиваться в противоположном направлении. Подсчитаем сумму моментов количеств движения. Пусть в момент  (рис. 187, II) насекомое находится в точке М. Обозначим через
(рис. 187, II) насекомое находится в точке М. Обозначим через  его полярные координаты, причем
его полярные координаты, причем  предполагается положительным. В тот же момент времени диаметр, выходящий из точки О, занимает положение
предполагается положительным. В тот же момент времени диаметр, выходящий из точки О, занимает положение  образующее с
образующее с  отрицательный угол, который мы обозначим через —а, так что а обозначает абсолютное значение угла
отрицательный угол, который мы обозначим через —а, так что а обозначает абсолютное значение угла  Момент количества движения насекомого равен
Момент количества движения насекомого равен  а сумма моментов количеств движения различных точек бумаги равна
а сумма моментов количеств движения различных точек бумаги равна  где
где  — момент инерции бумаги относительно
— момент инерции бумаги относительно  угловая скорость бумаги.
угловая скорость бумаги.
Имеем уравнение

Надо выразить, что дуга  окружности, которую пробежало насекомое, равна
окружности, которую пробежало насекомое, равна  Таким путем, так как
Таким путем, так как  получаем:
получаем:

где положено для краткости  . С другой стороны, из треугольника
. С другой стороны, из треугольника  имеем:
имеем:

Заменяя в равенстве  этим значением и а через
этим значением и а через  получим:
получим:

Написав это в виде

и выполнив интегрирование, получим;

причем постоянную присоединять не нужно, так как при  должно быть
должно быть  Таким образом, 0 выражено в функции
Таким образом, 0 выражено в функции  Обращаясь к уравнениям (3) и (2), найдем
Обращаясь к уравнениям (3) и (2), найдем  тоже в функции
тоже в функции  Таким образом, движение найдено.
Таким образом, движение найдено.
Найдем время Т, необходимое насекомому для достижения точки О, и соответствующие значения углов  . На основании равенств (2) и (4) имеем:
. На основании равенств (2) и (4) имеем:

Если насекомое будет продолжать перемещаться по окружности, то бумага будет продолжать поворачиваться в противоположном направлении.
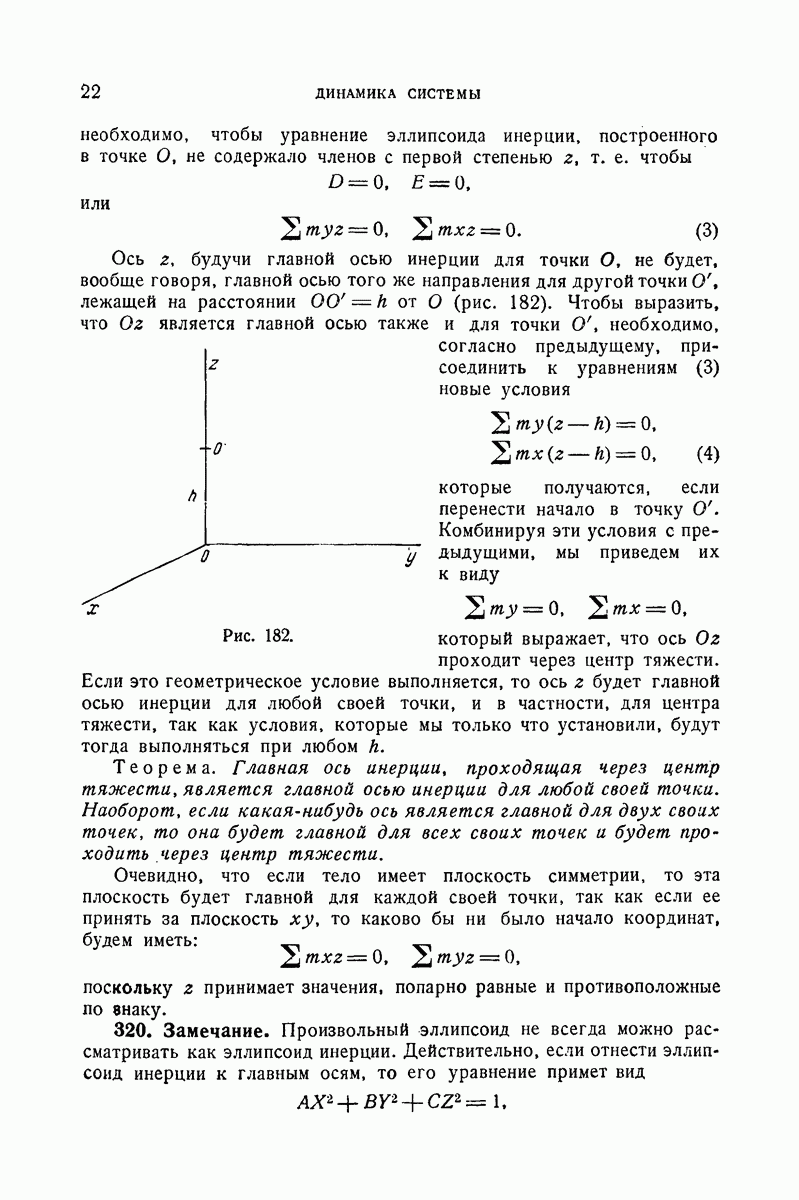
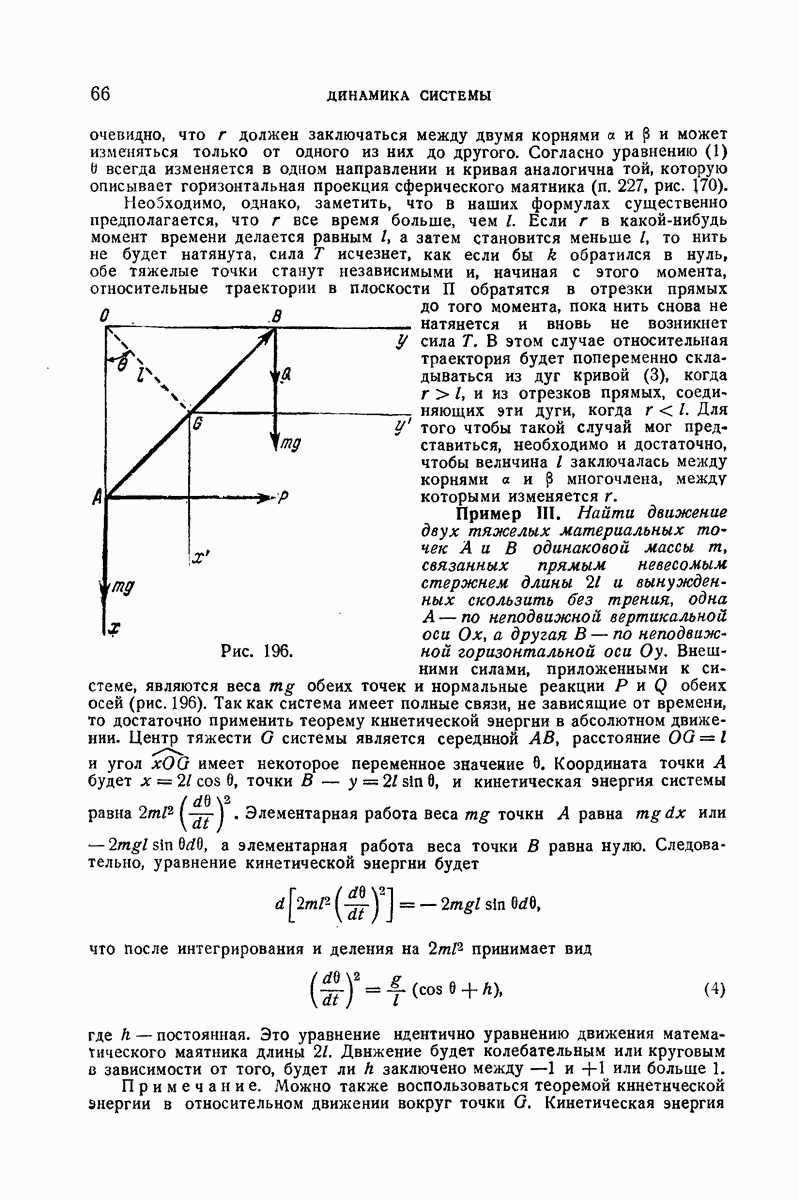
3°. В предыдущем примере точка О бумаги закреплена неподвижно. Но можно осуществить вращательное движение указанного рода, не закрепляя никакой точки, следующим образом. Предположим, что лист бумаги, имеющий центр тяжести в точке О, может скользить без трения по горизонтальной плоскости, и начертим на этом листке две одинаковые окружности, касающиеся в точке О (рис. 188). Вообразим теперь двух насекомых одинаковой массы находящихся вначале в покое в точках А и  диаметрально противоположных относительно точки О и начинающих затем перемещаться по обеим окружностям с одинаковой скоростью
диаметрально противоположных относительно точки О и начинающих затем перемещаться по обеим окружностям с одинаковой скоростью  и в одинаковом направлении вращения таким образом, что в произвольный момент времени они занимают симметричные относительно О положения М и М].
и в одинаковом направлении вращения таким образом, что в произвольный момент времени они занимают симметричные относительно О положения М и М].

Рис. 188.
Согласно теореме движения центра тяжести точка О, являющаяся центром тяжести всей системы, остается неподвижной, так как все начальные скорости равны нулю. Тогда листок бумаги будет вращаться вокруг неподвижной точки О в сторону, противоположную вращательному движению обоих насекомых, и уравнения движения будут идентичными с предыдущими, если предположить, как мы это сделали, что каждое из насекомых имеет половину массы насекомого из предыдущего примера.
Аналогичным образом наблюдатель, стоящий на идеально отполированной горизонтальной плоскости, может заставить себя вращаться. Для этого ему достаточно поднять оба кулака, расположив их симметрично относительно вертикали  проходящей через центр тяжести и затем описывать ими две окружности в одном и том же направлении, сохраняя все время симметрию относительно оси
проходящей через центр тяжести и затем описывать ими две окружности в одном и том же направлении, сохраняя все время симметрию относительно оси  Тогда корпус будет поворачиваться в противоположном направлении и по истечении некоторого промежутка времени может совершить полный оборот.
Тогда корпус будет поворачиваться в противоположном направлении и по истечении некоторого промежутка времени может совершить полный оборот.
4°. Вообразим наблюдателя, стоящего неподвижно на идеально гладкой горизонтальной плоскости, с надетым на него поясом в виде желоба, в котором лежат два тяжелых шара, вначале неподвижных. Если наблюдатель при помощи рук заставит шары перекатываться по желобу таким образом, чтобы они вращались вокруг его корпуса в каком-нибудь определенном направлении, то центр тяжести системы останется на неподвижной вертикали, а корпус будет вращаться вокруг этой вертикали в противоположном направлении.
Задачи того вида, какой мы сейчас изложили, рассмотрены в различных заметках Гюйу (Guyou), Мориса Леви (Maurice Levy), Марселя Депре (Marcel Deprez), Пикара (Picard), Аппеля, Лекорню (Lесогnu, Comptes ren-dus, 2-е semestre 1894 и Bulletin de la Soci6t6 mathematique, novembre 1894) и в заметке Сен-Жермена. (Saint-Geггаain, Nouvelles Annales de Mathematique, 1895), в которой подробно изложен четвертый из рассмотренных примеров.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
- 354. Пример I.
- V. Энергия
- 356. Потенциальная энергия. Механический смысл.
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
- 370. Пример I.
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
- 421. Твердое тело.
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели