| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
397. Интегрирование в эллиптических функциях.
Уравнение

однозначно определяет и через эллиптическую функцию от переменного  Чтобы выполнить это преобразование, достаточно применить метод, который был использован в задаче о сферическом маятнике (п. 277), заставив корни
Чтобы выполнить это преобразование, достаточно применить метод, который был использован в задаче о сферическом маятнике (п. 277), заставив корни  и играть ту же роль, какую играли корни -
и играть ту же роль, какую играли корни -  в задаче о маятнике. Эта аналогия отнюдь не является неожиданной и может быть доведена до полного совпадения, так как задача о сферическом маятнике является лишь частным случаем рассматриваемой задачи — случаем, когда тяжелое тело состоит из одной точки, помещенной в центре тяжести.
в задаче о маятнике. Эта аналогия отнюдь не является неожиданной и может быть доведена до полного совпадения, так как задача о сферическом маятнике является лишь частным случаем рассматриваемой задачи — случаем, когда тяжелое тело состоит из одной точки, помещенной в центре тяжести.
После того как а или, что то же,  будет выражено в функции
будет выражено в функции  можно определить
можно определить  в функции
в функции  из уравнений
из уравнений

в виде квадратур над эллиптическими функциями, которые могут быть выполнены при помощи функций Якоби  . Величина и является эллиптической функцией переменного
. Величина и является эллиптической функцией переменного  с вещественным периодом Т, причем
с вещественным периодом Т, причем

По истечении времени Т величины  , следовательно,
, следовательно,  принимают первоначальное значение. Функции
принимают первоначальное значение. Функции  увеличиваются каждая на постоянную
увеличиваются каждая на постоянную
величину. Мы не приводим выкладок. Для их выполнения мы отсылаем читателя к мемуару Лотгнера (Lott пег, Journal de Crelle, т. 50), к сочинениям Альфена (Haiphen) и Гринхилла (Greenhill), к сочинению Аппеля и Лакура, «Основы теории аналитических функций) (Principes de la Th6orie des Fonctions elliptiques), к сочинению Клейна и Зоммерфельда (Ueber die Theorie des Kreisels) и к заметке Лакура (Nouvelles Annales de Mathemati-ques, 3e serie, т. XVIII, 18Э9).
В уже цитированной работе Гринхилла (Proceedings of the London Mathematical Society, т. XXV) содержатся интересные примеры приведения эллиптических интегралов, входящих в общее решение, к интегралам псевдоэллиптическим. Несколько особенно изящных примеров мы укажем в упражнениях.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
- 354. Пример I.
- V. Энергия
- 356. Потенциальная энергия. Механический смысл.
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
- 370. Пример I.
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
- 421. Твердое тело.
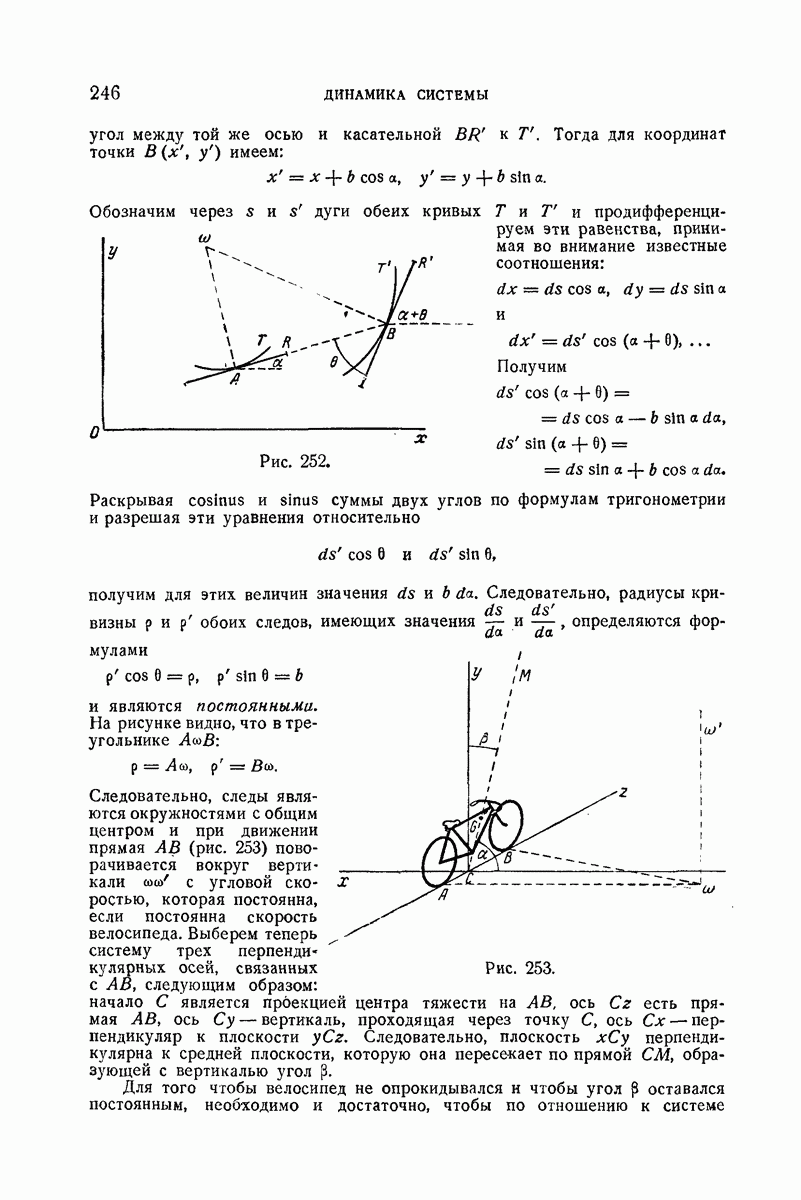
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
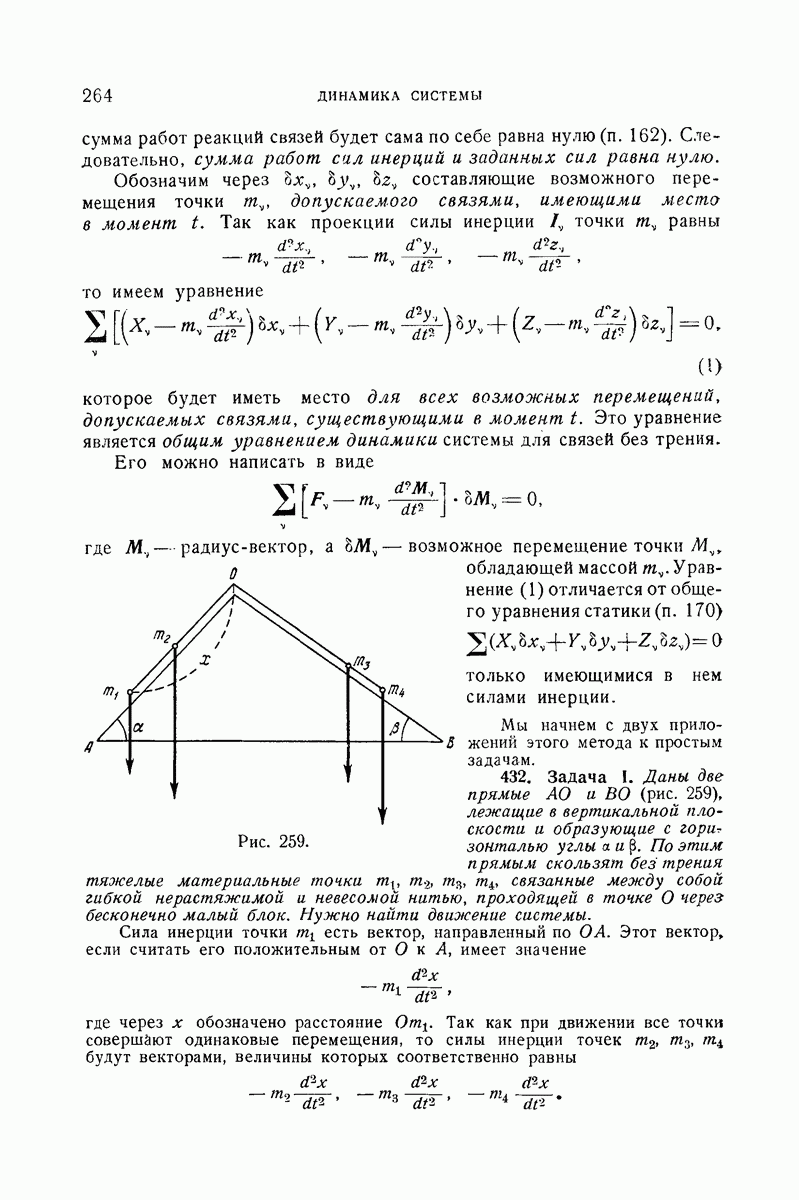
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
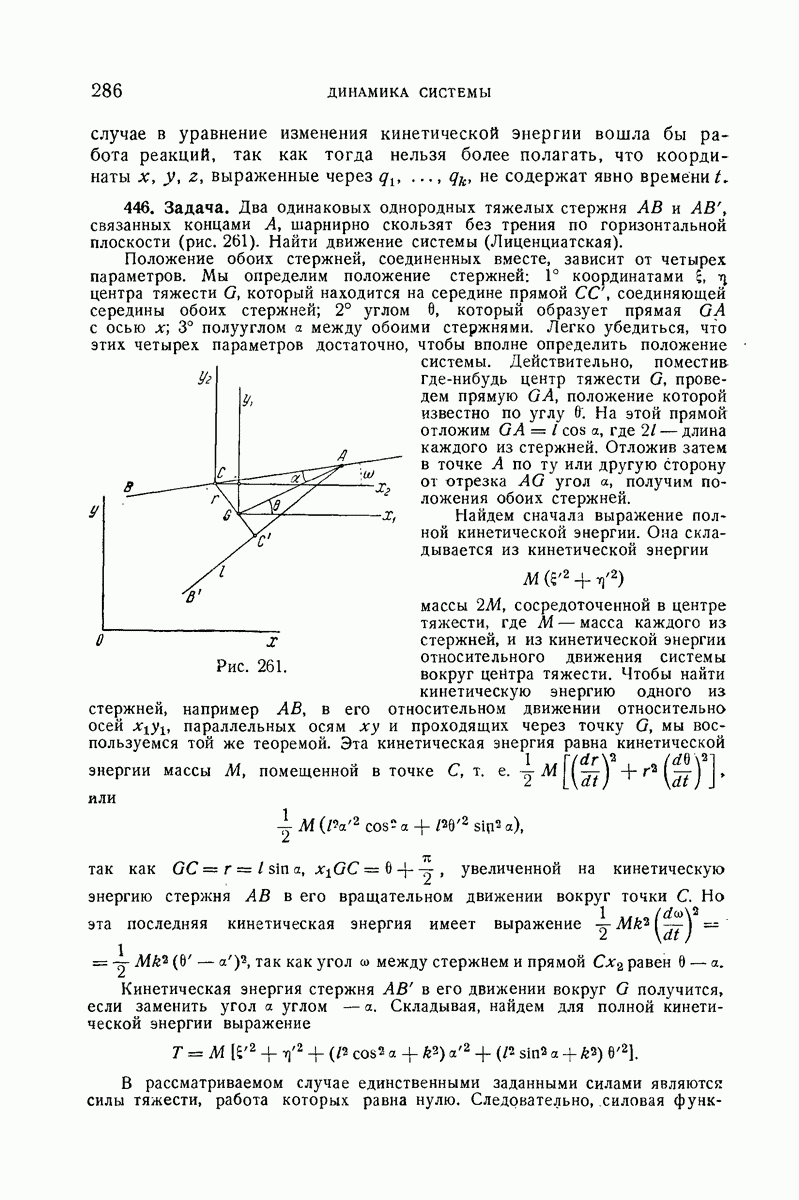
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели