| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
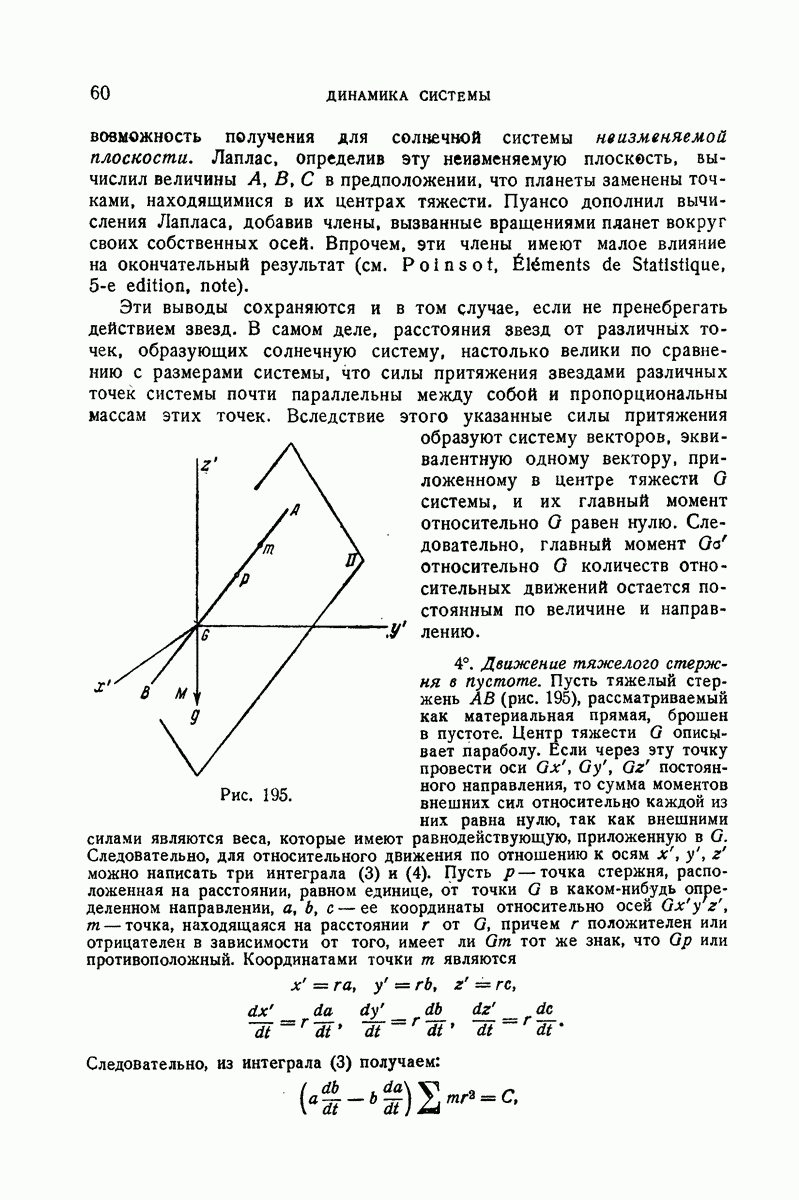
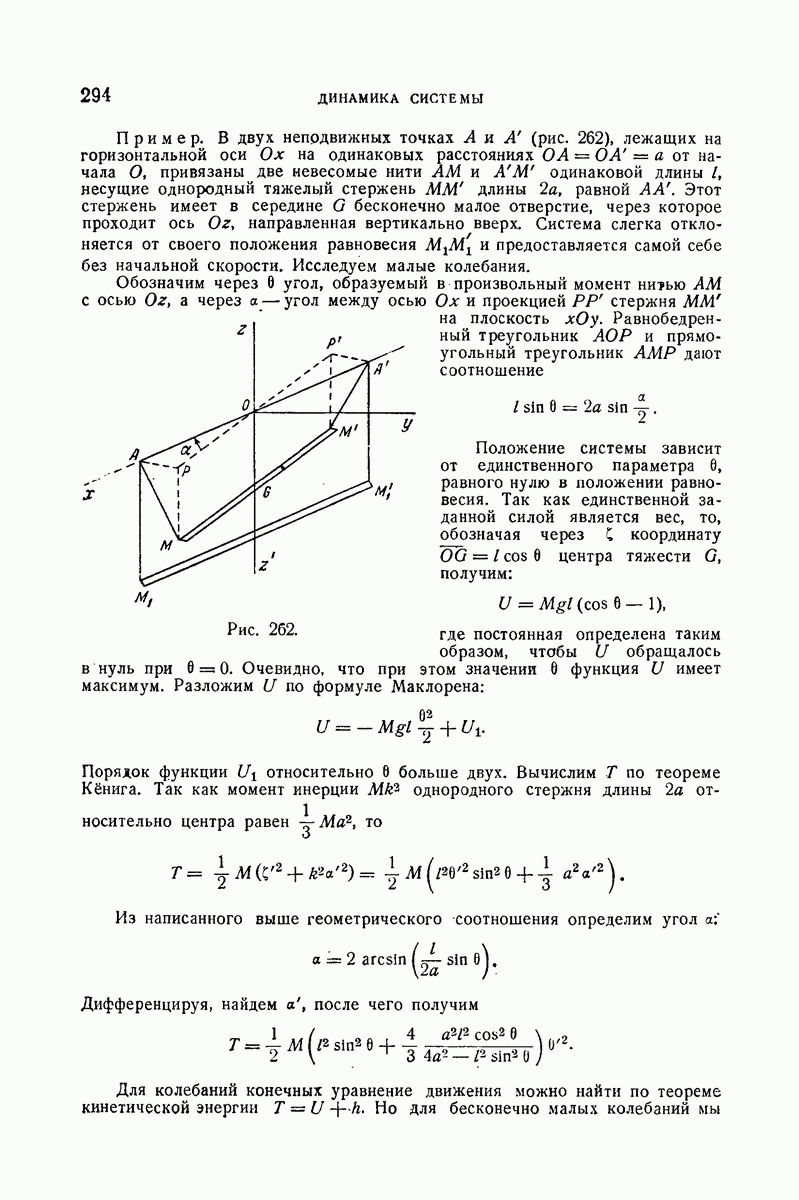
393. Уравнение герполодии.
Пуансо получил дифференциальное уравнение герполодии. заметив, что выражение дуги этой кривой функции радиуса От идентично выражению дуги полодии в функции того же радиуса, так как обе кривые катятся одна по другой. Мы применим другой метод, приводящий к несколько более коротким вычислениям, который мы заимствуем из заметки Дарбу к «Механике» Депейру (Despeyrous).
Пусть, как и выше,  — координаты полюса
— координаты полюса  относительно главных осей инерции
относительно главных осей инерции  Так как отношение постоянно и равно
Так как отношение постоянно и равно  то
то

Так как  являются эллиптическими функциями времени
являются эллиптическими функциями времени  то такими же будут и
то такими же будут и  Уравнения Эйлера, если в них заменить
Уравнения Эйлера, если в них заменить  через
через  приводятся к виду
приводятся к виду

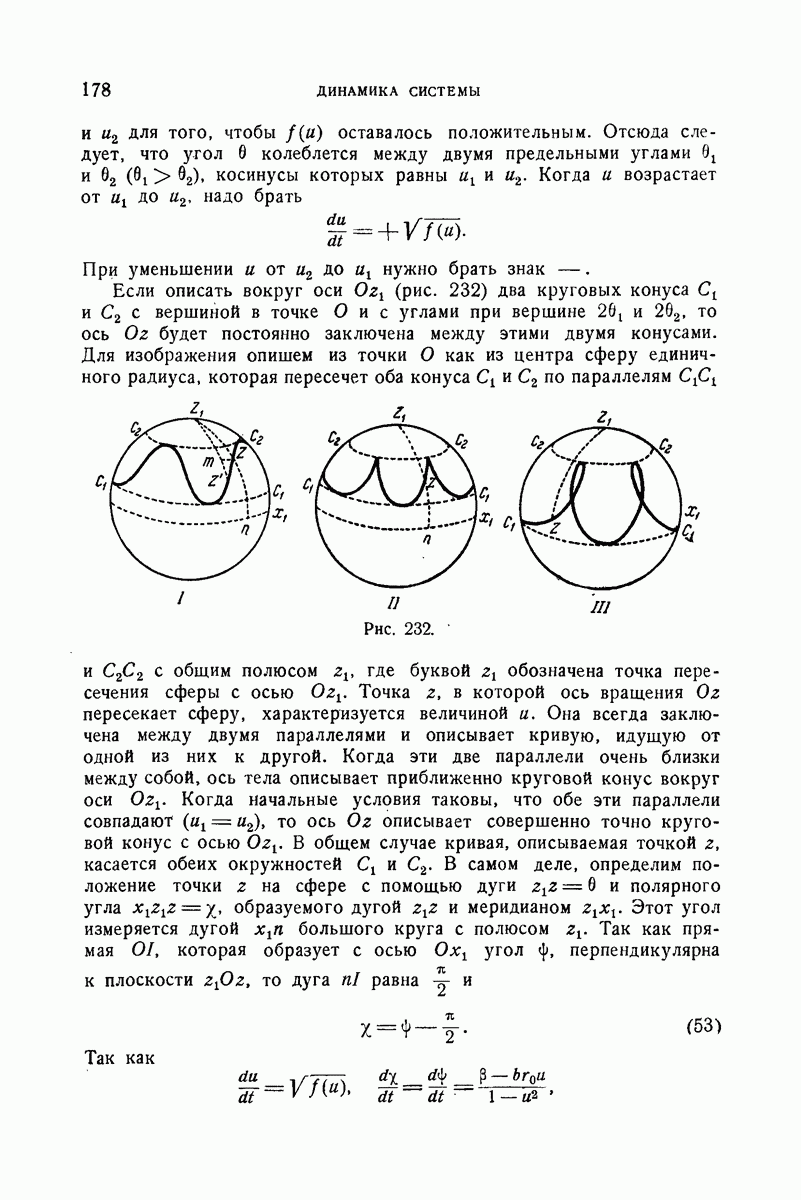
Обозначим, как и выше, через Р проекцию точки О на неподвижную плоскость II, которая содержит герполодию, и обозначим через  полярные координаты точки
полярные координаты точки  кривой, отнесенной к точке Р. Так как
кривой, отнесенной к точке Р. Так как

то имеем следующие уравнения:

из которых первое выражает, что  а последние суть уравнения полодии.
а последние суть уравнения полодии.
Разрешая эти уравнения относительно  и полагая
и полагая

получим:

Мы предположили, что  и что
и что  заключено между В и С. Тогда
заключено между В и С. Тогда  является отрицательным, и мы имеем
является отрицательным, и мы имеем  Следовательно,
Следовательно,  существенно положительно и никогда не обращается в нуль. Это находится в соответствии с тем, что
существенно положительно и никогда не обращается в нуль. Это находится в соответствии с тем, что  никогда не обращается в нуль. Для того чтобы
никогда не обращается в нуль. Для того чтобы  были положительны, необходимо, чтобы
были положительны, необходимо, чтобы  было положительно,
было положительно,  отрицательно. Следовательно,
отрицательно. Следовательно,  колеблется между а и
колеблется между а и  Таким образом, мы опять пришли к тому результату, что радиус-вектор
Таким образом, мы опять пришли к тому результату, что радиус-вектор
герполодии колеблется между минимумом  и максимумом
и максимумом  Дифференцируя перзое из уравнений (33), получим:
Дифференцируя перзое из уравнений (33), получим:

или, принимая во внимание уравнения (32),

Это уравнение, если заменить в нем х, у, z через их значения (34) и  через
через  принимает вид
принимает вид

Полученное уравнение позволяет найти  в функции
в функции  через эллиптическую функцию. Это выражение
через эллиптическую функцию. Это выражение  в функции
в функции  нам уже известно, так как х, у, z являются эллиптическими функциями времени
нам уже известно, так как х, у, z являются эллиптическими функциями времени 
Чтобы найти другое выражение, содержащее полярный угол  точки герполодии, нужно исходить из следующего замечания: если
точки герполодии, нужно исходить из следующего замечания: если  являются двумя бесконечно близкими положениями
являются двумя бесконечно близкими положениями  полюса в теле, то плоскость элементарного треугольника
полюса в теле, то плоскость элементарного треугольника  касательна к конусу мгновенных осей вращения в теле и проекции
касательна к конусу мгновенных осей вращения в теле и проекции  площади
площади  этого треугольника на главные плоскости эллипсоида равны
этого треугольника на главные плоскости эллипсоида равны

С другой стороны, так как конус мгновенных осей От в теле катится по неподвижному конусу с вершиной в точке О и с герполодией в качестве основания, то плоскость  касается также и неподвижного конуса, и элементарная площадь
касается также и неподвижного конуса, и элементарная площадь  равна также площади между двумя соответствующими бесконечно близкими образующими неподвижного конуса. Тогда проекция площади
равна также площади между двумя соответствующими бесконечно близкими образующими неподвижного конуса. Тогда проекция площади  на плоскость II, содержащую герполодию, есть элементарный сектор этой кривой
на плоскость II, содержащую герполодию, есть элементарный сектор этой кривой 
Так как плоскости  образуют с плоскостью П, перпендикулярной к
образуют с плоскостью П, перпендикулярной к  углы с косинусами
углы с косинусами 

Вычислим правую часть. Сначала находим

Далее, в силу уравнений, выводимых из уравнений Эйлера, и в силу уравнений (32) получаем:

Величина, заключенная в скобках, равна  как это видно после исключения
как это видно после исключения  из двух последних уравнений (33). Следовательно,
из двух последних уравнений (33). Следовательно,

Аналогичные выражения найдем путем перестановки букв для  и
и  Подставляя найденные выражения в равенство (36), получим после замены
Подставляя найденные выражения в равенство (36), получим после замены  величиной
величиной 

Заменим, наконец, в этом равенстве  их значениями (34) в функции
их значениями (34) в функции  и мы получим после сокращений соотношение вида
и мы получим после сокращений соотношение вида

где Е обозначает постоянную 
Соотношения (35) и (38) определяют  в функции времени. Исключая из
в функции времени. Исключая из  получим уравнение герполодин
получим уравнение герполодин

которое позволяет найти  через квадратуру.
через квадратуру.
Таким образом, можно построить герполодию и проверить, что она не имеет точек перегиба, для чего нужно вычислить радиус кривизны в функции  и доказать, что он никогда не обращается в бесконечность. Этот результат вытекает
и доказать, что он никогда не обращается в бесконечность. Этот результат вытекает  неравенства
неравенства  , связывающего три момента инерции. Кроме того, мы видим, что герполодия не имеет точек возврата, так как не обращается в нуль при значениях
, связывающего три момента инерции. Кроме того, мы видим, что герполодия не имеет точек возврата, так как не обращается в нуль при значениях  лежащих между а и
лежащих между а и 
Если эллипсоид инерции заменить произвольным эллипсоидом или гиперболоидом, который заставляли бы катиться и вертеться по неподвижной плоскости П, то соответствующая герполодия может иметь точки перегиба или возврата. Может также случиться, что радиус-вектор  не будет все время вращаться в одном и том же направлении. Мы отсылаем за более подробным рассмотрением этого вопроса геометрии к заметке Дарбу (Mecanique de Despeyrous) и к работе Гесса, а по поводу выражения к в функции времени к Traite Гринхилла (гл. III).
не будет все время вращаться в одном и том же направлении. Мы отсылаем за более подробным рассмотрением этого вопроса геометрии к заметке Дарбу (Mecanique de Despeyrous) и к работе Гесса, а по поводу выражения к в функции времени к Traite Гринхилла (гл. III).
В частном случае, когда  тогда Е, а и с обращаются в нуль, и квадратура, определяющая
тогда Е, а и с обращаются в нуль, и квадратура, определяющая  может быть выполнена в элементарных функциях. В этом случае
может быть выполнена в элементарных функциях. В этом случае

и, полагая  получим
получим

Это — уравнение спирали, изображенной на рис. 230.
Уравнения (35) и (38) можно получить, исходя также  замечания, что абсолютная скорость, с которой полюс
замечания, что абсолютная скорость, с которой полюс  описывает герполодию, равна в каждый момент времени относительной скорости по отношению к осям
описывает герполодию, равна в каждый момент времени относительной скорости по отношению к осям  с которой точка М описывает полодию. Это вытекает из того, что соответствующие дуги обеих кривых одинаковы. Тогда получаются два уравнения, если написать, что равны проекции этих двух скоростей на
с которой точка М описывает полодию. Это вытекает из того, что соответствующие дуги обеих кривых одинаковы. Тогда получаются два уравнения, если написать, что равны проекции этих двух скоростей на  и что равны моменты этих двух скоростей относительно
и что равны моменты этих двух скоростей относительно 
Герполддиограф Дарбу и Кёнигса. Картина движения, которую дал Пуансо, обладает тем недостатком, что в ней не представлено время. Действительно, если материально осуществить оба конуса, имеющих вершины в точке О, а основаниями полодию и герполодию и если при помощи какого-нибудь сцепления заставить один из них катиться по другому, то еще не будет получаться полное представление движения, так как, кроме того, необходимо катящемуся конусу сообщить мгновенную угловую скорость, которая в каждое мгновение пропорциональна От. Дарбу доказал (заметка в Mecanique de Despeyrous), что можно построить прибор, выполняющий это условие, если к предыдущему представлению движения присоединить другое представление, также принадлежащее Пуансо.
Пусть, как и раньше,  есть точка касания эллипсоида инерции с плоскостью
есть точка касания эллипсоида инерции с плоскостью  проекция центра О на плоскость П. Проведем через центр О (рис. 231) эллипсоида плоскость П, параллельную неподвижной плоскости П, и обозначим через
проекция центра О на плоскость П. Проведем через центр О (рис. 231) эллипсоида плоскость П, параллельную неподвижной плоскости П, и обозначим через  проекцию точки
проекцию точки  на плоскость П. Мгновенную угловую скорость вращения
на плоскость П. Мгновенную угловую скорость вращения  , направленную вдоль
, направленную вдоль  , можно разложить на две, из которых одна, направленная по
, можно разложить на две, из которых одна, направленная по  имеет постоянное значение
имеет постоянное значение  , а другая, направленная по От, равна
, а другая, направленная по От, равна  Если сообщить плоскости П постоянное вращение с угловой скоростью
Если сообщить плоскости П постоянное вращение с угловой скоростью  вокруг
вокруг  то движение эллипсоида относительно плоскости П, которая станет, таким образом, подвижной, приведется в каждый момент к одному вращению вокруг
то движение эллипсоида относительно плоскости П, которая станет, таким образом, подвижной, приведется в каждый момент к одному вращению вокруг  Во время движения положение прямой От меняется как в теле, так и в пространстве. В теле оно описывает конус
Во время движения положение прямой От меняется как в теле, так и в пространстве. В теле оно описывает конус  второго порядка, а в пространстве оно описывает плоскость П. Относительное движение эллипсоида по отношению к плоскости П, которая становится подвижной, приводится, следовательно, к качению конуса
второго порядка, а в пространстве оно описывает плоскость П. Относительное движение эллипсоида по отношению к плоскости П, которая становится подвижной, приводится, следовательно, к качению конуса  по этой плоскости, причем относительная угловая скорость качения постоянно равна
по этой плоскости, причем относительная угловая скорость качения постоянно равна 

Рис. 231.
Следовательно, движение тела представляется качением конуса  неизменно связанного с телом, по плоскости П, причем это качение осуществляется с мгновенной угловой скоростью
неизменно связанного с телом, по плоскости П, причем это качение осуществляется с мгновенной угловой скоростью  в то время как плоскость вращается с постоянной угловой скоростью
в то время как плоскость вращается с постоянной угловой скоростью  вокруг своей нормали
вокруг своей нормали 
Проверим теперь, будет  действительно конус
действительно конус  поверхностью второго порядка. Для составления уравнения этого конуса будем искать геометрическое место различных, положений точки
поверхностью второго порядка. Для составления уравнения этого конуса будем искать геометрическое место различных, положений точки  относительно осей
относительно осей  эллипсоида. Так как точка
эллипсоида. Так как точка  лежит на нормали к эллипсоиду инерции в полюсе
лежит на нормали к эллипсоиду инерции в полюсе  , то
, то

и так как эта точка лежит в плоскости П, параллельной касательной плоскости к эллипсоиду в точке  то имеем также
то имеем также

Мы обозначили через I общее значение отношений (40). Определим из них  и подставим в равенство (41). Получим
и подставим в равенство (41). Получим

На основании уравнений (29) и (30) полодин, первый член этого отношения равен 1, а второй равен  Следовательно,
Следовательно,

и из соотношений (40) получаем для координат точки  значения
значения

Таким путем можно определить геометрическое место точек  зная геометрические места точек
зная геометрические места точек  . Так как полодия, геометрическое место точек
. Так как полодия, геометрическое место точек  лежит на конусе
лежит на конусе

то геометрическое место точек  лежит на конусе
лежит на конусе  определяемом уравнением
определяемом уравнением

Таково уравнение конуса  геометрического места прямых
геометрического места прямых  в теле. Оно действительно второго порядка.
в теле. Оно действительно второго порядка.
Установив это, вернемся к движению. Сопоставляя оба способа воспроизведения движения, данных Пуансо, мы вндим, что, в то время как центральный эллипсоид катится по неподвижной плоскости П, конус  неизменно связанный с телом, катится по плоскости П, а последняя вращается с постоянной угловой скоростью (
неизменно связанный с телом, катится по плоскости П, а последняя вращается с постоянной угловой скоростью ( вокруг
вокруг 
Допустим теперь, что конус  с неподвижной вершиной в точке О и плоскость П осуществлены материально, причем плоскость П может вращаться вокруг
с неподвижной вершиной в точке О и плоскость П осуществлены материально, причем плоскость П может вращаться вокруг  а конус
а конус  при помощи зубчатого зацепления вынужден катиться по плоскости П. Предположим, с другой стороны, что полодня, материально осуществленная на эллипсоиде, вынуждена при помощи зубчатого зацепления или достаточно большого трения катиться по плоскости П. Наконец, вообразим, что тело совершает свое движение. Тогда оно увлекает конус
при помощи зубчатого зацепления вынужден катиться по плоскости П. Предположим, с другой стороны, что полодня, материально осуществленная на эллипсоиде, вынуждена при помощи зубчатого зацепления или достаточно большого трения катиться по плоскости П. Наконец, вообразим, что тело совершает свое движение. Тогда оно увлекает конус  который, катясь по плоскости П, заставляет ее вращаться с постоянной угловой скоростью. Наоборот, если при помощи часового механизма заставить плоскость П вращаться вокруг
который, катясь по плоскости П, заставляет ее вращаться с постоянной угловой скоростью. Наоборот, если при помощи часового механизма заставить плоскость П вращаться вокруг  с постоянной угловой скоростью, то эта плоскость увлечет конус
с постоянной угловой скоростью, то эта плоскость увлечет конус  который в свою очередь заставит полодию катиться по плоскости П в соответствии с законом движения. Именно по этому принципу Дарбу и Кённгс сконструировали прибор «герполоднограф», который позволяет вопроизводнть всю кинематику движения твердого тела. Мы не входим здесь в подробности конструкции этого прибора, описание которого можно найти в статье Кбнигса (Koenigs, Revue g6n6rale des Sciences, 30 апреля 1891). Закончим замечанием, принадлежащим Кёнигсу (Bulletin de la Soci6t6 mathmatique de France, т. XVIII, стр. 163 и 131). Главной целью прибора является демонстрация закона изменения скоростей, и поэтому желательно, чтобы это изменение было достаточно заметно и бросалось в глаза. К сожалению, в этом отношении приходится быть весьма ограниченным. Если по неподвижной плоскости заставить катиться произвольный эллипсоид с закрепленным центром при соблюдении закона Пуансо, т. е. с угловой скоростью, пропорциональной диаметру точки касания, то отношение наименьшего значения угловой скорости к Наибольшему ее значению может принимать любые желательные значения между
который в свою очередь заставит полодию катиться по плоскости П в соответствии с законом движения. Именно по этому принципу Дарбу и Кённгс сконструировали прибор «герполоднограф», который позволяет вопроизводнть всю кинематику движения твердого тела. Мы не входим здесь в подробности конструкции этого прибора, описание которого можно найти в статье Кбнигса (Koenigs, Revue g6n6rale des Sciences, 30 апреля 1891). Закончим замечанием, принадлежащим Кёнигсу (Bulletin de la Soci6t6 mathmatique de France, т. XVIII, стр. 163 и 131). Главной целью прибора является демонстрация закона изменения скоростей, и поэтому желательно, чтобы это изменение было достаточно заметно и бросалось в глаза. К сожалению, в этом отношении приходится быть весьма ограниченным. Если по неподвижной плоскости заставить катиться произвольный эллипсоид с закрепленным центром при соблюдении закона Пуансо, т. е. с угловой скоростью, пропорциональной диаметру точки касания, то отношение наименьшего значения угловой скорости к Наибольшему ее значению может принимать любые желательные значения между  .
.
Для этого достаточно подходящим образом выбрать эллипсоид и плоскость, по которой он катится. Этим путем можно получить легко заметные изменения угловой скорости, так как она удваивается или увеличивается в пять раз. Но в случае движения твердого тела катящийся эллипсоид является эллипсоидом инерции, и для него  . Это неравенство ограничивает выбор катящегося эллипсоида и приводит к тому, что отношение наименьшего значения угловой скорости к ее наибольшему значению будет обязательно заключено между 1 и
. Это неравенство ограничивает выбор катящегося эллипсоида и приводит к тому, что отношение наименьшего значения угловой скорости к ее наибольшему значению будет обязательно заключено между 1 и  Это будет доказано в упражнениях. Можно, наконец, осуществить условия, при которых указанное отношение будет сколь угодно близко к этий двум пределам. Изменение будет, таким образом, очень слабым и поневоле потребует большого внимания, чтобы быть замеченным. Следовательно, неравенство
Это будет доказано в упражнениях. Можно, наконец, осуществить условия, при которых указанное отношение будет сколь угодно близко к этий двум пределам. Изменение будет, таким образом, очень слабым и поневоле потребует большого внимания, чтобы быть замеченным. Следовательно, неравенство  , приводит, с одной стороны, к отсутствию точек перегиба у герполодии, а с другой —к некоторой устойчивости значения угловой скорости.
, приводит, с одной стороны, к отсутствию точек перегиба у герполодии, а с другой —к некоторой устойчивости значения угловой скорости.
Исследования Альфена а Гринхилла. Гринхилл, интересные исследования которого о случае, когда задача о сферическом маятнике приводится к псевдоэллиптическому интегралу, мы уже цитировали, указал также случай, когда и задача Пуансо приводится к псевдоэллиптическому интегралу. Эти исследования изложены в его «Эллиптических функциях» (Fonctions ellip-tiques) и в работе «On pseudo-elliptic integrals and their dynamical applications (Proceedings of the London Mathematical Society, т. XXV). Наиболее простой случай, приводящий к алгебраической герполодии четвертого порядка, отмечен впервые Гальфеном (Halphen). В этих исследованиях, имеющих исключительно геометрический и аналитический характер, Гальфен и Гринхилл предполагают, что по неподвижной плоскости П катится произвольная центральная поверхность второго порядка, так что в уравнении этой поверхности

коэффициенты произвольны и могут быть отрицательными (см. Halphen, Fonctions elliptiques, т. II, стр. 282).
Теорема Сильвестра. Сильвестр показал, что оба способа воспроизведения движения, предложенные Пуансо, являются частными случаями бесконечного множества других, которые могут быть получены следующим образом: построим поверхность второго порядка, подобную поверхности второго порядка, софокусной с эллипсоидом инерции, и заставим ее катиться и вертеться по плоскости П, параллельной неподвижной плоскости П, находящейся на постоянном расстоянии  от центра и совершающей равномерное вращение вокруг
от центра и совершающей равномерное вращение вокруг  (Philosophical Transactions, 1866). Мы ограничиваемся лишь формулировкой этого предложения, которое читатель может доказать в виде упражнения и доказательство которого было указано Дарбу (примечание к Mecanique de Despeyrous).
(Philosophical Transactions, 1866). Мы ограничиваемся лишь формулировкой этого предложения, которое читатель может доказать в виде упражнения и доказательство которого было указано Дарбу (примечание к Mecanique de Despeyrous).
| << Предыдущий параграф | Следующий параграф >> |
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
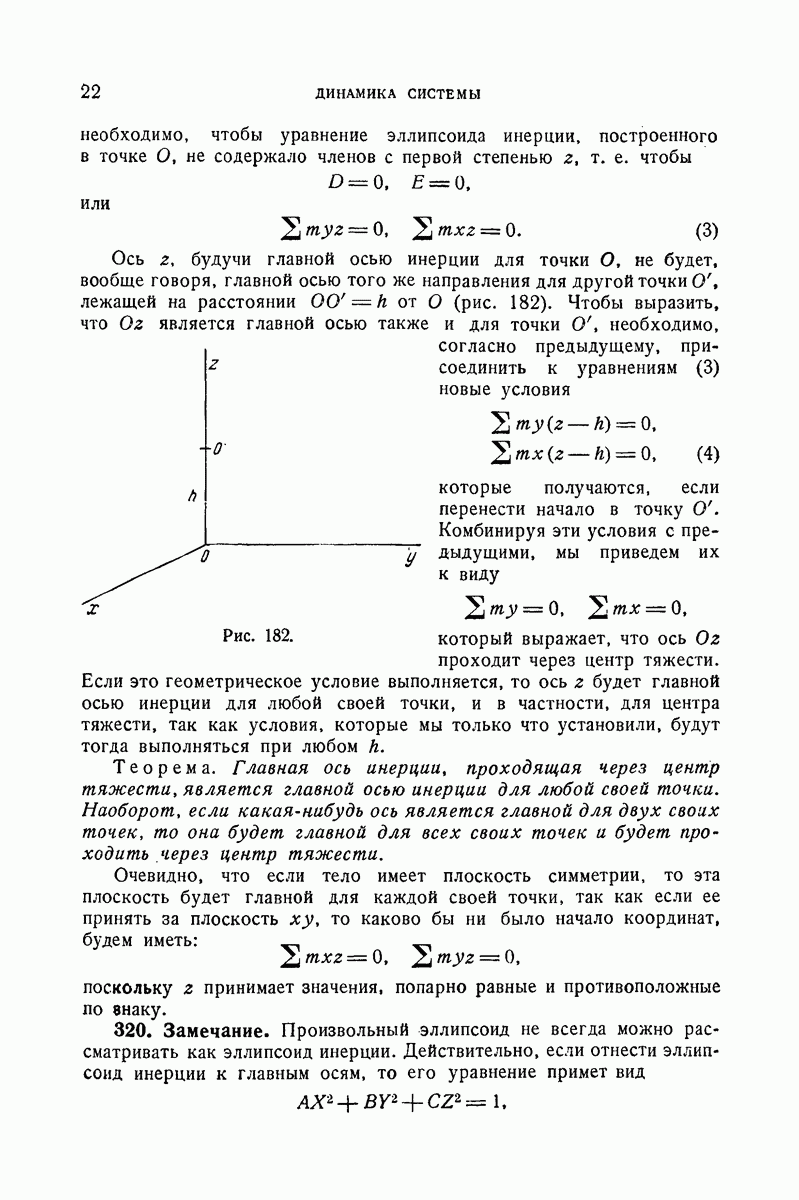
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
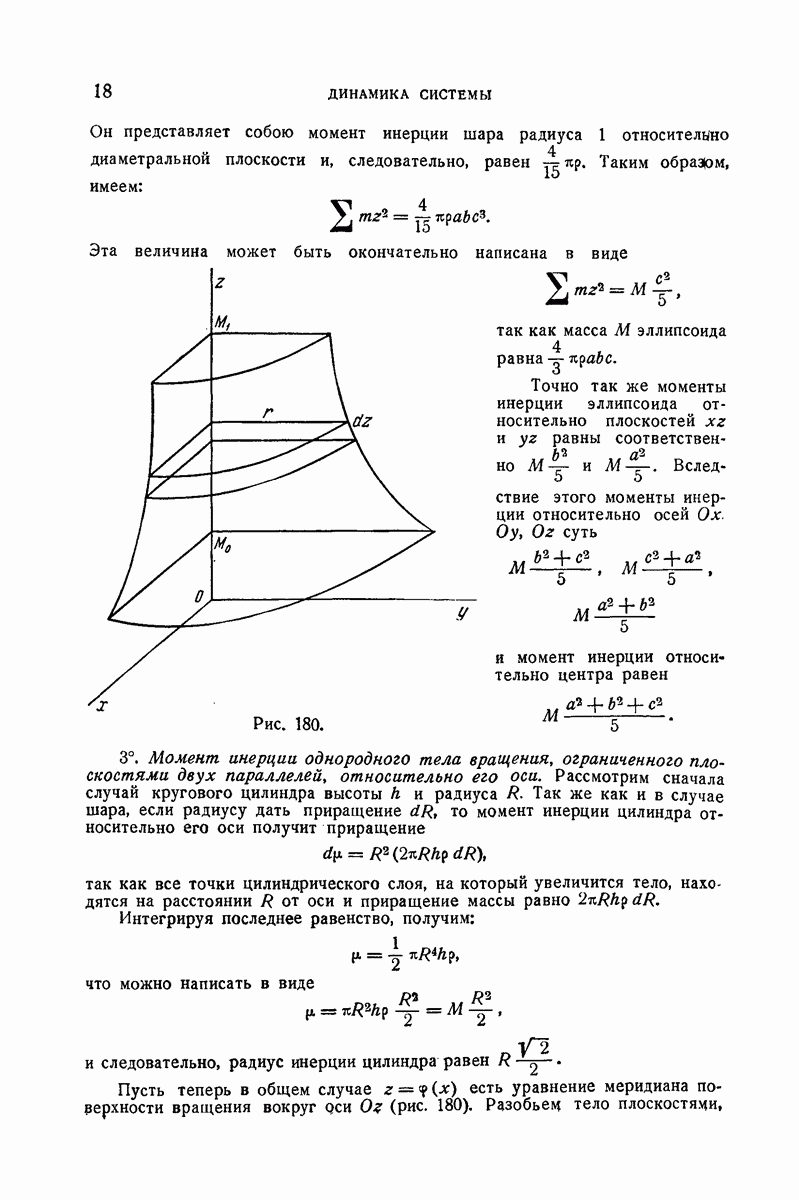
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
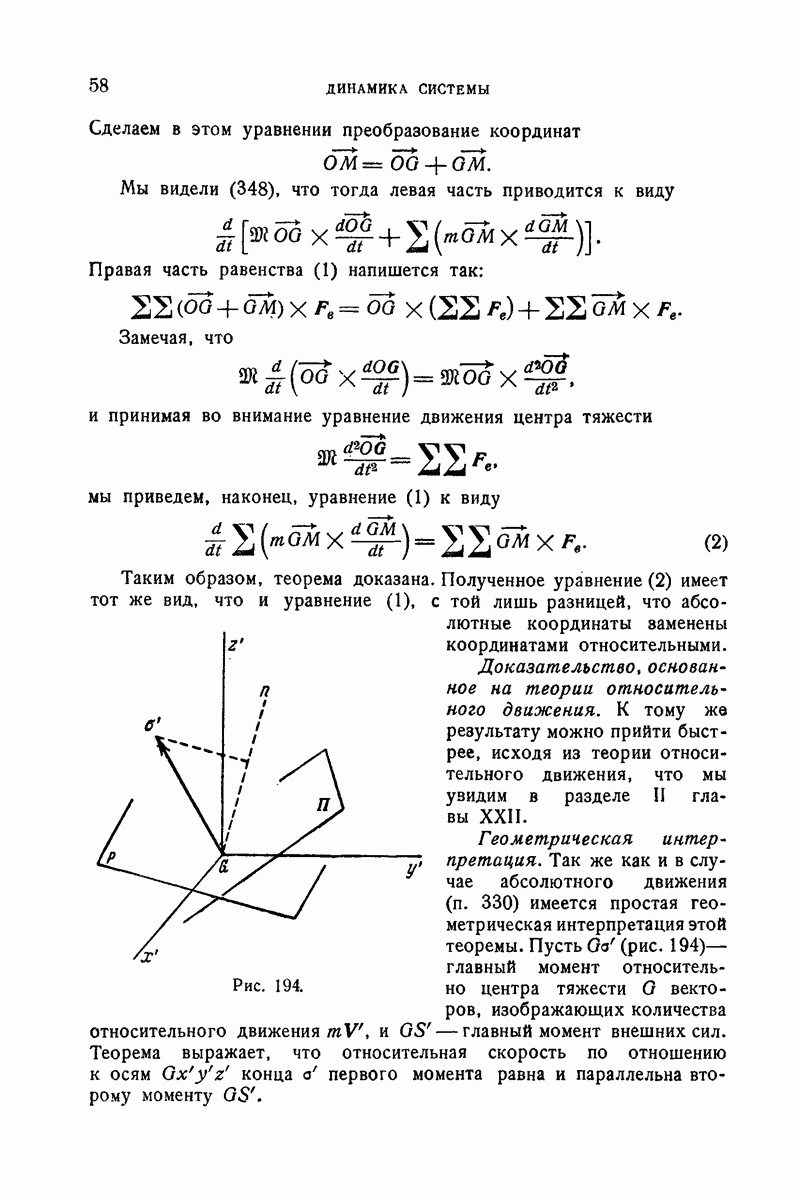
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
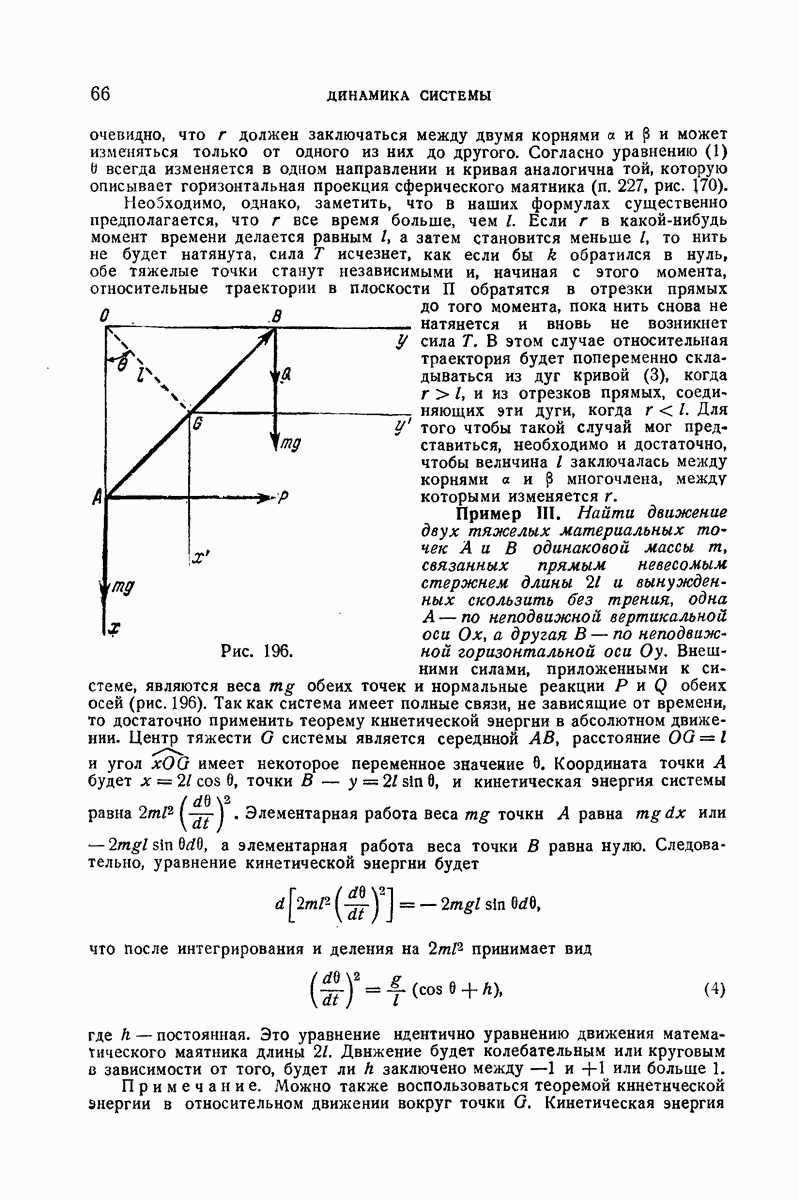
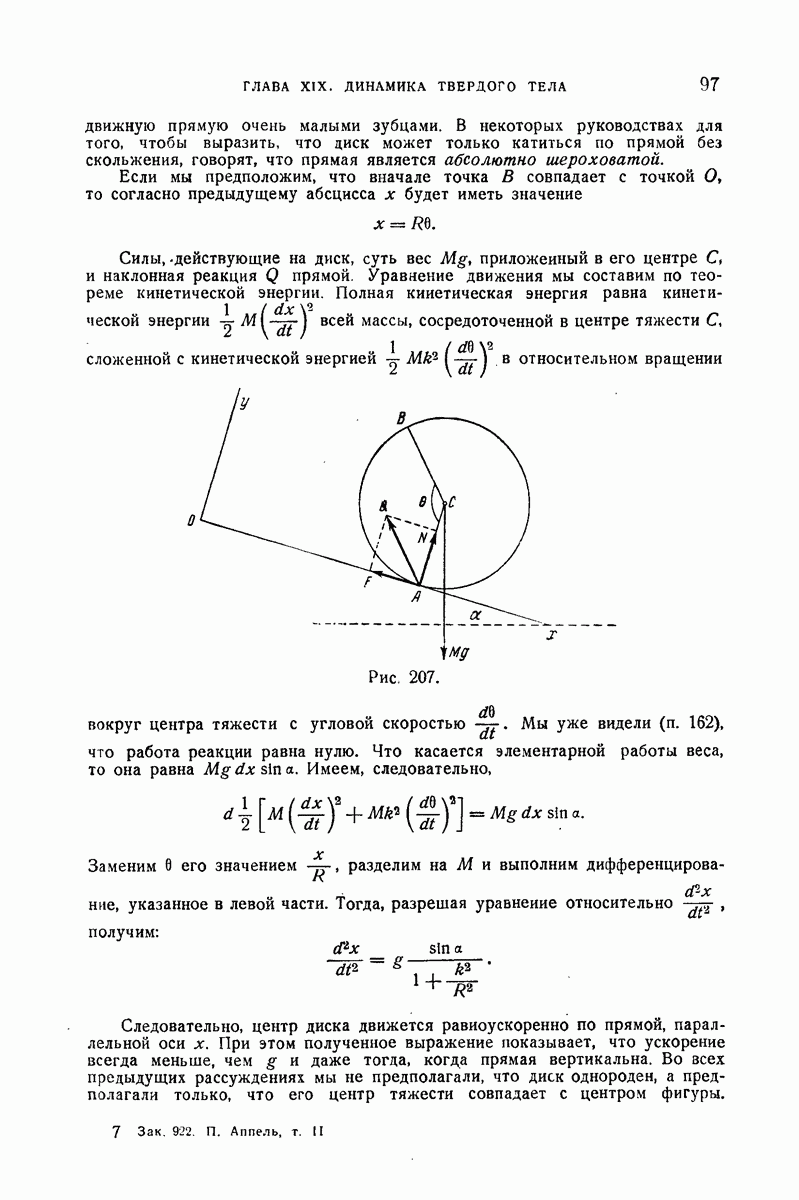
- 354. Пример I.
- V. Энергия
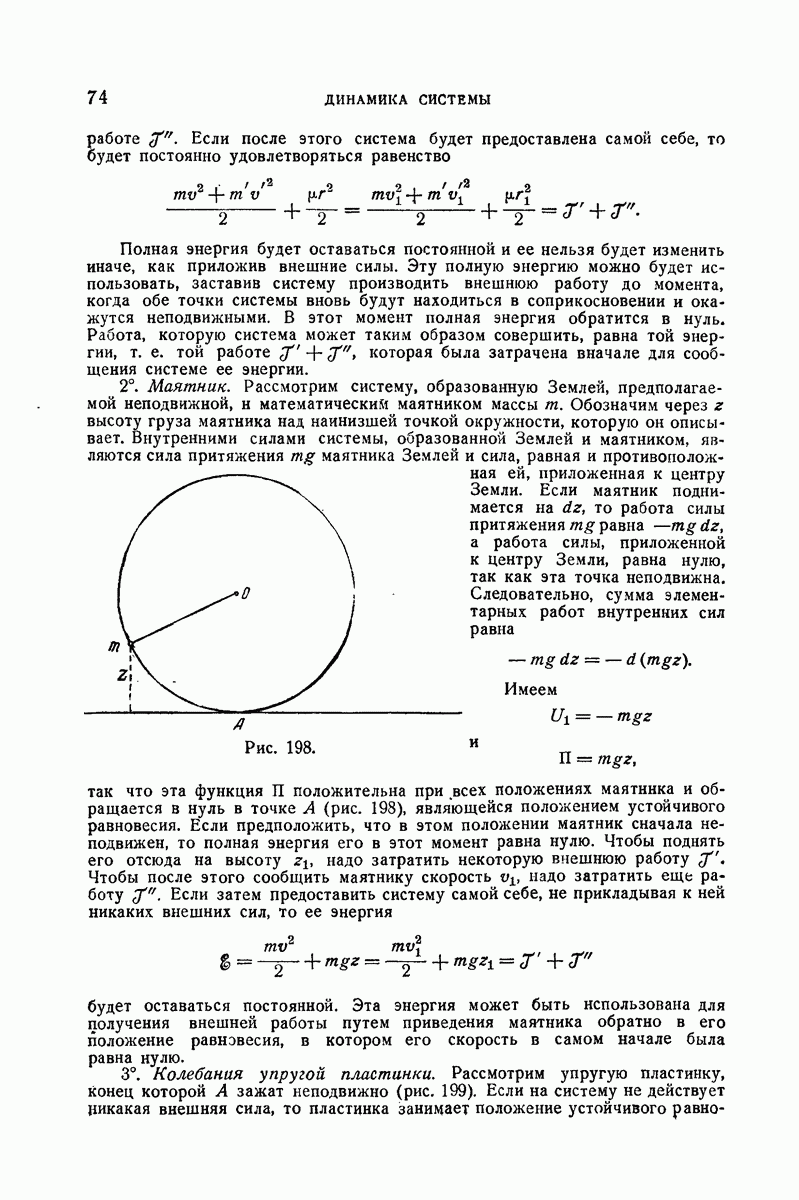
- 356. Потенциальная энергия. Механический смысл.
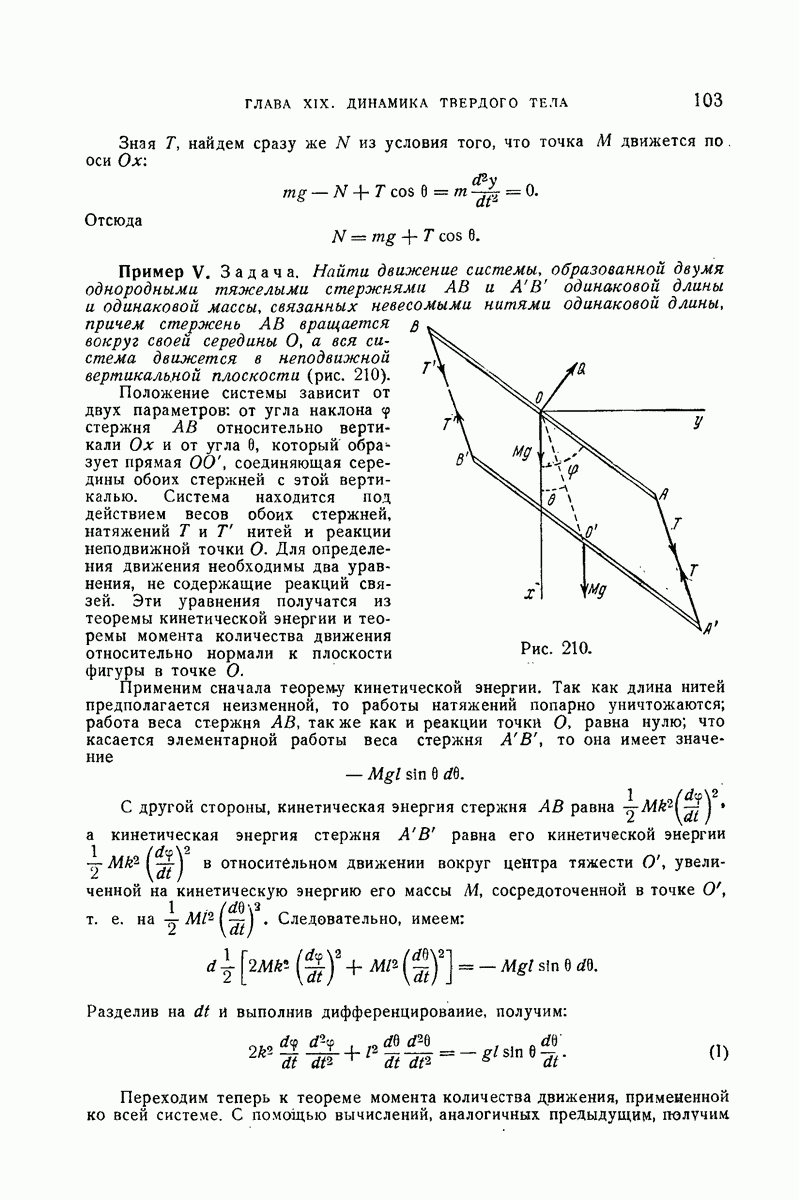
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
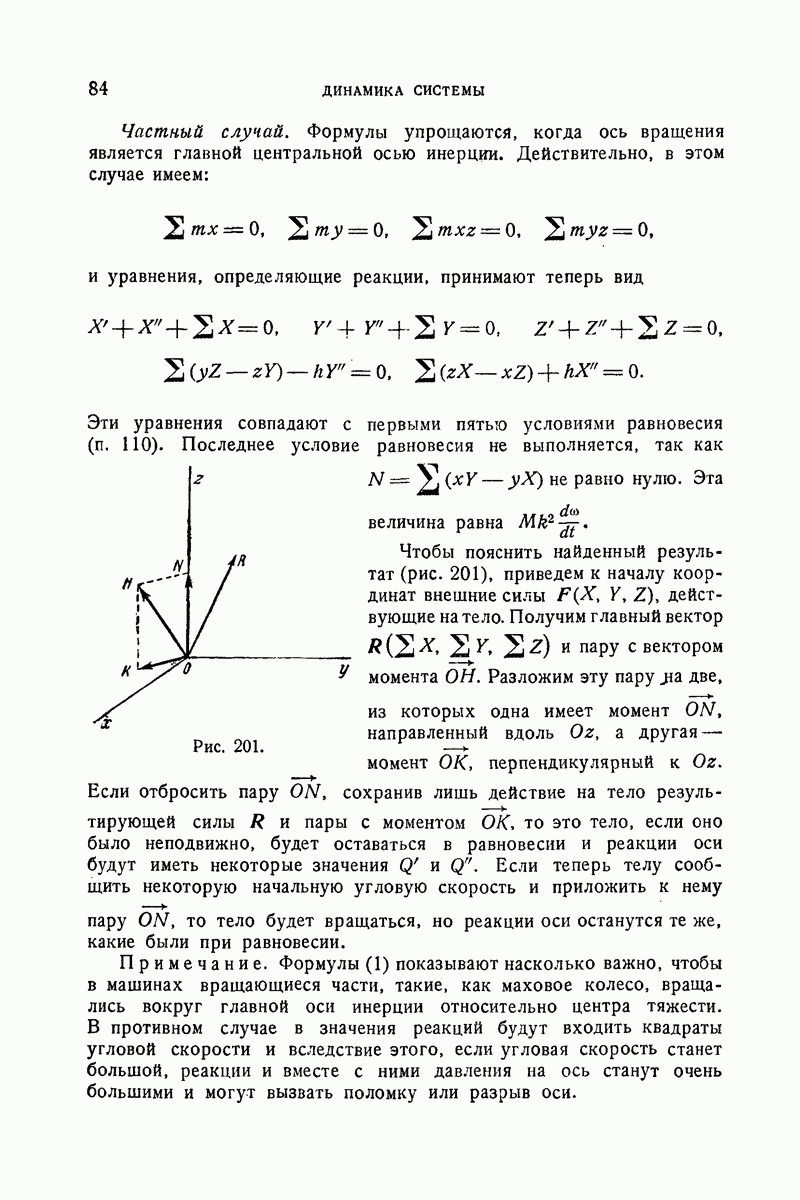
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
- 370. Пример I.
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
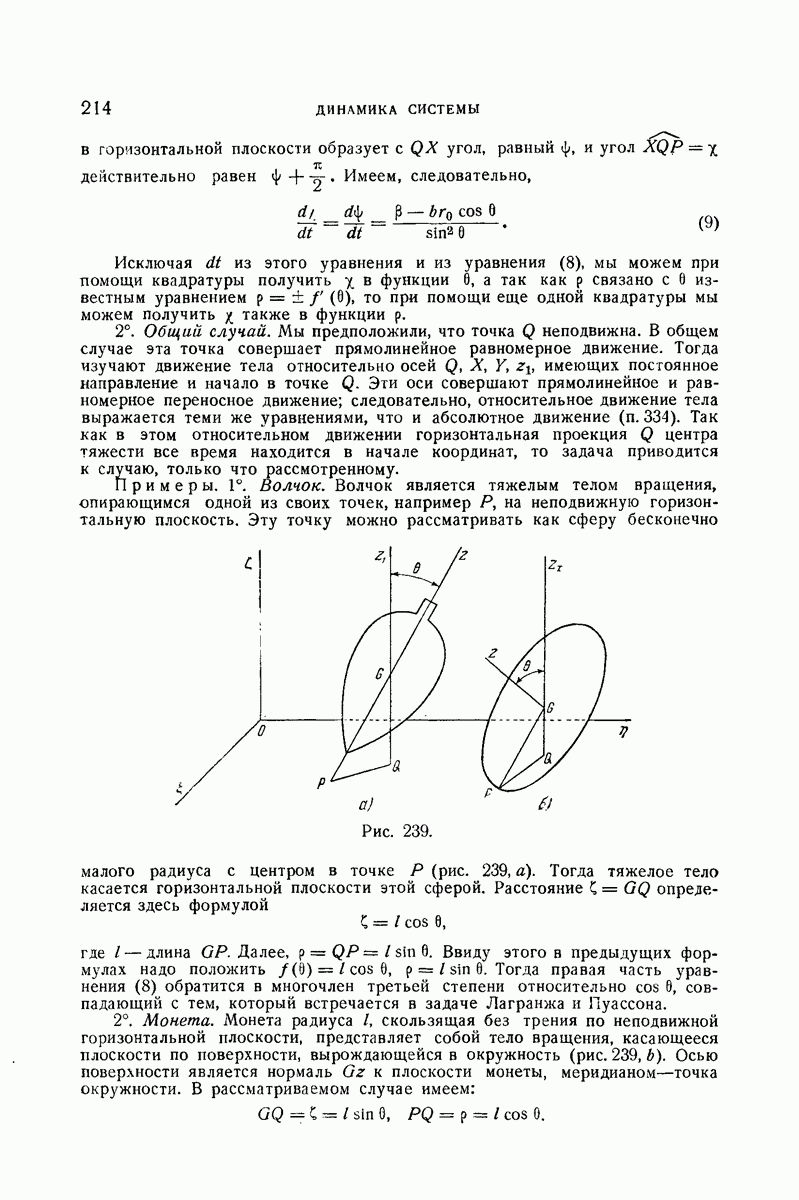
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
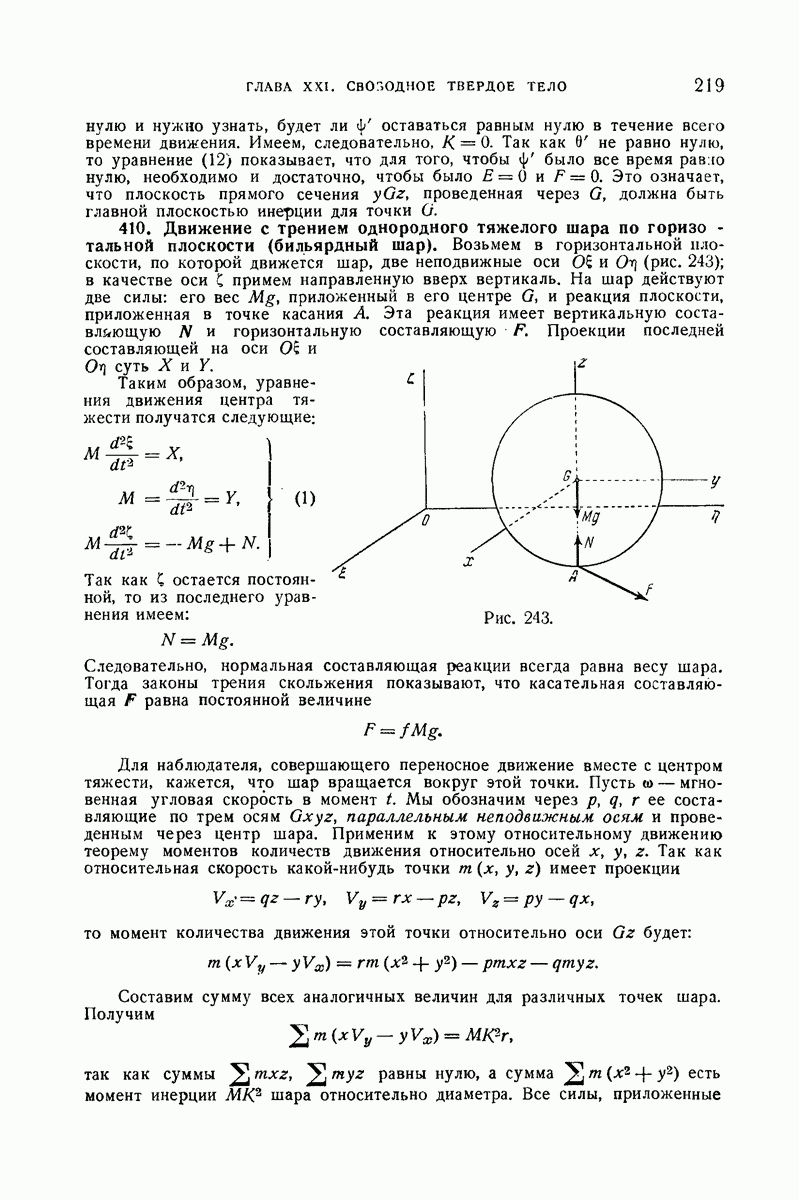
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
- 421. Твердое тело.
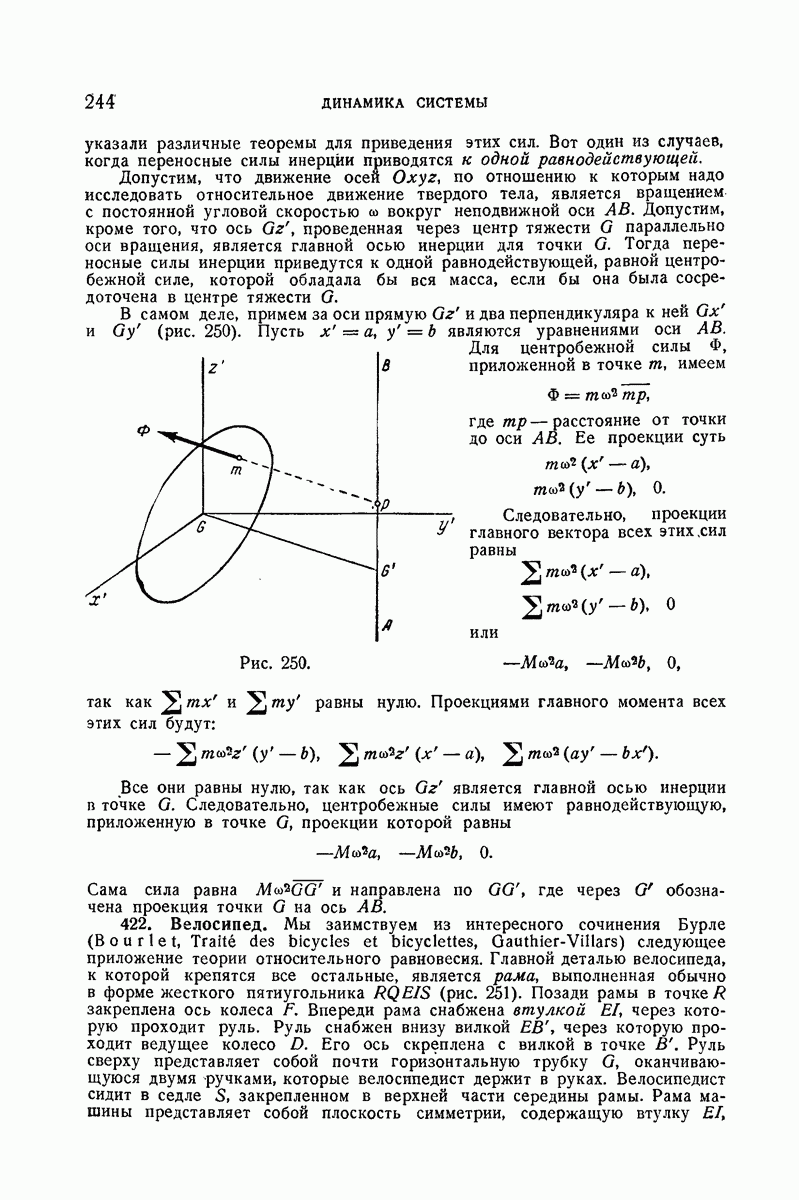
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
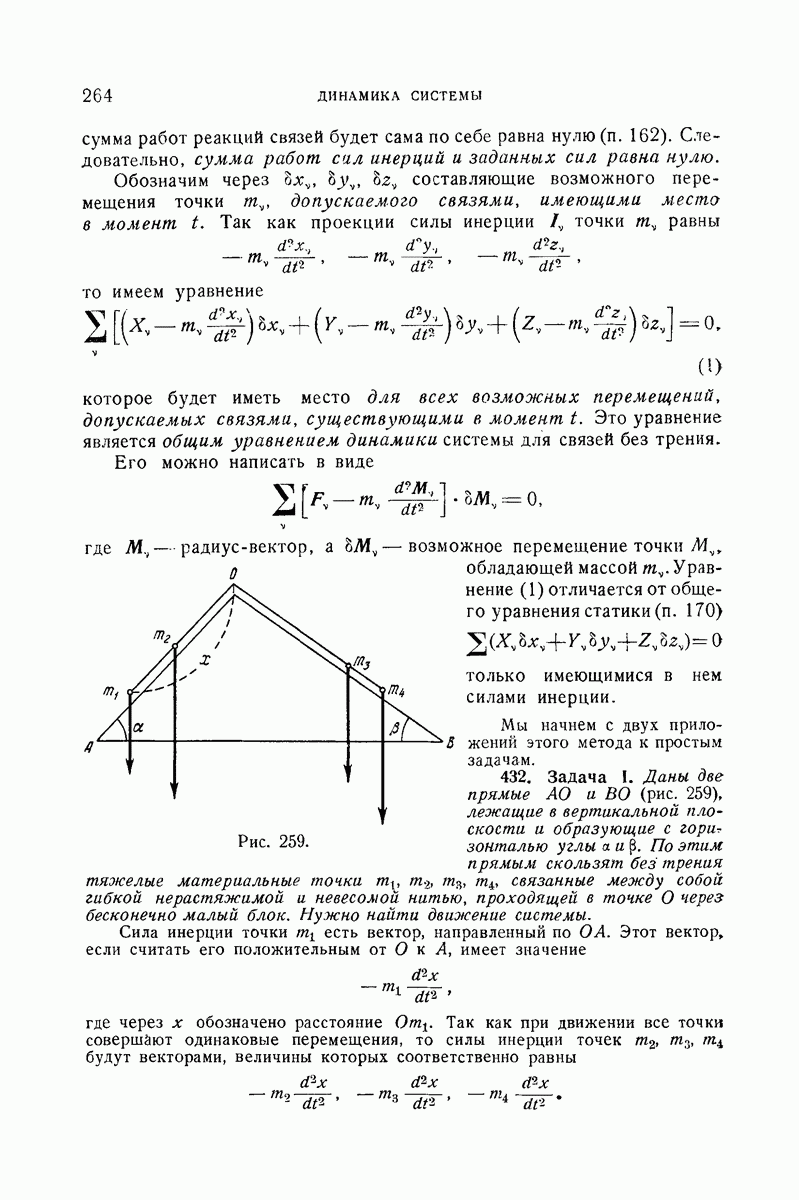
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
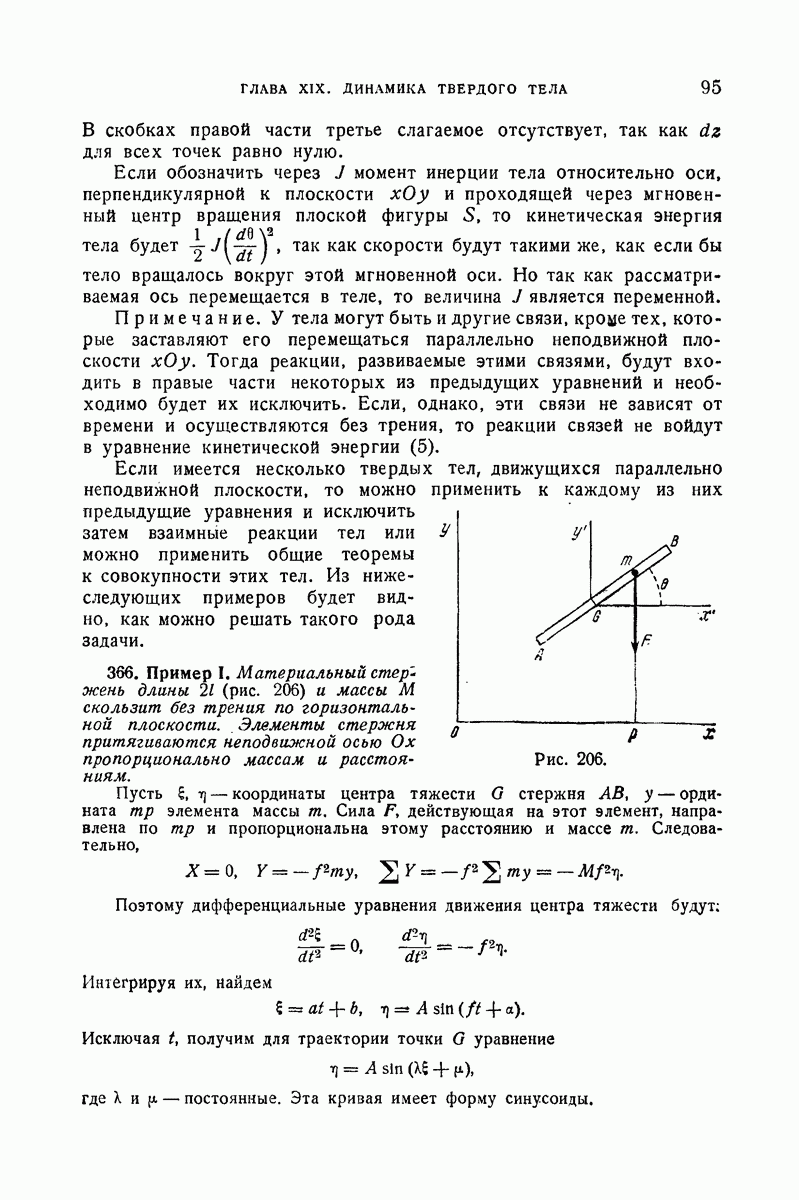
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели