| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
392. Геометрическое представление движения по Пуансо.
В работе, помещенной в т. XVI Journal de Liouville, Пуансо дал геометрическое представление движения, основанное на следующих теоремах кинематики, которые остаются справедливыми в любом случае движения твердого тела вокруг неподвижной точки.
Рассмотрим эллипсоид инерции тела, построенный в неподвижной точке О и пусть  — главные оси инерции этого эллипсоида. В некоторый момент времени мгновенная ось вращения
— главные оси инерции этого эллипсоида. В некоторый момент времени мгновенная ось вращения  пересекает поверхность эллипсоида в некоторой точке
пересекает поверхность эллипсоида в некоторой точке  которую Пуансо называет полюсом.
которую Пуансо называет полюсом.
Теорема I. Кинетическая энергия тела равна 
В самом деле, на основании самого определения эллипсоида инерции момент инерции тела относительно оси  равен
равен 
и так как скорости точек тела будут такими, как если бы тело вращалось с угловой скоростью  вокруг
вокруг  то кинетическая энергия
то кинетическая энергия  равна половине произведения момента инерции на квадрат угловой скорости (п. 359)
равна половине произведения момента инерции на квадрат угловой скорости (п. 359) 
Теорема II. В каждый момент времена касательная плоскость к эллипсоиду инерции в полюсе  перпендикулярна к главному моменту
перпендикулярна к главному моменту  количеств движения.
количеств движения.
В самом деле, эллипсоид инерции, отнесенный к осям  имеет уравнение
имеет уравнение

Направляющие косинусы вектора  равны координаты
равны координаты  полюса
полюса  относительно тех же осей можно представить в виде
относительно тех же осей можно представить в виде

Следовательно, уравнение касательной плоскости в точке 

принимает вид

Эта плоскость перпендикулярна к вектору  проекции которого равны
проекции которого равны 
Теорема III. Расстояние от неподвижной точки до плоскости, касательной к эллипсоиду инерции в полюсе, равно квадратному корню из удвоенной кинетической энергии, деленной на главный момент количеств движения.
В самом деле, расстояние от точки О до касательной плоскости

что и доказывает теорему.
Применим теперь эти три теоремы к частному случаю, когда силы, приложенные к твердому телу, приводятся к одной равнодействующей, проходящей через неподвижную точку. Тогда:
1°. Кинетическая энергия будет постоянной и равной  или
или  Следовательно, имеем
Следовательно, имеем

2°. Главный момент  количеств движения имеет фиксированное направление: плоскость, касательная к эллипсоиду в точке
количеств движения имеет фиксированное направление: плоскость, касательная к эллипсоиду в точке  будет также иметь фиксированное направление, перпендикулярное к
будет также иметь фиксированное направление, перпендикулярное к 
3°. Главный момент  имеет постоянную величину I или
имеет постоянную величину I или  и поэтому расстояние от точки О до касательной плоскости в точке
и поэтому расстояние от точки О до касательной плоскости в точке  равное
равное

будет также постоянным.
В результате плоскость П, касательная в точке  будет неподвижна, так как она имеет постоянное направление и находится на постоянном расстоянии от неподвижной точки О.
будет неподвижна, так как она имеет постоянное направление и находится на постоянном расстоянии от неподвижной точки О.
Мы пришли, следовательно, к выводу, что эллипсоид инерции постоянно касается неподвижной плоскости П. Точка касания  является полюсом, прямая
является полюсом, прямая  — мгновенной осью, а мгновенная угловая скорость
— мгновенной осью, а мгновенная угловая скорость  равная
равная  пропорциональна
пропорциональна  . Пуансо называет полодией кривую, описываемую полюсом
. Пуансо называет полодией кривую, описываемую полюсом  на поверхности эллипсоида, и герполодией — кривую, описываемую полюсом на неподвижной плоскости II (рис. 228).
на поверхности эллипсоида, и герполодией — кривую, описываемую полюсом на неподвижной плоскости II (рис. 228).

Рис. 228.
Конус, являющийся геометрическим местом мгновенных осей в теле, имеет вершину в точке О, и в качестве направляющей — полодию; конус, являющийся геометрическим местом мгновенных осей в пространстве, имеет вершину тоже в точке О, а в качестве основания — герполодию. Для получения движения нужно заставить первый конус катиться по второму таким образом, чтобы мгновенная угловая скорость  была в каждый момент пропорциональна От, так как
была в каждый момент пропорциональна От, так как

Так как точка эллипсоида, которая находится в соприкосновении с плоскостью П, имеет в каждый момент скорость, равную нулю, поскольку она находится на мгновенной оси, то можно также сказать, что движение получится, если заставить эллипсоид инерции катиться и вертеться (без скольжения) по неподвижной плоскости П. Положение этой неподвижной плоскости известно из начальных условий.
Можно еще иначе представить себе движение, допустив, что материально осуществлена поверхность катящегося конуса, ограниченная полодией: образованное таким образом тело катится по плоскости П, и его следом является герполодия (рис. 228а). Так как полодия катится по герполодии без скольжения, то соответствующие дуги обеих кривых имеют одинаковые длины.

Рис. 228а.
Полодия. Найдем уравнение полодии. С этой целью отнесем эллипсоид инерции к его осям. Мы можем определить полодию как геометрическое место точек  эллипсоида, в каждой из которых касательная плоскость
эллипсоида, в каждой из которых касательная плоскость

находится на постоянном расстоянии  начала координат. Это условие выражается уравнением
начала координат. Это условие выражается уравнением

Это уравнение совместно с уравнением эллипсоида

определяет полодию, которая является, таким образом, алгебраической кривой четвертого порядка. Можно себе представить вид этой кривой, если рассматривать ее как пересечение эллипсоида и конуса, являющегося геометрическим местом мгновенных осей вращения От в теле или, что то же, являющегося катящимся конусом. Уравнение этого конуса получится путем исключения правых частей из равенств (29) и (30), что приводит к уравнению

Для того чтобы этот конус был вещественным, необходимо, чтобы

Это — очевидное условие того, что расстояние  от касательной плоскости до начала координат должно быть меньше, чем наибольшая
от касательной плоскости до начала координат должно быть меньше, чем наибольшая
полуось  и больше, чем наименьшая полуось
и больше, чем наименьшая полуось  Конус вырождается в две мнимые плоскости, т. е. в прямую, совпадающую с осью
Конус вырождается в две мнимые плоскости, т. е. в прямую, совпадающую с осью  или с осью
или с осью  когда
когда  или
или  Это легко объяснить геометрически, поскольку концы
Это легко объяснить геометрически, поскольку концы  большой оси и концы а и а малой оси являются единственными вещественными точками, в которых касательная плоскость имеет максимальное или минимальное расстояние от начала. Полодия будет тогда состоять из двух точек с к с или а и а (рис. 229). При
большой оси и концы а и а малой оси являются единственными вещественными точками, в которых касательная плоскость имеет максимальное или минимальное расстояние от начала. Полодия будет тогда состоять из двух точек с к с или а и а (рис. 229). При  конус распадается на две вещественные плоскости, проходящие через среднюю ось
конус распадается на две вещественные плоскости, проходящие через среднюю ось


Рис. 229.
Это как раз те самые плоскости, с которыми мы встречались при аналитическом исследовании задачи. В этом случае полодии состоят из двух эллипсов  пересекающихся на двух концах
пересекающихся на двух концах  средней оси.
средней оси.
Таким образом, полодия является пересечением эллипсоида инерции и конуса второго порядка, имеющего те же плоскости симметрии. Она состоит из двух различных замкнутых ветвей, симметричных друг к другу относительно центра и одной из главных плоскостей эллипсоида. Каждая ветвь имеет в качестве плоскостей симметрии две другие главные плоскости эллипсоида (рис. 229) и обладает четырьмя вершинами 1, 2, 1, 2, для которых радиус-вектор  , выходящий из центра, имеет максимум или минимум. При движении одна из ветвей полодии катится по неподвижной плоскости П. Эта ветвь — единственная используемая; вторая ветвь катится по плоскости, симметричной к П относительно точки О.
, выходящий из центра, имеет максимум или минимум. При движении одна из ветвей полодии катится по неподвижной плоскости П. Эта ветвь — единственная используемая; вторая ветвь катится по плоскости, симметричной к П относительно точки О.
Важно дать себе отчет о различных формах, которые принимает полодия, в зависимости от начальных условий. Представим себе эллипсоид инерции (рис. 229). Так как мы предполагаем, что  то ось
то ось  является малой осью, а
является малой осью, а  — большой. Обозначим через
— большой. Обозначим через  , с вершины поверхности. В зависимости от начальных условий постоянная
, с вершины поверхности. В зависимости от начальных условий постоянная  изменяется между А и С. При
изменяется между А и С. При  конус, который является геометрическим местом мгновенных
конус, который является геометрическим местом мгновенных
осей вращения в теле, вырождается в ось  и полодия — пересечение этого конуса и эллипсоида — вырождается в точку
и полодия — пересечение этого конуса и эллипсоида — вырождается в точку  симметричную точку а. Когда
симметричную точку а. Когда  немного уменьшится, полодия будет состоять из маленькой замкнутой кривой
немного уменьшится, полодия будет состоять из маленькой замкнутой кривой  окружающей а, и из симметричной кривой окружающей а. Если
окружающей а, и из симметричной кривой окружающей а. Если  будет продолжать уменьшаться, то кривые
будет продолжать уменьшаться, то кривые  будут удаляться от
будут удаляться от  и при
и при  эти кривые соединятся в точках
эти кривые соединятся в точках  и
и  и распадутся на два эллипса
и распадутся на два эллипса  . Точно так же при
. Точно так же при  полодия выродится в две вершины
полодия выродится в две вершины  . При увеличении
. При увеличении  полодия будет вначале состоять из двух маленьких симметричных замкнутых кривых
полодия будет вначале состоять из двух маленьких симметричных замкнутых кривых  окружающих эти вершины; затем эти кривые будут увеличиваться, и при
окружающих эти вершины; затем эти кривые будут увеличиваться, и при  они опять обратятся в эллипсы
они опять обратятся в эллипсы  .
.
Таким образом, имеются два вида полодий. Одни из них окружают вершины малой оси, а другие вершины большой оси. Эти два вида полодий разделяются особой полодией, соответствующей  и образованной двумя эллипсами
и образованной двумя эллипсами  . Через каждую точку поверхности эллипсоида проходит одна и только одна полодия. Когда все эти кривые уже начерчены, то чтобы узнать, какая полодия соответствует заданным начальным условиям, достаточно знать точку
. Через каждую точку поверхности эллипсоида проходит одна и только одна полодия. Когда все эти кривые уже начерчены, то чтобы узнать, какая полодия соответствует заданным начальным условиям, достаточно знать точку  в которой ось начального мгновенного вращения пересекает эллипсоид. Искомой полодией будет та, которая проходит через
в которой ось начального мгновенного вращения пересекает эллипсоид. Искомой полодией будет та, которая проходит через  Что касается соответствующей неподвижной плоскости П, то это — плоскость, касающаяся в
Что касается соответствующей неподвижной плоскости П, то это — плоскость, касающаяся в  эллипсоида в его начальном положении.
эллипсоида в его начальном положении.
Герполодия. Если опустить из неподвижной точки перпендикуляр  на плоскость П (рис. 228), то длина
на плоскость П (рис. 228), то длина  равна Радиус-вектор
равна Радиус-вектор  какой-нибудь точки герполодии имеет длину
какой-нибудь точки герполодии имеет длину

Мы видели, на основании формы полодии, что расстояние. От. от полюса до центра изменяется между его минимумом и максимумом. Следовательно,  также изменяется между соответствующими минимумом и максимумом
также изменяется между соответствующими минимумом и максимумом  Герполодия заключена поэтому между двумя концентрическими окружностями радиусов
Герполодия заключена поэтому между двумя концентрическими окружностями радиусов  которых она последовательно касается в точках, таких, как
которых она последовательно касается в точках, таких, как  Она имеет форму, указанную на рис. 228. Это — кривая, обращенная всегда вогнутостью к точке Р и не имеющая точек перегиба. Это обстоятельство, впервые замеченное Гессом (диссертация, Мюнхен, 1880; Math. Annalen, т. XXVII) и вновь открытое де Спарром (de Sparre, Comptes rendus, 1884), заслуживает быть отмеченным, так как Пуансо в своей работе неточно изобразил герполоиду, приг дав ей синусообразную форму. Доказательство можно найти в статье Паде (Padd, Nouvelles Annales, 4 serie, т. VI, июль 1906).
Она имеет форму, указанную на рис. 228. Это — кривая, обращенная всегда вогнутостью к точке Р и не имеющая точек перегиба. Это обстоятельство, впервые замеченное Гессом (диссертация, Мюнхен, 1880; Math. Annalen, т. XXVII) и вновь открытое де Спарром (de Sparre, Comptes rendus, 1884), заслуживает быть отмеченным, так как Пуансо в своей работе неточно изобразил герполоиду, приг дав ей синусообразную форму. Доказательство можно найти в статье Паде (Padd, Nouvelles Annales, 4 serie, т. VI, июль 1906).
Дуга  герполодии есть четверть дуги 1, 2 полодии (рис. 228). Когда все точки полодии соприкоснутся последовательно с плоскостью, полюс
герполодии есть четверть дуги 1, 2 полодии (рис. 228). Когда все точки полодии соприкоснутся последовательно с плоскостью, полюс  займет в эллипсоиде первоначальное положение, но в плоскости II радиус-вектор
займет в эллипсоиде первоначальное положение, но в плоскости II радиус-вектор  повернется на угол, равный
повернется на угол, равный  поскольку на полодии имеются четыре вершины. Если этот угол
поскольку на полодии имеются четыре вершины. Если этот угол  несоизмерим с
несоизмерим с  то герполодия не будет замкнутой: полюс никогда не займет одновременно точно то же самое положение на эллипсоиде и на плоскости, которое он занимает в данный момент. Если же этот угол соизмерим с
то герполодия не будет замкнутой: полюс никогда не займет одновременно точно то же самое положение на эллипсоиде и на плоскости, которое он занимает в данный момент. Если же этот угол соизмерим с  то герполодия будет замкнутой и по истечении некоторого промежутка времени полюс займет опять прежнее положение и на эллипсоиде и на плоскости.
то герполодия будет замкнутой и по истечении некоторого промежутка времени полюс займет опять прежнее положение и на эллипсоиде и на плоскости.

Рис. 230.
Частные случаи. Если  или
или  то полодия и герполодия обратятся в точки. Эллипсоид будет вертеться, оставаясь в соприкосновении с плоскостью своей вершиной на большой или малой оси.
то полодия и герполодия обратятся в точки. Эллипсоид будет вертеться, оставаясь в соприкосновении с плоскостью своей вершиной на большой или малой оси.
Если  то полодия обратится в два эллипса
то полодия обратится в два эллипса  проходящих через среднюю ось. Малая ось одного из этих эллипсов, как это легко проверить, равна средней оси
проходящих через среднюю ось. Малая ось одного из этих эллипсов, как это легко проверить, равна средней оси  Движение в этом случае получится, если заставить один из эллипсов, центр которого неподвижен, катиться по плоскости II. Так как эта плоскость находится от центра на расстоянии, равном
Движение в этом случае получится, если заставить один из эллипсов, центр которого неподвижен, катиться по плоскости II. Так как эта плоскость находится от центра на расстоянии, равном  то минимум
то минимум  радиуса
радиуса  герполодии равен нулю; максимум имеет некоторое значение
герполодии равен нулю; максимум имеет некоторое значение  Герполодия будет тогда иметь форму двойной спирали (рис. 230), Имеющей вершину Т, соответствующую максимуму
Герполодия будет тогда иметь форму двойной спирали (рис. 230), Имеющей вершину Т, соответствующую максимуму  и состоящую из двух симметричных относительно
и состоящую из двух симметричных относительно  ветвей, приближающихся асимптотически к точке Р. Только одна часть этой герполодии будет в действительности описываться; это та ее часть, которая идет от начального положения
ветвей, приближающихся асимптотически к точке Р. Только одна часть этой герполодии будет в действительности описываться; это та ее часть, которая идет от начального положения  полюса до точки Р в том или другом направлении. Время, нужное для того, чтобы полюс пришел в положение Р, бесконечно, несмотря на то, что длина спирали конечна, так как она равна периметру катящегося эллипса.
полюса до точки Р в том или другом направлении. Время, нужное для того, чтобы полюс пришел в положение Р, бесконечно, несмотря на то, что длина спирали конечна, так как она равна периметру катящегося эллипса.
Когда эллипсоид является эллипсоидом вращения, полодия и герполодия будут окружностями. Если он является сферой, то. полодия и герполодия будут всегда точками.
Устойчивость вращения вокруг главных осей. В частных случаях, когда тело начинает вращаться вокруг одной из главных осей инерции, такое вращательное движение продолжается неопределенно долго; мгновенная ось будет неподвижной в теле и в пространстве. Легко видеть, что это единственные случаи, когда мгновенная ось остается неподвижной в теле. В самом деле, полагая мгновенную ось неподвижной в теле и обозначая через  с её направляющие косинусы относительно координатных осей
с её направляющие косинусы относительно координатных осей  имеем:
имеем:

где  — постоянные. Тогда интеграл кинетической энергии (12) показывает, что
— постоянные. Тогда интеграл кинетической энергии (12) показывает, что  постоянна. Следовательно, три составляющие
постоянна. Следовательно, три составляющие  будут постоянными и уравнения Эйлера будут иметь вид
будут постоянными и уравнения Эйлера будут иметь вид

Если эллипсоид инерции не является эллипсоидом вращения, то из этих уравнений вытекает, что две из величин  равны нулю, т. е. что тело вращается вокруг главной оси инерции. Если эллипсоид является эллипсоидом вращения вокруг оси
равны нулю, т. е. что тело вращается вокруг главной оси инерции. Если эллипсоид является эллипсоидом вращения вокруг оси  то
то  и либо
и либо  и тело вращается вокруг оси, лежашей в плоскости экватора, т. е. вокруг главной оси инерции, либо
и тело вращается вокруг оси, лежашей в плоскости экватора, т. е. вокруг главной оси инерции, либо  и тело вращается вокруг главной оси
и тело вращается вокруг главной оси  Наконец, в случае
Наконец, в случае  тело вращается вокруг главной оси инерции, так как все оси являются главными.
тело вращается вокруг главной оси инерции, так как все оси являются главными.
Теперь возникает вопрос, будет ли вращение тела вокруг одной из этих главных осей инерции устойчивым движением  нет. При этом вообще говорят, что движение является устойчивым, если произвольным бесконечно малым изменениям начальных условий соответствует бесконечно малое изменение самого движения. Движение называется неустойчивым, если некоторое бесконечно малое изменение начальных условий влечет за собой конечное изменение движения.
нет. При этом вообще говорят, что движение является устойчивым, если произвольным бесконечно малым изменениям начальных условий соответствует бесконечно малое изменение самого движения. Движение называется неустойчивым, если некоторое бесконечно малое изменение начальных условий влечет за собой конечное изменение движения.
Если  то вращения, вокруг большой и малой осей эллипсоида инерции являются устойчивыми, а вращение вокруг средней оси неустойчиво. В самом, деле, сообщим телу начальное вращение вокруг малой оси. Тогда эта ось останется неподвижной, полюс вращения совпадет с вершиной
то вращения, вокруг большой и малой осей эллипсоида инерции являются устойчивыми, а вращение вокруг средней оси неустойчиво. В самом, деле, сообщим телу начальное вращение вокруг малой оси. Тогда эта ось останется неподвижной, полюс вращения совпадет с вершиной  касательная плоскость
касательная плоскость  в точке
в точке  будет неподвижной. Если теперь изменить бесконечно мало начальные условия, сообщив телу начальное вращение вокруг оси, бесконечно близкой к
будет неподвижной. Если теперь изменить бесконечно мало начальные условия, сообщив телу начальное вращение вокруг оси, бесконечно близкой к  то полодия обратится в малую замкнутую кривую, бесконечно близкую к вершине малой оси. Следовательно, мгновенная ось опишет в теле вокруг своего первоначального положения конус с бесконечно малым углом раствора. Неподвижная плоскость П,
то полодия обратится в малую замкнутую кривую, бесконечно близкую к вершине малой оси. Следовательно, мгновенная ось опишет в теле вокруг своего первоначального положения конус с бесконечно малым углом раствора. Неподвижная плоскость П,
которой эллипсоид будет касаться в новом движении, будет бесконечно близкой к  и перпендикуляр
и перпендикуляр  опущенный из О на эту плоскость, будет бесконечно близким по величине и по положению к
опущенный из О на эту плоскость, будет бесконечно близким по величине и по положению к  Радиус-вектор От герполодии, имея длину, бесконечно близкую к
Радиус-вектор От герполодии, имея длину, бесконечно близкую к  отклонится бесконечно мало от перпендикуляра
отклонится бесконечно мало от перпендикуляра  т. е.
т. е.  Следовательно, мгновенная ось опишет также и в пространстве конус, бесконечно близкий к своему первоначальному положению. Таким образом, рассматриваемое вращение устойчиво. То же будет и в случае вращения вокруг большой оси.
Следовательно, мгновенная ось опишет также и в пространстве конус, бесконечно близкий к своему первоначальному положению. Таким образом, рассматриваемое вращение устойчиво. То же будет и в случае вращения вокруг большой оси.
Но если тбло начнет вначале вращаться вокруг средней оси, то бесконечно малое изменение начальных условий приведет полюс в положение  начиная от которого он будет описывать полодию, окружающую либо вершину а, либо вершину с. Тогда ось отклонится от своего первоначального положения на конечную величину; вращение будет неустойчивое.
начиная от которого он будет описывать полодию, окружающую либо вершину а, либо вершину с. Тогда ось отклонится от своего первоначального положения на конечную величину; вращение будет неустойчивое.
Эллипсы  (рис. 229) разделяют эллипсоид на четыре части: две, содержащие вершины
(рис. 229) разделяют эллипсоид на четыре части: две, содержащие вершины  , и две другие, содержащие вершины с и с.
, и две другие, содержащие вершины с и с.
Следуя замечанию Бура  естественно принять за меру устойчивости вращения вокруг оси
естественно принять за меру устойчивости вращения вокруг оси  отношение площади части, содержащей а, к половине площади эллипсоида инерции. Действительно, если начальные условия изменяются так, что полюс находится в этой части, то мгновенная ось описывает в теле конус вокруг своего первоначального положения
отношение площади части, содержащей а, к половине площади эллипсоида инерции. Действительно, если начальные условия изменяются так, что полюс находится в этой части, то мгновенная ось описывает в теле конус вокруг своего первоначального положения  Точно так же устойчивость вращения вокруг
Точно так же устойчивость вращения вокруг  измеряется площадью части, содержащей эту ось. Например, если эллипсоид очень близок к эллипсоиду вращения вокруг
измеряется площадью части, содержащей эту ось. Например, если эллипсоид очень близок к эллипсоиду вращения вокруг  т. е. если
т. е. если  очень мало, то часть, содержащая а, будет очень мала, так что устойчивость вращения вокруг
очень мало, то часть, содержащая а, будет очень мала, так что устойчивость вращения вокруг  будет слабой, так как маленькое смещение оси может вывести полюс из этой части и заставить вращаться вокруг
будет слабой, так как маленькое смещение оси может вывести полюс из этой части и заставить вращаться вокруг 
Если эллипсоид будет точно эллипсоидом вращения (продолговатые снаряды), то устойчивыми будут вращения только вокруг оси симметрии. В самом деле, если тело вращается вокруг одной из главных осей в плоскости экватора и если в каком-нибудь случае полюс  будет немного отклонен от этой плоскости, то он будет описывать на поверхности эллипсоида круг, параллельный экватору и почти совпадающий с ним. Следовательно, ось в теле сильно отклонится от своего первоначального положения. Интересно отметить, что в пространстве ось, напротив, останется очень близкой к своему первоначальному положению, так как длина От мало отличается от экваториального радиуса.
будет немного отклонен от этой плоскости, то он будет описывать на поверхности эллипсоида круг, параллельный экватору и почти совпадающий с ним. Следовательно, ось в теле сильно отклонится от своего первоначального положения. Интересно отметить, что в пространстве ось, напротив, останется очень близкой к своему первоначальному положению, так как длина От мало отличается от экваториального радиуса.
Если эллипсоид инерции является сферой, то все его оси будут одинаково устойчивыми или скорее безразличными, так как мгновенная ось, если она будет смещена со своего места в другое, снова станет неподвижной и в теле и в пространстве (см. Bour, Dynairrique, стр. 165).
| << Предыдущий параграф | Следующий параграф >> |
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
- 354. Пример I.
- V. Энергия
- 356. Потенциальная энергия. Механический смысл.
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
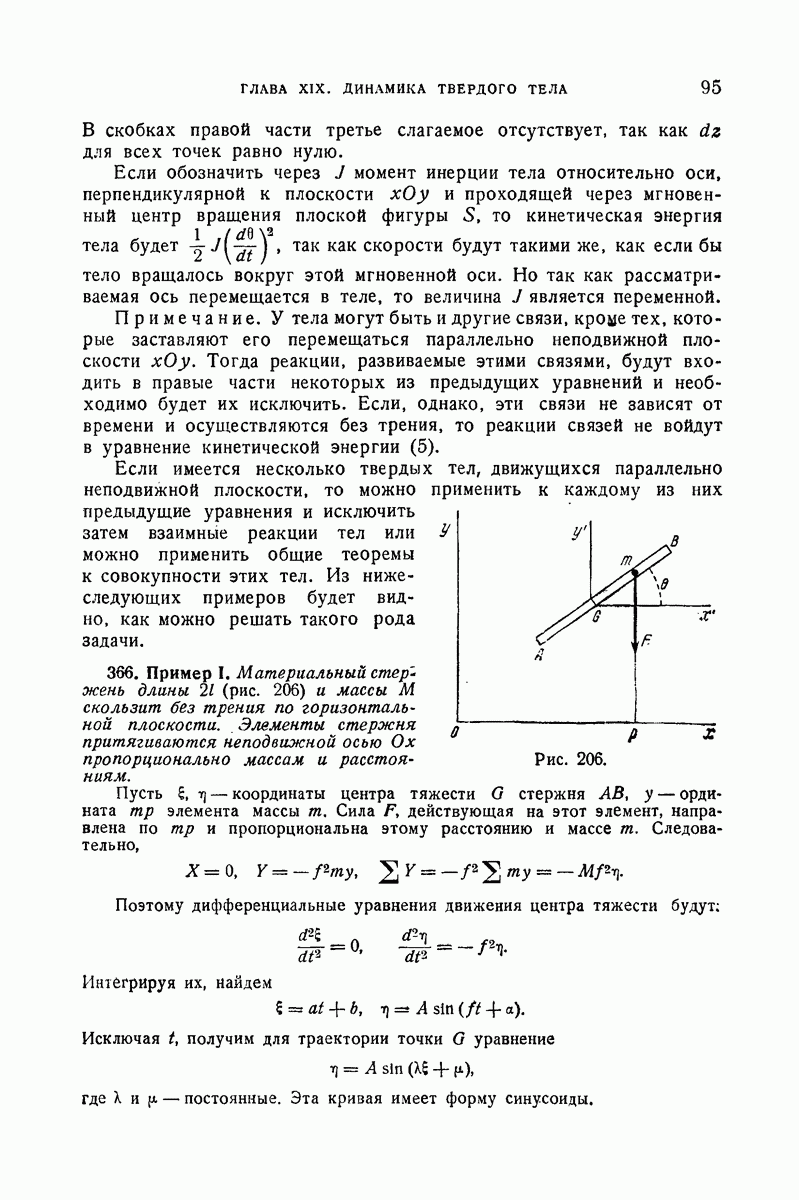
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
- 370. Пример I.
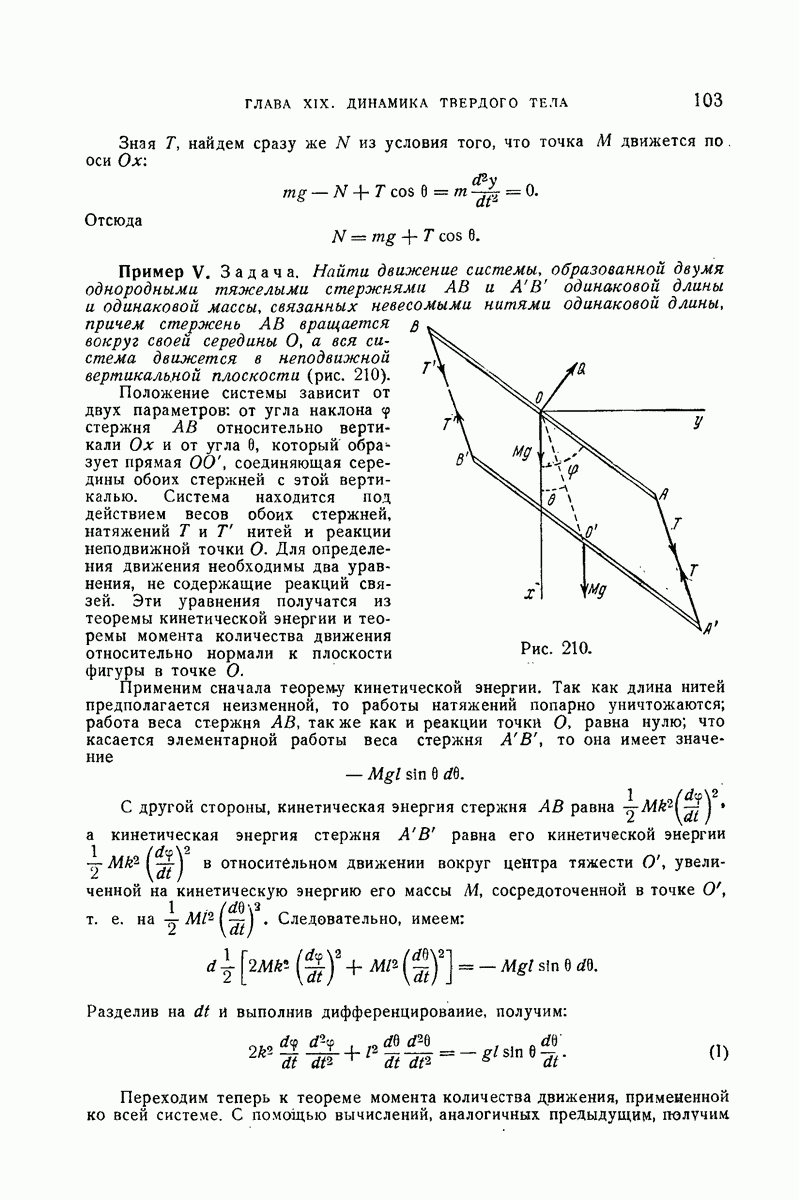
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
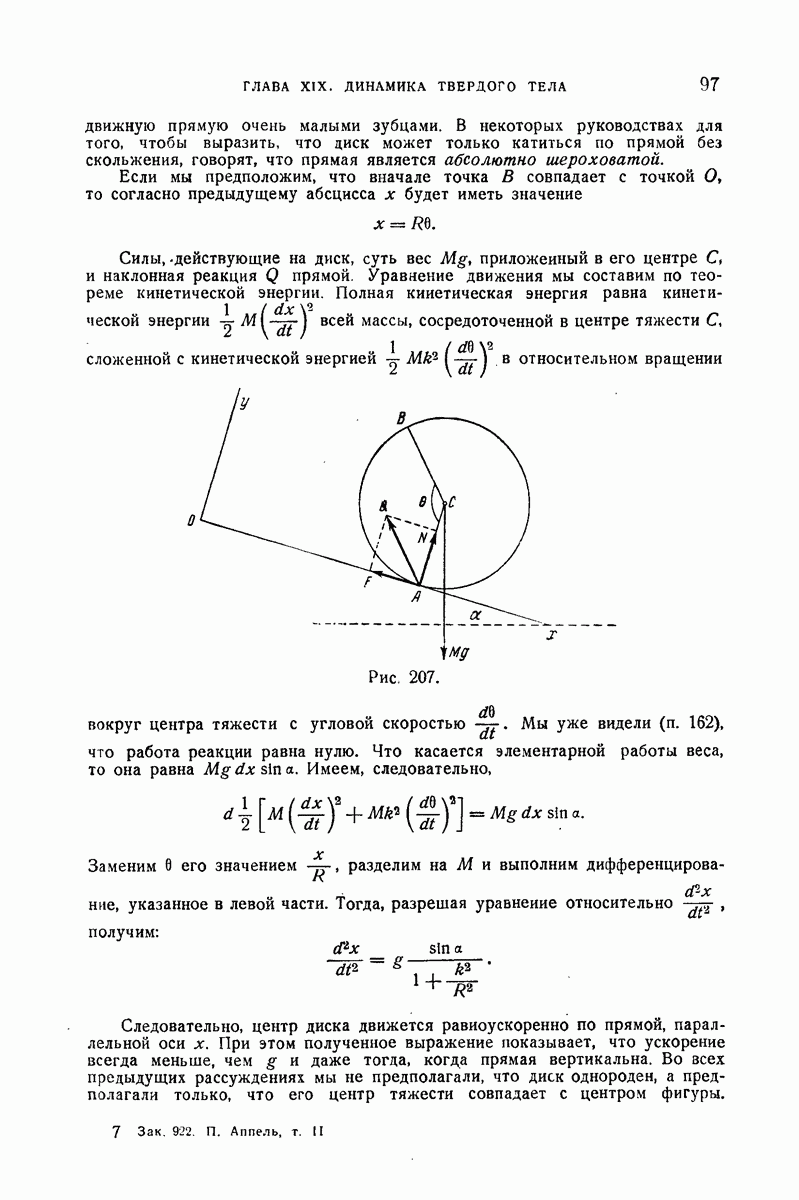
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
- 421. Твердое тело.
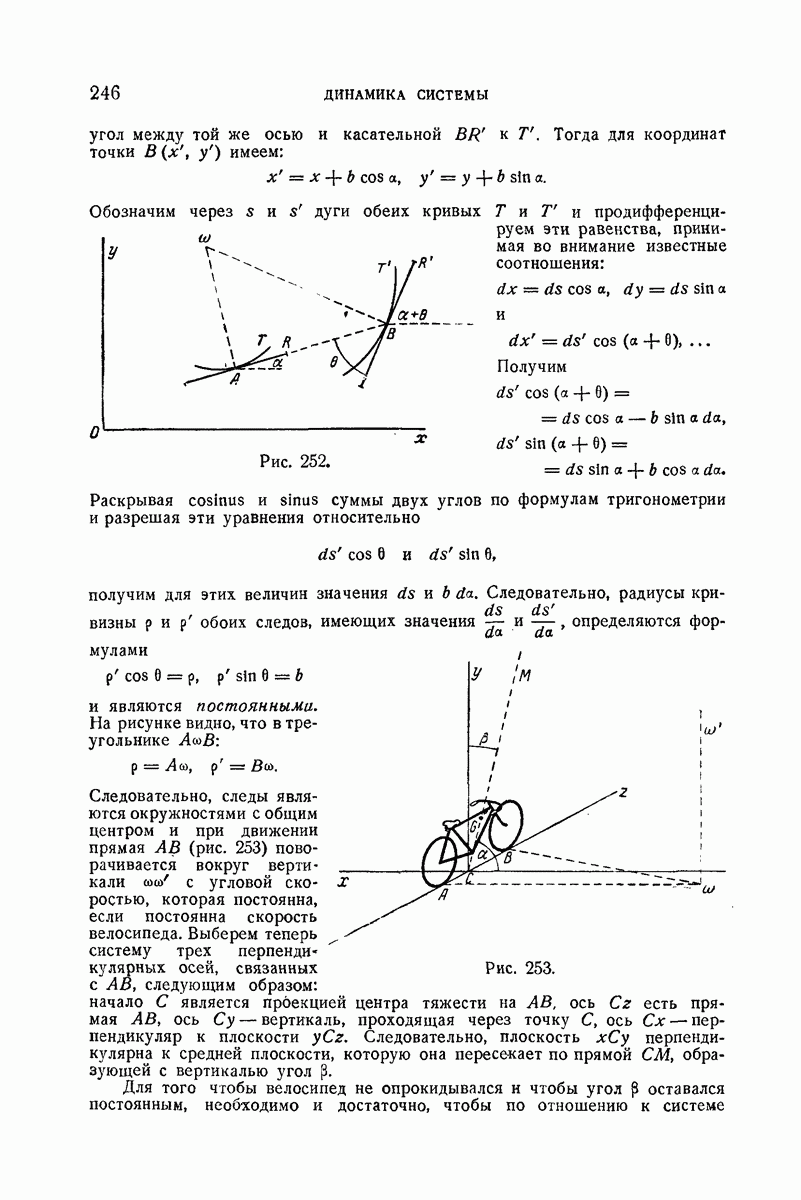
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
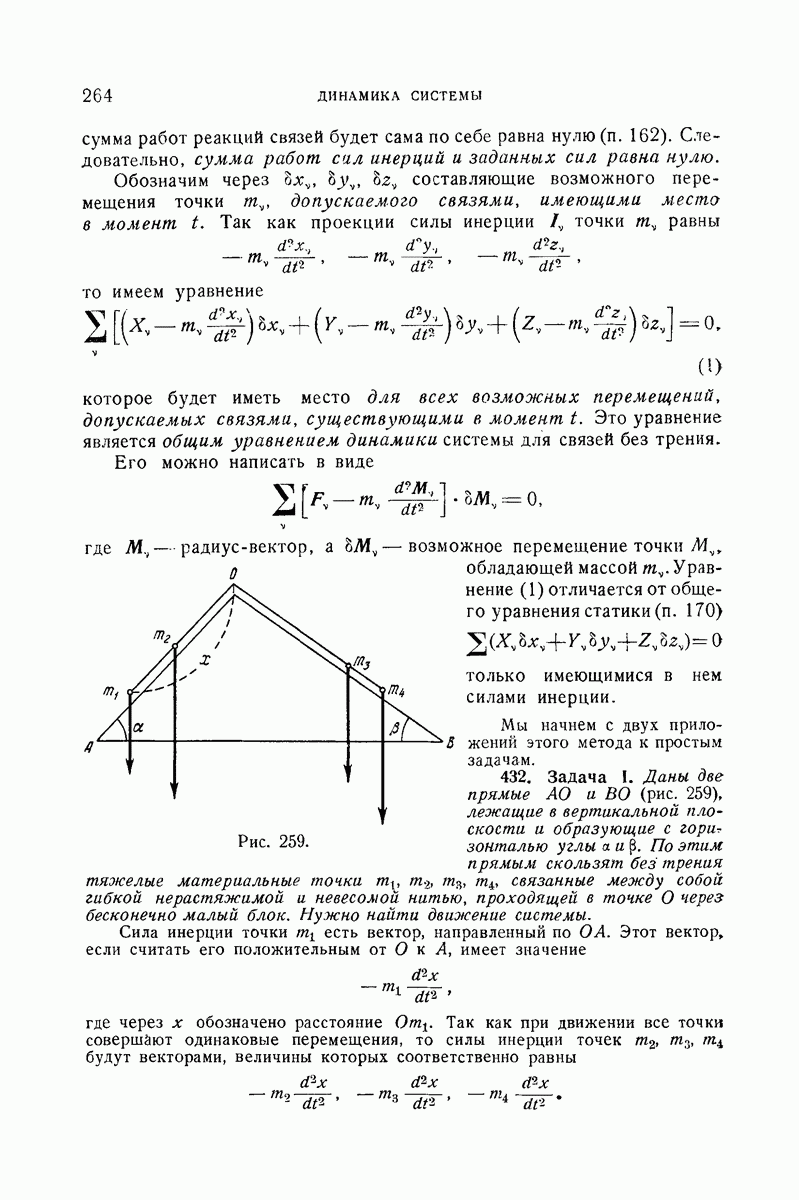
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
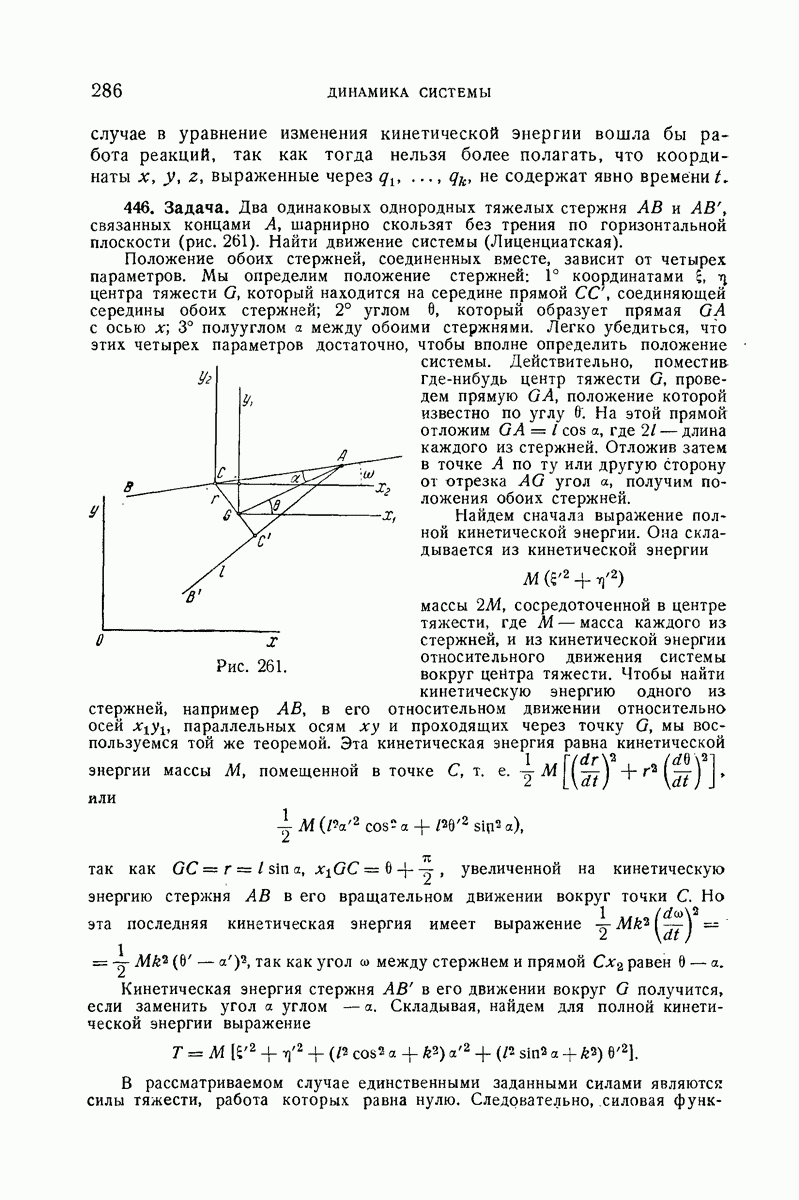
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели