| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
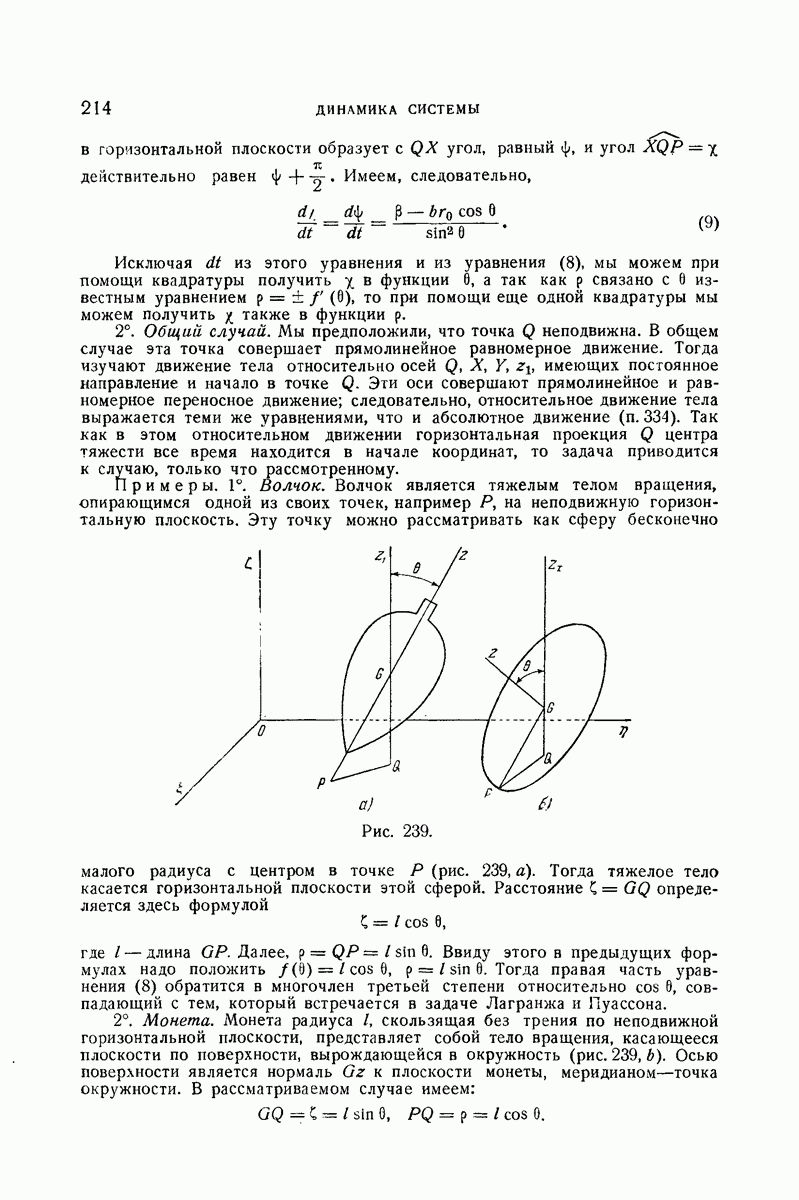
213
214
215
216
217
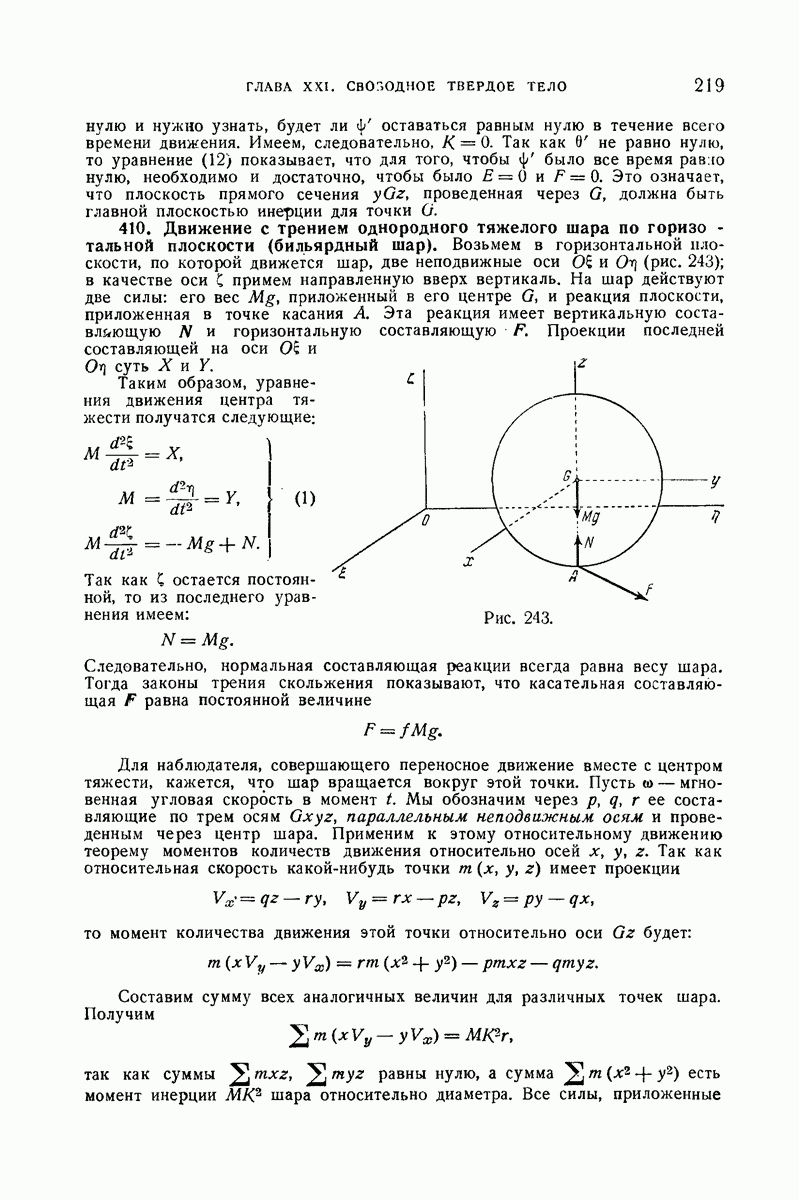
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
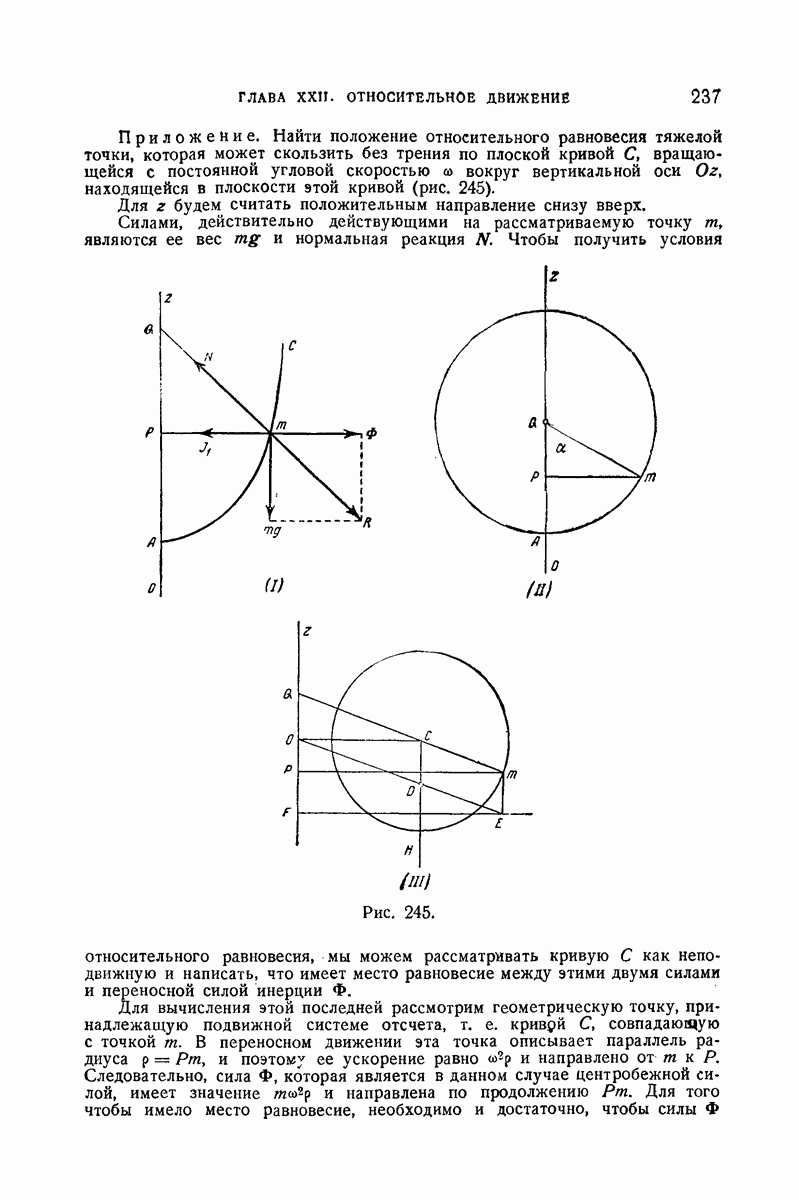
236
237
238
239
240
241
242
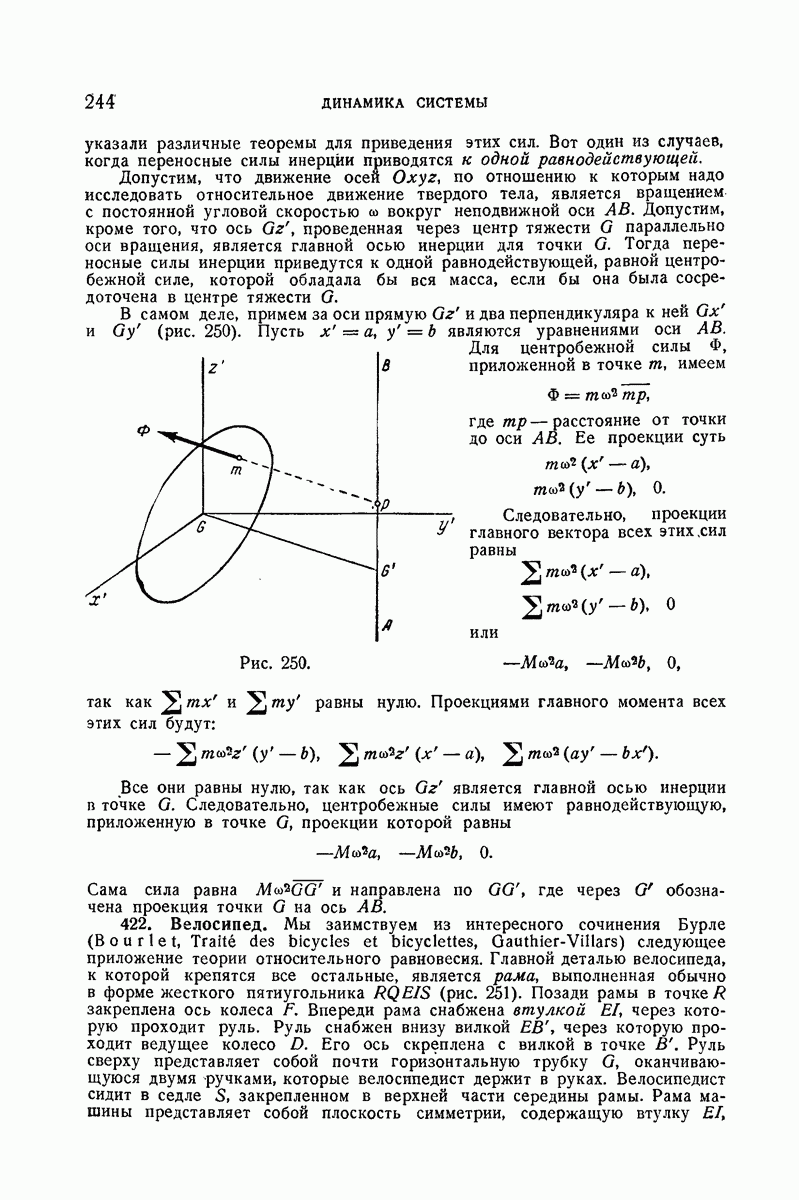
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
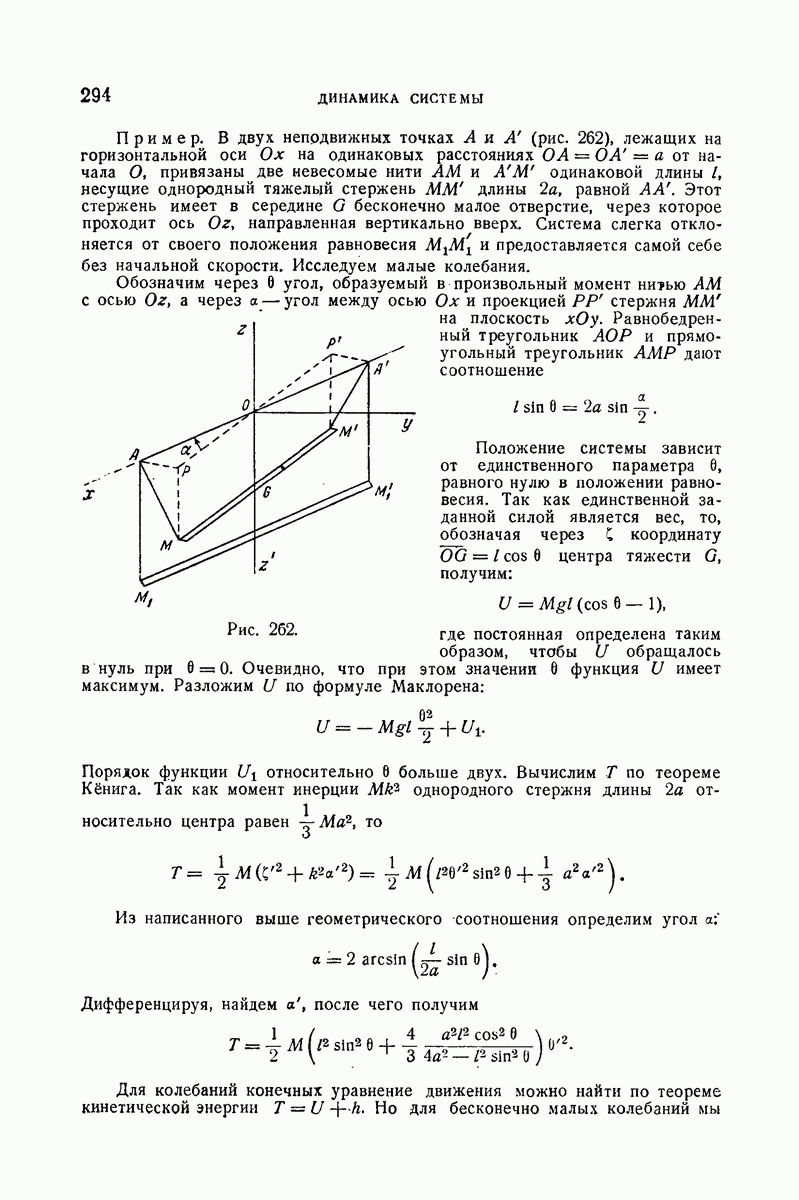
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
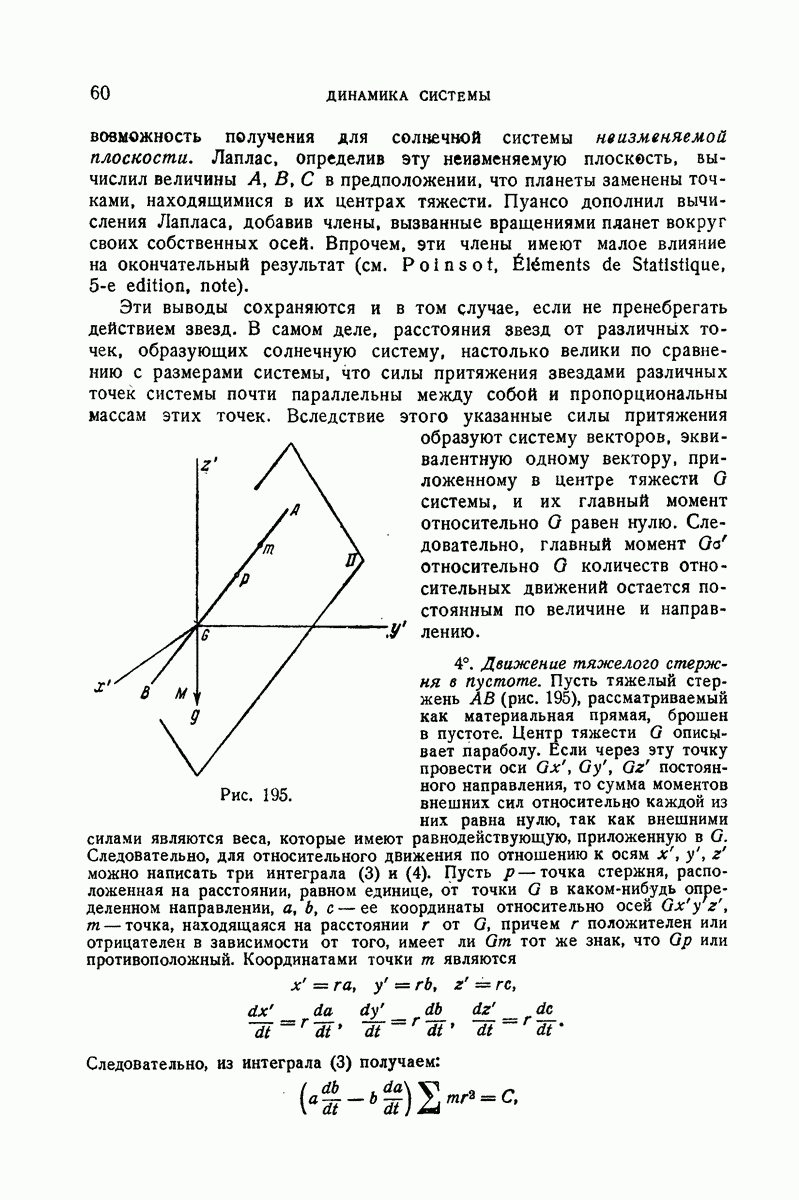
382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
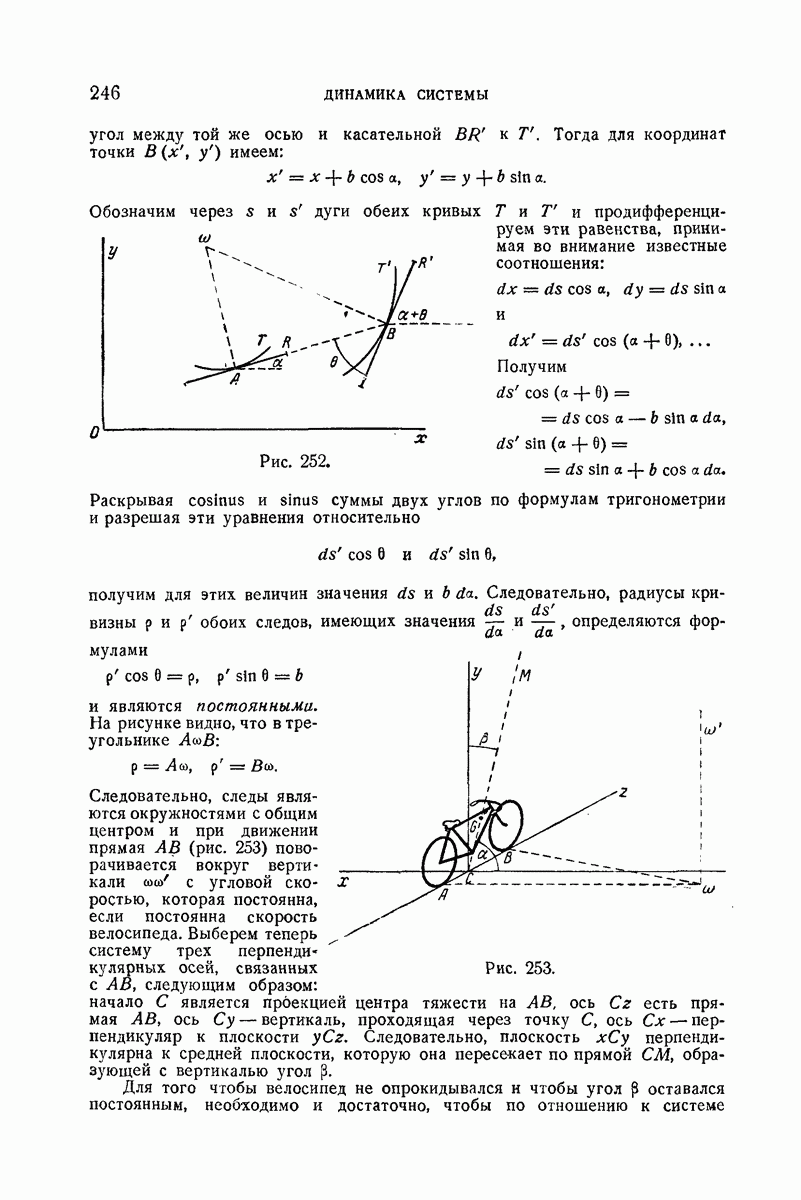
Рассмотрим триэдр  движущийся вокруг неподвижной точки О относительно триэдра
движущийся вокруг неподвижной точки О относительно триэдра  рассматриваемого как неподвижный. Для определения этого движения углы Эйлера
рассматриваемого как неподвижный. Для определения этого движения углы Эйлера  должны быть заданы в виде непрерывных функций времени.
должны быть заданы в виде непрерывных функций времени.
Мы видели в кинематике, что распределение скоростей в момент времени  в твердом теле, движущемся вокруг закрепленной точки, будет таким же, как если бы это тело совершало вращение с угловой скоростью
в твердом теле, движущемся вокруг закрепленной точки, будет таким же, как если бы это тело совершало вращение с угловой скоростью  вокруг оси, проходящей через неподвижную точку.
вокруг оси, проходящей через неподвижную точку.
Эта угловая скорость  называется мгновенной угловой скоростью вращения в момент
называется мгновенной угловой скоростью вращения в момент  и представляется, как мы Это указывали
и представляется, как мы Это указывали  некоторым вектором. Обозначим через
некоторым вектором. Обозначим через  проекции вектора мгновенной угловой скорости вращения подвижного триэдра на подвижные оси
проекции вектора мгновенной угловой скорости вращения подвижного триэдра на подвижные оси  Мы выразили
Мы выразили  в функции девяти косинусов и их производных по времени
в функции девяти косинусов и их производных по времени  Сейчас мы займемся вычислением
Сейчас мы займемся вычислением  в функции
в функции  их производных
их производных  по
по 
Чтобы перевести триэдр из положения, которое он занимает в момент времени  и которое соответствует значениям
и которое соответствует значениям  трех углов, в положение, бесконечно близкое, которое он занимает в момент
трех углов, в положение, бесконечно близкое, которое он занимает в момент  и которое соответствует углам
и которое соответствует углам  можно поступить следующим образом.
можно поступить следующим образом.
Сначала нужно повернуть триэдр на угол  вокруг оси
вокруг оси  тогда
тогда  увеличится на
увеличится на  не изменятся. Вокруг нового положения линии
не изменятся. Вокруг нового положения линии  нужно повернуть триэдр на угол
нужно повернуть триэдр на угол  Наконец, вокруг нового положения оси
Наконец, вокруг нового положения оси  нужно повернуть его на угол
нужно повернуть его на угол  Если предполагать, что эти три угловых перемещения делаются в пространстве в течение промежутка времени
Если предполагать, что эти три угловых перемещения делаются в пространстве в течение промежутка времени  то соответствующие угловые скорости вращений будут
то соответствующие угловые скорости вращений будут 
Можно сказать, что мгновенное вращение триэдра с угловой скоростью  является результирующим трех вращений вокруг осей
является результирующим трех вращений вокруг осей  с угловыми скоростями
с угловыми скоростями  Эти три составляющие вращения представляются векторами, равными
Эти три составляющие вращения представляются векторами, равными  и лежащими на осях
и лежащими на осях  (рис. 224). Результирующий вектор
(рис. 224). Результирующий вектор  является геометрической суммой этих трех векторов. Его проекция на произвольную ось равна сумме проекций составляющих векторов
является геометрической суммой этих трех векторов. Его проекция на произвольную ось равна сумме проекций составляющих векторов  на ту же ось.
на ту же ось.
Мы найдем сначала проекции мгновенного вектора  подвижного триэдра на взаимно-перпендикулярные оси
подвижного триэдра на взаимно-перпендикулярные оси  где ось
где ось  лежит в плоскости
лежит в плоскости  и образует с осью
и образует с осью  угол Обозначим через
угол Обозначим через  эти три проекции, из которых третья равна
эти три проекции, из которых третья равна  Чтобы их найти, достаточно заметить, что вектор
Чтобы их найти, достаточно заметить, что вектор  лежащий в плоскости
лежащий в плоскости  может быть разложен на его две проекции
может быть разложен на его две проекции  на оси
на оси  и
и  так что
так что

Тогда три составляющие вектора  по осям
по осям  будут
будут

Чтобы найти теперь  и
и  достаточно взять суммы проекций и
достаточно взять суммы проекций и  на оси
на оси  Так как взаимно-перпендикулярные оси
Так как взаимно-перпендикулярные оси  лежат в плоскости
лежат в плоскости  и ось
и ось  образует с осью
образует с осью  угол
угол  то
то
непосредственно получаем

откуда находим окончательные формулы, определяющие 

Примечание. В этих формулах первые члены каждой из трех правых частей представляют собой три проекции соответственно на оси  вектора
вектора  направленного по оси
направленного по оси  Отсюда получаются косинусы
Отсюда получаются косинусы  углов, которые образует ось
углов, которые образует ось  с осями
с осями 

что мы уже видели в предыдущем пункте.
Обратная задача. Мы только что видели, как, зная движение триэдра  , т. е. выражения
, т. е. выражения  или девяти косинусов
или девяти косинусов  в функции
в функции  можно вычислить проекции
можно вычислить проекции  мгновенной угловой скорости вращения триэдра в функции
мгновенной угловой скорости вращения триэдра в функции 
Обратно, допустим, что известны  в функции
в функции  и что требуется вычислить
и что требуется вычислить  или девять косинусов
или девять косинусов  в функции
в функции  Тогда надо будет проинтегрировать уравнения (2) первого порядка относительно
Тогда надо будет проинтегрировать уравнения (2) первого порядка относительно  Можно показать, что эта задача приводится к интегрированию одного уравнения Риккати с комплексными коэффициентами. [См. Darboux, Lemons sur la thdorie ?ёпёга1е des surfaces, т. I, глава II; Mayer, Simmetrische L6sung, ... (Berichte der Konigl. sSchs. Geselschaft der Wissenschaften zu Leipzig, 2 марта 1902) и курсы анализа, например, Гурса.]
Можно показать, что эта задача приводится к интегрированию одного уравнения Риккати с комплексными коэффициентами. [См. Darboux, Lemons sur la thdorie ?ёпёга1е des surfaces, т. I, глава II; Mayer, Simmetrische L6sung, ... (Berichte der Konigl. sSchs. Geselschaft der Wissenschaften zu Leipzig, 2 марта 1902) и курсы анализа, например, Гурса.]
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
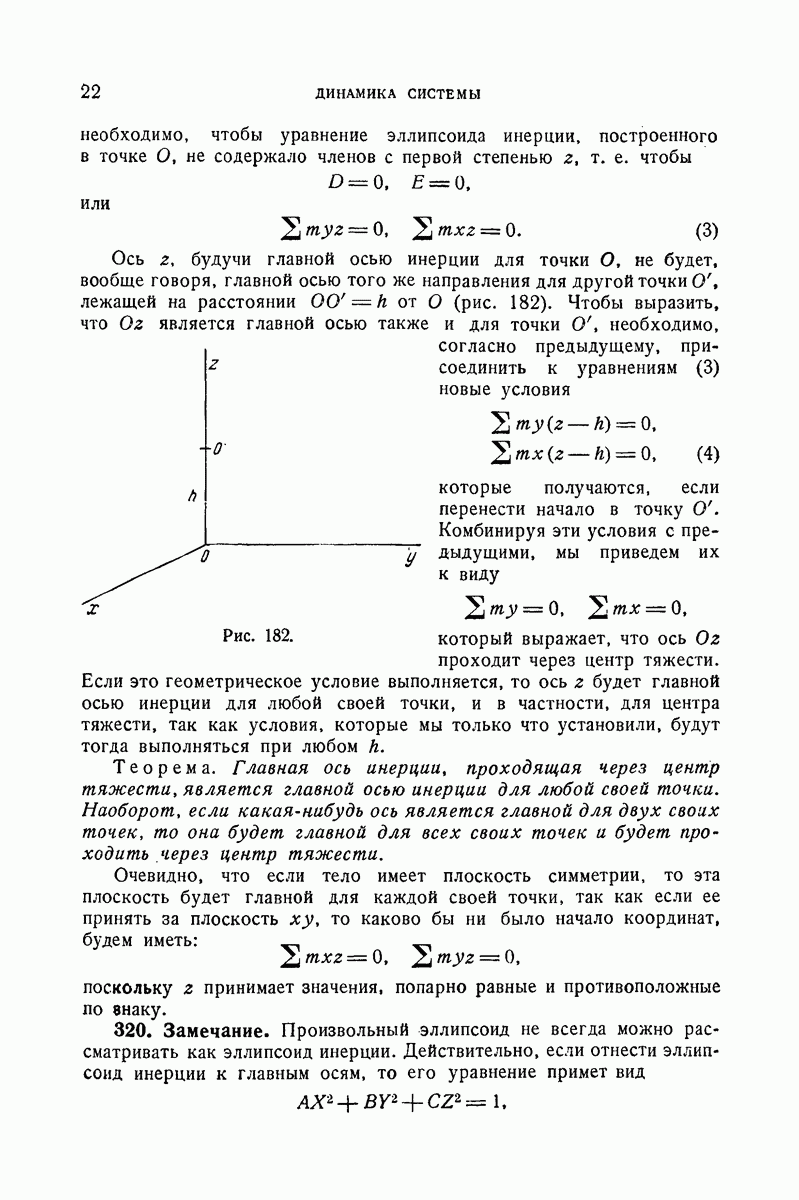
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
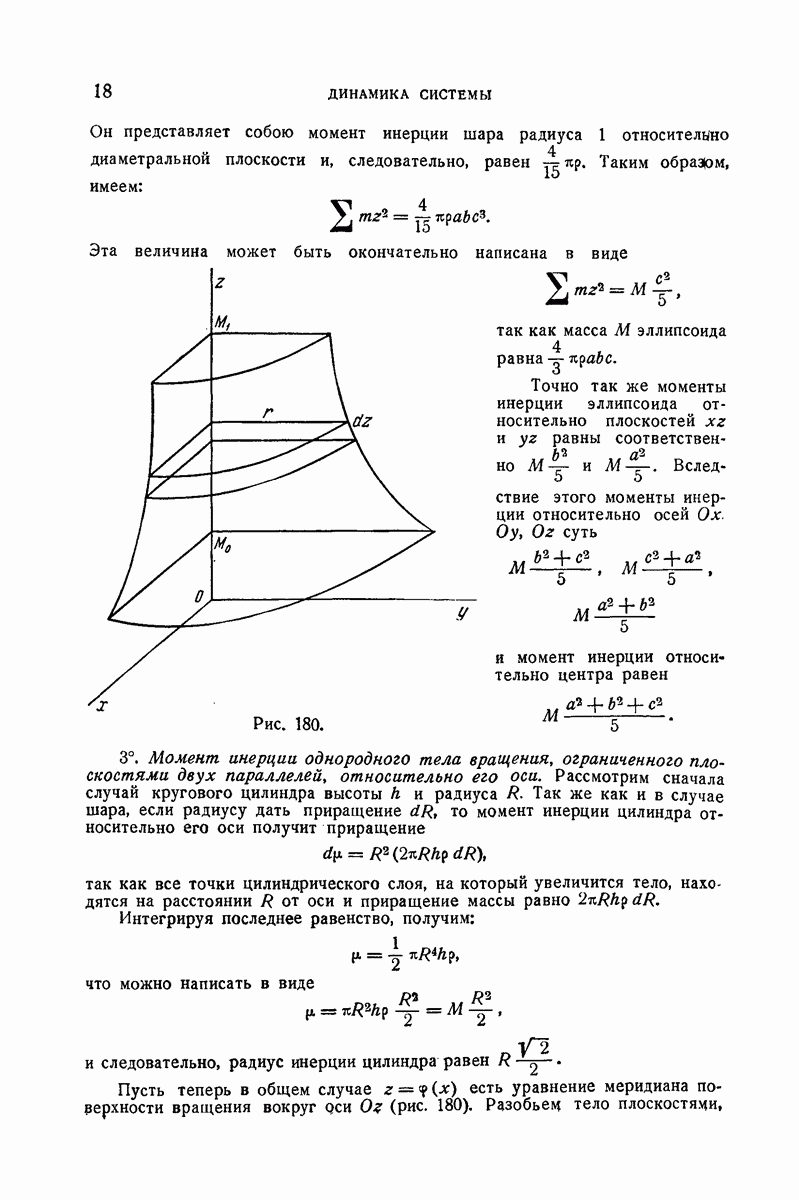
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
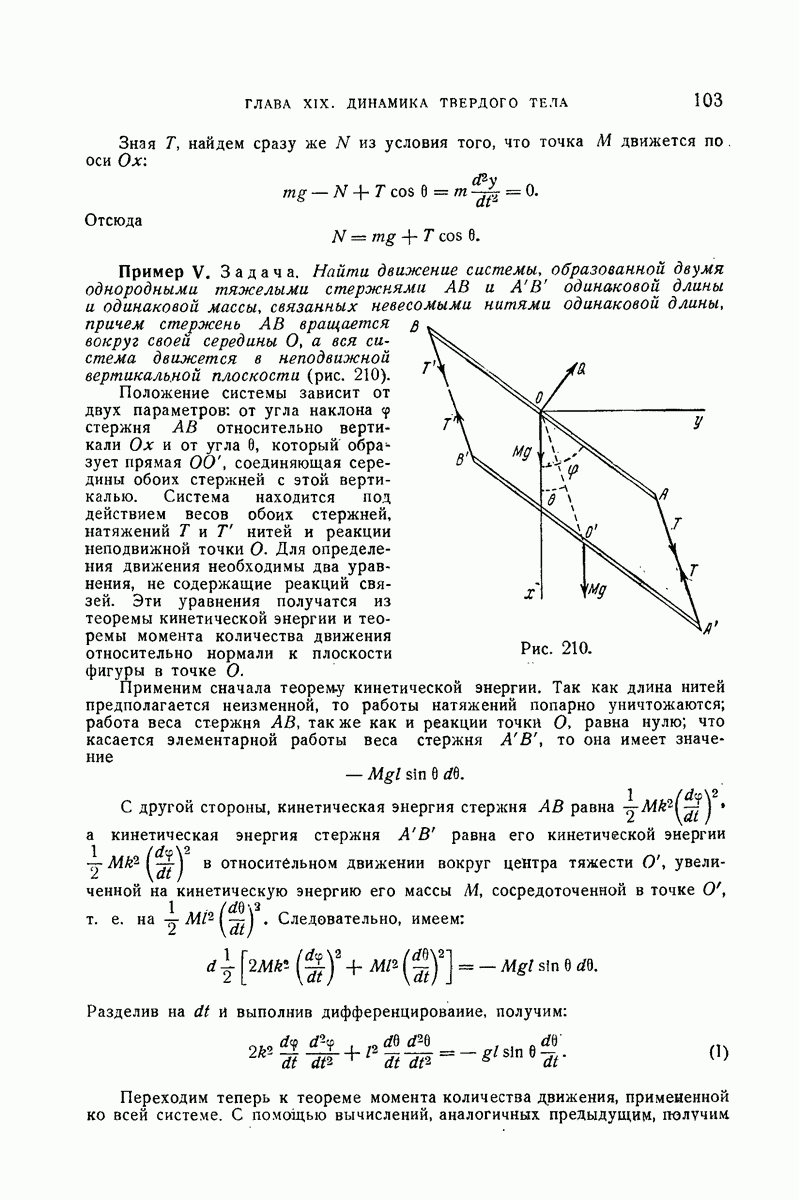
- 354. Пример I.
- V. Энергия
- 356. Потенциальная энергия. Механический смысл.
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
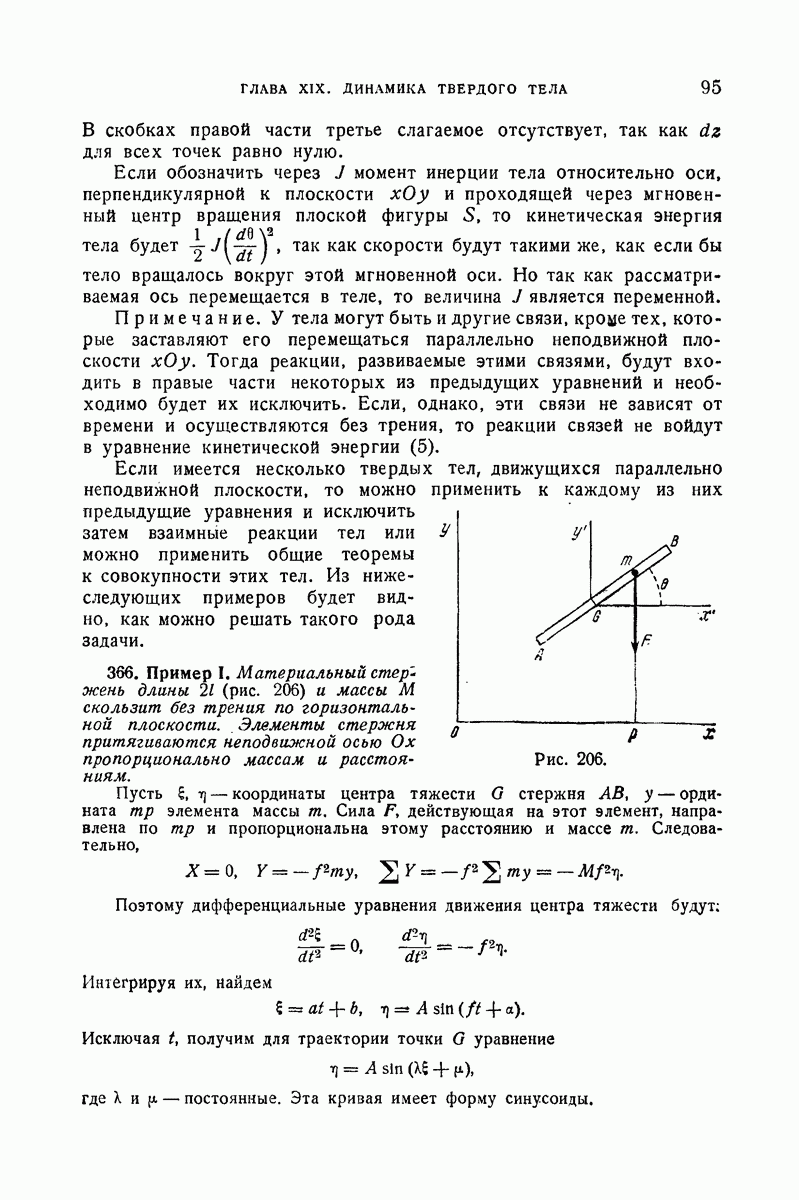
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
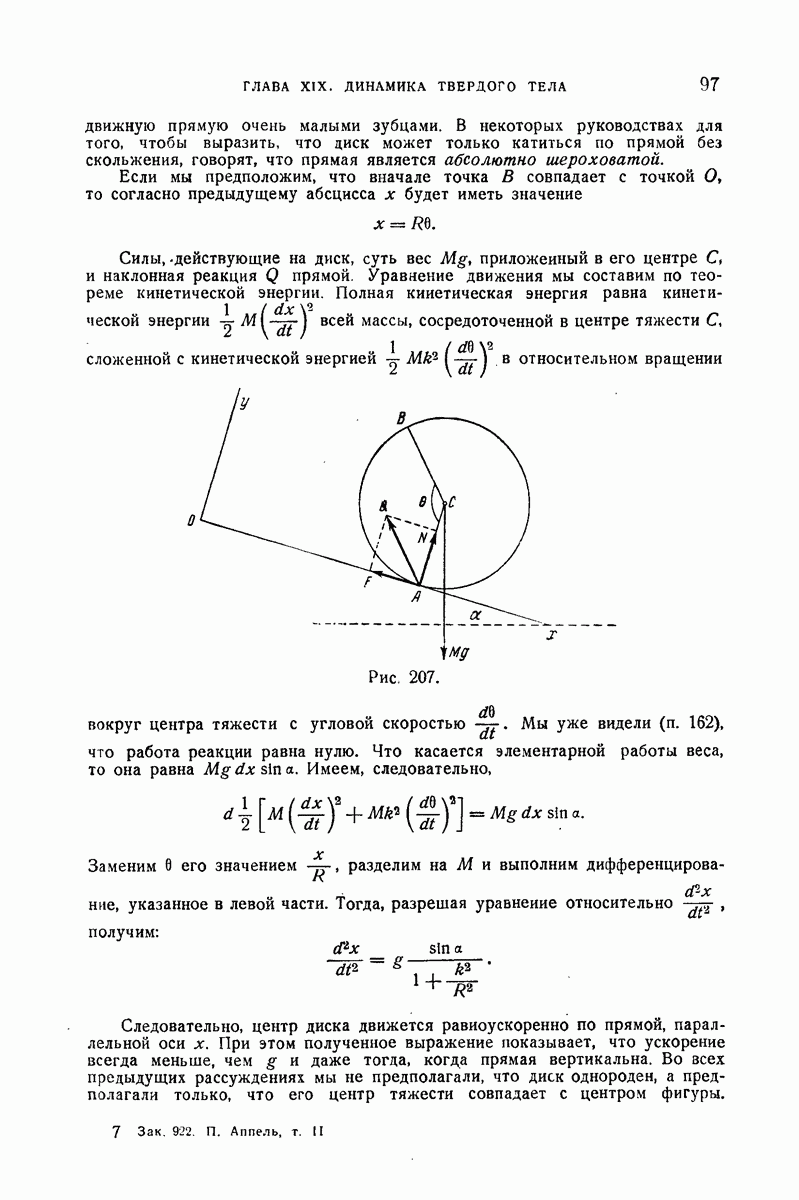
- 370. Пример I.
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
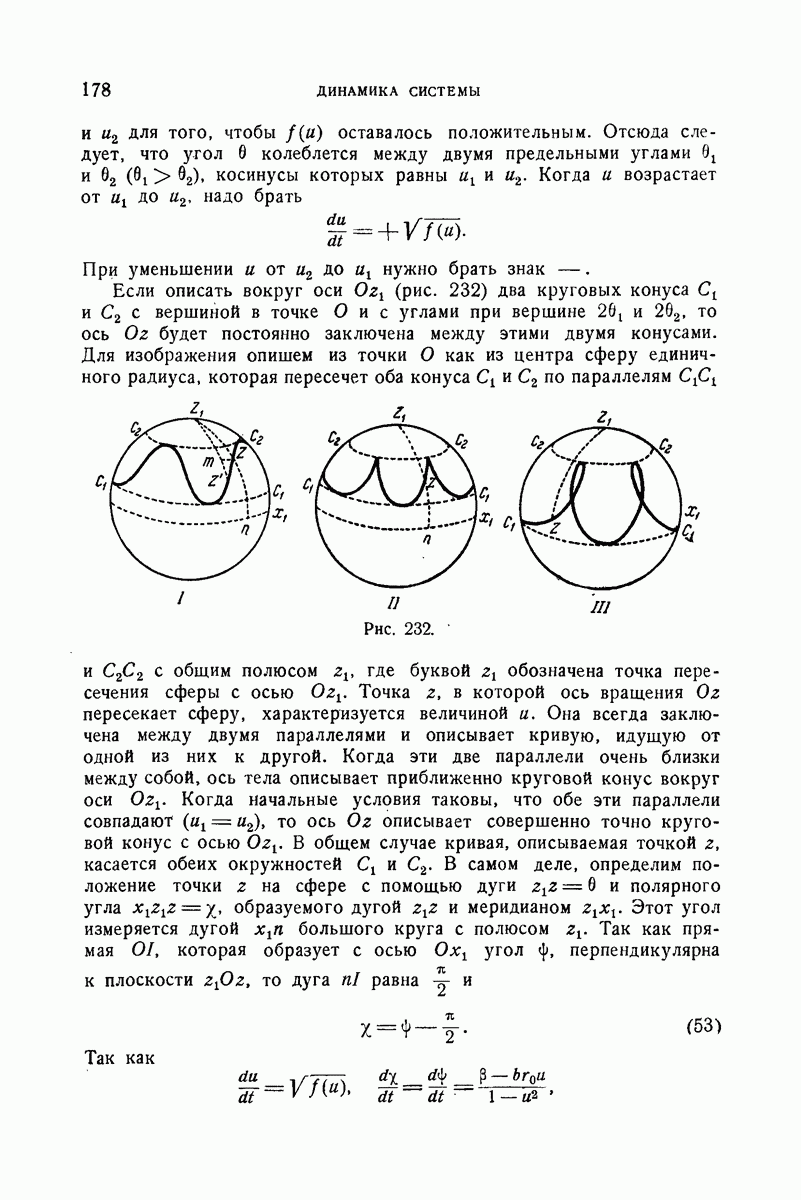
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
- 421. Твердое тело.
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
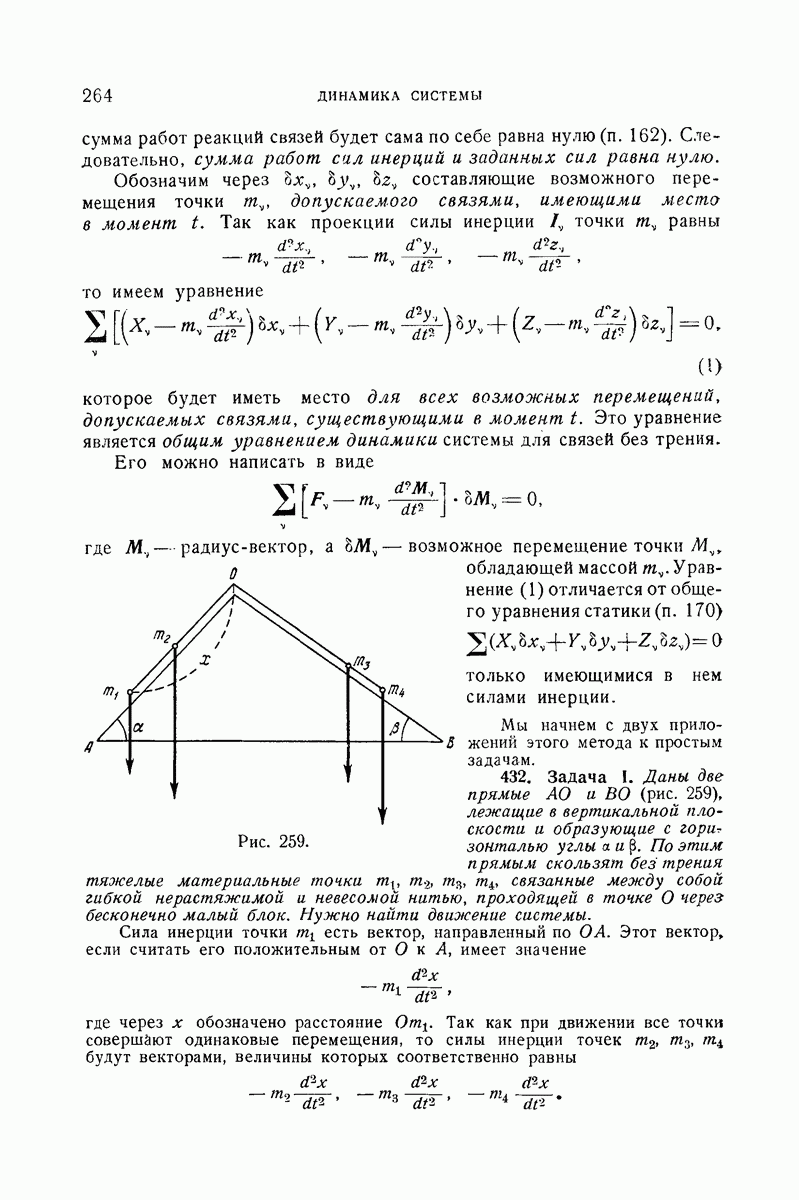
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
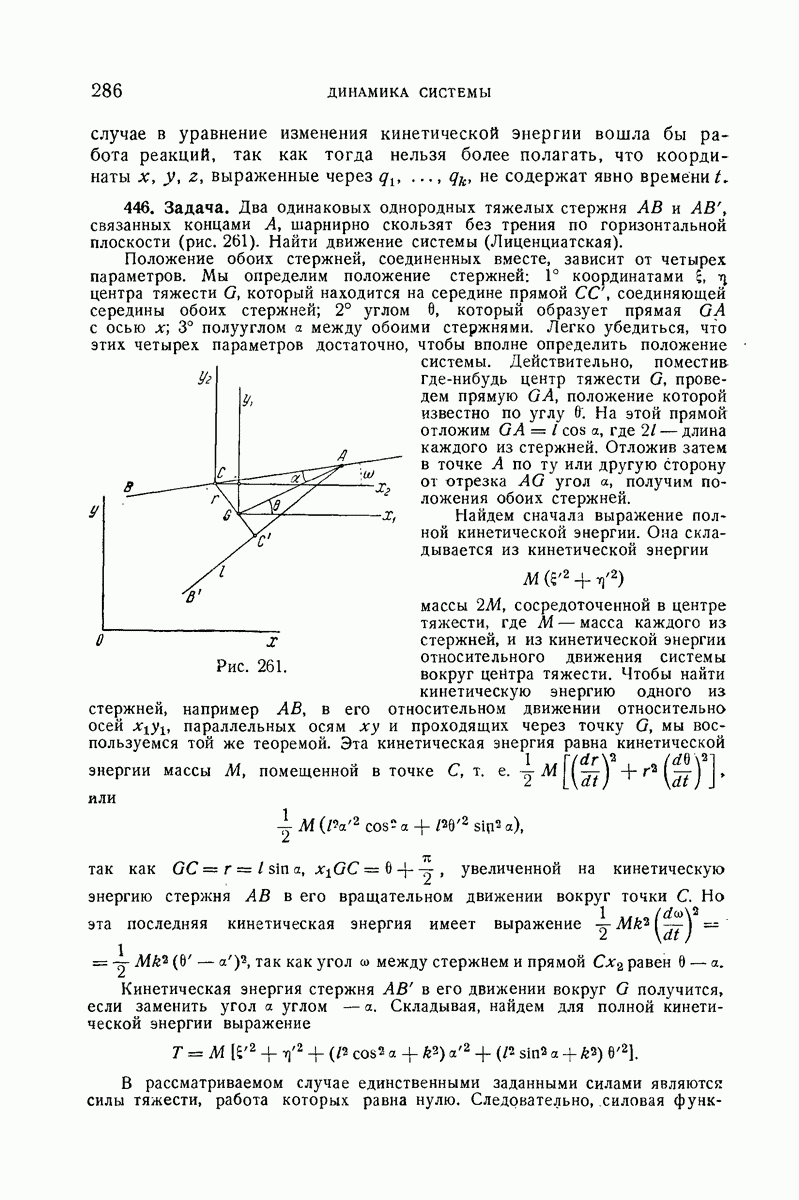
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели