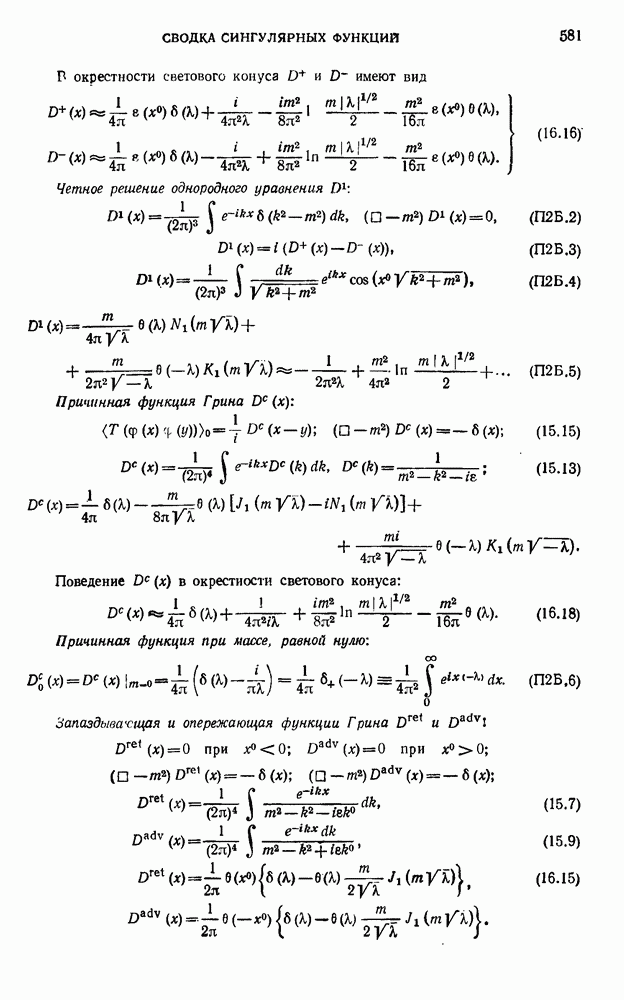| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
25.5. Двухчастичный распад.
Допустим теперь, что в начальном состоянии находится одна частица  массы М, а в конечном — две частицы
массы М, а в конечном — две частицы  с массами
с массами  Этот случай соответствует двухчастичному распаду частицы М, который кинематически возможен при
Этот случай соответствует двухчастичному распаду частицы М, который кинематически возможен при

Согласно формуле (18) среднее число частиц в конечном состоянии, попадающих в интервалы  в единицу времени и единицу объема, будет
в единицу времени и единицу объема, будет

Перейдем в систему покоя начальной частицы:

После интеграции по  получаем
получаем

С помощью остающейся  -функции снимаем интегрирование по
-функции снимаем интегрирование по 

Выполняя интегрирование по  , имеем
, имеем

Интегрируя это выражение по телесному углу, получаем полную вероятность двухчастичного распада в единицу времени

Величина w имеет размерность массы (в обычной системе единиц — сек и совпадает с энергетической шириной

В случае, если существует несколько каналов распада, полная ширина складывается из суммы выражений вида (33)

а время жизни исходной частицы  определяется соотношением
определяется соотношением

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
- § 23. Приведение S-матрицы к нормальной форме
- 23.2. Диаграммы Фейнмана и правила соответствия.
- 23.3. Примеры.
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
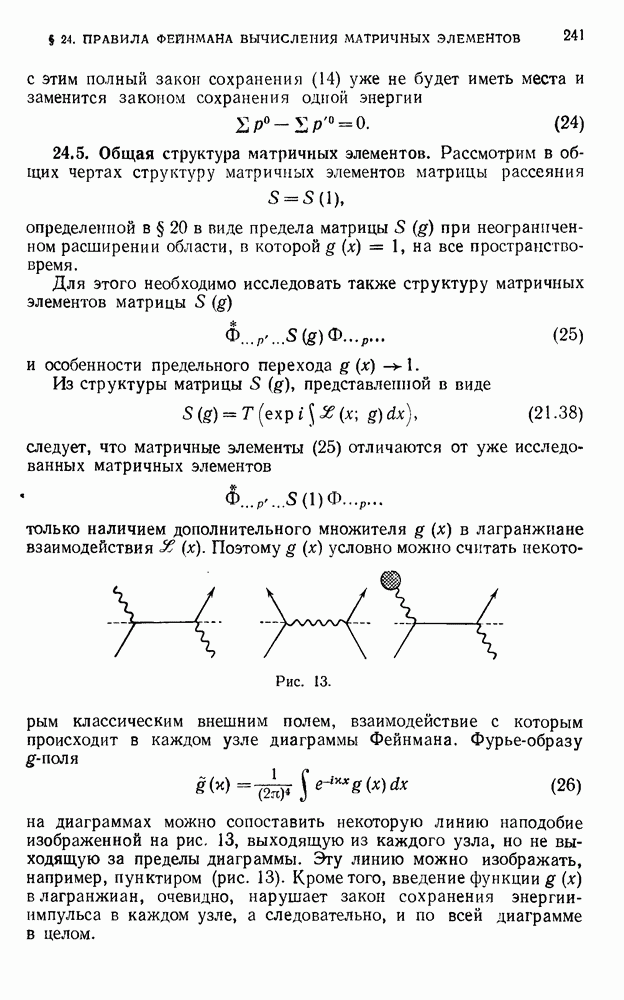
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
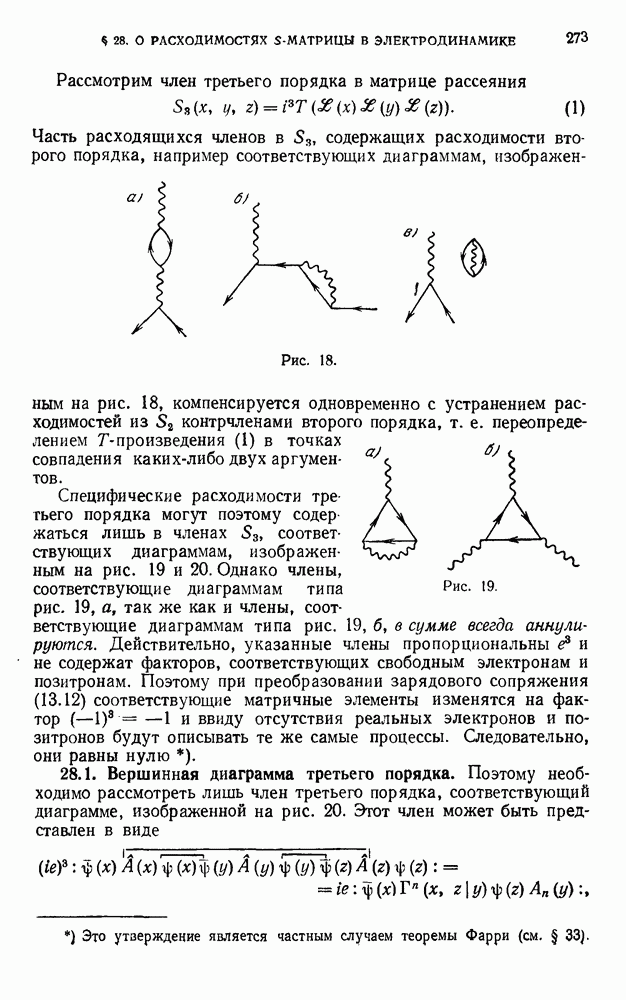
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
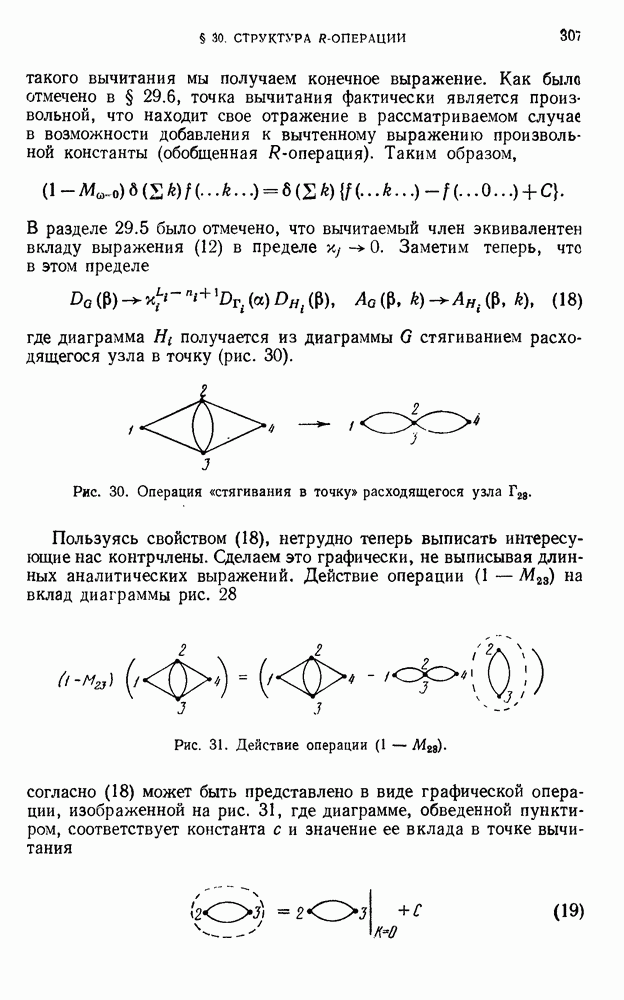
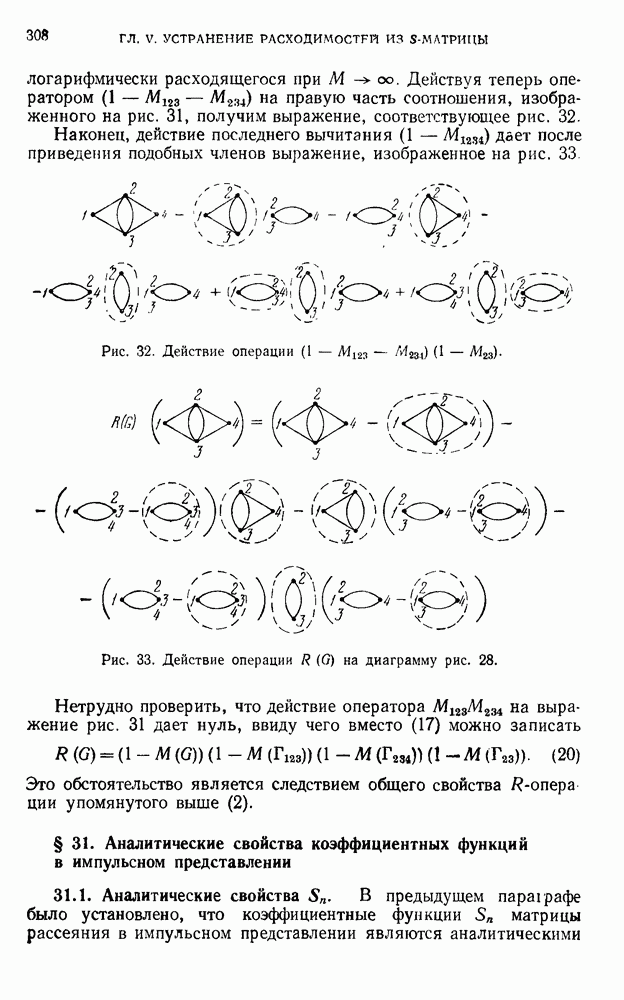
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
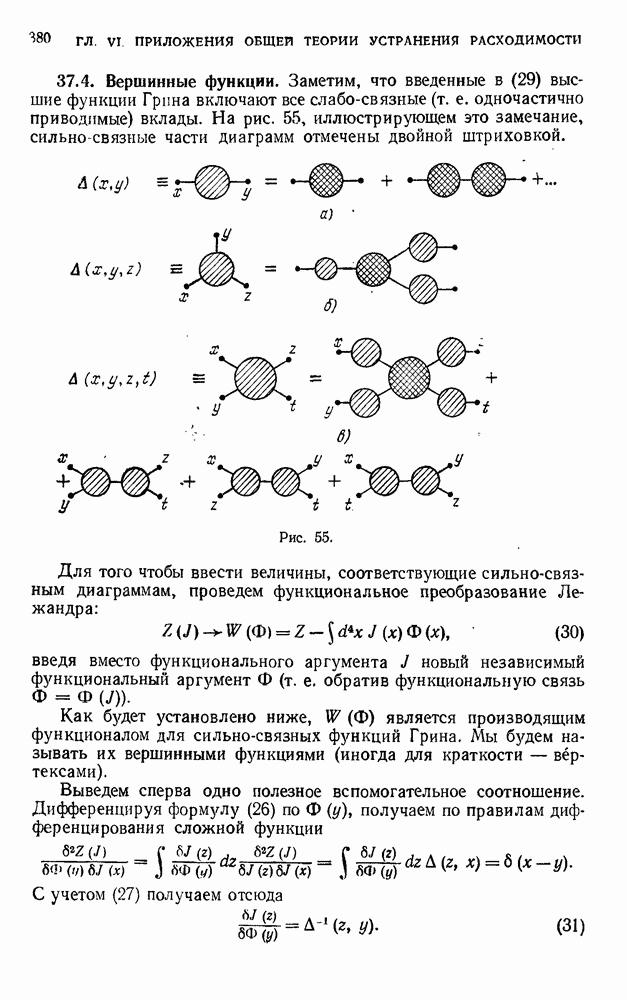
- 37.3. Производящий функционал для высших функций Грина.
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
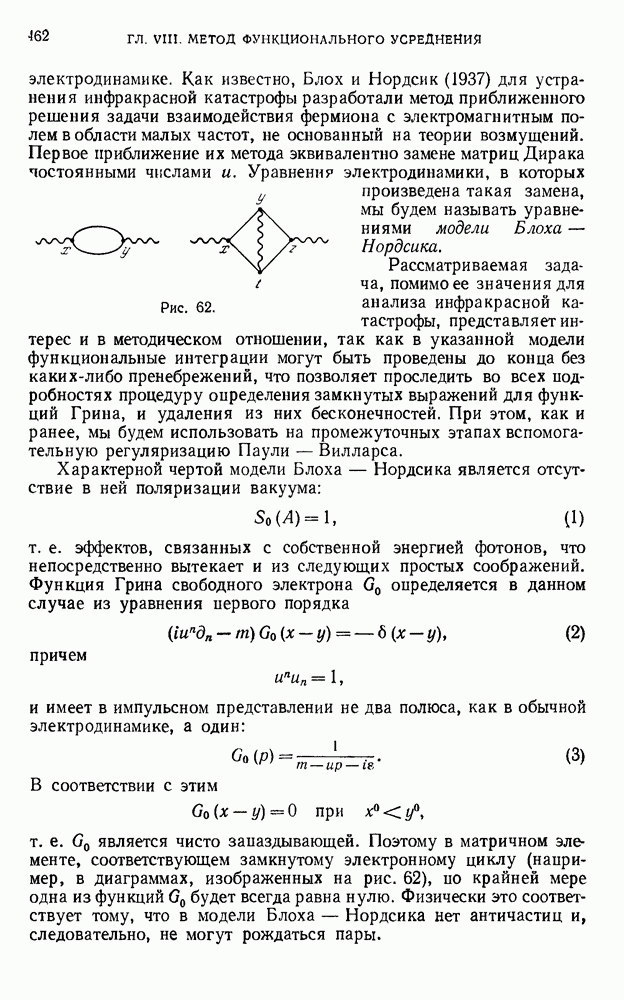
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
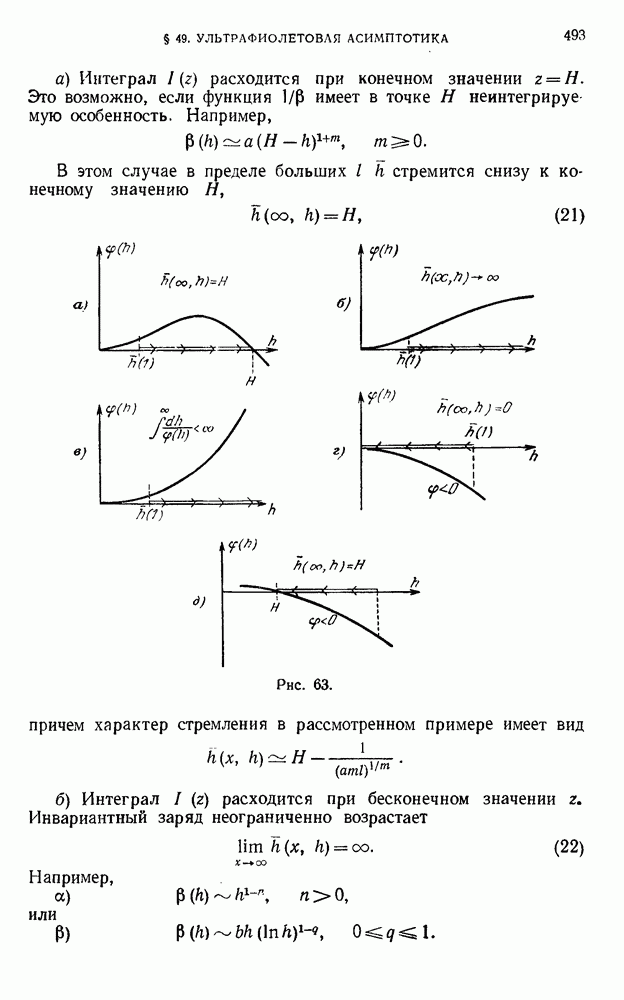
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
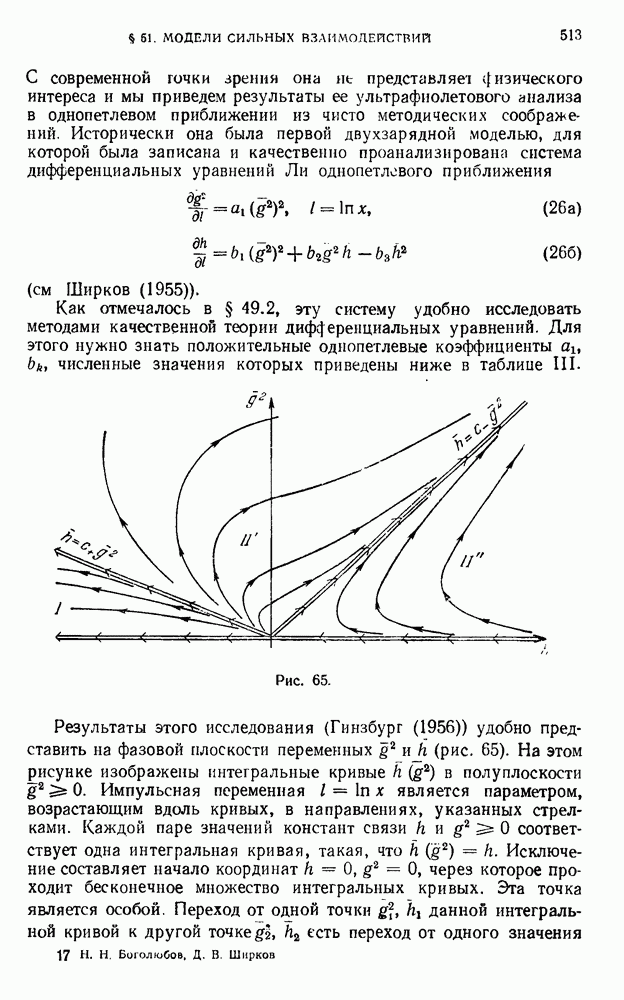
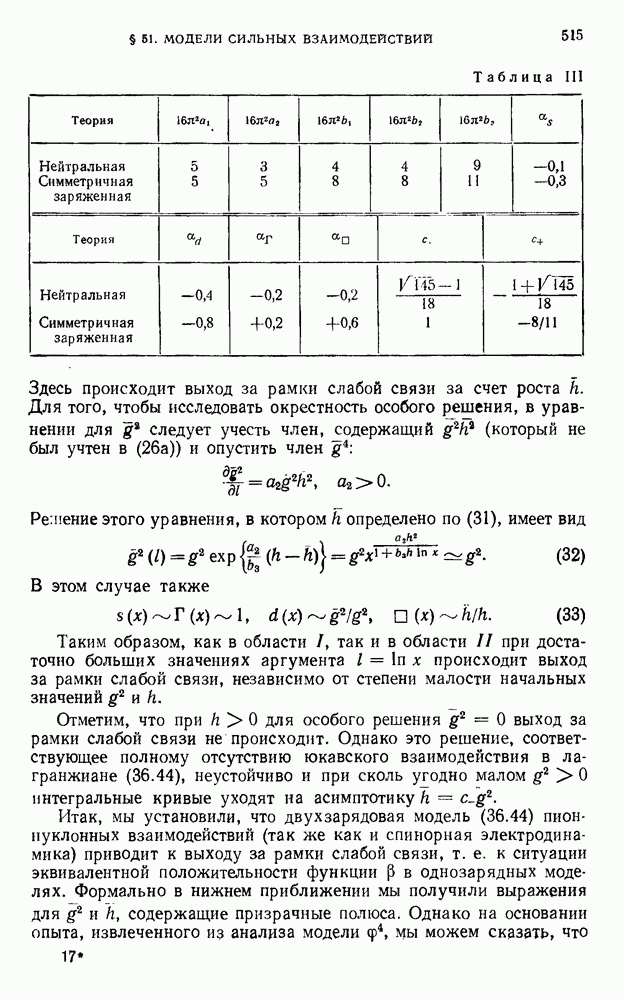
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
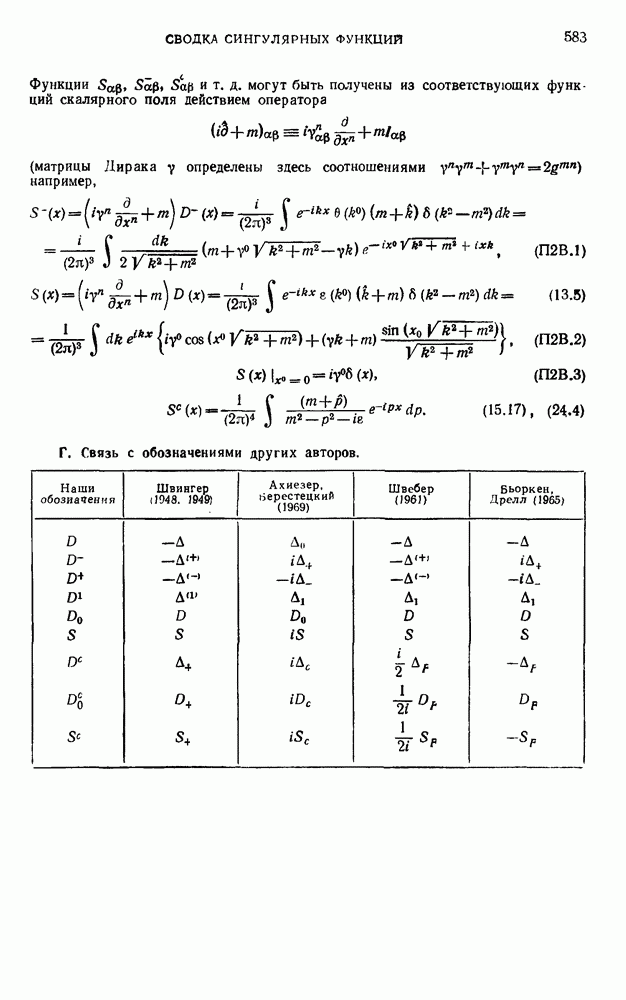
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА