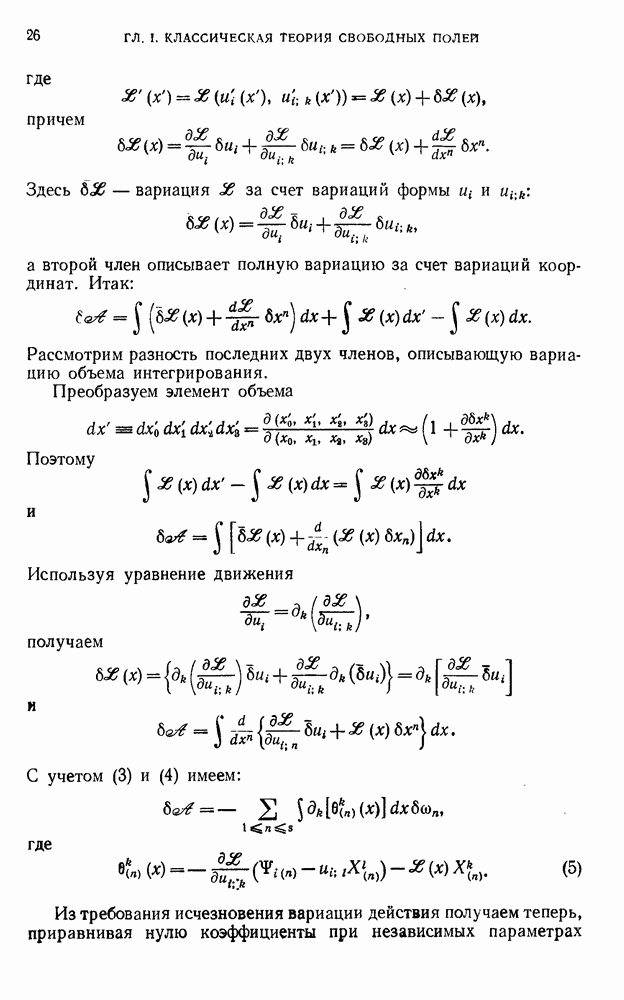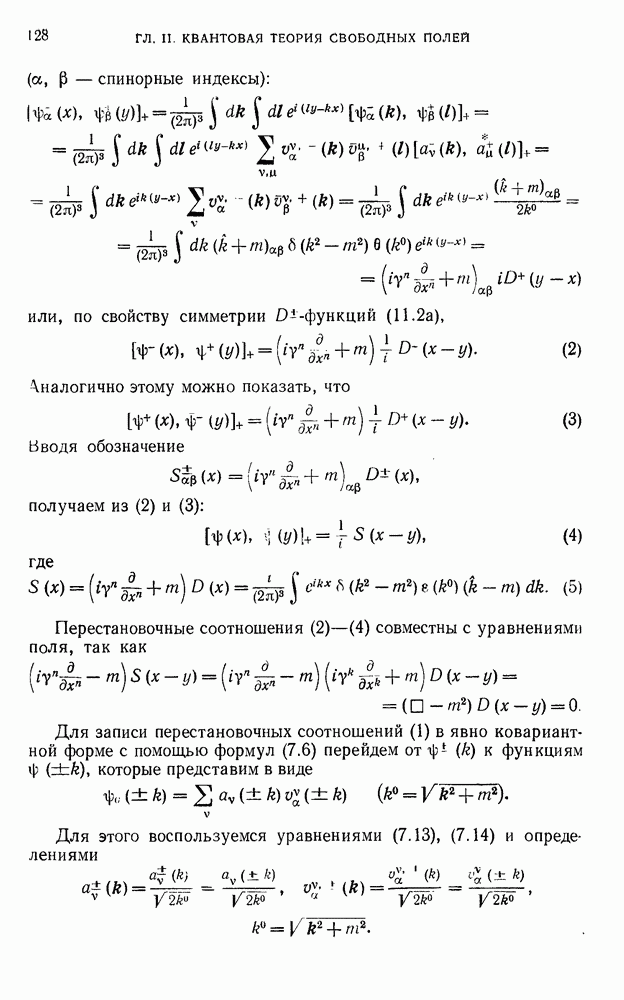| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 38. Уравнения Швингера и Дайсона
Теперь мы обратимся к задаче получения уравнений для введенных в предыдущем параграфе полных функций Грина. Как будет показано в § 38.2, эти функции Грина достаточно просто (вообще говоря, линейно) связаны с матричными элементами S-матрицы и полностью характеризуют поведение динамической системы. С другой стороны, рассматривая однородные уравнения для «обобщенных волновых функций», соответствующие неоднородным уравнениям для полных функций Грина, мы получаем возможность рассчитать радиационные поправки к собственным значениям энергии замкнутых систем и решать иные подобные задачи (см. ниже главу VII).
Можно было бы попытаться получить такие уравнения для полных функций Грина, «раскрывая» содержание радиационных поправок. Например, поляризационный оператор фотона в спинорной электродинамике можно выразить через интеграл от произведения электронных функций Грина и вершинных частей. В свою очередь сумму радиационных поправок к вершинной части можно выразить через одночастичные функции Грина и более сложные вершинные части и т. д.
Таким путем мы получили бы бесконечную последовательность все более усложняющихся уравнений, так называемых уравнений Дайсона. Как было показано Поливановым (1955), более элегантные соотношения можно получить на другом пути — используя метод производящего функционала, введенного в § 37.2. Здесь удается
получить вполне обозримую систему уравнений в функциональных производных — так называемых уравнений Швингера, из которой в свою очередь можно получать уравнения, связывающие различные функции Грина (уравнения Дайсона).
38.1. Обобщенная теорема Вика.
Прежде чем строить уравнения для функций Грина, рассмотрим вспомогательное предложение, которое уместно назвать «обобщенной теоремой Вика», утверждающее, что вакуумное ожидание от хронологического произведения  линейных операторов
линейных операторов  равно сумме
равно сумме  вакуумгых ожиданий тех же хронологических произведений со всеми возможными спариваниями одного из этих операторов (например, А) со всеми остальными, т. е.
вакуумгых ожиданий тех же хронологических произведений со всеми возможными спариваниями одного из этих операторов (например, А) со всеми остальными, т. е.

Обратим внимание на то, что в правой части (1) в отличие от обычной теоремы Вика (ср., например, (17.17)) не содержится выражений с числом спариваний, большим единицы.
Тем не менее, справедливость (1) непосредственно вытекает из обычной теоремы Вика. Ввиду исчезновения вакуумного ожидания нормального произведения любого отличного от нуля числа неспаренных операторов левая часть (1) равна сумме всех возможных вариантов полных взаимных спариваний внутри произведения операторов

т. е. спариваний, где спарены друг с другом все операторы. Совершенно аналогично любой из членов суммы в правой части (1), например первый, может быть представлен в виде

и равен произведению спаривания  на сумму всех возможных полных спариваний операторов
на сумму всех возможных полных спариваний операторов 
Выполняя суммирование по i в правой части (1), получаем сумму всех возможных полных спариваний операторов (2). Тем самым обобщенная теорема Вика доказана.
Имея в виду, что под знаком Т-произведений в вакуумных ожиданиях, определяющих полные функции Грина, содержится также матрица S, не являющаяся линейным оператором, обобщим теорему (1) и на этот случай. Рассмотрим для этого процесс спаривания линейного оператора  членом разложения матрицы рассеяния
членом разложения матрицы рассеяния

Введем операцию спаривания линейного оператора А с лагранжианом  также не являющимся линейным оператором. Выражение
также не являющимся линейным оператором. Выражение
 естественно определить как сумму произведений
естественно определить как сумму произведений  со всеми возможными спариваниями оператора А с операторами, входящими в X. Например, в случае спинорной электродинамики, когда с учетом члена внешнего тока
со всеми возможными спариваниями оператора А с операторами, входящими в X. Например, в случае спинорной электродинамики, когда с учетом члена внешнего тока  имеет вид
имеет вид

получаем, по определению,

Отметим в этой связи, что определенные выше полные функции Грина, которые являются суммами вкладов, соответствующих внутренним линиям диаграмм Фейнмана, естественно, содержат расходимости того же типа, что и матрица рассеяния. Для устранения этих расходимостей следовало бы с самого начала ввести в лагранжиан взаимодействия обычные контрчлены. Однако ради простоты изложения мы выведем сначала уравнения Швингера для функций Грина, исходя из лагранжиана (4), а затем произведем также и учет контрчленов.
Вернемся к спариванию (3) с линейным оператором А; мы получим сумму членов

которая благодаря симметрии (3) по отношению к переменным интеграции  может быть представлена следующим образом:
может быть представлена следующим образом:

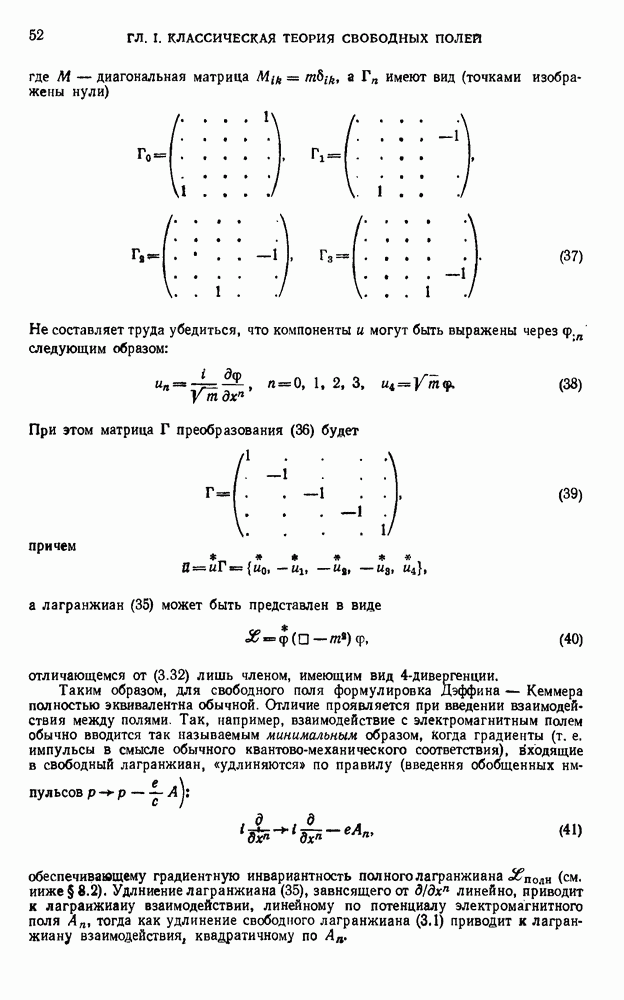
Суммируя по  , получаем результат спаривания оператора А с матрицей S в виде
, получаем результат спаривания оператора А с матрицей S в виде

Эту формулу можно переписать в другом виде, если использовать понятие вариационной производной S-матрицы но операторной функции поля.
Такие производные можно ввести, определив их как пределы соответствующих функциональных производных по аддитивным классическим добавкам  к квантовым и
к квантовым и 

при  , т. е.
, т. е.

Для того, чтобы полученные таким путем вариационные производные по ферми-полям  обладали надлежащими свойствами антикоммутативности, необходимо считать, что классические добавки к ферми-полям по своей алгебраической природе подобны введенным в § 37.3 источникам ферми-полей
обладали надлежащими свойствами антикоммутативности, необходимо считать, что классические добавки к ферми-полям по своей алгебраической природе подобны введенным в § 37.3 источникам ферми-полей  и удовлетворяют коммутационным соотношениям (37.15) грассмановой алгебры. Подобно тому, как это было сделано в § 37.3, мы условимся считать все вариационные производные по ферми-полям левыми производными. Замечая, что формулы (5—7) могут быть представлены в виде
и удовлетворяют коммутационным соотношениям (37.15) грассмановой алгебры. Подобно тому, как это было сделано в § 37.3, мы условимся считать все вариационные производные по ферми-полям левыми производными. Замечая, что формулы (5—7) могут быть представлены в виде

перепишем (8) в виде

Приведем еще формулы коммутации с S-матрицей и ее функциональными производными для бозе-оператора 

для ферми-оператора  :
:

Отметим, что коммутаторы ферми-операторов  с четными по ферми-полям функционалами (например, вариационными производными от S четного порядка по
с четными по ферми-полям функционалами (например, вариационными производными от S четного порядка по  ) имеют структуру (12а). В то же время структуру, подобную (126), имеют антикоммутаторы ферми-операторов
) имеют структуру (12а). В то же время структуру, подобную (126), имеют антикоммутаторы ферми-операторов  с нечетными по ферми-полям функционалами.
с нечетными по ферми-полям функционалами.
Выразим теперь вакуумные ожидания

на основе которых в § 37 строились высшие функции Грина, через вариационные производные S-матрицы.
Используя обобщенную теорему Вика относительно  получаем согласно (1) и (10)
получаем согласно (1) и (10)
 (13)
(13)
Здесь  обозначает величину, полученную из (37.1) вычеркиванием оператора
обозначает величину, полученную из (37.1) вычеркиванием оператора  — знаковые сомножители, учитывающие
— знаковые сомножители, учитывающие
четность перестановок ферми-операторов, в случае, если  поле с полуцелым спином.
поле с полуцелым спином.
Формула (13) выражает вакуумное ожидание от хронологического произведения k операторов и S-матрицы через сумму аналогичных ожиданий от  операторов и S-матрицы, либо ее вариационной производной, т. е. эффективно понижает на единицу степень линейности по u.
операторов и S-матрицы, либо ее вариационной производной, т. е. эффективно понижает на единицу степень линейности по u.
Применяя троекратно формулу (13) к выражению  связанному по формуле (37,24) с трехконцевой функцией Грина, получим после небольших преобразований
связанному по формуле (37,24) с трехконцевой функцией Грина, получим после небольших преобразований

Сравнивая (37.24) и (14), получаем связь между  и вакуумным ожиданием от третьей вариационной производной. Эта связь имеет вид
и вакуумным ожиданием от третьей вариационной производной. Эта связь имеет вид

Здесь многоточием обозначены слагаемые, пропорциональные Ф и обращающиеся в нуль в пределе выключения источников. Для  -концевой функции Грина соответствующее соотношение в отсутствии внешних источников имеет вид
-концевой функции Грина соответствующее соотношение в отсутствии внешних источников имеет вид

Переходя к импульсному представлению
 (17)
(17)
получим также

Формулы (16), (18) допускают очевидное обобщение на случай ферми-полей.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
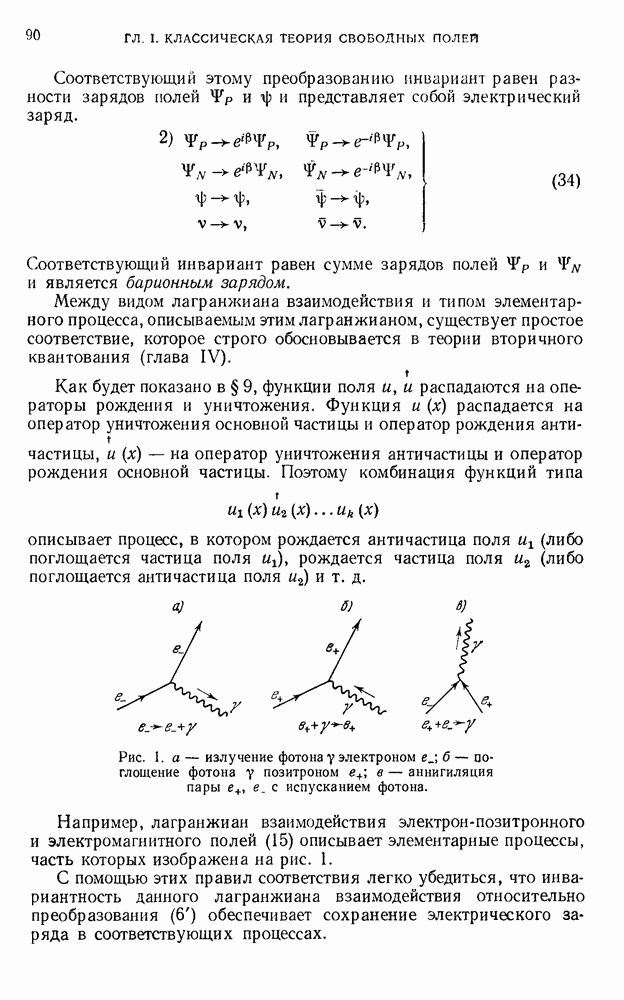
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
- § 23. Приведение S-матрицы к нормальной форме
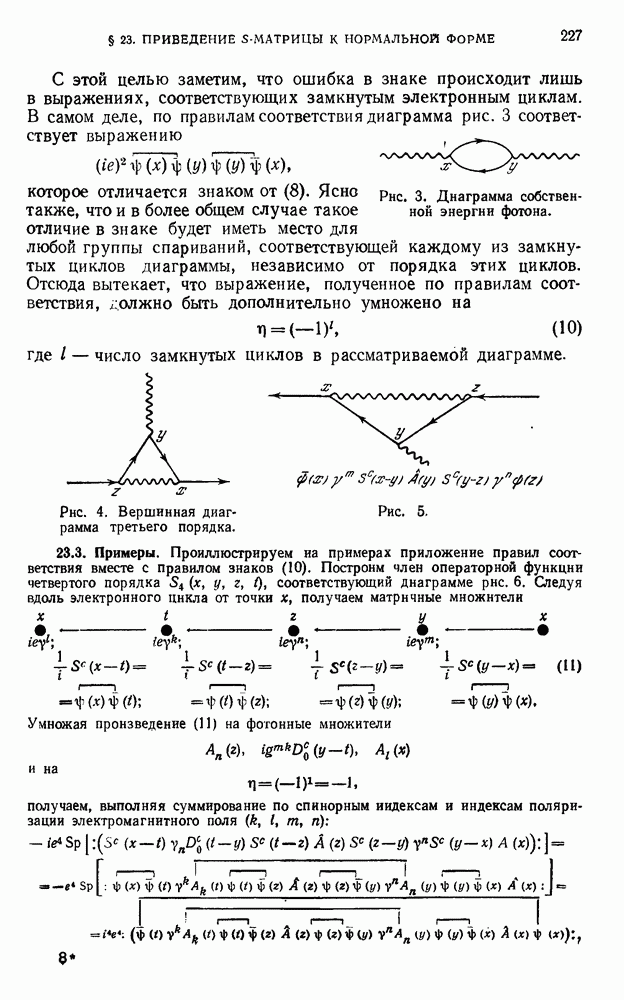
- 23.2. Диаграммы Фейнмана и правила соответствия.
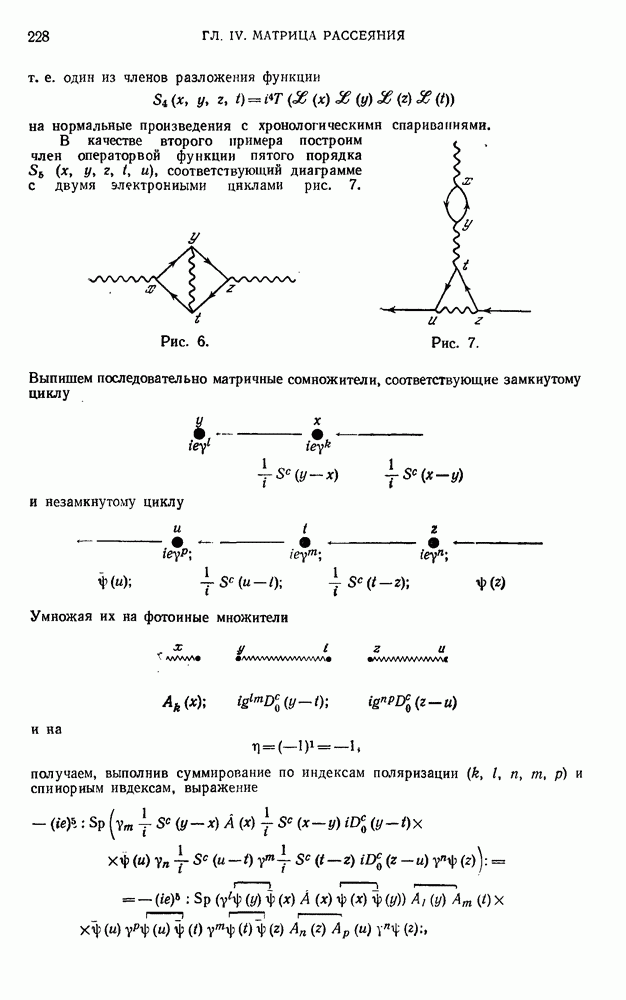
- 23.3. Примеры.
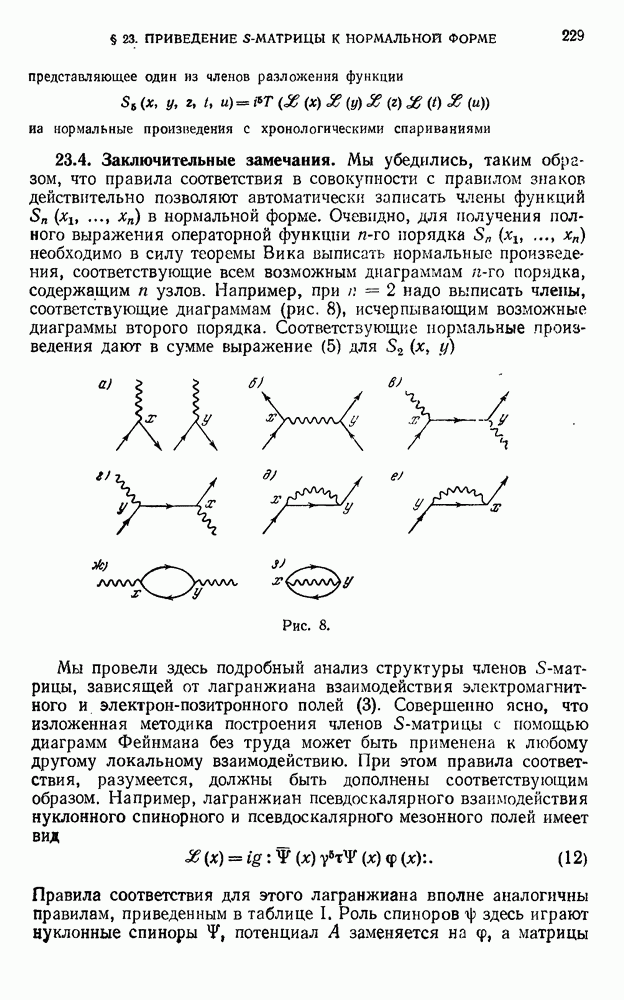
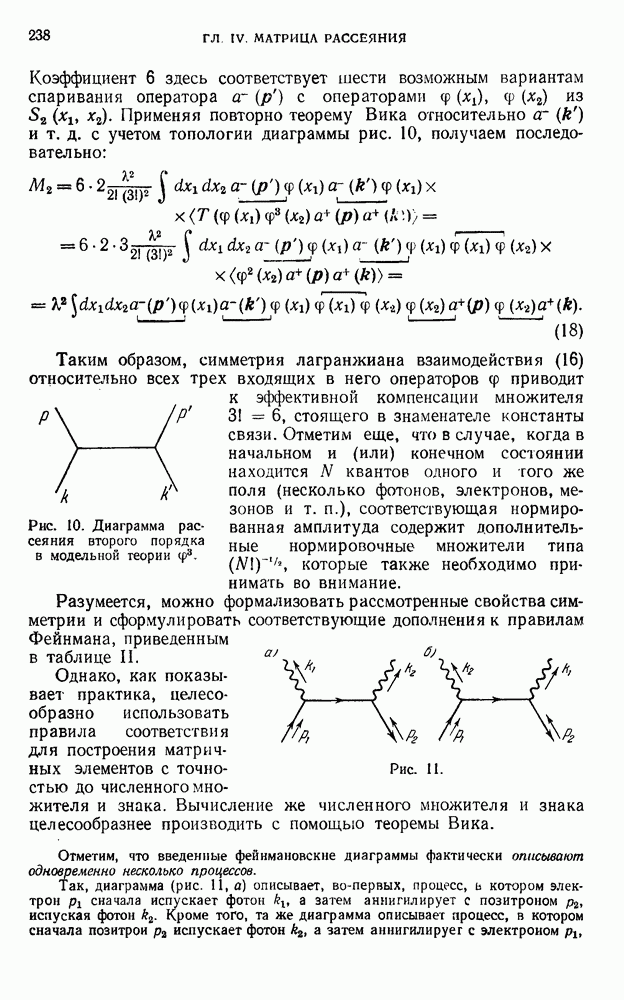
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
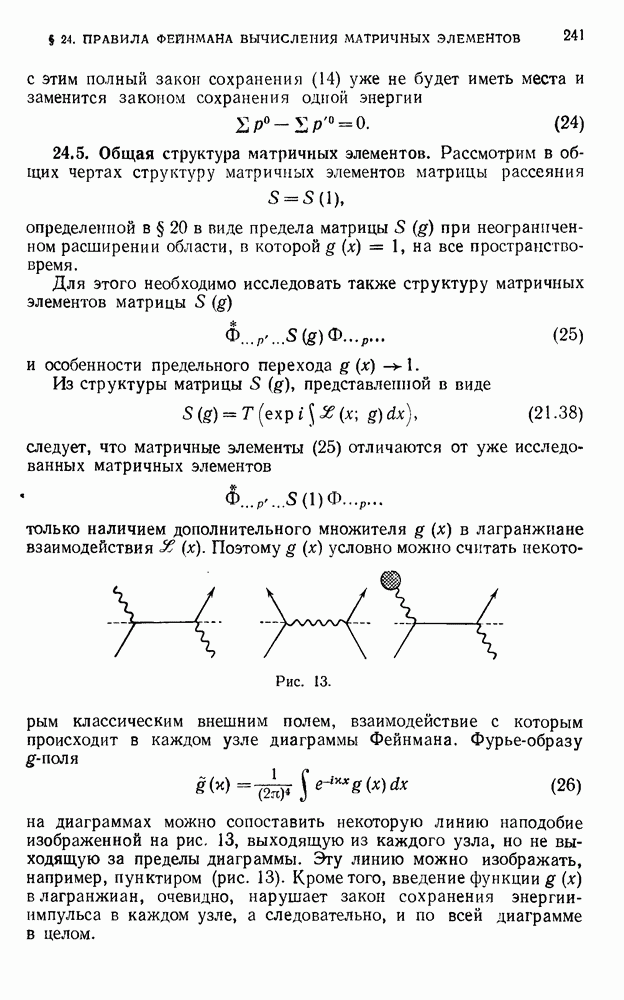
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
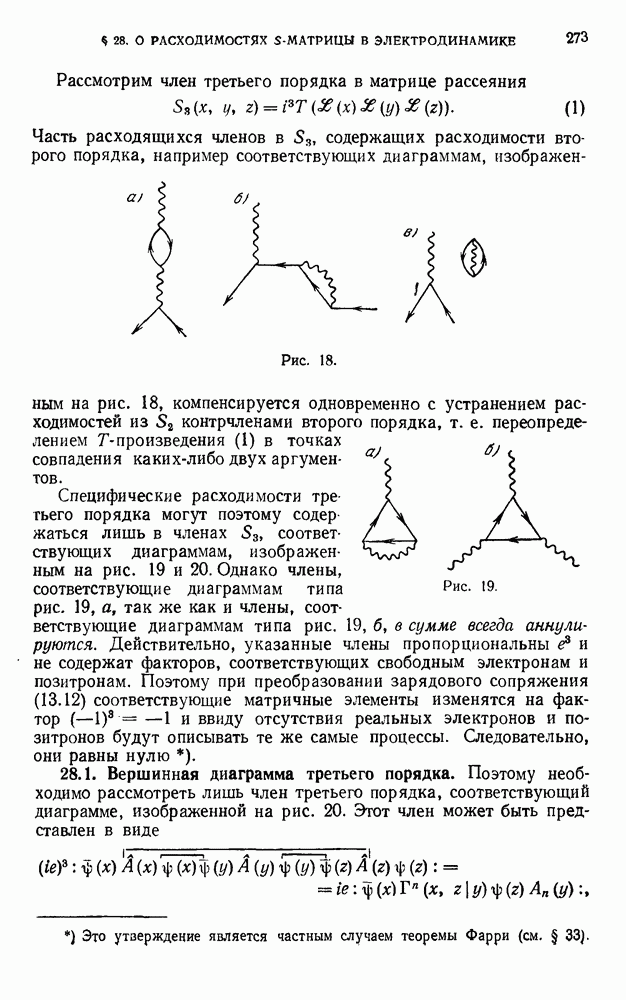
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
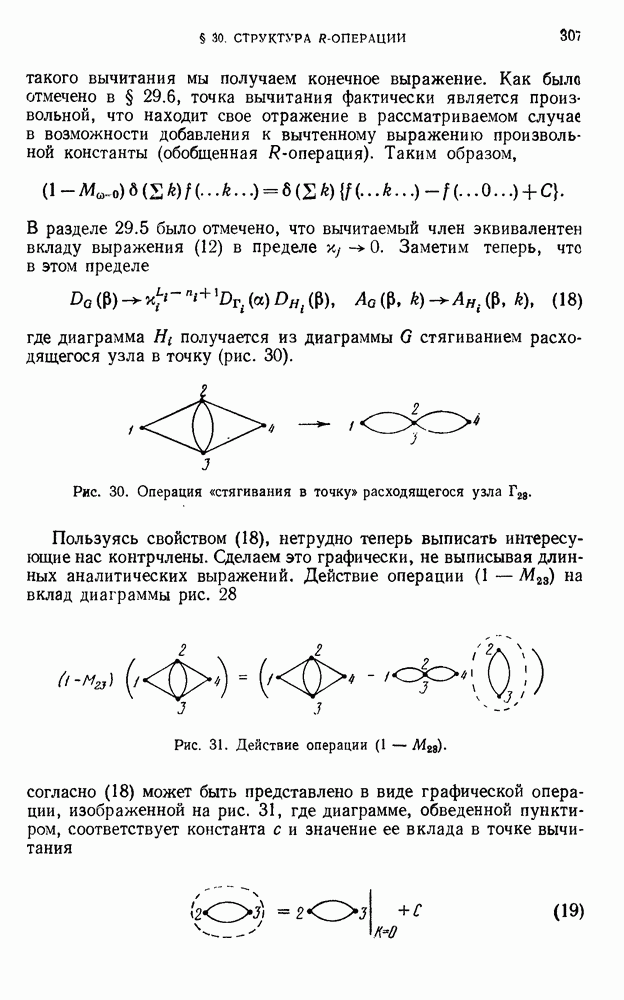
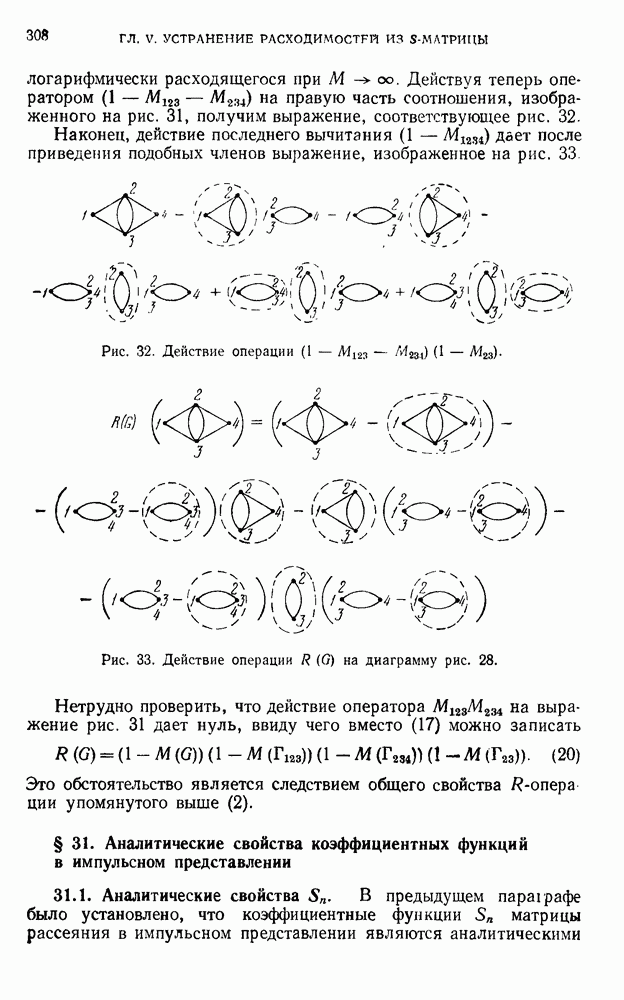
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
- 37.3. Производящий функционал для высших функций Грина.
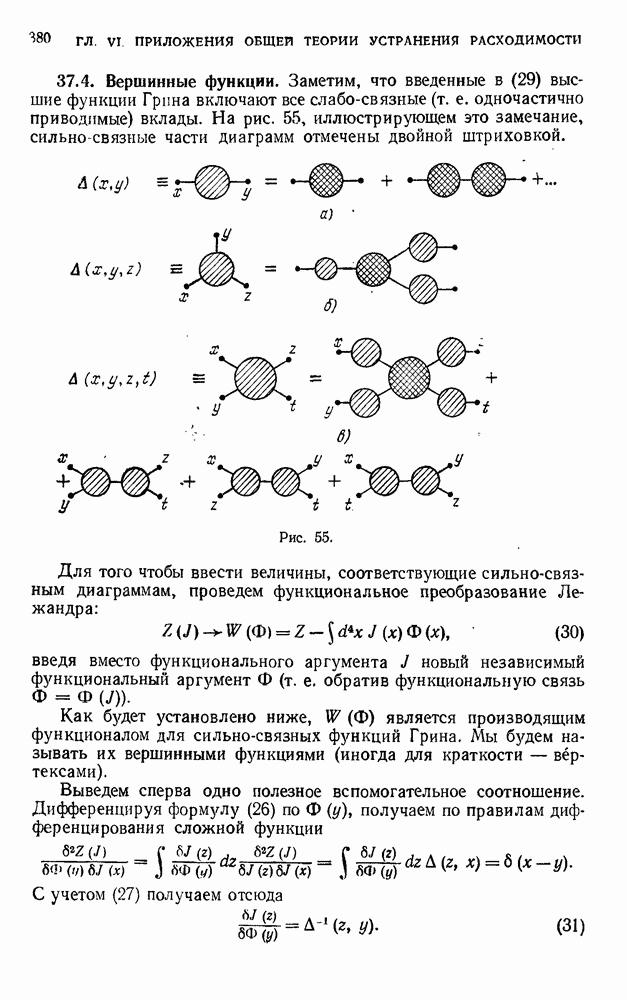
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
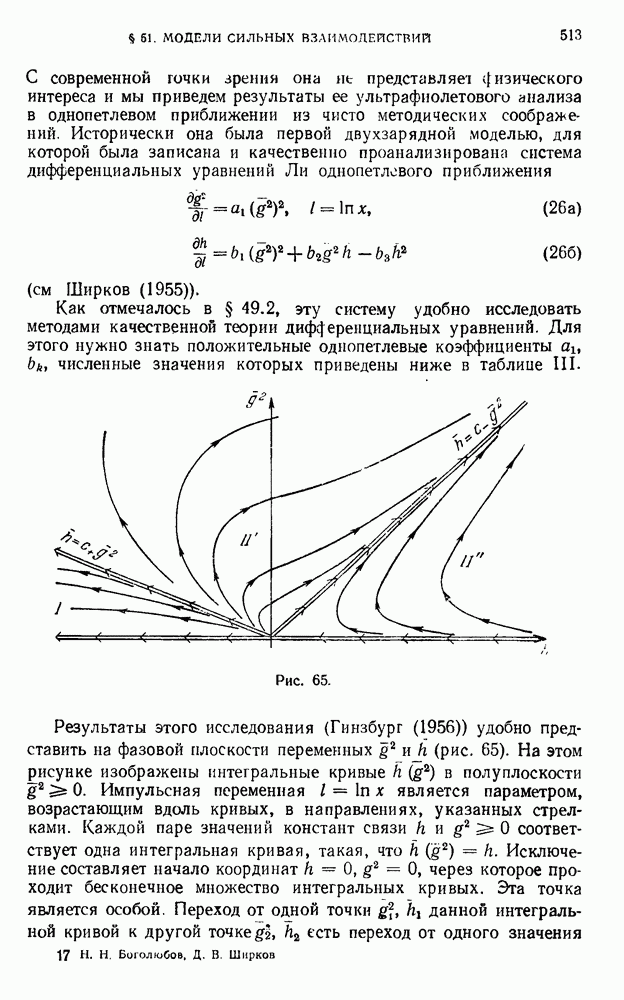
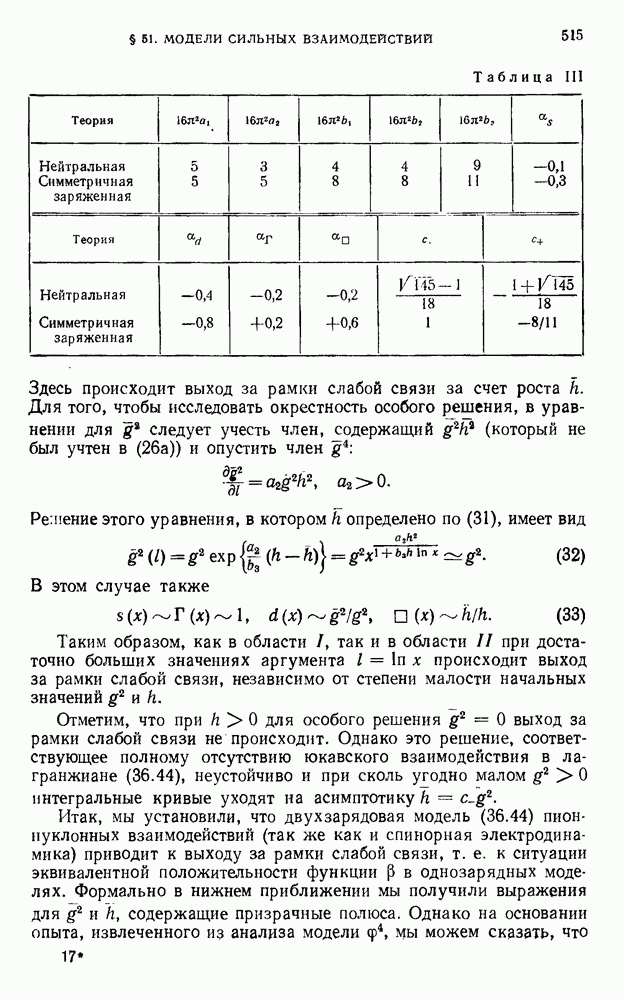
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА