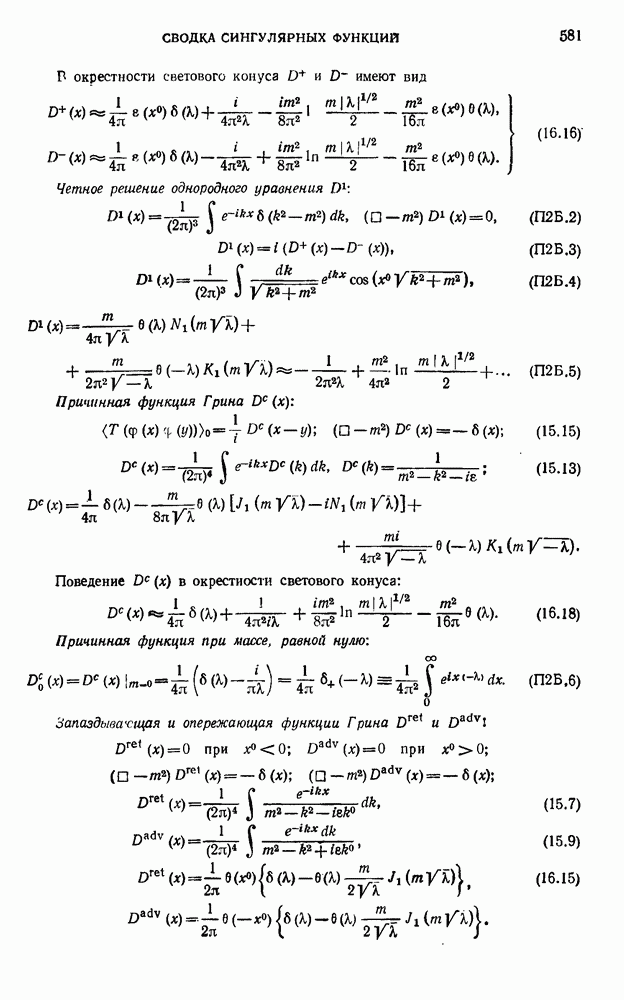| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
39.3. Сингулярности обобщенного гамильтониана.
Исследуем более подробно предельный переход, предписываемый формулой (14). При этом, чтобы не сталкиваться с дополнительными осложнениями, связанными с проблемой ультрафиолетовых расходимостей, будем исходить из регуляризованного выражения для  с конечными вспомогательными массами М.
с конечными вспомогательными массами М.
Начнем с члена второго порядка в  Из уравнений (21.12) и (21.41) находим
Из уравнений (21.12) и (21.41) находим

Если регуляризация проведена для каждой внутренней линии, то при конечных М выражение

является регулярным, и интеграл от произведения его на  по области (12) в пределе
по области (12) в пределе  обращается в нуль, поскольку сама область при этом сжимается в точку. В то же время соответствующий интеграл
обращается в нуль, поскольку сама область при этом сжимается в точку. В то же время соответствующий интеграл

с квазилокальным оператором, содержащим  -функцию, отличен от нуля.
-функцию, отличен от нуля.
Совершенно аналогичными рассуждениями можно установить, что в более общем случае имеет место предельное равенство

Для доказательства этого, представив  в виде суммы двух членов:
в виде суммы двух членов:

достаточно убедиться в том, что оператор  содержит число
содержит число  -функций, меньшее
-функций, меньшее  , и потому
, и потому  -кратная интеграция его по бесконечно малой области также даст нуль.
-кратная интеграция его по бесконечно малой области также даст нуль.
Итак, предельное (при  ) выражение для плотности гамильтониана имеет вид (Суханов (1962а))
) выражение для плотности гамильтониана имеет вид (Суханов (1962а))

Особенности этого выражения проиллюстрируем на двух примерах.
В теории с взаимодействием к  квазилокальные операторы
квазилокальные операторы  с производными относятся лишь к вакуумным членам, не содержащим операторов полей. Их вклад в предельный гамильтониан (15) пропорционален интегралу
с производными относятся лишь к вакуумным членам, не содержащим операторов полей. Их вклад в предельный гамильтониан (15) пропорционален интегралу

обращающемуся в нуль вследствие убывания функции g на бесконечности. В остальных членах квазилокальные операторы не содержат производных, и предельный переход (15) с учетом свойств симметрии операторов  (подробнее см. Суханов (1962 а)) дает:
(подробнее см. Суханов (1962 а)) дает:

где эффективный лагранжиан  теории
теории  определен формулой (36.7).
определен формулой (36.7).
В теории  производные в
производные в  содержатся уже в операторных членах. При выполнении интеграций по
содержатся уже в операторных членах. При выполнении интеграций по  в (15) эти производные перейдут как на поля
в (15) эти производные перейдут как на поля  , так и на функции
, так и на функции  . В членах
. В членах
первого типа предельный переход  допустим и (в совокупности с пределом членов без производных) дает выражение, аналогичное (17). Для членов же второго типа формального предела
допустим и (в совокупности с пределом членов без производных) дает выражение, аналогичное (17). Для членов же второго типа формального предела  не существует. Действительно, во втором порядке по
не существует. Действительно, во втором порядке по  будет давать вклад выражение
будет давать вклад выражение

По тем же соображениям, что и в (16), первый член разности здесь обращается в нуль. Во втором члене в пределе  появляется выражение неинтегрируемого типа, поскольку
появляется выражение неинтегрируемого типа, поскольку  . Подчеркнем, что эта трудность возникает и при конечных вспомогательных массах М, она связана с резким выключением взаимодействия на пространственно-подобной поверхности
. Подчеркнем, что эта трудность возникает и при конечных вспомогательных массах М, она связана с резким выключением взаимодействия на пространственно-подобной поверхности  Существование расходимостей такого типа впервые было отмечено Штюкельбергом (1951), который назвал их поверхностными.
Существование расходимостей такого типа впервые было отмечено Штюкельбергом (1951), который назвал их поверхностными.
Формально предел  можно доопределить как расширение функционала
можно доопределить как расширение функционала  определенного на основных функциях, обращающихся в О в точке
определенного на основных функциях, обращающихся в О в точке  на все основные функции класса
на все основные функции класса  . Такое расширение (см., например, Владимиров (1964)) имеет вид
. Такое расширение (см., например, Владимиров (1964)) имеет вид

где С — произвольная постоянная. В этом случае выражение (18) примет вид

Аналогичные вклады (с новыми произвольными постоянными) возникают от старших порядков по 
Таким образом, в теории  формальное доопределение (19) предельного перехода
формальное доопределение (19) предельного перехода  приводит к виду (Суханов, 19626):
приводит к виду (Суханов, 19626):

где эффективный лагранжиан  определен формулой (21.39), а
определен формулой (21.39), а  представляет собой сумму вкладов в переиормировочный множитель
представляет собой сумму вкладов в переиормировочный множитель  от различных порядков теории возмущений, умиожеииых на произвольные постоянные с (при
от различных порядков теории возмущений, умиожеииых на произвольные постоянные с (при  эти вклады расходятся).
эти вклады расходятся).
Посмотрим, как проявляет себя этот произвол в решении уравнения Томонага—Швингера (13), которое естественно искать в виде

Мы имеем

причем  определяется формулой (20). Очевидно, вклад второго члена в (20) сосредоточен на поверхности
определяется формулой (20). Очевидно, вклад второго члена в (20) сосредоточен на поверхности  Поскольку при этом
Поскольку при этом  коммутируют при равных временах, этот вклад можно вынести из-под знака Т-Экспоненты и выделить в отдельный экспоненциальный множитель слева:
коммутируют при равных временах, этот вклад можно вынести из-под знака Т-Экспоненты и выделить в отдельный экспоненциальный множитель слева:

Гаким образом, весь произвол в  появляющийся при доопределении предельного перехода
появляющийся при доопределении предельного перехода  удается выделить в унитарный операторный множитель, сосредоточенный на поверхности а. Заметим, что этот произвол не сказывается на полной S-матрице.
удается выделить в унитарный операторный множитель, сосредоточенный на поверхности а. Заметим, что этот произвол не сказывается на полной S-матрице.
Отметим, что рассуждения, приведшие нас к формулам (15) и (20), справедливы лишь в случае, когда регуляризация проводится для каждой внутренней линии диаграммы. Такая регуляризация, конечно, «избыточна»; для устранения расходимостей было бы достаточно регуляризовать только сильно связные части диаграмм: однако ее преимуществом является простота формул типа (15) и (20). При минимальной же регуляризации выражения типа

вообще говоря, не регулярны и содержат квазилокальную компоненту, если в лагранжиане имеются производные. Действительно, слабо связной диаграмме отвечает член с единственной сверткой, возникающий при раскрытии Г произведения лагранжианов, причем соответствующая линия теперь не регуляризуется. Поэтому, например, две временные производные, подействовав на свертку  дадут квазилокальный член, пропорциональный б
дадут квазилокальный член, пропорциональный б  (Ранее, при неминимальной регуляризации, множителем при этом члене стояла обращающаяся в нуль сумма коэффициентов Паули—Вилларса.)
(Ранее, при неминимальной регуляризации, множителем при этом члене стояла обращающаяся в нуль сумма коэффициентов Паули—Вилларса.)
В итоге, в каждом порядке по  наряду с вкладом от операторов
наряду с вкладом от операторов  в пределе
в пределе  появляется дополнительный квазилокальный вклад в
появляется дополнительный квазилокальный вклад в 

так что вместо (15) будет справедлива формула (Суханов (1961))

где

Заметим, что предельный переход  в члене с
в члене с  также приводит к поверхностным расходимостям, поскольку операторы
также приводит к поверхностным расходимостям, поскольку операторы  как и
как и  могут содержать производные.
могут содержать производные.
В примере теории  предельное выражение для обобщенного гамильтониана при минимальной регуляризации приобретает вид:
предельное выражение для обобщенного гамильтониана при минимальной регуляризации приобретает вид:

Последний член, как и ранее, приводит в матрице S (а) к (другому) унитарному множителю, сосредоточенному на поверхности а. Второй член, отличающий  от —X
от —X  , всегда присутствует в теориях с производными. Об этом отличии уже упоминалось в конце § 21 в связи с двумя формами S-матрицы — виковой и дайсоиовой.
, всегда присутствует в теориях с производными. Об этом отличии уже упоминалось в конце § 21 в связи с двумя формами S-матрицы — виковой и дайсоиовой.
Подчеркнем, что все рассуждения мы проводили при конечных вспомогательных массах. В пределе  перенормировочные константы в эффективном лагранжиане
перенормировочные константы в эффективном лагранжиане  расходятся.
расходятся.
Отсюда следует, что в некоторых случаях можно сразу записать «настоящее» уравнение Шредингера (с мгновенным выключением), но тогда в нем автоматически появляются расходящиеся члены.
Мы видим поэтому, что между матрицей рассеяния и уравнением Шредингера существует свойство дополнительности  смысле наличия бесконечноапей, даже после выделения поверхностных членов в унитарный множитель. Так, в обычной теории гамильтониан (т. е. уравнение Шредингера) регулярен, но в S-матрице содержатся бесконечные члены. С другой стороны, мы только что убедились, что если регуляризовать матрицу рассеяния, то расходимости автоматически появляются в уравнении Шредингера.
смысле наличия бесконечноапей, даже после выделения поверхностных членов в унитарный множитель. Так, в обычной теории гамильтониан (т. е. уравнение Шредингера) регулярен, но в S-матрице содержатся бесконечные члены. С другой стороны, мы только что убедились, что если регуляризовать матрицу рассеяния, то расходимости автоматически появляются в уравнении Шредингера.
В этой связи можно сделать следующее предположение о физической природе появления таких расходимостей. При мгновенном выключении взаимодействия влияние этого процесса на систему столь велико, что практически полностью невозможно определить какие-либо характеристики системы до процесса выключения. С формальной точки зрения мы имеем здесь некоторую аналогию с соотношениями неопределенности Гейзенберга, которые, как известно, связаны с самыми общими свойствами волновых процессов.
Мы приходим к выводу, что в общем случае можно довольно просто записать конечное уравнение для амплитуды  , где g — достаточно гладкая функция, но невозможно перейти к пределу
, где g — достаточно гладкая функция, но невозможно перейти к пределу  и получить имеющую смысл амплитуду
и получить имеющую смысл амплитуду  при снятии регуляризации, т. е. при
при снятии регуляризации, т. е. при 
Таким образом, вообще говоря, уравнения Шредингера и Томонага—Швингера в квантовой теории поля могут иметь лишь чисто формальное значение.
Итак, чтобы избежать появления бесконечностей в теории, мы должны работать с достаточно гладкими  При этом можно заметить, что для сходимости рассматриваемых интегралов нет необходимости требовать, чтобы
При этом можно заметить, что для сходимости рассматриваемых интегралов нет необходимости требовать, чтобы  была равна нулю всюду вне слоя толщиной
была равна нулю всюду вне слоя толщиной  . Достаточно потребовать, чтобы
. Достаточно потребовать, чтобы  достаточно быстро (например, экспоненциально) убывала вне этого слоя и была бы всюду достаточно гладкой. Совершенно очевидно, что класс G таких функций будет релятивистски-инвариантным по отношению к любому лоренцевому преобразованию L, т. е. если
достаточно быстро (например, экспоненциально) убывала вне этого слоя и была бы всюду достаточно гладкой. Совершенно очевидно, что класс G таких функций будет релятивистски-инвариантным по отношению к любому лоренцевому преобразованию L, т. е. если  , то также и
, то также и 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
- § 23. Приведение S-матрицы к нормальной форме
- 23.2. Диаграммы Фейнмана и правила соответствия.
- 23.3. Примеры.
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
- 37.3. Производящий функционал для высших функций Грина.
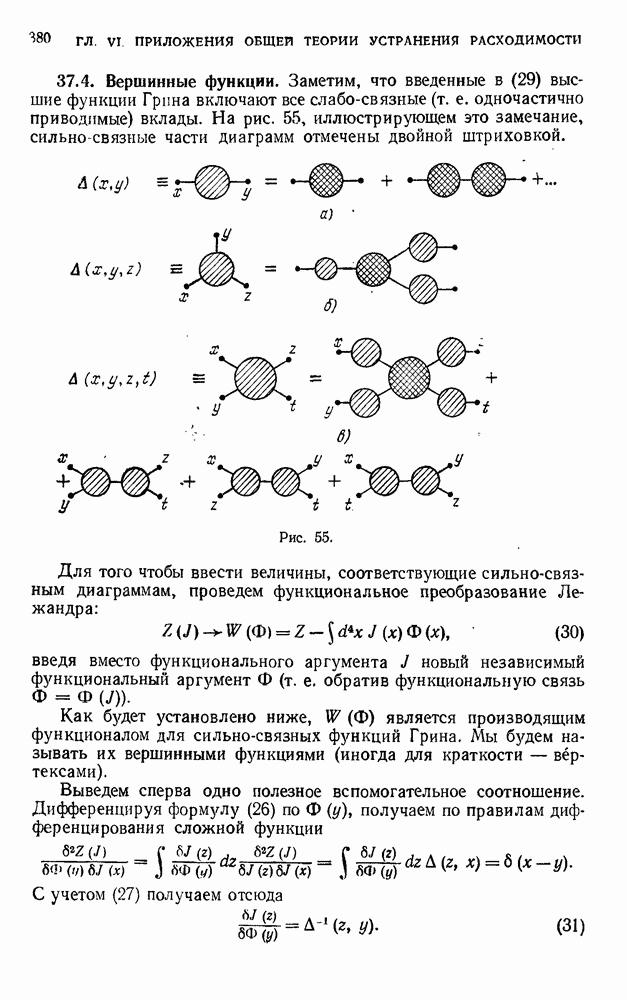
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
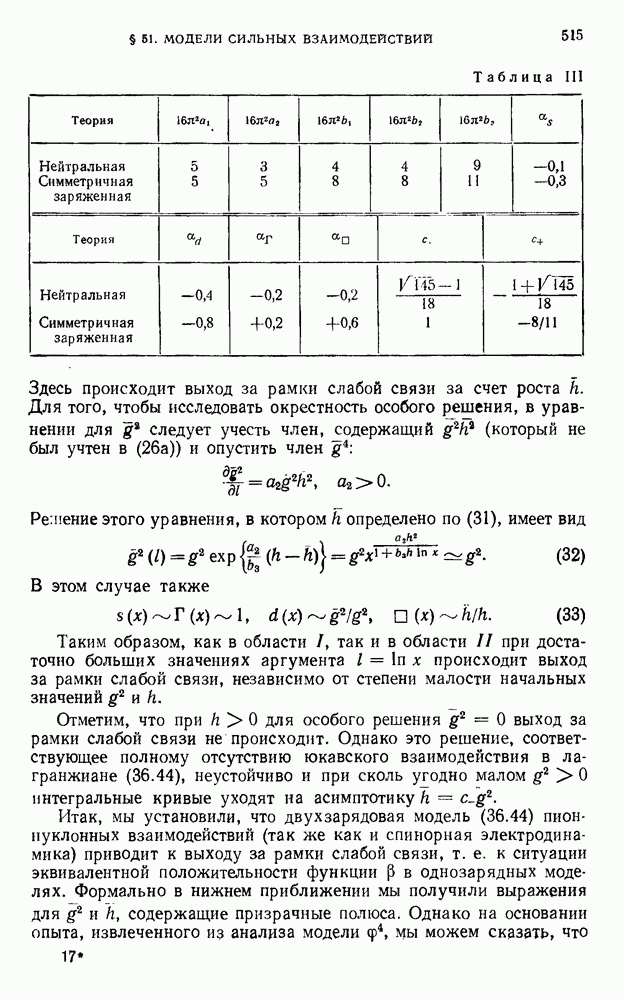
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
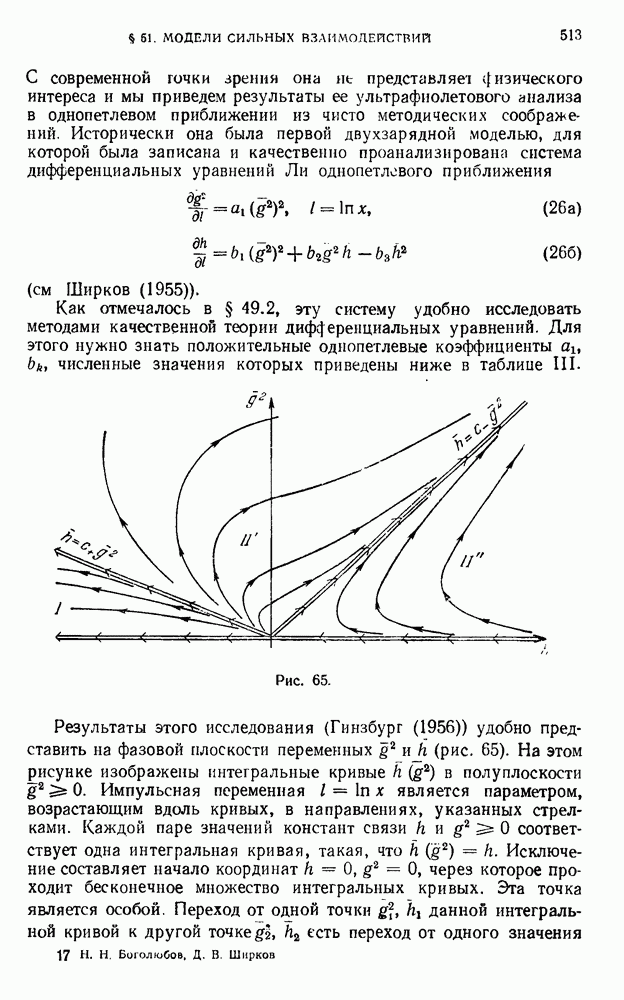
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
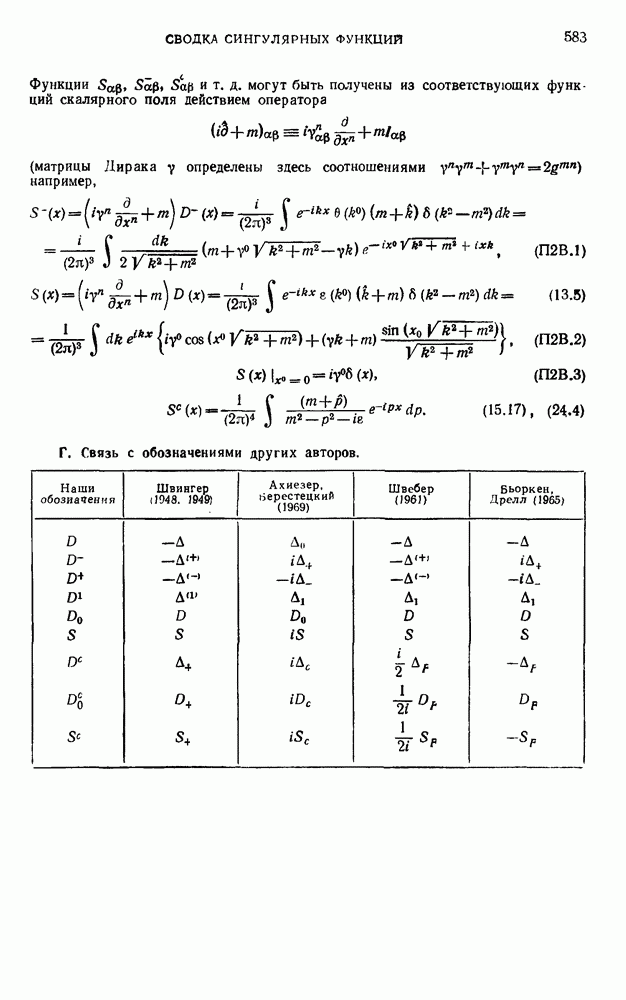
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА