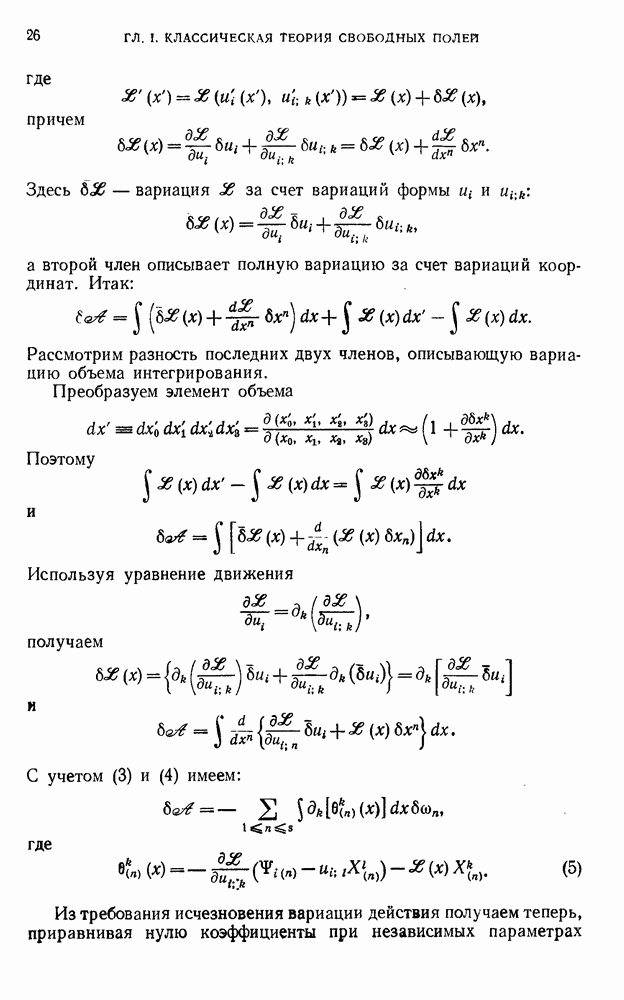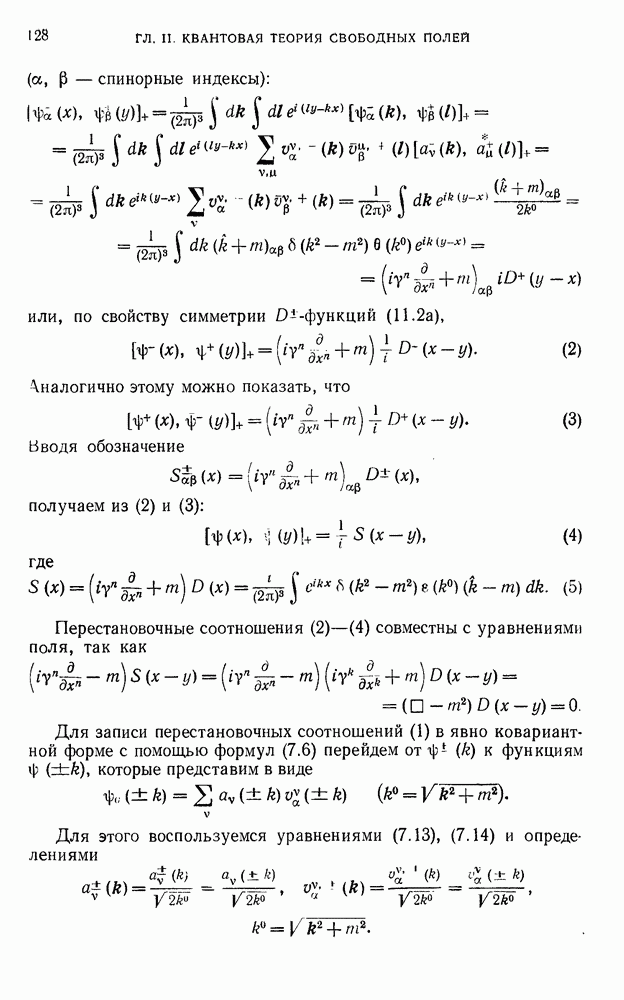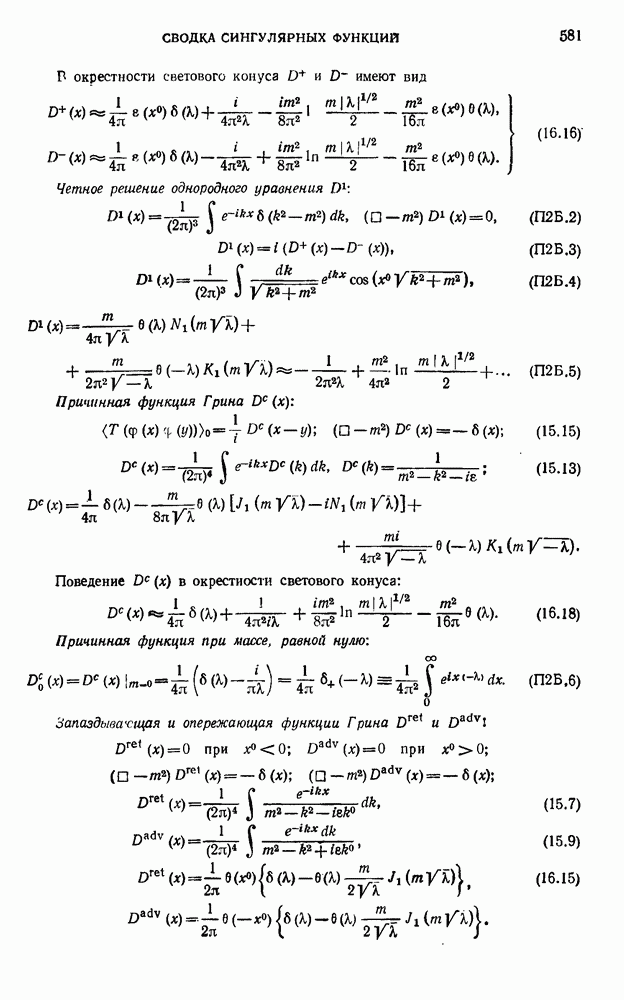| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
33.2. Градиентная инвариантность матрицы рассеяния.
Заметим, однако, что до сих пор не принималось во внимание требование градиентной инвариантности. Чтобы сформулировать это требование, рассмотрим сначала бесконечно малое градиентное преобразование потенциалов электромагнитного поля

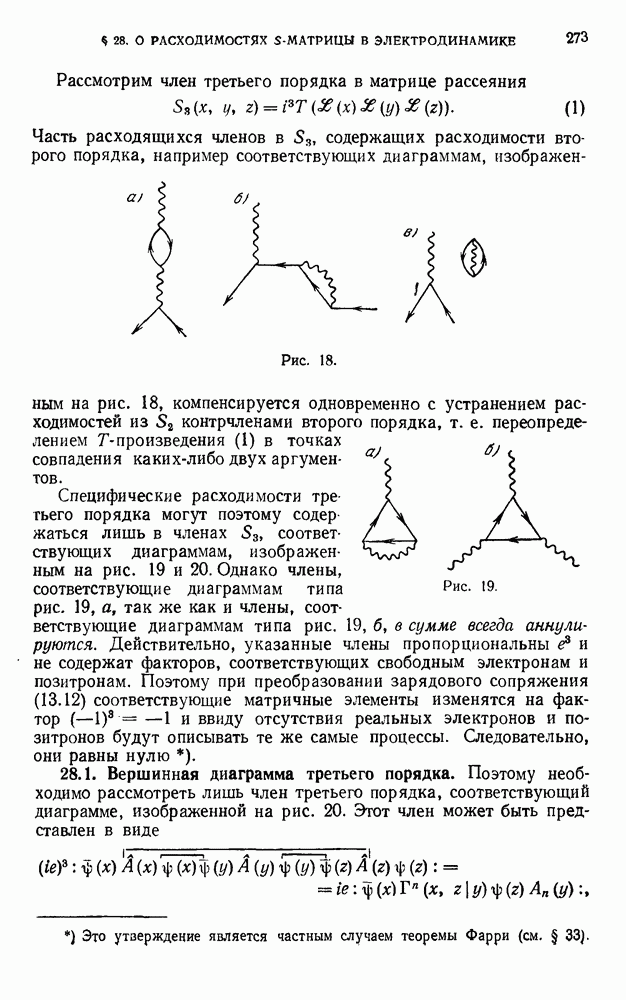
где f — произвольная бесконечно малая функция. При этом преобразовании член  порядка матрицы рассеяния
порядка матрицы рассеяния 

с учетом линейной зависимости  от потенциалов
от потенциалов  с различными аргументами, получит приращение
с различными аргументами, получит приращение

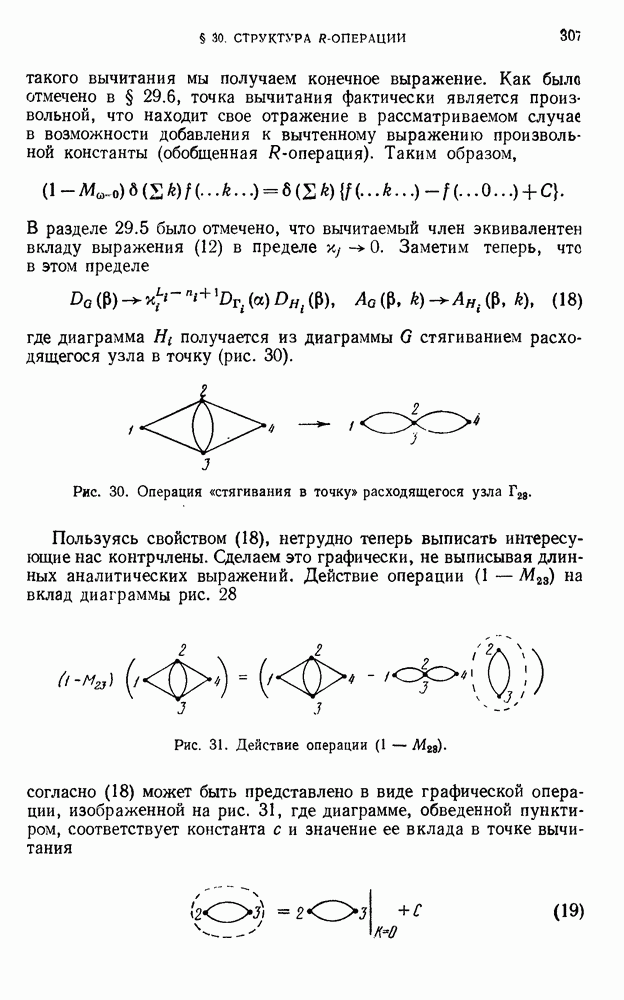
Интегрируя это выражение по частям, находим, что оно обращается в нуль, если тождественно

Нетрудно убедиться, что если выполняется это условие, выражение (11) не будет меняться и при конечном градиентном преобразовании. Это обусловлено тем, что коэффициенты при старших степенях  в приращении подынтегрального выражения можно записать через производные по
в приращении подынтегрального выражения можно записать через производные по  от (12).
от (12).
Исходя из указанных соображений, мы примем в качестве условия градиентной инвариантности теории условие (12). Ниже мы увидим (глава VII), что, кроме инвариантности S (1), это условие обеспечивает также выполнение дифференциального закона сохранения электрического тока.
Проанализируем теперь степень произвола в выборе коэффициентов  в выражениях
в выражениях  остающуюся после наложения условия градиентной инвариантности в форме (12). Рассмотрим, например, вершинную часть операторной функции
остающуюся после наложения условия градиентной инвариантности в форме (12). Рассмотрим, например, вершинную часть операторной функции

Для выполнения условия градиентной инвариантности эта величина должна удовлетворять соотношению

Сравнивая с (7), мы видим, что функция  определена с точностью до члена
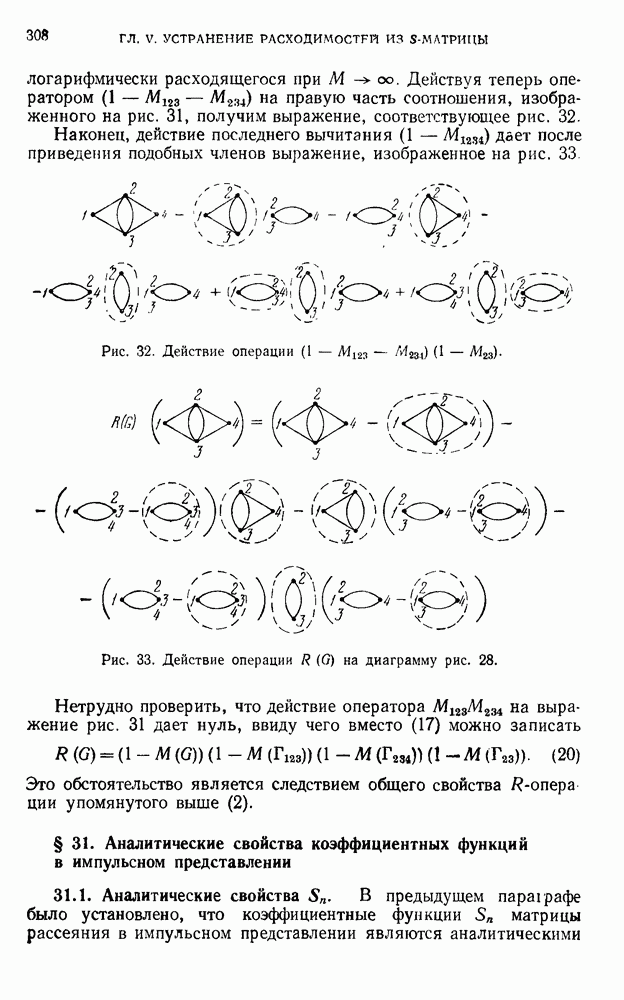
определена с точностью до члена

При этом ясно, что введение  соответствует изменению коэффициента
соответствует изменению коэффициента  . Однако нетрудно заметить, что если вершинная часть (13) удовлетворяет условию (12), то при добавлении к
. Однако нетрудно заметить, что если вершинная часть (13) удовлетворяет условию (12), то при добавлении к  члена (14) она это свойство теряет, так как
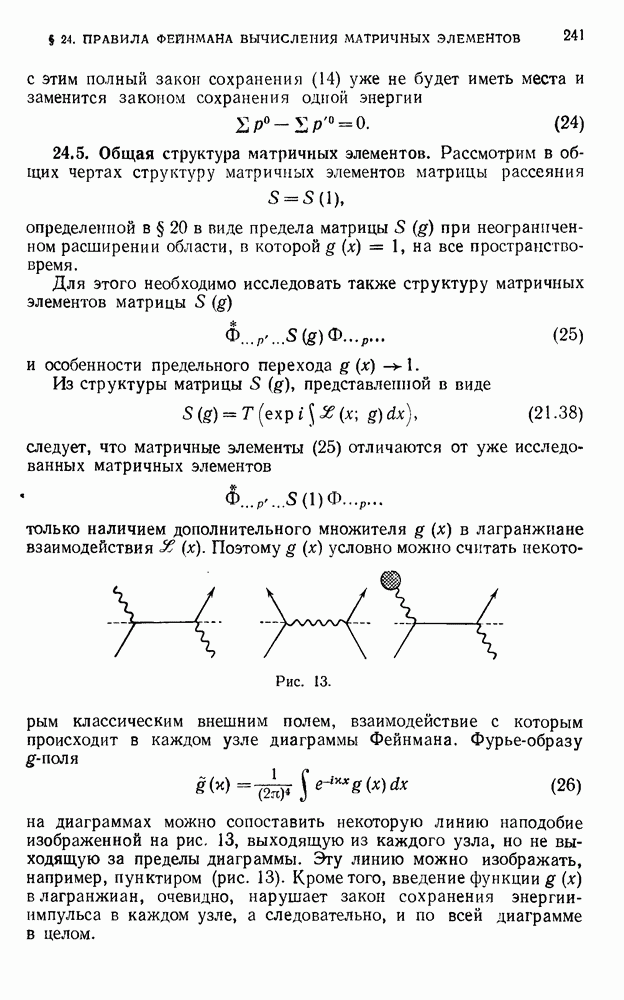
члена (14) она это свойство теряет, так как

Поэтому, если квазилокальные операторы (7) подобраны так, что результат вычитательной процедуры градиентно-инвариантен, то этот выбор вполне однозначен, т. е. неопределенность устраняется требованием градиентной инвариантности.
Совершенно аналогично можно убедиться в однозначности коэффициентов  в выражениях (6) и
в выражениях (6) и  в выражениях (8). Ясно также, что выражения (9), не содержащие потенциалов электромагнитного поля, допускают произвол в выборе коэффициентов
в выражениях (8). Ясно также, что выражения (9), не содержащие потенциалов электромагнитного поля, допускают произвол в выборе коэффициентов 
Рассмотрим еще неоднозначность операторных выражений типа

по отношению к членам с той же структурой, что и члены с коэффициентами  в выражении (8). Подставляя такой член
в выражении (8). Подставляя такой член

в условие (12), с учетом свойств производной  -функции
-функции

находим соотношение между 

оставляющее одну степень произвола в выборе этих коэффициентов, Таким образом, для каждого  имеются три неоднозначные константы
имеются три неоднозначные константы  и, например,
и, например,  но в контрчленах лагранжиана неоднозначными оказываются всего лишь три числа (ср. (21.44)):
но в контрчленах лагранжиана неоднозначными оказываются всего лишь три числа (ср. (21.44)):

В дальнейшем мы увидим, что эти три числа входят в результаты лишь в двух комбинациях и неоднозначность полностью устраняется выбором массы и заряда спинорной частицы.
Теперь необходимо показать, что подбором соответствующих контрчленов действительно можно получить градиентно-инвариантную теорию. Как известно, контрчлены лагранжиана служат для
описания того или иного вычитательного процесса, используемого в теории. Напомним, что принятая нами вычитательная процедура состоит в вычитании из расходящегося выражения достаточного числа членов его ряда Маклорена с центром разложения в точке  и добавлении к результату произвольного конечного полинома определенной степени. На основании только что полученных результатов этот произвол сводится к двум константам в членах типа (9) и одной константе в членах типа (8). Покажем, что в результате такого способа устранения расходимостей получаемая теория градиентно-инвариантна.
и добавлении к результату произвольного конечного полинома определенной степени. На основании только что полученных результатов этот произвол сводится к двум константам в членах типа (9) и одной константе в членах типа (8). Покажем, что в результате такого способа устранения расходимостей получаемая теория градиентно-инвариантна.
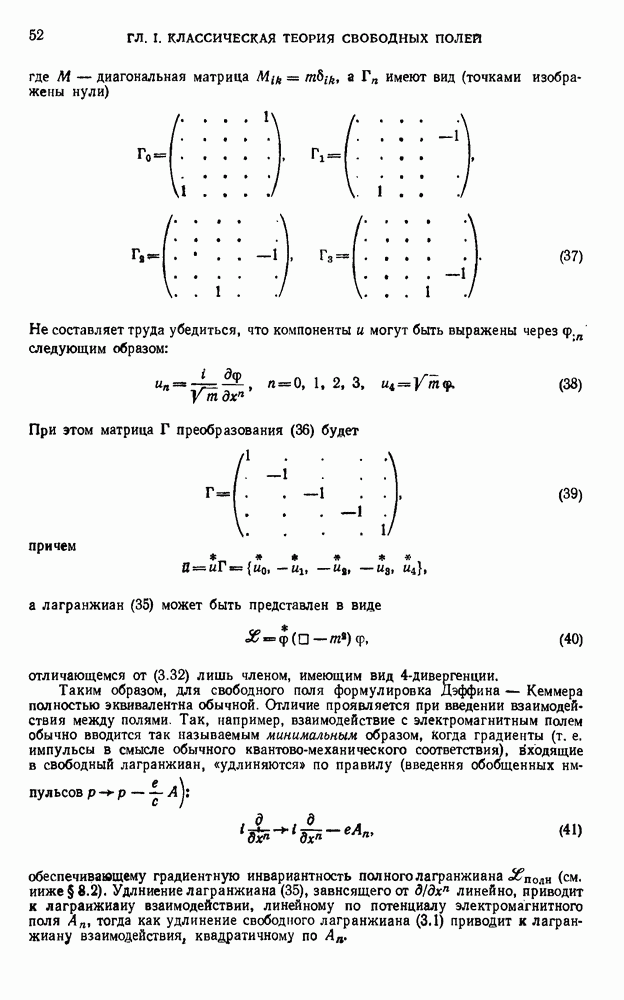
В доказательстве используем следующий вариант регуляризации с помощью вспомогательных масс. Фотонные причинные функции (24.3) регуляризуем обычным образом (см. (27.4)), а спинорные причинные функции будем регуляризовать не по отдельности, а заменяя их произведения, соответствующие замкнутым циклам:

выражениями

где  — причинная фермионная функция с массой
— причинная фермионная функция с массой 

Указанный способ регуляризации спинорных причинных функций представляет собой один из вариантов регуляризации Паули—Вилларса (1949).
Заметим в этой связи, что согласно общим свойствам регуляризуемых выражении, установленным в главе V, изменение способа вспомогательной регуляризации не влияет на общую структуру окончательных регуляризованных выражений, которые являются коэффициентными функциями операторов  определяющих не содержащую бесконечностей матрицу рассеяния.
определяющих не содержащую бесконечностей матрицу рассеяния.
Покажем теперь, что регуляризация по Паули—Вилларсу устраняет расходимости из матричных элементов, соответствующих замкнутым циклам. Рассмотрим для этого результат интеграции выражения (16), записанный в импульсном представлении:

Подынтегральное выражение при больших  ведет себя, как
ведет себя, как  и при
и при  интеграл расходится как
интеграл расходится как

Замечаем, что при больших  подынтегральное выражение в (19)
подынтегральное выражение в (19)

( — полином
— полином  степени по
степени по  ) может быть представлено в виде степенного ряда по
) может быть представлено в виде степенного ряда по  причем степень роста по
причем степень роста по  при
при  коэффициента при
коэффициента при  в степени k равна
в степени k равна  Ясно поэтому, что если коэффициенты См в сумме (17) удовлетворяют k соотношениям типа
Ясно поэтому, что если коэффициенты См в сумме (17) удовлетворяют k соотношениям типа

то подынтегральное выражение, соответствующее (17), при  ведет себя, как
ведет себя, как  и процедура Паули—Вилларса регуляризует рассматриваемые выражения вместе с их
и процедура Паули—Вилларса регуляризует рассматриваемые выражения вместе с их  первыми производными по
первыми производными по  Это свойство процедуры Паули—Вилларса можно было бы также непосредственно установить, переходя к
Это свойство процедуры Паули—Вилларса можно было бы также непосредственно установить, переходя к  -представлению» причинных функций.
-представлению» причинных функций.
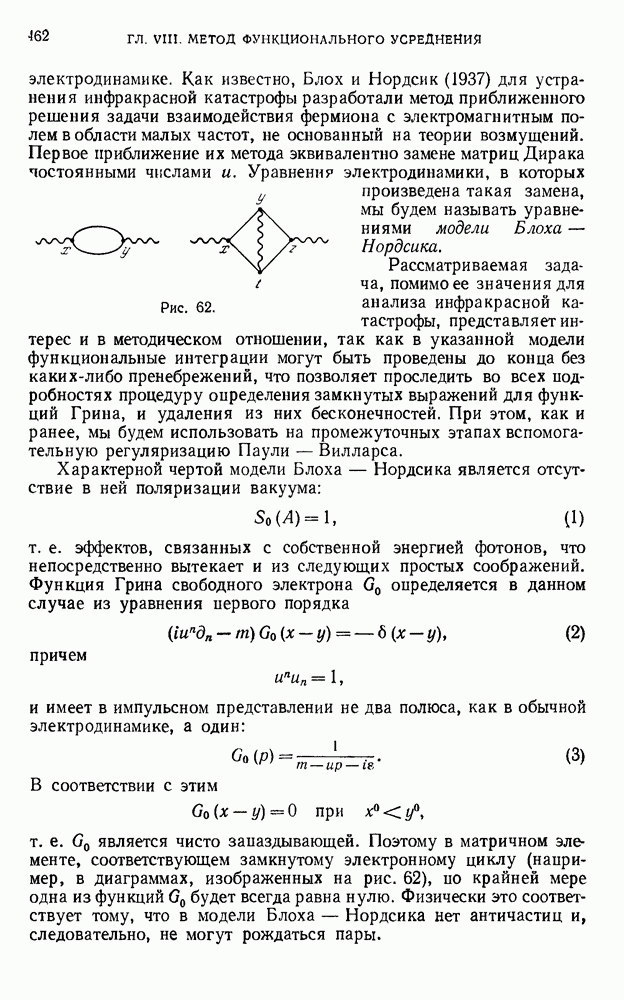
Таким образом, мы будем вводить вспомогательные массы лишь в фотонные линии и замкнутые спинорные циклы. Незамкнутые спинорные циклы мы вообще не будем подвергать регуляризации. Легко видеть, что в фотонные функции достаточно ввести одну вспомогательную массу, а в замкнутые спинорные циклы — две. Действительно, максимальная степень расходимости диаграмм с замкнутыми спинорными циклами равна двум (диаграммы типа рис. 35, в)  а введение двух вспомогательных масс снижает степень на четыре. В результате этой процедуры интеграл при
а введение двух вспомогательных масс снижает степень на четыре. В результате этой процедуры интеграл при  будет сходиться как
будет сходиться как

С другой стороны, максимальная степень расходимости диаграмм с внутренними фотонными линиями равна единице (диаграммы типа рис. 35, г). Введение в фотонную функцию одной вспомогательной массы снижает степень расходимости на два и интеграл становится сходящимся, как

Необходимости в регуляризации незамкнутых спинорных циклов, таким образом, не возникает. Мы видим отсюда, что при конечных значениях вспомогательных масс М, - все матричные элементы оказываются сходящимися.
Напомним, однако, что регуляризация методом вспомогательных масс является лишь техническим приемом, проводимым на промежуточной стадии рассуждений, и что фактическое устранение
расходимостей производится путем вычитательной процедуры. Поэтому к полученному регуляризованному выражению для матрицы рассеяния мы применим теперь обычную процедуру вычитания ряда Маклорена в импульсном представлении при одновременном добавлении трех произвольных конечных констант. Ввиду установленной ранее инвариантности результатов такого вычитания относительно способа введения вспомогательных масс нам остается лишь установить градиентную инвариантность регуляризации Паули—Вилларса и следующей за ней процедуры вычитания.

Рис. 36. Процесс вставки  -вершины.
-вершины.
Докажем градиентную инвариантность регуляризованной матрицы S (1) до применения к ней вычитательной процедуры. При этом мы воспользуемся тем обстоятельством, что совокупность диаграмм  порядка
порядка  внешними фотонными линиями может быть получена из диаграмм
внешними фотонными линиями может быть получена из диаграмм  порядка с
порядка с  внешними фотонными линиями посредством вставки дополнительной
внешними фотонными линиями посредством вставки дополнительной  вершины I в любую внешнюю или внутреннюю спинорную линию. Процесс вставки (который для краткости будем именовать
вершины I в любую внешнюю или внутреннюю спинорную линию. Процесс вставки (который для краткости будем именовать  -процессом) одновременно устанавливает графическое соответствие между выражениями
-процессом) одновременно устанавливает графическое соответствие между выражениями

Рассмотрим сначала  -процесс для внутренней спинорной линии. Вставляя
-процесс для внутренней спинорной линии. Вставляя  -вершину в линию
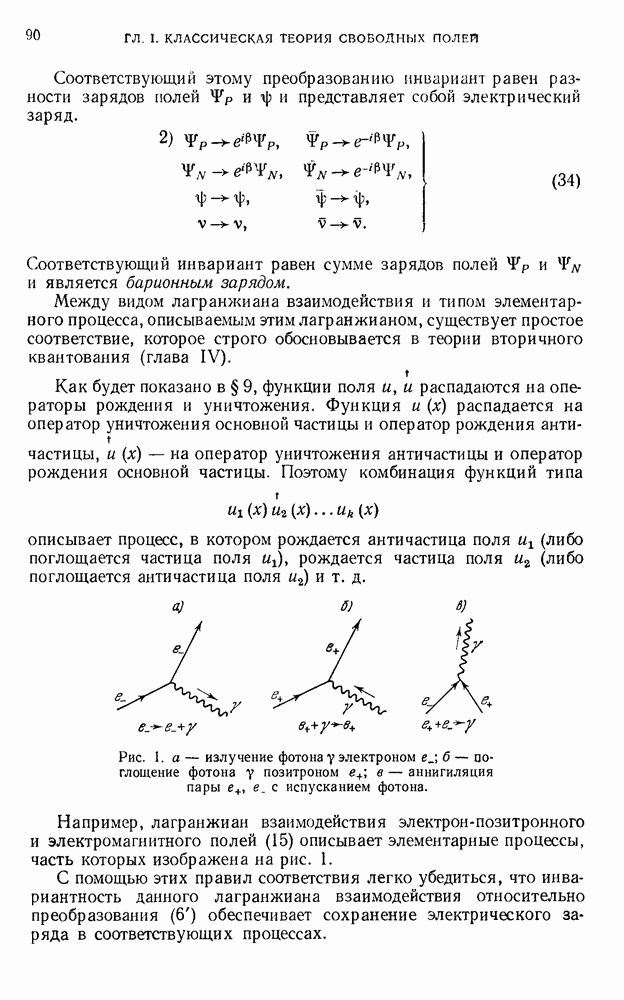
-вершину в линию  получим рис. 36. Вычисляя дивергенцию (12) по i от фактора
получим рис. 36. Вычисляя дивергенцию (12) по i от фактора

находим, пользуясь уравнениями для 

 -процесс для внутренних линий сложного фермионного цикла может быть представлен схемой рис. 37. Находя дивергенцию от суммы членов, соответствующих правой части схемы, с помощью (20) без труда убеждаемся, что она пропорциональна члену, отвечающему диаграмме в левой части схемы, с множителем пропорциональности, равным
-процесс для внутренних линий сложного фермионного цикла может быть представлен схемой рис. 37. Находя дивергенцию от суммы членов, соответствующих правой части схемы, с помощью (20) без труда убеждаемся, что она пропорциональна члену, отвечающему диаграмме в левой части схемы, с множителем пропорциональности, равным

Отсюда следует, что указанная дивергенция обращается в нуль для замкнутых циклов 

Рис. 37. g-процесс для внутренних линий фермионного цикла.
Применяя это рассуждение к более сложным диаграммам, состоящим из внутренних фотонных линий и произвольного числа замкнутых и незамкнутых фермионных циклов, приходим к соотношению

где суммирования  распространяются на все вершины диаграммы, в которые входят
распространяются на все вершины диаграммы, в которые входят  и из которых выходят
и из которых выходят  — внешние фермионные линии; здесь
— внешние фермионные линии; здесь  — коэффициентная функция
— коэффициентная функция  порядка,
порядка,  — полученная из нее -процессом коэффициентная функция
— полученная из нее -процессом коэффициентная функция  порядка.
порядка.

Рис. 38. g-процесс для внешних фермионных линий.
Для завершения доказательства рассмотрим еще  -процесс для внешних (входящей и выходящей) фермионных линий (рис. 38). Вычисляя соответствующие дивергенции, находим:
-процесс для внешних (входящей и выходящей) фермионных линий (рис. 38). Вычисляя соответствующие дивергенции, находим:

Сравнивая эти выражения с (22), убеждаемся, что  действительно удовлетворяют условию градиентной инвариантности (12). В самом деле, по только что доказанному, дивергенция факторов, описывающих замкнутые циклы, равна нулю. Дивергенция же оператора соответствующего незамкнутому циклу, слагается из дивергенции суммы
действительно удовлетворяют условию градиентной инвариантности (12). В самом деле, по только что доказанному, дивергенция факторов, описывающих замкнутые циклы, равна нулю. Дивергенция же оператора соответствующего незамкнутому циклу, слагается из дивергенции суммы  -вставок в коэффициентную функцию и вставок во внешние линии и также обращается в нуль, поскольку (24) компенсирует первый,
-вставок в коэффициентную функцию и вставок во внешние линии и также обращается в нуль, поскольку (24) компенсирует первый,  второй член в (21).
второй член в (21).
Этим формально доказана градиентная инвариантность матрицы S (1) до процесса регуляризации. Заметим, однако, что регуляризации по Паули—Вилларсу подвергаются лишь замкнутые фермионные циклы, причем в каждом из дополнительных членов в выражениях (17) для всех причинных функций  масса имеет одинаковое значение. Поэтому указанные дополнительные члены после
масса имеет одинаковое значение. Поэтому указанные дополнительные члены после  -процесса обладают также нулевой дивергенцией, и мы приходим к выводу, что и после применения процедуры Паули—Вилларса регуляризованная матрица S (1) удовлетворяет условию градиентной инвариантности. Отметим здесь, что указанное свойство сохранения градиентной инвариантности является важным преимуществом регуляризации по Паули—Вилларсу, которое мы и имели в виду, отступив от принятого нами ранее способа введения вспомогательных масс.
-процесса обладают также нулевой дивергенцией, и мы приходим к выводу, что и после применения процедуры Паули—Вилларса регуляризованная матрица S (1) удовлетворяет условию градиентной инвариантности. Отметим здесь, что указанное свойство сохранения градиентной инвариантности является важным преимуществом регуляризации по Паули—Вилларсу, которое мы и имели в виду, отступив от принятого нами ранее способа введения вспомогательных масс.
Подчеркнем, что формула (22) может рассматриваться как условие градиентной инвариантности для коэффициентных функций. В самом деле, мы только что убедились, что, (22) является достаточным для выполнения условия градиентной инвариантности матрицы рассеяния (12). Формулу (22) полезно переписать в импульсном представлении, переход к которому мы произведем, явно учитывая трансляционную инвариантность

Получаем вместо 

Формула (27) представляет собой условие градиентной инвариантности коэффициентных функций в импульсном представлении. Среди аргументов  в (27), так же как и среди аргументов
в (27), так же как и среди аргументов  в (22), существенными являются только те, которые соответствуют
в (22), существенными являются только те, которые соответствуют
внешним линиям. Для того чтобы убедиться в этом, достаточно подставить К, в  и выполнить интегрирование по всем
и выполнить интегрирование по всем  соответствующим внутренним вершинам диаграммы.
соответствующим внутренним вершинам диаграммы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
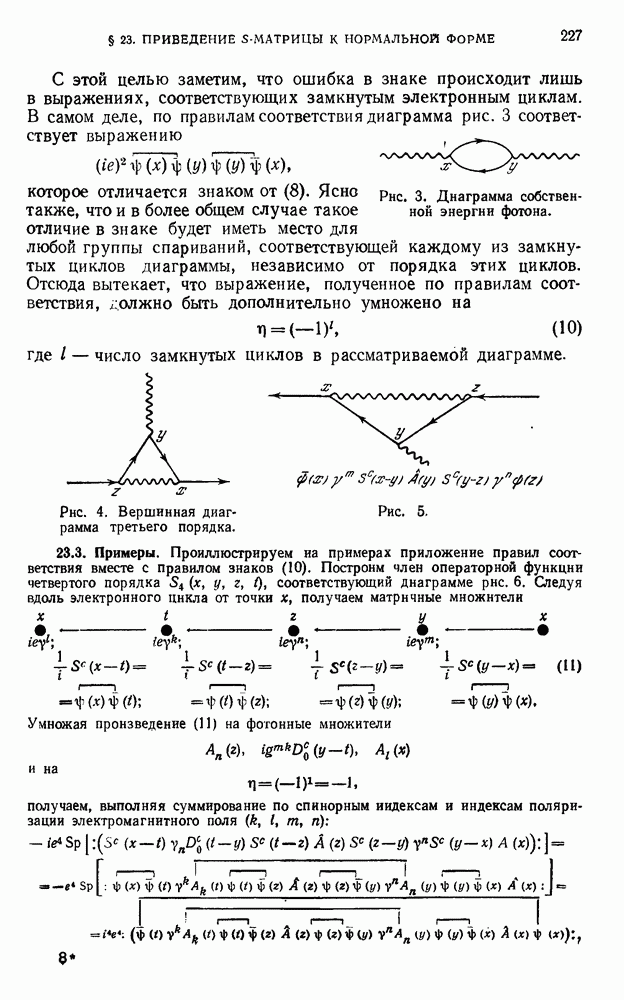
- § 23. Приведение S-матрицы к нормальной форме
- 23.2. Диаграммы Фейнмана и правила соответствия.
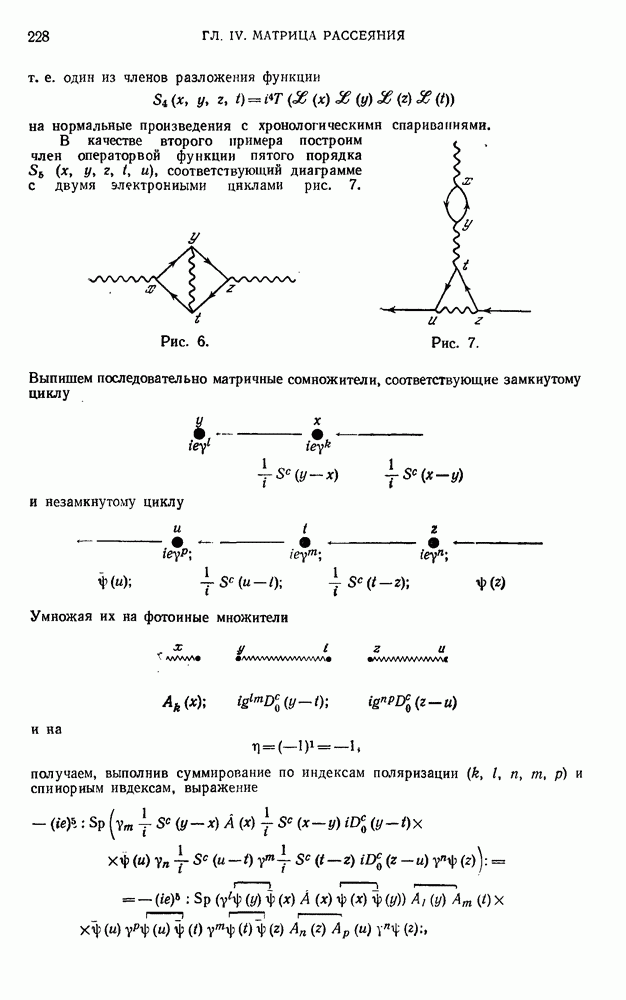
- 23.3. Примеры.
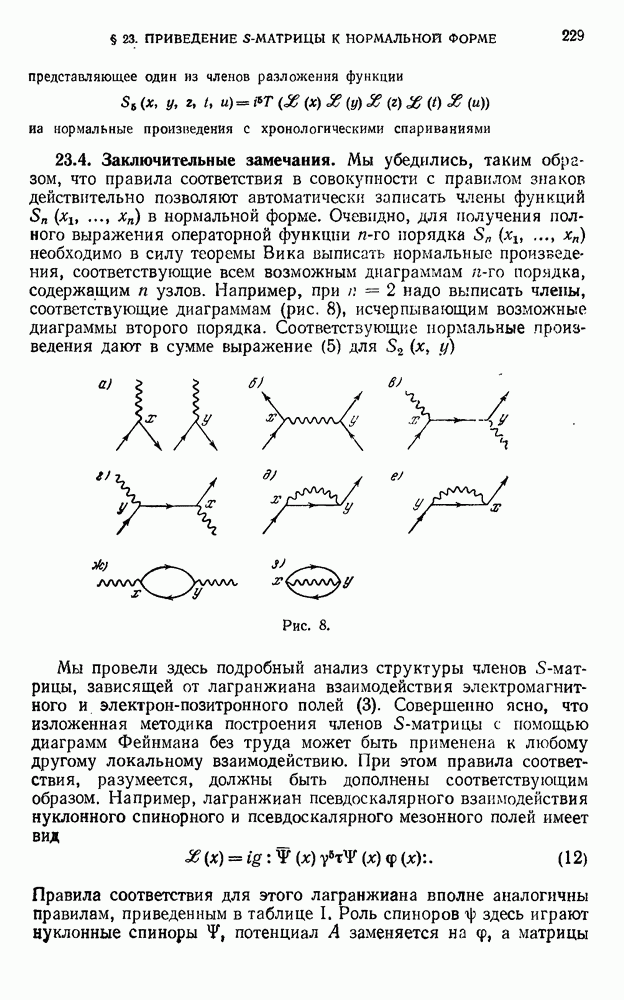
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
- 37.3. Производящий функционал для высших функций Грина.
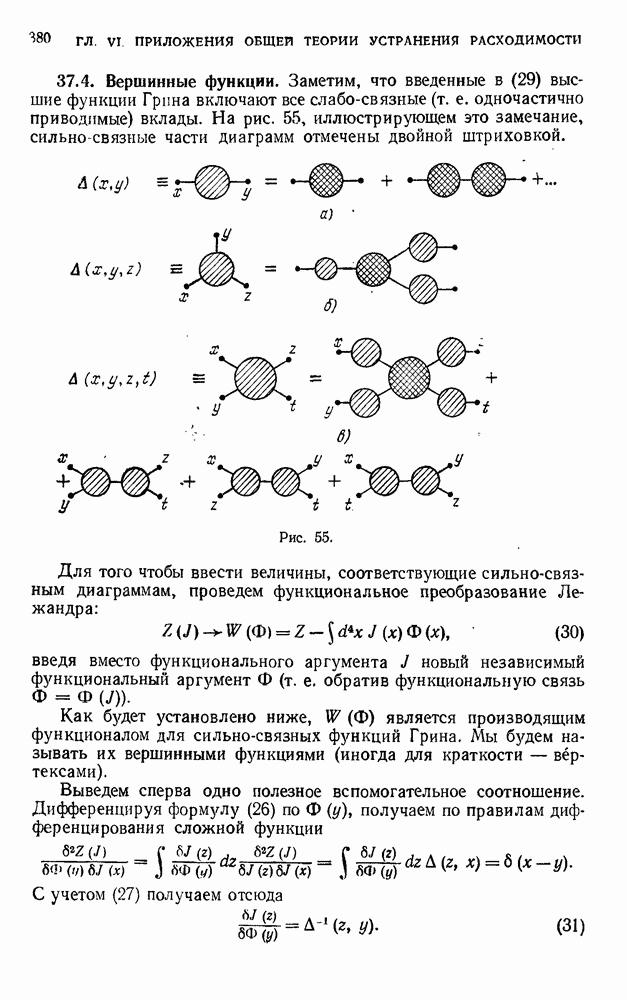
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
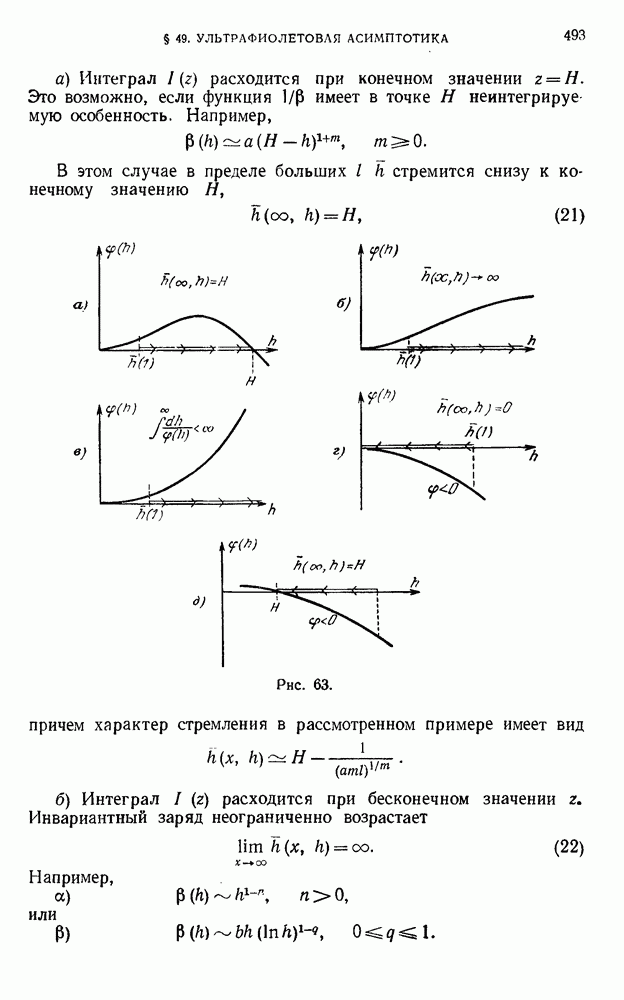
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
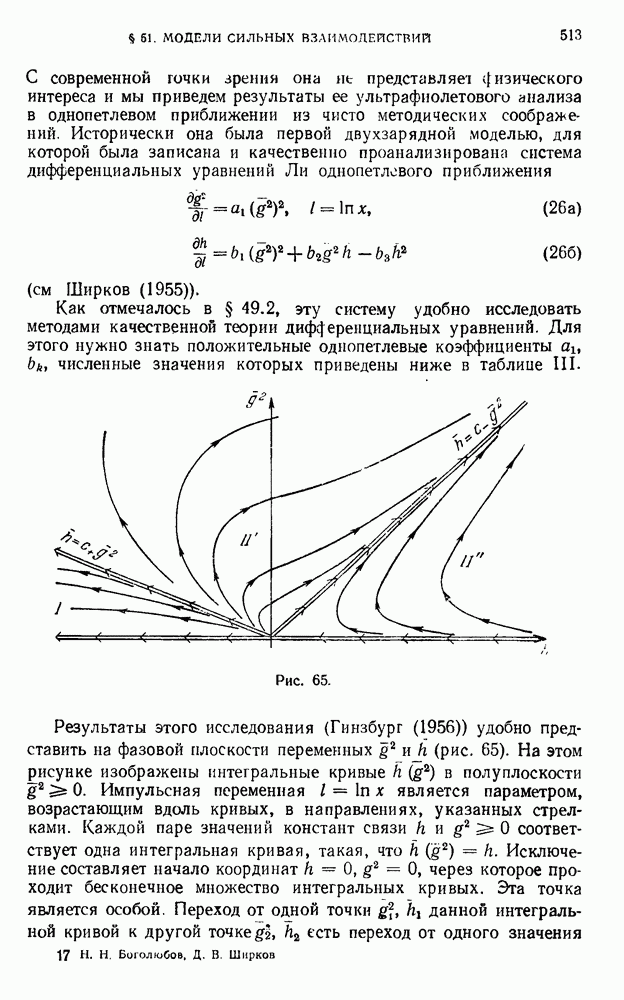
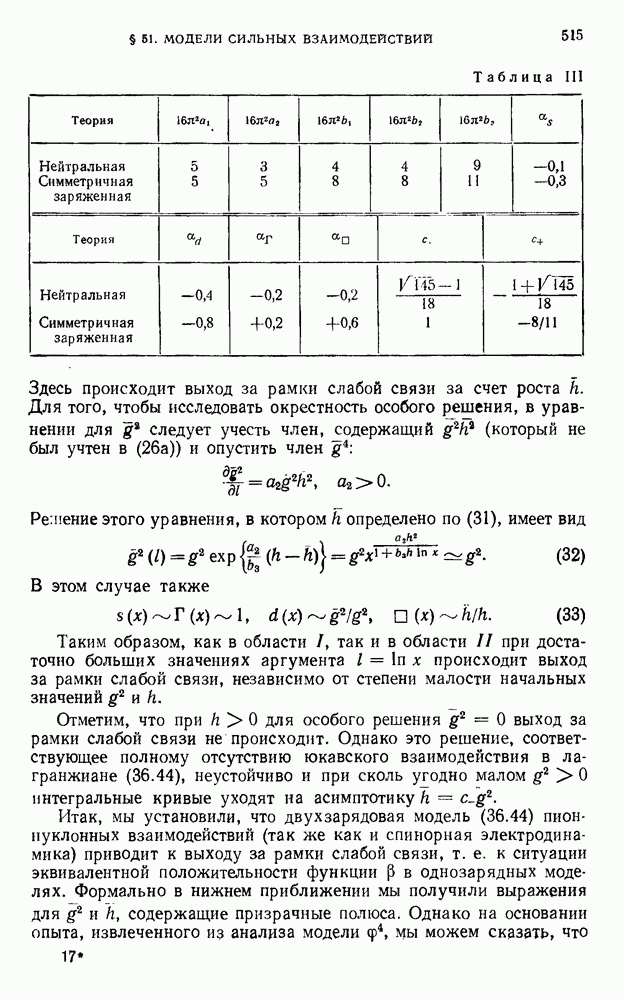
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
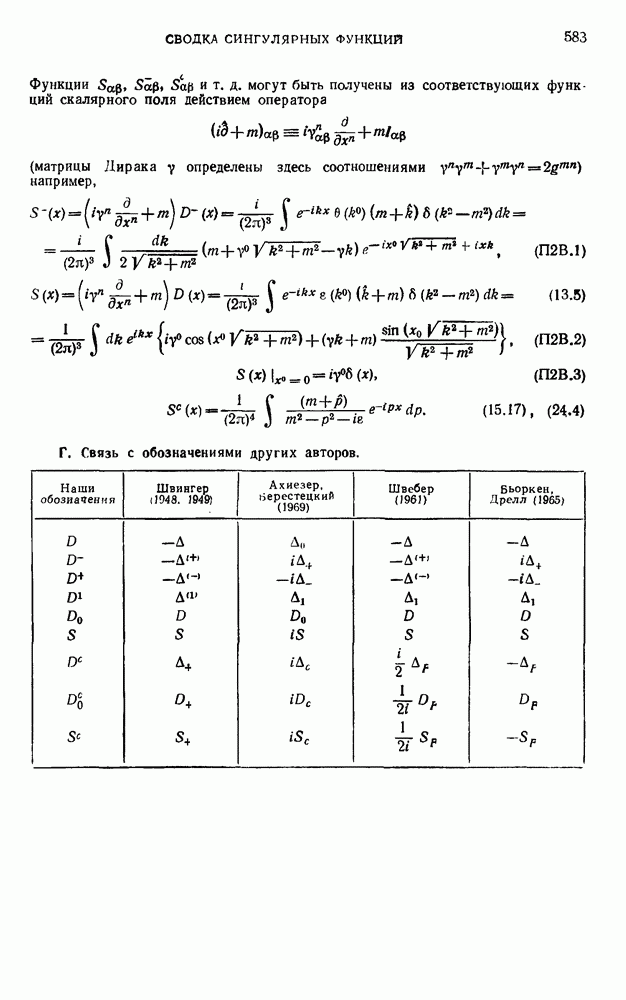
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА