| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
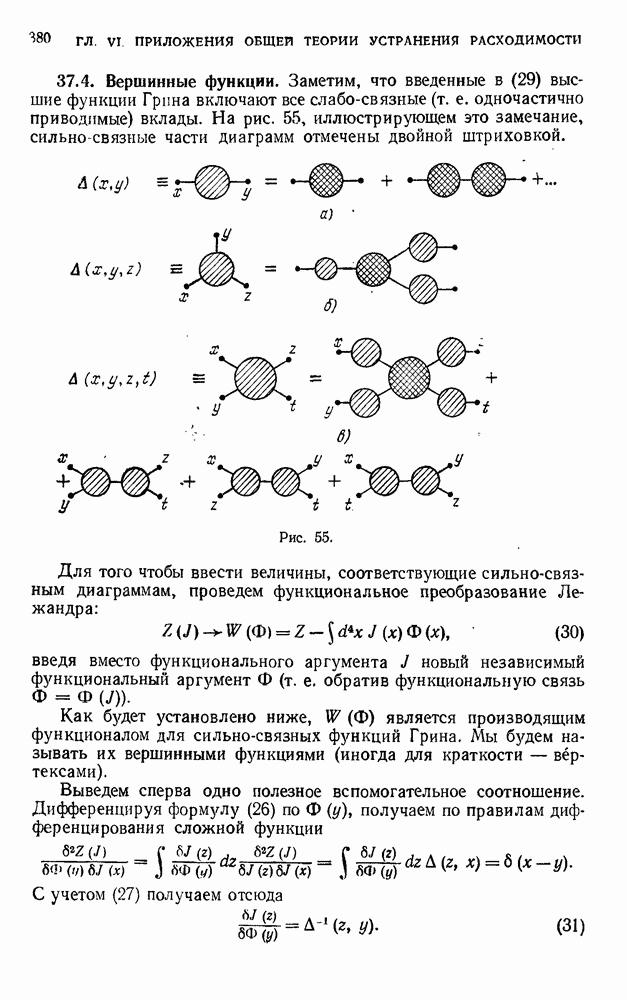
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
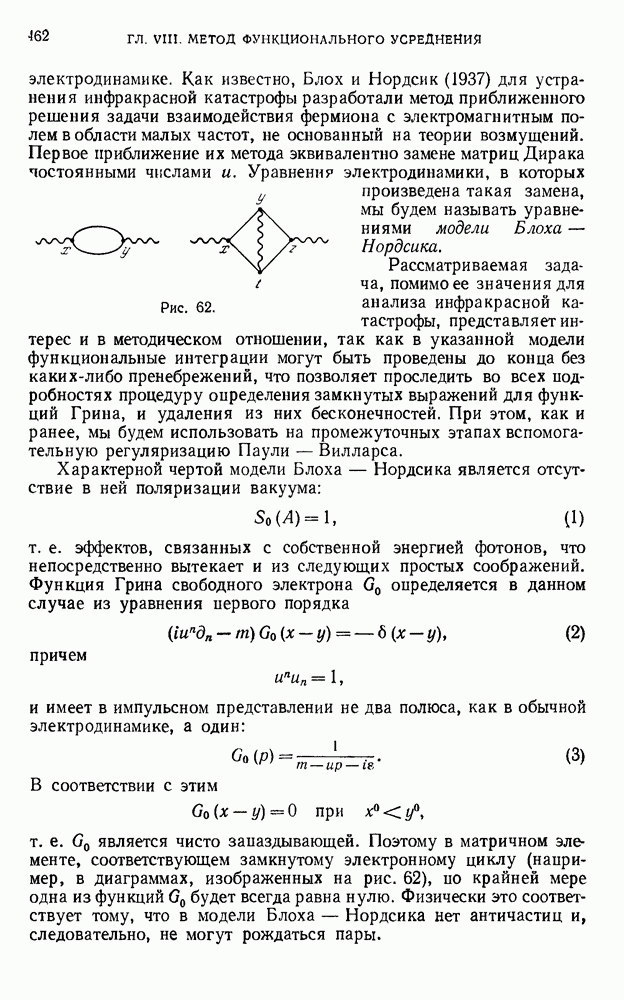
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
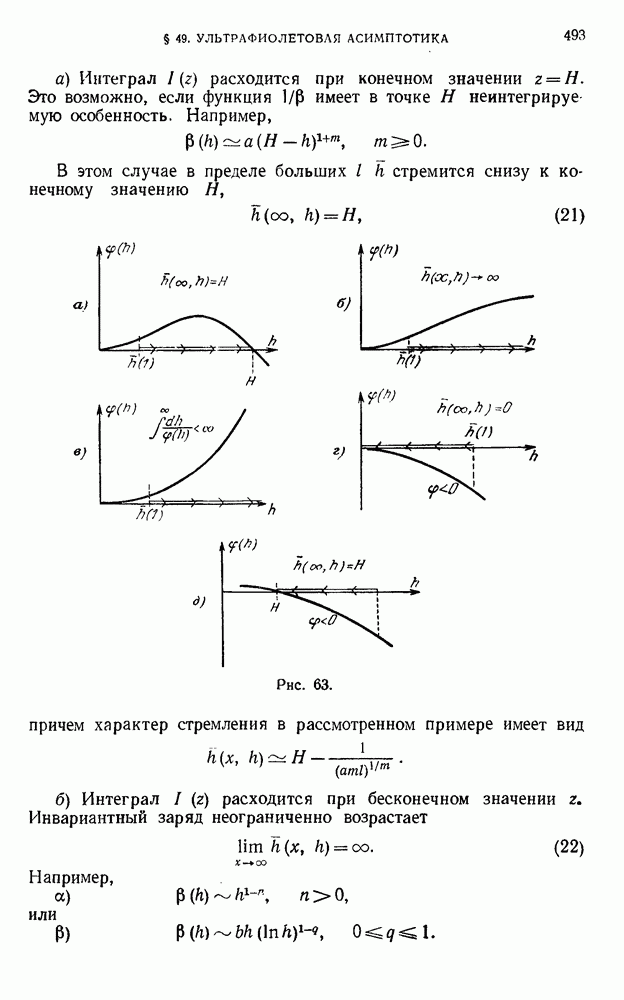
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
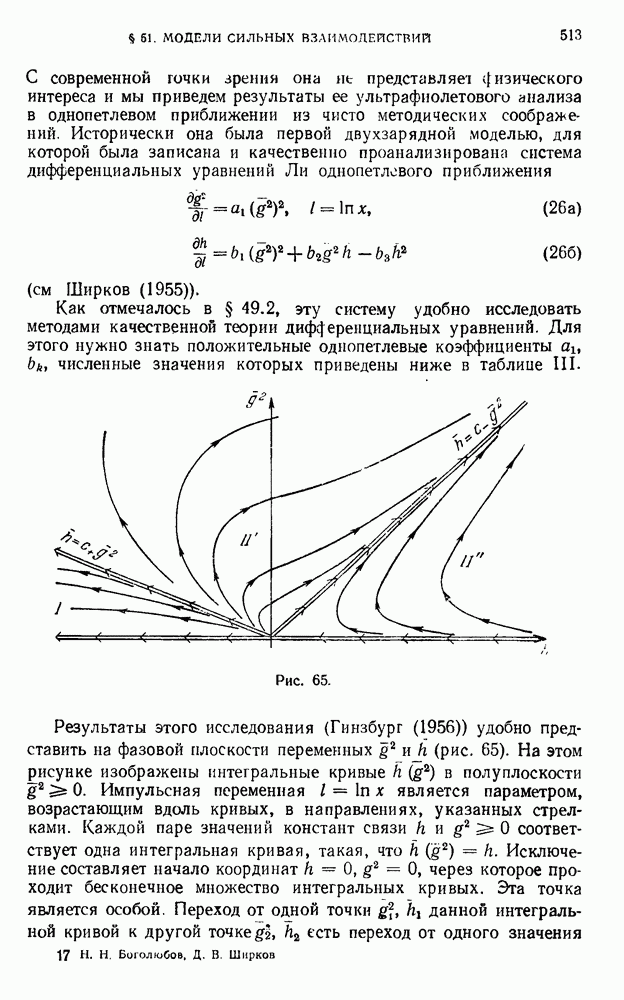
512
513
514
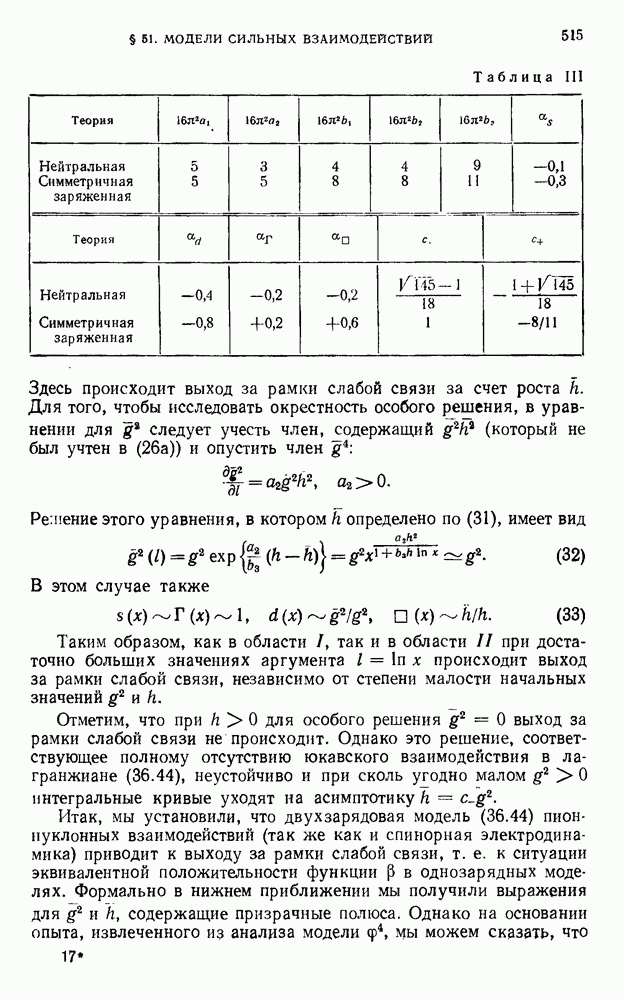
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
50.3. Инфракрасная асимптотика электронной функции Грина.
Рассмотрим теперь электронный пропагатор в окрестности точки  где радиационные поправки к нему имеют логарифмическую особенность. Отправляясь от резульгатов § 35.2, представим выражение (48.1) в виде
где радиационные поправки к нему имеют логарифмическую особенность. Отправляясь от резульгатов § 35.2, представим выражение (48.1) в виде

где символом  обозначено второе слагаемое в правой части (35.22), т. е. разность
обозначено второе слагаемое в правой части (35.22), т. е. разность  . В области
. В области  членами
членами  в числителе можно пренебречь, тогда как знаменатель представим в виде
в числителе можно пренебречь, тогда как знаменатель представим в виде

Таким образом, в окрестности массовой поверхности с учетом нормировки на импульс вычитания можем написать

и мы видим, что при  радиационные поправки неограниченно возрастают. Истинный характер инфракрасной особенности может быть восстановлен из (22) с помощью ренормгруппы. Подставляя вторую из формул (22) в (48.22), находим
радиационные поправки неограниченно возрастают. Истинный характер инфракрасной особенности может быть восстановлен из (22) с помощью ренормгруппы. Подставляя вторую из формул (22) в (48.22), находим

Используя это выражение в правой части  и принимая во внимание, что при
и принимая во внимание, что при  инвариантный заряд не имеет
инвариантный заряд не имеет
сингулярных поправок (вследствие чего можно положить  находим, выполняя простое интегрирование,
находим, выполняя простое интегрирование,

Таким образом, мы видим, что в окрестности точки  полная функция Грина электрона вместо простого полюса имеет особенность типа точки ветвления
полная функция Грина электрона вместо простого полюса имеет особенность типа точки ветвления

что находится в соответствии с результатами §§ 45.5 и 46.2.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЯ
- ВВЕДЕНИЕ
- ГЛАВА I. КЛАССИЧЕСКАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- 1.2. Гамильтонов и лагранжев формализмы.
- 1.3. Функция Лагранжа и принцип стационарного действия.
- 1.4. Трансформационные свойства функций поля.
- 1.5. Другие группы преобразований.
- § 2. Теорема Нётер и динамические инварианты
- 2.2. Вектор энергии-импульса.
- 2.3. Тензор момента количества движения и тензор спина.
- 2.4. Изотопический спин, заряд и вектор тока.
- § 3. Скалярное поле
- 3.2. Импульсное представление и частотные компоненты.
- 3.3. Дискретное импульсное представление.
- 3.4. Комплексное скалярное поле.
- 3.5. Поле пионов.
- § 4. Векторное поле
- 4.2. Переход к импульсному представлению.
- 4.3. Спин векторного поля.
- 4.4. Запись уравнений Клейна — Гордона в виде системы уравнений первого порядка.
- § 5. Электромагнитное поле
- 5.2. Градиентное преобразование и условие Лоренца.
- 5.3. Лагранжев формализм.
- 5.4. Поперечные, продольные и временные составляющие.
- 5.5. Спин.
- § 6. Спинорное поле. Матрицы Дирака и законы преобразования спинорных функций
- 6.2. Матрицы Дирака.
- 6.3. Уравнение Дирака.
- 6.4. Трансформационные свойства спинорного поля.
- § 7. Спинорное поле. Свойства решений и динамические инварианты
- 7.2. Разложения по спиновым состояниям и соотношения нормировки и ортогональности.
- 7.3. Лагранжев формализм и инварианты.
- 7.4. Спинорное поле с массой нуль.
- § 8. Лагранжиан системы полей
- 8.2. Локальные фазовые преобразования и калибровочные поля.
- 8.3. Поле Янга—Миллса.
- 8.4. Динамические инварианты системы полей.
- ГЛАВА II. КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ПОЛЕЙ
- § 9. Общие принципы квантования волновых полей
- 9.2. Представления уравнения Шредингера.
- 9.3. Трансформационные свойства амплитуды состояния и операторов поля.
- 9.4. Постулат квантования волновых полей.
- 9.5. Физический смысл положительно- и отрицательно-частотных составляющих и сопряженных функций.
- 9.6. Состояние вакуума и амплитуда состояния в фоковском представлении.
- § 10. Установление перестановочных соотношений
- 10.2. Перестановочные соотношения Ферми—Дирака и Бозе—Эйнштейна.
- 10.3. Связь спина со статистикой. Теорема Паули.
- 10.4. Нормальное произведение операторов и запись динамических переменных.
- 10.5. Перестановочные соотношения в дискретном импульсном представлении.
- § 11. Скалярное и векторное поля
- 11.2. Поле пи-мезонов.
- 11.3. Комплексное векторное поле.
- 11.4. Гамильтонов формализм и каноническое квантование.
- § 12. Электромагнитное поле
- 12.2. Индефинитная метрика.
- 12.3. Запись основных величин.
- § 13. Спинорное поле
- 13.2. Динамические переменные.
- 13.3. Зарядовое сопряжение.
- 13.4. Квантованное нейтринное поле.
- § 14. СРТ-теорема
- 14.2. P-преобразование.
- 14.3. Обращение времени.
- 14.4. СРТ-теорема.
- ГЛАВА III. СИНГУЛЯРНЫЕ ФУНКЦИИ И РЕГУЛЯРИЗАЦИЯ
- 15.2. Причинная функция Грина скалярного поля.
- 15.3. Причинные функции Грина различных полей.
- § 16. Особенности функций Грина и регуляризация
- 16.2. Явный вид и особенности функций …
- 16.3. Регуляризация Паули — Вилларса.
- 16.4. Размерная регуляризация.
- § 17. Приведение к нормальной форме
- 17.2. Теорема Вика для обычных произведений.
- 17.3. Некоторые определения.
- § 18. Коэффициентные функции
- 18.2. Некоторые свойства регуляризации Паули — Вилларса.
- § 19. Умножение операторных выражений
- 19.2. Некоторые свойства сингулярных функций.
- 19.3. Умножение операторных функций.
- ГЛАВА IV. МАТРИЦА РАССЕЯНИЯ
- § 20. Основные понятия теории взаимодействующих полей
- 20.2. Представление взаимодействия.
- 20.3. Матрица рассеяния.
- 20.4. Релятивистская ковариантность и унитарность S-матрицы.
- 20.5. Условие причинности.
- 20.6. «Классические поля» как функциональные аргументы.
- § 21. Лагранжиан взаимодействия и S-матрица
- 21.2. Условия ковариантности, унитарности и причинности для Sn.
- 21.3. Определение явного вида
- 21.4. Хронологическое произведение локальных операторов.
- 21.5. Определение функций Sn при любом n.
- 21.6. Анализ произвола в функциях Sn и наиболее общий вид S(g).
- § 22. Раскрытие хронологических произведений
- 22.2. Теорема Вика для хронологических произведений.
- § 23. Приведение S-матрицы к нормальной форме
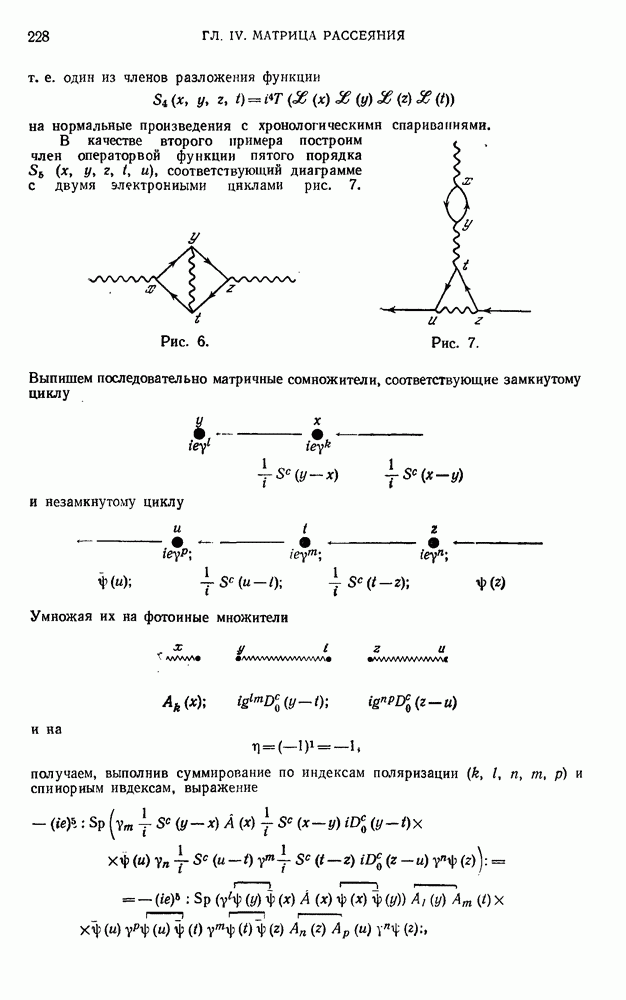
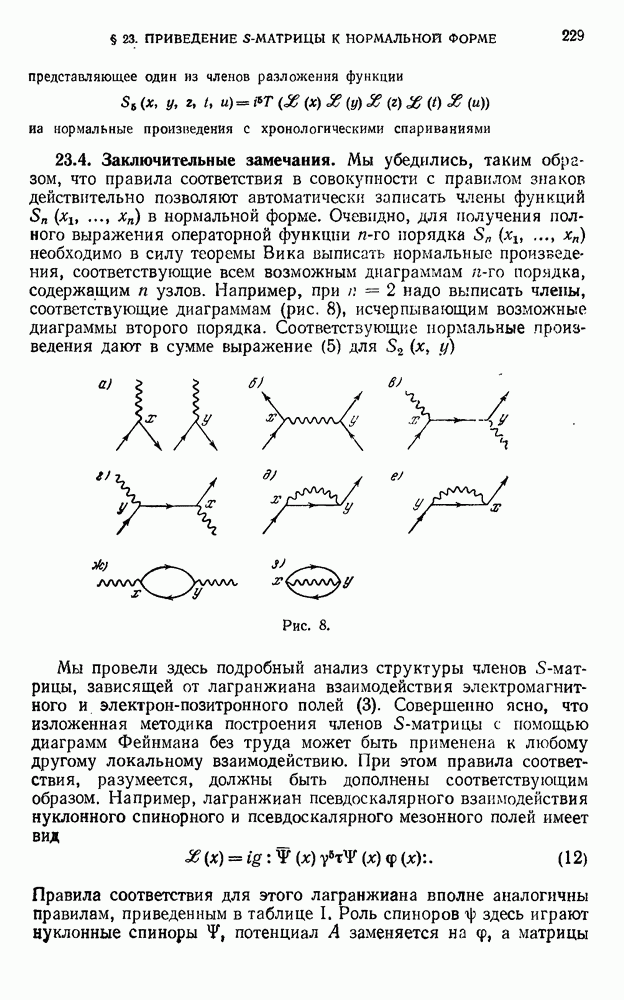
- 23.2. Диаграммы Фейнмана и правила соответствия.
- 23.3. Примеры.
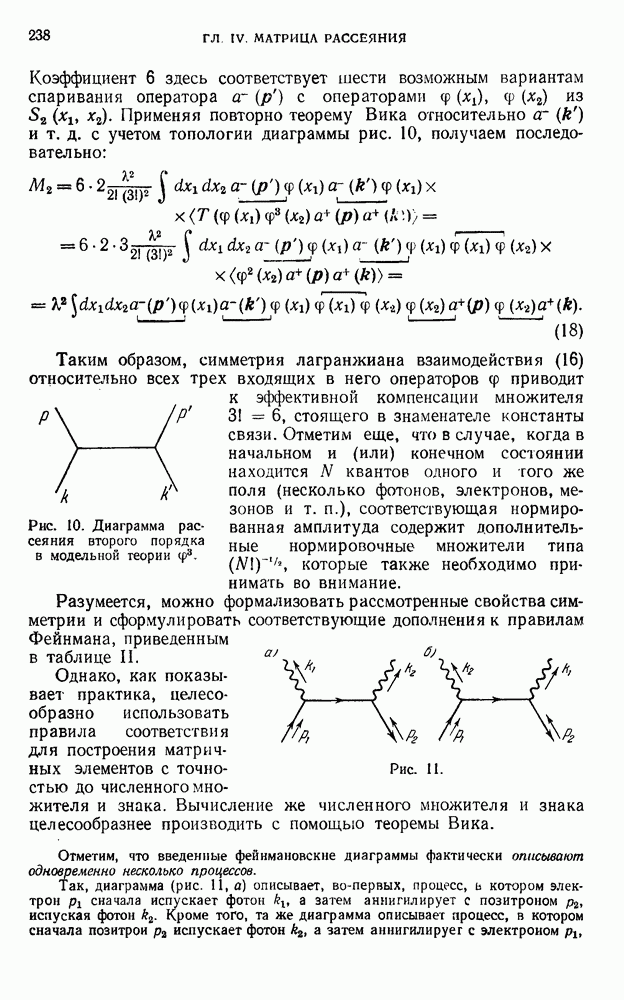
- 23.4. Заключительные замечания.
- § 24. Правила Фейнмана для вычисления матричных элементов матрицы рассеяния
- 24.2. Вычисление матричных элементов.
- 24.3. Учет свойств симметрии.
- 24.4. Рассеяние внешними полями.
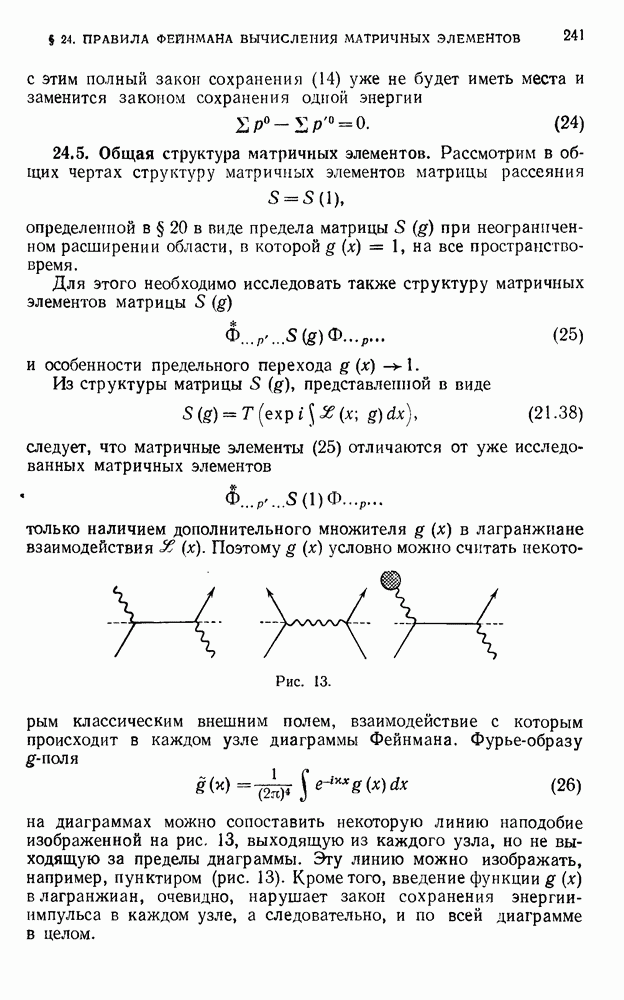
- 24.5. Общая структура матричных элементов.
- § 25. Вероятности процессов рассеяния и эффективные сечения
- 25.2. Вычисление вероятностей переходов.
- 25.3. Рассеяние двух частиц.
- 25.4. Эффективные сечения рассеяния.
- 25.5. Двухчастичный распад.
- § 26. Примеры расчета процессов второго порядка
- 26.2. Аннигиляция пары электрон — позитрон.
- 26.3. Тормозное излучение.
- ГЛАВА V. УСТРАНЕНИЕ РАСХОДИМОСТЕЙ ИЗ S-МАТРИЦЫ
- § 27. О расходимостях S-матрицы в электродинамике (второй порядок)
- 27.2. Выделение из расходящейся части.
- 27.3. Расходящаяся диаграмма с двумя внешними фотонными линиями П.
- 27.4. Выделение расходимостей из П и градиентная инвариантность.
- 27.5. Построение интегрируемой функции S2
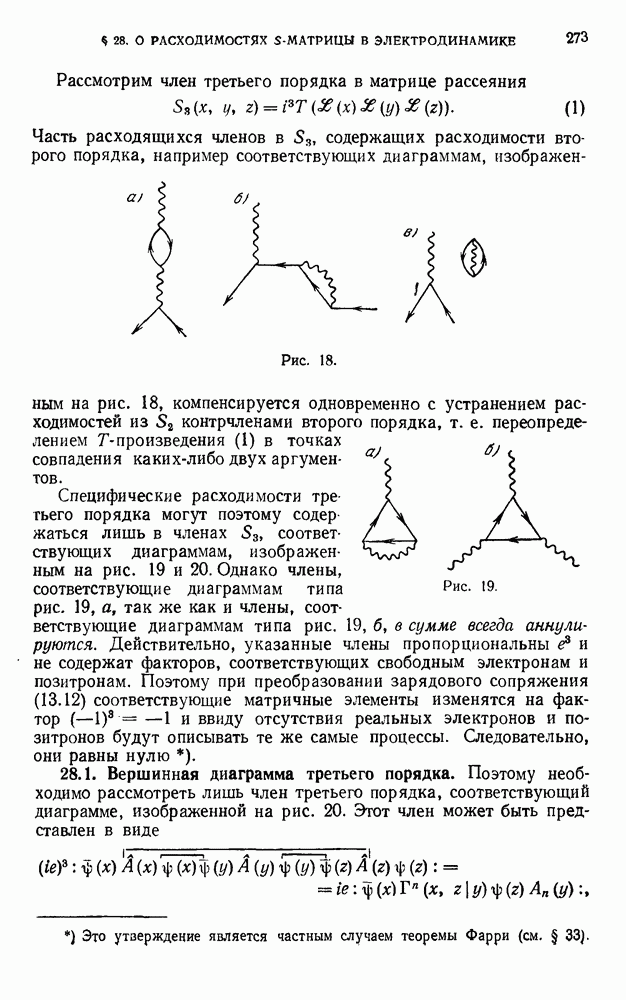
- § 28. О расходимостях S-матрицы в электродинамике (третий порядок)
- 28.2. Выделение расходимости из Г и градиентная инвариантность.
- 28.3. Тождество Уорда.
- 28.4. Получение интегрируемой функции S2.
- § 29. Общие правила устранения расходимостей из S-матрицы
- 29.2. Общий метод устранения расходимостей.
- 29.3. Графическое представление процедуры вычитания и R-операция.
- 29.4. Индекс диаграммы и степень расходимости.
- 29.5. Структура экспоненциальной квадратичной формы.
- 29.6. Выбор операции
- 29.7. Размерная перенормировка.
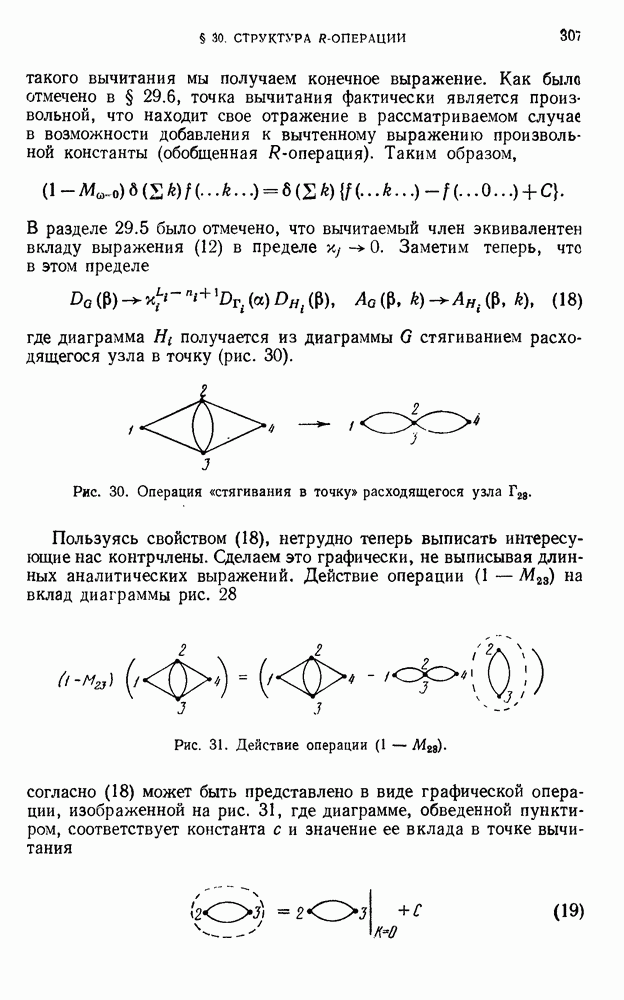
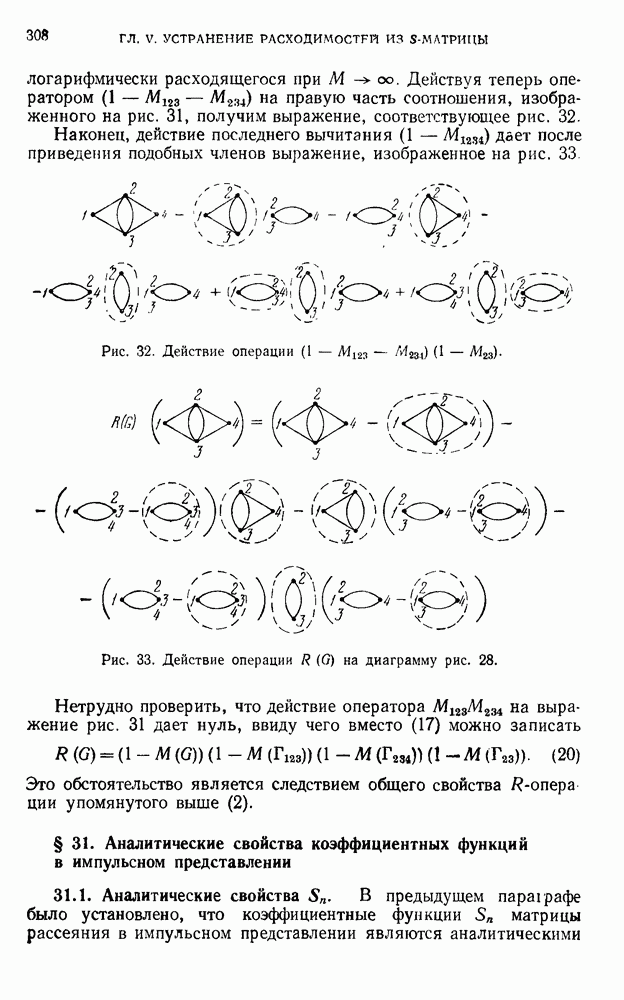
- § 30. Структура R-операции
- 30.2. Параметрическое представление.
- 30.3. Переход к пределу при е = 0.
- 30.4. Иллюстрация.
- § 31. Аналитические свойства коэффициентных функций в импульсном представлении
- 31.2. Структура функций Hn
- 31.3. Аналитические свойства функций Hn.
- § 32. Классификация ренормируемости теорий
- 32.2. Перечень взаимодействий первого рода.
- 32.3. Природа взаимодействий второго рода.
- 32.4. Фиксирование теории первого рода конечным числом констант.
- ГЛАВА VI. ПРИЛОЖЕНИЯ ОБЩЕЙ ТЕОРИИ УСТРАНЕНИЯ РАСХОДИМОСТЕЙ
- § 33. Спинорная электродинамика
- 33.2. Градиентная инвариантность матрицы рассеяния.
- 33.3. Тождества Уорда.
- 33.4. Контрчлены.
- § 34. Спинорная электродинамика.
- 34.2. Неоднозначность процесса устранения бесконечностей.
- 34.3. Полные функции Грина G, D и вершинная часть Г.
- 34.4. Радиационные поправки во внешние линии и выбор конечных постоянных.
- § 35. Спинорная электродинамика.
- 35.2. Поправки к электронной функции Грина.
- 35.3. Поправки к вершинной части.
- 35.4. Схема вычисления поправок к формуле Клейна—Нишины.
- § 36. Некоторые модели сильных взаимодействий
- 36.2. Псевдоскалярное поле с нелинейным взаимодействием.
- 36.3. Псевдоскалярная модель мезон-нуклонного взаимодействия.
- 36.4. Второй заряд, мультипликативные ренормировки и внешние линии.
- § 37. Полные функции Грина и вершинные функции
- 37.2. Источники и производящие функционалы.
- 37.3. Производящий функционал для высших функций Грина.
- 37.4. Вершинные функции.
- § 38. Уравнения Швингера и Дайсона
- 38.2. Редукционные формулы.
- 38.3. Уравнения Швингера.
- 38.4. Уравнения Дайсона.
- 38.5. Учет контрчленов.
- ГЛАВА VII. УРАВНЕНИЕ ШРЕДИНГЕРА И ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ
- § 39. Уравнение Шредингера для амплитуды состояний
- 39.2. Уравнение Шредингера в представлении взаимодействия и уравнение Томонага—Швингера.
- 39.3. Сингулярности обобщенного гамильтониана.
- 39.4. Основные свойства обобщенного гамильтониана.
- § 40. Динамические переменные системы взаимодействующих полей
- 40.2. Локальные динамические величины
- 40.3. Вектор тока.
- 40.4. Условие Лоренца.
- 40.5. Операторы волновых полей.
- § 41. Поляризация вакуума и аномальный магнитный момент электрона
- 41.2. Аномальный магнитный момент электрона.
- § 42. Уравнение Дирака с радиационными поправками
- 42.2. Обобщение уравнения Дирака.
- 42.3. Лэмбовский сдвиг уровней.
- 42.4. Заключительные замечания.
- ГЛАВА VIII. МЕТОД ФУНКЦИОНАЛЬНОГО УСРЕДНЕНИЯ
- § 43. Континуальный интеграл в квантовой теории поля
- 43.2. Вычисление …
- 43.3. Континуальные интегралы.
- 43.4. Континуальный интеграл по ферми-полям.
- § 44. Производящие функционалы и функции Грина
- 44.2. Представления для функций Грина в виде континуальных бозе-интегралов.
- § 45. Градиентные преобразования спинориой электродинамики
- 45.2. Градиентная инвариантность матрицы рассеяния.
- 45.3. Обобщенные тождества Уорда.
- 45.4. Переход к поперечной калибровке.
- 45.5. Градиентные преобразования функций Грина.
- § 46. Исследование модели Блоха — Нордсика
- 46.2. Вычисление G(х, у).
- ГЛАВА IX. РЕНОРМАЛИЗАЦИОННАЯ ГРУППА
- § 47. Группа мультипликативных ренормировок в квантовой теории поля
- 47.2. Групповой характер мультипликативных перенормировок.
- 47.3. Переход к импульсному представлению.
- 47.4. Вывод функциональных уравнений.
- 47.5. Свойства функциональных уравнений.
- § 48. Общий анализ групповых уравнений
- 48.2. Дифференциальные уравнения.
- 48.3. Общее решение уравнений.
- 48.4. Синтез ренормгруппы и теории возмущений.
- 48.5. Схемная зависимость.
- § 49. Асимптотический анализ в ультрафиолетовой области
- 49.2. Асимптотики инвариантного заряда.
- 49.3. Асимптотики функций Грина.
- 49.4. Высшие функции Грина.
- § 50. Анализ функций Грина спинорной электродинамики
- 50.2. Ультрафиолетовые асимптотики.
- 50.3. Инфракрасная асимптотика электронной функции Грина.
- 50.4. Матричные элементы и вероятности переходов.
- § 51. Модели сильных взаимодействий
- 51.2 Двухпетлевое приближение.
- 51.3. Надежность результатов. Высшие приближения.
- 51.4. Квантовая хромодинамика
- 51.5. Анализ двухзарядной модели.
- 51.6. Симметричные асимптотики высших функций Грина.
- ГЛАВА X. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- § 52. Основные свойства S-матрицы в локальной теории поля
- 52.2. Общие свойства матрицы рассеяния.
- 52.3. Локальные свойства.
- 52.4. Оптическая теорема.
- § 53. Спектральное представление пионной функции Грина
- 53.2. Вакуумное ожидание произведения и коммутатора двух токов.
- 53.3. Аналитические свойства …
- 53.4. Спектральное представление …
- § 54. Спектральное представление фермионной функции Грина
- 54.2. Вывод спектрального представления.
- 54.3. Близость к противоречию.
- § 55. Представление Йоста — Лемана — Дайсона
- 55.2. Общая форма представления.
- 55.3. Область интегрирования.
- 55.4. Некоторые следствия.
- § 56. Вывод дисперсионных соотношений для пион-нуклонного рассеяния
- 56.2. Переход к фиксированной системе отсчета. Трудности аналитического продолжения.
- 56.3. Схема получения дисперсионных соотношений для амплитуды рассеяния вперед.
- 56.4. Случай рассеяния при p <> 0
- § 57. Дисперсионные соотношения для пион-нуклонного рассеяния вперед
- 57.2. Изотопическая и спиновая структура.
- 57.3. Свойства симметрии по энергии.
- 57.4. Физические дисперсионные соотношения.
- 57.5. Дальнейшее развитие метода.
- ПРИЛОЖЕНИЕ 1. НЕКОТОРЫЕ СВЕДЕНИЯ ОБ ИЗОТОПИЧЕСКОМ ФОРМАЛИЗМЕ
- ПРИЛОЖЕНИЕ 2. СВОДКА СИНГУЛЯРНЫХ ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 3. СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ МАТРИЧНЫХ ЭЛЕМЕНТОВ
- ЛИТЕРАТУРА