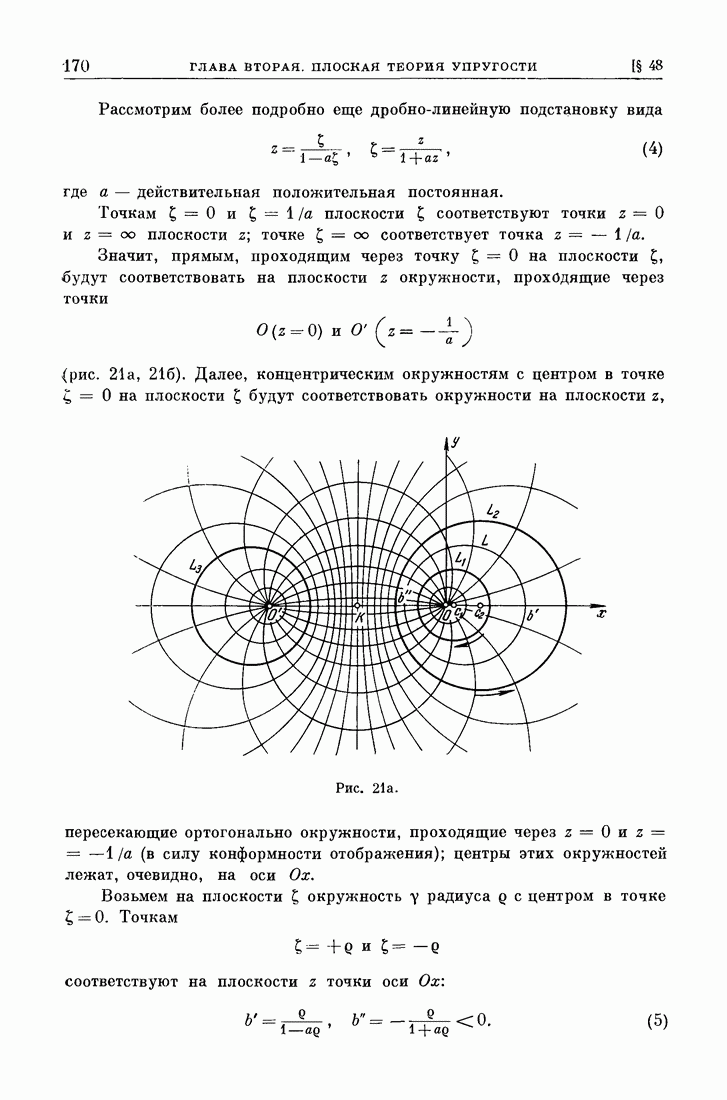
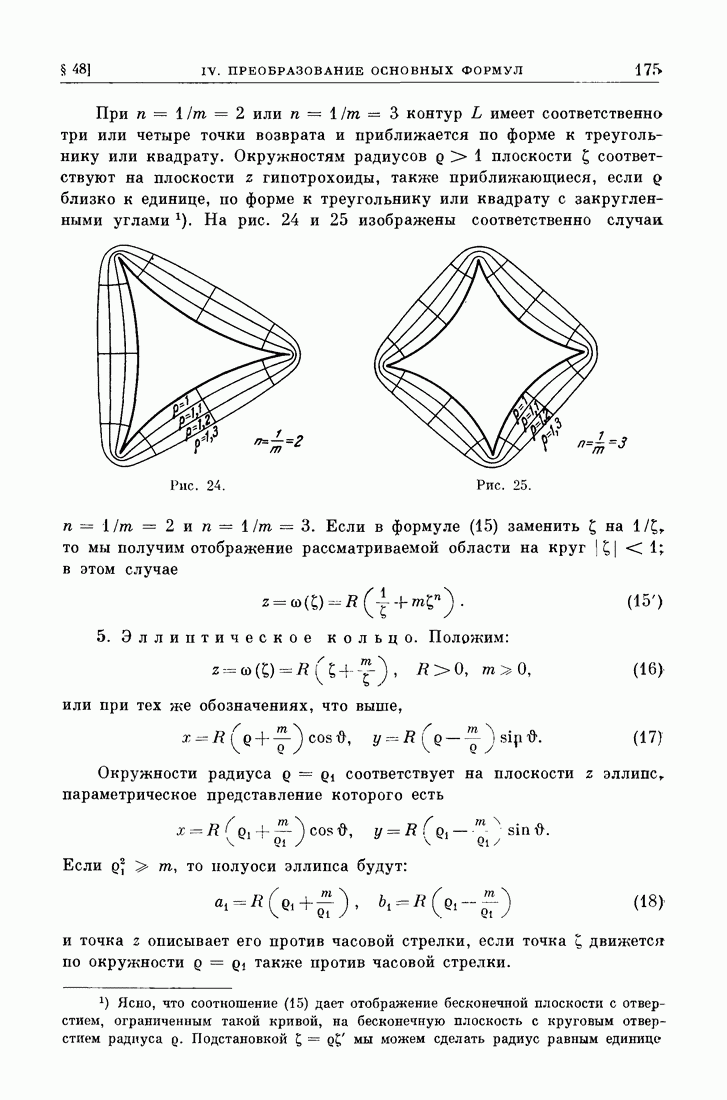
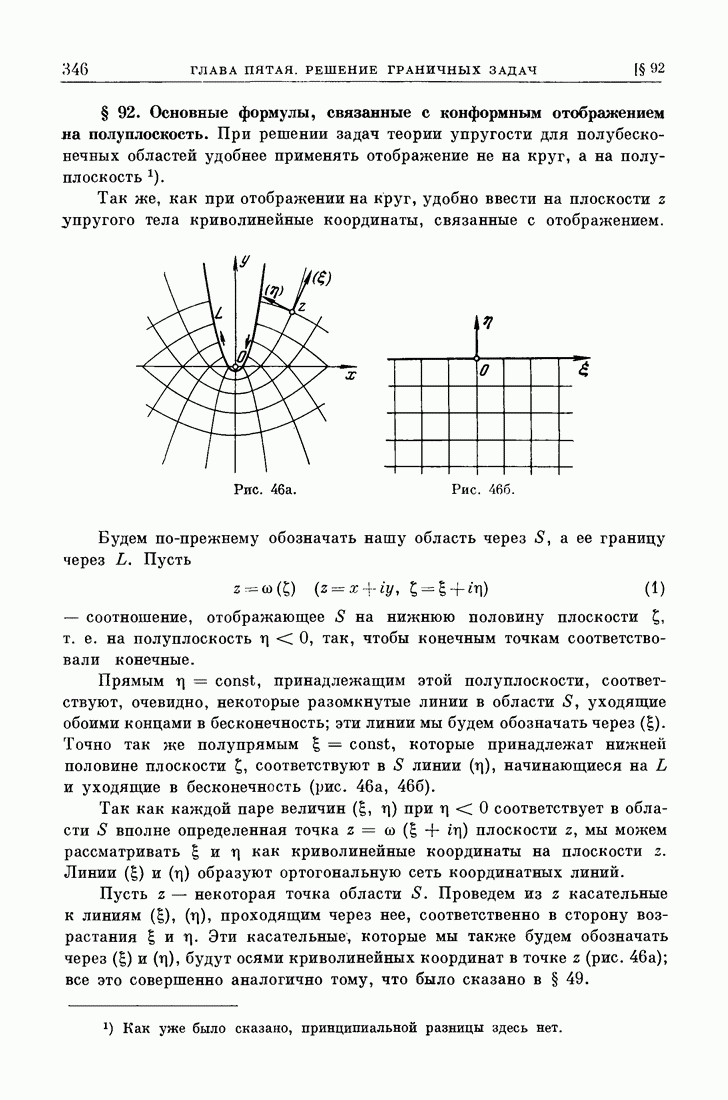
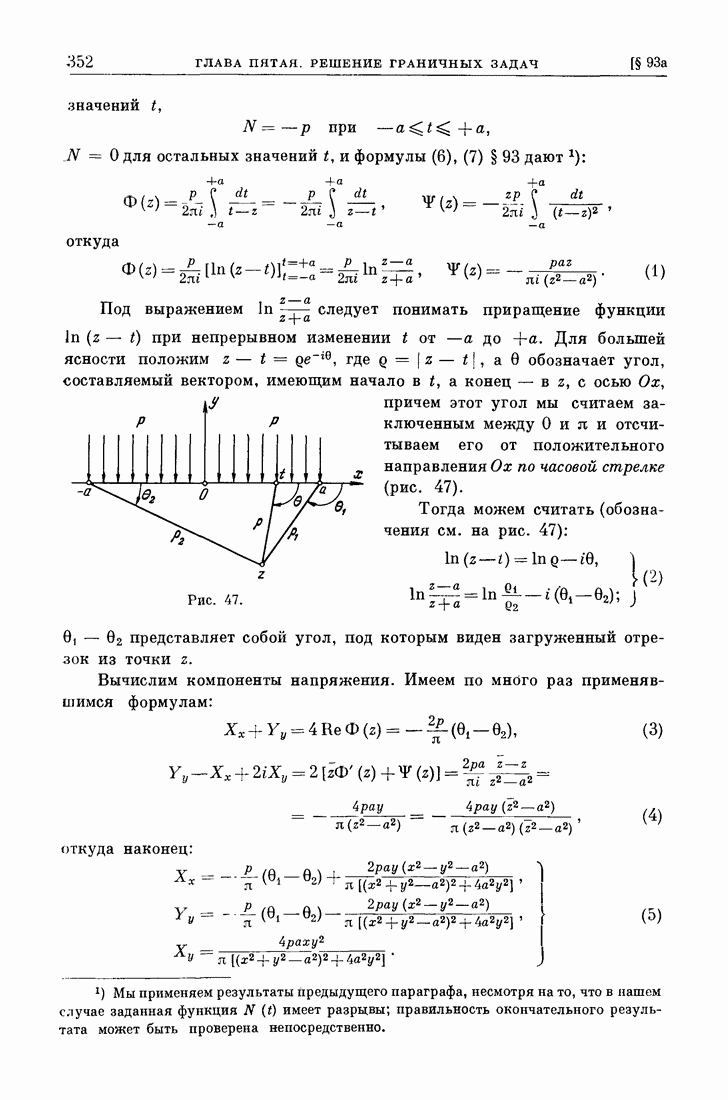
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
В § 14 мы вывели формулы, дающие возможность вычислять компоненты деформации по компонентам смещения, заданным как функции координат х, у, z. Мы ставим теперь обратную задачу: вычислить компоненты  смещения, если заданы компоненты деформации
смещения, если заданы компоненты деформации  как функции х, у, z. Решению этой задачи мы предпошлем несколько предварительных замечаний, позволяющих заранее предугадать некоторые результаты.
как функции х, у, z. Решению этой задачи мы предпошлем несколько предварительных замечаний, позволяющих заранее предугадать некоторые результаты.
Компоненты деформации определяют, как мы видели, изменение формы бесконечно малого элемента тела вблизи данной точки. Таким образом, задание компонент деформации как функций координат х, у, z определяет изменение формы каждого бесконечно малого элемента тела. На основании сказанного почти очевидно, что указанное задание определит и деформацию всего тела как целого, т. е. определит значения смещений  как функций от х, у, z; ясно также, что определение
как функций от х, у, z; ясно также, что определение  не может быть совершенно полным. Действительно, если найдены смещения, соответствующие данным компонентам деформации, то, присоединив произвольное (бесконечно малое) перемещение всего тела как жесткого целого, мы получим другие значения смещений, соответствующих тем же самым компонентам деформации, ибо жесткое перемещение всего тела никакого влияния на деформацию не оказывает. Чтобы сделать задачу определенной, можно, например, дополнительно задаться смещением какой-либо произвольно выбранной точки
не может быть совершенно полным. Действительно, если найдены смещения, соответствующие данным компонентам деформации, то, присоединив произвольное (бесконечно малое) перемещение всего тела как жесткого целого, мы получим другие значения смещений, соответствующих тем же самым компонентам деформации, ибо жесткое перемещение всего тела никакого влияния на деформацию не оказывает. Чтобы сделать задачу определенной, можно, например, дополнительно задаться смещением какой-либо произвольно выбранной точки  тела, а также компонентами вращения в этой точке.
тела, а также компонентами вращения в этой точке.
Заметим еще следующее. По принятому выше условию компоненты  однозначны и имеют непрерывные производные до третьего порядка. Значит, задаваемые компоненты деформации
однозначны и имеют непрерывные производные до третьего порядка. Значит, задаваемые компоненты деформации  должны быть также однозначны и иметь непрерывные производные до второго порядка; это условие мы будем считать выполненным. Легко, однако, убедиться заранее, что величины
должны быть также однозначны и иметь непрерывные производные до второго порядка; это условие мы будем считать выполненным. Легко, однако, убедиться заранее, что величины  должны удовлетворять еще определенным соотношениям, для того чтобы задача имела решение. Это следует уже из такого грубого рассмотрения. Представим себе тело разбитым на бесконечно малые элементы, скажем, кубики (не считая элементов, примыкающих к границе). Если мы подвергнем каждый кубик деформации с заданными компонентами и затем попытаемся вновь сложить полученные бесконечно малые параллелепипеды так, чтобы точки их граней, соприкасавшихся до деформации, снова соприкасались, то это окажется, вообще говоря, невозможным: при попытке сложить отдельные элементы между некоторыми из них или образуются зазоры, или грани элементов, которые должны были бы совпасть, окажутся сдвинутыми друг относительно друга, или, наконец, для некоторых элементов не окажется достаточно места. Это и показывает, что компоненты деформации должны удовлетворять некоторым соотношениям, для того чтобы была возможна деформация без разрывов.
должны удовлетворять еще определенным соотношениям, для того чтобы задача имела решение. Это следует уже из такого грубого рассмотрения. Представим себе тело разбитым на бесконечно малые элементы, скажем, кубики (не считая элементов, примыкающих к границе). Если мы подвергнем каждый кубик деформации с заданными компонентами и затем попытаемся вновь сложить полученные бесконечно малые параллелепипеды так, чтобы точки их граней, соприкасавшихся до деформации, снова соприкасались, то это окажется, вообще говоря, невозможным: при попытке сложить отдельные элементы между некоторыми из них или образуются зазоры, или грани элементов, которые должны были бы совпасть, окажутся сдвинутыми друг относительно друга, или, наконец, для некоторых элементов не окажется достаточно места. Это и показывает, что компоненты деформации должны удовлетворять некоторым соотношениям, для того чтобы была возможна деформация без разрывов.
Все это мы сейчас строго докажем, фактически решая поставленную задачу. Итак, пусть требуется найти функции  удовлетворяющие условиям:
удовлетворяющие условиям:

где  заданные однозначные функции от х, у, z, имеющие непрерывные производные до второго порядка.
заданные однозначные функции от х, у, z, имеющие непрерывные производные до второго порядка.
У нас, таким образом, имеется шесть уравнений для определения трех неизвестных функций. Это еще раз указывает на то, что задача не может иметь решения, если заданные функции  не подчинены некоторым дополнительным условиям; эти условия мы найдем, решая нашу задачу.
не подчинены некоторым дополнительным условиям; эти условия мы найдем, решая нашу задачу.
Пусть V — область, первоначально занятая телом; это есть область изменения х, у, z, в которой заданы функции  и в которой ищутся функции
и в которой ищутся функции 
Мы будем предполагать пока, что область V односвязна. Напомним, что односвязной называется область, обладающая следующим свойством: всякий замкнутый контур, проведенный внутри области, может быть стянут в одну точку путем непрерывного изменения, не выводящего контур из области. Такою областью является, например, область, занятая шаром, кубом и пр. (подробнее об этом см. в Добавлении II).
Пусть  какая-либо точка нашей области,
какая-либо точка нашей области,  значения компонент смещения, а
значения компонент смещения, а  значения компонент вращения в этой точке. Пусть
значения компонент вращения в этой точке. Пусть  какая-либо другая точка области
какая-либо другая точка области  Поставим себе задачей найти значения компонент смещения в этой точке.
Поставим себе задачей найти значения компонент смещения в этой точке.
Пусть  обозначает какую-либо линию, соединяющую точки
обозначает какую-либо линию, соединяющую точки  и находящуюся в области
и находящуюся в области  Если бы значения частных производных
Если бы значения частных производных  функции и были нам известны во всей области V, мы смогли бы найти значение
функции и были нам известны во всей области V, мы смогли бы найти значение  функции и в точке
функции и в точке  по формуле
по формуле

где интеграл взят по кривой  Но мы имеем:
Но мы имеем:

 определяются формулами (6) предыдущего параграфа. Следовательно,
определяются формулами (6) предыдущего параграфа. Следовательно,

Под знаком первого интеграла фигурируют исключительно заданные функции. Займемся теперь вторым. Имеем:

откуда, интегрируя по частям, получаем: 

Чтобы вычислить последний интеграл, необходимо знать выражения для  или, что все равно, выражения для частных производных первого порядка функций
или, что все равно, выражения для частных производных первого порядка функций  Но, как показывает непосредственная проверка,
Но, как показывает непосредственная проверка,

Подставляя эти значения в выражения

получаем на основании (а) и (б) первую из нижеследующих формул; две другие получены из первой путем круговой перестановки букв:

где для краткости введены обозначения:

Значения  получаются из предыдущих путем круговой перестановки букв (одновременно переставляются между собой буквы
получаются из предыдущих путем круговой перестановки букв (одновременно переставляются между собой буквы  и буквы х, у, z).
и буквы х, у, z).
Формулы (4) по существу совпадают с формулами, найденными Вольтерра (V. Volterra) путем преобразования формул, данных Кирхгоффом. Приведенный здесь вывод их принадлежит Чезаро (Е. Cesaro), который придал формулам Вольтерра более симметричный вид.
Полученные формулы (4) определяют компоненты  смещения в любой точке
смещения в любой точке  тела, если даны компоненты смещения
тела, если даны компоненты смещения  и вращения
и вращения  в какой-либо одной, раз навсегда выбранной, точке
в какой-либо одной, раз навсегда выбранной, точке 
Выражения, полученные для смещений, содержат интегралы, взятые по некоторой линии, соединяющей точки  Но ведь
Но ведь  должны быть функциями от
должны быть функциями от  и не зависеть от пути интегрирования
и не зависеть от пути интегрирования  Следовательно, для того чтобы наша задача имела решение, необходимо, чтобы интегралы, фигурирующие в формулах (4), не зависели от пути интегрирования.
Следовательно, для того чтобы наша задача имела решение, необходимо, чтобы интегралы, фигурирующие в формулах (4), не зависели от пути интегрирования.
Как легко видеть, для независимости интеграла

от выбора пути необходимы и достаточны условия 4)

Для двух других интегралов получим аналогичные условия путем круговой перестановки букв. Эти условия должны быть соблюдены во всех точках  в области V и для всех значений
в области V и для всех значений  в той же области.
в той же области.
Представляя эти условия в явной форме, увидим, что все они сводятся к шести следующим:

Например, условие

дает на основании формул (5) после некоторых сокращений

Так как это соотношение должно быть справедливо при всяких  в данной области, то должно быть:
в данной области, то должно быть:

Эти соотношения совпадают с двумя последними соотношениями правого столбца формул (6). Таким же образом получим все остальные. Заметим, что формулы, фигурирующие во второй и третьей строках (6), могут быть получены из формул первой строки путем круговой перестановки.
Условия (6) называются условиями совместимости Сен-Венана (Ваггё de Saint-Venant, 1797-1886), так как были впервые найдены им. Они дают нам математическое выражение тех соотношений, которым должны удовлетворять компоненты деформации, для того чтобы была возможна деформация без разрывов (см. начало настоящего параграфа), и потому называются иногда условиями неразрывности.
При соблюдении этих условий формулы (4) дают вполне определенные выражения для  не зависящие от выбора пути интегрирования, и легко непосредственно проверить, что найденные таким образом смещения действительно удовлетворяют уравнениям (1). При этом постоянные
не зависящие от выбора пути интегрирования, и легко непосредственно проверить, что найденные таким образом смещения действительно удовлетворяют уравнениям (1). При этом постоянные

остаются совершенно произвольными, как мы и предвидели заранее. Изменяя эти постоянные, мы сообщим только жесткое перемещение всему телу, как это видно из формул (8) § 12. В частности, если

80 всей области, то мы получим, полагая для простоты  и отбрасывая значки
и отбрасывая значки 

т. е. только жесткое перемещение тела как целого.
До сих пор мы предполагали, что область V односвязна. Рассмотрим теперь случай многосвязной области, т. е. такой области, что внутри
нее существуют замкнутые контуры, которые нельзя стянуть в одну точку, не разрывая их и не выводя из области. Примером многосвязной области может служить тор, т. е. тело, образованное вращением круга вокруг оси, лежащей в его плоскости и не пересекающей его (рис. 9).
Многосвязное тело можно превратить в односвязное, производя надлежащие разрезы; например, в случае тора достаточно разрезать его по одному из меридиональных кругов, изображенных на рис. 9. К разрезанной таким образом области применимо все сказанное выше. Именно, при соблюдении условий совместимости Сен-Венана компоненты  определяемые формулами (4), будут однозначными функциями кбординат точки
определяемые формулами (4), будут однозначными функциями кбординат точки  при этом, конечно, мы предполагаем, что путь интегрирования
при этом, конечно, мы предполагаем, что путь интегрирования  не выходит из разрезанной области, т. е. нигде не пересекает разрезов. Но при приближении точки
не выходит из разрезанной области, т. е. нигде не пересекает разрезов. Но при приближении точки  к какой-либо точке разреза величины
к какой-либо точке разреза величины  будут, вообще говоря, принимать различные значения в зависимости от того, с какой стороны приближается точка
будут, вообще говоря, принимать различные значения в зависимости от того, с какой стороны приближается точка  к разрезу.
к разрезу.

Рис. 9.
Пусть  суть значения
суть значения  получаемые при приближении к некоторой точке разреза с той или с другой стороны. Условие неразрывности деформации для всего тела в целом будет выполнено только в том случае, если наряду с условиями совместимости (6) соблюдены и дополнительные условия:
получаемые при приближении к некоторой точке разреза с той или с другой стороны. Условие неразрывности деформации для всего тела в целом будет выполнено только в том случае, если наряду с условиями совместимости (6) соблюдены и дополнительные условия:

вдоль всех разрезов, мысленно проведенных в теле с целью сделать его односвязным. При несоблюдении добавочных условий (7) придется допустить наличие разрывов вдоль упомянутых разрезов и даже проникновение частей тела друг в друга в этих местах.
Из сказанного ясно, что если условия (7) не соблюдены и если мы станем определять функции  по формулам (4) в неразрезанной области, т. е. допускать, что линия интегрирования может пересекать разрезы, тогда функции
по формулам (4) в неразрезанной области, т. е. допускать, что линия интегрирования может пересекать разрезы, тогда функции  окажутся многозначными функциями от
окажутся многозначными функциями от  при обходе по некоторым замкнутым контурам функции
при обходе по некоторым замкнутым контурам функции  не будут возвращаться к своим исходным значениям; это может иметь место, как легко видеть, только в случае контуров, не сводимых к точке путем непрерывного изменения (см. также Добавление II).
не будут возвращаться к своим исходным значениям; это может иметь место, как легко видеть, только в случае контуров, не сводимых к точке путем непрерывного изменения (см. также Добавление II).
На это обстоятельство впервые указал Мичелл (Michell [1]). Тимпе (Timpe [1]) указал для случая плоской задачи теории упругости возможность физической интерпретации многозначных смещений. Для общего
случая трех измерений вопрос о значении многозначных смещений был подробно исследован Вольтерра в ряде работ; сводка этих работ дана в его уже названном мемуаре. Этот вопрос будет нами подробно изучен для двумерного случая в главе II (отдел III).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
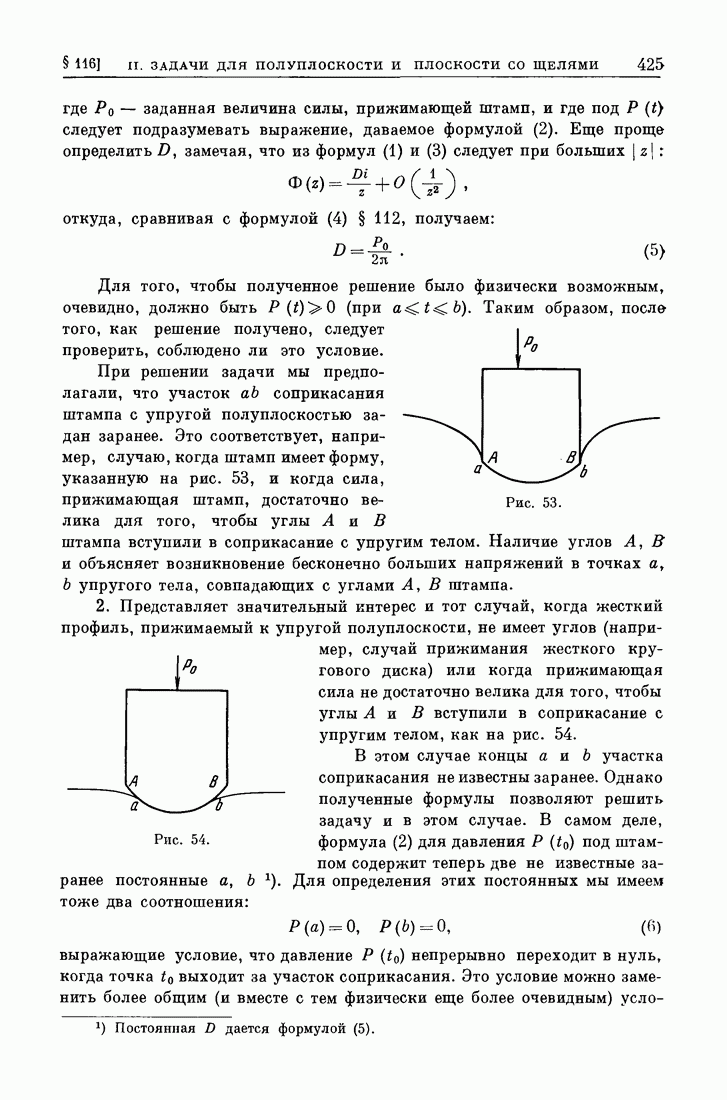
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
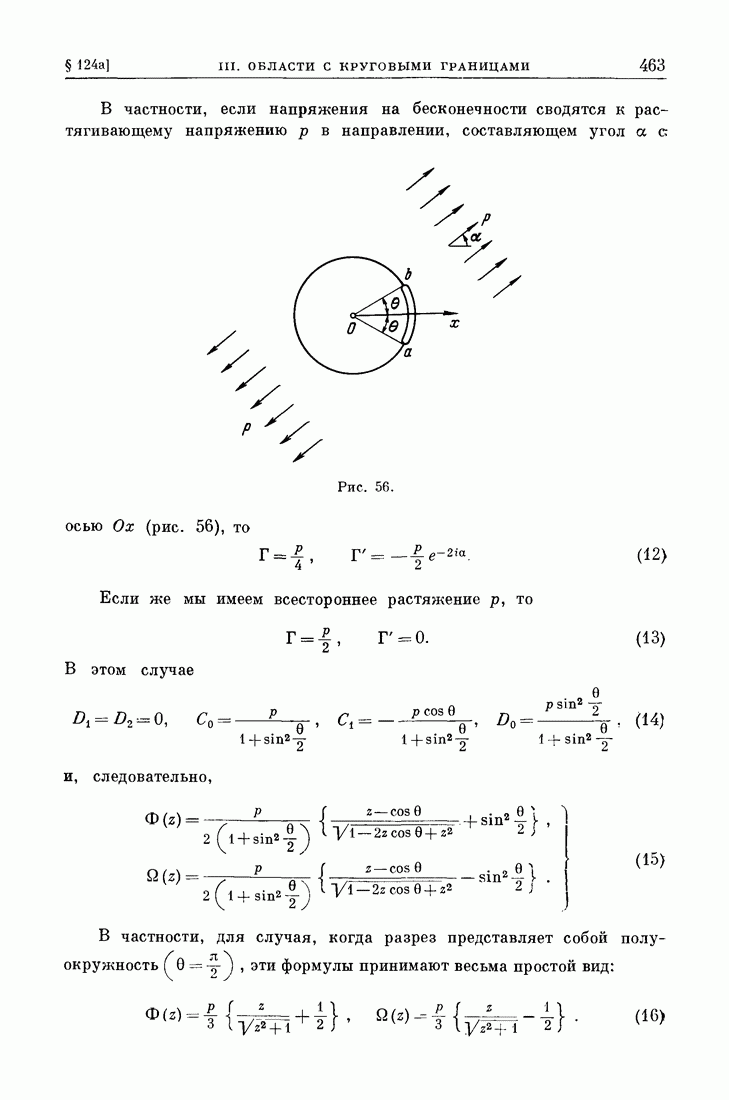
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
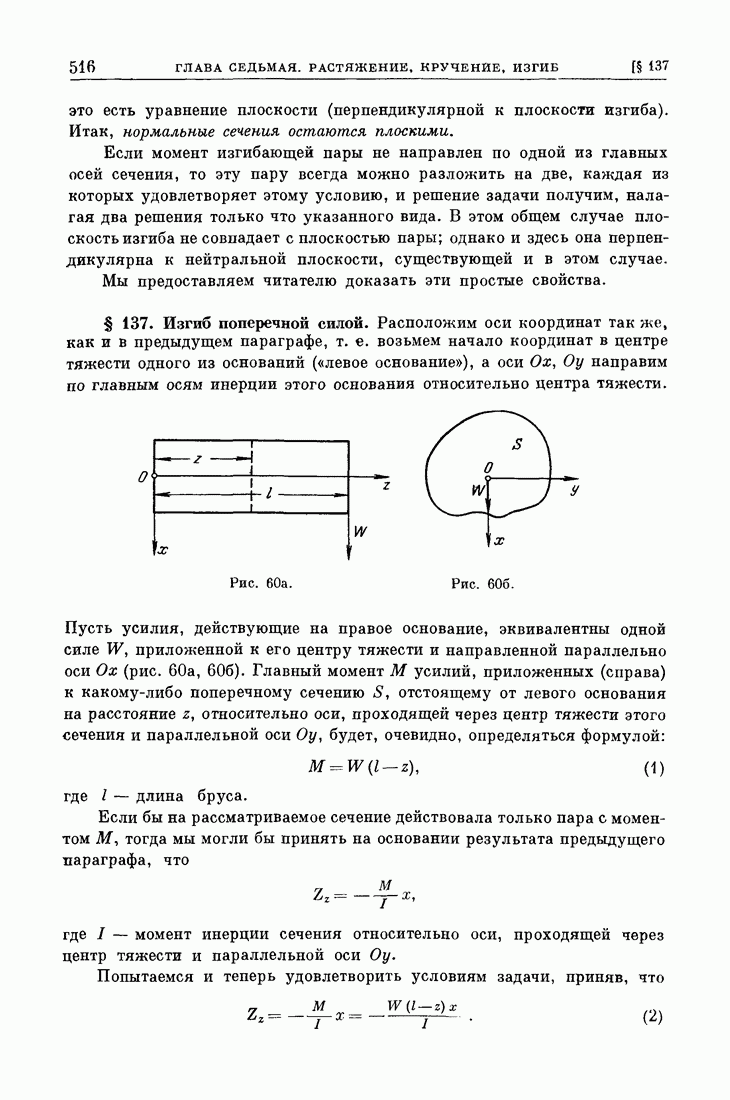
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
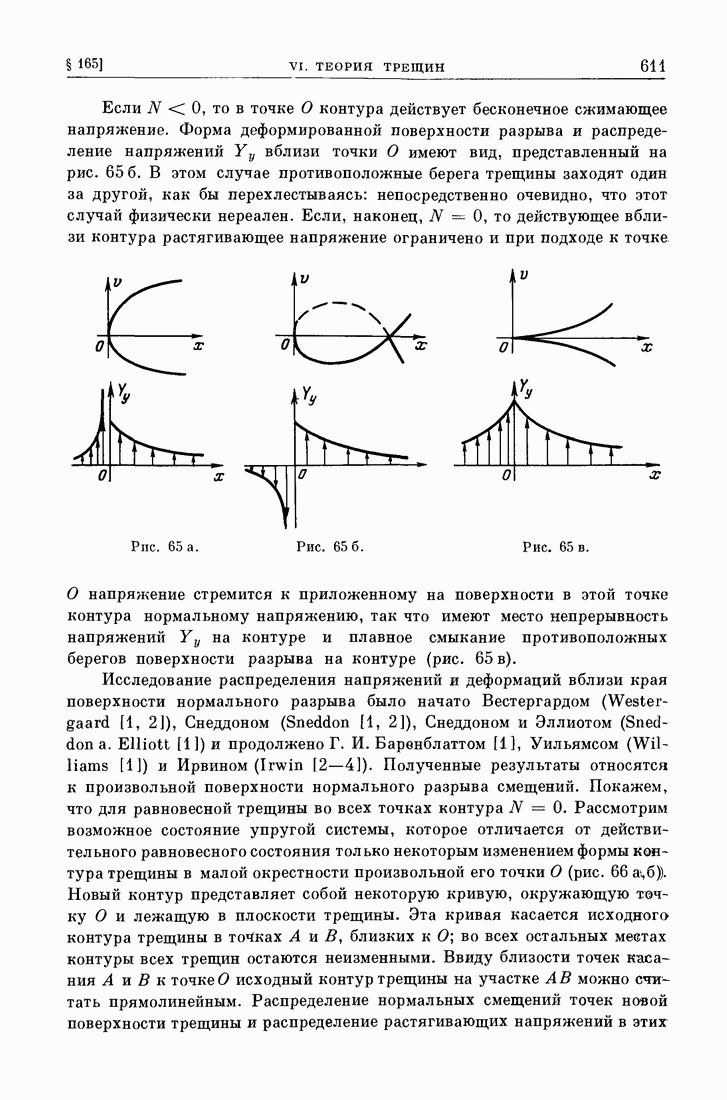
- VI. ТЕОРИЯ ТРЕЩИН
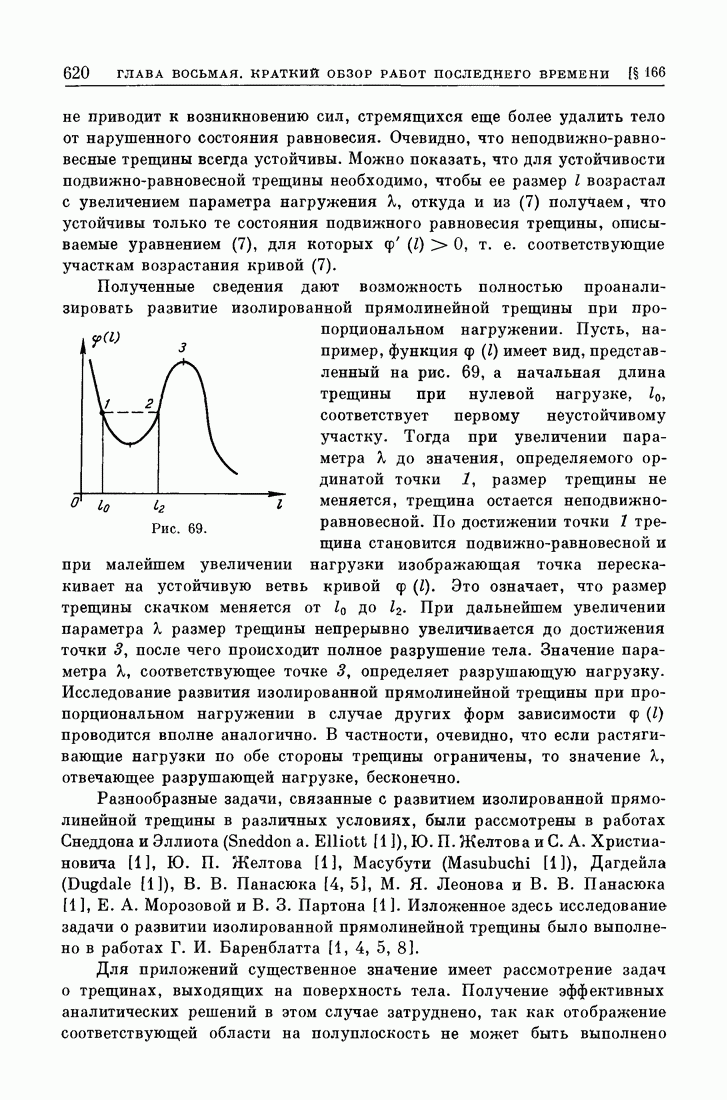
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ