| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
1. Начнем со случая двух измерений. Пусть  обозначает некоторую область на плоскости
обозначает некоторую область на плоскости  Мы будем рассматривать только такие связные области, которые ограничены одним или несколькими простыми замкнутыми контурами. Такие области могут быть и бесконечными (бесконечная плоскость с отверстиями), но пока мы ограничимся рассмотрением конечных областей.
Мы будем рассматривать только такие связные области, которые ограничены одним или несколькими простыми замкнутыми контурами. Такие области могут быть и бесконечными (бесконечная плоскость с отверстиями), но пока мы ограничимся рассмотрением конечных областей.
Область  называется односвязной, если любой разрез, проведенный от одной какой-либо точки ее границы до другой, нарушает ее связность, т. е. разбивает ее на раздельные области.
называется односвязной, если любой разрез, проведенный от одной какой-либо точки ее границы до другой, нарушает ее связность, т. е. разбивает ее на раздельные области.
Область называется многосвязной, если могут быть проведены такие разрезы, которые, идя от одной точки границы до другой, не разбивают область на части.
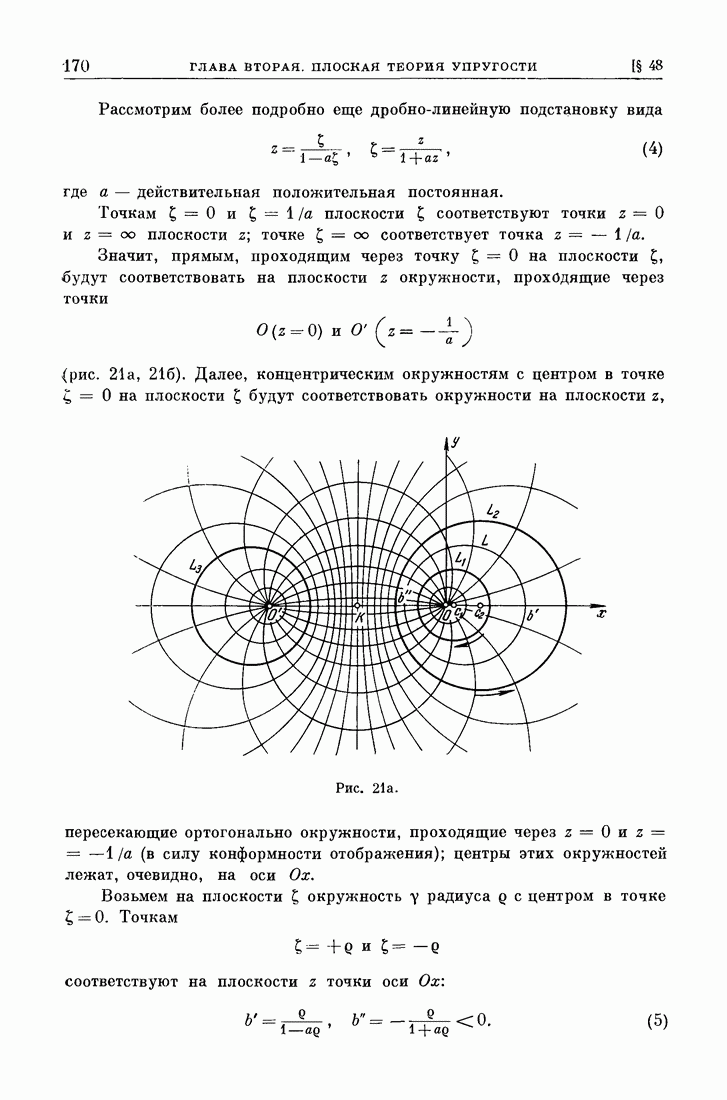
Легко видеть, что область, ограниченная одним простым замкнутым контуром, односвязна. Напротив, область, ограниченная несколькими простыми замкнутыми контурами, многосвязна. Действительно, пусть граница области состоит из контуров  из которых последний охватывает все остальные (рис. 73). Если разрезать область по какой-либо линии
из которых последний охватывает все остальные (рис. 73). Если разрезать область по какой-либо линии  соединяющей точку
соединяющей точку  контура
контура  с точкой внешнего контура
с точкой внешнего контура  то такой разрез («купюра») не нарушает ее связности.
то такой разрез («купюра») не нарушает ее связности.
Если, кроме  провести еще аналогичные разрезы
провести еще аналогичные разрезы  не пересекающие друг друга, то связность все же не нарушается, но, как легко видеть, всякий новый разрез уже нарушит связность. Таким образом, разрезы
не пересекающие друг друга, то связность все же не нарушается, но, как легко видеть, всякий новый разрез уже нарушит связность. Таким образом, разрезы  числом
числом  обращают нашу область в односвязную.
обращают нашу область в односвязную.
Если для превращения данной области в односвязную требуется провести  разрезов, то говорят, что область
разрезов, то говорят, что область  -связна или что ее связность равна
-связна или что ее связность равна 
Мы видим, что в нашем случае связность области равна числу замкнутых контуров, ее ограничивающих. Например, область, заключенная между двумя концентрическими окружностями, — двусвязная.
Односвязная область отличается от многосвязной еще следующим свойством. Если провести внутри односвязной области  любой простой замкнутый контур, то область, ограниченная этим контуром, целиком принадлежит области
любой простой замкнутый контур, то область, ограниченная этим контуром, целиком принадлежит области  этот контур путем непрерывной деформации может быть сжат в одну точку, все время оставаясь в области.
этот контур путем непрерывной деформации может быть сжат в одну точку, все время оставаясь в области.
В случае же многосвязной области существуют такие контуры, которые этим свойством не обладают. Например, на рис. 73 контур  (пунктир) есть один из таких контуров: его нельзя сжать в одну точку, не разрывая его и не выводя из области
(пунктир) есть один из таких контуров: его нельзя сжать в одну точку, не разрывая его и не выводя из области 

Рис. 73.
2. Пусть дано дифференциальное выражение

где  и
и  однозначные и непрерывные функции в некоторой области
однозначные и непрерывные функции в некоторой области  обладающие непрерывными производными первого порядка. Поставим себе вопрос: каким условиям должны удовлетворять функции
обладающие непрерывными производными первого порядка. Поставим себе вопрос: каким условиям должны удовлетворять функции  для того чтобы выражение (1) было полным дифференциалом некоторой однозначной функции
для того чтобы выражение (1) было полным дифференциалом некоторой однозначной функции  т. е. чтобы существовала однозначная фукция
т. е. чтобы существовала однозначная фукция  удовлетворяющая условию
удовлетворяющая условию

или, что сводится к тому же, условиям

Хотя этот вопрос излагается во всех, даже элементарных, курсах анализа, мы все же считаем нужным остановиться на нем, чтобы обратить внимание читателя на некоторые обстоятельства, весьма существенные для наших целей.
Предположим сперва, что область  односвязна. Возьмем в ней какую-либо постоянную точку
односвязна. Возьмем в ней какую-либо постоянную точку  и соединим ее произвольной линией
и соединим ее произвольной линией  не выходящей из
не выходящей из  с переменной точкой
с переменной точкой  Если функция
Если функция  удовлетворяющая условию (2), существует, то, интегрируя обе части этого равенства вдоль пути
удовлетворяющая условию (2), существует, то, интегрируя обе части этого равенства вдоль пути  получаем:
получаем:

где  — постоянная.
— постоянная.
По условию,  есть однозначная функция от х, у, значит, значение ее в точке
есть однозначная функция от х, у, значит, значение ее в точке  должно зависеть только от положения
должно зависеть только от положения  но не от пути интегрирования
но не от пути интегрирования  Таким образом, если функция
Таким образом, если функция  существует, то криволинейный интеграл
существует, то криволинейный интеграл

не должен зависеть от пути интегрирования (расположенного, разумеется, в области  Это условие можно выразить и так: интегралы
Это условие можно выразить и так: интегралы

взятые по любым замкнутым контурам  (целиком расположенным внутри
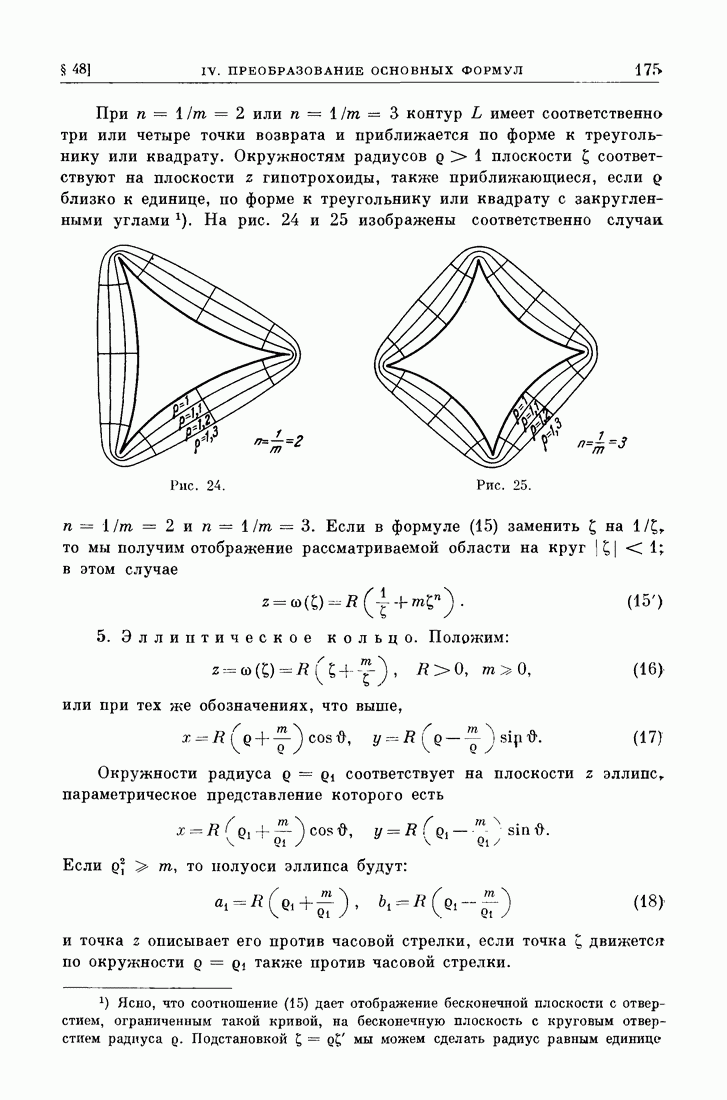
(целиком расположенным внутри  должны равняться нулю. Действительно, соединив какие-либо две точки
должны равняться нулю. Действительно, соединив какие-либо две точки  любого замкнутого контура
любого замкнутого контура  соответственно с точками
соответственно с точками  и
и  (рис. 74), будем иметь по условию:
(рис. 74), будем иметь по условию:

но так как интегралы по линиям  и
и  в обоих членах левой части равны между собой, то
в обоих членах левой части равны между собой, то

а это и требовалось доказать.

Рис. 74.
На основании известной формулы Остроградского — Грина имеем:

где о обозначает область, ограниченную контуром  Из сказанного следует, что интеграл в правой части должен равняться нулю для всякой части о области
Из сказанного следует, что интеграл в правой части должен равняться нулю для всякой части о области  Значит, подынтегральная функция должна быть равной нулю в каждой точке области
Значит, подынтегральная функция должна быть равной нулю в каждой точке области  т. е. мы должны иметь:
т. е. мы должны иметь:

во всей области  Это есть, как мы видим, необходимое условие существования функции
Это есть, как мы видим, необходимое условие существования функции  Оно оказывается также достаточным.
Оно оказывается также достаточным.
Действительно, при соблюдении этого условия криволинейный интеграл

не зависит от пути интегрирования, а только от конечной и начальной точек пути. Это непосредственно следует из предыдущего: если
А и В— две любые точки области  и
и  два любых пути, соединяющих эти точки, то
два любых пути, соединяющих эти точки, то

ибо (рис. 74)

а последний интеграл равен нулю в силу формулы (4) и условия (5). Мы подразумевали при этом, что пути  и
и  не пересекают друг друга, так что их соединение образует простой замкнутый контур. Но легко убедиться, что это несущественно: если пути пересекаются в одной или нескольких точках, то разность интегралов по этим путям может быть сведена к сумме интегралов по двум или большему числу замкнутых контуров.
не пересекают друг друга, так что их соединение образует простой замкнутый контур. Но легко убедиться, что это несущественно: если пути пересекаются в одной или нескольких точках, то разность интегралов по этим путям может быть сведена к сумме интегралов по двум или большему числу замкнутых контуров.
В частности, интеграл в правой части формулы (3) при зафиксированной точке  будет представлять собой однозначную функцию от х и у, и, значит, формула (3) определит однозначную функцию
будет представлять собой однозначную функцию от х и у, и, значит, формула (3) определит однозначную функцию  если придать С произвольное (постоянное) значение. Легко, далее, проверить, что мы действительно будем иметь равенства (2).
если придать С произвольное (постоянное) значение. Легко, далее, проверить, что мы действительно будем иметь равенства (2).
В самом деле, продолжив путь интегрирования в формуле (3) прямолинейным отрезком  параллельным
параллельным  до точки
до точки  будем, очевидно, иметь:
будем, очевидно, иметь:

откуда следует

т. е. первое из равенств (2); таким же образом доказывается и второе.
Мы видим, таким образом, что условие (5) необходимо и достаточно для существования однозначной функции  удовлетворяющей условию (2) или условиям (2). При соблюдении этого условия функция
удовлетворяющей условию (2) или условиям (2). При соблюдении этого условия функция  определяется формулой (3) с точностью до постоянной С, которая совершенно произвольна.
определяется формулой (3) с точностью до постоянной С, которая совершенно произвольна.
До сих пор мы считали область  односвязной. Посмотрим теперь, какие добавления требуются в случае многосвязной области.
односвязной. Посмотрим теперь, какие добавления требуются в случае многосвязной области.
Условие (5) и здесь является необходимым: вывод ничем не отличается от вывода для случая односвязной области. Надо только при применении формулы (4) брать такие контуры  чтобы области а, ими ограничиваемые, целиком принадлежали
чтобы области а, ими ограничиваемые, целиком принадлежали  (в случае односвязной области это выполняется само собой). Выясним теперь вопрос о достаточности этого условия. Мы покажем, что и в нашем случае условие это обеспечивает
(в случае односвязной области это выполняется само собой). Выясним теперь вопрос о достаточности этого условия. Мы покажем, что и в нашем случае условие это обеспечивает
существование функции  определяемой формулой (3), но что функция эта будет, вообще говоря, многозначной.
определяемой формулой (3), но что функция эта будет, вообще говоря, многозначной.
Начнем со следующего замечания. Разрежем область  купюрами
купюрами

как было указано в предыдущем пункте, и полученную таким образом односвязную область обозначим через 
Мы должны представлять себе, что вдоль каждой линии  соприкасаются два края разрезанной области, так что каждая точка этой линии должна считаться за две, одна из которых принадлежит одному, а другая — другому краю. В соответствии с этим на каждом разрезе мы будем различать два края, которые условно будем обозначать знаками
соприкасаются два края разрезанной области, так что каждая точка этой линии должна считаться за две, одна из которых принадлежит одному, а другая — другому краю. В соответствии с этим на каждом разрезе мы будем различать два края, которые условно будем обозначать знаками 
Так как область  односвязна, то функция
односвязна, то функция  определенная формулой (3), где путь интегрирования не должен выходить из
определенная формулой (3), где путь интегрирования не должен выходить из  т. е. не должен пересекать купюр, будет на основании сказанного выше однозначна в
т. е. не должен пересекать купюр, будет на основании сказанного выше однозначна в 
Это, однако, не значит, что в точках, принадлежащих различным краям одной и той же купюры, значения функции F будут одинаковы (ибо эти точки должны считаться различными точками области  Возьмем, например, какую-либо точку А на купюре
Возьмем, например, какую-либо точку А на купюре  и обозначим через.
и обозначим через.  значения функции F в точках
значения функции F в точках  краев (+) и (-), совмещенных в геометрической точке А. Имеем по формуле (3):
краев (+) и (-), совмещенных в геометрической точке А. Имеем по формуле (3):

где первый интеграл взят по любой линии  находящейся в
находящейся в  и идущей из
и идущей из  к точке А, подходя к ней со стороны (—); второй же интеграл взят по пути
к точке А, подходя к ней со стороны (—); второй же интеграл взят по пути  также выходящему из
также выходящему из  но подходящему к А со стороны (+) (рис. 73; на нем не изображены точка
но подходящему к А со стороны (+) (рис. 73; на нем не изображены точка  и упомянутые пути интегрирования). В качестве пути интегрирования для второго интеграла мы можем взять путь интегрирования
и упомянутые пути интегрирования). В качестве пути интегрирования для второго интеграла мы можем взять путь интегрирования  первого интеграла, дополнив его линией
первого интеграла, дополнив его линией  один раз окружающей контур
один раз окружающей контур  и ведущей от края (-) к краю (+), не выходя из разрезанной области
и ведущей от края (-) к краю (+), не выходя из разрезанной области  Таким образом, будем иметь:
Таким образом, будем иметь:

где определяется формулой

причем  есть простой замкнутый контур, ведущий по области
есть простой замкнутый контур, ведущий по области  от края (-) к краю (+) купюры
от края (-) к краю (+) купюры  и не пересекающий других купюр (рис. 73). Этот контур пересекает купюру
и не пересекающий других купюр (рис. 73). Этот контур пересекает купюру  переходя со стороны (+) на сторону
переходя со стороны (+) на сторону 
Легко видеть, что  не зависит от выбора контура
не зависит от выбора контура  лишь бы он один раз окружал контур
лишь бы он один раз окружал контур  идя по
идя по  от края (-) к краю (+) купюры
от края (-) к краю (+) купюры  Действительно, пусть
Действительно, пусть  есть другой такой контур, пересекающий в некоторой точке В. Рассмотрим замкнутый контур, не выходящий
есть другой такой контур, пересекающий в некоторой точке В. Рассмотрим замкнутый контур, не выходящий  составленный из отрезка
составленный из отрезка  положительного края купюры, пути
положительного края купюры, пути  пройденного в отрицательном направлении далее из отрезка
пройденного в отрицательном направлении далее из отрезка  отрицательного края купюры и, наконец, контура
отрицательного края купюры и, наконец, контура 
Имеем:

где интеграл взят по только что указанному замкнутому контуру. Так как, далее, интегралы по  и
и  взаимно уничтожаются, то остается:
взаимно уничтожаются, то остается:

а это и доказывает наше утверждение [перед первым интегралом мы взяли знак (-), считая, что обозначает контур, пройденный в положительном направлении].
Совершенно аналогично получим для любой купюры  что
что

где

 любой замкнутый контур, окружающий
любой замкнутый контур, окружающий  пересекающий только одну купюру
пересекающий только одну купюру  переходя со стороны (+) на сторону
переходя со стороны (+) на сторону 
Интеграл в формуле (6) может, в частности, быть взят по самой границе  если функции
если функции  непрерывны вплоть до границы.
непрерывны вплоть до границы.
Легко теперь выяснить, какую функцию  определяет формула (3), если рассматривать неразрезанную область, т. е. если допустить, что путь интегрирования может пересекать купюры.
определяет формула (3), если рассматривать неразрезанную область, т. е. если допустить, что путь интегрирования может пересекать купюры.
Обозначим через  то значение, которое дает формула (3) в разрезанной области, т. е. когда путь интегрирования не пересекает купюр.
то значение, которое дает формула (3) в разрезанной области, т. е. когда путь интегрирования не пересекает купюр.
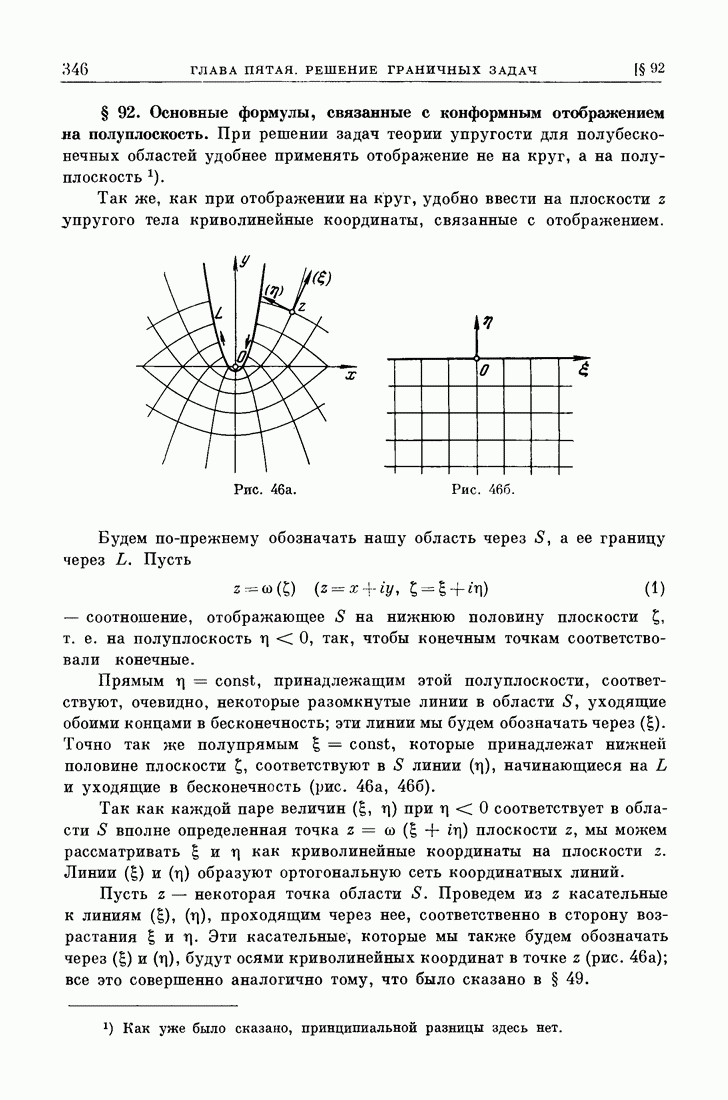
Рассмотрим теперь произвольный путь интегрирования  (рис. 75); пусть он пересекает купюры несколько, скажем
(рис. 75); пусть он пересекает купюры несколько, скажем  раз. Будем следовать из точки
раз. Будем следовать из точки  по пути интегрирования до первой встречи с одной из купюр
по пути интегрирования до первой встречи с одной из купюр  На части пути интегрирования после перехода через эту купюру, но до следующей встречи с какой-либо из купюр, возьмем две последовательные точки
На части пути интегрирования после перехода через эту купюру, но до следующей встречи с какой-либо из купюр, возьмем две последовательные точки  я заменим участок
я заменим участок  пути линией
пути линией  идущей из
идущей из  и возвращающейся в В, не пересекая ни одной из купюр. Это, конечно, не изменит значения интеграла (ибо при замене мы оставались
и возвращающейся в В, не пересекая ни одной из купюр. Это, конечно, не изменит значения интеграла (ибо при замене мы оставались
в разрезанной области). Первоначальный путь от  до
до  оказывается замененным замкнутым контуром
оказывается замененным замкнутым контуром  один раз охватывающим контур
один раз охватывающим контур  и путем
и путем  который пересекает купюры уже не
который пересекает купюры уже не  раз.
раз.
Интеграл, взятый по замкнутому контуру  равен на основании формулы
равен на основании формулы  или —
или —  в зависимости от того, пересекает ли путь интегрирования купюру
в зависимости от того, пересекает ли путь интегрирования купюру  переходя от края (+) к краю (-), или наоборот. Таким образом, мы можем выбросить из (видоизмененного) пути интегрирования замкнутую часть
переходя от края (+) к краю (-), или наоборот. Таким образом, мы можем выбросить из (видоизмененного) пути интегрирования замкнутую часть  при условии, что к окончательному результату прибавляется
при условии, что к окончательному результату прибавляется 

Рис. 75.
Продолжая действовать таким образом, мы можем свести путь интегрирования к пути, не пересекающему ни одной купюры. К интегралу, взятому по этому пути, надо будет добавить величины  каждую на них следует добавить столько раз, сколько раз первоначальный путь интегрирования пересекает соответствующую купюру; знак (+) надо брать в случае пересечения от стороны (+) к стороне (—); знак же (-) следует брать в противном случае.
каждую на них следует добавить столько раз, сколько раз первоначальный путь интегрирования пересекает соответствующую купюру; знак (+) надо брать в случае пересечения от стороны (+) к стороне (—); знак же (-) следует брать в противном случае.
Так как путь интегрирования, не пересекающий купюр, дает значение  то мы будем иметь окончательный результат в следующем виде:
то мы будем иметь окончательный результат в следующем виде:

где  целые числа (положительные или отрицательные), которые легко подсчитываются на основании сказанного выше по числу пересечений пути
целые числа (положительные или отрицательные), которые легко подсчитываются на основании сказанного выше по числу пересечений пути  с купюрами (при этом следует принимать во внимание направление пересечения). Например, в случае рис. 75
с купюрами (при этом следует принимать во внимание направление пересечения). Например, в случае рис. 75

Для того чтобы функция  была однозначной, необходимо и достаточно, чтобы наряду с условием (5) было соблюдено условие
была однозначной, необходимо и достаточно, чтобы наряду с условием (5) было соблюдено условие

Все сказанное выше можно применить и к случаю, когда контур  уходит целиком в бесконечность, так что область
уходит целиком в бесконечность, так что область  превращается в бесконечную плоскость с отверстиями.
превращается в бесконечную плоскость с отверстиями.
3. В случае трех измерений имеем совершенно аналогичные результаты. И здесь следует различать односвязные и многосвязные трехмерные области (тела). Односвязной называется область, обладающая тем свойством, что всякая замкнутая линия, проведенная внутри тела, может сжаться в одну точку путем непрерывной деформации,
не выходя из области (примеры: шар и куб). В противном случае область многосвязна. Примерами многосвязных областей могут служить, например, тор (т. е. тело, полученное вращением круга вокруг оси, лежащей в его плоскостии не пересекающей его) или куб, имеющий одно или несколько сквозных отверстий, и т. п.
Тор есть тело двусвязное, ибо его можно сделать односвязным путем проведения одного разреза (перегородки); здесь уже, в противоположность случаю двух измерений, разрез будет не линией, а поверхностью.
Вообще тело будет  -связным, если его можно сделать односвязным при помощи
-связным, если его можно сделать односвязным при помощи  разрезов. Обратим внимание на то, что тело, ограниченное одной замкнутой поверхностью, не обязательно односвязно (пример: тор); наоборот, тело может быть ограничено несколькими замкнутыми поверхностями, но быть односвязным (пример: область, заключенная между двумя концентрическими сферами). Пусть теперь дано дифференциальное выражение
разрезов. Обратим внимание на то, что тело, ограниченное одной замкнутой поверхностью, не обязательно односвязно (пример: тор); наоборот, тело может быть ограничено несколькими замкнутыми поверхностями, но быть односвязным (пример: область, заключенная между двумя концентрическими сферами). Пусть теперь дано дифференциальное выражение

где  однозначные и непрерывные функции, имеющие непрерывные первые производные в некоторой односвязной области
однозначные и непрерывные функции, имеющие непрерывные первые производные в некоторой односвязной области 
Совершенно аналогично сказанному в предыдущем пункте, можем показать, что для существования однозначной функции  удовлетворяющей условию
удовлетворяющей условию

необходимо и достаточно, чтобы

где  любой замкнутый контур в области
любой замкнутый контур в области 
При этом условии функция F определится формулой

где С — произвольная постоянная, а интеграл взят по любому пути (находящемуся в V), соединяющему постоянную точку  с переменной точкой
с переменной точкой  .
.
Преобразуем условие (3). Для этого вспомним известную формулу Стокса:

где  любая (разомкнутая) поверхность (не выходящая из
любая (разомкнутая) поверхность (не выходящая из  имеющая своей границей контур
имеющая своей границей контур  нормаль к этой поверхности а,
нормаль к этой поверхности а,
проведенная в определенную сторону. В силу этой формулы условие (3) примет вид

причем оно должно быть соблюдено для любой поверхности а (находящейся внутри  Взяв в качестве а какую-либо площадку, нормальную к оси
Взяв в качестве а какую-либо площадку, нормальную к оси  получим, в частности:
получим, в частности:

откуда выводим (ввиду произвольности площадки а) первую из следующих формул:

(две последние формулы выводятся круговой перестановкой).
Обратно, условия (7) являются, очевидно, достаточными для наличия условия (3) и, значит, для существования однозначной функции  определяемой формулой (3).
определяемой формулой (3).
В случае многосвязной области при наличии условий (7) функция F (х, у, z), определяемая равенством (4), может оказаться многозначной. Именно, рассуждениями, совершенно аналогичными рассуждениям предыдущего пункта (читатель легко воспроизведет их сам), можно установить следующее. Если мысленно провести  разрезов (перегородок) так, чтобы обратить данную
разрезов (перегородок) так, чтобы обратить данную  -связную область в односвязную, а через
-связную область в односвязную, а через  (х, у, z) обозначить функцию, определяемую формулой (4), при условии, что путь интегрирования не пересекает перегородок, то при произвольном пути интегрирования будем иметь:
(х, у, z) обозначить функцию, определяемую формулой (4), при условии, что путь интегрирования не пересекает перегородок, то при произвольном пути интегрирования будем иметь:

где  целые числа,
целые числа,  постоянные, представляющие собой интегралы по замкнутым путям. А именно:
постоянные, представляющие собой интегралы по замкнутым путям. А именно:

где  простой замкнутый контур, который пересекает только перегородку с номером к, переходя от стороны (+) к стороне (-). Целые числа
простой замкнутый контур, который пересекает только перегородку с номером к, переходя от стороны (+) к стороне (-). Целые числа  определяются по такому же правилу, как в предыдущем параграфе.
определяются по такому же правилу, как в предыдущем параграфе.
Для того чтобы функция F была однозначна, необходимо и достаточно, чтобы наряду с условиями (7) были соблюдены условия:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
- VI. ТЕОРИЯ ТРЕЩИН
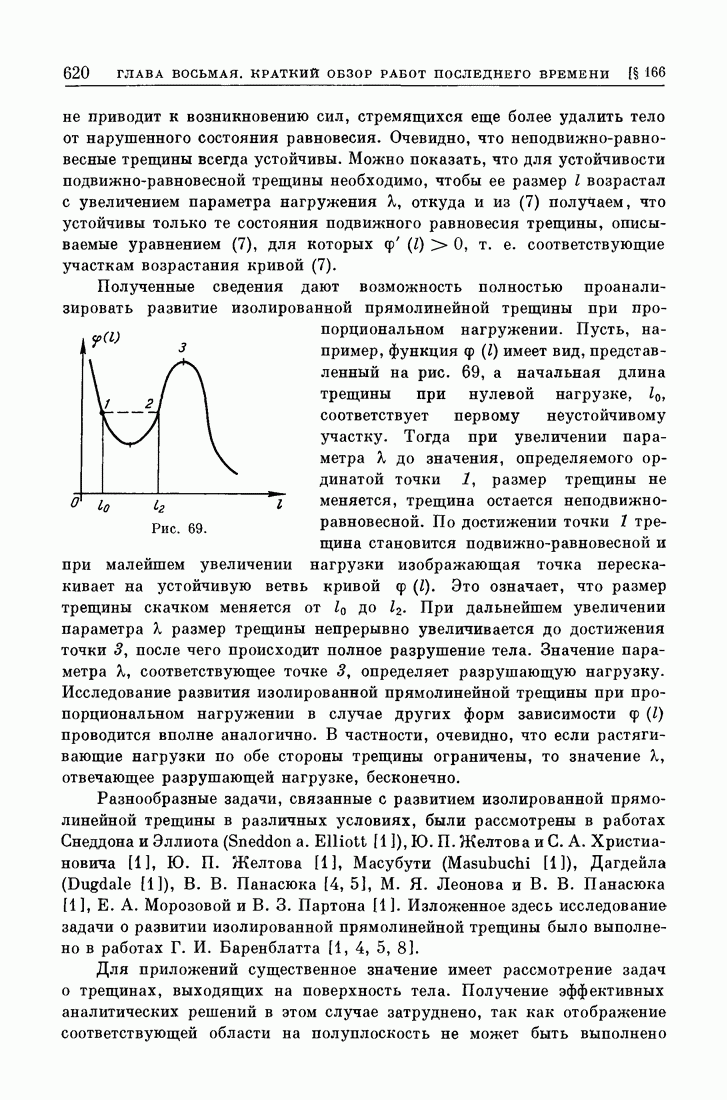
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ