| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
VI. ТЕОРИЯ ТРЕЩИН
В последние годы значительное внимание привлекли к себе задачи теории трещин, связанные с математической теорией хрупкого разрушения. Теория хрупкого разрушения, предполагающая, что тело сохраняет свойство линейной упругости (т. е. подчиняется обобщенному закону Гука) вплоть до разрушения, берет свое начало от работ Гриффитса (Griffith [1, 2]). Длительное время считалось, что область применимости этой теории ограничена немногими материалами типа стекла вследствие наличия в разрушающихся телах значительных областей пластических деформаций. Интенсивное развитие теории хрупкого разрушения началось после работ Ирвина (Irwin [1]) и Орована (Orowan [1]), показавших, что в большом числе практически важных случаев разрушение происходит квазихрупким образом, т. е. так, что пластическая область хотя и существует, но имеет очень малые размеры и сосредоточивается в непосредственной близости поверхности трещин. Эта важная идея открыла возможность применять теорию хрупкого разрушения во многих практических задачах.
Методы, развитые в настоящей книге, находят широкое применение в теории хрупкого разрушения. Изложение теории трещин, как и во всей этой главе, ведется, в основном, именно с точки зрения методов настоящей книги, поэтому в ряде случаев результаты различных авторов излагаются иначе, чем они были первоначально получены.
§ 165. Постановка задач. Основные представления.
Трещины математически рассматриваются как поверхности разрыва смещений в недеформированном теле, ограниченные некоторой гладкой линией — контуром трещины. Для простоты ограничимся здесь изложением теории трещин нормального разрыва, когда претерпевает разрыв только
нормальнормальная компонента смещения; теория непосредственно распространяется на общий случай.
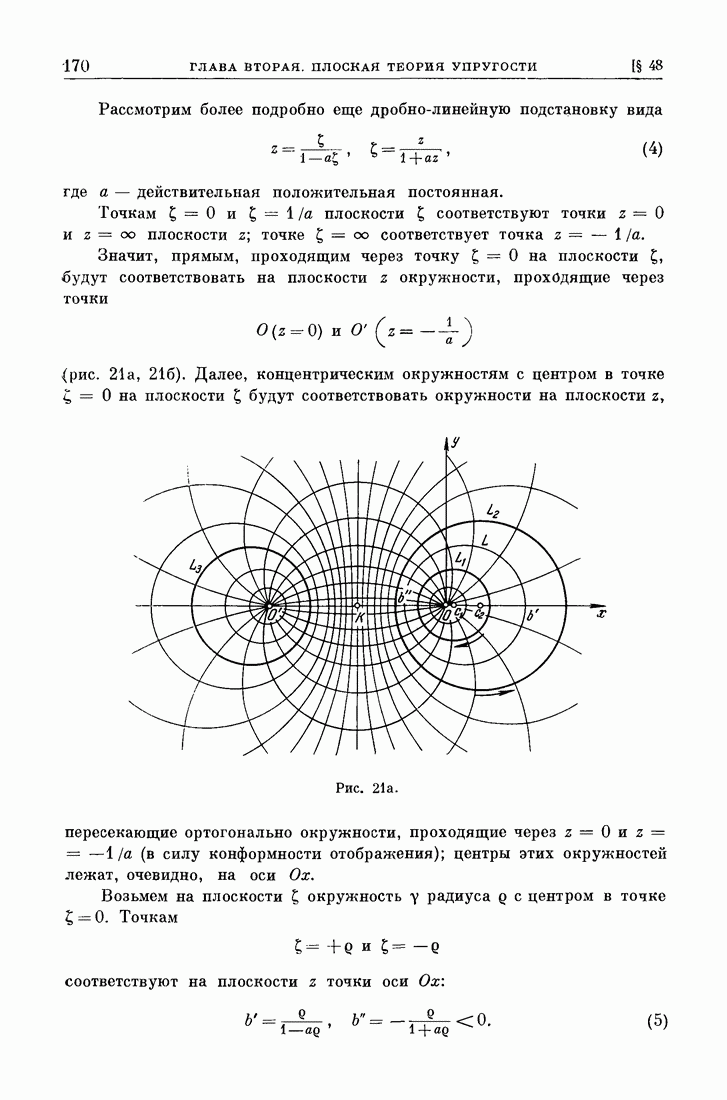
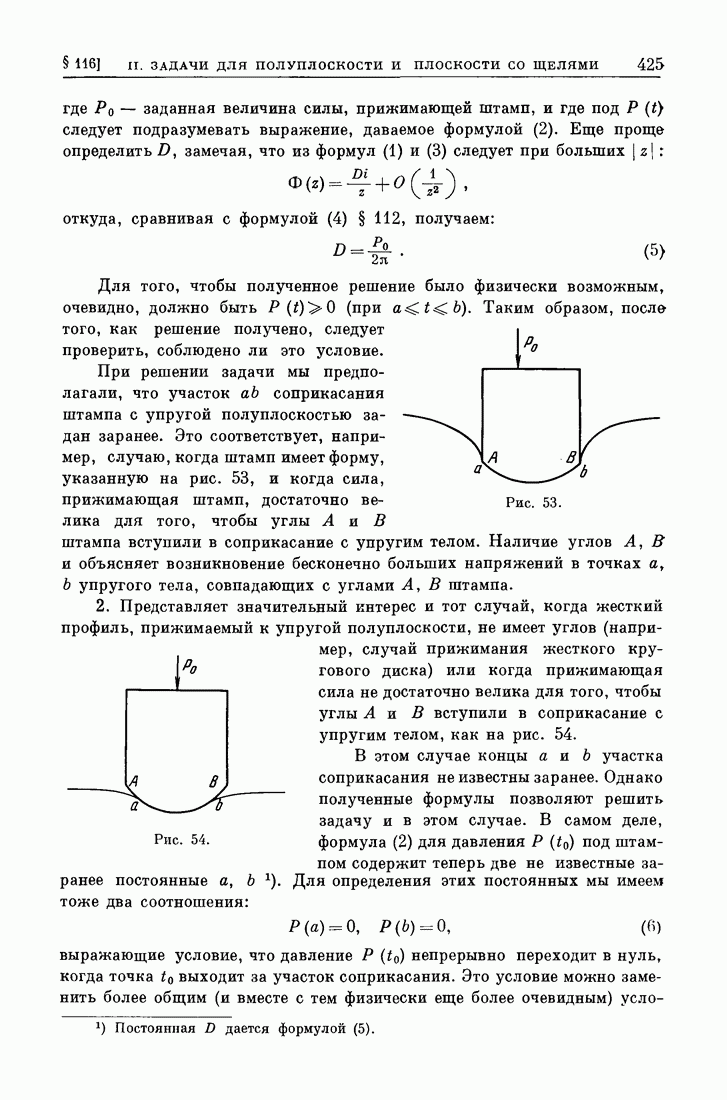
Возьмем вблизи произвольной точки О гладкого контура поверхности разрыва нормальных смещений окрестность, характерный размер которой мал сравнительно с радиусом кривизны контура в точке О. Деформацию в этой окрестности можно считать плоской и соответствующей прямолинейному бесконечному разрезу в бесконечном теле под действием некоторой системы симметричных относительно поверхности разреза нагрузок (рис. 64). Нагрузки могут быть приложены на поверхности разреза и внутри тела; нагрузки, приложенные на поверхности разреза, не уменьшая общности, можно считать нормальными.

Рис. 64.
Поле упругих элементов можно представить в виде суммы двух полей (рис. 64), первое из которых соответствует сплошному телу под действием нагрузок, приложенных внутри тела, а второе — телу с разрезом под действием симметричных нагрузок, приложенных только на поверхности разреза. Форма деформированной поверхности разреза определяется только вторым напряженным состоянием, так как нормальные смещения на месте разреза для первого напряженного состояния равны по симметрии нулю. Этот прием приведения нагрузки к распределенной по поверхности разрыва обоснован в наиболее общем виде Бюкнером (Bueckner [1]). Анализ первого напряженного состояния выполняется обычными методами; его можно считать известным.
Примем, что линия разреза (сечение поверхности разреза) соответствует положительной полуоси  нормальные напряжения
нормальные напряжения  приложенные на линии разреза во втором напряженном состоянии, представляют собой разность напряжений, приложенных на поверхности разреза в суммарном поле
приложенные на линии разреза во втором напряженном состоянии, представляют собой разность напряжений, приложенных на поверхности разреза в суммарном поле  и напряжений на месте разреза, соответствующих первому напряженному состоянию.
и напряжений на месте разреза, соответствующих первому напряженному состоянию.
Для определения второго напряженного состояния воспользуемся методом § 120. Имеем в силу формул (8) § 32 и формул (7) и (9) § 120:

(индексом 2 отмечены величины, относящиеся ко второму напряженному состоянию). В силу формул (20)-(22) § 120, без труда распространяемых на случай полубесконечного разреза, имеем:

На разрезе  и его продолжении
и его продолжении  выполняются соотношения
выполняются соотношения

Отсюда и из формул, описывающих поведение интеграла типа Коши вблизи концов линии интегрирования (Мусхелишвили [25]), получается выражение для растягивающих нормальных напряжений вблизи конца разреза на его продолжении

 малое расстояние рассматриваемой точки от конца разреза). Для распределения нормальных смещений точек линии разреза вблизи его конца получаем:
малое расстояние рассматриваемой точки от конца разреза). Для распределения нормальных смещений точек линии разреза вблизи его конца получаем:

 малое расстояние рассматриваемой точки линии разреза от его конца; знаки плюс и минус отвечают соответственно верхнему и нижнему берегам разреза).
малое расстояние рассматриваемой точки линии разреза от его конца; знаки плюс и минус отвечают соответственно верхнему и нижнему берегам разреза).
Из соотношений (7) и (8) непосредственно вытекают формулы для характеристик суммарного напряженного состояния вблизи контура произвольной поверхности нормального разрыва:

где  - «коэффициент интенсивности напряжений», т. е. величина, зависящая от действующих нагрузок, конфигурации тела и поверхностей разрыва в нем, а также от координат рассматриваемой точки О. В зависимости от знака
- «коэффициент интенсивности напряжений», т. е. величина, зависящая от действующих нагрузок, конфигурации тела и поверхностей разрыва в нем, а также от координат рассматриваемой точки О. В зависимости от знака  могут, вообще говоря, встретиться три возможности.
могут, вообще говоря, встретиться три возможности.
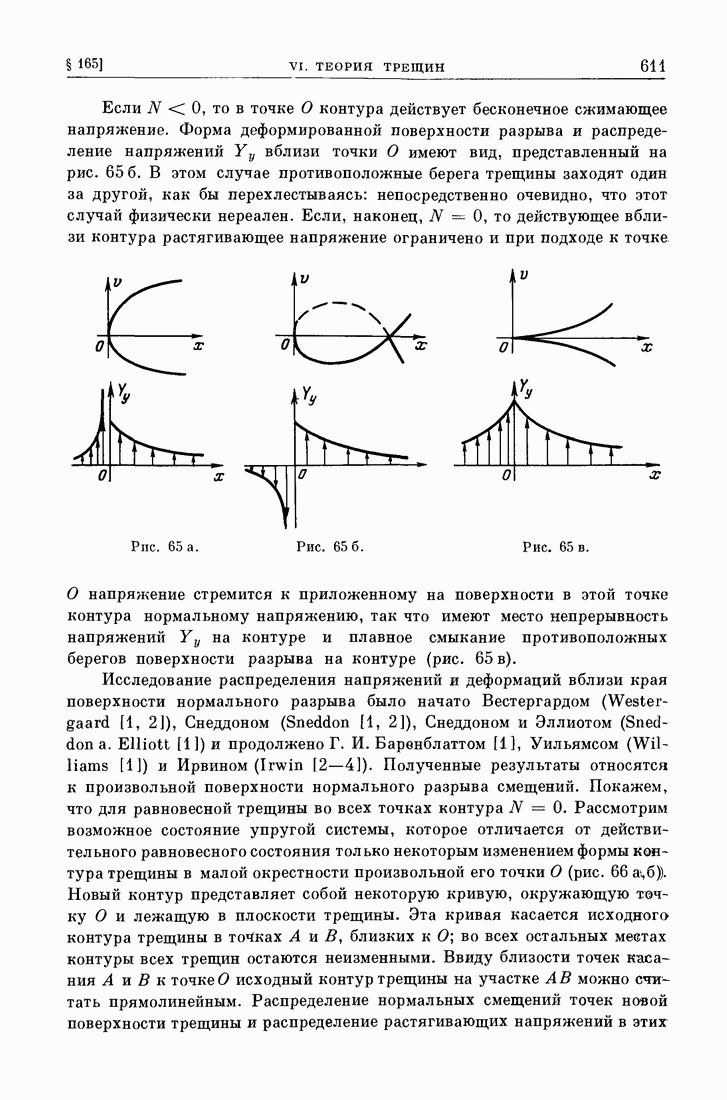
Если  то в точке О контура поверхности разрыва действует бесконечное растягивающее напряжение. Форма деформированной поверхности разрыва и распределение нормальных напряжений
то в точке О контура поверхности разрыва действует бесконечное растягивающее напряжение. Форма деформированной поверхности разрыва и распределение нормальных напряжений  вблизи точки О имеют вид, представленный на рис. 65 а.
вблизи точки О имеют вид, представленный на рис. 65 а.
Если  то в точке О контура действует бесконечное сжимающее напряжение. Форма деформированной поверхности разрыва и распределение напряжений
то в точке О контура действует бесконечное сжимающее напряжение. Форма деформированной поверхности разрыва и распределение напряжений  вблизи точки О имеют вид, представленный на рис. 65 б. В этом случае противоположные берега трещины заходят один за другой, как бы перехлестываясь: непосредственно очевидно, что этот случай физически нереален. Если, наконец,
вблизи точки О имеют вид, представленный на рис. 65 б. В этом случае противоположные берега трещины заходят один за другой, как бы перехлестываясь: непосредственно очевидно, что этот случай физически нереален. Если, наконец,  то действующее вблизи контура растягивающее напряжение ограничено и при подходе к точке
то действующее вблизи контура растягивающее напряжение ограничено и при подходе к точке

Рис. 65.а

Рис. 65 6.

Рис. 65 в.
О напряжение стремится к приложенному на поверхности в этой точке контура нормальному напряжению, так что имеют место непрерывность напряжений  на контуре и плавное смыкание противоположных берегов поверхности разрыва на контуре (рис. 65 в).
на контуре и плавное смыкание противоположных берегов поверхности разрыва на контуре (рис. 65 в).
Исследование распределения напряжений и деформаций вблизи края поверхности нормального разрыва было начато Вестергардом (Westergaard [1, 2]), Снеддоном (Sneddon [1, 2]), Снеддоном и Эллиотом (Sneddon а. Elliott [1]) и продолжено Г. И. Баренблаттом [1], Уильямсом (Williams [1]) и Ирвином (Irwin [2-4]). Полученные результаты относятся к произвольной поверхности нормального разрыва смещений. Покажем, что для равновесной трещины во всех точках контура  Рассмотрим возможное состояние упругой системы, которое отличается от действительного равновесного состояния только некоторым изменением формы контура трещины в малой окрестности произвольной его точки О (рис.
Рассмотрим возможное состояние упругой системы, которое отличается от действительного равновесного состояния только некоторым изменением формы контура трещины в малой окрестности произвольной его точки О (рис.  Новый контур представляет собой некоторую кривую, окружающую точку О и лежащую в плоскости трещины. Эта кривая касается исходного контура трещины в точках
Новый контур представляет собой некоторую кривую, окружающую точку О и лежащую в плоскости трещины. Эта кривая касается исходного контура трещины в точках  близких к
близких к  во всех остальных местах контуры всех трещин остаются неизменными. Ввиду близости точек касания
во всех остальных местах контуры всех трещин остаются неизменными. Ввиду близости точек касания  к точке О исходный контур трещины на участке А В можно считать прямолинейным. Распределение нормальных смещений точек новой поверхности трещины и распределение растягивающих напряжений в этих
к точке О исходный контур трещины на участке А В можно считать прямолинейным. Распределение нормальных смещений точек новой поверхности трещины и распределение растягивающих напряжений в этих
точках до образования новой поверхности трещины имеют, согласно предыдущему, с точностью до малых величин вид

где  коэффициент интенсивности напряжений в точке О.
коэффициент интенсивности напряжений в точке О.
Энергия  освободившаяся при образовании новой поверхности трещины и равная работе, потребной для закрытия этой новой поверхности, составляет
освободившаяся при образовании новой поверхности трещины и равная работе, потребной для закрытия этой новой поверхности, составляет

где  величина площади новой поверхности трещины.
величина площади новой поверхности трещины.
Равновесная трещина отличается от произвольной поверхности нормального разрыва именно тем, что освободившаяся энергия  обращается в нуль. Отсюда и из
обращается в нуль. Отсюда и из  следует:
следует:

Таким образом, справедливо важное утверждение, характеризующее структуру равновесной трещины вблизи ее контура:
1. Растягивающее напряжение на контуре трещины конечно.
2. Противоположные берега трещины плавно смыкаются на ее контуре. В гипотетической форме условие конечности напряжений и плавности смыкания противоположных берегов на краях трещины было впервые предложено С. А. Христиановичем (Желтов и Христианович [1], Баренблатт и Христианович [1]).

Рис. 66 а.

Рис. 66 б.
Приведенное выше доказательство этого условия дано в работе Г. И. Баренблатта [2]. Формула (11) для случая плоской деформации вне связи с конечностью напряжений и плавностью смыкания на краю трещины была указана в работах Ирвина (Irwin [2-4]).
Условие С. А. Христиановича (12) позволяет при заданной системе сил, действующих на тело, сформулировать задачу теории равновесных трещин. В рамках плоской задачи и для простейшего случая, когда симметрия тела и приложенных нагрузок обеспечивает развитие
прямолинейных трещин, эта задача ставится следующим образом. Для данного расположения начальных трещин и данной системы сил, действующих на тело, требуется найти напряжения, деформации и координаты концов трещин так, чтобы удовлетворить дифференциальным уравнениям равновесия, граничным условиям и обеспечить конечность напряжений и плавное смыкание противоположных берегов на краях трещин.

Рис. 67.
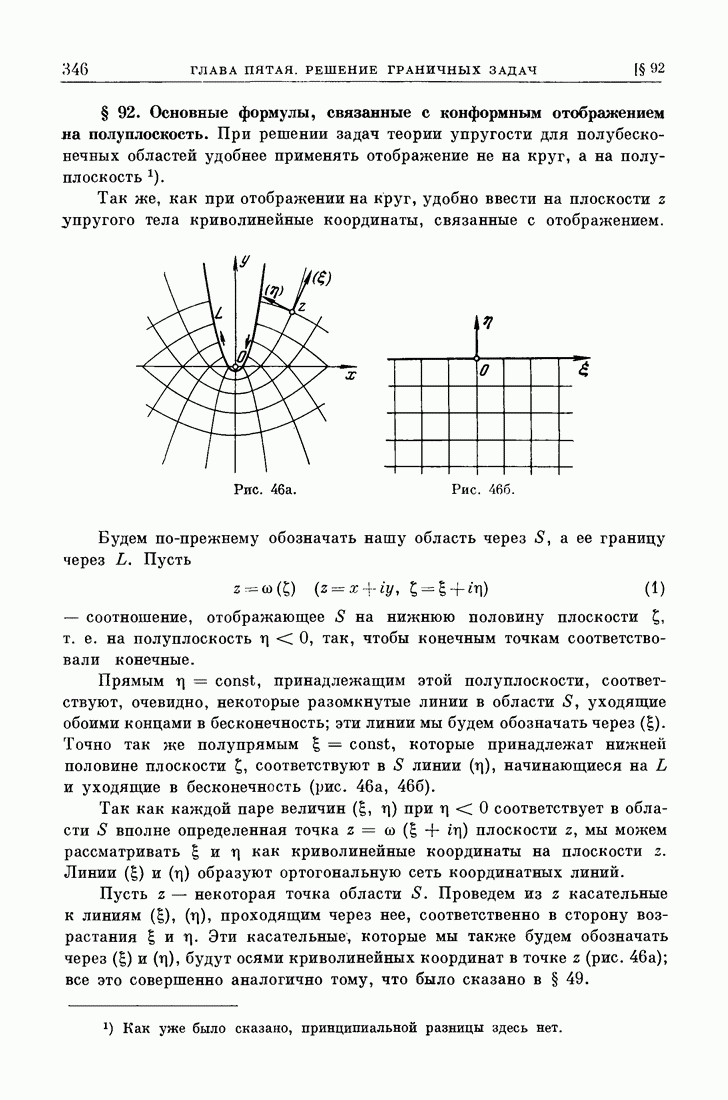
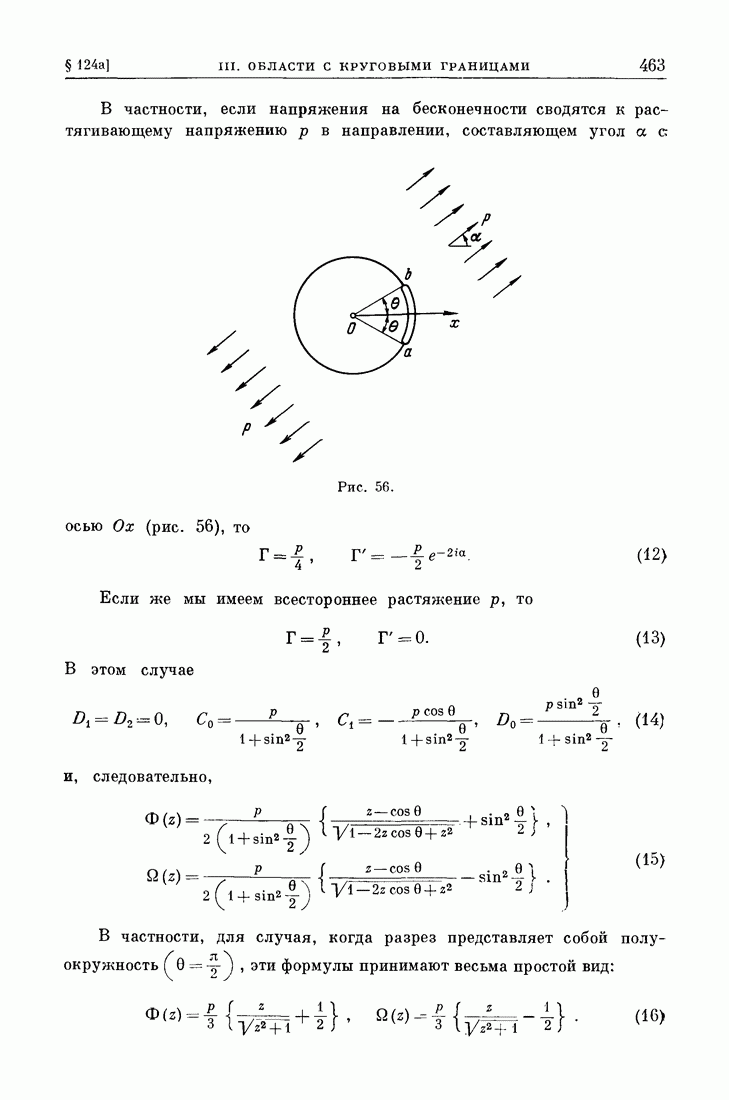
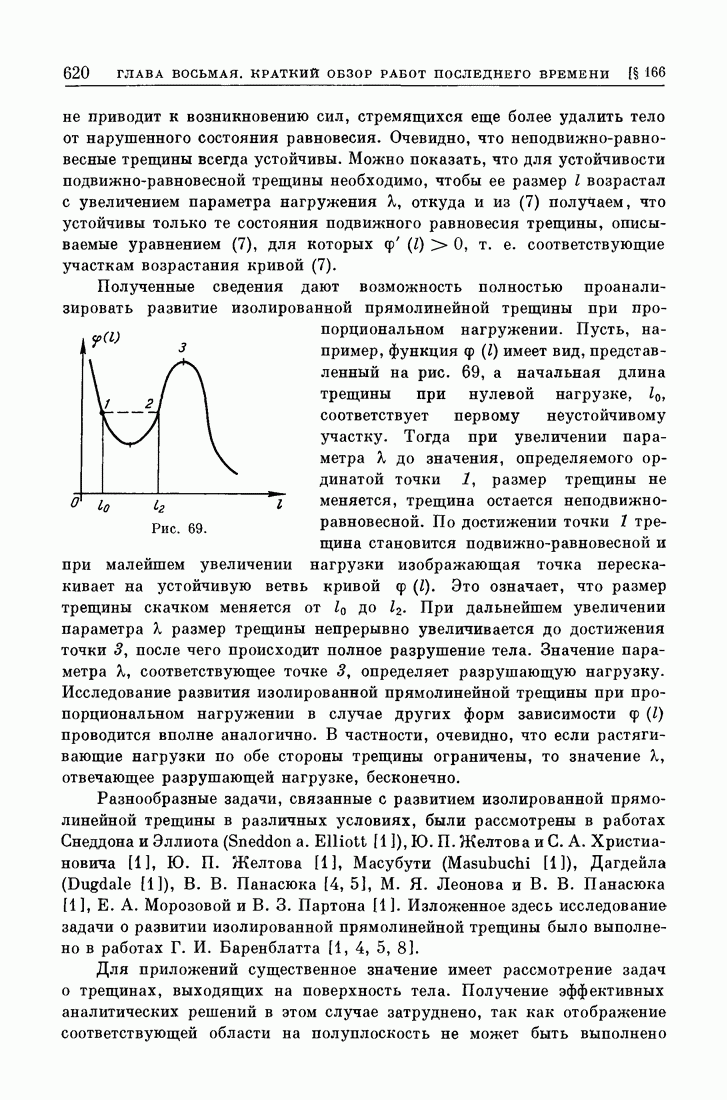
Разберем решение этой задачи на примере изолированной прямолинейной трещины в бесконечном упругом теле, сжатом на бесконечности всесторонним напряжением  Трещина поддерживается в раскрытом состоянии сосредоточенными силами
Трещина поддерживается в раскрытом состоянии сосредоточенными силами  приложенными в противоположных точках ее поверхности (рис. 67). Используя результаты § 82а, можно получить решение уравнений равновесия, удовлетворяющее граничным условиям, при произвольной длине трещины 21. Напряжения и смещения при этом выражаются формулами (1) и (8) § 32, причем
приложенными в противоположных точках ее поверхности (рис. 67). Используя результаты § 82а, можно получить решение уравнений равновесия, удовлетворяющее граничным условиям, при произвольной длине трещины 21. Напряжения и смещения при этом выражаются формулами (1) и (8) § 32, причем

Уравнения равновесия и граничные условия не определяют длины трещины 21. Распределения напряжений  на продолжении трещины и нормальных смещений
на продолжении трещины и нормальных смещений  точек линии трещины вблизи ее конца представляются в виде
точек линии трещины вблизи ее конца представляются в виде

Конечность напряжений и плавность смыкания берегов трещины на ее концах одновременно обеспечиваются при условии

которое и определяет размер трещины при данных нагрузках 
Попытаемся теперь определить размер 21 изолированной прямолинейной трещины в бесконечном теле, растягиваемом на бесконечности однородным напряжением  в направлении, перпендикулярном трещине. Если считать, что концы трещины свободны от напряжений, то из результатов п. 1 § 82а вытекает, что растягивающее напряжение на продолжении трещины вблизи ее конца зависит от расстояния от конца следующим
в направлении, перпендикулярном трещине. Если считать, что концы трещины свободны от напряжений, то из результатов п. 1 § 82а вытекает, что растягивающее напряжение на продолжении трещины вблизи ее конца зависит от расстояния от конца следующим
образом:

Отсюда получается, что ни при каком I напряжение  в конце трещины не будет конечным и равновесной трещины не существует. Этот парадоксальный результат объясняется тем, что из-за предположения о том, что поверхность трещины свободна от напряжений, здесь не приняты во внимание силы сцепления, действующие вблизи концов трещины на ее поверхности, и, таким образом, неполностью отражены нагрузки, действующие на тело.
в конце трещины не будет конечным и равновесной трещины не существует. Этот парадоксальный результат объясняется тем, что из-за предположения о том, что поверхность трещины свободна от напряжений, здесь не приняты во внимание силы сцепления, действующие вблизи концов трещины на ее поверхности, и, таким образом, неполностью отражены нагрузки, действующие на тело.
Итак, для построения адекватной теории трещин хрупкого разрушения необходимо дополнить модель хрупкого тела сравнительно с классической моделью упругого тела путем учета сил сцепления, действующих вблизи края трещины на ее поверхности. Известно, что интенсивность сил сцепления, действующих между двумя телами, существенно зависит от расстояния между этими телами, сначала возрастая с увеличением расстояния до некоторой весьма значительной максимальной величины и затем быстро убывая. В настоящее время не существует достоверных данных, позволяющих определить зависимость сил сцепления от расстояния и тем более распределение сил сцепления по поверхности трещины. Тем не менее имеющиеся сведения о силах сцепления дают возможность сформулировать весьма общие предположения, позволяющие существенно упростить анализ и, в конечном счете, вообще исключить силы сцепления из рассмотрения.

Рис. 68.
Поверхность трещины естественно разделить на две части (рис. 68). В первой части — внутренней области трещины — противоположные берега трещины далеко отстоят один от другого, так что их взаимодействие пренебрежимо мало и поверхность трещины можно считать свободной от напряжений, обусловленных взаимодействием противоположных берегов. Во второй части, прилегающей к контуру трещины, — концевой области трещины — противоположные берега трещины, близко подходят один к другому, так что действующие на этой части поверхности силы сцепления имеют значительную интенсивность. (Для трещин квазихрупкого разрушения за поверхность трещины следует принять границу пластической и упругой областей, так что концевая область включает в себя границу пластической головки трещины.)
Физический анализ приводит к следующим двум основным гипотезам.
Первая гипотеза. Ширина  концевой области мала сравнительно с размером всей трещины.
концевой области мала сравнительно с размером всей трещины.
Вторая гипотеза. Форма нормального сечения поверхности трещины в концевой области (и, следовательно, локальное распределение сил сцепления по поверхности трещины) не зависит от действующих нагрузок и для данного материала при данных условиях (температура, состав и давление окружающей атмосферы и т. п.) всегда одинакова. Под нормальным сечением здесь понимается сечение плоскостью, нормальной к контуру трещины. Вторая гипотеза означает, в частности, что вблизи концов форма поверхности трещин в условиях плоской задачи всегда одинакова.
Согласно второй гипотезе концевая область при расширении трещины как бы поступательно перемещается в другое место. Вторая гипотеза применима только для тех точек контура трещины, где достигается максимально возможная интенсивность сил сцепления, так что при сколь угодно малом увеличении приложенных к телу нагрузок в этой точке происходит расширение трещины.
Равновесные трещины, на контуре которых имеется хотя бы одна такая точка, естественно назвать подвижно-равновесными в отличие от неподвижно-равновесных трещин, этим свойством не обладающих и не расширяющихся при бесконечно малом увеличении нагрузки.
Приведенные выше гипотезы являются единственными предположениями, лежащими в основе теории трещин. В явной форме они были сформулированы в работах Г. И. Баренблатта [3-7].
Рассматриваемое тело, по предположению, является линейно упругим вплоть до разрушения, так что поле упругих элементов в теле с трещинами можно представить в виде суммы двух полей: поля, вычисленного без учета сил сцепления, и поля, соответствующего действию одних только сил сцепления. Поэтому величину  входящую в формулы (9) и равную, по доказанному, нулю, можно записать в виде
входящую в формулы (9) и равную, по доказанному, нулю, можно записать в виде  где
где  соответствует действующим на тело нагрузкам и той же конфигурации трещин, но без учета сил сцепления,
соответствует действующим на тело нагрузкам и той же конфигурации трещин, но без учета сил сцепления,  той же конфигурации трещин и одним только силам сцепления.
той же конфигурации трещин и одним только силам сцепления.
В силу первой гипотезы можно считать при определении  что упругое поле соответствует рассмотренной выше конфигурации бесконечного тела с полубесконечным прямолинейным разрезом, на поверхности которого приложены симметричные нормальные напряжения. Отсюда и из (7) следует, что
что упругое поле соответствует рассмотренной выше конфигурации бесконечного тела с полубесконечным прямолинейным разрезом, на поверхности которого приложены симметричные нормальные напряжения. Отсюда и из (7) следует, что

где  распределение сил сцепления, отличных от нуля только в концевой области
распределение сил сцепления, отличных от нуля только в концевой области
В силу второй гипотезы интеграл в правой части (15) представляет собой константу, являющуюся характеристикой данного материала при
данных условиях. Эта константа, обозначаемая через К:

и называемая модулем сцепления, является единственной характеристикой сил сцепления, входящей в формулировку задач о трещинах при принятых предположениях. В некоторых случаях используется другая характеристика сил сцепления: плотность поверхностной энергии — энергия, затрачиваемая на образование единицы площади новой поверхности трещины  Величины
Величины  связаны соотношением
связаны соотношением

Из формул (15) и (16) следует, что для точек контура трещины, в которых достигается максимальная интенсивность сил сцепления и, следовательно, выполняется вторая гипотеза, имеет место условие

так что растягивающее нормальное напряжение в точках тела, лежащих на продолжении трещины, вычисленное без учета сил сцепления, стремится к бесконечности по закону

где  малое расстояние до конца трещины. Выполнение условия (18) или (19) для одного из концов трещины означает достижение системой трещин в данном теле состояния подвижного равновесия. Важно отметить, что достижение трещиной состояния подвижного равновесия не следует, вообще говоря, связывать с началом неустойчивого быстрого развития трещины и тем более полным разрушением тела. Дело в том, что подвижно-равновесная трещина может быть как устойчивой, так и неустойчивой; только в случае неустойчивости подвижного равновесия условие (18) будет условием начала быстрого развития трещины.
малое расстояние до конца трещины. Выполнение условия (18) или (19) для одного из концов трещины означает достижение системой трещин в данном теле состояния подвижного равновесия. Важно отметить, что достижение трещиной состояния подвижного равновесия не следует, вообще говоря, связывать с началом неустойчивого быстрого развития трещины и тем более полным разрушением тела. Дело в том, что подвижно-равновесная трещина может быть как устойчивой, так и неустойчивой; только в случае неустойчивости подвижного равновесия условие (18) будет условием начала быстрого развития трещины.
Если на контуре трещины существуют точки, где интенсивность сил сцепления меньше максимально возможной (например, точки контуров нерасширенных надрезов или точки контуров трещин, получившихся при уменьшении нагрузки из трещин, существовавших при большей нагрузке), то в таких точках вторая гипотеза неприменима. Силы сцепления, действующие в концевой области поверхности трещины вблизи таких точек, меньше сил сцепления, действующих в концевой области вблизи точек рассмотренного выше типа. Поэтому для таких точек выполняется условие

При повышении нагрузки силы сцепления в концевой области возрастают, обеспечивая конечность напряжения и плавность смыкания на краю трещины. Однако трещина не распространяется, пока силы сцепления на данном ее конце не достигнут максимальной интенсивности, так что станет применима вторая гипотеза и будет выполняться условие (18).
Условия (18) и (20) позволяют при определении положений концов трещин вообще исключить силы сцепления из рассмотрения, ограничившись их суммарной интегральной характеристикой, модулем сцепления. Специальные оценки показывают, что влияние сил сцепления на поля напряжений и смещений существенно только в окрестности концов трещин, имеющей размер порядка ширины  концевой области. Силы сцепления определяют структуру трещин вблизи их концов и только через свою интегральную характеристику К — положение концов трещин.
концевой области. Силы сцепления определяют структуру трещин вблизи их концов и только через свою интегральную характеристику К — положение концов трещин.
Полученные условия дают возможность сформулировать основные задачи теории равновесных трещин. В общей форме основная задача теории равновесных трещин ставится следующим образом. Задается некоторая система начальных трещин в теле и процесс нагружения, т. е. система действующих на тело нагрузок, зависящая от одного монотонно возрастающего параметра  Для исходного состояния значение параметра К можно считать равным нулю. Требуется определить форму трещин, а также найти распределение напряжений и смещений в теле, соответствующее каждому
Для исходного состояния значение параметра К можно считать равным нулю. Требуется определить форму трещин, а также найти распределение напряжений и смещений в теле, соответствующее каждому  Предполагается, что изменения нагрузок достаточно медленные, так что динамические эффекты не учитываются.
Предполагается, что изменения нагрузок достаточно медленные, так что динамические эффекты не учитываются.
Решение этой задачи для общего случая криволинейных трещин весьма затруднительно. В принципе оно должно осуществляться методом последовательных шагов, причем направление развития трещины определяется условием локальной симметрии напряженного состояния вблизи конца трещины, вытекающим из второй гипотезы.
В случае, когда симметрия тела, нагрузок и начальных трещин обеспечивает возможность развития системы прямолинейных трещин и растягивающие нагрузки монотонно возрастают с увеличением X, конфигурация системы трещин в теле определяется только текущей нагрузкой, а не всей историей процесса нагружения, как в общем случае.
Задача теории трещин формулируется при этом следующим образом: в теле, ограниченном контуром 2, задана система начальных прямолинейных трещин  Требуется найти поле упругих элементов и положение системы прямолинейных трещин
Требуется найти поле упругих элементов и положение системы прямолинейных трещин  охватывающей первоначальную систему
охватывающей первоначальную систему  соответствующие данной нагрузке, т. е. данному значению
соответствующие данной нагрузке, т. е. данному значению 
Сформулированная задача математически сводится к решению системы дифференциальных уравнений равновесия теории упругости в области, ограниченной контуром 2 и прямолинейными разрезами, при граничных условиях, соответствующих данной нагрузке. При этом концы трещин
системы  должны быть определены так, чтобы в концах системы трещин
должны быть определены так, чтобы в концах системы трещин  выполнялись условия (18) или (20).
выполнялись условия (18) или (20).
Может оказаться, что решения поставленной задачи не существует. Это означает, что приложенная нагрузка превосходит разрушающую, так что при ее приложении наступает разрушение тела. Предельное значение параметра К, до достижения которого существует решение задачи, соответствует разрушающей нагрузке.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
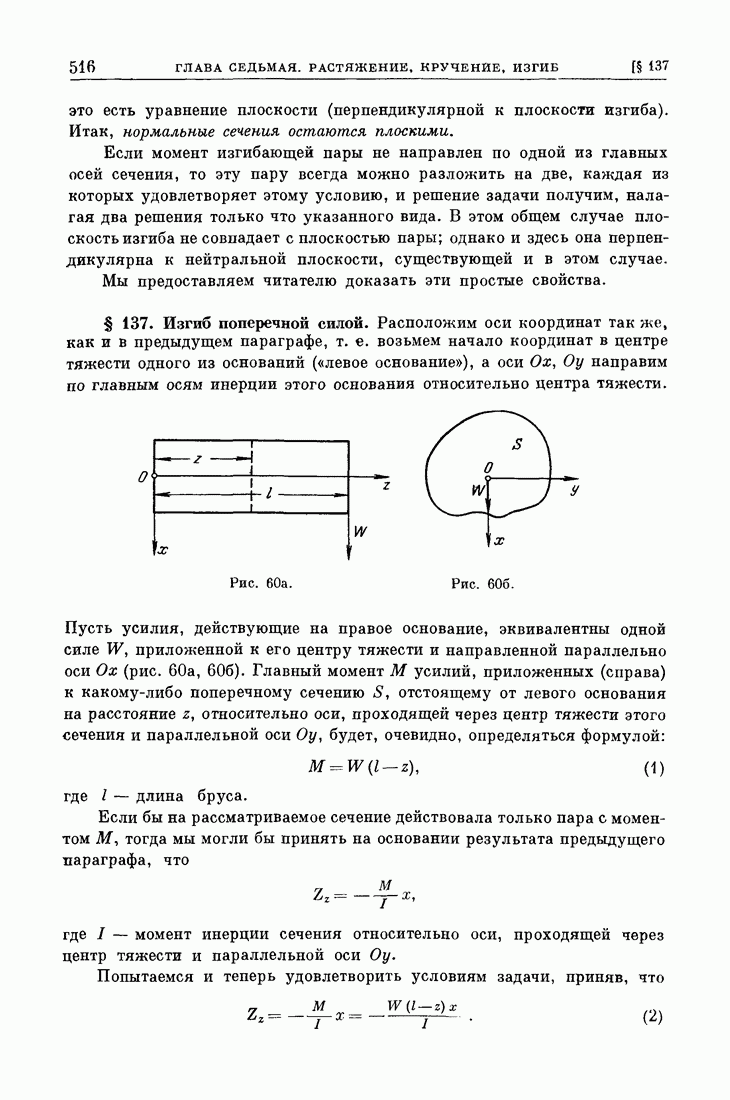
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
- VI. ТЕОРИЯ ТРЕЩИН
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ