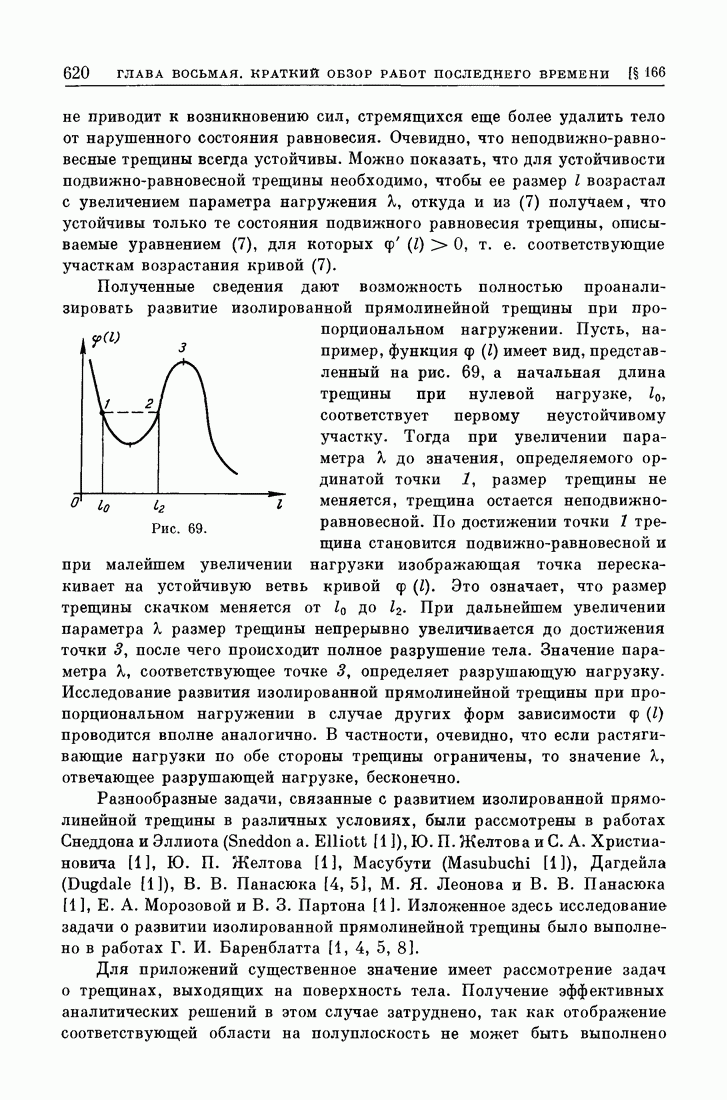
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 48. Простейшие примеры конформного отображения.
1. Дробно-линейная подстановка. Рассмотрим случай, когда z дробно-линейная функция от 

где  постоянные (вообще комплексные), причем
постоянные (вообще комплексные), причем  В этом случае говорят, что z получается из
В этом случае говорят, что z получается из  дробно-линейной подстановкой (или преобразованием). Решая соотношение (1) относительно получаем обратную подстановку, также дробно-линейную:
дробно-линейной подстановкой (или преобразованием). Решая соотношение (1) относительно получаем обратную подстановку, также дробно-линейную:

Значит, каждой точке плоскости  соответствует вполне определенная точка плоскости z, и обратно. Мы не исключаем и бесконечно удаленных точек. Именно, точке
соответствует вполне определенная точка плоскости z, и обратно. Мы не исключаем и бесконечно удаленных точек. Именно, точке  соответствует точка
соответствует точка  а точке
а точке  точка
точка 
Таким образом, мы имеем взаимно однозначное соответствие неограниченных плоскостей 
Дробно-линейная подстановка обладает тем замечательным свойством, что она сохраняет круги, т. е. любой окружности плоскости  она приводит в соответствие также окружность плоскости z, и обратно. При этом прямые рассматриваются как частные случаи окружностей. Проще всего это доказать следующим образом. Уравнение любой окружности на плоскости z, как известно, имеет следующий вид:
она приводит в соответствие также окружность плоскости z, и обратно. При этом прямые рассматриваются как частные случаи окружностей. Проще всего это доказать следующим образом. Уравнение любой окружности на плоскости z, как известно, имеет следующий вид:

где  действительные постоянные (при
действительные постоянные (при  имеем прямую).
имеем прямую).
Замечая, что  можно это уравнение написать и так:
можно это уравнение написать и так:

где  действительные, а
действительные, а  — сопряженные комплексные постоянные. Легко убедиться, что, обратно, уравнение предыдущего вида всегда приводится к виду
— сопряженные комплексные постоянные. Легко убедиться, что, обратно, уравнение предыдущего вида всегда приводится к виду  если вернуться к действительным переменным х и у. Чтобы теперь получить уравнение линии, соответствующей на плоскости
если вернуться к действительным переменным х и у. Чтобы теперь получить уравнение линии, соответствующей на плоскости  нашей окружности, достаточно внести в (б) выражение (1). После устранения знаменателя и элементарных приведений получаем уравнение
нашей окружности, достаточно внести в (б) выражение (1). После устранения знаменателя и элементарных приведений получаем уравнение

где  действительные, а
действительные, а  - сопряженные комплексные постоянные. Следовательно, мы опять получаем уравнение окружности, а это и требовалось доказать.
- сопряженные комплексные постоянные. Следовательно, мы опять получаем уравнение окружности, а это и требовалось доказать.
Одним из простейших частных случаев преобразования (1) является преобразование

где  действительная постоянная; мы будем считать
действительная постоянная; мы будем считать  Для того чтобы дать наглядное представление об этом преобразовании, напомним понятие отражения точки в окружности. Пусть
Для того чтобы дать наглядное представление об этом преобразовании, напомним понятие отражения точки в окружности. Пусть  окружность радиуса
окружность радиуса  на плоскости с центром в начале
на плоскости с центром в начале  пусть
пусть  некоторая точка на этой плоскости. Построим другую точку z, связанную с z следующим образом:
некоторая точка на этой плоскости. Построим другую точку z, связанную с z следующим образом:

Если  то, очевидно,
то, очевидно,  где
где  расстояния точек
расстояния точек  до 0, связанные соотношением
до 0, связанные соотношением

Таким образом, точки  расположены на одном и том же луче, выходящем из О, и их расстояния до О связаны соотношением (3).
расположены на одном и том же луче, выходящем из О, и их расстояния до О связаны соотношением (3).

Рис. 20.
Точка z, связанная с точкой z указанным образом, и называется отражением точки z в окружности  Ясно, что в свою очередь z является отражением z в том же смысле. Преобразование (3), связывающее
Ясно, что в свою очередь z является отражением z в том же смысле. Преобразование (3), связывающее  называется также инверсией. Точки
называется также инверсией. Точки  называются также сопряженными относительно окружности
называются также сопряженными относительно окружности  Когда дана одна из них, то другую легко построить при помощи циркуля и линейки: если, например, данная точка z расположена вне
Когда дана одна из них, то другую легко построить при помощи циркуля и линейки: если, например, данная точка z расположена вне  то для построения соответствующей точки z достаточно провести касательную из
то для построения соответствующей точки z достаточно провести касательную из  к
к  и из точки касания опустить перпендикуляр на луч Oz (рис. 20).
и из точки касания опустить перпендикуляр на луч Oz (рис. 20).
При инверсии, очевидно, точки окружности  соответствуют самим себе, точке
соответствуют самим себе, точке  соответствует точка
соответствует точка  внешние по отношению к
внешние по отношению к  точки переходят во внутренние, и наоборот.
точки переходят во внутренние, и наоборот.
Вернемся теперь к преобразованию (2). Представим себе для большей наглядности, что плоскость  наложена на плоскость z так, что начала и направления осей координат совпадают. Тогда, очевидно, точка соответствующая точке
наложена на плоскость z так, что начала и направления осей координат совпадают. Тогда, очевидно, точка соответствующая точке  будет определяться формулой
будет определяться формулой

Следовательно, точку  можно построить так: отразить точку z в окружности
можно построить так: отразить точку z в окружности  и полученное отражение z отразить (зеркально) в действительной оси; это последнее отражение и будет точкой
и полученное отражение z отразить (зеркально) в действительной оси; это последнее отражение и будет точкой  (рис. 20).
(рис. 20).
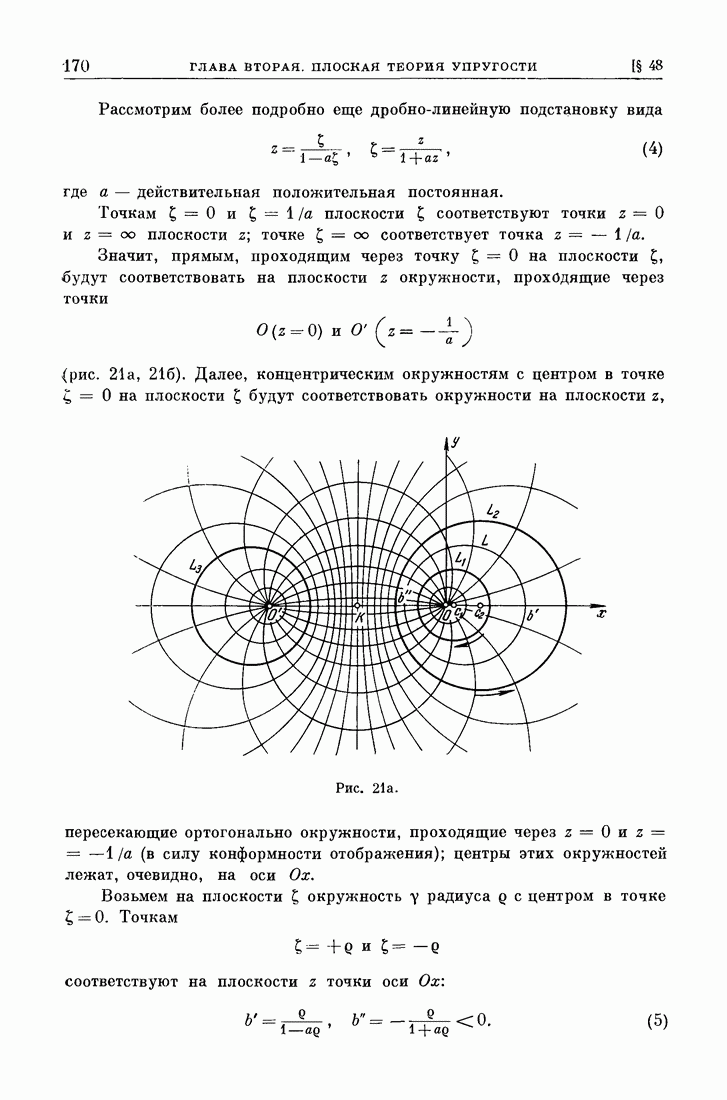
Рассмотрим более подробно еще дробно-линейную подстановку вида

где а — действительная положительная постоянная.
Точкам  плоскости
плоскости  соответствуют точки
соответствуют точки  плоскости
плоскости  точке
точке  соответствует точка
соответствует точка 
Значит, прямым, проходящим через точку  на плоскости будут соответствовать на плоскости z окружности, проходящие через точки
на плоскости будут соответствовать на плоскости z окружности, проходящие через точки

(рис. 21а, 216). Далее, концентрическим окружностям с центром в точке  на плоскости
на плоскости  будут соответствовать окружности на плоскости z, пересекающие ортогонально окружности, проходящие через
будут соответствовать окружности на плоскости z, пересекающие ортогонально окружности, проходящие через  (в силу конформности отображения);
(в силу конформности отображения);

Рис. 21а.
центры этих окружностей лежат, очевидно, на оси 
Возьмем на плоскости  окружность у радиуса
окружность у радиуса  с центром в точке
с центром в точке  Точкам
Точкам

соответствуют на плоскости z точки оси 

Значит, абсцисса с центра окружности  соответствующей окружности у, и радиус
соответствующей окружности у, и радиус  ее определятся формулами:
ее определятся формулами:

мы будем считать, что  если точка
если точка  расположена левее точки
расположена левее точки 
Если  то
то  Когда
Когда  приближается к
приближается к  то
то  и с беспредельно возрастают и окружность
и с беспредельно возрастают и окружность  обращается в прямую, перпендикулярную к
обращается в прямую, перпендикулярную к  проходящую через точку К с абсциссой —
проходящую через точку К с абсциссой — 
Если  то соответствующая окружность на плоскости z находится уже по другую сторону упомянутой прямой
то соответствующая окружность на плоскости z находится уже по другую сторону упомянутой прямой
Рассмотрим теперь две окружности  на плоскости z, соответствующие окружностям
на плоскости z, соответствующие окружностям  с радиусами
с радиусами  плоскости и будем считать, что
плоскости и будем считать, что 

Рис. 216.
Тогда, очевидно, соотношение (4) дает конформное отображение области, заключенной между эксцентрическими окружностями и  на кольцо, заключенное между
на кольцо, заключенное между 
Если даны элементы, определяющие первую область, т. е. радиусы

окружностей  и расстояние I между их центрами
и расстояние I между их центрами  то легко найти величину а, фигурирующую в формуле (4), и радиусы
то легко найти величину а, фигурирующую в формуле (4), и радиусы  окружностей
окружностей  Именно, для определения этих величин имеем
Именно, для определения этих величин имеем
уравнения

откуда после элементарных выкладок получаем:

Таким же образом легко найти отображение бесконечной области, состоящей из точек, расположенных вне двух данных окружностей  (рис. 21а), на кольцо, заключенное между двумя концентрическими окружностями
(рис. 21а), на кольцо, заключенное между двумя концентрическими окружностями  с радиусами
с радиусами  В этом случае
В этом случае  Улитка Паскаля. Положим:
Улитка Паскаля. Положим:

Полагая  получаем:
получаем:

откуда

Когда точка  описывает окружность у радиуса
описывает окружность у радиуса  то точка
то точка  описывает на плоскости z кривую
описывает на плоскости z кривую  параметрически представляемую равенствами
параметрически представляемую равенствами

Эта кривая называется улиткой Паскаля. Если, как мы предполагаем,

то кривая эта не пересекает саму себя и при изменении  от
от  до
до  точка z описывает ее в одном и том же направлении. Значит, на основании сказанного в конце предыдущего параграфа соотношение (9) дает конформное отображение области, заключенной внутри улитки Паскаля, на круг радиуса 1.
точка z описывает ее в одном и том же направлении. Значит, на основании сказанного в конце предыдущего параграфа соотношение (9) дает конформное отображение области, заключенной внутри улитки Паскаля, на круг радиуса 1.
При  улитка Паскаля обращается в окружность, при
улитка Паскаля обращается в окружность, при  в кардиоиду. В этом последнем случае кривая имеет точку
в кардиоиду. В этом последнем случае кривая имеет точку
возврата при z, соответствующем значению  для этого значения
для этого значения 
Окружностям радиусов  на плоскости
на плоскости  соответствуют также улитки Паскаля, параметрическое представление которых получим, полагая
соответствуют также улитки Паскаля, параметрическое представление которых получим, полагая

в уравнениях (10). Радиусам окружности у соответствуют на плоскости z кривые, параметрическое представление которых получим, полагая в формулах. (10)

(параметром будет  кривые эти, как легко убедиться, — параболы.
кривые эти, как легко убедиться, — параболы.

Рис. 22а.

Рис. 226.
На рис. 22а изображены кривые, соответствующие окружностям  и лучам
и лучам  изображенным на рис. 226. Эти кривые пересекаются под прямыми углами, в силу конформности отображения.
изображенным на рис. 226. Эти кривые пересекаются под прямыми углами, в силу конформности отображения.
3. Эпитрохоида. Положим:

где  целое число, большее единицы. Если, как раньше, положить
целое число, большее единицы. Если, как раньше, положить  то
то

Окружности  плоскости
плоскости  соответствует на плоскости z кривая
соответствует на плоскости z кривая  имеющая следующее параметрическое представление:
имеющая следующее параметрическое представление:

Эта кривая есть эпитрохоида. Действительно, если круг радиуса  катится без скольжения (на плоскости
катится без скольжения (на плоскости  по кругу радиуса
по кругу радиуса  касаясь
касаясь
его извне, то точка  связанная с подвижным кругом и находящаяся на расстоянии I от его центра, описывает кривую
связанная с подвижным кругом и находящаяся на расстоянии I от его центра, описывает кривую

где  обозначает полярный угол точки взаимного касания кругов, а
обозначает полярный угол точки взаимного касания кругов, а  Если положить:
Если положить:

то кривая (14) совпадает с кривой (14). Так как, по условию,  то
то  При
При  точка
точка  находится внутри катящегося круга, и поэтому кривая не пересекает саму себя. В предельном случае
находится внутри катящегося круга, и поэтому кривая не пересекает саму себя. В предельном случае  точка
точка  находится на окружности катящегося круга, и наша кривая обращается в эпициклоиду, имеющую
находится на окружности катящегося круга, и наша кривая обращается в эпициклоиду, имеющую  точек возврата. На рис. 23 изображен случай
точек возврата. На рис. 23 изображен случай 
На основании теоремы, указанной в § 47, легко заключить, что соотношение (12) отображает область  заключенную внутри кривой
заключенную внутри кривой  на область
на область 
Окружностям  плоскости
плоскости  соответствуют на плоскости z также эпитрохоиды, параметрическое представление которых мы получим, полагая
соответствуют на плоскости z также эпитрохоиды, параметрическое представление которых мы получим, полагая  в формулах (13).
в формулах (13).
При  кривая
кривая  обращается в улитку Паскаля, рассмотренную в предыдущем пункте.
обращается в улитку Паскаля, рассмотренную в предыдущем пункте.

Рис. 23.
4. Гипотрохоида. Положим:

где  целое положительное число.
целое положительное число.
В этом случае контур  соответствующий окружности
соответствующий окружности  есть, как легко видеть, гипотрохоида, не пересекающая саму себя, описываемая точкой
есть, как легко видеть, гипотрохоида, не пересекающая саму себя, описываемая точкой  круга радиуса
круга радиуса  катящегося без скольжения по кругу радиуса
катящегося без скольжения по кругу радиуса  и касающегося его изнутри, причем если I обозначает расстояние точки
и касающегося его изнутри, причем если I обозначает расстояние точки  до центра катящегося круга, то
до центра катящегося круга, то

Легко видеть, что соотношение (15) отображает часть плоскости z, находящуюся вне  на область
на область  плоскости
плоскости  Окружностям
Окружностям  плоскости
плоскости  соответствуют на плоскости z также гипотрохоиды. В случае
соответствуют на плоскости z также гипотрохоиды. В случае  контур
контур  обращается в эллипс; этот случай будет рассмотрен в следующем пункте. При
обращается в эллипс; этот случай будет рассмотрен в следующем пункте. При  контур
контур  обращается в гипоциклоиду, имеющую в
обращается в гипоциклоиду, имеющую в  точек возврата.
точек возврата.
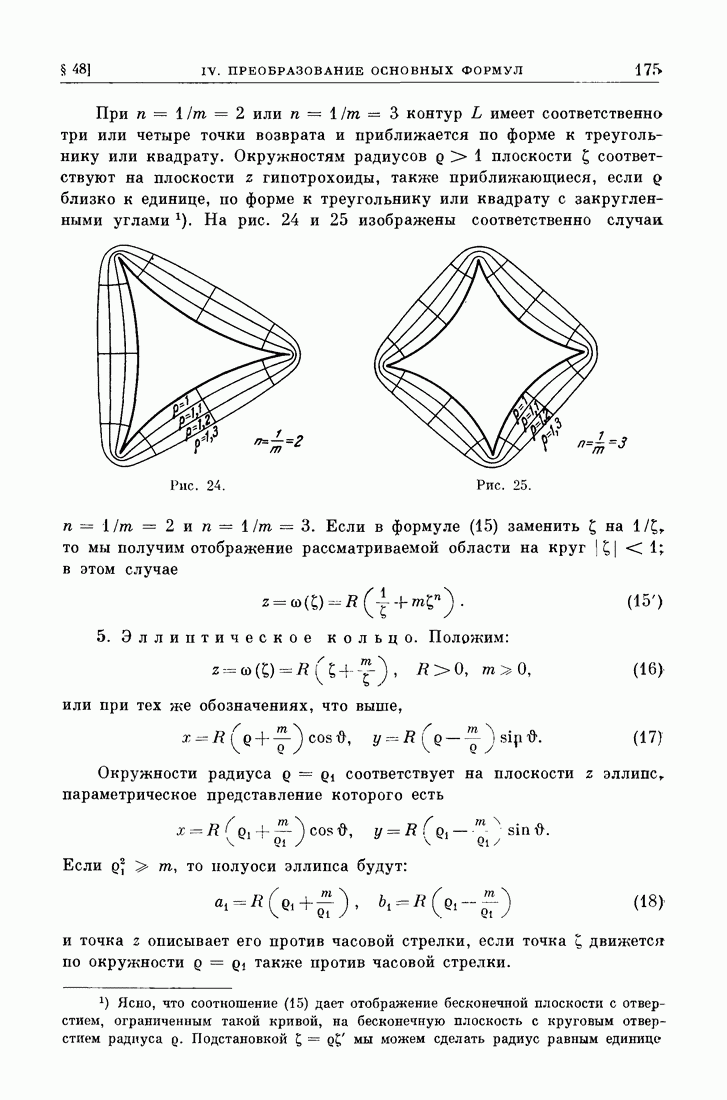
При  или
или  контур
контур  имеет соответственно три или четыре точки возврата и приближается по форме к треугольнику или квадрату. Окружностям радиусов
имеет соответственно три или четыре точки возврата и приближается по форме к треугольнику или квадрату. Окружностям радиусов  плоскости
плоскости  соответствуют на плоскости z гипотрохоиды, также приближающиеся, если
соответствуют на плоскости z гипотрохоиды, также приближающиеся, если  близко к единице, по форме к треугольнику или квадрату с закругленными углами. На рис. 24 и 25 изображены соответственно случаи
близко к единице, по форме к треугольнику или квадрату с закругленными углами. На рис. 24 и 25 изображены соответственно случаи 

Рис. 24.

Рис. 25.
Если в формуле (15) заменить  на 1 то мы получим отображение рассматриваемой области на круг С 1; в этом случае
на 1 то мы получим отображение рассматриваемой области на круг С 1; в этом случае

5. Эллиптическое кольцо. Положим:

или при тех же обозначениях, что выше,

Окружности радиуса  соответствует на плоскости z эллипс, параметрическое представление которого есть
соответствует на плоскости z эллипс, параметрическое представление которого есть

Если  то полуоси эллипса будут:
то полуоси эллипса будут:

и точка  описывает его против часовой стрелки, если точка
описывает его против часовой стрелки, если точка  движется по окружности
движется по окружности  также против часовой стрелки.
также против часовой стрелки.
Значит, если мы на плоскости  возьмем две окружности
возьмем две окружности  радиусов
радиусов  причем
причем  на основании сказанного в конце § 47 получим отображение области, заключенной между эллипсами и
на основании сказанного в конце § 47 получим отображение области, заключенной между эллипсами и  соответствующими этим окружностям, на круговое кольцо, заключенное между
соответствующими этим окружностям, на круговое кольцо, заключенное между  Наши эллипсы будут конфокальны, так как расстояние с от фокусов эллипса
Наши эллипсы будут конфокальны, так как расстояние с от фокусов эллипса  до начала координат дается формулой
до начала координат дается формулой  не зависит от
не зависит от 
Окружностям, соответствующим различным значениям  будут соответствовать эллипсы, заключенные между
будут соответствовать эллипсы, заключенные между  и конфокальные с ними. Лучам
и конфокальные с ними. Лучам  плоскости
плоскости  будут соответствовать конфокальные гиперболы, имеющие те же фокусы, что и эллипсы. Эти эллипсы и гиперболы пересекаются, конечно, под прямыми углами (рис. 26).
будут соответствовать конфокальные гиперболы, имеющие те же фокусы, что и эллипсы. Эти эллипсы и гиперболы пересекаются, конечно, под прямыми углами (рис. 26).

Рис. 26.
Мы можем увеличить  до бесконечности. Тогда мы получим отображение бесконечной области, состоящей из точек, расположенных вне эллипса
до бесконечности. Тогда мы получим отображение бесконечной области, состоящей из точек, расположенных вне эллипса  на бесконечную область, состоящую из точек, находящихся вне
на бесконечную область, состоящую из точек, находящихся вне  этом случае мы всегда будем брать для простоты
этом случае мы всегда будем брать для простоты  следовательно,
следовательно,  При
При  эллипс обращается в прямолинейную щель. При
эллипс обращается в прямолинейную щель. При  мы получим окружность. Если в формуле (16) заменим
мы получим окружность. Если в формуле (16) заменим  на
на  т. е. положим:
т. е. положим:

то получим отображение плоскости с эллиптическим отверстием на круг 
6. Как было только что сказано, соотношение

отображает на круг  бесконечную плоскость
бесконечную плоскость  с эллиптическим отверстием. Уравнение границы отверстия будет
с эллиптическим отверстием. Уравнение границы отверстия будет

Как было сказано, при  эллипс обращается в прямолинейную щель. Произвздя подстановку
эллипс обращается в прямолинейную щель. Произвздя подстановку

что приводит к соотношению

получим отображение на круг  конечной области, ограниченной так называемой лемнискатой Бута (Booth).
конечной области, ограниченной так называемой лемнискатой Бута (Booth).

Рис. 27.
Когда  мало отличается от единицы, то область эта мало отличается от фигуры, состоящей из двух касающихся друг друга кругов. На рис. 27 изображена кривая, соответствующая
мало отличается от единицы, то область эта мало отличается от фигуры, состоящей из двух касающихся друг друга кругов. На рис. 27 изображена кривая, соответствующая 
Если же вместо подстановки (21) произвести подстановку

где точка с расположена вне эллипса (20), то, как легко видеть, получим отображение на круг  некоторой области, которая при
некоторой области, которая при  обращается в бесконечную плоскость, разрезанную вдоль дуги окружности
обращается в бесконечную плоскость, разрезанную вдоль дуги окружности 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
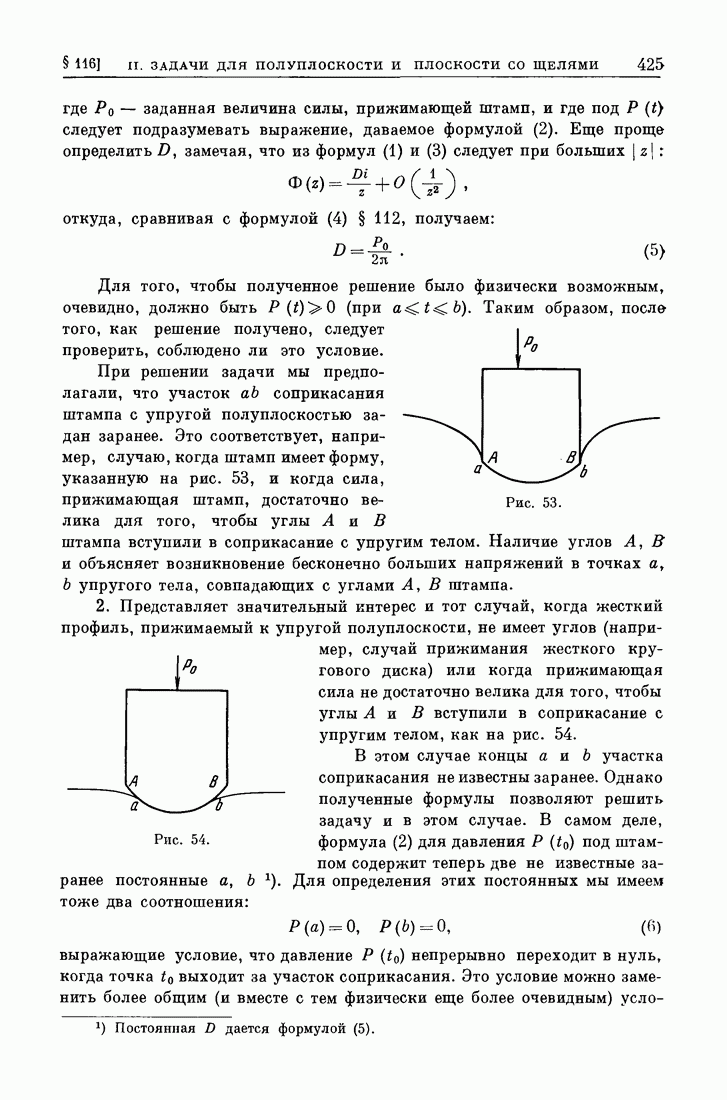
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
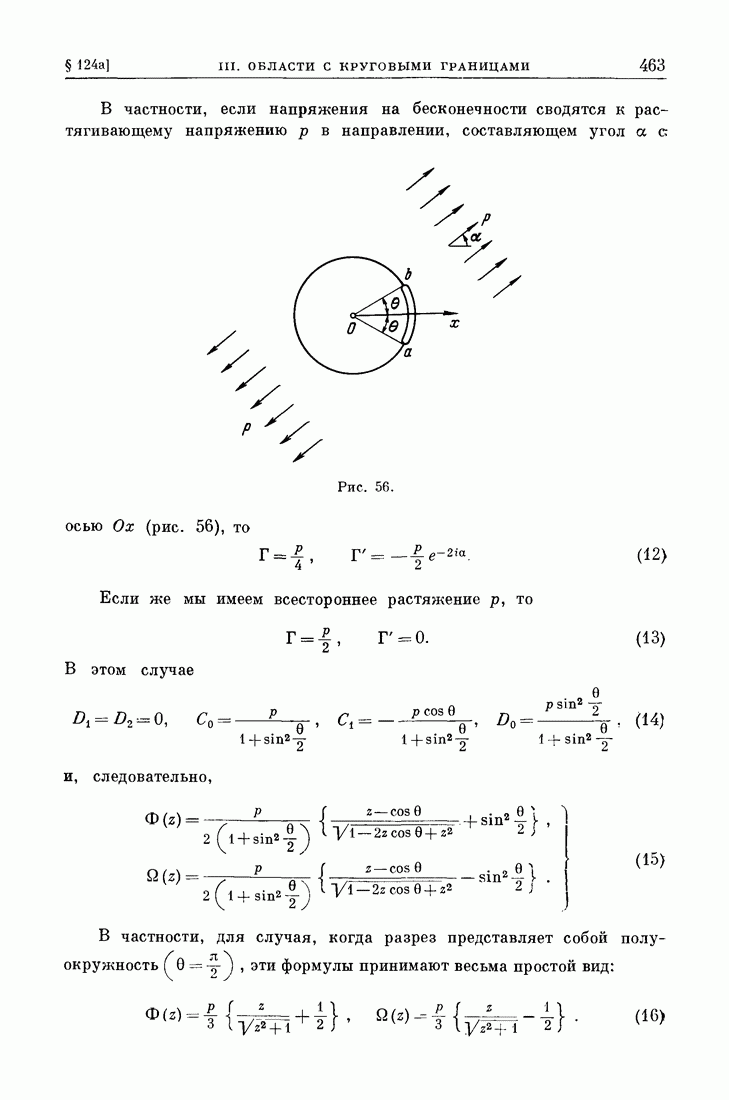
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
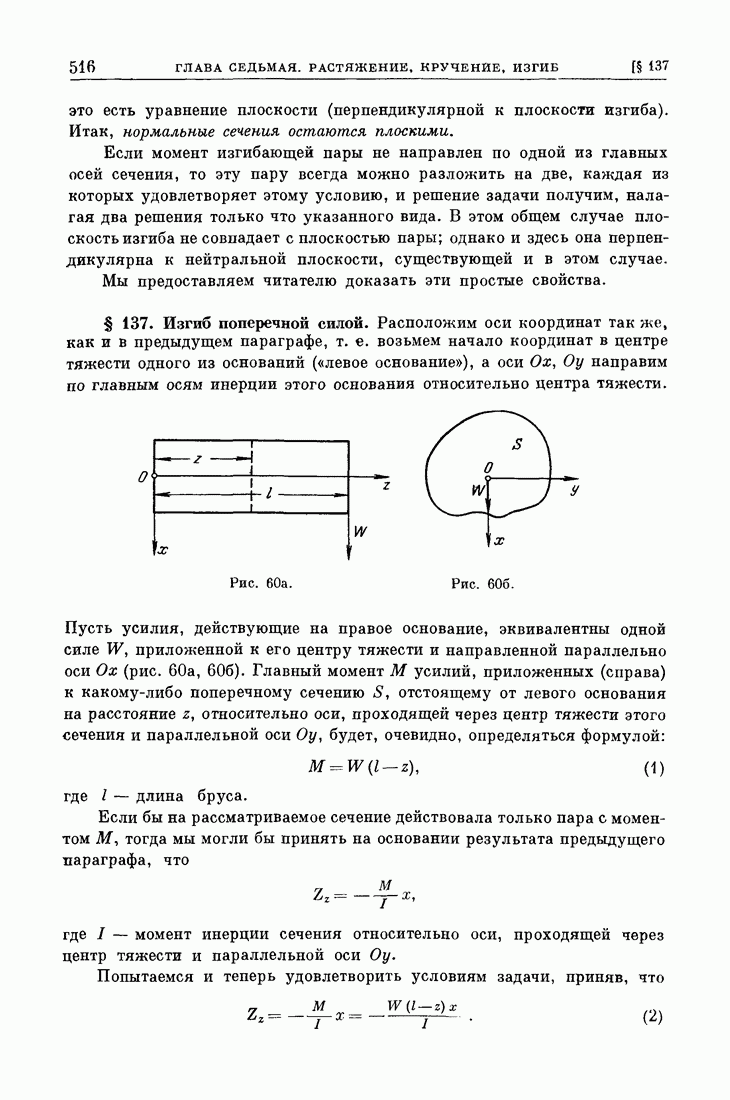
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
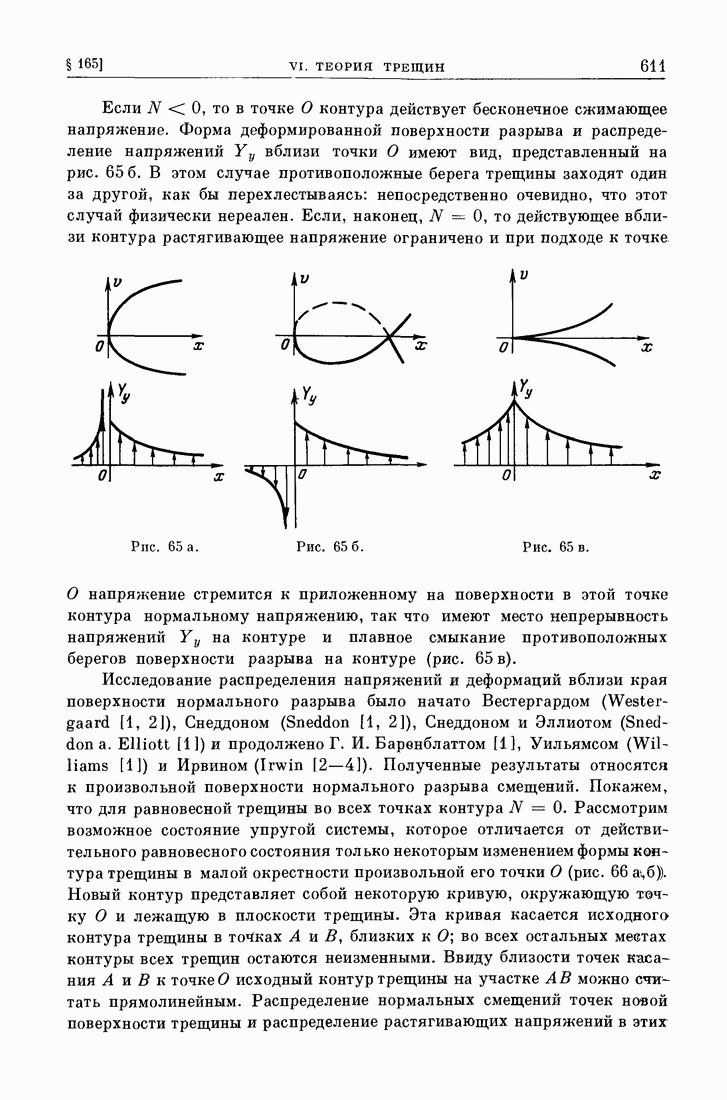
- VI. ТЕОРИЯ ТРЕЩИН
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ