| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 55. Решение второй основной задачи для круга.
Это решение совершенно аналогично предыдущему. Именно, из условия (1) § 41 имеем:

Представляя заданное выражение  в виде комплексного ряда Фурье
в виде комплексного ряда Фурье

и внося в формулу (1) разложения (6) предыдущего параграфа, получаем, как в упомянутом параграфе:

откуда (ср. предыдущий параграф)

Предыдущими формулами определяются все коэффициенты. Коэффициент а также вполне определяется формулой (3), в противоположность случаю предыдущего параграфа. Именно, из равенства (3) и равенства, получаемого переходом к сопряженным значениям, следует:

откуда

(вспомним, что всегда 
Как в предыдущем параграфе, легко покажем, что найденные ряды действительно удовлетворяют условиям задачи, если, например,  имеют производные второго порядка, удовлетворяющие условиям Дирихле.
имеют производные второго порядка, удовлетворяющие условиям Дирихле.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
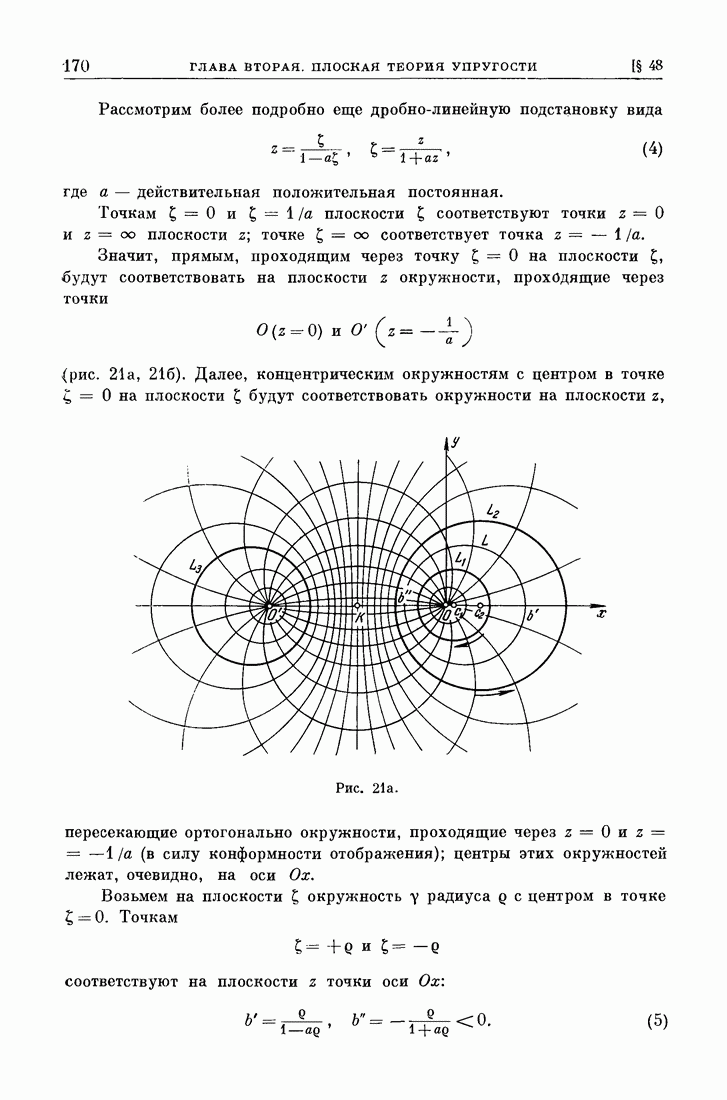
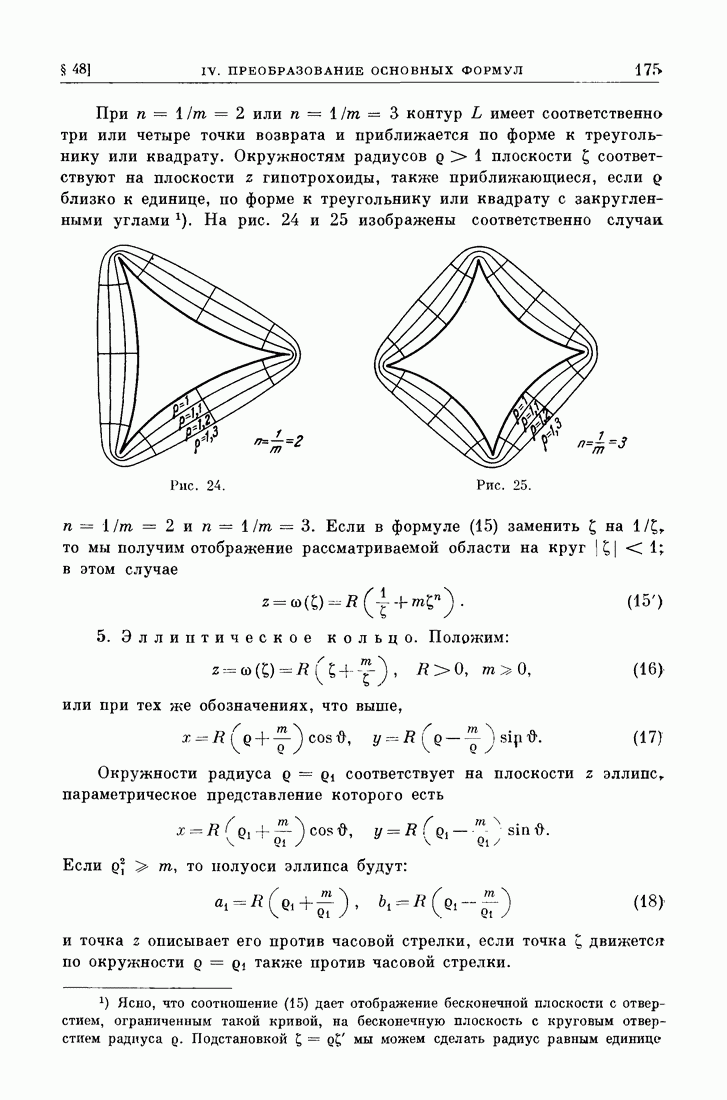
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
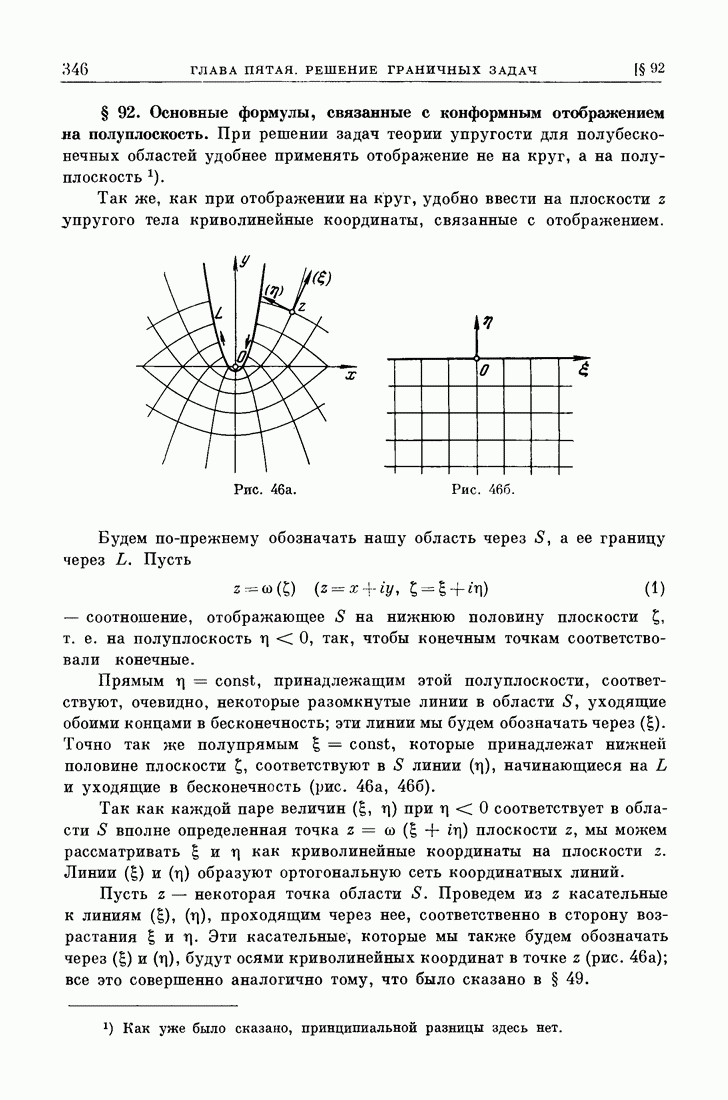
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
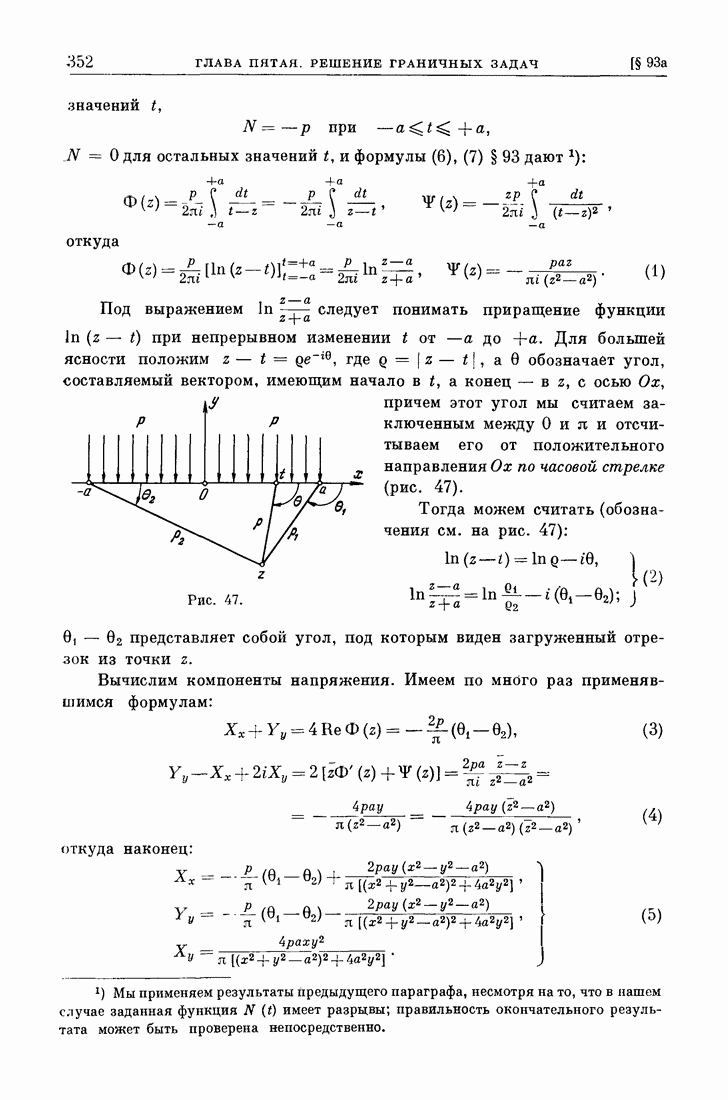
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
- VI. ТЕОРИЯ ТРЕЩИН
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ