| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 140. Решение при помощи интегральных уравнений.
Будем считать, что мы имеем дело с основным случаем (§ 139, п. 1).
Принимая во внимание непрерывность искомой функции  во всей области
во всей области  и разрывность ее нормальных производных на контурах
и разрывность ее нормальных производных на контурах  естественно попытаться представить эту функцию в виде потенциала простого слоя, распределенного на этих контурах, так как потенциал простого слоя обладает как раз этими свойствами. Мы придем
естественно попытаться представить эту функцию в виде потенциала простого слоя, распределенного на этих контурах, так как потенциал простого слоя обладает как раз этими свойствами. Мы придем
таким образом к обобщению известной задачи Робена — Пуанкаре. Итак, положим:

здесь  обозначает расстояние точки
обозначает расстояние точки  до точки
до точки  расположенной на одном из контуров
расположенной на одном из контуров  (плотность слоя) обозначает искомую непрерывную функцию точки
(плотность слоя) обозначает искомую непрерывную функцию точки  Буквой
Буквой  мы вместе с тем обозначаем дугу того из контуров
мы вместе с тем обозначаем дугу того из контуров  по которому производится интегрирование.
по которому производится интегрирование.
На основании известных свойств потенциала простого слоя функция  определяемая предыдущим равенством, будет непрерывной во всей области. Нормальная же производная будет разрывна при переходе через контуры
определяемая предыдущим равенством, будет непрерывной во всей области. Нормальная же производная будет разрывна при переходе через контуры  именно, имеют место известные соотношения:
именно, имеют место известные соотношения:

здесь и относятся к точке  одного из контуров
одного из контуров  обозначает расстояние между точками
обозначает расстояние между точками  угол между вектором
угол между вектором  и нормалью
и нормалью  в точке
в точке  (напомним, что
(напомним, что  всегда обозначает нормаль, внешнюю но отношению к области
всегда обозначает нормаль, внешнюю но отношению к области  рис. 61).
рис. 61).
Граничные условия (7) § 139 обращаются на основании равенств (2) в уравнения:

где  обозначает точку на контуре
обозначает точку на контуре 
Мы получили, таким образом, уравнение Фредгольма, которое можно записать так:

где положено:

 Выясним, при каких условиях уравнение (4) имеет решение. Однородное уравнение
Выясним, при каких условиях уравнение (4) имеет решение. Однородное уравнение

получаемое из уравнения (4), если положить  т. е. то
т. е. то 

имеет одно-единственное линейно независимое решение.
Действительно, функция  определяемая равенством (1), где
определяемая равенством (1), где  есть решение однородного уравнения (6), будет удовлетворять граничным условиям (7) § 139 при
есть решение однородного уравнения (6), будет удовлетворять граничным условиям (7) § 139 при  На основании доказанного в предыдущем параграфе такая функция
На основании доказанного в предыдущем параграфе такая функция  есть постоянная во всей области
есть постоянная во всей области  Но при
Но при  равенства (2) дают:
равенства (2) дают:

Итак, решение  однородного уравнения (6) есть плотность слоя, распределенного на внешней границе
однородного уравнения (6) есть плотность слоя, распределенного на внешней границе  области
области  и дающего постоянный потенциал в этой области; это, таким образом, есть двумерный аналог «естественного распределения» электричества на проводнике. Как известно, плотность такого распределения определена с точностью до постоянного множителя, а это и доказывает наше утверждение.
и дающего постоянный потенциал в этой области; это, таким образом, есть двумерный аналог «естественного распределения» электричества на проводнике. Как известно, плотность такого распределения определена с точностью до постоянного множителя, а это и доказывает наше утверждение.
На основании известной теоремы Фредгольма союзное однородное уравнение, т. е. уравнение

будет также допускать одно-единственное (линейно независимое) решение. Легко найти это последнее. Именно, легко проверить, что этим решением будет

Действительно, если точка  взята на
взята на  то
то

Все это следует из хорошо известных формул:

 знак меняется на обратный, так как в этом случае по нашим обозначениям
знак меняется на обратный, так как в этом случае по нашим обозначениям  будет внешней нормалью по отношению к этому контуру, а не внутренней, как по отношению к другим контурам
будет внешней нормалью по отношению к этому контуру, а не внутренней, как по отношению к другим контурам 
Принимая во внимание эти формулы, сразу устанавливаем, что величина  определяемая формулой (8), удовлетворяет уравнению (7), если точка
определяемая формулой (8), удовлетворяет уравнению (7), если точка  взята на
взята на  Наконец, если точка
Наконец, если точка  взята на
взята на
(страница пропущена)
§ 140а. Примеры.
В некоторых частных случаях можно, конечно, получить решение задачи, не прибегая к интегральным уравнениям. И здесь конформное отображение может иногда оказать большие услуги, как это будет показано в первом из нижеследующих примеров.
1. Кручение кругового цилиндра, армированного продольным круговым стержнем из другого материала. Пусть сечение  бруса состоит из области
бруса состоит из области  ограниченной окружностью и области
ограниченной окружностью и области  ограниченной той же окружностью
ограниченной той же окружностью  и окружностью
и окружностью  охватывающей первую. Пусть первой области соответствует модуль сдвига
охватывающей первую. Пусть первой области соответствует модуль сдвига  а второй — модуль
а второй — модуль 
Легко непосредственно убедиться, что если окружности  концентрические и если начало координат взято в центре, то функция кручения будет постоянной. Следовательно, закручивание стержня и окружающего полого цилиндра происходит так, как если бы эти тела не были связаны друг с другом и жесткость при кручении составного бруса равна сумме жесткостей составных частей.
концентрические и если начало координат взято в центре, то функция кручения будет постоянной. Следовательно, закручивание стержня и окружающего полого цилиндра происходит так, как если бы эти тела не были связаны друг с другом и жесткость при кручении составного бруса равна сумме жесткостей составных частей.
Случай же, когда и  не концентричны, значительно сложнее. Будем пользоваться обозначениями § 48, п. 1, только вместо
не концентричны, значительно сложнее. Будем пользоваться обозначениями § 48, п. 1, только вместо  будем теперь писать Пусть
будем теперь писать Пусть

— соотношение, отображающее плоскость  на плоскость
на плоскость  так, чтобы окружностям
так, чтобы окружностям  соответствовали концентрические окружности
соответствовали концентрические окружности  на плоскости радиусов
на плоскости радиусов  Эти радиусы и постоянная а связаны с радиусами и
Эти радиусы и постоянная а связаны с радиусами и  окружностей и
окружностей и  и с расстоянием I между их центрами формулами (7) и (8) § 48. Не забудем, что (§ 48)
и с расстоянием I между их центрами формулами (7) и (8) § 48. Не забудем, что (§ 48)

Области  будет в силу формулы (1) соответствовать круг
будет в силу формулы (1) соответствовать круг  а области
а области  круговое кольцо
круговое кольцо 
Пусть  функция кручения; ее значения в областях
функция кручения; ее значения в областях  будем обозначать соответственно через
будем обозначать соответственно через  Пусть
Пусть  функция, сопряжен
функция, сопряжен  (определяемая отдельно в областях
(определяемая отдельно в областях  ее значения в
ее значения в  будем обозначать через
будем обозначать через  Функций
Функций  гармони» ческие в соответствующих областях.
гармони» ческие в соответствующих областях.
Граничные условия, которым удовлетворяют  таковы (см. § 139):
таковы (см. § 139):

В настоящем параграфе под  мы будем понимать нормаль, направленную от центра соответствующей окружности, под
мы будем понимать нормаль, направленную от центра соответствующей окружности, под  дугу, отсчитываемую против часовой стрелки.
дугу, отсчитываемую против часовой стрелки.
Считая, что частные производные первого порядка функций  непрерывны вплоть до границ областей их определения (это подтвердится после получения решения), и принимая во внимание соотношения
непрерывны вплоть до границ областей их определения (это подтвердится после получения решения), и принимая во внимание соотношения

вытекающие из соотношений Коши — Римана, мы можем заменить условия (3) следующими:

Пусть  комплексная функция кручения и пусть
комплексная функция кручения и пусть

— та же функция, выраженная через переменную  . Пусть
. Пусть  значения этой функции в областях
значения этой функции в областях  где
где  есть круг
есть круг  кольцо
кольцо 
Тогда мы будем иметь:

откуда, полагая 

Заметим далее, что

Но мы имеем:

Предыдущий ряд (абсолютно) сходится при  Значит, мы будем иметь:
Значит, мы будем иметь:

Подставляя ряды (6), (7) и (8) в условия (3) и сравнивая коэффициенты при  получаем без всякого труда для
получаем без всякого труда для 

где

 равны расстояниям центров окружностей и
равны расстояниям центров окружностей и  до начала координат [см. § 48, формула (6)].
до начала координат [см. § 48, формула (6)].
Постоянные  остаются совершенно произвольными, как и следовало ожидать. Условие же непрерывности
остаются совершенно произвольными, как и следовало ожидать. Условие же непрерывности  дает, как легко видеть,
дает, как легко видеть,  общее значение
общее значение  остается произвольным. Мы можем поэтому положить:
остается произвольным. Мы можем поэтому положить:

Из формул (9) следует:

где

Подставляя эти значения в формулы (6) и (7), получаем окончательно:

Эти ряды и их производные, как легко видеть, сходятся абсолютно и равномерно в соответствующих областях, включая и контуры.
Если  т. е. если
т. е. если  получим для и
получим для и  одно и то же выражение
одно и то же выражение

т. е.

Это — комплексная функция кручения, соответствующая случаю однородного цилиндра. Если начало координат возьмем в центре, то получим:

(см. § 131, замечание 2).
Таким образом, можем сказать, что функция  определяемая второй из формул (13), состоит из двух частей: части, соответствующей случаю, когда мы имеем сплошной однородный брус (первый член), и части, выражающей «возмущение», вызванное присутствием стержня.
определяемая второй из формул (13), состоит из двух частей: части, соответствующей случаю, когда мы имеем сплошной однородный брус (первый член), и части, выражающей «возмущение», вызванное присутствием стержня.
Раз функции  найдены, то вычисление компонент напряжения при помощи формул § 134 не представляет никаких затруднений
найдены, то вычисление компонент напряжения при помощи формул § 134 не представляет никаких затруднений  Жесткость при кручении
Жесткость при кручении  тоже легко вычисляется при помощи формул § 134. После элементарных выкладок и преобразований получим:
тоже легко вычисляется при помощи формул § 134. После элементарных выкладок и преобразований получим:

где

 обозначает полярный момент инерции сплошного круга радиуса
обозначает полярный момент инерции сплошного круга радиуса  относительно его центра, а
относительно его центра, а  полярный момент инерции сплошного круга радиуса
полярный момент инерции сплошного круга радиуса  относительно центра первого круга.
относительно центра первого круга.
Если  обозначает жесткость при кручении отдельно взятого стержня с модулем сдвига
обозначает жесткость при кручении отдельно взятого стержня с модулем сдвига  жесткость при кручении окиужаюшего
жесткость при кручении окиужаюшего
полого цилиндра, из которого удален стержень, то

Из формул (16) и (14) выводим:

откуда следует, что

как это можно было предвидеть заранее.
Для однородного цилиндра  мы вместо
мы вместо  имели бы
имели бы

В общем случае при малом имеем приближенно, пренебрегая четвертой и высшими степенями 

откуда следует приближенная формула

Эта формула совпадает при  с формулой Макдональда (Macdonald [1]) для полого цилиндра.
с формулой Макдональда (Macdonald [1]) для полого цилиндра.
Если цилиндр армирован не одним, а несколькими продольными стержнями из одного и того же материала и если стержни настолько тонки и удалены друг от друга, что районы вызываемых ими «возмущений» практически не перекрываются, то, очевидно, приближенная формула (19) может быть применена и к этому случаю, если подразумевать под I сумму моментов инерции их сечений относительно центра окружности 
Еще проще решается задача о кручении в случае, когда  конфокальные эллипсы, а также и для случая, когда границы — определенным образом расположенные эпитрохоиды.
конфокальные эллипсы, а также и для случая, когда границы — определенным образом расположенные эпитрохоиды.
2. Кручение прямоугольного бруса, составленного из двух также прямоугольных брусьев. Можно часто также получить решение задачи кручения в случаях,
исключенных нами из рассмотрения при приведении задачи к интегральному уравнению, например в случаях, когда контуры имеют угловые точки. Один из таких случаев рассмотрен в нижеследующем примере.
Рассмотрим прямоугольный брус, составленный из двух также прямоугольных брусьев, сечения которых — прямоугольники со сторонами  спаянных вдоль грани шириной
спаянных вдоль грани шириной  (рис. 62).
(рис. 62).

Рис. 62.
Модули сдвигов составляющих брусьев обозначим соответственно через  Направим ось Оу по линии раздела областей
Направим ось Оу по линии раздела областей  соответствующих различным материалам, и возьмем начало координат в середине этой линии; обозначим через
соответствующих различным материалам, и возьмем начало координат в середине этой линии; обозначим через  значения функции кручения
значения функции кручения  в областях
в областях 
Введем, далее, гармоническую функцию  значения которой в областях
значения которой в областях  обозначим через
обозначим через  Как легко непосредственно убедиться, граничные условия сводятся к следующим:
Как легко непосредственно убедиться, граничные условия сводятся к следующим:

Будем искать гармонические функции  в виде рядов:
в виде рядов:

где для краткости введено обозначение

Каждый член обоих предыдущих рядов есть, очевидно, гармоническая функция. При этом числа  подобраны так, что удовлетворены условия
подобраны так, что удовлетворены условия  ясно также, что удовлетворено условие
ясно также, что удовлетворено условие 
Остается удовлетворить условиям (а) и  Для этого заметим, что функцию
Для этого заметим, что функцию  можно в промежутке
можно в промежутке  представить в виде ряда
представить в виде ряда

где для краткости введено обозначение

т. е.

На основании  условия (а) будут удовлетворены, если
условия (а) будут удовлетворены, если

а условия  если
если

Решая три предыдущих уравнения относительно  и подставляя найденные значения в ряды
и подставляя найденные значения в ряды  получаем после некоторых очевидных преобразований:
получаем после некоторых очевидных преобразований:

Форма коэффициентов показывает, что полученные ряды сходятся довольно быстро (притом равномерно и абсолютно). Так же очевидна законность почленного дифференцирования, которым мы пользовались в процессе вывода.
Функция кручения дается формулами:

Жесткость при кручении  вычисляется по формуле (6) § 139, которая в нашем случае принимает вид:
вычисляется по формуле (6) § 139, которая в нашем случае принимает вид:

Внося в эту формулу предыдущие выражения для  получаем путем совершенно элементарных выкладок (ср. случай однородного бруса, Love [1], § 225):
получаем путем совершенно элементарных выкладок (ср. случай однородного бруса, Love [1], § 225):

Если  велики по сравнению с
велики по сравнению с  (практически при
(практически при  то можем с достаточной точностью принять:
то можем с достаточной точностью принять:

и тогда получим для  приближенную формулу (ср. аналогичное значение для случая однородного бруса, Love [1], § 225):
приближенную формулу (ср. аналогичное значение для случая однородного бруса, Love [1], § 225):

3. Отметим в заключение сравнительно недавно опубликованную статью Д. И. Шермана [27], в которой решена задача кручения эллиптического цилиндра, армированного круговым стержнем. Метод решения, указанный в этой статье, может быть с успехом применен для приближенного решения задач интересующего нас здесь типа и в ряде других случаев, представляющих практический интерес.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
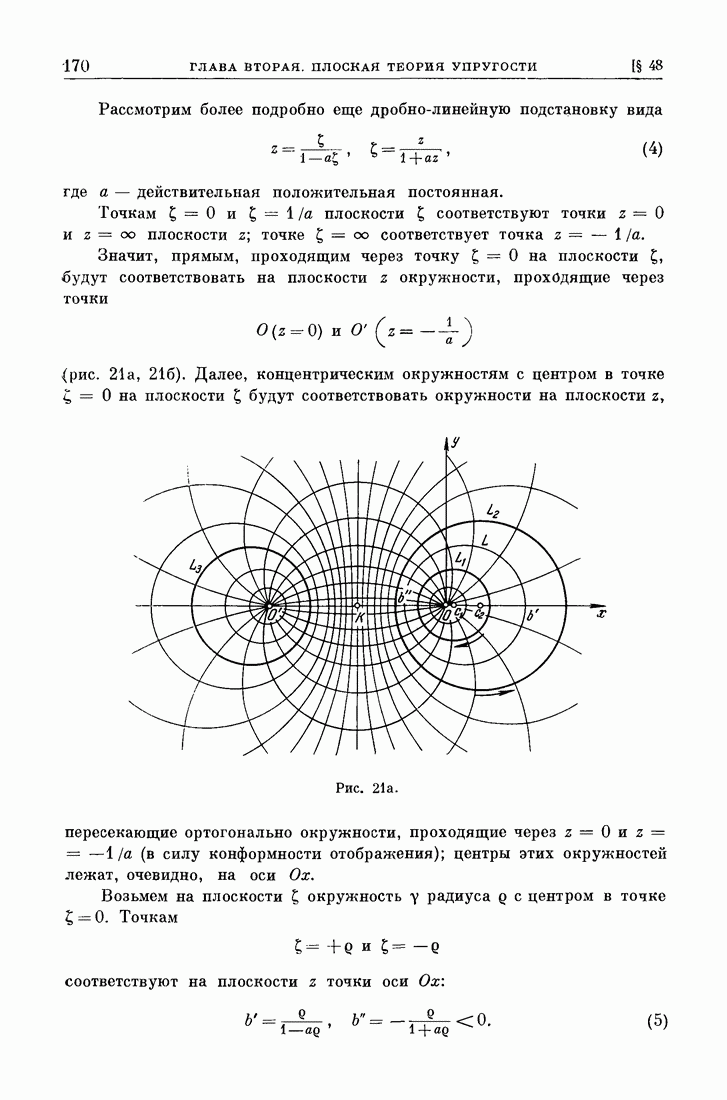
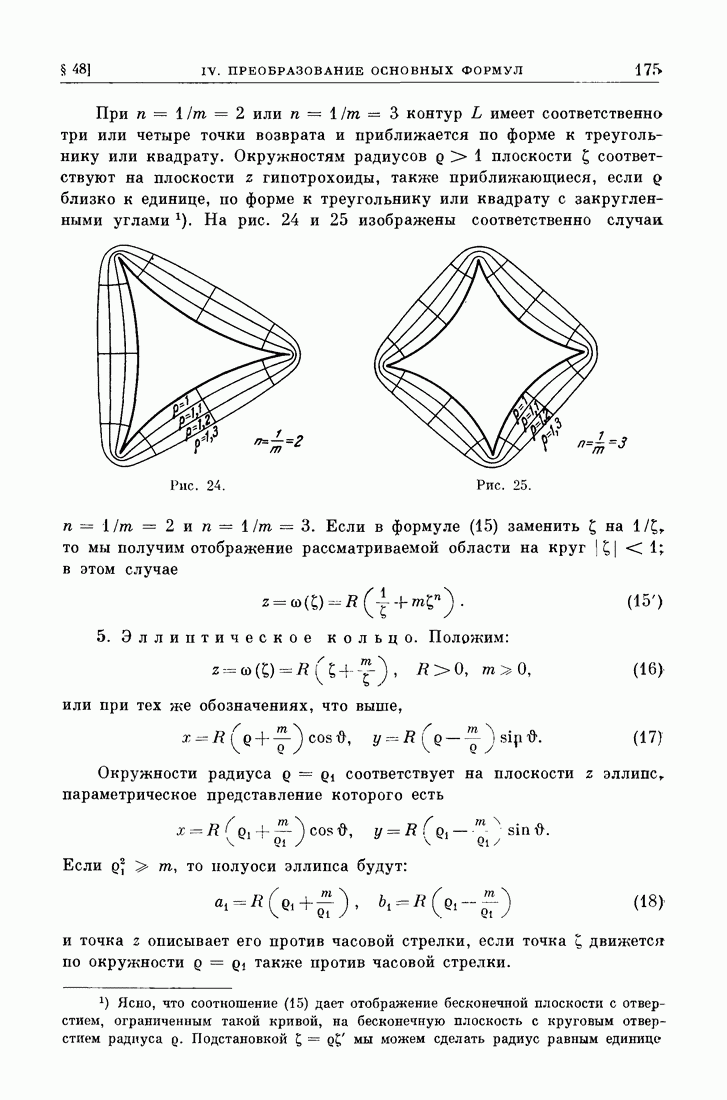
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
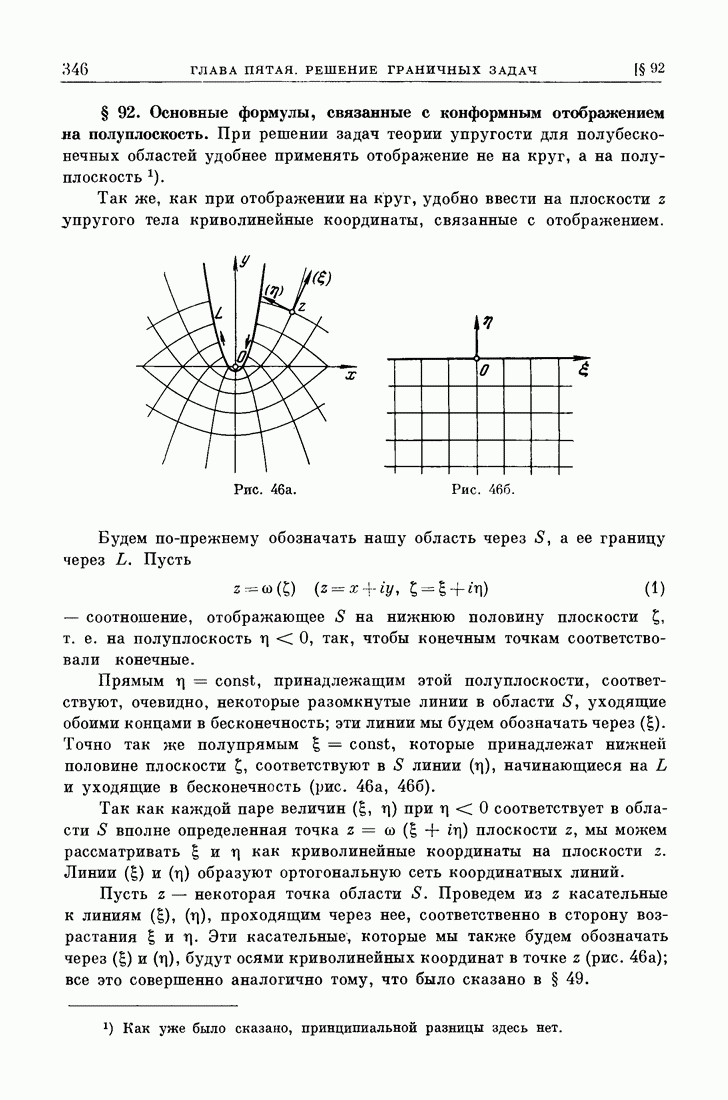
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
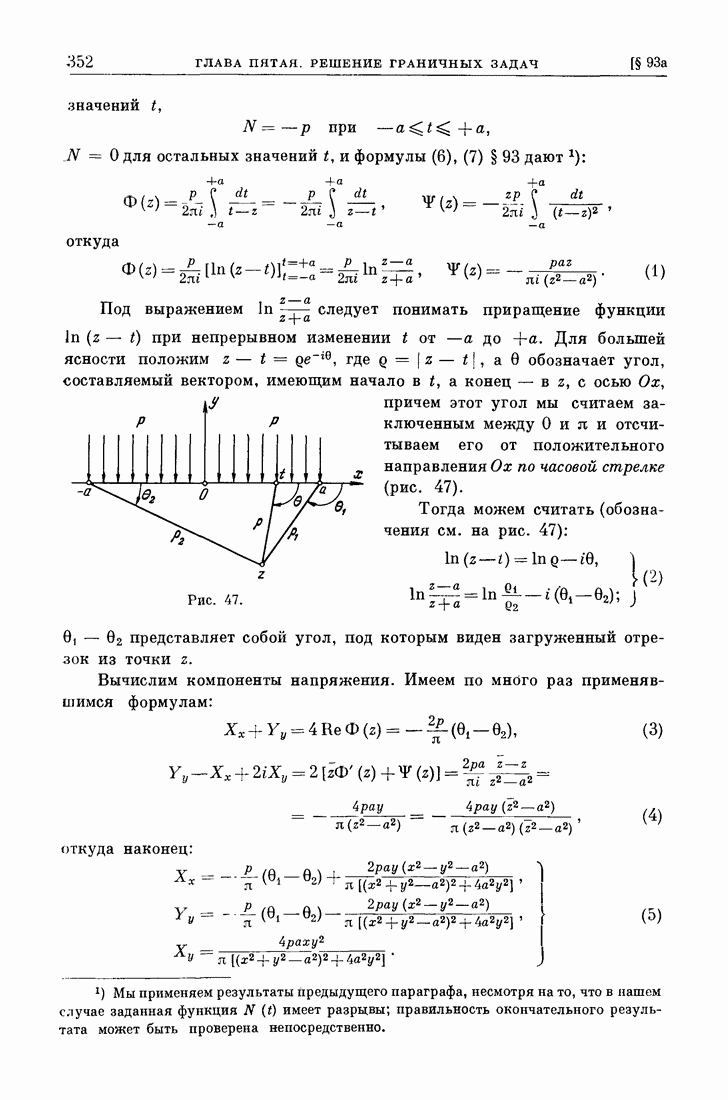
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
- VI. ТЕОРИЯ ТРЕЩИН
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ