| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
Все сказанное до сих пор может быть отнесено к любым сплошным телам. Для того, чтобы получить уравнения, характеризующие тела, которые мы называем упругими (вернее, идеально упругими) твердыми телами, необходимо еще иметь закон, выражающий связь между напряженным состоянием тела и вызванной им деформацией.
§ 16. Основной закон теории упругости (обобщенный закон Гука).
1. Первая, весьма неполная, формулировка закона, связывающего напряжение с деформацией, принадлежит Гуку (Robert Hooke, 1635-1702). Закон, называемый его именем, был найден им в 1660 г., опубликовав в виде анаграммы в 1676 г., а в явном виде в 1678 г. В переводе на современный язык содержание, которое вкладывает Гук в свой закон, можно передать приблизительно так: «Деформация упругого тела пропорциональна действующему на него усилию». В эту формулировку можно вложить определенное содержание в том только случае, когда «усилие», действующее на тело, и вызванная им деформация могут быть охарактеризованы одной величиной каждая.
Например, если мы имеем длинный и тонкий цилиндрический стержень, растягиваемый продольными силами, приложенными на концах, то можно принять, что усилие, которому подвержено тело, характеризуется заданием величины F растягивающей силы, а деформация — удлинением  стержня. В этом случае закон Гука дает
стержня. В этом случае закон Гука дает  где С — постоянная зависящая только от первоначальной длины I стержня, формы и размеров поперечного сечения и материала стержня. Можно привести еще много примеров подобного рода.
где С — постоянная зависящая только от первоначальной длины I стержня, формы и размеров поперечного сечения и материала стержня. Можно привести еще много примеров подобного рода.
Эксперименты подтвердили, что закон Гука хорошо согласуется с действительностью для многих твердых тел, но всегда при условии достаточно малых деформаций. Начиная с определенной величины деформации, закон пропорциональности перестает быть даже приблизительно справедливым.
Однако и в случае малых деформаций, когда закон пропорциональности можно считать справедливым, приведенный выше закон Гука
не может дать полной картины того, что в действительности происходит в деформированном теле. В самом деле, мы видели, что деформированное и напряженное состояния характеризуются шестью величинами каждое, причем эти величины изменяются от одной точки тела к другой, так что мы в действительности имеем дело с бесчисленным множеством величин, характеризующих состояние тела в целом.
Например, в приведенном выше случае мы говорили о растягивающих силах  приложенных к концам цилиндрического стержня. На самом деле «сила» F выражает только суммарный эффект внешних напряжений, приложенных вблизи концов стержня. Эти напряжения могут быть распределены самым различным образом; например: могут быть распределены на основаниях или на участках боковой поверхности вблизи оснований; распределение может быть равномерным или неравномерным и пр.
приложенных к концам цилиндрического стержня. На самом деле «сила» F выражает только суммарный эффект внешних напряжений, приложенных вблизи концов стержня. Эти напряжения могут быть распределены самым различным образом; например: могут быть распределены на основаниях или на участках боковой поверхности вблизи оснований; распределение может быть равномерным или неравномерным и пр.
Ясно, что от способа распределения внешних напряжений существенно зависит распределение напряжений и деформаций внутри стержня. Только в том случае, когда размеры поперечного сечения стержня малы в сравнении с длиной, способ распределения внешних усилий около концов не отражается заметно на состоянии стержня (и то только в частях, не очень близких к концам), и мы можем ограничиться рассмотрением только суммарной «силы» F (об этом см. также § 23).
Итак, очевидно, что если мы не хотим ограничиться грубым, примитивным описанием явлений, мы должны заменить закон Гука более общим, глубже проникающим в сущность дела.
Наиболее естественным обобщением закона простой пропорциональности двух величин можно считать закон линейной зависимости между несколькими величинами. Поэтому как наиболее естественное обобщение первоначального закона можно рассматривать следующий основной закон теории упругости или обобщенный закон Гука:
Компоненты напряжения в данной точке тела суть линейные и однородные функции компонент деформации в той же точке (и обратно).
Речь, конечно, идет о малых деформациях.
В этом, по существу, виде закон был дан Коши в несколько уже раз упомянутом (см. стр. 18) мемуаре, доложенном Парижской Академии в 1822 г. В следующей работе, опубликованной в 1828 г., Коши выводит этот закон, базируясь на молекулярной теории, при простейших предположениях относительно сил взаимодействия между молекулами, которые рассматриваются им как материальные точки. Тот же результат был получен Пуассоном (S. D. Poisson, 1781-1840) аналогичным методом в мемуаре, доложенном Парижской Академии в 1828 г. и опубликованном в 1829 г.
Мы не станем здесь излагать выводов Коши и Пуассона, тем более что они оказались недостаточными (см. ниже), и примем обобщенный
закон Гука как исходный пункт нашей теории, базируясь на том, что закон этот при малых деформациях достаточно хорошо согласуется с действительностью для очень многих материалов.
2. Прежде, чем идти дальше, необходимо сделать следующее замечание. Так как вообще напряжения и деформации различны в различных местах тела, то можно говорить только об их компонентах в данной точке. Так мы и поступали выше. Однако выражение в «данной точке» мы понимали различным образом в применении к компонентам деформации и к компонентам напряжения. Именно, когда мы говорили, например, что  есть функция координат
есть функция координат  мы под (х, у, z) понимали положение точки до деформации. Это же относится к компонентам
мы под (х, у, z) понимали положение точки до деформации. Это же относится к компонентам  смещения. Когда же мы говорили, например, что
смещения. Когда же мы говорили, например, что  есть функция от х, у, z, мы под (х, у, z) понимали положение точки при окончательном (напряженном, а следовательно, и деформированном) состоянии тела.
есть функция от х, у, z, мы под (х, у, z) понимали положение точки при окончательном (напряженном, а следовательно, и деформированном) состоянии тела.
Однако при рассматриваемых вами малых деформациях это различие несущественно, так как, например, значения величины  в точках
в точках  где (х, у, z) есть положение точки
где (х, у, z) есть положение точки  до деформации, различаются на величину, малую по сравнению с
до деформации, различаются на величину, малую по сравнению с  Таким образом, значение функции
Таким образом, значение функции  в данной точке
в данной точке  деформированного тела мы можем заменять значением этой функции в точке (х, у, z).
деформированного тела мы можем заменять значением этой функции в точке (х, у, z).
Во всем последующем мы будем брать значения всех рассматриваемых функций в (геометрических) точках, представляющих собой начальные положения точек деформированного тела.
В соответствии с этим, говоря в дальнейшем об области V, занятой телом, и о ее границе  мы всегда будем иметь в виду Область, занятую телом до деформации, и ее границу.
мы всегда будем иметь в виду Область, занятую телом до деформации, и ее границу.
3. Вернемся к обобщенному закону Гука. Этот закон при помощи формул может быть записан следующим образом. Если  суть компоненты напряжения в данной точке тела, а
суть компоненты напряжения в данной точке тела, а  компоненты деформации, то
компоненты деформации, то

множитель 2 в некоторых членах правых частей введен для удобства; см. ниже соотношения (2).
Так как на основании принятого основного закона компоненты деформации суть также определенные линейные функции от компонент напряжения, то предыдущие уравнения должны быть разрешимы относительно  т. е. определитель, составленный из коэффициентов
т. е. определитель, составленный из коэффициентов  должен быть отличен от нуля.
должен быть отличен от нуля.
Величины  суть постоянные, характеризующие упругие свойства тела в данной точке. Они носят названия упругих постоянных. Слово «постоянные» надо понимать в том смысле, что эти величины не зависят от значений компонент деформации и соответствующего напряжения в данной точке. Однако они могут иметь различные значения в различных точках тела. Тогда мы будем говорить, что тело (в смысле упругих свойств) неоднородно. Если же упругие постоянные одни и те же для всех точек тела, то тело будет однородным.
суть постоянные, характеризующие упругие свойства тела в данной точке. Они носят названия упругих постоянных. Слово «постоянные» надо понимать в том смысле, что эти величины не зависят от значений компонент деформации и соответствующего напряжения в данной точке. Однако они могут иметь различные значения в различных точках тела. Тогда мы будем говорить, что тело (в смысле упругих свойств) неоднородно. Если же упругие постоянные одни и те же для всех точек тела, то тело будет однородным.
Формулы (1) содержат, как мы видим, 36 упругих постоянных.
Однако при помощи соображений, основанных на законе сохранения энергии и на рассмотрении потенциальной энергии деформации, можно показать, что между этими постоянными должны существовать соотношения

иначе говоря, что таблица коэффициентов  симметрична. Таким образом, число упругих постоянных в самом общем случае может быть сведено к 21.
симметрична. Таким образом, число упругих постоянных в самом общем случае может быть сведено к 21.
Как мы увидим в следующем параграфе, в случае изотропного тела число упругих постоянных сводится к двум.
По старой теории Коши, основанной на рассмотрении молекулярных сил, число упругих постоянных в самом общем случае равно не 21, а 15; в случае же изотропного тела, по теории Коши, мы должны иметь всего одну упругую постоянную. К тому же результату пришел Пуассон. Однако это не подтвердилось на опыте. Не надо, впрочем, думать, что к неправильному результату привела молекулярная теория и что, исходя из нее, нельзя получить должного числа постоянных. Дело только в том, что Коши и Пуассон применяли молекулярную теорию в слишком упрощенном виде. Основываясь на современных взглядах на строение материи, можно получить полный результат, т. е. все 21 постоянную. Это и было сделано сравнительно недавно Борном (М. Born).
Мы не останавливаемся подробнее на всем этом, так как в дальнейшем будем изучать только изотропные тела. В этом же случае можно получить окончательные формулы при помощи очень простых соображений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
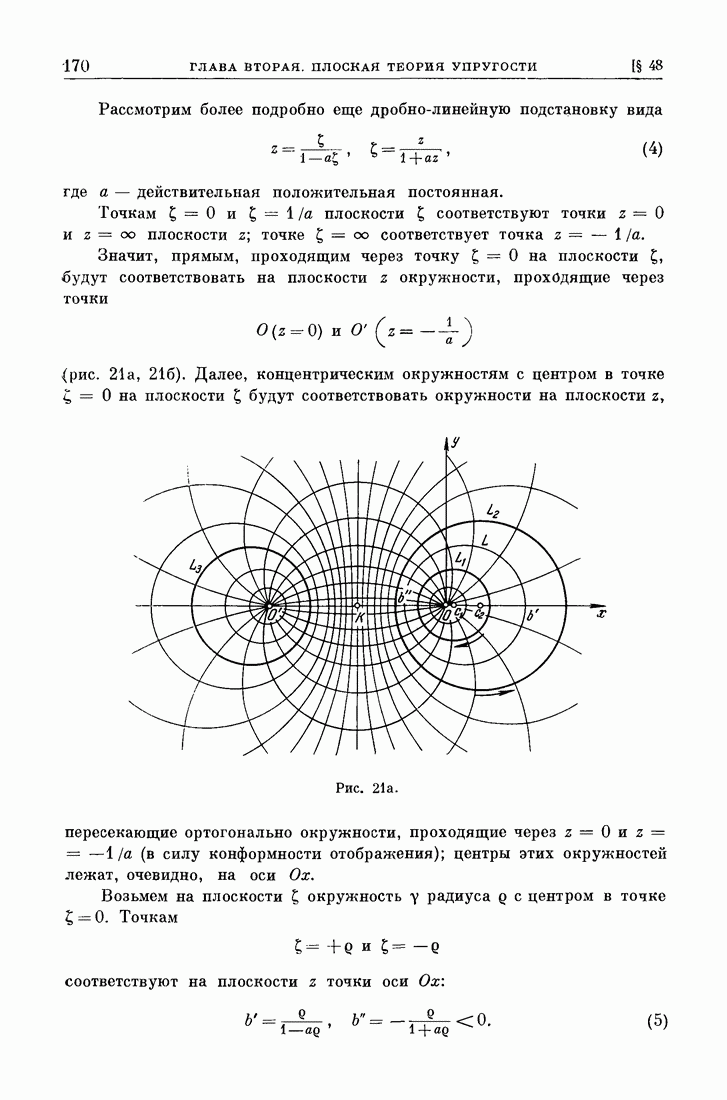
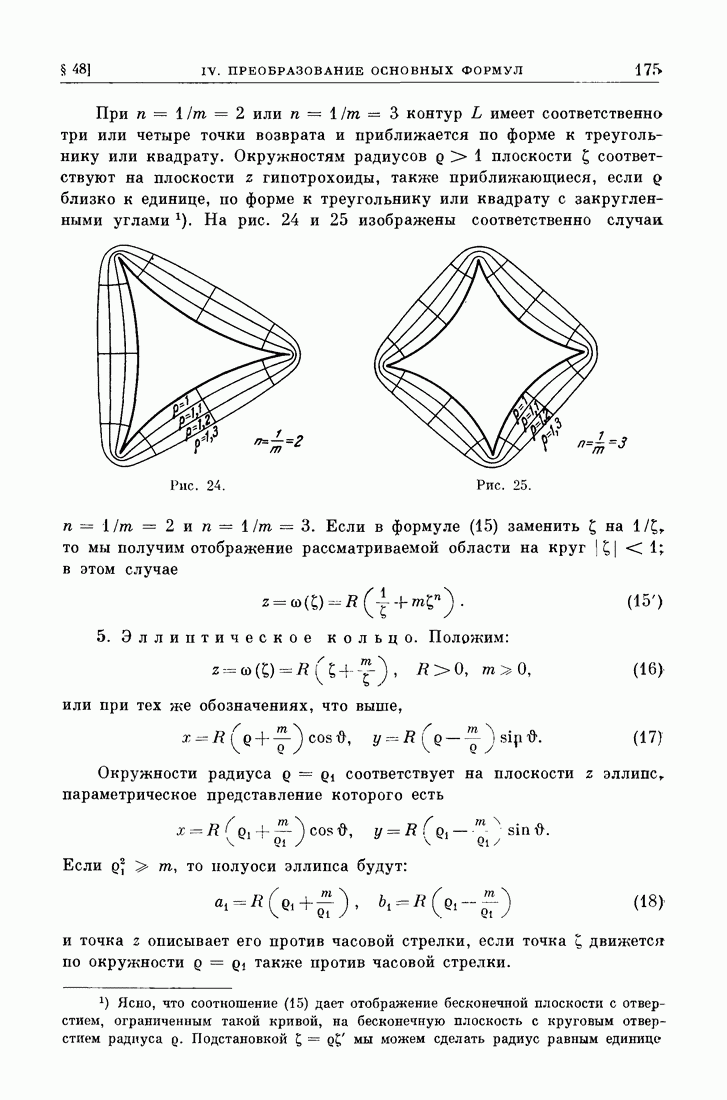
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
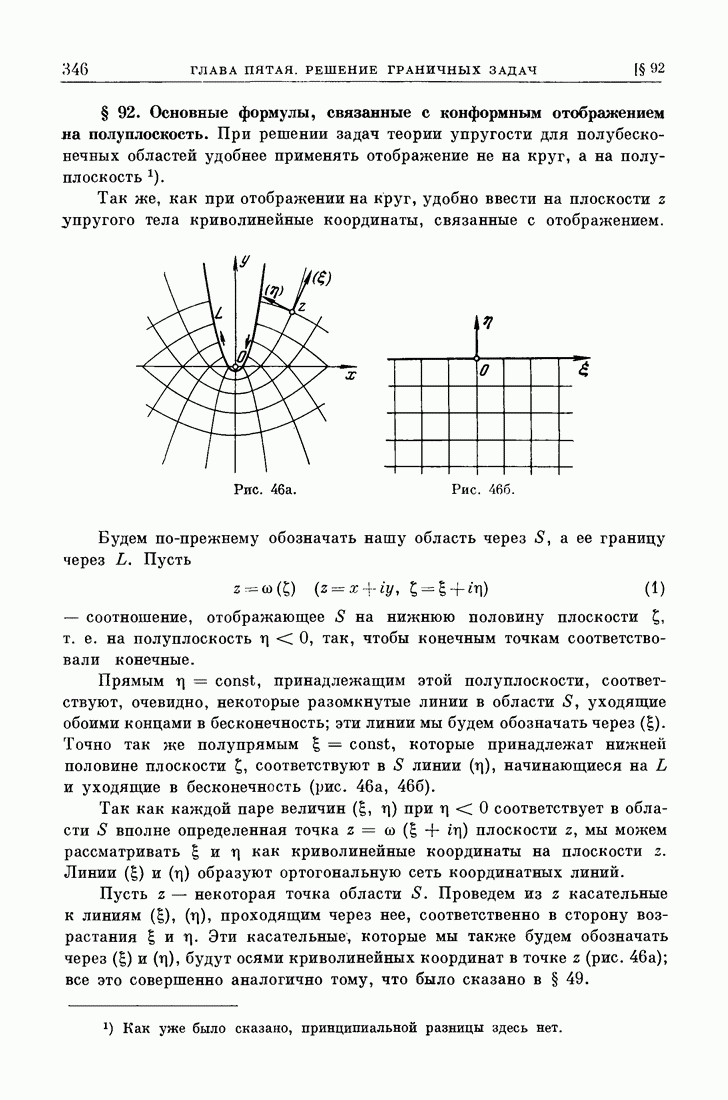
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
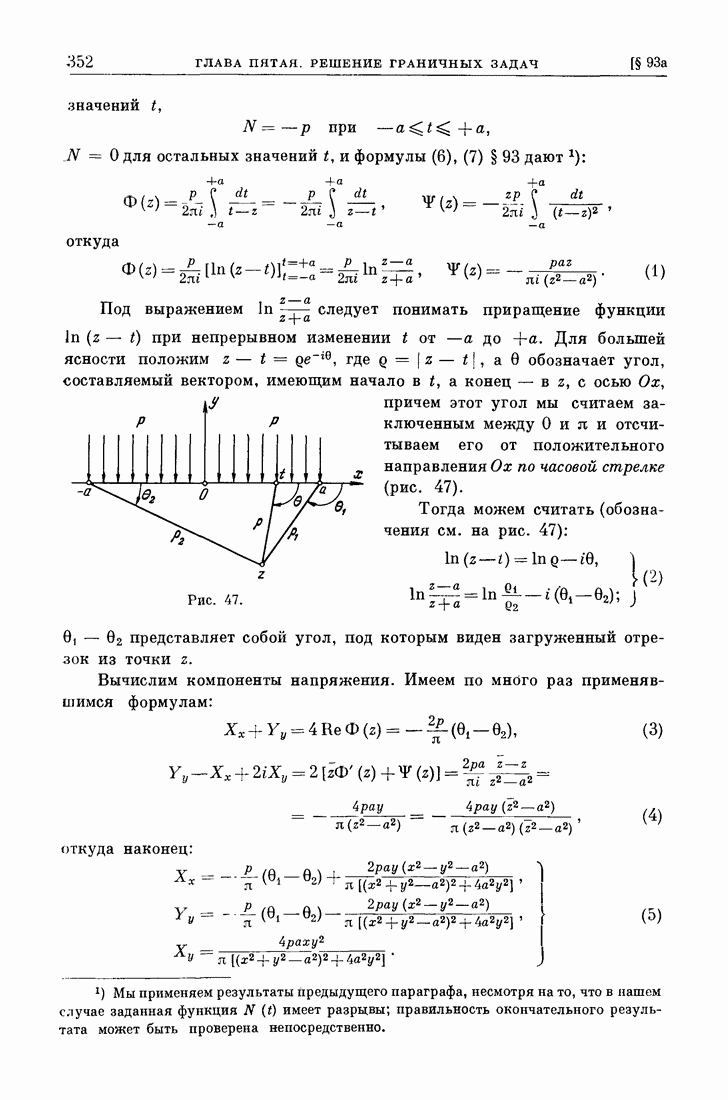
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
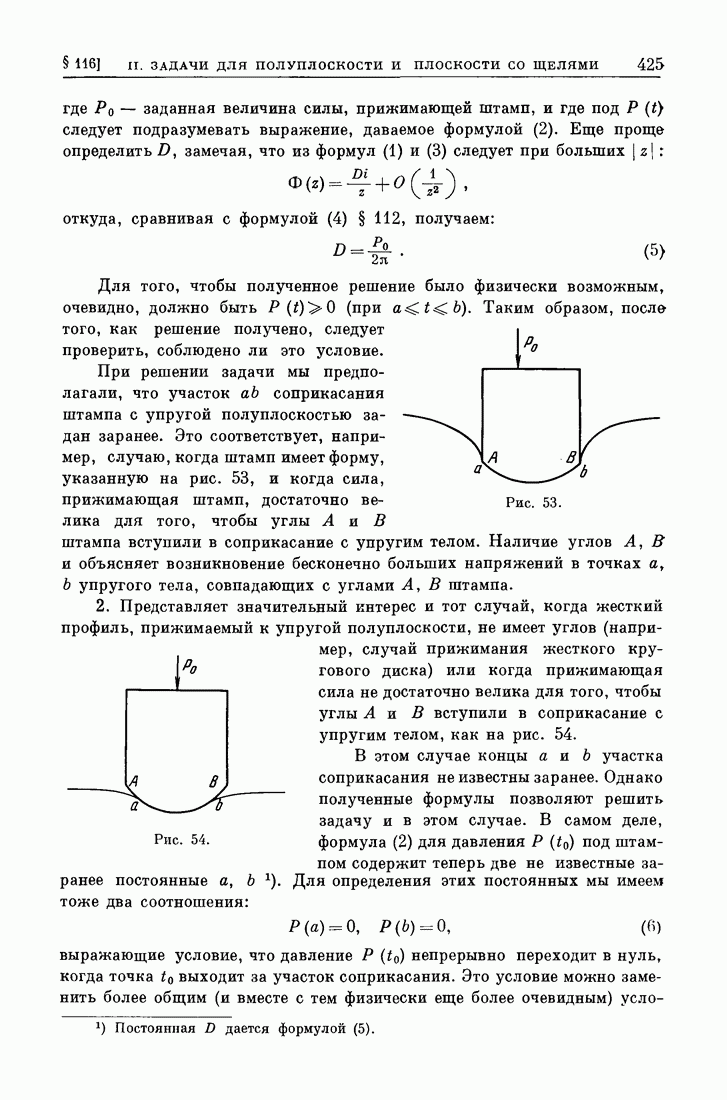
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
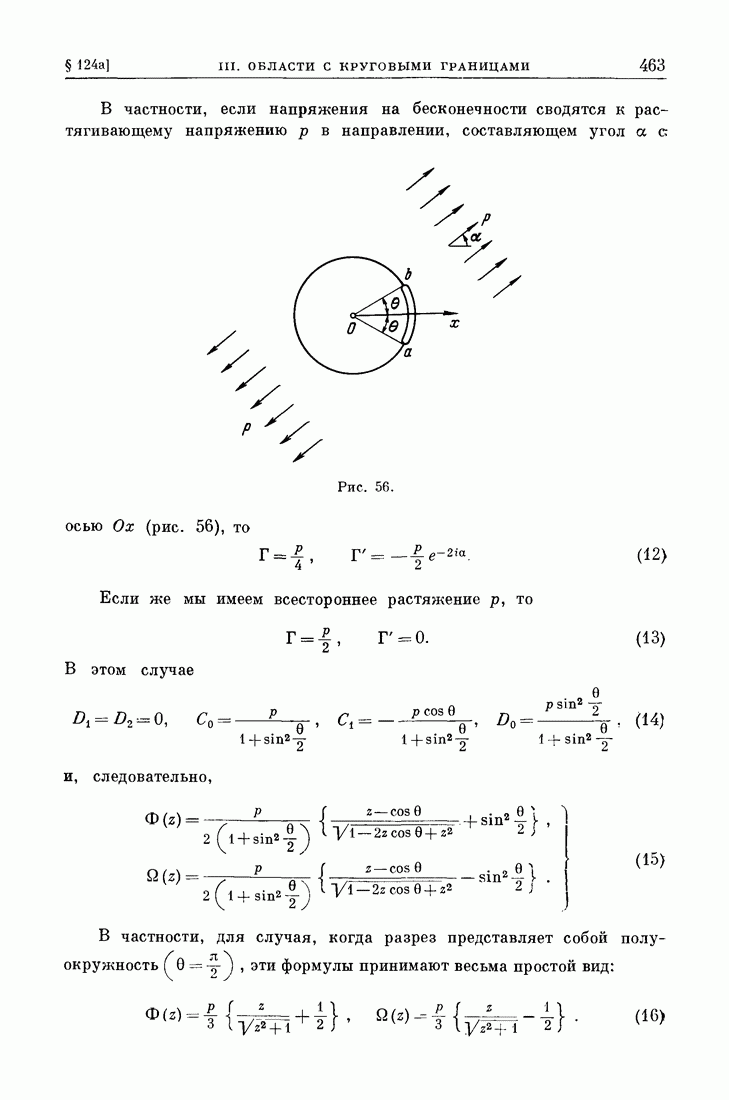
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
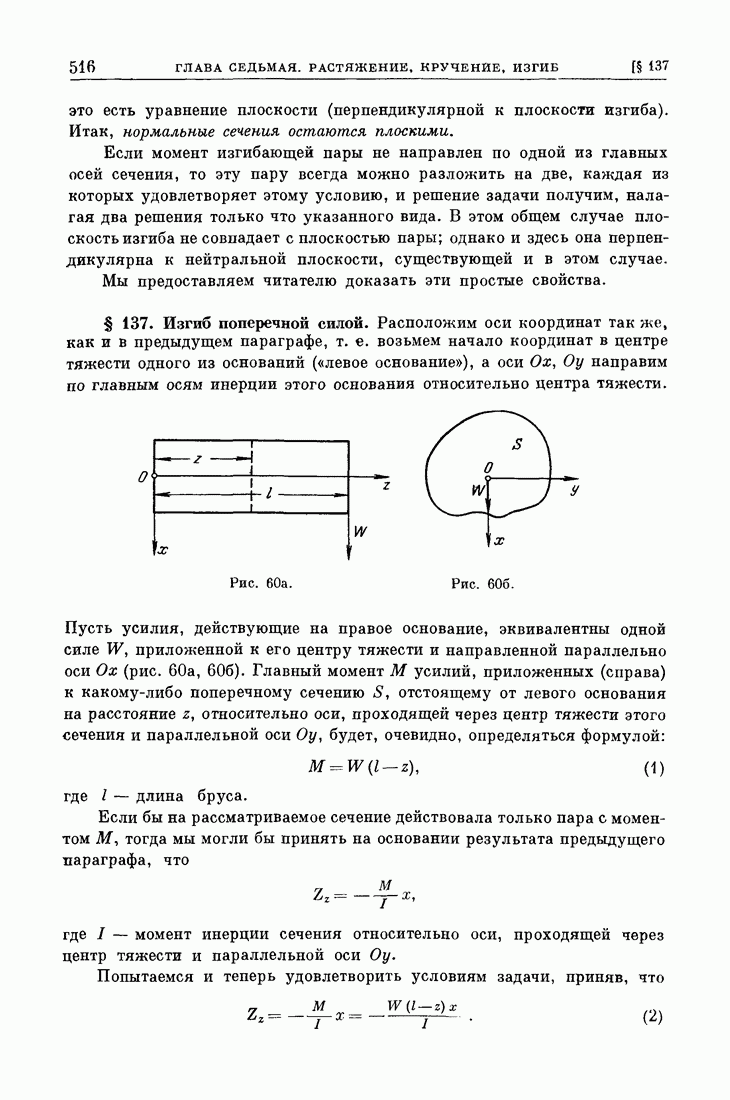
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
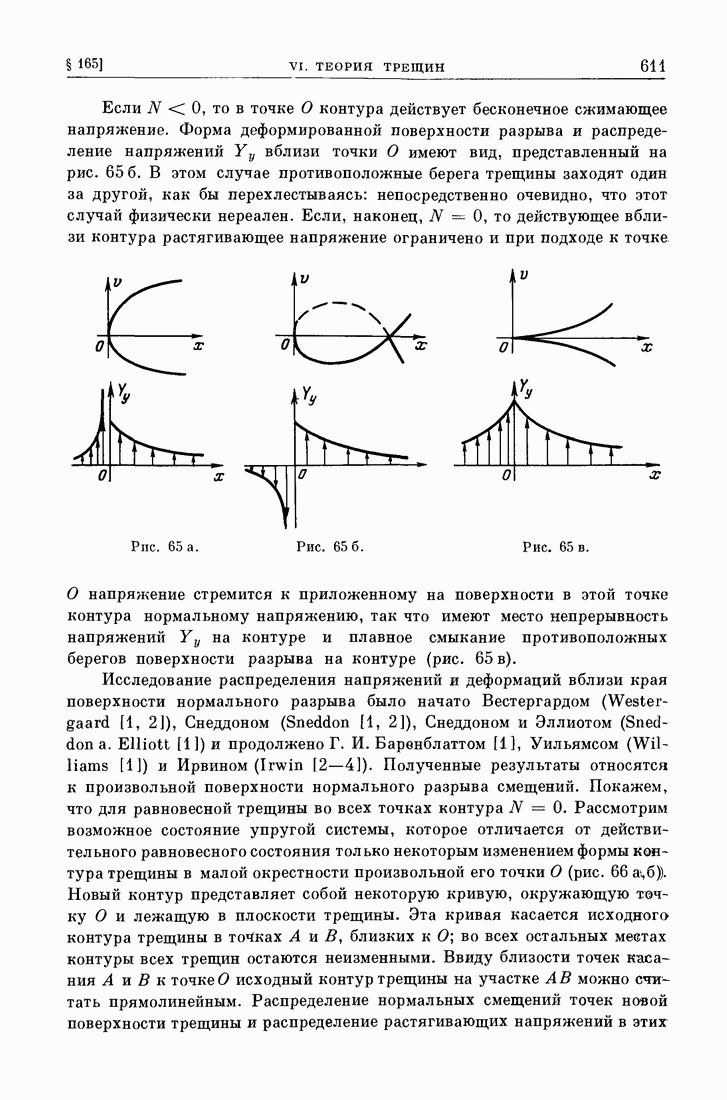
- VI. ТЕОРИЯ ТРЕЩИН
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ