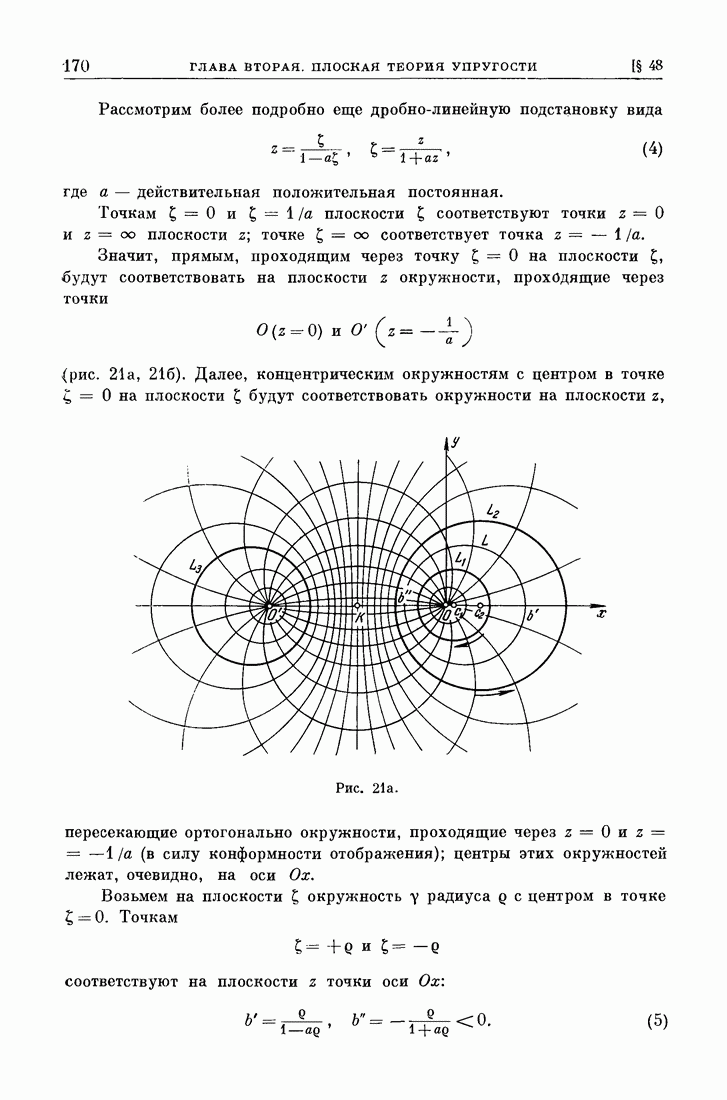
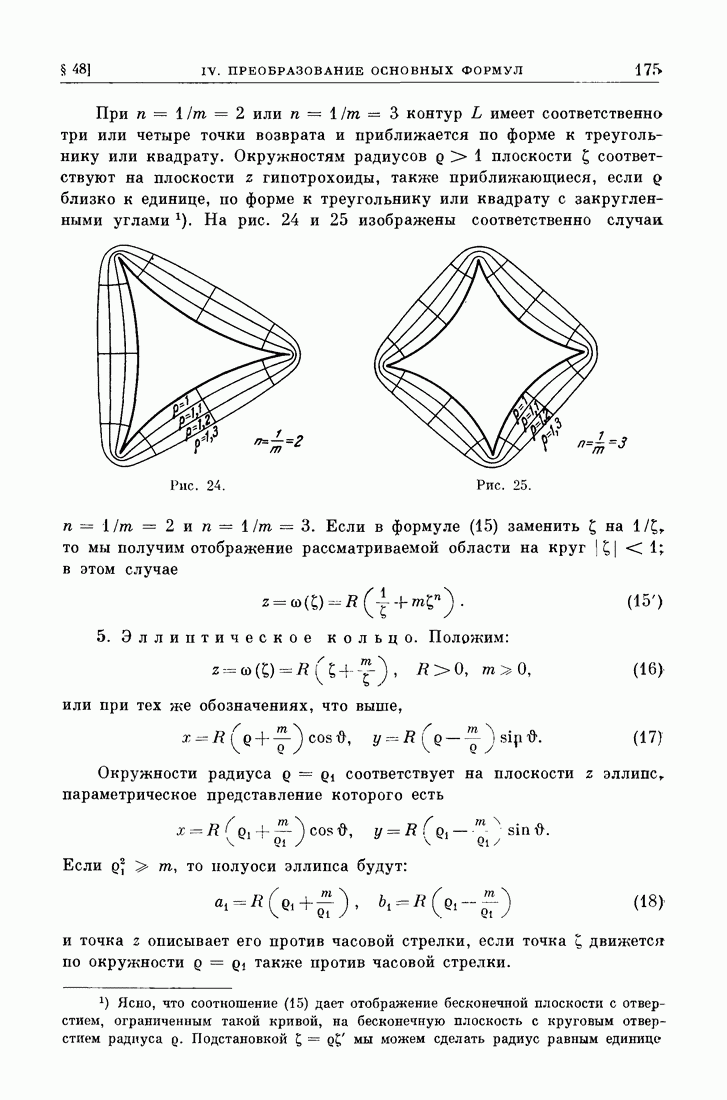
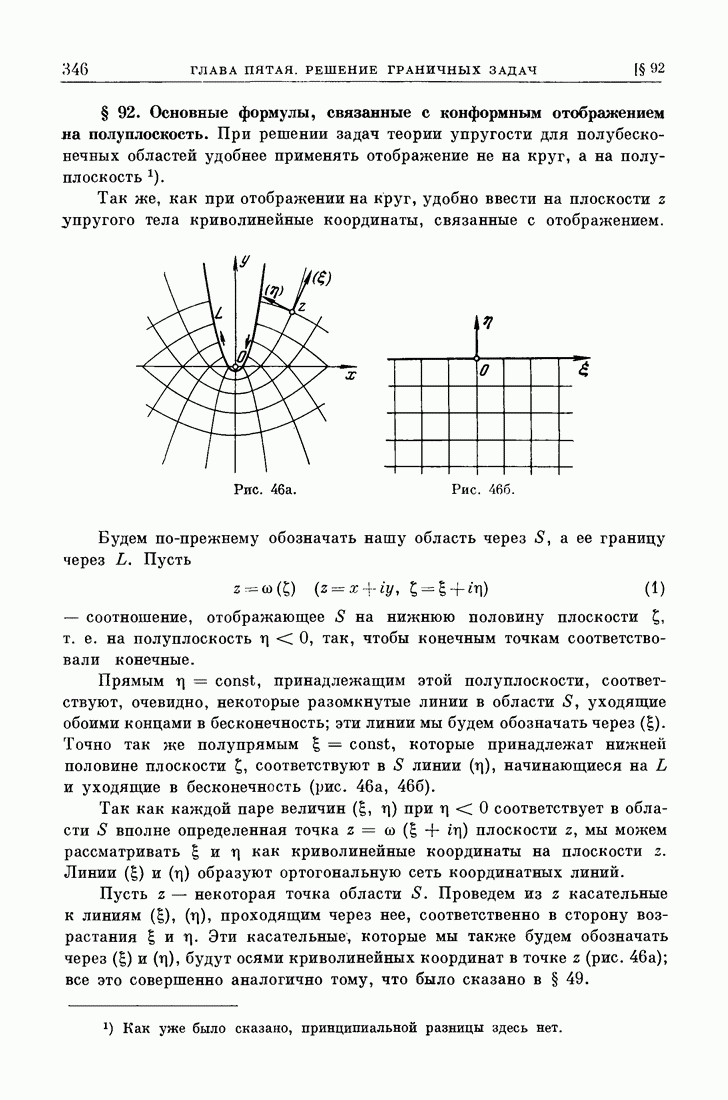
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
До сих пор мы предполагали, что в формуле (1) § 66 точка z не расположена на линии интегрирования  Пусть теперь точка z совпадает с некоторой точкой
Пусть теперь точка z совпадает с некоторой точкой  расположенной на
расположенной на  Напишем пока чисто формально:
Напишем пока чисто формально:

Если  то подынтегральная функция обращается при
то подынтегральная функция обращается при  в бесконечность, как
в бесконечность, как  Поэтому интеграл в правой части не имеет смысла, если оставаться в рамках обычного определения. Однако интегралу (1) можно при некоторых предположениях относительно функции
Поэтому интеграл в правой части не имеет смысла, если оставаться в рамках обычного определения. Однако интегралу (1) можно при некоторых предположениях относительно функции  приписать вполне определенный смысл. Именно, предположим, что точка
приписать вполне определенный смысл. Именно, предположим, что точка  не совпадает ни с одним из концов линии
не совпадает ни с одним из концов линии  (если таковые имеются), и выделим из
(если таковые имеются), и выделим из  около точки
около точки  достаточно малую дугу
достаточно малую дугу  содержащую
содержащую  и такую, что расстояния точек и
и такую, что расстояния точек и  до
до  равны между собой, т. е.
равны между собой, т. е.

Обозначим дугу  через I, а оставшуюся часть линии
через I, а оставшуюся часть линии  через
через  и рассмотрим интеграл
и рассмотрим интеграл

Этот интеграл имеет уже вполне определенный обычный смысл, так как, когда  пробегает путь интегрирования
пробегает путь интегрирования  всегда
всегда  где
где  некоторое положительное число.
некоторое положительное число.
Предположим теперь, что  стремятся к
стремятся к  так, однако, что все время соблюдается условие (2). Если при этом интеграл (3) стремится к определенному пределу, то этот предел называется главным значением интеграла (1) по Ноши.
так, однако, что все время соблюдается условие (2). Если при этом интеграл (3) стремится к определенному пределу, то этот предел называется главным значением интеграла (1) по Ноши.
Ясно, что если интеграл (1) имеет обычный (риманов) смысл, то существует и его главное значение, но обратное утверждение, вообще говоря, несправедливо.

Рис. 31.
Главное значение интеграла, если оно существует, мы будем обозначать тем же символом, что и обычный интеграл, т. е. символом (1), подразумевая, что если интеграл не имеет обычного смысла, то берется его главное значение (когда оно существует).
Мы не станем заниматься разысканием возможно общих условий существования главного значения, а укажем один весьма важный случай (вполне достаточный для наших целей), когда это существование наверное обеспечено. А именно, главное значение интеграла (1) существует, если функция  удовлетворяет в окрестности точки
удовлетворяет в окрестности точки  условию
условию  условию (см. § 65, п. 3):
условию (см. § 65, п. 3):

Мы докажем это утверждение путем фактического выражения главного значения интеграла через обычный интеграл.
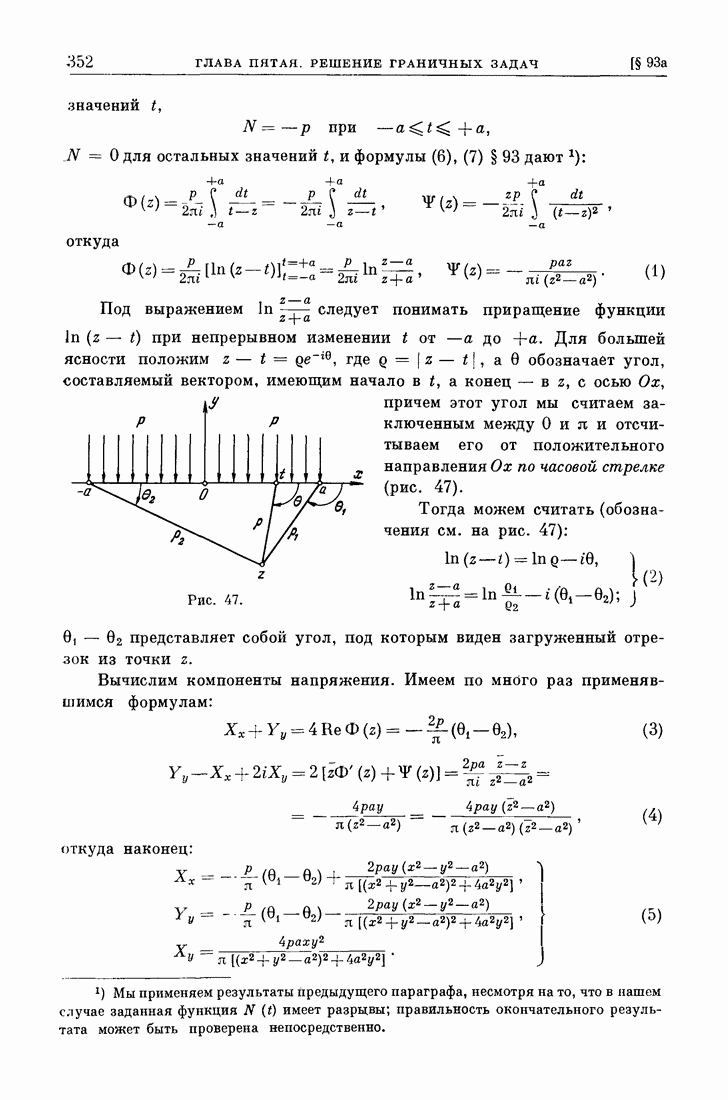
Вернемся для этого к интегралу (3) и рассмотрим сперва случай (рис. 31), когда  состоит из одной простой разомкнутой дуги
состоит из одной простой разомкнутой дуги  т. е. рассмотрим интеграл
т. е. рассмотрим интеграл

Обозначения мы выбрали так, что положительное направление на  ведет от а к
ведет от а к 
Этот интеграл мы можем представить следующим образом: 

Первый интеграл правой части стремится при  к вполне определенному пределу
к вполне определенному пределу

ибо этот интеграл — сходящийся в обычном (т. е. римановом) смысле. Действительно, на основании условия (4) имеем:

и так как  то это неравенство обеспечивает сходимость нашего интеграла в силу хорошо известного элементарного признака сходимости.
то это неравенство обеспечивает сходимость нашего интеграла в силу хорошо известного элементарного признака сходимости.
Обратимся ко второму интегралу правой Части формулы (5). Он легко вычисляется в конечном виде 

где под  на частях
на частях  линии
линии  подразумеваются любые ветви этой функции, непрерывно изменяющиеся вместе с
подразумеваются любые ветви этой функции, непрерывно изменяющиеся вместе с  на каждой из частей
на каждой из частей  в отдельности. Эти ветви могут быть выбраны произвольно на каждой из упомянутых частей, но для определенности мы свяжем их следующим условием: значение
в отдельности. Эти ветви могут быть выбраны произвольно на каждой из упомянутых частей, но для определенности мы свяжем их следующим условием: значение  при
при  получается из значения
получается из значения  при
при  путем непрерывного изменения
путем непрерывного изменения  при движении точки
при движении точки  из положения в положение
из положения в положение  по (бесконечно малой) полуокружности, расположенной слева от
по (бесконечно малой) полуокружности, расположенной слева от  (по отношению к наблюдателю, смотрящему вдоль положительного направления, выбранного на
(по отношению к наблюдателю, смотрящему вдоль положительного направления, выбранного на  рис. 31, пунктир). Тогда выбор ветви
рис. 31, пунктир). Тогда выбор ветви  на
на  вполне определяет выбор ветви на
вполне определяет выбор ветви на  подразумевая, что этот выбор сделан, мы можем написать:
подразумевая, что этот выбор сделан, мы можем написать:

где следует подразумевать

при только что указанном выборе логарифмов. Так как, далее, по условию  то
то

где  — угол, указанный на рис. 31. Ясно, далее, что при
— угол, указанный на рис. 31. Ясно, далее, что при  будем иметь:
будем иметь:  Поэтому, переходя к пределу в выражении
Поэтому, переходя к пределу в выражении  получаем:
получаем:

Следовательно, интеграл (3) стремится к определенному пределу; этот предел и есть по определению главное значение интеграла

оно дается формулой, вытекающей из предыдущих:

где в правой части фигурирует интеграл в обычном (римановом) смысле.
Пусть теперь  произвольная линия указанного в п. 1 § 65 вида. Тогда, выделив на
произвольная линия указанного в п. 1 § 65 вида. Тогда, выделив на  произвольную дугу
произвольную дугу  содержащую точку
содержащую точку  (так, чтобы
(так, чтобы  не совпадали с
не совпадали с  можем переписать интеграл (3) так:
можем переписать интеграл (3) так:

При  если при этом соблюдается условие (2), первый интеграл правой части стремится, как было показано, к определенному пределу; второй же интеграл от
если при этом соблюдается условие (2), первый интеграл правой части стремится, как было показано, к определенному пределу; второй же интеграл от  не зависит. Следовательно, интеграл (3) стремится к определенному пределу, который и есть по определению главное значение интеграла (1); на основании предыдущего это главное значение дается формулой:
не зависит. Следовательно, интеграл (3) стремится к определенному пределу, который и есть по определению главное значение интеграла (1); на основании предыдущего это главное значение дается формулой:

Эта формула мало симметрична, и мы ею в дальнейшем пользоваться не будем; мы вывели ее лишь для того, чтобы показать, что главное
значение по Коши, при указанном выше условии насчет функции  существует и может быть выражено при помощи обычных интегралов.
существует и может быть выражено при помощи обычных интегралов.
Замечание 1. Формула (8) значительно упрощается, если  простой замкнутый контур. Мы можем получить формулу для этого случая исходя из формулы (7), представив себе, что конец
простой замкнутый контур. Мы можем получить формулу для этого случая исходя из формулы (7), представив себе, что конец  дуги
дуги  приближается к концу а, так что в пределе мы получим замкнутый контур
приближается к концу а, так что в пределе мы получим замкнутый контур  Считая для определенности, что положительное направление на этом контуре выбрано так, что, идя в этом направлении, мы оставляем конечную часть плоскости, ограниченную контуром
Считая для определенности, что положительное направление на этом контуре выбрано так, что, идя в этом направлении, мы оставляем конечную часть плоскости, ограниченную контуром  слева, будем, как легко видеть, иметь в пределе (при
слева, будем, как легко видеть, иметь в пределе (при 

и формула (7) примет вид

Замечание 2. Считая, что  удовлетворяет условию
удовлетворяет условию  при рассматриваемых значениях
при рассматриваемых значениях  отметим следующее обстоятельство.
отметим следующее обстоятельство.
При определении главного значения интеграла по Коши нет необходимости полагать, что условие (2), т. е. условие  соблюдается точно. Достаточно считать, что при
соблюдается точно. Достаточно считать, что при 

т. е. что  эквивалентные бесконечно малые величины. Действительно ясно, что и при этом условии мы будем также иметь
эквивалентные бесконечно малые величины. Действительно ясно, что и при этом условии мы будем также иметь

и что поэтому все наши предыдущие рассуждения и формулы останутся в силе. В частности, условие (2) можно заменить следующим:

где  обозначают длины дуг и
обозначают длины дуг и  иначе говоря, точка
иначе говоря, точка  разделяет дугу
разделяет дугу  на две равные по длине части.
на две равные по длине части.
Замечание 3. Очевидно, что формулы и заключения этого параграфа останутся в силе и в случае, если функция  удовлетворяет при данном
удовлетворяет при данном  условию
условию  лишь в точке
лишь в точке  (§ 65, п. 3, замечание), т. е. условию
(§ 65, п. 3, замечание), т. е. условию

(при t достаточно близком к  не обязательно удовлетворяя условию
не обязательно удовлетворяя условию  для любых двух точек в окрестности
для любых двух точек в окрестности  Однако в этом случае заключения и формулы будут, вообще говоря, справедливы лишь для данного значения
Однако в этом случае заключения и формулы будут, вообще говоря, справедливы лишь для данного значения 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
- VI. ТЕОРИЯ ТРЕЩИН
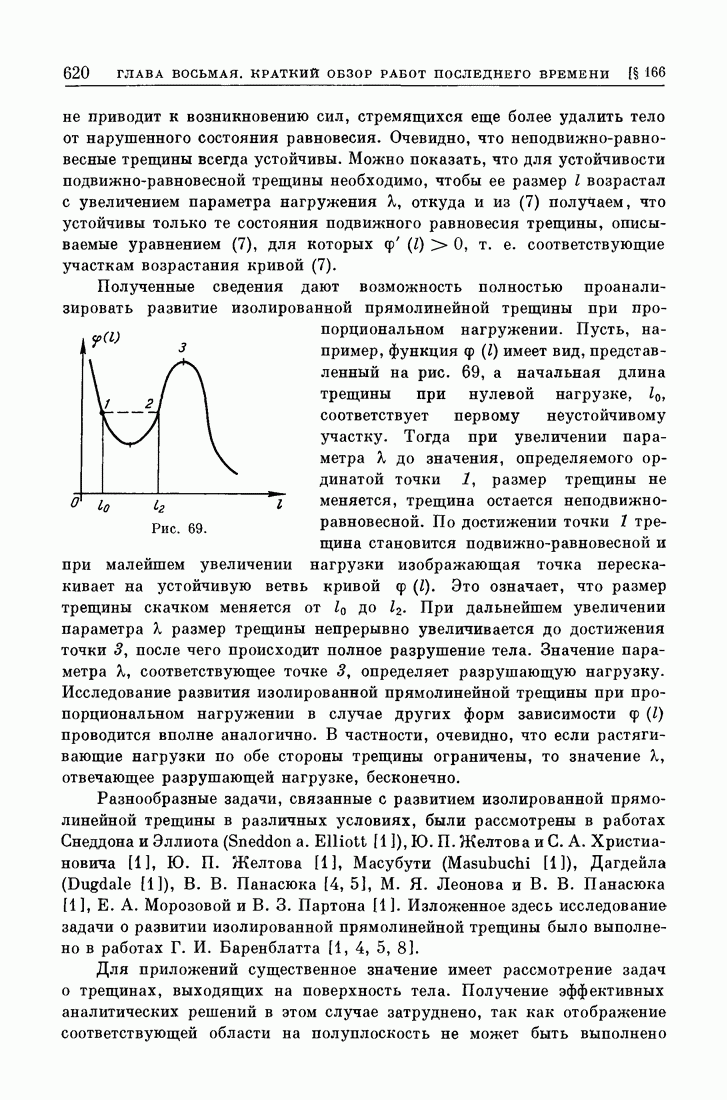
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ