| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ
1. В гл. II был приведен простой вывод формул общего представления решения уравнений плоской теории упругости при отсутствии объемных сил, по существу совпадающих с формулами Г. В. Колосова.
Эти формулы можно, разумеется, вывести и другими простыми способами. Одним из них является тот, которым пользовался сам Г. В. Колосов [1, 2]. Я не остановился на этом в основном тексте, так как способ получения формул общего представления существенного значения не имеет: существенно лишь то, как используются эти формулы для решения конкретных задач. Однако вследствие того, что некоторые авторы придают способу вывода формул общего представления определенное (на мой взгляд — преувеличенное) значение, я счел целесообразным сказать здесь несколько слов об упомянутых способах и привести один из них, охватывающий также случай наличия объемных сил.
2. Большинство выводов, приводимых различными авторами, основано на следующем приеме. Вместо действительных переменных х, у вводятся комплексные переменные

так что различные функции действительных переменных, скажем функция  представляются в виде функций двух переменных
представляются в виде функций двух переменных 

при этом с функцией  оперируют иногда как с функцией двух независимых комплексных переменных
оперируют иногда как с функцией двух независимых комплексных переменных  Например, общее решение уравнения
Например, общее решение уравнения

где  заданная и
заданная и  искомая функции, пишут в виде
искомая функции, пишут в виде

где  - «произвольная» (подразумевается — аналитическая) функция
- «произвольная» (подразумевается — аналитическая) функция
от  Очевидно, что таким рассуждениям можно придать определенный смысл лишь в частных случаях (о некоторых из них см. ниже п. 3) и при весьма существенных оговорках. Формулы вида
Очевидно, что таким рассуждениям можно придать определенный смысл лишь в частных случаях (о некоторых из них см. ниже п. 3) и при весьма существенных оговорках. Формулы вида  иногда применял и Г. В. Колосов; см.-, например, его книгу [6], § 8 и статью [3]. Следует, однако, отметить, что выводы формул общего представления (при отсутствии объемных сил), данные в его основных работах [1, 2], предшествующих названным, можно считать вполне строгим, если добавить к ним некоторые, впрочем почти очевидные, пояснения.
иногда применял и Г. В. Колосов; см.-, например, его книгу [6], § 8 и статью [3]. Следует, однако, отметить, что выводы формул общего представления (при отсутствии объемных сил), данные в его основных работах [1, 2], предшествующих названным, можно считать вполне строгим, если добавить к ним некоторые, впрочем почти очевидные, пояснения.
Ниже, в п. 4, приведем один вывод, аналогичный упомянутым выше, но строго обоснованный, и начнем с некоторых предварительных замечаний. 3. Введем в рассмотрение следующие операции:

применимые к любым дифференцируемым в некоторой области  функциям
функциям  где
где  действительные функции действительных переменных х, у.
действительные функции действительных переменных х, у.

Если

то, в силу условий Коши — Римана,  где
где  аналитическая функция от z, и обратно, а если
аналитическая функция от z, и обратно, а если

то  где
где  аналитическая функция от z, и обратно. Рассмотрим теперь дифференциальное уравнение
аналитическая функция от z, и обратно. Рассмотрим теперь дифференциальное уравнение

где  искомая, а
искомая, а  заданная функции, или в раскрытом виде систему дифференциальных уравнений
заданная функции, или в раскрытом виде систему дифференциальных уравнений

Если  то уравнение (3) и эквивалентная ему система (3а) обращаются в однородные и выражают условие Коши — Римана. Ясно, что общим решением однородного уравнения, соответствующего
то уравнение (3) и эквивалентная ему система (3а) обращаются в однородные и выражают условие Коши — Римана. Ясно, что общим решением однородного уравнения, соответствующего
уравнению (3), является произвольная аналитическая функция  комплексного переменного z и что общее решение неоднородного уравнения (3) получим, прибавив к какому-либо его частному решению произвольную аналитическую функцию от
комплексного переменного z и что общее решение неоднородного уравнения (3) получим, прибавив к какому-либо его частному решению произвольную аналитическую функцию от 
Что же касается частных решений, то при некоторых общих условиях, которые будут указаны ниже, одним из таких решений будет функция  определяемая формулой
определяемая формулой

где  произвольная точка области
произвольная точка области 
Мы будем считать здесь и в дальнейшем, что область  подчинена тем же общим условиям, как и в основном тексте книги, и что в случае бесконечной области
подчинена тем же общим условиям, как и в основном тексте книги, и что в случае бесконечной области

Справедливость утверждения, что функция  определяемая формулой (4), является (частным) решением уравнения (3), можно доказать при некоторых условиях, налагаемых на функцию
определяемая формулой (4), является (частным) решением уравнения (3), можно доказать при некоторых условиях, налагаемых на функцию  непосредственной проверкой, не совсем, впрочем, простой, так как дифференцирование под знаком интеграла здесь недопустимо вследствие сильной сингулярности подынтегрального выражения. В п. 5 настоящего Добавления мы приведем доказательство, применимое к случаю, когда функция
непосредственной проверкой, не совсем, впрочем, простой, так как дифференцирование под знаком интеграла здесь недопустимо вследствие сильной сингулярности подынтегрального выражения. В п. 5 настоящего Добавления мы приведем доказательство, применимое к случаю, когда функция  непрерывно дифференцируема в области
непрерывно дифференцируема в области  В п. 6 будут указаны и более общие условия, при которых наше утверждение остается справедливым. Общее решение уравнения (3) будет дано формулой
В п. 6 будут указаны и более общие условия, при которых наше утверждение остается справедливым. Общее решение уравнения (3) будет дано формулой

где  произвольная аналитическая функция.
произвольная аналитическая функция.
Аналогично одно из частных решений  уравнения
уравнения

дается формулой

а общее решение — формулой

где  произвольная аналитическая функция.
произвольная аналитическая функция.
Отметим еще, что во многих частных случаях можно получить решение уравнений (3) или (5) совершенно элементарно.
Например, если  представляет собою полином или, более общо, рациональную функцию от ее,
представляет собою полином или, более общо, рациональную функцию от ее,  то эту функцию можно представить в виде полинома или рациональной функции от
то эту функцию можно представить в виде полинома или рациональной функции от 

(теперь уже такое представление имеет определенный смысл) и тогда, например, решение уравнения (5), как легко непосредственно проверить, представится в виде

где  произвольная аналитическая функция от z, а интеграл вычисляется так, как если бы величина z оставалась постоянной. Как было уже сказано в п. 2, формула (7) теряет смысл в общем случае.
произвольная аналитическая функция от z, а интеграл вычисляется так, как если бы величина z оставалась постоянной. Как было уже сказано в п. 2, формула (7) теряет смысл в общем случае.
Вообще на практике можно часто обойтись без применения формул (4) или (6), пользуясь теми или иными приемами. Приведем два простых примера, которые нам понадобятся в дальнейшем. Пусть требуется решить уравнение вида (5): 

 заданная непрерывная функция в
заданная непрерывная функция в  удовлетворяющая в случае бесконечной области условию (4а) при
удовлетворяющая в случае бесконечной области условию (4а) при  Замечая, что, очевидно,
Замечая, что, очевидно,

можем представить уравнение (8) в виде

(дифференцирование под знаком интеграла здесь допустимо), откуда непосредственно следует, что одним из частных решений уравнения (8) будет

Поступая аналогично, мы можем представить частное решение уравнения

в виде

4. Перейдем теперь к упомянутому выше выводу формул общего представления. Будем исходить из уравнений плоской теории упругости в смещениях  формула (4)]:
формула (4)]:

в области  где, как всегда,
где, как всегда,  компоненты смещения,
компоненты смещения,  компоненты объемной силы и
компоненты объемной силы и

Уравнения (1) можно записать в виде одного комплексного уравнения:

где положено

Отметим, что

Операцию  следует рассматривать как
следует рассматривать как  понимая операции
понимая операции  как указано в п. 3 [формулы (1)].
как указано в п. 3 [формулы (1)].
Уравнение (2) можно еще представить в виде

откуда, применяя формулу (4) п. 3, выводим

где  произвольная аналитическая функция, которую мы представили в виде производной от произвольной аналитической функции, а множитель
произвольная аналитическая функция, которую мы представили в виде производной от произвольной аналитической функции, а множитель  введен для удобства; как всегда,
введен для удобства; как всегда,

Складывая формулу (4) с формулой, полученной переходом к сопряженным значениям, находим:

Подставляя это значение  в формулу (4) и пользуясь на этот раз формулами (9) и
в формулу (4) и пользуясь на этот раз формулами (9) и  п. 3, получим после простых выкладок и введения
п. 3, получим после простых выкладок и введения
надлежащих обозначений следующую формулу:

где  некоторая произвольная аналитическая функция.
некоторая произвольная аналитическая функция.
Формула (5) дает общее представление решения уравнений плоской теории упругости в смещениях. Если в (5) положить  то получим формулу, относящуюся к случаю отсутствия объемных сил, которой мы постоянно пользовались в основном тексте. Полагая же
то получим формулу, относящуюся к случаю отсутствия объемных сил, которой мы постоянно пользовались в основном тексте. Полагая же  мы получим как раз то частное решение уравнений плоской теории упругости при наличии объемных сил, которое было найдено иным путем в § 57а.
мы получим как раз то частное решение уравнений плоской теории упругости при наличии объемных сил, которое было найдено иным путем в § 57а.
Для вывода формул, выражающих компоненты напряжения, воспользуемся формулами:

вытекающими из формул (2) § 25.
Подставляя в эти формулы выражение (5) для  получим без труда:
получим без труда:

Эти формулы при отсутствии объемных сил, т. е. при  совпадают с приведенными в основном тексте.
совпадают с приведенными в основном тексте.
Следует еще отметить, что аналогичные выводы формул общего представления при наличии объемных сил имеются и в некоторых работах Г. В. Колосова, например в его книге [6]. Однако выводы эти нельзя признать строгими (по крайней мере без существенных оговорок), так как автор пользуется приемом, о котором говорилось в п. 2, в частности формулами вида 
Для случая, когда существует потенциал объемных сил, т. е. когда

где  некоторая функция от х, у, формулы общего представления были даны С. Г. Михлиным [10].
некоторая функция от х, у, формулы общего представления были даны С. Г. Михлиным [10].
Этот же случай был позднее рассмотрен Стевенсоном (Stevenson [1, 2]). В первой из указанных работ этот автор пользуется формулами вида  п. 2, во второй же он дает вывод формул общего представления, не пользуясь формулами вида
п. 2, во второй же он дает вывод формул общего представления, не пользуясь формулами вида  В полученных им формулах общего представления фигурирует некоторая функция
В полученных им формулах общего представления фигурирует некоторая функция  определяемая условием
определяемая условием

автор не дает явного выражения для этой функции.
Формулы общего представления при наличии объемных сил и некоторые их приложения даны также Ю (Yi-Yuan Yu [1 ]) и Ф. Шеленговским [1].
5. Приведем в заключение временно опущенное нами доказательство утверждения, что формула (4) п. 3 дает одно из частных решений уравнения (3) п. 3. Это относительно простое доказательство было сообщено мне  Векуа.
Векуа.
Для упрощения обозначений мы будем теперь вместо  писать
писать  где по-прежнему
где по-прежнему  а вместо
а вместо  писать
писать  или
или  так что формула (4) п. 3 представится в виде
так что формула (4) п. 3 представится в виде

Мы будем по-прежнему считать, что в случае бесконечной области при больших 

Кроме того, мы будем считать, что функция  т. е. функция
т. е. функция  формулы (4) п. 3, непрерывно дифференцируема, т. е. имеет непрерывные частные производные по и
формулы (4) п. 3, непрерывно дифференцируема, т. е. имеет непрерывные частные производные по и 
Нам надлежит доказать, что в любой точке  области
области 

Очевидно, достаточно доказать справедливость этой формулы для сколь угодно малой окрестности произвольно фиксированной точки  области
области  В качестве
В качестве  мы возьмем круг радиуса
мы возьмем круг радиуса  с центром в точке
с центром в точке  целиком расположенный в области
целиком расположенный в области  В дальнейшем мы будем считать, что z изменяется внутри круга
В дальнейшем мы будем считать, что z изменяется внутри круга 
Функцию  можно теперь представить в виде
можно теперь представить в виде

где  обозначают интегралы вида (1), но взятые соответственно по областям
обозначают интегралы вида (1), но взятые соответственно по областям 
Очевидно, что  голоморфная в
голоморфная в  функция и поэтому
функция и поэтому

в области  Следовательно, нам остается показать, что в этой области
Следовательно, нам остается показать, что в этой области

где

Распространим теперь функцию  фигурирующую в предыдущем интеграле и заданную в круге
фигурирующую в предыдущем интеграле и заданную в круге  на всю плоскость так, чтобы полученная новая функция
на всю плоскость так, чтобы полученная новая функция  определенная уже на всей плоскости и совпадающая в области
определенная уже на всей плоскости и совпадающая в области  с функцией
с функцией  была непрерывна и непрерывно дифференцируема всюду и удовлетворяла условию (1а). Такое распространение можно, как легко видеть, осуществить бесчисленным множеством способов. Положим теперь:
была непрерывна и непрерывно дифференцируема всюду и удовлетворяла условию (1а). Такое распространение можно, как легко видеть, осуществить бесчисленным множеством способов. Положим теперь:

где  обозначает всю плоскость,
обозначает всю плоскость,  и
и  интегралы, распространенные соответственно по областям
интегралы, распространенные соответственно по областям 
Ясно, что  голоморфная в
голоморфная в  функция и поэтому
функция и поэтому

Таким образом, нам остается показать, что в области 

Заменой переменных интегрирования функцию  можно представить в виде
можно представить в виде

Отсюда сразу вытекает, что функция  непрерывно дифференцируема на всей плоскости
непрерывно дифференцируема на всей плоскости  Дифференцируя под знаком интеграла (что теперь допустим
Дифференцируя под знаком интеграла (что теперь допустим  ), получим:
), получим:

или еще

где  обозначает область, заключенную между концентрическими окружностями
обозначает область, заключенную между концентрическими окружностями  положительная величина.
положительная величина.
Применим теперь формулу Остроградского — Грина, преобразующую двойной интеграл в простой. Как легко видеть, эту формулу можно в комплексной форме представить так:

где  некоторая конечная область на плоскости,
некоторая конечная область на плоскости,  ее граница, снабженная определенным положительным направлением; мы предполагаем, что область
ее граница, снабженная определенным положительным направлением; мы предполагаем, что область  и ее граница
и ее граница  подчинены тем же условиям, что в основном тексте книги.
подчинены тем же условиям, что в основном тексте книги.
В нашем случае эта формула дает

и утверждение доказано.
6. Можно показать, что равенство (2) п. 5 имеет место и в случае, когда функция  не будучи дифференцируемой, удовлетворяет условию Гёльдера. Доказательство этого предложения дано в монографии И. Н. Векуа [8], гл. 1, § 8.
не будучи дифференцируемой, удовлетворяет условию Гёльдера. Доказательство этого предложения дано в монографии И. Н. Векуа [8], гл. 1, § 8.
Если функция  лишь непрерывна, то формула (2) п. 5, вообще говоря, несправедлива, так как в этом случае функция
лишь непрерывна, то формула (2) п. 5, вообще говоря, несправедлива, так как в этом случае функция  может не иметь частных производных по х и у в обычном смысле. Но можно обобщить понятие частных производных таким образом, чтобы функция
может не иметь частных производных по х и у в обычном смысле. Но можно обобщить понятие частных производных таким образом, чтобы функция  оставалась дифференцируемой и в этом случае. А именно, если понимать частные производные в смысле С. Л. Соболева, то в случае, когда функция
оставалась дифференцируемой и в этом случае. А именно, если понимать частные производные в смысле С. Л. Соболева, то в случае, когда функция  лишь непрерывна, равенство
лишь непрерывна, равенство  имеет место почти всюду в
имеет место почти всюду в  Более того, это равенство имеет место почти всюду в
Более того, это равенство имеет место почти всюду в  если функция
если функция  лишь интегрируема по Лебегу. Доказательство этих результатов дано И. Н. Векуа [8].
лишь интегрируема по Лебегу. Доказательство этих результатов дано И. Н. Векуа [8].
ЦИТИРОВАННАЯ ЛИТЕРАТУРА
(см. скан)
(см. скан)
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ УПРУГОГО ТЕЛА
- § 2. Напряжения.
- § 3. Компоненты напряжения. Зависимость напряжения от ориентировки площадки.
- § 4. Уравнения, связывающие компоненты напряжения.
- § 5. Замена координат. Инвариантная квадратичная форма. Тензор напряжений.
- § 6. Поверхность напряжений. Главные напряжения.
- § 7. Нахождение главных напряжений и главных осей.
- § 8. Случай плоского напряженного состояния.
- II. ДЕФОРМАЦИЯ
- § 10. Аффинное преобразование.
- § 11. Бесконечно малое аффинное преобразование.
- § 12. Разложение бесконечно малого преобразования на чистую деформацию и жесткое перемещение.
- § 13. Инвариантная квадратичная форма, связанная с деформацией. Поверхность деформаций, главные оси. Замена координат.
- § 14. Деформация общего вида.
- § 15. Определение смещений по компонентам деформации. Условия совместимости Сен-Венана.
- III. ОСНОВНОЙ ЗАКОН ТЕОРИИ УПРУГОСТИ. ОСНОВНЫЕ УРАВНЕНИЯ
- § 16. Основной закон теории упругости (обобщенный закон Гука).
- § 17. Случай изотропного тела.
- § 18. Основные уравнения статики упругого изотропного тела.
- § 19. Простейшие случаи упругого равновесия. Основные упругие постоянные.
- § 20. Основные граничные задачи статики упругого тела. Единственность решения.
- § 21. Основные уравнения в компонентах смещения.
- § 22. Уравнения в компонентах напряжения.
- § 23. Замечание о фактическом решении основных задач. Принцип Сен-Венана.
- § 24. Динамические уравнения. Об основных задачах динамика упругого тела.
- ГЛАВА ВТОРАЯ. ОБЩИЕ ФОРМУЛЫ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 25. Плоская деформация.
- § 26. Деформация тонкой пластинки силами, действующими в ее плоскости.
- § 27. Основные уравнения плоской теории упругости.
- § 28. Приведение к случаю отсутствия объемных сил.
- II. ФУНКЦИЯ НАПРЯЖЕНИЙ. КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ОБЩЕГО РЕШЕНИЯ УРАВНЕНИЙ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 30. Функция напряжений.
- § 31. Комплексное представление бигармонической функции.
- § 32. Комплексное представление смещений и напряжений.
- § 33. Механическое значение функции f. Выражения для главного вектора и главного момента.
- § 34. Степень определенности введенных функций.
- § 35. Общие формулы для конечной многосвязной области.
- § 36. Случай бесконечной области.
- § 37. Некоторые свойства, вытекающие из аналитического характера решения. Об аналитическом продолжении через данный контур.
- § 38. Замена прямоугольных координат.
- § 39. Полярные координаты.
- § 40. Основные граничные задачи. Единственность решения.
- § 41. Приведение основных задач к задачам теории функций комплексного переменного.
- § 41а. Дополнительные замечания.
- § 42. Понятие регулярного решения. Единственность регулярного решения.
- § 43. О сосредоточенных силах, приложенных к границе.
- § 44. Зависимость напряженного состояния от упругих постоянных.
- III. МНОГОЗНАЧНЫЕ СМЕЩЕНИЯ. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ
- § 45. Многозначные смещения. Дислокации.
- § 46. Температурные напряжения.
- IV. ПРЕОБРАЗОВАНИЕ ОСНОВНЫХ ФОРМУЛ ПРИ КОНФОРМНОМ ОТОБРАЖЕНИИ
- § 47. Конформное отображение.
- § 48. Простейшие примеры конформного отображения.
- § 49. Криволинейные координаты, связанные с конформным отображением на круговую область.
- § 51. Граничные условия в преобразованной области.
- ГЛАВА ТРЕТЬЯ. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПРИ ПОМОЩИ СТЕПЕННЫХ РЯДОВ
- § 52. О рядах Фурье в комплексной форме.
- § 53. О характере сходимости рядов Фурье.
- II. РЕШЕНИЕ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОКРУЖНОСТЬЮ
- § 54. Решение первой основной задачи для круга.
- § 55. Решение второй основной задачи для круга.
- § 56. Решение первой основной задачи для бесконечной плоскости с круговым отверстием.
- § 56а. Примеры.
- § 57. О сосредоточенных силах вообще.
- § 57а. Применение к случаю наличия объемных сил.
- § 58. Некоторые случаи равновесия бесконечной пластинки со вставленной круговой шайбой из другого материала.
- III. РЕШЕНИЕ ДЛЯ КРУГОВОГО КОЛЬЦА
- § 59. Решение первой основной задачи для кругового кольца.
- § 59а. Примеры и обобщения.
- § 60. Многозначные смещения в случае кругового кольца.
- § 61. Приложение.
- § 62. Температурные напряжения в полом круговом цилиндре.
- IV. ПРИМЕНЕНИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
- § 64. Пример применения отображения на круговое кольцо. Решение основных задач для сплошного эллипса.
- ГЛАВА ЧЕТВЕРТАЯ. ОБ ИНТЕГРАЛАХ ТИПА КОШИ
- I. ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛОВ ТИПА КОШИ
- § 66. Интегралы типа Коши.
- § 67. Значения интеграла типа Коши на линии интегрирования. Главное значение интеграла по Коши.
- § 68. Граничные значения интеграла типа Коши. Формулы Сохоцкого — Племеля.
- § 69. О производных интеграла типа Коши.
- § 70. Некоторые элементарные формулы, облегчающие вычисление интегралов типа Коши.
- § 71. Об интегралах типа Коши по бесконечной прямой.
- § 72. Продолжение.
- II. О ГРАНИЧНЫХ ЗНАЧЕНИЯХ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 74. Обобщение.
- § 75. Теорема Гарнака (Harnack).
- § 76. Некоторые специальные формулы для круга и полуплоскости.
- § 77. Простейшие приложения: решение основных задач теории потенциала для круга и полуплоскости.
- ГЛАВА ПЯТАЯ. ПРИМЕНЕНИЕ ИНТЕГРАЛОВ ТИПА КОШИ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- I. ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ ОДНИМ ЗАМКНУТЫМ КОНТУРОМ
- § 78. Приведение основных задач к функциональным уравнениям.
- § 79. Приведение к уравнениям Фредгольма. Теоремы существования.
- § 79а. О некоторых других применениях предыдущих интегральных уравнений.
- II. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ. ПРИЛОЖЕНИЕ К ПРИБЛИЖЕННОМУ РЕШЕНИЮ ДЛЯ ОБЛАСТЕЙ ОБЩЕГО ВИДА
- § 80а. Примеры.
- § 81. Решение второй основной задачи для круга.
- § 82. Решение первой основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 82а. Примеры.
- § 83. Решение второй основной задачи для бесконечной плоскости с эллиптическим отверстием.
- § 83а. Примеры.
- § 84. Общее решение первой основной задачи для областей, отображаемых на круг при помощи полиномов.
- § 85. Обобщение на случай отображения при помощи рациональных функций.
- § 86. Решение второй основной задачи. О решении основной смешанной задачи.
- § 87. Другой способ решения основных задач.
- § 87a. Пример.
- § 88. Дальнейшие примеры. Приложение к некоторым другим граничным задачам.
- § 89. Приложение к приближенному решению в общем случае.
- III. РЕШЕНИЕ ОСНОВНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ОБЛАСТЕЙ
- § 91. Общие формулы для полубесконечных областей.
- § 92. Основные формулы, связанные с конформным отображением на полуплоскость.
- § 93. Решение первой основной задачи для полуплоскости.
- § 93а. Пример.
- § 94. Решение второй основной задачи.
- § 95. Решение основных задач для областей, отображаемых на полуплоскость при помощи рациональных функций. Случай параболического контура.
- IV. НЕКОТОРЫЕ ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ. ОБОБЩЕНИЯ
- § 97. Об одном общем методе решения задач для многосвязных областей.
- § 98. Интегральные уравнения, предложенные автором.
- § 99. Применение к контурам с угловыми точками.
- § 100. О численном решении интегральных уравнений плоской теории упругости.
- § 101. Интегральные уравнения Шермана — Лауричелла.
- § 102. Решение первой и второй основных задач по методу Д. И. Шермана.
- § 103. О решении основной смешанной задачи и некоторых других граничных задач по способу Д. И. Шермана.
- § 104. Обобщения на случай анизотропных тел.
- § 105. О других применениях общих представлений решения.
- ГЛАВА ШЕСТАЯ. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ ПУТЕМ ПРИВЕДЕНИЯ К ЗАДАЧЕ СОПРЯЖЕНИЯ
- § 106. Кусочно-голоморфные функции.
- § 107. Задача сопряжения.
- § 108. Определение кусочно-голоморфной функции по заданному скачку.
- § 109. Одно приложение.
- § 109а. Пример.
- § 110. Решение задачи …
- § 111. Случай разрывного коэффициента.
- II. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ПОЛУПЛОСКОСТИ И ДЛЯ ПЛОСКОСТИ С ПРЯМОЛИНЕЙНЫМИ ЩЕЛЯМИ
- § 113. Решение первой и второй основных задач для полуплоскости
- § 114. Решение основной смешанной задачи.
- § 114а. Примеры.
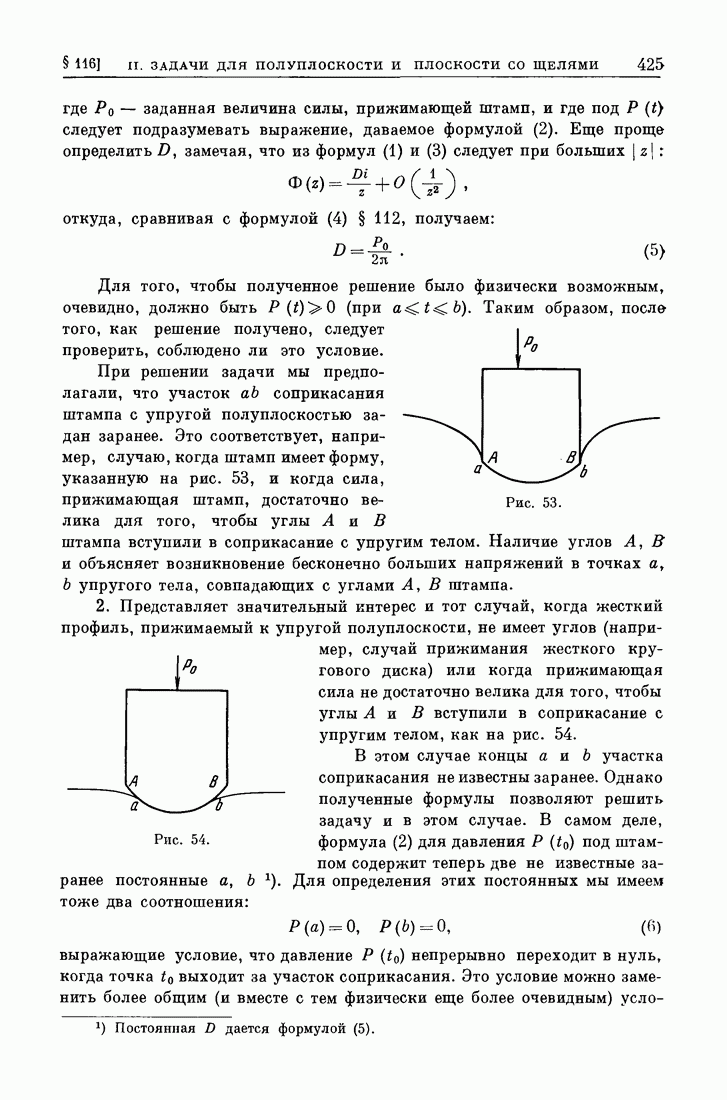
- § 115. Задача давления жестких штампов при отсутствии трения.
- § 116. Продолжение.
- § 116а. Примеры
- § 117. Равновесие жесткого штампа на границе упругой полуплоскости при наличии трения.
- § 117а. Примеры
- § 118. Другой способ решения граничных задач для полуплоскости.
- § 119. Задача соприкасания двух упругих тел (обобщенная плоская задача Герца).
- § 120. Граничные задачи для плоскости с прямолинейными разрезами
- III. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТИ, ОГРАНИЧЕННОЙ ОКРУЖНОСТЬЮ, И ДЛЯ БЕСКОНЕЧНОЙ ПЛОСКОСТИ, РАЗРЕЗАННОЙ ВДОЛЬ ДУГ ОКРУЖНОСТИ
- § 121. Преобразование общих формул для области, ограниченной окружностью.
- § 122. Решение первой и второй основных задач для области, ограниченной окружностью.
- § 123. Основная смешанная задача для области, ограниченной окружностью.
- § 123а. Пример.
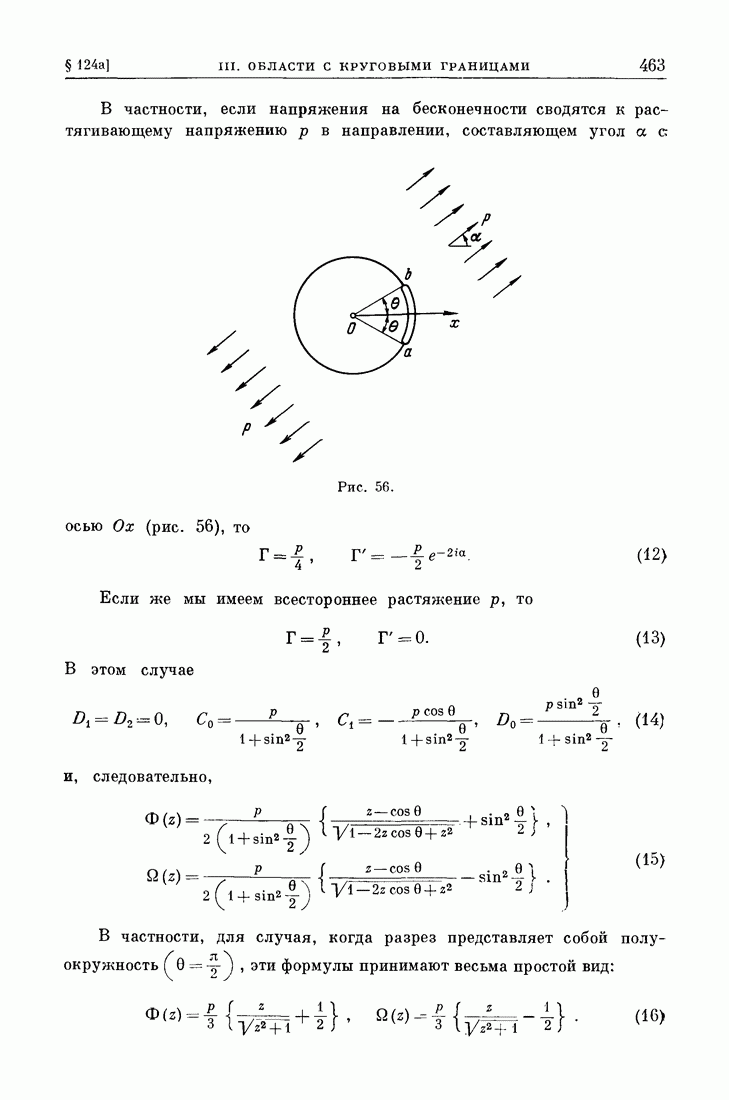
- § 124. Граничные задачи для плоскости, разрезанной вдоль дуг окружности.
- § 124а. Пример.
- IV. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЛАСТЕЙ, ОТОБРАЖАЕМЫХ НА КРУГ ПРИ ПОМОЩИ РАЦИОНАЛЬНЫХ ФУНКЦИИ
- § 126. Решение первой и второй основных задач.
- § 127. Решение основной смешанной задачи.
- § 127а. Пример.
- § 128. Задача соприкасания с жестким профилем.
- § 128а. Примеры.
- ГЛАВА СЕДЬМАЯ. РАСТЯЖЕНИЕ, КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ И СОСТАВНЫХ БРУСЬЕВ
- I. КРУЧЕНИЕ И ИЗГИБ ОДНОРОДНЫХ БРУСЬЕВ (ЗАДАЧА СЕН-ВЕНАНА)
- § 130. Некоторые формулы.
- § 131. Общее решение задачи кручения.
- § 132. Комплексная функция кручения. Функция напряжений.
- § 133. О решении задачи кручения для различных частных случаев.
- § 134. Применение конформного отображения.
- § 134а. Примеры.
- § 135. Растяжение продольными силами.
- § 136. Изгиб парами, приложенными на концах.
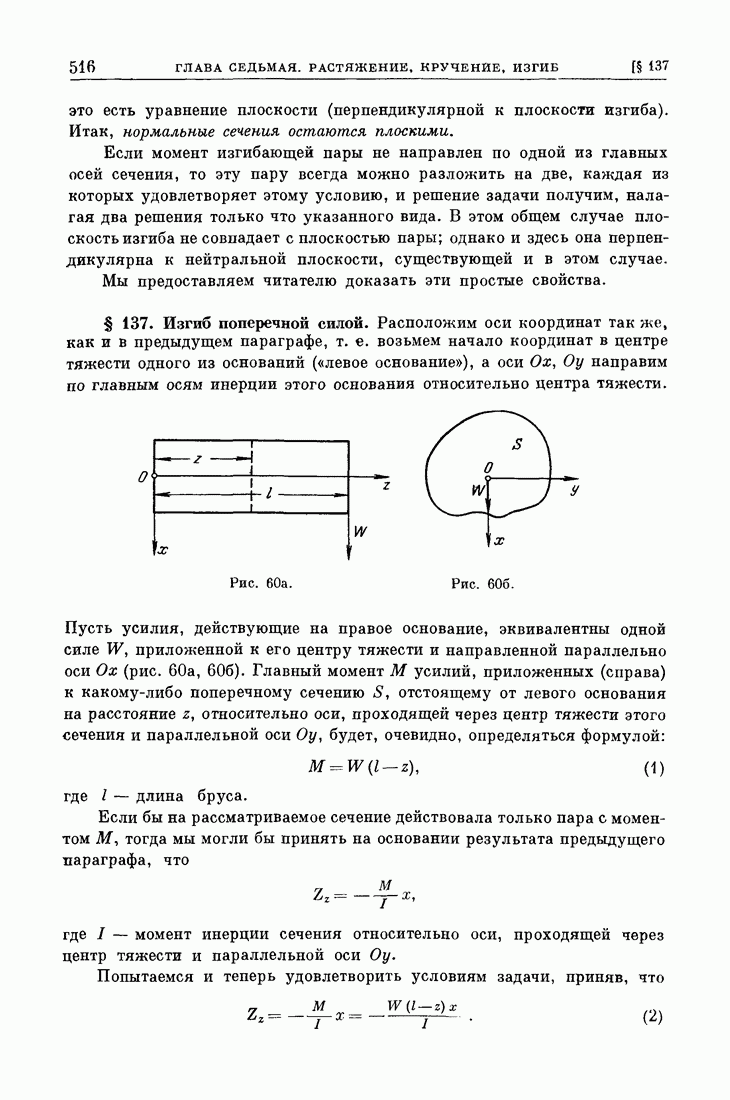
- § 137. Изгиб поперечной силой.
- § 138. О решении задачи изгиба для различных сечений.
- II. КРУЧЕНИЕ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ
- § 140. Решение при помощи интегральных уравнений.
- III. РАСТЯЖЕНИЕ И ИЗГИБ БРУСЬЕВ, СОСТАВЛЕННЫХ ИЗ РАЗЛИЧНЫХ МАТЕРИАЛОВ С ОДНИМ И ТЕМ ЖЕ КОЭФФИЦИЕНТОМ ПУАССОНА
- § 142. Растяжение.
- § 143. Изгиб парой.
- § 144. Изгиб поперечной силой.
- IV. РАСТЯЖЕНИЕ И ИЗГИБ В СЛУЧАЕ РАЗЛИЧНЫХ КОЭФФИЦИЕНТОВ ПУАССОНА
- § 146. Задача растяжения и изгиба парами.
- § 147. Частные случаи.
- § 148. Главная ось растяжения и главные плоскости изгиба.
- § 149. Применение комплексного представления. Примеры.
- § 150. Задача об изгибе поперечной силой.
- ГЛАВА ВОСЬМАЯ. КРАТКИЙ ОБЗОР НЕКОТОРЫХ РАБОТ ПОСЛЕДНЕГО ВРЕМЕНИ
- I. ОДНОРОДНАЯ СРЕДА С ОДНИМ ИЛИ НЕСКОЛЬКИМИ ОТВЕРСТИЯМИ
- § 151. Эффективные решения граничных задач для двусвязных областей. Метод Д. И. Шермана.
- § 151а. Некоторые конкретные задачи.
- § 152. Пластинки со многими отверстиями. Периодическая задача.
- § 153. Бесконечная плоскость с одним отверстием.
- § 154. Продолжение.
- II. КУСОЧНО-ОДНОРОДНАЯ СРЕДА. ПОДКРЕПЛЕННЫЕ ОТВЕРСТИЯ
- § 155. Включения из того же материала.
- § 156. Включения из различных материалов.
- § 157. Усиление отверстий тонкими кольцами.
- III. СПЛОШНАЯ ОДНОРОДНАЯ СРЕДА (СПЕЦИАЛЬНЫЕ СЛУЧАИ). НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОПРОСЫ
- § 158. Пластинки с полигональным контуром. Разрывные нагрузки.
- § 159. Пластинки с границами, уходящими в бесконечность.
- § 160. Различные специальные вопросы.
- IV. СМЕШАННЫЕ И КОНТАКТНЫЕ ЗАДАЧИ ПЛОСКОЙ ТЕОРИИ УПРУГОСТИ
- § 162. Контактные задачи плоской теории упругости.
- V. НЕКОТОРЫЕ ЗАДАЧИ, ПРИВОДЯЩИЕ К ОБОБЩЕННОМУ БИГАРМОНИЧЕСКОМУ УРАВНЕНИЮ
- § 163. Плоская статическая задача теории упругости для анизотропных тел, обладающих плоскостью упругой симметрии.
- § 164. Стационарные динамические смешанные задачи.
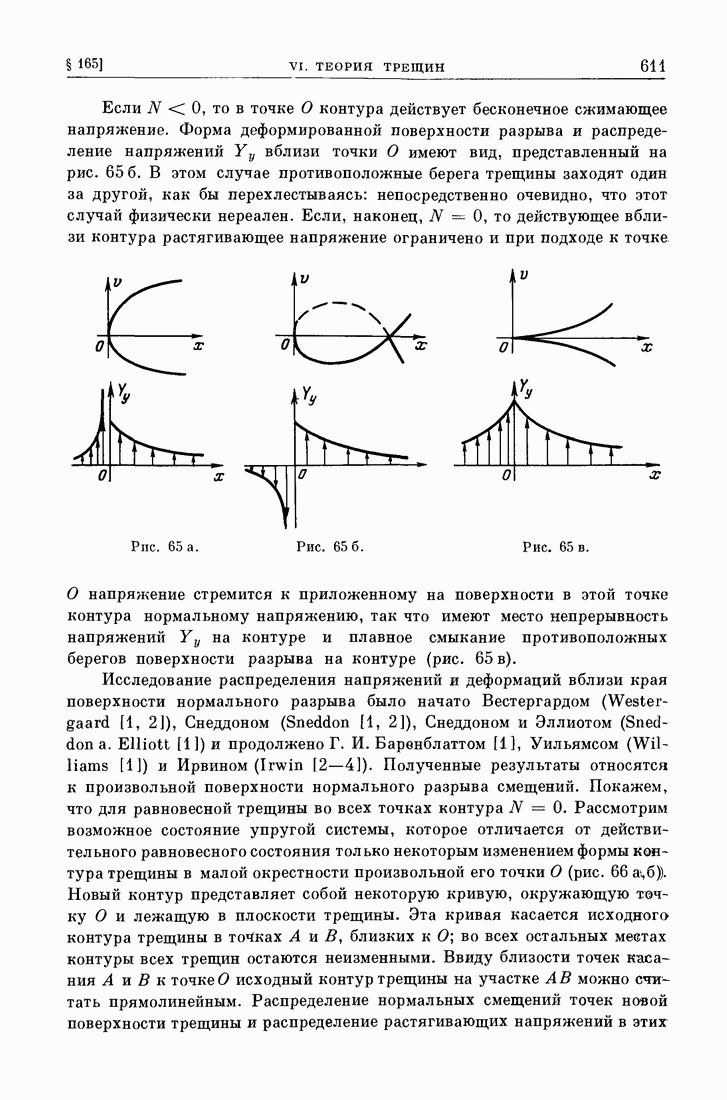
- VI. ТЕОРИЯ ТРЕЩИН
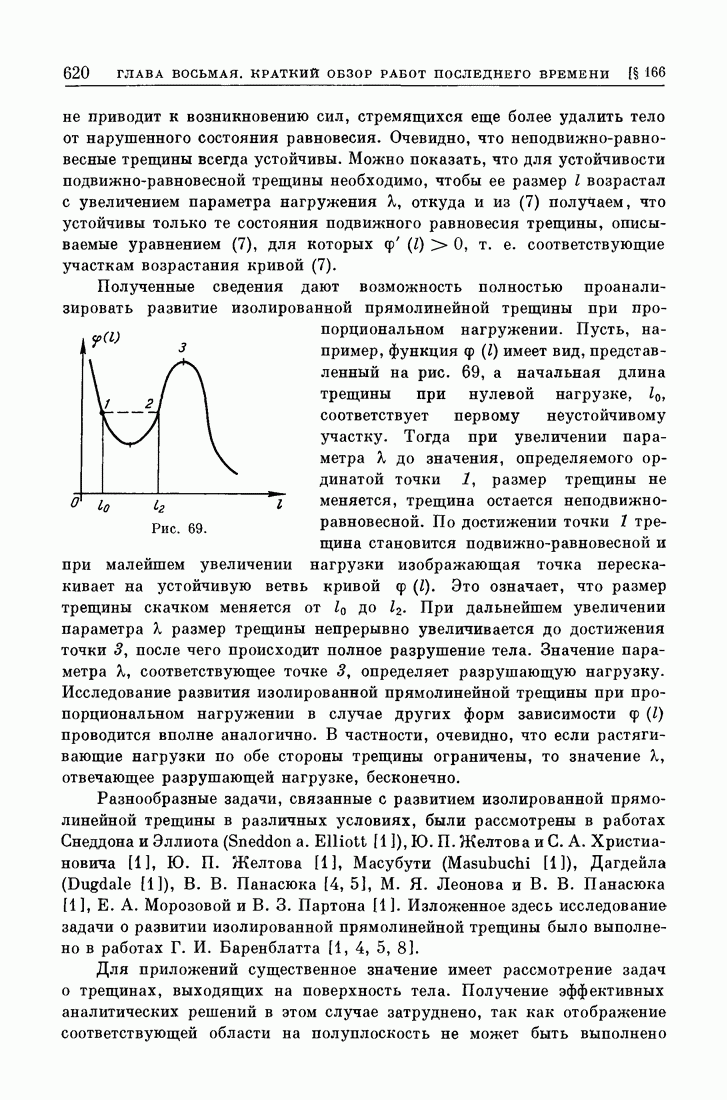
- § 166. Частные задачи.
- VII. КРУЧЕНИЕ И ИЗГИБ БРУСЬЕВ
- § 168. Составные брусья.
- VIII. ПРОСТРАНСТВЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- § 170. Применение p-аналитических функций.
- ДОБАВЛЕНИЕ I. О ПОНЯТИИ ТЕНЗОРА
- ДОБАВЛЕНИЕ II. ОБ ОПРЕДЕЛЕНИИ ФУНКЦИИ ПО ЕЕ ПОЛНОМУ ДИФФЕРЕНЦИАЛУ В МНОГОСВЯЗНОЙ ОБЛАСТИ
- ДОБАВЛЕНИЕ III. ОПРЕДЕЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО ПО ЗАДАННОЙ ДЕЙСТВИТЕЛЬНОЙ ЧАСТИ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ОТ ГОЛОМОРФНОЙ ФУНКЦИИ
- ДОБАВЛЕНИЕ IV. ОДИН ВЫВОД ФОРМУЛ КОМПЛЕКСНОГО ПРЕДСТАВЛЕНИЯ