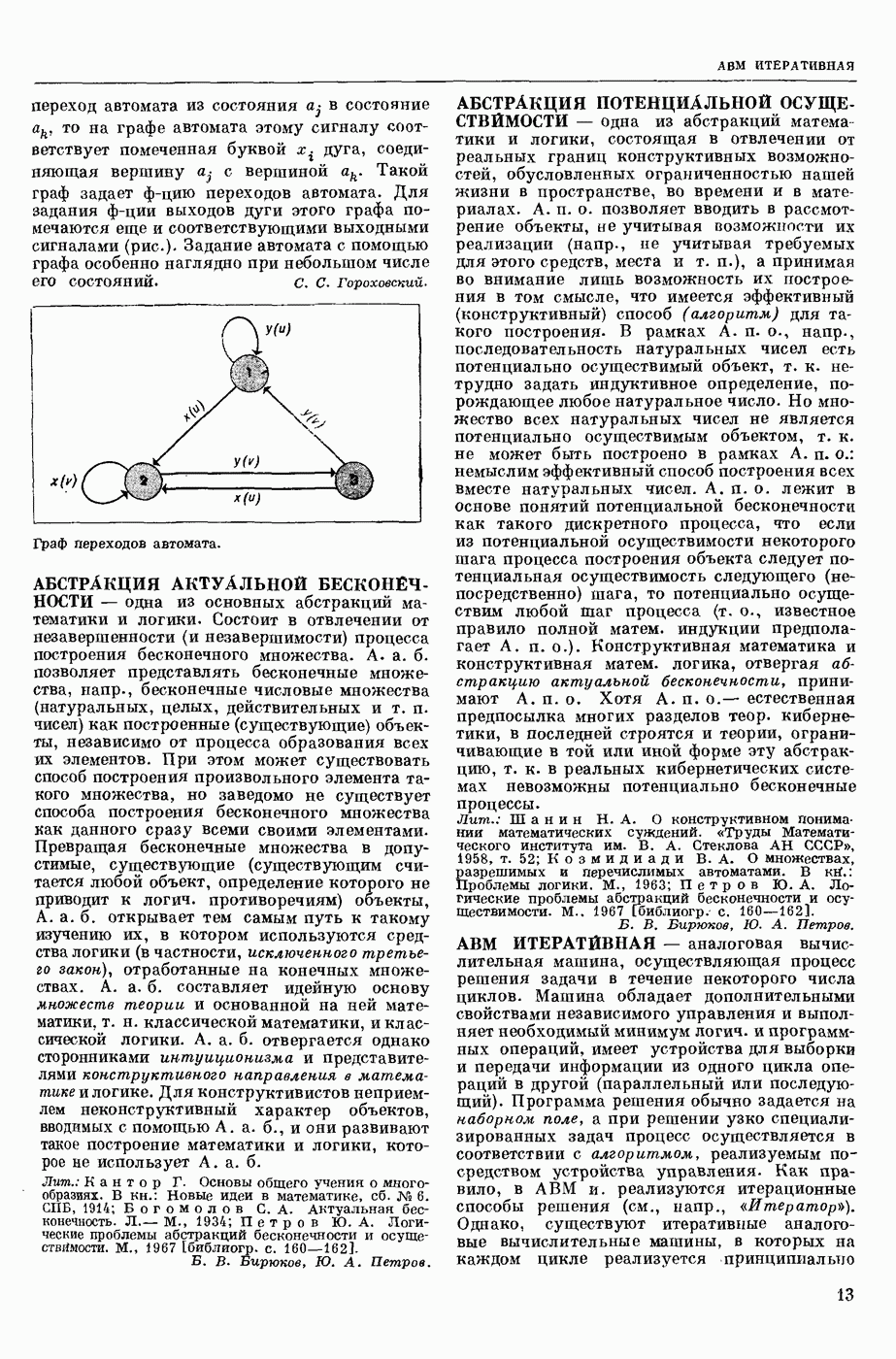
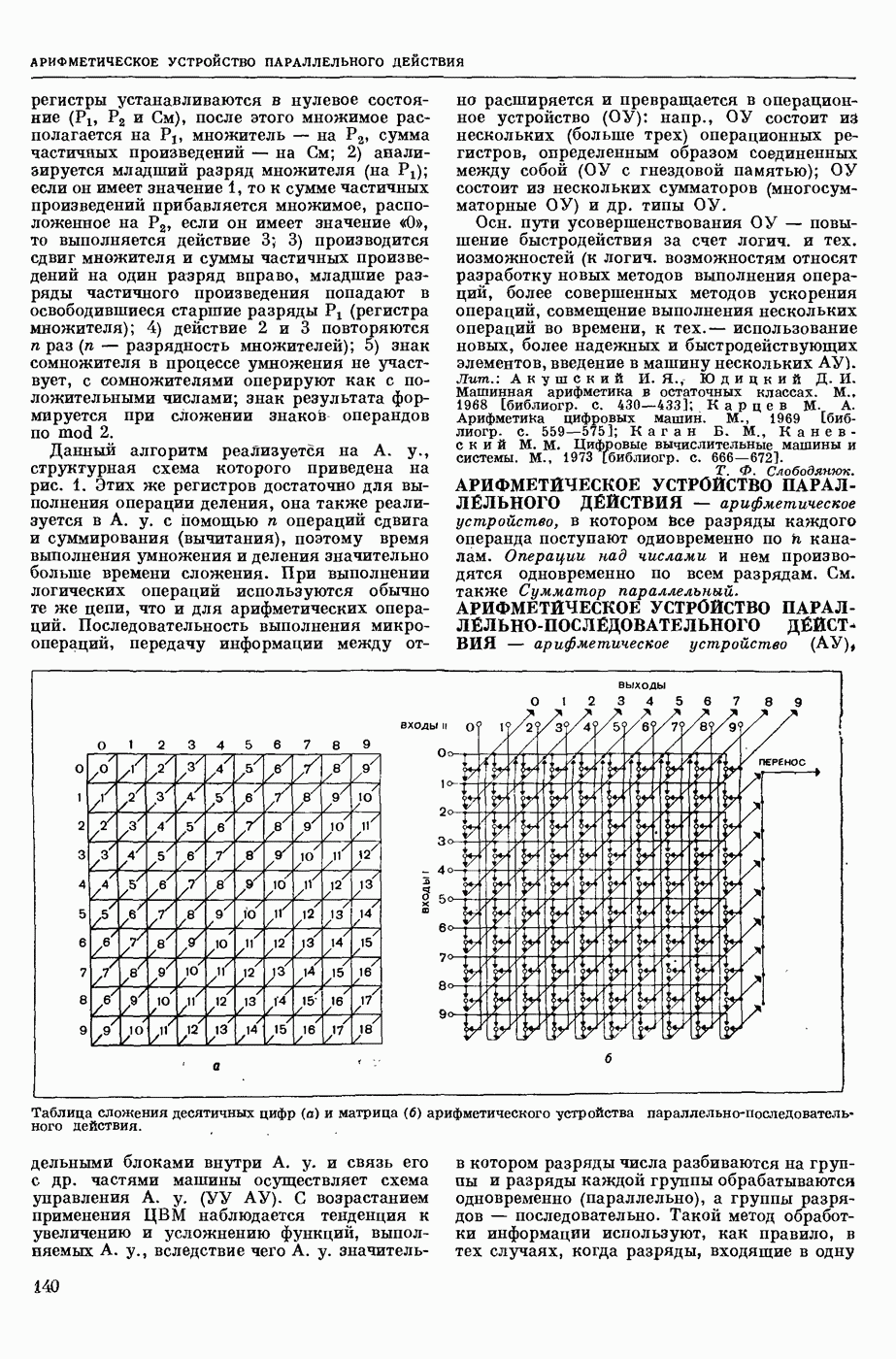
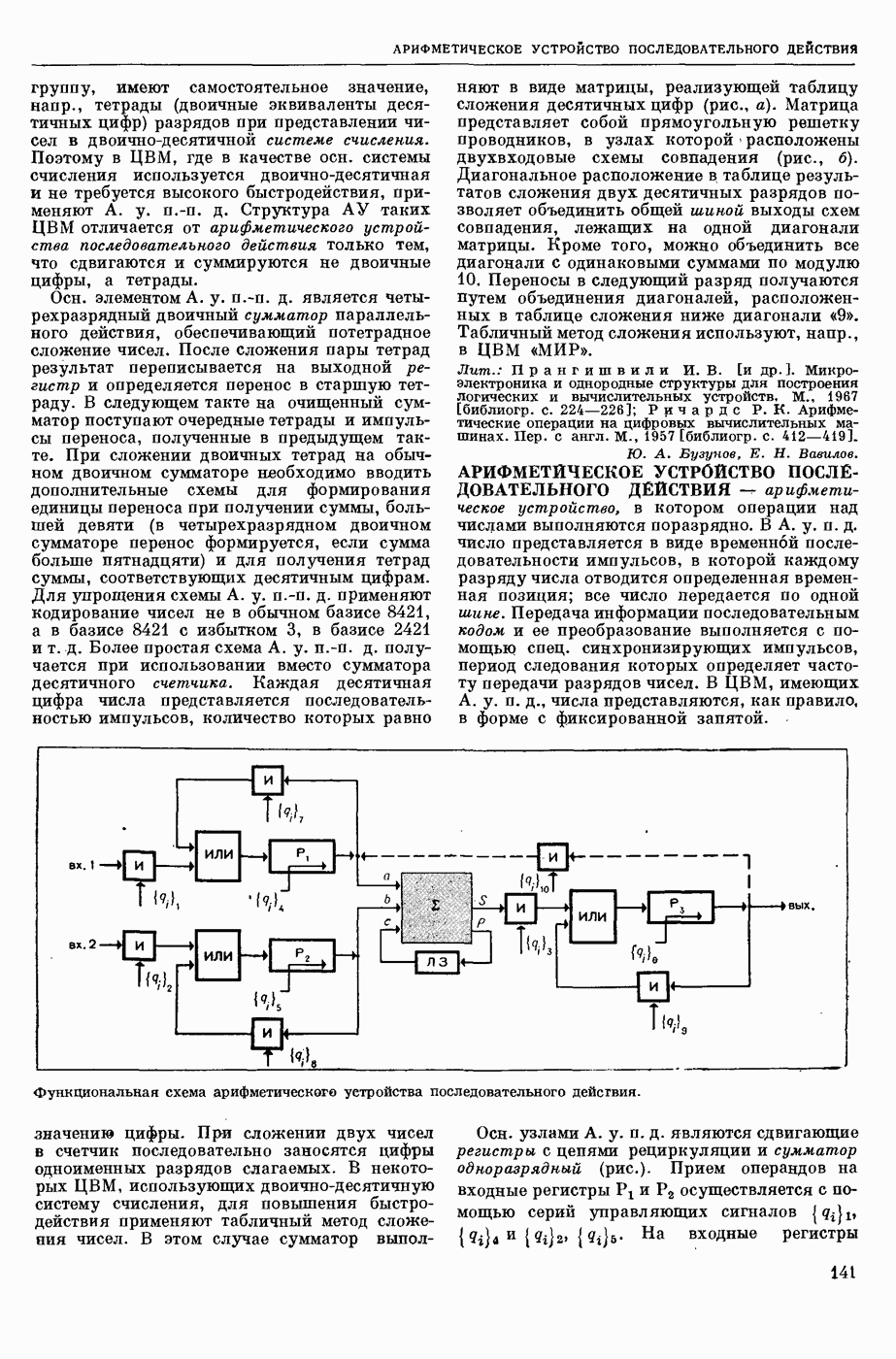
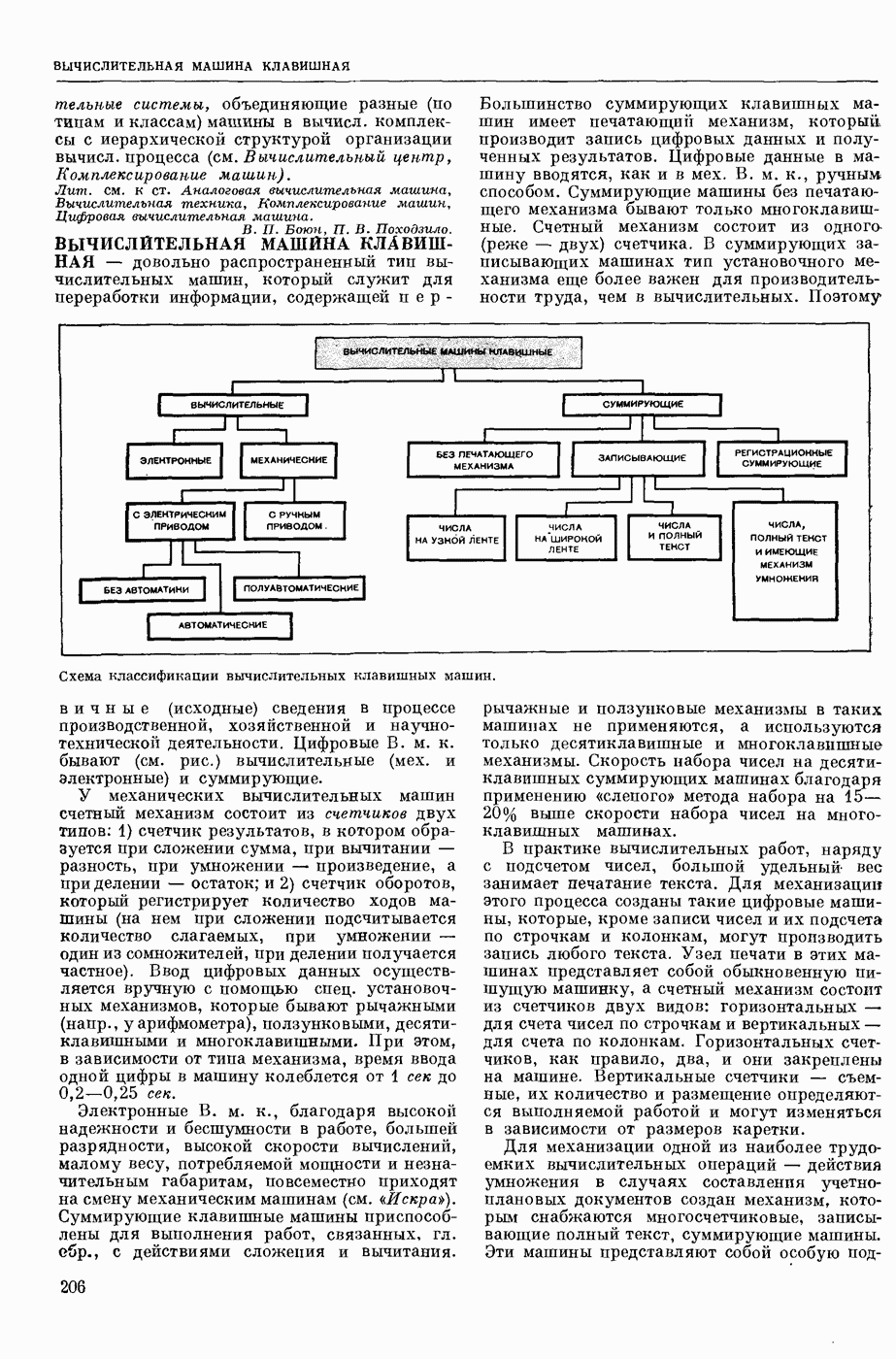
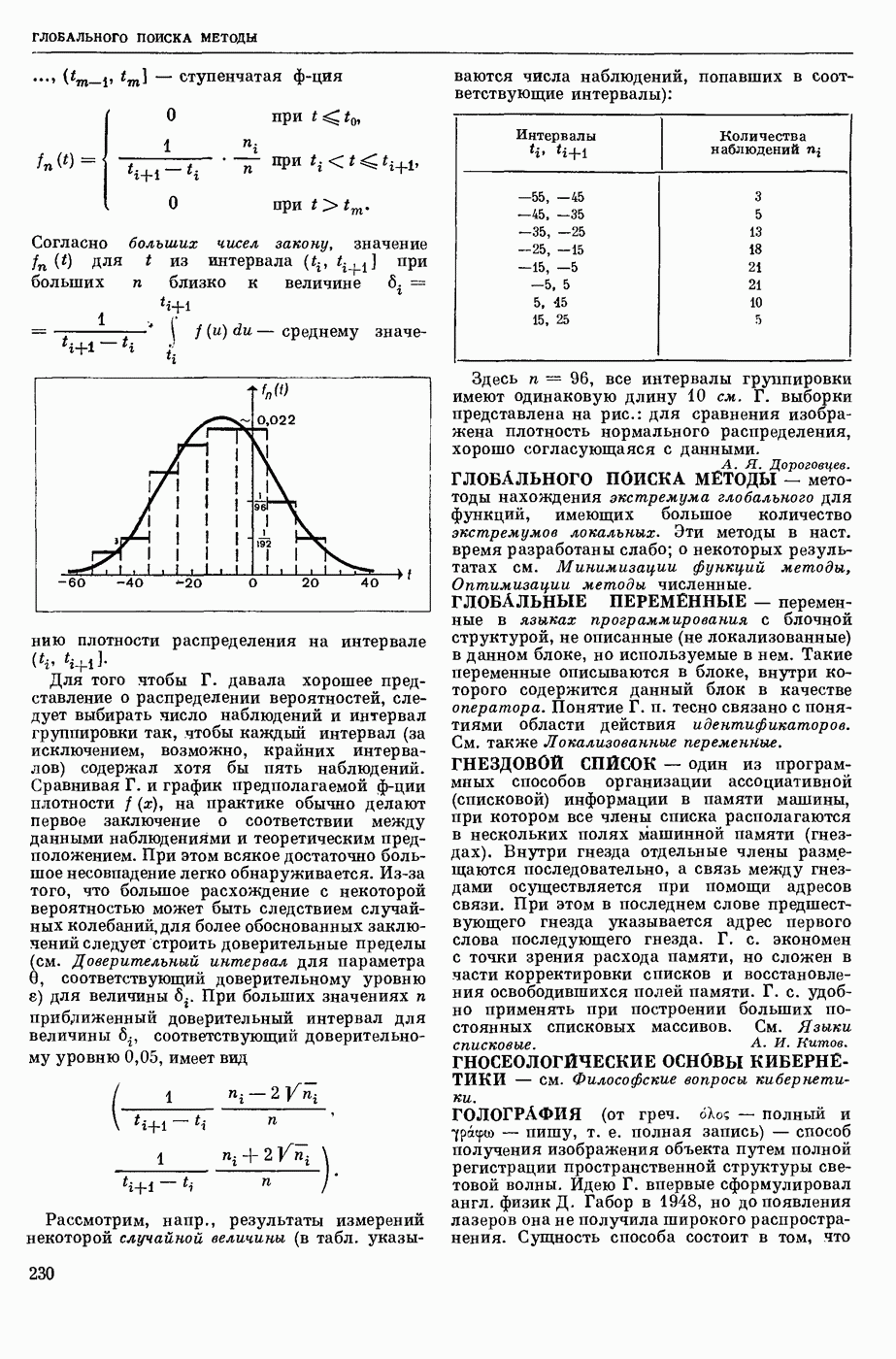
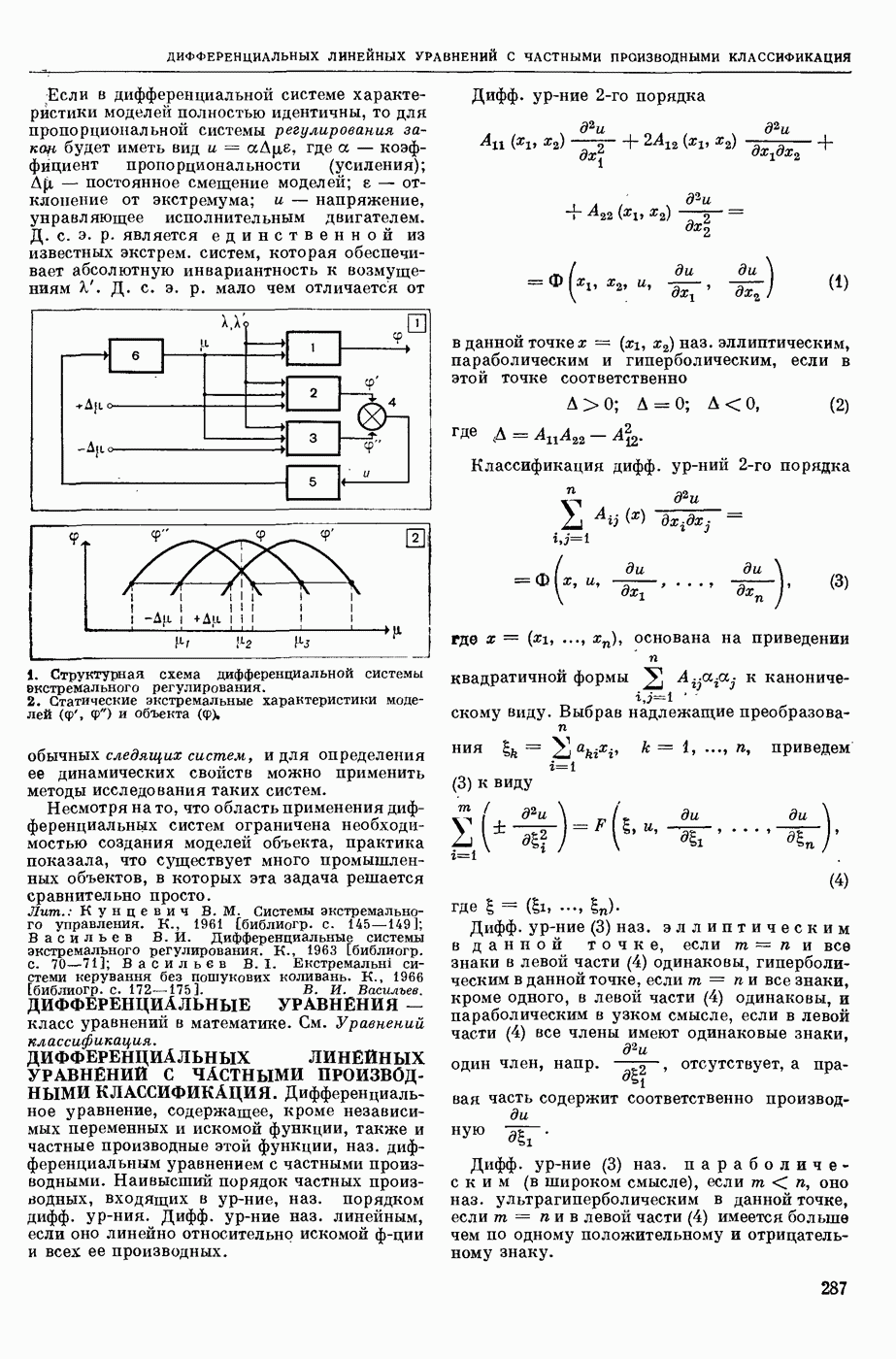
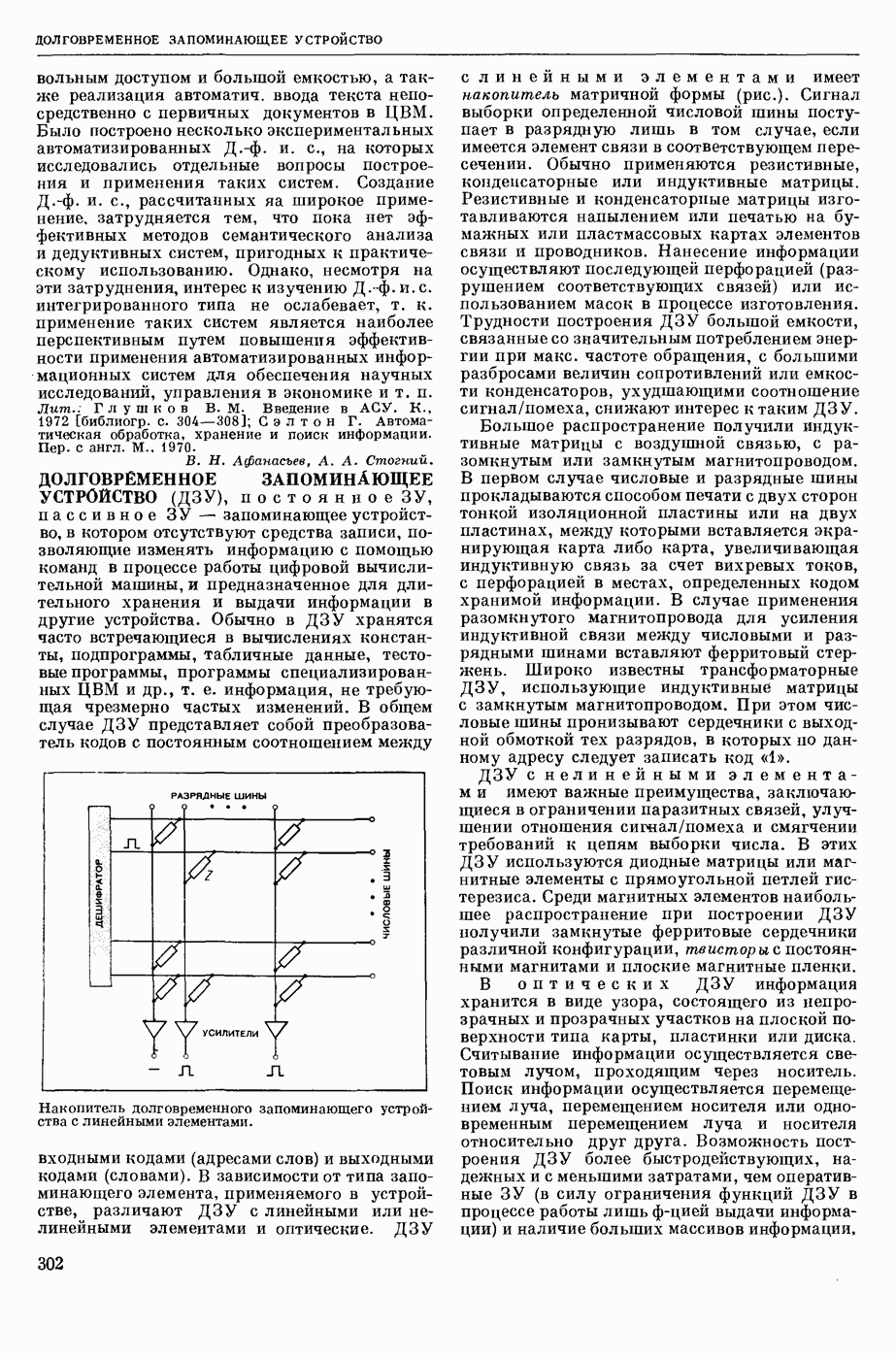
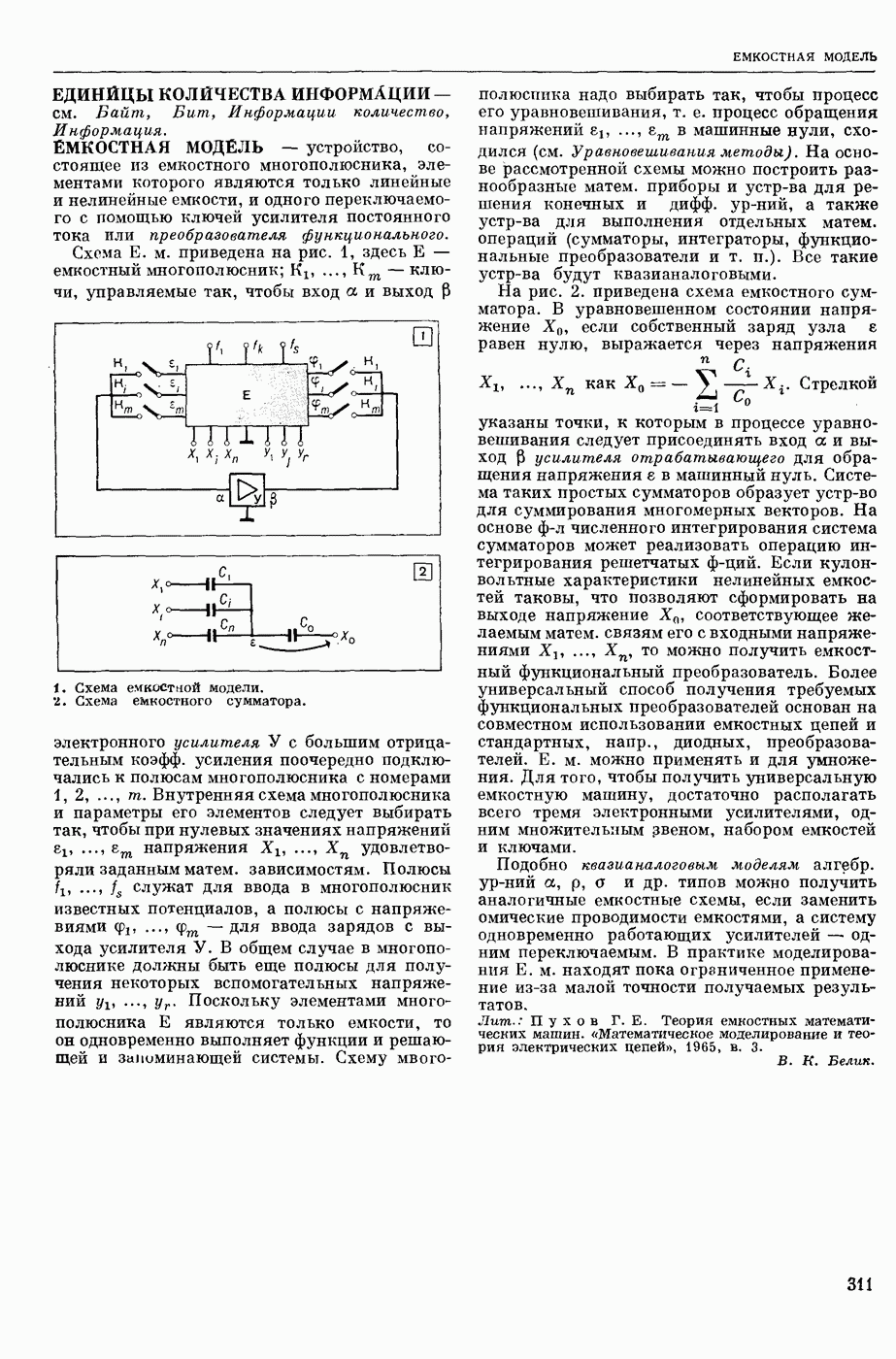
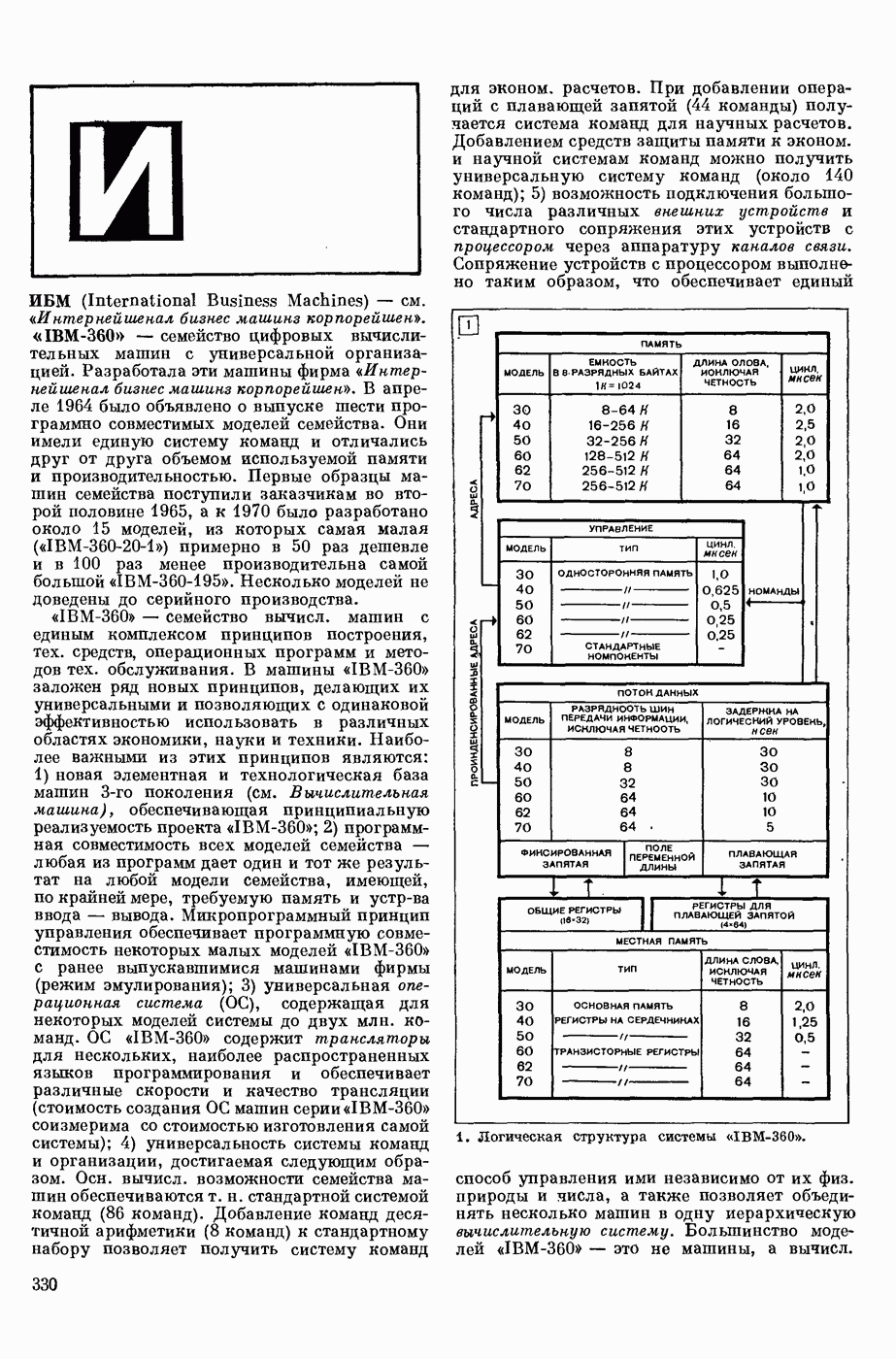
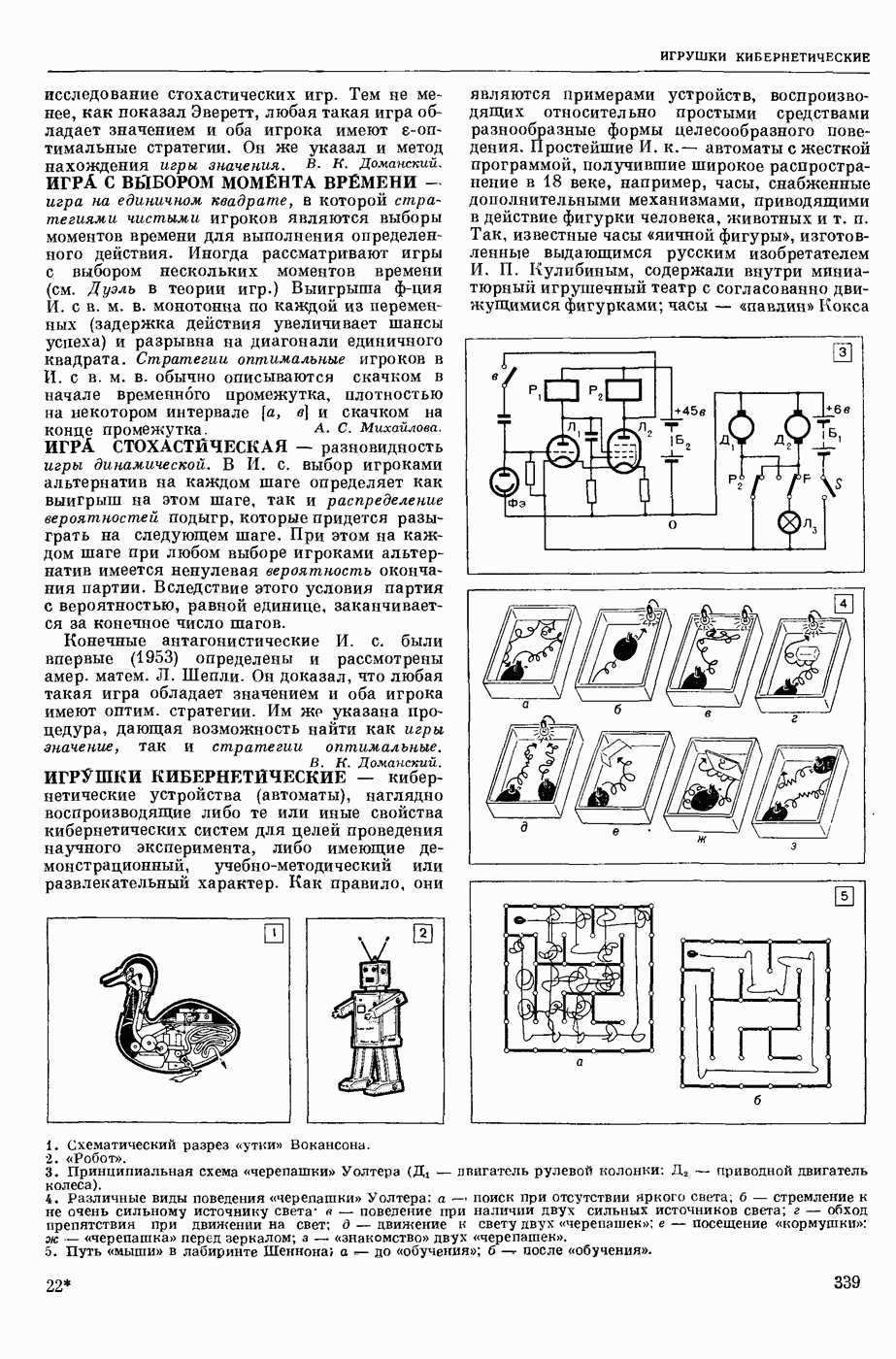
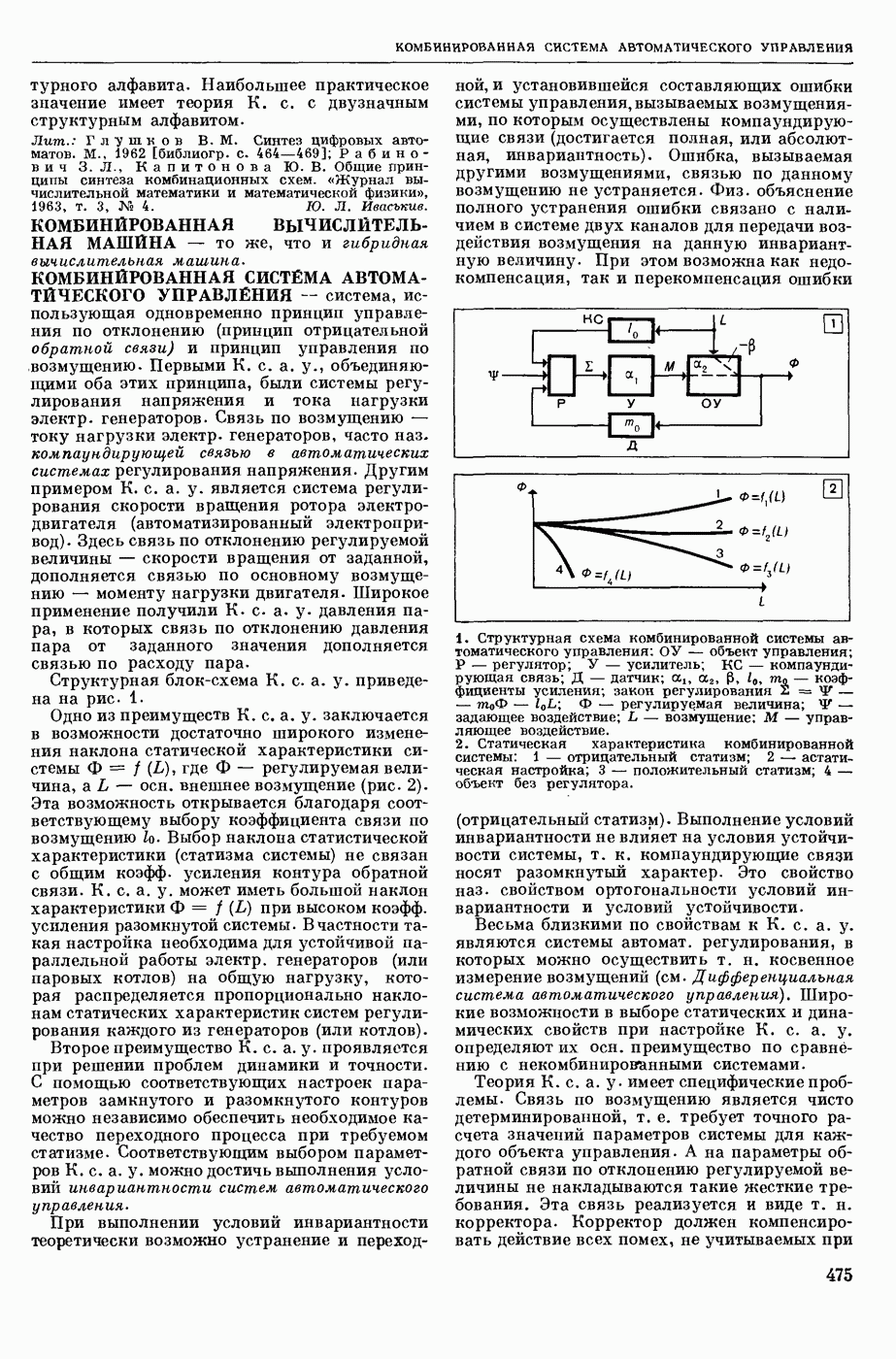
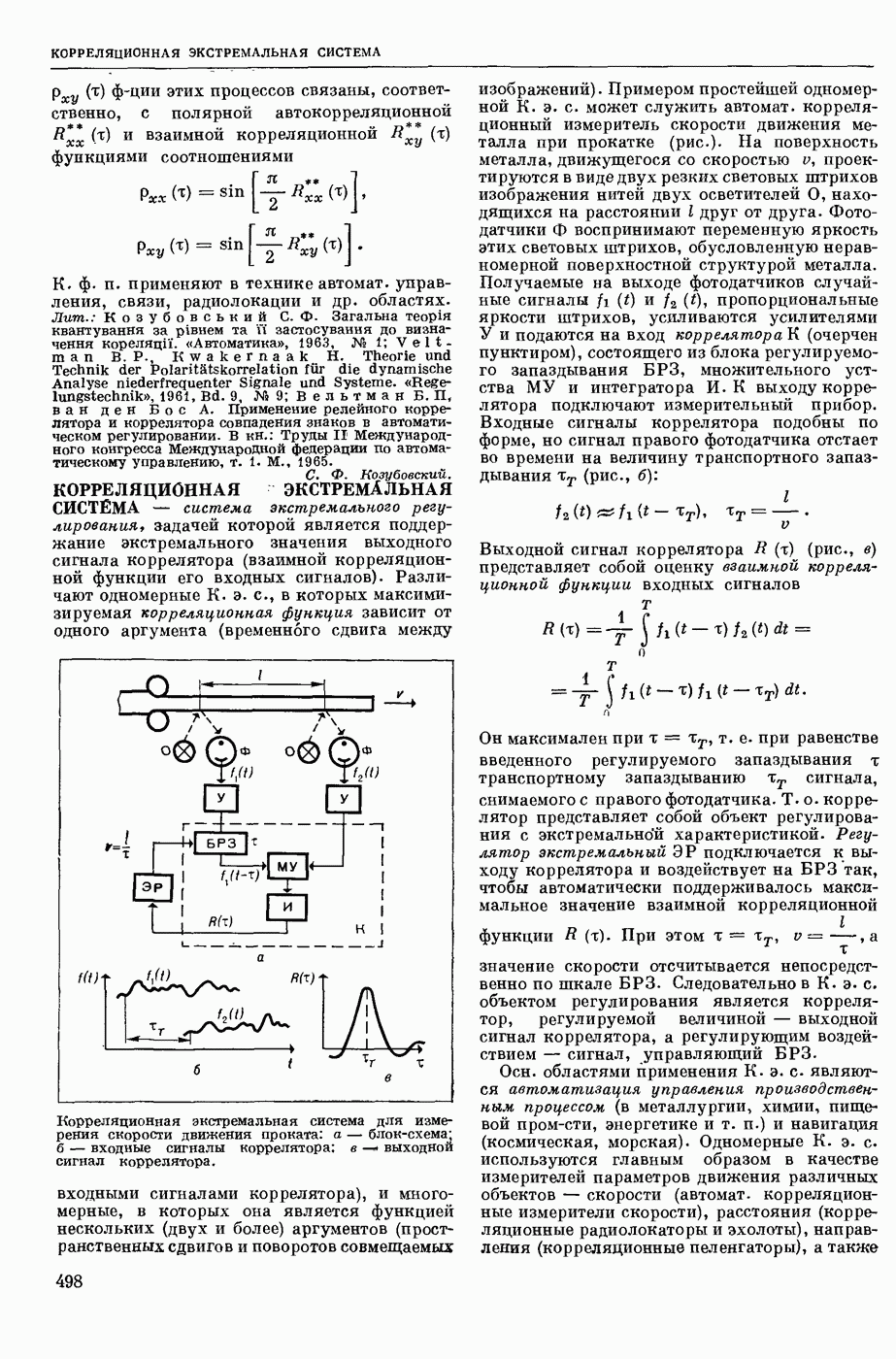
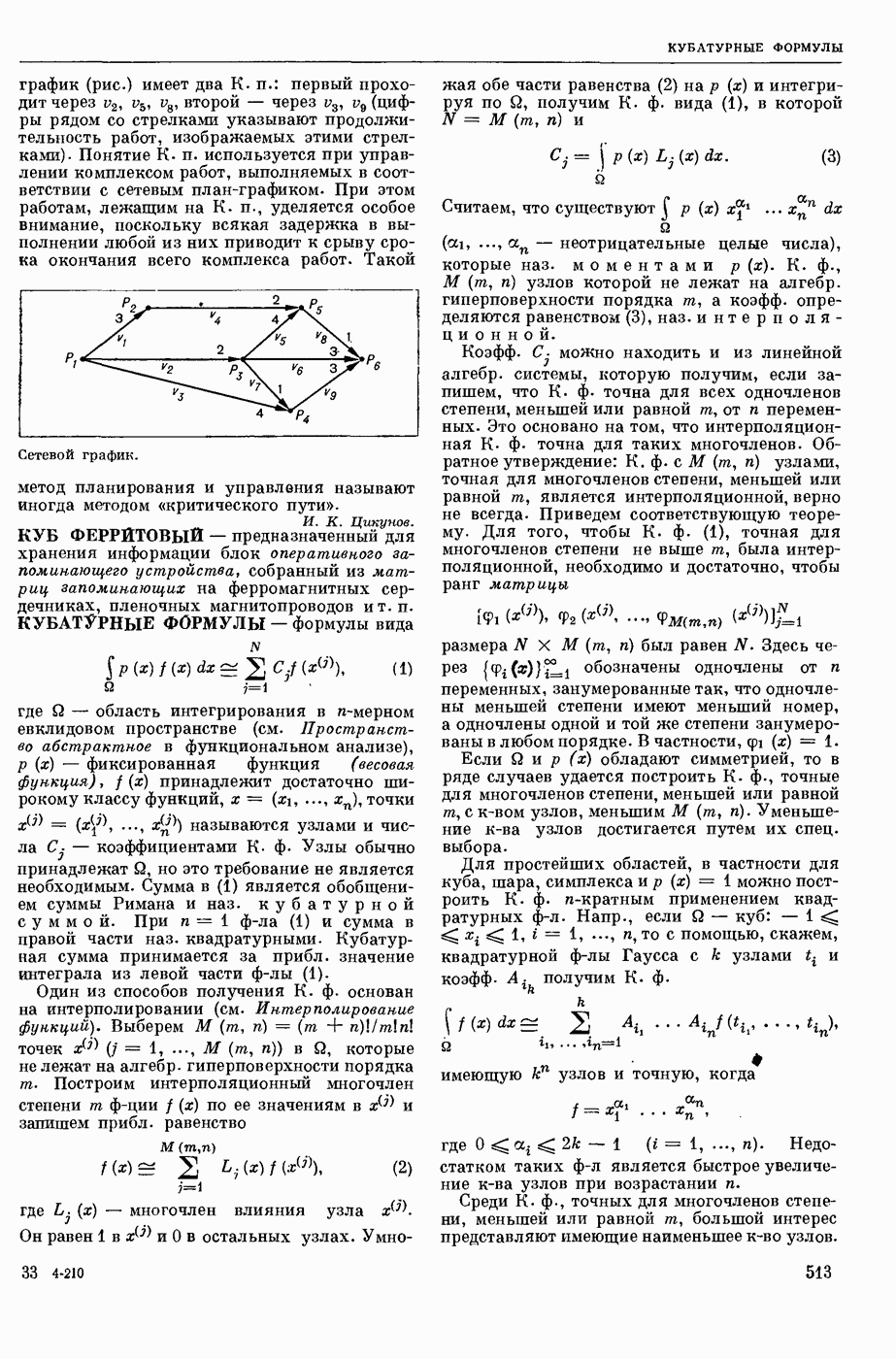
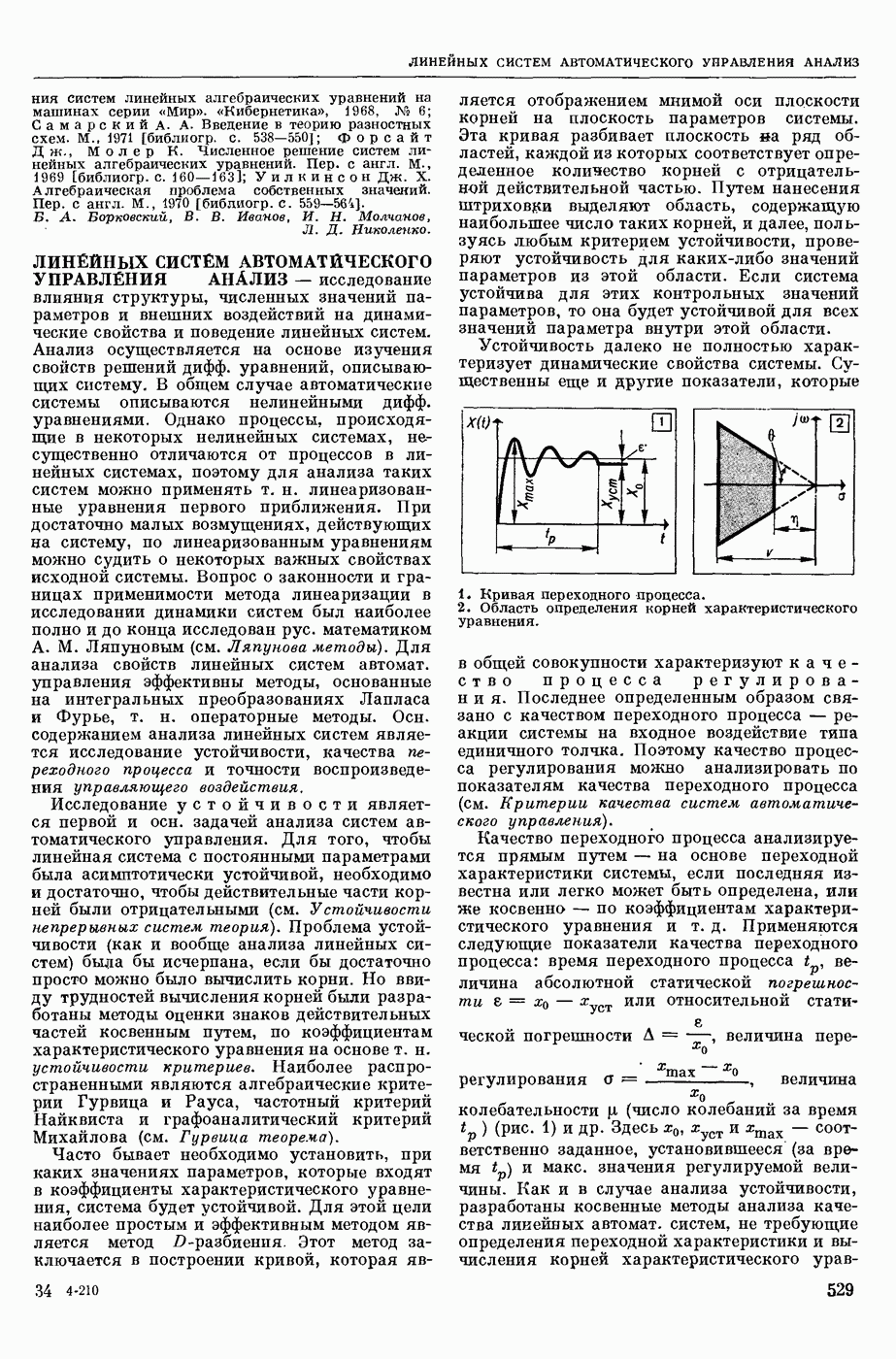
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
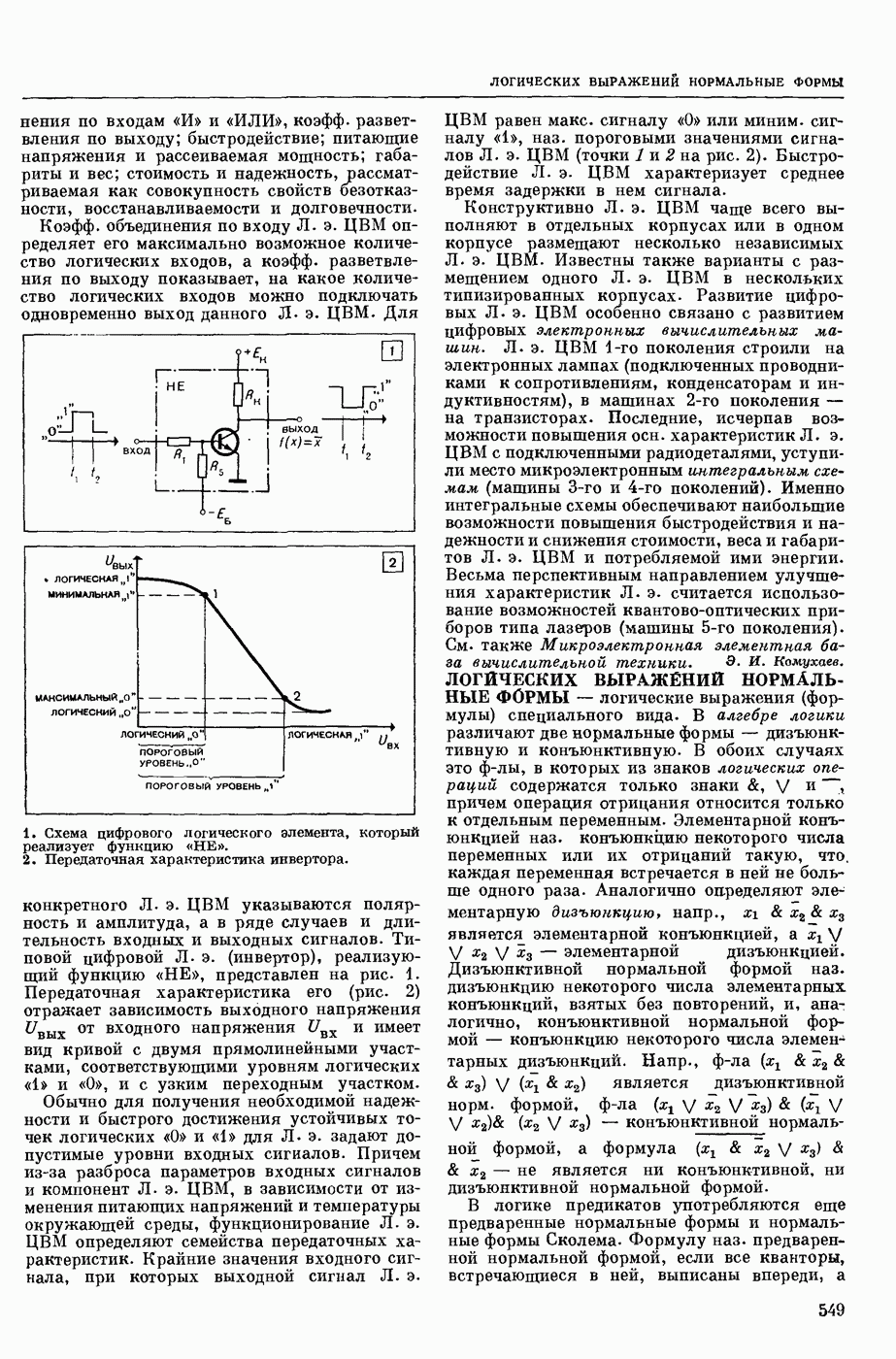
— раздел математики, изучающий методы получения решения различных математических задач в виде числового (точного или приближенного) результата (см. Численные методы). Свое начало В. м. ведет от глубокой древности и началом ее можно считать правила вычисления иррациональных чисел. Современная В. м. состоит из многих разделов; важнейшие из них: вычисление значений ф-ций, вычисл. методы линейной алгебры, численное решение алгебр, и трансцендентных ур-ний, численное дифференцирование и интегрирование, численное решение дифф. и интегро-дифф. ур-ний и численные методы отыскания экстремумов функционалов (оптимизации методы). В. м. развивается вместе с развитием математики вообще, представляя собой как бы завершающий этап в решении матем. проблем. Напр., развивающийся в последнее время дискретный анализ порождает вычисл. методы дискретного анализа, которые также относятся к В. м.Любой числ. результат можно получить только с помощью арифм. и логич. действий, поэтому задачу В. м. можно сформулировать как задачу представления решений (точно или приближенно) в виде последовательности арифм. операций. Т. о., любой числ. метод состоит из алгоритма решения, т. е. точного описания последовательности арифм. операций, и оценки погрешности алгоритма (см. Погрешностей вычислений теория). Лишь в очень редких случаях точный результат может быть достигнут при конечном к-ве арифм. операций. Почти всегда этот результат представляется как предел бесконечной последовательности операций. Поэтому оценка погрешностп часто сводится к оценке сходимости алгоритма. Однако сходимость отнюдь не является необходимым требованием, когда ставится задача о получении результата с заданной точностью (а не с любой степенью точности), при этом необходимая точность устанавливается обычно из практических соображений. Примером может служить вычисление значений ф-ций с помощью расходящихся асимптотических рядов, которые не могут дать приближения с любой степенью точности, но позволяют быстро и точно при соответствующих условиях вычислять значения ф-ций с конечной, но достаточной точностью.
Для практического применения алгоритма весьма важна его эффективность. Ее иногда оценивают по к-ву арифм. операций, необходимых для получения решения. Однако весьма часто уменьшение к-ва арифм. операций достигается в результате логич. усложнения алгоритма, и поэтому программы для ЭВМ (особенно при трансляции с алгоритмических языков) для такого логически усложненного алгоритма получаются столь неэкономичными, что весь выигрыш вследствие снижения к-ва арифм. операций может потеряться.
Аналитической основой вычисления значений трансцендентных ф-ций является теория разложения в ряды (степенные, ряды по ортогональным ф-циям, ряды факториалов и др.). приближение многочленами, реже — разложение в непрерывные дроби, а также другие спец. методы, связанные со специфическими свойствами конкретных ф-ций. Приближение ф-ций многочленами (которое в частных случаях может совпадать с разложением в ряд но ортогональным многочленам) получило в последнее время значительное распространение для составления стандартных программ вычисления трансцендентных ф-ций на ЭВМ, при этом чаще всего используются многочлены Чебышева. Для широкого практического использования трансцендентных ф-ций вычисляют таблицы их значений для некоторой последовательности значений аргумента. Промежуточные значения находят с помощью интерполирования (см. Интерполирование функций). Практически осуществимо табулирование функций, зависящих лишь от одной, максимум двух, переменных.
Раздел вычисл. методов линейной алгебры рассматривает в основном две задачи: 1) решение систем линейных алгебр, ур-ний и 2) определение собственных значений и собственных векторов матриц (см. Собственных значений и собственных векторов матриц способы вычисления). Первая задача является «арифмети-зированной», т. е. ее точное решение можно получить с помощью конечной последовательности арифм. операций. К-во этих операций (сложений и умножений) для системы с  неизвестными в общем случае составляет величину порядка
неизвестными в общем случае составляет величину порядка 
К системам линейных алгебр, ур-ний приближенно сводится решение краевых задач для линейных дифф. ур-ний. В случае ур-ний с частными производными порядок системы алгебр, ур-ний может быть очень высок (тысячи и десятки тысяч неизвестных), и решение таких систем прямыми точными методами практически невыполнимо. Поэтому, помимо точных методов решения больших систем алгебр. ур-ний, применяют и прибл. итерационные методы. Смысл их заключается в том, что матрицу А исходной системы  представляют в виде
представляют в виде  , причем для матрицы
, причем для матрицы  обратную матрицу можно легко вычислить. После этого систему решают последовательными приближениями
обратную матрицу можно легко вычислить. После этого систему решают последовательными приближениями

или, в более общей форме,

(здесь а — некоторый параметр, используемый для улучшения сходимости, при а = - 1 получают предыдущий случай). Если достаточно точное решение можно получить при небольшом к-ве итераций, то к-во арифм. операций, необходимое для получения этого решения, составит величину порядка  .
.
Прямые методы вычисления собственных значений матрицы приводят к задаче нахождения корней многочлена га-ной степени ( - порядок матрицы) относительно собственного значения X. При тех высоких порядках матриц, к которым приближенно приводится, напр., задача о собственных значениях для краевых задач в частных производных, такой метод является часто практически невыполнимым. Для этих задач интерес представляет обычно вычисление небольшого к-ва первых собственных значений, для чего можно ограничиться вычислением сумм
- порядок матрицы) относительно собственного значения X. При тех высоких порядках матриц, к которым приближенно приводится, напр., задача о собственных значениях для краевых задач в частных производных, такой метод является часто практически невыполнимым. Для этих задач интерес представляет обычно вычисление небольшого к-ва первых собственных значений, для чего можно ограничиться вычислением сумм  которые выражаются через следы степеней обратпой матрицы. При достаточно высоких степенях к эти суммы приближенно можно заменять суммами нескольких первых членов. Однако и такой подход требует большой вычисл. работы, так как произведение матриц требует к-ва арифм. операций порядка
которые выражаются через следы степеней обратпой матрицы. При достаточно высоких степенях к эти суммы приближенно можно заменять суммами нескольких первых членов. Однако и такой подход требует большой вычисл. работы, так как произведение матриц требует к-ва арифм. операций порядка 
Широкое применение в задачах матем. физики получил метод возмущений. В этом методе исходную матрицу А заменяют суммой  и задачу определения собственных значений матрицы
и задачу определения собственных значений матрицы  заменяют задачей
заменяют задачей

и при  сводят ее к исходной задаче. Матрица
сводят ее к исходной задаче. Матрица  выбирается так, чтобы ее собственные значения и собственные векторы легко вычислялись. Задача (2) решается методом разложения по степеням
выбирается так, чтобы ее собственные значения и собственные векторы легко вычислялись. Задача (2) решается методом разложения по степеням  Эффективность этого метода существенно зависит от того, насколько близко к исходной матрице А удается подобрать матрицу
Эффективность этого метода существенно зависит от того, насколько близко к исходной матрице А удается подобрать матрицу  Если это удалось так, что для вычисления собственных значений с необходимой точностью достаточно ограничиться небольшим к-вом членов разложения в ряд по е, то это дает для матриц высокого порядка значительное сокращение к-ва арифм. операций.
Если это удалось так, что для вычисления собственных значений с необходимой точностью достаточно ограничиться небольшим к-вом членов разложения в ряд по е, то это дает для матриц высокого порядка значительное сокращение к-ва арифм. операций.
Проблема определения корней алгебр, или трансцендентных ур-ний исчерпывающим образом разработана для случая ф-ций одного переменного. В основе многочисленных методов лежит замена ф-ции в окрестности нуля простейшей близкой к пей кривой (прямой или параболой). Такие методы требуют предварительной грубой локализации нуля, но для одной переменной эта задача весьма простая.
Для отыскания корней многочленов и целых ф-ций используются также методы, основанные на том, что суммы вида  распространенные по всем нулям, могут точно выражаться через коэфф. разложения ф-ции в ряды Тейлора. Значительно сложнее обстоит дело при определении корней системы ур-ний
распространенные по всем нулям, могут точно выражаться через коэфф. разложения ф-ции в ряды Тейлора. Значительно сложнее обстоит дело при определении корней системы ур-ний

Конечно, если корни системы грубо локализованы, то замена ф-ций системы простейшими поверхностями (например, плоскостями) дает возможность при определенных условиях определить корень с любой степенью точности. Однако для многомерных пространств нет еще сколь-нибудь универсальных подходов хотя бы для грубой локализации нулей. Развитые за последние годы эффективные прямые методы решения экстрем, задач стали применяться также для нахождения корней системы ур-ний, путем замены исходной задачи задачей отыскания минимума ф-ции

Числ. дифференцирование и интегрирование непосредственно основывается на определении этих операций как предела отношения приращения ф-ции к приращению аргумента при стремлении последнего к нулю (дифференцирование) или как предела сумм произведений элементов объема области интегрирования на значения ф-ции в некоторой точке этого элемента. Несмотря на теор. простоту этой проблемы, большие вычисл. трудности возникают при вычислении многократных интегралов. Напр., в задачах кинетики разреженных газов, где приходится вычислять семикратные интегралы, вычисление их даже с очень малой точностью обычными методами разбиения на равные элементы объема приводит к десяткам миллиардов арифм. операций. Поэтому многие исследования были направлены на оптимизацию Кубатурных формул с целью уменьшения к-ва узловых точек. Другой подход к вычислению многократных интегралов основан на аналогии между этими интегралами и вероятностью некоторого случайного процесса (Монте-Карло метод или метод статических испытаний). Преимущество метода Монте-Карло состоит в том, что в нем объем необходимых вычислений растет пропорционально к-ву измерений, а не экспоненциально возрастает с ростом к-ва измерений.
Числ. методы решения дифф. ур-ний составляют важнейший раздел вычисл. математики. Задачи механики, физики и хим. кинетики — это, в подавляющем числе случаев, задачи теории дифф. (иногда интегро-дифф.) ур-ний. Если числ. методы решения обыкновенных дифф. ур-ний начали разрабатываться почти одновременно с возникновением понятия дифф. ур-ний и ведут свое начало от Л. Эйлера (1707—83), то числ. методы решения ур-ний в частных производных, по существу, начали
развиваться только после создания ЭВМ. Причиной этого является т. н. «барьер многомерности» — резкий рост необходимого к-ва арифм. операций с возрастанием числа независимых переменных. Если для решения одномерного (т. е. обыкновенного) дифф. ур-ния с заданной точностью нужно определять решения в  узловых точках, то для получения решения с той же точностью для
узловых точках, то для получения решения с той же точностью для  -мерного ур-ния в частных производных потребуется уже
-мерного ур-ния в частных производных потребуется уже  узловых точек. Поскольку при числ. решениях дифф. ур-ний часто приходится решать системы линейных алгебр, ур-ний относительно неизвестных значений ф-ции в узловых точках, то это значит, что в одномерном случае необходимо выполнить
узловых точек. Поскольку при числ. решениях дифф. ур-ний часто приходится решать системы линейных алгебр, ур-ний относительно неизвестных значений ф-ции в узловых точках, то это значит, что в одномерном случае необходимо выполнить  арифм. операций, а в А-мерном —
арифм. операций, а в А-мерном —  операций. Практическая невозможность проведения такого рода вычислений «ручным» способом делала бессмысленной разработку числ. методов решения ур-ний в частных производных до появления ЭВМ. Лишь самые элементарные подходы были предложены в «домашинную ару», которые могли применяться только для простейших, как правило, линейных задач на ур-ния в частных производных.
операций. Практическая невозможность проведения такого рода вычислений «ручным» способом делала бессмысленной разработку числ. методов решения ур-ний в частных производных до появления ЭВМ. Лишь самые элементарные подходы были предложены в «домашинную ару», которые могли применяться только для простейших, как правило, линейных задач на ур-ния в частных производных.
В общем можно отметить два главных подхода к решению дифф. ур-ний: 1) представление решения в виде рядов по некоторой полной системе ф-ций (обычно ортогональной) и нахождение коэфф. этих рядов и 2) замена производных их конечноразностными приближениями (или интегралов — конечными суммами). Первый подход имеет ограниченное применение — он эффективен только в применении к линейным ур-ниям или в некоторых методах последовательных приближений, когда на каждой итерации решается линейное ур-ние. Именно этот подход чаще всего использовали до создания ЭВМ. В наст, время наибольшее применение имеют конечноразностные методы (в широком смысле этого слова); метод прямых или метод интегр. соотношений и метод характеристик мы также относим к конечноразностным. Важнейшей проблемой конечноразностных методов является устойчивость вычисл. процесса.
Простым примером можно проиллюстрировать значение этого явления. Дифф. ур-ние  можно аппроксимировать, напр. следующими двумя конечноразностными формами:
можно аппроксимировать, напр. следующими двумя конечноразностными формами:

или

Точность аппроксимации первой формы имеет порядок h, второй  , т. е. вторая форма на порядок точнее. Легко получить точные решения этих конечноразностных ур-ний.
, т. е. вторая форма на порядок точнее. Легко получить точные решения этих конечноразностных ур-ний.
Общее решение первой формы

второй формы

Первое решение дает прибл. решение (с точностью до  ) исходного дифф. ур-ния, во втором решении лишь первое слагаемое дает нужное решение (точность его по отношению к решению дифф. ур-ния выше — равна О №2)), но второе осциллирующее и возрастающее по
) исходного дифф. ур-ния, во втором решении лишь первое слагаемое дает нужное решение (точность его по отношению к решению дифф. ур-ния выше — равна О №2)), но второе осциллирующее и возрастающее по  величине слагаемое является паразитным решением. Однако при счете с конечным к-вом знаков оно обязательно появится (хотя
величине слагаемое является паразитным решением. Однако при счете с конечным к-вом знаков оно обязательно появится (хотя  и будет малой величиной) и при большом к-ве шагов полностью перекроет истинное решение. Т. о., попытка повысить точность аппроксимации привела к неустойчивости вычисл. процесса и решения вторым способом нельзя получить при достаточно большом интервале переменной х. Исследование устойчивости проводят обычно методом локальной линеаризации и фиксации переменных коэфф. ур-ний, так как полное исследование устойчивости конечноразностных ур-ний с переменными коэфф. и нелинейных ур-ний пока еще далеко от полного решения.
и будет малой величиной) и при большом к-ве шагов полностью перекроет истинное решение. Т. о., попытка повысить точность аппроксимации привела к неустойчивости вычисл. процесса и решения вторым способом нельзя получить при достаточно большом интервале переменной х. Исследование устойчивости проводят обычно методом локальной линеаризации и фиксации переменных коэфф. ур-ний, так как полное исследование устойчивости конечноразностных ур-ний с переменными коэфф. и нелинейных ур-ний пока еще далеко от полного решения.
Неустойчивость вычисл. процесса является причиной того, что в вычисл. практике почти не используются явные схемы для ур-ний в частных производных. Если одной из независимых переменных является время и решается задача с начальными условиями, то формально ур-ние вида

где Ф — некоторый оператор, содержащий дифференцирование лдшь по пространственным переменным, можно аппроксимировать конечноразностной формой:

и т. о. свести задачу определения искомой ф-ции (системы ф-ций — в общем случае) в момент  по известным ее значениям в момент t к элементарным вычислениям. Но такой метод в общем случае является неустойчивым пли устойчивым лишь при очень малых значениях
по известным ее значениям в момент t к элементарным вычислениям. Но такой метод в общем случае является неустойчивым пли устойчивым лишь при очень малых значениях  Однако и в последнем случае, когда устойчивости все же можно достигнуть, общий объем вычислений превосходит практические возможности. Для корректно поставленных задач (см. Некорректно поставленные задачи) всегда можно добиться устойчивости вычисл. процесса применением неявных схем
Однако и в последнем случае, когда устойчивости все же можно достигнуть, общий объем вычислений превосходит практические возможности. Для корректно поставленных задач (см. Некорректно поставленные задачи) всегда можно добиться устойчивости вычисл. процесса применением неявных схем

при этом существенно в неявной форме записывать старшие производные по координатам.
Однако в этом случае для многомерных задач на каждом шаге по времени необходимо решать системы ур-ний весьма высокого порядка (хотя они будут и линейными для квазилинейных ур-ний в частных производных). Выше уже говорилось, сколь большого к-ва арифм. операций требует решение таких задач. Выходом из положения явилась разработка схем, в некотором смысле промежуточных между чисто явными и чисто неявными, и которые приводят к тому, что система ур-ний высокого порядка неявной схемы расщепляется на последовательность систем существенно более низкого порядка, при этом устойчивость таких схем существенно превышает устойчивость явных схем. Одним из наиболее часто применяемых методов этого направления является т. н. метод переменных направлений, в котором на каждом шаге по времени поочередно в неявном виде записываются производные лишь по одной из простр. переменных. Т. о., порядок систем линейных алгебр, ур-ний будет здесь на каяздом шаге по времени таким же, как и при решении одномерных задач.
Упомянутые методы во много раз упростили решение многомерных задач, однако никакие методы не позволяют уменьшить необходимый для вычислений объем памяти ЭВМ. Поэтому убыстрение методов решения не приведет к цели, если объем оперативной памяти вычисл. машины недостаточный. Стационарные задачи матем. физики также можно решать описанным выше путем, применяя метод установления, т. е. записывая систему в виде некоторой нестационарной системы, выходящей на установившийся режим. При этом, конечно, не обязательно использовать физ. реальную нестационарную систему. Важно лишь обеспечить устойчивость стационарного режима. Процесс установления здесь нужно понимать просто как некоторый итерационный процесс.
Широкое применение для решения стационарных задач получили также вариационные методы. В физ. задачах системы yp-ний часто являются вариационными ур-ниями Эйлера для некоторого функционала. Но если даже и нельзя построить функционал Эйлера, то задачу решения системы дифф. ур-ний с заданным граничным условием  всегда можно свести к нахождению минимума функционала
всегда можно свести к нахождению минимума функционала

Числ. методы отыскания экстремумов (числ. методы оптимизации) имеют широкое применение в самых различных областях. Сюда относятся не только научные задачи физ. цикла, но и задачи оптим. управления в тех. и административных системах, оптим. планирования в экономике и др. При аналитических решениях задач опт-ции эти задачи сводились к дифф. ур-ииям (вариационные ур-ния Эйлера) или к системам трансцендентных (в общем случае) ур-ний — при поиске экстремума ф-ций. Но для числ. методов прямые методы нахождения экстремума являются наиболее эффективными, так что, как говорилось выше, наоборот, задачи дифф. ур-ний или решения систем трансцендентных ур-ний приводят к эквивалентным вариационным задачам. Задачи поиска экстремума (для определенности будем говорить о минимуме) обладают тем преимуществом, что всегда можно построить итерационный процесс, приводящий к уменьшению функционала, причем процесс этот можно составлять из простейших одномерных вариаций. Не представляет обычно труда обосновать сходимость процесса. Главная теор. трудность проблемы опт-ции для невыпуклых функционалов состоит в том, что может существовать несколько минимумов. Итерационный процесс приведет к к.-н. из этих минимумов, но не обязательно к наименьшему из них, и пока еще не разработаны регулярные методы поиска наименьшего минимума.
В. м. начала весьма быстро развиваться с созданием ЭВМ. Возникают новые ее разделы, как, например, вычисл. методы игр теории, массового обслуживания теории, минимизации логических ф-ций, комбинаторики и др. В статье же были рассмотрены установившиеся разделы, которые вышли из состояния первых поисков и имеют уже широкое применение.
Лит.: Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. М.- Л., 1963 [библиогр. с. 677—734]; Ремез Е. Я. Основы численных методов чебышевского приближения. К., 1969 [библиогр. с. 613—623]; Самарский А. А. Введение в теорию разностных схем. М., 1971 [библиогр. с. 538—550]; Моисеев Н. Н. Численные методы в теории оптимальных систем. М., 1971; Уиттекер Э., Робинсон Г. Математическая обработка результатов наблюдений. Пер. с англ. Л.- М., 1935; Уилкинсон Дж. X. Алгебраическая проблема собственных значений. Пер. с англ. М.. 1970 [библиогр. с. 559 — 564].
А. А. Дородницын.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- КАК ПОЛЬЗОВАТЬСЯ ЭНЦИКЛОПЕДИЕЙ КИБЕРНЕТИКИ
- ОСНОВНЫЕ СОКРАЩЕНИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
- АБСТРАКТНАЯ ТЕОРИЯ АВТОМАТОВ
- АБСТРАКТНОГО АВТОМАТА ГРАФ
- АБСТРАКЦИЯ АКТУАЛЬНОЙ БЕСКОНЕЧНОСТИ
- АБСТРАКЦИЯ ПОТЕНЦИАЛЬНОЙ ОСУЩЕСТВИМОСТИ
- АВМ ИТЕРАТИВНАЯ
- АВМ МЕХАНИЧЕСКАЯ
- АВМ ПНЕВМАТИЧЕСКАЯ
- АВМ ЭЛЕКТРОМЕХАНИЧЕСКАЯ
- АВТОКОД
- АВТОКОЛЕБАНИЯ
- АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- АВТОМАТ
- АВТОМАТ АВТОНОМНЫЙ
- АВТОМАТ АСИНХРОННЫЙ
- АВТОМАТ БЕЗ ПАМЯТИ
- АВТОМАТ ВЕРОЯТНОСТНЫЙ
- АВТОМАТ ДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ДЕФИНИТНЫЙ
- АВТОМАТ ИНИЦИАЛЬНЫЙ
- АВТОМАТ КОНЕЧНЫЙ
- АВТОМАТ ЛИНЕЙНЫЙ
- АВТОМАТ МАГАЗИННЫЙ
- АВТОМАТ МИКРОПРОГРАММНЫЙ
- АВТОМАТ МИНИМАЛЬНЫЙ
- АВТОМАТ НЕДЕТЕРМИНИРОВАННЫЙ
- АВТОМАТ ОПЕРАЦИОННЫЙ
- АВТОМАТ ПРИВЕДЁННЫЙ
- АВТОМАТ ПУШ-ДАУН
- АВТОМАТ РЕГИСТРОВЫЙ
- АВТОМАТ С МАГАЗИННОЙ ПАМЯТЬЮ
- АВТОМАТ САМОВОСПРОИЗВОДЯЩИЙСЯ
- АВТОМАТ СВОБОДНЫЙ.
- АВТОМАТ СВЯЗНЫЙ
- АВТОМАТ УПРАВЛЯЮЩИЙ
- АВТОМАТ ЧАСТИЧНЫЙ
- АВТОМАТА ДИАГРАММА
- АВТОМАТА МАТРИЦА ПЕРЕХОДОВ
- АВТОМАТА ПАМЯТЬ
- АВТОМАТА ТАБЛИЦА
- АВТОМАТА ФУНКЦИЯ
- АВТОМАТИЗАЦИЯ КОМПЛЕКСНАЯ
- АВТОМАТИЗАЦИЯ ЛИНГВИСТИЧЕСКИХ ИССЛЕДОВАНИЙ
- АВТОМАТИЗАЦИЯ МЕДИЦИНСКОЙ ДИАГНОСТИКИ
- АВТОМАТИЗАЦИЯ ПРОГРАММИРОВАНИЯ
- АВТОМАТИЗАЦИЯ ПРОЕКТИРОВАНИЯ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНИЯ ПРОИЗВОДСТВЕННЫМ ПРОЦЕССОМ
- АВТОМАТИЗАЦИЯ УПРАВЛЕНЧЕСКОГО ТРУДА
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
- АВТОМАТИЗИРОВАННАЯ СИСТЕМА ПРОЕКТИРОВАНИЯ
- АВТОМАТИЗИРОВАННОГО ОБУЧЕНИЯ КЛАСС
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ (АСУП)
- АВТОМАТИЗИРОВАННЫЙ ПОИСК ДОКАЗАТЕЛЬСТВ ТЕОРЕМ
- «АВТОМАТИКА»
- «АВТОМАТИКА И ТЕЛЕМЕХАНИКА»
- АВТОМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- АВТОМАТИЧЕСКИЙ АНАЛИЗ МЕДИКО-БИОЛОГИЧЕСКИХ ПРОЦЕССОВ
- АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- АВТОМАТИЧЕСКОЕ ЦИФРО-ПЕЧАТАЮЩЕЕ УСТРОЙСТВО
- АВТОМАТНОЕ ОТОБРАЖЕНИЕ
- АВТОМАТОВ АБСТРАКТНАЯ ТЕОРИЯ
- АВТОМАТОВ АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ
- АВТОМАТОВ АНАЛИЗ
- АВТОМАТОВ ГОМОМОРФИЗМ.
- АВТОМАТОВ ДЕКОМПОЗИЦИЯ
- АВТОМАТОВ ИГРЫ
- АВТОМАТОВ ИЗОМОРФИЗМ
- АВТОМАТОВ КОМПОЗИЦИИ
- АВТОМАТОВ МИНИМИЗАЦИЯ
- АВТОМАТОВ ПОВЕДЕНИЕ
- АВТОМАТОВ ПРОИЗВЕДЕНИЕ
- АВТОМАТОВ ПРЯМАЯ СУММА
- АВТОМАТОВ СИНТЕЗ
- АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ
- АВТОМАТОВ СТРУКТУРНАЯ ТЕОРИЯ
- АВТОМАТОВ СУПЕРПОЗИЦИЯ
- АВТОМАТОВ ТЕОРИЯ
- АВТОМАТОВ ЭКВИВАЛЕНТНОСТЬ
- АВТОМАТЫ БЕСКОНЕЧНЫЕ
- АВТОМАТЫ ИТЕРАТИВНЫЕ
- АВТОМАТЫ РАСТУЩИЕ
- АВТОНОМНОСТЬ
- АВТОПИЛОТИРОВАНИЕ
- АГРЕГАТНАЯ УНИФИЦИРОВАННАЯ СИСТЕМА (АУС)
- АГРЕГАТНО-БЛОЧНОЕ ПОСТРОЕНИЕ СРЕДСТВ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- АДАМСА МЕТОД
- АДАПТАЦИЯ В КИБЕРНЕТИКЕ
- АДАПТИВНАЯ СИСТЕМА
- АДРЕС В ПРОГРАММИРОВАНИИ
- АДРЕС МАТЕМАТИЧЕСКИЙ
- АДРЕСНЫЙ ЯЗЫК
- АДРЕСОВ МОДИФИКАЦИЯ
- АИКА
- АЛГЕБРА АЛГОРИТМОВ
- АЛГЕБРА ЛИНЕЙНАЯ
- АЛГЕБРА ЛОГИКИ
- АЛГЕБРА МАТРИЦ
- АЛГЕБРА МНОЖЕСТВ
- АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ АВТОМАТОВ
- АЛГЕБРАИЧЕСКАЯ ТОПОЛОГИЯ
- АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
- АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
- АЛГЕБРЫ СОБЫТИЙ
- АЛГЕБРЫ УНИВЕРСАЛЬНЫЕ.
- АЛГОЛ-60
- АЛГОЛ-68
- АЛГОРИТМ, АЛГОРИФМ
- АЛГОРИТМ ЛОКАЛЬНЫЙ
- АЛГОРИТМ РАСПОЗНАВАНИЯ
- АЛГОРИТМИЗАЦИЯ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ
- АЛГОРИТМИЗАЦИЯ ТВОРЧЕСКИХ ПРОЦЕССОВ
- АЛГОРИТМИЧЕСКАЯ СТРУКТУРА ЦВМ
- АЛГОРИТМИЧЕСКИЙ СИНТЕЗ ЦВМ
- АЛГОРИТМИЧЕСКИЙ ЯЗЫК
- АЛГОРИТМИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- АЛГОРИТМОВ ГРАФ-СХЕМЫ, ГРАФ-СХЕМЫ АЛГОРИТМОВ
- АЛГОРИТМОВ РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ
- АЛГОРИТМОВ СЛОЖНОСТЬ
- АЛГОРИТМОВ СХЕМА
- АЛГОРИТМОВ ТЕОРИЯ
- АЛГОРИТМОВ ЭКВИВАЛЕНТНОСТЬ
- АЛГЭК
- АЛГЭМ
- АЛМО
- АЛФАВИТНО-ЦИФРОВОЕ ПЕЧАТАЮЩЕЕ УСТРОЙСТВО (АЦПУ)
- АЛФАВИТНЫЙ ОПЕРАТОР
- АЛЬГИБР
- АЛЬФА-СИСТЕМА
- АЛЬФА-ЯЗЫК
- АМПЛИТУДНО-ИМПУЛЬСНАЯ МОДЕЛЬ
- АНАЛИЗАТОРНЫЕ СИСТЕМЫ
- АНАЛИТИК
- АНАЛИТИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ НА ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ.
- АНАЛОГ ЦИФРОВОЙ, ЦИФРОВАЯ МОДЕЛЬ
- АНАЛОГИИ
- АНАЛОГОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ABM)
- АНАЛОГО-ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- АНАЛОГО-ЦИФРОВАЯ СИСТЕМА
- АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ, ПРЕОБРАЗОВАТЕЛЬ АНАЛОГ-КОД
- АННОТИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- АНСАМБЛЬ СООБЩЕНИЙ
- АНТИГРАДИЕНТ ФУНКЦИИ
- АППРОКСИМАЦИЯ ФУНКЦИИ СРЕДНЕКВАДРАТИЧНАЯ
- АППРОКСИМАЦИЯ ФУНКЦИЙ
- АППРОКСИМАЦИЯ ФУНКЦИЙ РАВНОМЕРНАЯ (чебышевская)
- АРИФМЕТИЗАЦИЯ МАТЕМАТИКИ
- АРИФМЕТИКА С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
- АРИФМЕТИКА С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- АРИФМЕТИКА ФОРМАЛЬНАЯ
- АРИФМЕТИЧЕСКАЯ И АНАЛИТИЧЕСКАЯ ИЕРАРХИИ
- АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ ЦВМ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО (АУ)
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- АРХИВ в автоматизированных системах управления или системах обработки данных
- АСИНХРОННЫХ АВТОМАТОВ ТЕОРИЯ
- «АСОР», автоматизированная система организации работ
- АССЕМБЛЕР
- АССОЦИАТИВНЫЙ ЭЛЕМЕНТ
- АСТАТИЗМ n-ПОРЯДКА
- БАЗА ДАННЫХ
- БАЙЕСА ФОРМУЛА, формула вероятностей гипотез
- БАЙЕСОВСКИЙ МЕТОД
- БАЙЕСОВСКОЕ ОБУЧЕНИЕ
- БАЙЕСОВСКОЕ РЕШАЮЩЕЕ ПРАВИЛО
- БАЙТ (англ. byte)
- БАЛАНС МЕЖОТРАСЛЕВОЙ
- БАЛАНСОВЫЕ МОДЕЛИ
- БАНК ДАННЫХ
- БАРАБАН МАГНИТНЫЙ
- ВЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ
- ВЕЛЛМАНА УРАВНЕНИЕ
- БЕЛЫЙ ШУМ
- БЕРЖА ГРАФ
- БЕРНУЛЛИ РАСПРЕДЕЛЕНИЕ
- «БЕРРАУЗ КОРПОРЕЙШЕН» (Burroughs Corporation)
- БИАКС
- БИБЛИОГРАФИЧЕСКИЙ ПОИСК
- БИБЛИОТЕКА СТАНДАРТНЫХ ПОДПРОГРАММ
- БИБЛИОТЕЧНЫХ ПОДПРОГРАММ МЕТОД
- БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ.
- БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- БИОЛОГИЧЕСКИЕ СИСТЕМЫ
- БИОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- БИОЛОГИЧЕСКИХ СИСТЕМ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- БИОЛОГИЧЕСКИХ СИСТЕМ ОРГАНИЗАЦИЯ
- БИОМЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- БИОНИКА
- БИОЭЛЕКТРИЧЕСКОЕ УПРАВЛЕНИЕ
- БИТ
- БЛЕЙКА АЛГОРИТМ
- БЛОК в программировании
- БЛОК ПЕРЕМЕННЫХ КОЭФФИЦИЕНТОВ
- БЛОК ХРАНЕНИЯ ИНФОРМАЦИИ
- БЛОКИ ЦВМ ТИПОВЫЕ
- БЛОКИРОВКА ОБСЛУЖИВАНИЯ
- БЛОК-СХЕМА ПРОГРАММЫ
- БЛОЧНЫЙ СИНТЕЗ ЦВМ
- БОЛЬЦА ЗАДАЧА
- БОЛЬШАЯ ИНТЕГРАЛЬНАЯ СХЕМА (БИС)
- БОЛЬШИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- БОЛЬШИХ ЧИСЕЛ ЗАКОН
- БУБНОВА — ГАЛЕРКИНА МЕТОД
- БУЛЕВА АЛГЕБРА
- БУЛЕВЫ ФУНКЦИИ
- БУХГАЛТЕРСКОГО УЧЁТА АВТОМАТИЗАЦИЯ
- БЫСТРОДЕЙСТВИЕ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- БЫСТРОДЕЙСТВИЕ ЦВМ
- БЭКУСА НОРМАЛЬНАЯ ФОРМА
- «БЭСМ»
- ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
- ВАРИАЦИОННЫЕ МЕТОДЫ
- ВАРИАЦИОННЫЙ РЯД
- ВВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЕЙЧА ДИАГРАММА
- ВЕКТОР ОБОБЩЕННОГО ГРАДИЕНТА
- ВЕНГЕРСКИЙ МЕТОД
- ВЕРОЯТНОСТЕЙ РАСПРЕДЕЛЕНИЕ
- ВЕРОЯТНОСТЕЙ ТЕОРИЯ
- ВЕРОЯТНОСТНАЯ МАШИНА
- ВЕРОЯТНОСТНЫЙ ПРОЦЕСС
- ВЕРОЯТНОСТЬ
- ВЕРОЯТНОСТЬ УСЛОВНАЯ
- «ВЕСНА»
- ВЕСОВАЯ ФУНКЦИЯ
- ВЕТВЕЙ И ГРАНИЦ МЕТОД
- ВЕТВЯЩИЙСЯ ПРОЦЕСС
- ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- ВЗАИМОДЕЙСТВИЕ ЧЕЛОВЕКА С ВЫЧИСЛИТЕЛЬНОЙ МАШИНОЙ
- ВИНЕРА—ХОПФА УРАВНЕНИЕ первого рода
- ВНЕШНЕЕ ОБОРУДОВАНИЕ
- ВНЕШНИЕ УСТРОЙСТВА
- «ВНИИЭМ»
- ВОЗБУЖДЕНИЯ КЛЕТКИ ТЕОРИЯ
- ВОЗМОЖНЫХ НАПРАВЛЕНИЙ МЕТОД
- ВОЗМУЩАЮЩЕЕ ВОЗДЕЙСТВИЕ,
- ВОЛЬТЕРРЫ УРАВНЕНИЕ
- ВОССТАНОВЛЕНИЯ ТЕОРИЯ
- ВРЕМЕННОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ
- ВРЕМЕННЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ВРЕМЯ ВОССТАНОВЛЕНИЯ после отказа
- ВРЕМЯ ВЫБОРКИ ИНФОРМАЦИИ
- ВРЕМЯ МОДЕЛИРОВАНИЯ ДЕЙСТВИТЕЛЬНОЕ
- ВРЕМЯ ОБРАЩЕНИЯ К ЗАПОМИНАЮЩЕМУ УСТРОЙСТВУ
- ВРЕМЯ ОЖИДАНИЯ
- ВРЕМЯ РАБОТЫ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ ПОЛЕЗНОЕ
- ВСЕСОЮЗНЫЙ ИНСТИТУТ НАУЧНОЙ И ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ (ВИНИТИ)
- ВСПОМОГАТЕЛЬНОГО ОПЕРАТОРА МЕТОД
- ВХОДНОЕ УСТРОЙСТВО
- ВЫБОРКА ТРЕНИРОВОЧНАЯ
- ВЫВОДА ИНФОРМАЦИИ УСТРОЙСТВО
- ВЫДЕЛЕНИЕ СИГНАЛОВ НА ФОНЕ ПОМЕХ
- ВЫИГРЫША ФУНКЦИЯ
- ВЫИГРЫШЕЙ МАТРИЦА
- ВЫПУКЛАЯ ОБОЛОЧКА
- ВЫПУКЛАЯ ФУНКЦИЯ
- ВЫПУКЛОЕ МНОГОГРАННОЕ МНОЖЕСТВО
- ВЫПУКЛОЕ МНОЖЕСТВО
- ВЫПУКЛЫЙ КОНУС
- ВЫПУКЛЫЙ МНОГОГРАННИК
- ВЫПУКЛЫЙ МНОГОГРАННЫЙ КОНУС
- ВЫСКАЗЫВАНИЙ ИСЧИСЛЕНИЕ
- ВЫСКАЗЫВАНИЯ ЛОГИЧЕСКИ ИСТИННЫЕ, высказывания тождественно истинные
- ВЫСКАЗЫВАНИЯ ЭКЗИСТЕНЦИАЛЬНЫЕ
- ВЫХОДНОЕ УСТРОЙСТВО
- ВЫЧИСЛЕНИЯ В РЕАЛЬНОЕ ВРЕМЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА КЛАВИШНАЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- ВЫЧИСЛИТЕЛЬНАЯ МАШИНА ОБЩЕГО НАЗНАЧЕНИЯ
- ВЫЧИСЛИТЕЛЬНАЯ СИСТЕМА
- ВЫЧИСЛИТЕЛЬНАЯ СХЕМА
- ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА ПОГРЕШНОСТЬ
- ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА СХОДИМОСТЬ
- ВЫЧИСЛИТЕЛЬНЫЕ СРЕДЫ
- ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК АРМЯНСКОЙ ССР И ЕРЕВАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР СИБИРСКОГО ОТДЕЛЕНИЯ АКАДЕМИИ НАУК СССР
- ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ ХАРАКТЕРИСТИКИ
- ВЫЧИСЛИТЕЛЬНЫХ МАШИН И СИСТЁМ КОМПЛЕКСЫ
- ВЫЧИСЛИТЕЛЬНЫХ РАБОТ МЕТОДЫ ОРГАНИЗАЦИИ
- ВЫЧИСЛИТЕЛЬНЫХ ЦЕНТРОВ СЕТИ
- ГАМИЛЬТОНОВ ПУТЬ (контур)
- ГАМИЛЬТОНОВА ЦЕПЬ
- ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- ГАУССА МЕТОД
- ГАУССА РАСПРЕДЕЛЕНИЕ
- ГАУССОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ГЕДЕЛЯ ТЕОРЕМЫ О НЕПОЛНОТЕ
- ГЕНЕРАТОР ПРОГРАММ
- ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ
- ГЕНЦЕНА ФОРМАЛЬНЫЕ СИСТЕМЫ
- ГИБРИДНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- ГИДРОБИОНИКА
- ГИПЕРБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ГИПЕРГРАФ
- ГИПЕРПЛОСКОСТИ ОТСЕКАЮЩЕЙ МЕТОД
- ГИПОТЕЗА КОМПАКТНОСТИ
- ГИСТОГРАММА
- ГЛОБАЛЬНОГО ПОИСКА МЕТОДЫ
- ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
- ГНЕЗДОВОЙ СПИСОК
- ГНОСЕОЛОГИЧЕСКИЕ ОСНОВЫ КИБЕРНЕТИКИ
- ГОЛОГРАФИЯ
- ГОМЕОСТАЗИС
- ГОМЕОСТАТИЧЕСКАЯ СИСТЕМА
- ГОМОРИ МЕТОД
- ГОНОК ПРОБЛЕМА
- ГОРНЕРА СХЕМА
- ГОСУДАРСТВЕННЫЙ ФОНД АЛГОРИТМОВ И ПРОГРАММ (ГФАП)
- ГРАДИЕНТ
- ГРАДИЕНТНЫЙ МЕТОД
- ГРАММАТИКА АВТОМАТНАЯ, грамматика с конечным числом состояний
- ГРАММАТИКА БЕСКОНТЕКСТНАЯ, грамматика контекстно-свободная
- ГРАММАТИКА ЗАВИСИМОСТЕЙ, грамматика управлений
- ГРАММАТИКА КАТЕГОРИАЛЬНАЯ
- ГРАММАТИКА ЛИНЕЙНАЯ
- ГРАММАТИКА ПОРОЖДАЮЩАЯ
- ГРАММАТИКА РАСПОЗНАЮЩАЯ
- ГРАММАТИКА СОСТАВЛЯЮЩИХ, грамматика непосредственно составляющих
- ГРАММАТИКА ТРАНСФОРМАЦИОННАЯ
- ГРАММАТИКА ФОРМАЛЬНАЯ
- ГРАНИЧНАЯ ЗАДАЧА
- ГРАФ
- ГРАФ ВЗВЕШЕННЫЙ
- ГРАФ РАСКРАШЕННЫЙ
- ГРАФИЧЕСКОЕ РЕГИСТРИРУЮЩЕЕ УСТРОЙСТВО
- ГРАФОВ СВЯЗНОСТЬ
- ГРАФОВ ТЕОРИЯ
- ГРАФОПОСТРОИТЕЛЬ
- ГРУПП ТЕОРИЯ
- ГРУППА в алгебре
- ГРУППОВОЙ ИСТОЧНИК НАПРЯЖЕНИЯ
- ГРУППЫ НЕПРЕРЫВНЫЕ.
- ГУРВИЦА КРИТЕРИЙ
- ГУРВИЦА ТЕОРЕМА
- ДАННЫЕ
- ДАТЧИК ВРЕМЕНИ,
- ДАТЧИК ОДИНОЧНЫХ ИМПУЛЬСОВ
- ДАТЧИК РАБОЧЕГО ЦИКЛА
- ДАТЧИК СЛУЧАЙНЫХ ЧИСЕЛ
- ДВИГАТЕЛЬ ПОЛИМЕРНЫЙ
- ДВОЙСТВЕННАЯ ЗАДАЧА ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ.
- ДВОЙСТВЕННАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- ДВОЙСТВЕННОСТИ ЗАКОН, принцип двойственности
- ДВОЙСТВЕННОСТИ ТЕОРИЯ в программировании линейном
- ДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ДВОЙСТВЕННЫЙ ГРАДИЕНТНЫЙ МЕТОД
- ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД, метод последовательного уточнения оценок
- ДВОЙСТВЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ДВУПОЛЮСНИК КОНТАКТНЫЙ
- ДВУХТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ДЕЙСТВИТЕЛЬНОЕ ВРЕМЯ МОДЕЛИРОВАНИЯ
- ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО
- ДЕКОМПОЗИЦИИ МЕТОД, блочный метод
- ДЕЛЕЖ в теории игр
- ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ
- ДЕЛЬТА-ФУНКЦИЯ
- ДЕМОДУЛЯТОР, детектор
- ДЕМПФИРОВАНИЕ
- «ДЕРЕВО» в теории графов
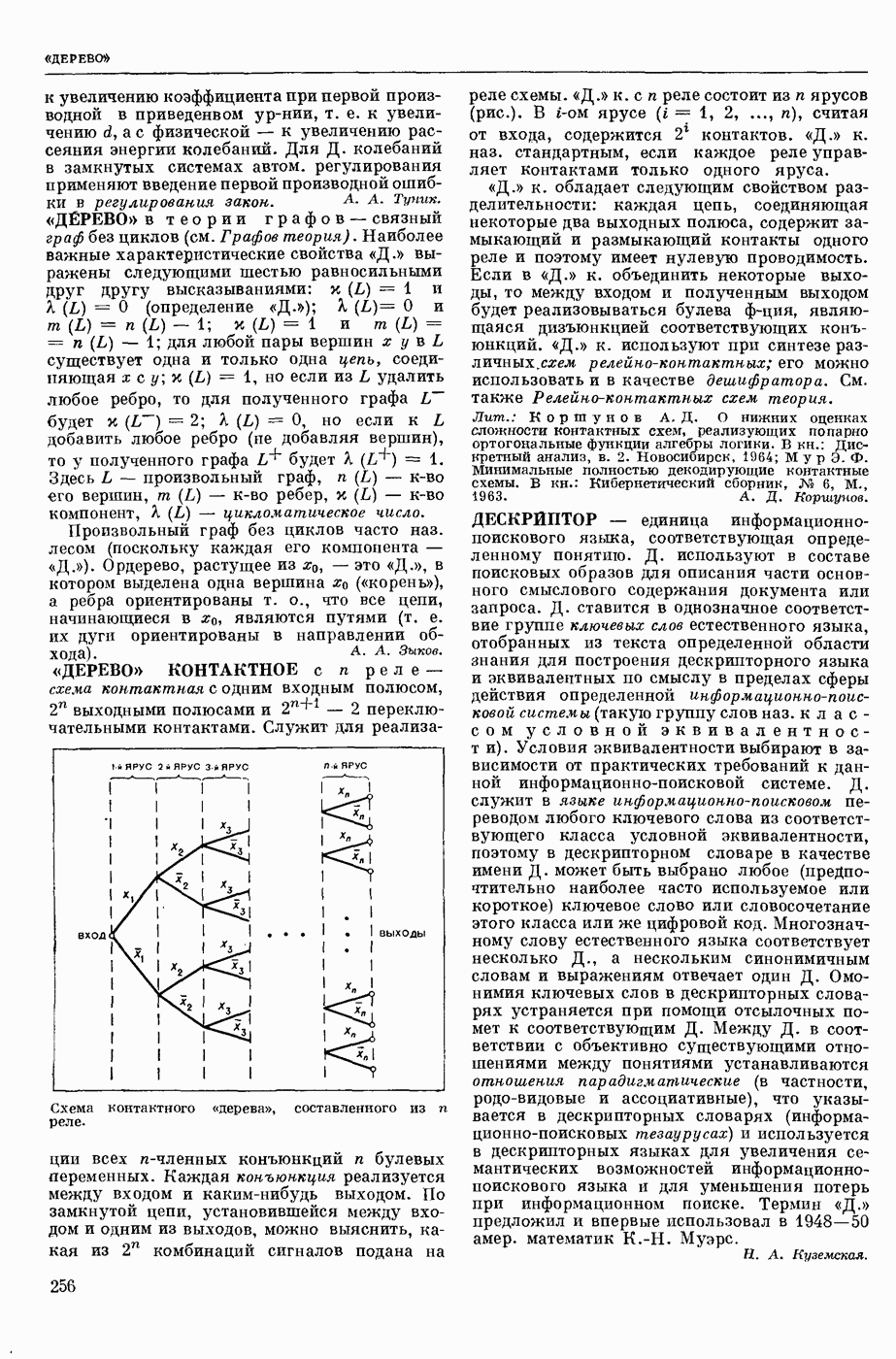
- «ДЕРЕВО» КОНТАКТНОЕ с n реле
- ДЕСКРИПТОР
- ДЕТЕРМИНИРОВАННЫЕ СИСТЕМЫ
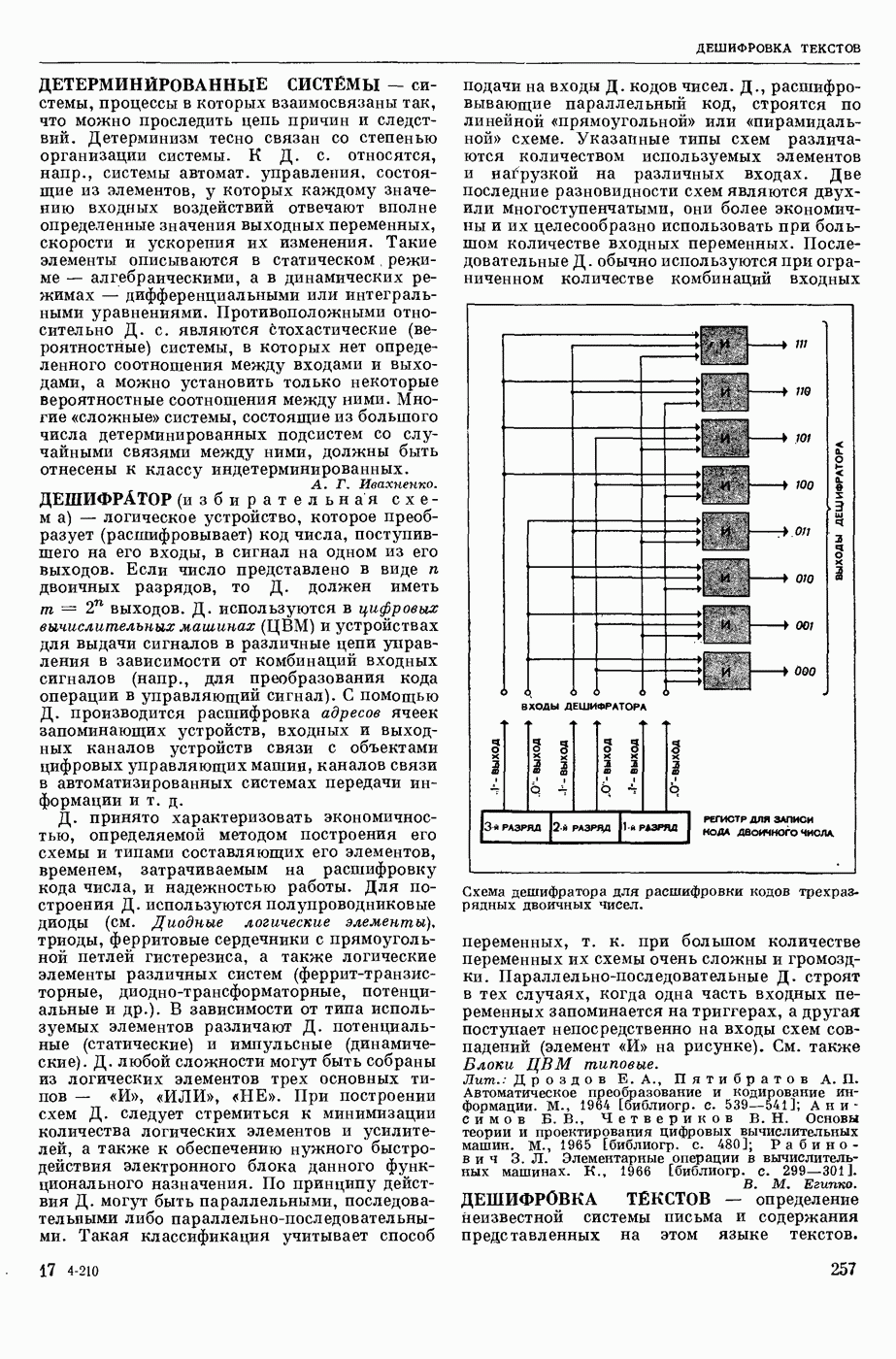
- ДЕШИФРАТОР
- ДЕШИФРОВКА ТЕКСТОВ
- ДИАГНОСТИКА АВТОМАТИЧЕСКАЯ
- ДИАГНОСТИКА НЕИСПРАВНОСТЕЙ ЦВМ
- ДИАГНОСТИРОВАНИЕ СЛОЖНЫХ ТЕХНИЧЕСКИХ КОМПЛЕКСОВ, техническая диагностика
- ДИАЛОГА РЕЖИМ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (ДНФ)
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА ТУПИКОВАЯ.
- ДИЗЪЮНКЦИЯ
- ДИЗЪЮНКЦИЯ СЛАБАЯ
- ДИЗЪЮНКЦИЯ СТРОГАЯ, антиэквивалентность, сложение по модулю 2
- ДИНАМИЧЕСКИХ СИСТЕМ ТЕОРИЯ ЧУВСТВИТЕЛЬНОСТИ
- ДИНАМИЧЕСКИХ СИСТЕМ УСЛОВИЯ ГРУБОСТИ
- ДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ МЕТОД
- ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ
- ДИОД ПОЛУПРОВОДНИКОВЫЙ
- ДИОДНАЯ ЛИНЕЙКА
- ДИОДНАЯ МАТРИЦА
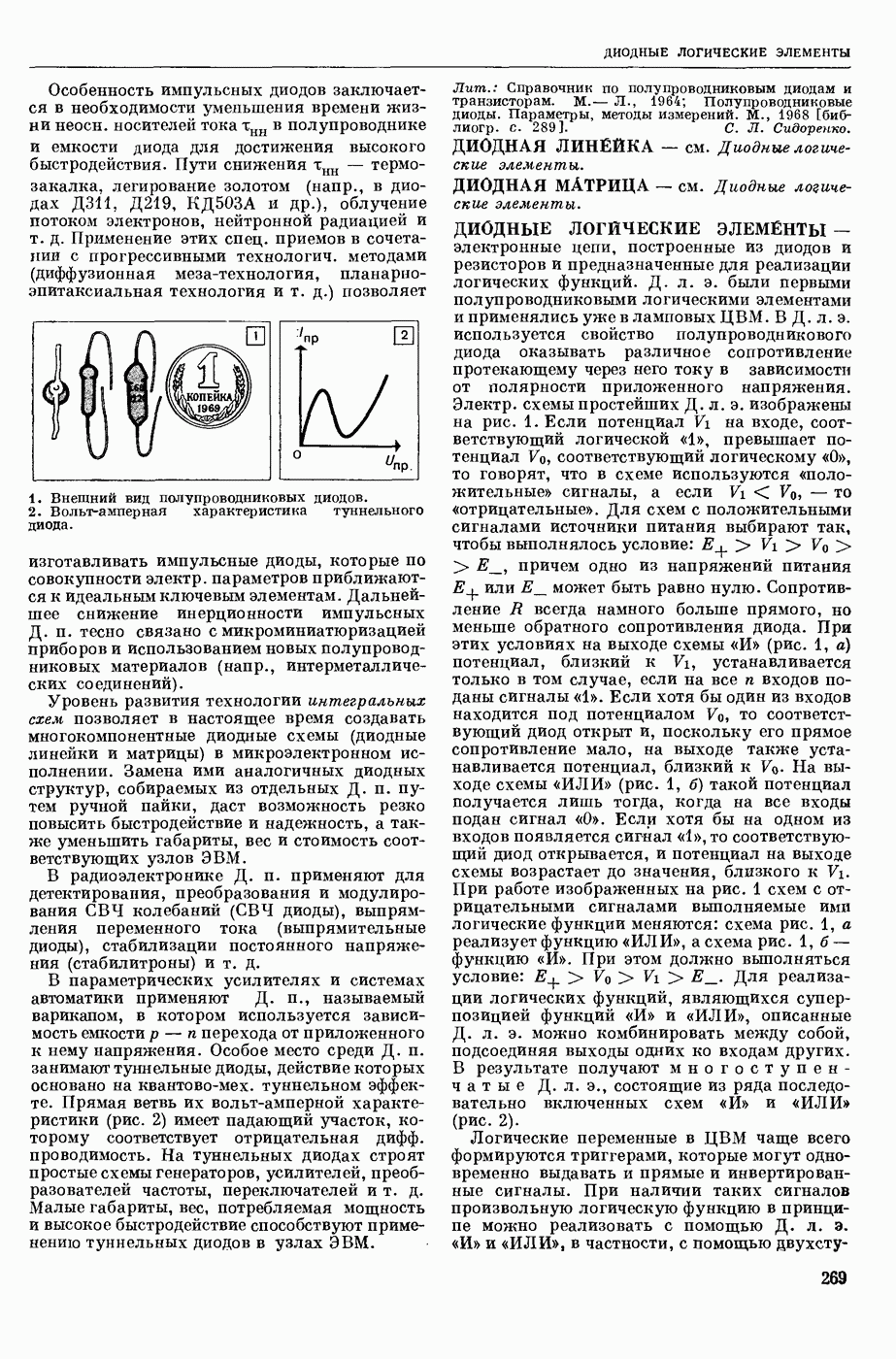
- ДИОДНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ДИРАКА ФУНКЦИЯ
- ДИСК МАГНИТНЫЙ
- ДИСКРЕТИЗАЦИЯ ИЗОБРАЖЕНИЙ
- ДИСКРЕТНАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- ДИСКРЕТНАЯ СИСТЕМА
- ДИСКРЕТНАЯ СИСТЕМА УПРАВЛЕНИЯ, импульсная система управления
- ДИСКРЕТНЫЙ АНАЛИЗ
- ДИСКРЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ ТЕОРИЯ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- ДИСКРЕТНЫХ ЭЛЕМЕНТОВ СИСТЕМА
- ДИСПЕРСИОННЫЙ АНАЛИЗ
- ДИСПЕРСИЯ
- ДИСПЕТЧЕР в программировании
- ДИСПЕТЧЕРСКОГО УПРАВЛЕНИЯ АВТОМАТИЗАЦИЯ
- ДИСТАНЦИОННОЕ УПРАВЛЕНИЕ
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ДИФФЕРЕНЦИАЛЬНАЯ СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ДИФФЕРЕНЦИАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ КЛАССИФИКАЦИЯ.
- ДИФФЕРЕНЦИАЛЬНЫХ РЕНТ МЕТОД
- ДИФФЕРЕНЦИАТОР
- ДИФФЕРЕНЦИРОВАНИЕ СИГНАЛОВ
- ДИФФЕРЕНЦИРОВАНИЕ СИМВОЛЬНОЕ, дифференцирование аналитическое
- ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ
- ДИФФУЗИОННЫЙ ПРОЦЕСС
- ДЛИНА ОЧЕРЕДИ
- ДЛИТЕЛЬНОСТЬ ОЖИДАНИЯ
- «ДНЕПР»
- ДОВЕРИТЕЛЬНАЯ ОБЛАСТЬ
- ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
- ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ
- ДОВЕРИТЕЛЬНЫЙ УРОВЕНЬ
- ДОКАЗАТЕЛЬСТВ ТЕОРИЯ, метаматематика
- ДОКАЗАТЕЛЬСТВО ТЕОРЕМ НА ЭВМ, машинный поиск логического вывода
- ДОКУМЕНТ НАУЧНЫЙ
- ДОКУМЕНТАЛЬНАЯ ИНФОРМАЦИОННОПОИСКОВАЯ СИСТЕМА
- ДОКУМЕНТАЛЬНО-ФАКТОГРАФИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
- ДОЛГОВРЕМЕННОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ДЗУ)
- ДОМИНИРОВАНИЕ в теории игр.
- ДОПУСТИМАЯ ОБЛАСТЬ
- ДОПУСТИМАЯ ТОЧКА
- ДОПУСТИМОЕ МНОЖЕСТВО
- ДОПУСТИМОЕ УПРАВЛЕНИЕ
- ДОПУСТИМЫЙ ВЕКТОР
- ДОПУСТИМЫЙ ПУТЬ в теории графов
- ДОПУСТИМЫХ НАПРАВЛЕНИЙ МЕТОД
- ДОСТАТОЧНОСТЬ ПРИЗНАКОВ.
- ДОСТАТОЧНЫЕ СТАТИСТИКИ
- ДОСТУП ПОСЛЕДОВАТЕЛЬНЫЙ
- ДОСТУП ПРОИЗВОЛЬНЫЙ
- ДРЕЙФ НУЛЕВОГО УРОВНЯ операционного усилителя
- ДРОБНО-ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ЗАДАЧА
- ДРОБНЫХ ШАГОВ МЕТОД
- ДУАЛЬНОЕ УПРАВЛЕНИЕ
- ДУГА графа
- ДУЭЛЬ в теории игр
- ЕДИНАЯ СИСТЕМА ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН (ЕС ЭВМ)
- ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ
- ЕМКОСТНАЯ МОДЕЛЬ
- ЖЕГАЛКИНА АЛГЕБРА
- ЗАГРУЗЧИК в программировании
- ЗАДАЧА О КОММИВОЯЖЕРЕ
- ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ
- ЗАДАЧА О НАЗНАЧЕНИЯХ
- ЗАДАЧА О ПЕРЕВОЗКАХ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
- ЗАДАЧА О РАСПРЕДЕЛЕНИИ ПОСТАВОК
- ЗАДАЧА О РЮКЗАКЕ
- ЗАДАЧА О СКЛАДЕ
- ЗАДАЧА ОБ ОПТИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
- ЗАДАЧА ОБ УЗКИХ МЕСТАХ
- ЗАДАЧА С ЗАКРЕПЛЕННЫМ ВРЕМЕНЕМ
- ЗАДАЧА С ПОДВИЖНЫМИ КОНЦАМИ
- ЗАМЫКАНИЕ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА
- ЗАПАЗДЫВАНИЯ БЛОК
- ЗАПАСОВ ТЕОРИЯ, теория управления запасами
- ЗАПИСЬ
- ЗАПИСЬ БЕССКОБОЧНАЯ, польская запись
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЕМКОСТЬ
- ЗАПОМИНАЮЩЕГО УСТРОЙСТВА ЗОНА
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ЗУ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АВМ (ЗУ АВМ)
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АДРЕСНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО АССОЦИАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО БУФЕРНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ВНЕШНЕЕ, внешний накопитель
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ДОЛГОВРЕМЕННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО МАГАЗИННОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО НА ЛИНИЯХ ЗАДЕРЖКИ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ОПЕРАТИВНОЕ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПОСЛЕДОВАТЕЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПРОИЗВОЛЬНЫМ ОБРАЩЕНИЕМ
- ЗАПОМИНАЮЩИЙ ЭЛЕМЕНТ
- ЗАЦИКЛИВАНИЕ
- ЗАЩИТА ПАМЯТИ
- ЗНАКОВЫЙ РАЗРЯД
- ЗНАЧАЩИЕ ЦИФРЫ приближенного числа
- ИБМ (International Business Machines)
- ИГР ТЕОРИЯ
- ИГРА АЗАРТНАЯ
- ИГРА БЕЗ ПОБОЧНЫХ ПЛАТЕЖЕЙ
- ИГРА БЕСКОАЛИЦИОННАЯ
- ИГРА ВЫПУКЛАЯ
- ИГРА ВЫРОЖДЕННАЯ
- ИГРА ДИНАМИЧЕСКАЯ
- ИГРА КООПЕРАТИВНАЯ
- ИГРА НА ГРАФЕ
- ИГРА НА ЕДИНИЧНОМ КВАДРАТЕ
- ИГРА ПОЗИЦИОННАЯ
- ИГРА ПРОСТАЯ
- ИГРА РЕКУРСИВНАЯ
- ИГРА С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ
- ИГРА СТОХАСТИЧЕСКАЯ
- ИГРУШКИ КИБЕРНЕТИЧЕСКИЕ
- ИГРЫ АНТАГОНИСТИЧЕСКИЕ
- ИГРЫ ДИФФЕРЕНЦИАЛЬНЫЕ
- ИГРЫ ЗНАЧЕНИЕ
- ИГРЫ МАТРИЧНЫЕ
- ИГРЫ НА ВЫЖИВАНИЕ
- ИГРЫ РЕФЛЕКСИВНЫЕ
- ИДЕНТИФИКАТОР
- ИДЕНТИФИКАЦИЯ ОБЪЕКТОВ УПРАВЛЕНИЯ
- ИЕРАРХИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ (ИСУ)
- ИЕРАРХИЧНОСТЬ УПРАВЛЕНИЯ
- ИЗБЫТОЧНОСТЬ СИСТЕМЫ
- ИЗБЫТОЧНОСТЬ СООБЩЕНИЙ
- ИМПЛИКАЦИЯ в алгебре логики
- ИМПЛИКАЦИЯ СТРОГАЯ
- ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ
- ИМПУЛЬСНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ИНВАРИАНТНОСТЬ ПРИЗНАКОВ
- ИНВАРИАНТНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ИНВЕРТОР
- ИНГВЕ ГИПОТЕЗА, гипотеза глубины
- ИНДЕКСИРОВАНИЕ
- ИНДИКАТОРЫ ИНФОРМАЦИИ
- ИНЖЕНЕРНЫЕ МЕТОДЫ СИНТЕЗА ДИСКРЕТНЫХ АВТОМАТОВ
- ИНЖЕНЕРНЫХ РАСЧЕТОВ АВТОМАТИЗАЦИЯ
- ИНСТИТУТ АВТОМАТИКИ АКАДЕМИИ НАУК КИРГИЗСКОЙ ССР
- ИНСТИТУТ АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ (ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ) АКАДЕМИИ НАУК СССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК АЗЕРБАЙДЖАНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК ЭСТОНСКОЙ ССР
- ИНСТИТУТ КИБЕРНЕТИКИ С ВЫЧИСЛИТЕЛЬНЫМ ЦЕНТРОМ АКАДЕМИИ НАУК УЗБЕКСКОЙ ССР
- ИНСТИТУТ ПРИКЛАДНОЙ МАТЕМАТИКИ И МЕХАНИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- ИНСТИТУТ СИСТЕМ УПРАВЛЕНИЯ АКАДЕМИИ НАУК ГРУЗИНСКОЙ ССР
- ИНСТИТУТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ АКАДЕМИИ НАУК БЕЛОРУССКОЙ ССР
- ИНСТИТУТ ТОЧНОЙ МЕХАНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК СССР
- ИНСТИТУТ ЭЛЕКТРОНИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ АКАДЕМИИ НАУК ЛАТВИЙСКОЙ ССР
- ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ, приборная погрешность
- ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ИНТЕГРАЛЬНАЯ СХЁМА
- ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ СИНГУЛЯРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАЛЬНЫХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ИНТЕГРАТОР
- ИНТЕГРИРОВАНИЕ СИМВОЛЬНОЕ, интегр ирование аналитическое
- ИНТЕГРИРОВАНИЕ ЧИСЛЕННОЕ
- ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- ИНТЕНСИВНОСТЬ ПОТОКА в теории массового обслуживания
- «ИНТЕРНЕЙШЕНАЛ БИЗНЕС МАШЙНЗ КОРПОРЕЙШЕН», ИБМ (International Business Machines Corporation, IBM)
- «ИНТЕРНЕЙШЕНАЛ КОМПЬЮТЕРЗ ЛЙМИТЕД» (International Computers Limited, I. С. L.)
- ИНТЕРПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
- ИНТЕРПОЛЯТОР
- ИНТЕРПРЕТАЦИЯ ЯЗЫКА СТРУКТУРНАЯ
- ИНТЕРПРЕТИРУЮЩАЯ СИСТЕМА
- ИНТУИЦИОНИЗМ
- ИНФОРМАТИВНОСТЬ ПРИЗНАКОВ
- ИНФОРМАТИКА
- ИНФОРМАЦИИ КОЛИЧЕСТВО
- ИНФОРМАЦИИ ПЕРЕДАЧА
- ИНФОРМАЦИИ ТЕОРИЯ
- ИНФОРМАЦИИ ХРАНЕНИЕ
- ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНЫЙ ЦЕНТР ПРЕДПРИЯТИЯ
- ИНФОРМАЦИОННО-ЛОГИЧЕСКАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ ЯЗЫК
- ИНФОРМАЦИОННО-ПЛАНИРУЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА ФАКТОГРАФИЧЕСКАЯ
- ИНФОРМАЦИОННО-ПОИСКОВОЕ УСТРОЙСТВО
- ИНФОРМАЦИОННО-ПОИСКОВЫЙ ЯЗЫК
- ИНФОРМАЦИОННО-СПРАВОЧНАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩАЯ СИСТЕМА
- ИНФОРМАЦИОННО-УПРАВЛЯЮЩИХ СИСТЕМ ТЕХНИЧЕСКОЕ ОСНАЩЕНИЕ
- ИНФОРМАЦИОННЫЕ ПОТОКИ НАУКИ
- ИНФОРМАЦИОННЫХ РАБОТ АВТОМАТИЗАЦИЯ
- ИНФОРМАЦИЯ (лат. informatio — разъяснение, изложение, осведомленность)
- ИНФОРМАЦИЯ ДОКУМЕНТАЛЬНАЯ
- ИНФОРМАЦИЯ НАУЧНАЯ
- ИНФОРМАЦИЯ СЕМАНТИЧЕСКАЯ
- ИСКЛЮЧЕННОГО ТРЕТЬЕГО ЗАКОН
- «ИСКРА»
- ИСКУССТВЕННАЯ МЫШЦА
- ИСКУССТВЕННЫЙ РАЗУМ
- ИСПОЛНИТЕЛЬНЫЙ МЕХАНИЗМ
- ИСТОЧНИК ОПОРНОГО НАПРЯЖЕНИЯ
- ИСТОЧНИК СООБЩЕНИЙ
- ИСЧИСЛЕНИЕ, дедуктивная система
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ, пропозициональное исчисление
- ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ МИНИМАЛЬНОЕ, логика минимальная
- ИСЧИСЛЕНИЕ ЗАДАЧ, теория задач
- ИСЧИСЛЕНИЕ ПРЕДИКАТОВ УЗКОЕ, исчисление предикатов первой ступени
- ИСЧИСЛЕНИЕ ПРОПОЗИЦИОНАЛЬНОЕ
- «ИТЕРАТОР»
- ИТЕРАЦИОННЫЕ МЕТОДЫ
- ИТЕРАЦИЯ СОБЫТИЯ
- ИФАК (International Federation of Automatic Control)
- ИФИП (International Federation for Information Processing)
- КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ
- КАНАЛ МАШИННЫЙ
- КАНАЛОВ СВЯЗИ ПРОПУСКНАЯ СПОСОБНОСТЬ
- КАНАЛЫ СВЯЗИ
- КАРДИНАЛЬНЫЕ ЧИСЛА
- КАРНАУ КАРТА, Вейча диаграмма
- КАРТА МАГНИТНАЯ
- КАСКАДОВ МЕТОД
- КАТАЛОГ
- КАТЕГОРИЙ ТЕОРИЯ
- КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ
- КВАДРАТУРНЫЕ ФОРМУЛЫ
- КВАЗИАНАЛОГОВАЯ МОДЕЛИРУЮЩАЯ СРЕДА
- КВАЗИАНАЛОГОВАЯ МОДЕЛЬ
- КВАЗИАНАЛОГОВОЕ МОДЕЛИРОВАНИЕ
- КВАЗИРЕЗИСТОР
- КВАЙНА МЕТОД МИНИМИЗАЦИИ
- КВАНТОВАНИЕ
- КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ
- КВАНТОРЫ
- КИБЕРНЕТИКА
- «КИБЕРНЕТИКА»
- «КИБЕРНЕТИКА» — реферативный журнал,
- КИБЕРНЕТИКА БИОЛОГИЧЕСКАЯ
- КИБЕРНЕТИКА В ВОЕННОМ ДЕЛЕ
- КИБЕРНЕТИКА МЕДИЦИНСКАЯ
- КИБЕРНЕТИКА ТЕХНИЧЕСКАЯ
- КИБЕРНЕТИКА ЭКОНОМИЧЕСКАЯ
- КЛАСС ЗАМКНУТЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ИНВАРИАНТНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАСС ПРЕДПОЛНЫЙ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ
- КЛАССИФИКАЦИИ ИЕРАРХИЧЕСКИЕ
- КЛАССИФИКАЦИЯ АВТОМАТИЧЕСКАЯ
- КЛЮЧЕВОЕ СЛОВО
- КОБОЛ
- КОД (от лат. codex)
- КОД СЕМАНТИЧЕСКИЙ
- КОДИРОВАНИЕ АВТОМАТНОЕ
- КОДИРОВАНИЕ СОСТОЯНИЙ АВТОМАТА
- КОДИРОВАНИЯ ТЕОРИЯ
- КОДЫ КОРРЕКТИРУЮЩИЕ
- КОЛЕБАНИЯ СКРЫТЫЕ
- КОЛМОГОРОВА УРАВНЕНИЯ
- КОМАНД МОДИФИКАЦИЯ
- КОМАНД СИСТЕМА
- КОМАНДА МАШИННАЯ
- КОМАНДЫ ФОРМАТ
- КОМБИНАТОРНЫЙ АНАЛИЗ
- КОМБИНАЦИОННАЯ СХЕМА
- КОМБИНИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- КОМБИНИРОВАННАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОМБИНИРОВАННЫЕ МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- КОМИТ
- КОММУНИКАЦИОННЫЙ ПРОЦЕССОР
- «КОМПАНИ ИНТЕРНАСЬОНАЛЬ ПУР Л’ИНФОРМАТИК» (Compagnie internationale pour l’informatique)
- КОМПАУНДИРУЮЩИЕ СВЯЗИ В АВТОМАТИЧЕСКИХ СИСТЕМАХ
- КОМПЕНСАЦИОННЫЙ СПОСОБ НАСТРОЙКИ И ИЗМЕРЕНИЯ РЕЗУЛЬТАТОВ РЕШЕНИЯ
- КОМПЛЕКСИРОВАНИЕ МАШИН
- КОМПЛЕКТ ПЕРФОРАЦИОННЫЙ ВЫЧИСЛИТЕЛЬНЫЙ
- КОМПЬЮТЕР
- КОНЕЧНОРАЗНОСТНЫЕ МЕТОДЫ, методы сеток
- КОНКУРЕНЦИИ МОДЕЛИ
- КОНСТРУКТИВНОЕ НАПРАВЛЕНИЕ В МАТЕМАТИКЕ, конструктивная математика
- КОНСТРУКТИВНЫЙ АНАЛИЗ, рекурсивный анализ, вычислимый анализ
- «КОНТРОЛ ДЕЙТА КОРПОРЁЙШЕН» (Control Data Corporation)
- КОНТРОЛЬ ABM
- КОНТРОЛЬ НАБОРА ЗАДАЧ В АВМ
- КОНТРОЛЬ ПРОГРАММНЫЙ
- КОНТРОЛЬ ЦВМ
- КОНТРОЛЬНИК
- КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
- КОНЪЮНКЦИЯ
- КООРДИНАЦИОННО — УПРАВЛЯЮЩИЙ ЦЕНТР ПРЕДПРИЯТИЯ
- КОРНЕВОГО ГОДОГРАФА МЕТОД
- КОРНЕЙ АЛГЕБРАИЧЕСКИХ МНОГОЧЛЕНОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРНЕЙ НЕПРЕРЫВНЫХ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- КОРРЕКЦИЯ ДРЕЙФА НУЛЯ
- КОРРЕКЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КОРРЕЛЯТОР, коррелометр, коррелограф
- КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ ПОЛЯРНАЯ (знаковая)
- КОРРЕЛЯЦИОННАЯ ЭКСТРЕМАЛЬНАЯ СИСТЕМА
- КОРРЕЛЯЦИОННЫЙ АППАРАТУРНЫЙ АНАЛИЗ случайных процессов
- КОРРЕЛЯЦИОННЫЙ МЕТОД РАСПОЗНАВАНИЯ
- КОРРЕЛЯЦИОННЫЙ ЧИТАЮЩИЙ АВТОМАТ
- КОРРЕЛЯЦИЯ в теории вероятностей
- КОШИ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ СПОСОБЫ РЕШЕНИЯ.
- КОЭФФИЦИЕНТ ПЕРЕДАЧИ АВМ
- КОЭФФИЦИЕНТ ПОЛНОТЫ ПОИСКА
- КОЭФФИЦИЕНТ ТОЧНОСТИ ПОИСКА
- КРАЕВАЯ ЗАДАЧА
- КРАЕВЫЕ УСЛОВИЯ
- КРАЕВЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- КРАЙНЯЯ ТОЧКА
- КРАТНЫХ ИНТЕГРАЛОВ СПОСОБЫ ПРИБЛИЖЁННОГО ВЫЧИСЛЕНИЯ
- КРИОГЕННЫЕ ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- КРИОТРОН
- КРИТЕРИИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- КРИТЕРИЙ СЕМАНТИЧЕСКОГО СООТВЕТСТВИЯ
- КРИТИЧЕСКИЙ ПУТЬ
- КУБ ФЕРРИТОВЫЙ
- КУБАТУРНЫЕ ФОРМУЛЫ
- «КИIВ-67»
- ЛАГ И ТАГ СИСТЕМЫ
- ЛАГРАНЖА ЗАДАЧА
- ЛАГРАНЖА ПРАВИЛО МНОЖИТЕЛЕЙ
- ЛАПЛАСА ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЛАПЛАСА ПРЕОБРАЗОВАНИЯ
- ЛЕЖАНДРА—КЛЕБША УСЛОВИЕ
- ЛЕНТА МАГНИТНАЯ
- ЛИНГВИСТИКА МАТЕМАТИЧЕСКАЯ
- ЛИНГВИСТИКА ПРИКЛАДНАЯ
- ЛИНГВИСТИЧЕСКАЯ СТАТИСТИКА
- ЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- ЛИНЕЙНАЯ ФОРМА, линейный функционал, ковектор
- ЛИНЕЙНЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ СИСТЕМ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ
- ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- ЛИСП
- ЛОГИКА КОНСТРУКТИВНАЯ
- ЛОГИКА МАЖОРИТАРНАЯ
- ЛОГИКА МАТЕМАТИЧЕСКАЯ, формальная логика
- ЛОГИКА МИНИМАЛЬНАЯ
- ЛОГИКА МНОГОЗНАЧНАЯ
- ЛОГИКА ПОРОГОВАЯ
- ЛОГИКА ПРЕДИКАТОВ ВЫСШИХ СТУПЕНЕЙ
- ЛОГИКИ НЕКЛАССИЧЕСКИЕ
- ЛОГИКО-МАТЕМАТИЧЕСКОЕ ИСЧИСЛЕНИЕ
- ЛОГИЧЕСКАЯ РАСПОЗНАЮЩАЯ СИСТЕМА
- ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- ЛОГИЧЕСКИЙ ЗАДЕРЖИВАЮЩИЙ ЭЛЕМЕНТ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ АВМ
- ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ЦВМ
- ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ НОРМАЛЬНЫЕ ФОРМЫ
- ЛОКАЛИЗОВАННЫЕ ПЕРЕМЕННЫЕ
- ЛОКАЛЬНОГО КОДИРОВАНИЯ ПРИНЦИП
- ЛЯПАС
- ЛЯПУНОВА МЕТОДЫ
- «М-20»
- МАЖОРИТАРНЫЙ ЭЛЕМЕНТ
- МАЙЕРА ЗАДАЧА
- МАК-КЛАСКИ АЛГОРИТМ
- МАКРОКОМАНДА
- МАКРОМОДЕЛИ ЭКОНОМИЧЕСКИЕ
- МАКСИМИНА ПРИНЦИП
- МАКСИМУМА ПРАВДОПОДОБИЯ МЕТОД
- МАНИПУЛЯТОР
- «MARK-1»
- МАРКЕР
- МАРКОВА ЦЕПЬ
- МАРКОВСКИЙ ПРОЦЕСС
- МАССИВ
- МАССИВ ИНФОРМАЦИОННЫЙ
- МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА
- МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ, теория очередей
- МАТЕМАТИКА ВЫЧИСЛИТЕЛЬНАЯ
- МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА
- МАТЕМАТИЧЕСКИЕ МЁТОДЫ В ПОЭТИКЕ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ
- МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЦВМ ВНУТРЕННЕЕ
- МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, среднее значение
- МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- МАТРИЦА
- МАТРИЦА ВТОРЫХ МОМЕНТОВ
- МАТРИЦА ЗАПОМИНАЮЩАЯ
- МАТРИЦА ОБУЧАЕМАЯ
- МАТРИЦА ФЕРРИТОВАЯ МНОГООТВЕРСТНАЯ
- МАТРИЦА ФЕРРИТОВАЯ СЛОИСТАЯ
- МАТРИЧНЫЕ ИГРЫ
- МАШИНА
- МАШИНА ЦЕНТРАЛИЗОВАННОГО КОНТРОЛЯ
- МАШИННАЯ ПЕРЕМЕННАЯ
- МАШИННОЕ ПРОЕКТИРОВАНИЕ ИНТЕГРАЛЬНЫХ СХЕМ
- МАШИННОЕ СЛОВО
- МАШИННЫЙ «ИНТЕЛЛЕКТ»
- МАШИННЫЙ ПЕРЕВОД, автоматический перевод
- МЕДИЦИНСКАЯ ИНФОРМАЦИОННАЯ СИСТЕМА
- МЕДИЦИНСКАЯ ЭЛЕКТРОНИКА
- МЕЖДУНАРОДНАЯ АССОЦИАЦИЯ ПО АНАЛОГОВЫМ ВЫЧИСЛЕНИЯМ
- МЕЖДУНАРОДНАЯ ОРГАНИЗАЦИЯ ПО СТАНДАРТИЗАЦИИ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО АВТОМАТИЧЕСКОМУ УПРАВЛЕНИЮ
- МЕЖДУНАРОДНАЯ ФЕДЕРАЦИЯ ПО ОБРАБОТКЕ ИНФОРМАЦИИ
- МЕМИСТОР
- МЕРЫ СЛОЖНОСТИ в теории автоматов.
- МЕТАЛОГИКА
- МЕТАМАТЕМАТИКА
- МЕТАСИМВОЛЫ
- МЕТАТЕОРИЯ
- МЕТАТРАНСЛЯТОР
- МЕТАЯЗЫК
- МЕТКА
- МЕТОД ЗАМЕНЫ ЯДРА ВЫРОЖДЕННЫМ
- МЕТРИЧЕСКИЕ СВОЙСТВА ДИЗЪЮНКТИВНЫХ НОРМАЛЬНЫХ ФОРМ
- МИКРОКОМАНДА
- МИКРОМОДЕЛЬ ЭКОНОМИЧЕСКАЯ
- МИКРООПЕРАЦИЯ
- МИКРОПРОГРАММ ПРЕОБРАЗОВАНИЯ.
- МИКРОПРОГРАММА
- МИКРОПРОГРАММНАЯ АЛГЕБРА
- МИКРОПРОГРАММНОЕ УПРАВЛЕНИЕ
- МИКРОСХЕМА
- МИКРОЭЛЕКТРОННАЯ ЭЛЕМЕНТНАЯ БАЗА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
- МИЛИ АВТОМАТ
- МИНИМАКС
- МИНИМАКСНОЕ РЕШАЮЩЕЕ ПРАВИЛО
- МИНИМАЛЬНО-ФАЗОВАЯ СИСТЕМА
- МИНИМИЗАЦИИ ФУНКЦИЙ МЕТОДЫ
- МИНИМИЗАЦИЯ НАБОРА ПРИЗНАКОВ
- МИНИМИЗАЦИЯ СХЕМ ЦВМ
- МИНИМИЗАЦИЯ ЧИСЛА СОСТОЯНИЙ АВТОМАТА
- «МИНСК»
- «МИР», машина для инженерных расчетов
- «МИР-2» (разработана в 1969)