| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 11.2. Составление дифференциальных уравнений для однородной линии с распределенными параметрами.
Пусть  — продольное активное сопротивление единицы длины линии;
— продольное активное сопротивление единицы длины линии;  — индуктивность единицы длины линии;
— индуктивность единицы длины линии;  — емкость единицы длины линии;
— емкость единицы длины линии;  — поперечная проводимость единицы длины линии. Поперечная проводимость
— поперечная проводимость единицы длины линии. Поперечная проводимость  не является обратной величиной продольного сопротивления
не является обратной величиной продольного сопротивления  .
.
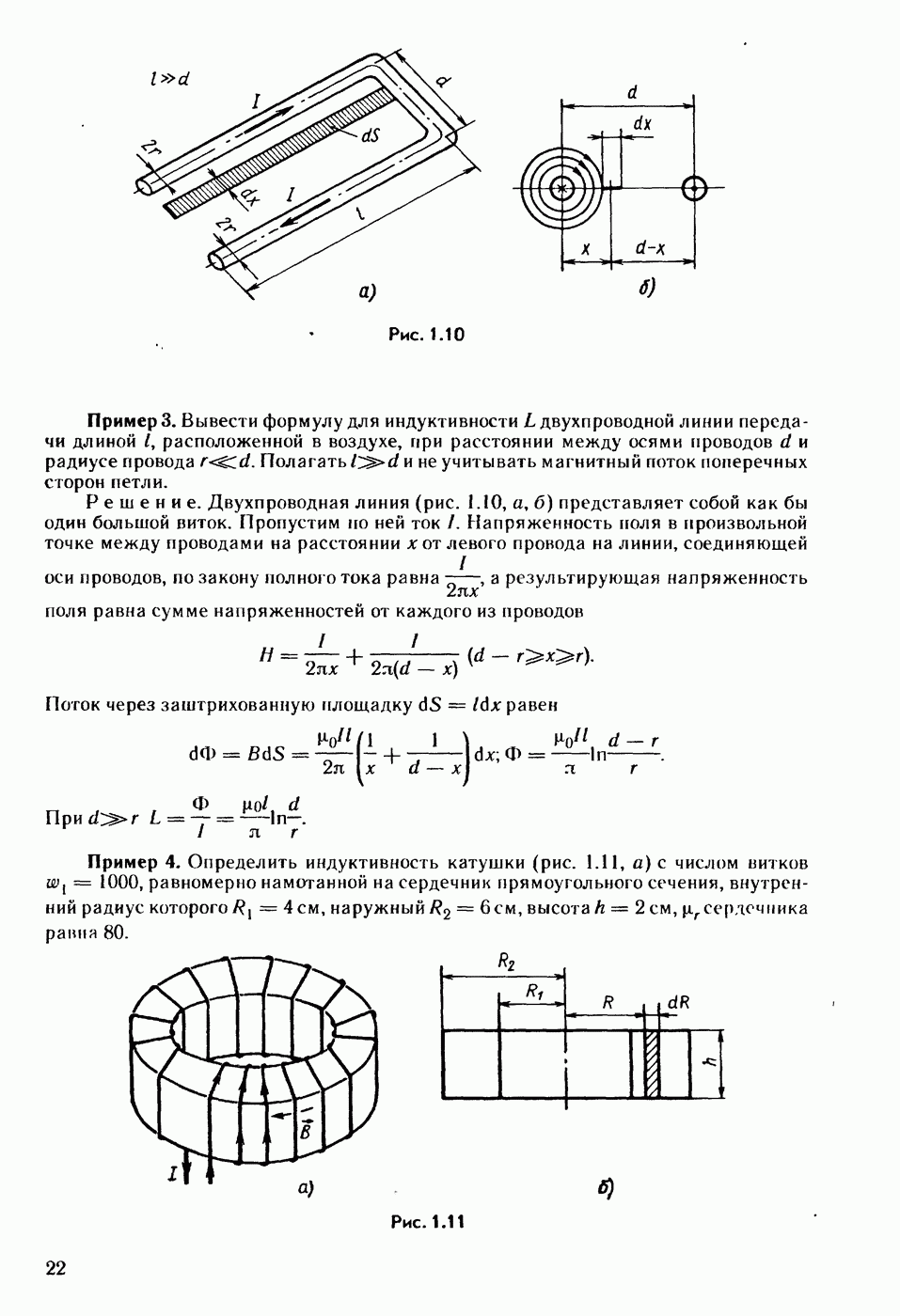
Разобьем линию на участки длиной  (рис. 11.2), где
(рис. 11.2), где  — расстояние, отсчитываемое от начала линии. На длине
— расстояние, отсчитываемое от начала линии. На длине  активное сопротивление равно
активное сопротивление равно  индуктивность —
индуктивность —  проводимость утечки —
проводимость утечки —  и емкость —
и емкость —  Обозначим ток в начале рассматриваемого участка линии через i, а напряжение между проводами линии — через и. И ток и напряжение являются в общем случае функциями расстояния вдоль линии
Обозначим ток в начале рассматриваемого участка линии через i, а напряжение между проводами линии — через и. И ток и напряжение являются в общем случае функциями расстояния вдоль линии  и времени t. Поэтому в дальнейшем в уравнениях использованы частные производные от
и времени t. Поэтому в дальнейшем в уравнениях использованы частные производные от  по времени t и расстоянию
по времени t и расстоянию 
Если для некоторого момента времени t ток в начале рассматриваемого участка равен i, то в результате утечки через поперечный элемент ток в конце участка для того же момента времени равен  где
где  — скорость изменения тока в направлении
— скорость изменения тока в направлении  Скорость, умноженная на расстояние
Скорость, умноженная на расстояние  является приращением тока на пути
является приращением тока на пути 
Аналогично, если напряжение в начале участка и, то в конце Участка для того же момента времени напряжение равно и 
Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной  обойдя его По часовой стрелке:
обойдя его По часовой стрелке:

После упрощения и деления уравнения на  получим
получим

По первому закону Кирхгофа,

Ток  (рис. 11.2) равен сумме токов, проходящих через проводимость
(рис. 11.2) равен сумме токов, проходящих через проводимость  и емкость
и емкость 

Пренебрегаем слагаемыми второго порядка малости. Тогда

Подставим (11.3) в (11.2), упростим и поделим уравнение на 

Уравнения (11.1) и (11.4) являются основными дифференциальными уравнениями для линии с распределенными параметрами.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть I. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
- § 1.2. Интегральные и дифференциальные соотношения между основными величинами, характеризующими поле.
- § 1.3. Подразделение электротехнических задач на цепные и полевые.
- § 1.4. Конденсатор.
- § 1.5. Индуктивность. Явление самоиндукции.
- § 1.6. Взаимная индуктивность. Явление взаимоиндукции.
- § 1.7. Схемы замещения реальных электротехнических устройств.
- Вопросы для самопроверки
- Глава вторая. СВОЙСТВА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И МЕТОДЫ ИХ РАСЧЕТА. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
- § 2.1. Определение линейных и нелинейных электрических цепей.
- § 2.2. Источник ЭДС и источник тока.
- § 2.3. Неразветвленные и разветвленные электрические цепи.
- § 2.4. Напряжение на участке цепи.
- § 2.5. Закон Ома для участка цепи, не содержащего источника ЭДС.
- § 2.6. Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома.
- § 2.7. Законы Кирхгофа.
- § 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа.
- § 2.9. Заземление одной точки схемы.
- § 2.10. Потенциальная диаграмма.
- § 2.11. Энергетический баланс в электрических цепях.
- § 2.12. Метод пропорциональных величин.
- § 2.13. Метод контурных токов.
- § 2.14. Принцип наложения и метод наложения.
- § 2.15. Входные и взаимные проводимости ветвей. Входное сопротивление.
- § 2.16. Теорема взаимности.
- § 2.17. Теорема компенсации.
- § 2.18. Линейные соотношения в электрических цепях.
- § 2.19. Изменения токов ветвей, вызванные приращением сопротивления одной ветви (теорема вариаций).
- § 2.20. Замена нескольких параллельных ветвей, содержащих источники ЭДС и источники тока, одной эквивалентной.
- § 2.21. Метод двух узлов.
- § 2.22. Метод узловых потенциалов.
- § 2.23. Преобразование звезды в треугольник и треугольника в звезду.
- § 2.24. Перенос источников ЭДС и источников тока.
- § 2.25. Активный и пассивный двухполюсники.
- § 2.26. Метод эквивалентного генератора.
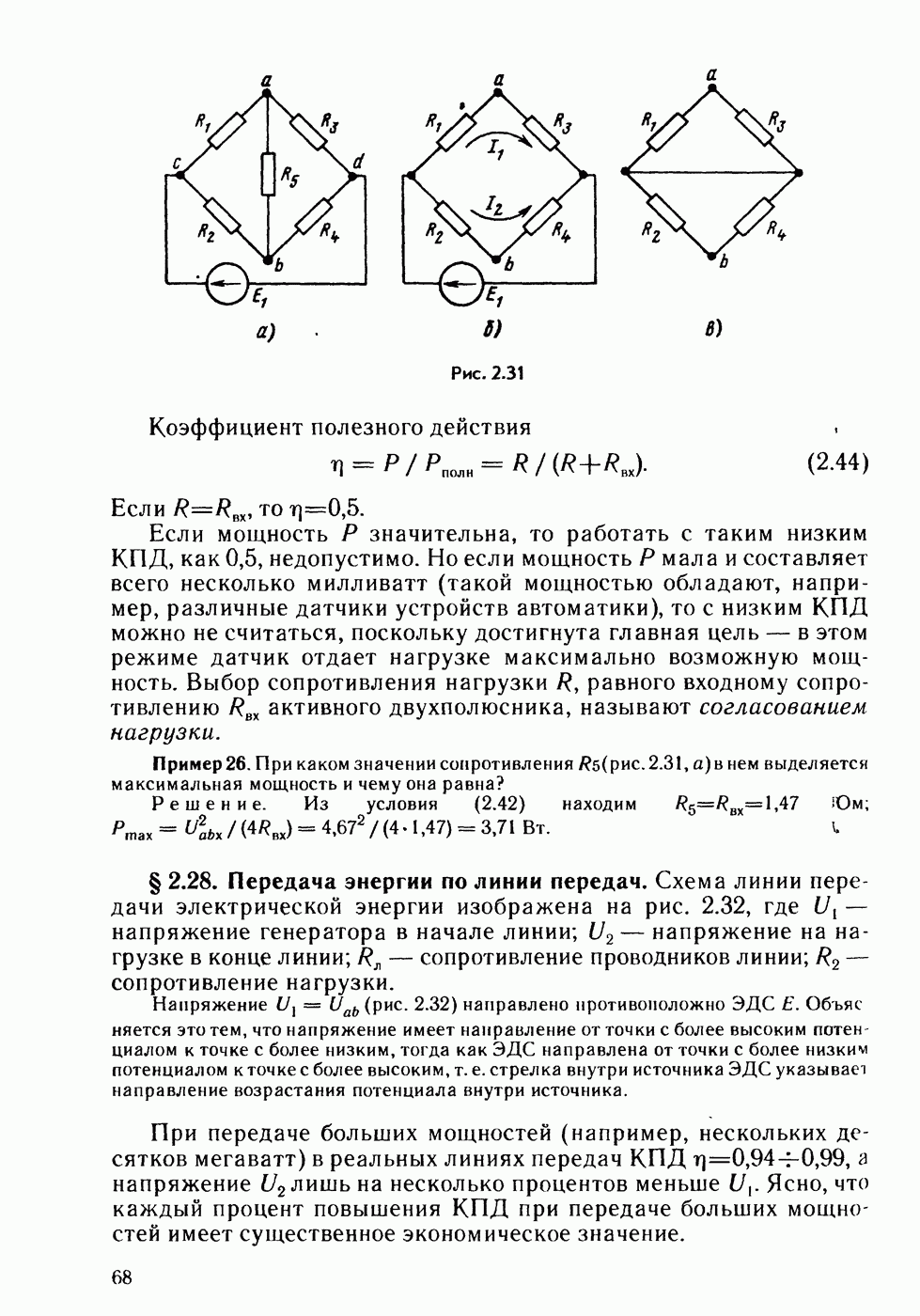
- § 2.27. Передача энергии от активного двухполюсника нагрузке.
- § 2.28. Передача энергии по линии передач.
- § 2.29. Некоторые выводы по методам расчета электрических цепей.
- § 2.30. Основные свойства матриц и простейшие операции с ними.
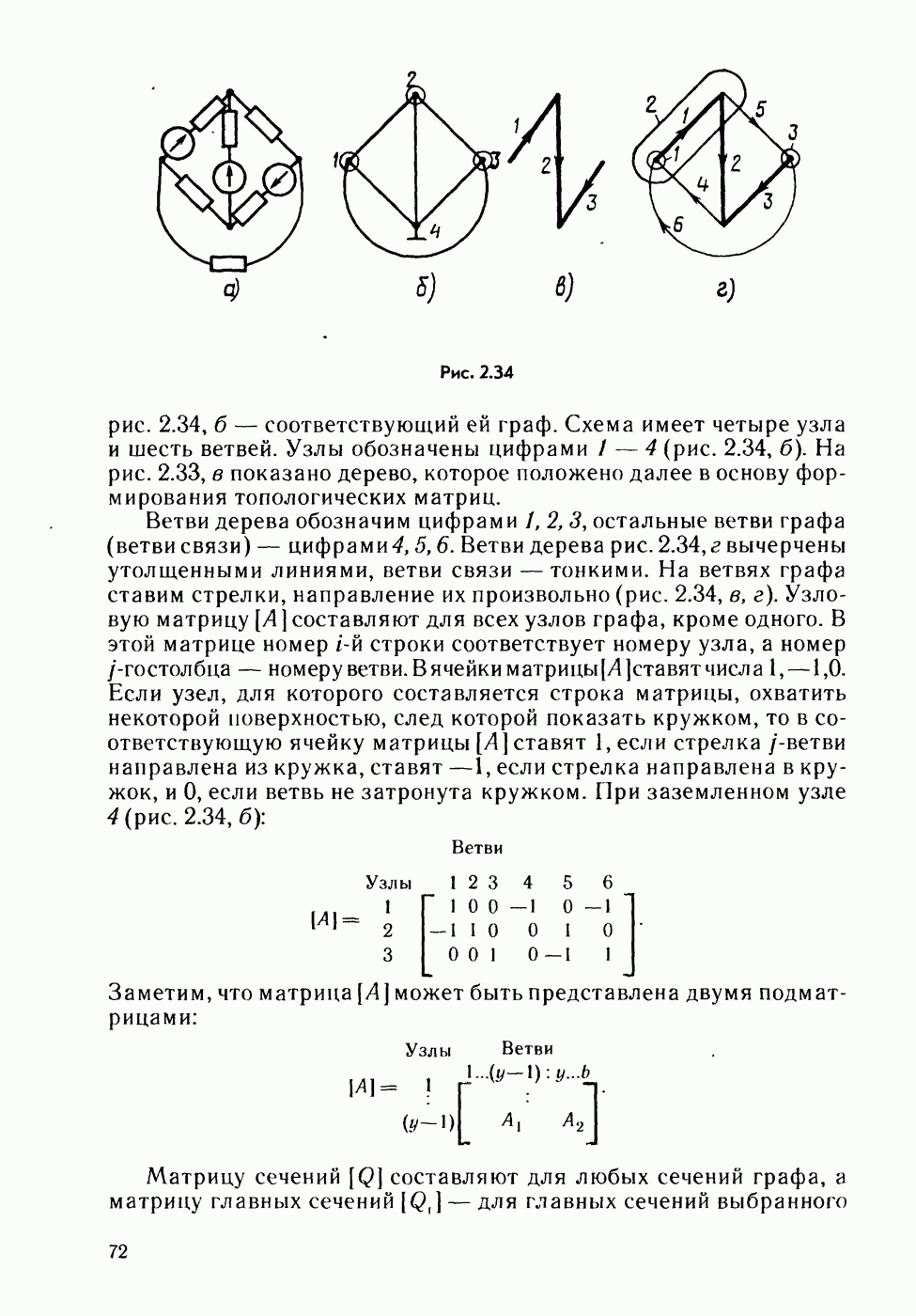
- § 2.31. Некоторые топологические понятия и топологические матрицы.
- § 2.32. Запись уравнений по законам Кирхгофа с помощью топологических матриц.
- § 2.33. Обобщенная ветвь электрической цепи.
- § 2.34. Вывод уравнений метода контурных токов с помощью топологических матриц.
- § 2.35. Вывод уравнений метода узловых потенциалов с помощью топологических матриц.
- § 2.36. Соотношения между топологическими матрицами.
- § 2.37. Сопоставление матрично-топологического и традиционного направлений теории цепей.
- Вопросы для самопроверки
- Глава третья. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА
- § 3.1. Синусоидальный ток и основные характеризующие его величины.
- § 3.2. Среднее и действующее значения синусоидально изменяющейся величины.
- § 3.3. Коэффициент амплитуды и коэффициент формы.
- § 3.4. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения.
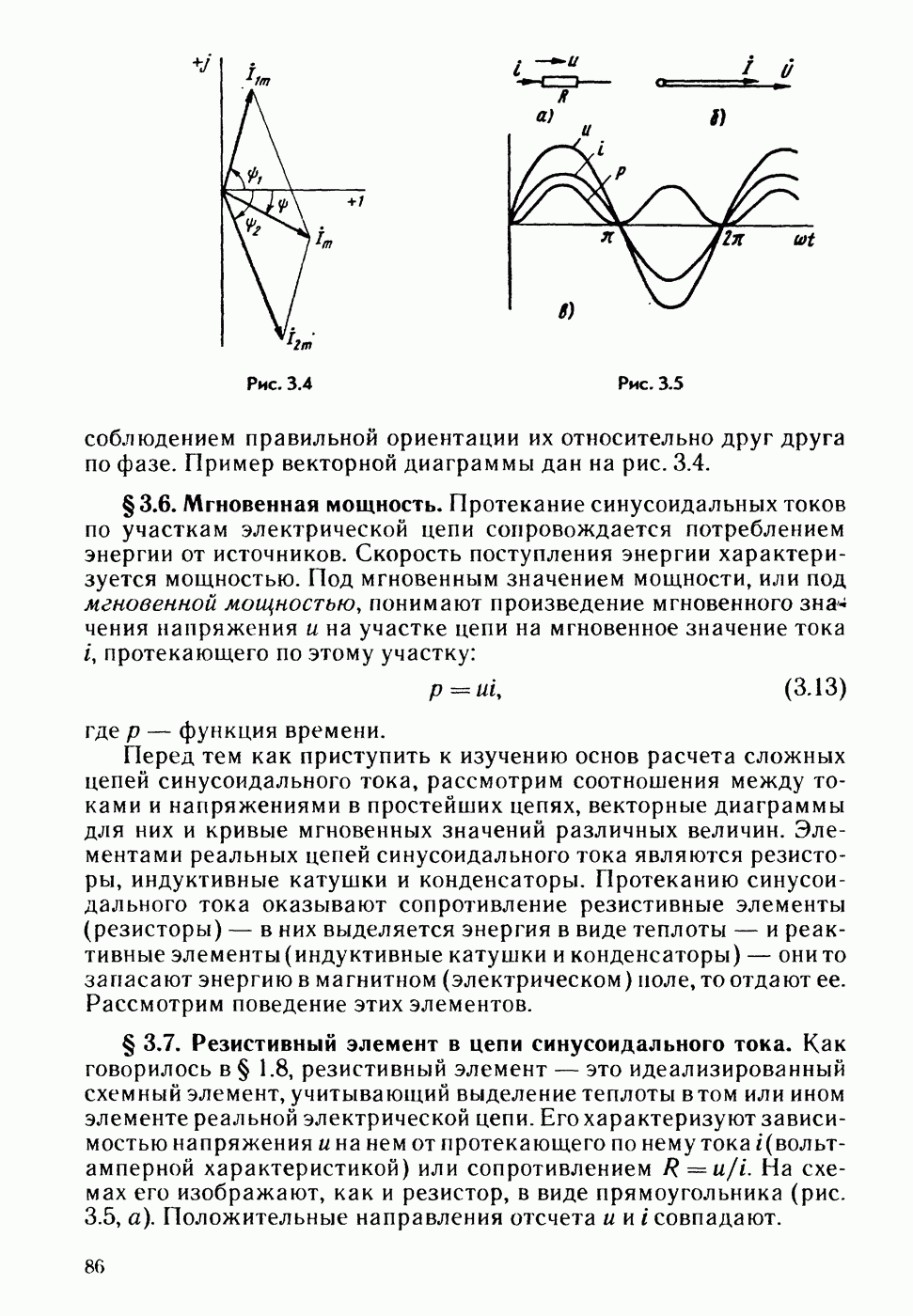
- § 3.5. Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма.
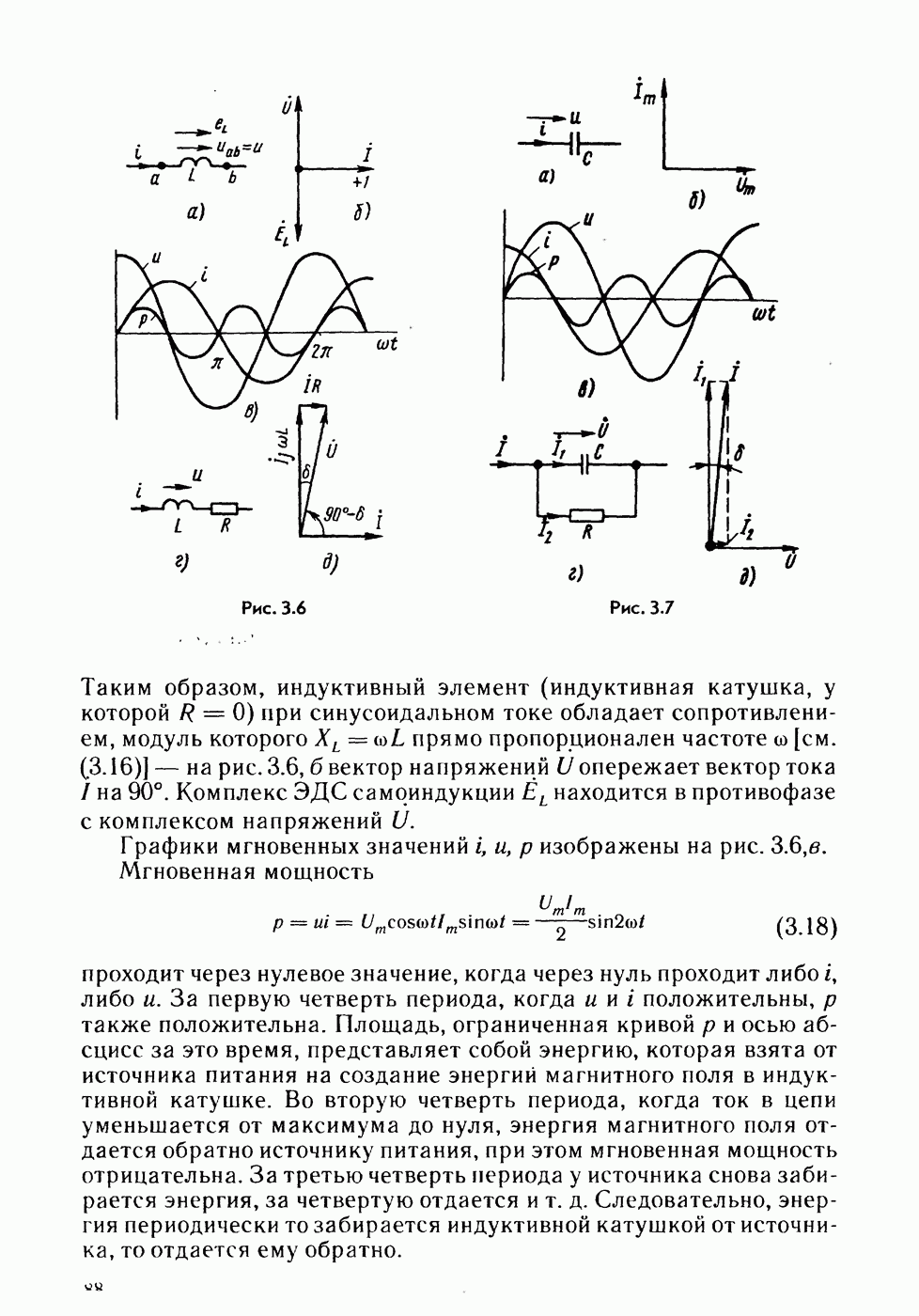
- § 3.6. Мгновенная мощность.
- § 3.7. Резистивный элемент в цепи синусоидального тока.
- § 3.8. Индуктивный элемент в цепи синусоидального тока.
- § 3.9. Емкостный элемент в цепи синусоидального тока.
- § 3.10. Умножение вектора на j и —j.
- § 3.11. Основы символического метода расчета цепей синусоидального тока.
- § 3.12. Комплексное сопротивление. Закон Ома для цепи синусоидального тока.
- § 3.13. Комплексная проводимость.
- § 3.14. Треугольник сопротивлений и треугольник проводимостей.
- § 3.15. Работа с комплексными числами.
- § 3.16. Законы Кирхгофа в символической форме записи.
- § 3.17. Применение к расчету цепей синусоидального тока методов, рассмотренных в главе «Электрические цепи постоянного тока».
- § 3.18. Применение векторных диаграмм при расчете электрических цепей синусоидального тока.
- § 3.19. Изображение разности потенциалов на комплексной плоскости.
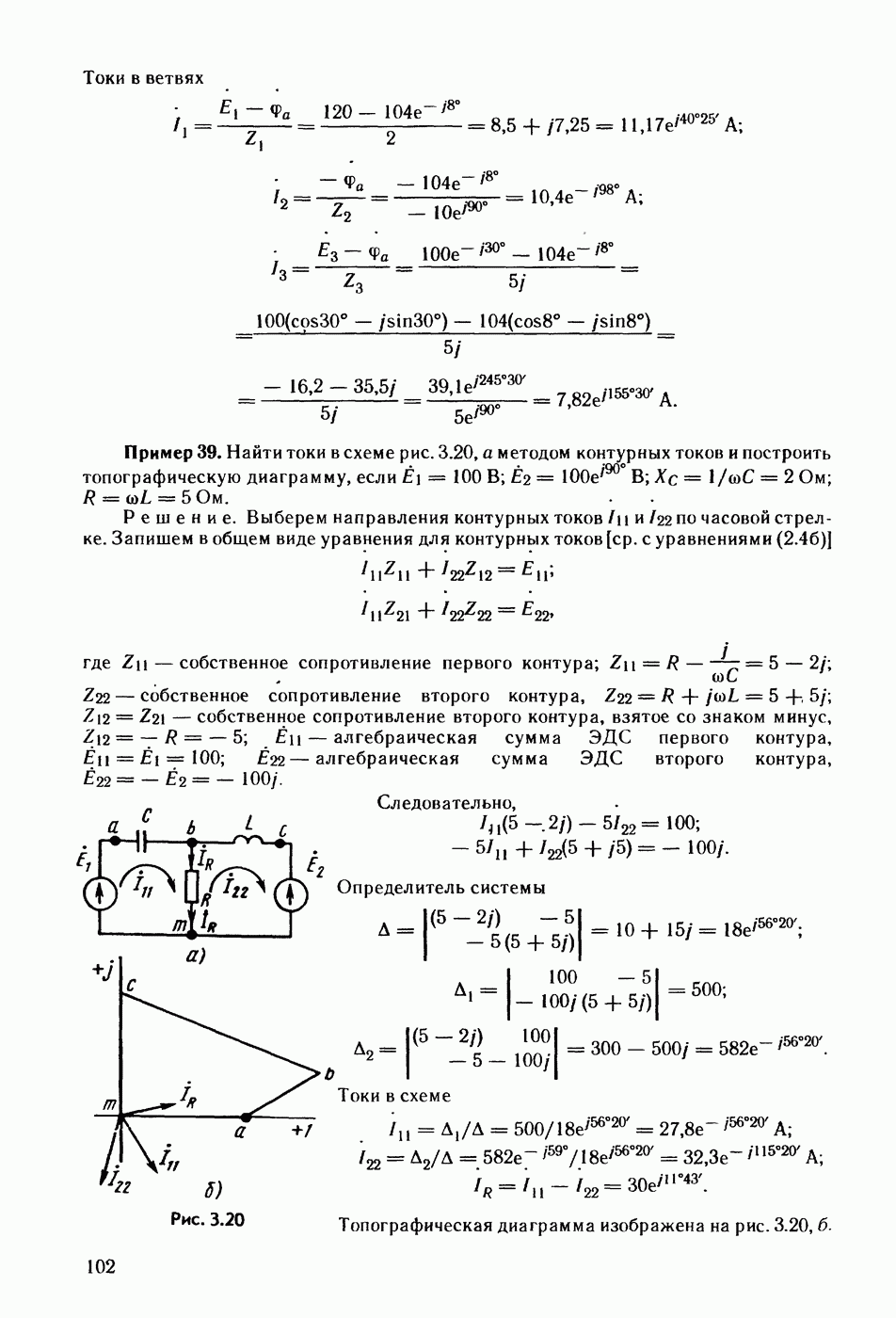
- § 3.20. Топографическая диаграмма.
- § 3.21. Активная, реактивная и полная мощности.
- § 3.22. Выражение мощности в комплексной форме записи.
- § 3.23. Измерение мощности ваттметром.
- § 3.24. Двухполюсник в цепи синусоидального тока.
- § 3.25. Резонансный режим работы двухполюсника.
- § 3.26. Резонанс токов.
- § 3.27. Компенсация сдвига фаз.
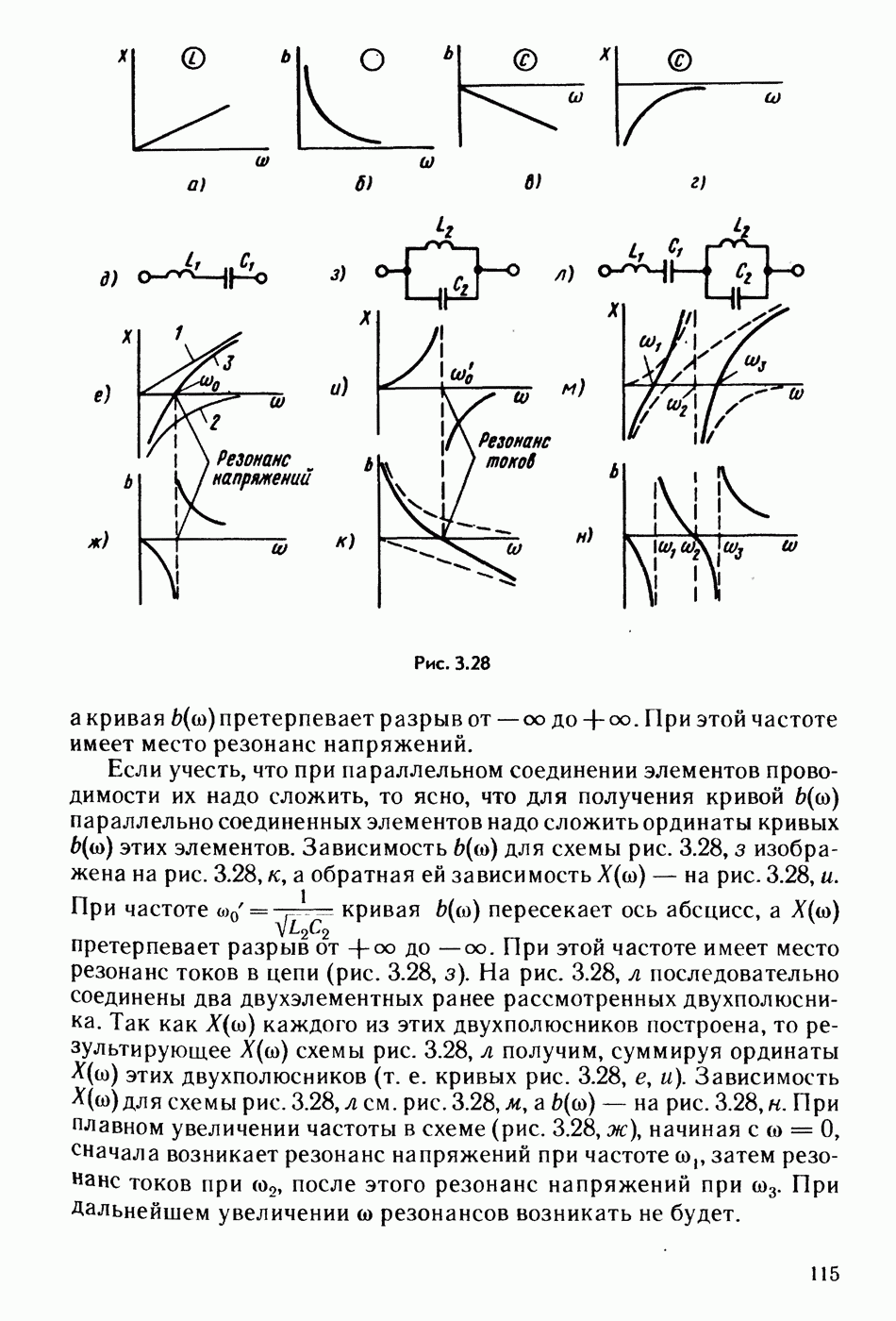
- § 3.28. Резонанс напряжений.
- § 3.29. Исследование работы схемы рис. 3.26, а при изменении частоты и индуктивности.
- § 3.30. Частотные характеристики двухполюсников.
- § 3.31. Канонические схемы. Эквивалентные двухполюсники.
- § 3.32. Передача энергии от активного двухполюсника нагрузке.
- § 3.33. Согласующий трансформатор.
- § 3.34. Идеальный трансформатор.
- § 3.35. Падение и потеря напряжения в линии передачи энергии.
- § 3.36. Расчет электрических цепей при наличии в них магнитносвязанных катушек.
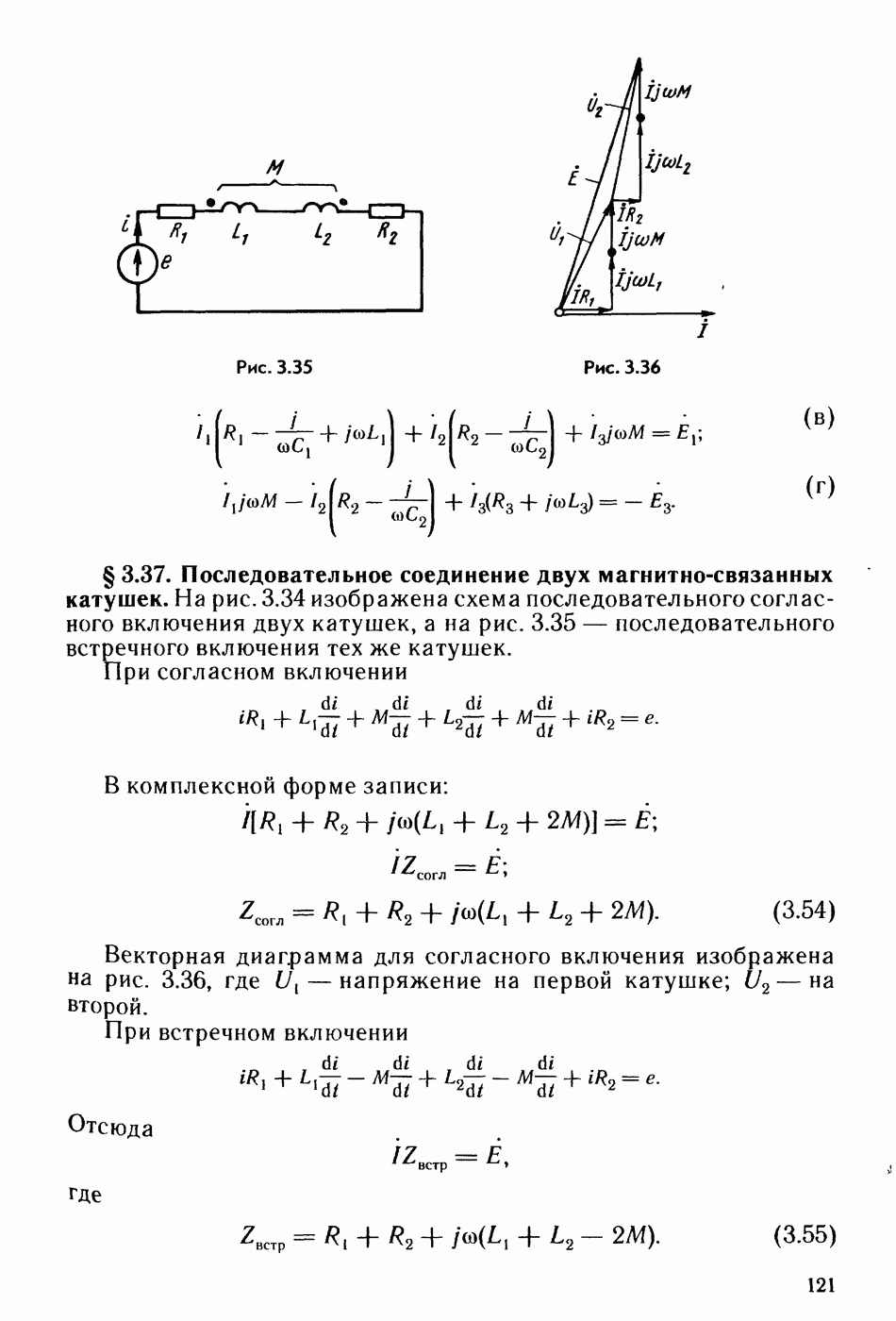
- § 3.37. Последовательное соединение двух магнитно-связанных катушек.
- § 3.38. Определение взаимной индуктивности опытным путем.
- § 3.39. Трансформатор. Вносимое сопротивление.
- § 3.40. Резонанс в магнитно-связанных колебательных контурах.
- § 3.41. «Развязывание» магнитно-связанных цепей.
- § 3.42. Теорема о балансе активных и реактивных мощностей (теорема Лонжевена).
- § 3.43. Теорема Теллегена.
- § 3.44. Определение дуальной цепи.
- § 3.45. Преобразование исходной схемы в дуальную.
- Вопросы для самопроверки
- Глава четвертая. ЧЕТЫРЕХПОЛЮСНИКИ. ЦЕПИ С УПРАВЛЯЕМЫМИ ИСТОЧНИКАМИ. КРУГОВЫЕ ДИАГРАММЫ
- § 4.1. Определение четырехполюсника.
- § 4.2. Шесть форм записи уравнений четырехполюсника.
- § 4.3. Вывод уравнений в А-форме.
- § 4.4. Определение коэффициентов A-формы записи уравнений четырехполюсника.
- § 4.5. Т- и П-схемы замещения пассивного четырехполюсника.
- § 4.6. Определение коэффициентов Y-, Z-, G- и H-форм записи уравнений четырехполюсника.
- § 4.7. Определение коэффициентов одной формы уравнений через коэффициенты другой формы.
- § 4.8. Применение различных форм записи уравнений четырехполюсника. Соединения четырехполюсников. Условия регулярности.
- § 4.9. Характеристические и повторные сопротивления четырехполюсников.
- § 4.10. Постоянная передача и единицы измерения затухания.
- § 4.11. Уравнения четырехполюсника, записанные через гиперболические функции.
- § 4.12. Конвертор и инвертор сопротивления.
- § 4.13. Гиратор.
- § 4.14. Операционный усилитель.
- § 4.15. Управляемые источники напряжения (тока).
- § 4.16. Активный четырехполюсник.
- § 4.17. Многополюсник.
- § 4.18. Построение дуги окружности по хорде и вписанному углу.
- § 4.19. Уравнение дуги окружности в векторной форме записи.
- § 4.20. Круговые диаграммы.
- § 4.21. Круговая диаграмма тока двух последовательно соединенных сопротивлений.
- § 4.22. Круговая диаграмма напряжения двух последовательно соединенных сопротивлений.
- § 4.23. Круговая диаграмма тока активного двухполюсника.
- § 4.24. Круговая диаграмма напряжения четырехполюсника.
- § 4.25. Линейные диаграммы.
- Вопросы для самопроверки
- Глава пятая. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- § 5.1. Назначение и типы фильтров.
- § 5.2. Основы теории k-фильтров.
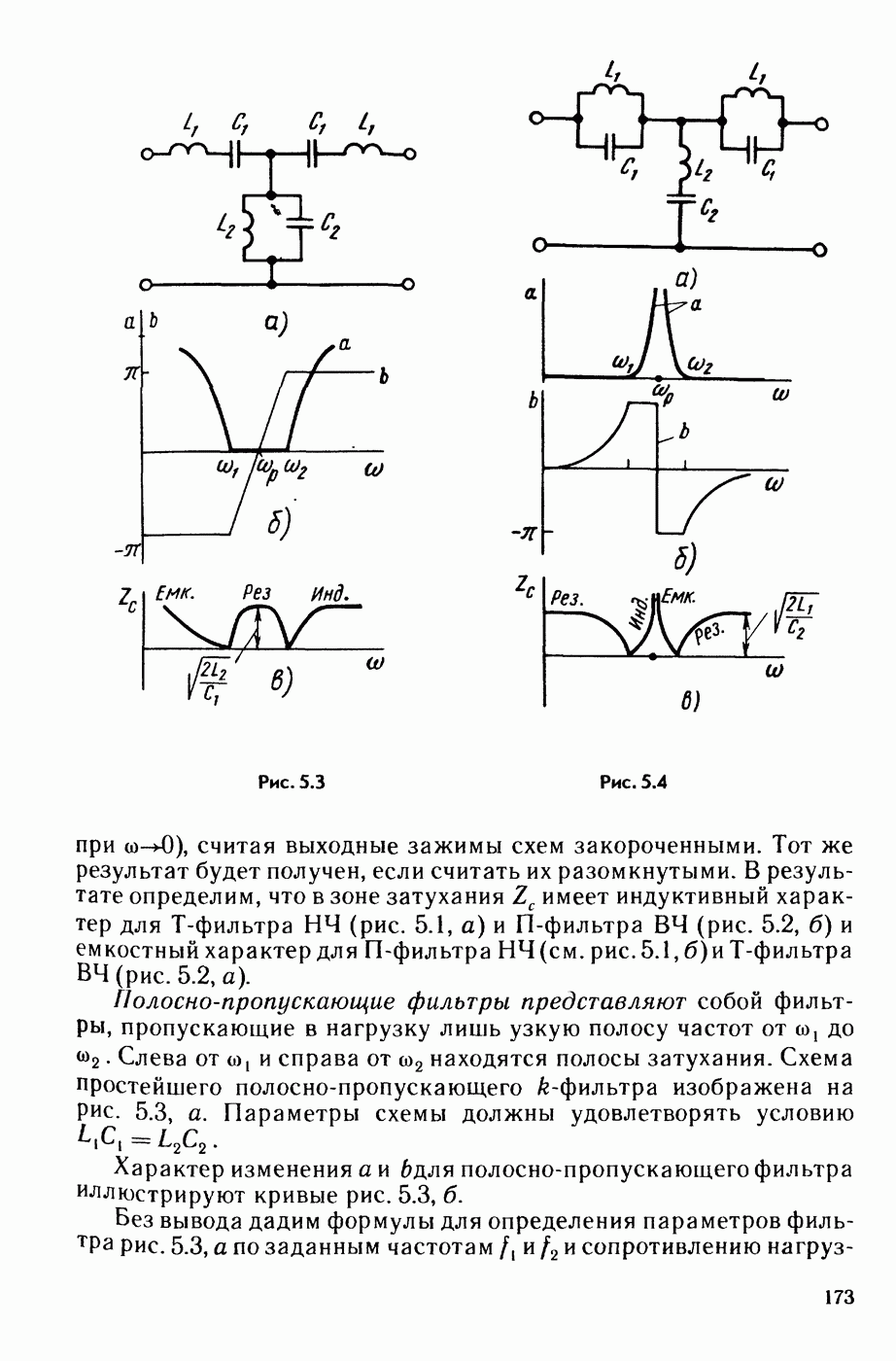
- § 5.3. K-фильтры НЧ и ВЧ, полосно-пропускающие и полосно-заграждающие k-фильтры.
- § 5.4. Качественное определение k-фильтра.
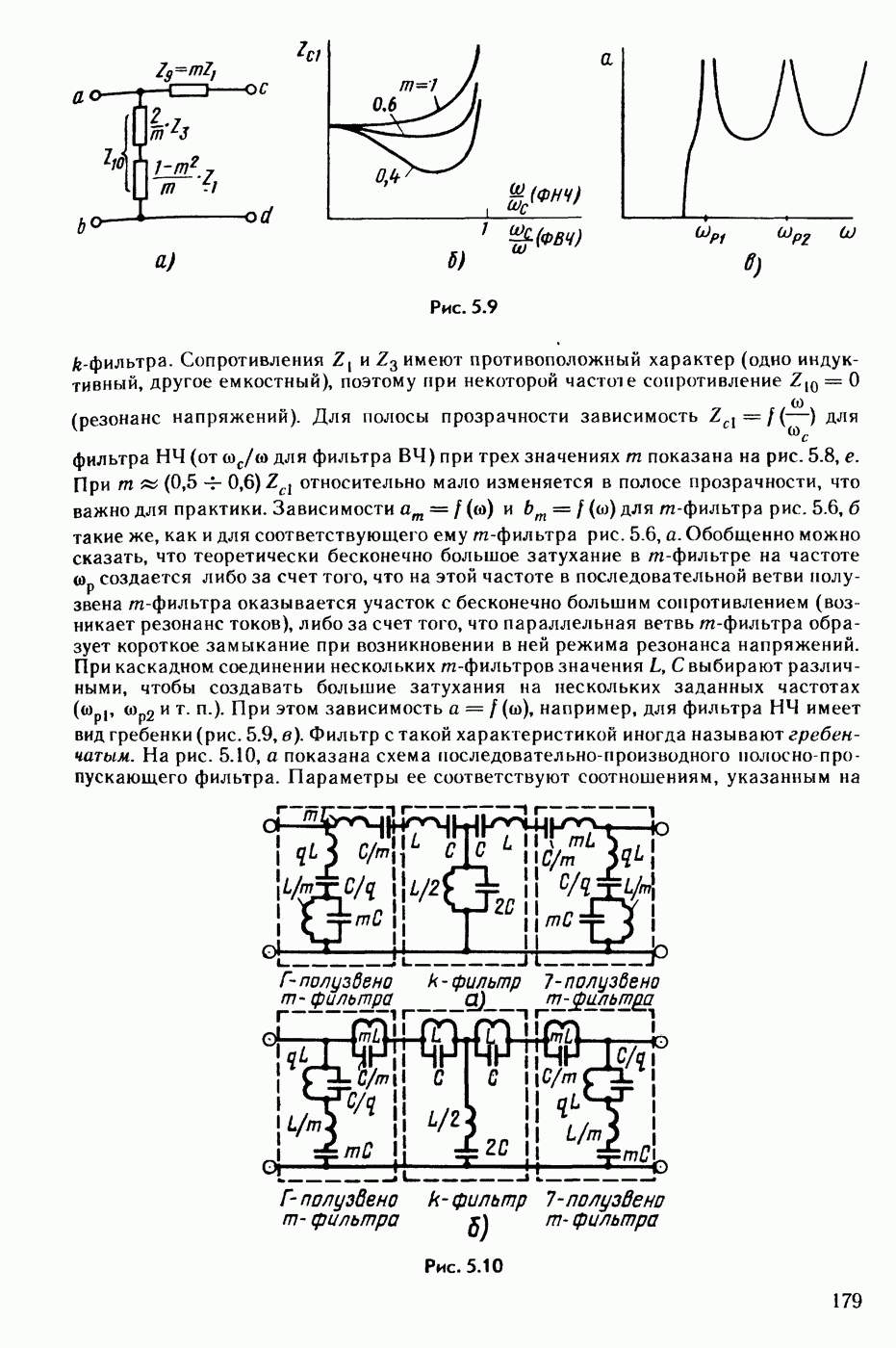
- § 5.5. Основы теории m-фильтров. Каскадное включение фильтров.
- § 5.6. RC-фильтры.
- § 5.7. Активные RС-фильтры.
- § 5.8. Передаточные функции активных RС-фильтров в нормированном виде.
- § 5.9. Получение передаточной функции низкочастотного активного RС-фильтра, выбор схемы и определение ее параметров.
- § 5.10. Получение передаточной функции полосно-пропускающего активного RС-фильтра.
- Вопросы для самопроверки
- Глава шестая. ТРЕХФАЗНЫЕ ЦЕПИ
- § 6.1. Трехфазная система ЭДС.
- § 6.2. Принцип работы трехфазного машинного генератора.
- § 6.3. Трехфазная цепь. Расширение понятия фазы.
- § 6.4. Основные схемы соединения трехфазных цепей, определение линейных и фазовых величин.
- § 6.5. Соотношения между линейными и фазовыми напряжениями и токами.
- § 6.6. Преимущества трехфазных систем.
- § 6.7. Расчет трехфазных цепей.
- § 6.8. Соединение звезда — звезда с нулевым проводом.
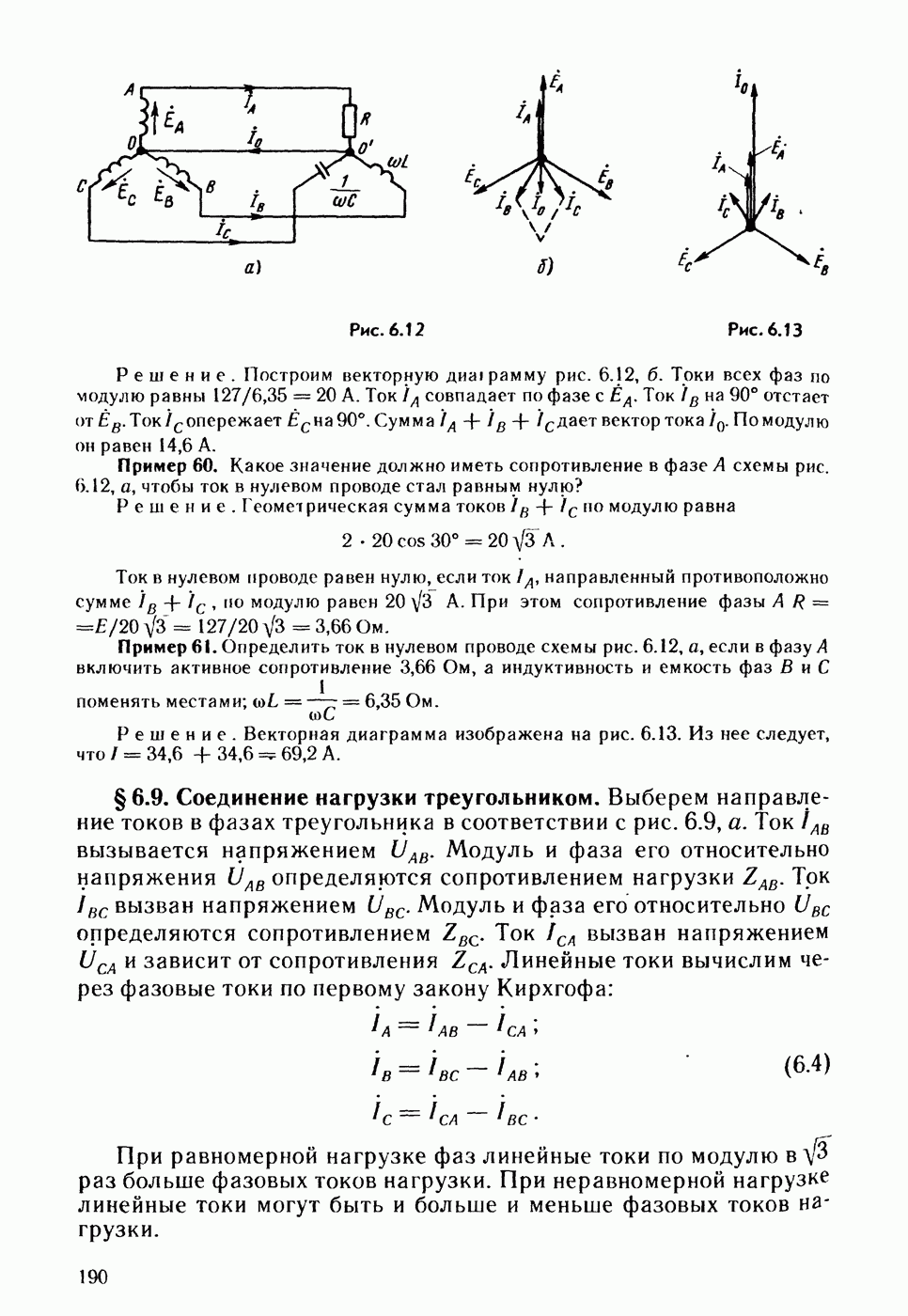
- § 6.9. Соединение нагрузки треугольником.
- § 6.10 Оператор а трехфазной системы.
- § 6.11 Соединение звезда — звезда без нулевого провода.
- § 6.12. Трехфазные цепи при наличии взаимоиндукции.
- § 6.13. Активная, реактивная и полная мощности трехфазной системы.
- § 6.14. Измерение активной мощности в трехфазной системе.
- § 6.15. Круговые и линейные диаграммы в трехфазных цепях.
- § 6.16. Указатель последовательности чередования фаз.
- § 6.17. Магнитное поле катушки с синусоидальным током.
- § 6.18. Получение кругового вращающегося магнитного поля.
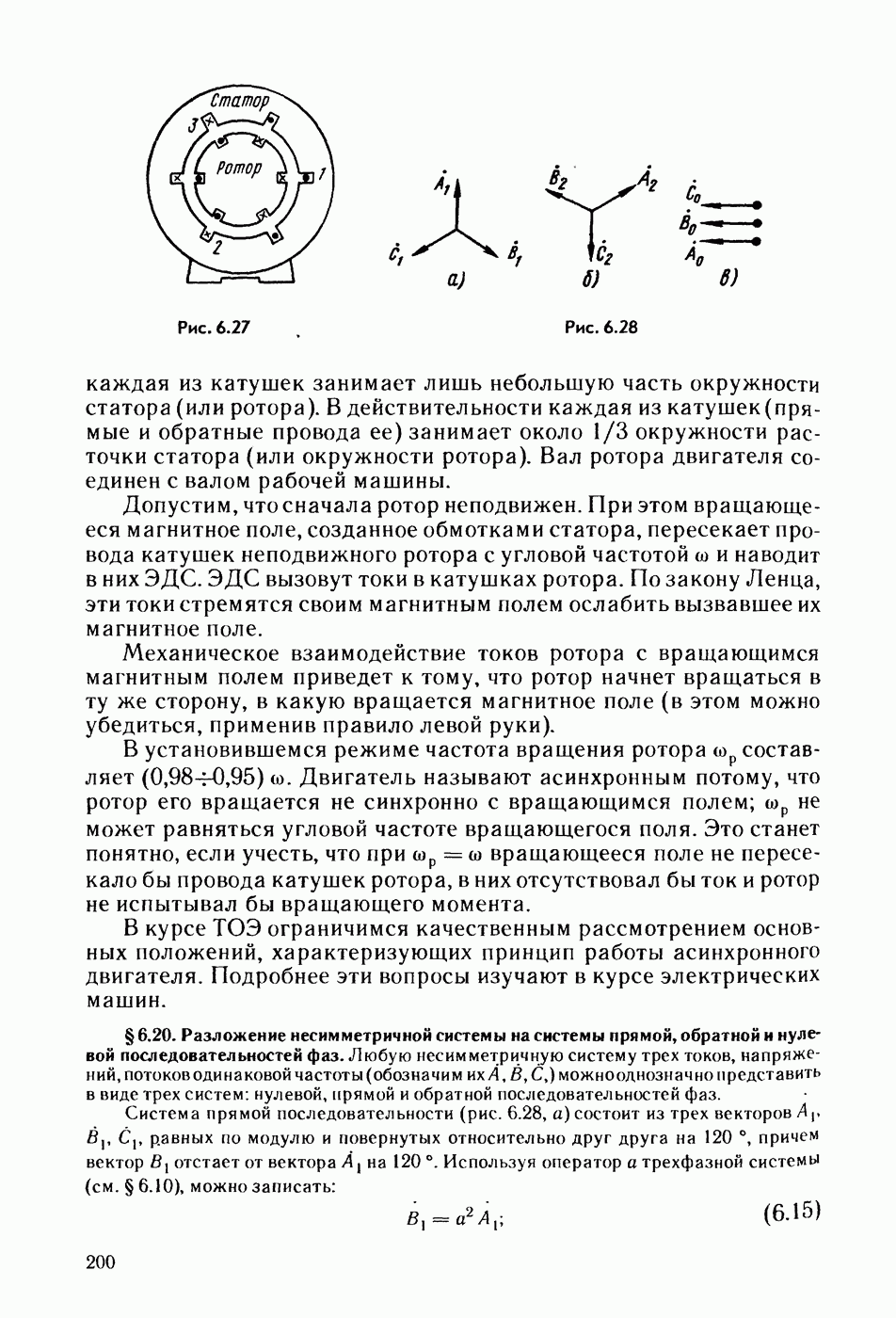
- § 6.19. Принцип работы асинхронного двигателя.
- § 6.20. Разложение несимметричной системы на системы прямой, обратной и нулевой последовательностей фаз.
- § 6.21. Основные положения метода симметричных составляющих.
- Вопросы для самопроверки
- Глава седьмая. ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 7.1. Определение периодических несинусоидальных токов и напряжений.
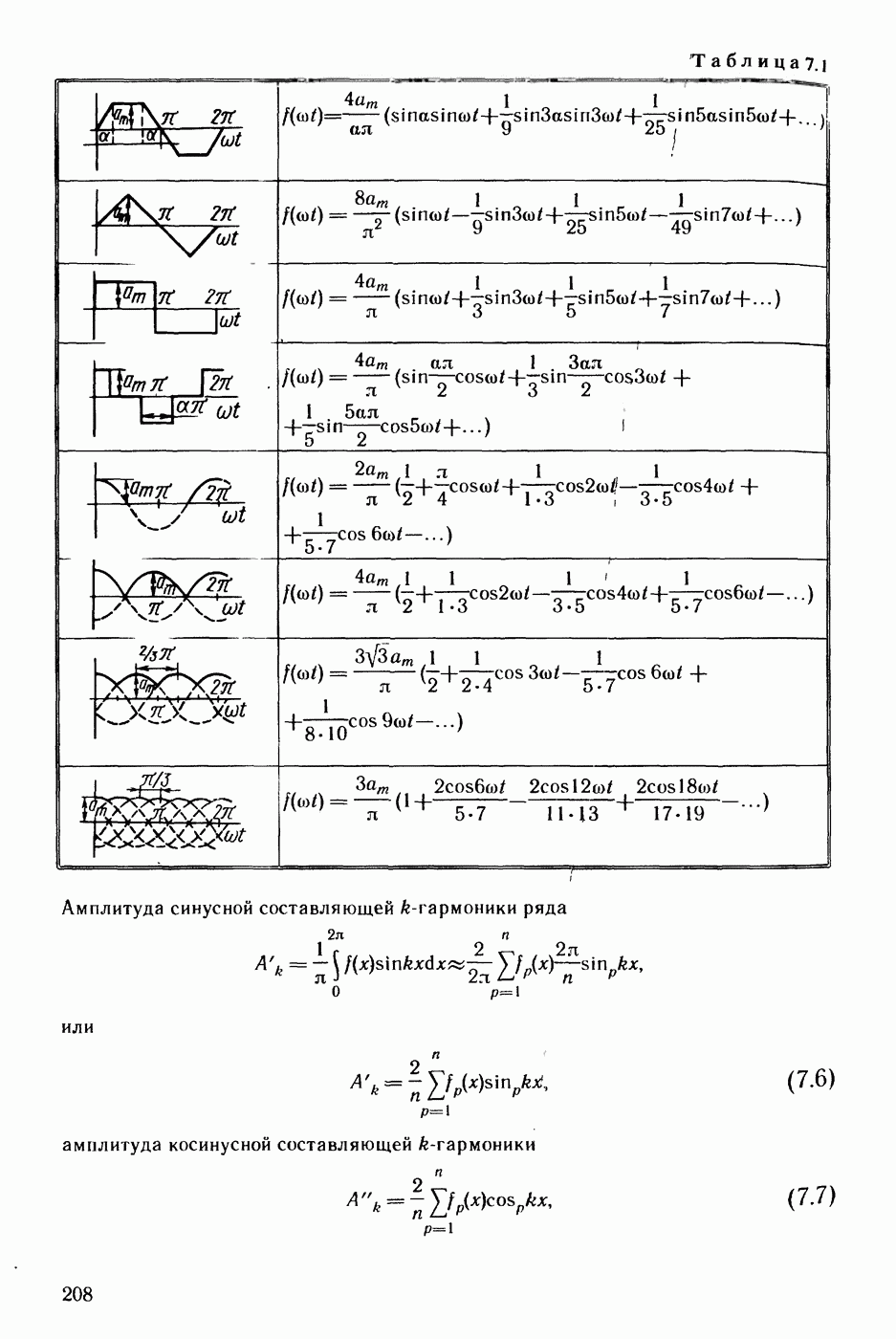
- § 7.2. Изображение несинусоидальных токов и напряжений с помощью рядов Фурье.
- § 7.3. Некоторые свойства периодических кривых, обладающих симметрией.
- § 7.4. О разложении вряд Фурье кривых геометрически правильной и неправильной форм.
- § 7.5. Графический (графоаналитический) метод определения гармоник ряда Фурье.
- § 7.6. Расчет токов и напряжений при несинусоидальных источниках питания.
- § 7.7. Резонансные явления при несинусоидальных токах.
- § 7.8. Действующие значения несинусоидального тока и несинусоидального напряжения.
- § 7.9. Среднее по модулю значение несинусоидальной функции.
- § 7.10. Величины, которые измеряют амперметры и вольтметры при несинусоидальных токах.
- § 7.11. Активная и полная мощности несинусоидального тока.
- § 7.12. Замена несинусоидальных токов и напряжений эквивалентными синусоидальными.
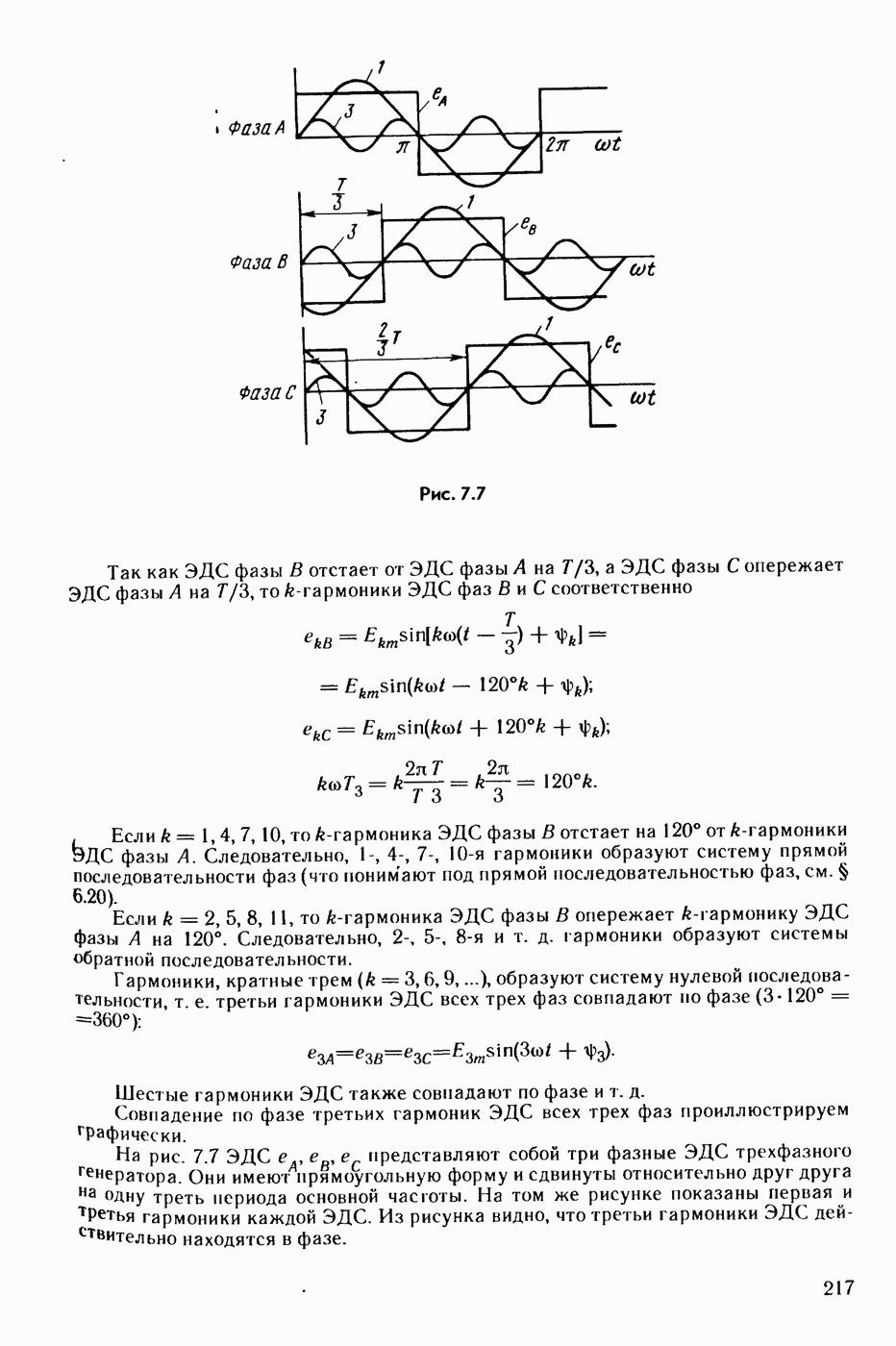
- § 7.13. Особенности работы трехфазных систем, вызываемых гармониками, кратными трем.
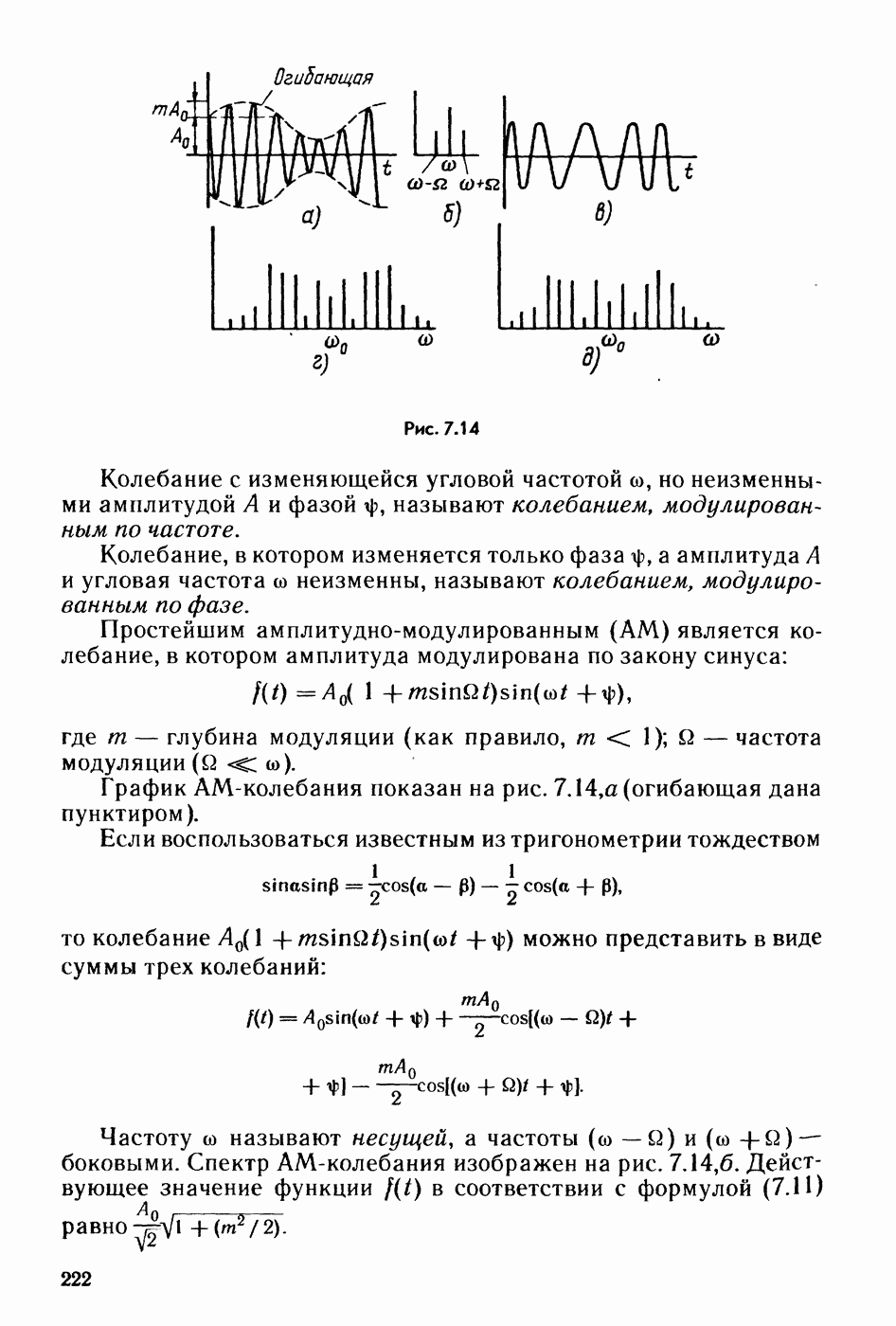
- § 7.14. Биения.
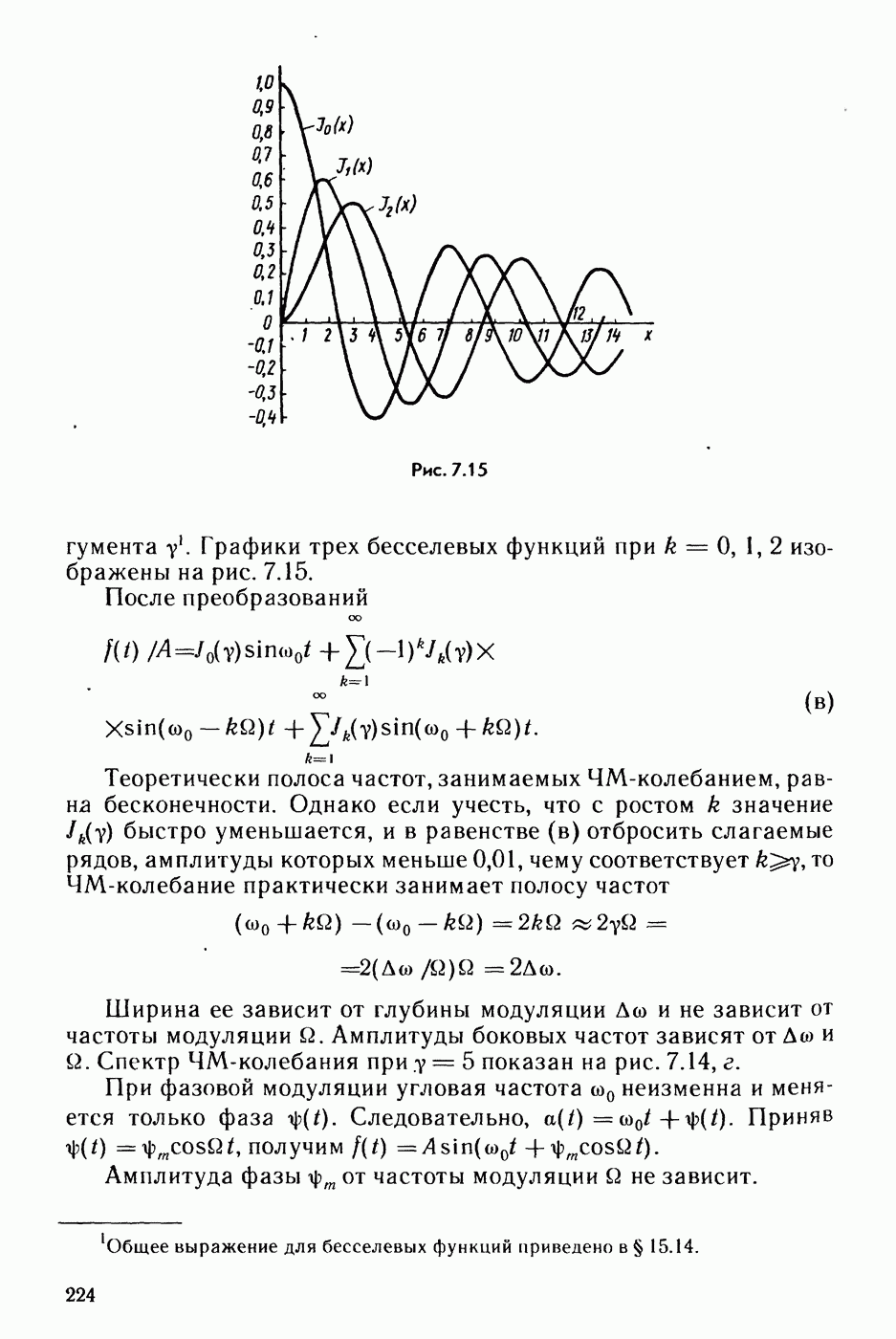
- § 7.15. Модулированные колебания.
- § 7.16. Расчет линейных цепей при воздействии модулированных колебаний.
- Вопросы для самопроверки
- Глава восьмая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 8.1. Определение переходных процессов.
- § 8.2. Приведение задачи о переходном процессе к решению линейного дифференциального уравнения с постоянными коэффициентами.
- § 8.3. Принужденные и свободные составляющие токов и напряжений.
- § 8.4. Обоснование невозможности скачка тока через индуктивную катушку и скачка напряжения на конденсаторе.
- § 8.5. Первый закон (правило) коммутации.
- § 8.6. Второй закон (правило) коммутации.
- § 8.7. Начальные значения величин.
- § 8.8. Независимые и зависимые (послекоммутационные) начальные значения.
- § 8.9. Нулевые и ненулевые начальные условия.
- § 8.10. Составление уравнений для свободных токов и напряжений.
- § 8.11. Алгебраизация системы уравнений для свободных токов.
- § 8.12. Составление характеристического уравнения системы.
- § 8.13. Составление характеристического уравнения путем использования выражения для входного сопротивления цепи на переменном токе.
- § 8.14. Основные и неосновные зависимые начальные значения.
- § 8.15. Определение степени характеристического уравнения.
- § 8.16. Свойства корней характеристического уравнения.
- § 8.17. Отрицательные зшаки действительных частей корней характеристических уравнений.
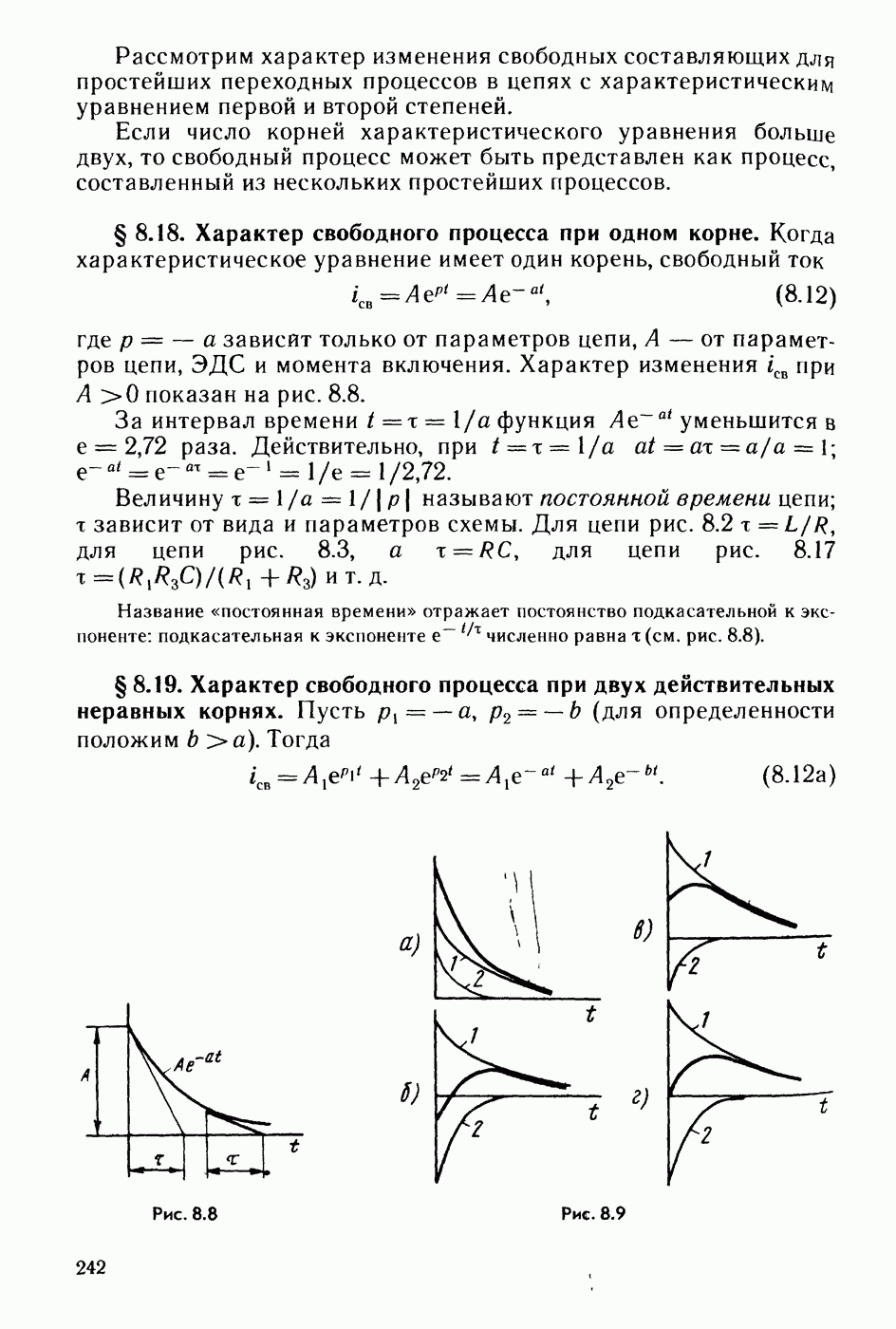
- § 8.18. Характер свободного процесса при одном корне.
- § 8.19. Характер свободного процесса при двух действительных неравных корнях.
- § 8.20. Характер свободного процесса при двух равных корнях.
- § 8.21. Характер свободного процесса при двух комплексно-сопряженных корнях.
- § 8.22. Некоторые особенности переходных процессов.
- § 8.23. Переходные процессы, сопровождающиеся электрической искрой (дугой).
- § 8.24. Опасные перенапряжения, вызываемые размыканием ветвей в цепях, содержащих индуктивные катушки.
- § 8.25. Общая характеристика методов анализа переходных процессов в линейных электрических цепях.
- § 8.26. Определение классического метода расчета переходных процессов.
- § 8.27. Определение постоянных интегрирования в классическом методе.
- § 8.28. О переходных процессах, при макроскопическом рассмотрении которых не выполняются законы коммутации.
- § 8.29. Логарифм как изображение числа.
- § 8.30. Комплексные изображения синусоидальных функций.
- § 8.31. Введение в операторный метод.
- § 8.32. Преобразование Лапласа.
- § 8.33. Изображение постоянной.
- § 8.34. Изображение показательной функции exp(at).
- § 8.35. Изображение первой производной.
- § 8.36. Изображение напряжения на индуктивном элементе.
- § 8.37. Изображение второй производной.
- § 8.38. Изображение интеграла.
- § 8.39. Изображение напряжения на конденсаторе.
- § 8.40. Некоторые теоремы и предельные соотношения.
- § 8.41. Закон Ома в операторной форме. Внутренние ЭДС.
- § 8.42. Первый закон Кирхгофа в операторной форме.
- § 8.43. Второй закон Кирхгофа в операторной форме.
- § 8.44. Составление уравнений для изображений путем использования методов, рассмотренных в третьей главе.
- § 8.45. Последовательность расчета операторным методом.
- § 8.46. Изображение функции времени в виде отношения N(p)/M(p) двух полиномов по степеням p.
- § 8.47. Переход от изображения к функции времени.
- § 8.48. Разложение сложной дроби на простые.
- § 8.49. Формула разложения.
- § 8.50. Дополнения к операторному методу.
- § 8.51. Переходная проводимость.
- § 8.52. Понятие о переходной функции.
- § 8.53. Интеграл Дюамеля.
- § 8.54. Последовательность расчета с помощью интеграла Дюамеля.
- § 8.55. Применение интеграла Дюамеля при сложной форме напряжения.
- § 8.56. Сравнение различных методов расчета переходных процессов.
- § 8.57. Дифференцирование электрическим путем.
- § 8.58. Интегрирование электрическим путем.
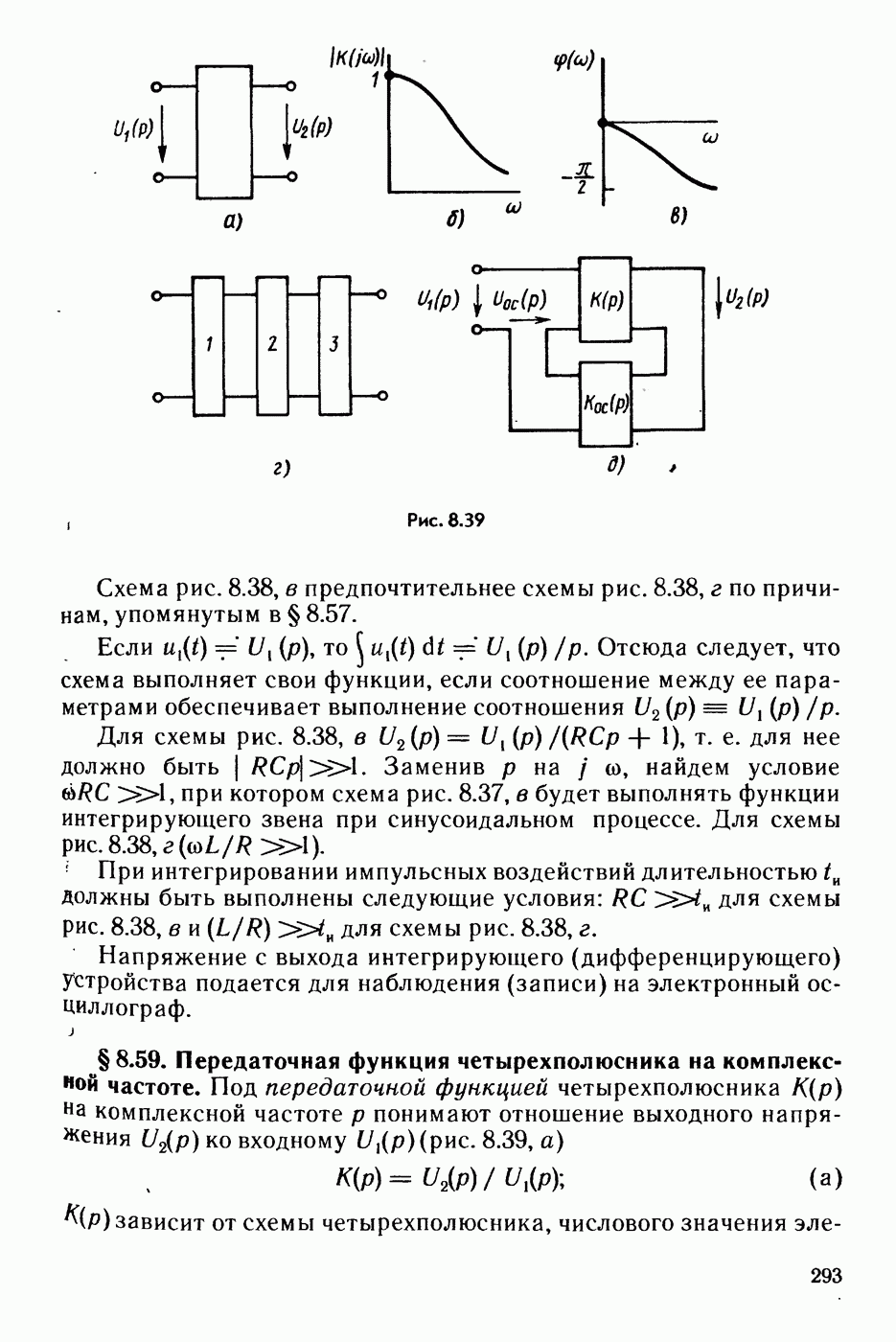
- § 8.59. Передаточная функция четырехполюсника на комплексной частоте.
- § 8.60. Переходные процессы при воздействии импульсов напряжения.
- § 8.61. Дельта-функция, единичная функция и их свойства. Импульсная переходная проводимость.
- § 8.62. Определение h(t) и h'(t) через K(р).
- § 8.63. Метод пространства состояний.
- § 8.64. Дополняющие двухполюсники.
- § 8.65. Системные функции и понятие о видах чувствительности.
- § 8.66. Обобщенные функции и их применение к расчету переходных процессов.
- § 8.67. Интеграл Дюамеля для огибающей.
- Вопросы для самопроверки
- Глава девятая. ИНТЕГРАЛ ФУРЬЕ. СПЕКТРАЛЬНЫЙ МЕТОД. СИГНАЛЫ
- § 9.1. Ряд Фурье в комплексной форме записи.
- § 9.2. Спектр функции и интеграл Фурье.
- § 9.3. Спектр функции, смещенной во времени. Спектр суммы функций времени.
- § 9.4. Теорема Рейли.
- § 9.5. Применение спектрального метода.
- § 9.6. Текущий спектр функции времени.
- § 9.7. Основные сведения по теории сигналов.
- § 9.8. Узкополосный и аналитический сигналы.
- § 9.9. Частотный спектр аналитического сигнала.
- § 9.10. Прямое и обратное преобразование Гильберта.
- Вопросы для самопроверки
- Глава десятая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- § 10.1. Характеристика синтеза.
- § 10.2. Условия, которым должны удовлетворять входные сопротивления двухполюсников.
- § 10.3. Реализация двухполюсников лестничной (цепной) схемой.
- § 10.4. Реализация двухполюсников путем последовательного выделения простейших составляющих.
- § 10.5. Метод Бруне.
- § 10.6. Понятие о минимально-фазовом и неминимально-фазовом четырехполюсниках.
- § 10.7. Синтез четырехполюсников Г-образными RC-схемами.
- § 10.8. Четырехполюсник для фазовой коррекции.
- § 10.9. Четырехполюсник для амплитудной коррекции.
- § 10.10. Аппроксимация частотных характеристик.
- Вопросы для самопроверки
- Глава одиннадцатая. УСТАНОВИВШИЕСЯ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- § 11.2. Составление дифференциальных уравнений для однородной линии с распределенными параметрами.
- § 11.3. Решение уравнений линии с распределенными параметрами при установившемся синусоидальном процессе.
- § 11.4. Постоянная распространения и волновое сопротивление.
- § 11.5. Формулы для определения комплексов напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии.
- § 11.6. Графическая интерпретация гиперболических синуса и косинуса от комплексного аргумента.
- § 11.7. Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии.
- § 11.8. Падающие и отраженные волны в линии.
- § 11.9. Коэффициент отражения.
- § 11.10. Фазовая скорость.
- § 11.11. Длина волны.
- § 11.12. Линия без искажений.
- § 11.13. Согласованная нагрузка.
- § 11.14. Определение напряжения и тока при согласованной нагрузке.
- § 11.15. Коэффициент полезного действия линии передачи при согласованной нагрузке.
- § 11.16. Входное сопротивление нагруженной линии.
- § 11.17. Определение напряжения и тока в линии без потерь.
- § 11.18. Входное сопротивление линии без потерь при холостом ходе.
- § 11.19. Входное сопротивление линии без потерь при коротком замыкании на конце линии.
- § 11.20. Входное сопротивление линии без потерь при реактивной нагрузке.
- § 11.21. Определение стоячих электромагнитных волн.
- § 11.22. Стоячие волны в линии без потерь при холостом ходе линии.
- § 11.23. Стоячие волны в линии без потерь при коротком замыкании на конце линии.
- § 11.24. Четвертьволновый трансформатор.
- § 11.25. Бегущие, стоячие и смешанные волны в линиях без потерь.
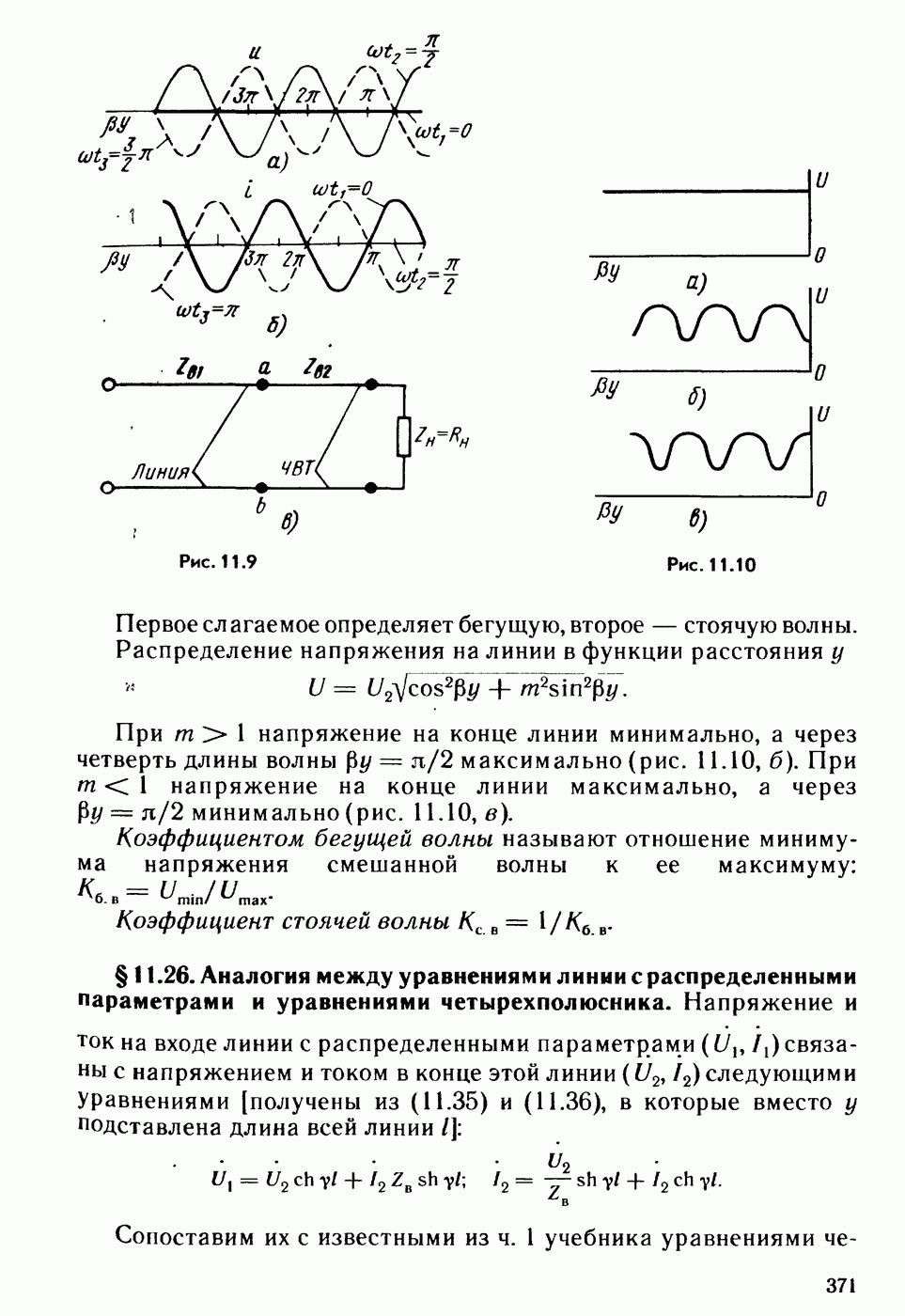
- § 11.26. Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника.
- § 11.27. Замена четырехполюсника эквивалентной ему линией с распределенными параметрами и обратная замена.
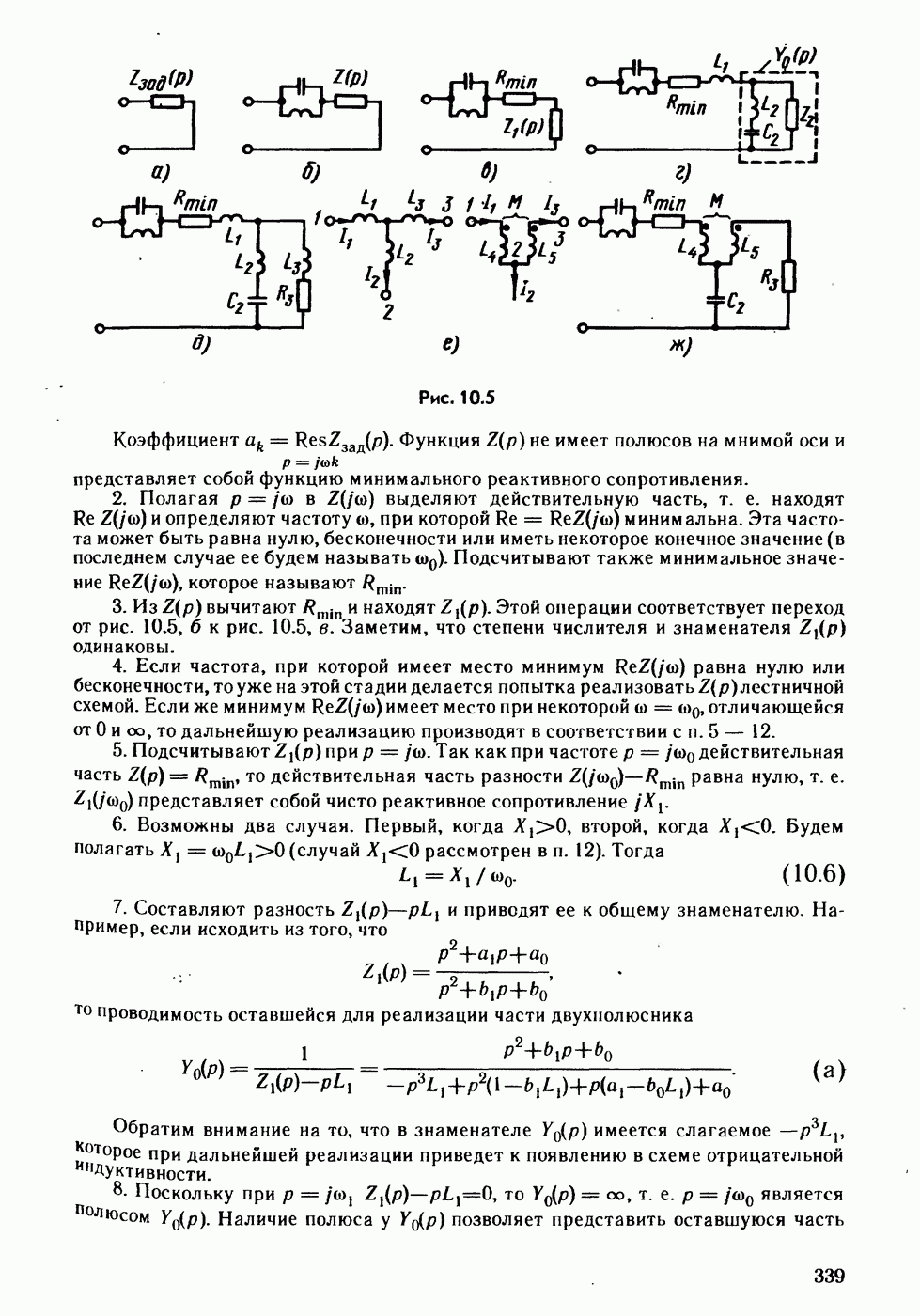
- § 11.28. Четырехполюсник заданного затухания.
- § 11.29. Цепная схема.
- Вопросы для самопроверки
- Глава двенадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- § 12.2. Исходные уравнения и их решение.
- § 12.3. Падающие и отраженные волны на линиях.
- § 12.4. Связь между функциями f1, f2 и функциями.
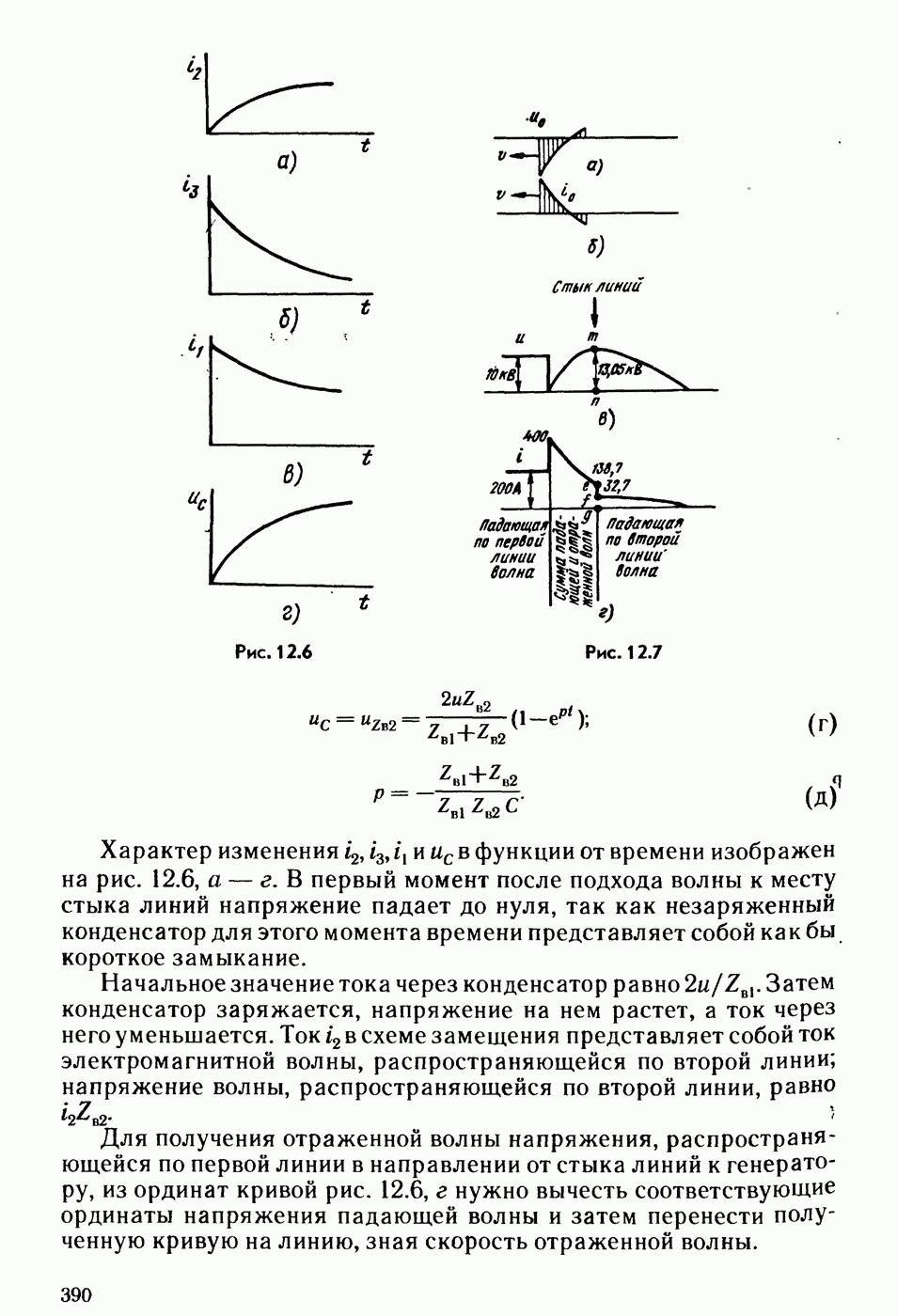
- § 12.5. Электромагнитные процессы при движении прямоугольной волны по линии.
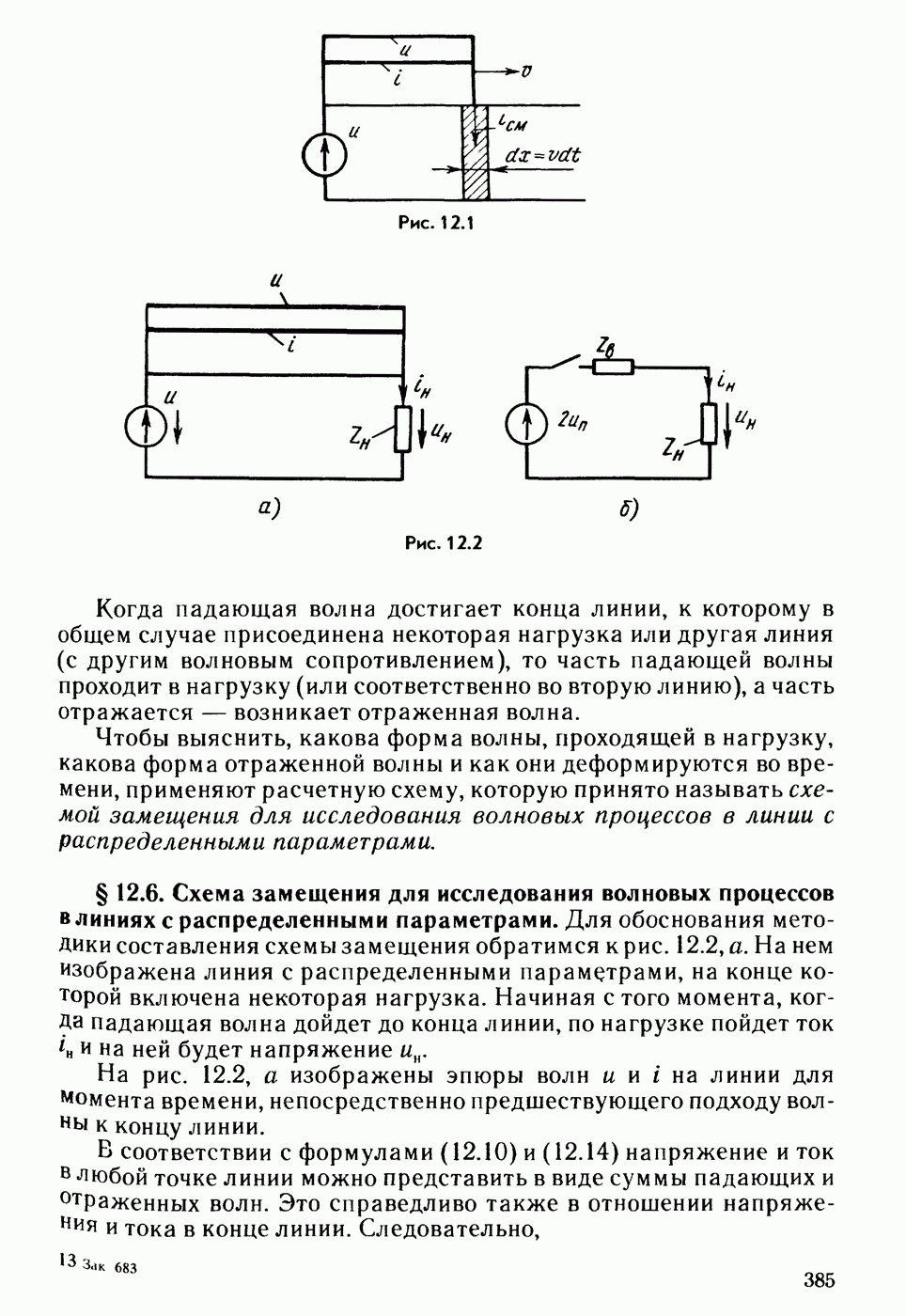
- § 12.6. Схема замещения для исследования волновых процессов в линиях с распределенными параметрами.
- § 12.7. Подключение разомкнутой на конце линии к источнику постоянного напряжения.
- § 12.8. Переходный процесс при подключении источника постоянного напряжения к двум последовательно соединенным линиям при наличии емкости в месте стыка линий.
- § 12.9. Линия задержки.
- § 12.10. Использование линий для формирования кратковременных импульсов.
- § 12.11. Исходные положения по применению операторного метода к расчету переходных процессов в линиях.
- § 12.12. Подключение линии без потерь конечной длины l, разомкнутой на конце, к источнику постоянного напряжения.
- § 12.13. Подключение линии без искаженйя конечной длины l, разомкнутой на конце, к источнику постоянного напряжения U.
- § 12.14. Подключение бесконечно протяженного кабеля без индуктивности и утечки к источнику постоянного напряжения U.
- § 12.15. Подключение бесконечно протяженной линии без утечки к источнику постоянного напряжения.
- Вопросы для самопроверки
- Часть II. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
- Глава тринадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
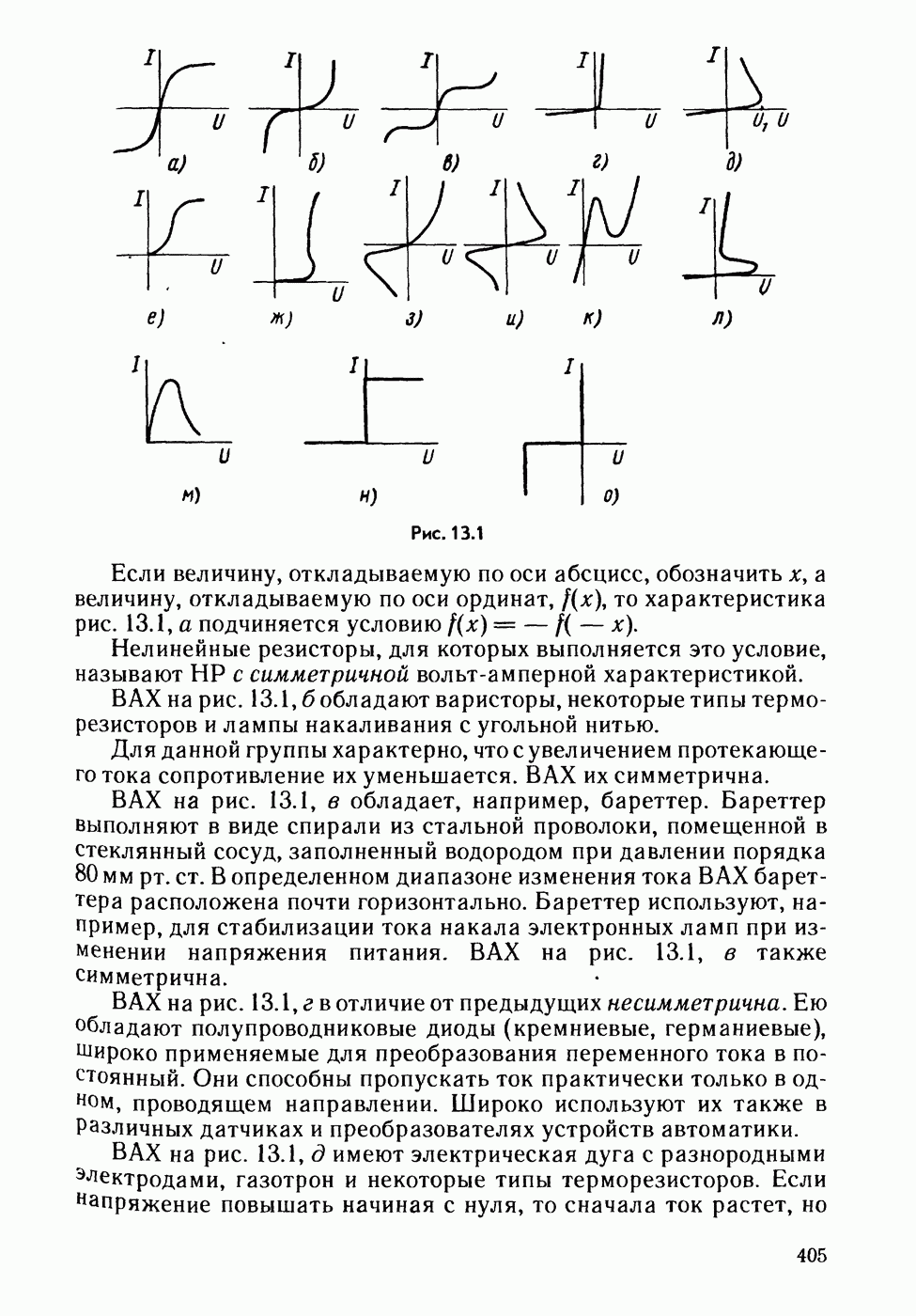
- § 13.2. ВАХ нелинейных резисторов.
- § 13.3. Общая характеристика методов расчета нелинейных электрических цепей постоянного тока.
- § 13.4. Последовательное соединение HP.
- § 13.5. Параллельное соединение HP.
- § 13.6. Последовательно-параллельное соединение сопротивлений.
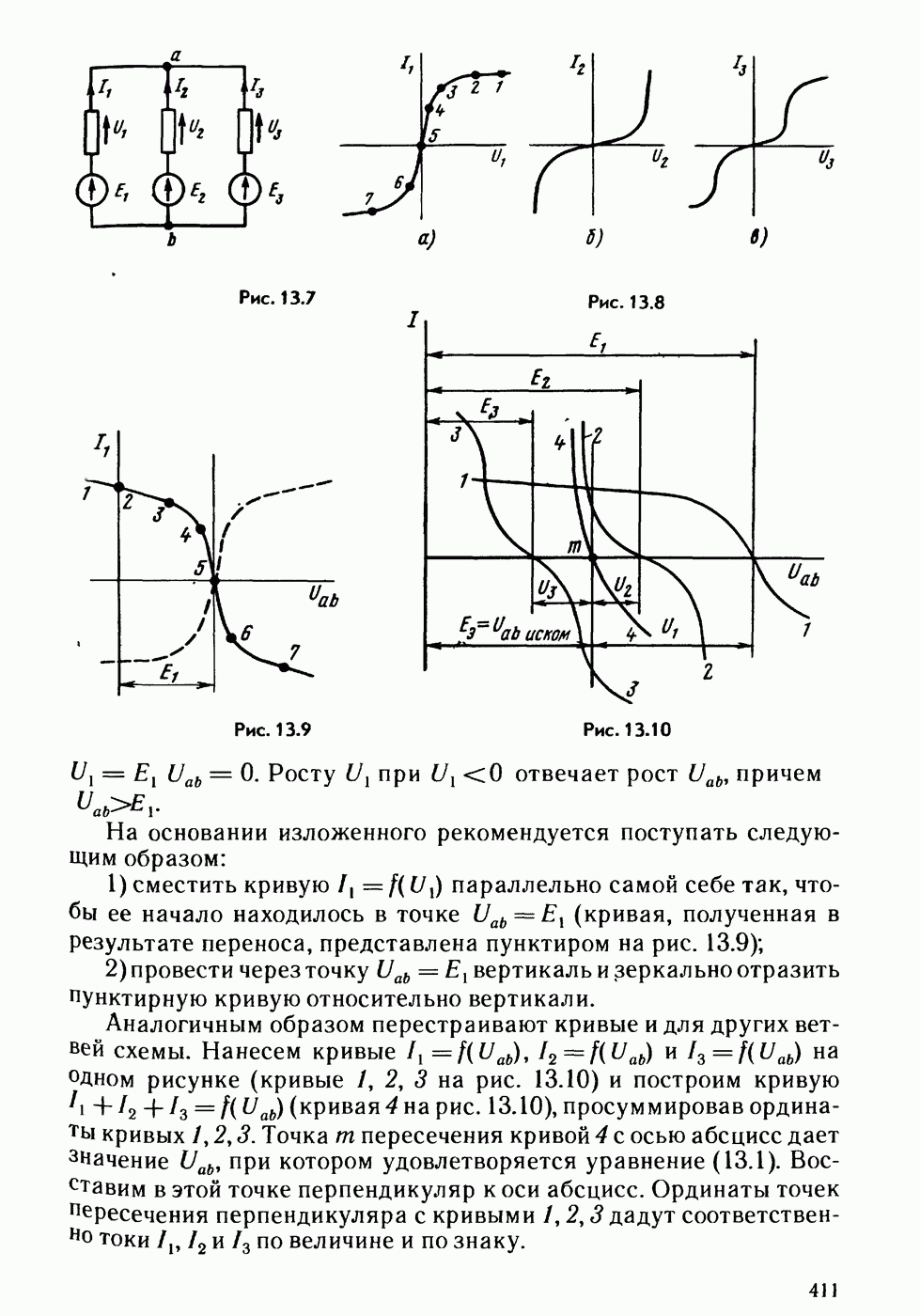
- § 13.8. Замена нескольких параллельных ветвей, содержащих HP и ЭДС, одной эквивалентной.
- § 13.9. Расчет нелинейных цепей методом эквивалентного генератора.
- § 13.10. Статическое и дифференциальное сопротивления.
- § 13.11. Замена нелинейного резистора эквивалентным линейным сопротивлением и ЭДС.
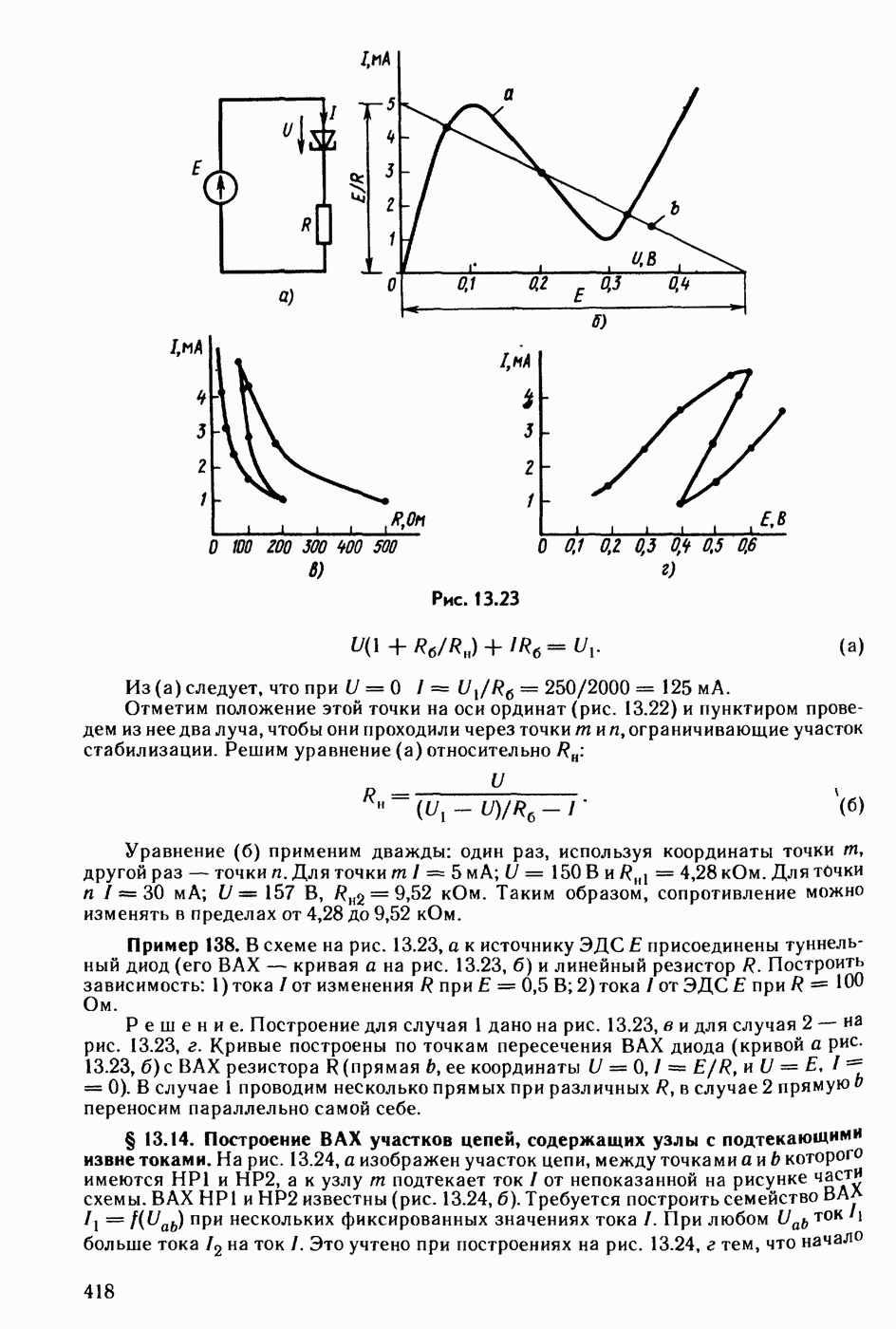
- § 13.12. Стабилизатор тока.
- § 13.13. Стабилизатор напряжения.
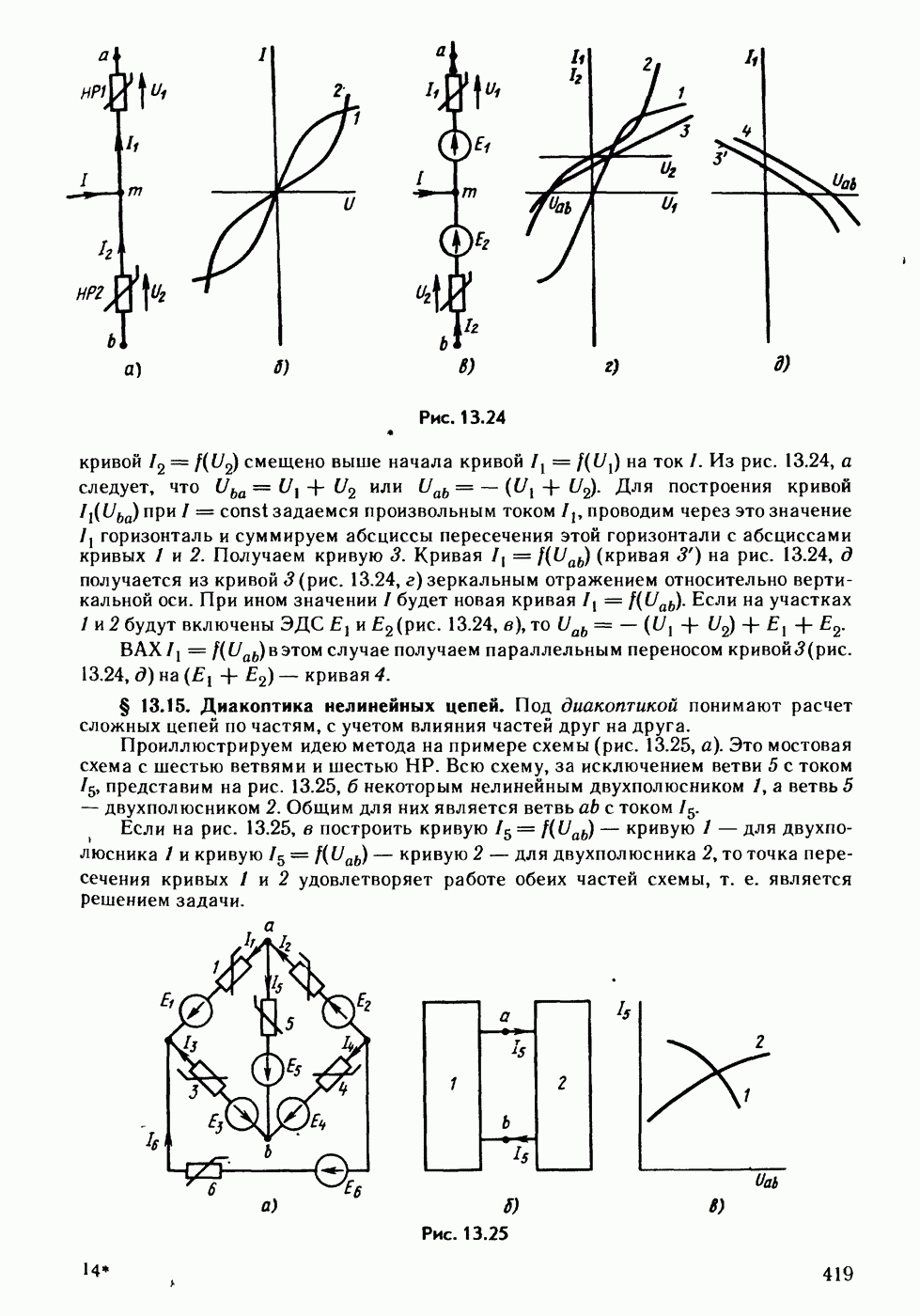
- § 13.14. Построение ВАХ участков цепей, содержащих узлы с подтекающими извне токами.
- § 13.15. Диакоптика нелинейных цепей.
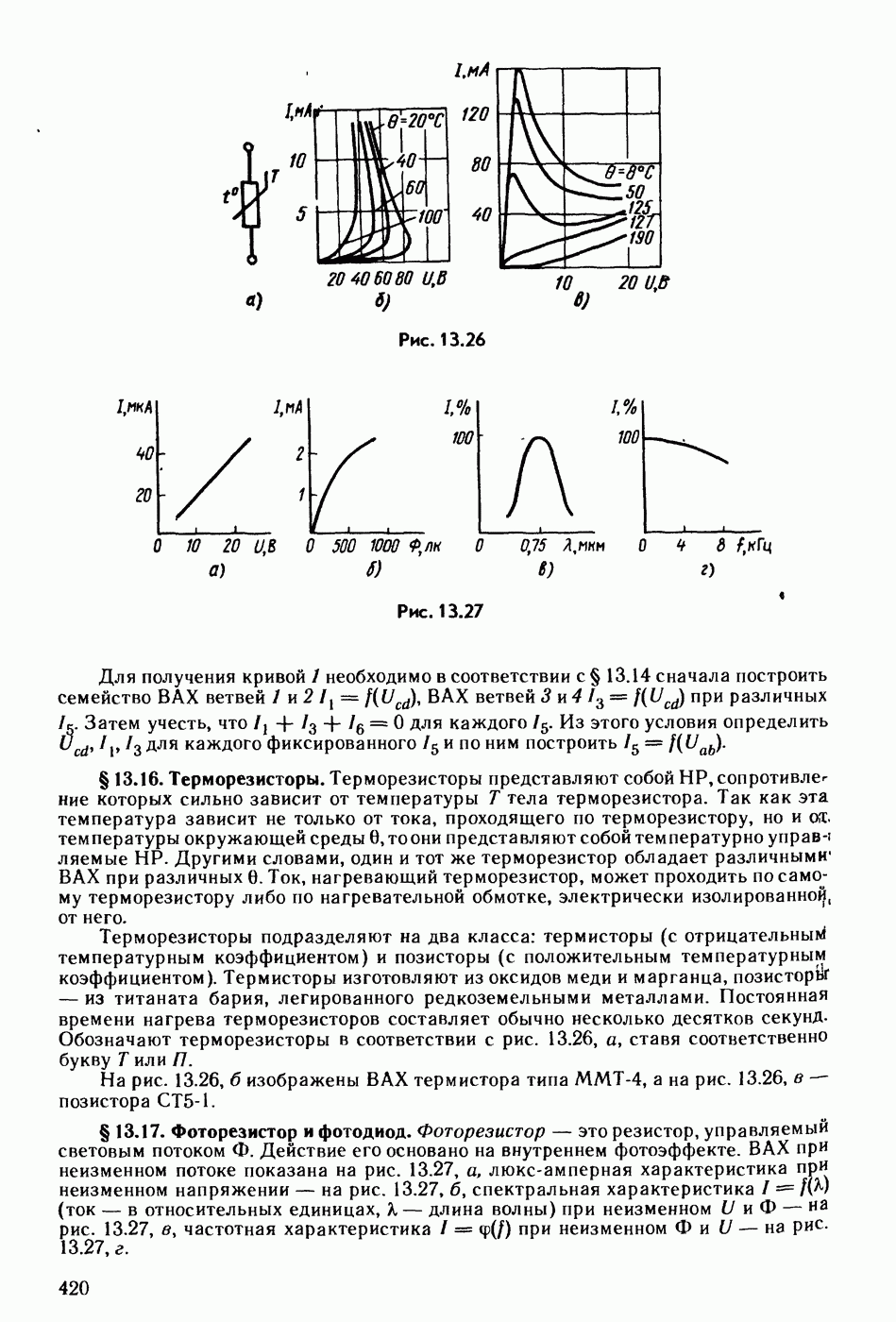
- § 13.16. Терморезисторы.
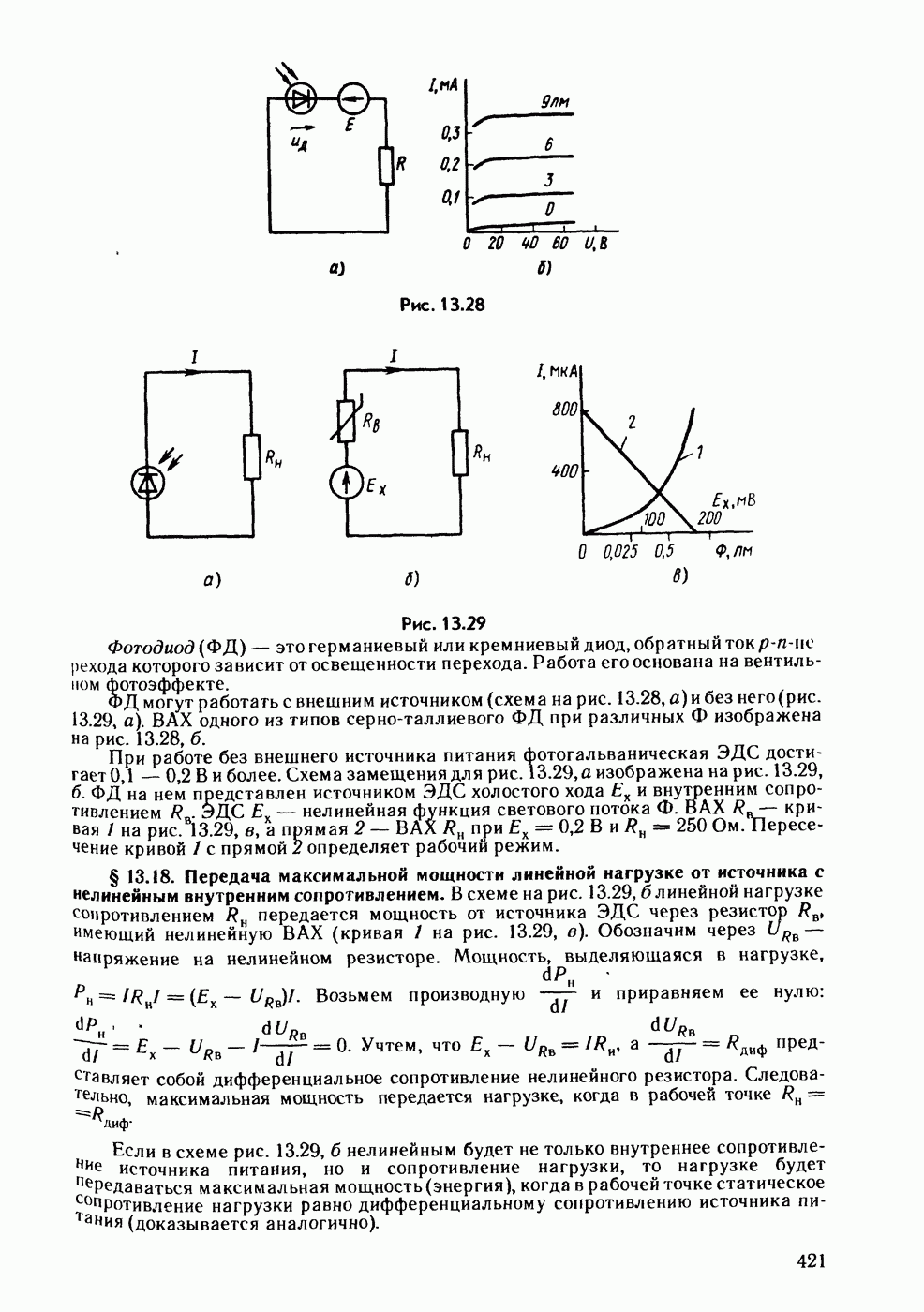
- § 13.17. Фоторезистор и фотодиод.
- § 13.18. Передача максимальной мощности линейной нагрузке от источника с нелинейным внутренним сопротивлением.
- § 13.19. Магниторезисторы и магнитодиоды.
- Вопросы для самопроверки
- Глава четырнадцатая. МАГНИТНЫЕ ЦЕПИ
- § 14.1. Подразделение веществ на сильномагнитные и слабомагнитные.
- § 14.2. Основные величины, характеризующие магнитное поле.
- § 14.3. Основные характеристики ферромагнитных материалов.
- § 14.4. Потери, обусловленные гистерезисом.
- § 14.5. Магнитомягкие и магнитотвердые материалы.
- § 14.6. Магнитодиэлектрики и ферриты.
- § 14.7. Закон полного тока.
- § 14.8. Магнитодвижущая (намагничивающая) сила.
- § 14.9. Разновидности магнитных цепей.
- § 14.10. Роль ферромагнитных материалов в магнитной цепи.
- § 14.11. Падение магнитного напряжения.
- § 14.12. Вебер-амперные характеристики.
- § 14.13. Построение вебер-амперных характеристик.
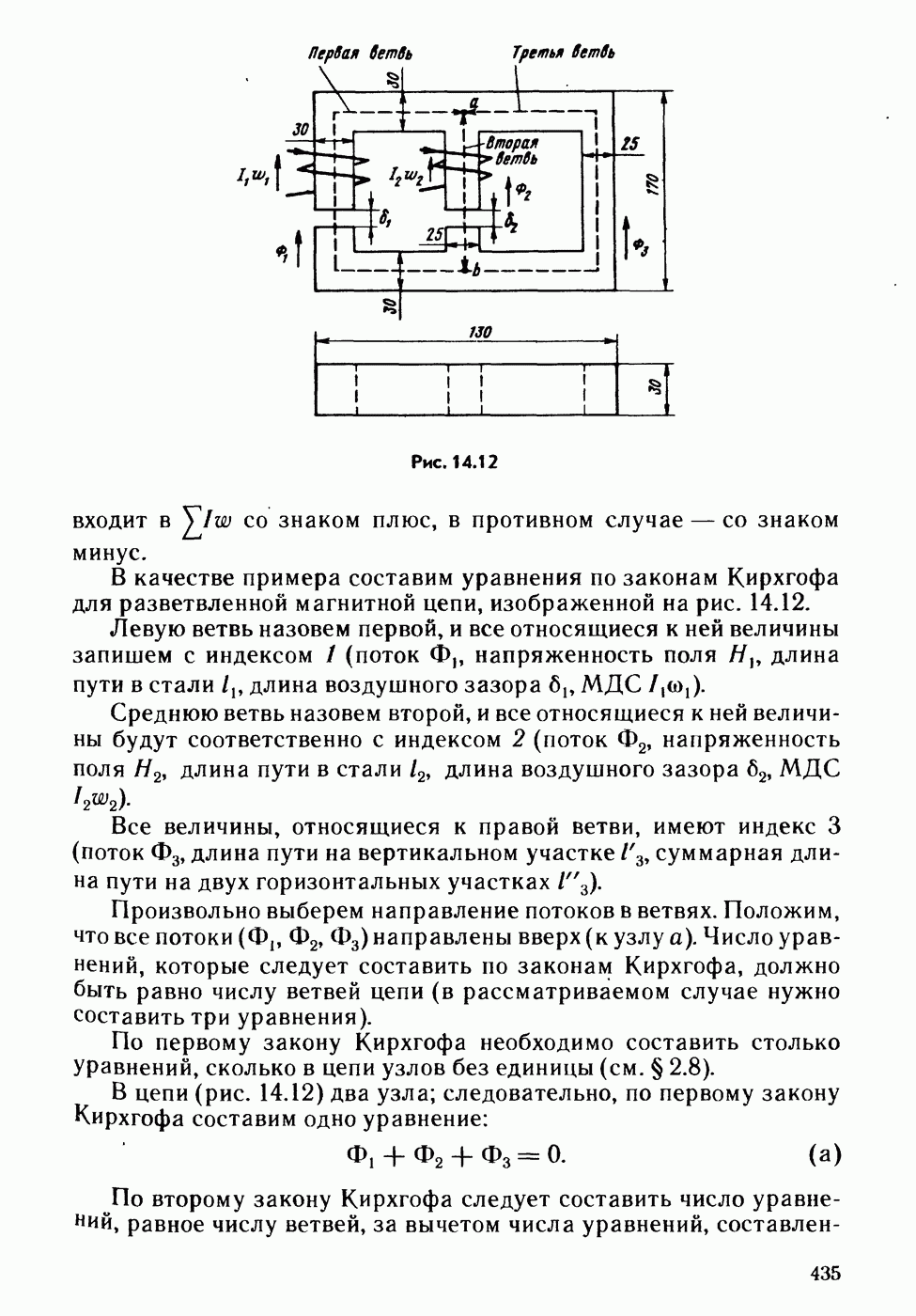
- § 14.14. Законы Кирхгофа для магнитных цепей.
- § 14.15. Применение к магнитным цепям всех методов, используемых для расчета электрических цепей с нелинейными резисторами.
- § 14.16. Определение МДС неразветвленной магнитной цепи по заданному потоку.
- § 14.17. Определение потока в неразветвленной магнитной цепи по заданной МДС.
- § 14.18. Расчет разветвленной магнитной цепи методом двух узлов.
- § 14.19. Дополнительные замечания к расчету магнитных цепей.
- § 14.20. Получение постоянного магнита.
- § 14.21. Расчет магнитной цепи постоянного магнита.
- § 14.22. Прямая и коэффициент возврата.
- § 14.23. Магнитное сопротивление и магнитная проводимость участка магнитной цепи. Закон Ома для магнитной цепи.
- § 14.24. Магнитная линия с распределенными параметрами.
- § 14.25. Пояснения к формуле
- Вопросы для самопроверки
- Глава пятнадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- § 15.1. Подразделение нелинейных элементов.
- § 15.2. Общая характеристика нелинейных резисторов.
- § 15.3. Общая характеристика нелинейных индуктивных элементов.
- § 15.4. Потери в сердечниках нелинейных индуктивных катушек, обусловленные вихревыми токами.
- § 15.5. Потери в ферромагнитном сердечнике, обусловленные гистерезисом.
- § 15.6. Схема замещения нелинейной индуктивной катушки.
- § 15.7. Общая характеристика нелинейных емкостных элементов.
- § 15.8. Нелинейные элементы как генераторы высших гармоник тока и напряжения.
- § 15.9. Основные преобразования, осуществляемые с помощью нелинейных электрических цепей.
- § 15.10. Некоторые физические явления, наблюдаемые в нелинейных цепях.
- § 15.11. Разделение нелинейных элементов по степени симметрии характеристик относительно осей координат.
- § 15.12. Аппроксимация характеристик нелинейных элементов.
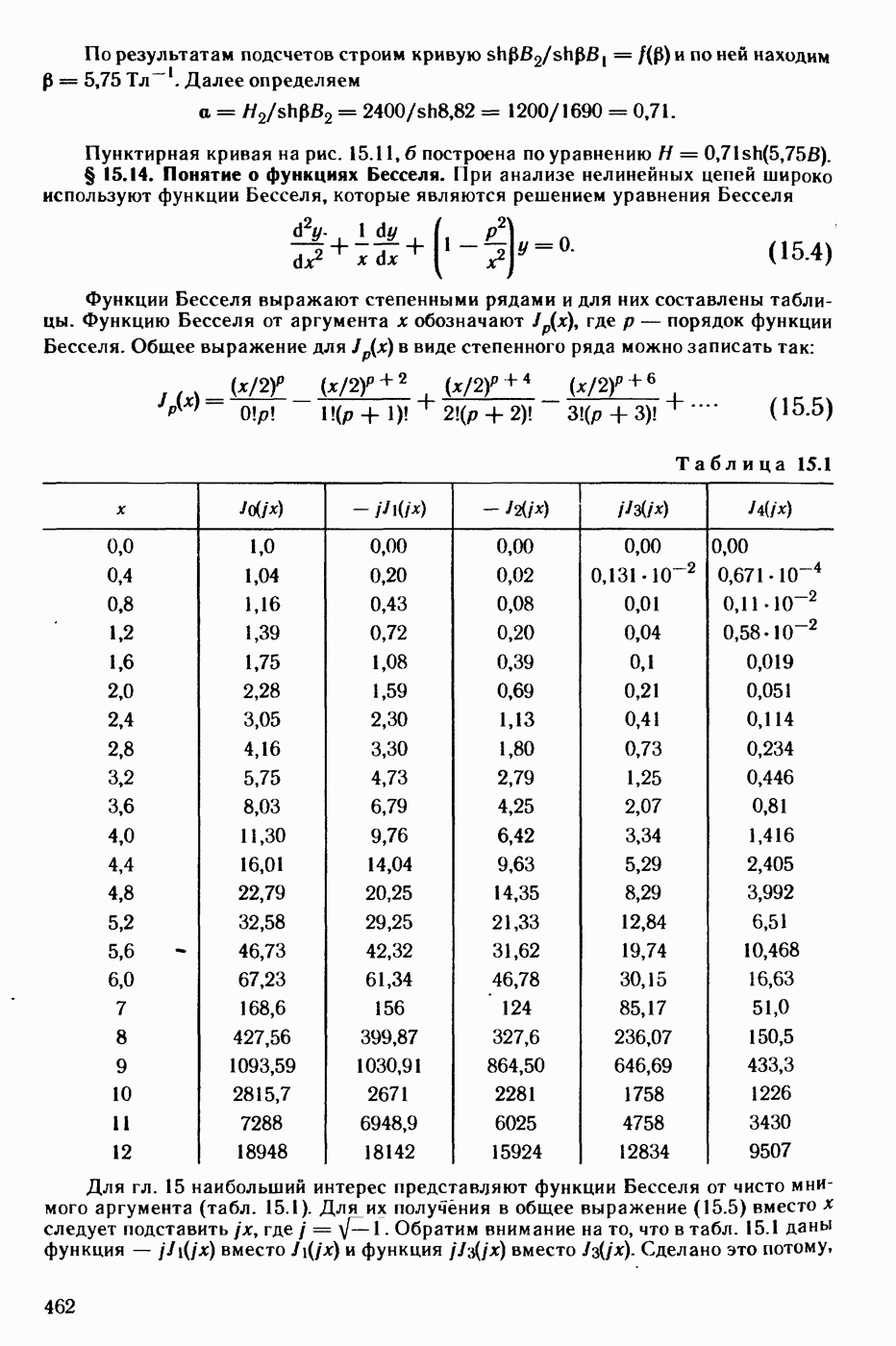
- § 15.13. Аппроксимация симметричных характеристик для мгновенных значений гиперболическим синусом.
- § 15.15. Разложение гиперболических синуса и косинуса от периодического аргумента в ряды Фурье.
- § 15.16. Разложение гиперболического синуса от постоянной и синусоидально меняющейся составляющих в ряд Фурье.
- § 15.17. Некоторые общие свойства симметричных нелинейных элементов.
- § 15.18. Появление постоянной составляющей тока (напряжения, потока, заряда) на нелинейном элементе с симметричной характеристикой.
- § 15.19. Типы характеристик нелинейных элементов.
- § 15.20. Характеристики для мгновенных значений.
- § 15.21. ВАХ по первым гармоникам.
- § 15.22. ВАХ для действующих значений.
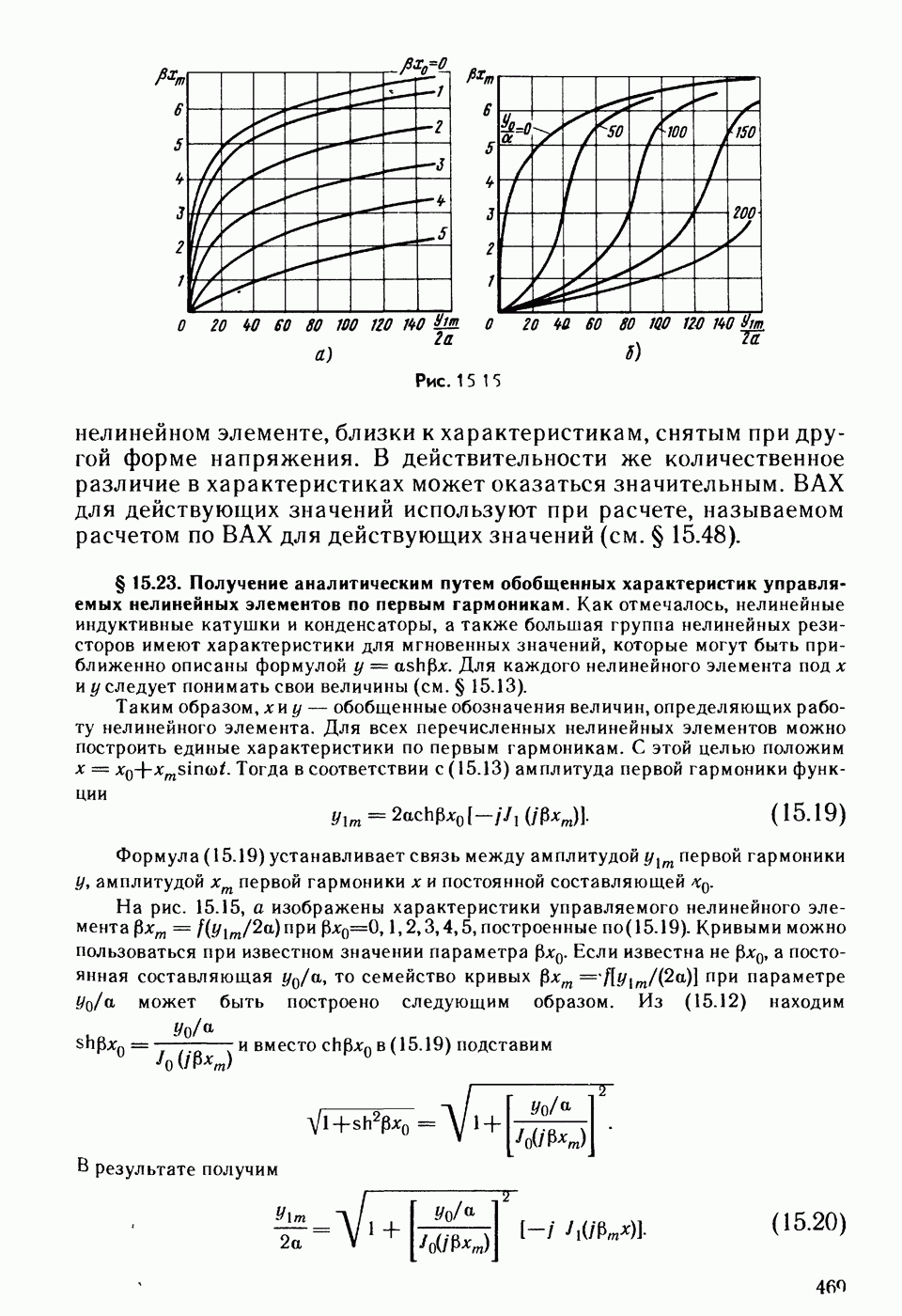
- § 15.23. Получение аналитическим путем обобщенных характеристик управляемых нелинейных элементов по первым гармоникам.
- § 15.24. Простейшая управляемая нелинейная индуктивная катушка.
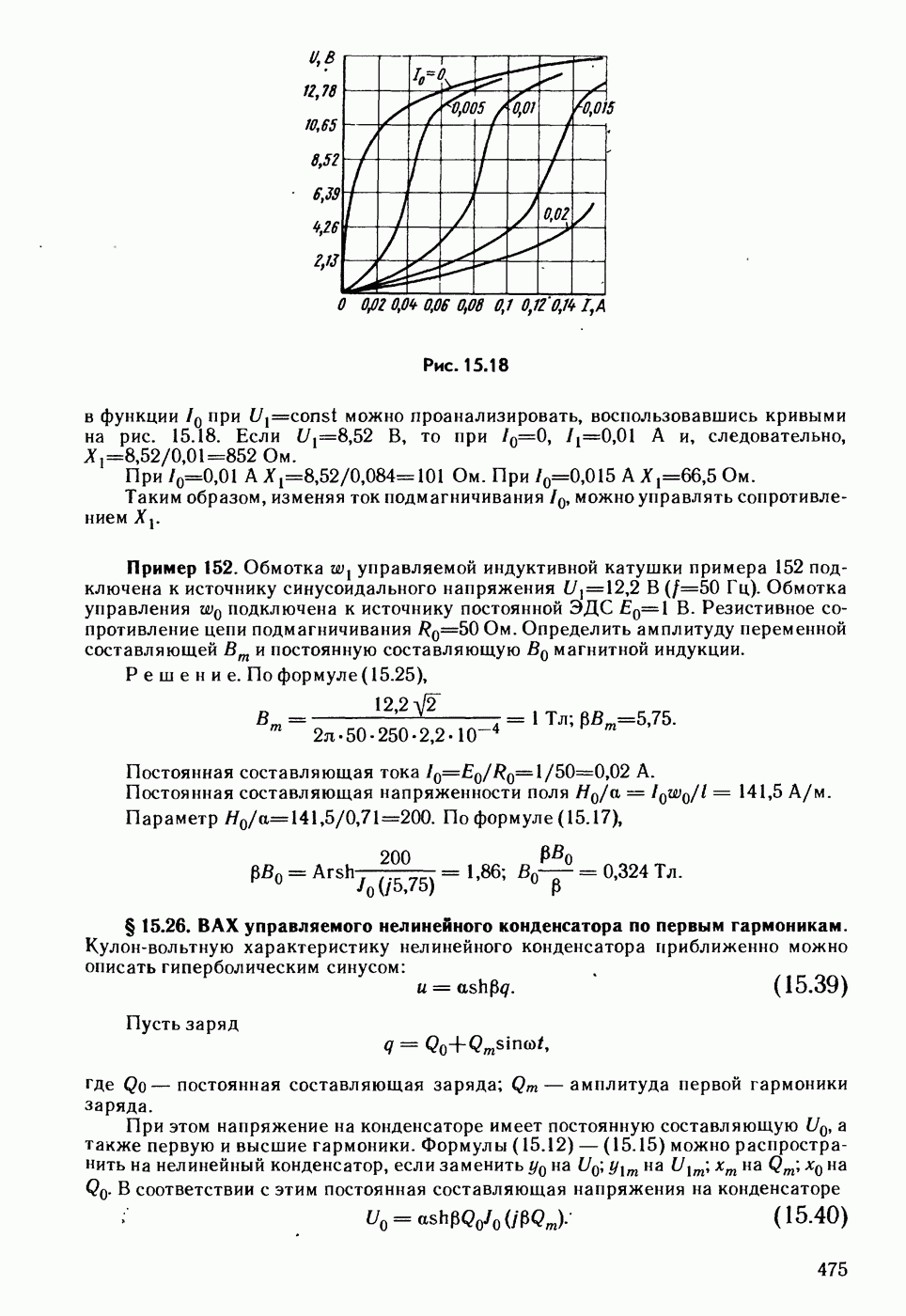
- § 15.25. ВАХ управляемой нелинейной индуктивной катушки по первым гармоникам.
- § 15.26. ВАХ управляемого нелинейного конденсатора по первым гармоникам.
- § 15.27. Основные сведения об устройстве биполярного транзистора.
- § 15.28. Основные способы включения биполярных транзисторов в схему.
- § 15.29. Принцип работы биполярного транзистора.
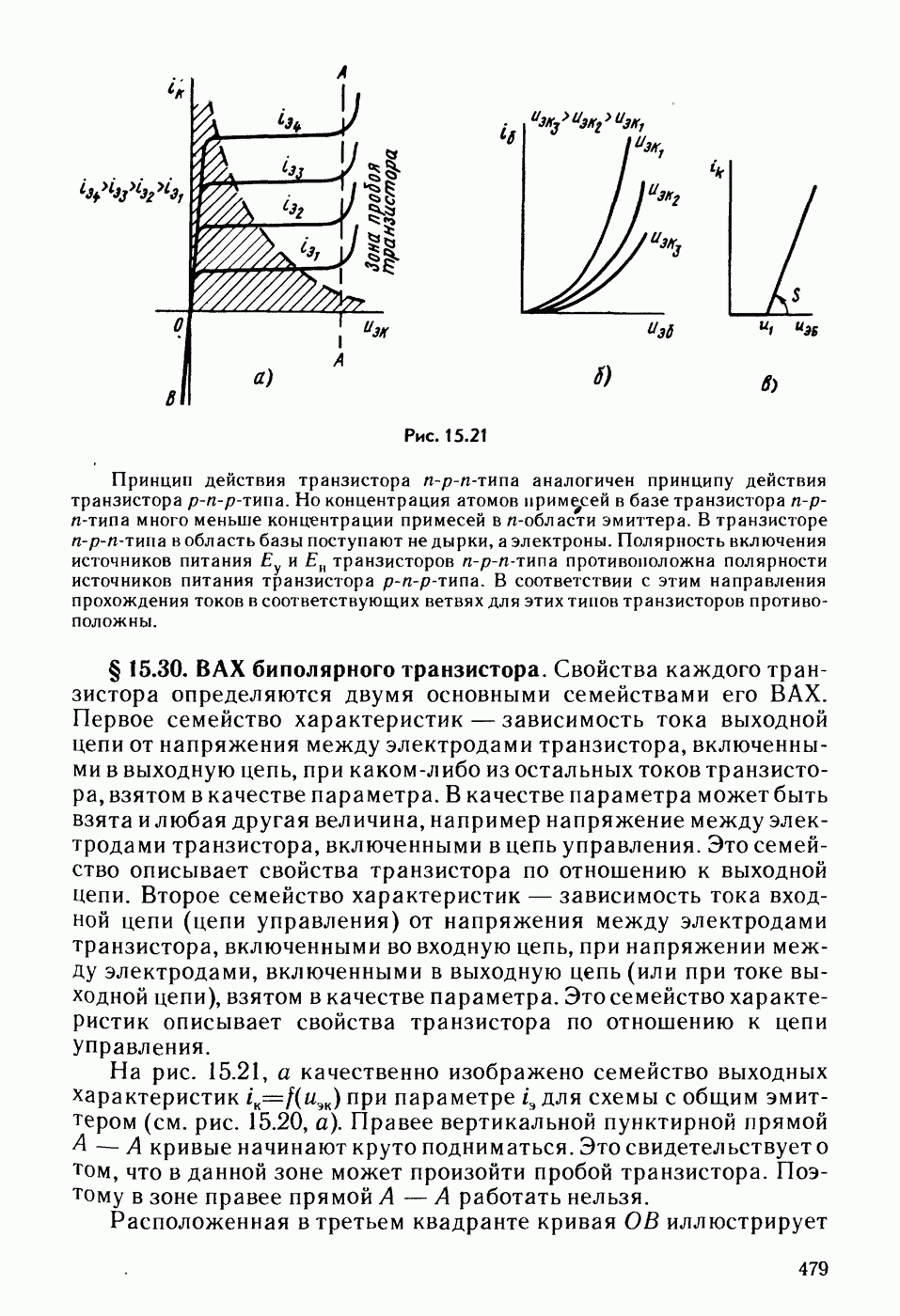
- § 15.30. ВАХ биполярного транзистора.
- § 15.31. Биполярный транзистор в качестве усилителя тока, напряжения, мощности.
- § 15.32. Связь между приращениями входных и выходных величин биполярного транзистора.
- § 15.33. Схема замещения биполярного транзистора для малых приращений. Методика расчета схем суправляемыми источниками с учетом ихчастотных свойств.
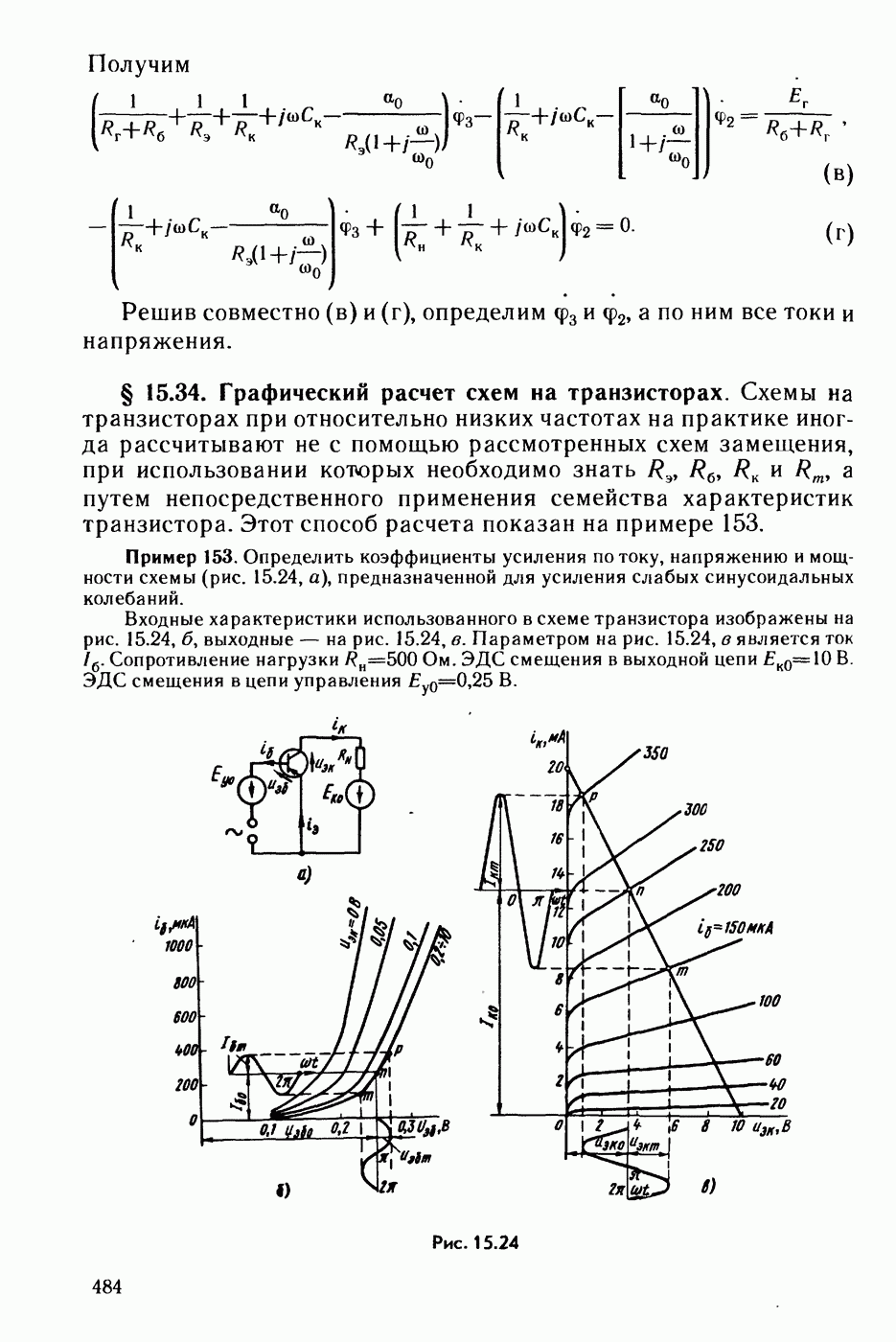
- § 15.34. Графический расчет схем на транзисторах.
- § 15.35. Принцип работы полевого транзистора.
- § 15.36. ВАХ полевого транзистора.
- § 15.37. Схемы включения полевого транзистора.
- § 15.38. Основные сведения о трехэлектродной лампе.
- § 15.39. ВАХ трехэлектродной лампы для мгновенных значений.
- § 15.40. Аналитическое выражение сеточной характеристики электронной лампы.
- § 15.41. Связь между малыми приращениями входных и выходных величин электронной лампы.
- § 15.42. Схема замещения электронной лампы для малых приращений.
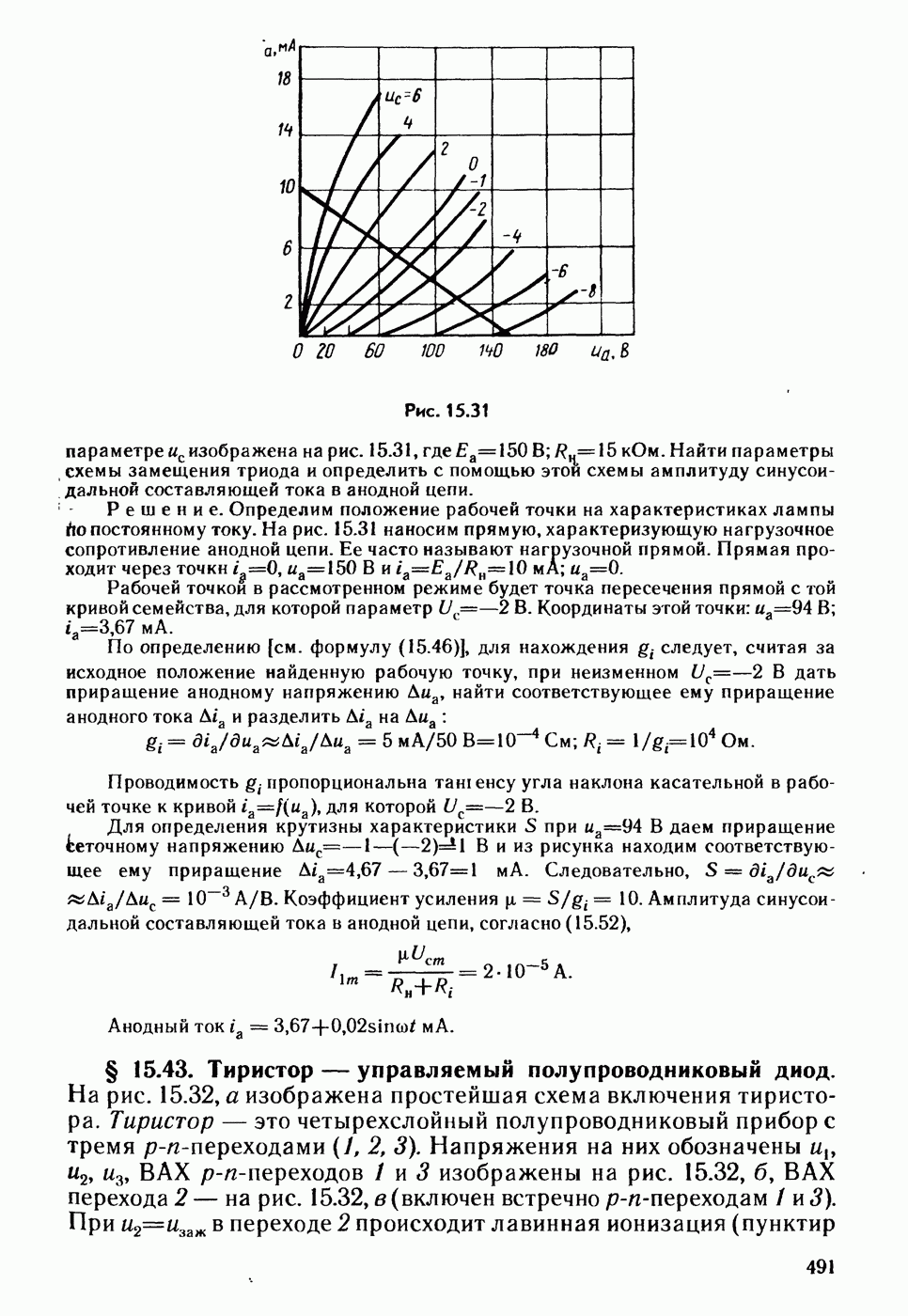
- § 15.43. Тиристор — управляемый полупроводниковый диод.
- § 15.44. Общая характеристика методов анализа и расчета нелинейных электрических цепей переменного тока.
- § 15.45. Графический метод расчета при использовании характеристик нелинейных элементов для мгновенных значений.
- § 15.46. Аналитический метод расчета при использовании характеристик нелинейных элементов для мгновенных значений при их кусочно-линейной аппроксимации.
- § 15.47. Аналитический (графический) метод расчета по первым гармоникам токов и напряжений.
- § 15.48. Анализ нелинейных цепей переменного тока путем использования ВАХ для действующих значений.
- § 15.49. Аналитический метод расчета цепей по первой и одной или нескольким высшим или низшим гармоникам.
- § 15.50. Расчет цепей с помощью линейных схем замещения.
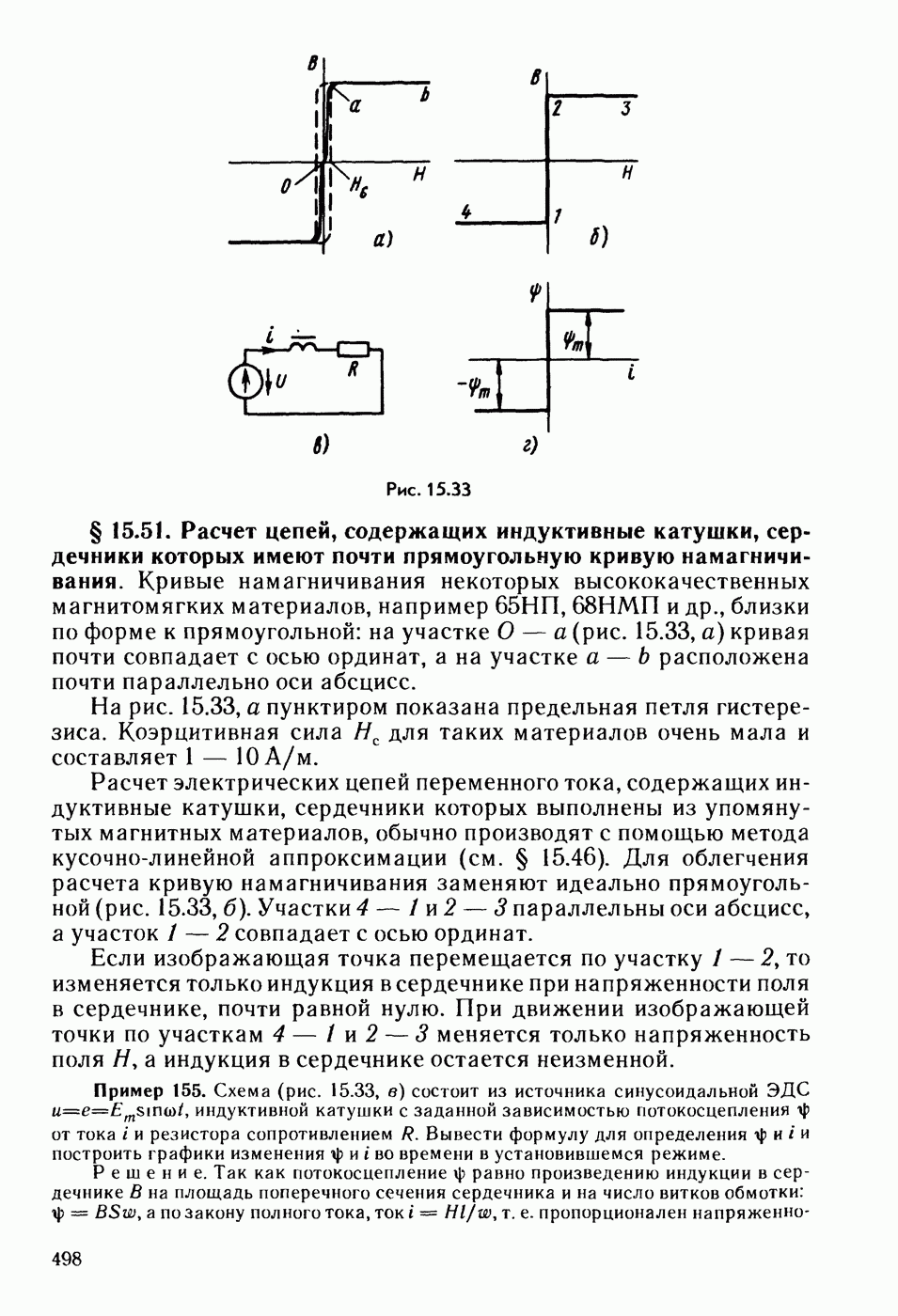
- § 15.51. Расчет цепей, содержащих индуктивные катушки, сердечники которых имеют почти прямоугольную кривую намагничивания.
- § 15.52. Расчет цепей, содержащих нелинейные конденсаторы с прямоугольной кулон-вольтной характеристикой.
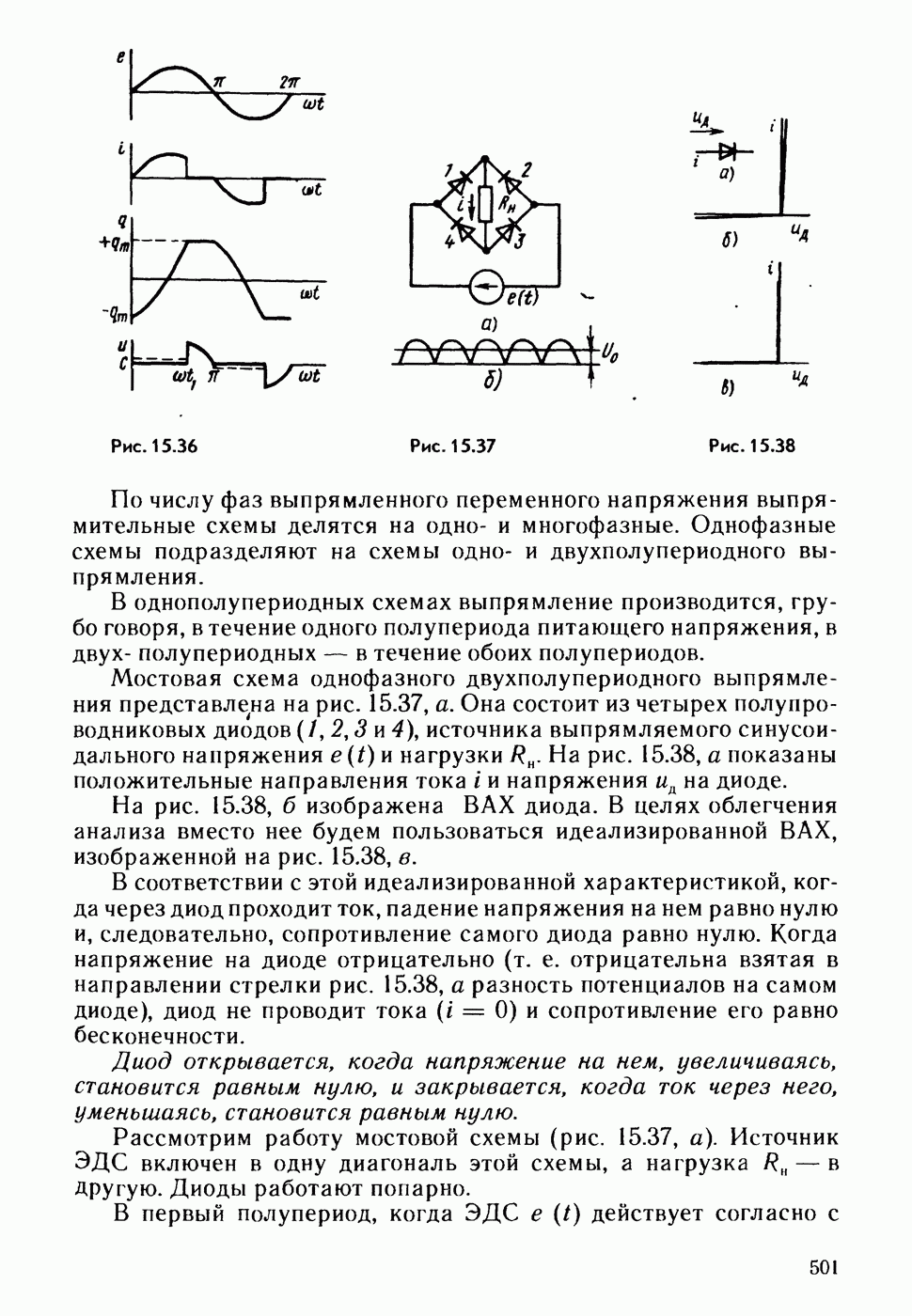
- § 15.53. Выпрямление переменного напряжения.
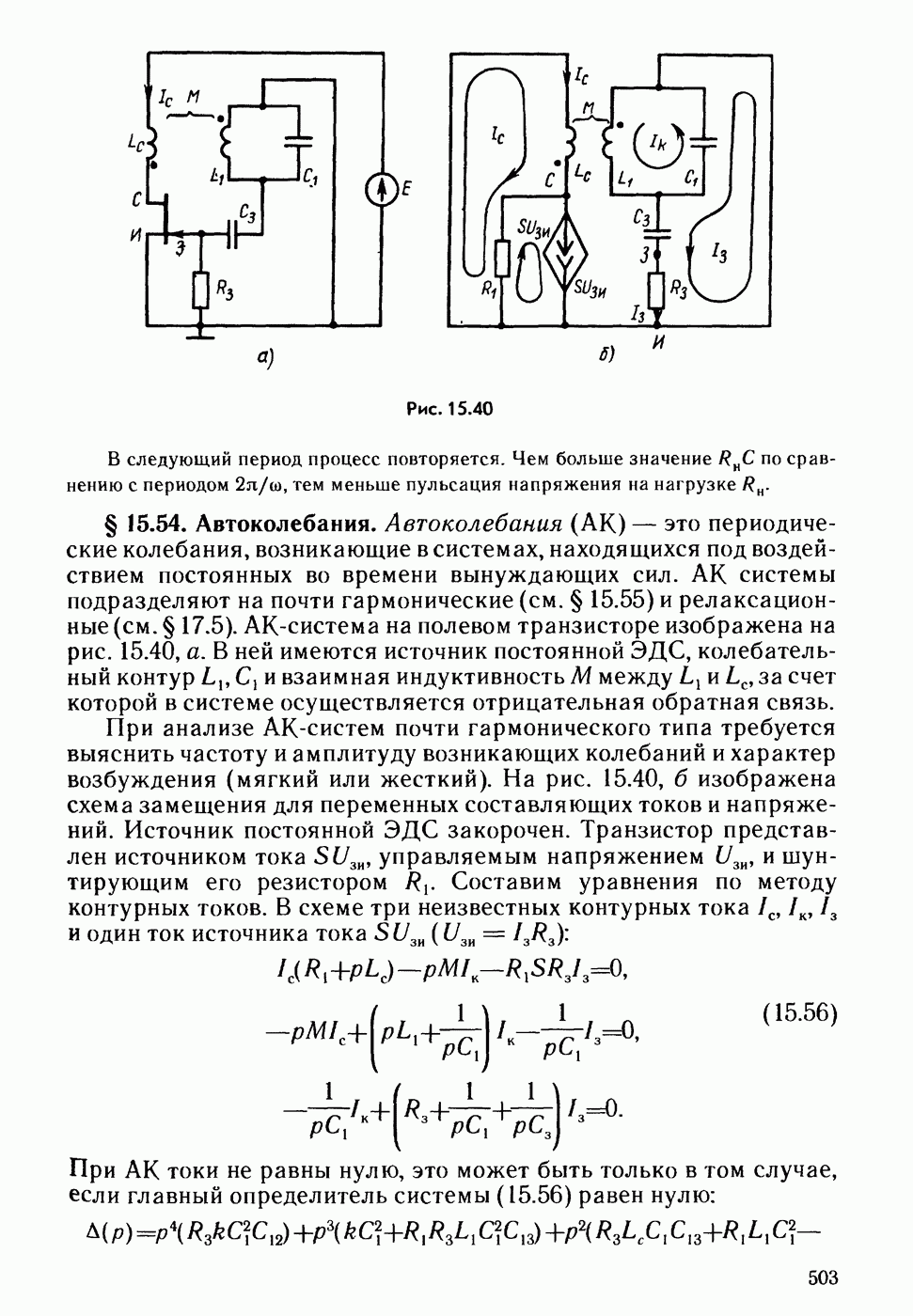
- § 15.54. Автоколебания.
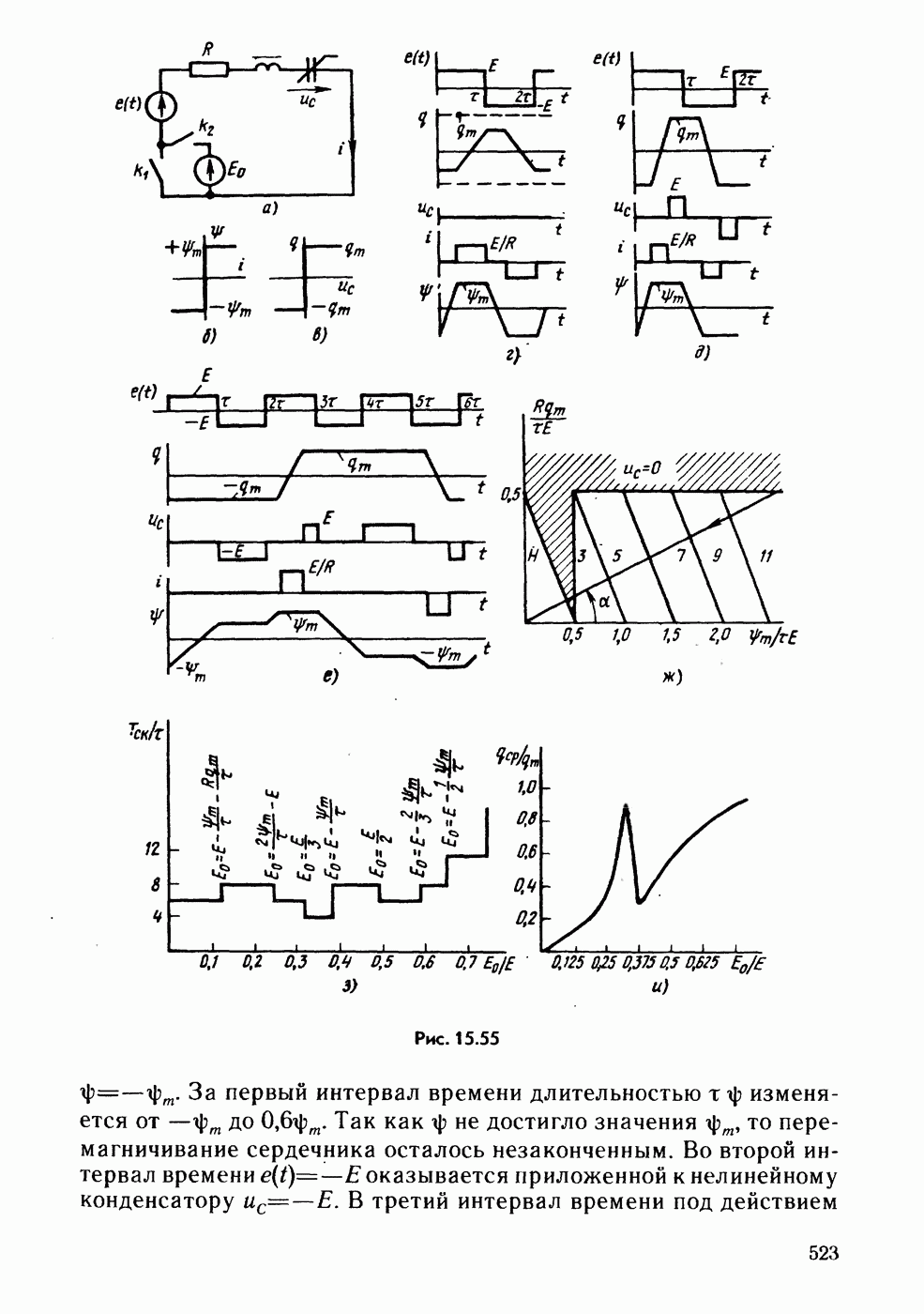
- § 15.55. Мягкое и жесткое возбуждение автоколебаний.
- § 15.56. Определение феррорезонансных цепей.
- § 15.57. Построение ВАХ последовательной феррорезонансной цепи.
- § 15.58. Триггерный эффект в последовательной феррорезонансной цепи. Феррорезонанс напряжений.
- § 15.59. ВАХ параллельного соединения конденсатора и катушки со стальным сердечником. Феррорезонанс токов.
- § 15.60. Триггерный эффект в параллельной феррорезонансной цепи.
- § 15.61. Частотные характеристики нелинейных цепей.
- § 15.62. Применение символического метода для расчета нелинейных цепей. Построение векторных и топографических диаграмм.
- § 15.63. Метод эквивалентного генератора.
- § 15.64. Векторная диаграмма нелинейной индуктивной катушки.
- § 15.65. Определение намагничивающего тока.
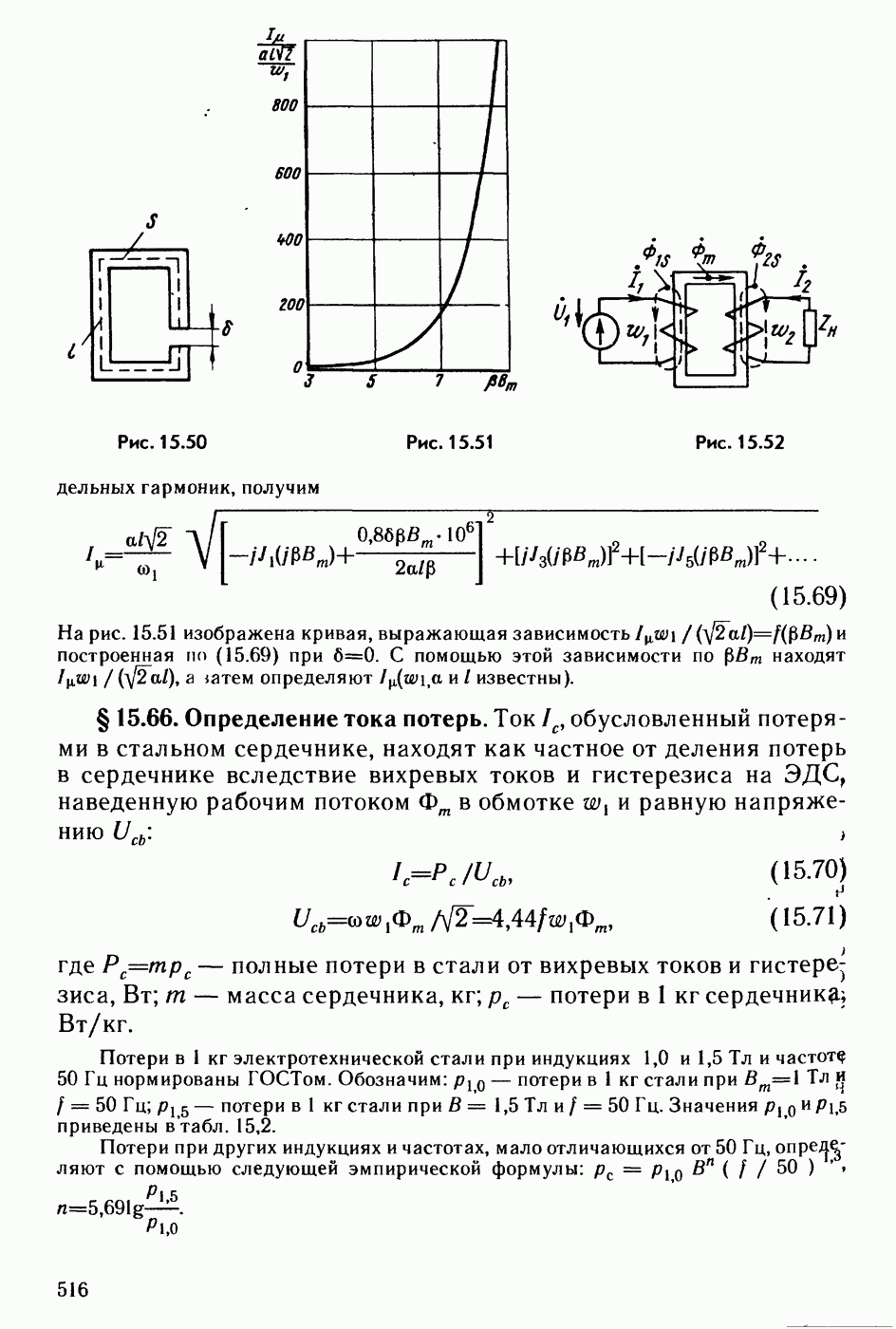
- § 15.66. Определение тока потерь.
- § 15.67. Основные соотношения для трансформатора со стальным сердечником.
- § 15.68. Векторная диаграмма трансформатора со стальным сердечником.
- § 15.69. Субгармонические колебания. Многообразие типов движений в нелинейных цепях.
- § 15.70. Автомодуляция. Хаотические колебания (странные аттракторы).
- Вопросы для самопроверки
- Глава шестнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 16.1. Общая характеристика методов анализа и расчета переходных процессов.
- § 16.2. Расчет, основанный на графическом подсчете определенного интеграла.
- § 16.3. Расчет методом интегрируемой нелинейной аппроксимации.
- § 16.4. Расчет методом кусочно-линейной аппроксимации.
- § 16.5. Расчет переходных процессов в нелинейных цепях методом переменных состояния на ЭВМ.
- § 16.6. Метод медленно меняющихся амплитуд.
- § 16.7. Метод малого параметра.
- § 16.8. Метод интегральных уравнений.
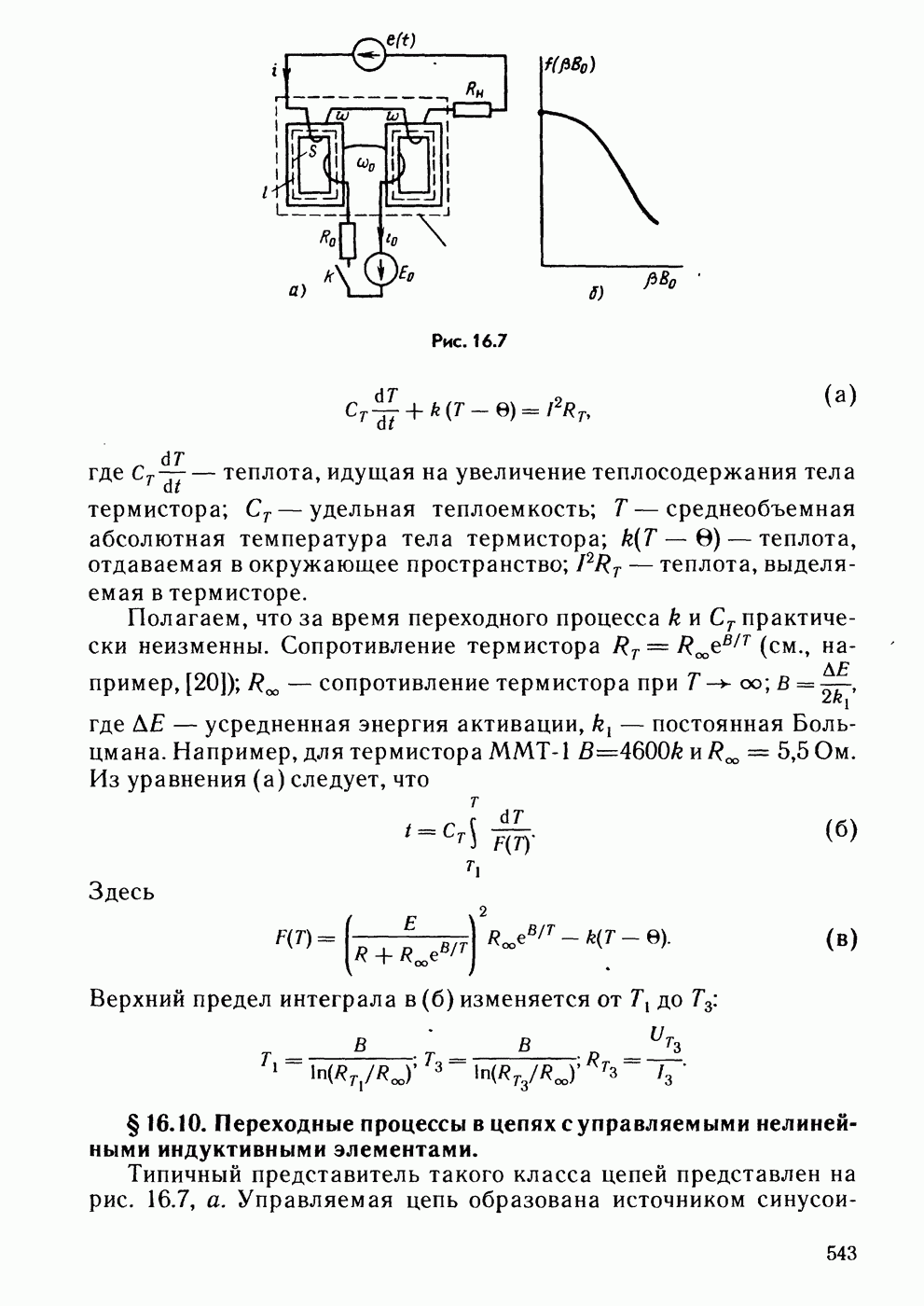
- § 16.9. Переходные процессы в цепях с терморезисторами.
- § 16.10. Переходные процессы в цепях с управляемыми нелинейными индуктивными элементами.
- § 16.11. Переходные процессы в нелинейных электромеханических системах.
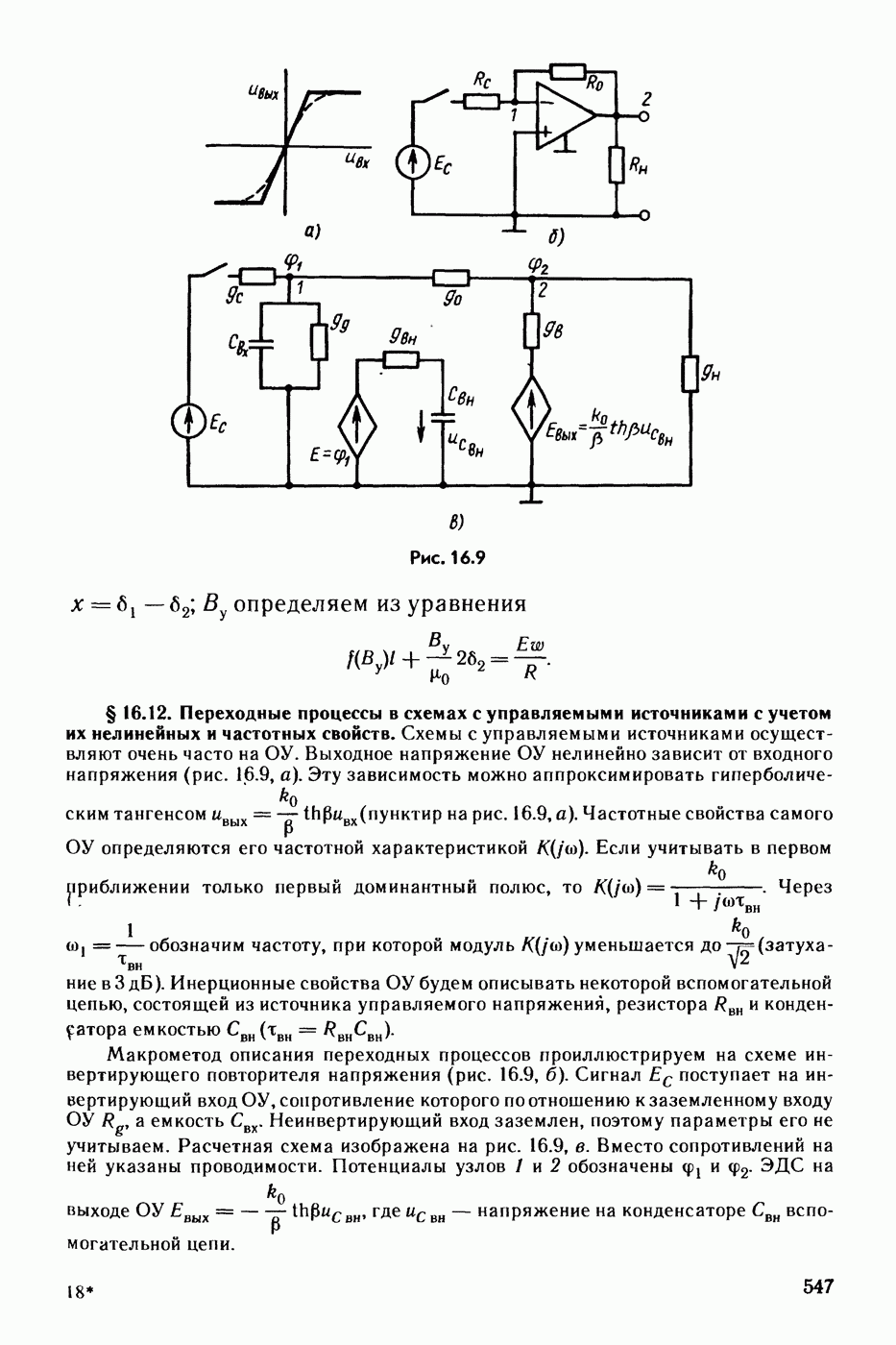
- § 16.12. Переходные процессы в схемах с управляемыми источниками с учетом их нелинейных и частотных свойств.
- § 16.13. Перемагничивание ферритовых сердечников импульсами тока.
- § 16.14. Фазовая плоскость и характеристика областей ее применения.
- § 16.15. Интегральные кривые, фазовая траектория и предельный цикл.
- § 16.16. Изображение простейших процессов на фазовой плоскости.
- § 16.17. Изоклины. Особые точки. Построение фазовых траекторий.
- Вопросы для самопроверки
- Глава семнадцатая. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ РЕЖИМОВ РАБОТЫ НЕЛИНЕЙНЫХ ЦЕПЕЙ
- § 17.1. Устойчивость «в малом» и «в большом». Устойчивость по Ляпунову.
- § 17.2. Общие основы исследования устойчивости «в малом».
- § 17.3. Исследование устойчивости состояния равновесия в системах с постоянной вынуждающей силой.
- § 17.4. Исследование устойчивости автоколебаний и вынужденных колебаний по первой гармонике.
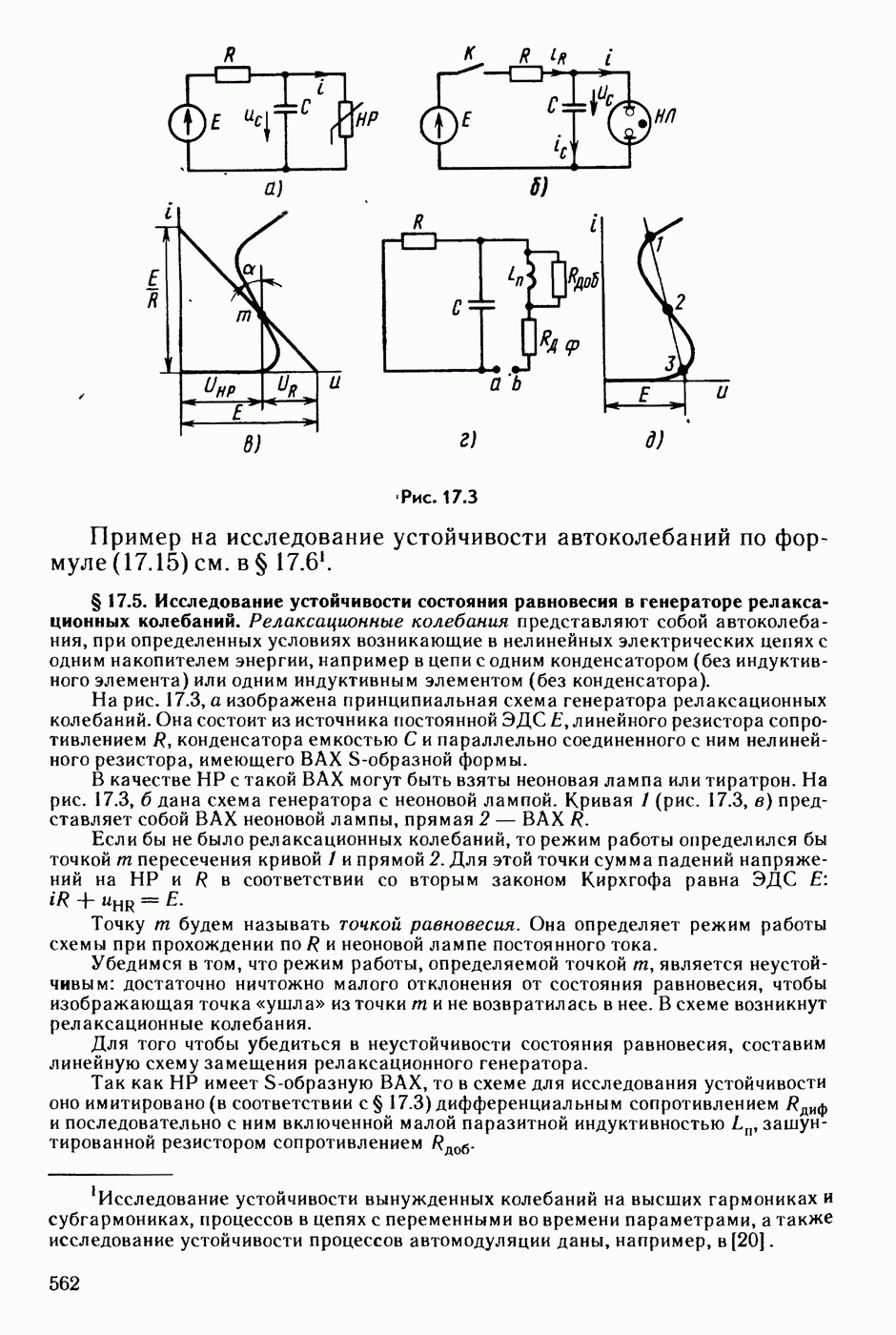
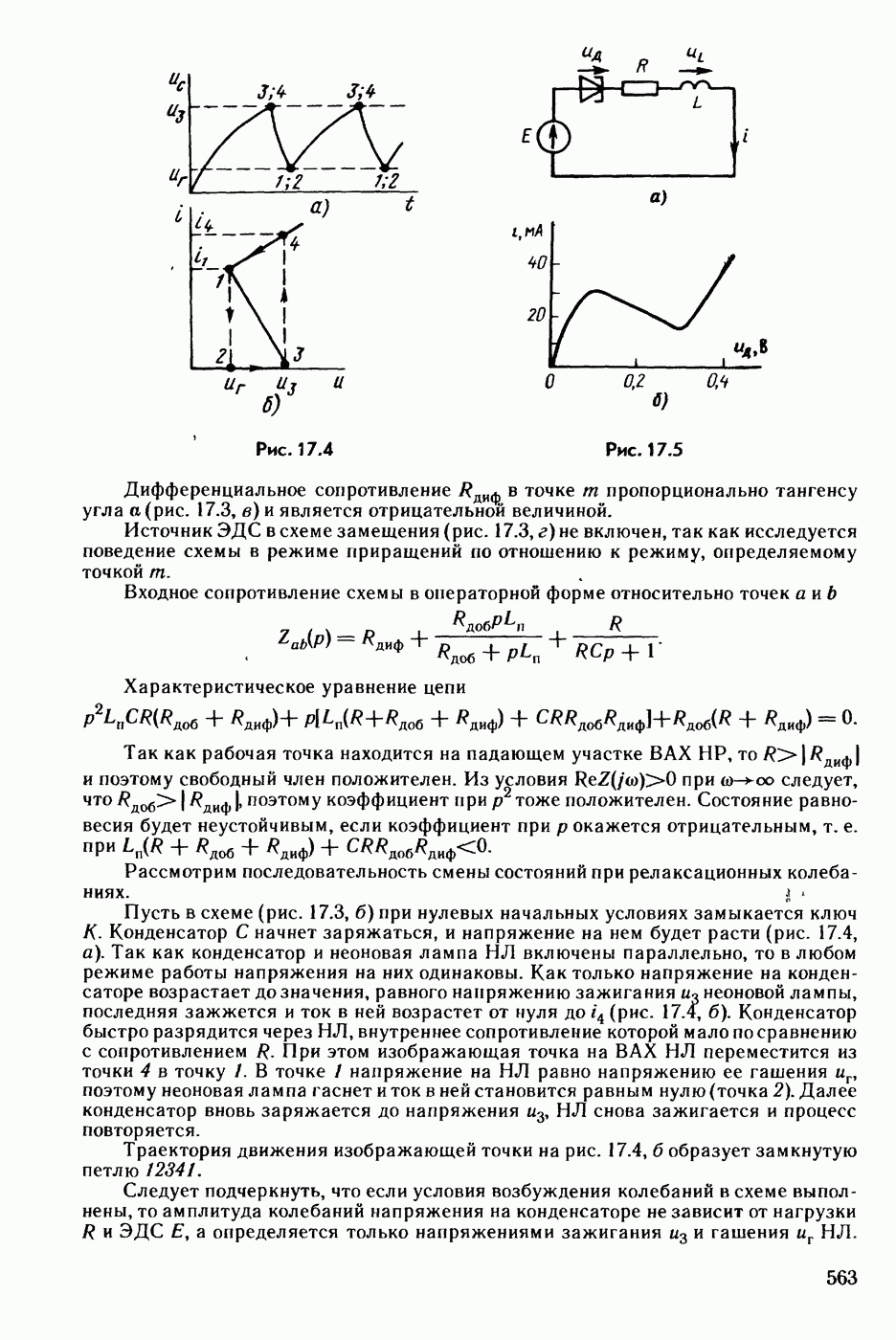
- § 17.5. Исследование устойчивости состояния равновесия в генераторе релаксационных колебаний.
- § 17.6. Исследование устойчивости периодического движения в ламповом генераторе синусоидальных колебаний.
- § 17.7. Исследование устойчивости работы электрических цепей, содержащих управляемые источники напряжения (тока) с учетом их неидеальности.
- Вопросы для самопроверки
- Глава восемнадцатая. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ПЕРЕМЕННЫМИ ВО ВРЕМЕНИ ПАРАМЕТРАМИ
- § 18.1. Элементы цепей.
- § 18.2. Общие свойства электрических цепей.
- § 18.3. Расчет электрических цепей в установившемся режиме.
- § 18.4. Параметрические колебания.
- § 18.5. Параметрические генератор и усилитель.
- Вопросы для самопроверки