| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5.2. Основы теории k-фильтров.
Из § 4.10 известно, что если нагрузка  согласована с характеристическим сопротивлением
согласована с характеристическим сопротивлением  четырехполюсника, то напряжение
четырехполюсника, то напряжение  и ток в нагрузке
и ток в нагрузке  связаны с напряжением
связаны с напряжением  и током
и током  на входе четырехполюсника следующими соотношениями:
на входе четырехполюсника следующими соотношениями:

где 
Тогда

Множитель  определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения (тока) на его входе.
определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения (тока) на его входе.
Если  то
то  и фильтр пропускает колебания без затухания. Таким образом, в полосе прозрачности
и фильтр пропускает колебания без затухания. Таким образом, в полосе прозрачности  .
.
В полосе затухания а > 0. Множитель  по модулю равный 1, свидетельствует о том, что напряжение
по модулю равный 1, свидетельствует о том, что напряжение  и ток
и ток  отстают соответственно от
отстают соответственно от  на угол
на угол 
Фильтрующие свойства четырехполюсника рассмотрим путем сравнения выражения для коэффициента А четырехполюсника с равным ему выражением гиперболического косинуса от аргумента 

Гиперболический косинус от суммы двух аргументов (с учетом того, что  ) можно представить следующим образом:
) можно представить следующим образом:

Для любого фильтра, собранного по Т-схеме (см. § 4.5), 
Для фильтра, собранного по П-схеме (см. § 4.5),  Из каких бы реактивных сопротивлений ни был собран фильтр, отношения
Из каких бы реактивных сопротивлений ни был собран фильтр, отношения  в Т-схеме и
в Т-схеме и  в П-схеме всегда будут действительными (не мнимыми и не комплексными) числами — отношение двух мнимых чисел всегда есть число действительное. Следовательно, всегда будет действительным и коэффициент А. Но если коэффициент А действителен, то действительным должно быть и выражение равного ему
в П-схеме всегда будут действительными (не мнимыми и не комплексными) числами — отношение двух мнимых чисел всегда есть число действительное. Следовательно, всегда будет действительным и коэффициент А. Но если коэффициент А действителен, то действительным должно быть и выражение равного ему 

Это выражение действительно, если

При этом

Уравнения (5.1) и (5.2) используют для определения границ полосы прозрачности и характера изменения угла b в этой полосе, а также характера изменения коэффициента затухания в полосе (полосах) затухания.
Равенство (5.1) для полосы прозрачности  удовлетворяется, так как
удовлетворяется, так как  . В силу того что
. В силу того что  уравнение (5.2) Для полосы прозрачности переходит в следующее:
уравнение (5.2) Для полосы прозрачности переходит в следующее:

Круговой косинус ( ) может изменяться в пределах от
) может изменяться в пределах от  до
до  Поэтому крайние значения коэффициента А [являющегося Функцией частоты
Поэтому крайние значения коэффициента А [являющегося Функцией частоты  в полосе прозрачности равны ± 1. Полоса прозрачности в общем случае лежит в диапазоне частот от
в полосе прозрачности равны ± 1. Полоса прозрачности в общем случае лежит в диапазоне частот от  до
до 
Значения  для фильтров НЧ и ВЧ (подробнее см. § 5.3) определяют путем решения уравнений
для фильтров НЧ и ВЧ (подробнее см. § 5.3) определяют путем решения уравнений

Для полосовых и заграждающих фильтров (см. § 5.3)  находят как корни уравнения
находят как корни уравнения 
Частоту, являющуюся граничной между полосой прозрачности и полосой затухания, называют частотой среза.
Характер изменения угла  в функции от о для полосы прозрачности определяют в соответствии с уравнением (5.3) следующим образом:
в функции от о для полосы прозрачности определяют в соответствии с уравнением (5.3) следующим образом:
 (5.5)
(5.5)
Определим а и  для полосы затухания. В полосе затухания
для полосы затухания. В полосе затухания  Уравнение (5.1) удовлетворяется при условии
Уравнение (5.1) удовлетворяется при условии

т. е. при

и (или) при

Согласно уравнению (5.2), при 

а при 

Уравнения (5.9) и (5.10) позволяют по значениям А как функции со рассчитать  в полосе затухания, а по
в полосе затухания, а по  определить а и, таким образом, построить кривую
определить а и, таким образом, построить кривую  Из уравнений (5.7) и (5.8) следует, что в полосе затухания напряжение
Из уравнений (5.7) и (5.8) следует, что в полосе затухания напряжение  на выходе фильтра находится либо в фазе (при
на выходе фильтра находится либо в фазе (при  либо в противофазе (при
либо в противофазе (при  ) с напряжением
) с напряжением  на входе фильтра.
на входе фильтра.
В заключение необходимо отметить два важных положения:
1) с изменением частоты  меняются коэффициенты В и С четырехполюсника, поэтому изменяется и характеристическое сопротивление
меняются коэффициенты В и С четырехполюсника, поэтому изменяется и характеристическое сопротивление  Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная! теория фильтров), при изменении частоты нужно менять и сопротивление нагрузки;
Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная! теория фильтров), при изменении частоты нужно менять и сопротивление нагрузки;
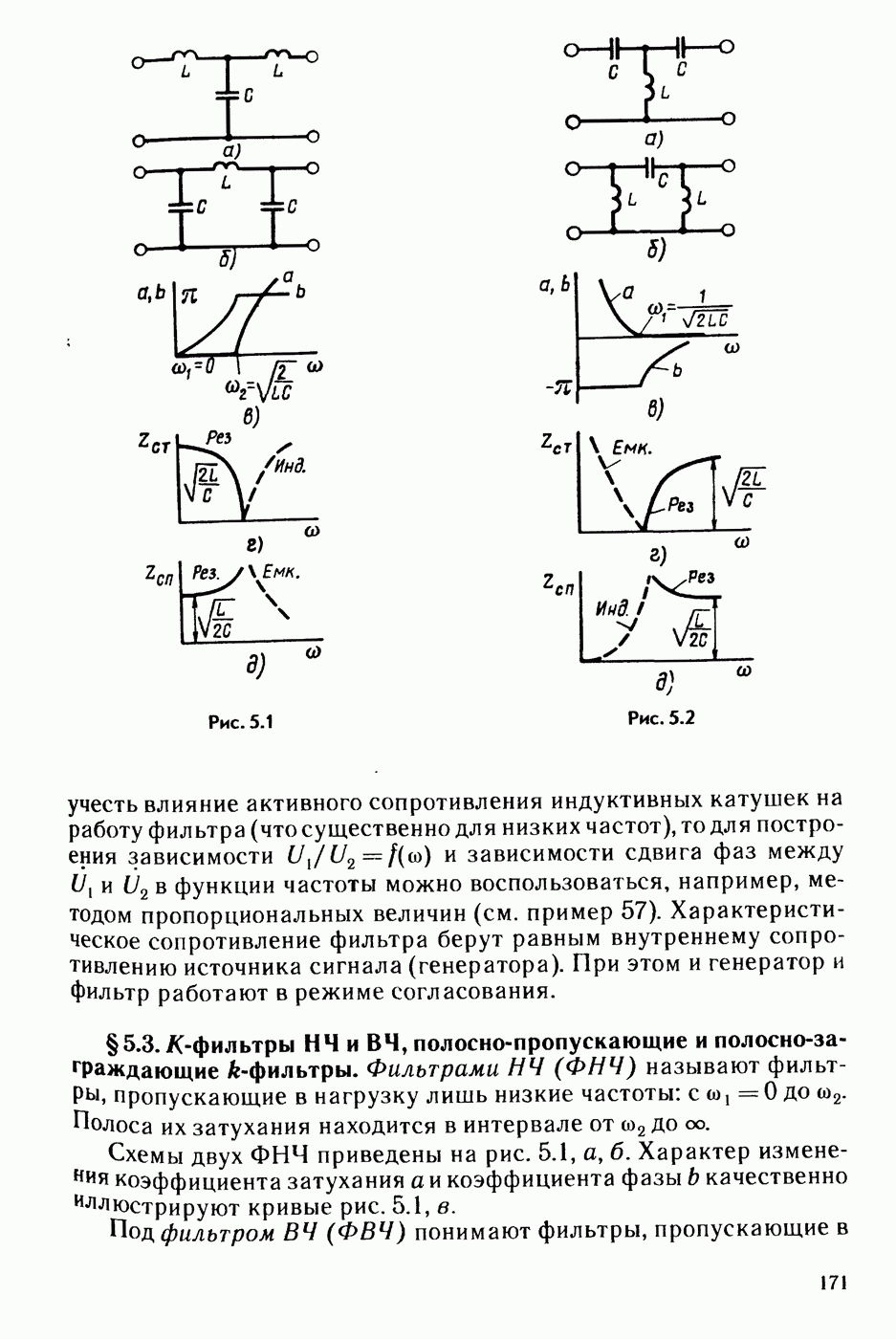
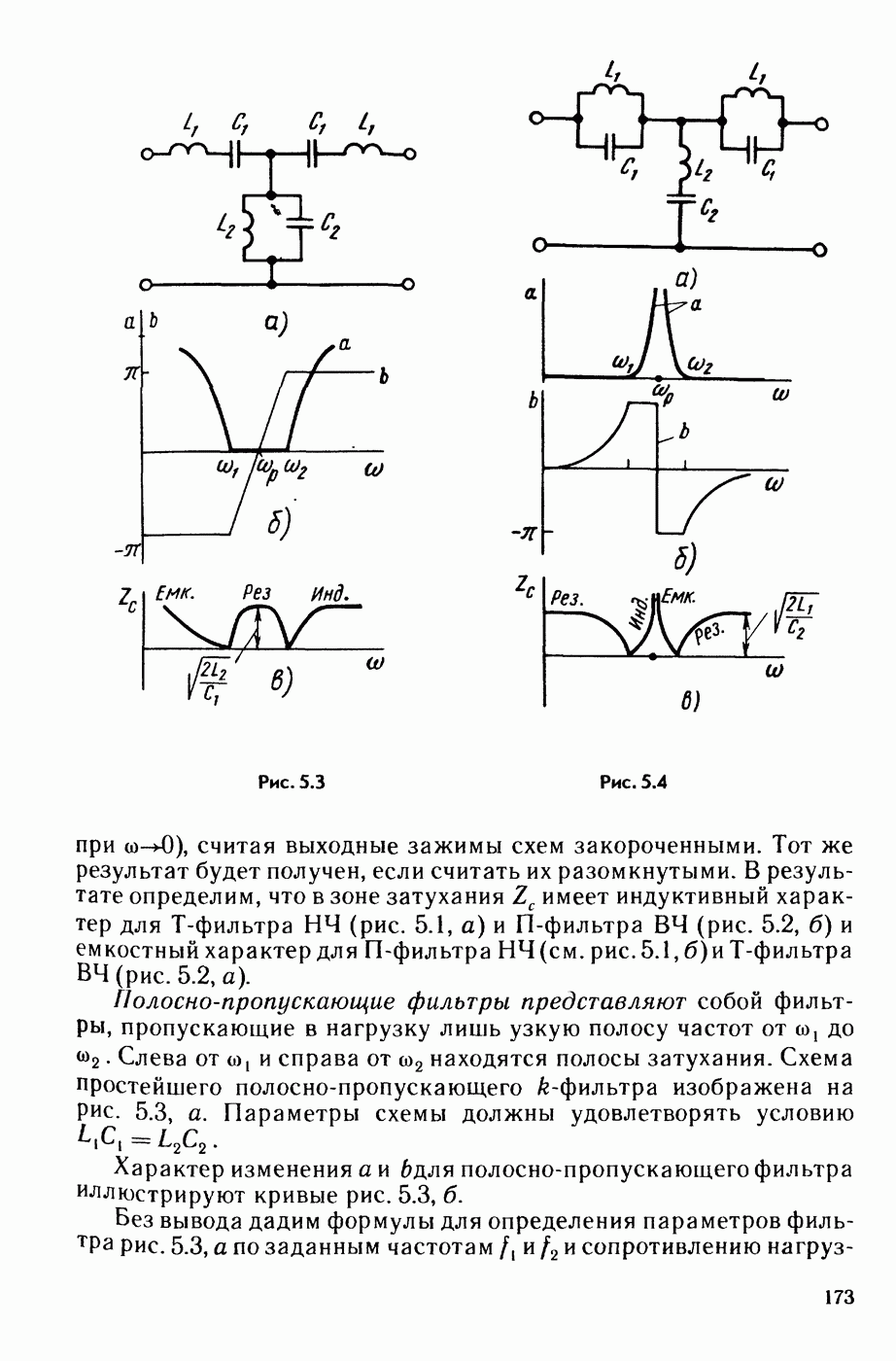
2) в полосе прозрачности характеристическое сопротивление К-фильтров (§ 5.3) активное, а в полосе затухания — чисто реактивное (индуктивное или емкостное).

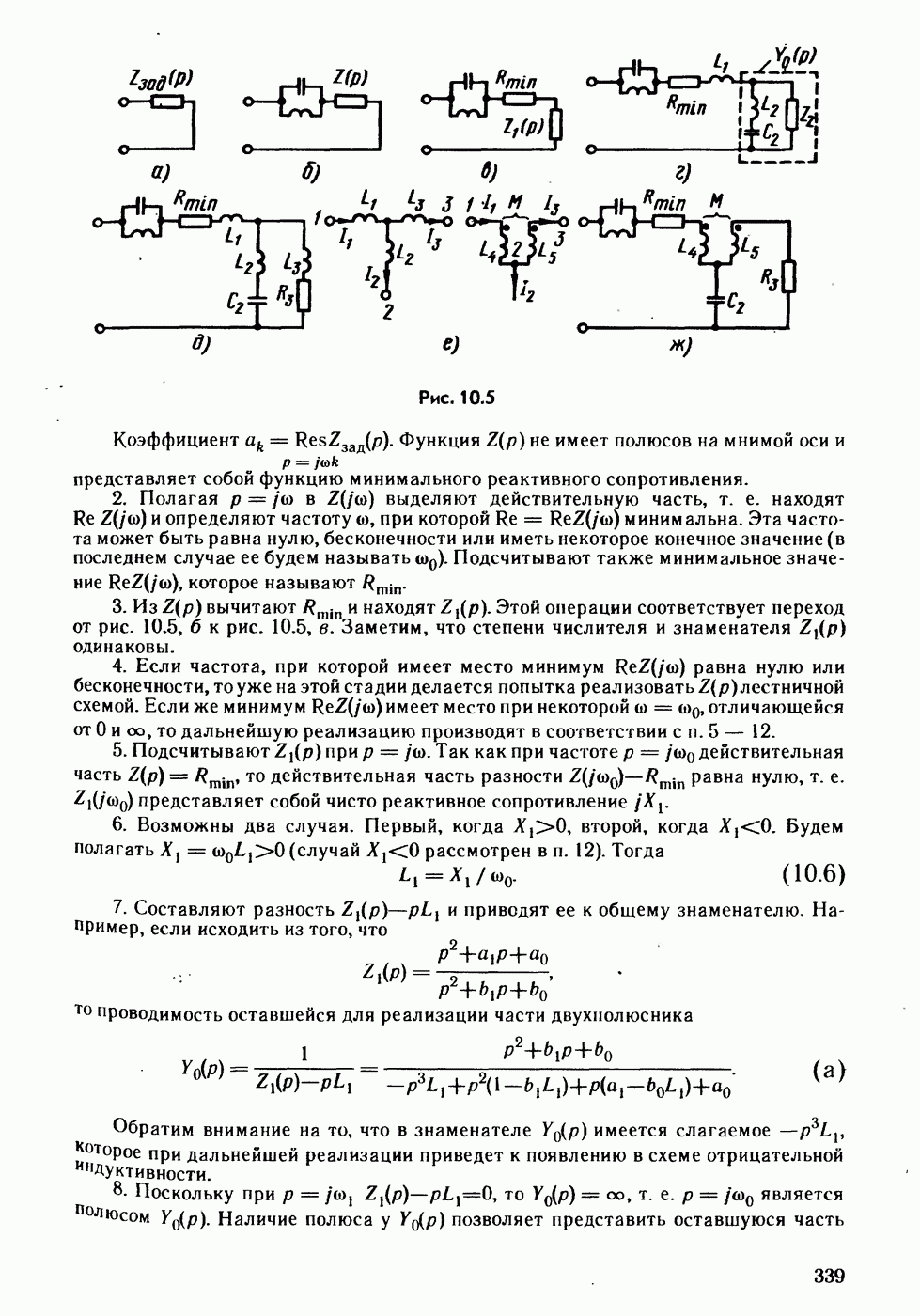
Рис. 5.1

Рис. 5.2
Если нагрузка фильтра не чисто активная или не согласована с характеристическим сопротивлением фильтра, а также требуется учесть влияние активного сопротивления индуктивных катушек на работу фильтра (что существенно для низких частот), то для построения зависимости  и зависимости сдвига фаз между и
и зависимости сдвига фаз между и  в функции частоты можно воспользоваться, например, методом пропорциональных величин (см. пример 57). Характеристическое сопротивление фильтра берут равным внутреннему сопротивлению источника сигнала (генератора). При этом и генератор и фильтр работают в режиме согласования.
в функции частоты можно воспользоваться, например, методом пропорциональных величин (см. пример 57). Характеристическое сопротивление фильтра берут равным внутреннему сопротивлению источника сигнала (генератора). При этом и генератор и фильтр работают в режиме согласования.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Часть I. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
- § 1.2. Интегральные и дифференциальные соотношения между основными величинами, характеризующими поле.
- § 1.3. Подразделение электротехнических задач на цепные и полевые.
- § 1.4. Конденсатор.
- § 1.5. Индуктивность. Явление самоиндукции.
- § 1.6. Взаимная индуктивность. Явление взаимоиндукции.
- § 1.7. Схемы замещения реальных электротехнических устройств.
- Вопросы для самопроверки
- Глава вторая. СВОЙСТВА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И МЕТОДЫ ИХ РАСЧЕТА. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
- § 2.1. Определение линейных и нелинейных электрических цепей.
- § 2.2. Источник ЭДС и источник тока.
- § 2.3. Неразветвленные и разветвленные электрические цепи.
- § 2.4. Напряжение на участке цепи.
- § 2.5. Закон Ома для участка цепи, не содержащего источника ЭДС.
- § 2.6. Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома.
- § 2.7. Законы Кирхгофа.
- § 2.8. Составление уравнений для расчета токов в схемах с помощью законов Кирхгофа.
- § 2.9. Заземление одной точки схемы.
- § 2.10. Потенциальная диаграмма.
- § 2.11. Энергетический баланс в электрических цепях.
- § 2.12. Метод пропорциональных величин.
- § 2.13. Метод контурных токов.
- § 2.14. Принцип наложения и метод наложения.
- § 2.15. Входные и взаимные проводимости ветвей. Входное сопротивление.
- § 2.16. Теорема взаимности.
- § 2.17. Теорема компенсации.
- § 2.18. Линейные соотношения в электрических цепях.
- § 2.19. Изменения токов ветвей, вызванные приращением сопротивления одной ветви (теорема вариаций).
- § 2.20. Замена нескольких параллельных ветвей, содержащих источники ЭДС и источники тока, одной эквивалентной.
- § 2.21. Метод двух узлов.
- § 2.22. Метод узловых потенциалов.
- § 2.23. Преобразование звезды в треугольник и треугольника в звезду.
- § 2.24. Перенос источников ЭДС и источников тока.
- § 2.25. Активный и пассивный двухполюсники.
- § 2.26. Метод эквивалентного генератора.
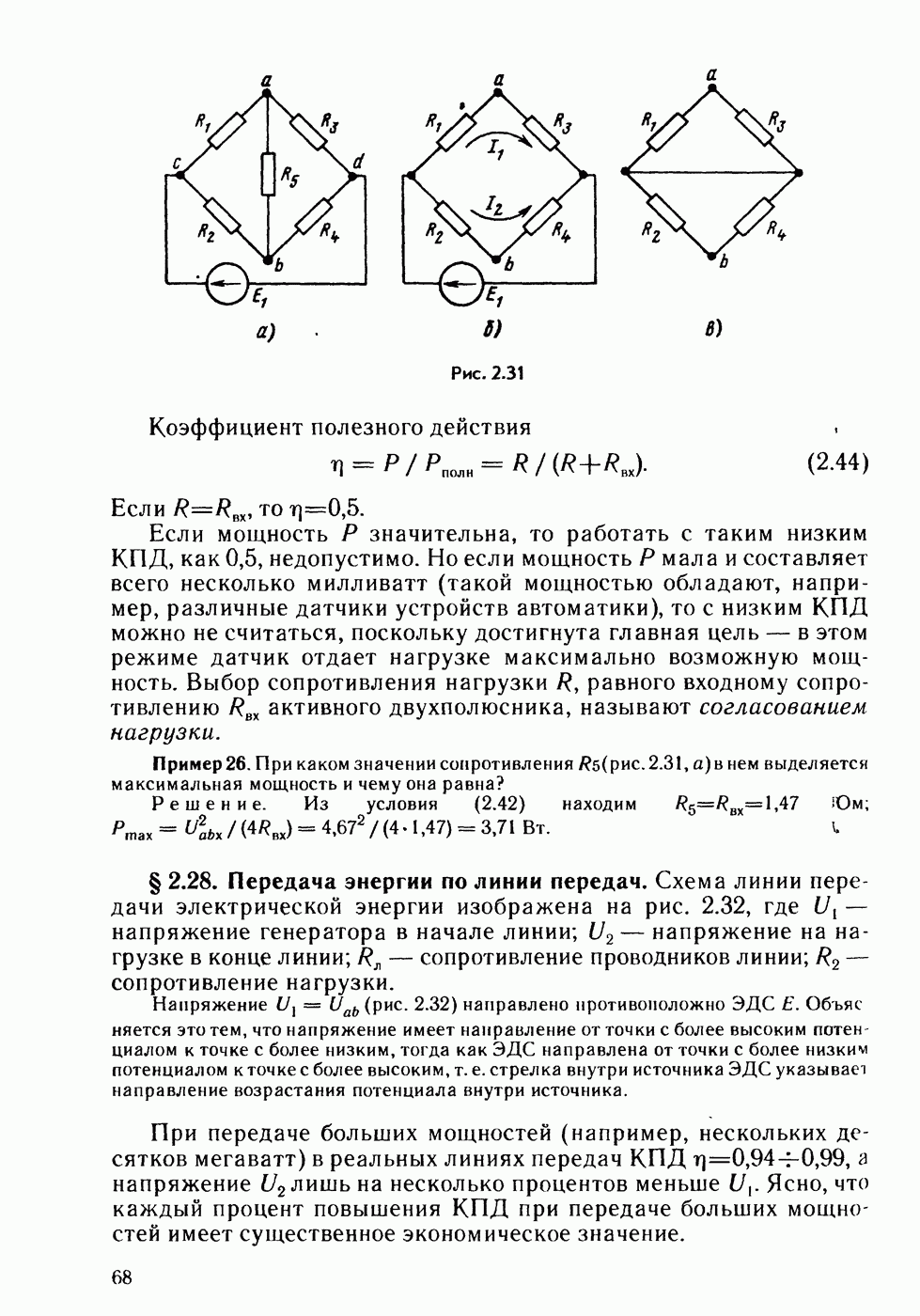
- § 2.27. Передача энергии от активного двухполюсника нагрузке.
- § 2.28. Передача энергии по линии передач.
- § 2.29. Некоторые выводы по методам расчета электрических цепей.
- § 2.30. Основные свойства матриц и простейшие операции с ними.
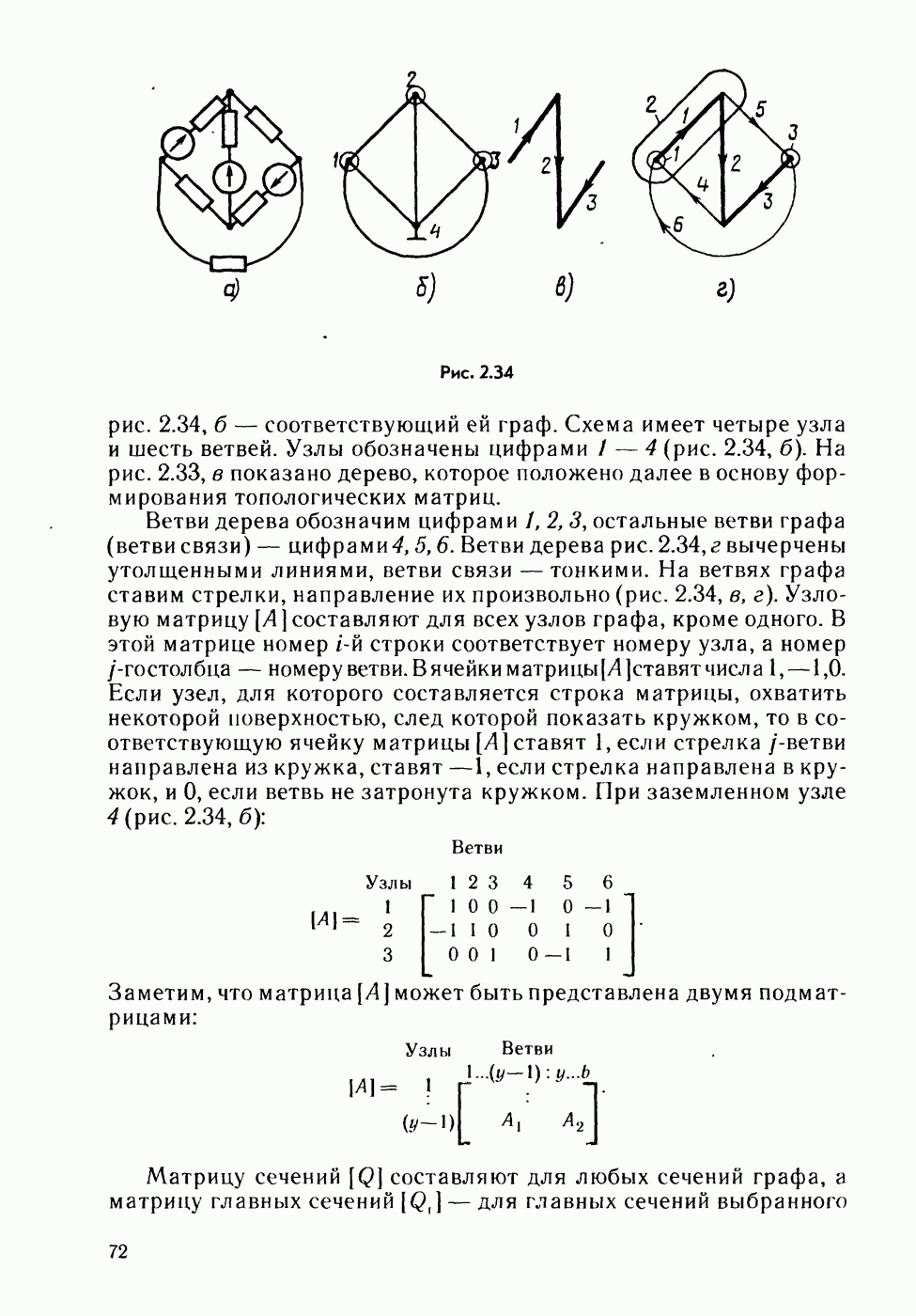
- § 2.31. Некоторые топологические понятия и топологические матрицы.
- § 2.32. Запись уравнений по законам Кирхгофа с помощью топологических матриц.
- § 2.33. Обобщенная ветвь электрической цепи.
- § 2.34. Вывод уравнений метода контурных токов с помощью топологических матриц.
- § 2.35. Вывод уравнений метода узловых потенциалов с помощью топологических матриц.
- § 2.36. Соотношения между топологическими матрицами.
- § 2.37. Сопоставление матрично-топологического и традиционного направлений теории цепей.
- Вопросы для самопроверки
- Глава третья. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА
- § 3.1. Синусоидальный ток и основные характеризующие его величины.
- § 3.2. Среднее и действующее значения синусоидально изменяющейся величины.
- § 3.3. Коэффициент амплитуды и коэффициент формы.
- § 3.4. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости. Комплексная амплитуда. Комплекс действующего значения.
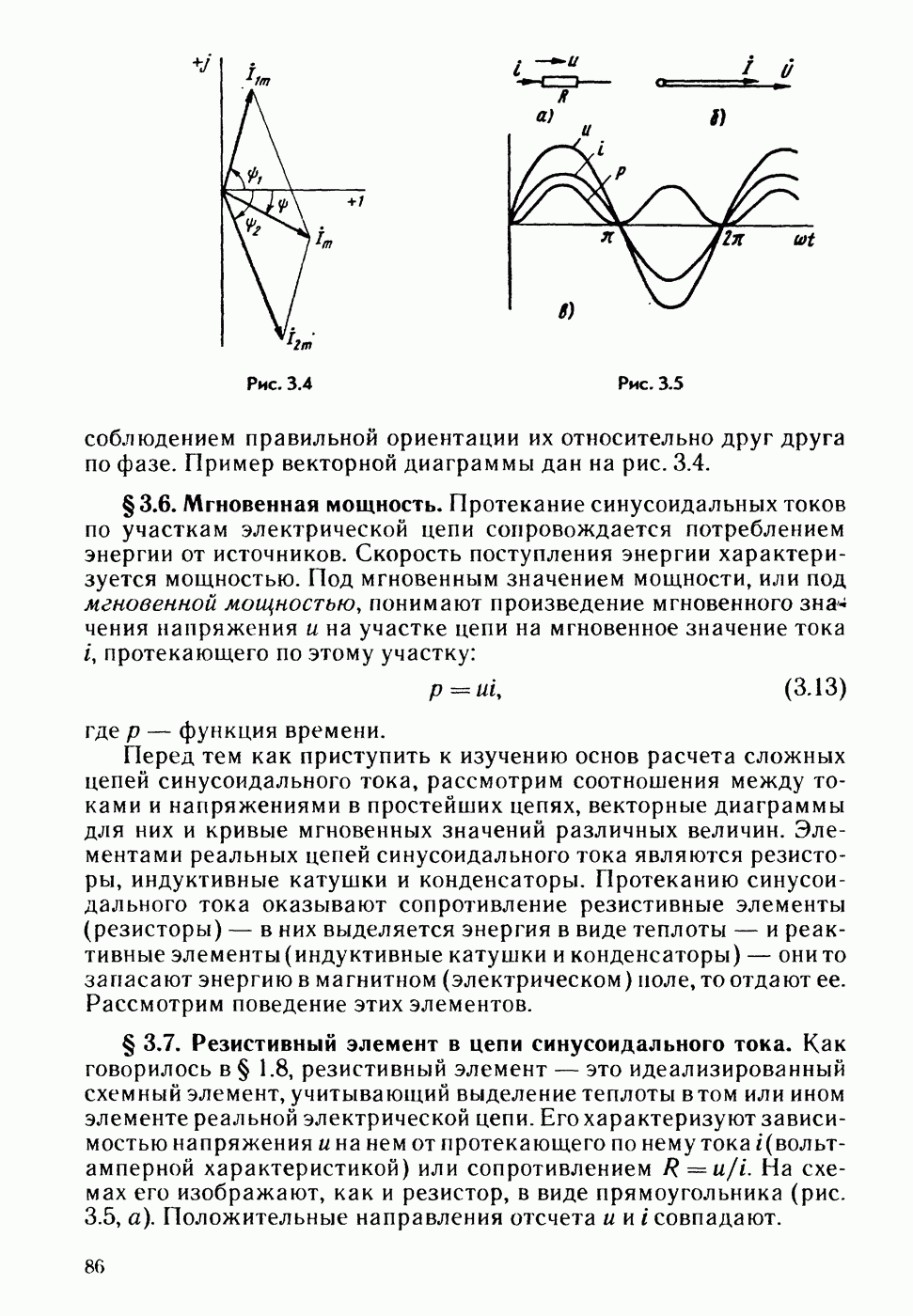
- § 3.5. Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма.
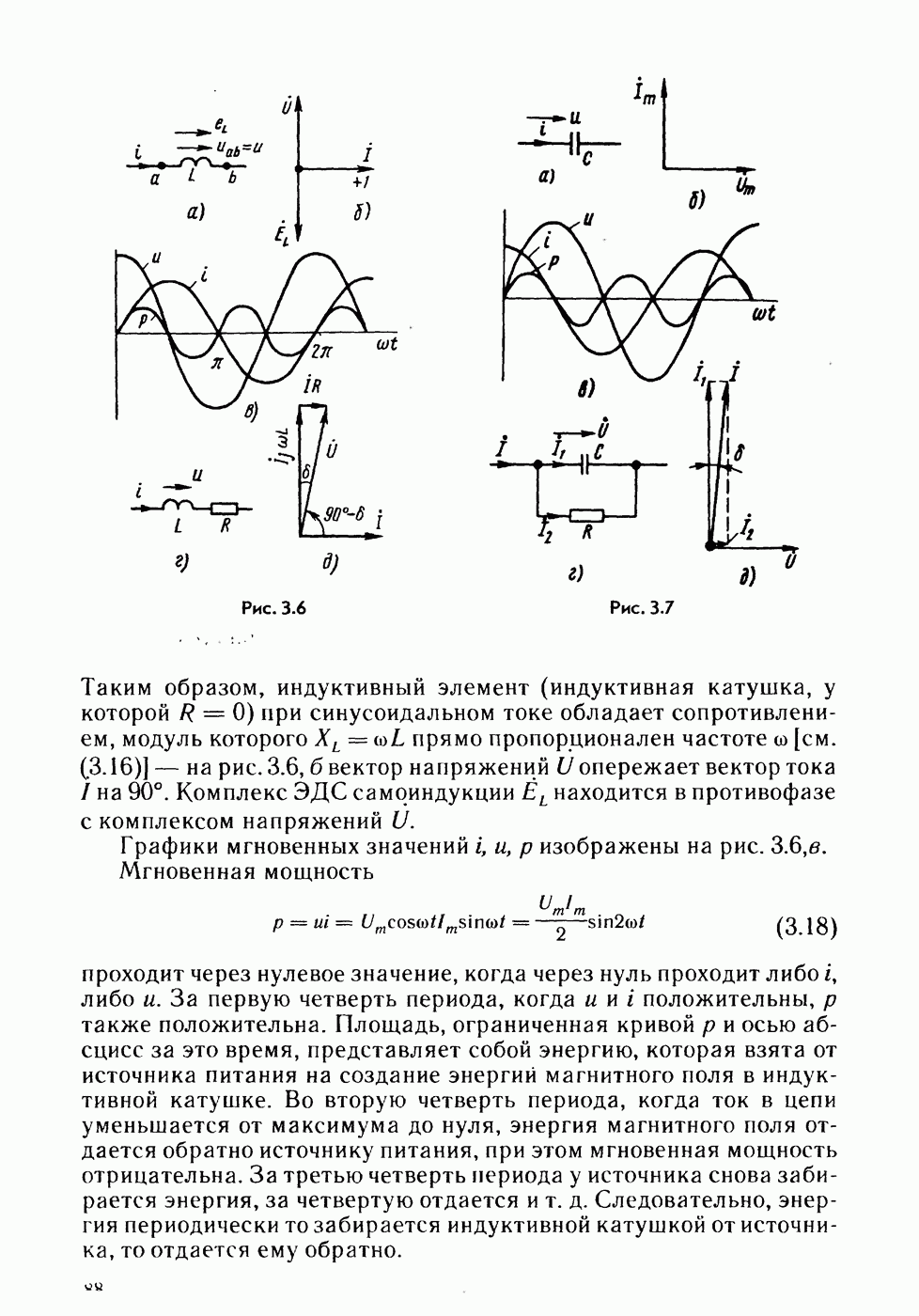
- § 3.6. Мгновенная мощность.
- § 3.7. Резистивный элемент в цепи синусоидального тока.
- § 3.8. Индуктивный элемент в цепи синусоидального тока.
- § 3.9. Емкостный элемент в цепи синусоидального тока.
- § 3.10. Умножение вектора на j и —j.
- § 3.11. Основы символического метода расчета цепей синусоидального тока.
- § 3.12. Комплексное сопротивление. Закон Ома для цепи синусоидального тока.
- § 3.13. Комплексная проводимость.
- § 3.14. Треугольник сопротивлений и треугольник проводимостей.
- § 3.15. Работа с комплексными числами.
- § 3.16. Законы Кирхгофа в символической форме записи.
- § 3.17. Применение к расчету цепей синусоидального тока методов, рассмотренных в главе «Электрические цепи постоянного тока».
- § 3.18. Применение векторных диаграмм при расчете электрических цепей синусоидального тока.
- § 3.19. Изображение разности потенциалов на комплексной плоскости.
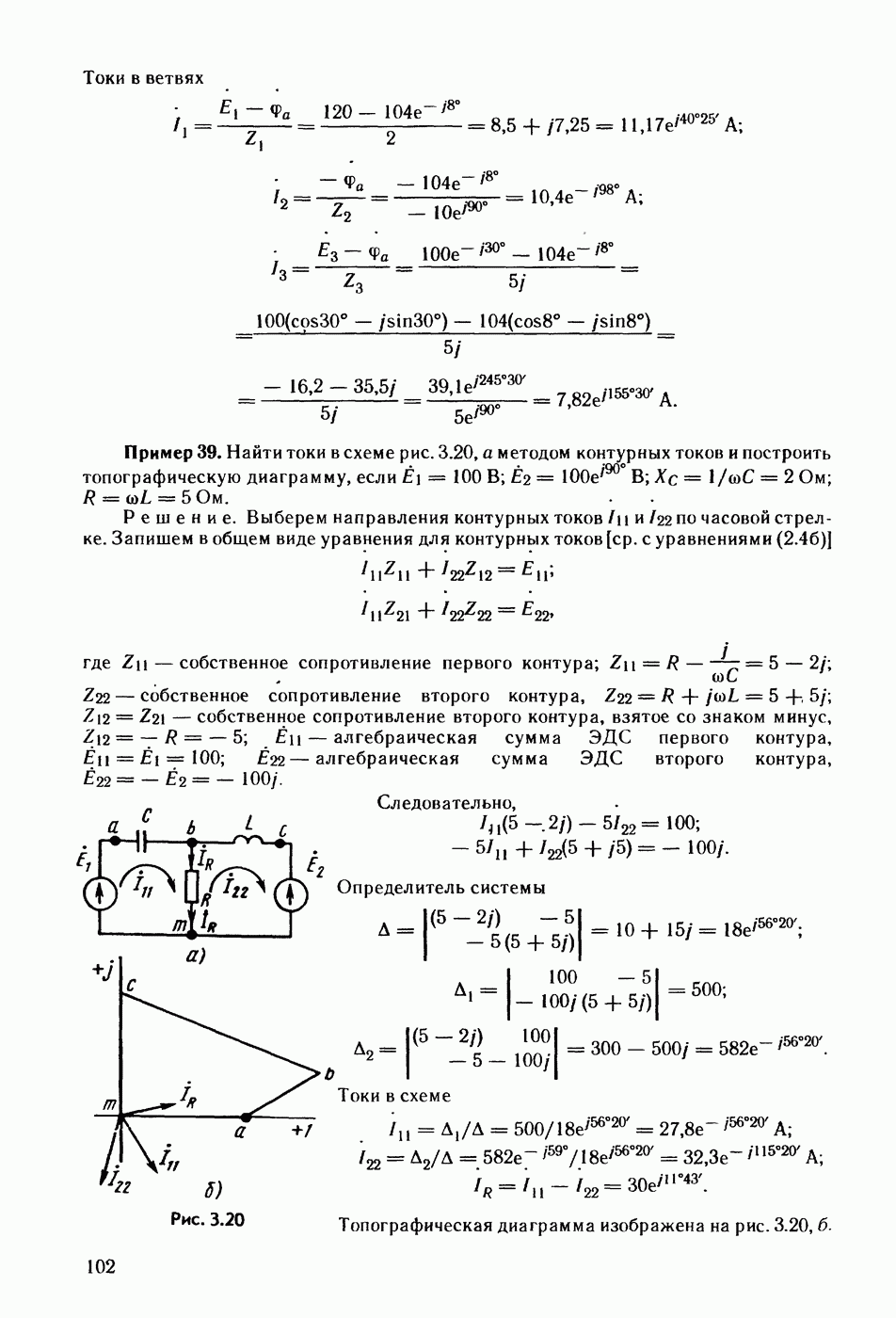
- § 3.20. Топографическая диаграмма.
- § 3.21. Активная, реактивная и полная мощности.
- § 3.22. Выражение мощности в комплексной форме записи.
- § 3.23. Измерение мощности ваттметром.
- § 3.24. Двухполюсник в цепи синусоидального тока.
- § 3.25. Резонансный режим работы двухполюсника.
- § 3.26. Резонанс токов.
- § 3.27. Компенсация сдвига фаз.
- § 3.28. Резонанс напряжений.
- § 3.29. Исследование работы схемы рис. 3.26, а при изменении частоты и индуктивности.
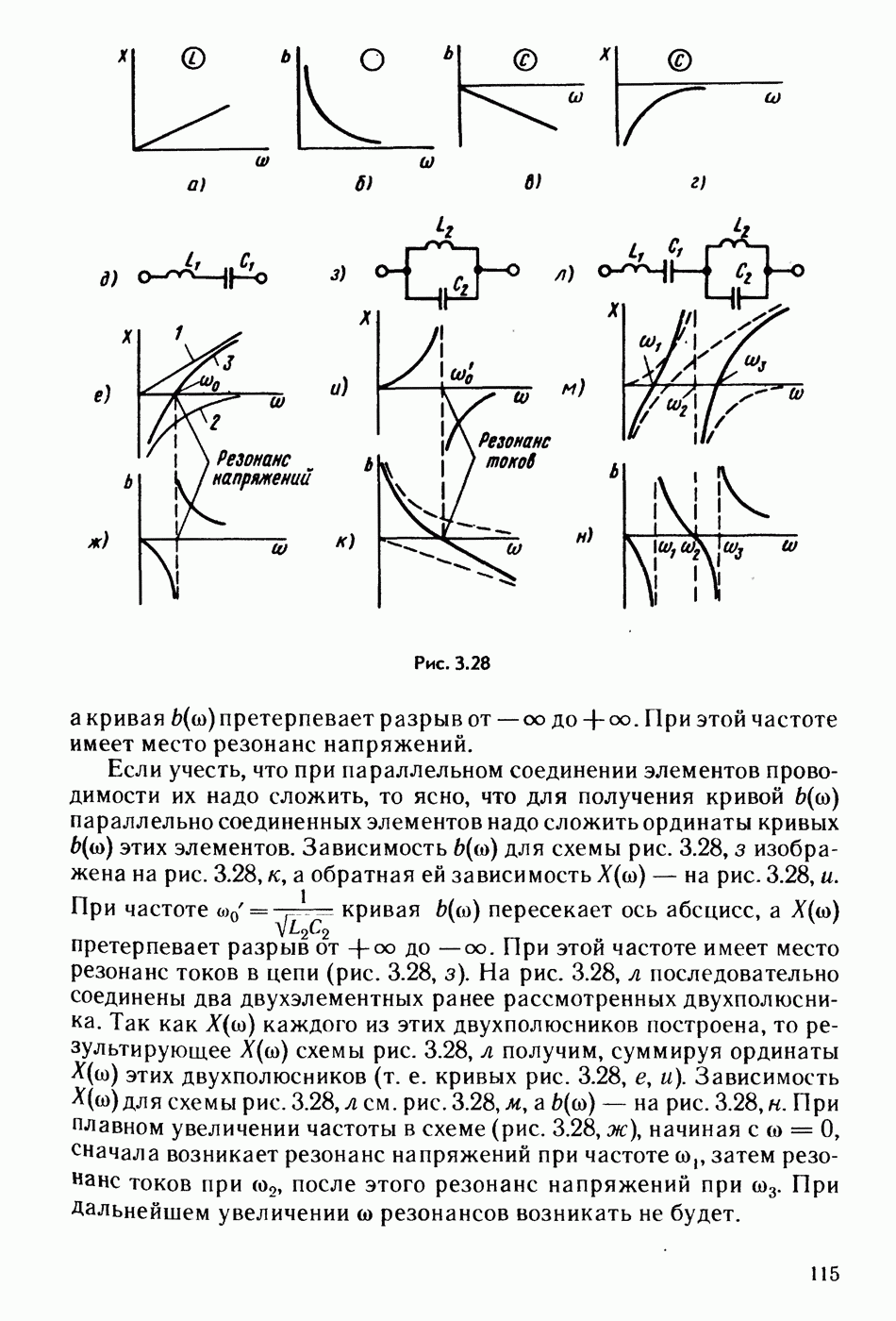
- § 3.30. Частотные характеристики двухполюсников.
- § 3.31. Канонические схемы. Эквивалентные двухполюсники.
- § 3.32. Передача энергии от активного двухполюсника нагрузке.
- § 3.33. Согласующий трансформатор.
- § 3.34. Идеальный трансформатор.
- § 3.35. Падение и потеря напряжения в линии передачи энергии.
- § 3.36. Расчет электрических цепей при наличии в них магнитносвязанных катушек.
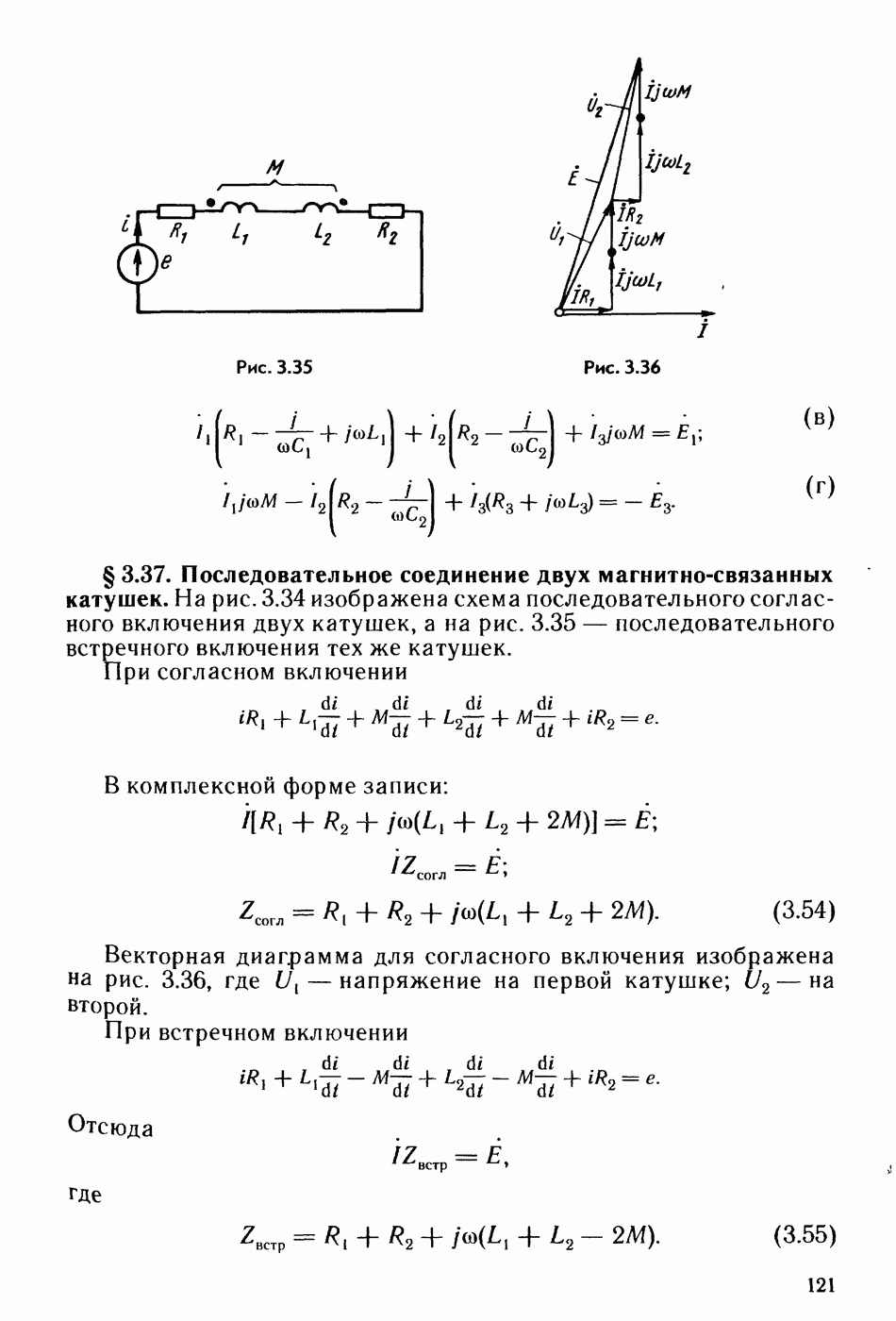
- § 3.37. Последовательное соединение двух магнитно-связанных катушек.
- § 3.38. Определение взаимной индуктивности опытным путем.
- § 3.39. Трансформатор. Вносимое сопротивление.
- § 3.40. Резонанс в магнитно-связанных колебательных контурах.
- § 3.41. «Развязывание» магнитно-связанных цепей.
- § 3.42. Теорема о балансе активных и реактивных мощностей (теорема Лонжевена).
- § 3.43. Теорема Теллегена.
- § 3.44. Определение дуальной цепи.
- § 3.45. Преобразование исходной схемы в дуальную.
- Вопросы для самопроверки
- Глава четвертая. ЧЕТЫРЕХПОЛЮСНИКИ. ЦЕПИ С УПРАВЛЯЕМЫМИ ИСТОЧНИКАМИ. КРУГОВЫЕ ДИАГРАММЫ
- § 4.1. Определение четырехполюсника.
- § 4.2. Шесть форм записи уравнений четырехполюсника.
- § 4.3. Вывод уравнений в А-форме.
- § 4.4. Определение коэффициентов A-формы записи уравнений четырехполюсника.
- § 4.5. Т- и П-схемы замещения пассивного четырехполюсника.
- § 4.6. Определение коэффициентов Y-, Z-, G- и H-форм записи уравнений четырехполюсника.
- § 4.7. Определение коэффициентов одной формы уравнений через коэффициенты другой формы.
- § 4.8. Применение различных форм записи уравнений четырехполюсника. Соединения четырехполюсников. Условия регулярности.
- § 4.9. Характеристические и повторные сопротивления четырехполюсников.
- § 4.10. Постоянная передача и единицы измерения затухания.
- § 4.11. Уравнения четырехполюсника, записанные через гиперболические функции.
- § 4.12. Конвертор и инвертор сопротивления.
- § 4.13. Гиратор.
- § 4.14. Операционный усилитель.
- § 4.15. Управляемые источники напряжения (тока).
- § 4.16. Активный четырехполюсник.
- § 4.17. Многополюсник.
- § 4.18. Построение дуги окружности по хорде и вписанному углу.
- § 4.19. Уравнение дуги окружности в векторной форме записи.
- § 4.20. Круговые диаграммы.
- § 4.21. Круговая диаграмма тока двух последовательно соединенных сопротивлений.
- § 4.22. Круговая диаграмма напряжения двух последовательно соединенных сопротивлений.
- § 4.23. Круговая диаграмма тока активного двухполюсника.
- § 4.24. Круговая диаграмма напряжения четырехполюсника.
- § 4.25. Линейные диаграммы.
- Вопросы для самопроверки
- Глава пятая. ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ
- § 5.1. Назначение и типы фильтров.
- § 5.2. Основы теории k-фильтров.
- § 5.3. K-фильтры НЧ и ВЧ, полосно-пропускающие и полосно-заграждающие k-фильтры.
- § 5.4. Качественное определение k-фильтра.
- § 5.5. Основы теории m-фильтров. Каскадное включение фильтров.
- § 5.6. RC-фильтры.
- § 5.7. Активные RС-фильтры.
- § 5.8. Передаточные функции активных RС-фильтров в нормированном виде.
- § 5.9. Получение передаточной функции низкочастотного активного RС-фильтра, выбор схемы и определение ее параметров.
- § 5.10. Получение передаточной функции полосно-пропускающего активного RС-фильтра.
- Вопросы для самопроверки
- Глава шестая. ТРЕХФАЗНЫЕ ЦЕПИ
- § 6.1. Трехфазная система ЭДС.
- § 6.2. Принцип работы трехфазного машинного генератора.
- § 6.3. Трехфазная цепь. Расширение понятия фазы.
- § 6.4. Основные схемы соединения трехфазных цепей, определение линейных и фазовых величин.
- § 6.5. Соотношения между линейными и фазовыми напряжениями и токами.
- § 6.6. Преимущества трехфазных систем.
- § 6.7. Расчет трехфазных цепей.
- § 6.8. Соединение звезда — звезда с нулевым проводом.
- § 6.9. Соединение нагрузки треугольником.
- § 6.10 Оператор а трехфазной системы.
- § 6.11 Соединение звезда — звезда без нулевого провода.
- § 6.12. Трехфазные цепи при наличии взаимоиндукции.
- § 6.13. Активная, реактивная и полная мощности трехфазной системы.
- § 6.14. Измерение активной мощности в трехфазной системе.
- § 6.15. Круговые и линейные диаграммы в трехфазных цепях.
- § 6.16. Указатель последовательности чередования фаз.
- § 6.17. Магнитное поле катушки с синусоидальным током.
- § 6.18. Получение кругового вращающегося магнитного поля.
- § 6.19. Принцип работы асинхронного двигателя.
- § 6.20. Разложение несимметричной системы на системы прямой, обратной и нулевой последовательностей фаз.
- § 6.21. Основные положения метода симметричных составляющих.
- Вопросы для самопроверки
- Глава седьмая. ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 7.1. Определение периодических несинусоидальных токов и напряжений.
- § 7.2. Изображение несинусоидальных токов и напряжений с помощью рядов Фурье.
- § 7.3. Некоторые свойства периодических кривых, обладающих симметрией.
- § 7.4. О разложении вряд Фурье кривых геометрически правильной и неправильной форм.
- § 7.5. Графический (графоаналитический) метод определения гармоник ряда Фурье.
- § 7.6. Расчет токов и напряжений при несинусоидальных источниках питания.
- § 7.7. Резонансные явления при несинусоидальных токах.
- § 7.8. Действующие значения несинусоидального тока и несинусоидального напряжения.
- § 7.9. Среднее по модулю значение несинусоидальной функции.
- § 7.10. Величины, которые измеряют амперметры и вольтметры при несинусоидальных токах.
- § 7.11. Активная и полная мощности несинусоидального тока.
- § 7.12. Замена несинусоидальных токов и напряжений эквивалентными синусоидальными.
- § 7.13. Особенности работы трехфазных систем, вызываемых гармониками, кратными трем.
- § 7.14. Биения.
- § 7.15. Модулированные колебания.
- § 7.16. Расчет линейных цепей при воздействии модулированных колебаний.
- Вопросы для самопроверки
- Глава восьмая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 8.1. Определение переходных процессов.
- § 8.2. Приведение задачи о переходном процессе к решению линейного дифференциального уравнения с постоянными коэффициентами.
- § 8.3. Принужденные и свободные составляющие токов и напряжений.
- § 8.4. Обоснование невозможности скачка тока через индуктивную катушку и скачка напряжения на конденсаторе.
- § 8.5. Первый закон (правило) коммутации.
- § 8.6. Второй закон (правило) коммутации.
- § 8.7. Начальные значения величин.
- § 8.8. Независимые и зависимые (послекоммутационные) начальные значения.
- § 8.9. Нулевые и ненулевые начальные условия.
- § 8.10. Составление уравнений для свободных токов и напряжений.
- § 8.11. Алгебраизация системы уравнений для свободных токов.
- § 8.12. Составление характеристического уравнения системы.
- § 8.13. Составление характеристического уравнения путем использования выражения для входного сопротивления цепи на переменном токе.
- § 8.14. Основные и неосновные зависимые начальные значения.
- § 8.15. Определение степени характеристического уравнения.
- § 8.16. Свойства корней характеристического уравнения.
- § 8.17. Отрицательные зшаки действительных частей корней характеристических уравнений.
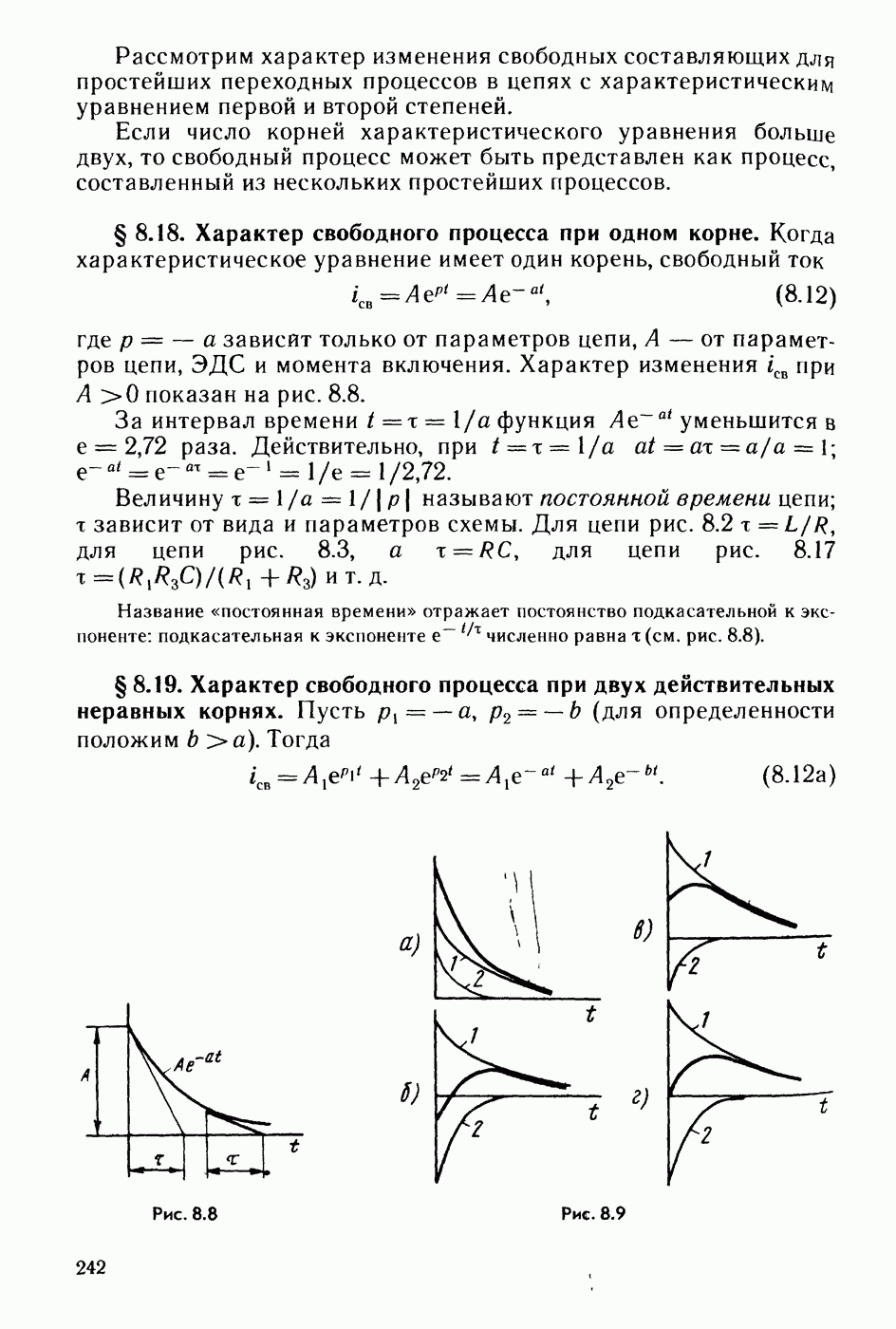
- § 8.18. Характер свободного процесса при одном корне.
- § 8.19. Характер свободного процесса при двух действительных неравных корнях.
- § 8.20. Характер свободного процесса при двух равных корнях.
- § 8.21. Характер свободного процесса при двух комплексно-сопряженных корнях.
- § 8.22. Некоторые особенности переходных процессов.
- § 8.23. Переходные процессы, сопровождающиеся электрической искрой (дугой).
- § 8.24. Опасные перенапряжения, вызываемые размыканием ветвей в цепях, содержащих индуктивные катушки.
- § 8.25. Общая характеристика методов анализа переходных процессов в линейных электрических цепях.
- § 8.26. Определение классического метода расчета переходных процессов.
- § 8.27. Определение постоянных интегрирования в классическом методе.
- § 8.28. О переходных процессах, при макроскопическом рассмотрении которых не выполняются законы коммутации.
- § 8.29. Логарифм как изображение числа.
- § 8.30. Комплексные изображения синусоидальных функций.
- § 8.31. Введение в операторный метод.
- § 8.32. Преобразование Лапласа.
- § 8.33. Изображение постоянной.
- § 8.34. Изображение показательной функции exp(at).
- § 8.35. Изображение первой производной.
- § 8.36. Изображение напряжения на индуктивном элементе.
- § 8.37. Изображение второй производной.
- § 8.38. Изображение интеграла.
- § 8.39. Изображение напряжения на конденсаторе.
- § 8.40. Некоторые теоремы и предельные соотношения.
- § 8.41. Закон Ома в операторной форме. Внутренние ЭДС.
- § 8.42. Первый закон Кирхгофа в операторной форме.
- § 8.43. Второй закон Кирхгофа в операторной форме.
- § 8.44. Составление уравнений для изображений путем использования методов, рассмотренных в третьей главе.
- § 8.45. Последовательность расчета операторным методом.
- § 8.46. Изображение функции времени в виде отношения N(p)/M(p) двух полиномов по степеням p.
- § 8.47. Переход от изображения к функции времени.
- § 8.48. Разложение сложной дроби на простые.
- § 8.49. Формула разложения.
- § 8.50. Дополнения к операторному методу.
- § 8.51. Переходная проводимость.
- § 8.52. Понятие о переходной функции.
- § 8.53. Интеграл Дюамеля.
- § 8.54. Последовательность расчета с помощью интеграла Дюамеля.
- § 8.55. Применение интеграла Дюамеля при сложной форме напряжения.
- § 8.56. Сравнение различных методов расчета переходных процессов.
- § 8.57. Дифференцирование электрическим путем.
- § 8.58. Интегрирование электрическим путем.
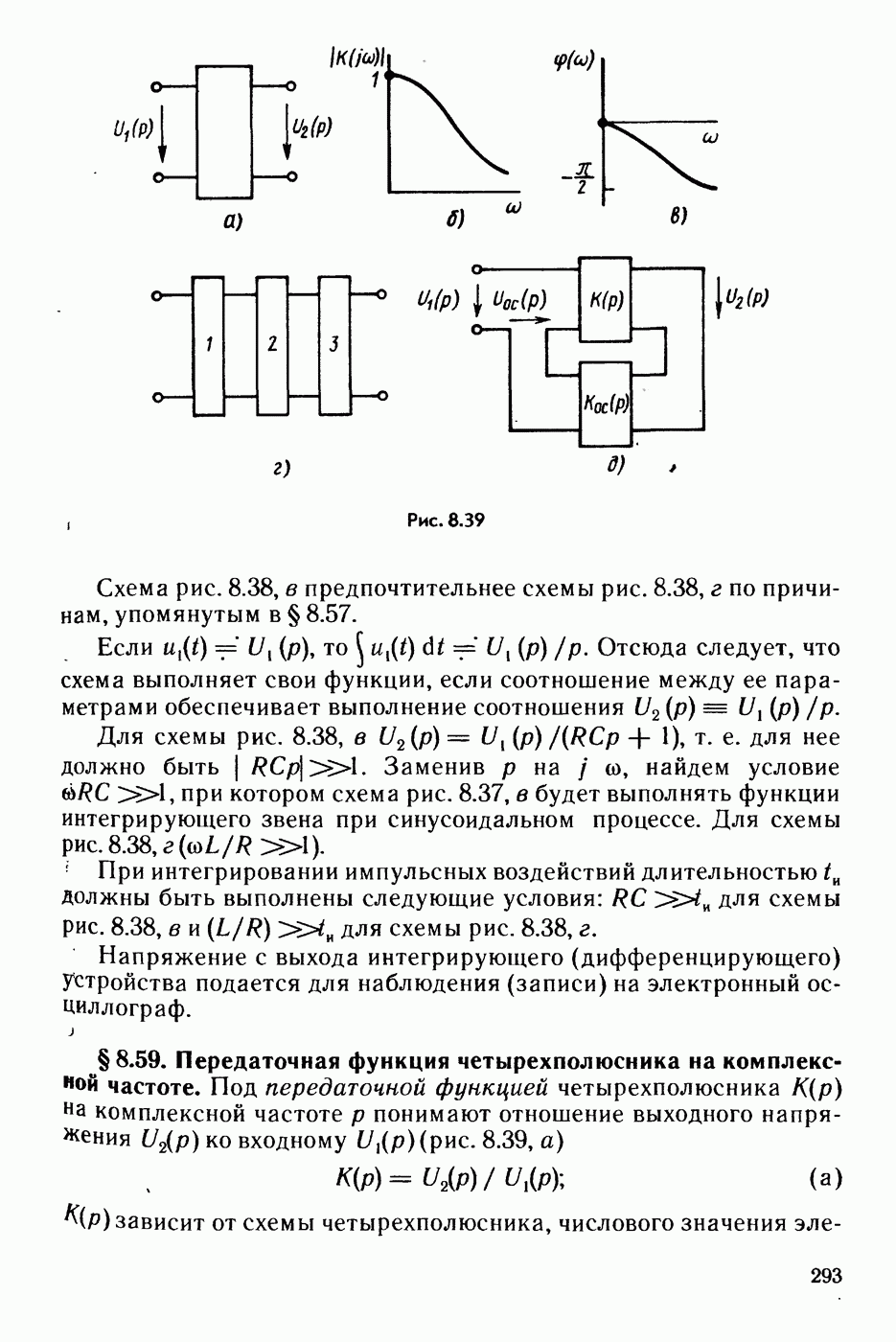
- § 8.59. Передаточная функция четырехполюсника на комплексной частоте.
- § 8.60. Переходные процессы при воздействии импульсов напряжения.
- § 8.61. Дельта-функция, единичная функция и их свойства. Импульсная переходная проводимость.
- § 8.62. Определение h(t) и h'(t) через K(р).
- § 8.63. Метод пространства состояний.
- § 8.64. Дополняющие двухполюсники.
- § 8.65. Системные функции и понятие о видах чувствительности.
- § 8.66. Обобщенные функции и их применение к расчету переходных процессов.
- § 8.67. Интеграл Дюамеля для огибающей.
- Вопросы для самопроверки
- Глава девятая. ИНТЕГРАЛ ФУРЬЕ. СПЕКТРАЛЬНЫЙ МЕТОД. СИГНАЛЫ
- § 9.1. Ряд Фурье в комплексной форме записи.
- § 9.2. Спектр функции и интеграл Фурье.
- § 9.3. Спектр функции, смещенной во времени. Спектр суммы функций времени.
- § 9.4. Теорема Рейли.
- § 9.5. Применение спектрального метода.
- § 9.6. Текущий спектр функции времени.
- § 9.7. Основные сведения по теории сигналов.
- § 9.8. Узкополосный и аналитический сигналы.
- § 9.9. Частотный спектр аналитического сигнала.
- § 9.10. Прямое и обратное преобразование Гильберта.
- Вопросы для самопроверки
- Глава десятая. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- § 10.1. Характеристика синтеза.
- § 10.2. Условия, которым должны удовлетворять входные сопротивления двухполюсников.
- § 10.3. Реализация двухполюсников лестничной (цепной) схемой.
- § 10.4. Реализация двухполюсников путем последовательного выделения простейших составляющих.
- § 10.5. Метод Бруне.
- § 10.6. Понятие о минимально-фазовом и неминимально-фазовом четырехполюсниках.
- § 10.7. Синтез четырехполюсников Г-образными RC-схемами.
- § 10.8. Четырехполюсник для фазовой коррекции.
- § 10.9. Четырехполюсник для амплитудной коррекции.
- § 10.10. Аппроксимация частотных характеристик.
- Вопросы для самопроверки
- Глава одиннадцатая. УСТАНОВИВШИЕСЯ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- § 11.2. Составление дифференциальных уравнений для однородной линии с распределенными параметрами.
- § 11.3. Решение уравнений линии с распределенными параметрами при установившемся синусоидальном процессе.
- § 11.4. Постоянная распространения и волновое сопротивление.
- § 11.5. Формулы для определения комплексов напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии.
- § 11.6. Графическая интерпретация гиперболических синуса и косинуса от комплексного аргумента.
- § 11.7. Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии.
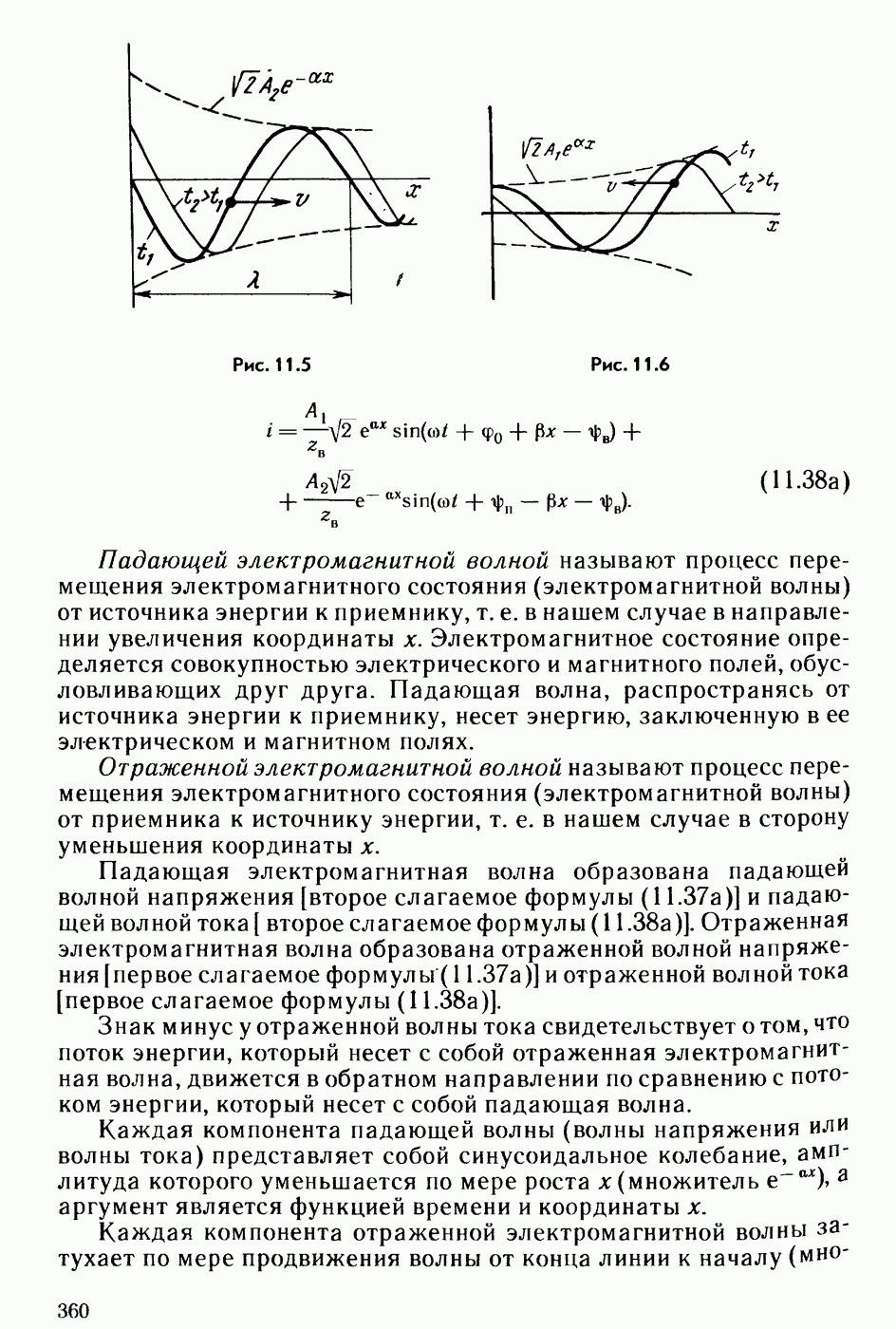
- § 11.8. Падающие и отраженные волны в линии.
- § 11.9. Коэффициент отражения.
- § 11.10. Фазовая скорость.
- § 11.11. Длина волны.
- § 11.12. Линия без искажений.
- § 11.13. Согласованная нагрузка.
- § 11.14. Определение напряжения и тока при согласованной нагрузке.
- § 11.15. Коэффициент полезного действия линии передачи при согласованной нагрузке.
- § 11.16. Входное сопротивление нагруженной линии.
- § 11.17. Определение напряжения и тока в линии без потерь.
- § 11.18. Входное сопротивление линии без потерь при холостом ходе.
- § 11.19. Входное сопротивление линии без потерь при коротком замыкании на конце линии.
- § 11.20. Входное сопротивление линии без потерь при реактивной нагрузке.
- § 11.21. Определение стоячих электромагнитных волн.
- § 11.22. Стоячие волны в линии без потерь при холостом ходе линии.
- § 11.23. Стоячие волны в линии без потерь при коротком замыкании на конце линии.
- § 11.24. Четвертьволновый трансформатор.
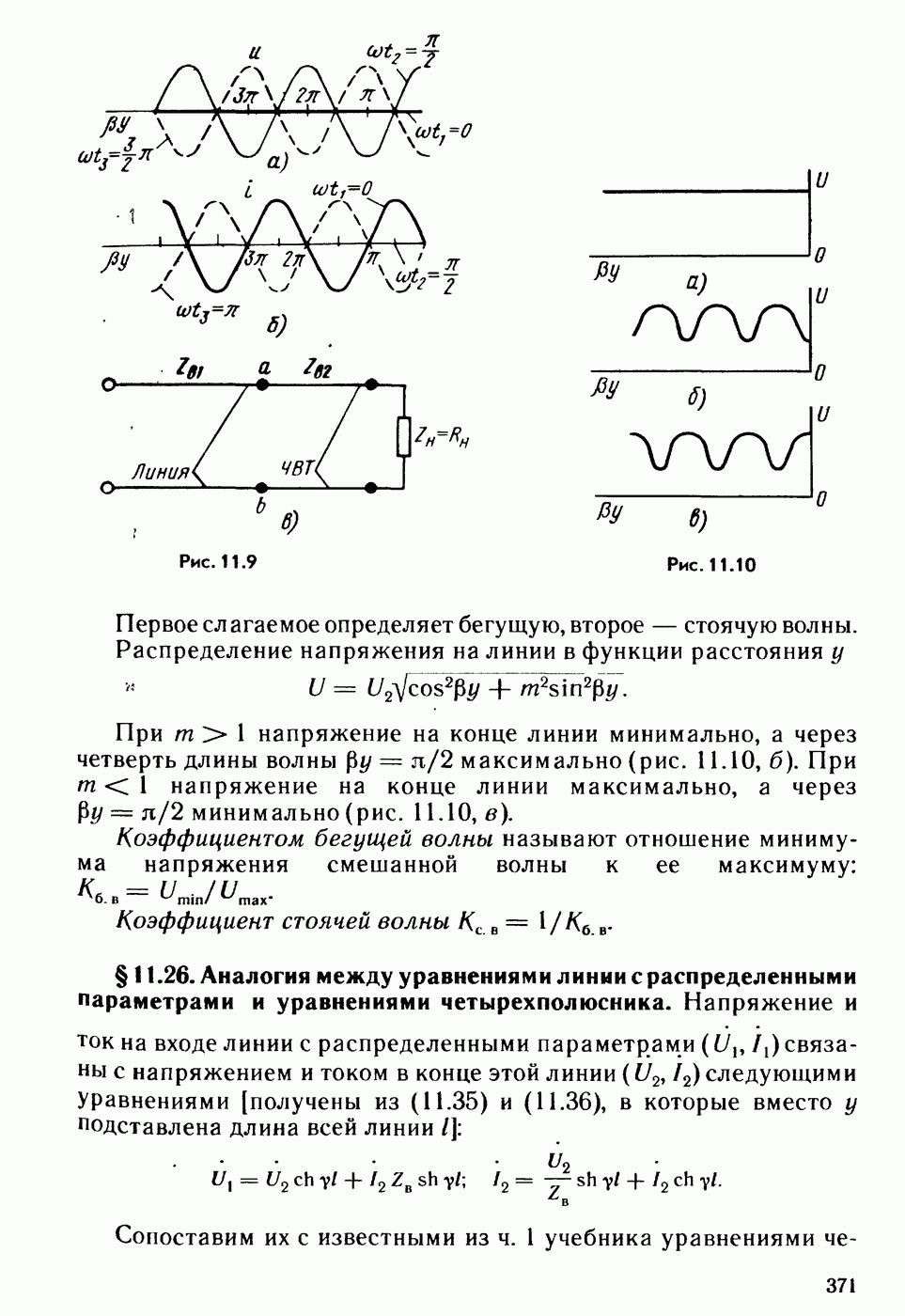
- § 11.25. Бегущие, стоячие и смешанные волны в линиях без потерь.
- § 11.26. Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника.
- § 11.27. Замена четырехполюсника эквивалентной ему линией с распределенными параметрами и обратная замена.
- § 11.28. Четырехполюсник заданного затухания.
- § 11.29. Цепная схема.
- Вопросы для самопроверки
- Глава двенадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- § 12.2. Исходные уравнения и их решение.
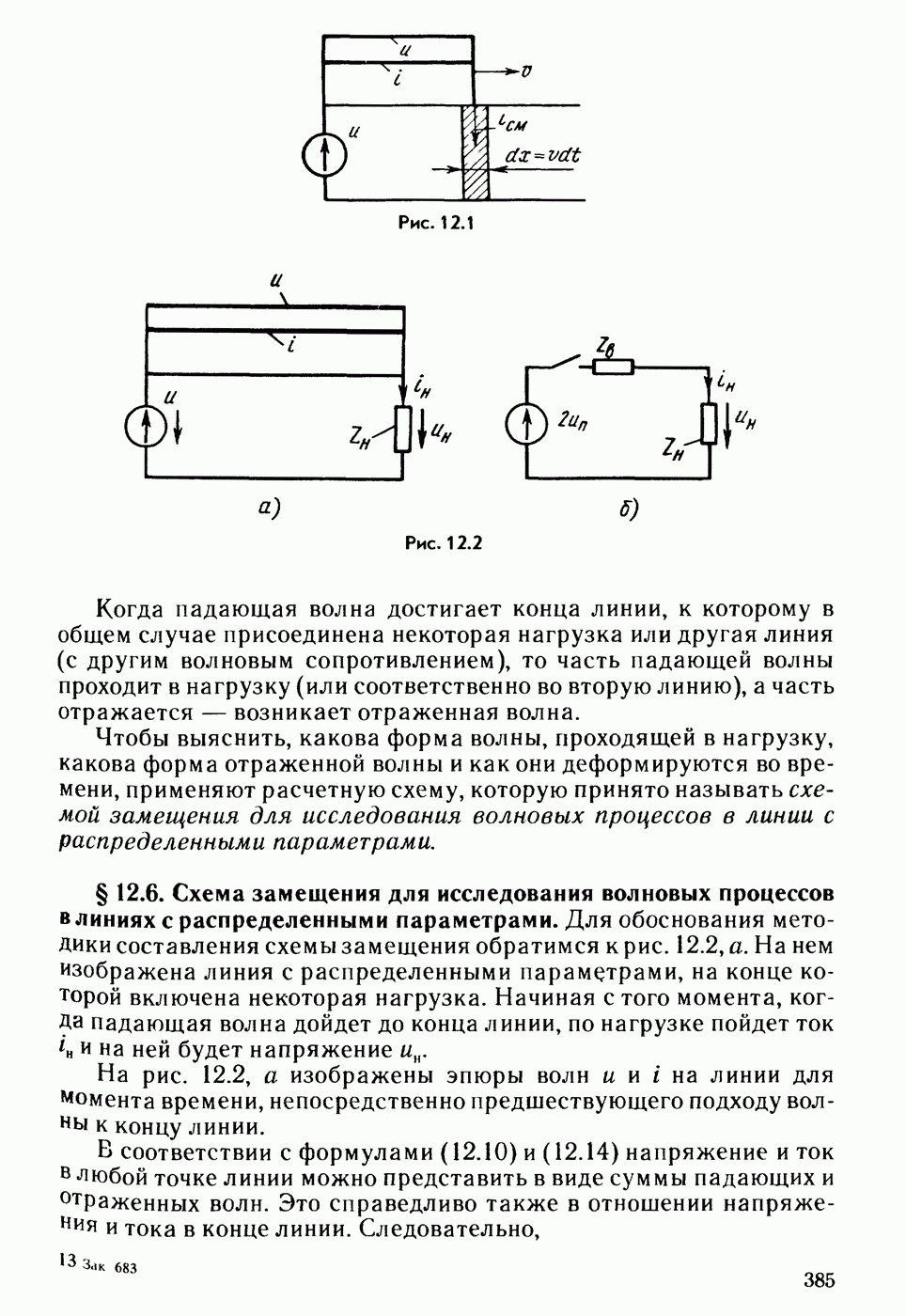
- § 12.3. Падающие и отраженные волны на линиях.
- § 12.4. Связь между функциями f1, f2 и функциями.
- § 12.5. Электромагнитные процессы при движении прямоугольной волны по линии.
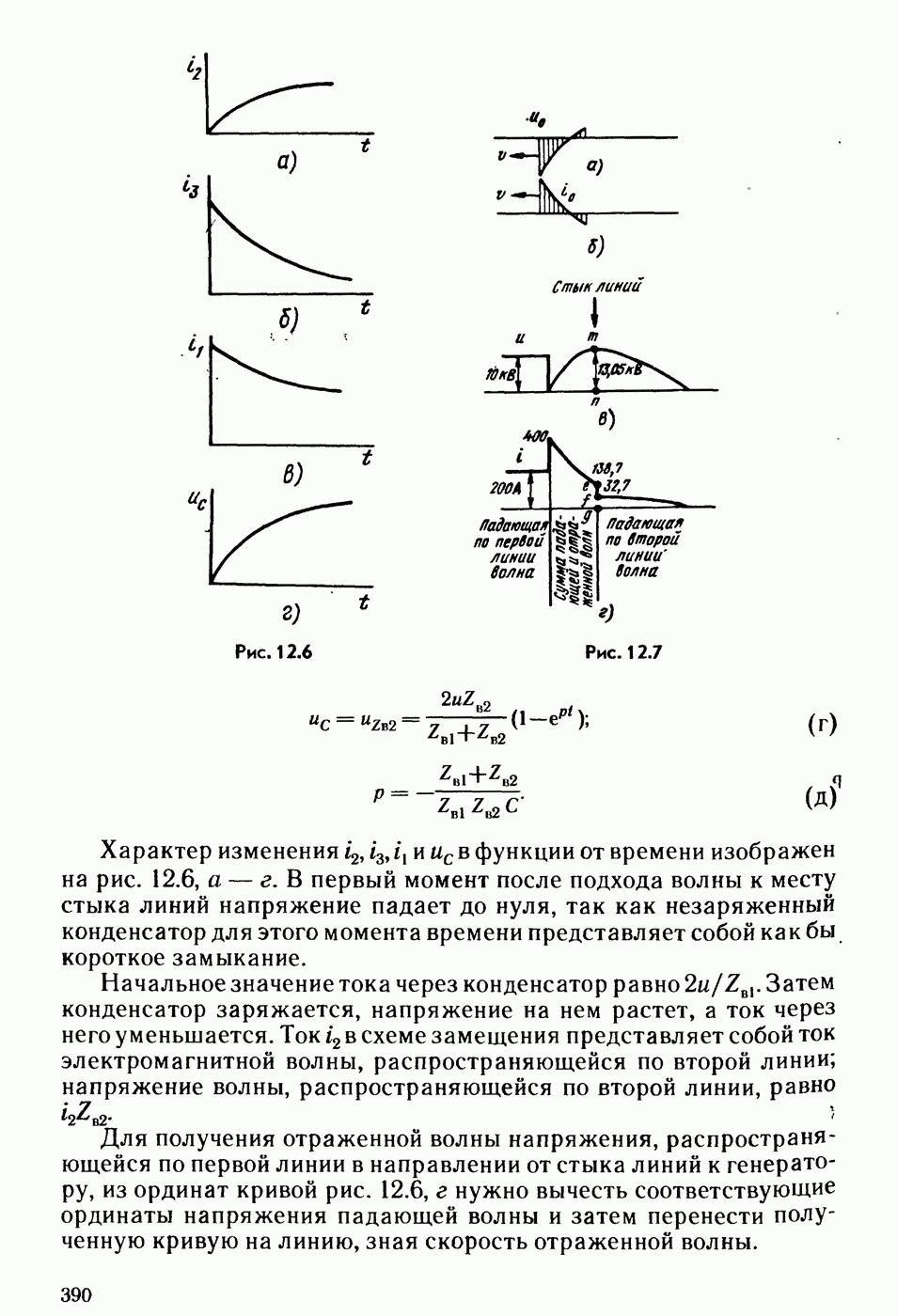
- § 12.6. Схема замещения для исследования волновых процессов в линиях с распределенными параметрами.
- § 12.7. Подключение разомкнутой на конце линии к источнику постоянного напряжения.
- § 12.8. Переходный процесс при подключении источника постоянного напряжения к двум последовательно соединенным линиям при наличии емкости в месте стыка линий.
- § 12.9. Линия задержки.
- § 12.10. Использование линий для формирования кратковременных импульсов.
- § 12.11. Исходные положения по применению операторного метода к расчету переходных процессов в линиях.
- § 12.12. Подключение линии без потерь конечной длины l, разомкнутой на конце, к источнику постоянного напряжения.
- § 12.13. Подключение линии без искаженйя конечной длины l, разомкнутой на конце, к источнику постоянного напряжения U.
- § 12.14. Подключение бесконечно протяженного кабеля без индуктивности и утечки к источнику постоянного напряжения U.
- § 12.15. Подключение бесконечно протяженной линии без утечки к источнику постоянного напряжения.
- Вопросы для самопроверки
- Часть II. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
- Глава тринадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
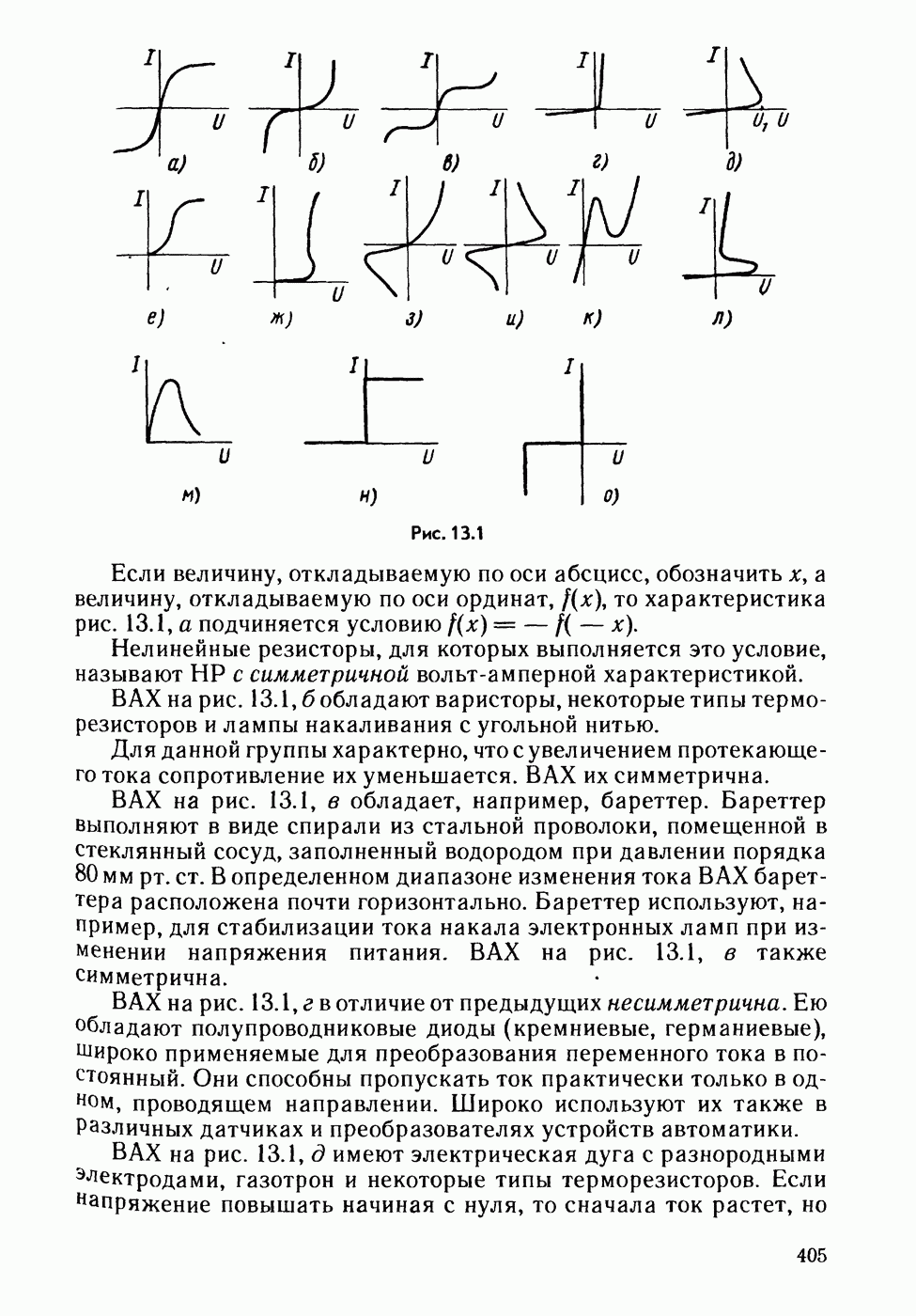
- § 13.2. ВАХ нелинейных резисторов.
- § 13.3. Общая характеристика методов расчета нелинейных электрических цепей постоянного тока.
- § 13.4. Последовательное соединение HP.
- § 13.5. Параллельное соединение HP.
- § 13.6. Последовательно-параллельное соединение сопротивлений.
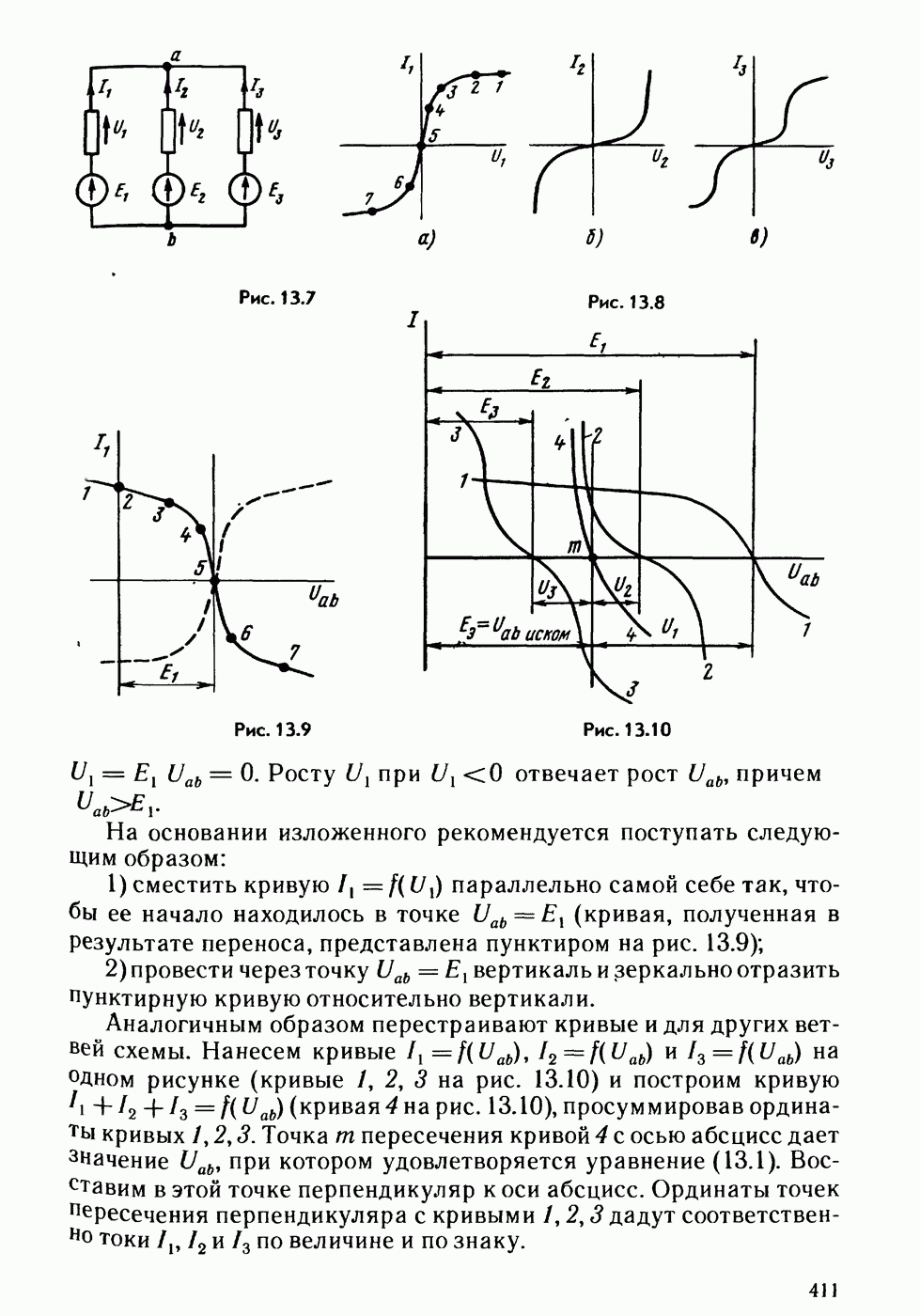
- § 13.8. Замена нескольких параллельных ветвей, содержащих HP и ЭДС, одной эквивалентной.
- § 13.9. Расчет нелинейных цепей методом эквивалентного генератора.
- § 13.10. Статическое и дифференциальное сопротивления.
- § 13.11. Замена нелинейного резистора эквивалентным линейным сопротивлением и ЭДС.
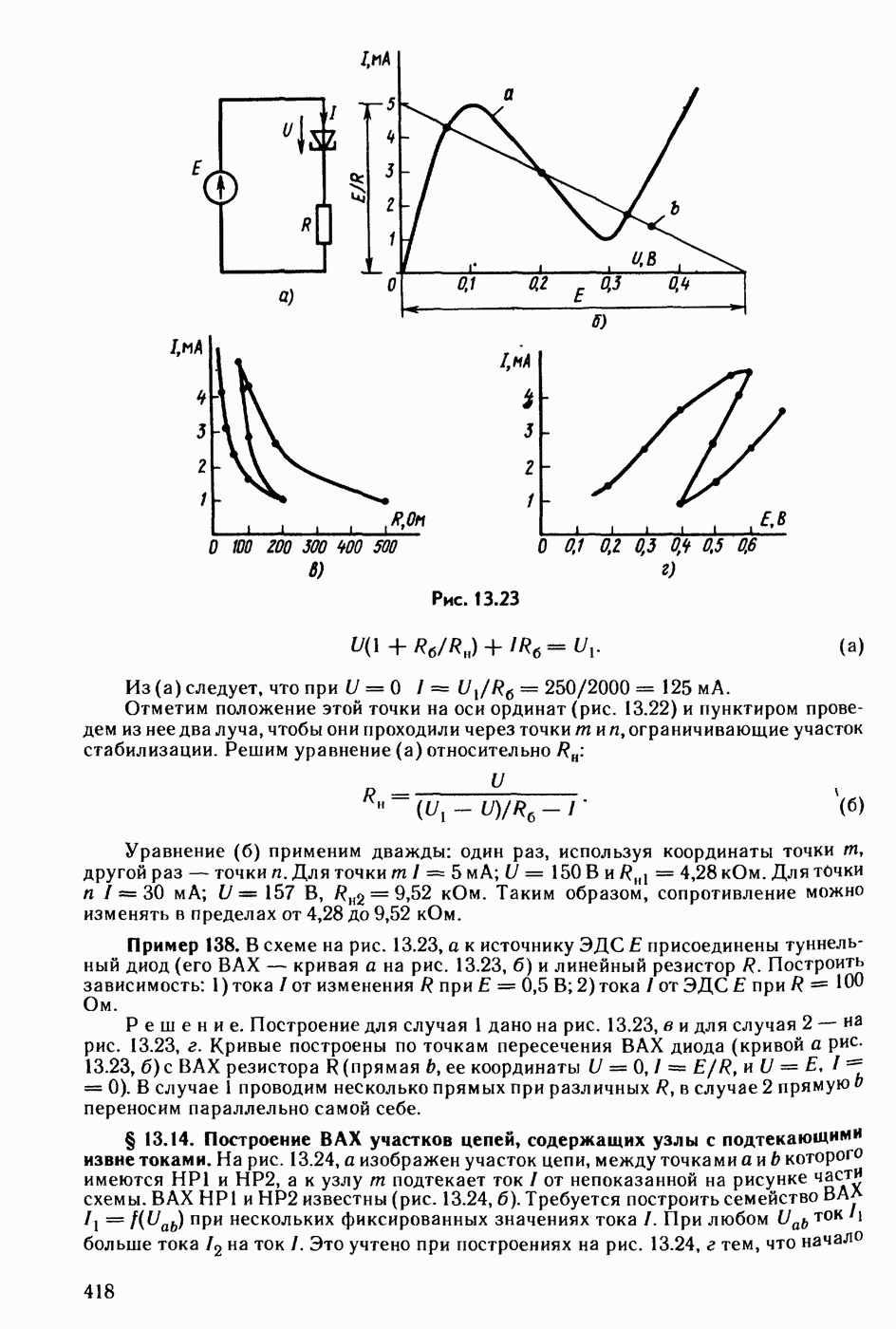
- § 13.12. Стабилизатор тока.
- § 13.13. Стабилизатор напряжения.
- § 13.14. Построение ВАХ участков цепей, содержащих узлы с подтекающими извне токами.
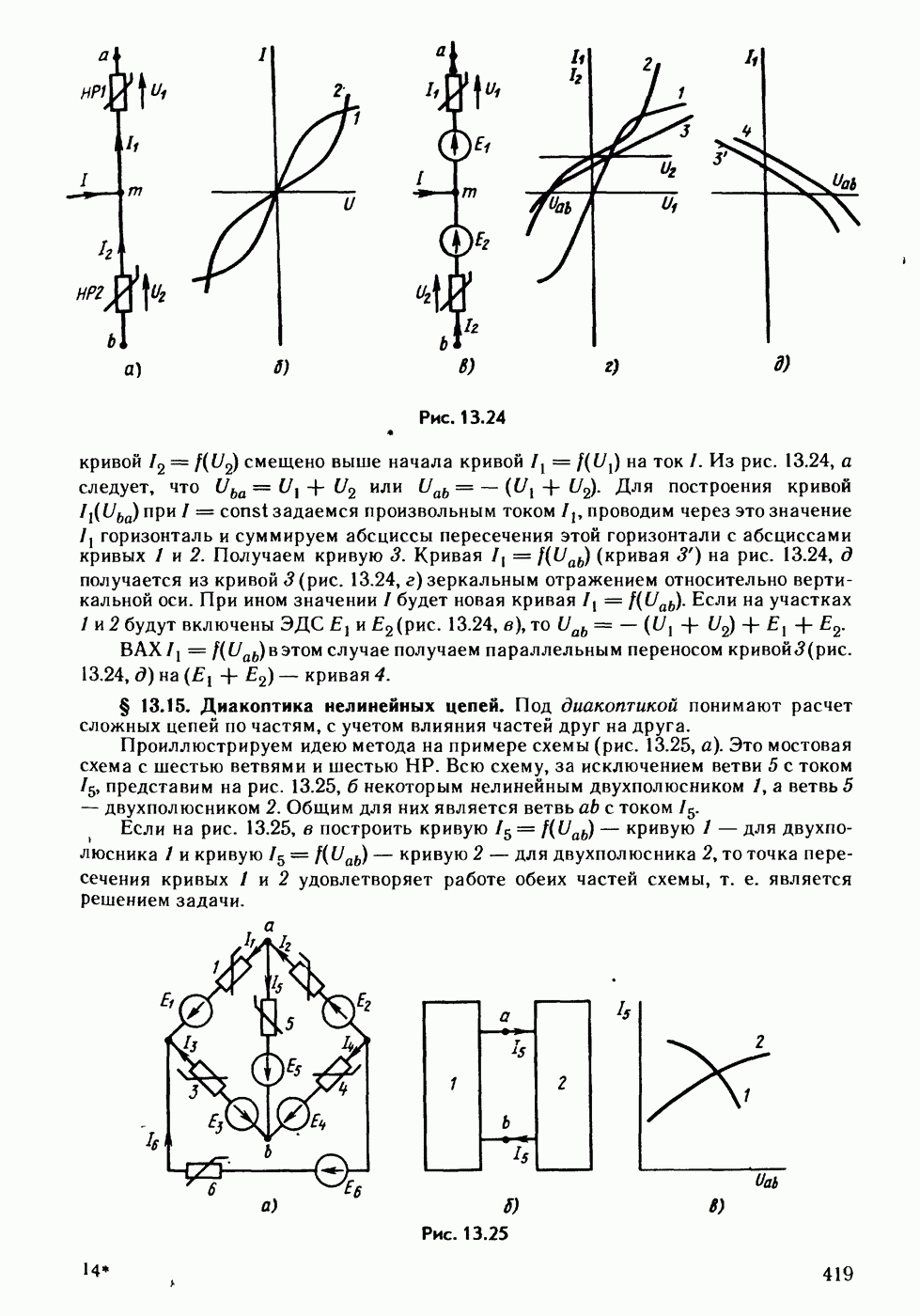
- § 13.15. Диакоптика нелинейных цепей.
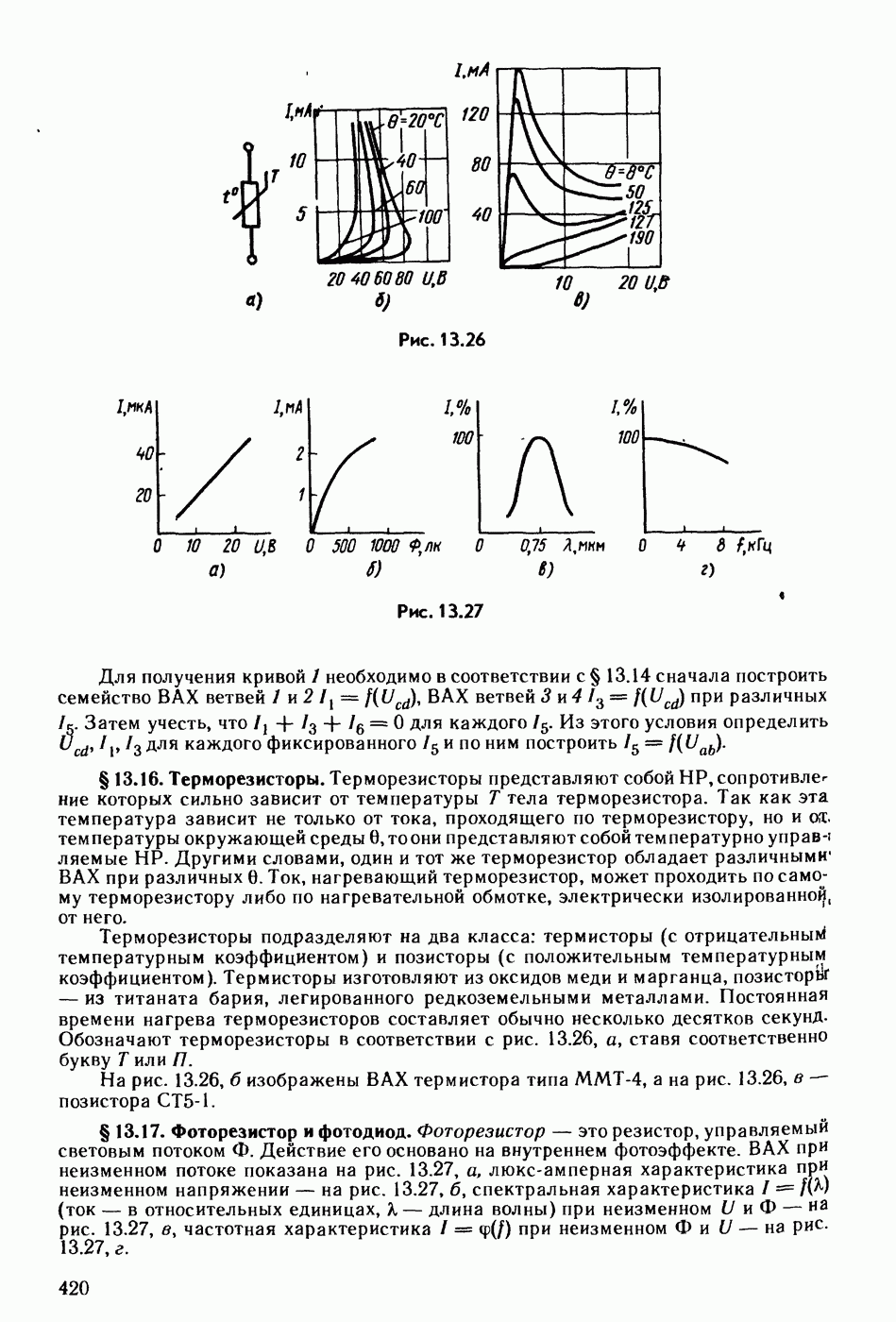
- § 13.16. Терморезисторы.
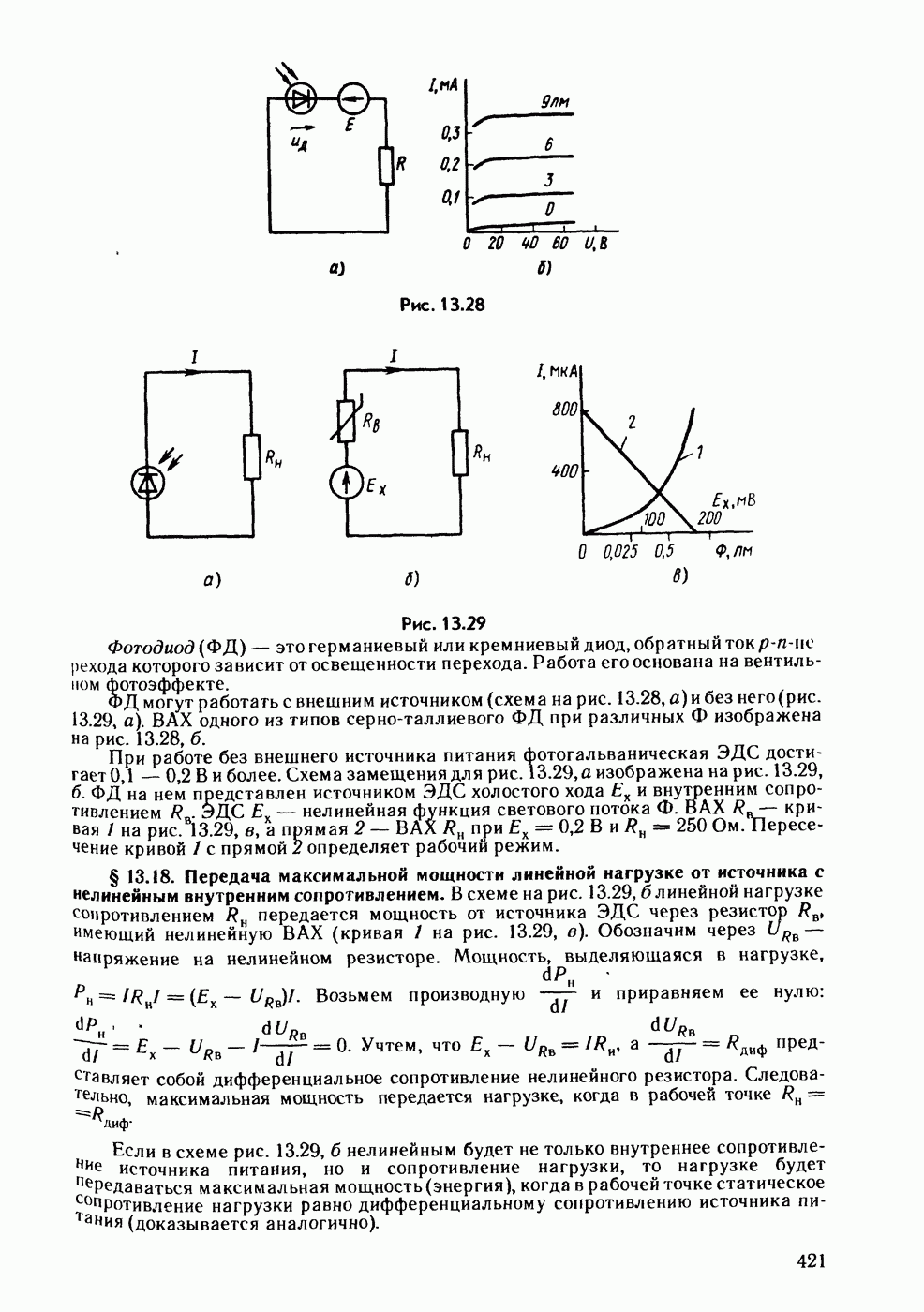
- § 13.17. Фоторезистор и фотодиод.
- § 13.18. Передача максимальной мощности линейной нагрузке от источника с нелинейным внутренним сопротивлением.
- § 13.19. Магниторезисторы и магнитодиоды.
- Вопросы для самопроверки
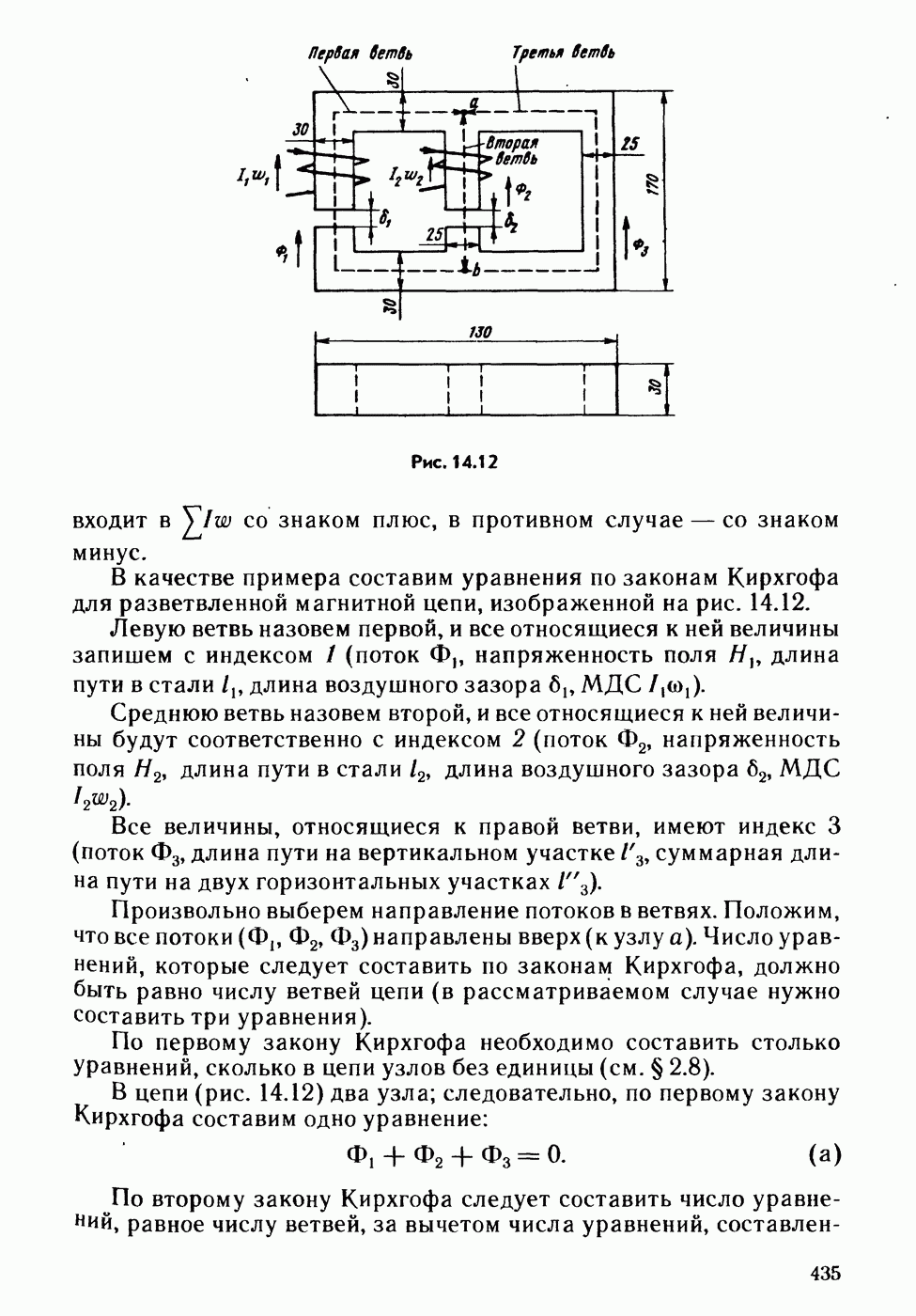
- Глава четырнадцатая. МАГНИТНЫЕ ЦЕПИ
- § 14.1. Подразделение веществ на сильномагнитные и слабомагнитные.
- § 14.2. Основные величины, характеризующие магнитное поле.
- § 14.3. Основные характеристики ферромагнитных материалов.
- § 14.4. Потери, обусловленные гистерезисом.
- § 14.5. Магнитомягкие и магнитотвердые материалы.
- § 14.6. Магнитодиэлектрики и ферриты.
- § 14.7. Закон полного тока.
- § 14.8. Магнитодвижущая (намагничивающая) сила.
- § 14.9. Разновидности магнитных цепей.
- § 14.10. Роль ферромагнитных материалов в магнитной цепи.
- § 14.11. Падение магнитного напряжения.
- § 14.12. Вебер-амперные характеристики.
- § 14.13. Построение вебер-амперных характеристик.
- § 14.14. Законы Кирхгофа для магнитных цепей.
- § 14.15. Применение к магнитным цепям всех методов, используемых для расчета электрических цепей с нелинейными резисторами.
- § 14.16. Определение МДС неразветвленной магнитной цепи по заданному потоку.
- § 14.17. Определение потока в неразветвленной магнитной цепи по заданной МДС.
- § 14.18. Расчет разветвленной магнитной цепи методом двух узлов.
- § 14.19. Дополнительные замечания к расчету магнитных цепей.
- § 14.20. Получение постоянного магнита.
- § 14.21. Расчет магнитной цепи постоянного магнита.
- § 14.22. Прямая и коэффициент возврата.
- § 14.23. Магнитное сопротивление и магнитная проводимость участка магнитной цепи. Закон Ома для магнитной цепи.
- § 14.24. Магнитная линия с распределенными параметрами.
- § 14.25. Пояснения к формуле
- Вопросы для самопроверки
- Глава пятнадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- § 15.1. Подразделение нелинейных элементов.
- § 15.2. Общая характеристика нелинейных резисторов.
- § 15.3. Общая характеристика нелинейных индуктивных элементов.
- § 15.4. Потери в сердечниках нелинейных индуктивных катушек, обусловленные вихревыми токами.
- § 15.5. Потери в ферромагнитном сердечнике, обусловленные гистерезисом.
- § 15.6. Схема замещения нелинейной индуктивной катушки.
- § 15.7. Общая характеристика нелинейных емкостных элементов.
- § 15.8. Нелинейные элементы как генераторы высших гармоник тока и напряжения.
- § 15.9. Основные преобразования, осуществляемые с помощью нелинейных электрических цепей.
- § 15.10. Некоторые физические явления, наблюдаемые в нелинейных цепях.
- § 15.11. Разделение нелинейных элементов по степени симметрии характеристик относительно осей координат.
- § 15.12. Аппроксимация характеристик нелинейных элементов.
- § 15.13. Аппроксимация симметричных характеристик для мгновенных значений гиперболическим синусом.
- § 15.15. Разложение гиперболических синуса и косинуса от периодического аргумента в ряды Фурье.
- § 15.16. Разложение гиперболического синуса от постоянной и синусоидально меняющейся составляющих в ряд Фурье.
- § 15.17. Некоторые общие свойства симметричных нелинейных элементов.
- § 15.18. Появление постоянной составляющей тока (напряжения, потока, заряда) на нелинейном элементе с симметричной характеристикой.
- § 15.19. Типы характеристик нелинейных элементов.
- § 15.20. Характеристики для мгновенных значений.
- § 15.21. ВАХ по первым гармоникам.
- § 15.22. ВАХ для действующих значений.
- § 15.23. Получение аналитическим путем обобщенных характеристик управляемых нелинейных элементов по первым гармоникам.
- § 15.24. Простейшая управляемая нелинейная индуктивная катушка.
- § 15.25. ВАХ управляемой нелинейной индуктивной катушки по первым гармоникам.
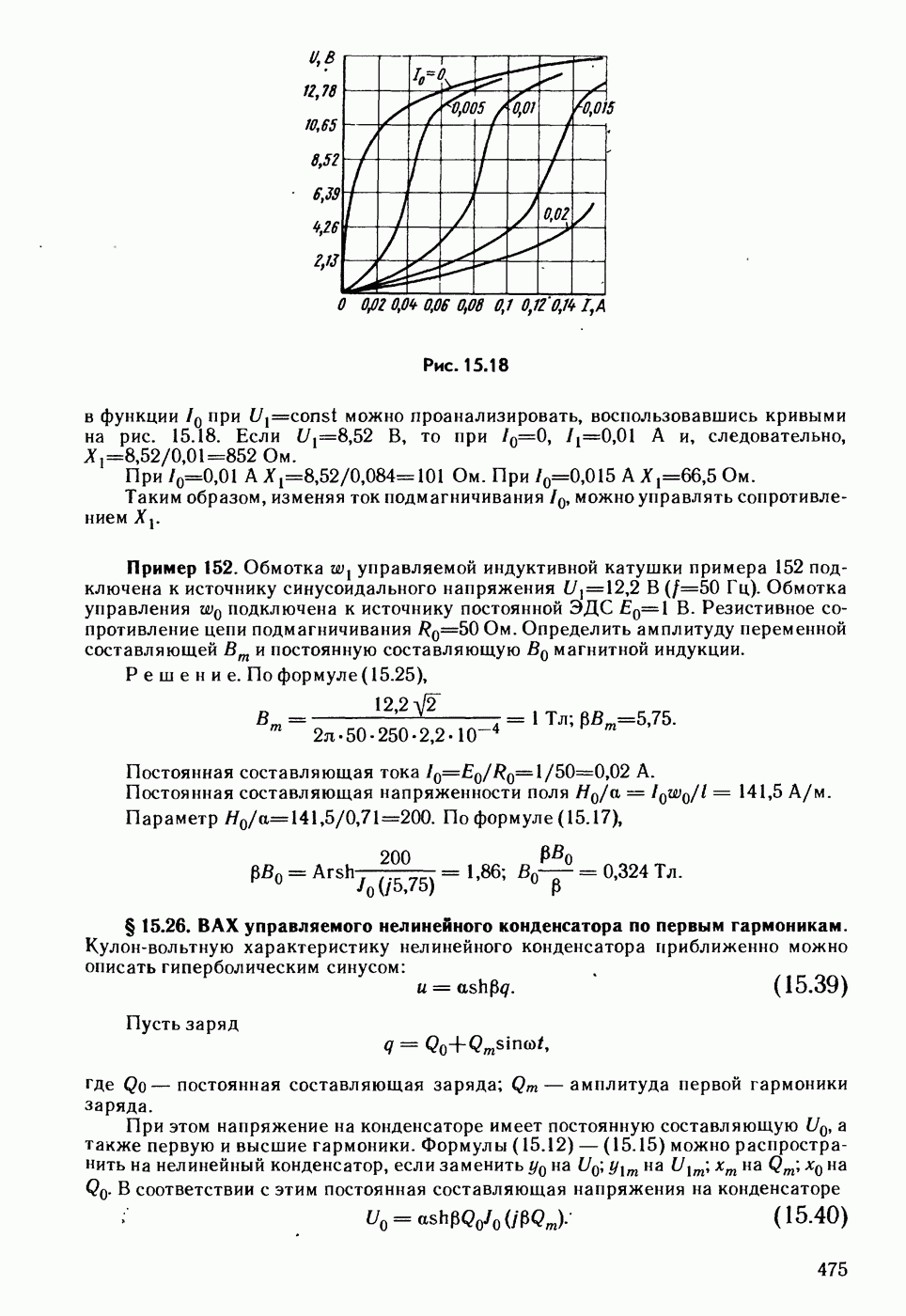
- § 15.26. ВАХ управляемого нелинейного конденсатора по первым гармоникам.
- § 15.27. Основные сведения об устройстве биполярного транзистора.
- § 15.28. Основные способы включения биполярных транзисторов в схему.
- § 15.29. Принцип работы биполярного транзистора.
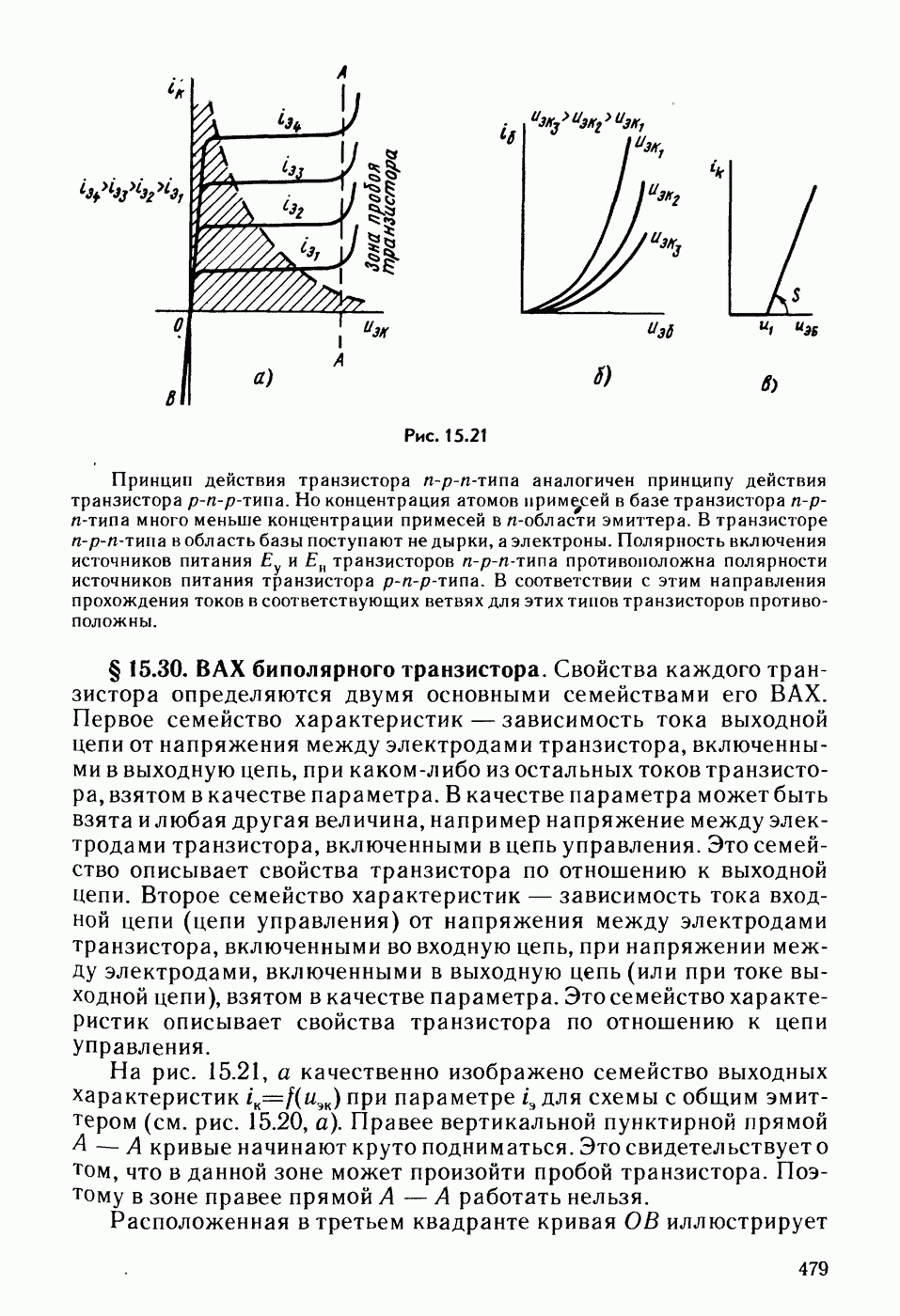
- § 15.30. ВАХ биполярного транзистора.
- § 15.31. Биполярный транзистор в качестве усилителя тока, напряжения, мощности.
- § 15.32. Связь между приращениями входных и выходных величин биполярного транзистора.
- § 15.33. Схема замещения биполярного транзистора для малых приращений. Методика расчета схем суправляемыми источниками с учетом ихчастотных свойств.
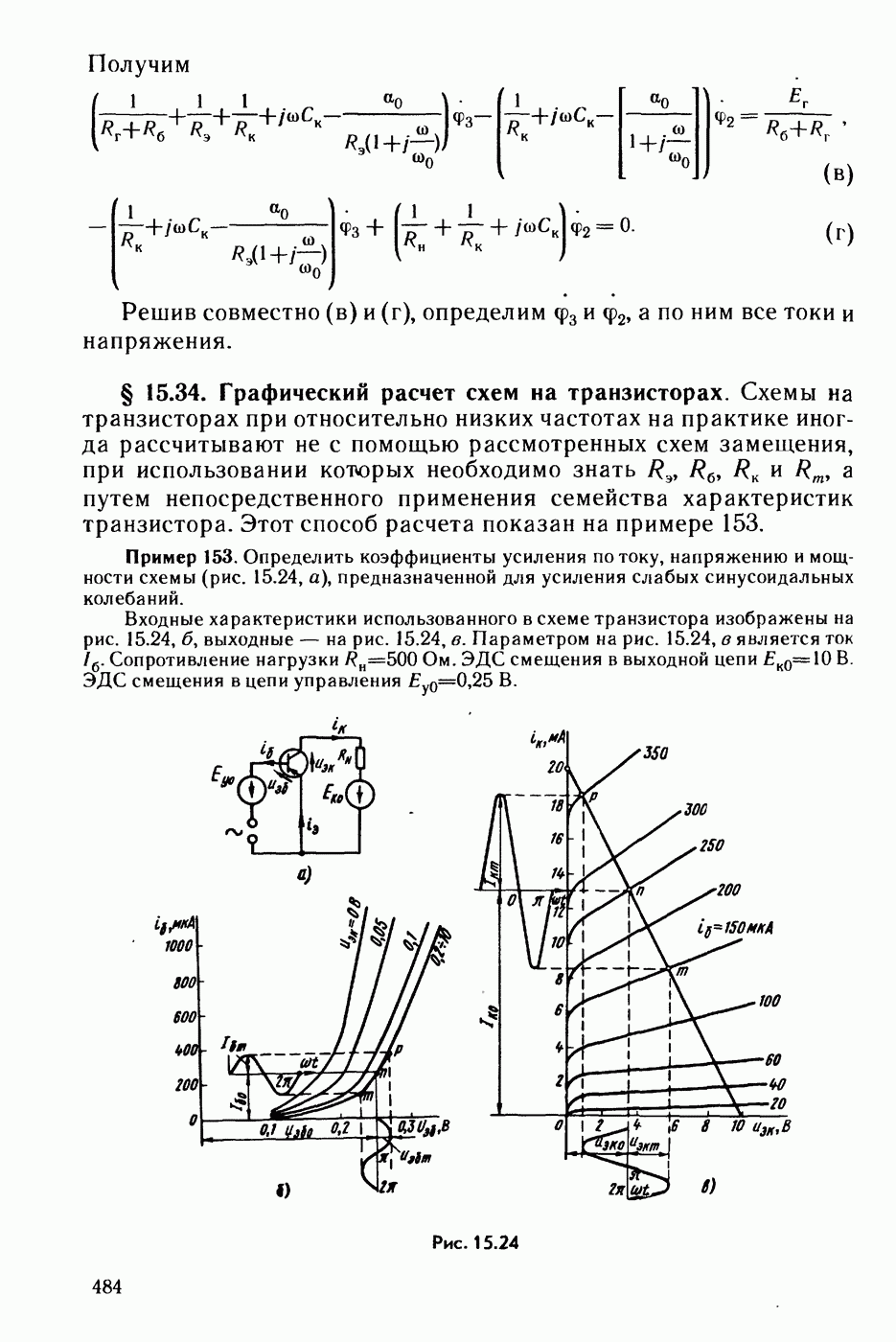
- § 15.34. Графический расчет схем на транзисторах.
- § 15.35. Принцип работы полевого транзистора.
- § 15.36. ВАХ полевого транзистора.
- § 15.37. Схемы включения полевого транзистора.
- § 15.38. Основные сведения о трехэлектродной лампе.
- § 15.39. ВАХ трехэлектродной лампы для мгновенных значений.
- § 15.40. Аналитическое выражение сеточной характеристики электронной лампы.
- § 15.41. Связь между малыми приращениями входных и выходных величин электронной лампы.
- § 15.42. Схема замещения электронной лампы для малых приращений.
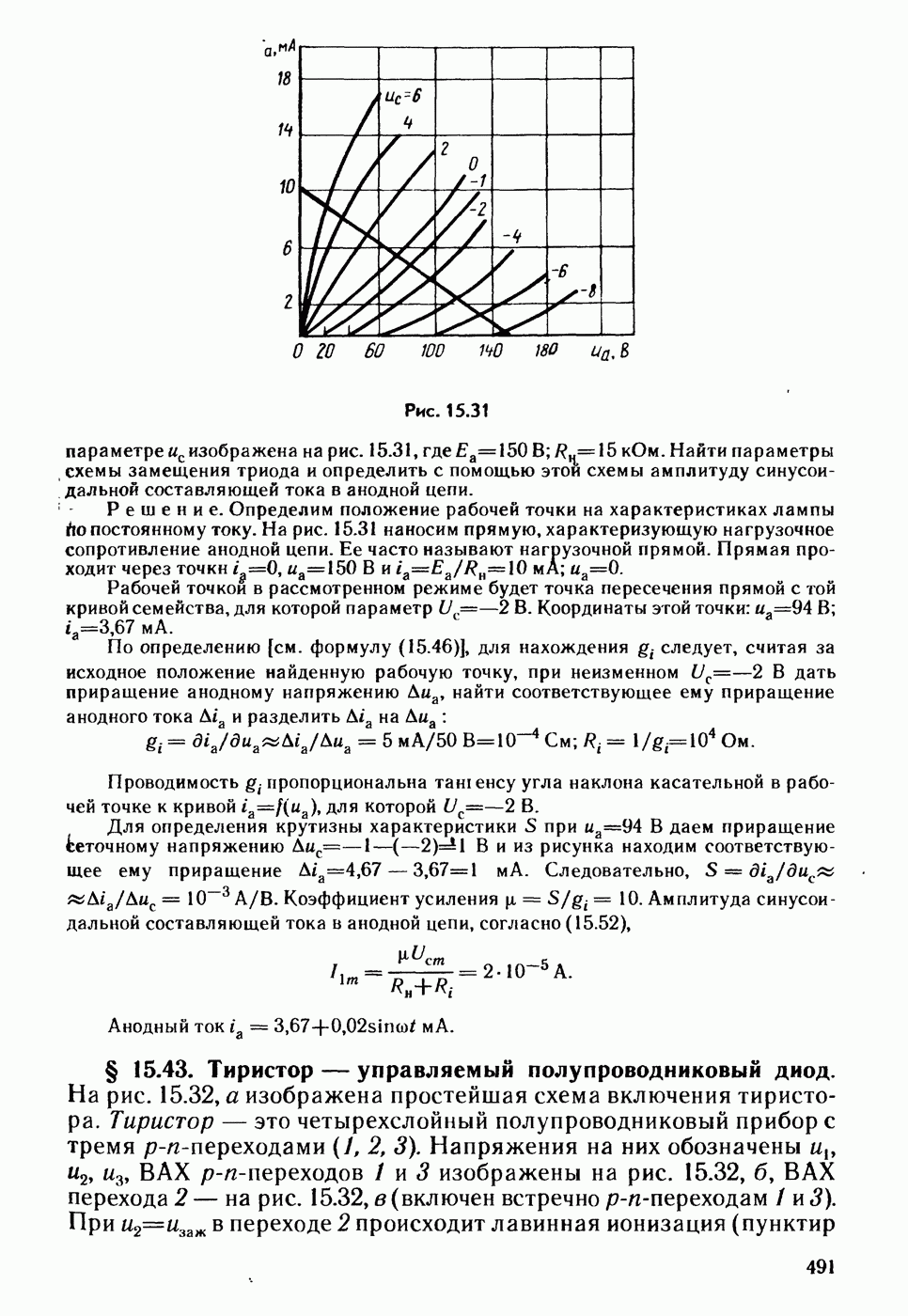
- § 15.43. Тиристор — управляемый полупроводниковый диод.
- § 15.44. Общая характеристика методов анализа и расчета нелинейных электрических цепей переменного тока.
- § 15.45. Графический метод расчета при использовании характеристик нелинейных элементов для мгновенных значений.
- § 15.46. Аналитический метод расчета при использовании характеристик нелинейных элементов для мгновенных значений при их кусочно-линейной аппроксимации.
- § 15.47. Аналитический (графический) метод расчета по первым гармоникам токов и напряжений.
- § 15.48. Анализ нелинейных цепей переменного тока путем использования ВАХ для действующих значений.
- § 15.49. Аналитический метод расчета цепей по первой и одной или нескольким высшим или низшим гармоникам.
- § 15.50. Расчет цепей с помощью линейных схем замещения.
- § 15.51. Расчет цепей, содержащих индуктивные катушки, сердечники которых имеют почти прямоугольную кривую намагничивания.
- § 15.52. Расчет цепей, содержащих нелинейные конденсаторы с прямоугольной кулон-вольтной характеристикой.
- § 15.53. Выпрямление переменного напряжения.
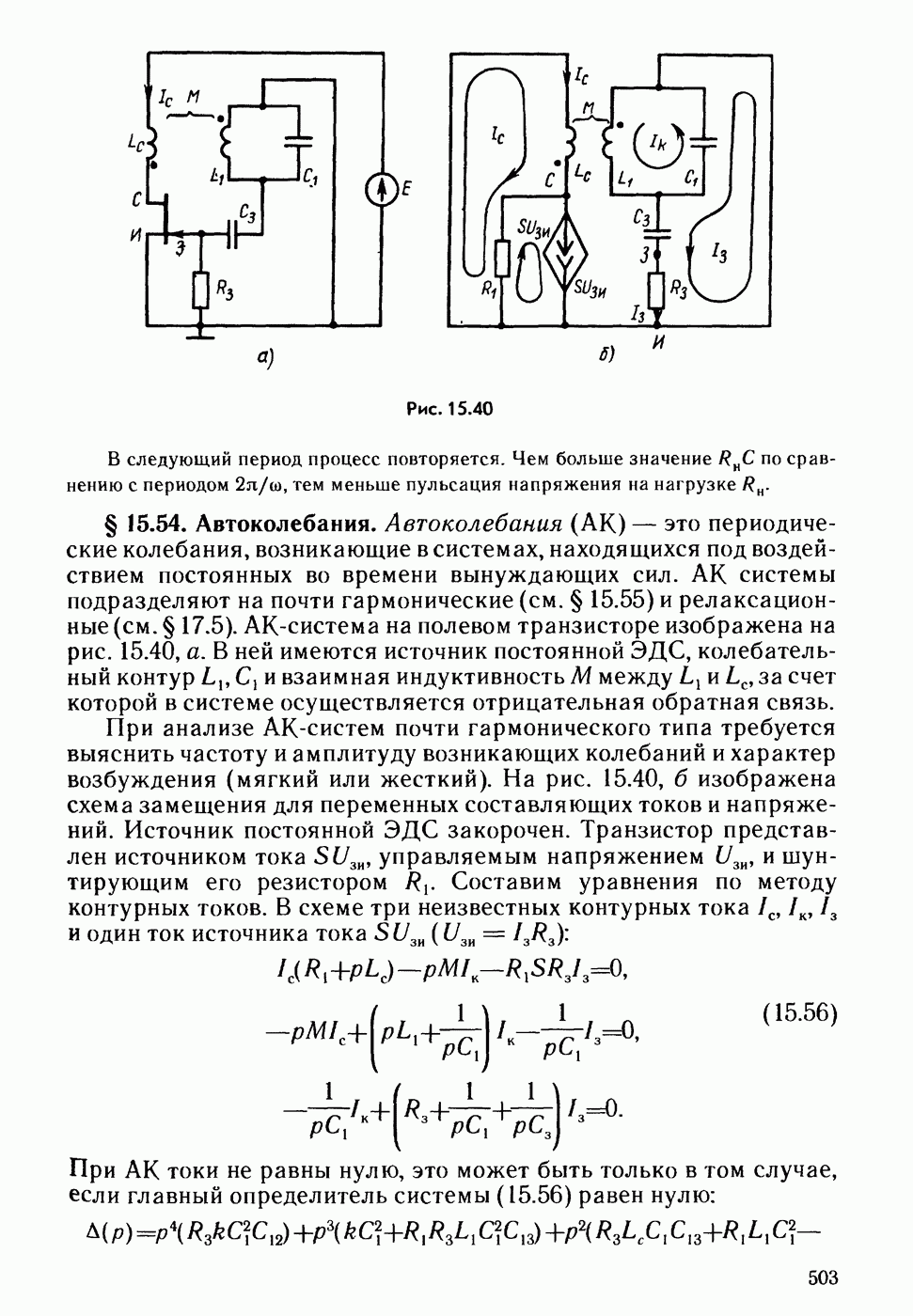
- § 15.54. Автоколебания.
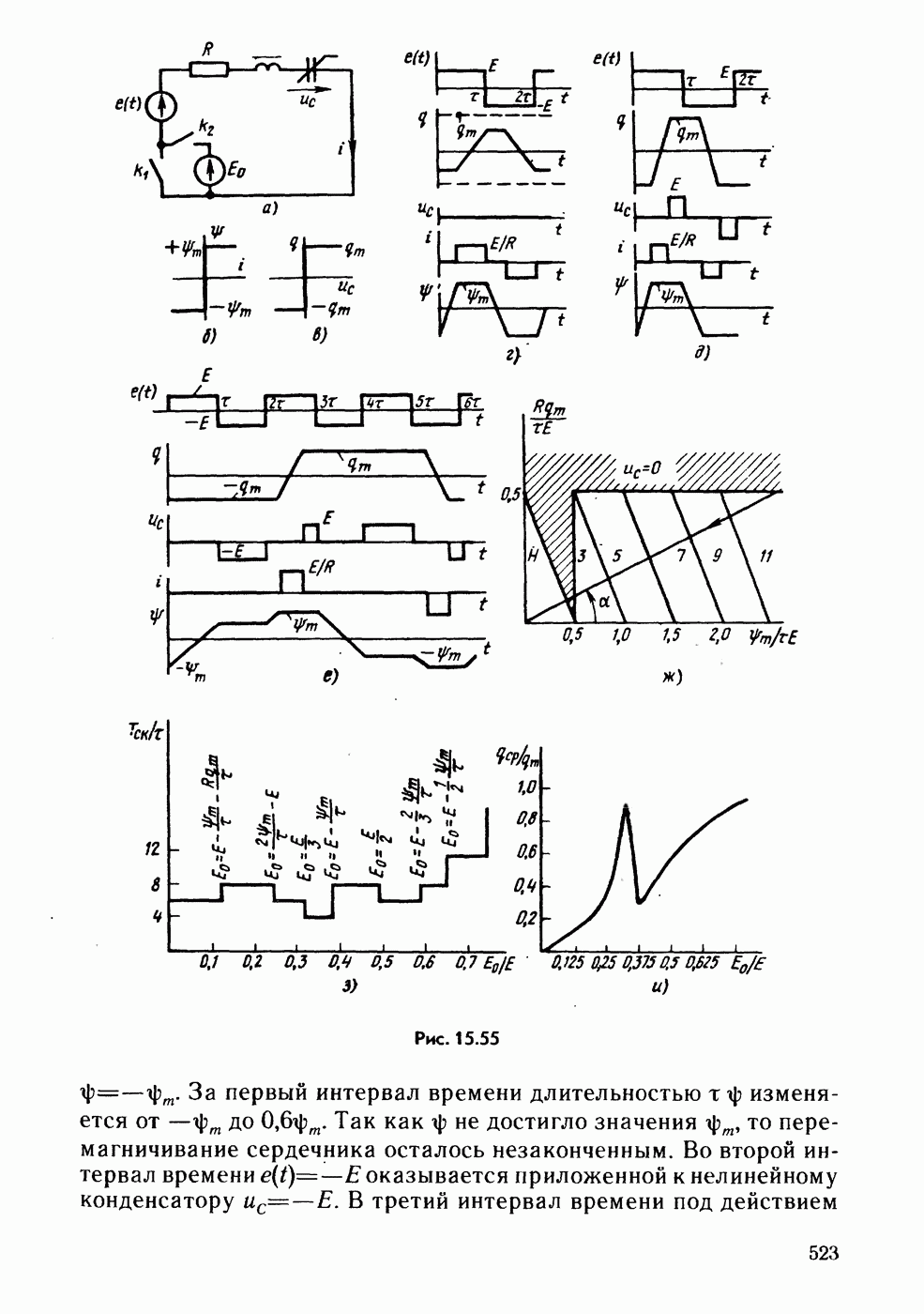
- § 15.55. Мягкое и жесткое возбуждение автоколебаний.
- § 15.56. Определение феррорезонансных цепей.
- § 15.57. Построение ВАХ последовательной феррорезонансной цепи.
- § 15.58. Триггерный эффект в последовательной феррорезонансной цепи. Феррорезонанс напряжений.
- § 15.59. ВАХ параллельного соединения конденсатора и катушки со стальным сердечником. Феррорезонанс токов.
- § 15.60. Триггерный эффект в параллельной феррорезонансной цепи.
- § 15.61. Частотные характеристики нелинейных цепей.
- § 15.62. Применение символического метода для расчета нелинейных цепей. Построение векторных и топографических диаграмм.
- § 15.63. Метод эквивалентного генератора.
- § 15.64. Векторная диаграмма нелинейной индуктивной катушки.
- § 15.65. Определение намагничивающего тока.
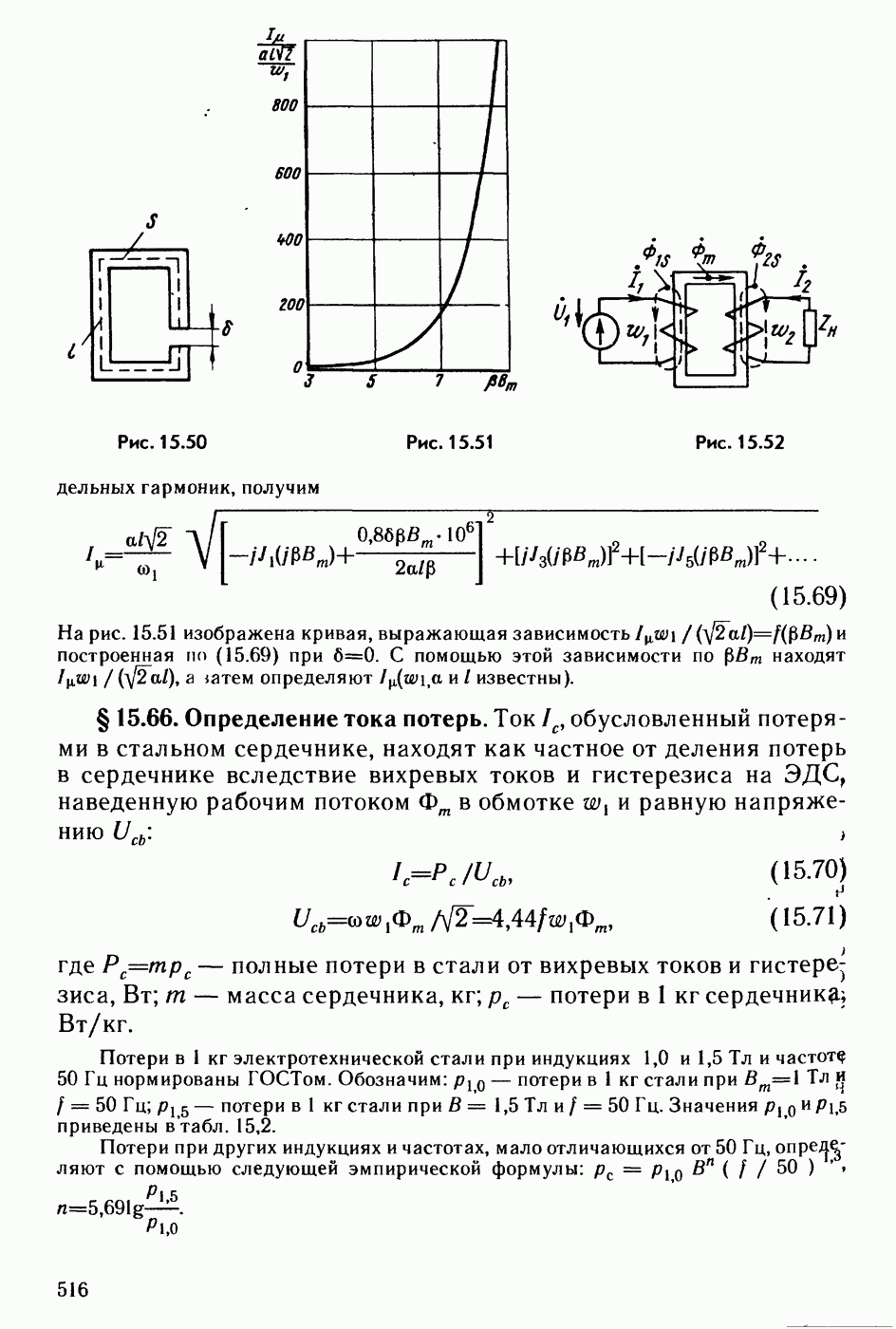
- § 15.66. Определение тока потерь.
- § 15.67. Основные соотношения для трансформатора со стальным сердечником.
- § 15.68. Векторная диаграмма трансформатора со стальным сердечником.
- § 15.69. Субгармонические колебания. Многообразие типов движений в нелинейных цепях.
- § 15.70. Автомодуляция. Хаотические колебания (странные аттракторы).
- Вопросы для самопроверки
- Глава шестнадцатая. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 16.1. Общая характеристика методов анализа и расчета переходных процессов.
- § 16.2. Расчет, основанный на графическом подсчете определенного интеграла.
- § 16.3. Расчет методом интегрируемой нелинейной аппроксимации.
- § 16.4. Расчет методом кусочно-линейной аппроксимации.
- § 16.5. Расчет переходных процессов в нелинейных цепях методом переменных состояния на ЭВМ.
- § 16.6. Метод медленно меняющихся амплитуд.
- § 16.7. Метод малого параметра.
- § 16.8. Метод интегральных уравнений.
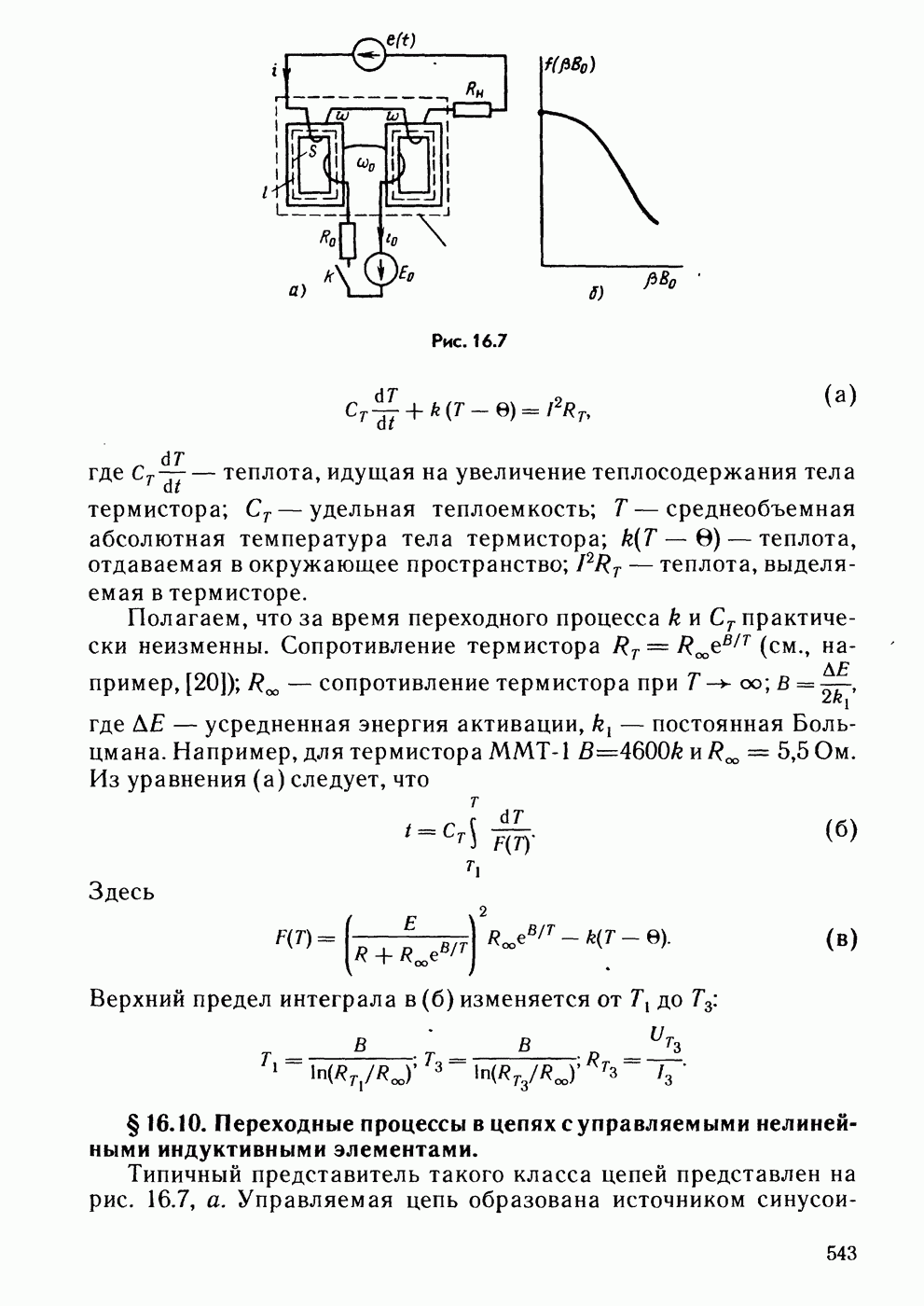
- § 16.9. Переходные процессы в цепях с терморезисторами.
- § 16.10. Переходные процессы в цепях с управляемыми нелинейными индуктивными элементами.
- § 16.11. Переходные процессы в нелинейных электромеханических системах.
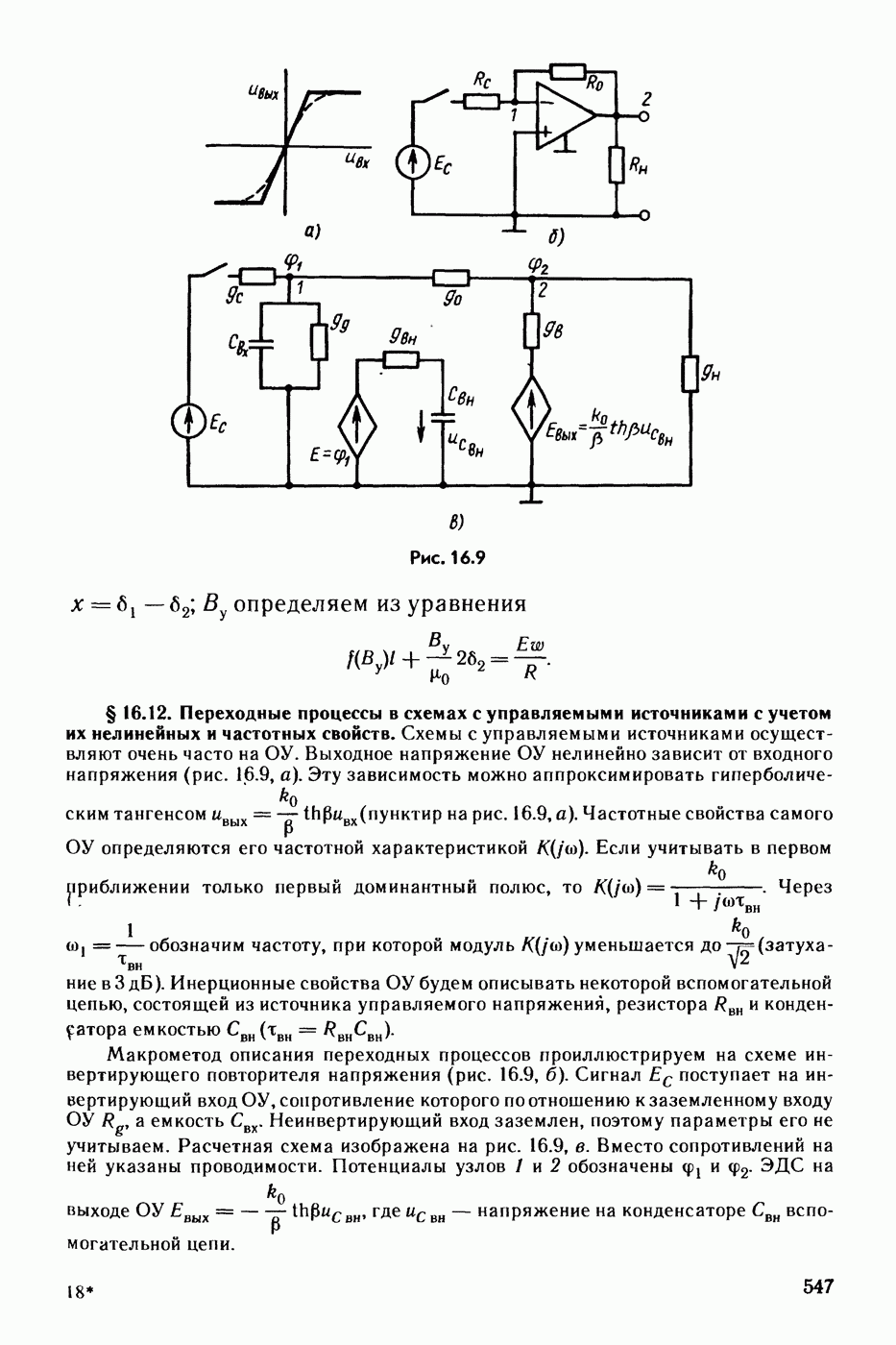
- § 16.12. Переходные процессы в схемах с управляемыми источниками с учетом их нелинейных и частотных свойств.
- § 16.13. Перемагничивание ферритовых сердечников импульсами тока.
- § 16.14. Фазовая плоскость и характеристика областей ее применения.
- § 16.15. Интегральные кривые, фазовая траектория и предельный цикл.
- § 16.16. Изображение простейших процессов на фазовой плоскости.
- § 16.17. Изоклины. Особые точки. Построение фазовых траекторий.
- Вопросы для самопроверки
- Глава семнадцатая. ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ РЕЖИМОВ РАБОТЫ НЕЛИНЕЙНЫХ ЦЕПЕЙ
- § 17.1. Устойчивость «в малом» и «в большом». Устойчивость по Ляпунову.
- § 17.2. Общие основы исследования устойчивости «в малом».
- § 17.3. Исследование устойчивости состояния равновесия в системах с постоянной вынуждающей силой.
- § 17.4. Исследование устойчивости автоколебаний и вынужденных колебаний по первой гармонике.
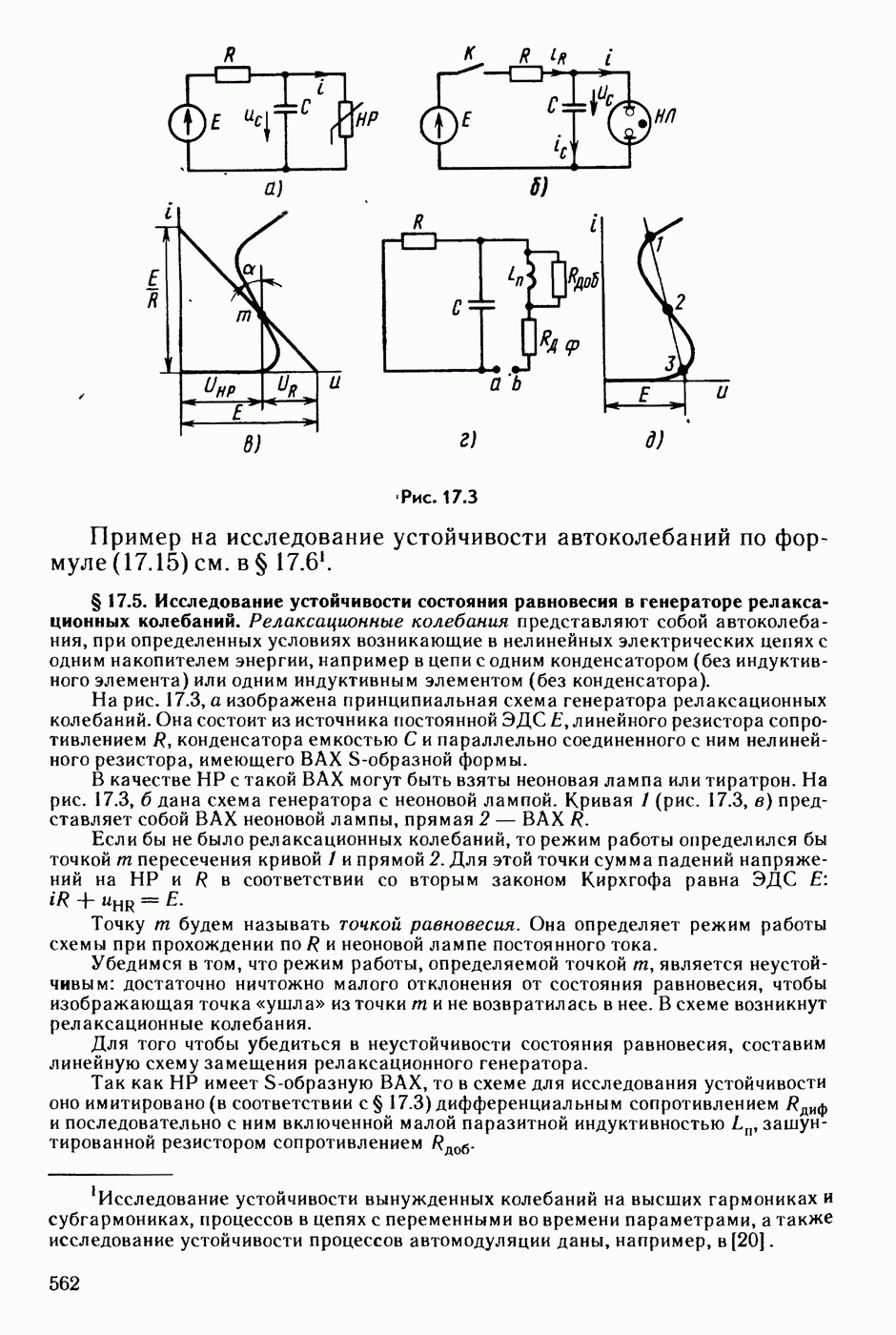
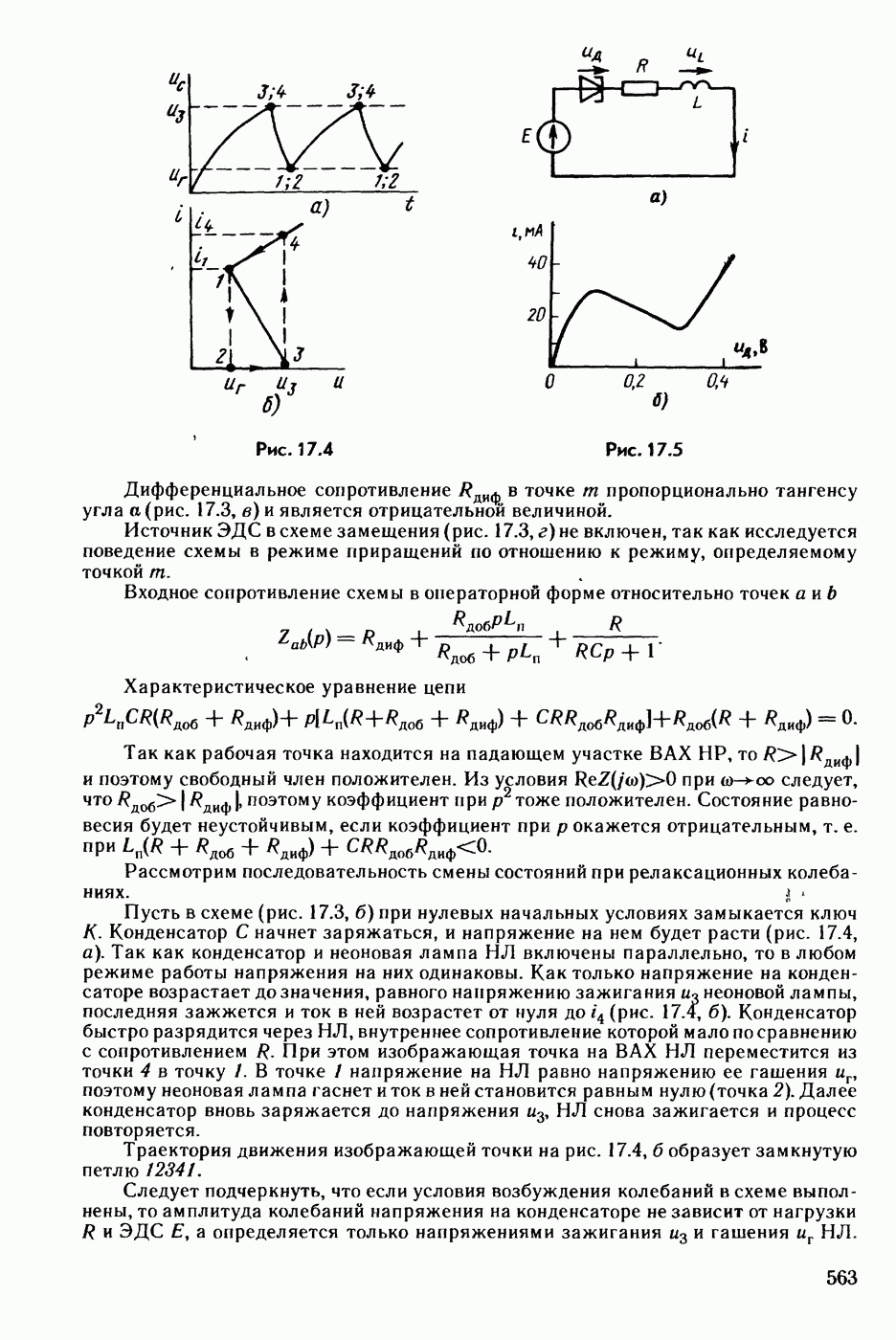
- § 17.5. Исследование устойчивости состояния равновесия в генераторе релаксационных колебаний.
- § 17.6. Исследование устойчивости периодического движения в ламповом генераторе синусоидальных колебаний.
- § 17.7. Исследование устойчивости работы электрических цепей, содержащих управляемые источники напряжения (тока) с учетом их неидеальности.
- Вопросы для самопроверки
- Глава восемнадцатая. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ПЕРЕМЕННЫМИ ВО ВРЕМЕНИ ПАРАМЕТРАМИ
- § 18.1. Элементы цепей.
- § 18.2. Общие свойства электрических цепей.
- § 18.3. Расчет электрических цепей в установившемся режиме.
- § 18.4. Параметрические колебания.
- § 18.5. Параметрические генератор и усилитель.
- Вопросы для самопроверки