| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
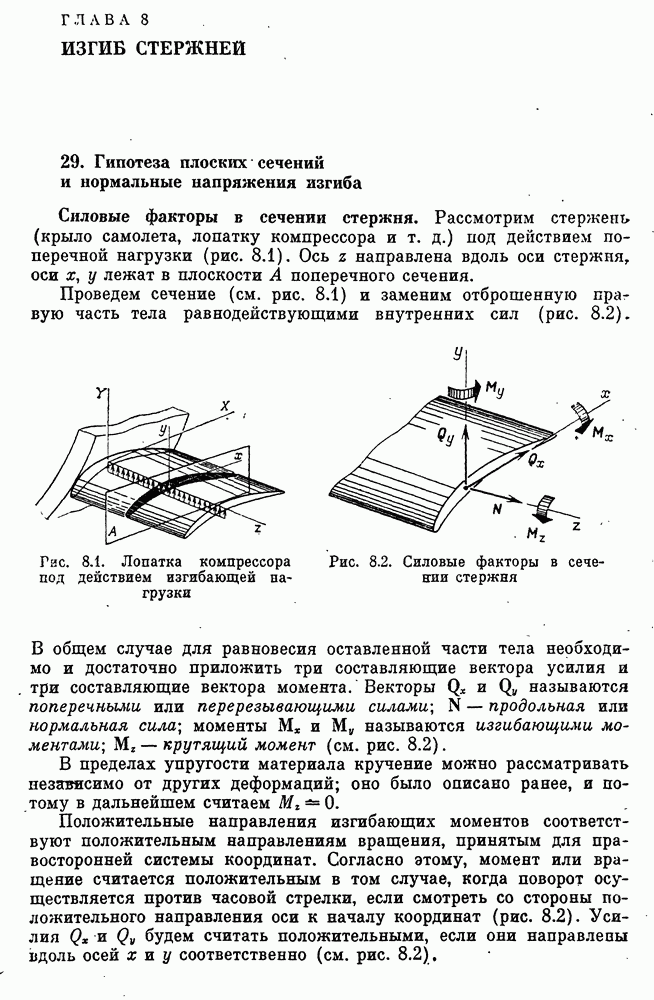
31. Условия равновесия элемента стержня и касательные напряжения изгиба
Вводные замечания.
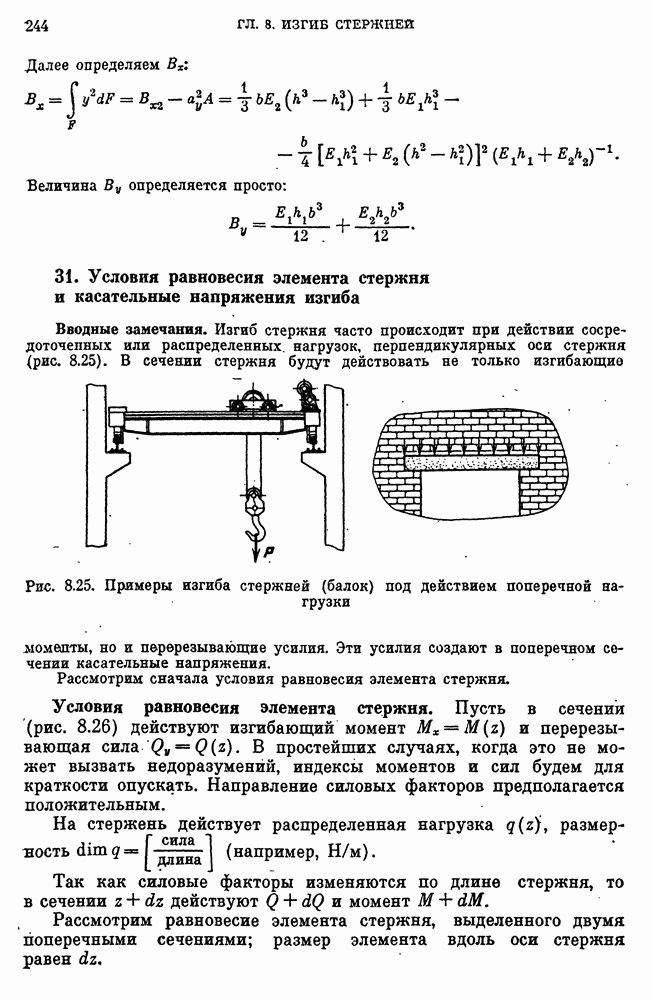
Изгиб стержня часто происходит при действии сосредоточенных или распределенных, нагрузок, перпендикулярных оси стержня (рис. 8.25).

Рис. 8.25. Примеры изгиба стержней (балок) под действием поперечной нагрузки
В сечении стержня будут действовать не только изгибающие моменты, но и перерезывающие усилия. Эти усилия создают в поперечном сечении касательные напряжения.
Рассмотрим сначала условия равновесия элемента стержня.
Условия равновесия элемента стержня.
Пусть в сечении (рис. 8.26) действуют изгибающий момент  и перерезывающая сила
и перерезывающая сила  . В простейших случаях, когда это не может вызвать недоразумений, индексы моментов и сил будем для краткости опускать. Направление силовых факторов предполагается положительным.
. В простейших случаях, когда это не может вызвать недоразумений, индексы моментов и сил будем для краткости опускать. Направление силовых факторов предполагается положительным.
На стержень действует распределенная нагрузка  размервость
размервость  — (например, Н/м).
— (например, Н/м).
Так как силовые факторы изменяются по длине стержня, то в сечении  действуют
действуют  и момент
и момент 
Рассмотрим равновесие элемента стержня, выделенного двумя поперечными сечениями; размер элемента вдоль оси стержня равен dz.
Проектируя все силы на вертикальное направление, находим

Составим сумму моментов относительно оси х, лежащей в сечении z + dz:

Отбрасывая  как бесконечно малую второго порядка, получим
как бесконечно малую второго порядка, получим

Производная изгибающего момента равна перерезывающей силе. Уравнения (81) и (82) образуют условия равновесия элемента стержня при изгибе.

Рис. 8.26. Условия равновесия элемента стержня
Замечание. Полученные условия равновесия справедливы для стержня постоянного или переменного сечений; при любых свойствах материала стержня они являются прямым следствием состояния равновесия.
При движении с ускорением элемента стержня к распределенным усилиям следует добавить по принципу Даламбера инерционные усилия.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
- 1. Сопротивление материалов — наука о прочности и надежности конструкций
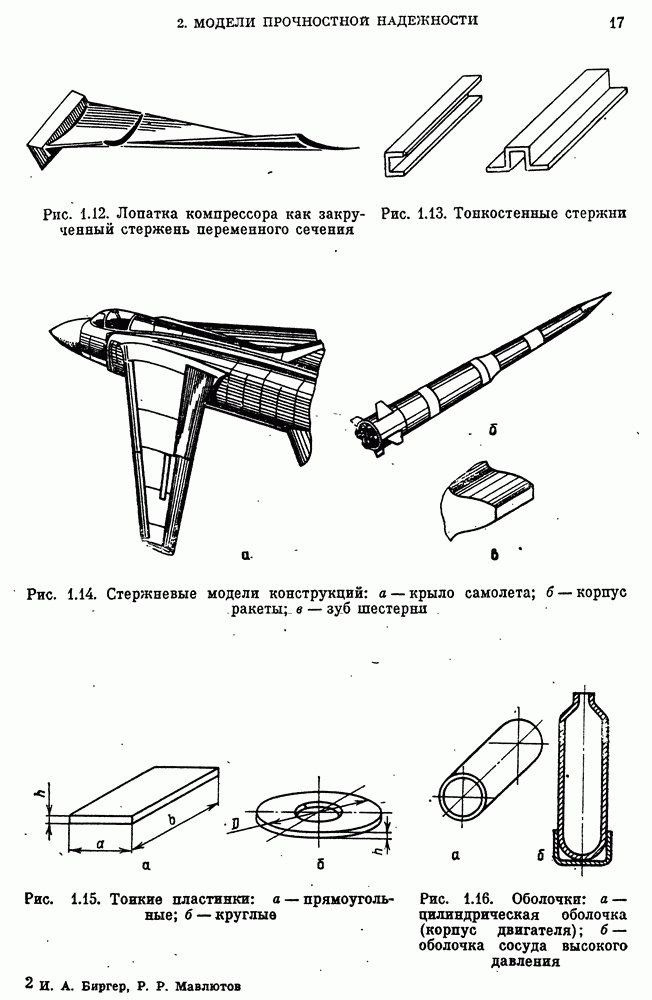
- 2. Модели прочностной надежности
- Модели прочностной надежности.
- Конструкционные материалы.
- Три уровня моделей материала.
- Модели материала в общей модели прочностной надежности.
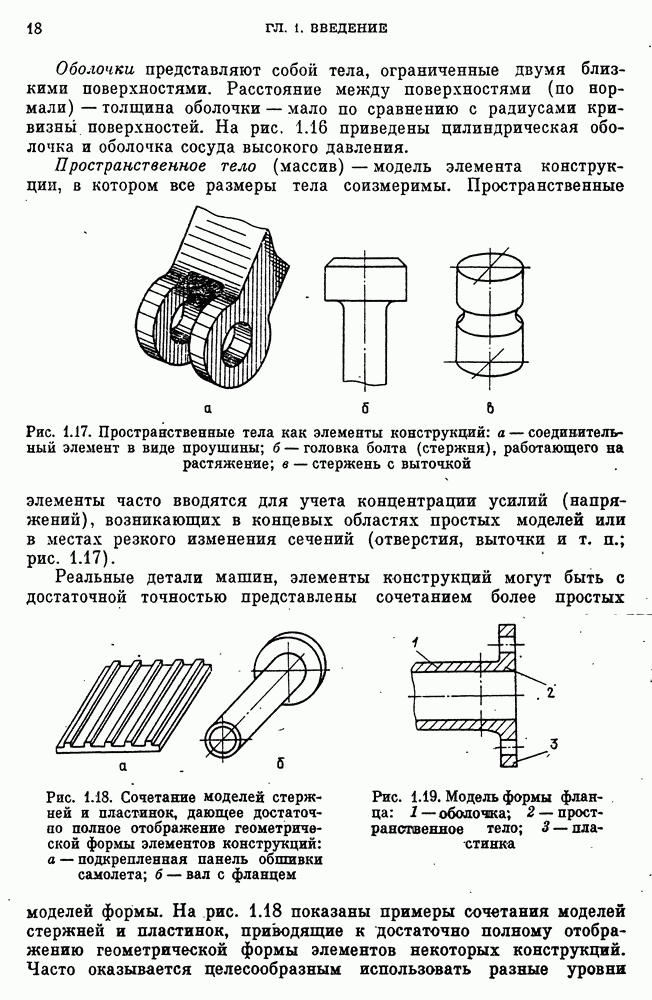
- Модели формы.
- Модели нагружения.
- Модели разрушения.
- ГЛАВА 2. НАПРЯЖЕНИЯ
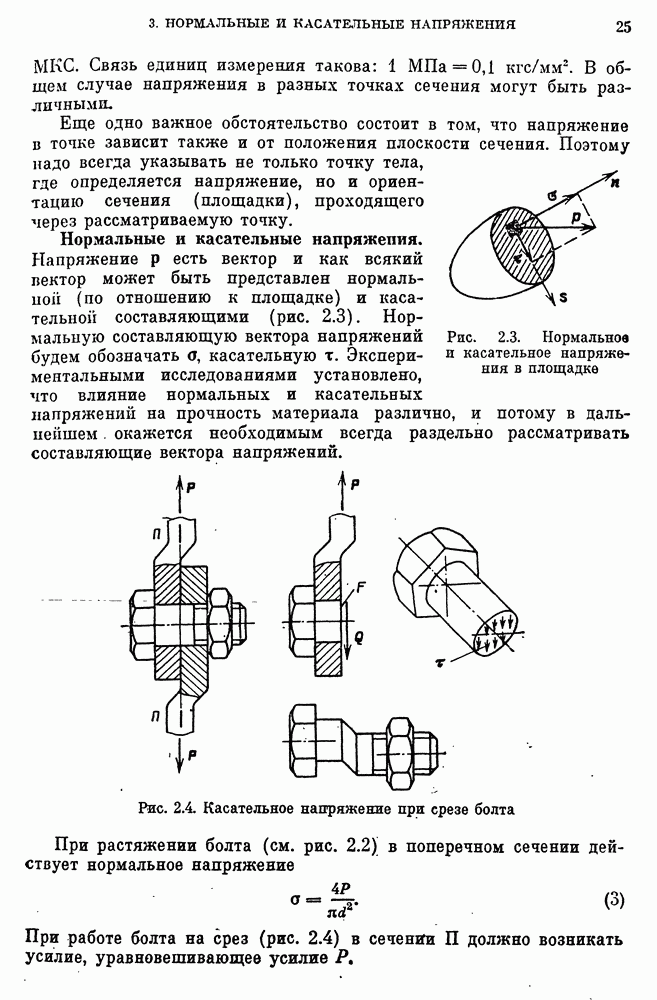
- 3. Нормальные и касательные напряжения
- Нормальные и касательные напряжения.
- 4. Напряженное состояние в точке
- Свойства парности касательных напряжений.
- 5. Плоское напряженное состояние
- Главные площадки при плоском напряженном состоянии.
- Главные напряжения при плоском напряженном состоянии.
- Наибольшие касательные напряжения.
- 6. Объемное напряженное состояние
- Напряжения в произвольной косой площадке.
- Главные площадки и главные напряжения при объемном напряженном состоянии.
- Инварианты напряженного состояния в точке.
- Понятие о тензоре напряженного состояния.
- 7. Дифференциальные уравнения равновесия элемента тела и краевые условия
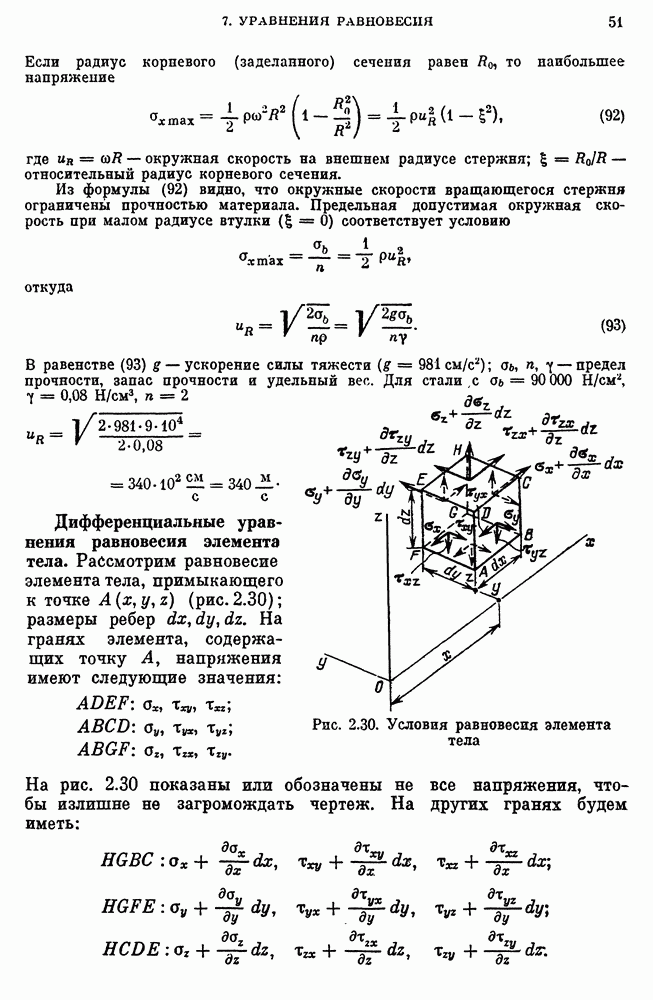
- Дифференциальные уравнения равновесия элемента тела.
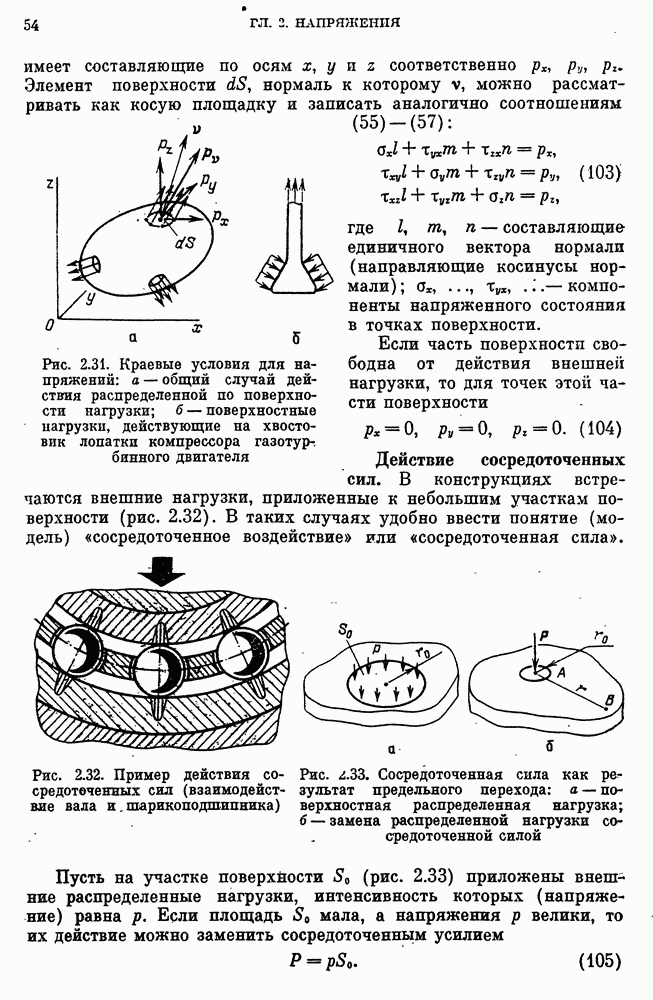
- Краевые условия для напряжений.
- Действие сосредоточенных сил.
- Принцип Сен-Венана для краевых условий.
- ГЛАВА 3. ДЕФОРМАЦИИ
- 8. Перемещения и деформации
- Определение линейной деформации.
- Определение угловой деформации.
- 9. Связь перемещений и деформаций
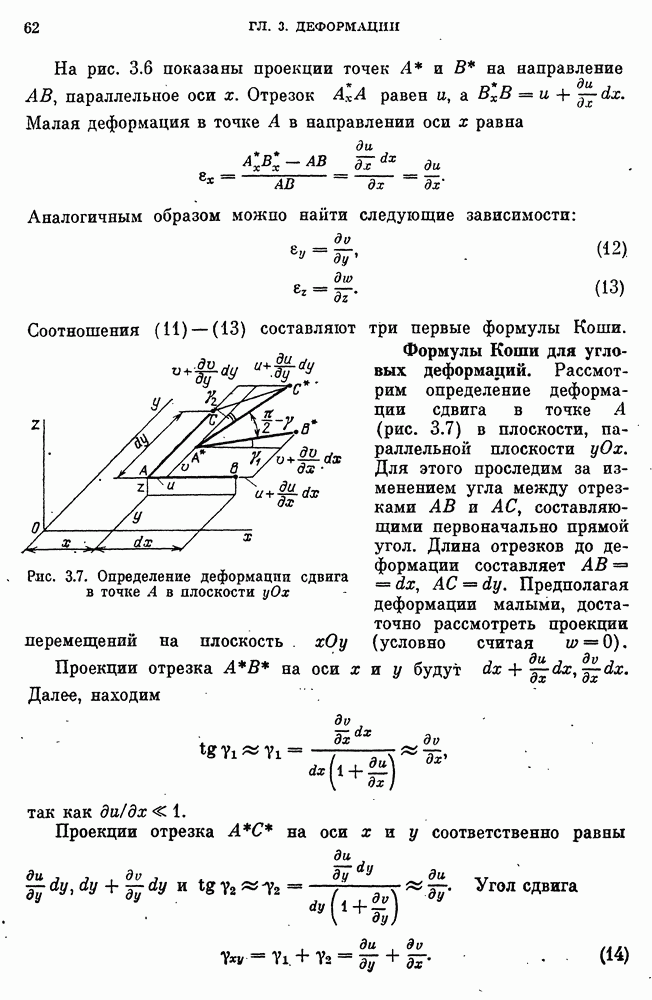
- Формулы Коши для линейных деформаций.
- 10. Линейная деформация в произвольном направлении. Главные деформации, тензор деформаций
- Главные направления и главные деформации.
- 11. Уравнения совместности деформаций
- ГЛАВА 4. МЕХАНИЧЕСКИЕ СВОЙСТВА КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
- 12. Диаграммы деформирования, пределы текучести и прочности
- Упругость, модуль упругости, пластичность, закон разгрузки и закон упрочнения.
- Пределы текучести и прочности при сжатии.
- Определение предела прочности материала с помощью испытания твердости.
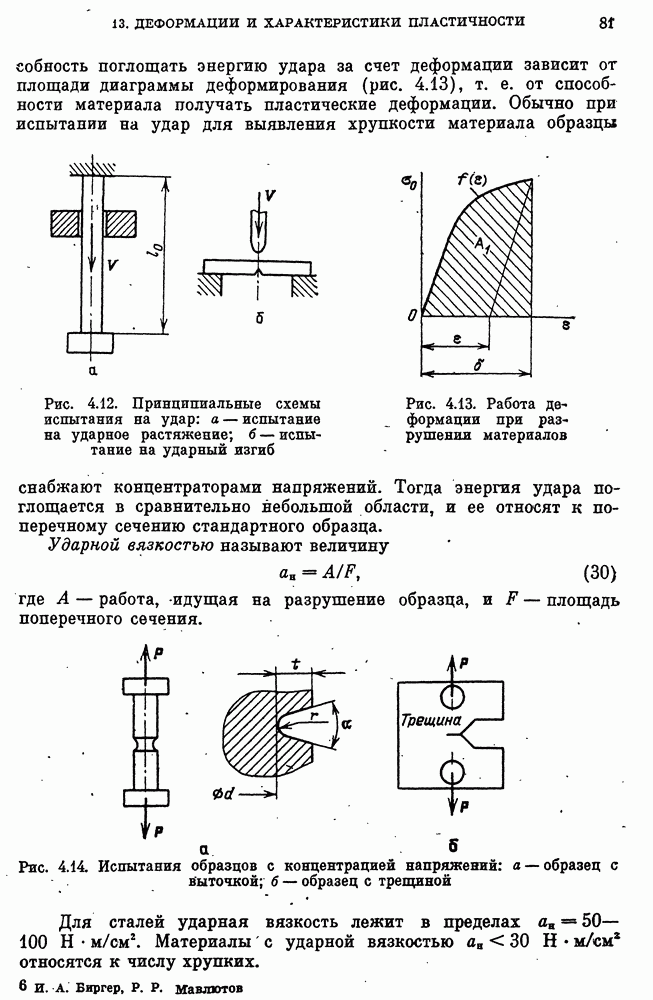
- 13. Деформации и характеристики пластичности
- Дополнительные характеристики хрупкости и пластичности материала.
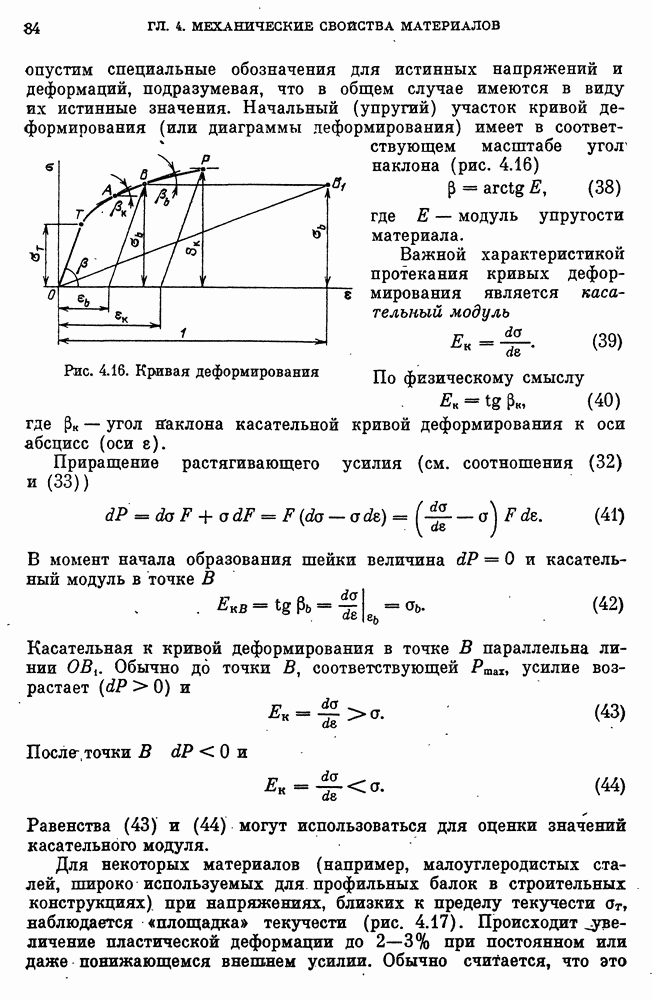
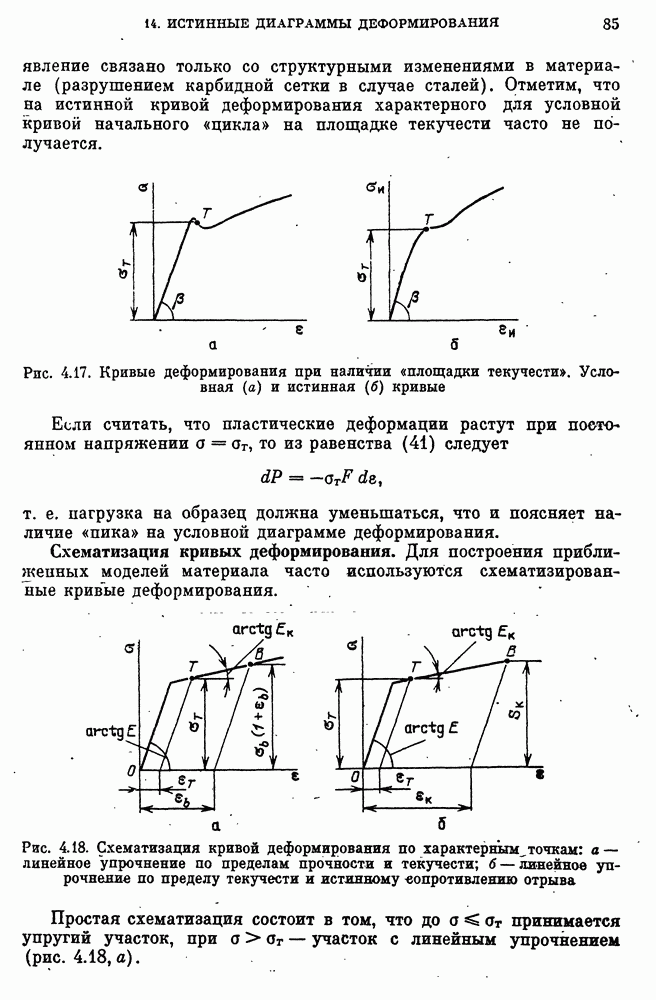
- 14. Истинные диаграммы деформирования и их схематизация
- Особенности кривых деформирования
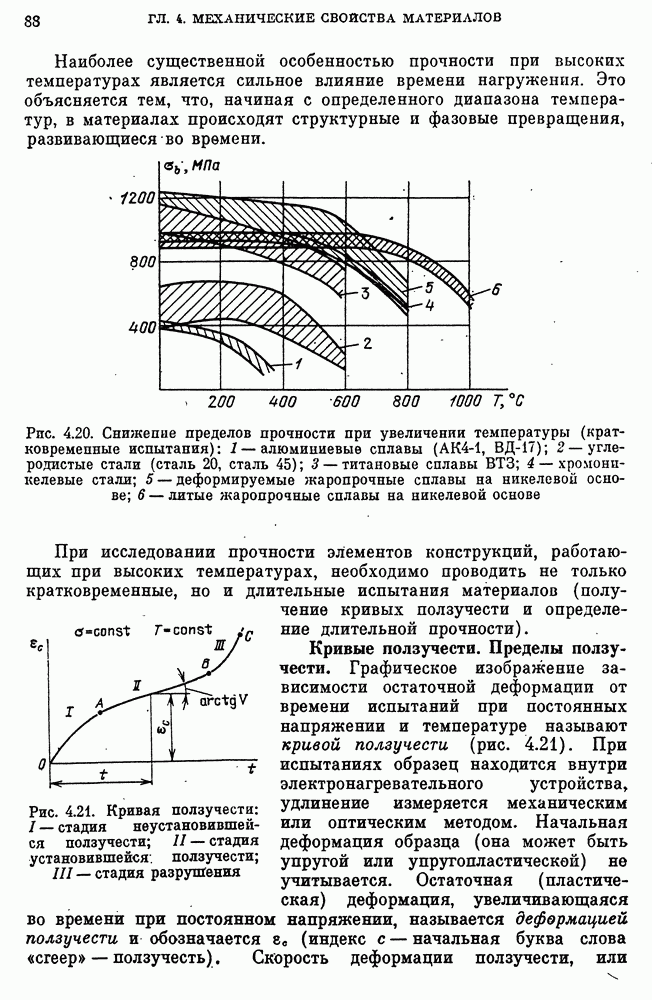
- 15. Ползучесть и длительная прочность
- Кривые ползучести. Пределы ползучести.
- Влияние ползучести на напряженное состояние в элементах конструкций.
- Длительная прочность, предел длительной прочности.
- Зависимость пределов длительной прочности от времени нагружения.
- Рассеяние долговечности при испытаниях длительной прочности.
- Зависимость пределов длительной прочности от температуры.
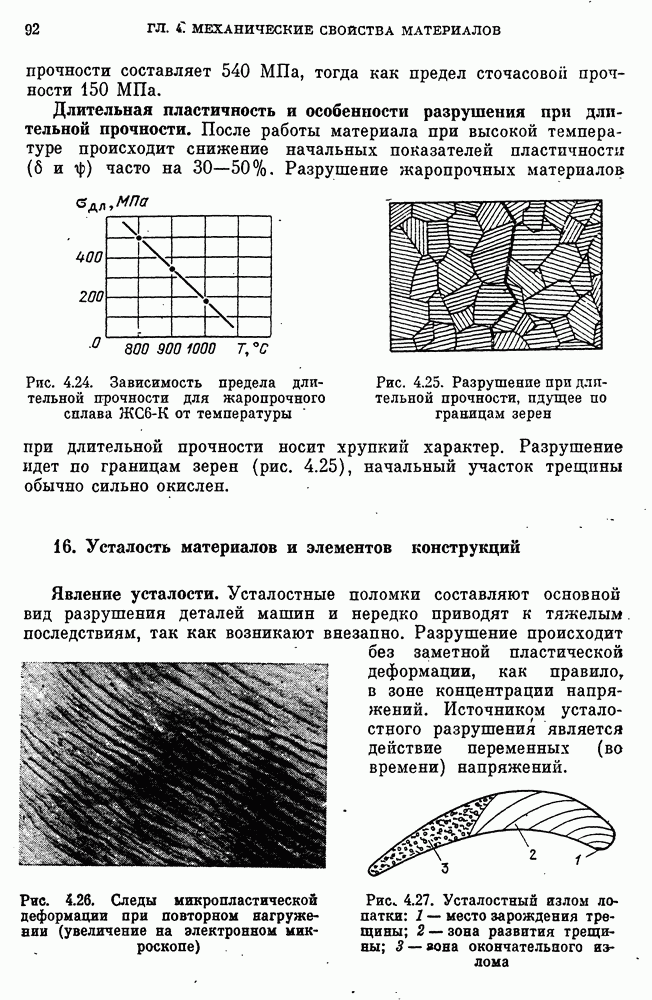
- Длительная пластичность и особенности разрушения при длительной прочности.
- 16. Усталость материалов и элементов конструкций
- Циклы переменных напряжений.
- Испытания на усталость.
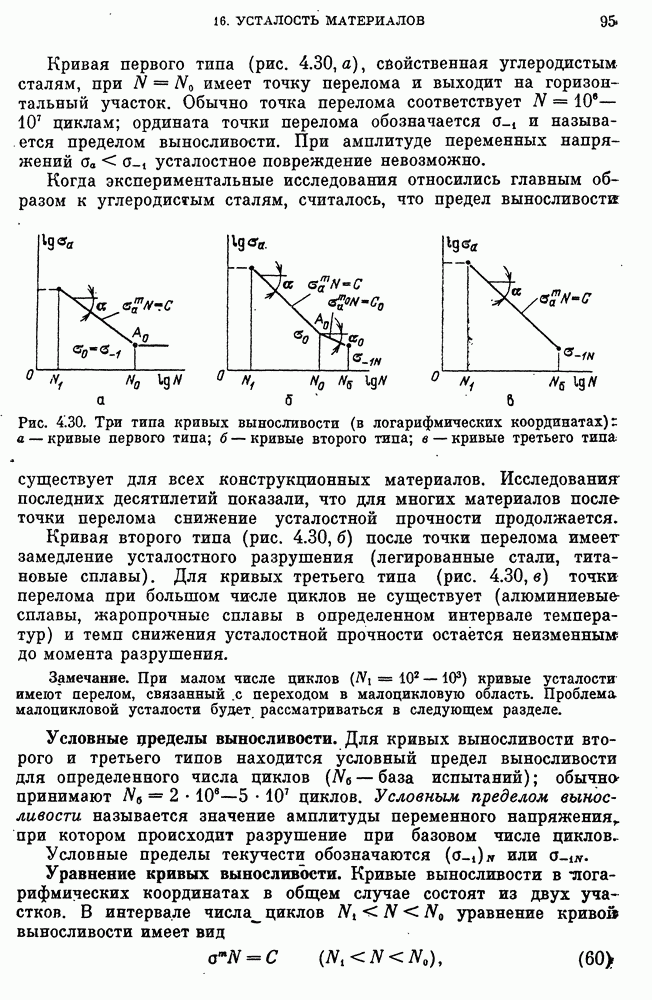
- Влияние числа циклов нагружения на усталостную прочность, кривые выносливости, пределы выносливости.
- Уравнение кривых выносливости.
- Влияние постоянных напряжений на усталостную прочность.
- Влияние концентрации напряжений.
- Влияние поверхностного слоя.
- Влияние абсолютных размеров деталей.
- Рассеяние усталостной долговечности.
- 17. Малоцикловая усталость
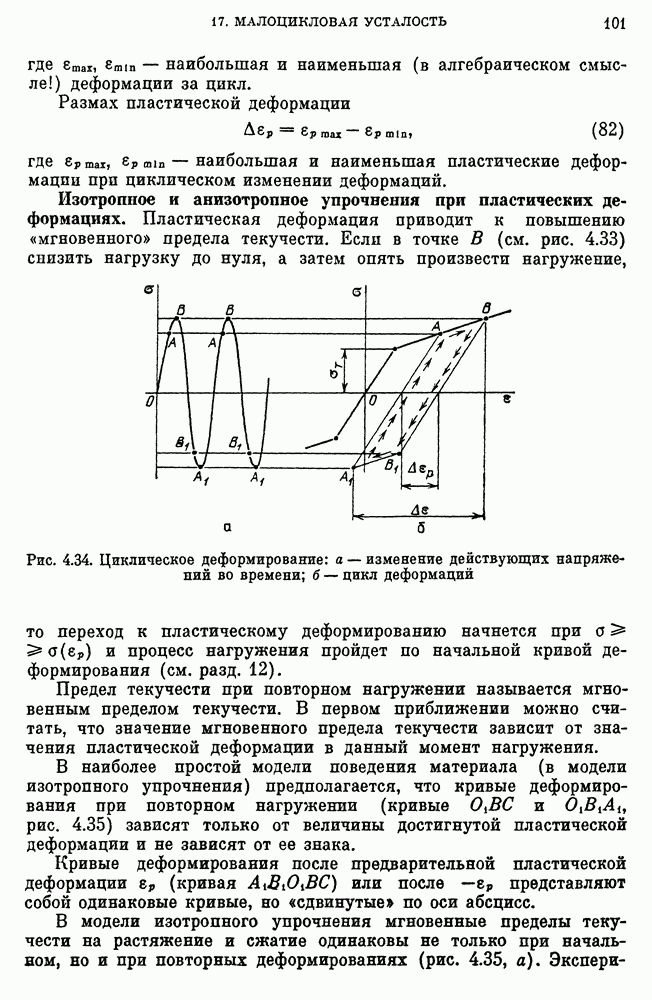
- Изотропное и анизотропное упрочнения при пластических деформациях.
- Явление малоцикловой усталости.
- ГЛАВА 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- Связь деформаций сдвига и касательных напряжений.
- Связь модуля сдвига с модулем упругости и коэффициентом Пуассона.
- Температурная деформация.
- Общая форма закона упругости.
- Другие формы закона упругости.
- Матричная запись закона упругости.
- Модель упругости для анизотропного тела.
- 19. Модели пластичности
- Уравнения пластичности в векторной форме.
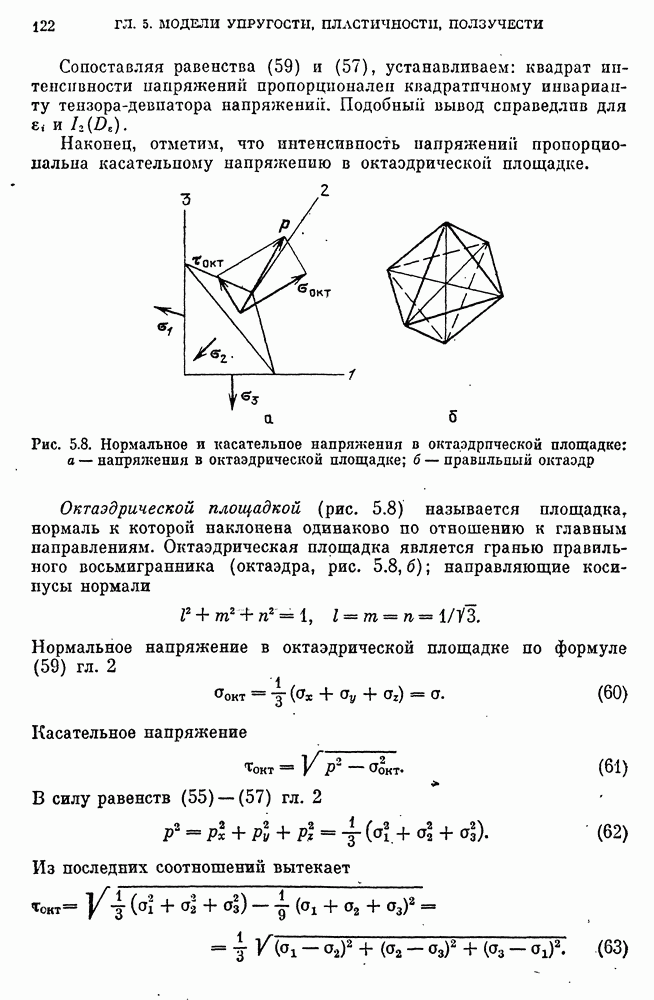
- Интенсивность напряжений и деформаций.
- Интенсивность упругих и пластических деформаций.
- Обобщенная кривая деформирования.
- Еще одна форма уравнений Генки — Ильюшина.
- Коэффициент Пуассона при упругопластических деформациях.
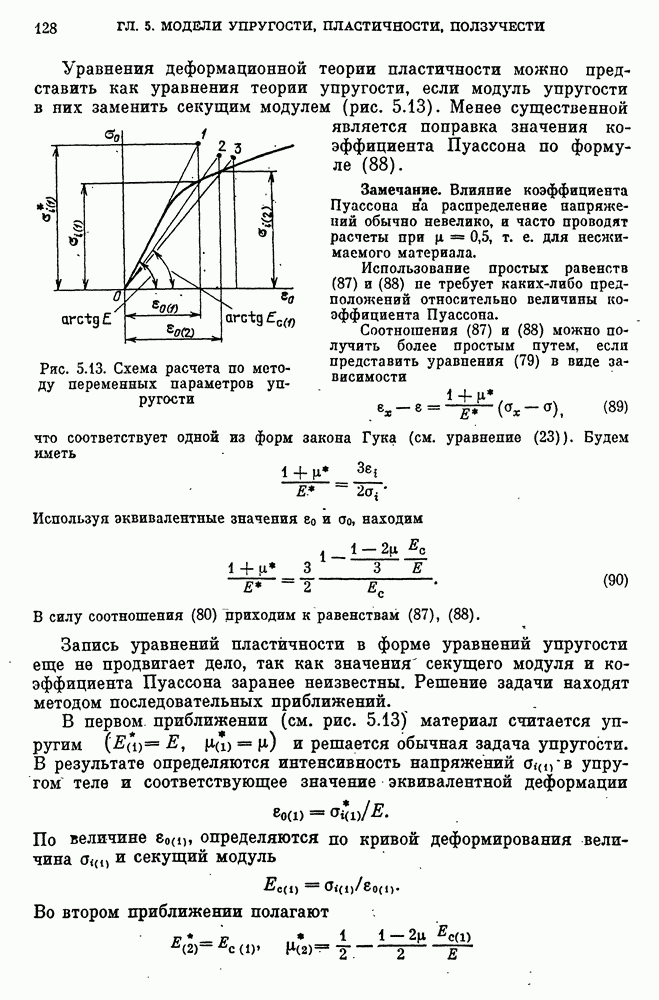
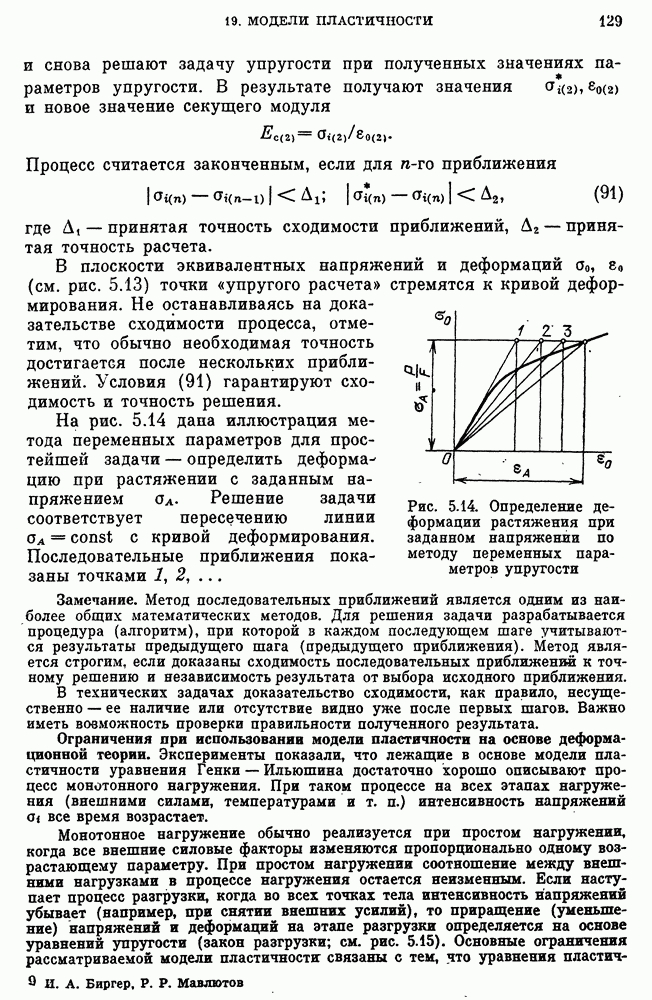
- Метод переменных параметров упругости.
- Ограничения при использовании модели пластичности на основе деформационной теории.
- 20. Модели ползучести и вязкоупругости
- Модели ползучести, основанные на теории старения. Изохронные кривые ползучести.
- Модели ползучести, основанные на теории течения и теории упрочнения.
- Установившаяся ползучесть.
- Модели вязкоупругости.
- ГЛАВА 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
- 21. Растяжение и сжатие стержней сосредоточенными и распределенными силами
- Приближенные модели растяжения и сжатия стержней.
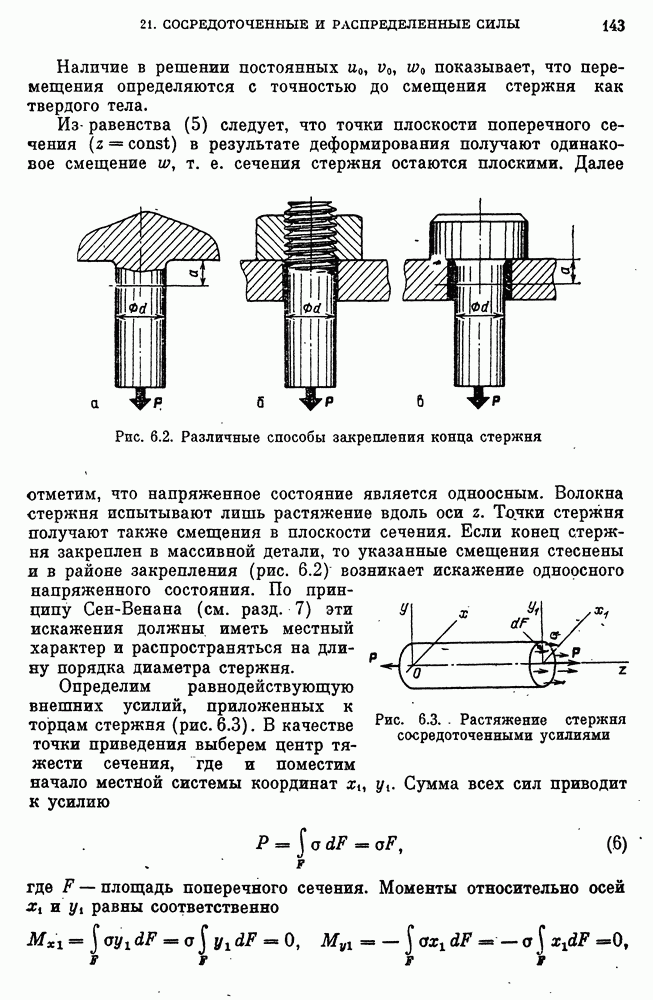
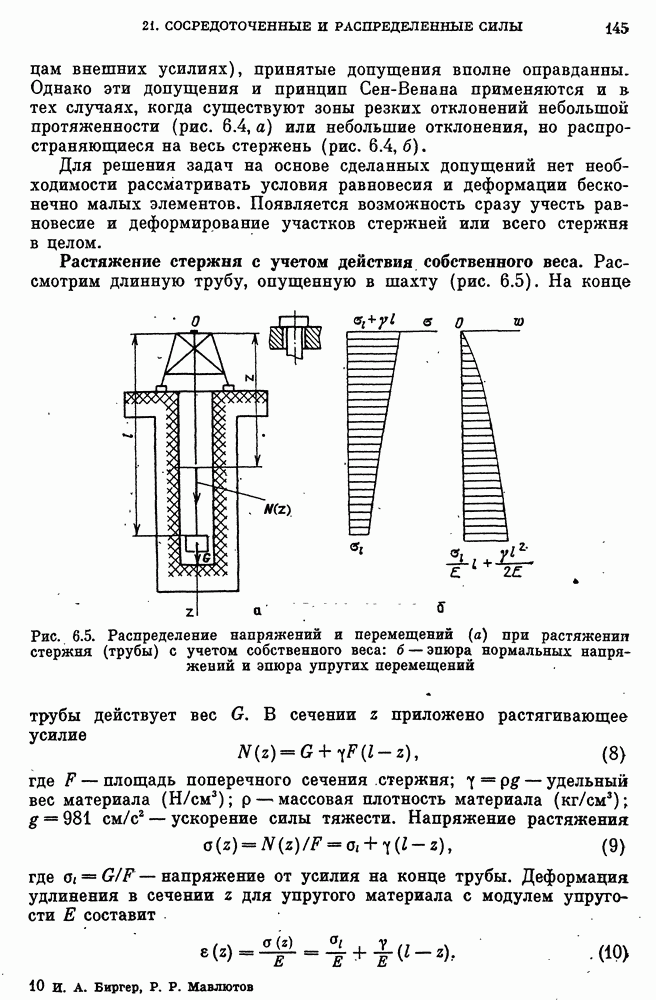
- Растяжение стержня с учетом действия собственного веса.
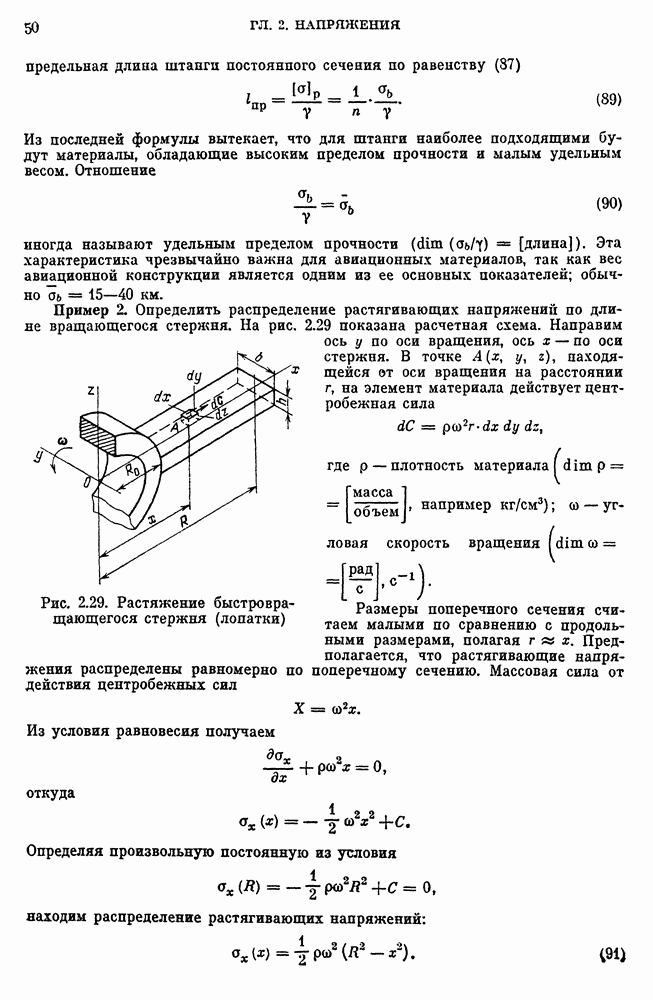
- Растяжение стержня в поле центробежных сил.
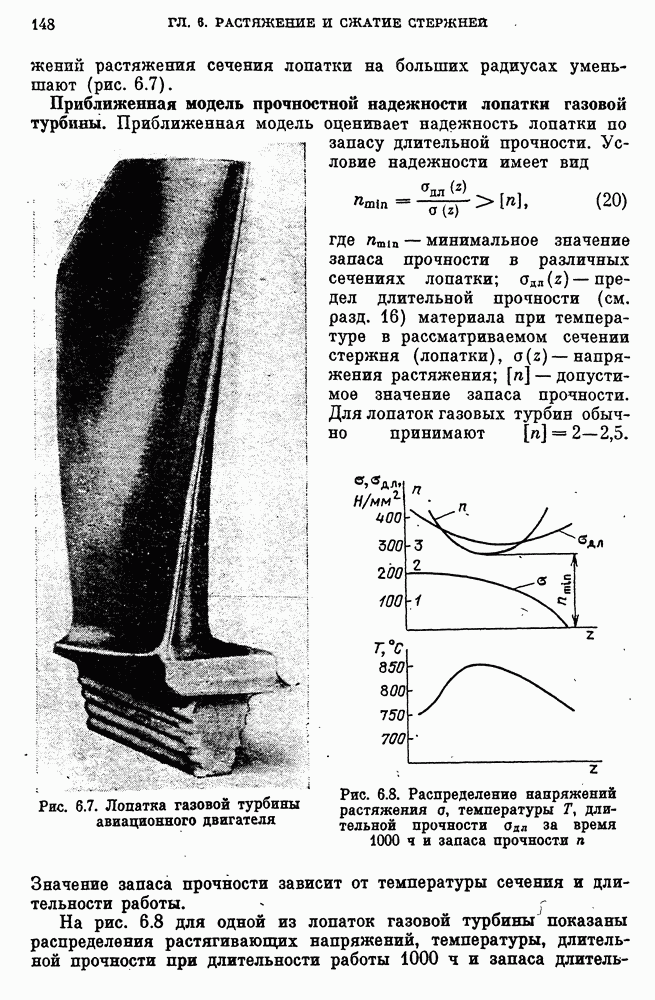
- Приближенная модель прочностной надежности лопатки газовой турбины.
- Связь запаса прочности по напряжениям и запаса прочности по долговечности.
- 22. Статически неопределимые задачи растяжения и сжатия стержней
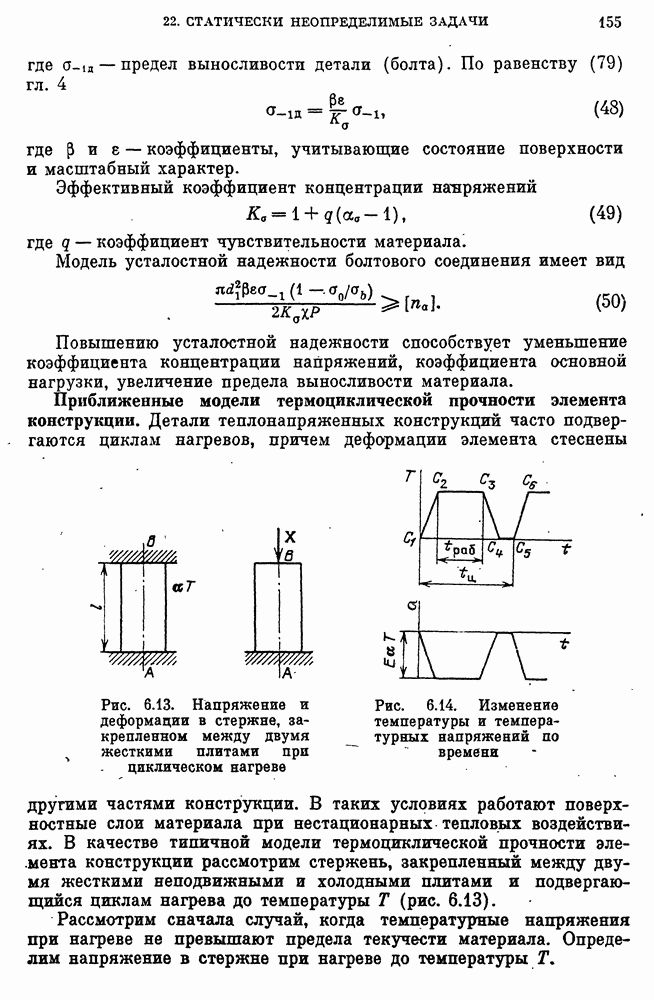
- Прочностная модель болтового соединения.
- Модель прочностной надежности болта при действии переменных нагрузок.
- Приближенные модели термоциклической прочности элемента конструкции.
- Учет ползучести материала при определении температурных напряжений.
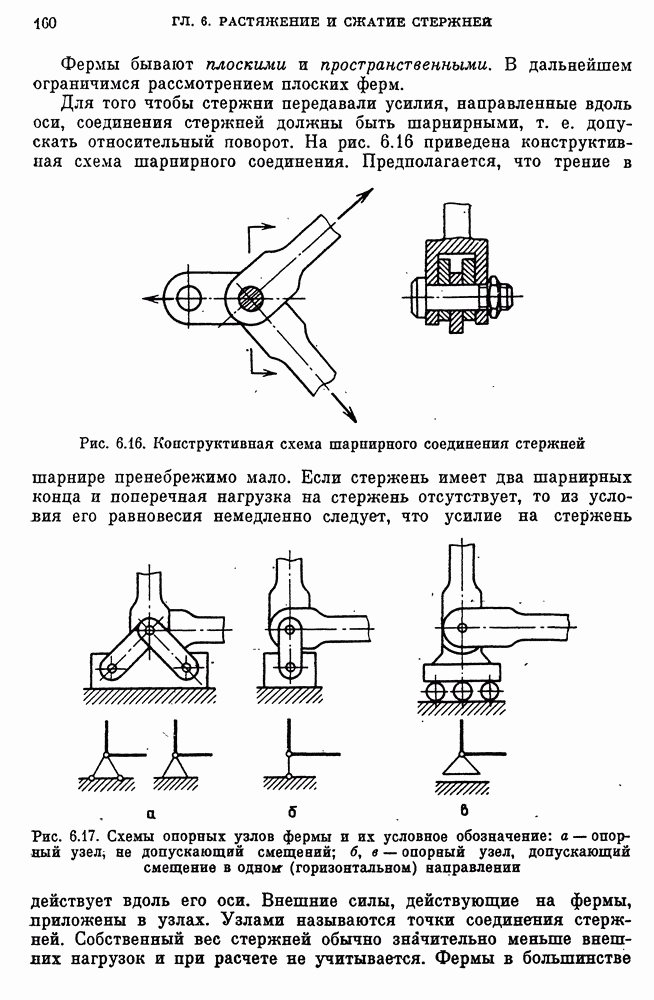
- 23. Стержневые системы (фермы)
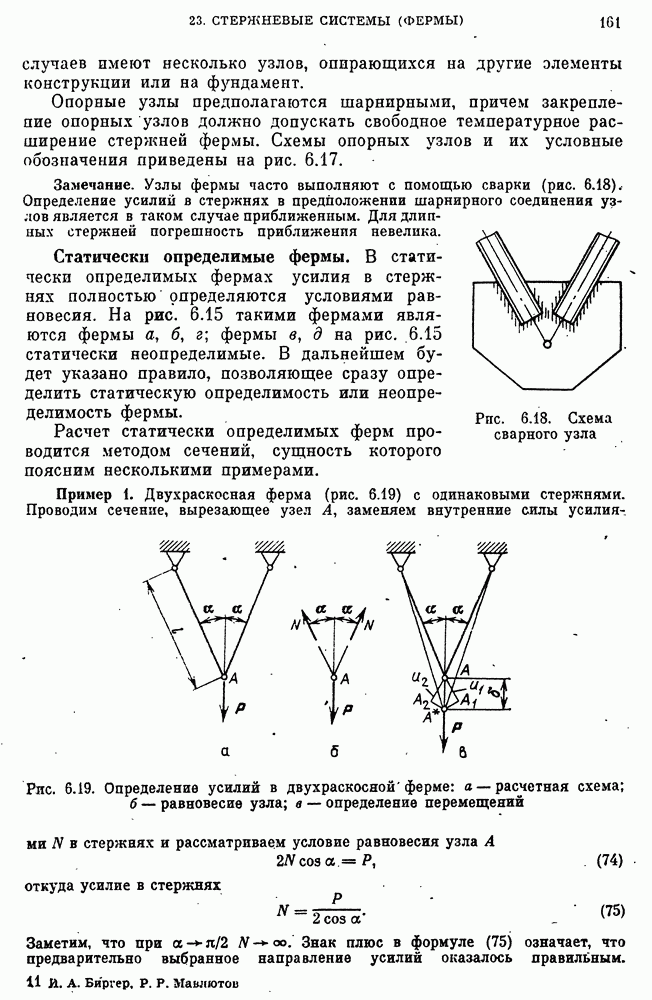
- Статически определимые фермы.
- Общие замечания о статически определимых фермах и сопоставление со статически неопределимыми.
- 24. Статически неопределимые стержневые системы
- Работа статически неопределимой системы после возникновения пластических деформаций.
- Модель надежности по несущей способности.
- Сопоставление двух моделей надежности.
- Расчет в упругопластической стадии методом переменных параметров упругости.
- 25. Гибкие нити
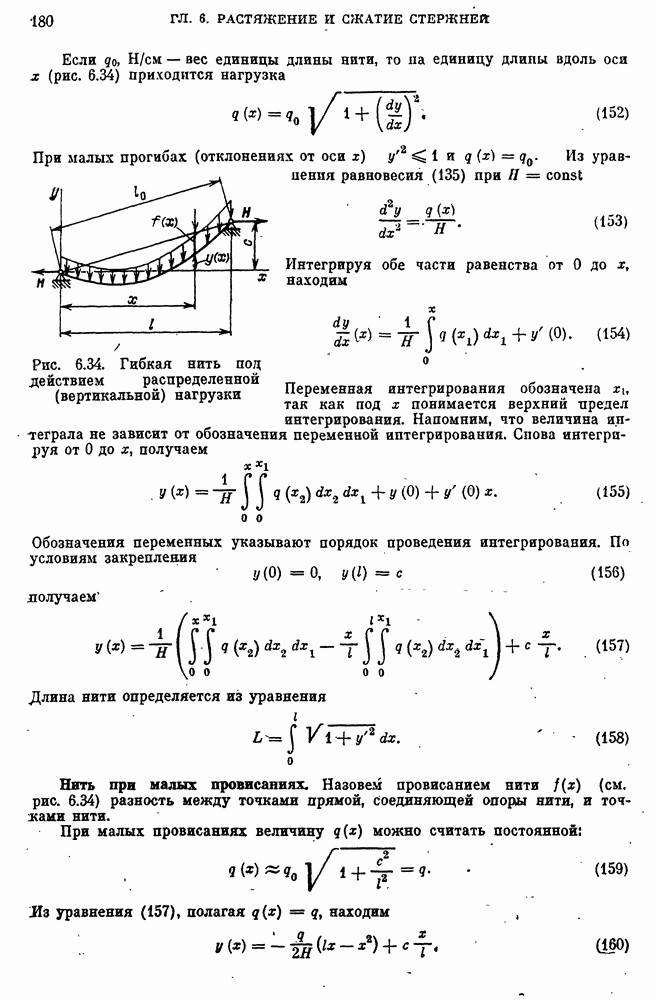
- Гибкая нить под действием распределенной нагрузки.
- Нить при малых провисаниях.
- ГЛАВА 7. КРУЧЕНИЕ СТЕРЖНЕЙ
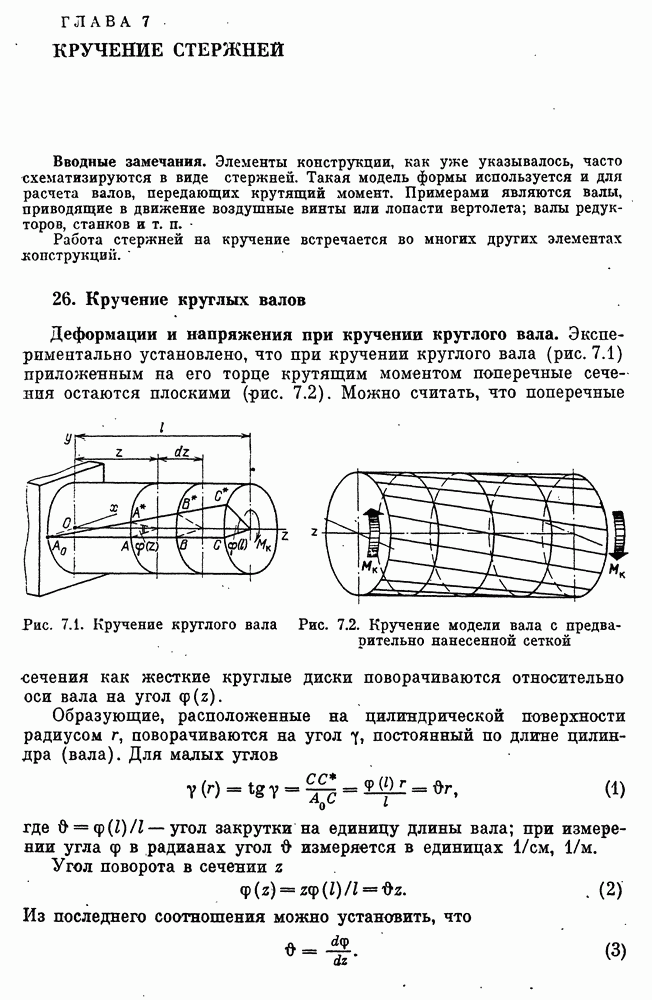
- 26. Кручение круглых валов
- Кручение полого вала.
- Кручение вала в упругопластической стадии.
- Кручение вала в стадии установившейся ползучести.
- Модели прочностной надежности вала при кручении.
- 27. Общая задача кручения стержней и концентрация напряжений
- Математическая постановка задачи. Функция кручения.
- Функция напряжения.
- Примеры точных решений. Стержень эллиптического сечения.
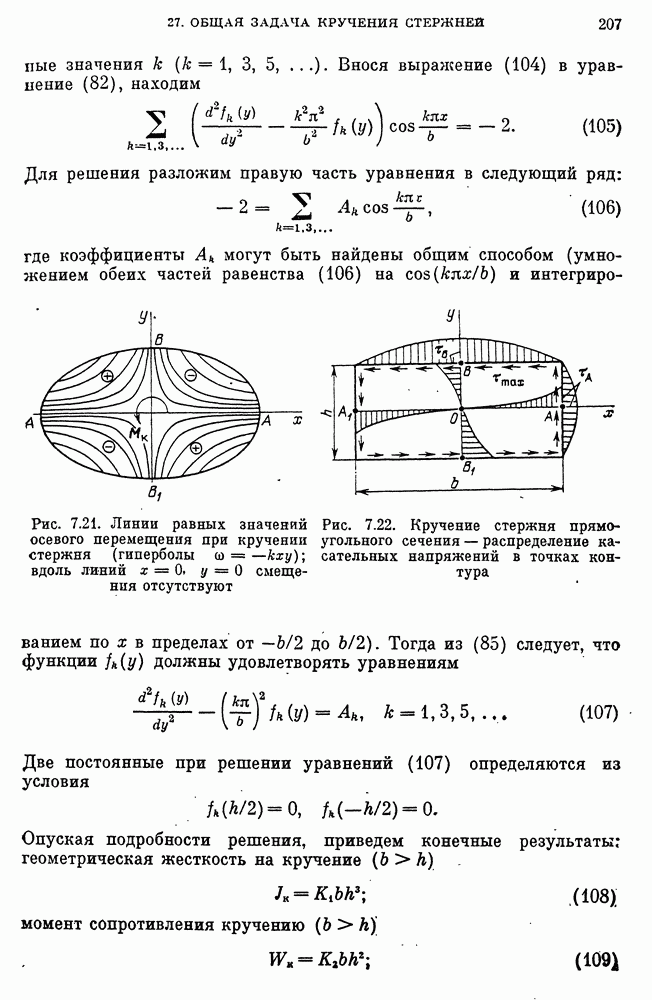
- Стержень прямоугольного сечения.
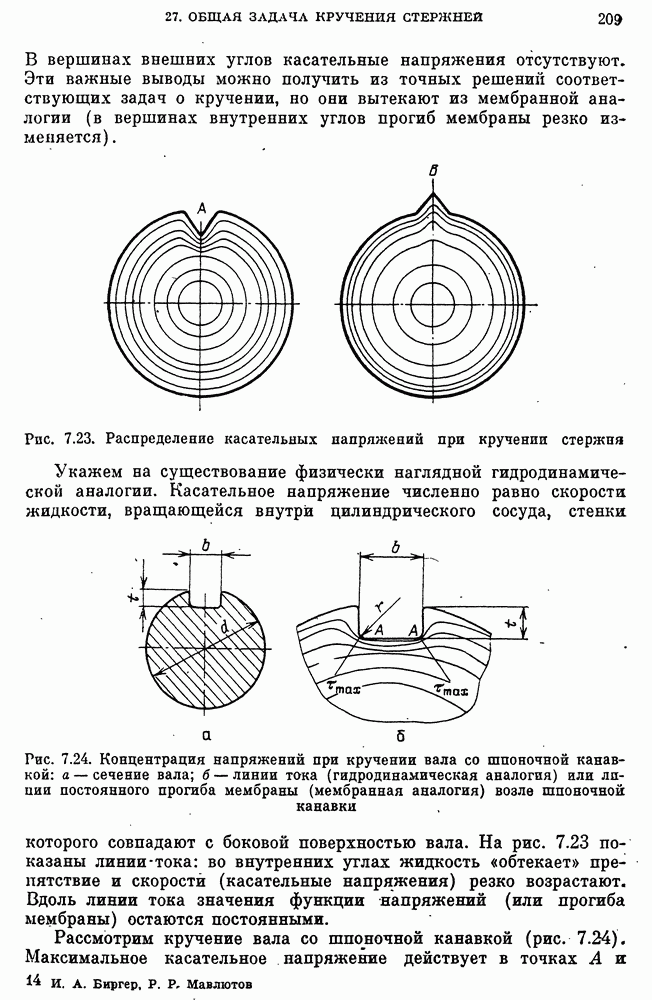
- Концентрация напряжений при кручении.
- 28. Кручение тонкостенных стержней
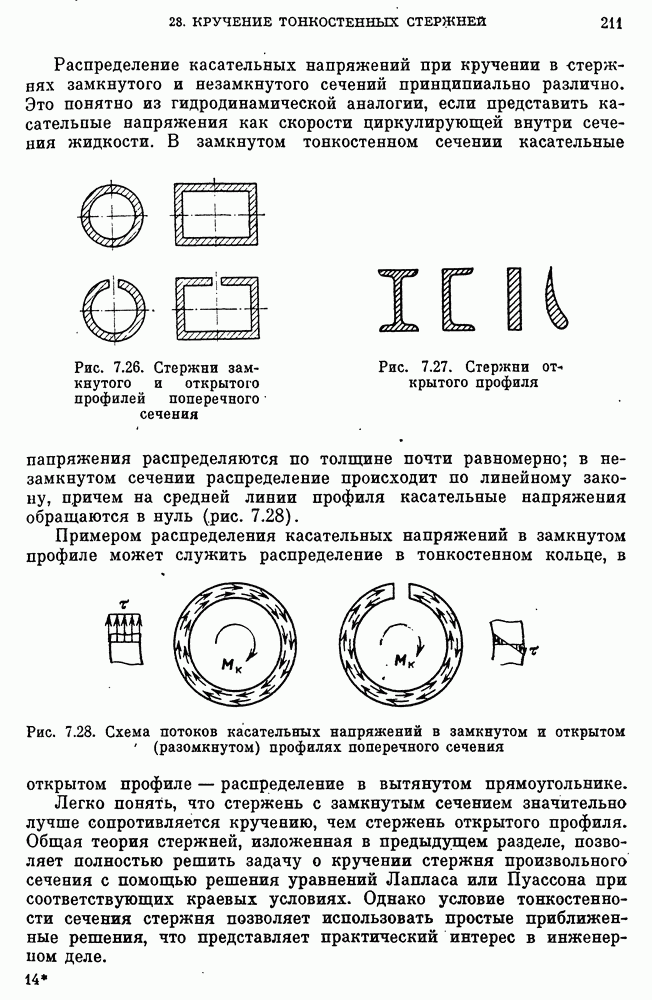
- Кручение стержня замкнутого профиля.
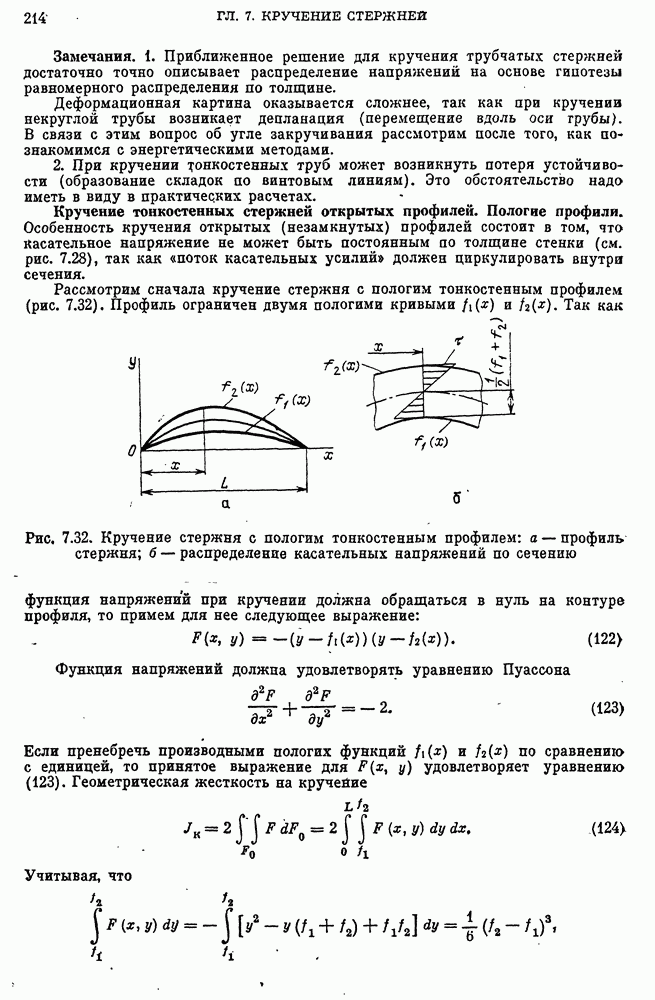
- Кручение тонкостенных стержней открытых профилей. Пологие профили.
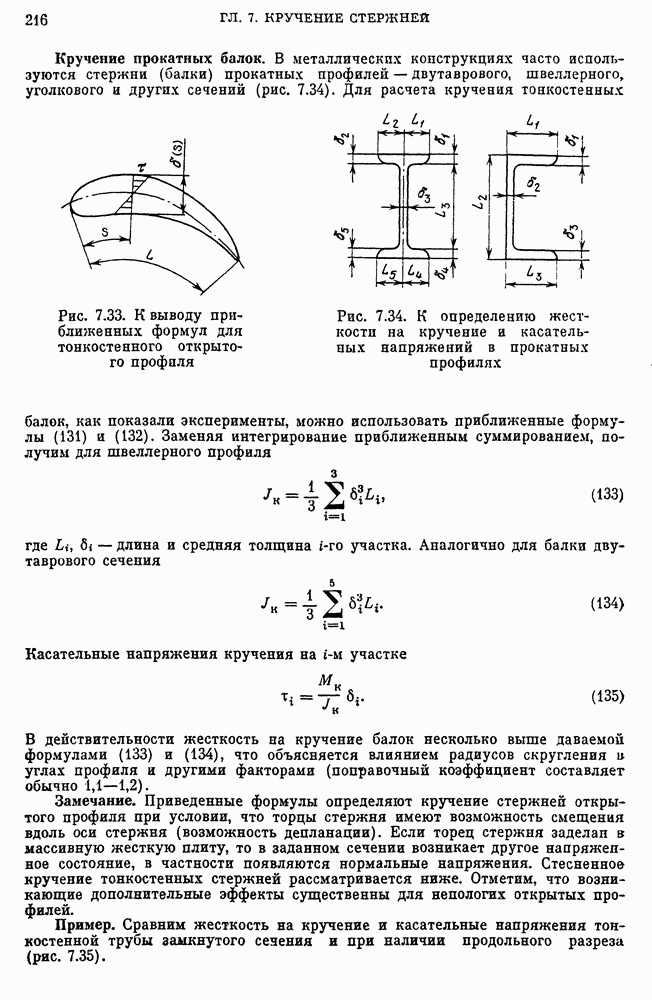
- Кручение прокатных балок.
- Кручение тонкостенных стержней открытого профиля с переменными параметрами упругости.
- ГЛАВА 8. ИЗГИБ СТЕРЖНЕЙ
- 29. Гипотеза плоских сечений и нормальные напряжения изгиба
- Распределение нормальных напряжений изгиба.
- Система уравнений для определения нормальных напряжений изгиба и растяжения стержня и ее упрощение.
- Напряжения растяжения и изгиба в стержне от действия внешних сил.
- Температурные напряжения.
- Обоснование гипотезы плоских сечений.
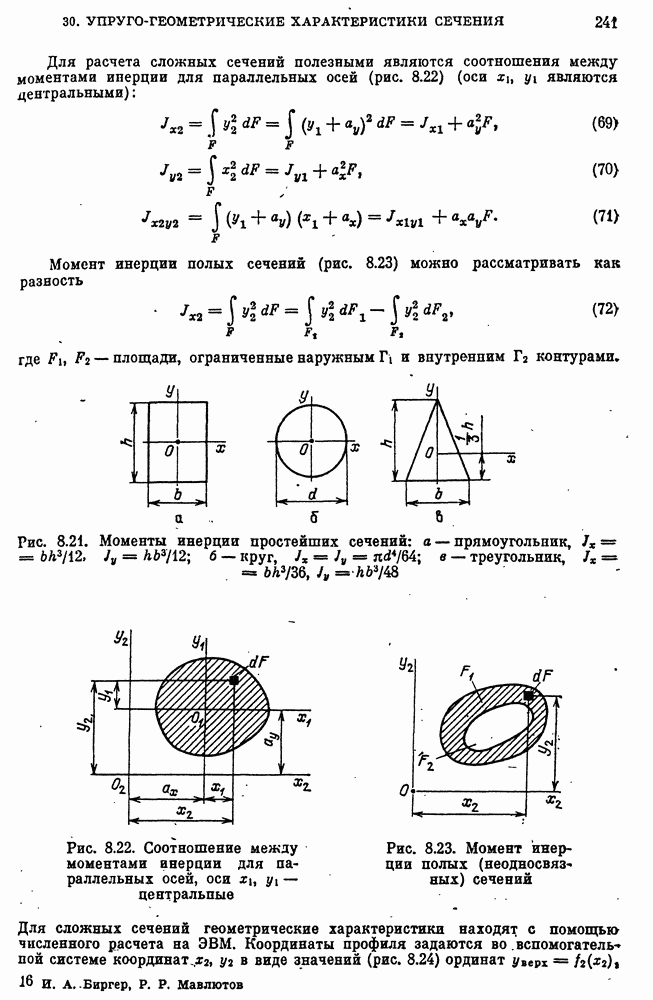
- 30. Упруго-геометрические характеристики сечения стержня при изгибе. Главные оси, главные моменты инерции
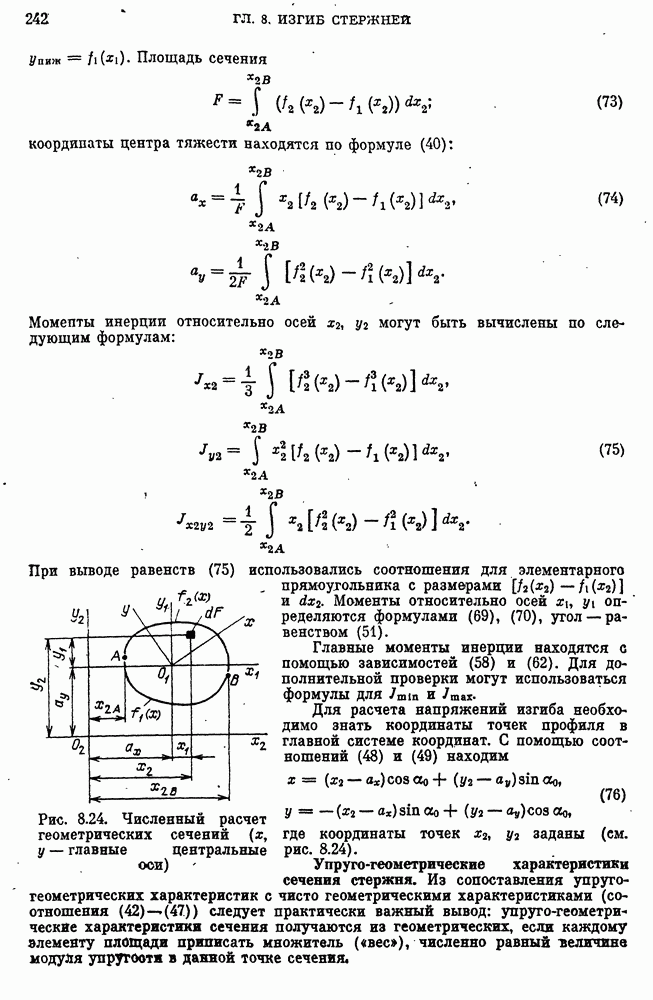
- Геометрические характеристики сечения стержня.
- Главные моменты инерции сечения.
- Упруго-геометрические характеристики сечения стержня.
- 31. Условия равновесия элемента стержня и касательные напряжения изгиба
- Скачки перерезывающей силы и изгибающего момента.
- Условие равновесия элемента стержня при наличии распределенных изгибающих моментов.
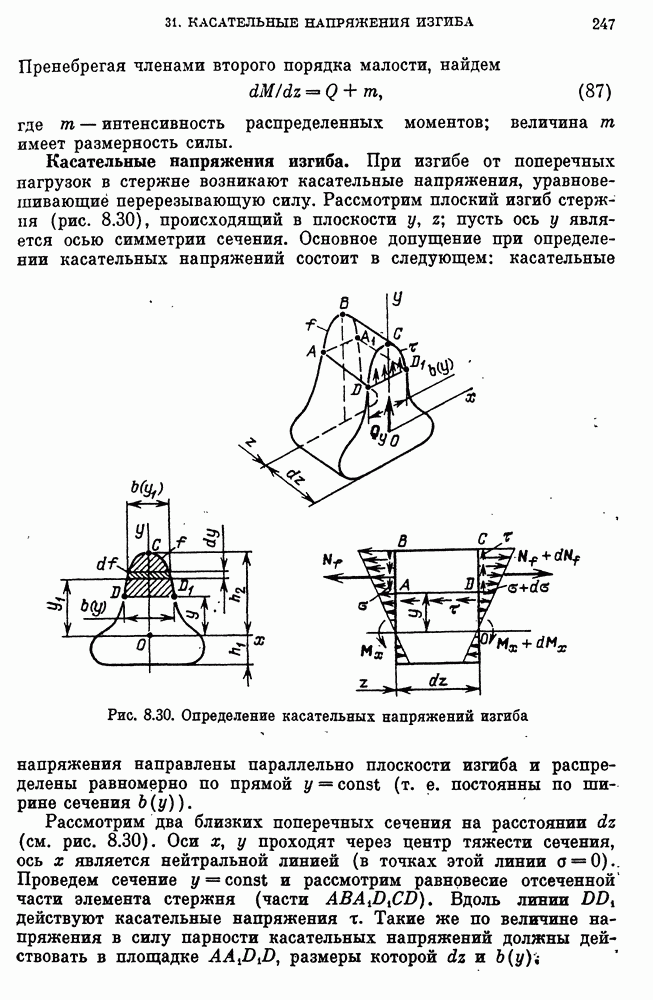
- Распределение касательных напряжений в стержне постоянного сечения.
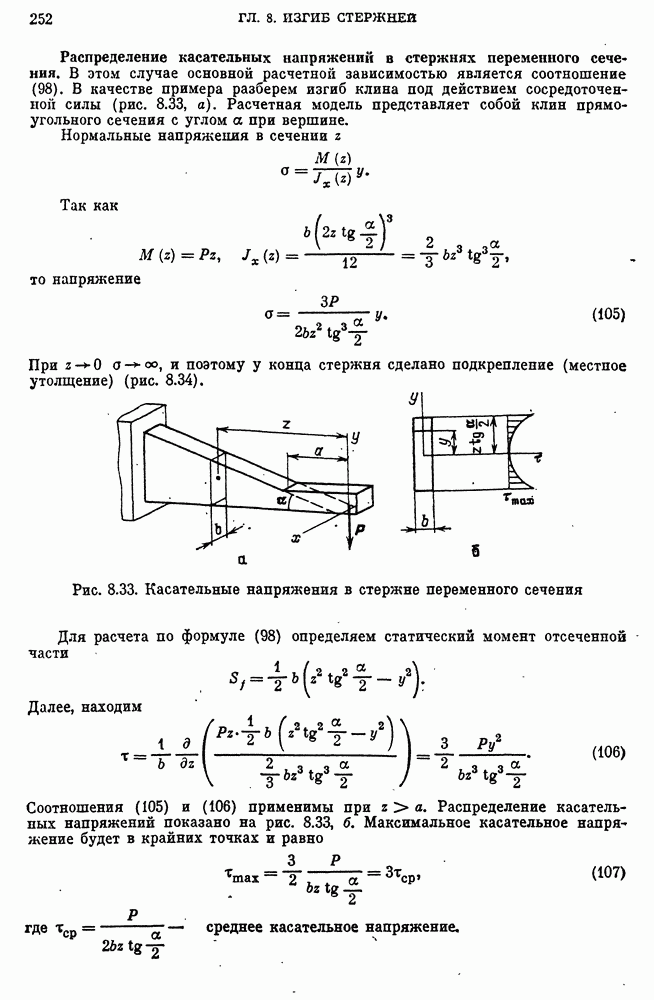
- Распределение касательных напряжений в стержнях переменного сечения.
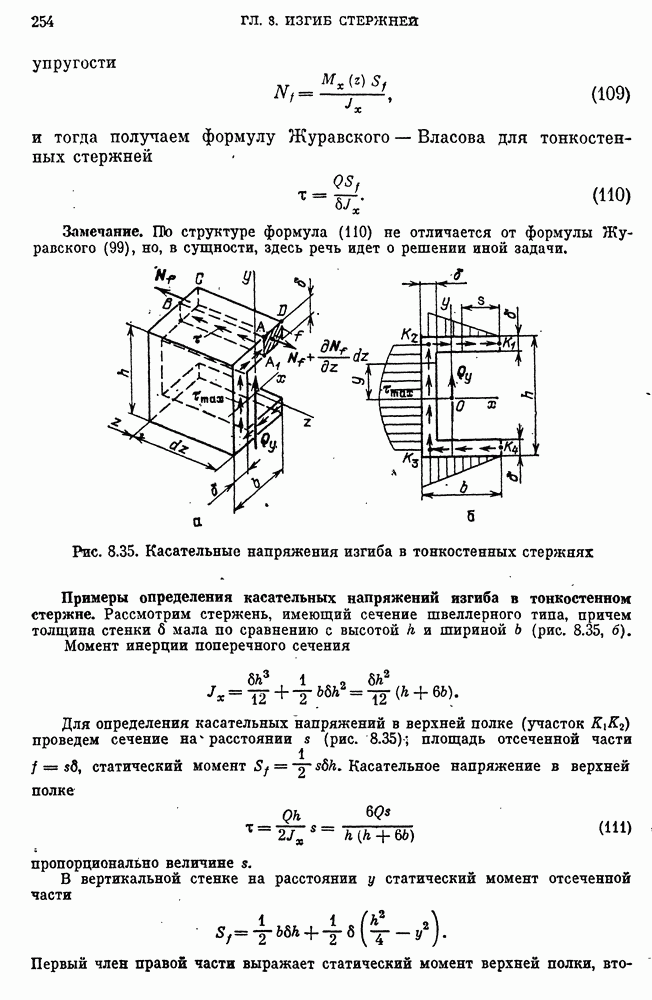
- Касательные напряжения изгиба в тонкостенных стержнях.
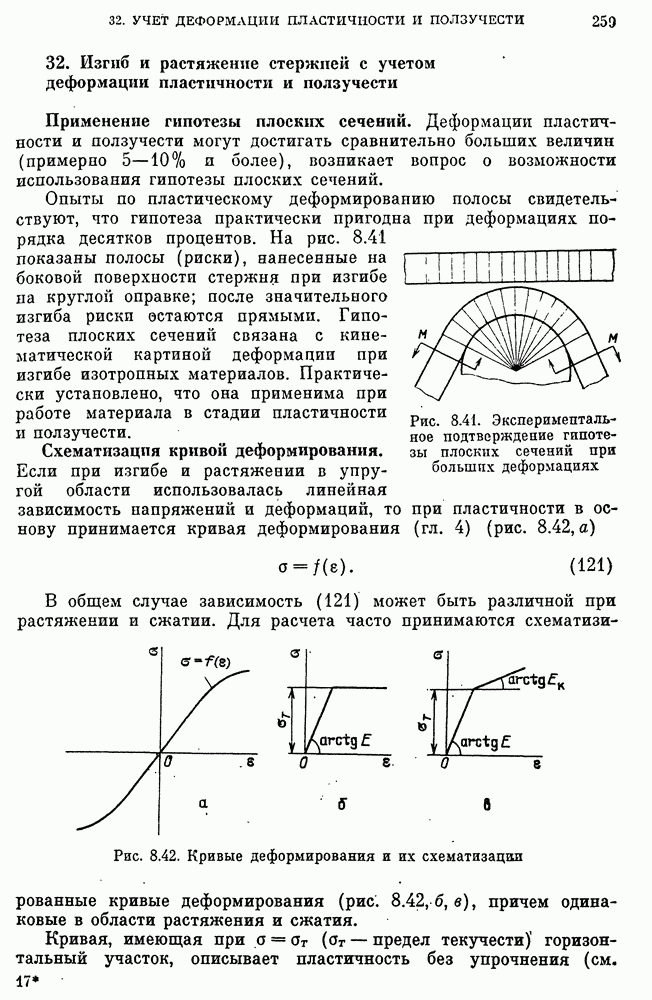
- 32. Изгиб и растяжение стержней с учетом деформации пластичности и ползучести
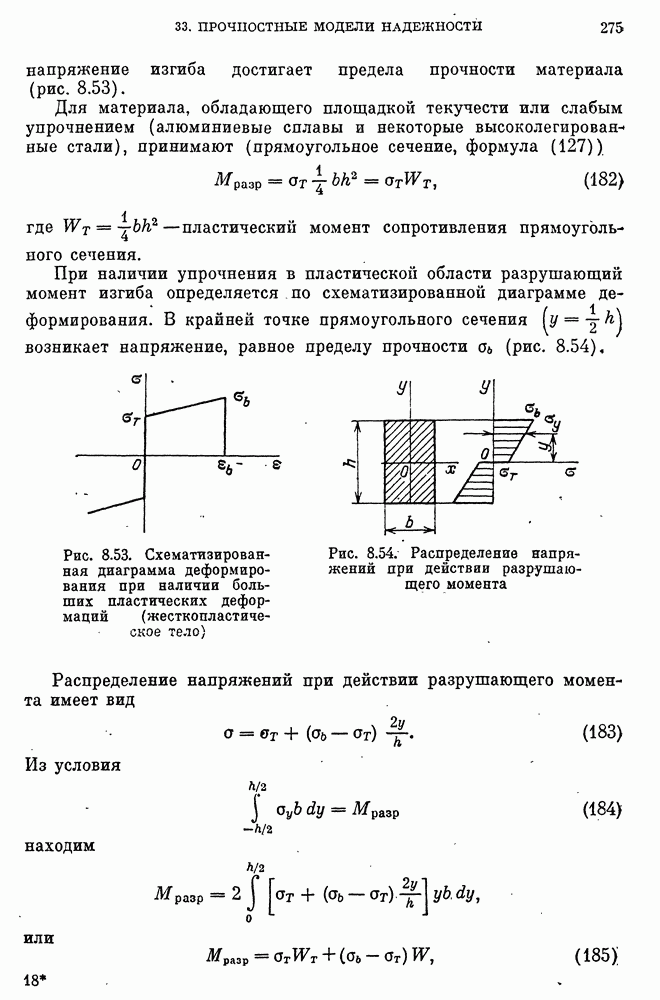
- Изгиб стержней при пластичности без упрочнения. Предельный изгибающий момент.
- Остаточные напряжения.
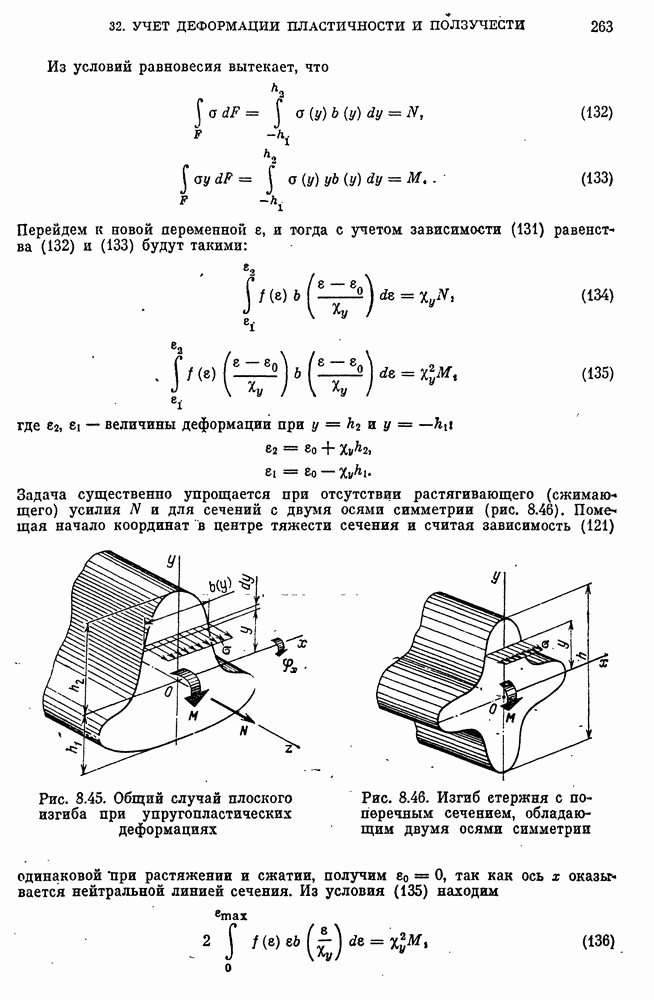
- Общий случай расчета стержня в упругопластнческой стадии. Метод переменных параметров упругости.
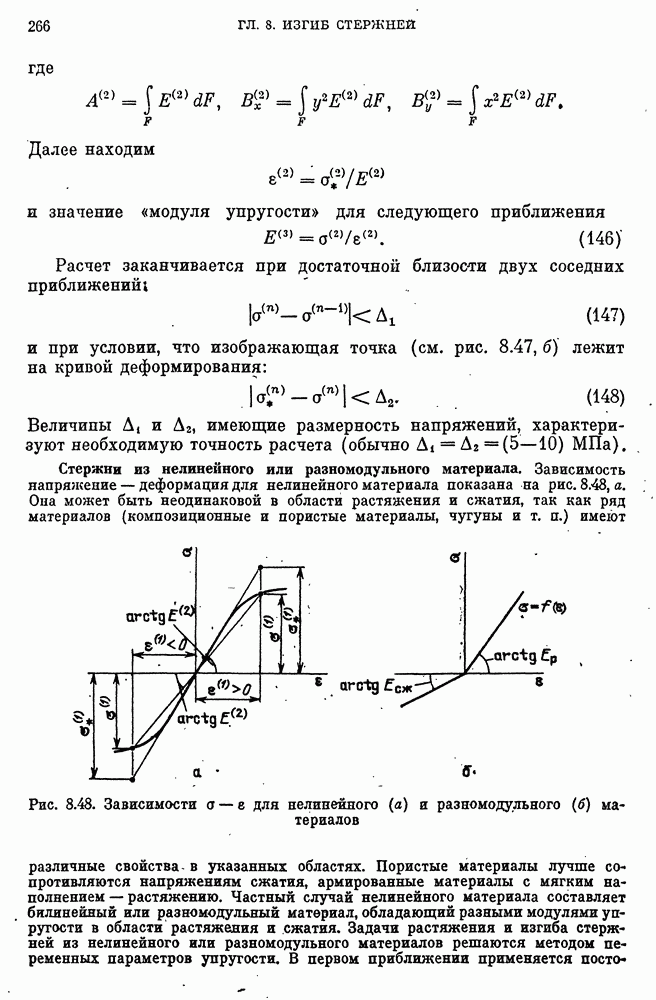
- Стержни из нелинейного или разномодульного материала.
- Касательные напряжения при изгибе стержней в упругопластической стадии.
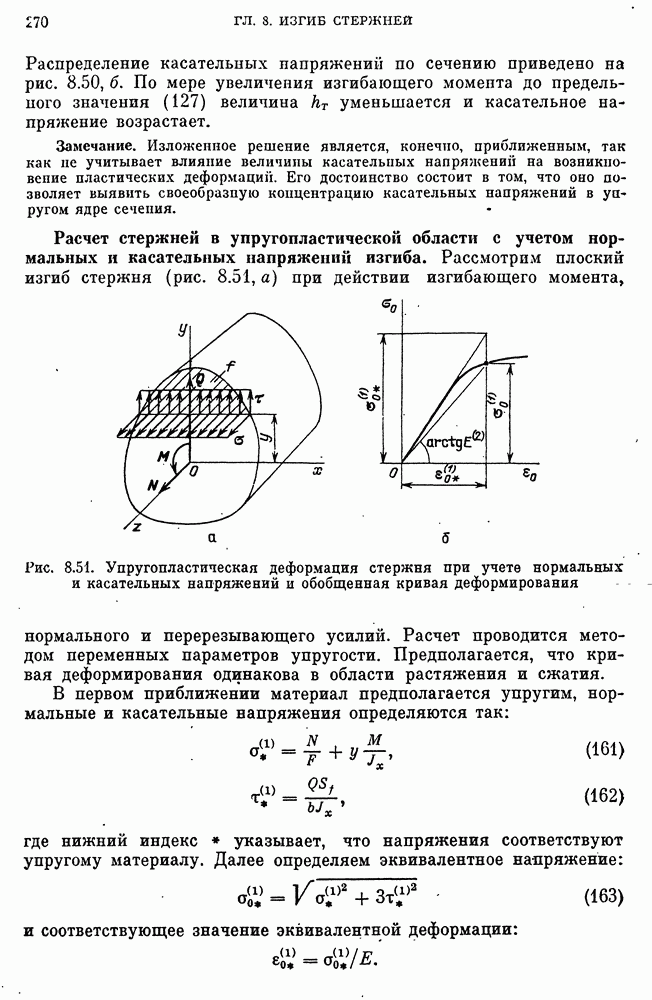
- Расчет стержней в упругопластической области с учетом нормальных и касательных напряжений изгиба.
- Учет деформации ползучести при изгибе стержня.
- Общий случай расчета стержней на изгиб при учете ползучести материала.
- 33. Прочностные модели надежности при изгибе
- Прочностная модель надежности при статической нагрузке по напряжениям.
- Прочностная модель надежности при переменной нагрузке.
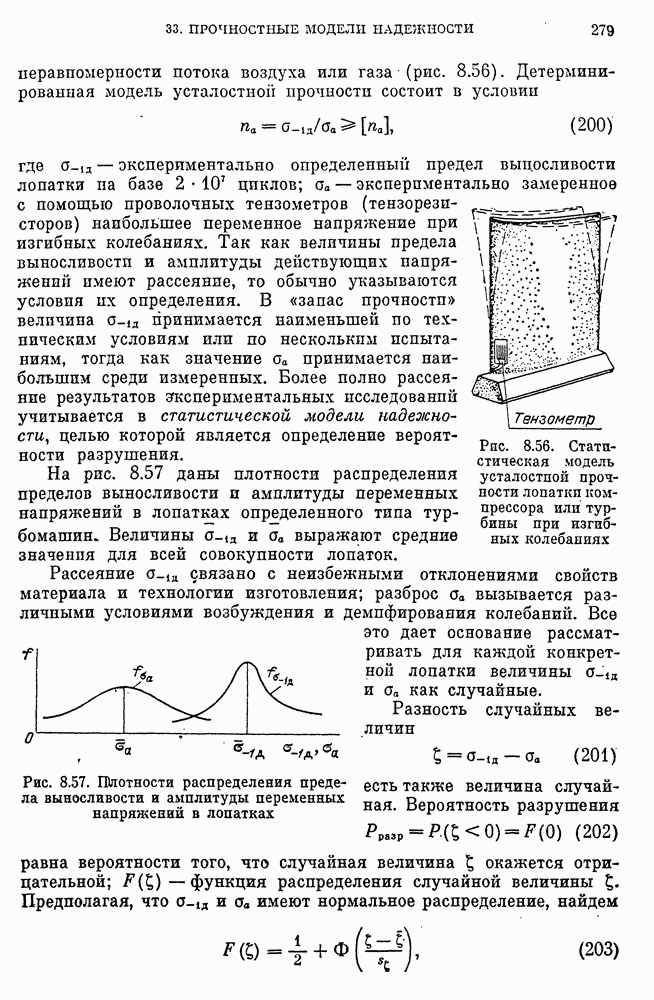
- Детерминированная и статистическая модели усталостней прочности лопатки компрессора или турбины, вероятность разрушения.
- Прочностная модель надежности валов.
- 34. Прогибы стержней
- Геометрическая картина изгибной деформации.
- Уравнение упругой линии стержня.
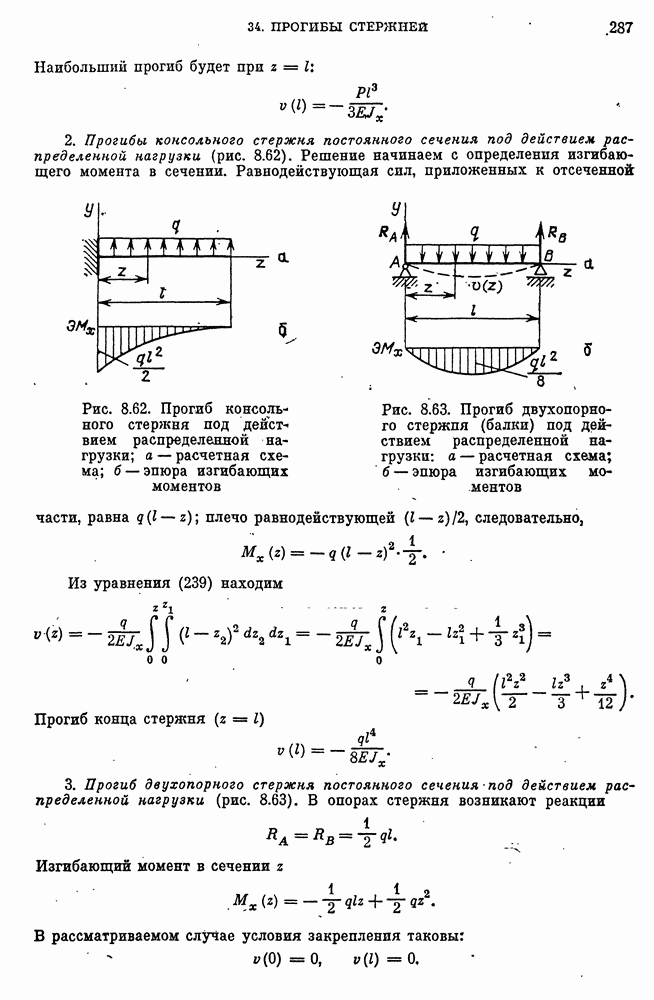
- Уравнение упругой линии при изгибе стержней постоянного сечения.
- Основная форма дифференциального уравнения плоского изгиба стержня.
- Дифференциальное уравнение плоского изгиба в матричной форме.
- Нормальные фундаментальные функции дифференциального уравнения изгиба и начальные параметры.
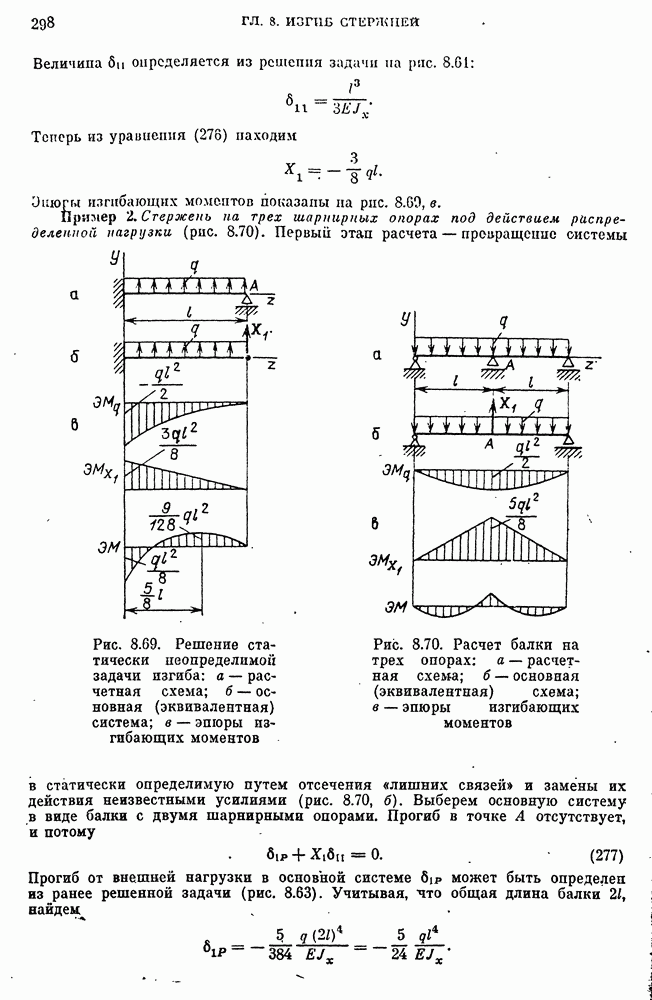
- Статически неопределимые задачи изгиба стержней.
- Учет деформации сдвига при изгибе стержня.
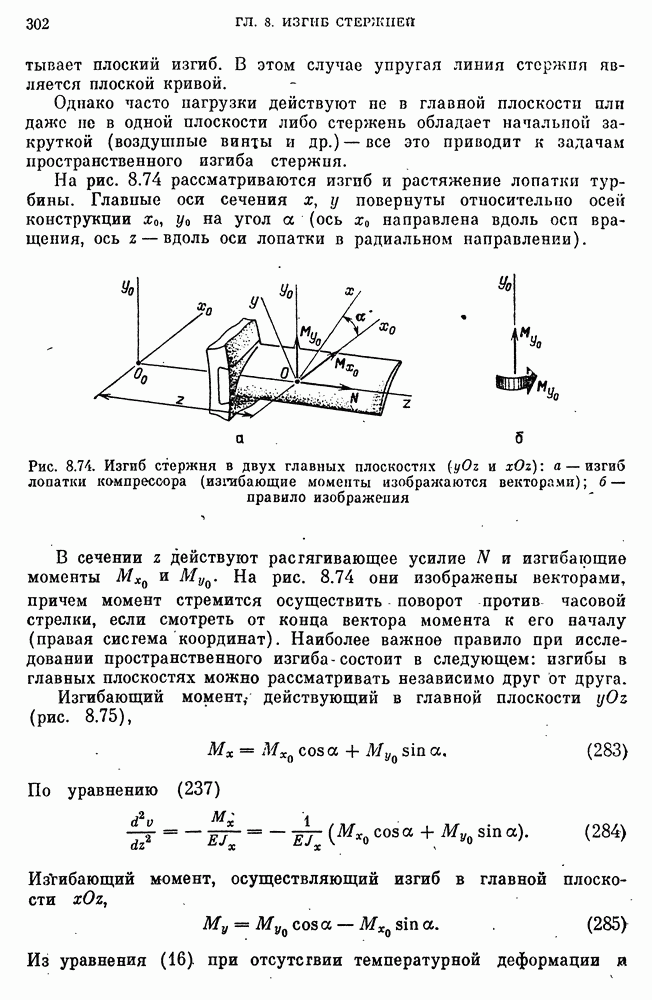
- Уравнение упругой линии стержня при изгибе в двух главных плоскостях.
- ГЛАВА 9. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ, ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ, ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
- 35. Потенциальная энергия деформации
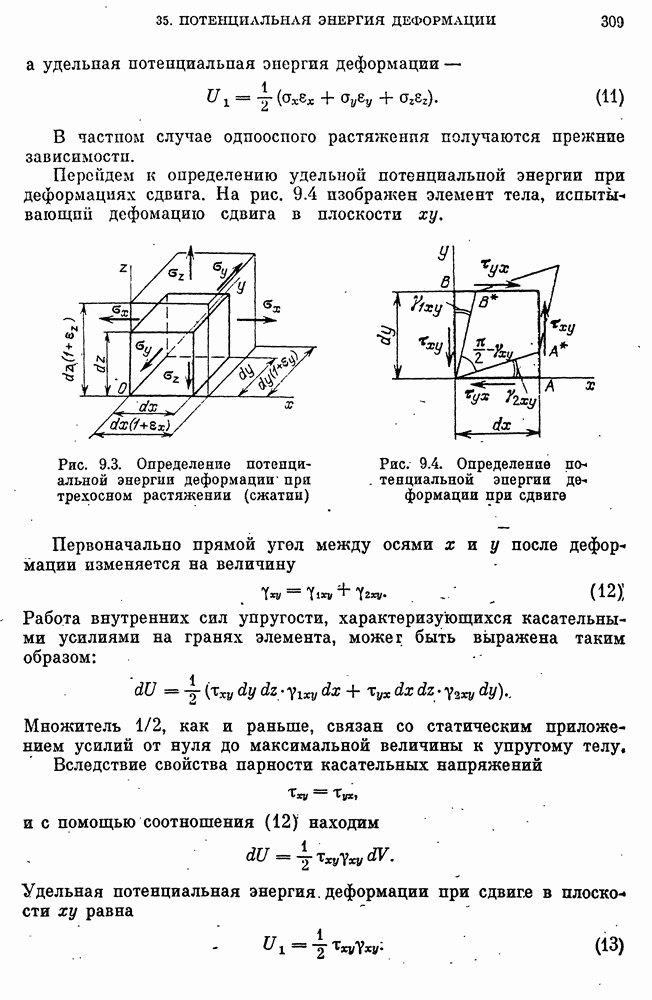
- Удельная потенциальная энергия деформации.
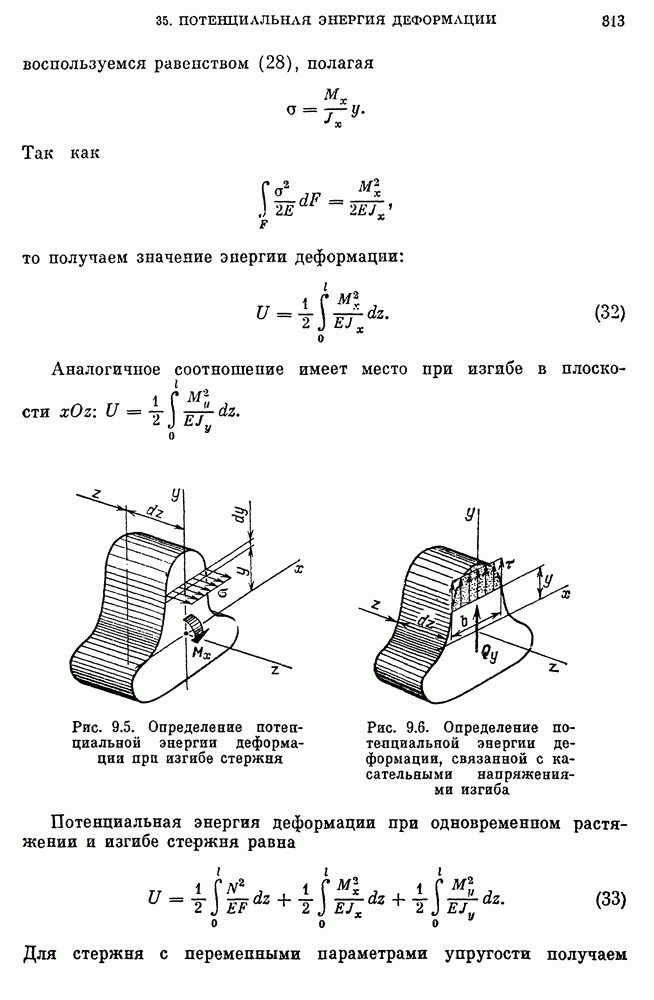
- Потенциальная энергия деформации стержней при растяжении и изгибе.
- Потенциальная энергия деформации, связанная с касательными напряжениями изгиба.
- 36. Вариационные методы
- Условия экстремума функционала, уравнение Эйлера — Пуассона, метод Рэлея — Ритца.
- Применение начала возможных перемещений, вариационное уравнение Лагранжа.
- Вариационное уравнение изгиба стержня.
- Применение метода Рэлея — Ритца к задаче изгиба стержня.
- Применение начала возможных перемещений для определения прогибов стержней. Интеграл Мора.
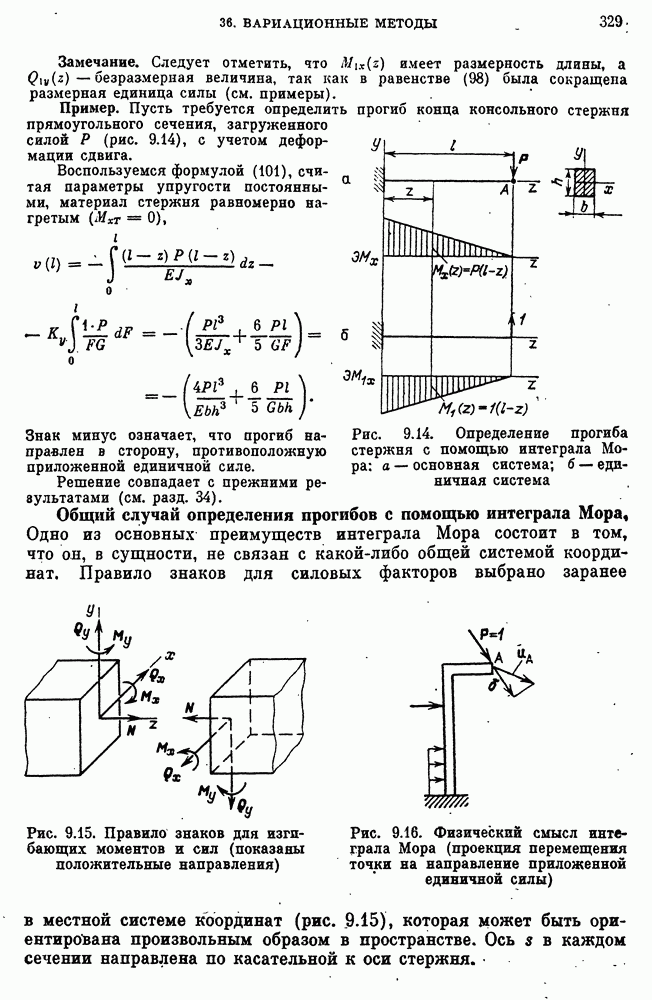
- Общий случай определения прогибов с помощью интеграла Мора.
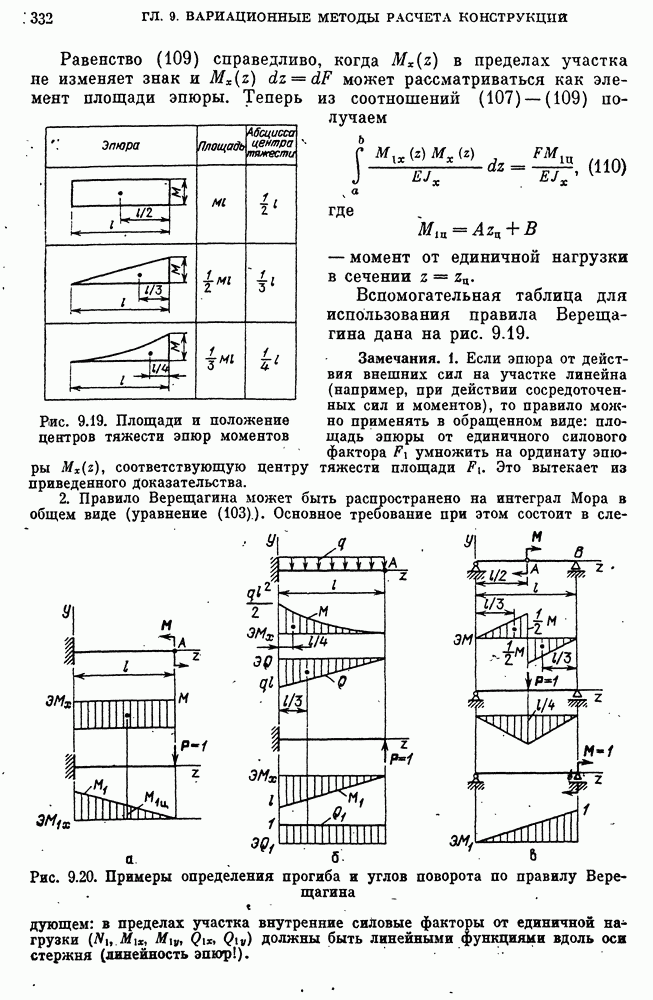
- Вычисление интеграла Мора по правилу Верещагина.
- 37. Вариационные методы и общие свойства упругих систем
- Вариационное уравнение метода вариации напряжений.
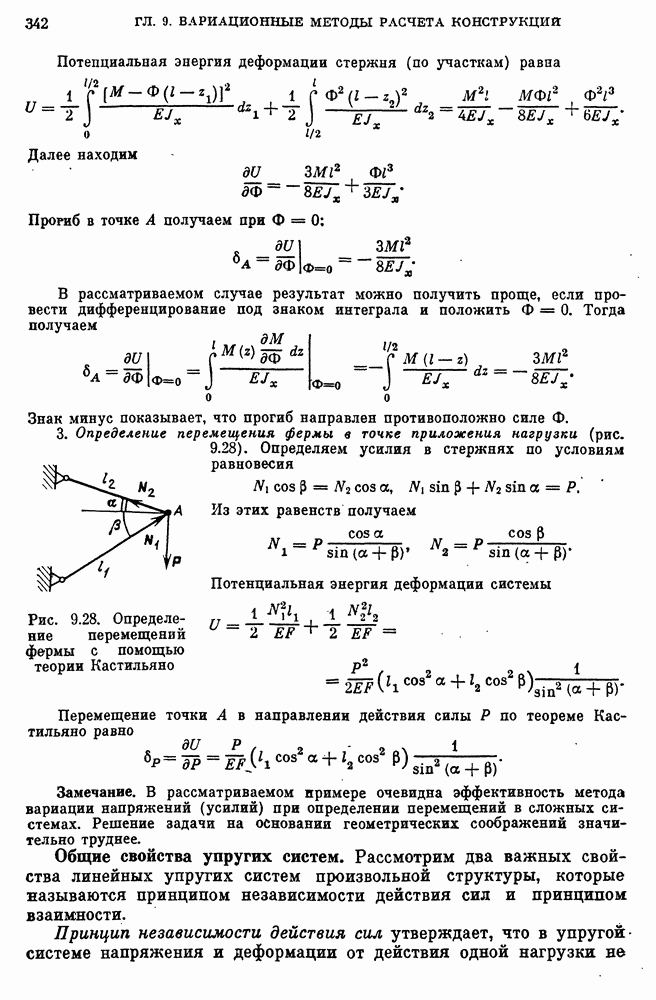
- Следствия вариационного уравнения. Теорема Кастильяно.
- Общие свойства упругих систем.
- ГЛАВА 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
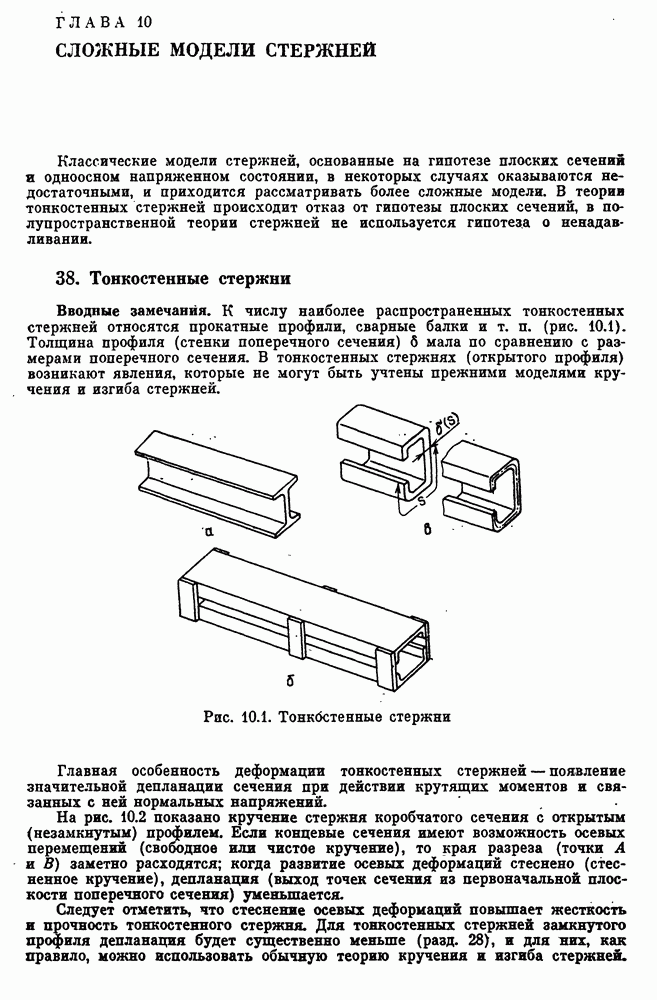
- 38. Тонкостенные стержни
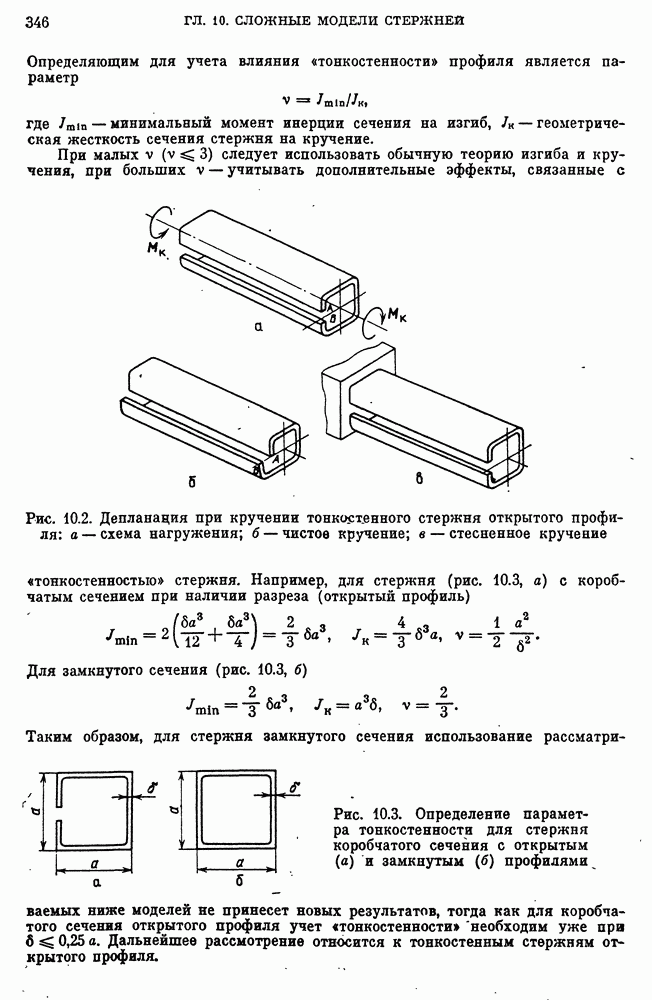
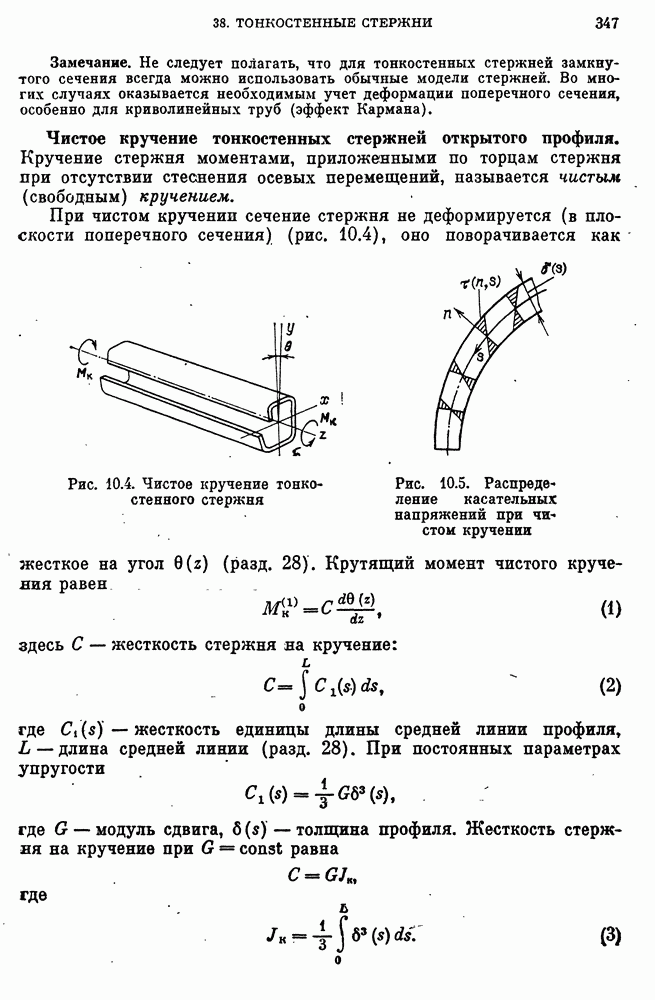
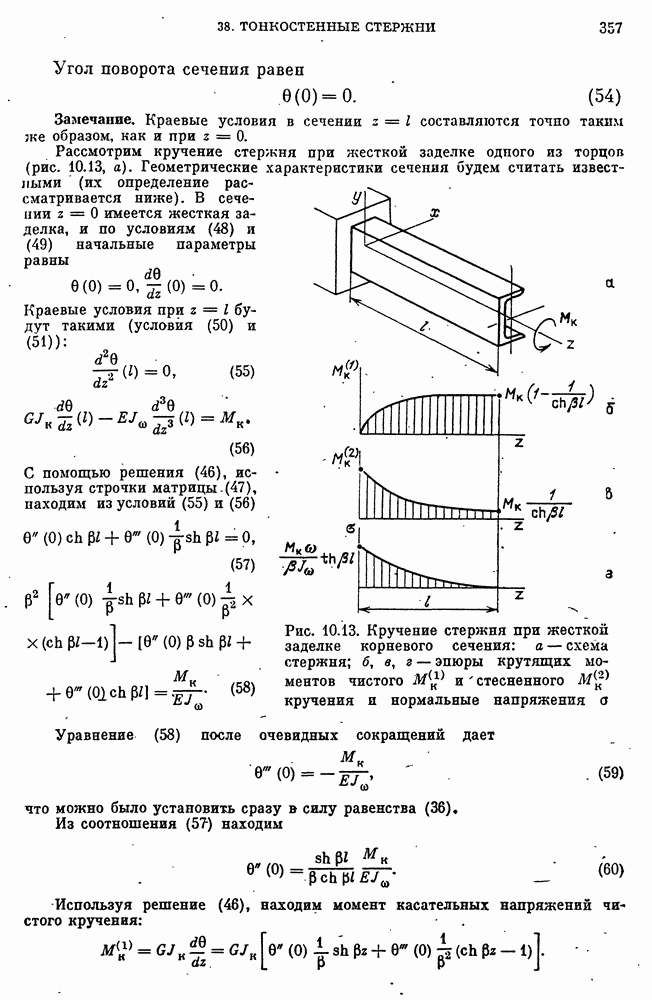
- Чистое кручение тонкостенных стержней открытого профиля.
- Стесненное кручение тонкостенных стержней. Основные гипотезы.
- Нормальные напряжения стесненного кручения.
- Касательные напряжения стесненного кручения.
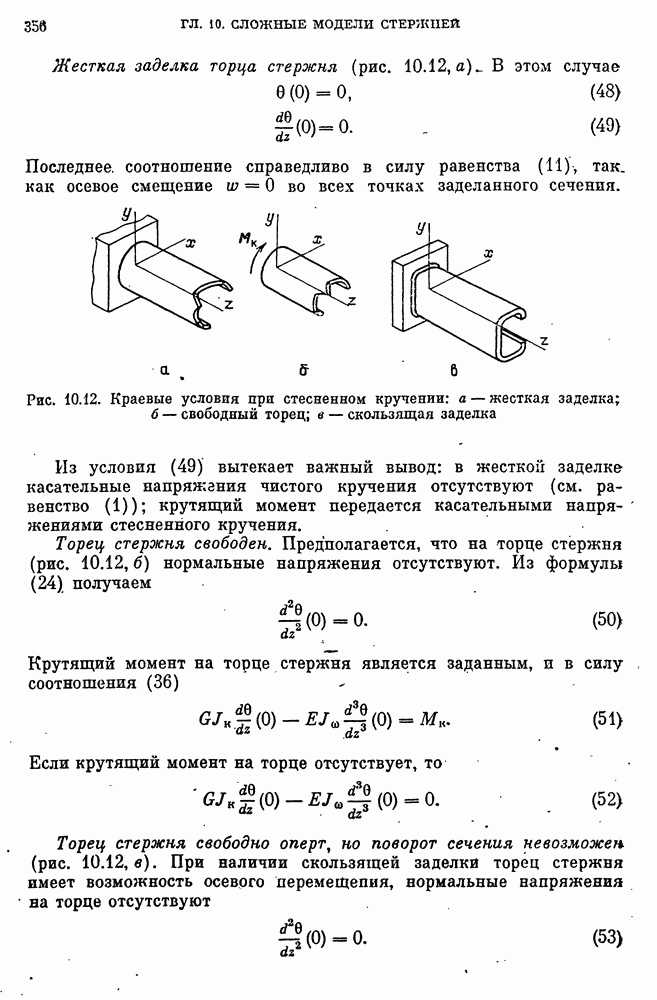
- Решение уравнения стесненного кручения тонкостенных стержней и краевые условия.
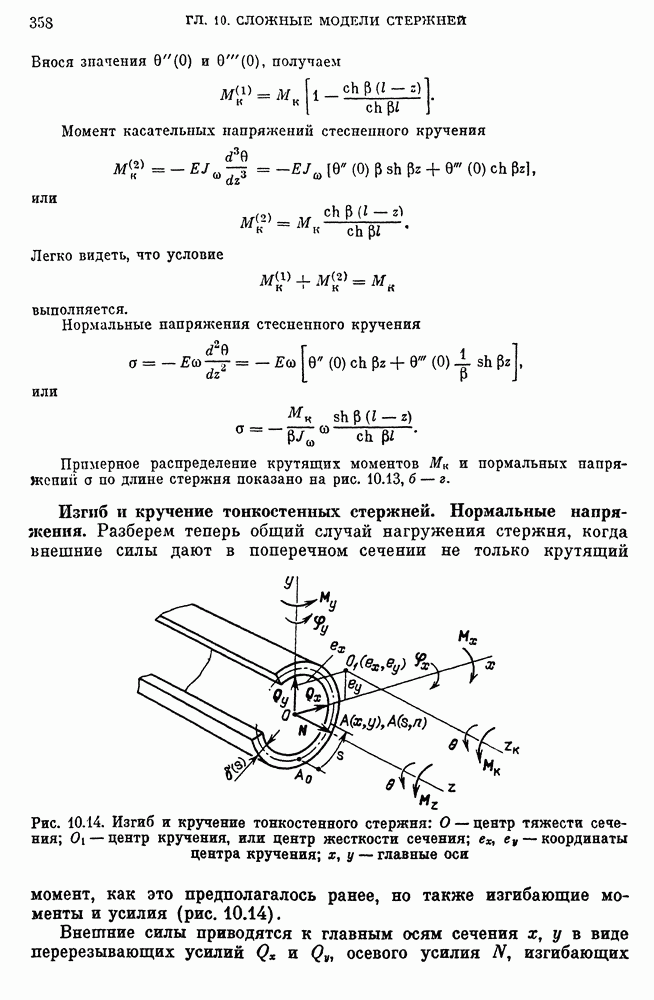
- Изгиб и кручение тонкостенных стержней. Нормальные напряжения.
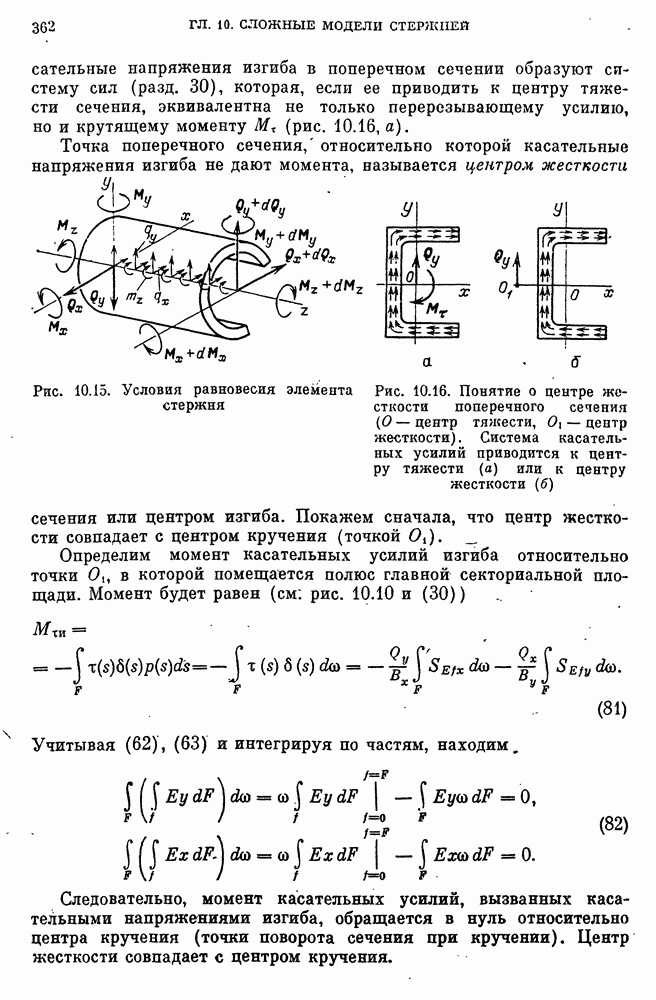
- Касательные напряжения изгиба. Центр жесткости сечения.
- Уравнения изгибно-крутильных деформаций тонкостенного стержня.
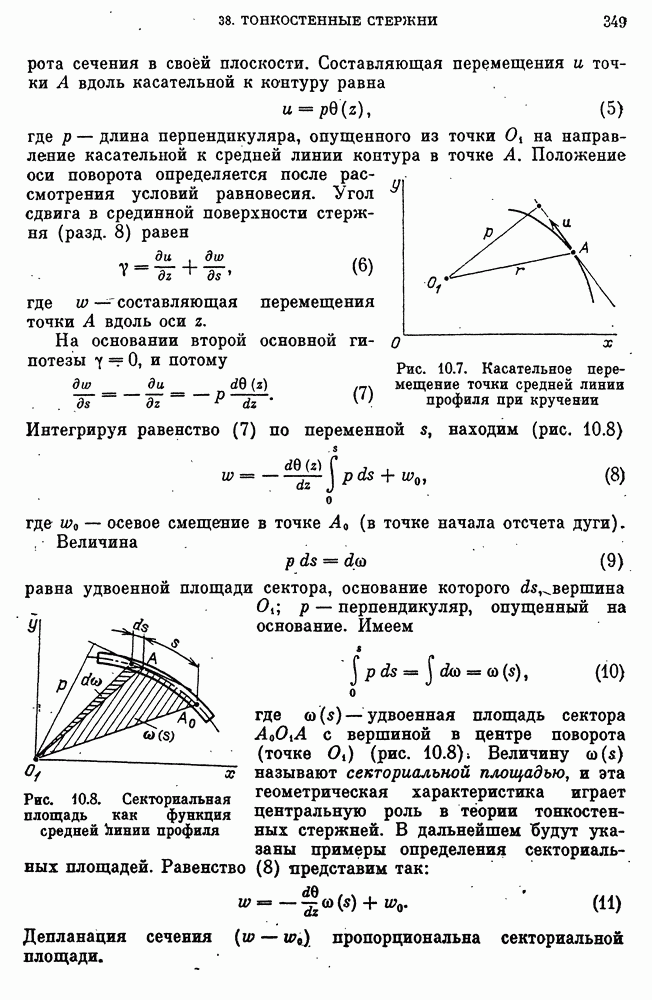
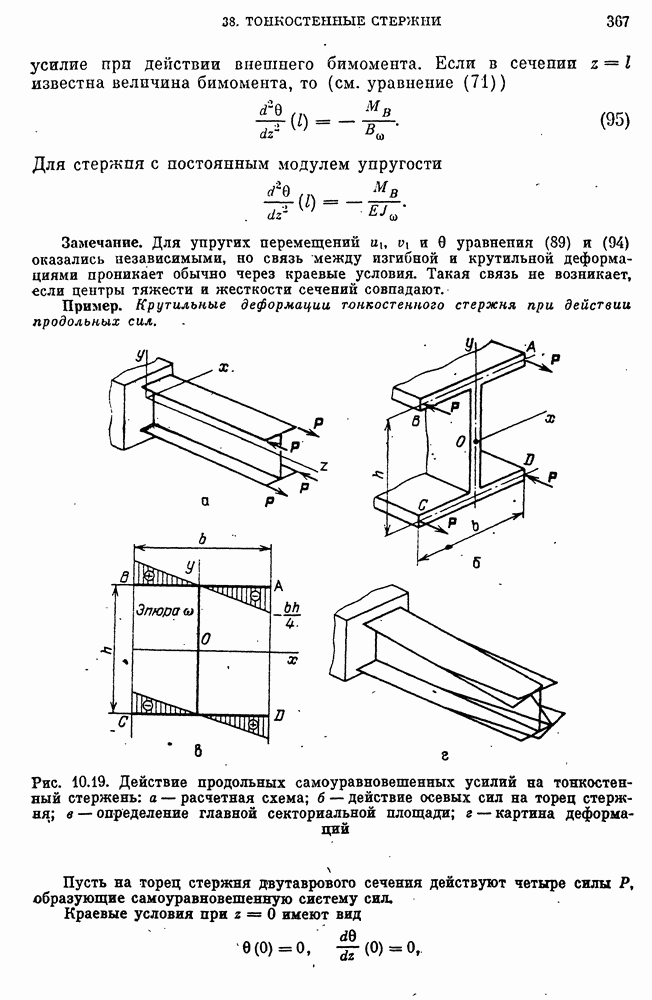
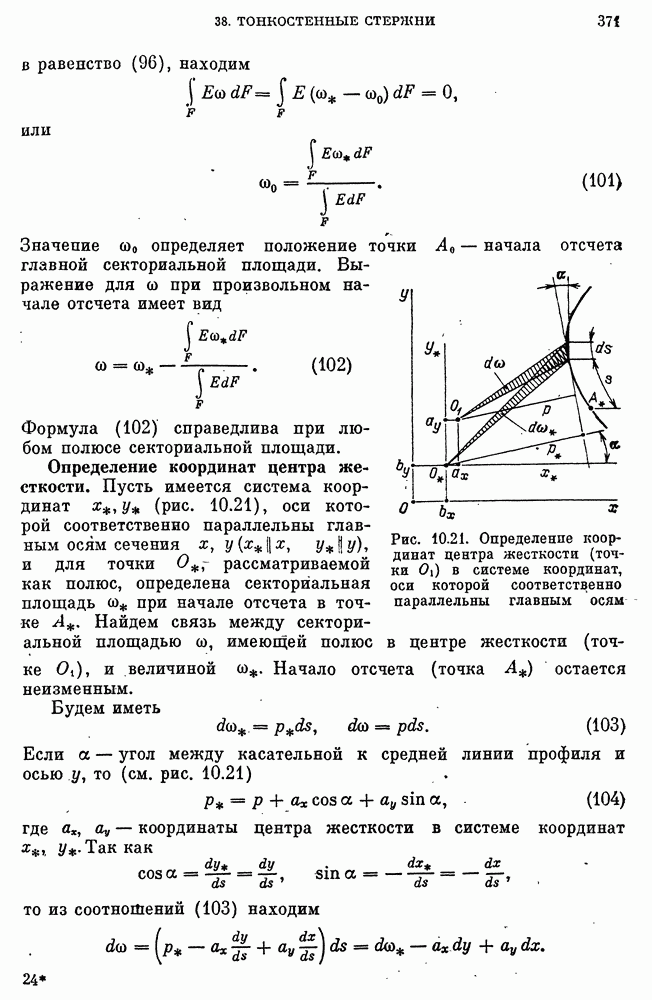
- Определение секториальных упруго-геометрических характеристик сечения и координат центра жесткости.
- Общие свойства расположения центра жесткости.
- Расчет секториальных характеристик сечений.
- 39. Полупространственные модели стержня
- Напряжения в плоскости поперечного сечения.
- Расчет стержней по полупространствениой теории.
- ГЛАВА 11. КОЛЬЦА
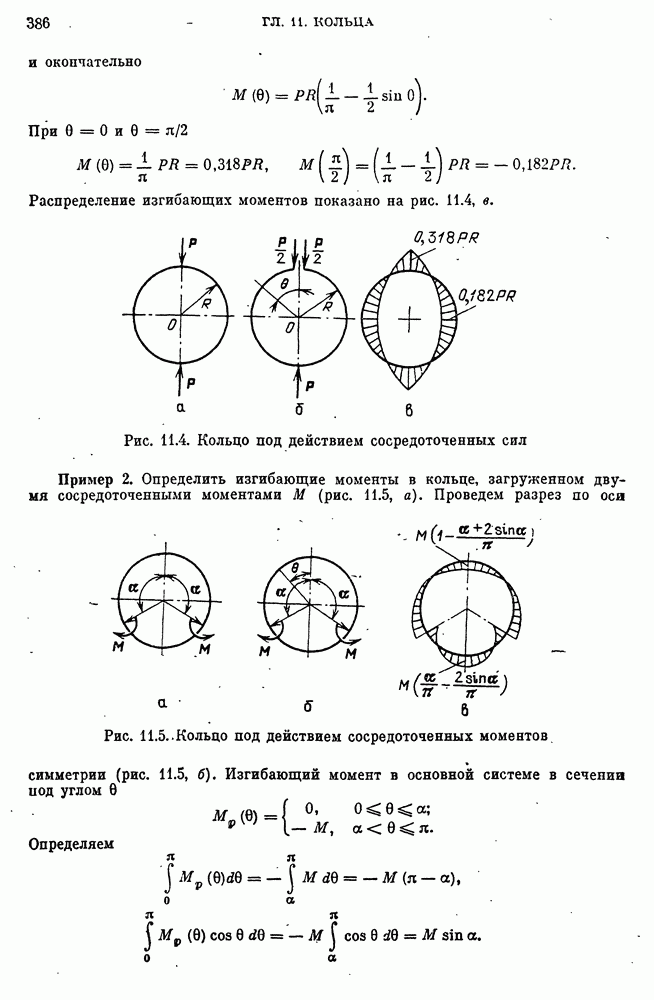
- 40. Изгиб колец
- 41. Осесимметричная деформация колец
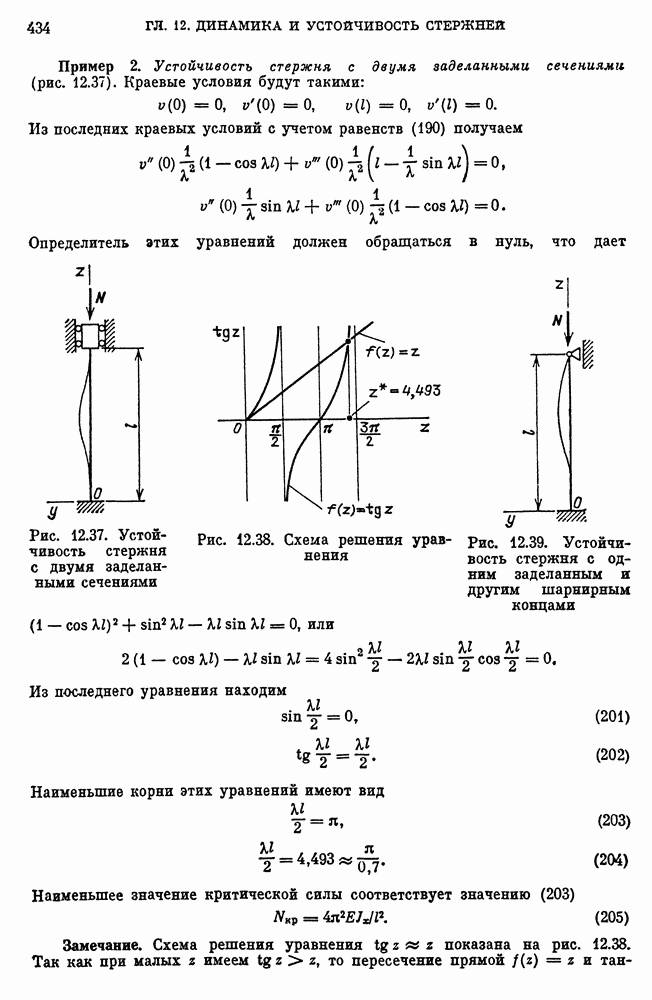
- ГЛАВА 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
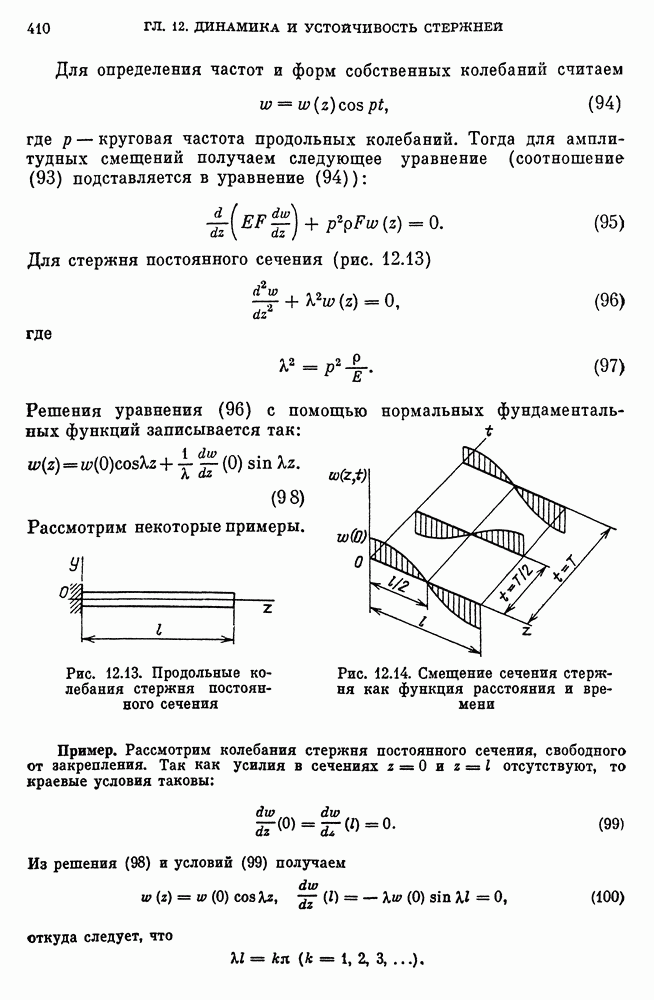
- 42. Изгибные и продольные колебания стержней
- Собственные колебания груза.
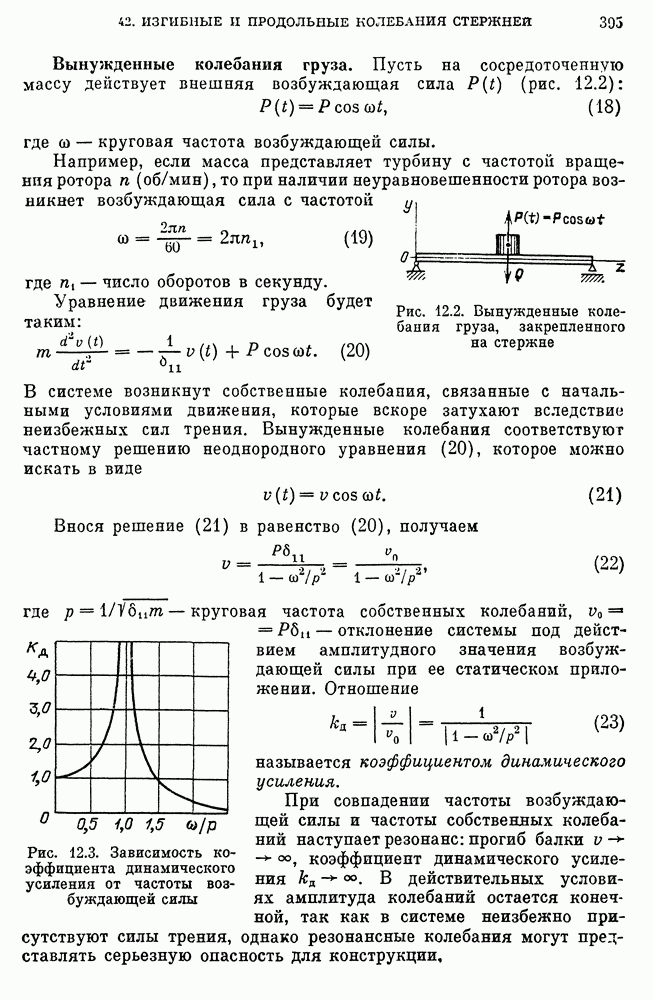
- Вынужденные колебания груза.
- Собственные колебания стержня с несколькими сосредоточенными массами.
- Дифференциальное уравнение изгибных колебаний стержней.
- Изгибные колебания стержней постоянного сечения.
- Изгибные колебания балки переменного сечения. Решение с помощью интегральных уравнений.
- Применение вариационного метода для определения частот и форм изгибных колебаний стержня.
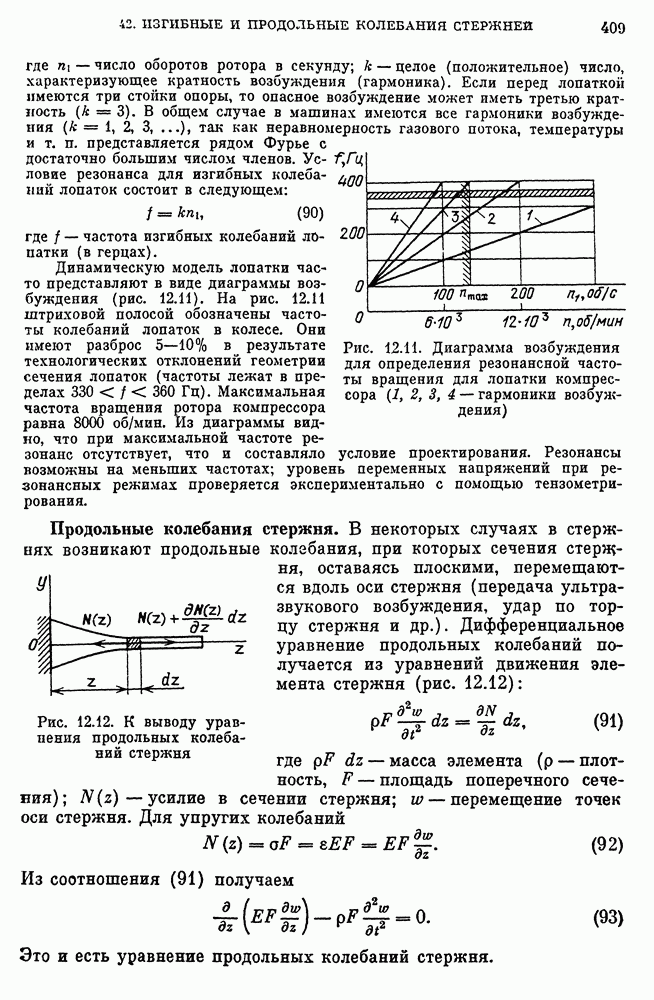
- Динамическая модель лопатки осевого компрессора при изгибных колебаниях.
- Продольные колебания стержня.
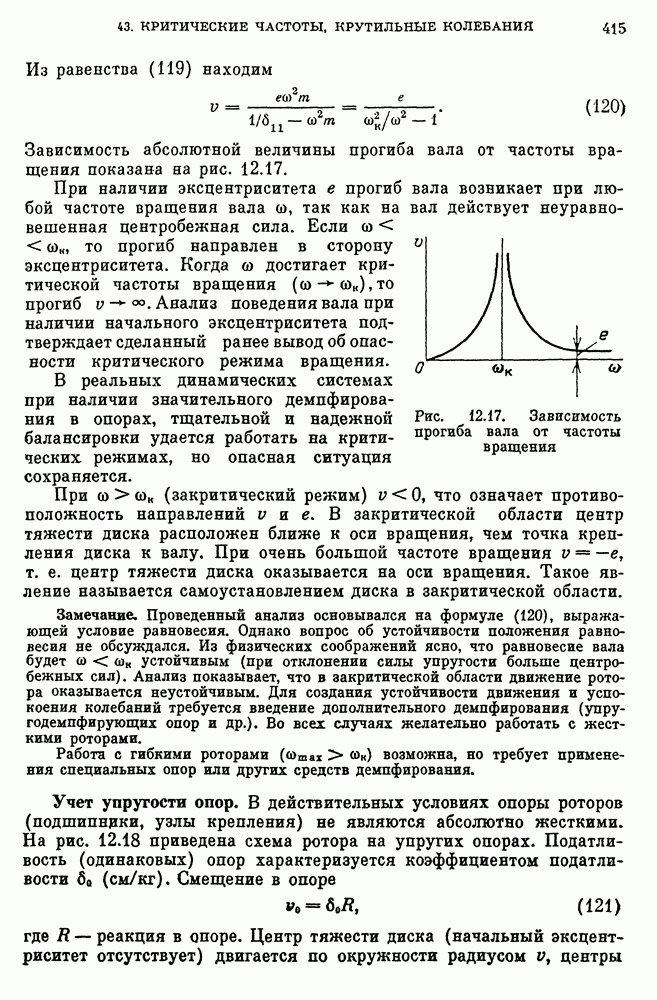
- 43. Критические частоты вращения и крутильные колебания валов
- Учет начального эксцентриситета центра тяжести диска.
- Учет упругости опор.
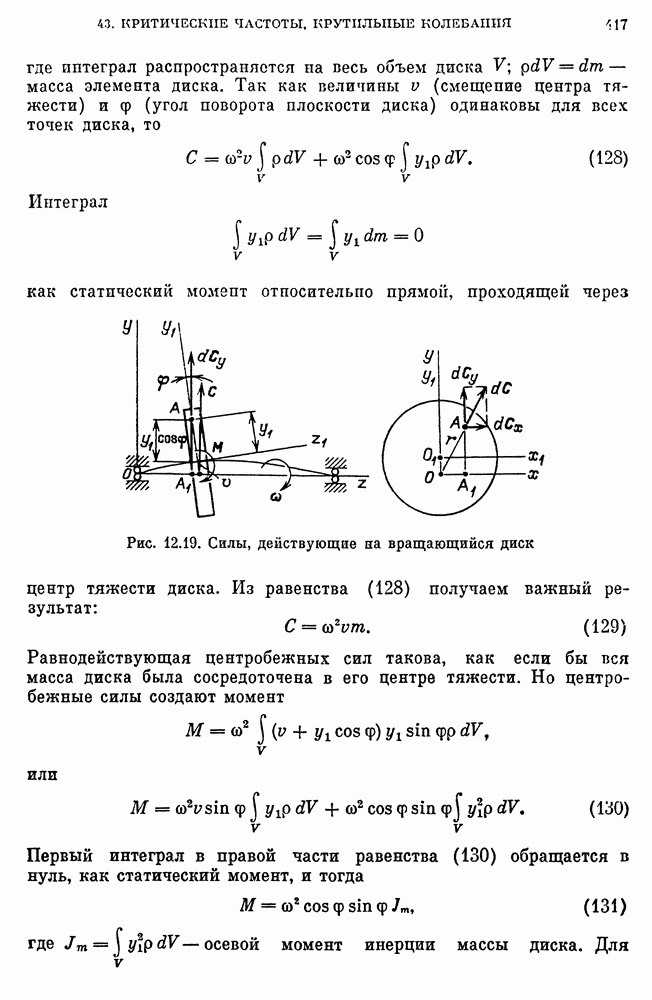
- Силы, действующие на вращающийся диск при прогибах вала.
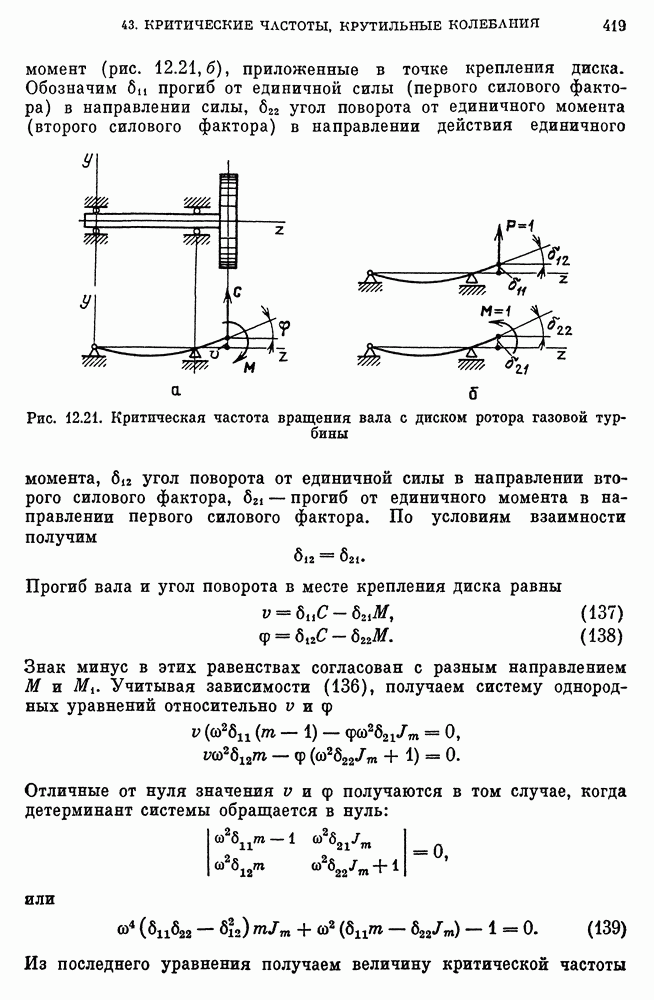
- Критическая частота вращения вала с дисками.
- Критическая частота вращения вала переменного сечения с непрерывно распределенными массами.
- Крутильные колебания валов.
- 44. Устойчивость стержней
- Критическая нагрузка для стержня с шарнирно закрепленными концами. Формула Эйлера.
- Общее дифференциальное уравнение устойчивости стержня и краевые условия.
- Решение дифференциального уравнения устойчивости для стержня постоянного сечения.
- Влияние условий закрепления концов стержня на величину критической силы.
- Приведенная длина стержня. Обобщенная формула Эйлера.
- Интегральное уравнение устойчивости стержня.
- Устойчивость стержней при упругопластических деформациях. Модуль Кармана.
- Устойчивость стержней в условиях продолжающегося нагружения в пластической области.
- Практические расчеты на устойчивость.
- ГЛАВА 13. МОДЕЛИ РАЗРУШЕНИЯ
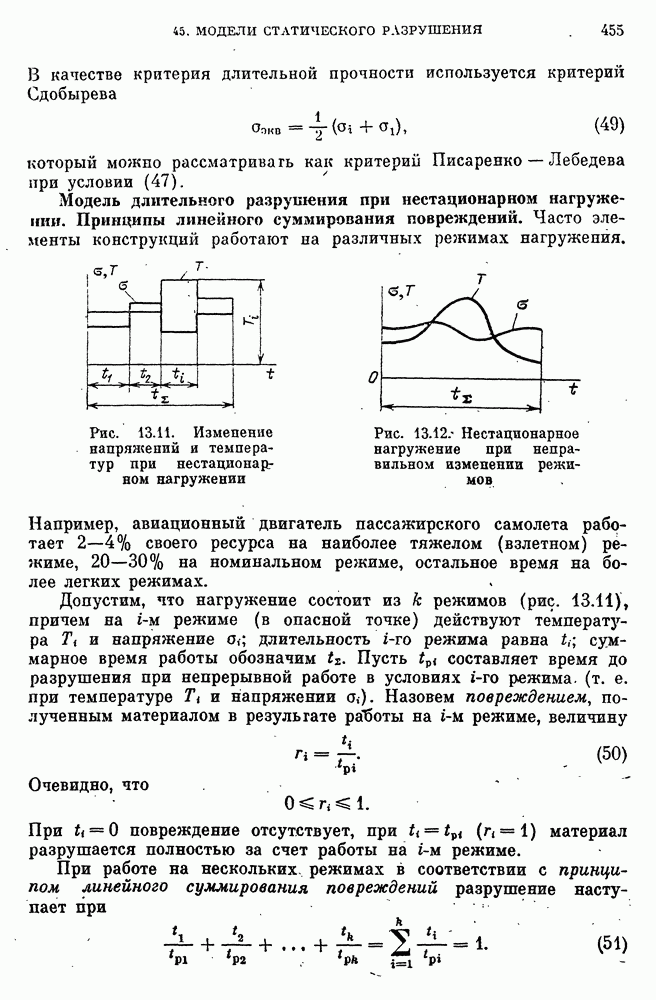
- 45. Модели статического и длительного разрушения
- Модели статического разрушения пластичных материалов.
- Критерий максимальных касательных напряжений.
- Предельные поверхности по критериям интенсивности напряжений и максимальных касательных напряжений.
- Модель статического разрушения пластичных материалов, дополненная условием отрыва.
- Модели статического разрушения хрупких материалов.
- Более общие модели статического разрушения.
- Предельная поверхность в пространстве главных напряжений по критерию Мора.
- Предельная поверхность в пространстве главных напряжений по критерию Писаренко — Лебедева.
- Модели длительного разрушения.
- Прочность при наличии трещин. Линейная механика разрушения.
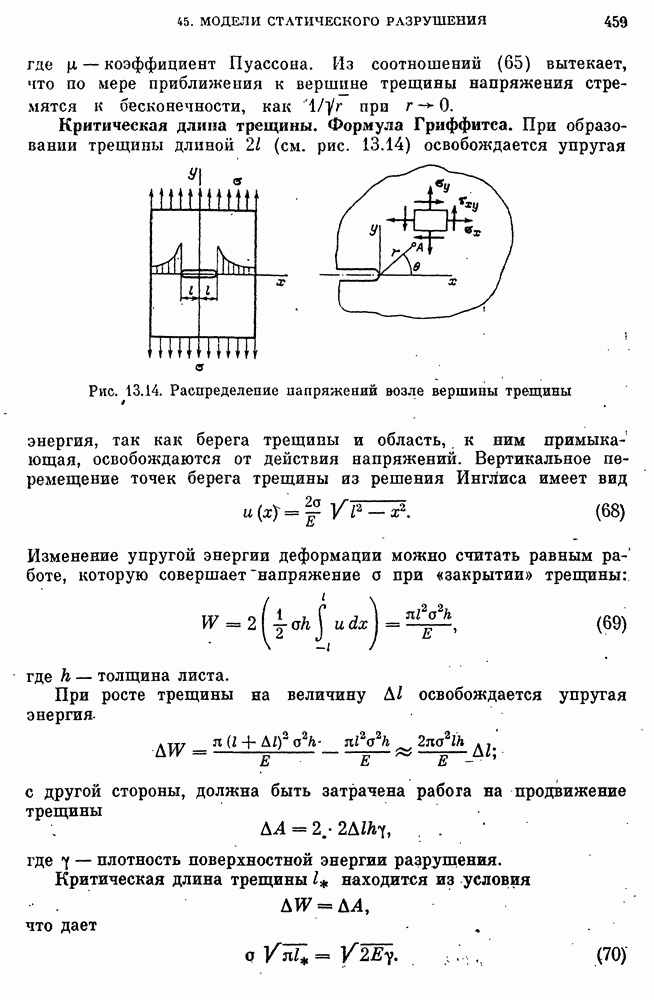
- Критическая длина трещины. Формула Гриффитса.
- 46. Модели усталостного и малоциклового разрушения
- Модели усталостного разрушения при многоосном (многокомпонентном) напряженном состоянии.
- Модели усталостного разрушения при стационарном нагружении с учетом числа циклов нагружений.
- Модели малоциклового разрушения при одноосном и сложном напряженных состояниях.
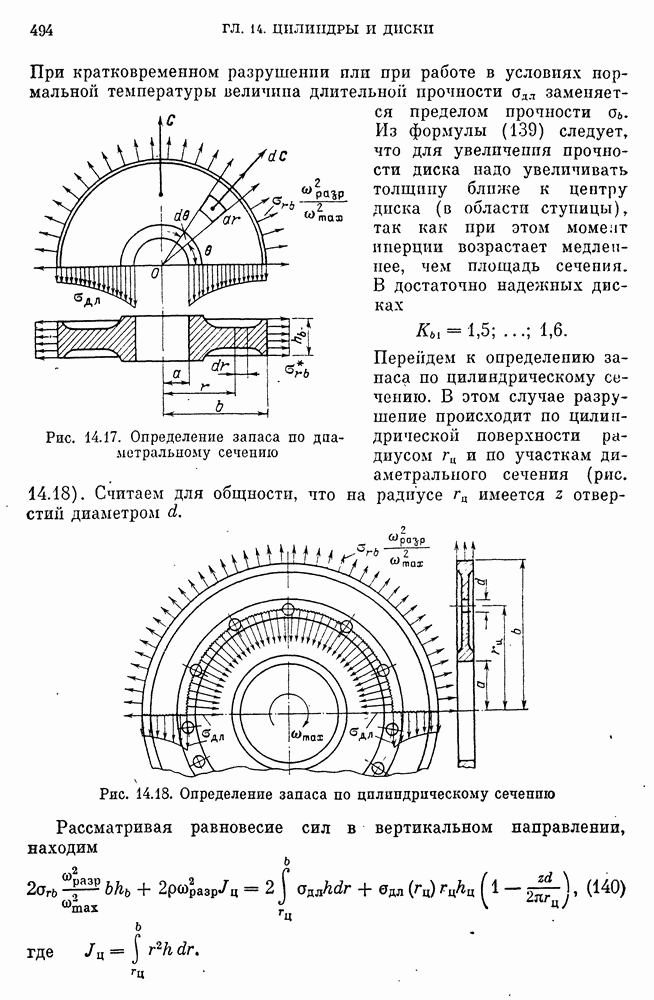
- ГЛАВА 14. ЦИЛИНДРЫ И ДИСКИ
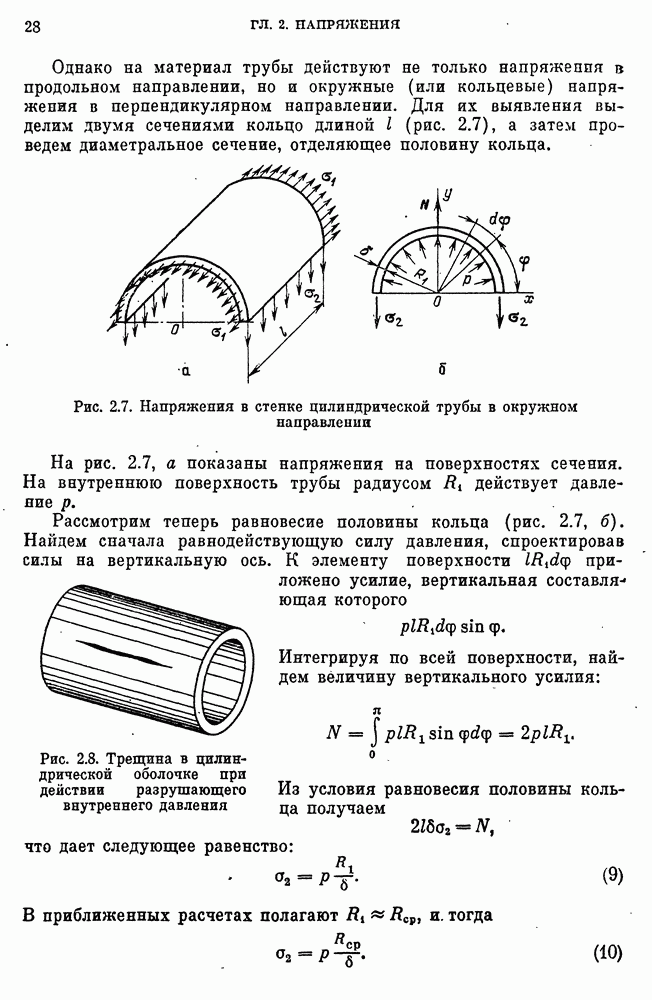
- 47. Прочностные модели толстостенных труб и цилиндров. Напряжения и деформации
- Уравнения равновесия элемента цилиндра.
- Толстостенная труба под действием внутреннего и внешдего давлений.
- Действие осевого усилия.
- Прочностная модель цилиндрической части сосуда высокого давления.
- Прочностная модель прессового соединения.
- Температурные напряжения и, напряжения от центробежных сил.
- Цилиндр с переменными параметрами упругости.
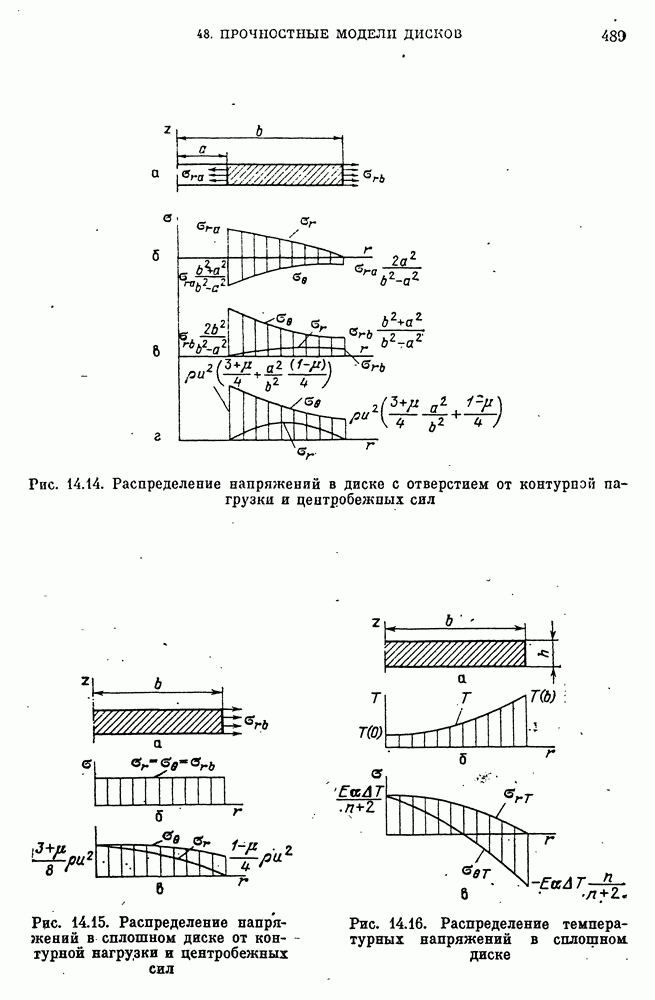
- 48. Прочностные модели дисков
- Дифференциальное уравнение для диска постоянной толшины с постоянными параметрами упругости.
- Распределение напряжений в диске постоянной толщины.
- Напряжения в диске переменной толщины с переменными параметрами упругости.
- Модели общей статической и длительной прочности диска.
- Эквивалентный запас по разрушающей частоте вращения.
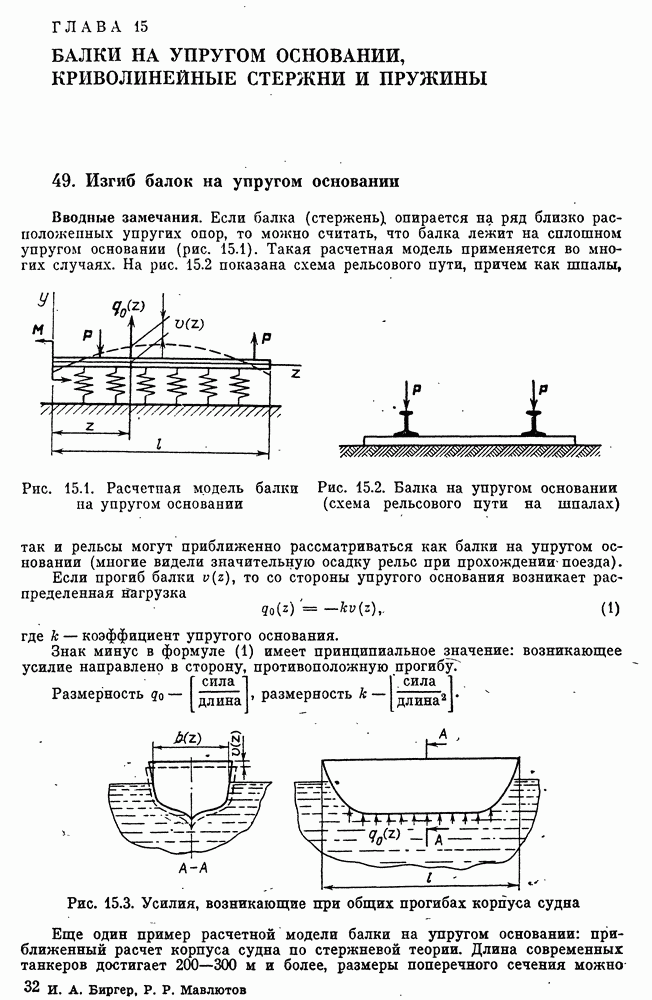
- ГЛАВА 15. БАЛКИ НА УПРУГОМ ОСНОВАНИИ, КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
- 49. Изгиб балок на упругом основании
- Уравнения изгиба для балки постоянного сечения на упругом основании. Структура решения.
- Метод начальных параметров и решение уравнения изгиба балки на упругом основании в матричной форме.
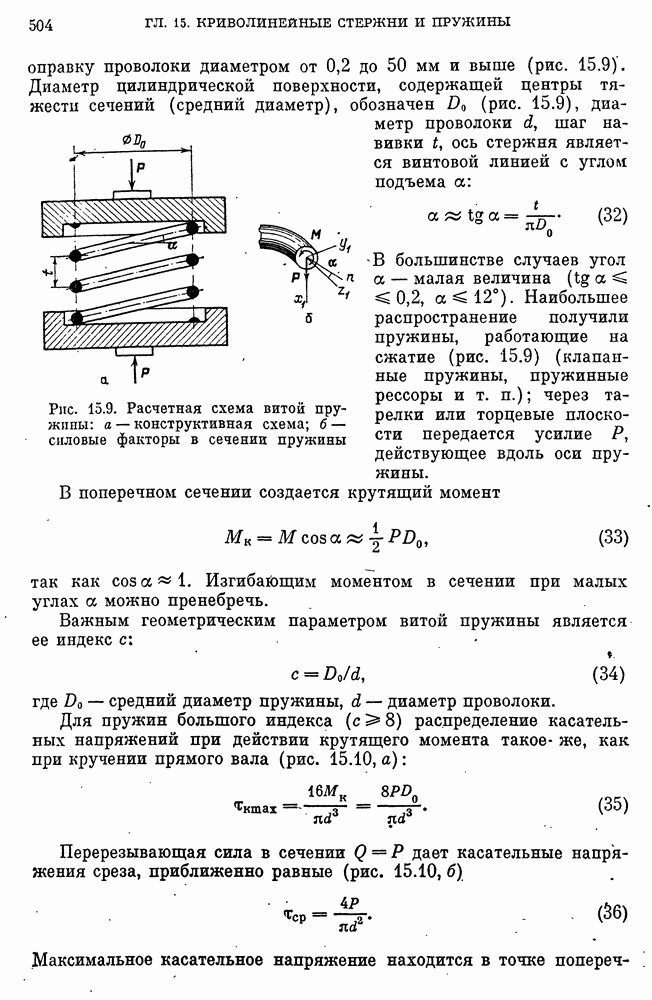
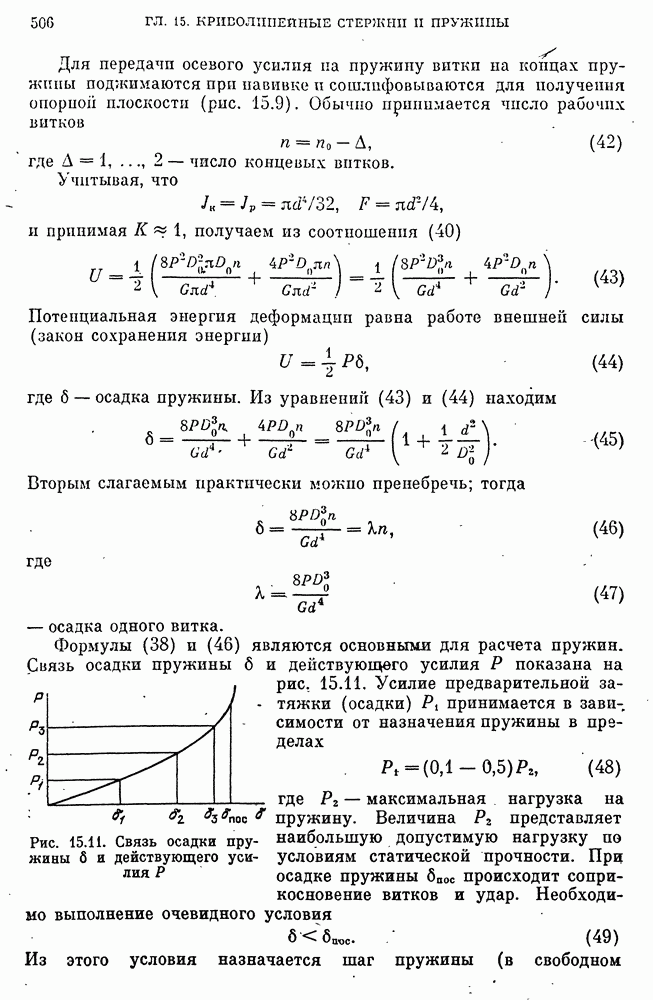
- 50. Криволинейные стержни и пружины
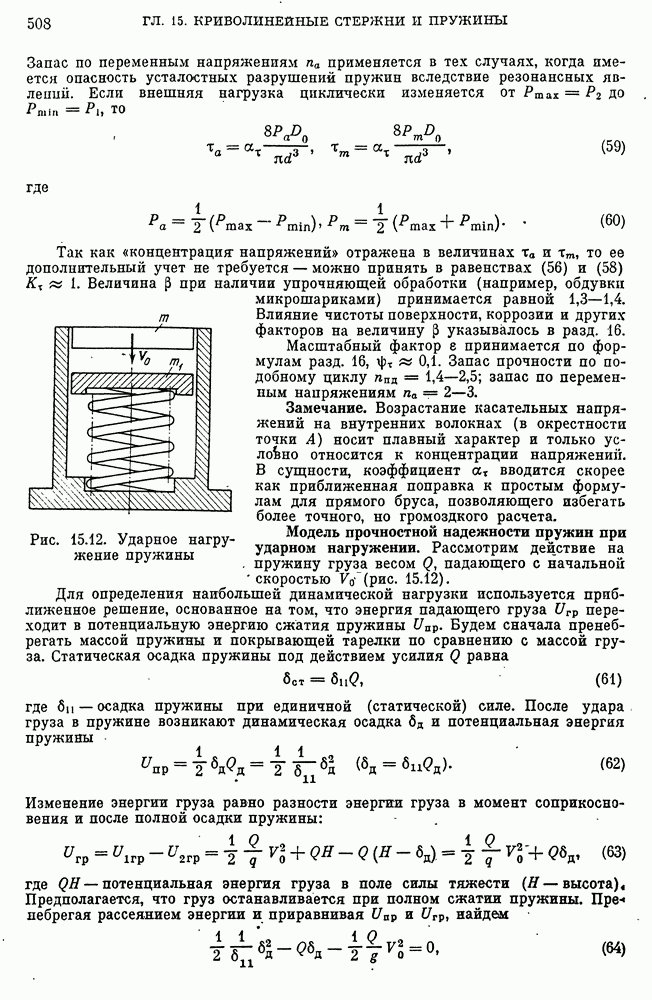
- Модели прочностной надежности пружин.
- Модель прочностной надежности пружин при ударном нагружении.
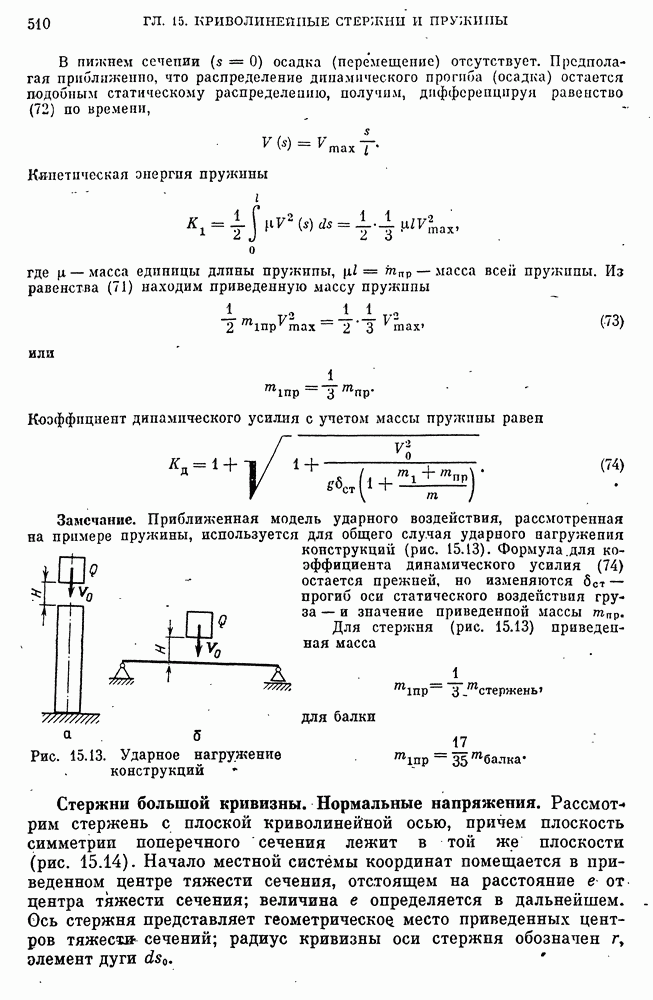
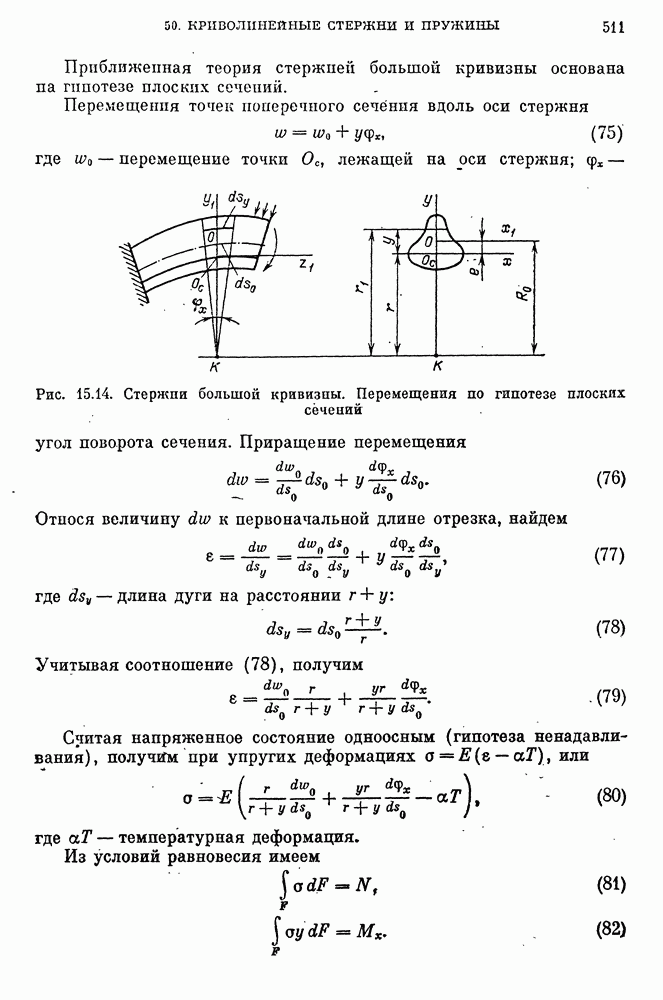
- Стержни большой кривизны. Нормальные напряжения.
- Определение приведенного центра тяжести сечения криволинейного стержня. Примеры.
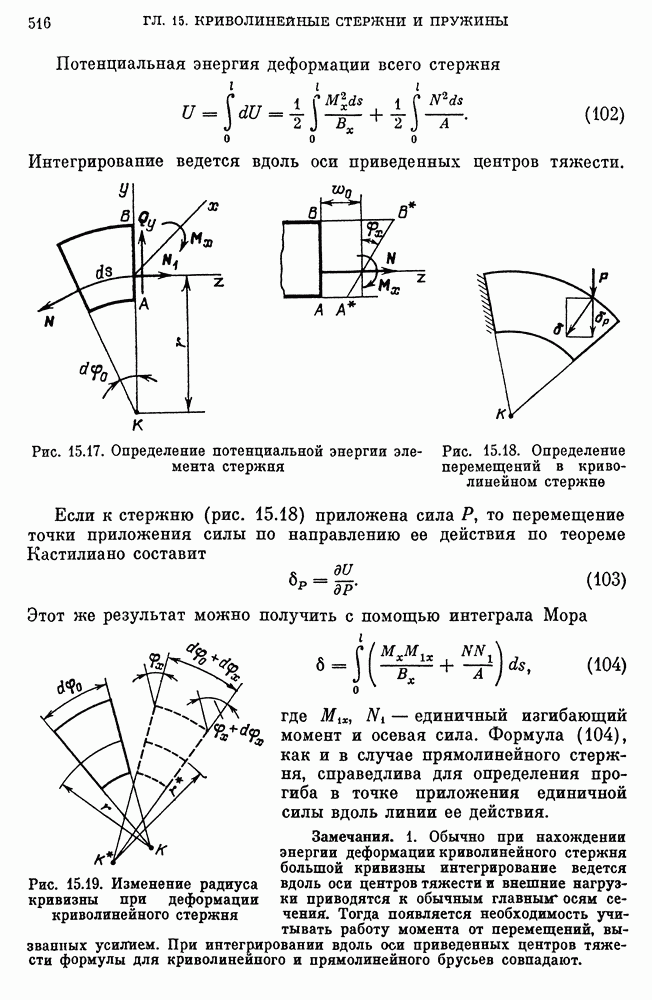
- Касательные напряжения при изгибе криволинейного стержня.
- Перемещения на изгибе криволинейного стержня.
- ГЛАВА 16. ПЛАСТИНКИ И ОБОЛОЧКИ
- 51. Пластинки
- Деформация круглых пластинок.
- Круглая пластинка постоянной толщины с постоянными параметрами упругости.
- Напряжения изгиба в круглой пластинке.
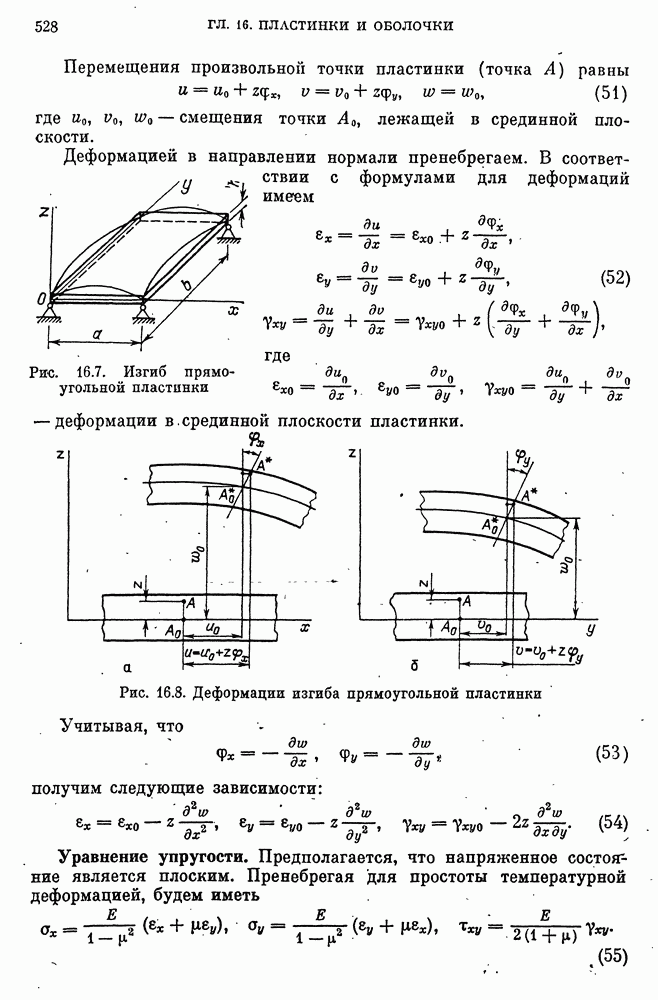
- Изгиб прямоугольных пластинок. Деформации.
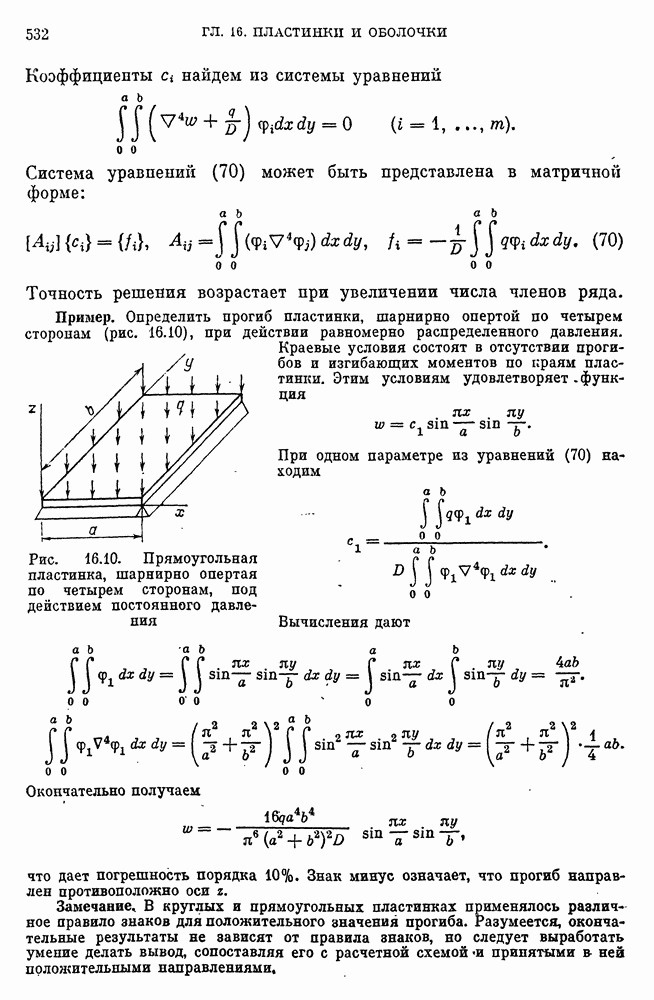
- Определение прогибов и напряжений в пластинке вариационным методом.
- 52. Цилиндрические оболочки
- Краевой эффект и безмоментное напряженное состояние в длинных цилиндрических оболочках.
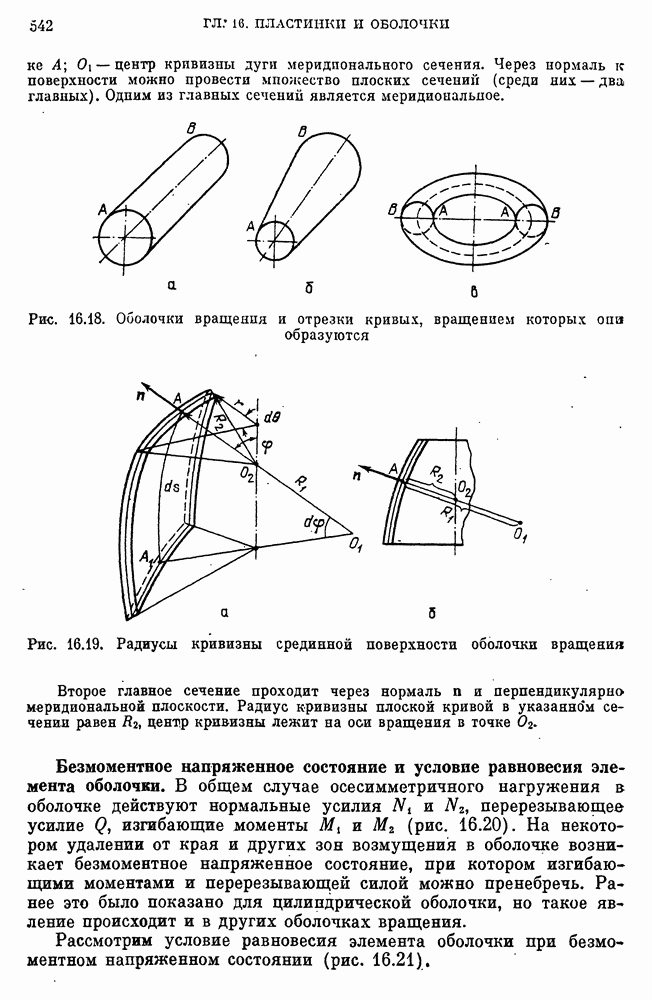
- 53. Приближенные методы расчета прочности и устойчивости рболочек вращения при осесимметричном нагружении
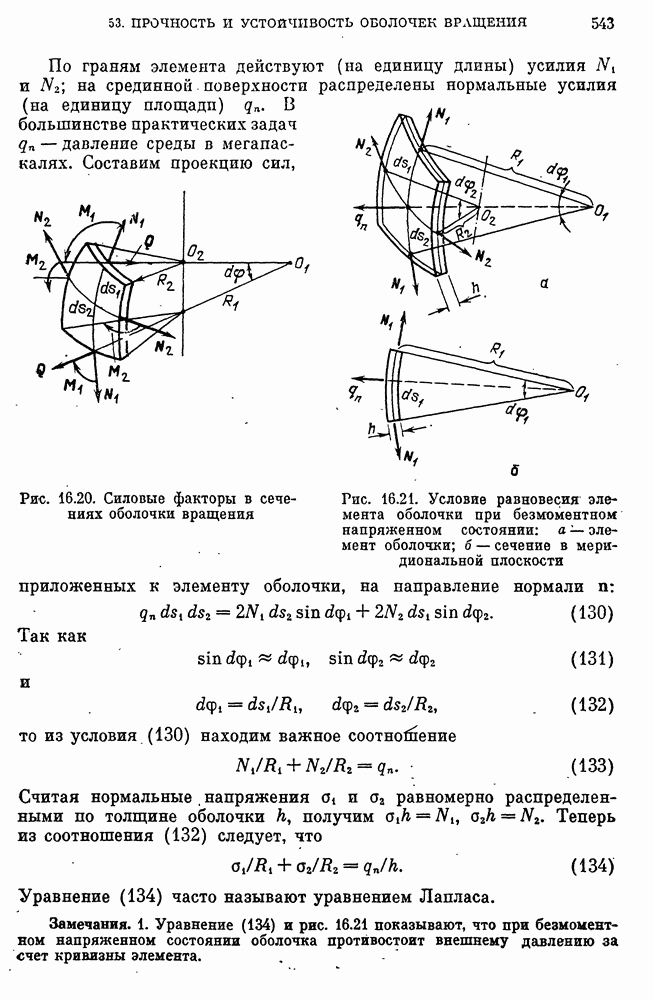
- Безмоментное напряженное состояние и условие равновесия элемента оболочки.
- Общее условие равновесия произвольной части оболочки.
- Приближенная модель прочности оболочки вращения при осесимметричном нагружении.
- Приближенные модели устойчивости оболочки.
- ГЛАВА 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- 54. Введение в метод конечных элементов
- 55. Основные уравнения метода конечных элементов
- Вариационное уравнение метода конечных элементов.