| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Дифференциальные уравнения равновесия элемента тела.
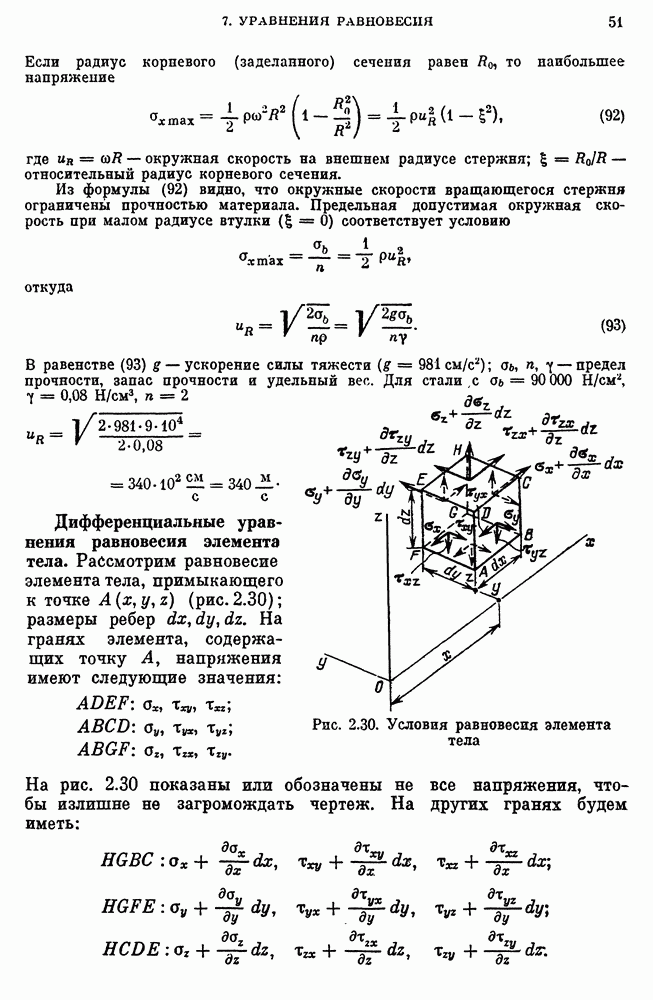
Рассмотрим равновесие элемента тела, примыкающего к точке  (рис. 2.30); размеры ребер
(рис. 2.30); размеры ребер  На гранях элемента, содержащих точку А, напряжения имеют следующие значения:
На гранях элемента, содержащих точку А, напряжения имеют следующие значения:

На рис. 2.30 показаны или обозначены не все напряжения, чтобы излишне не загромождать чертеж. На других гранях будем иметь:


Рис. 2.30. Условия равновесия элемента тела
Приращение напряжений по отношению к другой параллельной грани связано с приращением одной из координат. Кроме напряжений на гранях элемента, на него действует массовая сила, компоненты которой обычно обозначают  .
.
Составим суммы проекций всех сил на оси координат. Удобно сразу рассматривать две параллельные грани, так как напряжения на них направлены в разные стороны. Рассмотрим проекцию сил на ось х. На гранях ADEF и BCHG составляющие по оси х имеют только нормальные напряжения:

Среди сил, действующих по граням ADCB и FEHG, проекцию на ось х дают касательные напряжения

Силы на гранях ABGF и DCHE составляют проекцию на ось х

Сумма проекций всех сил с учетом массовой силы дает следующее условие:

и аналогично для других осей:

Уравнения (94) — (96) представляют собой три дифференциальных уравнения равновесия элемента тела в прямоугольных (декартовых) координатах.
Из механики известно, что в общем случае для любого тела, находящегося в равновесии, должны выполняться шесть условий равновесия (три — относительно составляющих усилия и три — для составляющих момента). Три условия для моментов были рассмотрены ранее, и они не изменяются при учете приращения напряжений по граням элемента. Эти три условия представляют свойства парности касательных напряжений

Пример. Покажем, что для случая плоского напряженного состояния, когда

И массовые силы отсутствуют  условия равновесия будут удовлетворены, если положить
условия равновесия будут удовлетворены, если положить

 — произвольная непрерывная функция координат. Действительно, надо позаботиться только об условиях (94) и (95), так как уравнение (96) удовлетворяется в силу равенства (98). Подстановка соотношений (90) в уравнения (94) и (95) приводит к тождествам
— произвольная непрерывная функция координат. Действительно, надо позаботиться только об условиях (94) и (95), так как уравнение (96) удовлетворяется в силу равенства (98). Подстановка соотношений (90) в уравнения (94) и (95) приводит к тождествам

так как частные производные непрерывных функций не зависят от порядка дифференцирования.
Замечание. Не следует думать, что равенства (99) дают полное решение плоской задачи. Используя соотношения (99), удается удовлетворить только уравнения равновесия, однако, как будет ясно из дальнейшего, для полного решения задачи функция  должна еще удовлетворить условия совместности деформаций всех элементов.
должна еще удовлетворить условия совместности деформаций всех элементов.
Дифференциальное уравнение равновесия элемента в тензорной форме.
Вспоминая тензорные обозначения и учитывая свойство парности касательных напряжений  можно записать уравнения равновесия в следующем виде:
можно записать уравнения равновесия в следующем виде:

Числовая индексация осей позволяет применить приемы сокращенной записи. Три уравнения (101) запишем в виде

В уравнении (102) запятая в индексе означает дифференцирование по координате, указываемой следующим за запятой индексом. Далее в тензорной записи используется правило Эйнштейна: по двум одинаковым индексам проводится суммирование от 1 до 3, В уравнении (102) такое суммирование проводится по индексу  Давая индексу i значения 1, 2, 3, получаем каждый раз одно из уравнений (101).
Давая индексу i значения 1, 2, 3, получаем каждый раз одно из уравнений (101).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
- 1. Сопротивление материалов — наука о прочности и надежности конструкций
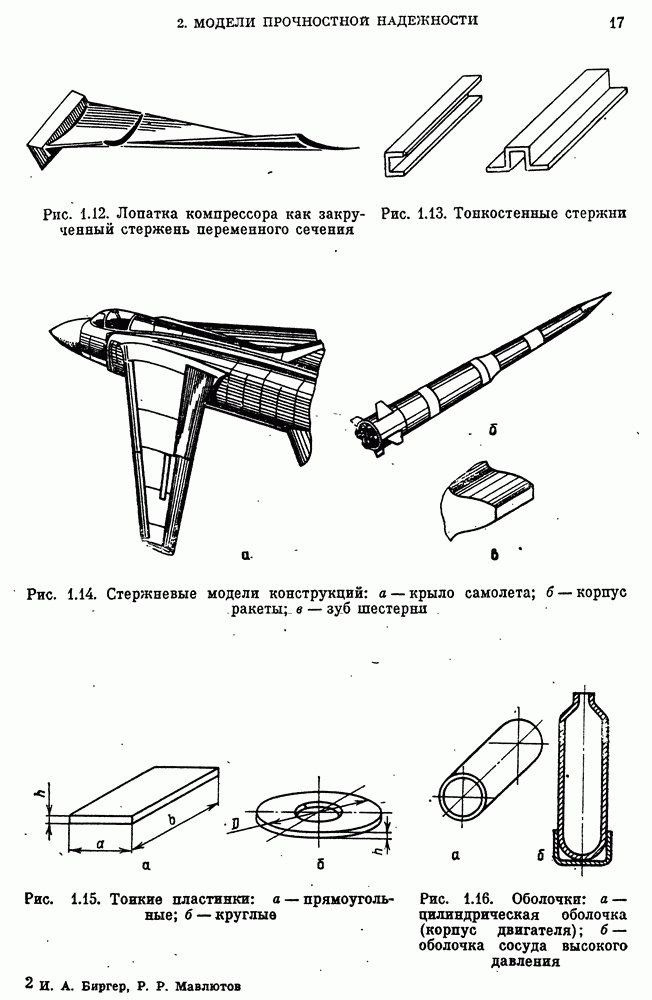
- 2. Модели прочностной надежности
- Модели прочностной надежности.
- Конструкционные материалы.
- Три уровня моделей материала.
- Модели материала в общей модели прочностной надежности.
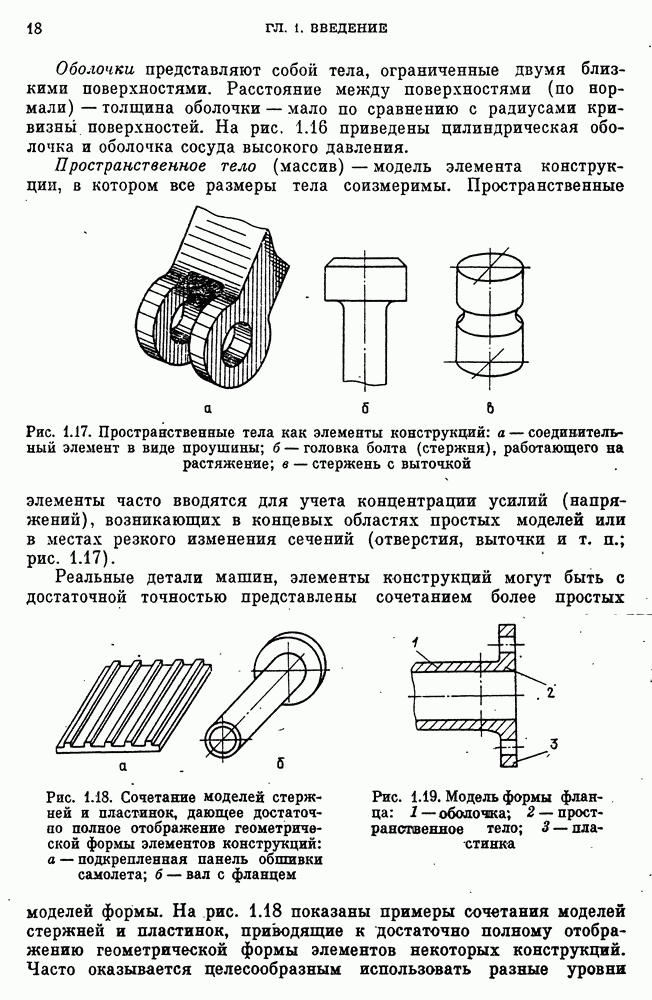
- Модели формы.
- Модели нагружения.
- Модели разрушения.
- ГЛАВА 2. НАПРЯЖЕНИЯ
- 3. Нормальные и касательные напряжения
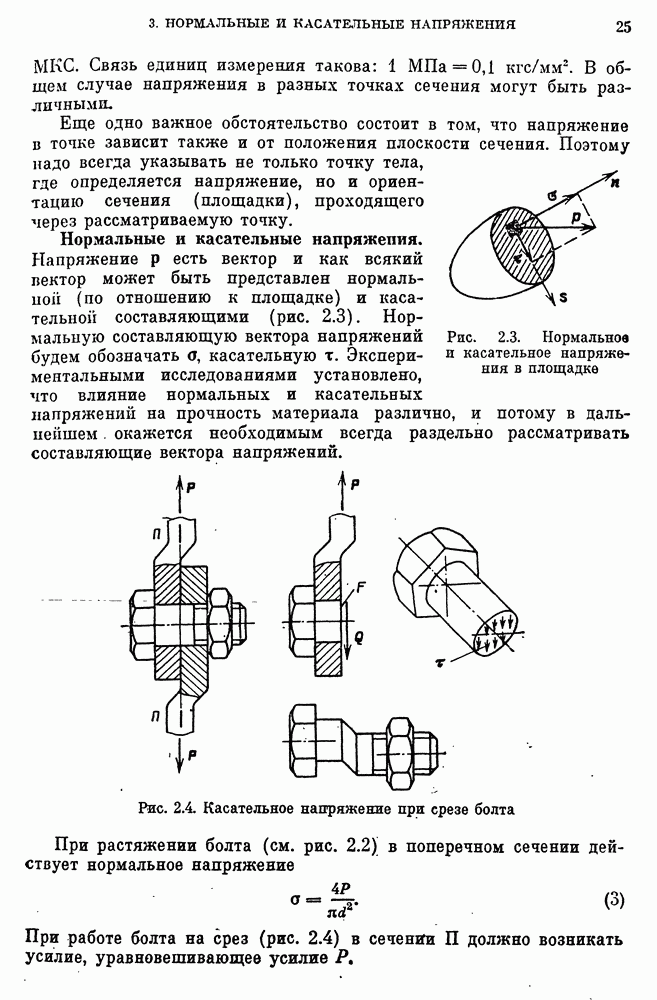
- Нормальные и касательные напряжения.
- 4. Напряженное состояние в точке
- Свойства парности касательных напряжений.
- 5. Плоское напряженное состояние
- Главные площадки при плоском напряженном состоянии.
- Главные напряжения при плоском напряженном состоянии.
- Наибольшие касательные напряжения.
- 6. Объемное напряженное состояние
- Напряжения в произвольной косой площадке.
- Главные площадки и главные напряжения при объемном напряженном состоянии.
- Инварианты напряженного состояния в точке.
- Понятие о тензоре напряженного состояния.
- 7. Дифференциальные уравнения равновесия элемента тела и краевые условия
- Дифференциальные уравнения равновесия элемента тела.
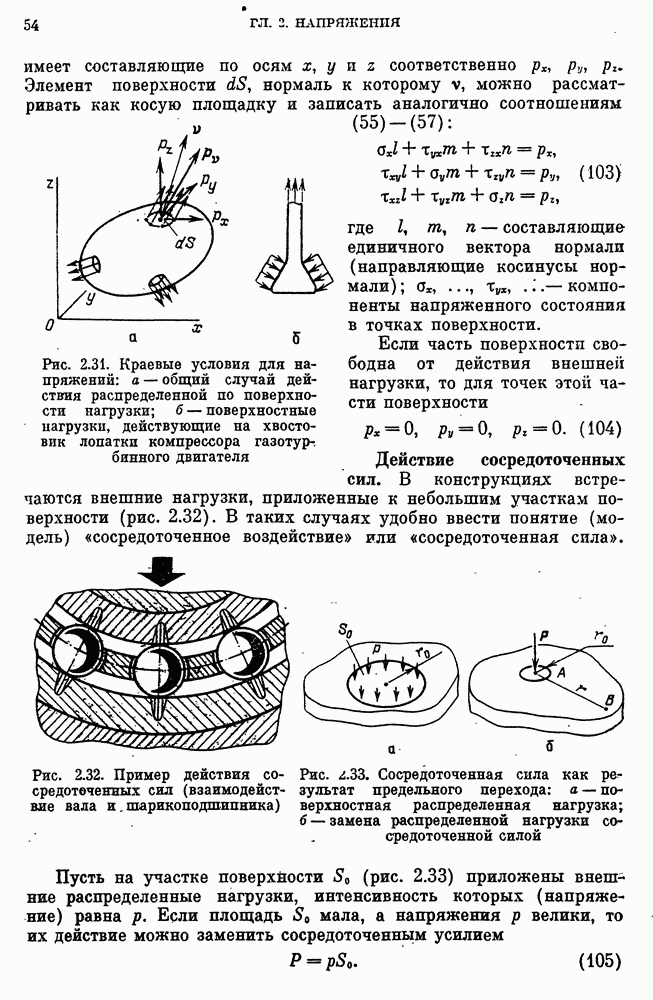
- Краевые условия для напряжений.
- Действие сосредоточенных сил.
- Принцип Сен-Венана для краевых условий.
- ГЛАВА 3. ДЕФОРМАЦИИ
- 8. Перемещения и деформации
- Определение линейной деформации.
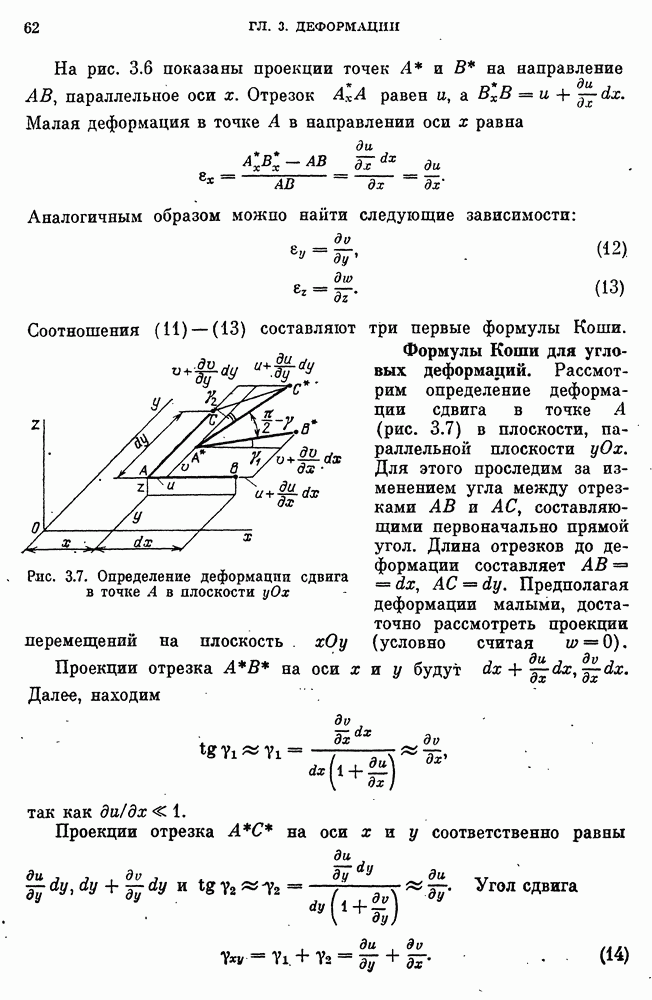
- Определение угловой деформации.
- 9. Связь перемещений и деформаций
- Формулы Коши для линейных деформаций.
- 10. Линейная деформация в произвольном направлении. Главные деформации, тензор деформаций
- Главные направления и главные деформации.
- 11. Уравнения совместности деформаций
- ГЛАВА 4. МЕХАНИЧЕСКИЕ СВОЙСТВА КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
- 12. Диаграммы деформирования, пределы текучести и прочности
- Упругость, модуль упругости, пластичность, закон разгрузки и закон упрочнения.
- Пределы текучести и прочности при сжатии.
- Определение предела прочности материала с помощью испытания твердости.
- 13. Деформации и характеристики пластичности
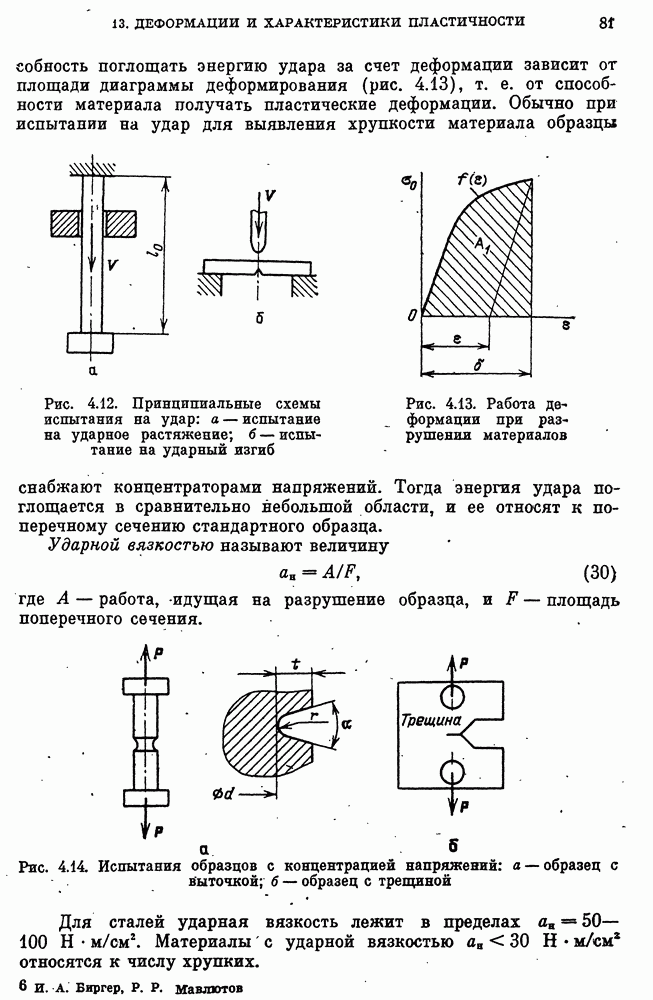
- Дополнительные характеристики хрупкости и пластичности материала.
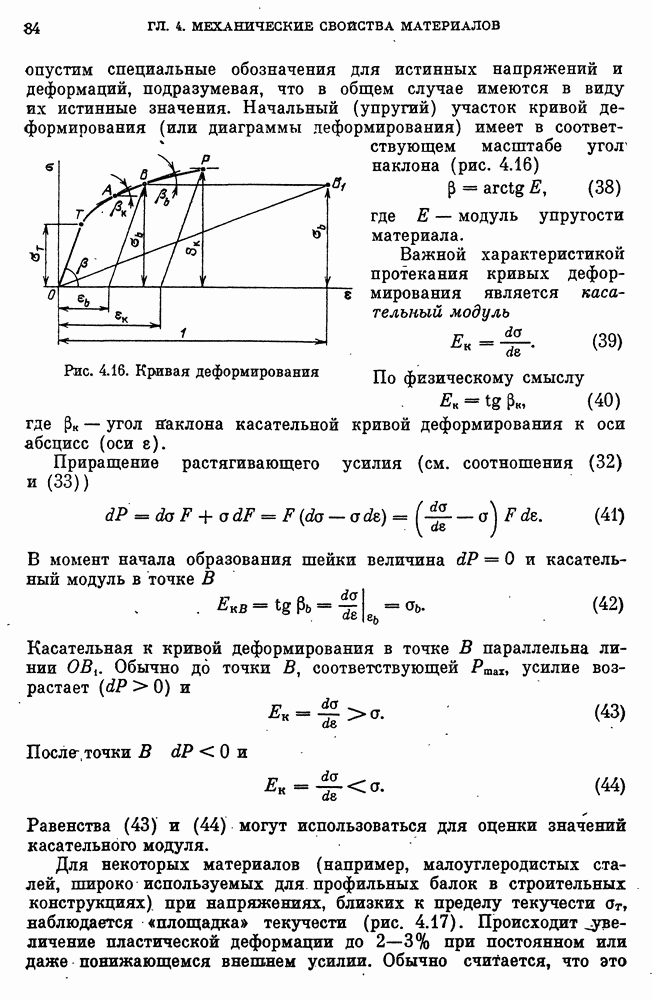
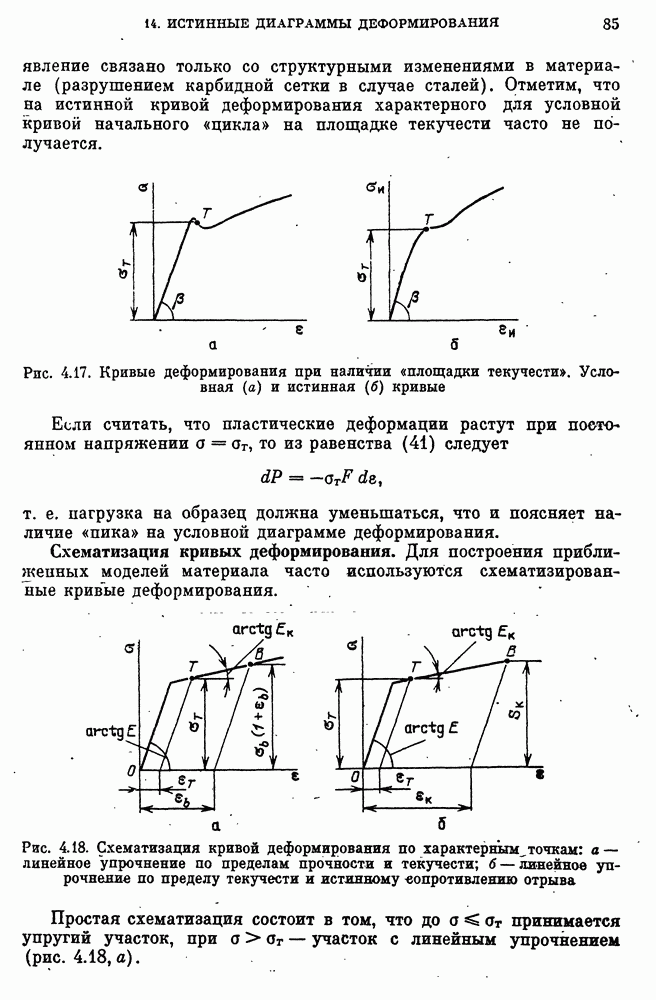
- 14. Истинные диаграммы деформирования и их схематизация
- Особенности кривых деформирования
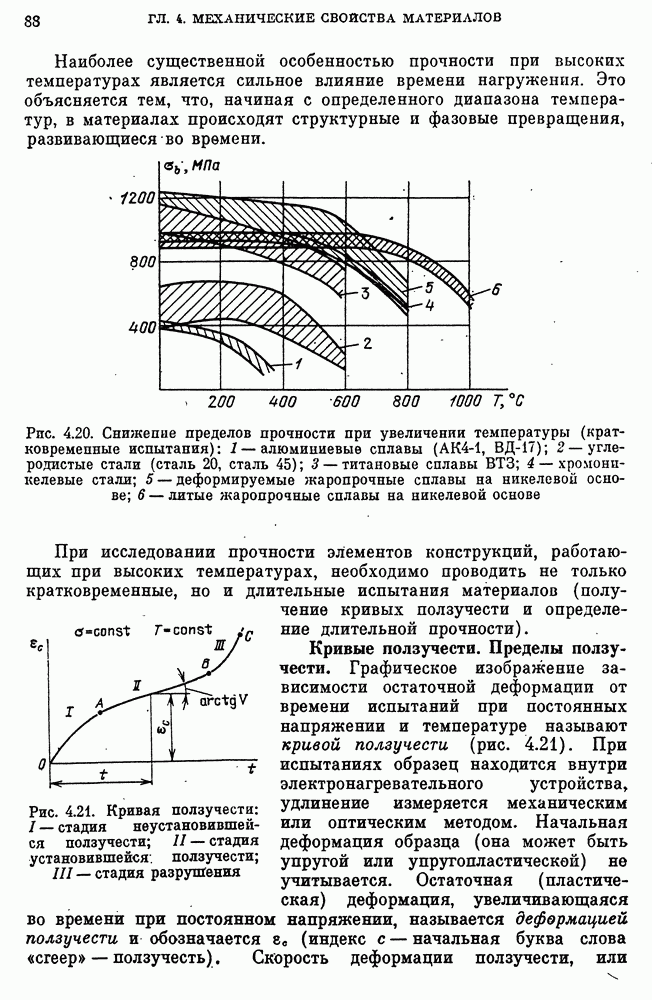
- 15. Ползучесть и длительная прочность
- Кривые ползучести. Пределы ползучести.
- Влияние ползучести на напряженное состояние в элементах конструкций.
- Длительная прочность, предел длительной прочности.
- Зависимость пределов длительной прочности от времени нагружения.
- Рассеяние долговечности при испытаниях длительной прочности.
- Зависимость пределов длительной прочности от температуры.
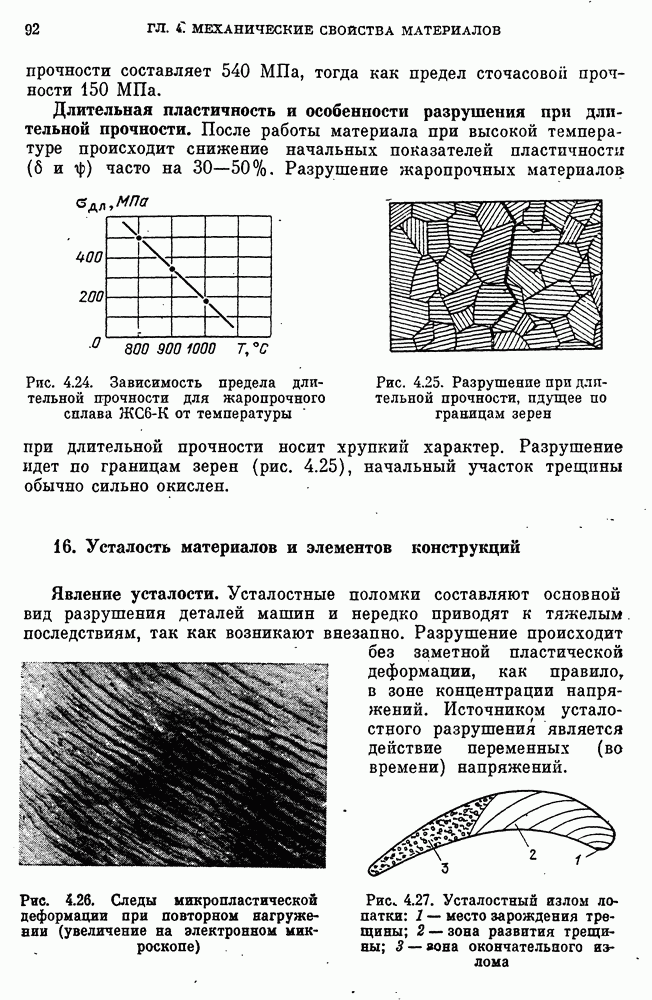
- Длительная пластичность и особенности разрушения при длительной прочности.
- 16. Усталость материалов и элементов конструкций
- Циклы переменных напряжений.
- Испытания на усталость.
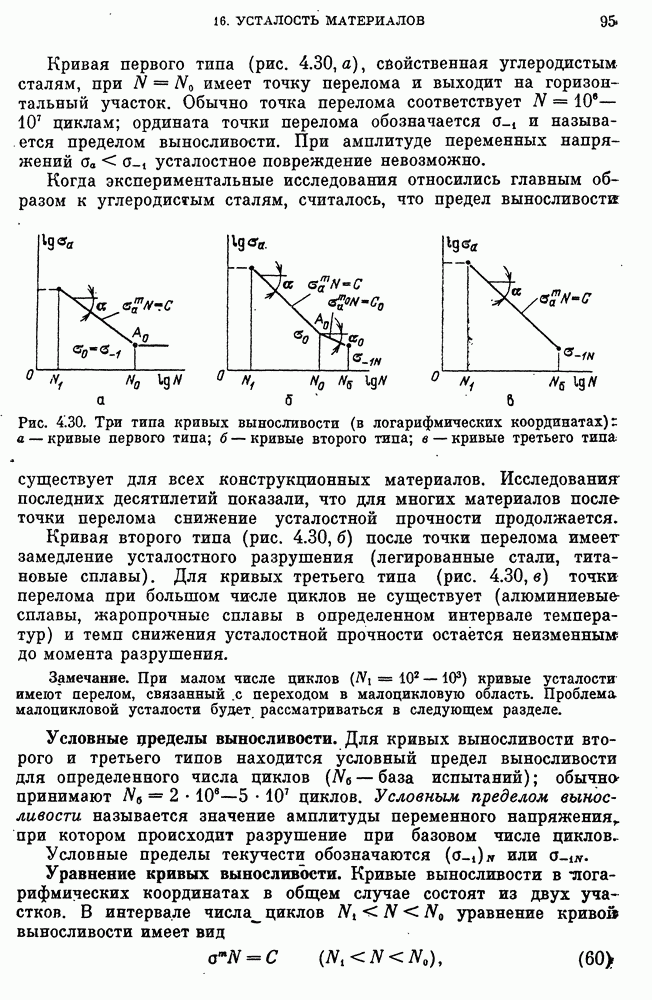
- Влияние числа циклов нагружения на усталостную прочность, кривые выносливости, пределы выносливости.
- Уравнение кривых выносливости.
- Влияние постоянных напряжений на усталостную прочность.
- Влияние концентрации напряжений.
- Влияние поверхностного слоя.
- Влияние абсолютных размеров деталей.
- Рассеяние усталостной долговечности.
- 17. Малоцикловая усталость
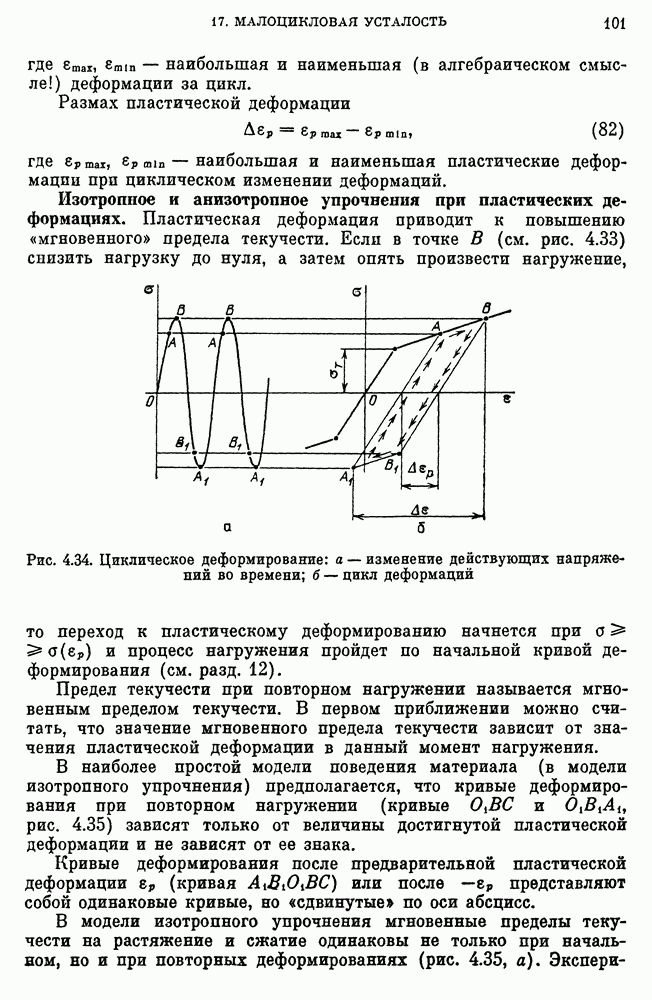
- Изотропное и анизотропное упрочнения при пластических деформациях.
- Явление малоцикловой усталости.
- ГЛАВА 5. МОДЕЛИ УПРУГОСТИ, ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ
- Связь деформаций сдвига и касательных напряжений.
- Связь модуля сдвига с модулем упругости и коэффициентом Пуассона.
- Температурная деформация.
- Общая форма закона упругости.
- Другие формы закона упругости.
- Матричная запись закона упругости.
- Модель упругости для анизотропного тела.
- 19. Модели пластичности
- Уравнения пластичности в векторной форме.
- Интенсивность напряжений и деформаций.
- Интенсивность упругих и пластических деформаций.
- Обобщенная кривая деформирования.
- Еще одна форма уравнений Генки — Ильюшина.
- Коэффициент Пуассона при упругопластических деформациях.
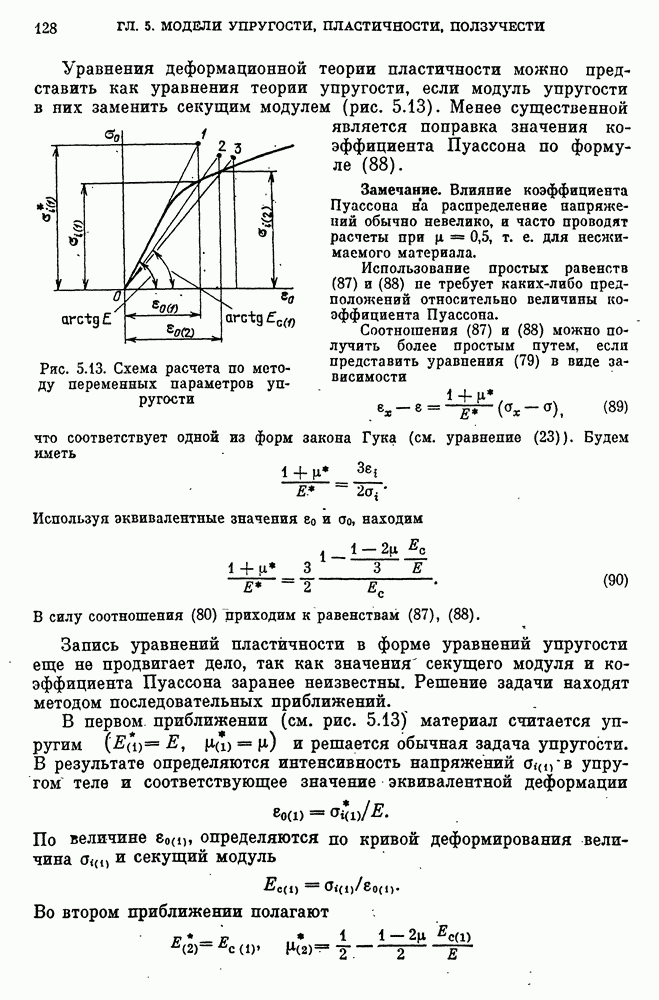
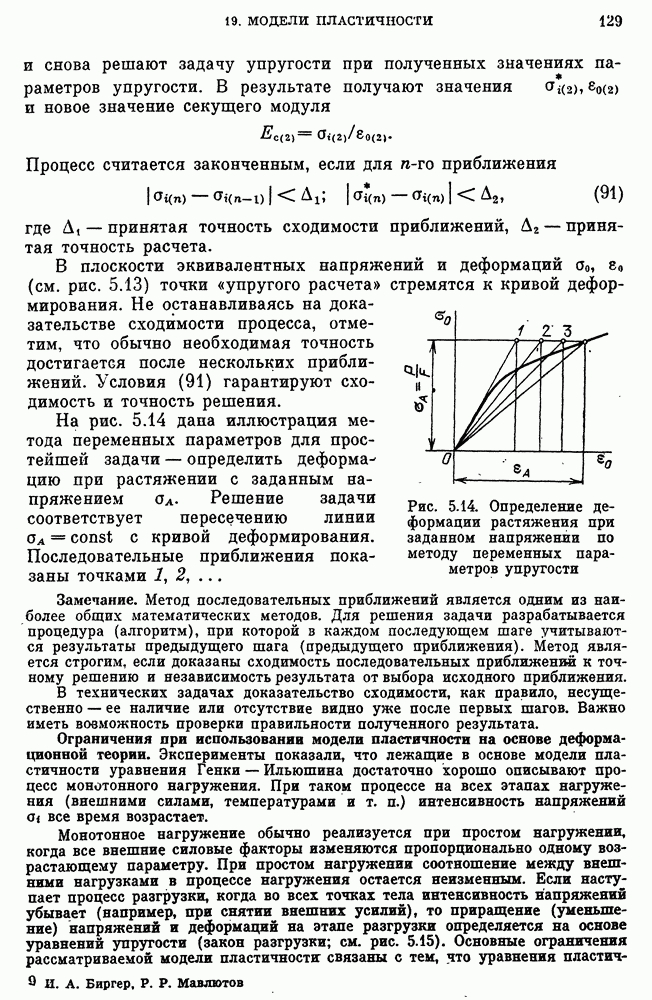
- Метод переменных параметров упругости.
- Ограничения при использовании модели пластичности на основе деформационной теории.
- 20. Модели ползучести и вязкоупругости
- Модели ползучести, основанные на теории старения. Изохронные кривые ползучести.
- Модели ползучести, основанные на теории течения и теории упрочнения.
- Установившаяся ползучесть.
- Модели вязкоупругости.
- ГЛАВА 6. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
- 21. Растяжение и сжатие стержней сосредоточенными и распределенными силами
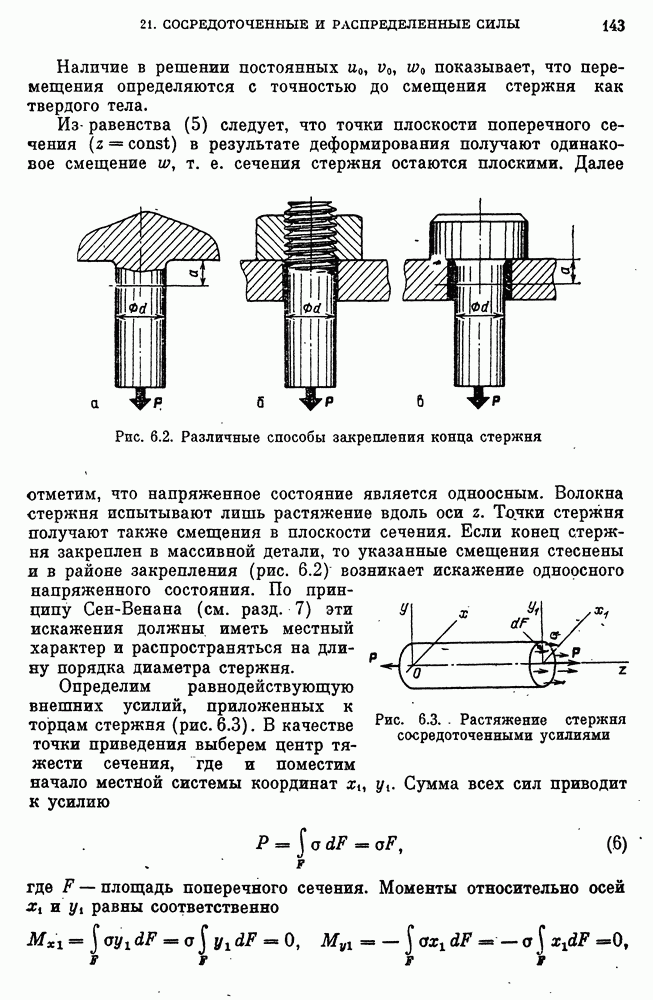
- Приближенные модели растяжения и сжатия стержней.
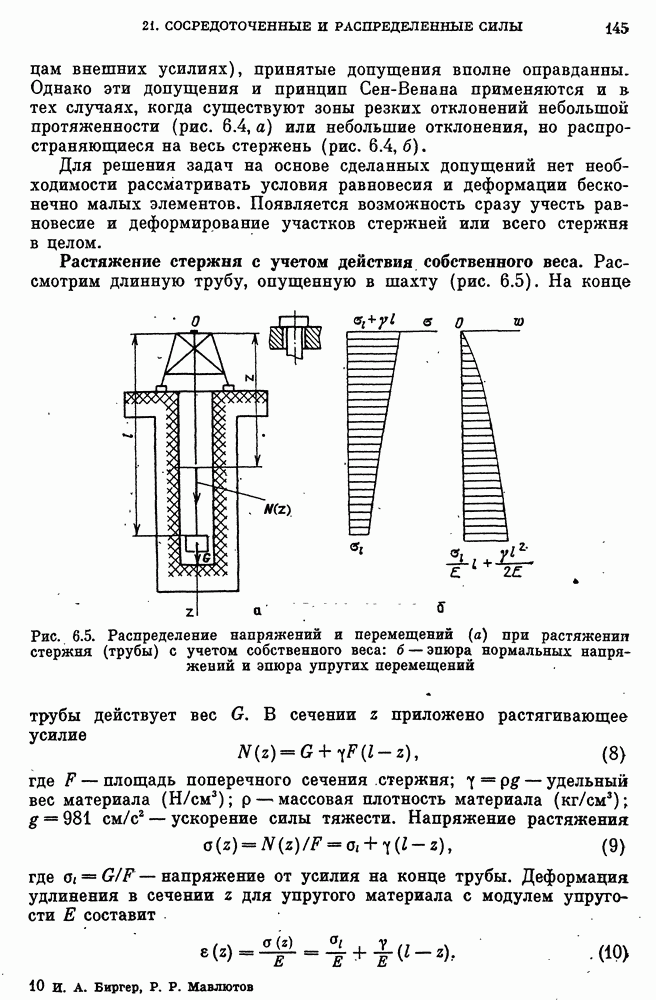
- Растяжение стержня с учетом действия собственного веса.
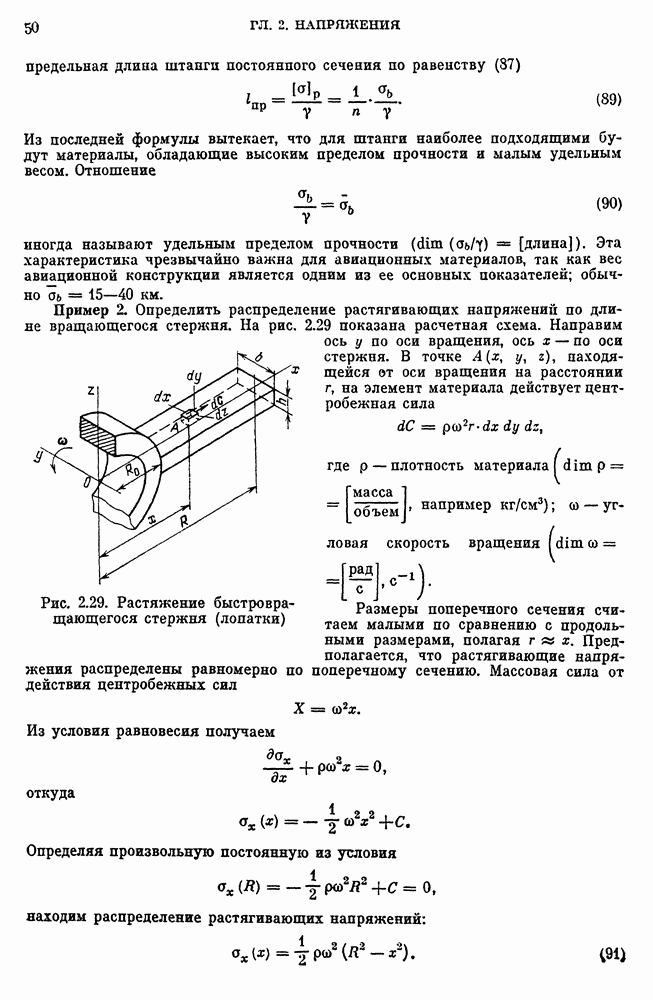
- Растяжение стержня в поле центробежных сил.
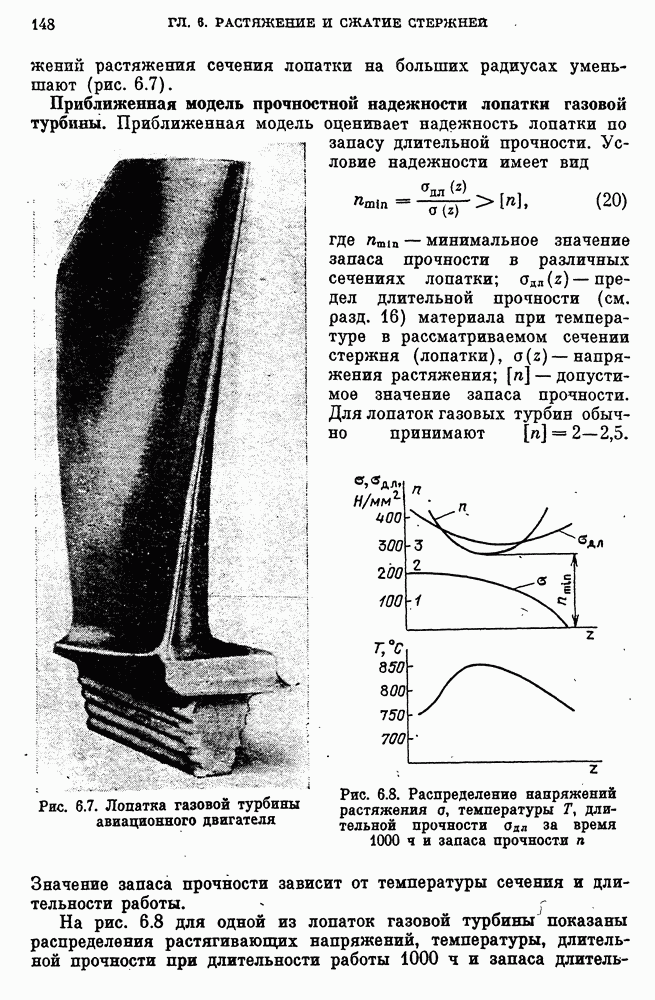
- Приближенная модель прочностной надежности лопатки газовой турбины.
- Связь запаса прочности по напряжениям и запаса прочности по долговечности.
- 22. Статически неопределимые задачи растяжения и сжатия стержней
- Прочностная модель болтового соединения.
- Модель прочностной надежности болта при действии переменных нагрузок.
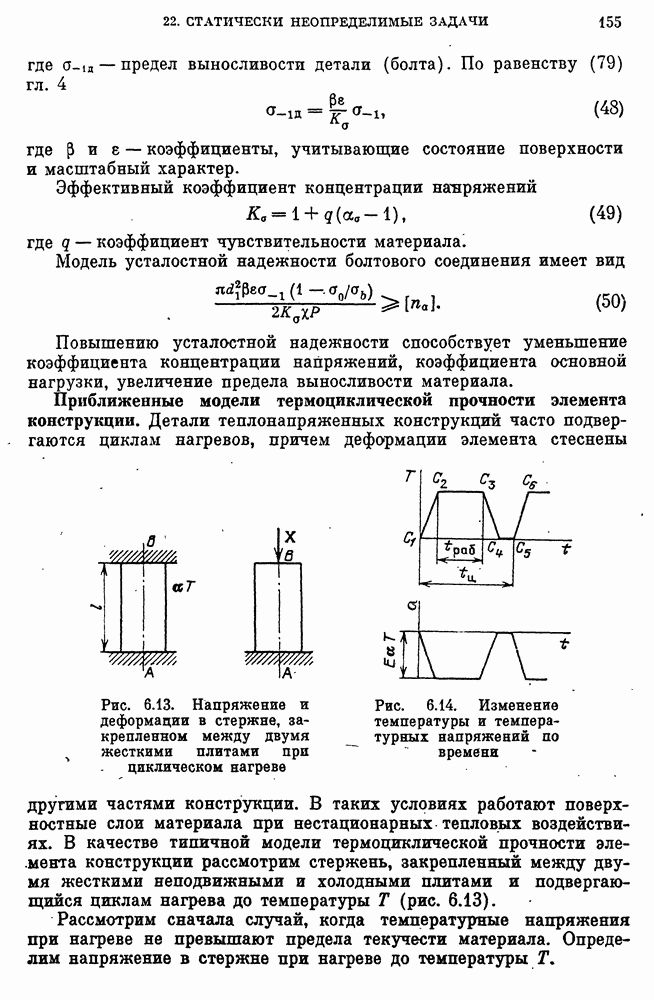
- Приближенные модели термоциклической прочности элемента конструкции.
- Учет ползучести материала при определении температурных напряжений.
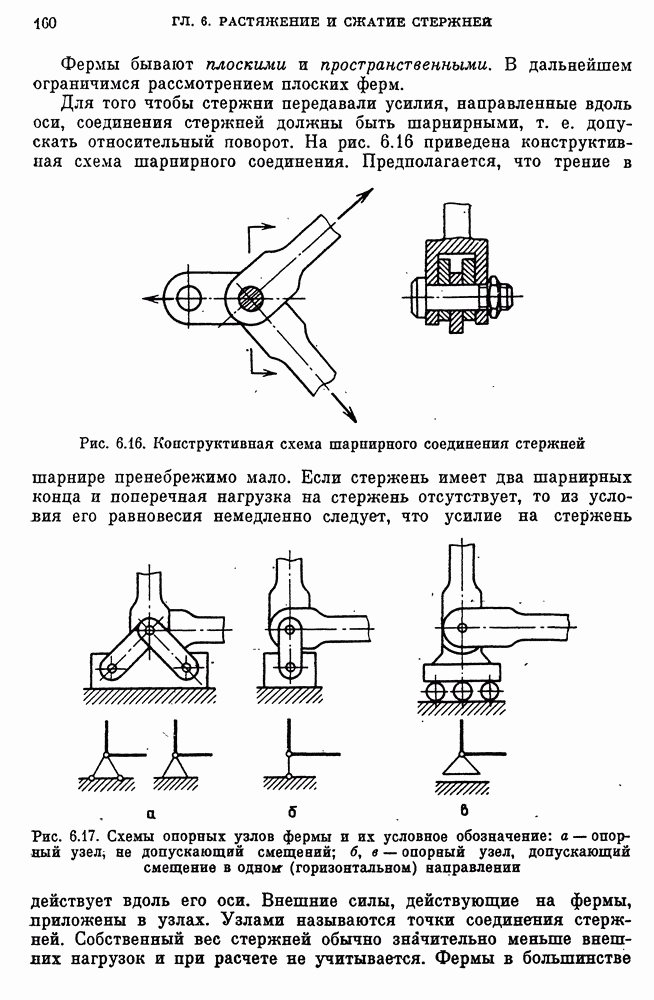
- 23. Стержневые системы (фермы)
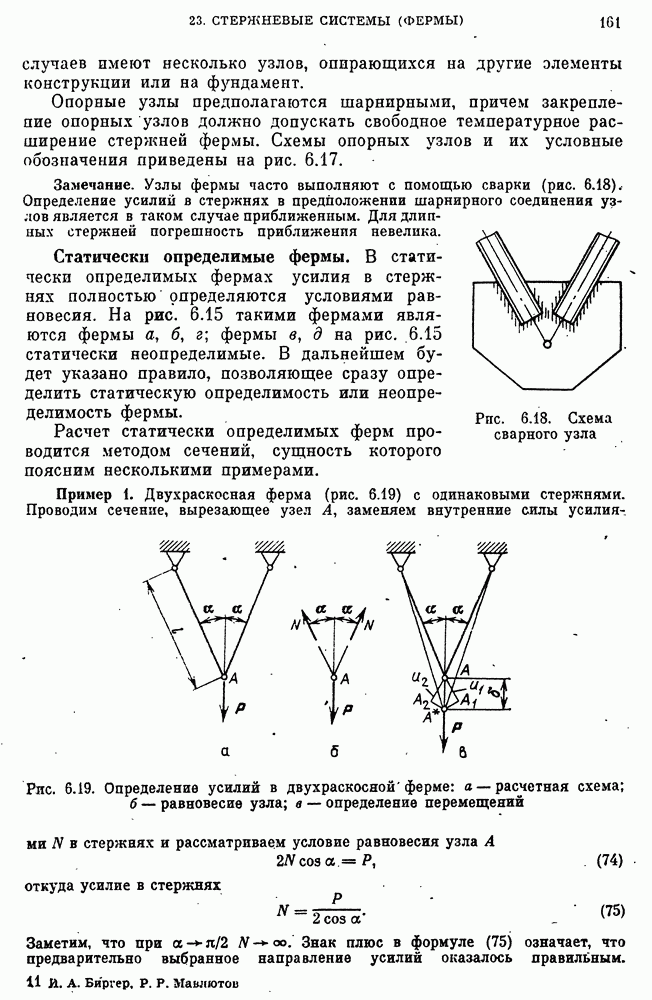
- Статически определимые фермы.
- Общие замечания о статически определимых фермах и сопоставление со статически неопределимыми.
- 24. Статически неопределимые стержневые системы
- Работа статически неопределимой системы после возникновения пластических деформаций.
- Модель надежности по несущей способности.
- Сопоставление двух моделей надежности.
- Расчет в упругопластической стадии методом переменных параметров упругости.
- 25. Гибкие нити
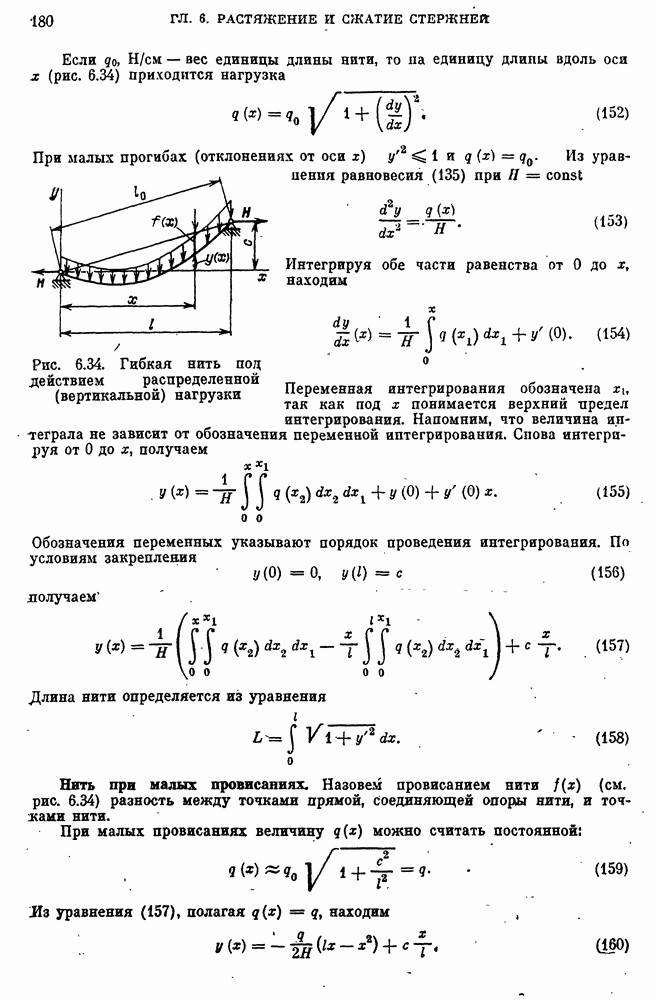
- Гибкая нить под действием распределенной нагрузки.
- Нить при малых провисаниях.
- ГЛАВА 7. КРУЧЕНИЕ СТЕРЖНЕЙ
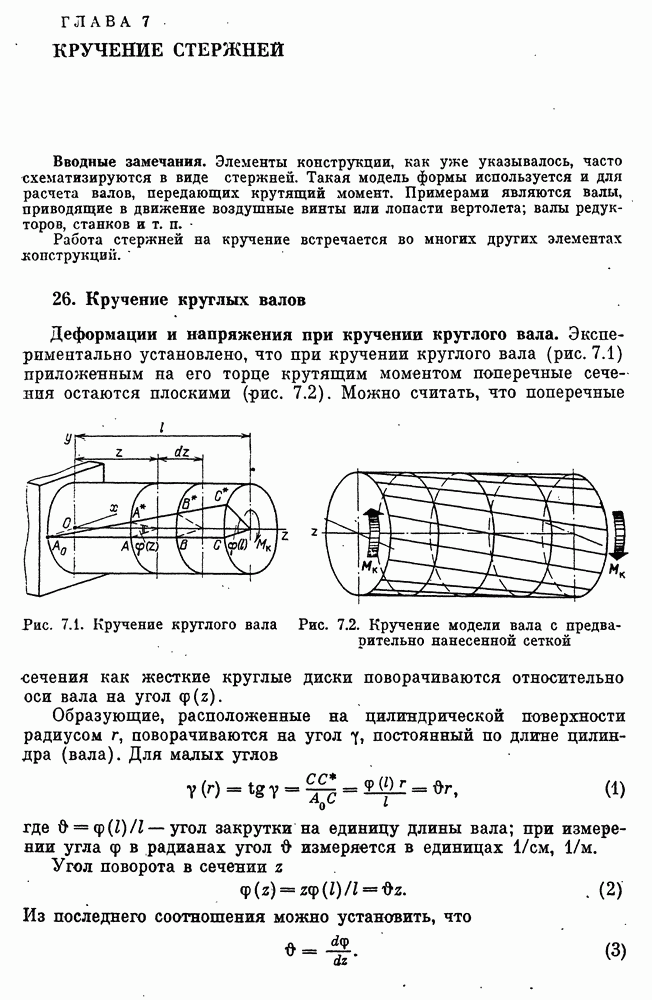
- 26. Кручение круглых валов
- Кручение полого вала.
- Кручение вала в упругопластической стадии.
- Кручение вала в стадии установившейся ползучести.
- Модели прочностной надежности вала при кручении.
- 27. Общая задача кручения стержней и концентрация напряжений
- Математическая постановка задачи. Функция кручения.
- Функция напряжения.
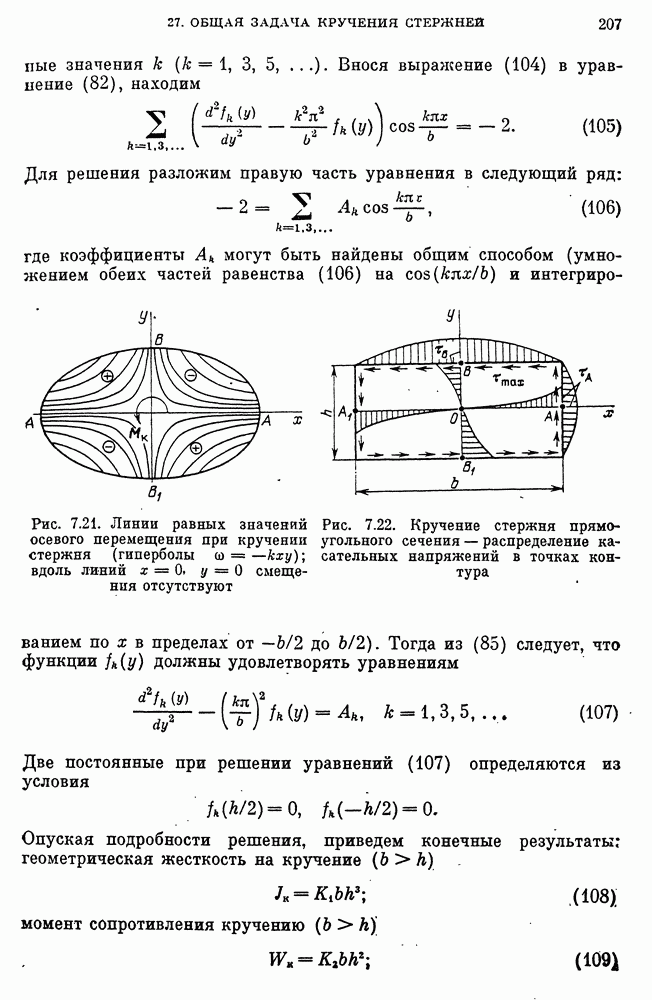
- Примеры точных решений. Стержень эллиптического сечения.
- Стержень прямоугольного сечения.
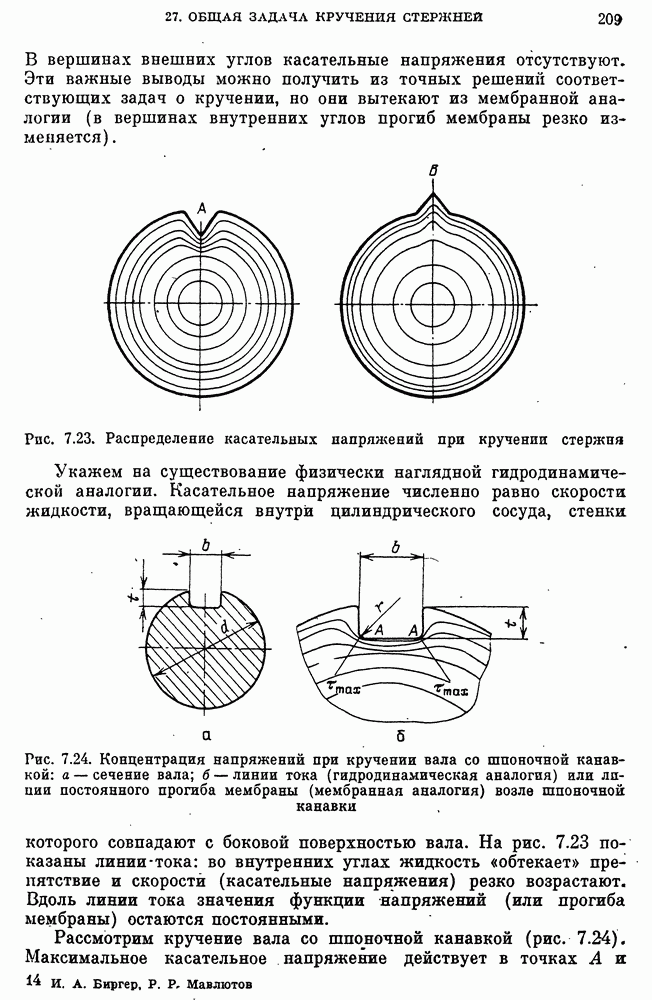
- Концентрация напряжений при кручении.
- 28. Кручение тонкостенных стержней
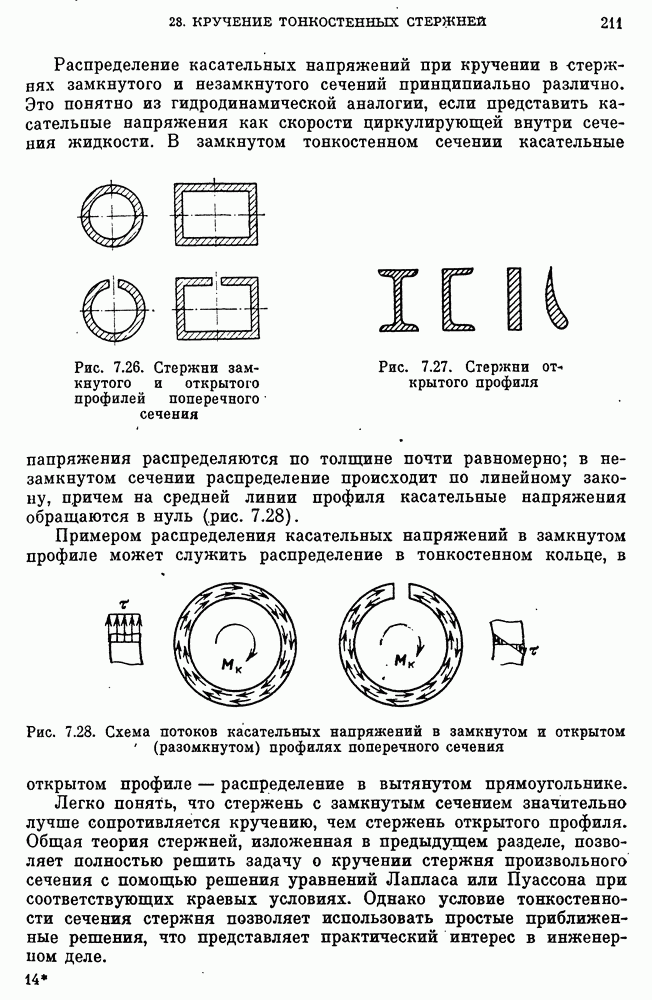
- Кручение стержня замкнутого профиля.
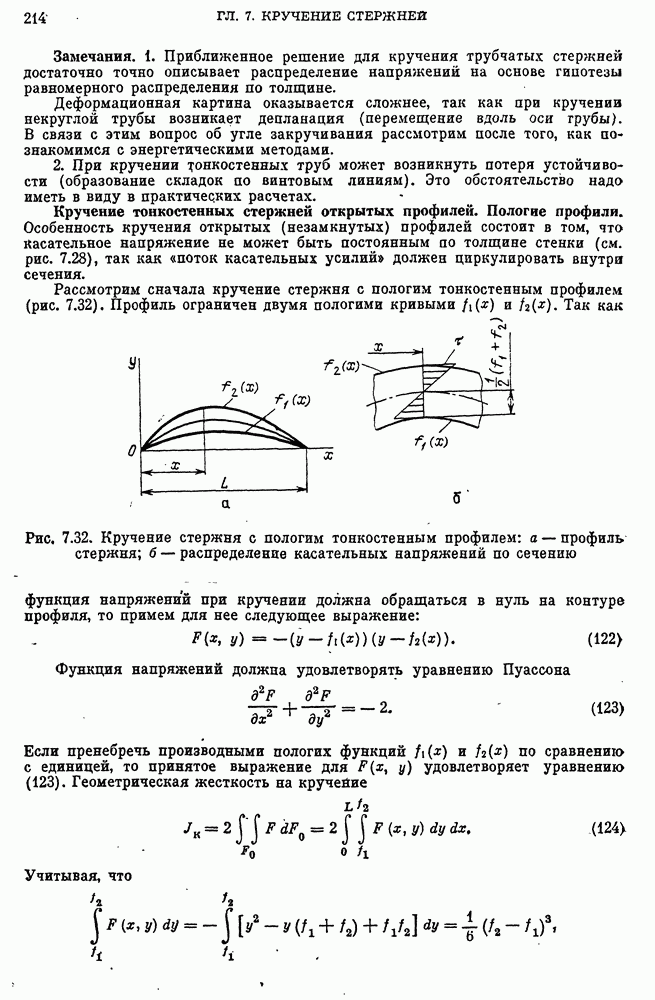
- Кручение тонкостенных стержней открытых профилей. Пологие профили.
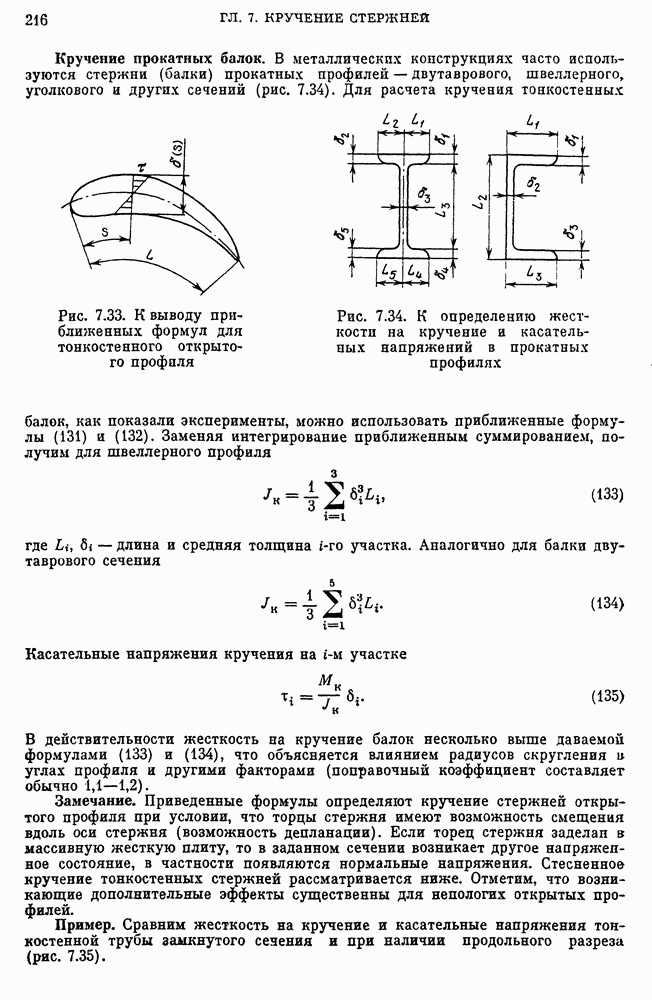
- Кручение прокатных балок.
- Кручение тонкостенных стержней открытого профиля с переменными параметрами упругости.
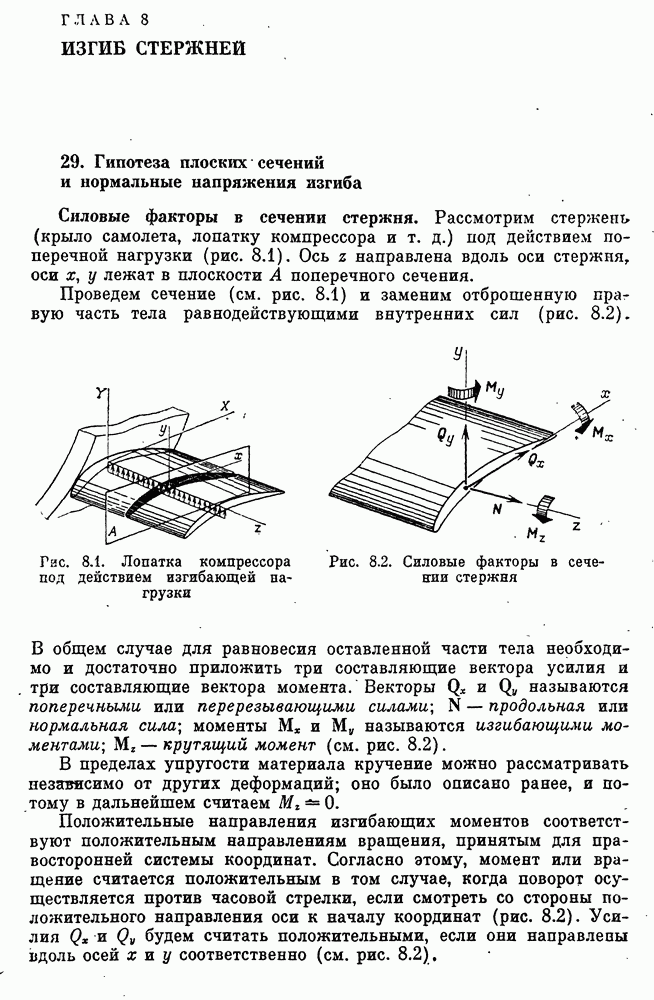
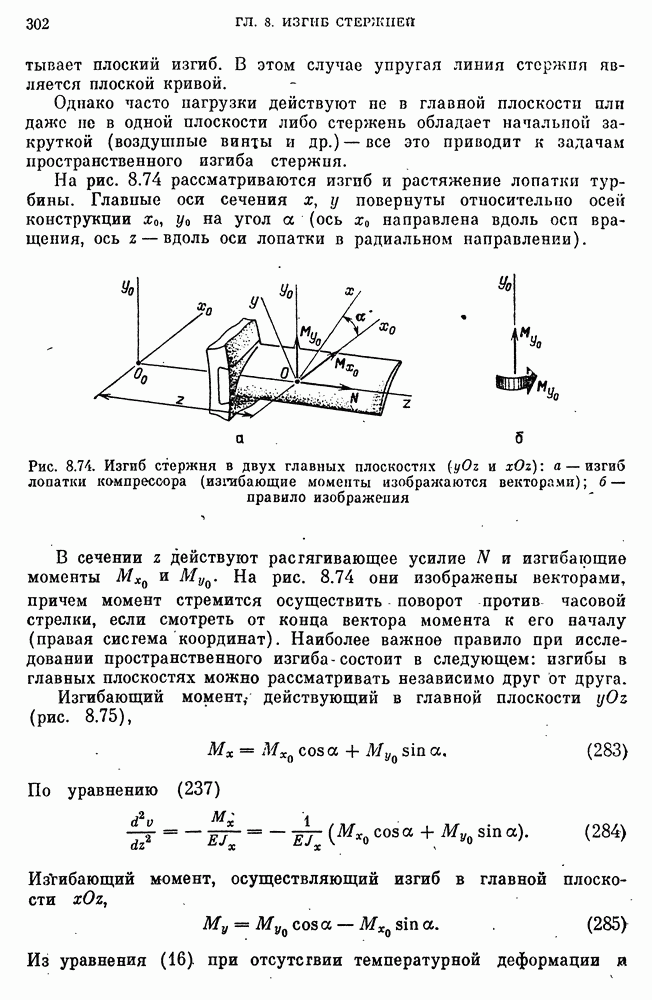
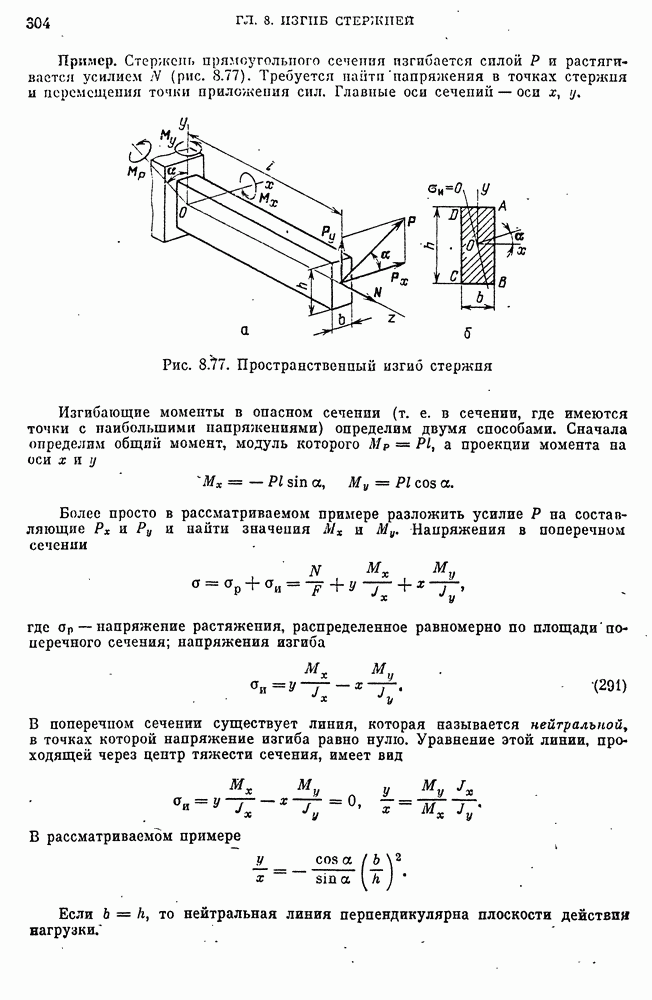
- ГЛАВА 8. ИЗГИБ СТЕРЖНЕЙ
- 29. Гипотеза плоских сечений и нормальные напряжения изгиба
- Распределение нормальных напряжений изгиба.
- Система уравнений для определения нормальных напряжений изгиба и растяжения стержня и ее упрощение.
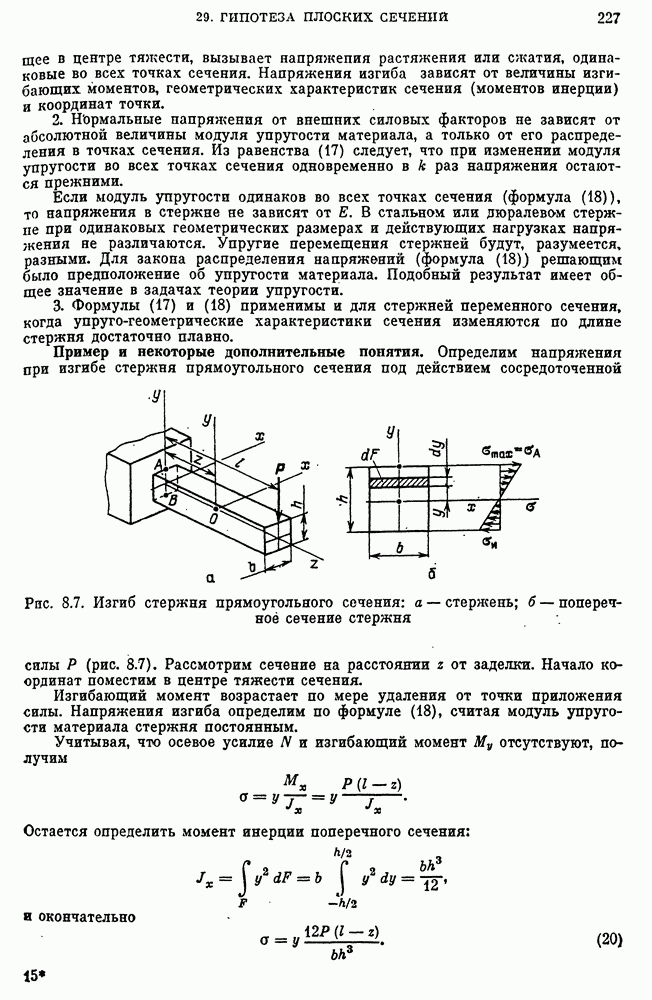
- Напряжения растяжения и изгиба в стержне от действия внешних сил.
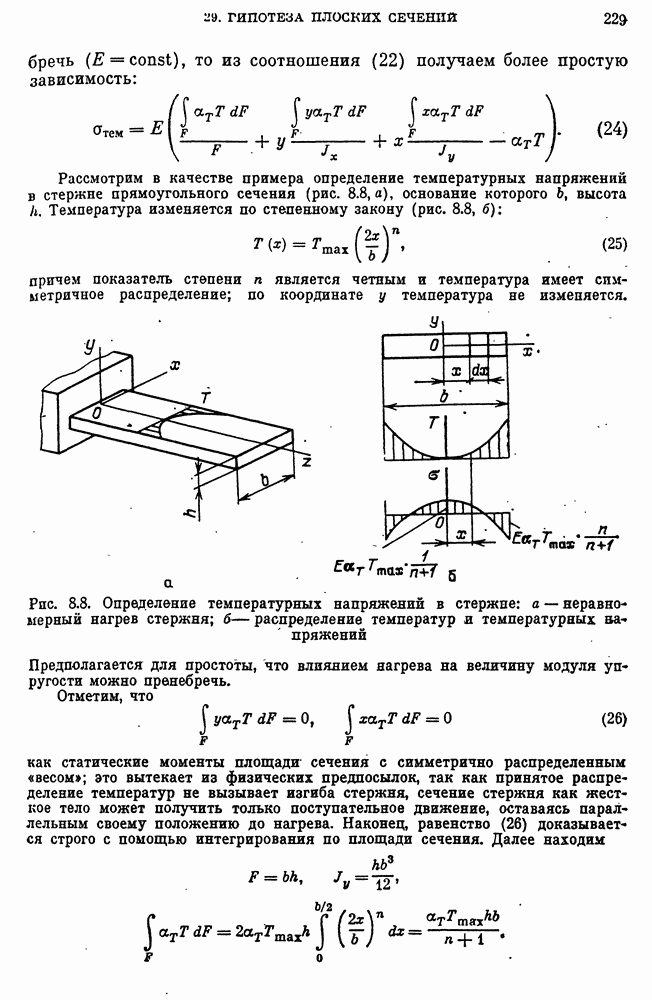
- Температурные напряжения.
- Обоснование гипотезы плоских сечений.
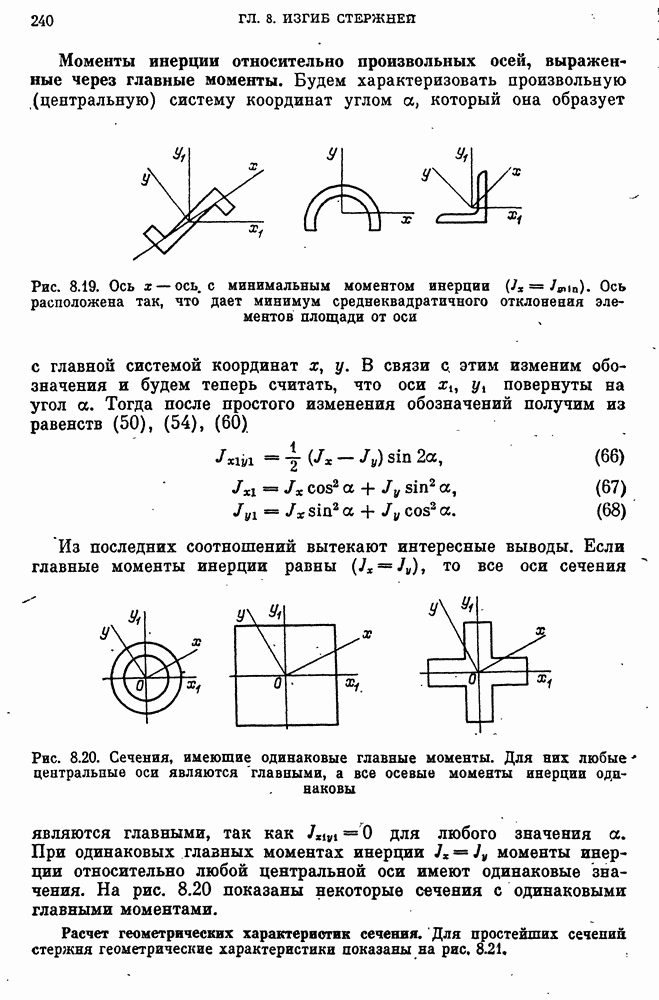
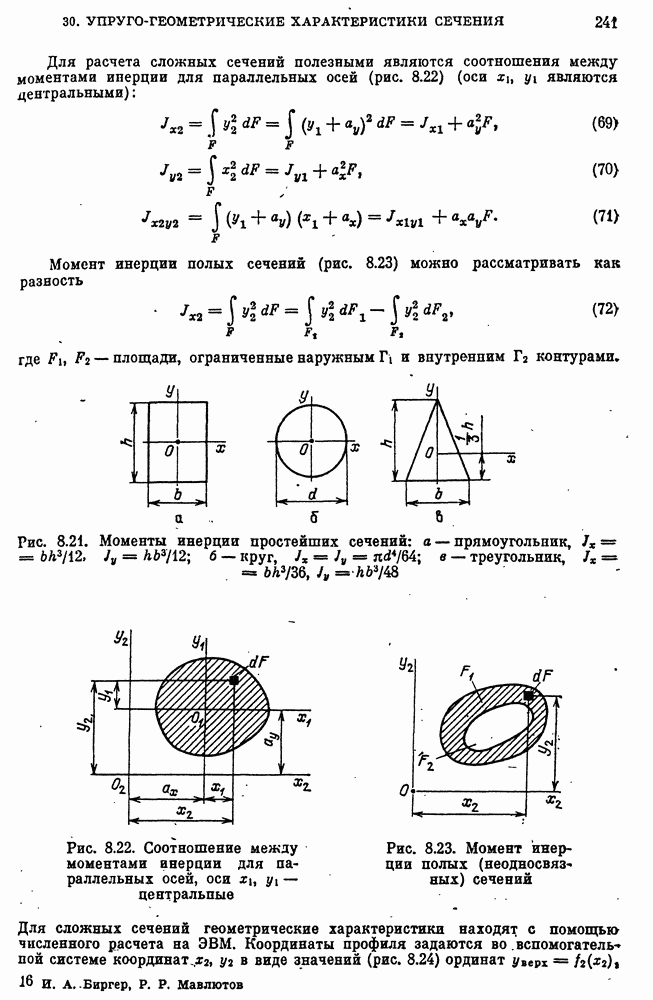
- 30. Упруго-геометрические характеристики сечения стержня при изгибе. Главные оси, главные моменты инерции
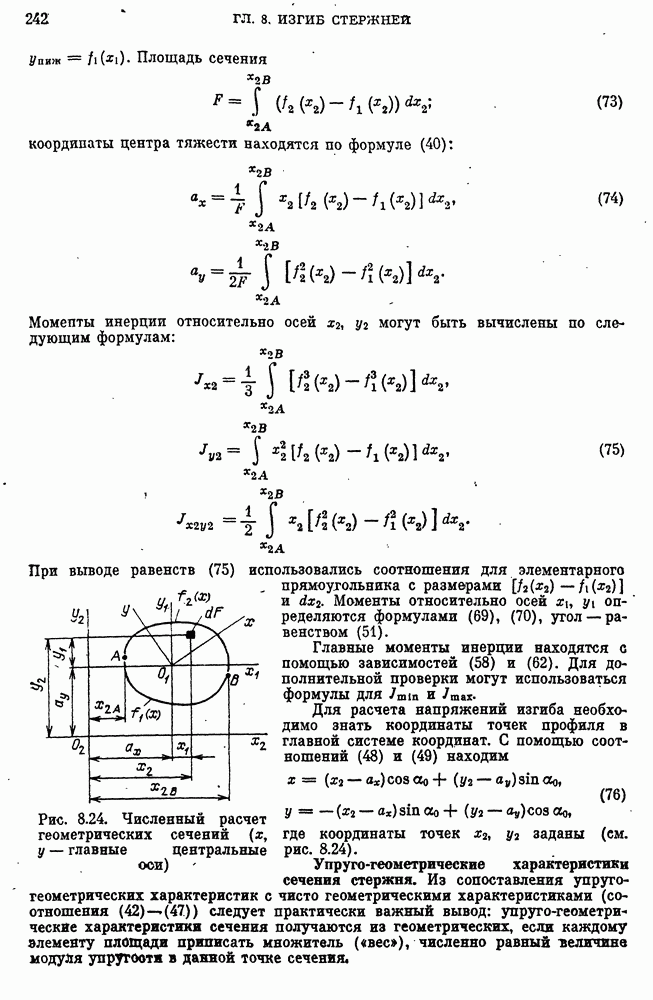
- Геометрические характеристики сечения стержня.
- Главные моменты инерции сечения.
- Упруго-геометрические характеристики сечения стержня.
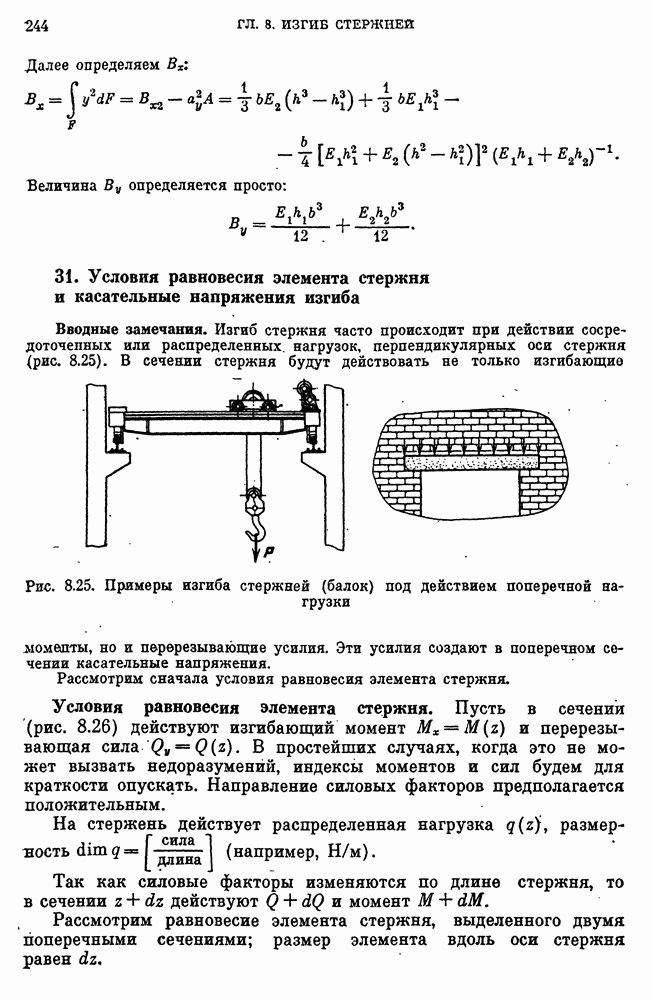
- 31. Условия равновесия элемента стержня и касательные напряжения изгиба
- Скачки перерезывающей силы и изгибающего момента.
- Условие равновесия элемента стержня при наличии распределенных изгибающих моментов.
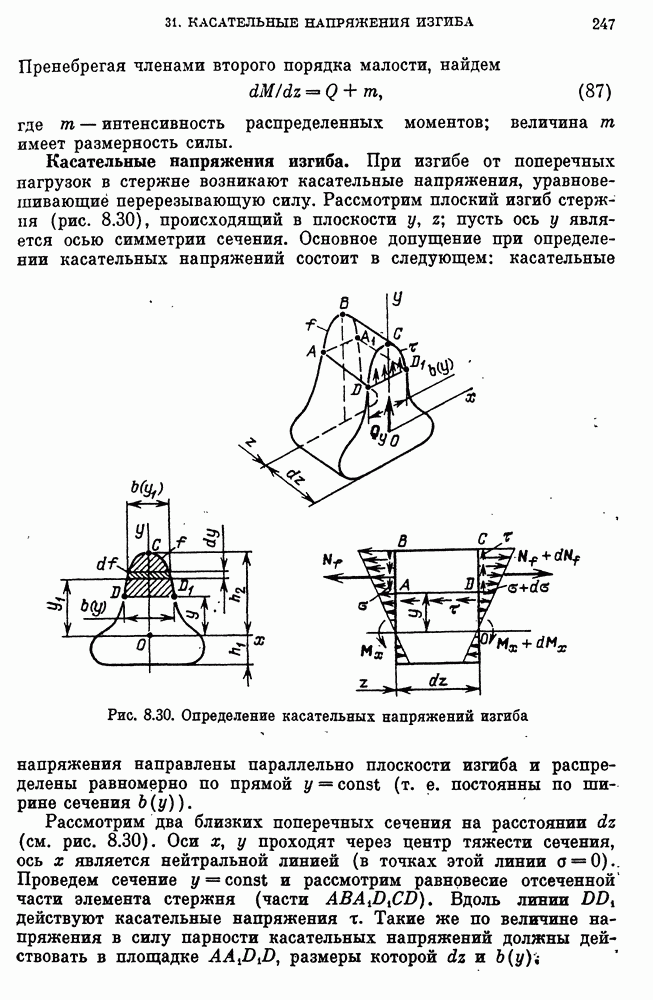
- Распределение касательных напряжений в стержне постоянного сечения.
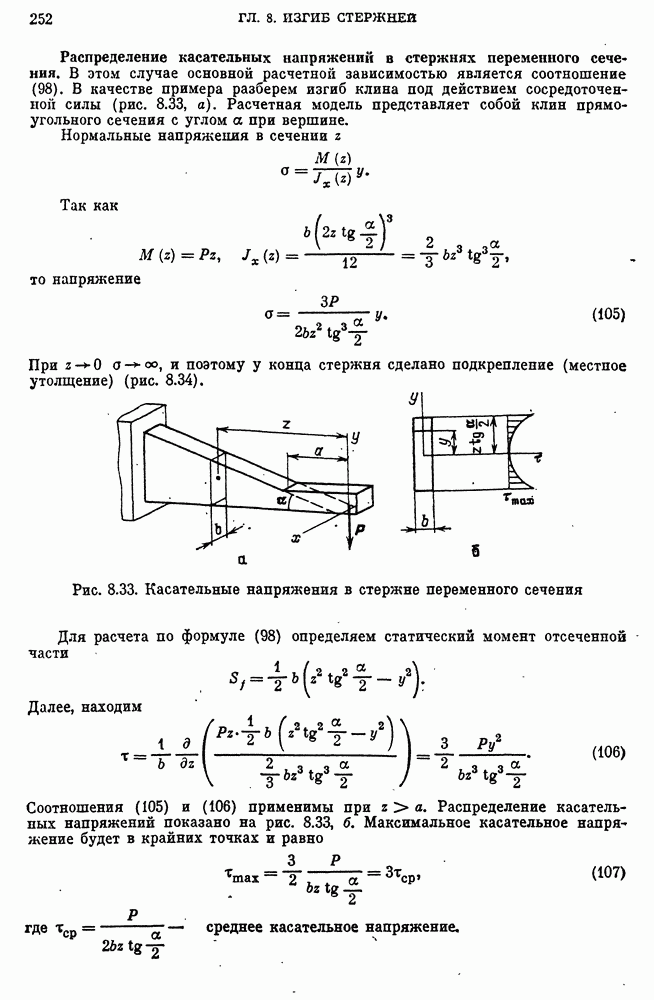
- Распределение касательных напряжений в стержнях переменного сечения.
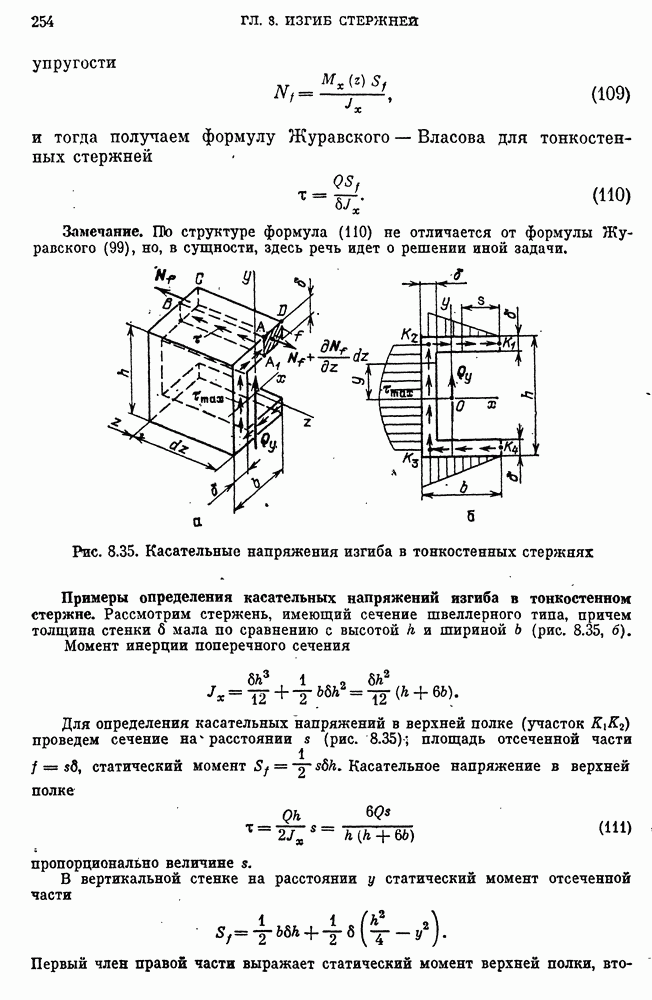
- Касательные напряжения изгиба в тонкостенных стержнях.
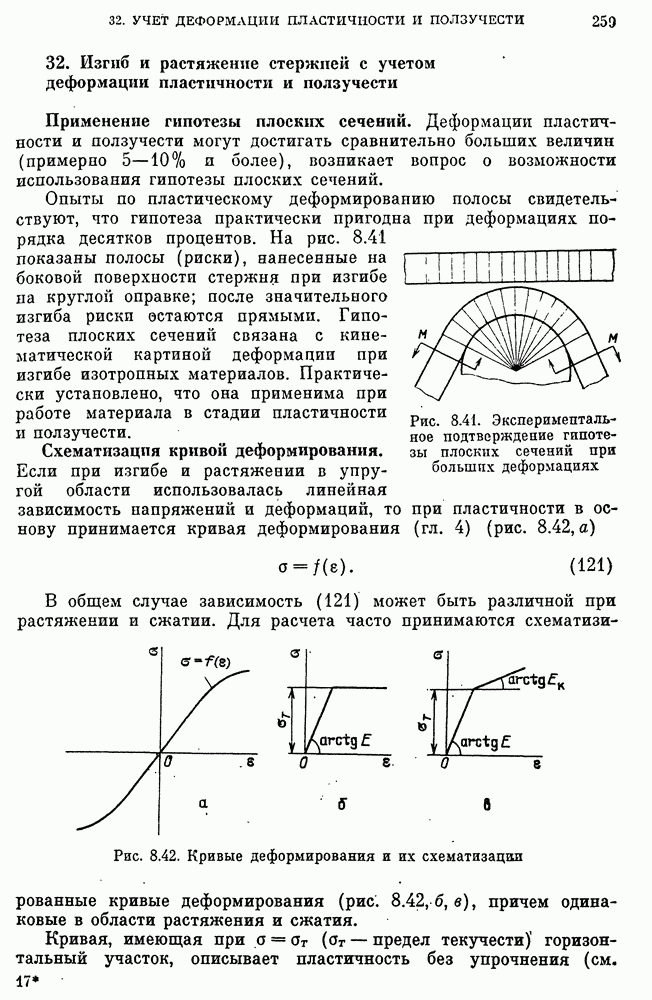
- 32. Изгиб и растяжение стержней с учетом деформации пластичности и ползучести
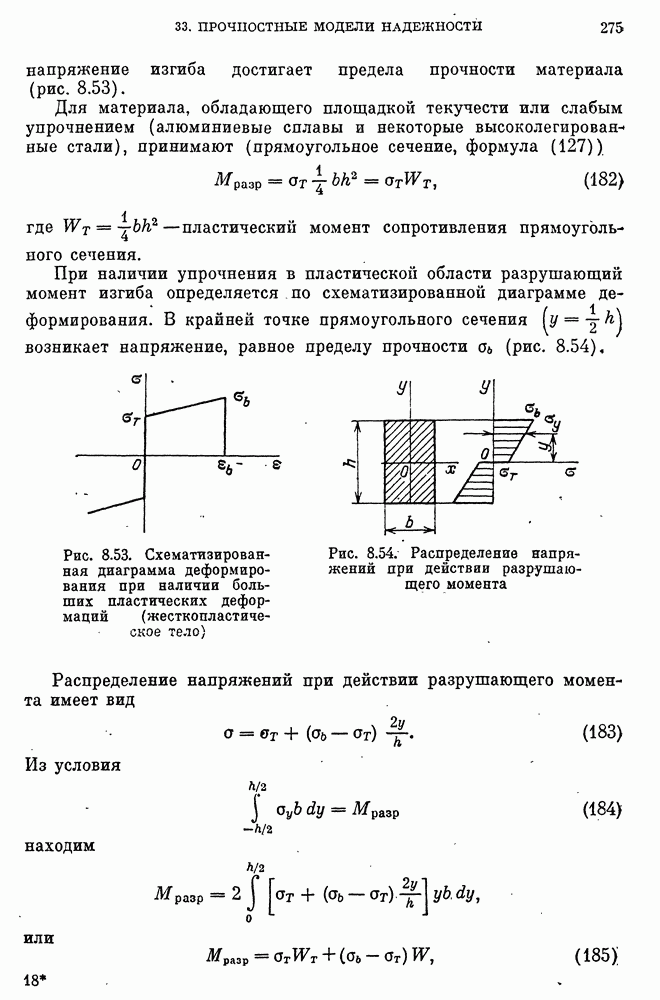
- Изгиб стержней при пластичности без упрочнения. Предельный изгибающий момент.
- Остаточные напряжения.
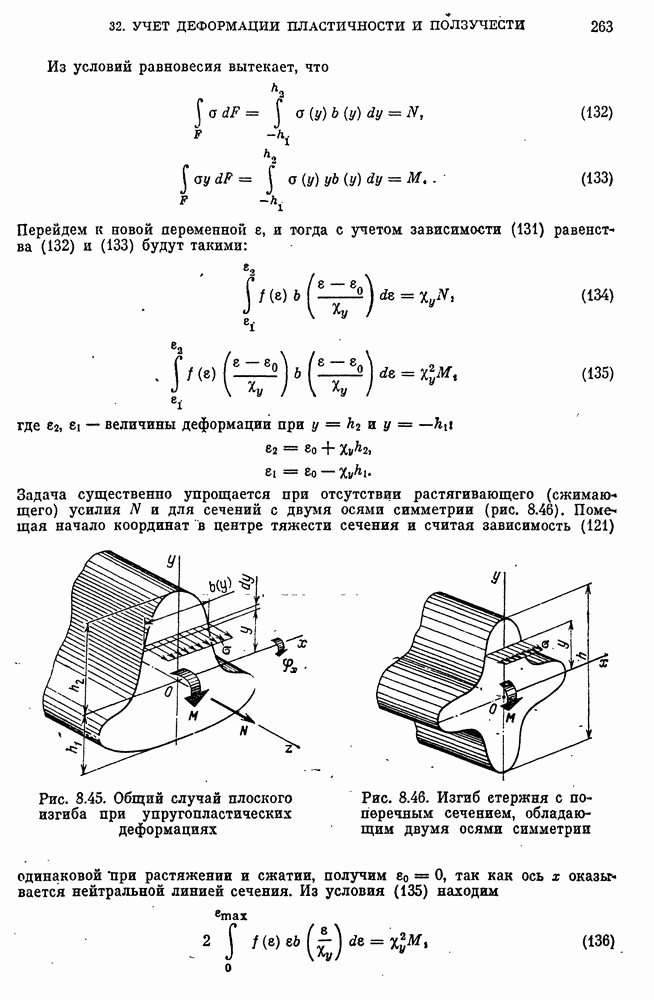
- Общий случай расчета стержня в упругопластнческой стадии. Метод переменных параметров упругости.
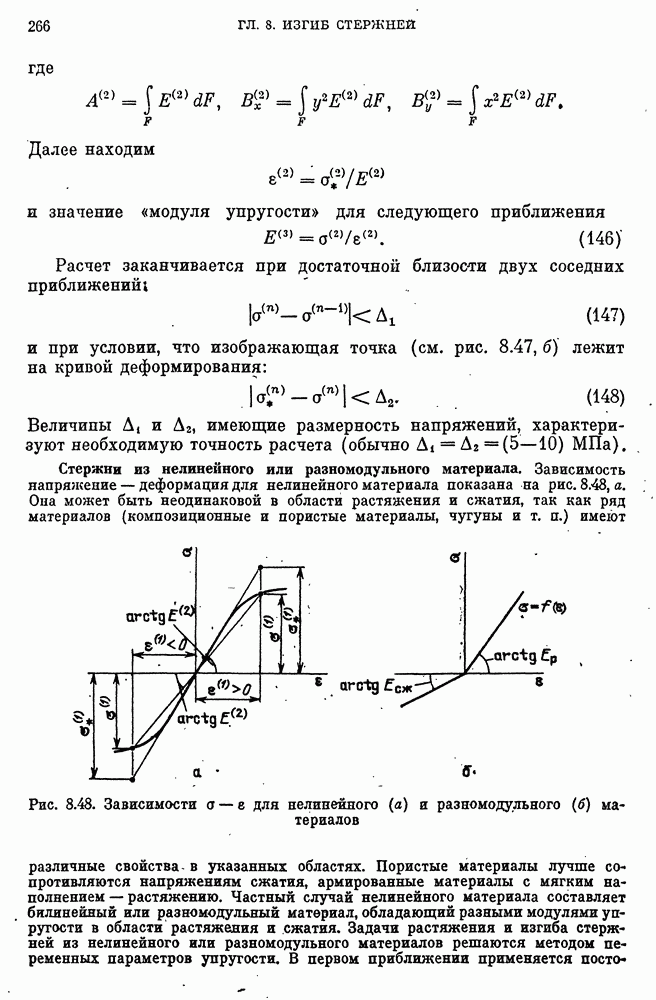
- Стержни из нелинейного или разномодульного материала.
- Касательные напряжения при изгибе стержней в упругопластической стадии.
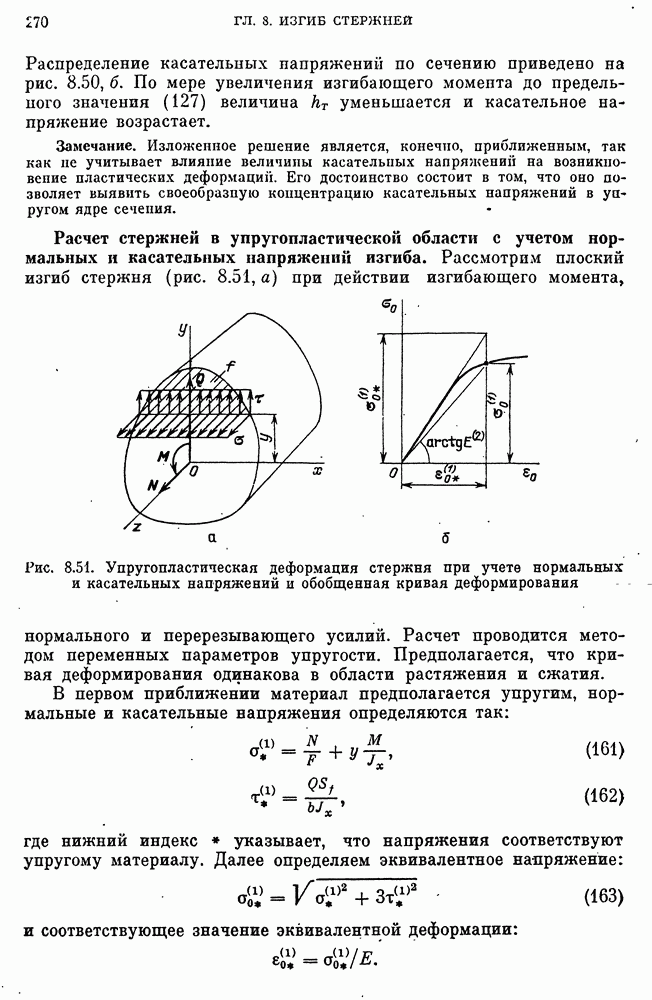
- Расчет стержней в упругопластической области с учетом нормальных и касательных напряжений изгиба.
- Учет деформации ползучести при изгибе стержня.
- Общий случай расчета стержней на изгиб при учете ползучести материала.
- 33. Прочностные модели надежности при изгибе
- Прочностная модель надежности при статической нагрузке по напряжениям.
- Прочностная модель надежности при переменной нагрузке.
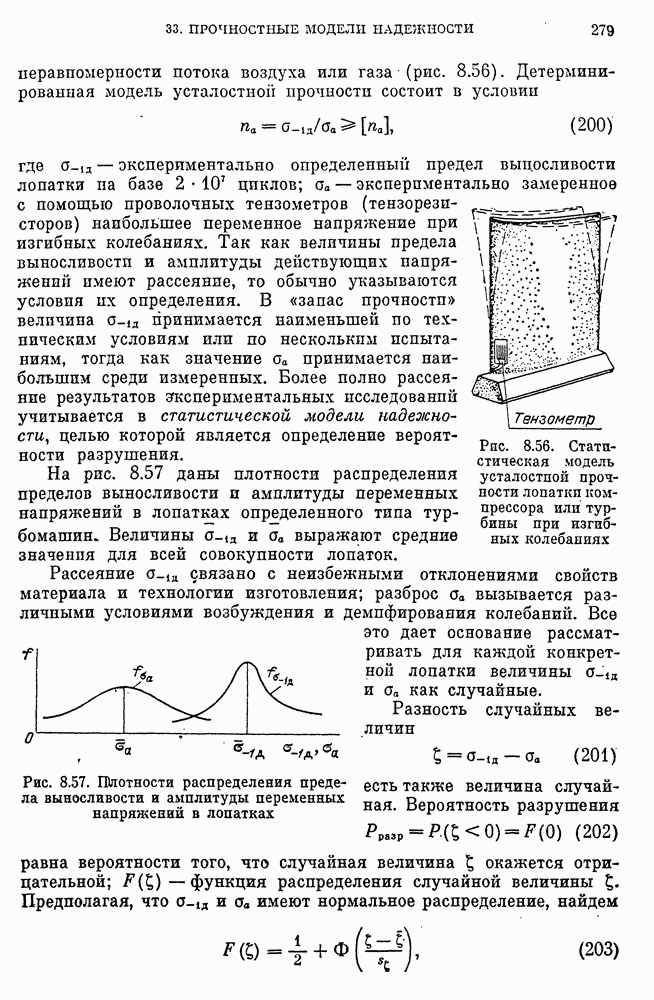
- Детерминированная и статистическая модели усталостней прочности лопатки компрессора или турбины, вероятность разрушения.
- Прочностная модель надежности валов.
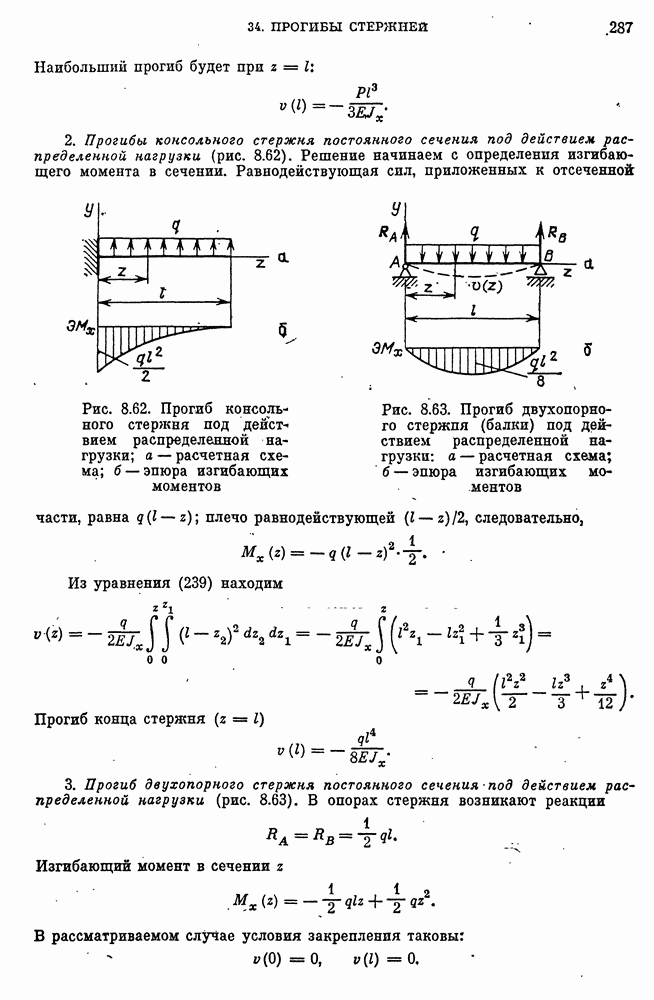
- 34. Прогибы стержней
- Геометрическая картина изгибной деформации.
- Уравнение упругой линии стержня.
- Уравнение упругой линии при изгибе стержней постоянного сечения.
- Основная форма дифференциального уравнения плоского изгиба стержня.
- Дифференциальное уравнение плоского изгиба в матричной форме.
- Нормальные фундаментальные функции дифференциального уравнения изгиба и начальные параметры.
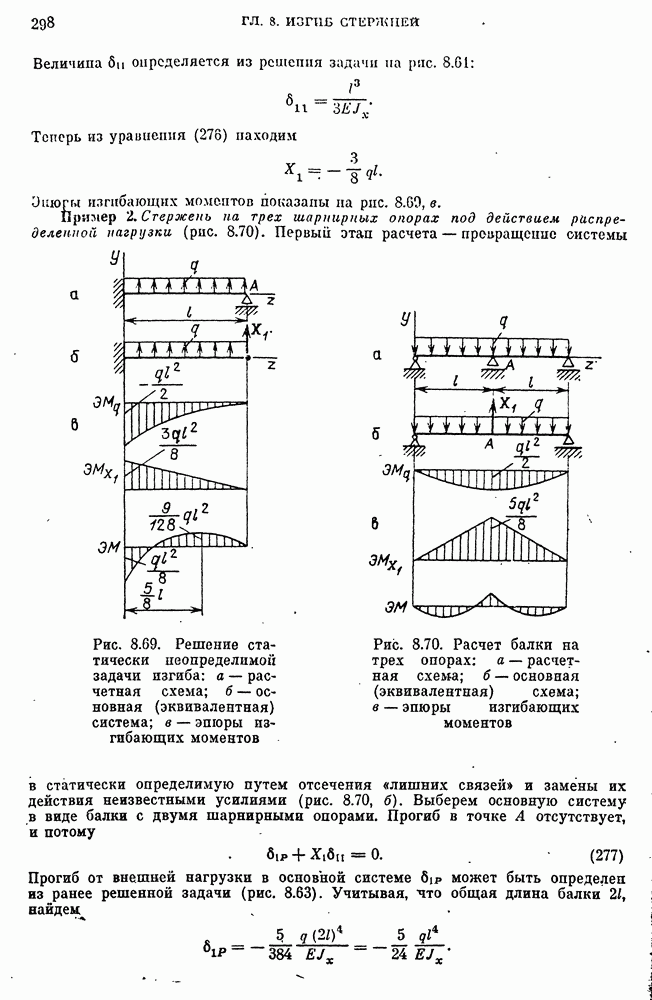
- Статически неопределимые задачи изгиба стержней.
- Учет деформации сдвига при изгибе стержня.
- Уравнение упругой линии стержня при изгибе в двух главных плоскостях.
- ГЛАВА 9. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ, ВАРИАЦИОННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ, ОБЩИЕ СВОЙСТВА УПРУГИХ СИСТЕМ
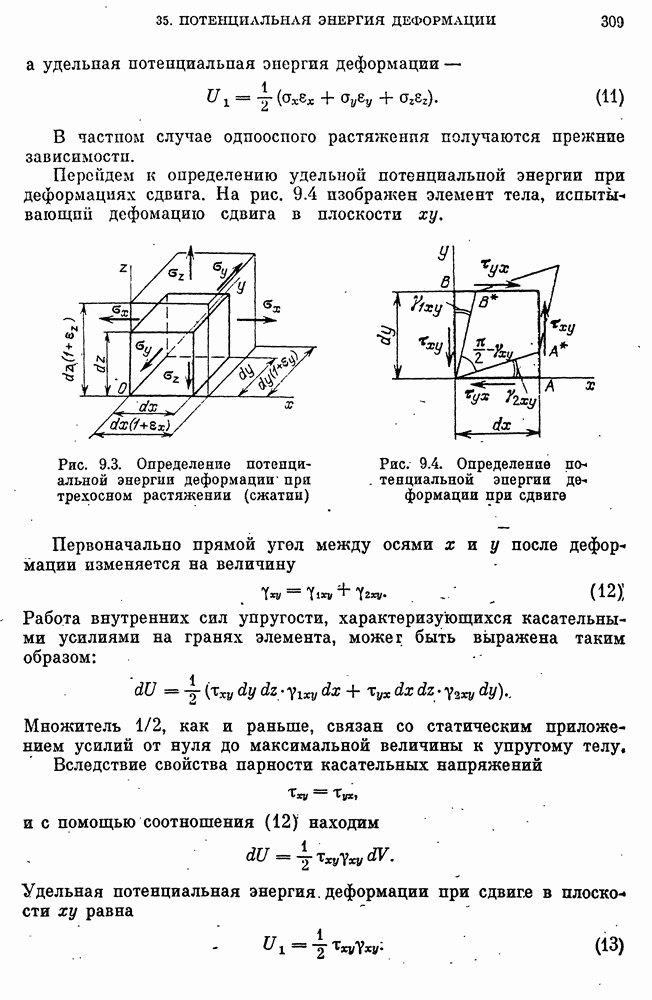
- 35. Потенциальная энергия деформации
- Удельная потенциальная энергия деформации.
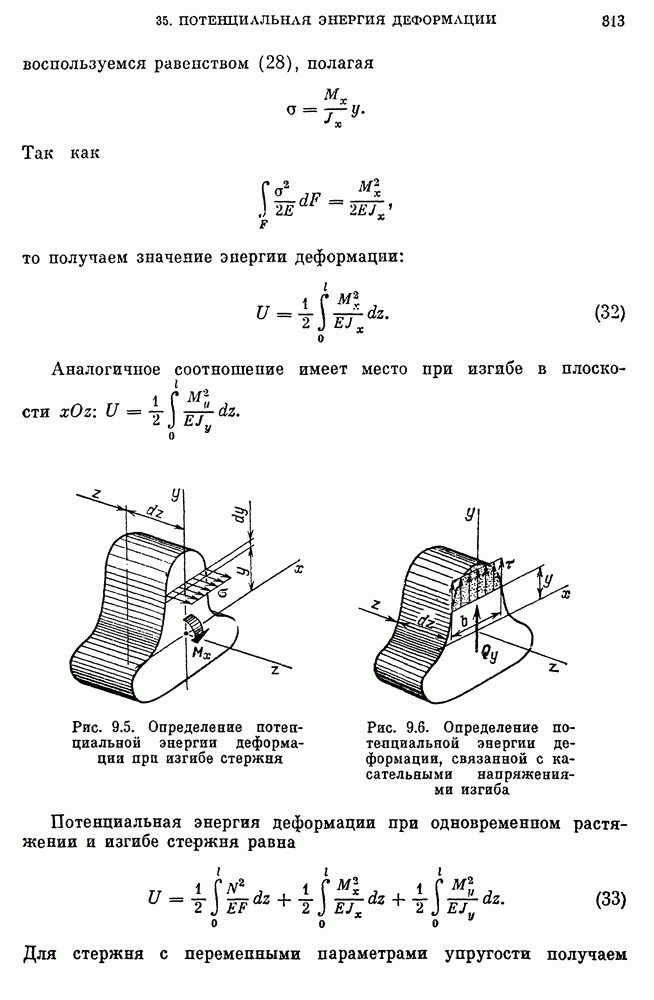
- Потенциальная энергия деформации стержней при растяжении и изгибе.
- Потенциальная энергия деформации, связанная с касательными напряжениями изгиба.
- 36. Вариационные методы
- Условия экстремума функционала, уравнение Эйлера — Пуассона, метод Рэлея — Ритца.
- Применение начала возможных перемещений, вариационное уравнение Лагранжа.
- Вариационное уравнение изгиба стержня.
- Применение метода Рэлея — Ритца к задаче изгиба стержня.
- Применение начала возможных перемещений для определения прогибов стержней. Интеграл Мора.
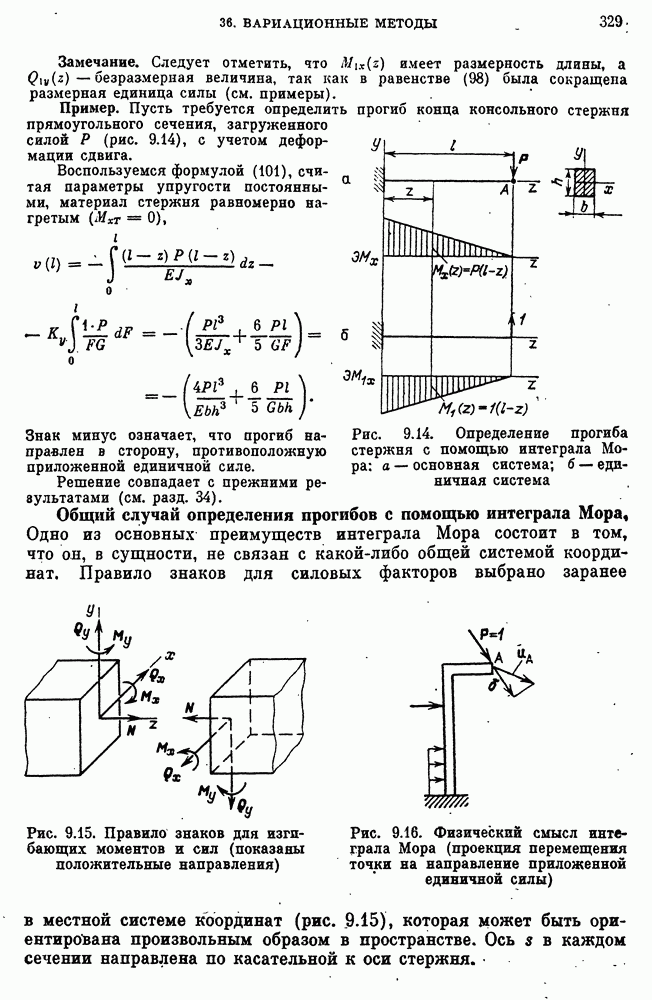
- Общий случай определения прогибов с помощью интеграла Мора.
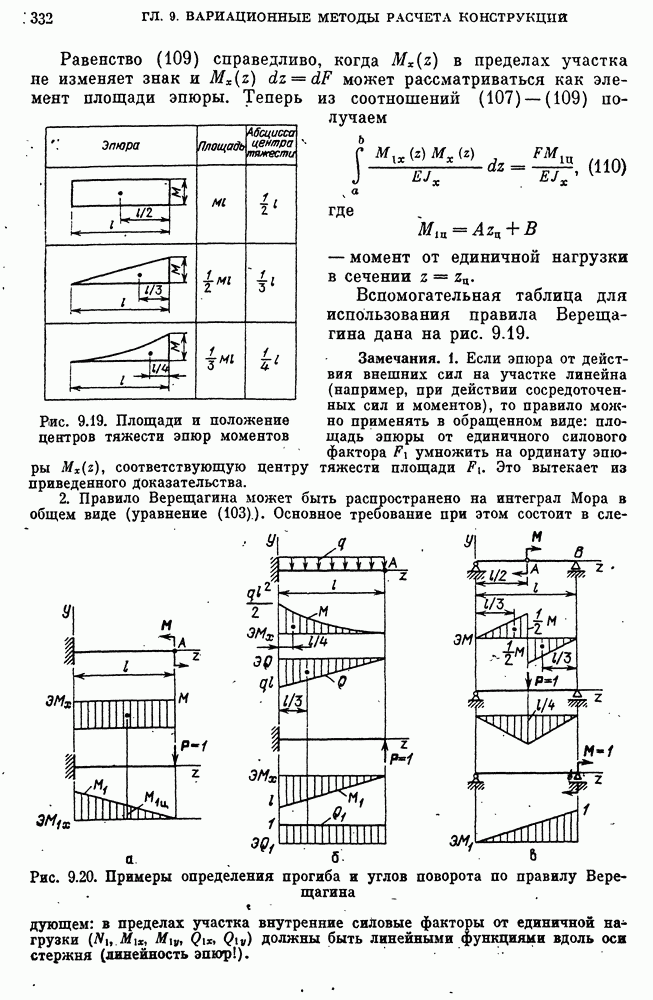
- Вычисление интеграла Мора по правилу Верещагина.
- 37. Вариационные методы и общие свойства упругих систем
- Вариационное уравнение метода вариации напряжений.
- Следствия вариационного уравнения. Теорема Кастильяно.
- Общие свойства упругих систем.
- ГЛАВА 10. СЛОЖНЫЕ МОДЕЛИ СТЕРЖНЕЙ
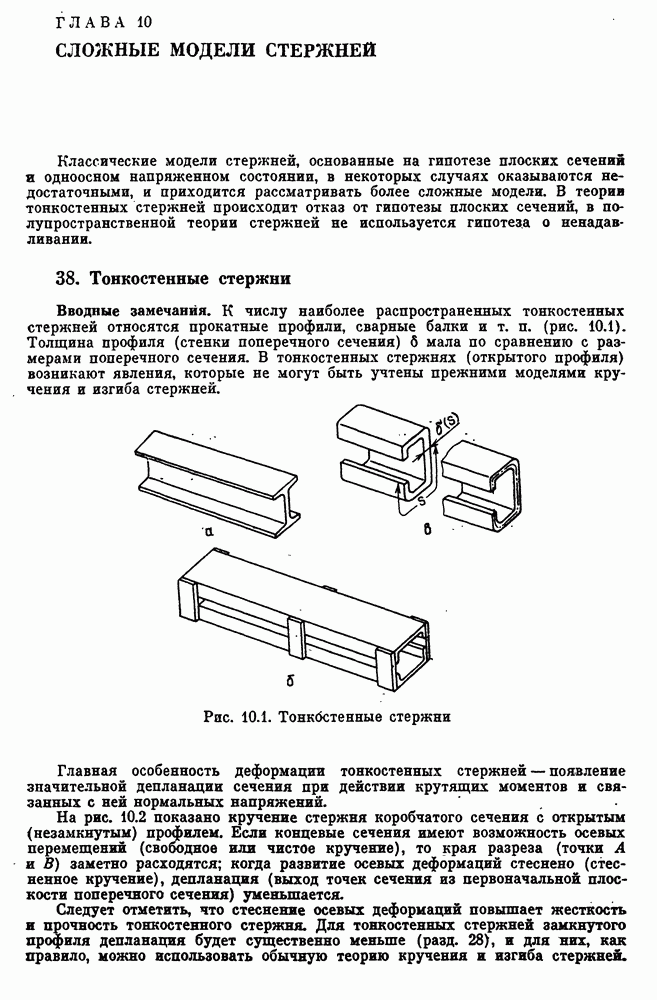
- 38. Тонкостенные стержни
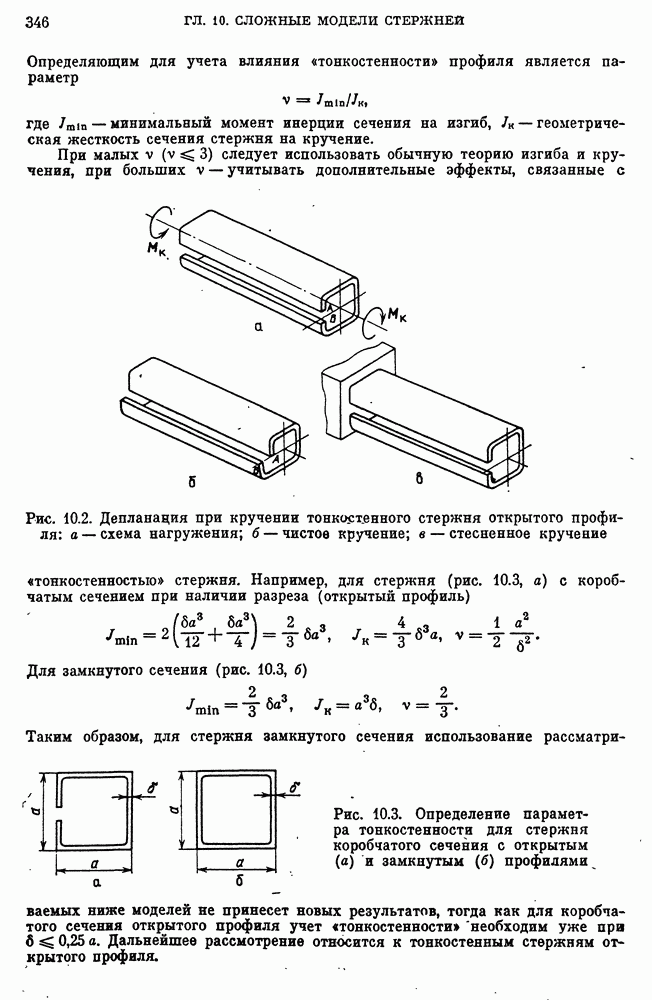
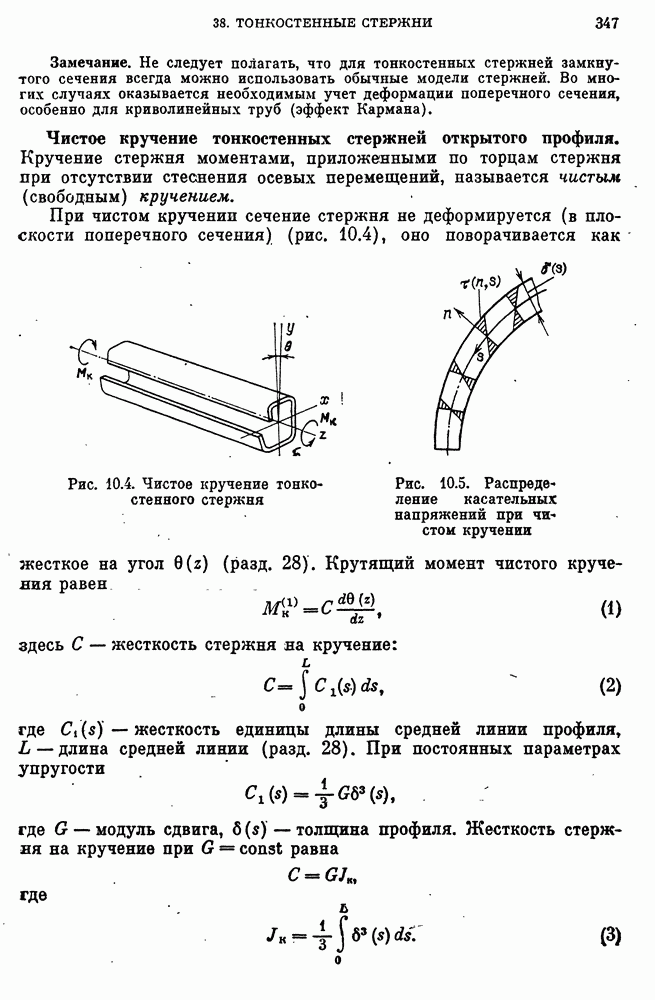
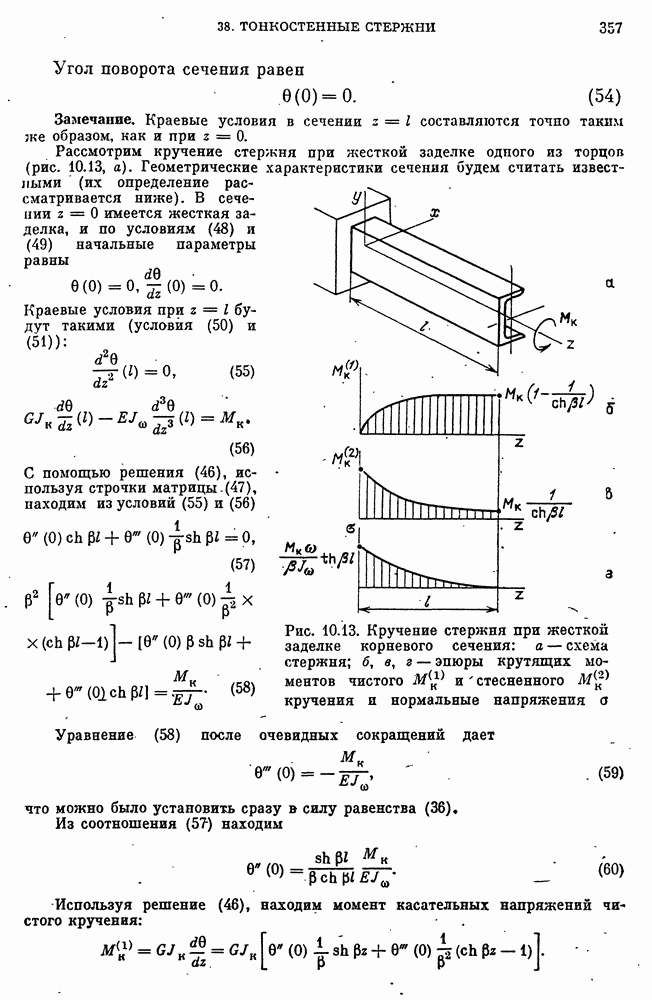
- Чистое кручение тонкостенных стержней открытого профиля.
- Стесненное кручение тонкостенных стержней. Основные гипотезы.
- Нормальные напряжения стесненного кручения.
- Касательные напряжения стесненного кручения.
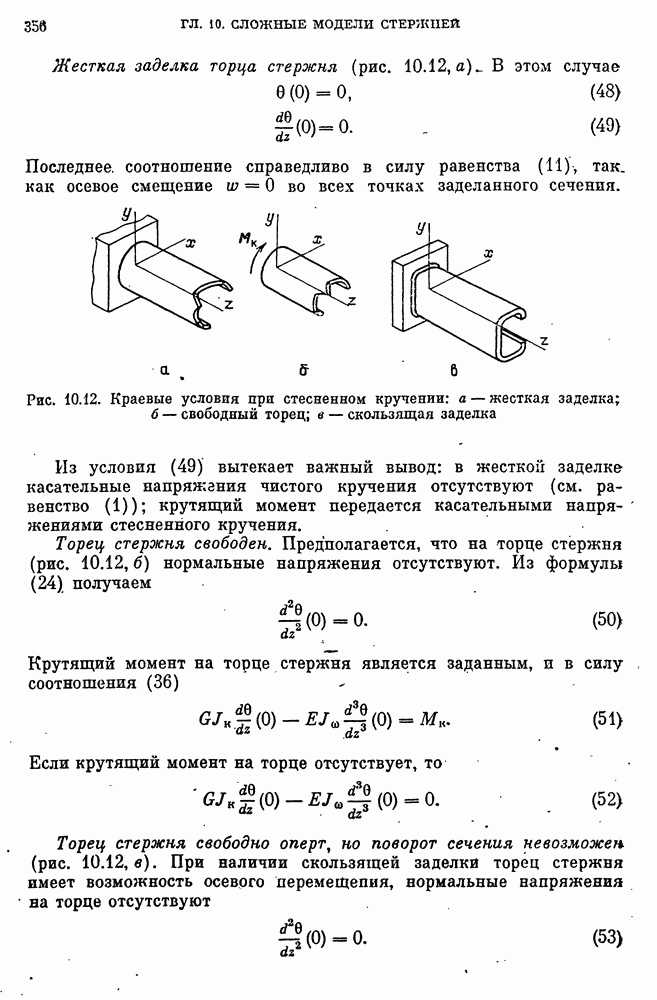
- Решение уравнения стесненного кручения тонкостенных стержней и краевые условия.
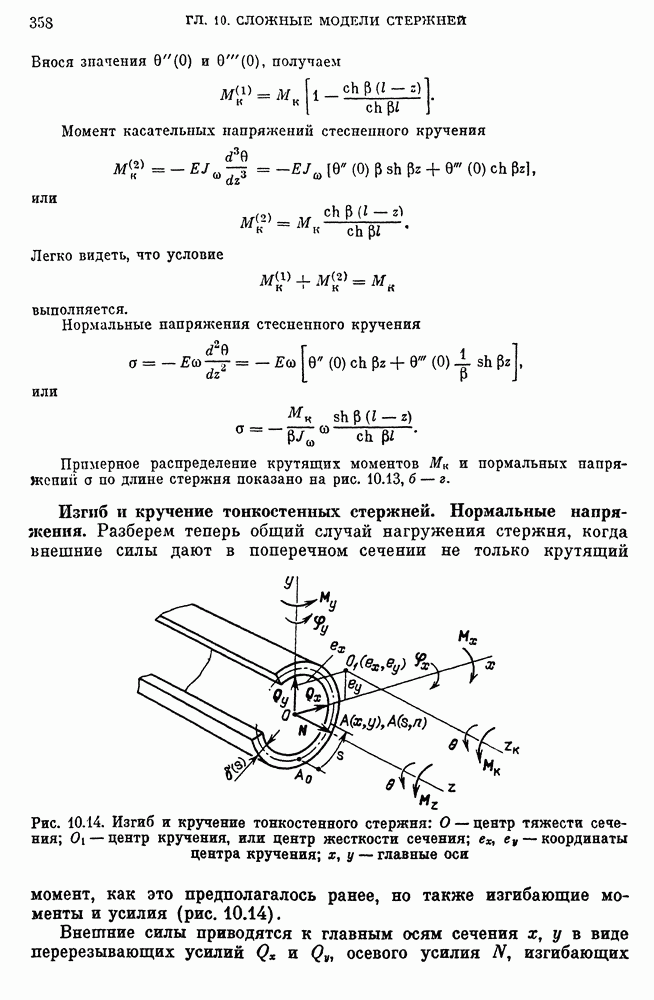
- Изгиб и кручение тонкостенных стержней. Нормальные напряжения.
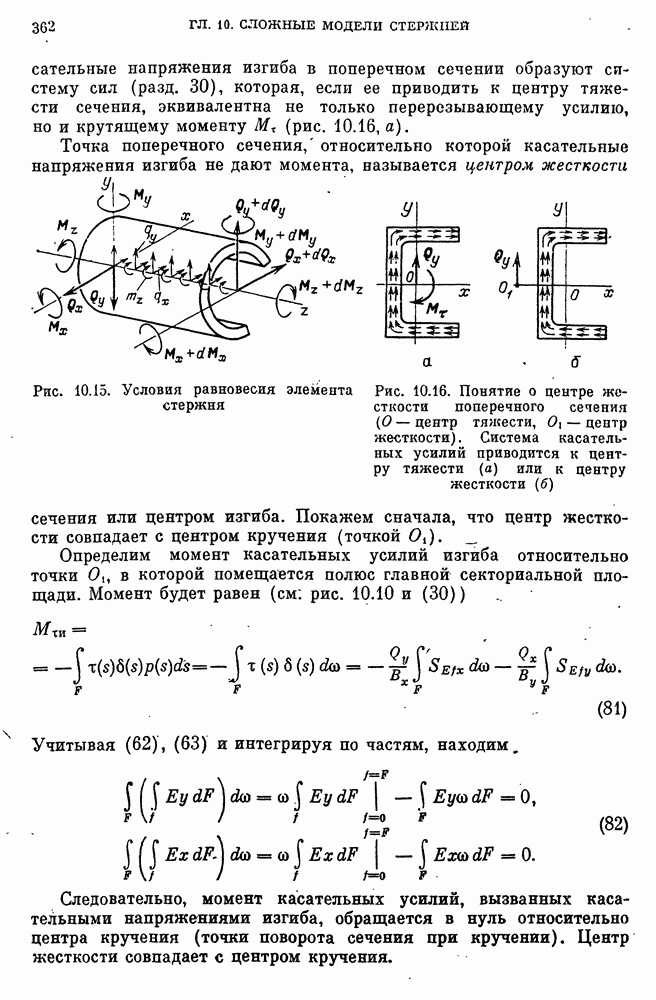
- Касательные напряжения изгиба. Центр жесткости сечения.
- Уравнения изгибно-крутильных деформаций тонкостенного стержня.
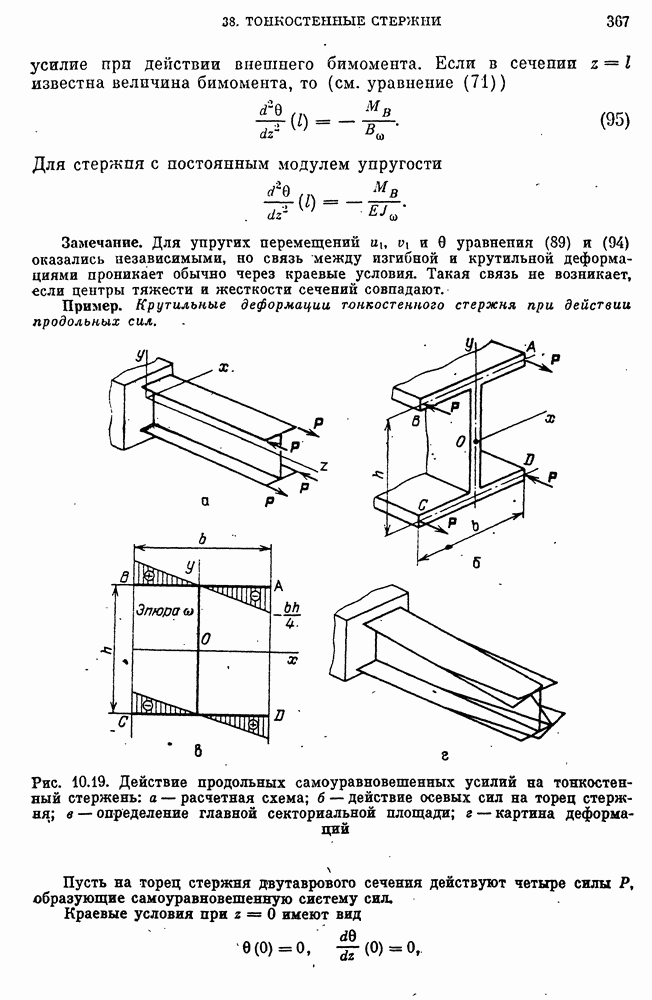
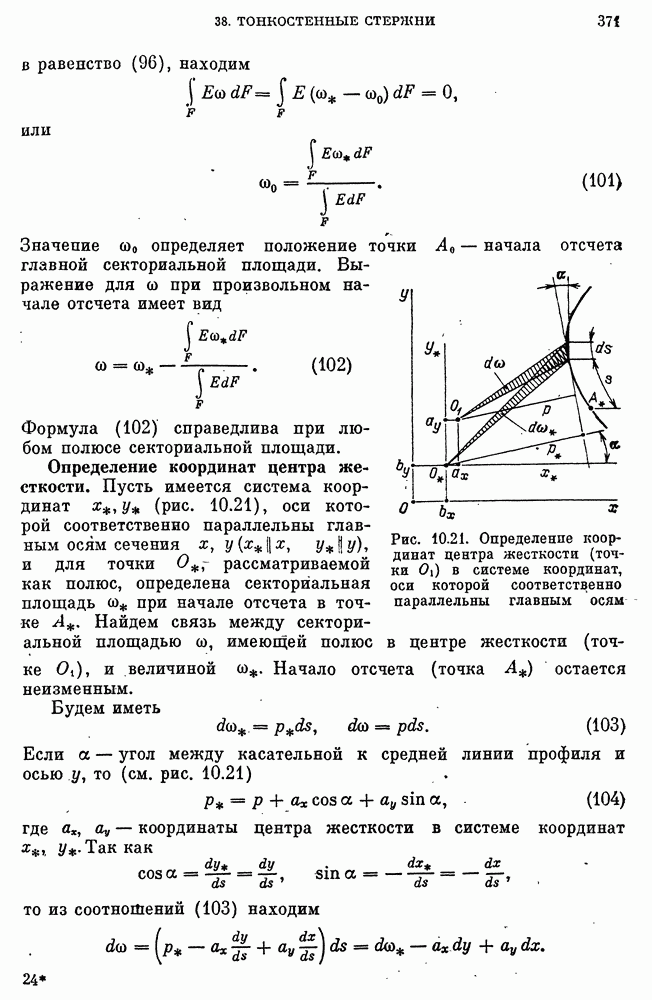
- Определение секториальных упруго-геометрических характеристик сечения и координат центра жесткости.
- Общие свойства расположения центра жесткости.
- Расчет секториальных характеристик сечений.
- 39. Полупространственные модели стержня
- Напряжения в плоскости поперечного сечения.
- Расчет стержней по полупространствениой теории.
- ГЛАВА 11. КОЛЬЦА
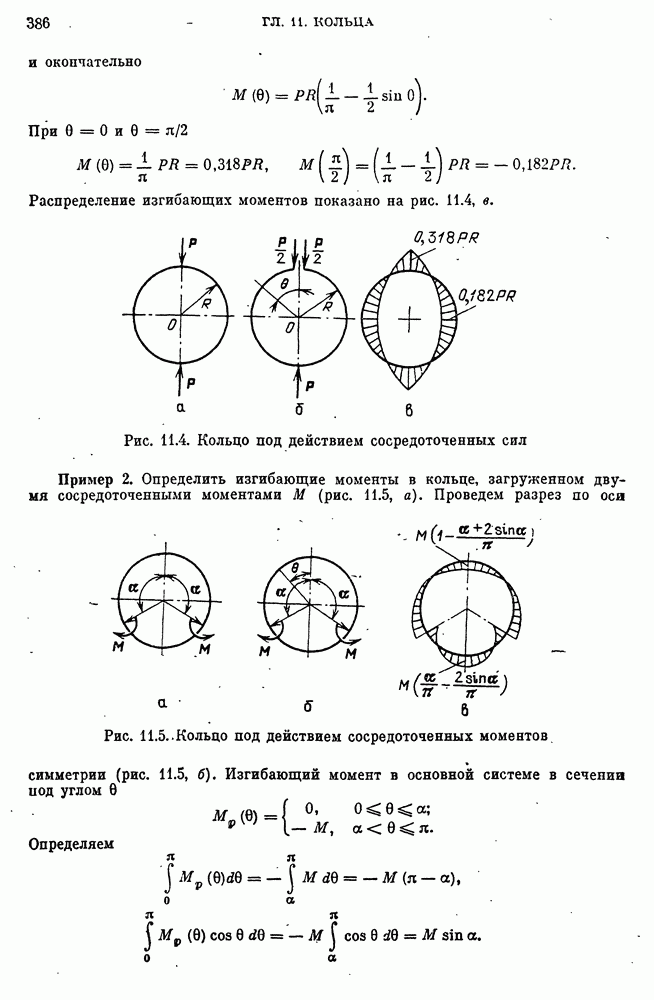
- 40. Изгиб колец
- 41. Осесимметричная деформация колец
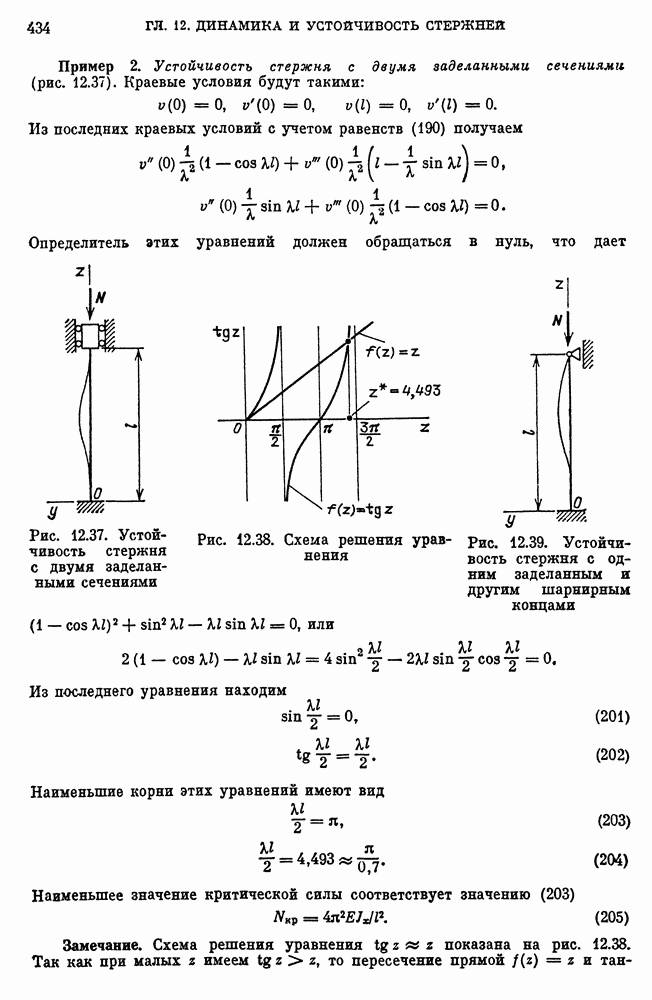
- ГЛАВА 12. ДИНАМИКА И УСТОЙЧИВОСТЬ СТЕРЖНЕЙ
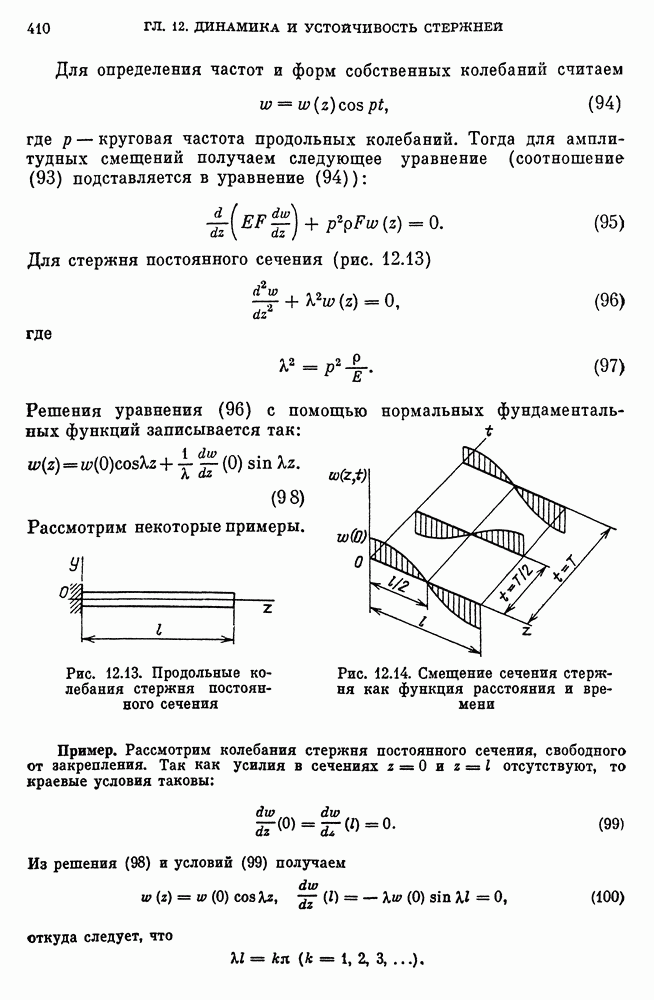
- 42. Изгибные и продольные колебания стержней
- Собственные колебания груза.
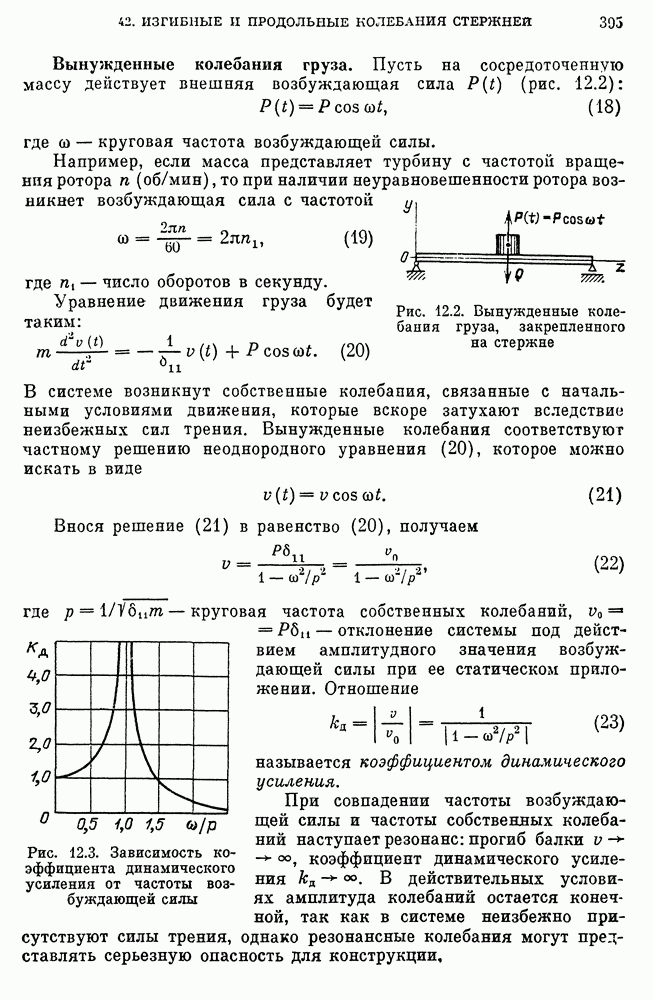
- Вынужденные колебания груза.
- Собственные колебания стержня с несколькими сосредоточенными массами.
- Дифференциальное уравнение изгибных колебаний стержней.
- Изгибные колебания стержней постоянного сечения.
- Изгибные колебания балки переменного сечения. Решение с помощью интегральных уравнений.
- Применение вариационного метода для определения частот и форм изгибных колебаний стержня.
- Динамическая модель лопатки осевого компрессора при изгибных колебаниях.
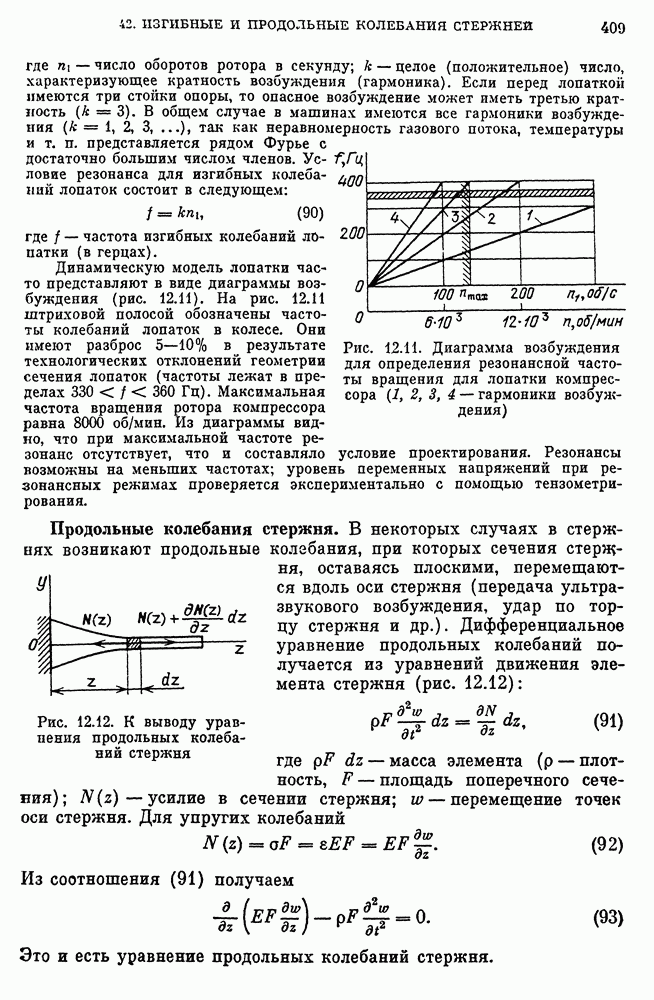
- Продольные колебания стержня.
- 43. Критические частоты вращения и крутильные колебания валов
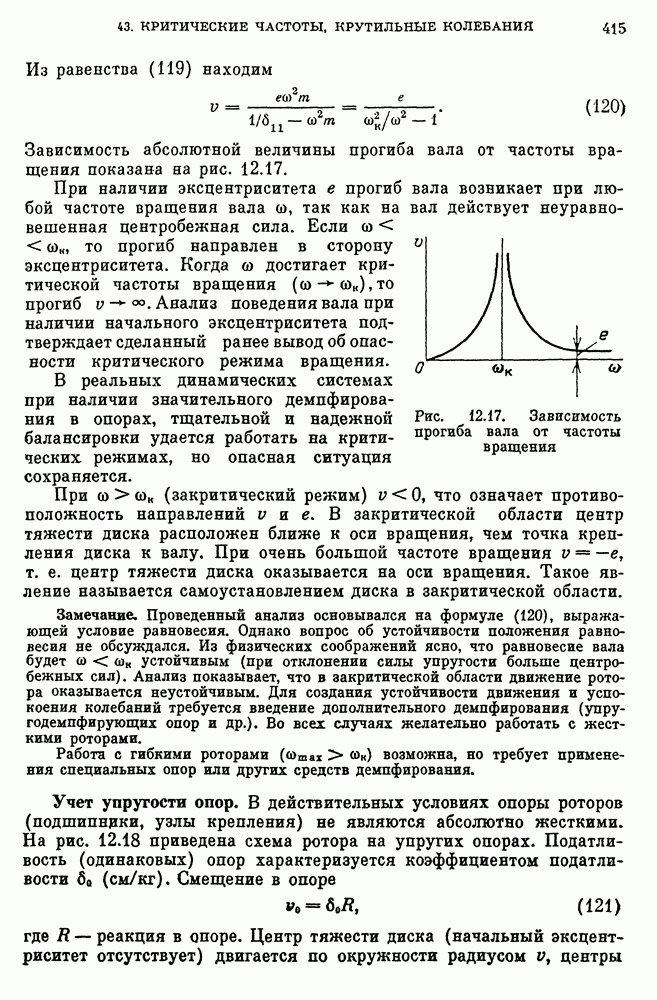
- Учет начального эксцентриситета центра тяжести диска.
- Учет упругости опор.
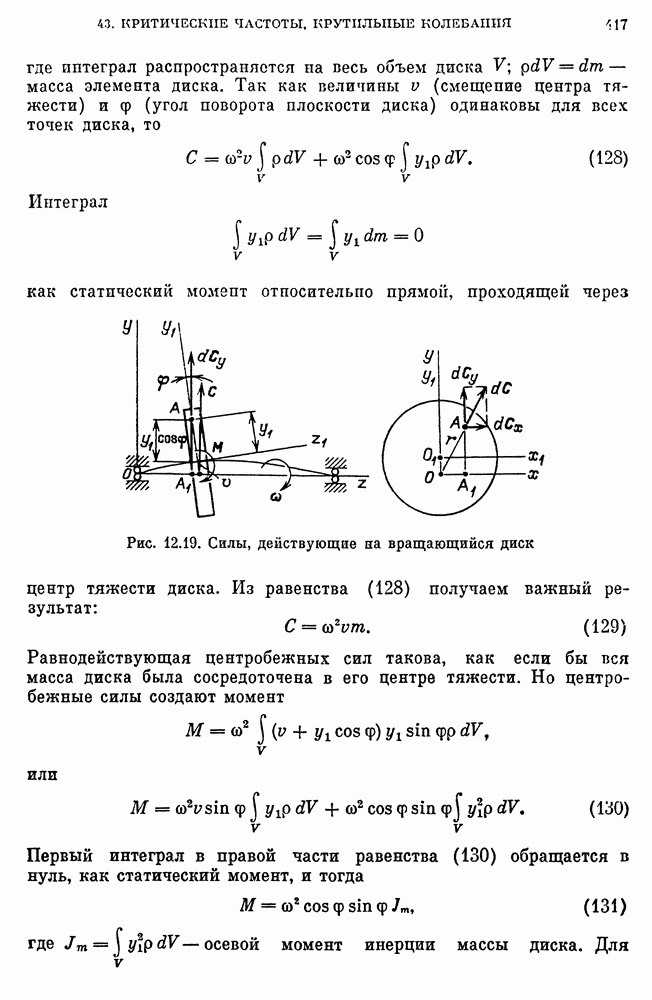
- Силы, действующие на вращающийся диск при прогибах вала.
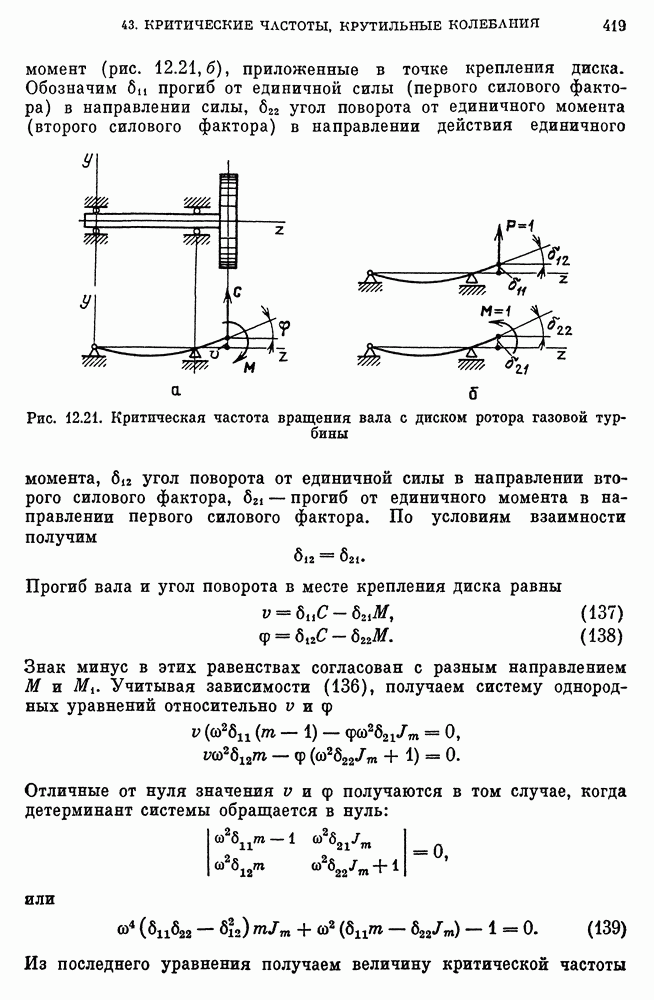
- Критическая частота вращения вала с дисками.
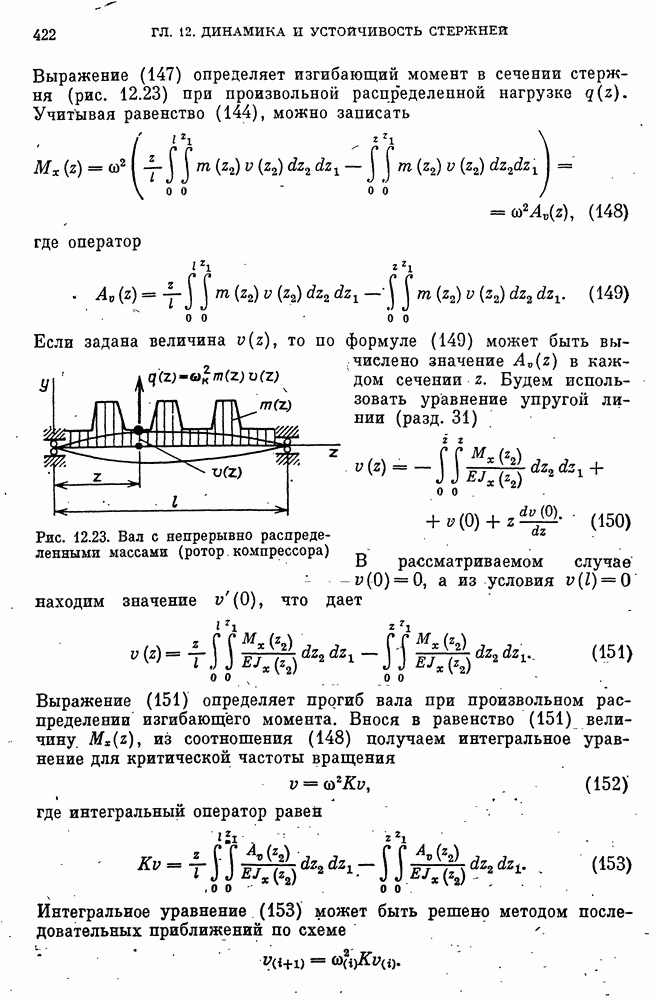
- Критическая частота вращения вала переменного сечения с непрерывно распределенными массами.
- Крутильные колебания валов.
- 44. Устойчивость стержней
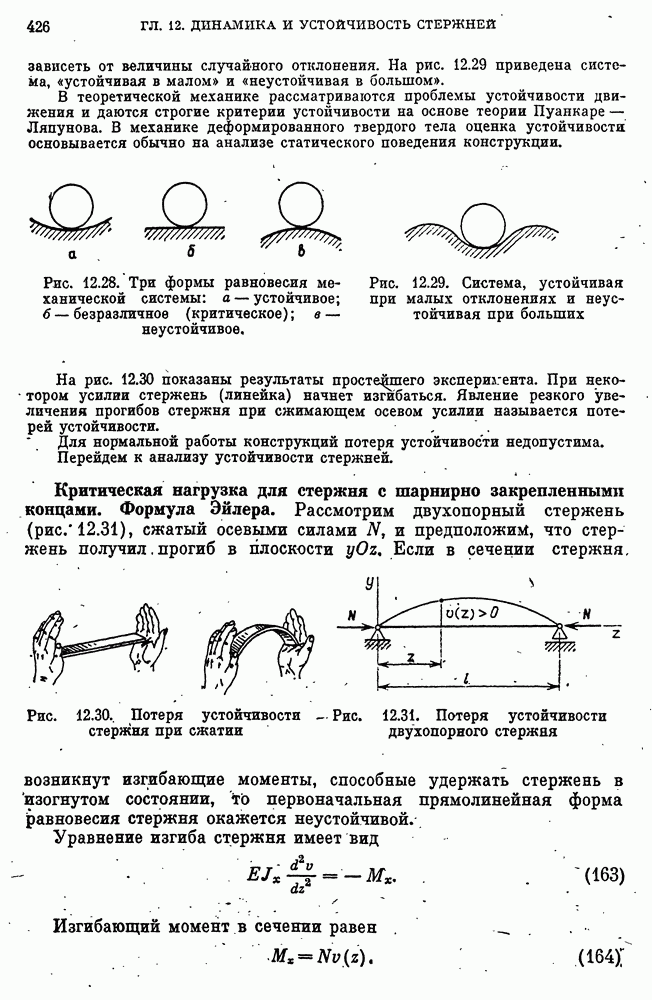
- Критическая нагрузка для стержня с шарнирно закрепленными концами. Формула Эйлера.
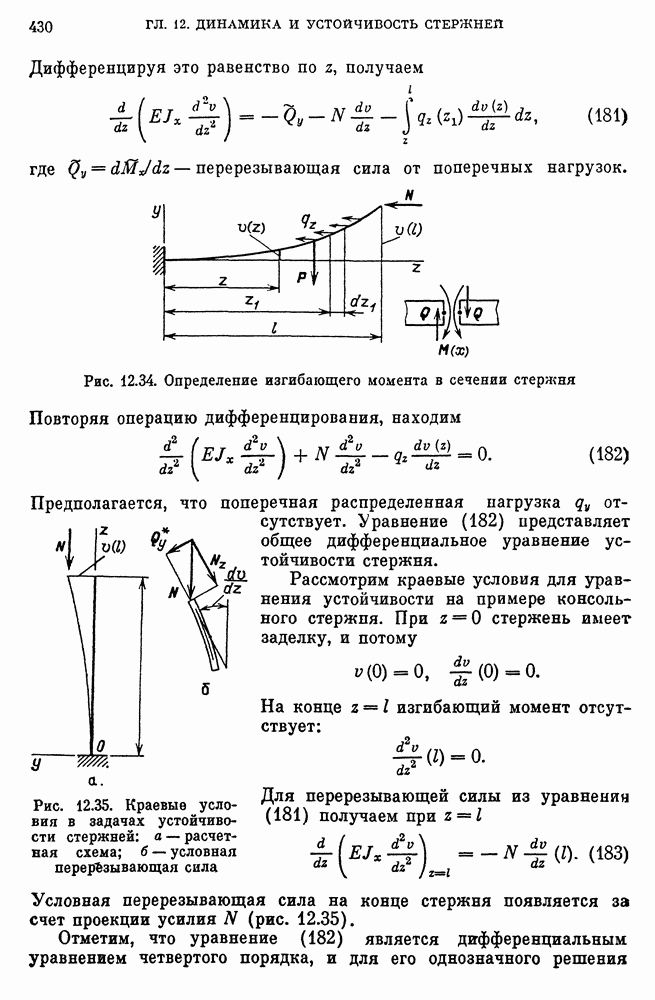
- Общее дифференциальное уравнение устойчивости стержня и краевые условия.
- Решение дифференциального уравнения устойчивости для стержня постоянного сечения.
- Влияние условий закрепления концов стержня на величину критической силы.
- Приведенная длина стержня. Обобщенная формула Эйлера.
- Интегральное уравнение устойчивости стержня.
- Устойчивость стержней при упругопластических деформациях. Модуль Кармана.
- Устойчивость стержней в условиях продолжающегося нагружения в пластической области.
- Практические расчеты на устойчивость.
- ГЛАВА 13. МОДЕЛИ РАЗРУШЕНИЯ
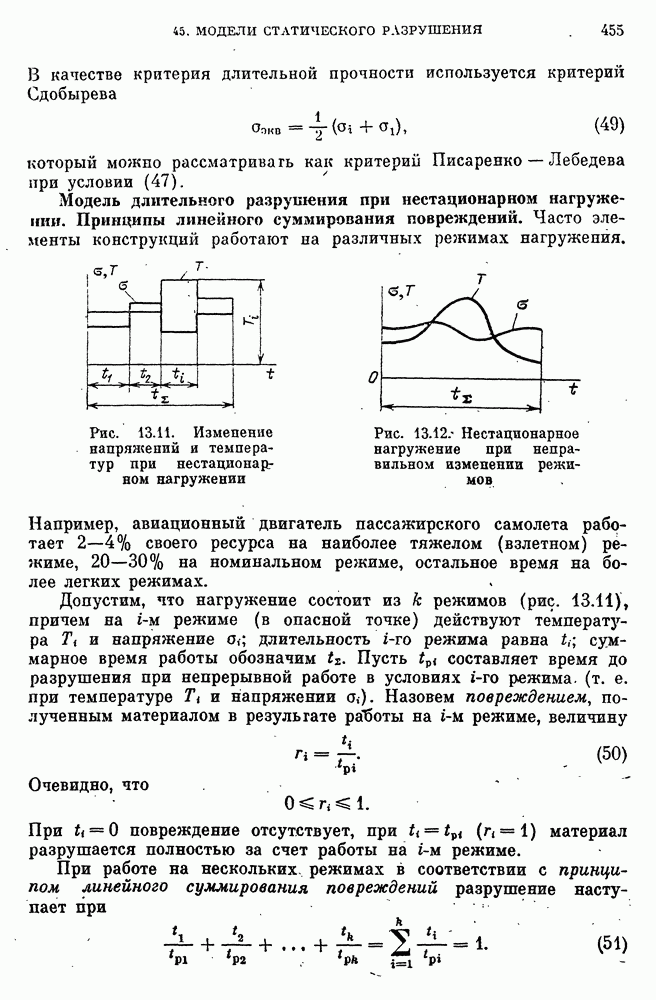
- 45. Модели статического и длительного разрушения
- Модели статического разрушения пластичных материалов.
- Критерий максимальных касательных напряжений.
- Предельные поверхности по критериям интенсивности напряжений и максимальных касательных напряжений.
- Модель статического разрушения пластичных материалов, дополненная условием отрыва.
- Модели статического разрушения хрупких материалов.
- Более общие модели статического разрушения.
- Предельная поверхность в пространстве главных напряжений по критерию Мора.
- Предельная поверхность в пространстве главных напряжений по критерию Писаренко — Лебедева.
- Модели длительного разрушения.
- Прочность при наличии трещин. Линейная механика разрушения.
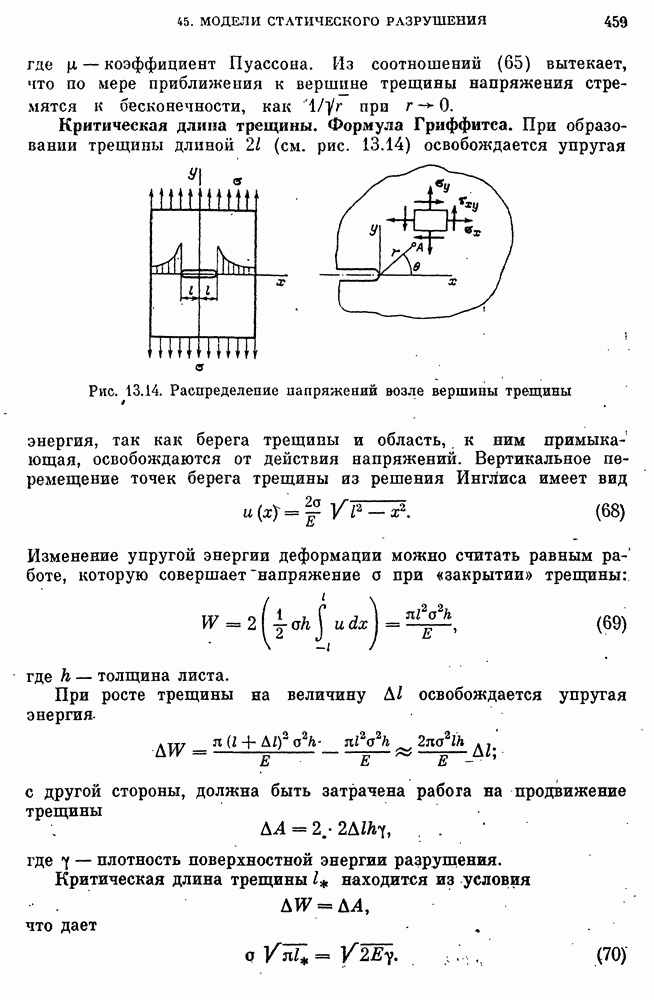
- Критическая длина трещины. Формула Гриффитса.
- 46. Модели усталостного и малоциклового разрушения
- Модели усталостного разрушения при многоосном (многокомпонентном) напряженном состоянии.
- Модели усталостного разрушения при стационарном нагружении с учетом числа циклов нагружений.
- Модели малоциклового разрушения при одноосном и сложном напряженных состояниях.
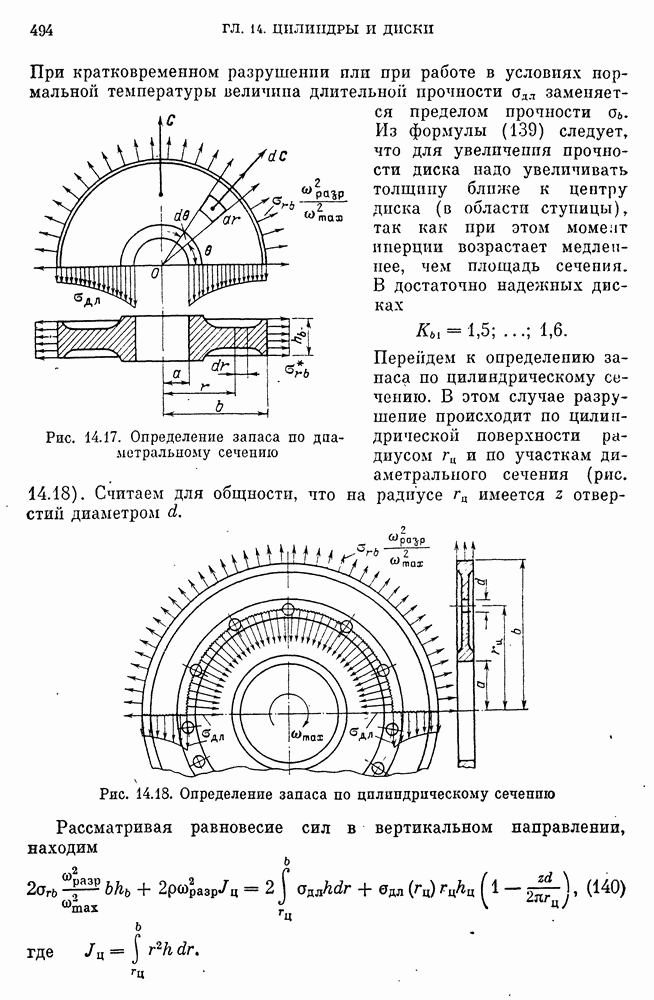
- ГЛАВА 14. ЦИЛИНДРЫ И ДИСКИ
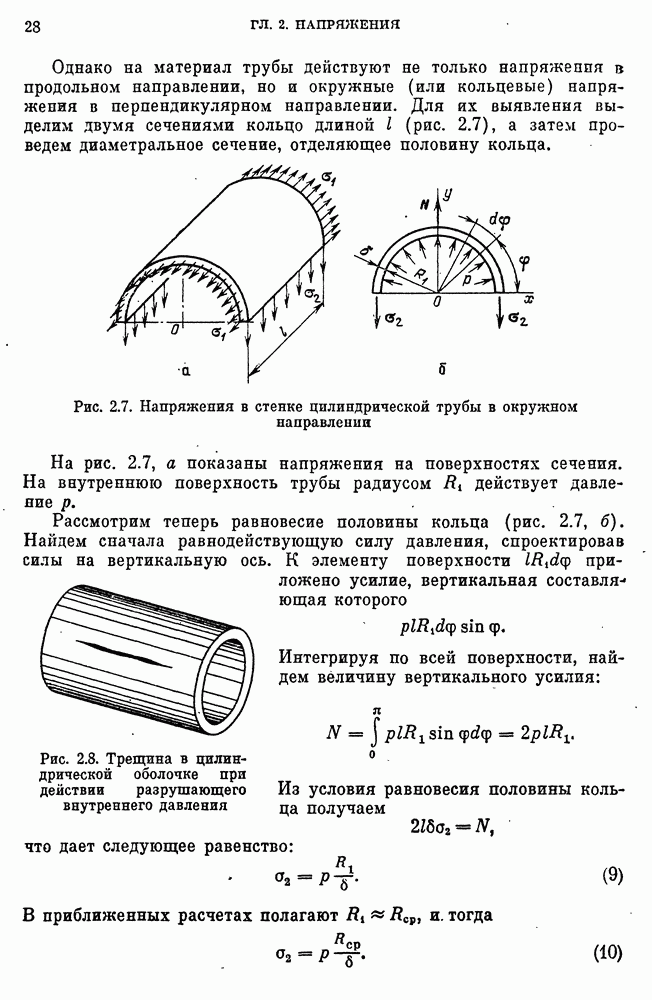
- 47. Прочностные модели толстостенных труб и цилиндров. Напряжения и деформации
- Уравнения равновесия элемента цилиндра.
- Толстостенная труба под действием внутреннего и внешдего давлений.
- Действие осевого усилия.
- Прочностная модель цилиндрической части сосуда высокого давления.
- Прочностная модель прессового соединения.
- Температурные напряжения и, напряжения от центробежных сил.
- Цилиндр с переменными параметрами упругости.
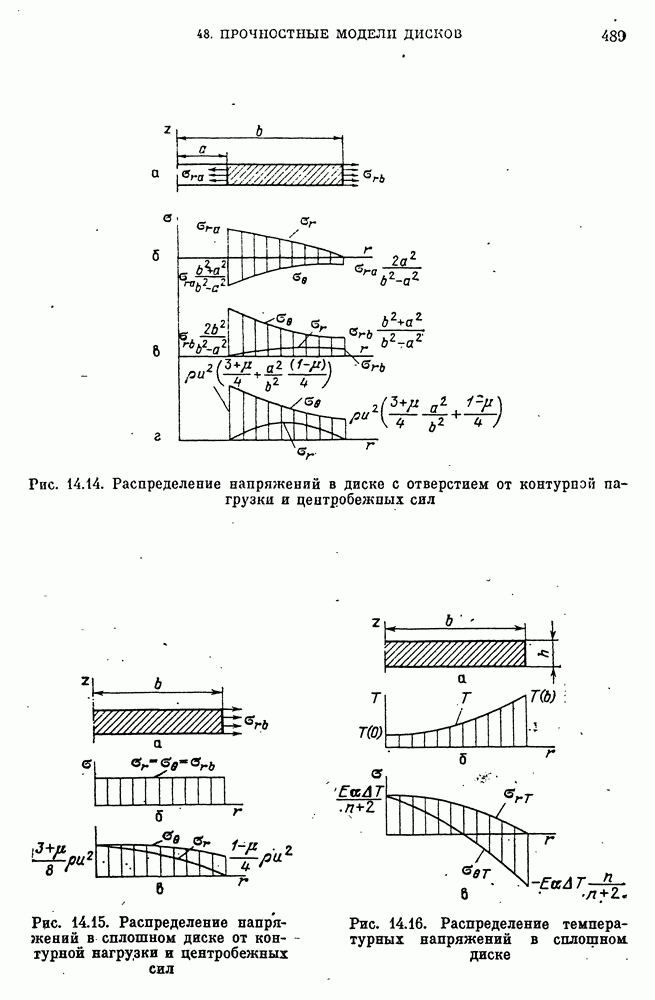
- 48. Прочностные модели дисков
- Дифференциальное уравнение для диска постоянной толшины с постоянными параметрами упругости.
- Распределение напряжений в диске постоянной толщины.
- Напряжения в диске переменной толщины с переменными параметрами упругости.
- Модели общей статической и длительной прочности диска.
- Эквивалентный запас по разрушающей частоте вращения.
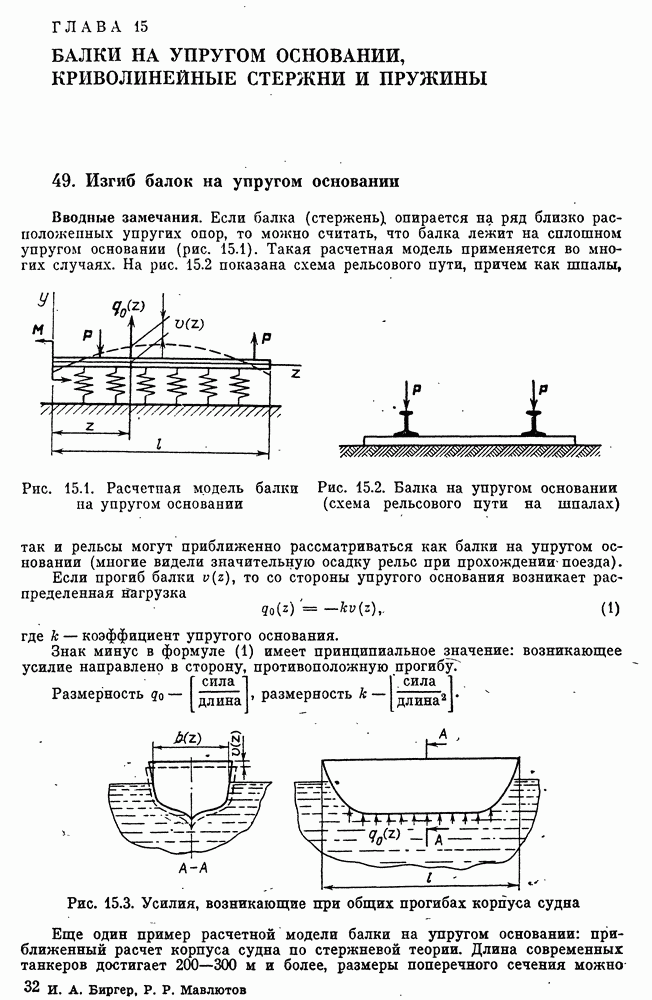
- ГЛАВА 15. БАЛКИ НА УПРУГОМ ОСНОВАНИИ, КРИВОЛИНЕЙНЫЕ СТЕРЖНИ И ПРУЖИНЫ
- 49. Изгиб балок на упругом основании
- Уравнения изгиба для балки постоянного сечения на упругом основании. Структура решения.
- Метод начальных параметров и решение уравнения изгиба балки на упругом основании в матричной форме.
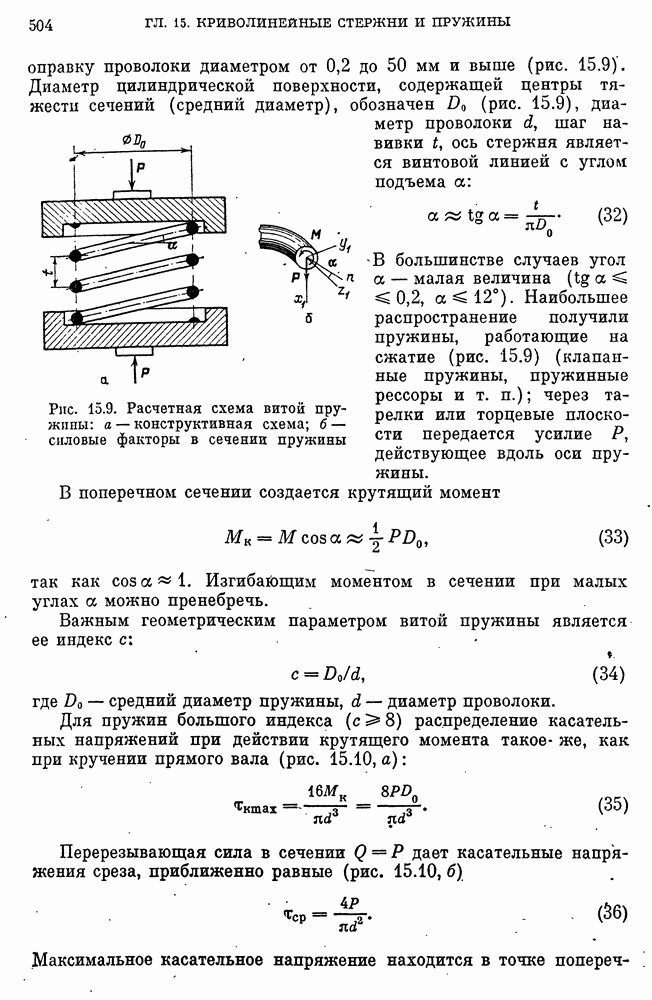
- 50. Криволинейные стержни и пружины
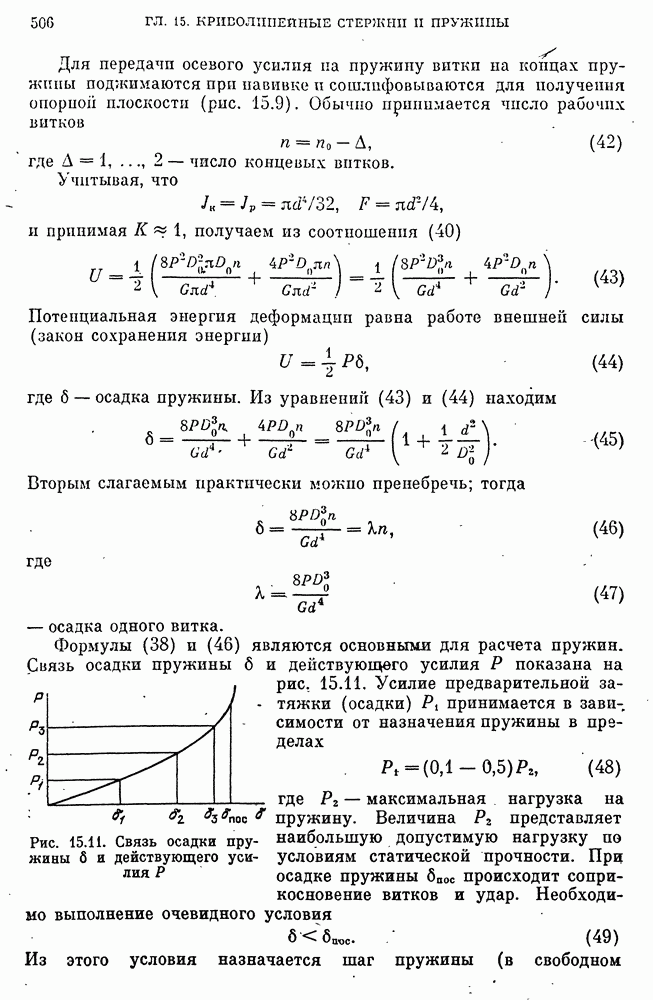
- Модели прочностной надежности пружин.
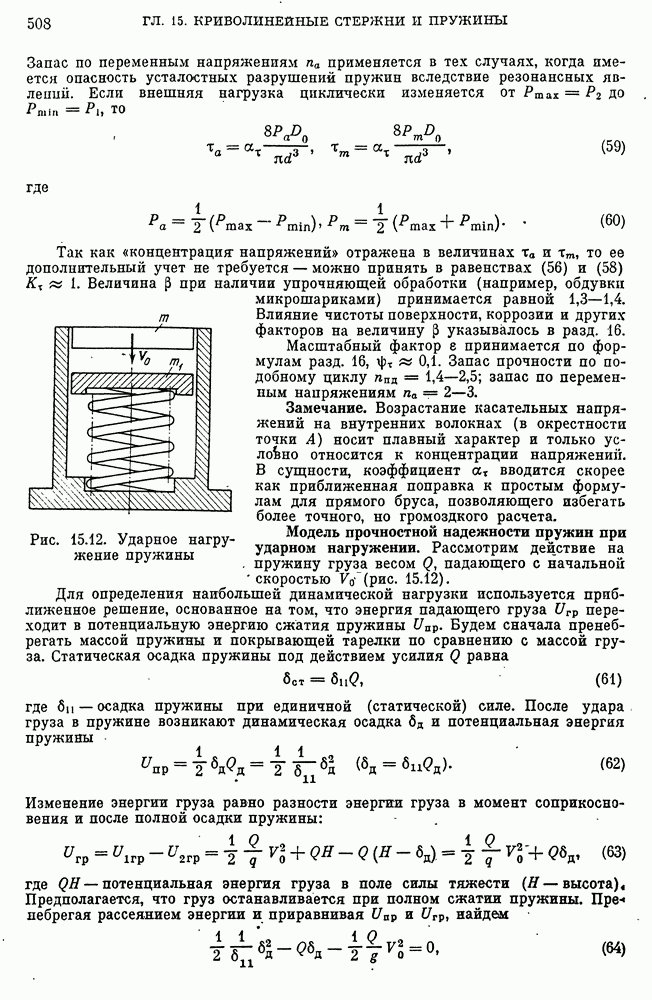
- Модель прочностной надежности пружин при ударном нагружении.
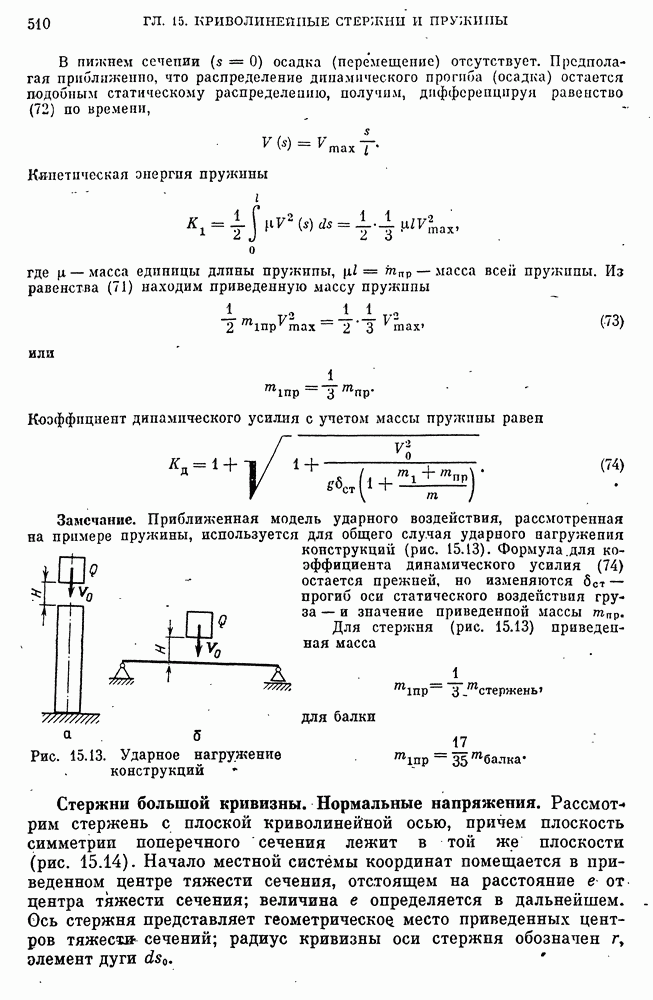
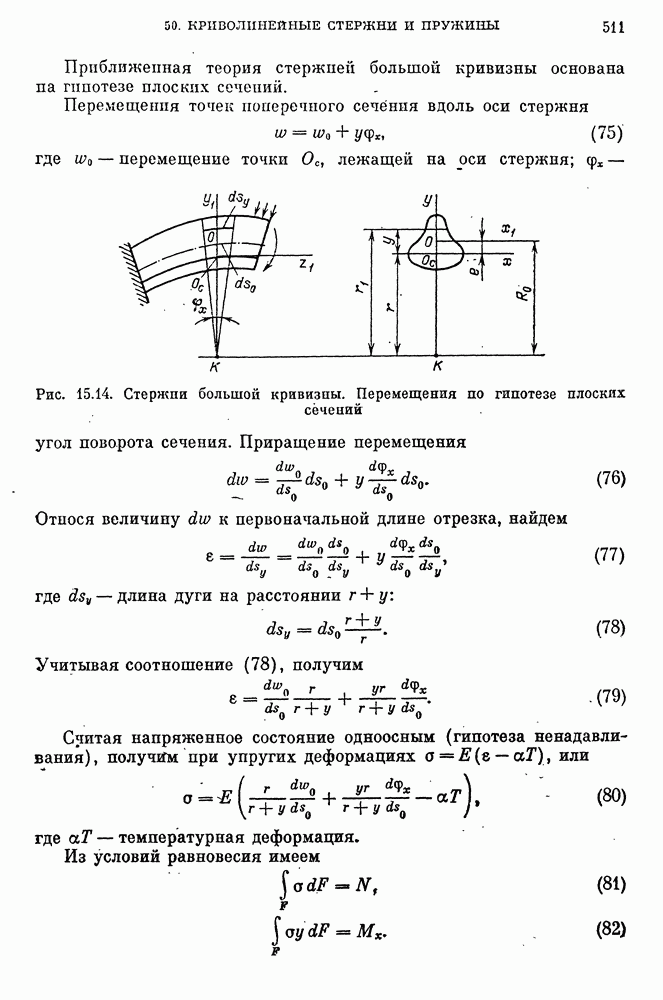
- Стержни большой кривизны. Нормальные напряжения.
- Определение приведенного центра тяжести сечения криволинейного стержня. Примеры.
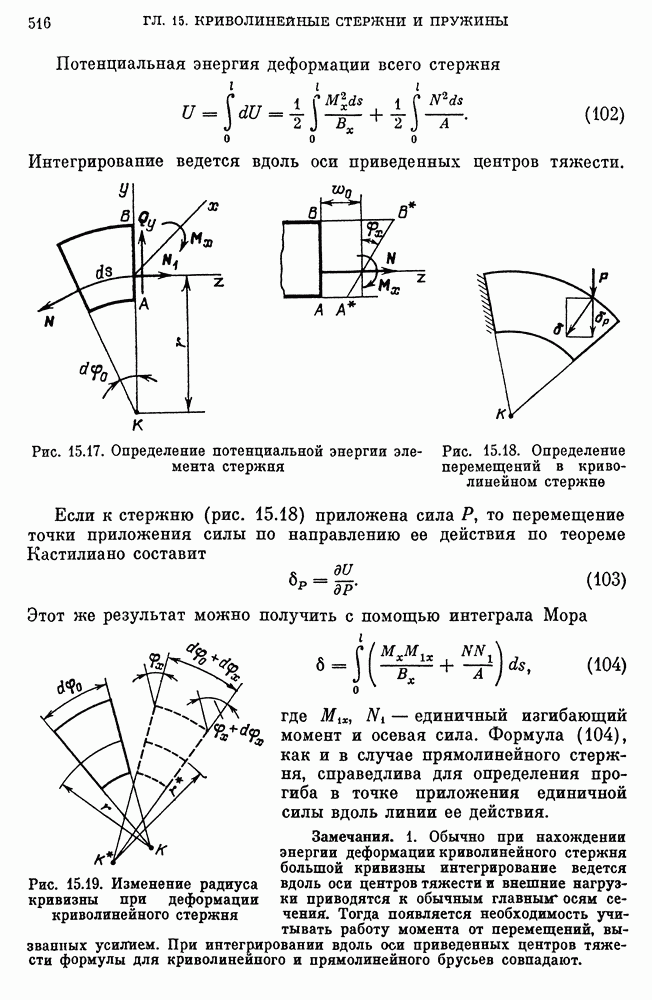
- Касательные напряжения при изгибе криволинейного стержня.
- Перемещения на изгибе криволинейного стержня.
- ГЛАВА 16. ПЛАСТИНКИ И ОБОЛОЧКИ
- 51. Пластинки
- Деформация круглых пластинок.
- Круглая пластинка постоянной толщины с постоянными параметрами упругости.
- Напряжения изгиба в круглой пластинке.
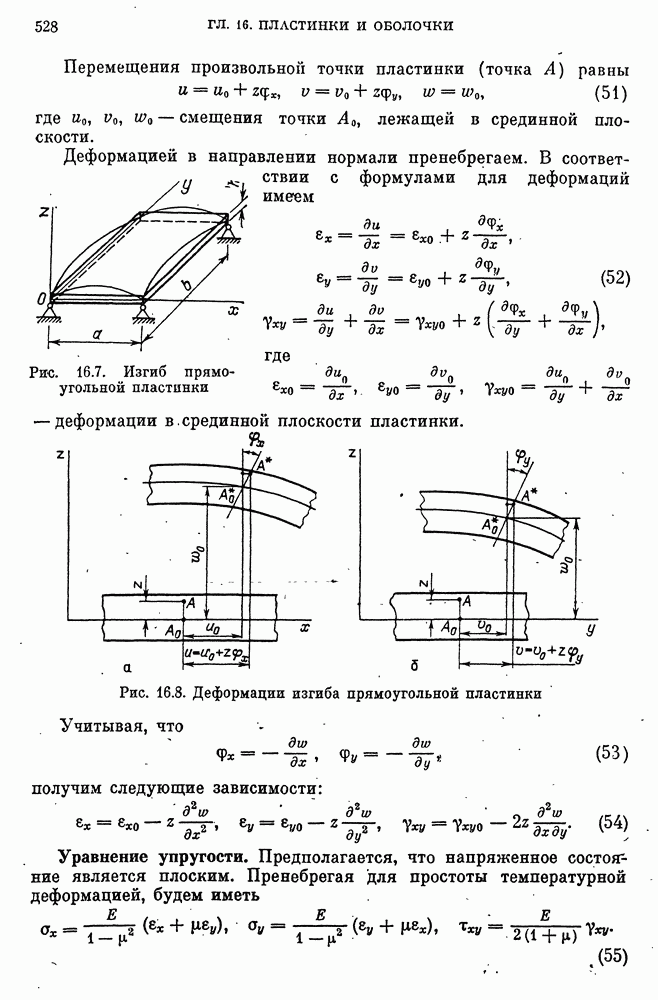
- Изгиб прямоугольных пластинок. Деформации.
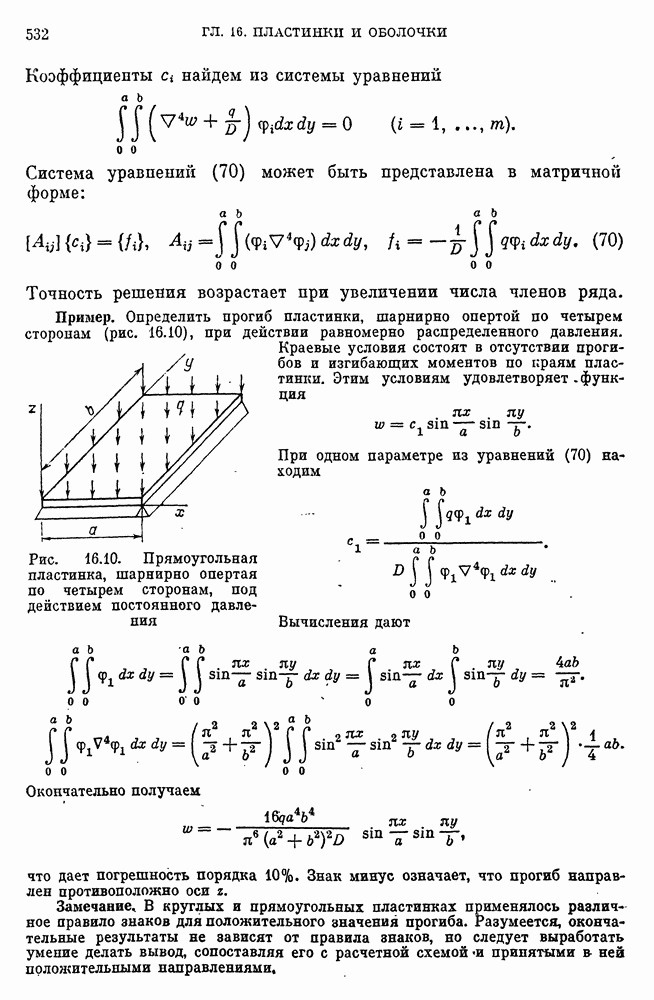
- Определение прогибов и напряжений в пластинке вариационным методом.
- 52. Цилиндрические оболочки
- Краевой эффект и безмоментное напряженное состояние в длинных цилиндрических оболочках.
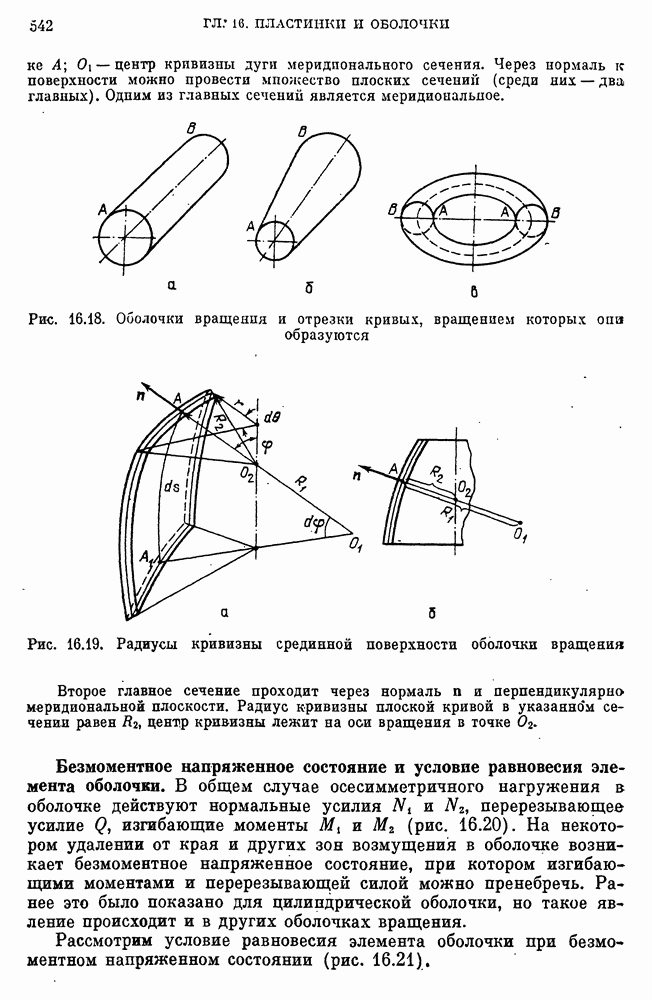
- 53. Приближенные методы расчета прочности и устойчивости рболочек вращения при осесимметричном нагружении
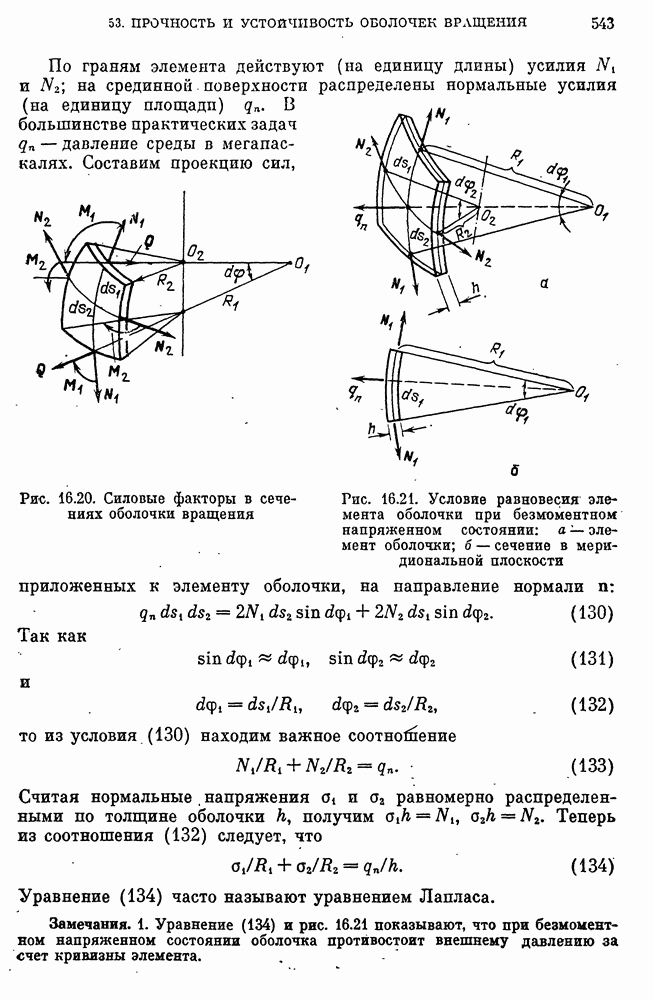
- Безмоментное напряженное состояние и условие равновесия элемента оболочки.
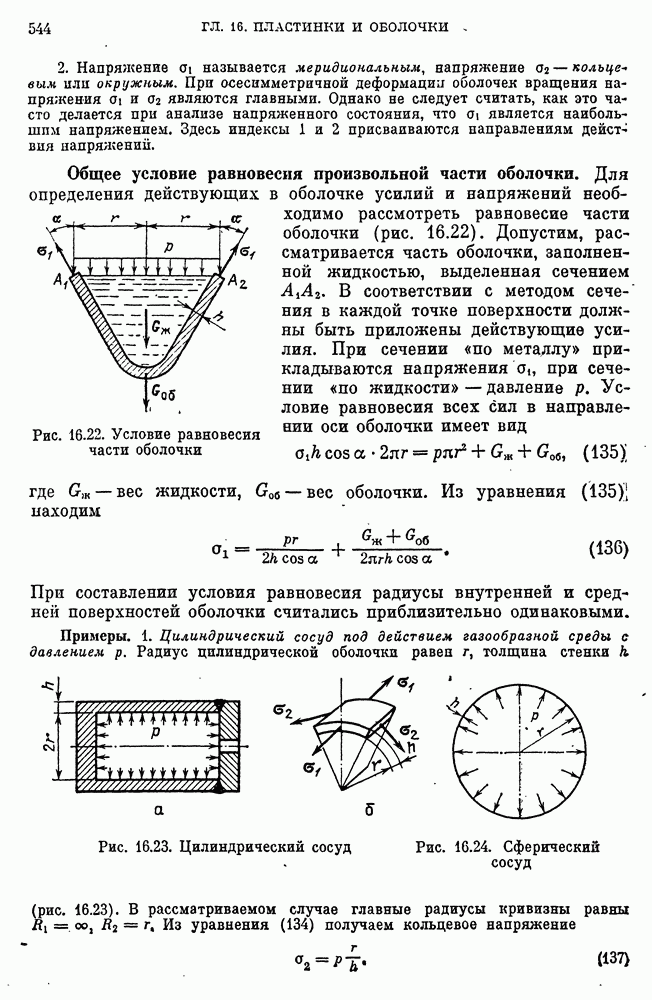
- Общее условие равновесия произвольной части оболочки.
- Приближенная модель прочности оболочки вращения при осесимметричном нагружении.
- Приближенные модели устойчивости оболочки.
- ГЛАВА 17. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
- 54. Введение в метод конечных элементов
- 55. Основные уравнения метода конечных элементов
- Вариационное уравнение метода конечных элементов.