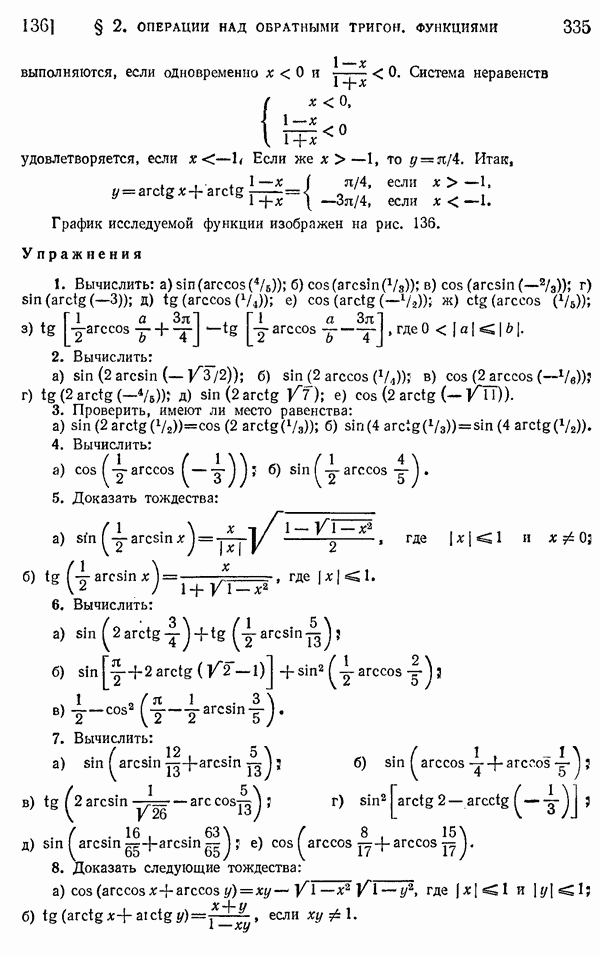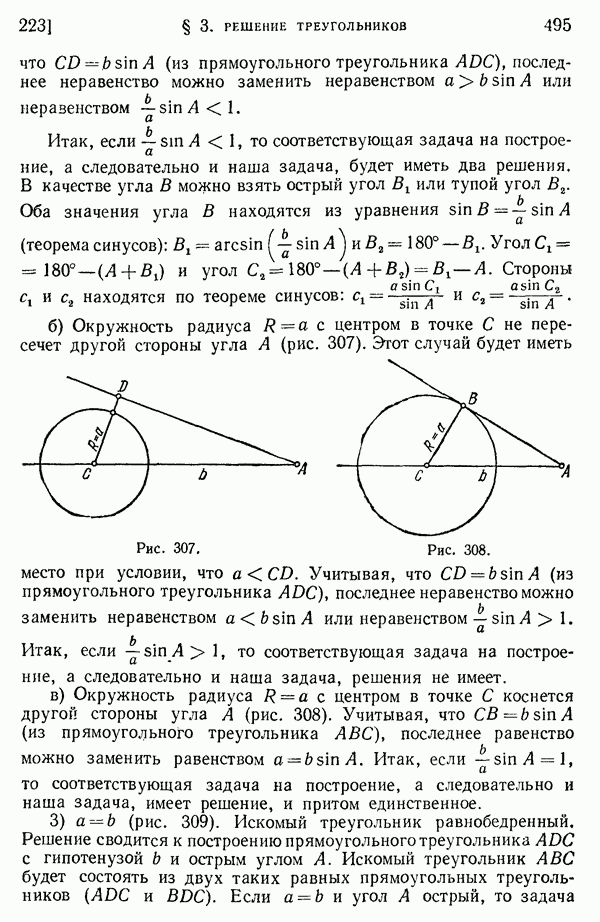| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
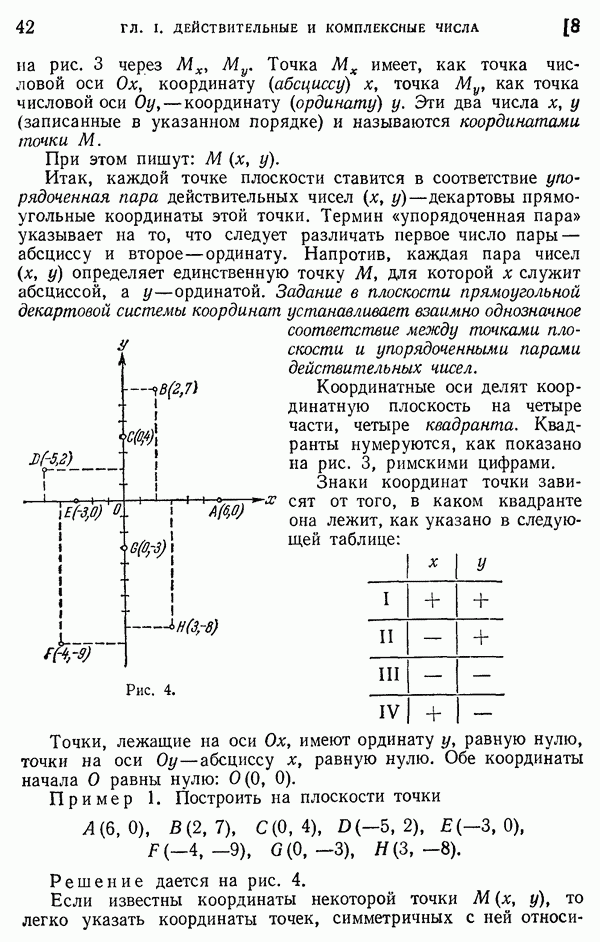
42
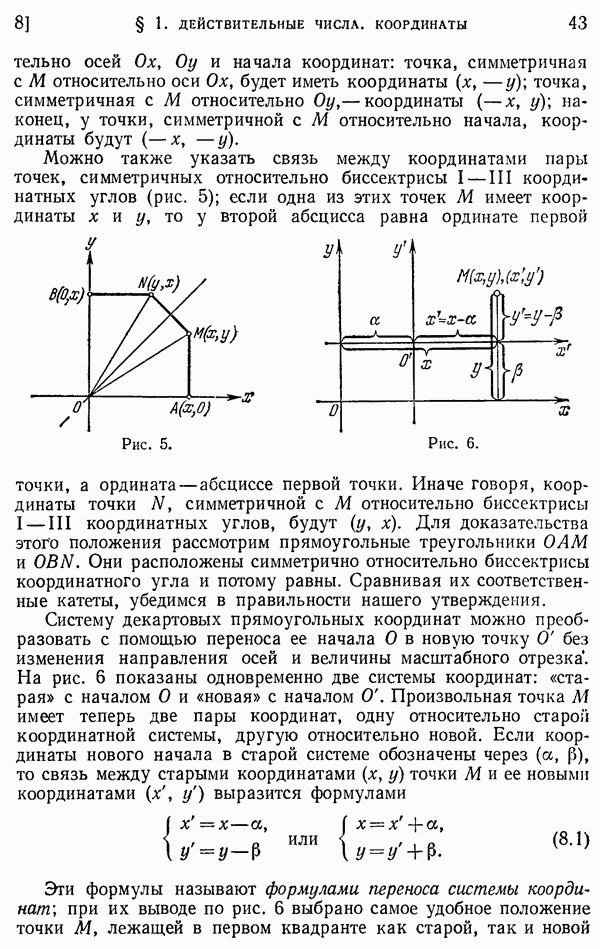
43
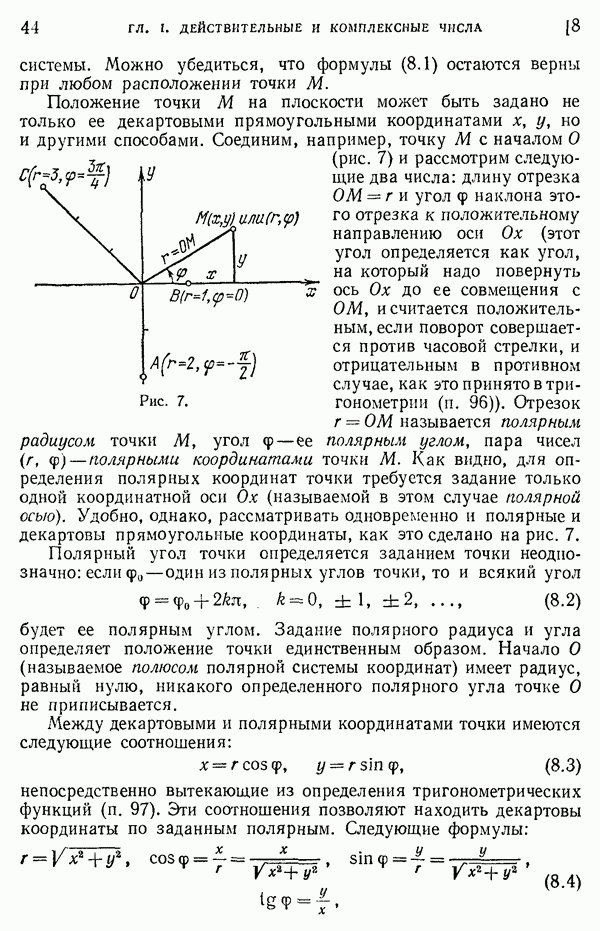
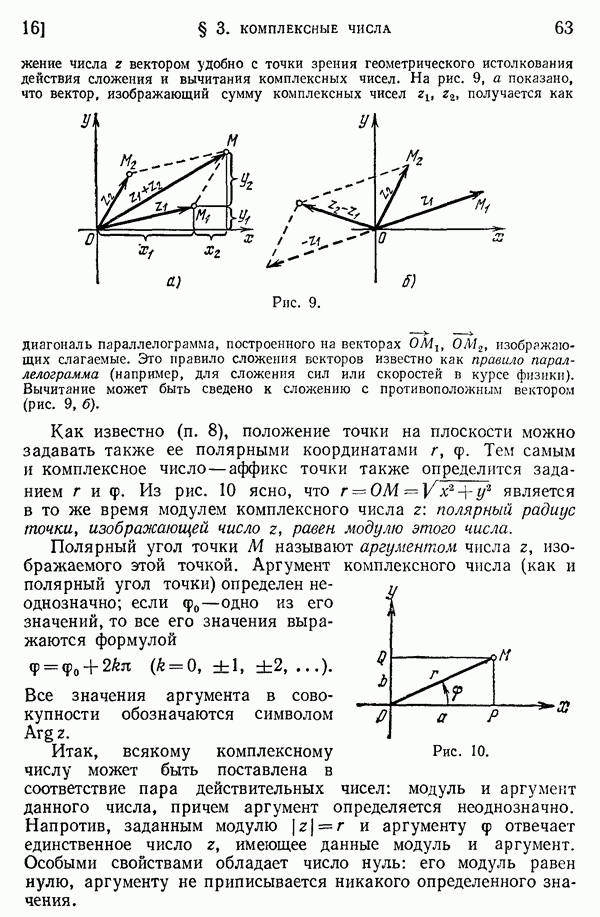
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
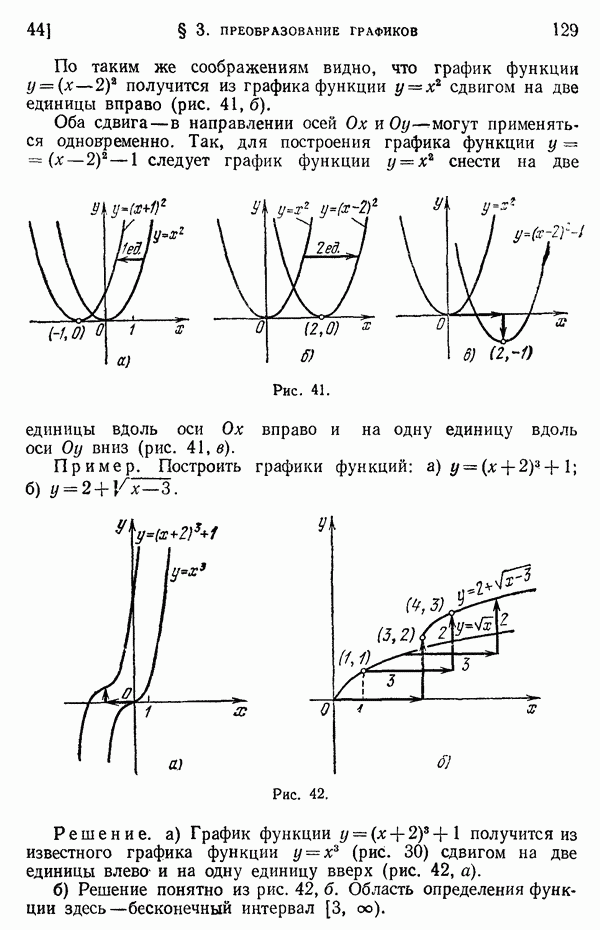
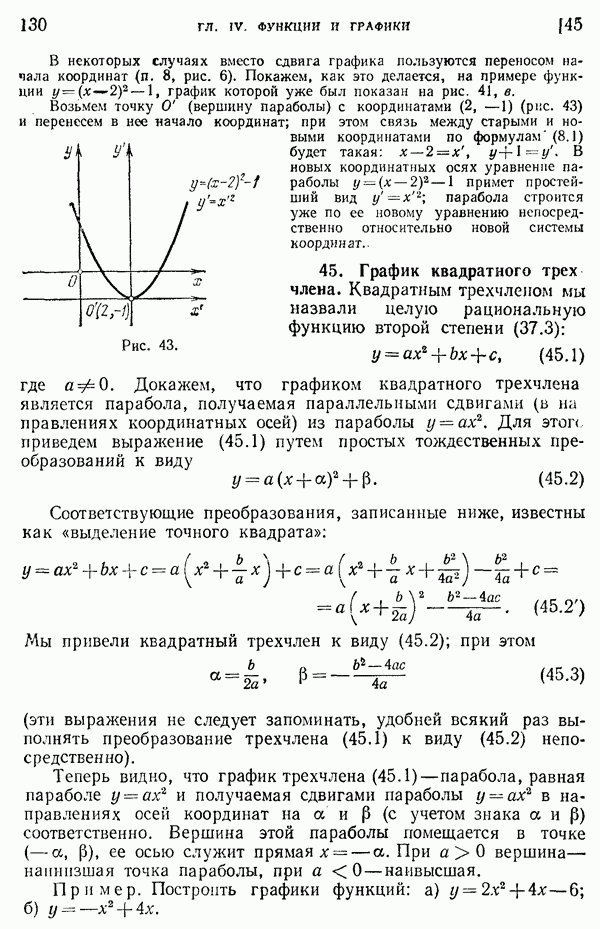
129
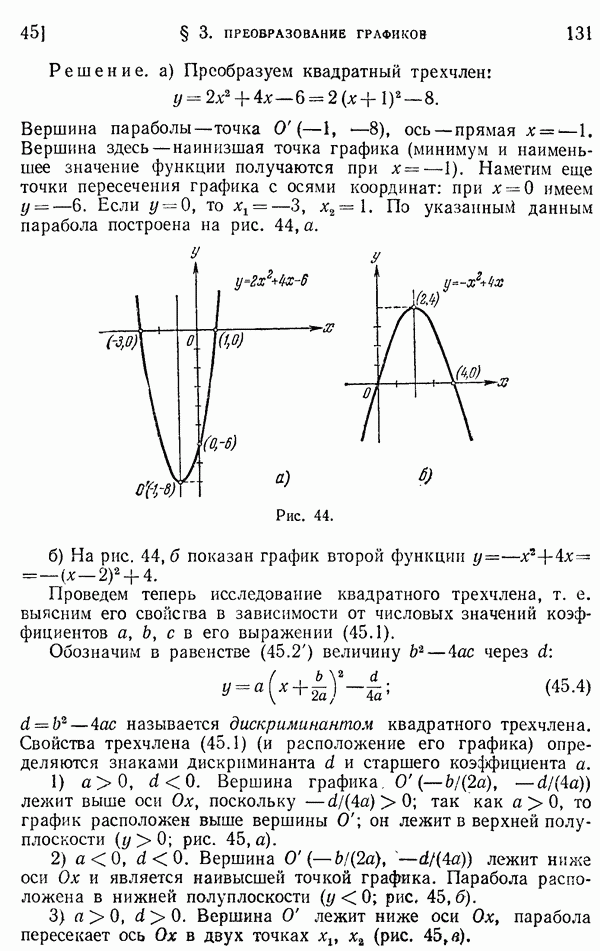
130
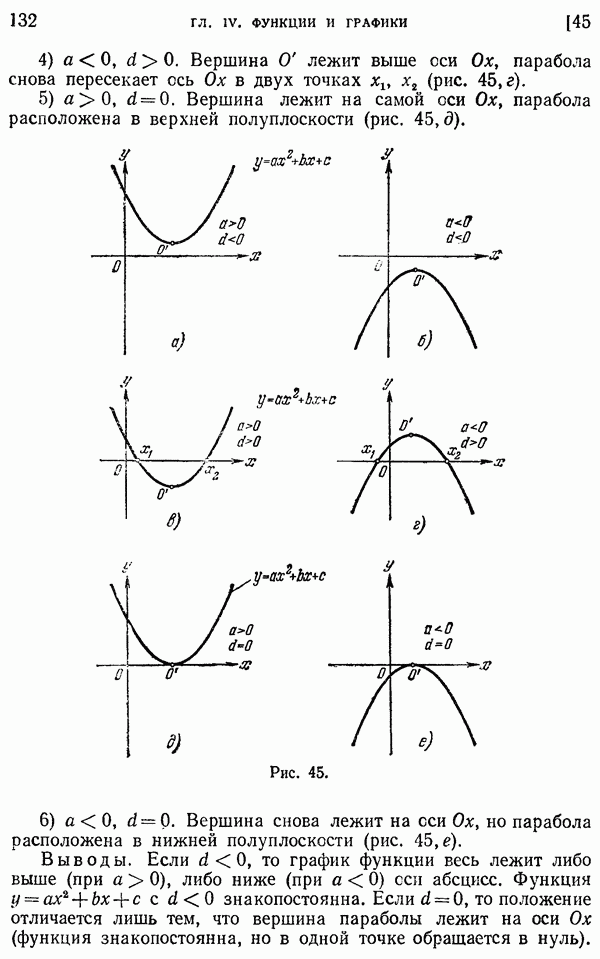
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
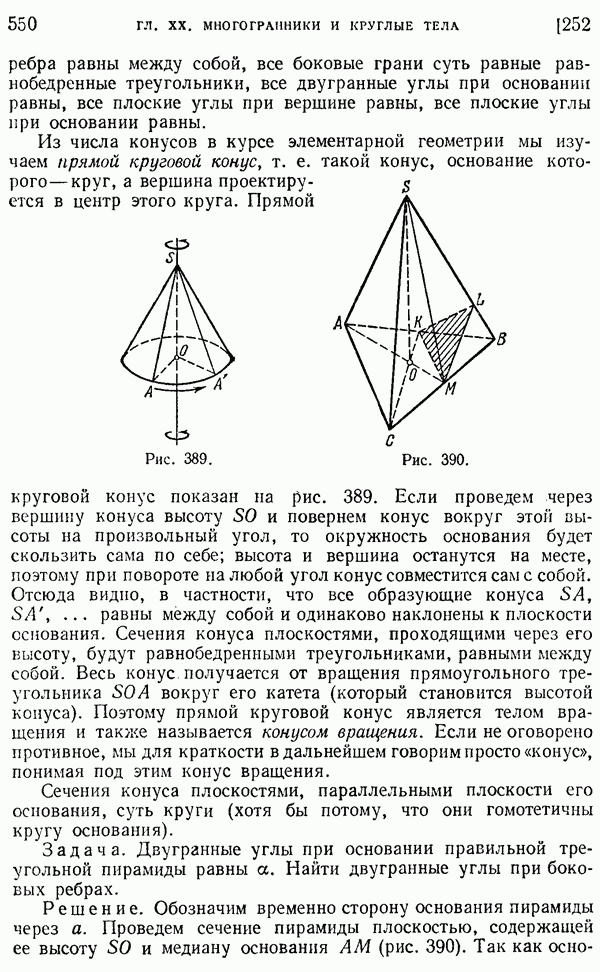
550
551
552
553
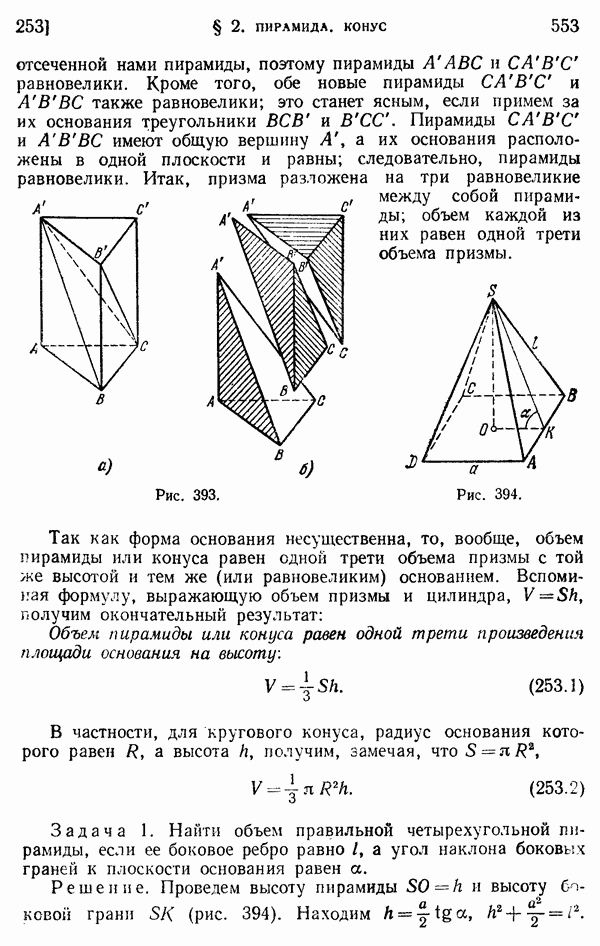
554
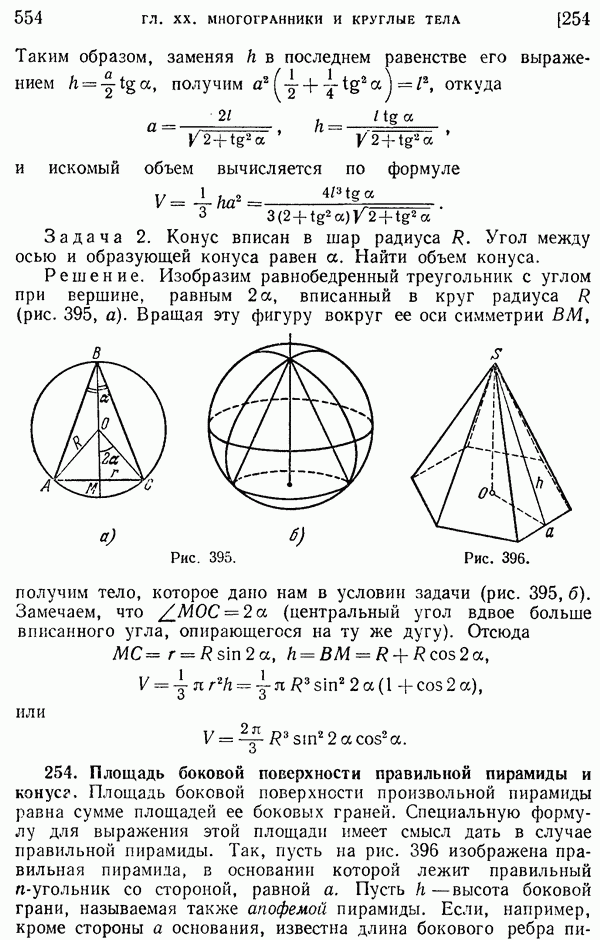
555
556
557
558
559
560
561
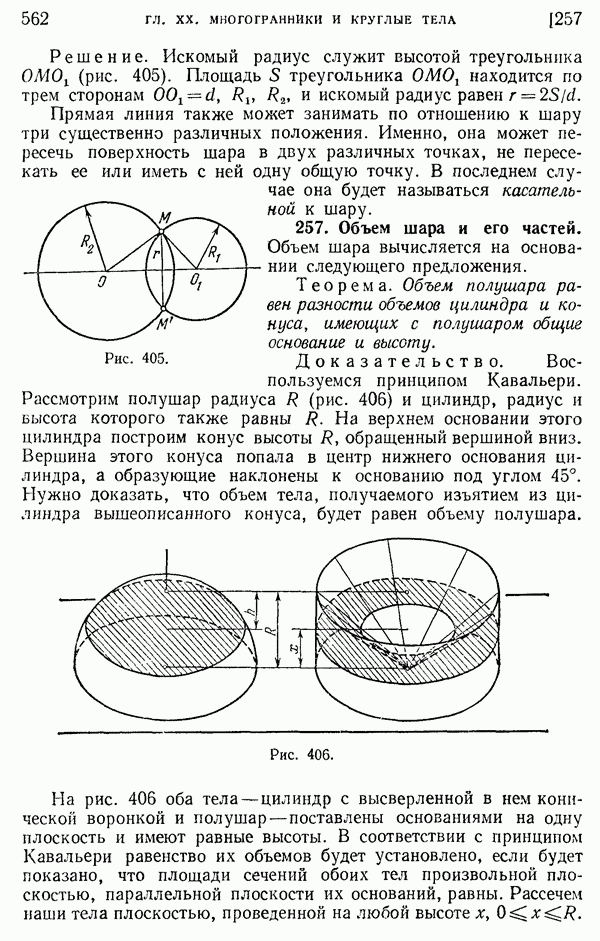
562
563
564
565
566
567
568
569
570
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
32. График функции. Способы задания функций.
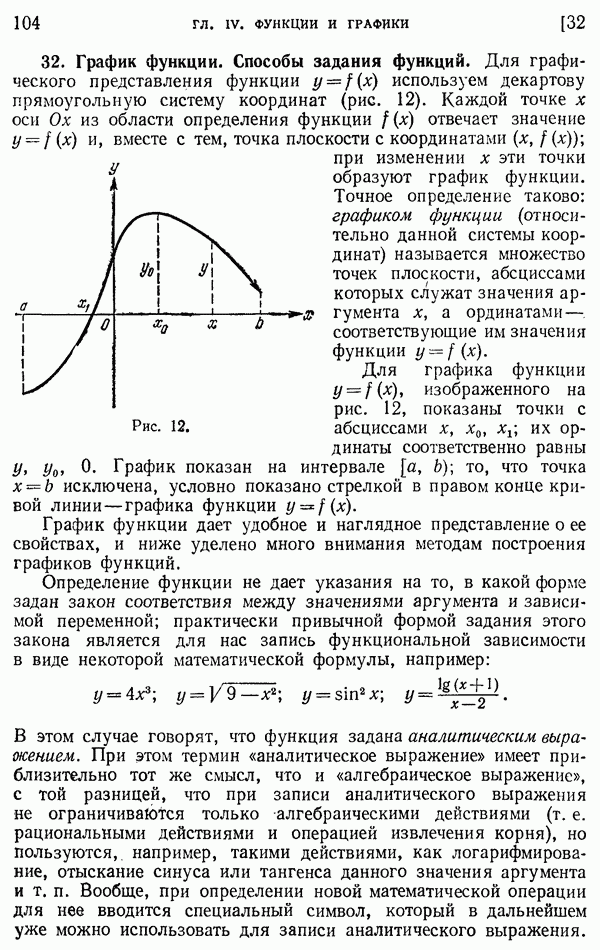
Для графического представления функции  используем декартову прямоугольную систему координат (рис. 12). Каждой точке х оси Ох из области определения функции
используем декартову прямоугольную систему координат (рис. 12). Каждой точке х оси Ох из области определения функции  отвечает значение
отвечает значение  и, вместе с тем, точка плоскости с координатами
и, вместе с тем, точка плоскости с координатами  при изменении
при изменении  эти точки образуют график функции. Точное определение таково: графиком функции (относительно данной системы координат) называется множество точек плоскости, абсциссами которых служат значения аргумента
эти точки образуют график функции. Точное определение таково: графиком функции (относительно данной системы координат) называется множество точек плоскости, абсциссами которых служат значения аргумента  а ординатами — соответствующие им значения функции y = f(x).
а ординатами — соответствующие им значения функции y = f(x).

Рис. 12.
Для графика функции  изображенного на рис. 12, показаны точки с абсциссами
изображенного на рис. 12, показаны точки с абсциссами  их ординаты соответственно равны
их ординаты соответственно равны  График показан на интервале
График показан на интервале  то, что точка
то, что точка  исключена, условно показано стрелкой в правом конце кривой линии — графика функции
исключена, условно показано стрелкой в правом конце кривой линии — графика функции 
График функции дает удобное и наглядное представление о ее свойствах, и ниже уделено много внимания методам построения графиков функций.
Определение функции не дает указания на то, в какой форме задан закон соответствия между значениями аргумента и зависимой переменной; практически привычной формой задания этого закона является для нас запись функциональной зависимости в виде некоторой математической формулы, например:

В этом случае говорят, что функция задана аналитическим выражением. При этом термин «аналитическое выражение» имеет приблизительно тот же смысл, что и «алгебраическое выражение», с той разницей, что при записи аналитического выражения не ограничиваются только алгебраическими действиями (т. е. рациональными действиями и операцией извлечения корня), но пользуются, например, такими действиями, как логарифмирование, отыскание синуса или тангенса данного значения аргумента и т. п. Вообще, при определении новой математической операции для нее вводится специальный символ, который в дальнейшем уже можно использовать для записи аналитического выражения.
Для функции, заданной аналитическим выражением, область определения может состоять только из значений  входящих в о. д. з. этого выражения. Область определения функции оказывается в этом случае частью области допустимых значений аналитического выражения, задающего функцию, или совпадает с этой областью. Например, площадь S круга, как функция радиуса R, задается выражением
входящих в о. д. з. этого выражения. Область определения функции оказывается в этом случае частью области допустимых значений аналитического выражения, задающего функцию, или совпадает с этой областью. Например, площадь S круга, как функция радиуса R, задается выражением  Область определения этой функции по смыслу дела есть
Область определения этой функции по смыслу дела есть  взятое же само по себе аналитическое выражение
взятое же само по себе аналитическое выражение  определено при всех значениях R. Если функция задана аналитическим выражением относительно аргумента
определено при всех значениях R. Если функция задана аналитическим выражением относительно аргумента  и область определения не указана, то подразумевают, что область определения совпадает с о. д. з. задающего ее выражения.
и область определения не указана, то подразумевают, что область определения совпадает с о. д. з. задающего ее выражения.
Иногда функция задается разными аналитическими выражениями в разных частях области определения. Самый простой пример: будем рассматривать  как функцию от
как функцию от  . Тогда
. Тогда

Можно записать  виде
виде  . Вообще, одна и та же функция может быть задана различными способами и в разных видах.
. Вообще, одна и та же функция может быть задана различными способами и в разных видах.
Кроме аналитического способа задания применяют графическое и табличное задание функций. Если функция задана графиком, то можно по чертежу находить значения у, отвечающие данным значениям  разумеется, приближенно.
разумеется, приближенно.
Табличный способ задания функции заключается в том, что для избранных значений аргумента  обычно отстоящих друг от друга на некоторую постоянную величину — шаг таблицы, указываются соответствующие значения у (с определенной степенью точности). Небольшой фрагмент таблицы может выглядеть так:
обычно отстоящих друг от друга на некоторую постоянную величину — шаг таблицы, указываются соответствующие значения у (с определенной степенью точности). Небольшой фрагмент таблицы может выглядеть так:

В данном примере шаг таблицы равен 0,02.
Графическое и табличное задание функций часто возникает в результате проведения измерений, опытов, применения самопишущих приборов.
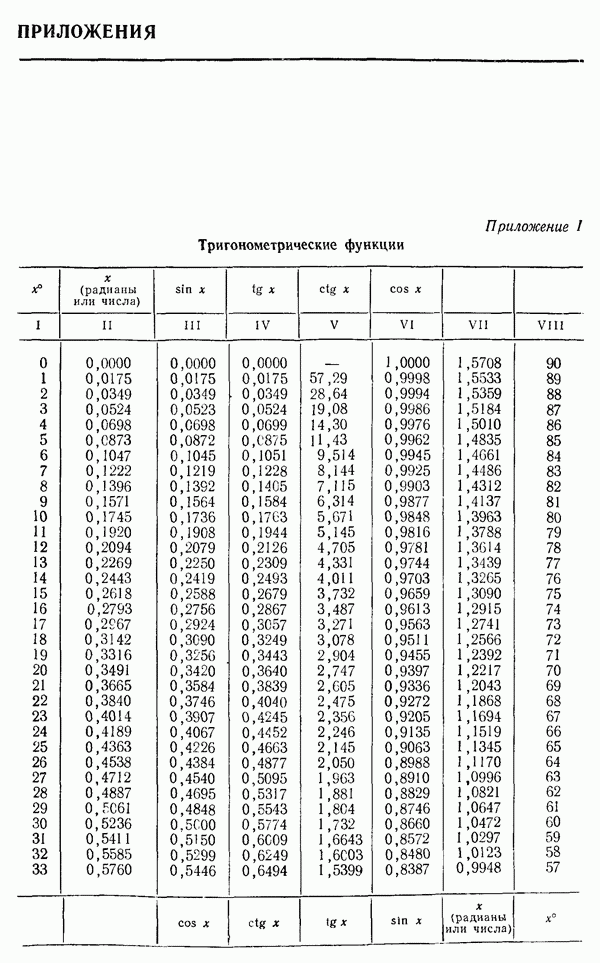
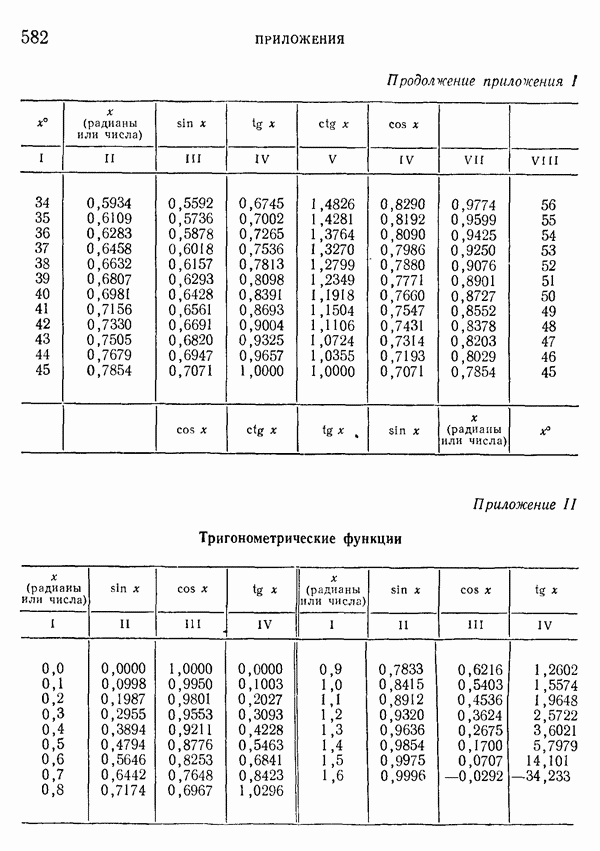
Для многих функций, заданных аналитически, также составлены таблицы, облегчающие применение этих функций (таблицы квадратных и кубических корней, таблицы логарифмов, тригонометрических функций и др.).
Необходимо приобрести навыки в пользовании таблицами функций (см. п. 220).
В восемнадцатом и в начале девятнадцатого века математики представляли себе функцию только с точки зрения ее аналитического выражения. Лишь в первой половине девятнадцатого столетия некоторыми математиками, в том числе великим русским ученым Н. И. Лобачевским, было сформулировано современное определение функции: существенным является наличие закона соответствия, а не возможность представить его «формулой». В частности, допускается и словесное описание закона соответствия: например,  целая часть
целая часть  определяется как «наибольшее целое число, не превосходящее х».
определяется как «наибольшее целое число, не превосходящее х».
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
- 2. Простые и составные числа. Признаки делимости.
- 3. Наибольший общий делитель и наименьшее общее кратное.
- 4. Целые числа. Рациональные числа.
- 5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
- 6. Иррациональные числа. Действительные числа.
- 7. Действия с приближенными числами.
- 8. Числовая ось. Координаты точки на плоскости.
- § 2. Степени и корни
- 9. Степени с натуральными показателями.
- 10. Степени с целыми показателями.
- 11. Корни.
- 12. Степени с рациональными показателями. Степени с действительными показателями.
- 13. Алгоритм извлечения квадратного корня.
- § 3. Комплексные числа
- 14. Основные понятия и определения.
- 15. Рациональные действия с комплексными числами.
- 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
- 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
- 18. Извлечение корня из комплексного числа.
- Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
- 19. Алгебраические выражения. Одночлены и многочлены.
- 20. Формулы сокращенного умножения.
- 21. Бином Ньютона.
- 22. Разложение многочлена на множители.
- 23. Дробные алгебраические выражения.
- § 2. Иррациональные алгебраические выражения
- 24. Радикалы из алгебраических выражений.
- 25. Освобождение от иррациональности в знаменателе дроби.
- Глава III. ЛОГАРИФМЫ
- 26. Определение и свойства логарифмов.
- 27. Логарифмы по различным основаниям. Модуль перехода.
- § 2. Десятичные логарифмы
- 28. Характеристика и мантисса десятичного логарифма.
- 29. Применение десятичных логарифмов к вычислениям.
- Глава IV. ФУНКЦИИ И ГРАФИКИ
- 30. Величина. Числовые множества.
- 31. Определение функции.
- 32. График функции. Способы задания функций.
- 33. Элементарное исследование поведения функции.
- 34. Сложная функция.
- 35. Обратная функция.
- 36. Функции нескольких переменных.
- § 2. Элементарные функции
- 37. Обзор элементарных функций.
- 38. Линейная функция.
- 39. Квадратичная функция у=ах^2.
- 40. Степенная функция у = х^n.
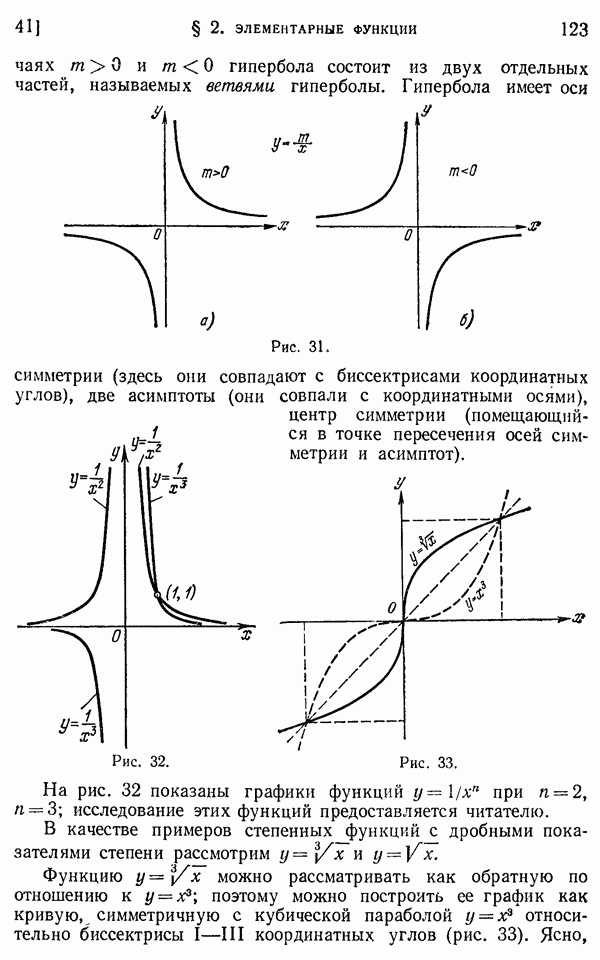
- 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
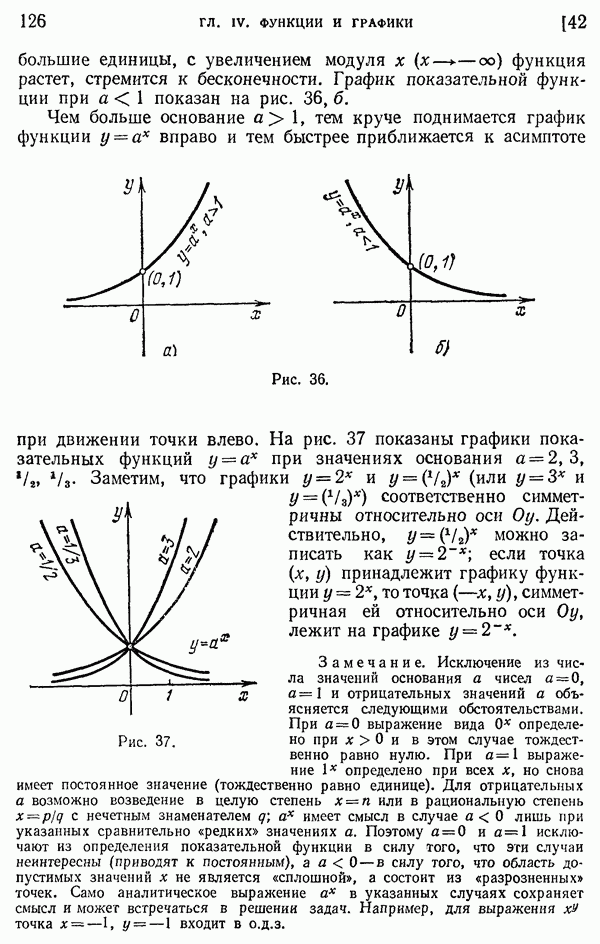
- 42. Показательная функция.
- 43. Логарифмическая функция.
- § 3. Преобразование графиков
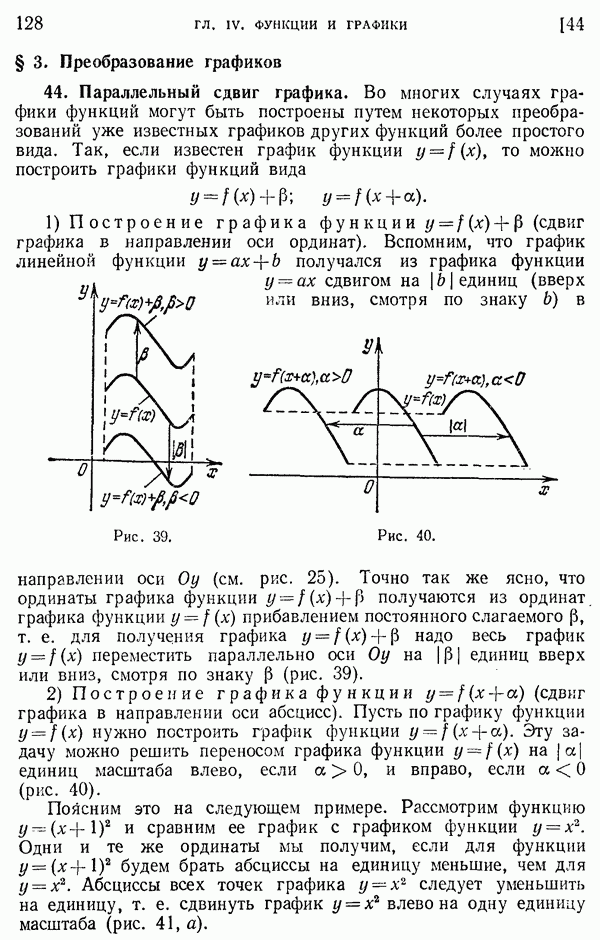
- 44. Параллельный сдвиг графика.
- 45. График квадратного трех члена.
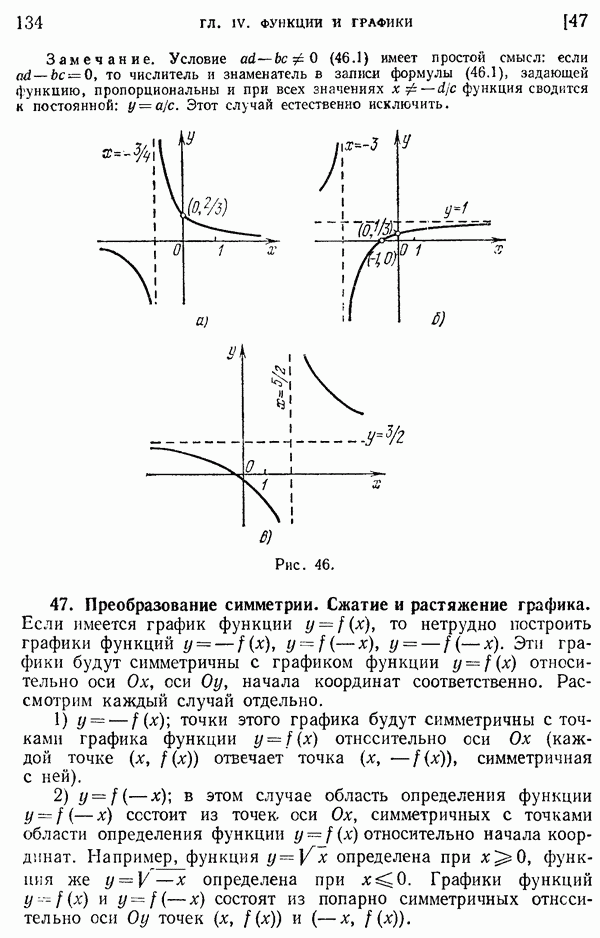
- 46. График дробно-линейной функции.
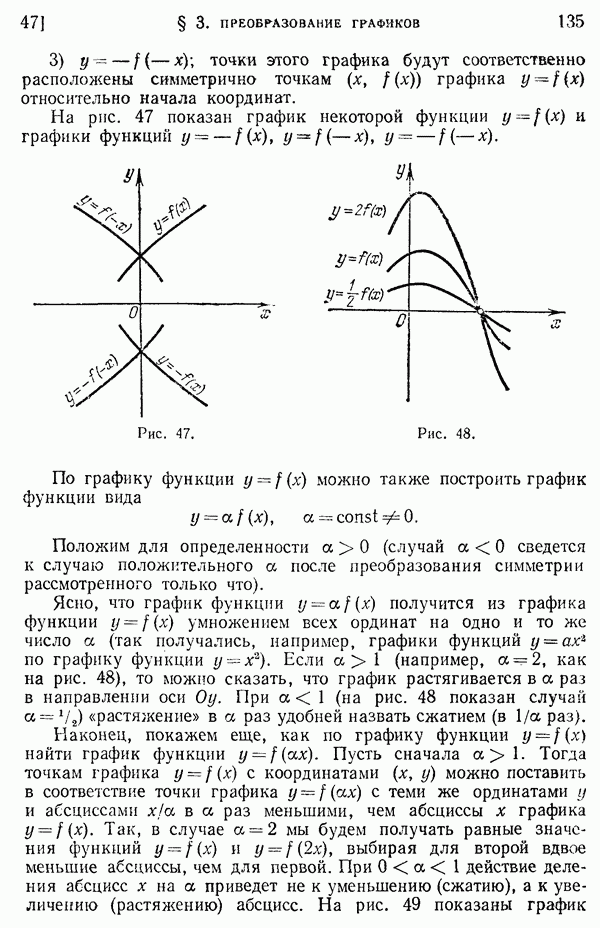
- 47. Преобразование симметрии. Сжатие и растяжение графика.
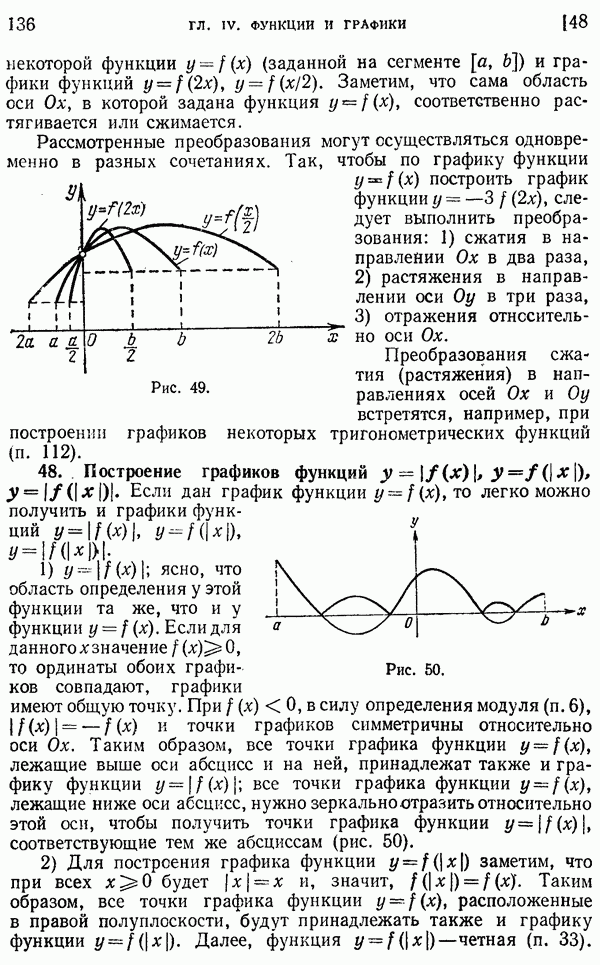
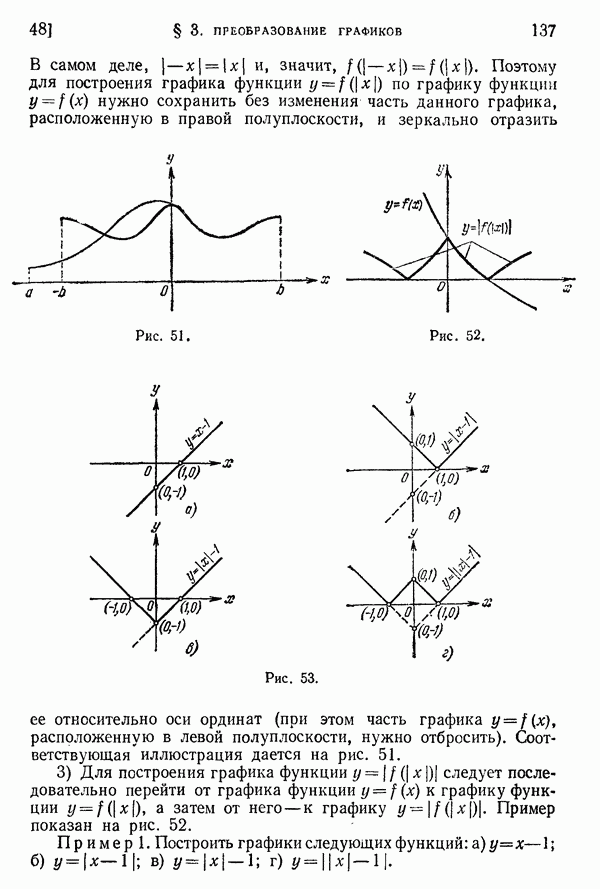
- 48. Построение графиков функций.
- 49. Сложение графиков.
- § 4. Некоторые сведения о рациональных функциях
- 50. Целые и дробные рациональные функции. Деление многочленов.
- 51. Схема Горнера. Теорема Безу.
- 52. Нули многочлена. Разложение многочлена на множители.
- Глава V. УРАВНЕНИЯ
- 53. Уравнение. Корни уравнения.
- 54. Равносильные уравнения.
- 55. Системы уравнений.
- 56. Графическое решение уравнений.
- §. 2. Алгебраические уравнения с одной неизвестной
- 57. Число и кратность корней.
- 58. Уравнения первой степени (линейные уравнения).
- 59. Уравнения второй степени (квадратные уравнения).
- 60. Формулы Виета. Разложение квадратного трехчлена на множители.
- 61. Исследование квадратного уравнения.
- 62. Уравнения высших степеней. Целые корни.
- 63. Двучленные уравнения.
- 64. Уравнения, сводящиеся к квадратным.
- 65. Возвратные уравнения.
- § 3. Системы алгебраических уравнений
- 66. Линейные системы.
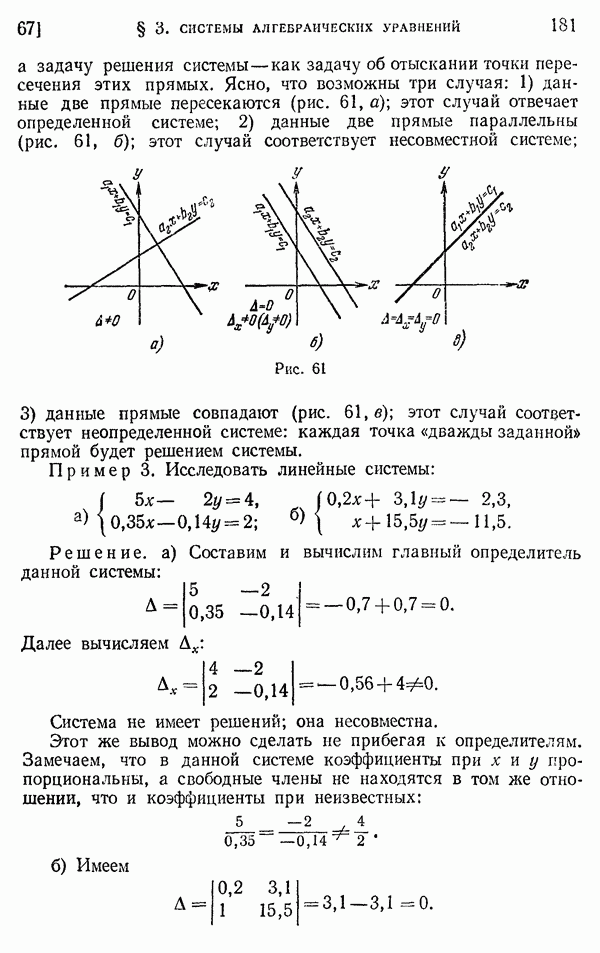
- 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
- 68. Системы, состоящие из уравнения второй степени и линейного уравнения.
- 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
- § 4. Иррациональные, показательные и логарифмические уравнения
- 70. Иррациональные уравнения.
- 71. Показательные уравнения.
- 72. Логарифмические уравнения.
- 73. Разные уравнения. Системы уравнений.
- Глава VI. НЕРАВЕНСТВА
- 74. Свойства неравенств. Действия над неравенствами.
- 75. Алгебраические неравенства.
- § 2. Решение неравенств
- 76. Множество решений неравенства. Равносильные неравенства.
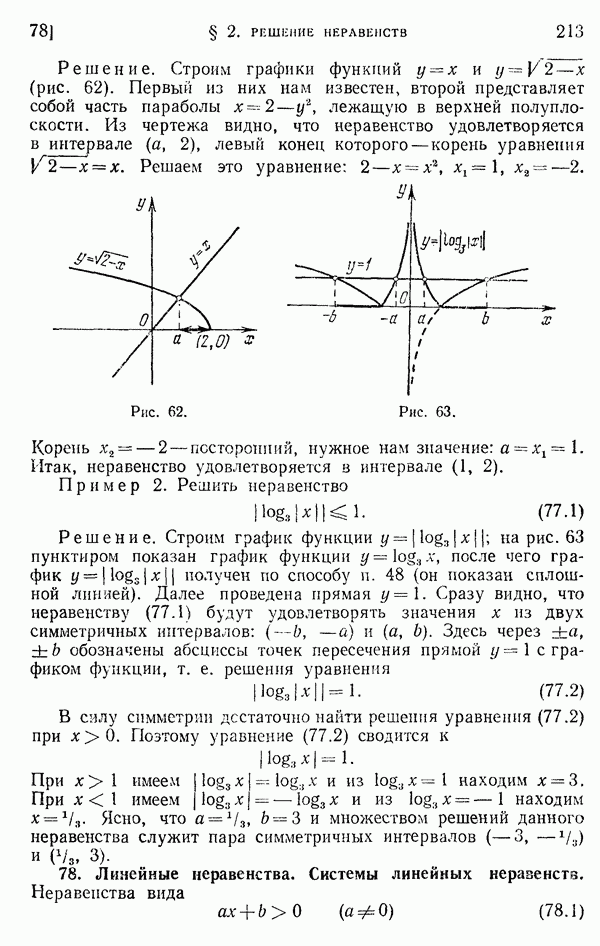
- 77. Графическое решение неравенств.
- 79. Квадратные неравенства.
- 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
- 81. Иррациональные, показательные и логарифмические неравенства.
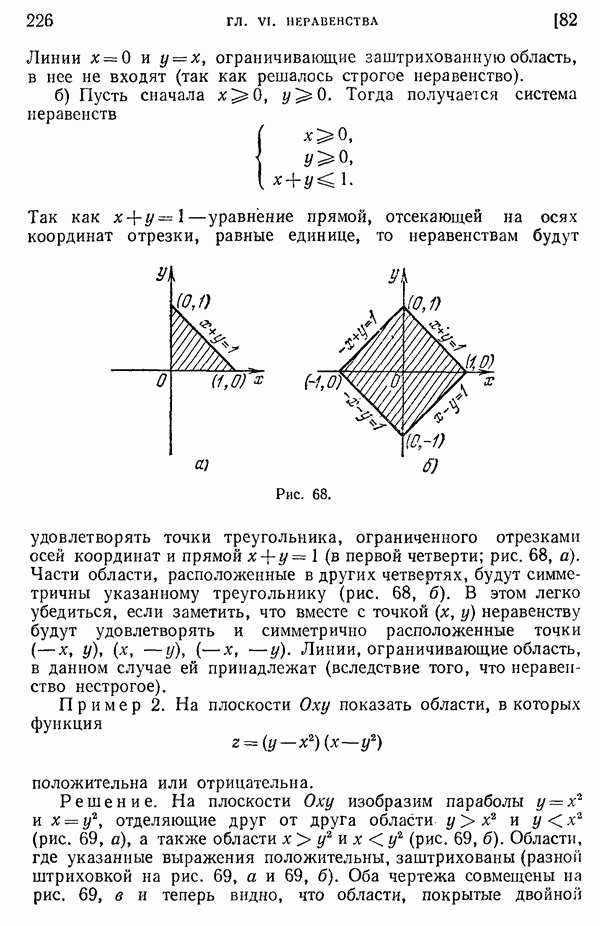
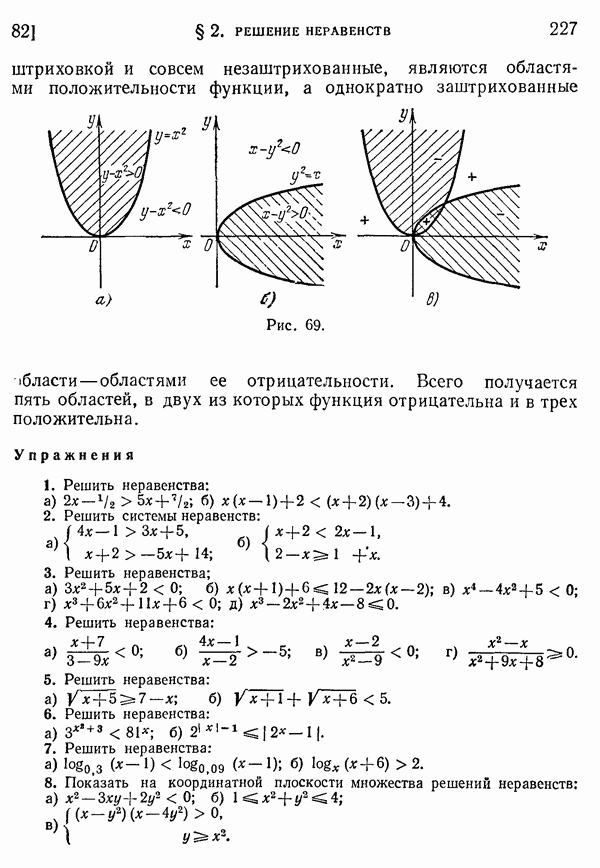
- 82. Неравенства с двумя неизвестными.
- Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
- 83. Числовая последовательность.
- 84. Предел числовой последовательности.
- 85. Бесконечно малые. Правила предельного перехода.
- § 2. Арифметическая прогрессия
- 86. Арифметическая прогрессия. Формула общего члена.
- 87. Свойства арифметической прогрессии.
- 88. Формула для суммы n членов арифметической прогрессии.
- § 3. Геометрическая прогрессия
- 89. Геометрическая прогрессия. Формула общего члена.
- 90. Свойства геометрической прогрессии.
- 91. Формулы для суммы n членов геометрической прогрессии.
- 92. Бесконечно убывающая геометрическая прогрессия.
- Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
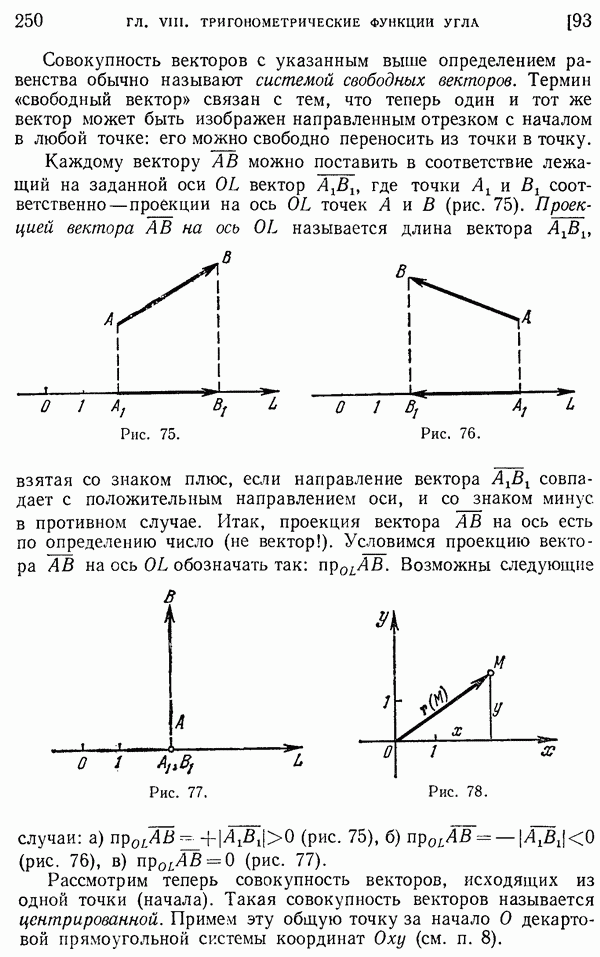
- 93. Вектор, проекция вектора.
- 94. Положительные углы и дуги, меньшие 360°.
- 95. Углы и дуги, большие 360°.
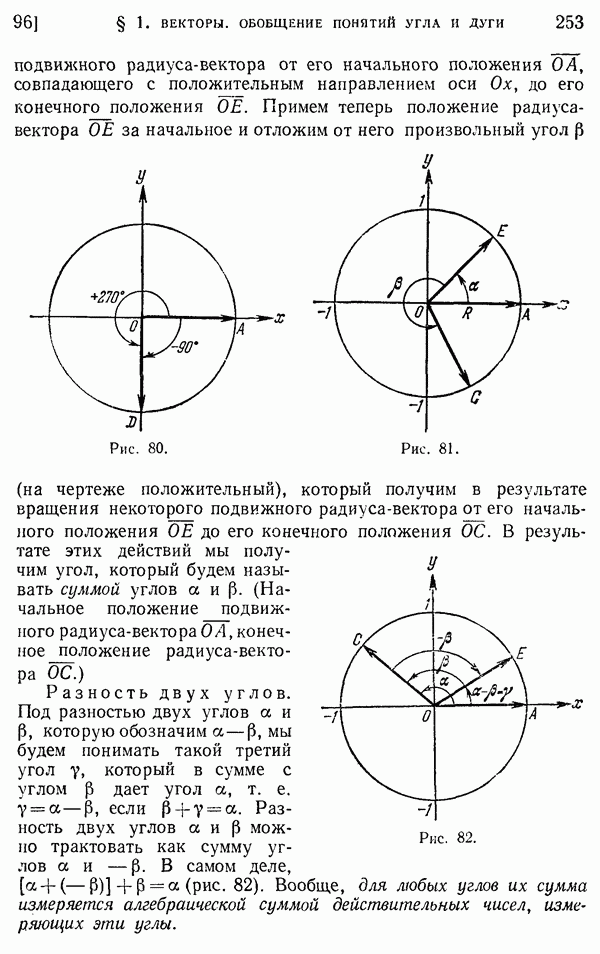
- 96. Отрицательные углы. Сложение и вычитание углов.
- § 2. Тригонометрические функции произвольного угла
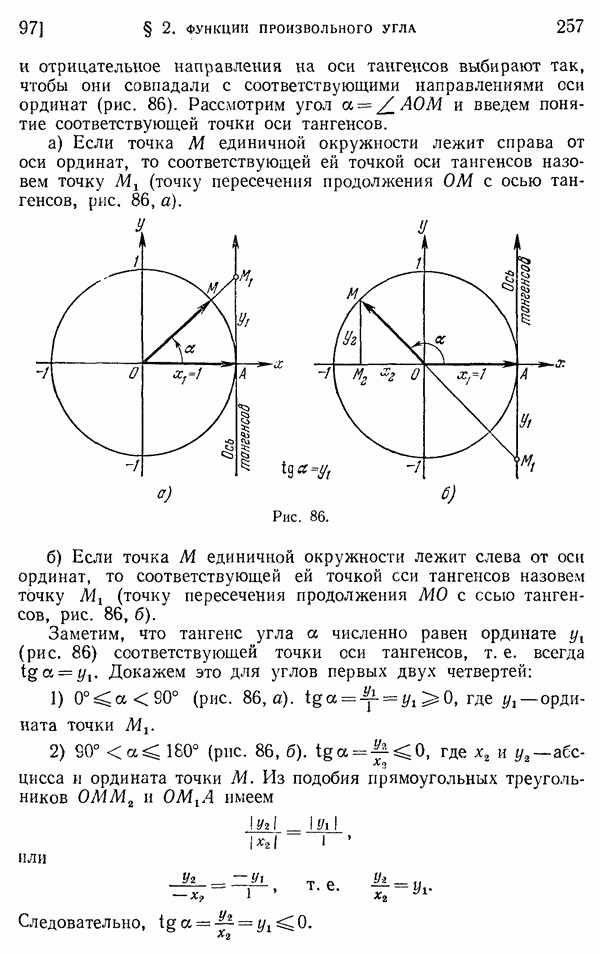
- 97. Определение основных тригонометрических функций.
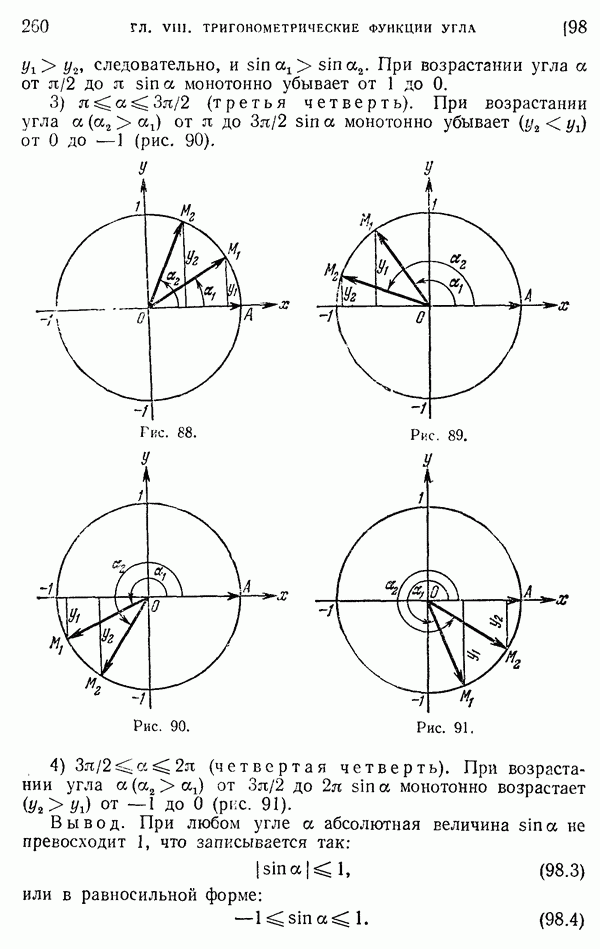
- 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
- § 3. Соотношения между тригонометрическими функциями одного и того же угла
- 99. Основные тригонометрические тождества.
- 100. Вычисление значений тригонометрических функций по значению одной из них.
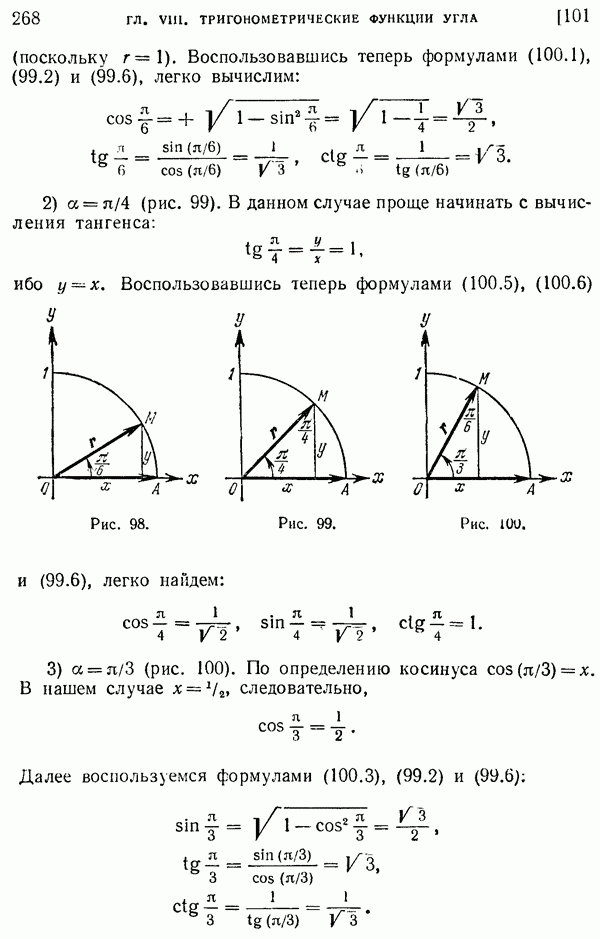
- 101. Значения тригонометрических функций некоторых углов.
- § 4. Четность, нечетность и периодичность тригонометрических функций
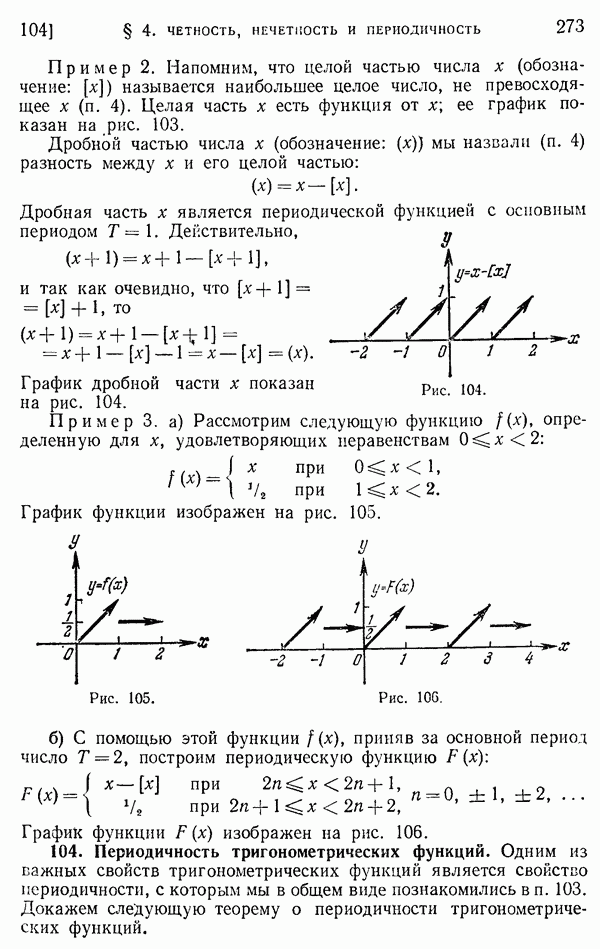
- 102. Четность и нечетность.
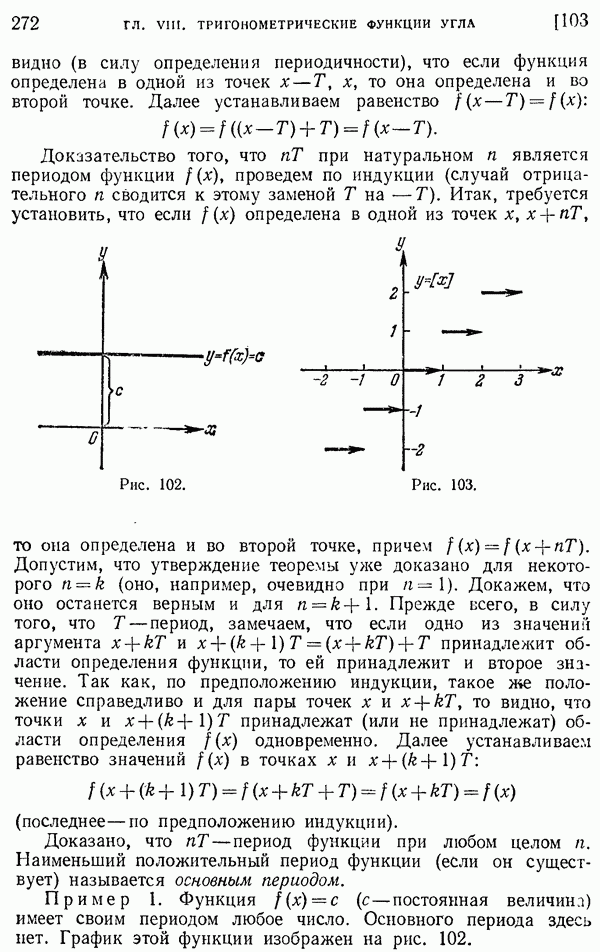
- 103. Понятие периодической функции.
- 104. Периодичность тригонометрических функций.
- § 5. Формулы приведения
- 105. Зависимость между тригонометрическими функциями дополнительных углов.
- 106. Формулы приведения.
- Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
- § 1. Тригонометрические функции числового аргумента
- 108. Области определения и области изменения значений тригонометрических функций.
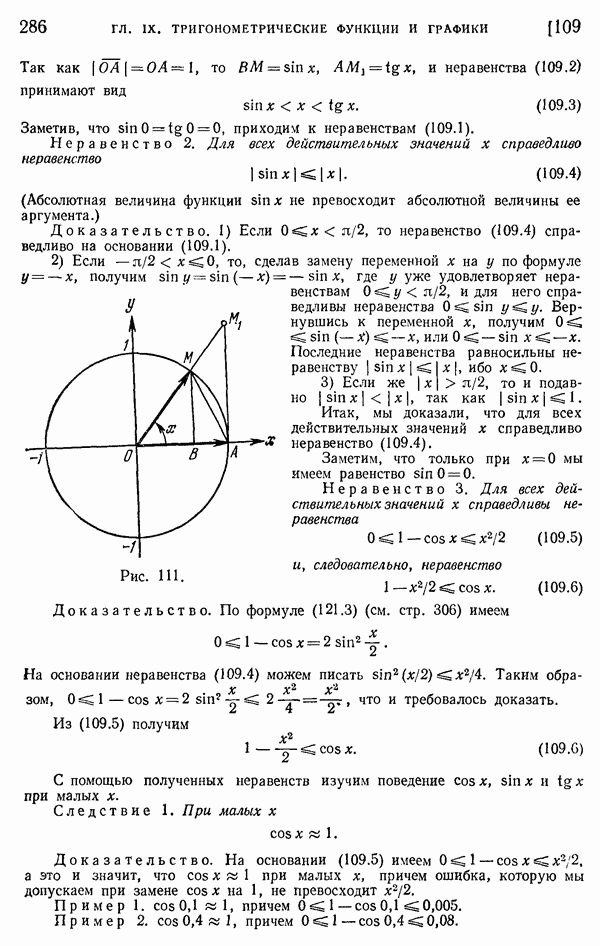
- 109. Некоторые неравенства и их следствия.
- § 2. Графики тригонометрических функций
- 110. Первоначальные сведения о таблицах тригонометрических функций.
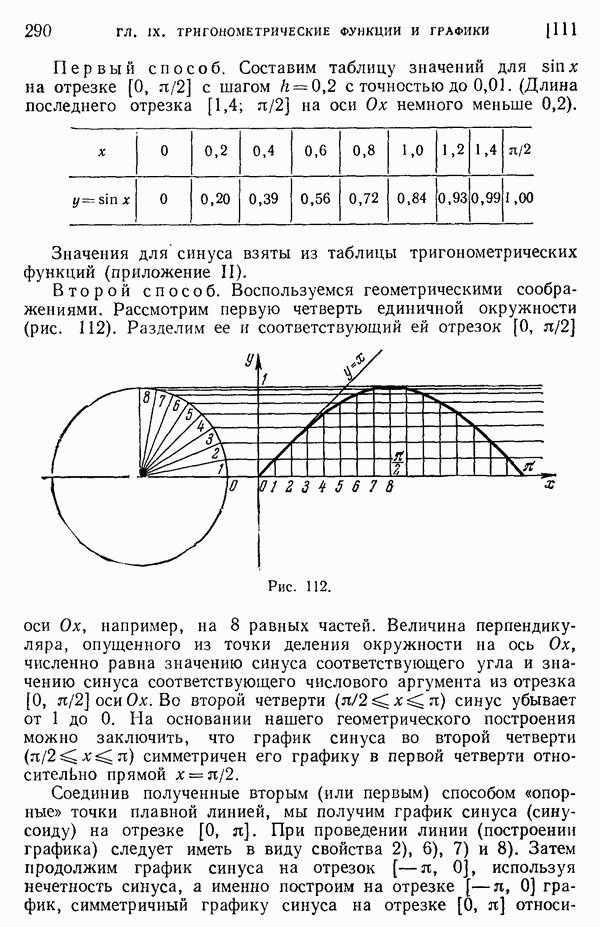
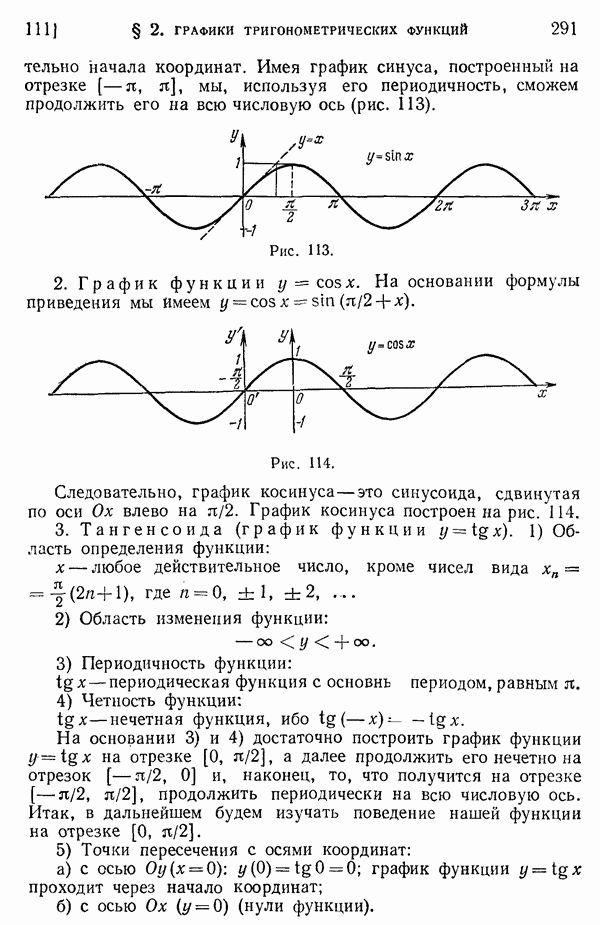
- 111. Основные графики.
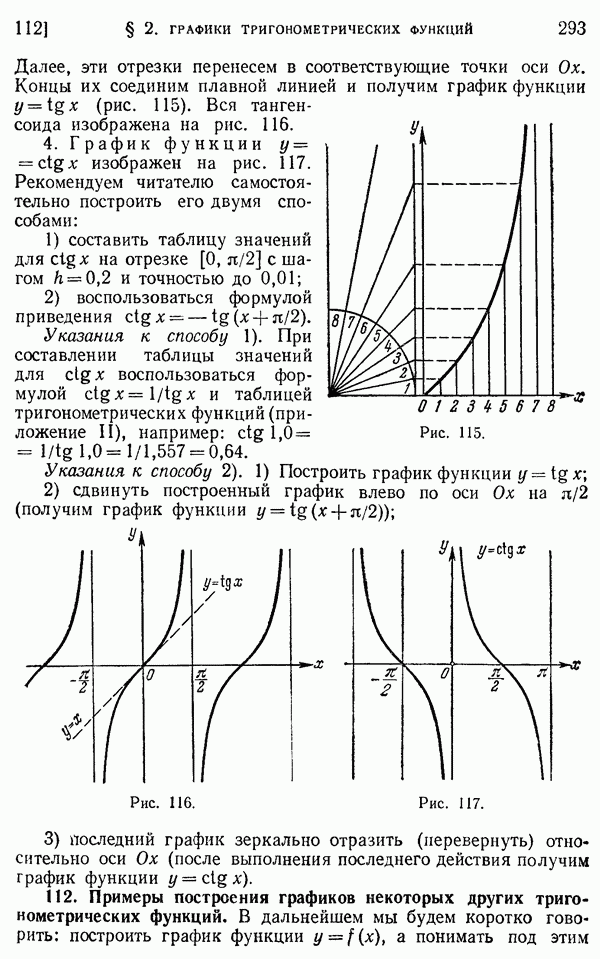
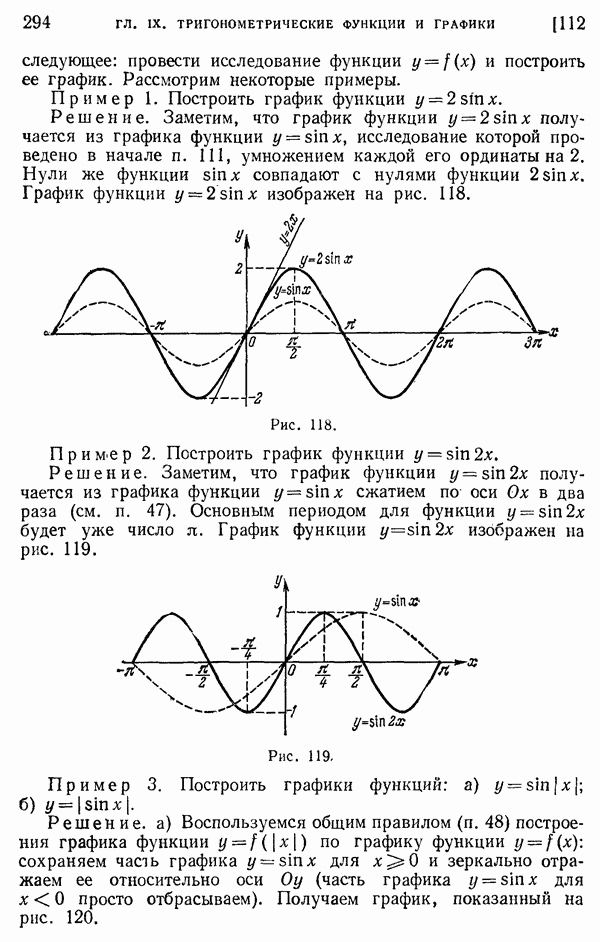
- 112. Примеры построения графиков некоторых других тригонометрических функций.
- 113. Дальнейшие примеры построения графиков функций.
- Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
- 114. Расстояние между двумя точками на плоскости.
- 115. Косинус суммы и разности двух аргументов.
- 116. Синус суммы и разности двух аргументов.
- 117. Тангенс суммы и разности двух аргументов.
- 118. О формулах сложения для нескольких аргументов.
- § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
- 119. Тригонометрические функции двойного аргумента.
- 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
- 121. Тригонометрические функции половинного аргумента.
- 122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
- § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
- § 4. Преобразование в произведение сумм вида
- § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
- 127. Преобразование в произведение выражения a•sina + b•cosa.
- 128. Преобразование в произведение выражений a•sina+b и a•cosa+b
- 129. Преобразование в произведение выражения a•tga+b.
- Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
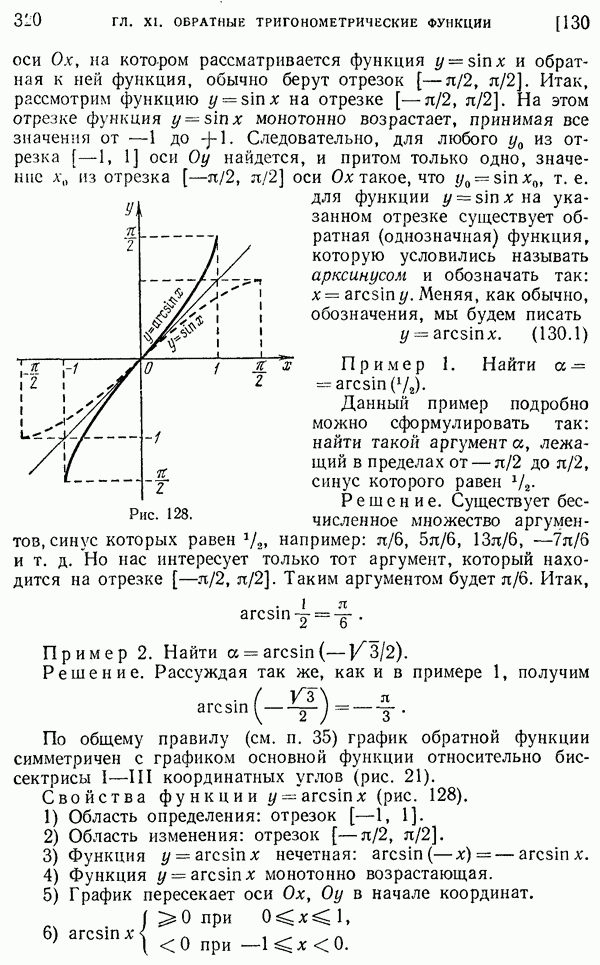
- 130. Функция у = arcsin x (арксинус).
- 131. Функция y = arccos x (арккосинус).
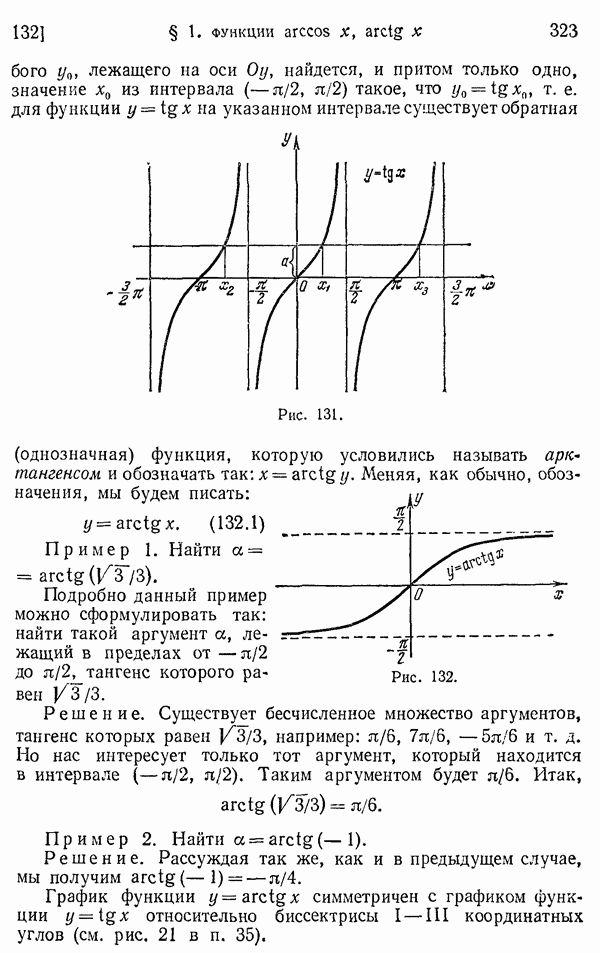
- 132. Функция y = arctg x (арктангенс).
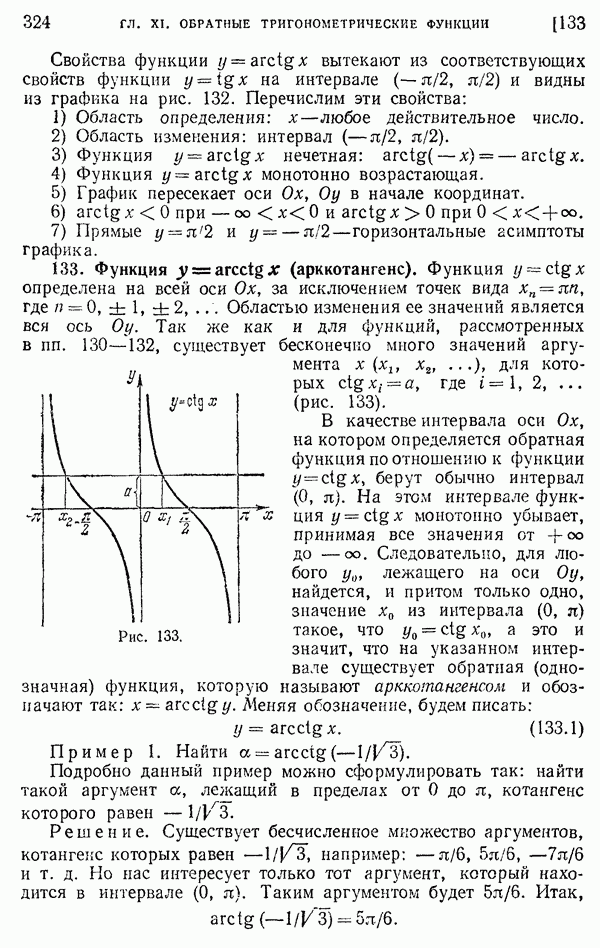
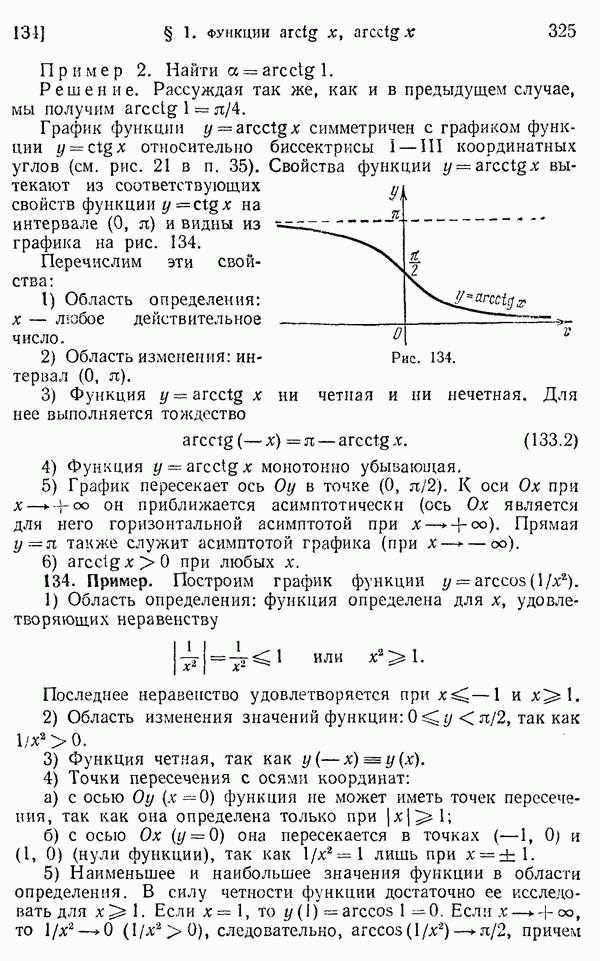
- 133. Функция y = arcctg x (арккотангенс).
- 134. Пример.
- § 2. Операции над обратными тригонометрическими функциями
- 135. Тригонометрические операции.
- 136. Операции сложения (вычитания).
- § 3. Обратные тригонометрические операции над тригонометрическими функциями
- 137. Функция у = arcsin (sin x).
- 138. Функция y = arctg (tg x).
- Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- 139. Уравнение sin х = а.
- 140. Уравнение cos х = a.
- 141. Уравнение tg x = a.
- 142. Уравнение ctg x = a.
- 143. Некоторые дополнения.
- § 2. Способ приведения к одной функции одного и того же аргумента
- 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
- 146. Способ разложения на множители.
- 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
- § 3. Некоторые частные приемы решения тригонометрических уравнений и систем
- 148. Введение вспомогательного аргумента.
- 149. Преобразование произведения в сумму или разность.
- 150. Переход к функциям удвоенного аргумента.
- 151. Решение уравнения типа…
- 152. Применение подстановок sinx ± соsx = y.
- § 4. Решение тригонометрических неравенств
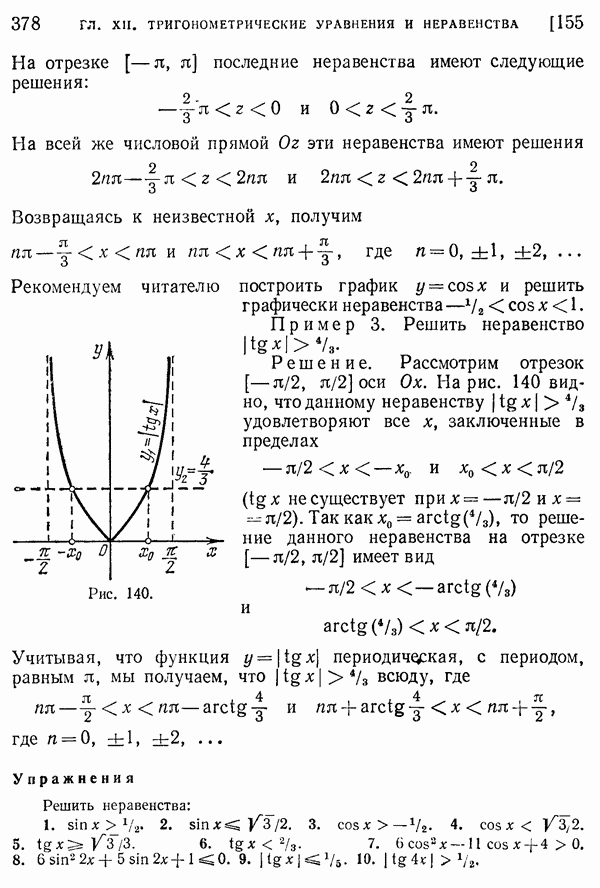
- 154. Простейшие тригонометрические неравенства.
- 155. Примеры тригонометрических неравенств, сводящихся к простейшим.
- Часть вторая. ГЕОМЕТРИЯ
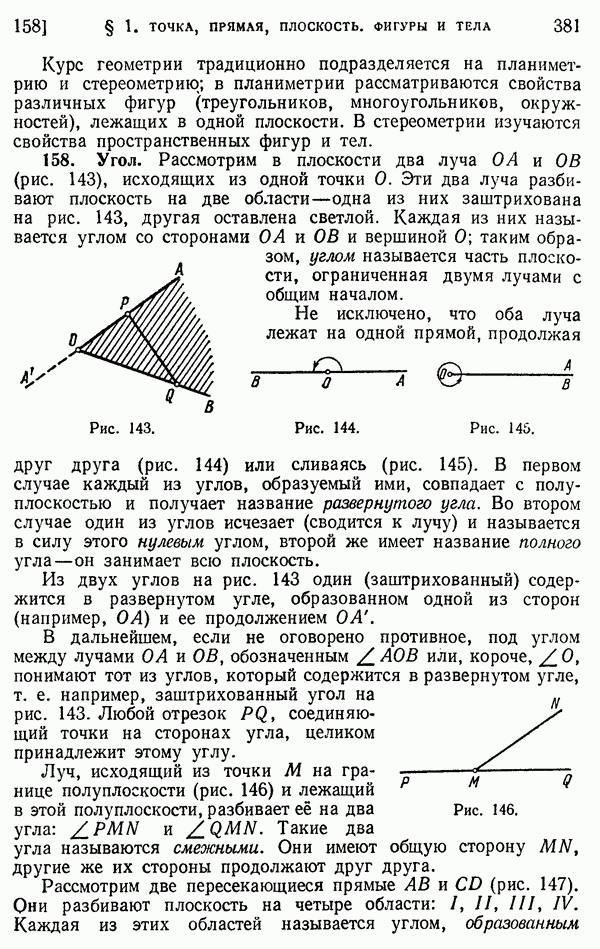
- 156. Точка. Прямая. Луч. Отрезок.
- 157. Плоскость. Фигуры и тела.
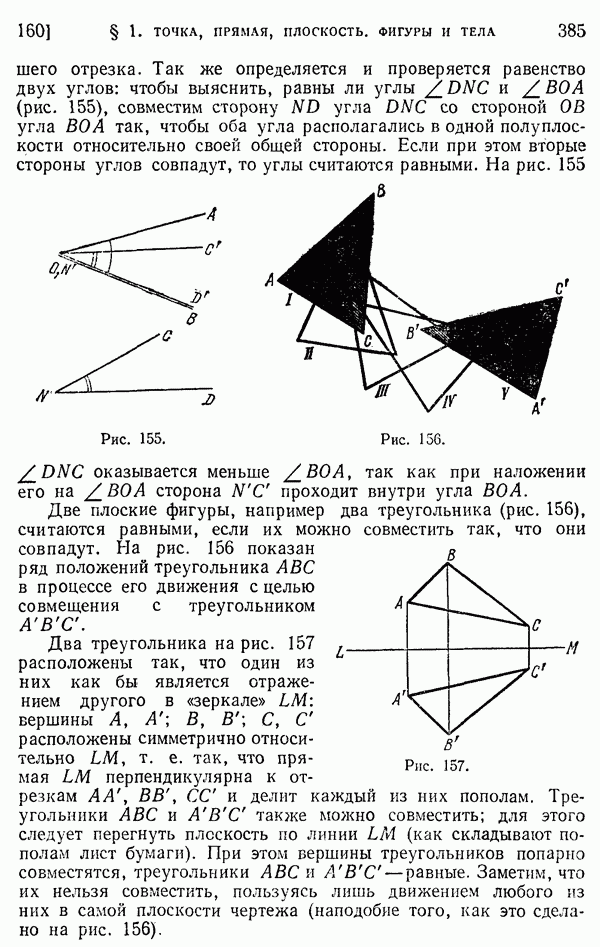
- 160. Равенство фигур. Движение.
- 161. Равенство тел.
- § 2. Измерение геометрических величин
- 162. Сложение отрезков. Длина отрезка.
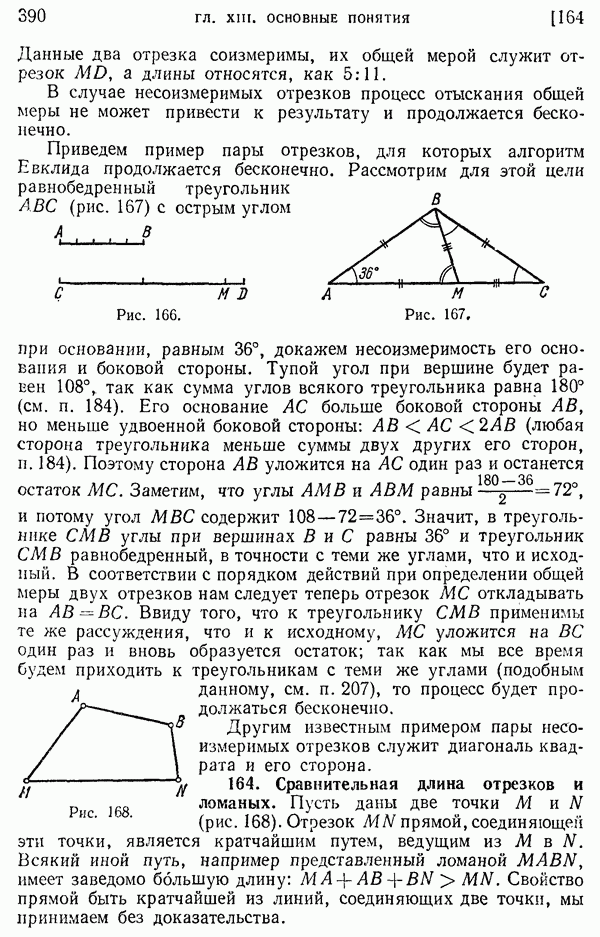
- 163. Общая мера двух отрезков.
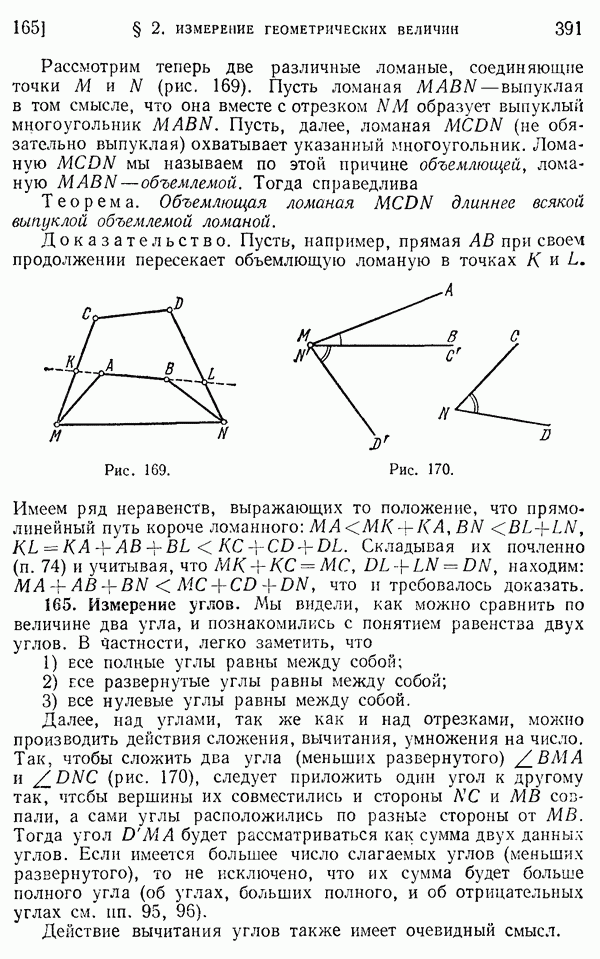
- 164. Сравнительная длина отрезков и ломаных.
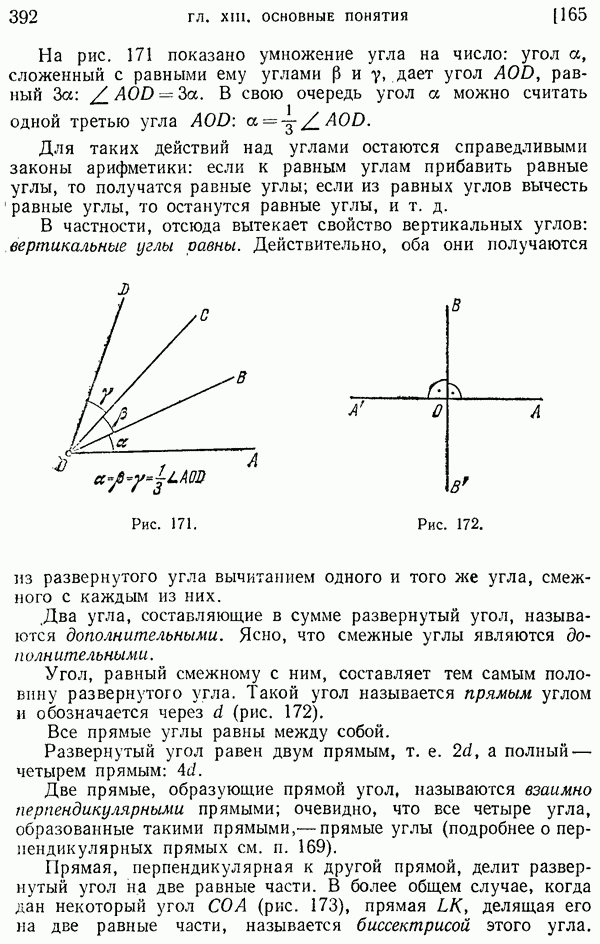
- 165. Измерение углов.
- 166. Радианная мера угла.
- 167. Измерение площадей.
- 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
- Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
- 169. Перпендикуляр и наклонные.
- 170. Свойство перпендикуляра, проведенного к отрезку в его середине.
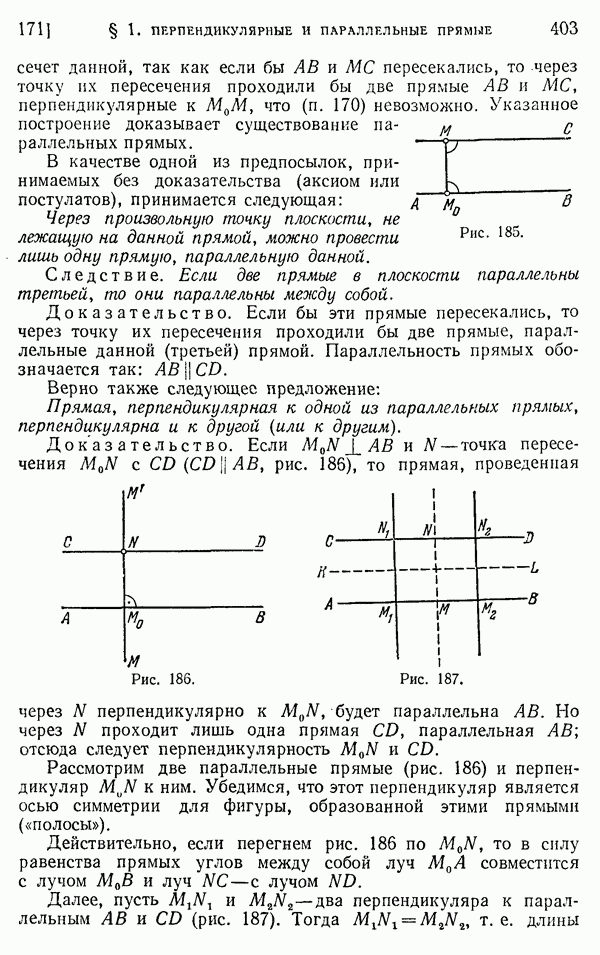
- 171. Параллельные прямые.
- 172. Углы, образованные двумя параллельными прямыми и секущей.
- 173. Углы с параллельными или перпендикулярными сторонами.
- § 2. Геометрические места точек. Окружность
- 174. Геометрическое место точек.
- 175. Свойство биссектрисы угла.
- 176. Окружность.
- 177. Взаимное расположение прямой и окружности. Касательная и секущая.
- 178. Хорда и диаметр. Сектор и сегмент.
- 179. Взаимное расположение двух окружностей.
- § 3. Основные задачи на построение
- 181. Деление отрезка пополам. Построение перпендикуляров.
- 182. Построение углов.
- 183. Другие задачи на построение.
- Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
- 184. Стороны и углы треугольника.
- 185. Биссектрисы треугольника. Вписанная окружность.
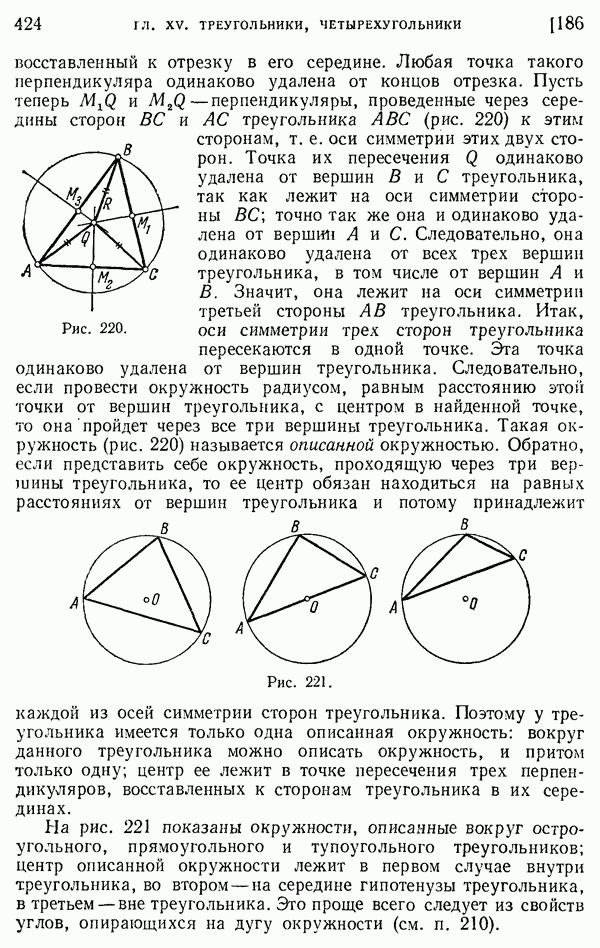
- 186. Оси симметрии сторон треугольника. Описанная окружность.
- 187. Медианы и выcоты треугольника.
- 188. Равенство треугольников.
- 189. Построение треугольников.
- 190. Равнобедренные треугольники.
- 191. Прямоугольные треугольники.
- § 2. Параллелограммы
- 192. Четырехугольники.
- 193. Параллелограмм и его свойства.
- 194. Прямоугольник.
- § 3. Трапеция
- 196. Трапеция.
- 197. Средняя линия треугольника.
- 198. Средняя линия трапеции.
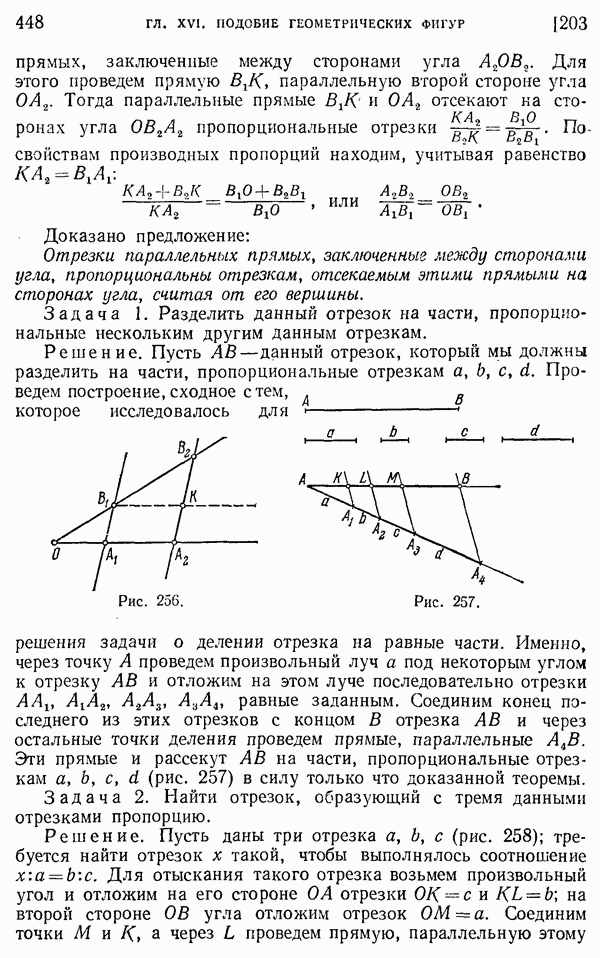
- 199. Деление отрезка на равные части.
- § 4. Площади треугольников и четырехугольников
- 200. Площадь параллелограмма.
- 201. Площадь треугольника.
- 202. Площадь трапеции.
- Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
- 203. Пропорциональные отрезки.
- 204. Свойства биссектрис внутреннего и внешнего углов треугольника.
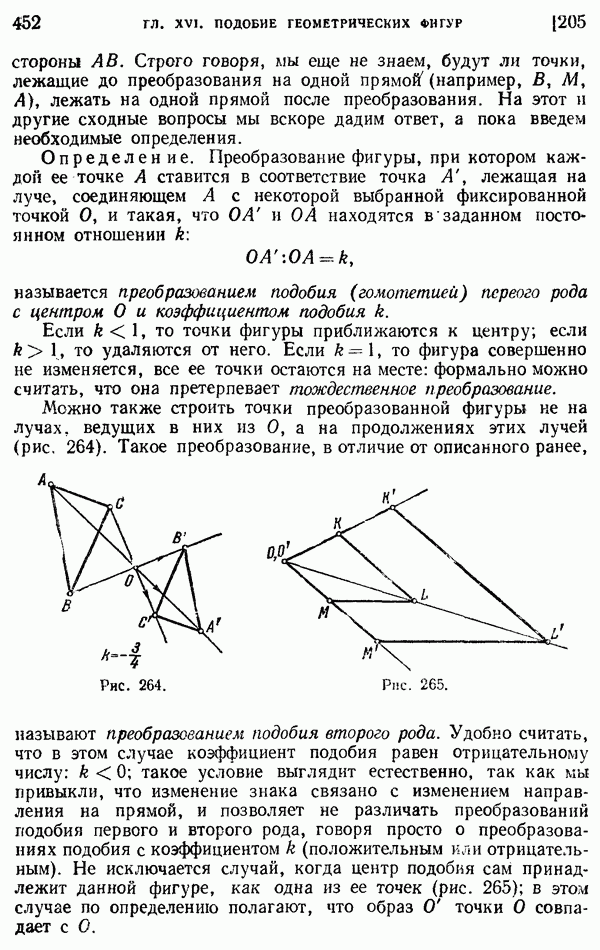
- § 2. Подобное преобразование фигур (гомотетия)
- 205. Определение гомотетичных фигур.
- 206. Свойства преобразования подобия.
- § 3. Общее подобное соответствие фигур
- 207. Подобные фигуры.
- 208. Периметры и площади подобных треугольников.
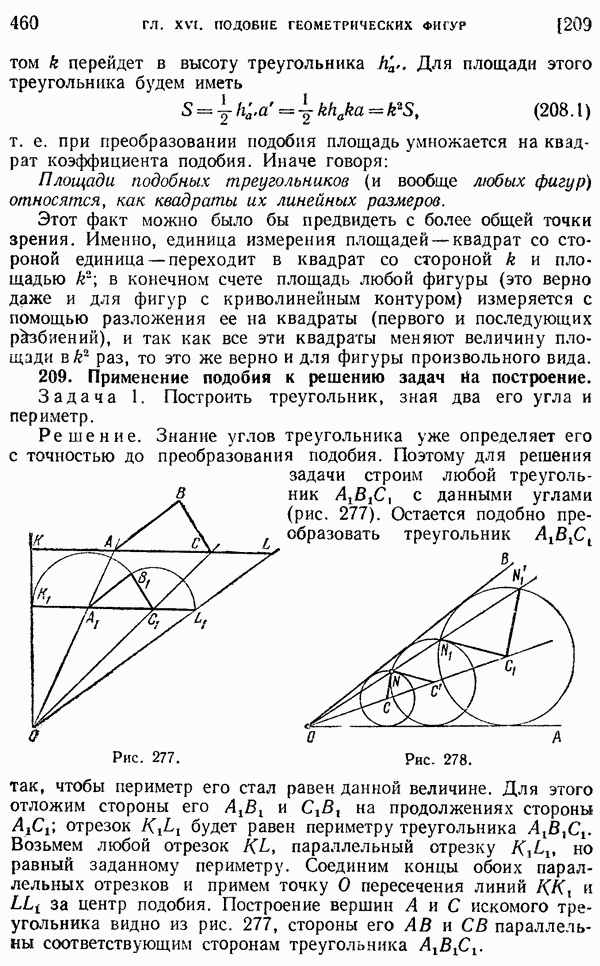
- 209. Применение подобия к решению задач на построение.
- Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
- 210. Углы с вершиной на окружности.
- 211. Углы с вершиной внутри и вне круга.
- 212. Угол, под которым виден данный отрезок.
- 213. Четырехугольники, вписанные в окружность.
- 214. Пропорциональные отрезки в круге.
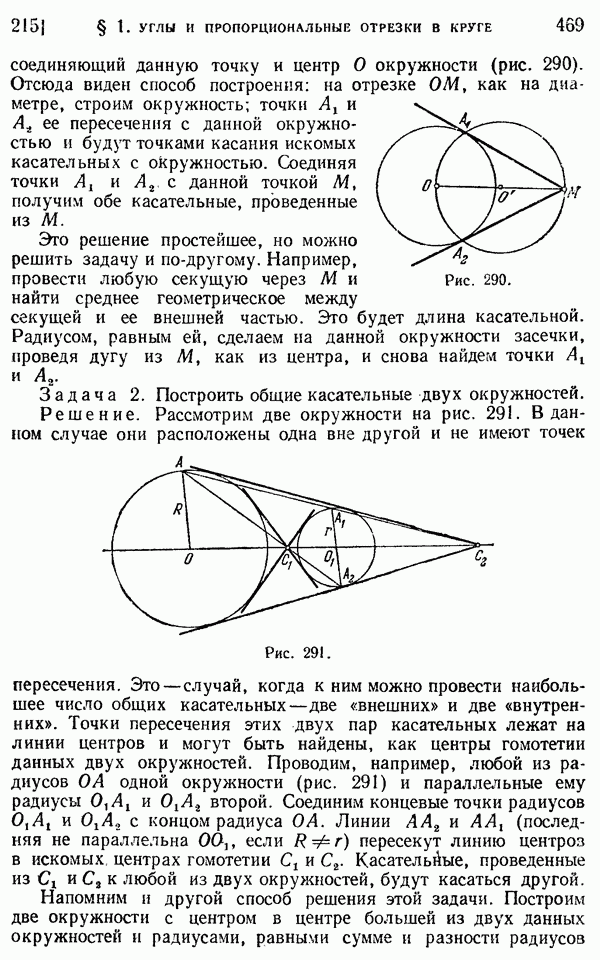
- 215. Задачи на построение.
- § 2. Метрические соотношения в треугольнике
- 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора.
- 218. Теорема синусов. Формула Герона.
- 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
- 218. Теорема синусов. Формула Герона.
- 219. Радиусы вписанной и описанной окружностей.
- § 3. Решение треугольников
- 220. Таблицы функций.
- 221. Решение треугольников. Сводка основных формул.
- 222. Решение прямоугольных треугольников.
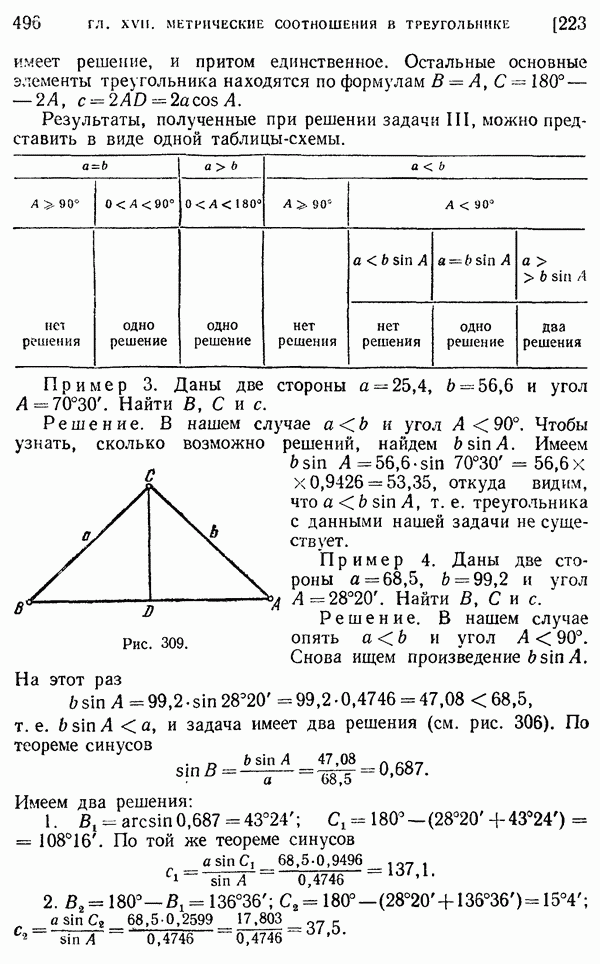
- 223. Решение косоугольных треугольников.
- Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
- 224. Выпуклые многоугольники.
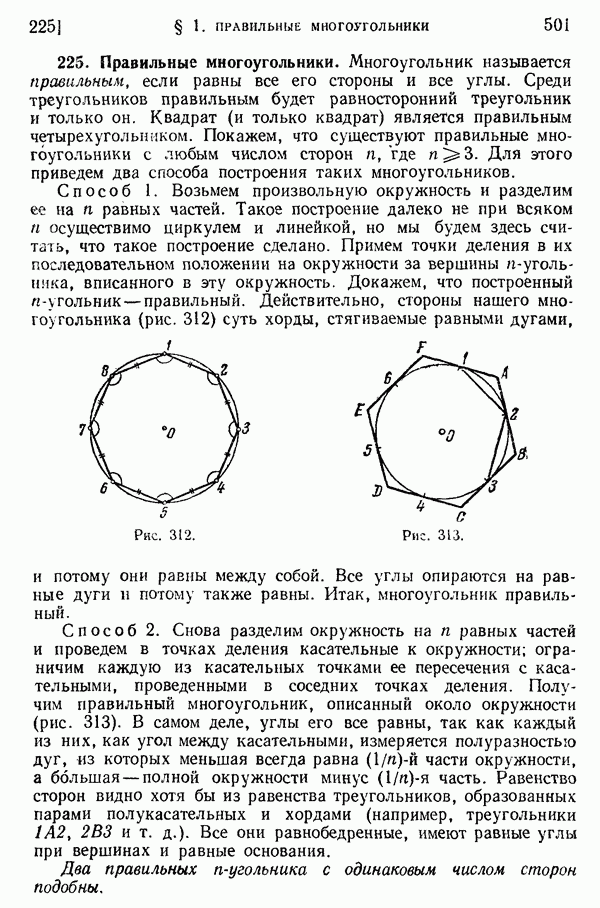
- 225. Правильные многоугольники.
- 226. Соотношения между стороной, радиусом и апофемой.
- 227. Периметр и площадь правильного n-угольника.
- 228. Удвоение числа сторон правильного многоугольника.
- § 2. Длина окружности. Площадь круга и его частей
- 229. Длина окружности.
- 230. Площадь круга и его частей.
- Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- 231. Взаимное расположение двух прямых в пространстве.
- 232. Взаимное расположение прямой линии и плоскости.
- 233. Взаимное расположение двух плоскостей.
- 234. Свойства параллельных прямых и плоскостей.
- 235. Построения в стереометрии.
- § 2. Перпендикулярность прямых и плоскостей
- 236. Перпендикуляр к плоскости.
- 237. Перпендикуляр и наклонные.
- 238. Угол между прямой и плоскостью.
- 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
- 240. Общий перпендикуляр двух скрещивающихся прямых.
- § 3. Двугранные и многогранные углы
- 241. Двугранный угол.
- 242. Взаимно перпендикулярные плоскости.
- 243. Трехгранные углы.
- 244. Многогранные углы.
- § 4. Многогранники
- 245. Многогранники.
- 246. Правильные многогранники.
- Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
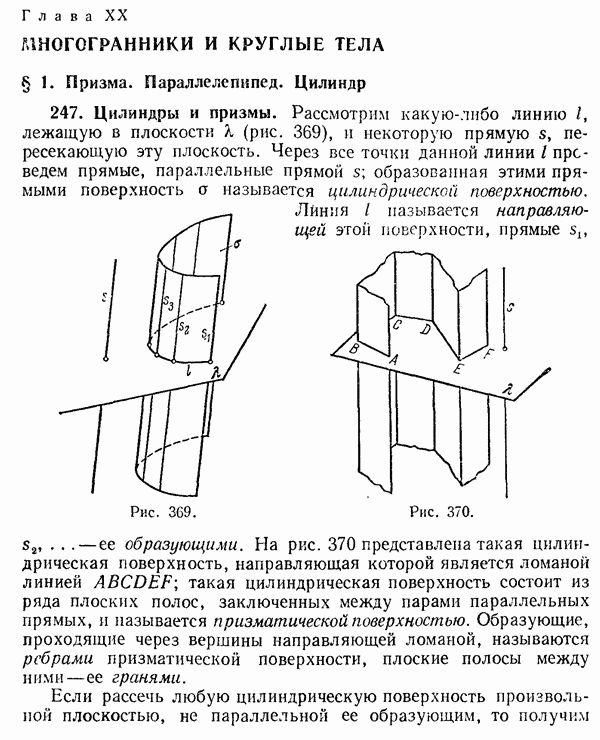
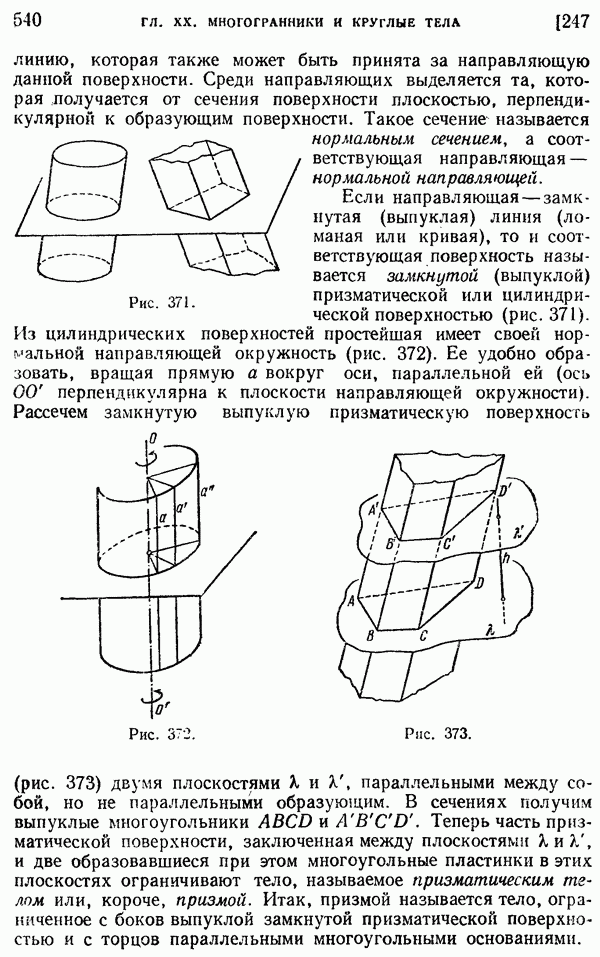
- 247. Цилиндры и призмы.
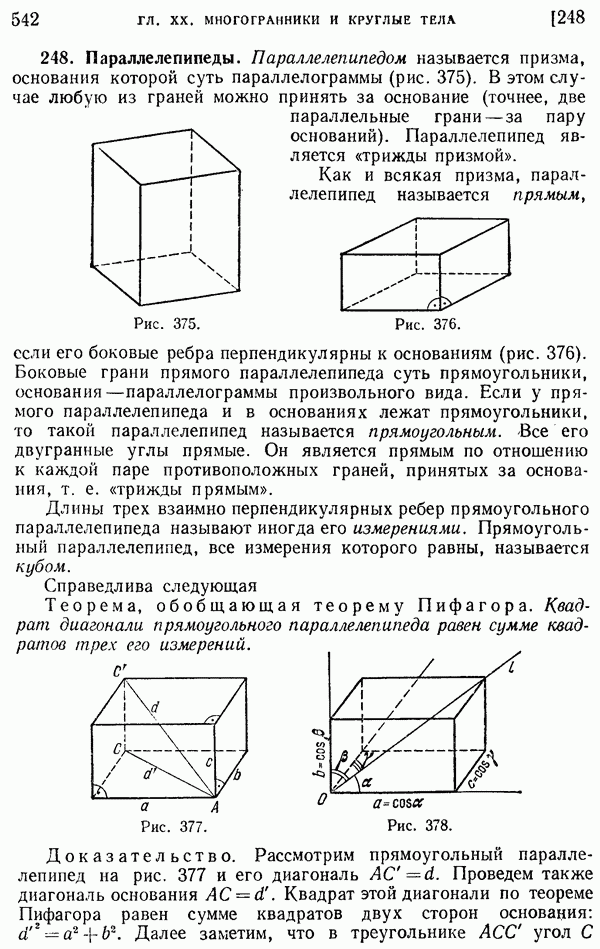
- 248. Параллелепипеды.
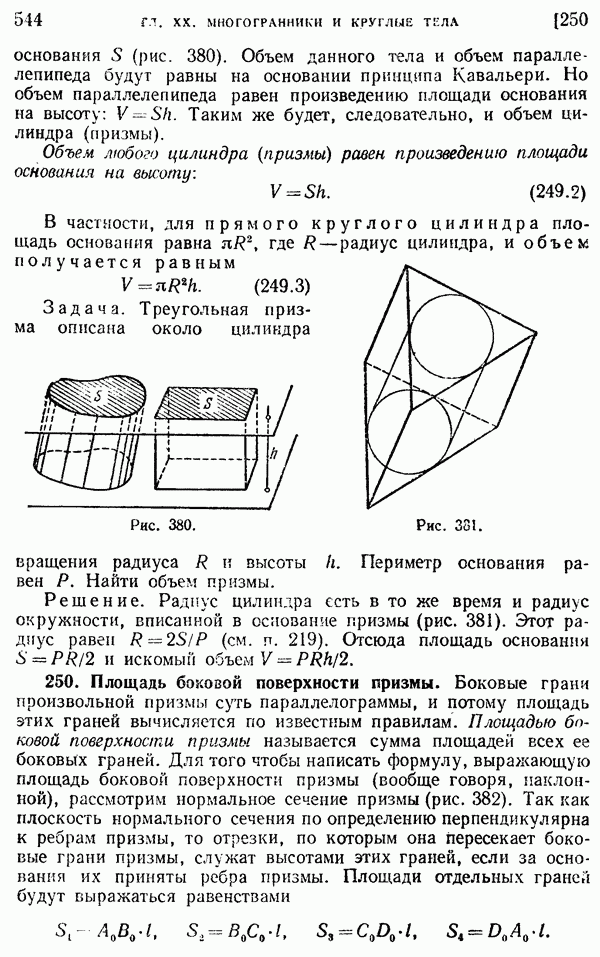
- 249. Объемы призм и цилиндров.
- 250. Площадь боковой поверхности призмы.
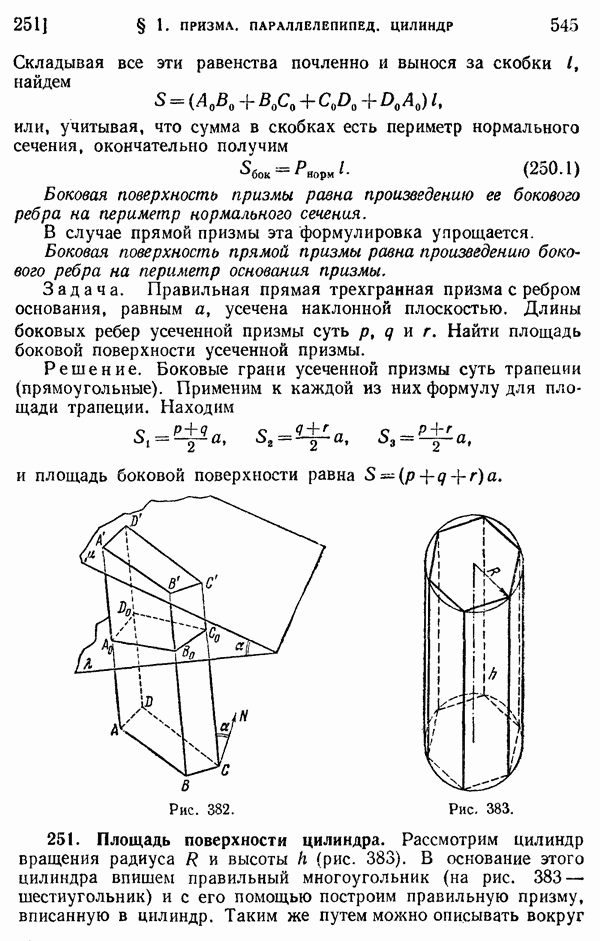
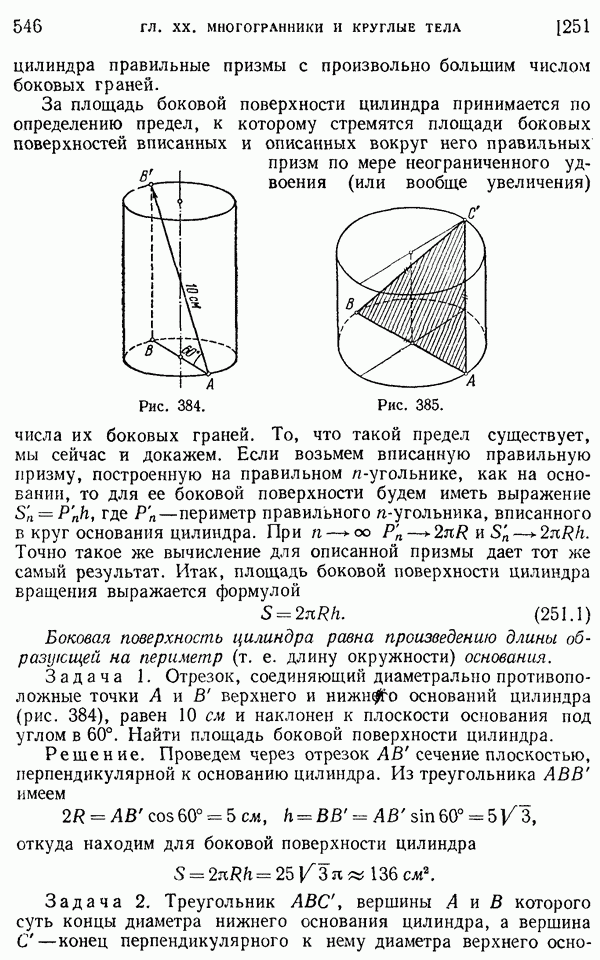
- 251. Площадь поверхности цилиндра.
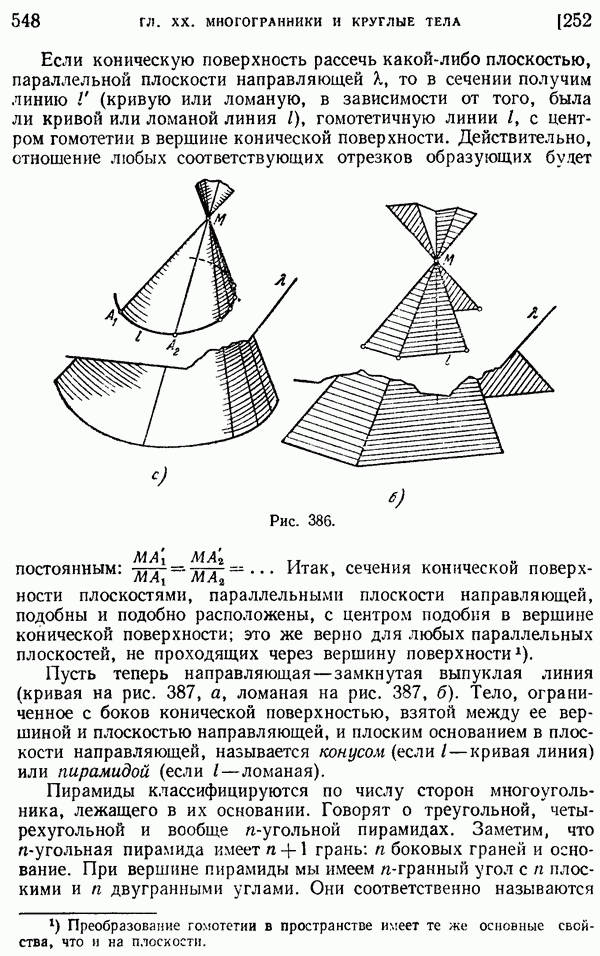
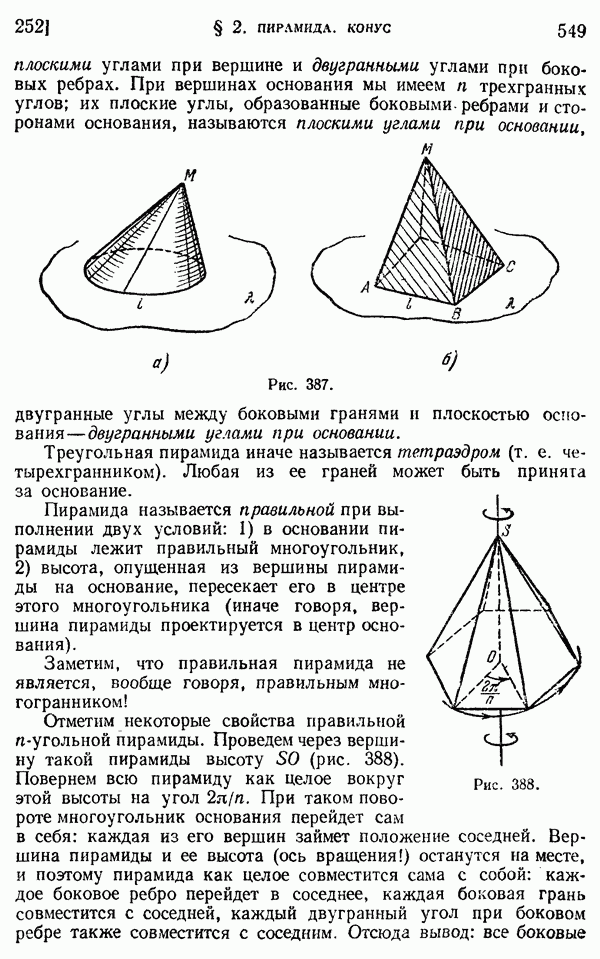
- § 2. Пирамида. Конус
- 252. Свойства пирамиды и конуса.
- 253. Объем пирамиды и конуса.
- 254. Площадь боковой поверхности правильной пирамиды и конуса.
- 255. Усеченный конус и усеченная пирамида.
- § 3. Шаровая поверхность. Шар
- 256. Шар и шаровая поверхность.
- 257. Объем шара и его частей.
- 258. Площадь поверхности шара и ее частей.
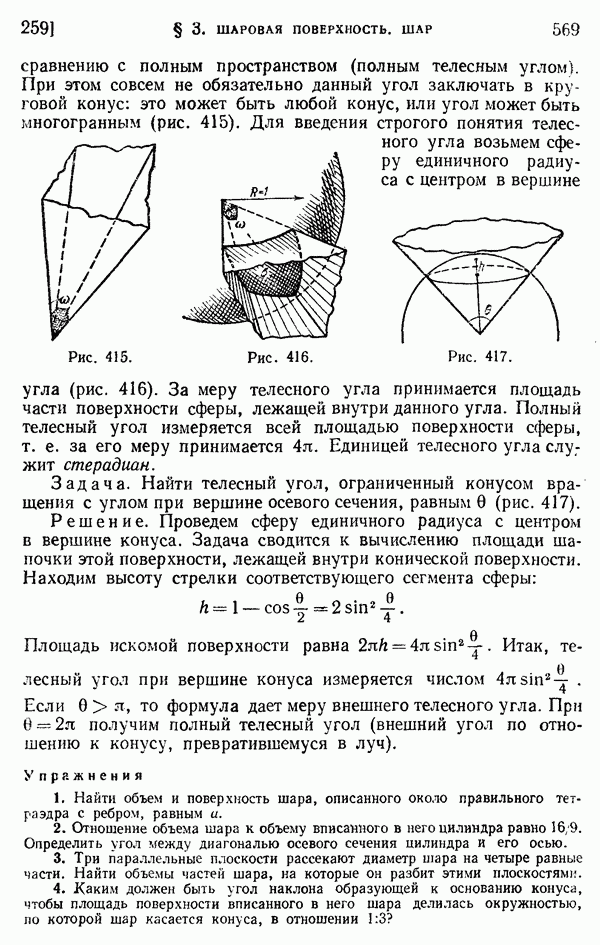
- 259. Понятие телесного угла.
- Ответы к упражнениям
- Приложения