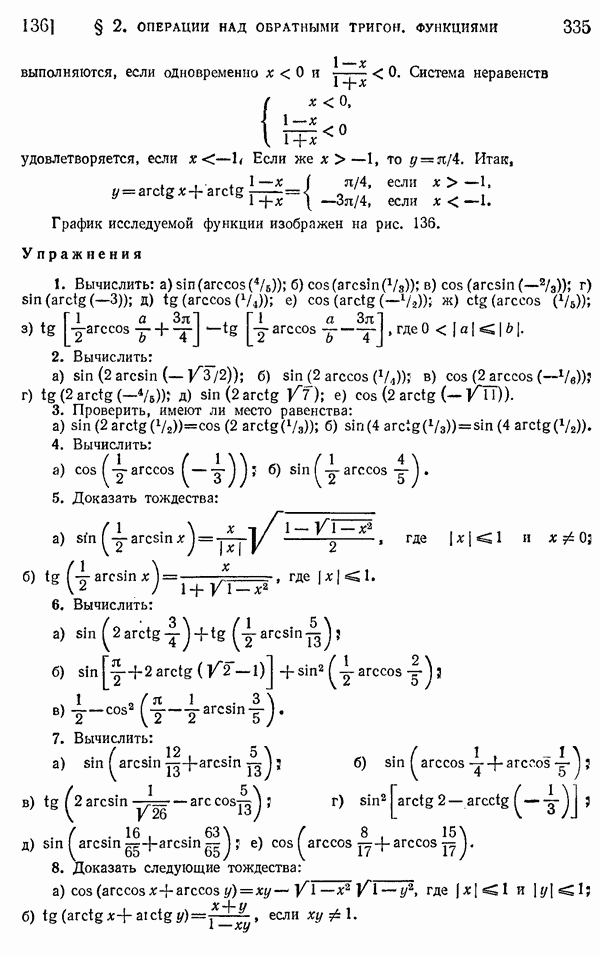| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
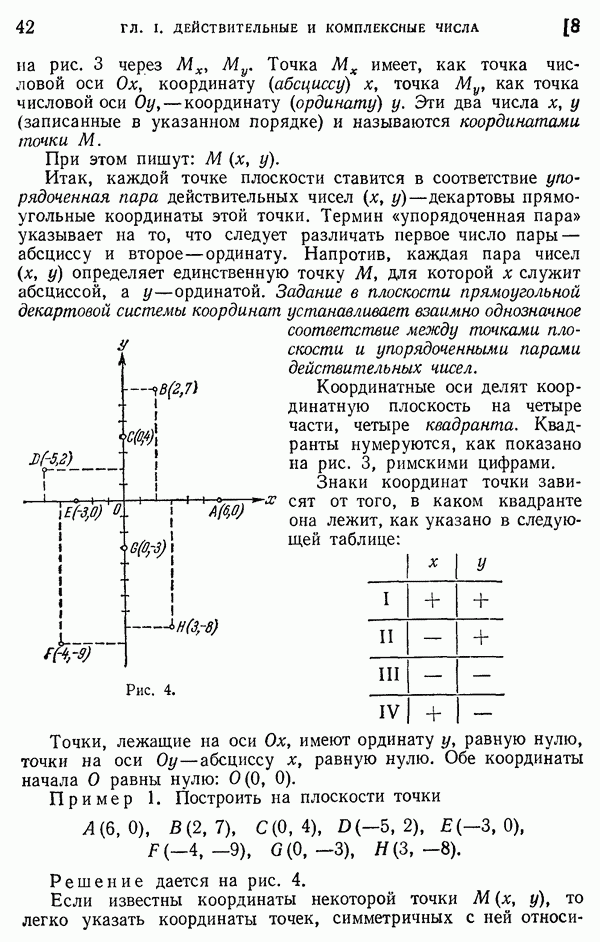
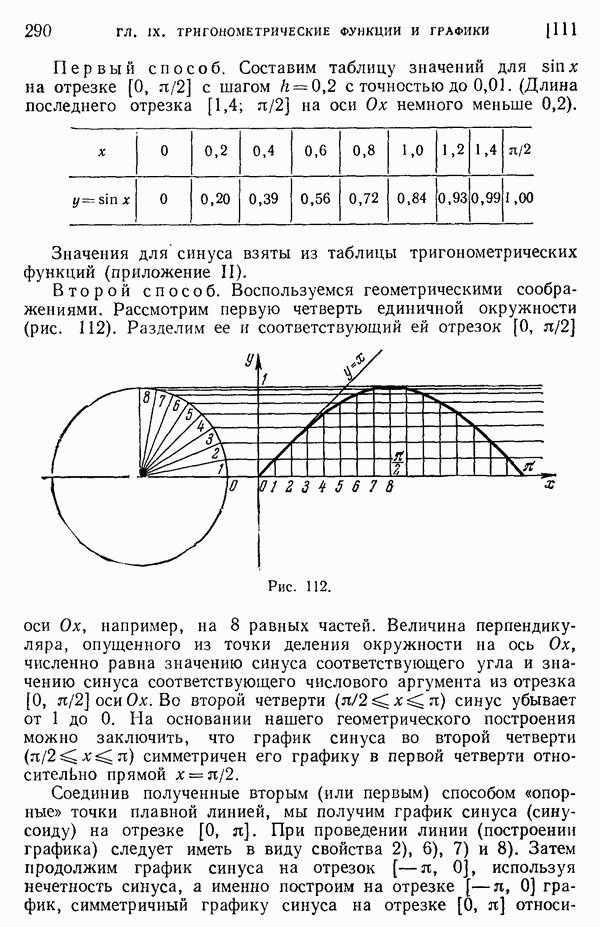
94. Положительные углы и дуги, меньшие 360°.
На координатной плоскости  рассмотрим окружность радиуса R с центром в начале координат (рис. 79).
рассмотрим окружность радиуса R с центром в начале координат (рис. 79).

Рис. 79.
Будем считать, что угол  образован вращением некоторого подвижного радиуса-вектора, абсолютная величина которого равна R, в направлении, противоположном движению часовой стрелки, от начального положения ОА, совпадающего с положительным направлением оси
образован вращением некоторого подвижного радиуса-вектора, абсолютная величина которого равна R, в направлении, противоположном движению часовой стрелки, от начального положения ОА, совпадающего с положительным направлением оси  до конечного положения ОЕ. Такой угол а считается положительным. При вращении (в направлении против движения часовой стрелки) подвижный радиус-вектор описывает углы от 0° до 360° (определение градуса см. в п. 165). Осями координат круг на рис. 79 делится на четыре четверти: первая четверть АОВ, вторая ВОС, третья COD и четвертая DOA. Если сторона ОЕ угла АОЕ расположена в первой, второй, третьей или четвертой четверти, то угол АОЕ будем называть соответственно углом первой, второй, третьей или четвертой четверти. В первой четверти угол а изменяется в пределах от 0° да 90° (0° < а < 90°), во второй — от 90° до 180°
до конечного положения ОЕ. Такой угол а считается положительным. При вращении (в направлении против движения часовой стрелки) подвижный радиус-вектор описывает углы от 0° до 360° (определение градуса см. в п. 165). Осями координат круг на рис. 79 делится на четыре четверти: первая четверть АОВ, вторая ВОС, третья COD и четвертая DOA. Если сторона ОЕ угла АОЕ расположена в первой, второй, третьей или четвертой четверти, то угол АОЕ будем называть соответственно углом первой, второй, третьей или четвертой четверти. В первой четверти угол а изменяется в пределах от 0° да 90° (0° < а < 90°), во второй — от 90° до 180°  , в третьей — от 180° до 270°
, в третьей — от 180° до 270°  , в четвертой — от 270° до 360° (270° < а < 360°).
, в четвертой — от 270° до 360° (270° < а < 360°).
Если подвижный радиус-вектор описал угол АОЕ, равный а угловым градусам, то его конец описал дугу окружности АЕ, равную а дуговым градусам. Начало этой дуги находится в точке А, а конец — в точке Е. Все сказанное выше об углах относится и к дугам.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
- 2. Простые и составные числа. Признаки делимости.
- 3. Наибольший общий делитель и наименьшее общее кратное.
- 4. Целые числа. Рациональные числа.
- 5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
- 6. Иррациональные числа. Действительные числа.
- 7. Действия с приближенными числами.
- 8. Числовая ось. Координаты точки на плоскости.
- § 2. Степени и корни
- 9. Степени с натуральными показателями.
- 10. Степени с целыми показателями.
- 11. Корни.
- 12. Степени с рациональными показателями. Степени с действительными показателями.
- 13. Алгоритм извлечения квадратного корня.
- § 3. Комплексные числа
- 14. Основные понятия и определения.
- 15. Рациональные действия с комплексными числами.
- 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
- 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
- 18. Извлечение корня из комплексного числа.
- Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
- 19. Алгебраические выражения. Одночлены и многочлены.
- 20. Формулы сокращенного умножения.
- 21. Бином Ньютона.
- 22. Разложение многочлена на множители.
- 23. Дробные алгебраические выражения.
- § 2. Иррациональные алгебраические выражения
- 24. Радикалы из алгебраических выражений.
- 25. Освобождение от иррациональности в знаменателе дроби.
- Глава III. ЛОГАРИФМЫ
- 26. Определение и свойства логарифмов.
- 27. Логарифмы по различным основаниям. Модуль перехода.
- § 2. Десятичные логарифмы
- 28. Характеристика и мантисса десятичного логарифма.
- 29. Применение десятичных логарифмов к вычислениям.
- Глава IV. ФУНКЦИИ И ГРАФИКИ
- 30. Величина. Числовые множества.
- 31. Определение функции.
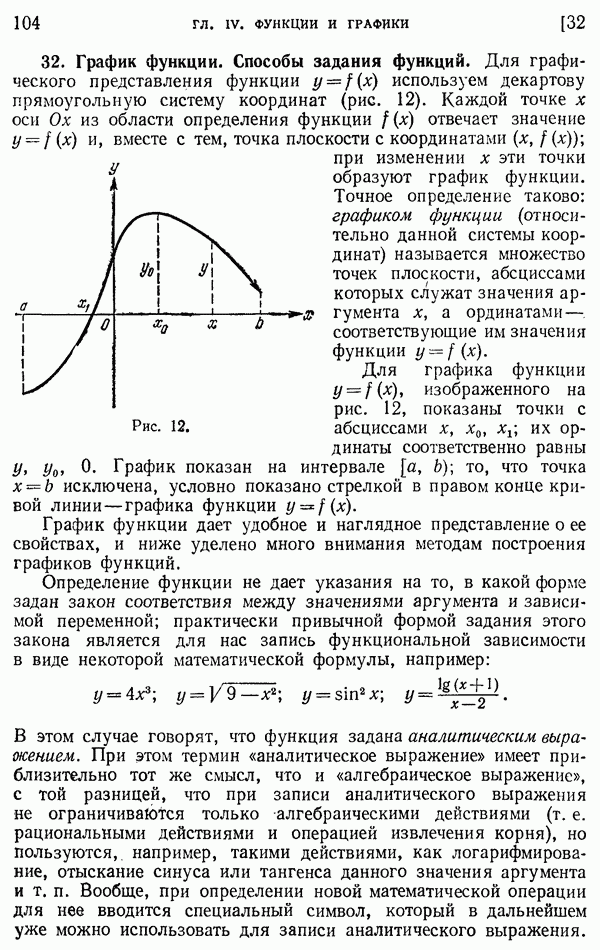
- 32. График функции. Способы задания функций.
- 33. Элементарное исследование поведения функции.
- 34. Сложная функция.
- 35. Обратная функция.
- 36. Функции нескольких переменных.
- § 2. Элементарные функции
- 37. Обзор элементарных функций.
- 38. Линейная функция.
- 39. Квадратичная функция у=ах^2.
- 40. Степенная функция у = х^n.
- 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
- 42. Показательная функция.
- 43. Логарифмическая функция.
- § 3. Преобразование графиков
- 44. Параллельный сдвиг графика.
- 45. График квадратного трех члена.
- 46. График дробно-линейной функции.
- 47. Преобразование симметрии. Сжатие и растяжение графика.
- 48. Построение графиков функций.
- 49. Сложение графиков.
- § 4. Некоторые сведения о рациональных функциях
- 50. Целые и дробные рациональные функции. Деление многочленов.
- 51. Схема Горнера. Теорема Безу.
- 52. Нули многочлена. Разложение многочлена на множители.
- Глава V. УРАВНЕНИЯ
- 53. Уравнение. Корни уравнения.
- 54. Равносильные уравнения.
- 55. Системы уравнений.
- 56. Графическое решение уравнений.
- §. 2. Алгебраические уравнения с одной неизвестной
- 57. Число и кратность корней.
- 58. Уравнения первой степени (линейные уравнения).
- 59. Уравнения второй степени (квадратные уравнения).
- 60. Формулы Виета. Разложение квадратного трехчлена на множители.
- 61. Исследование квадратного уравнения.
- 62. Уравнения высших степеней. Целые корни.
- 63. Двучленные уравнения.
- 64. Уравнения, сводящиеся к квадратным.
- 65. Возвратные уравнения.
- § 3. Системы алгебраических уравнений
- 66. Линейные системы.
- 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
- 68. Системы, состоящие из уравнения второй степени и линейного уравнения.
- 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
- § 4. Иррациональные, показательные и логарифмические уравнения
- 70. Иррациональные уравнения.
- 71. Показательные уравнения.
- 72. Логарифмические уравнения.
- 73. Разные уравнения. Системы уравнений.
- Глава VI. НЕРАВЕНСТВА
- 74. Свойства неравенств. Действия над неравенствами.
- 75. Алгебраические неравенства.
- § 2. Решение неравенств
- 76. Множество решений неравенства. Равносильные неравенства.
- 77. Графическое решение неравенств.
- 79. Квадратные неравенства.
- 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
- 81. Иррациональные, показательные и логарифмические неравенства.
- 82. Неравенства с двумя неизвестными.
- Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
- 83. Числовая последовательность.
- 84. Предел числовой последовательности.
- 85. Бесконечно малые. Правила предельного перехода.
- § 2. Арифметическая прогрессия
- 86. Арифметическая прогрессия. Формула общего члена.
- 87. Свойства арифметической прогрессии.
- 88. Формула для суммы n членов арифметической прогрессии.
- § 3. Геометрическая прогрессия
- 89. Геометрическая прогрессия. Формула общего члена.
- 90. Свойства геометрической прогрессии.
- 91. Формулы для суммы n членов геометрической прогрессии.
- 92. Бесконечно убывающая геометрическая прогрессия.
- Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
- 93. Вектор, проекция вектора.
- 94. Положительные углы и дуги, меньшие 360°.
- 95. Углы и дуги, большие 360°.
- 96. Отрицательные углы. Сложение и вычитание углов.
- § 2. Тригонометрические функции произвольного угла
- 97. Определение основных тригонометрических функций.
- 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
- § 3. Соотношения между тригонометрическими функциями одного и того же угла
- 99. Основные тригонометрические тождества.
- 100. Вычисление значений тригонометрических функций по значению одной из них.
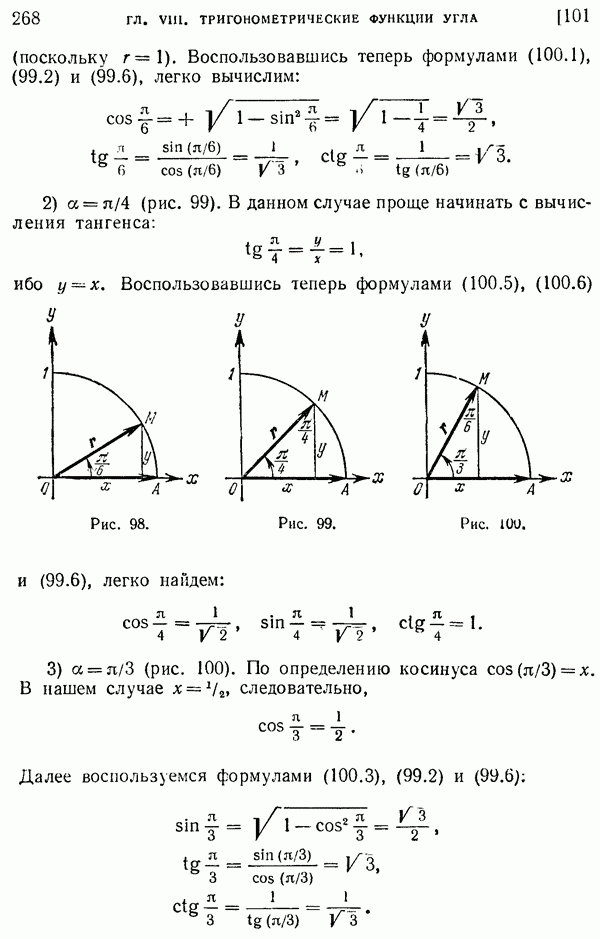
- 101. Значения тригонометрических функций некоторых углов.
- § 4. Четность, нечетность и периодичность тригонометрических функций
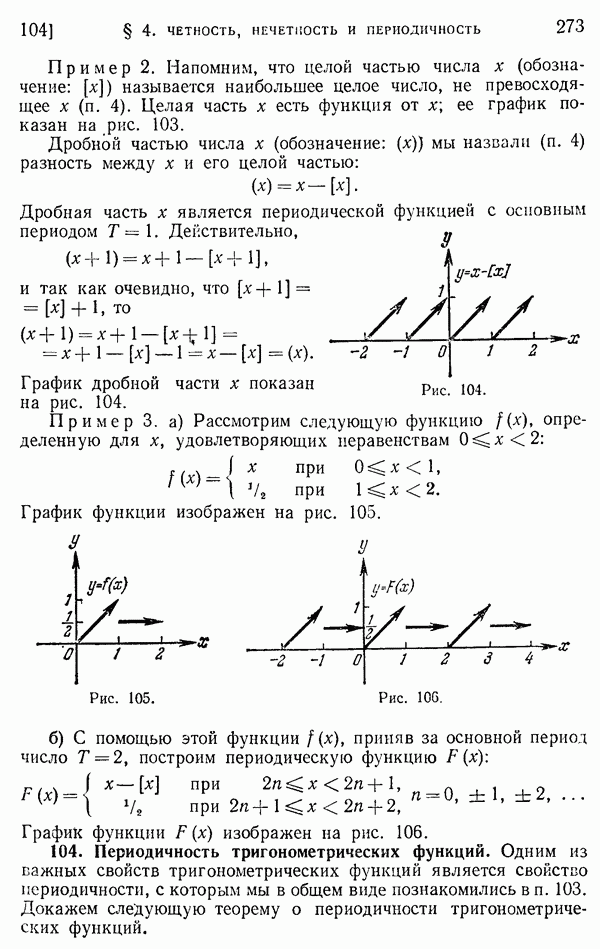
- 102. Четность и нечетность.
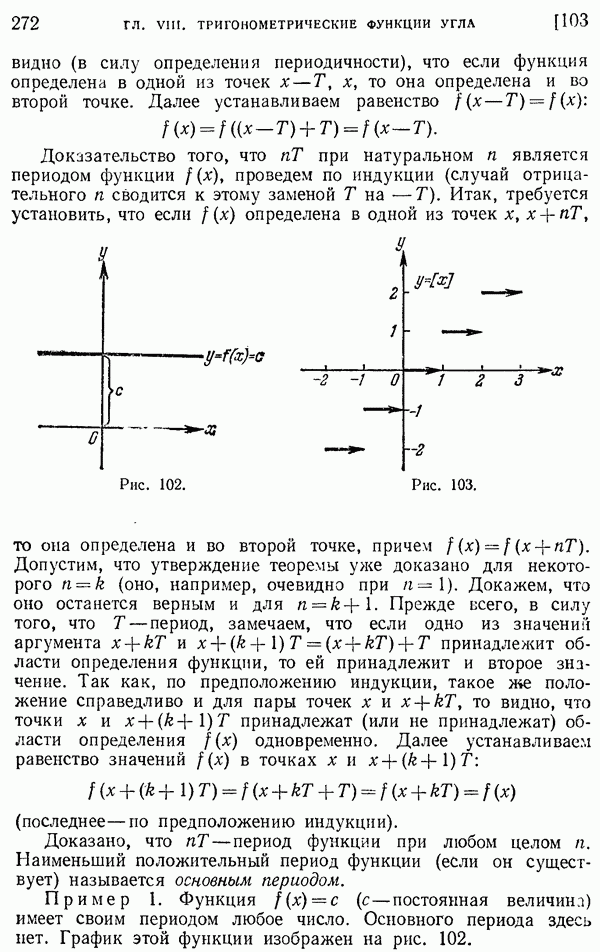
- 103. Понятие периодической функции.
- 104. Периодичность тригонометрических функций.
- § 5. Формулы приведения
- 105. Зависимость между тригонометрическими функциями дополнительных углов.
- 106. Формулы приведения.
- Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
- § 1. Тригонометрические функции числового аргумента
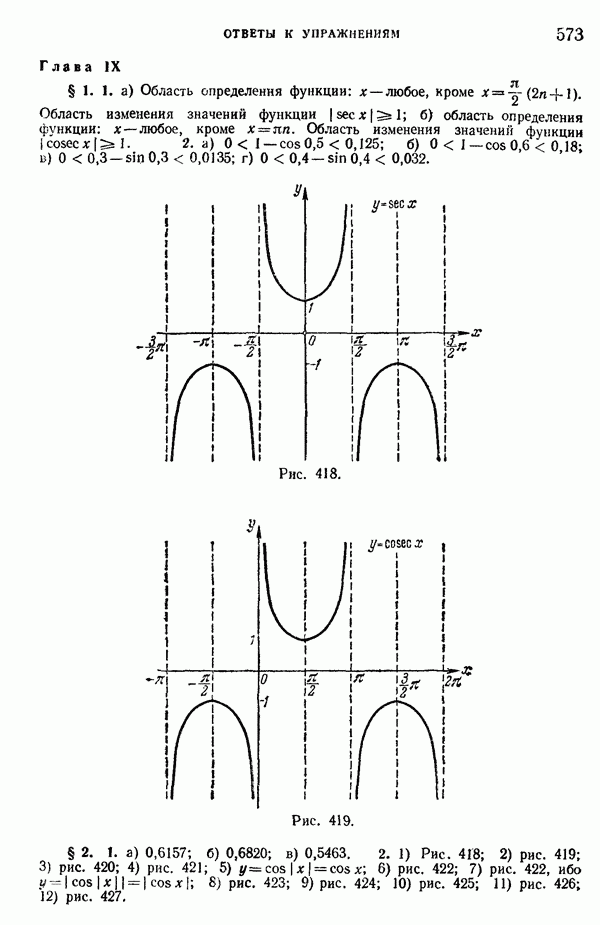
- 108. Области определения и области изменения значений тригонометрических функций.
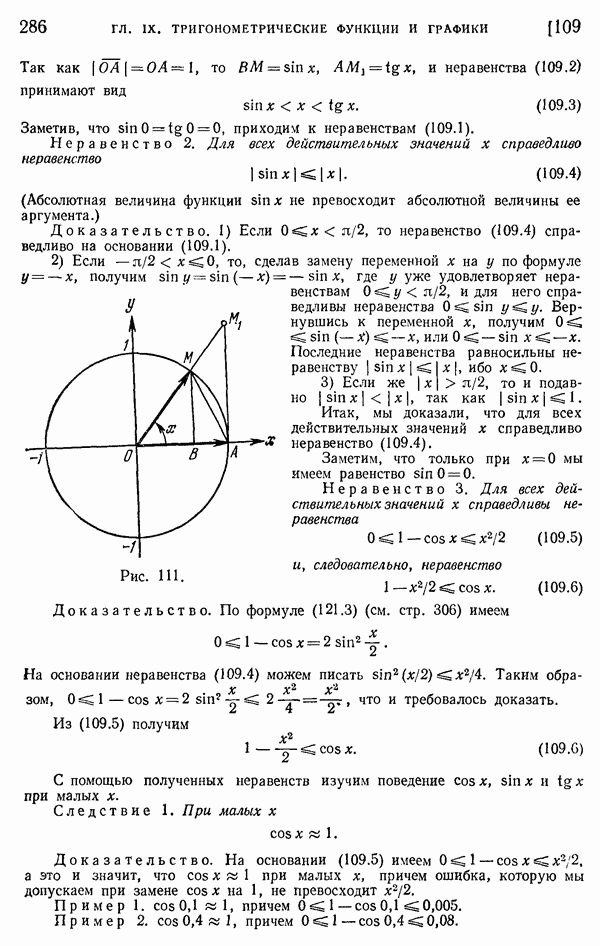
- 109. Некоторые неравенства и их следствия.
- § 2. Графики тригонометрических функций
- 110. Первоначальные сведения о таблицах тригонометрических функций.
- 111. Основные графики.
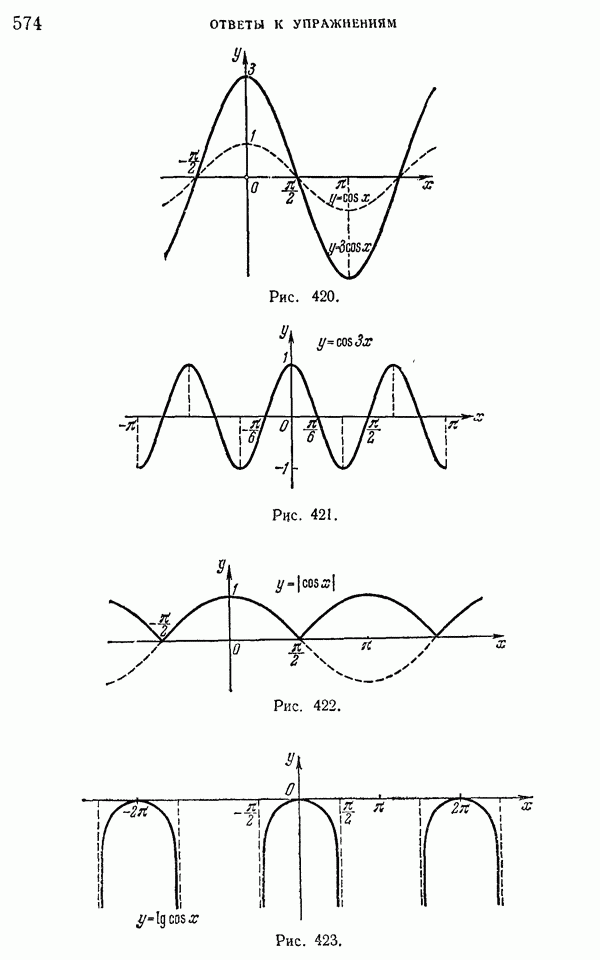
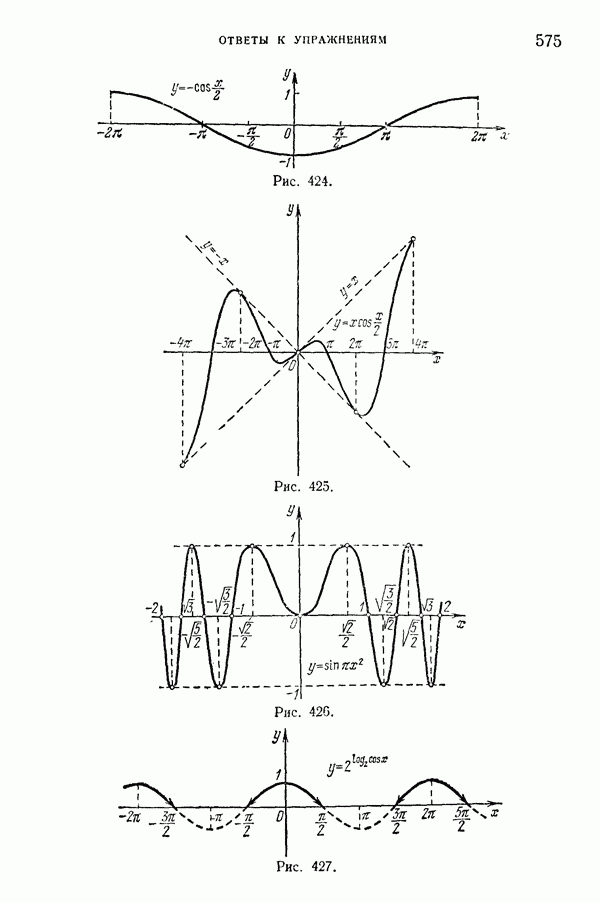
- 112. Примеры построения графиков некоторых других тригонометрических функций.
- 113. Дальнейшие примеры построения графиков функций.
- Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
- 114. Расстояние между двумя точками на плоскости.
- 115. Косинус суммы и разности двух аргументов.
- 116. Синус суммы и разности двух аргументов.
- 117. Тангенс суммы и разности двух аргументов.
- 118. О формулах сложения для нескольких аргументов.
- § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
- 119. Тригонометрические функции двойного аргумента.
- 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
- 121. Тригонометрические функции половинного аргумента.
- 122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
- § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
- § 4. Преобразование в произведение сумм вида
- § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
- 127. Преобразование в произведение выражения a•sina + b•cosa.
- 128. Преобразование в произведение выражений a•sina+b и a•cosa+b
- 129. Преобразование в произведение выражения a•tga+b.
- Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
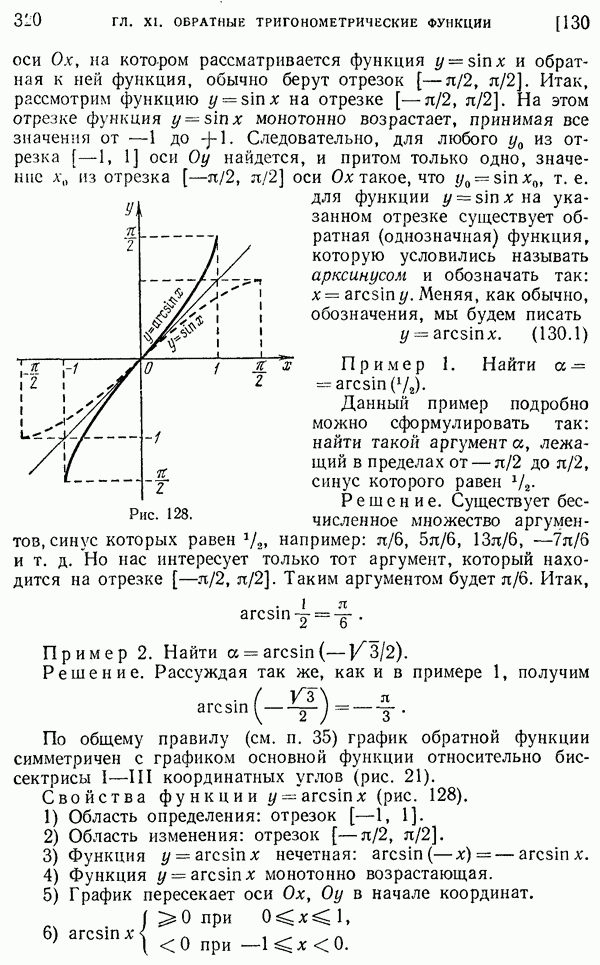
- 130. Функция у = arcsin x (арксинус).
- 131. Функция y = arccos x (арккосинус).
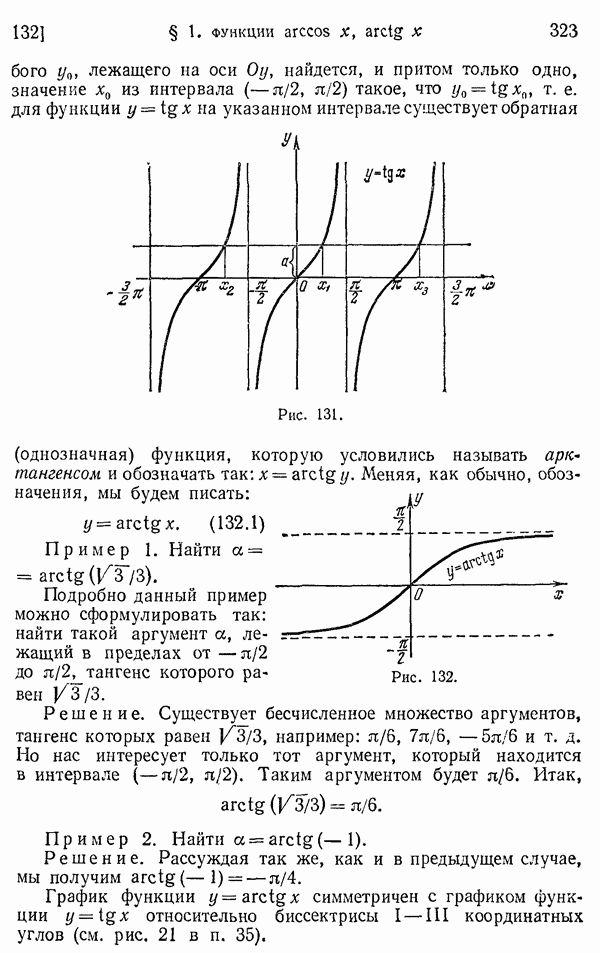
- 132. Функция y = arctg x (арктангенс).
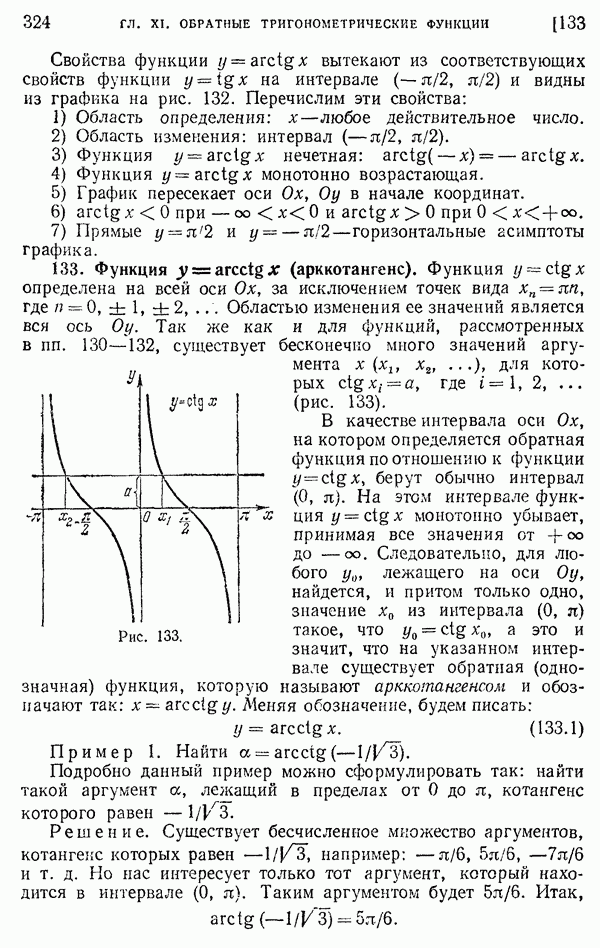
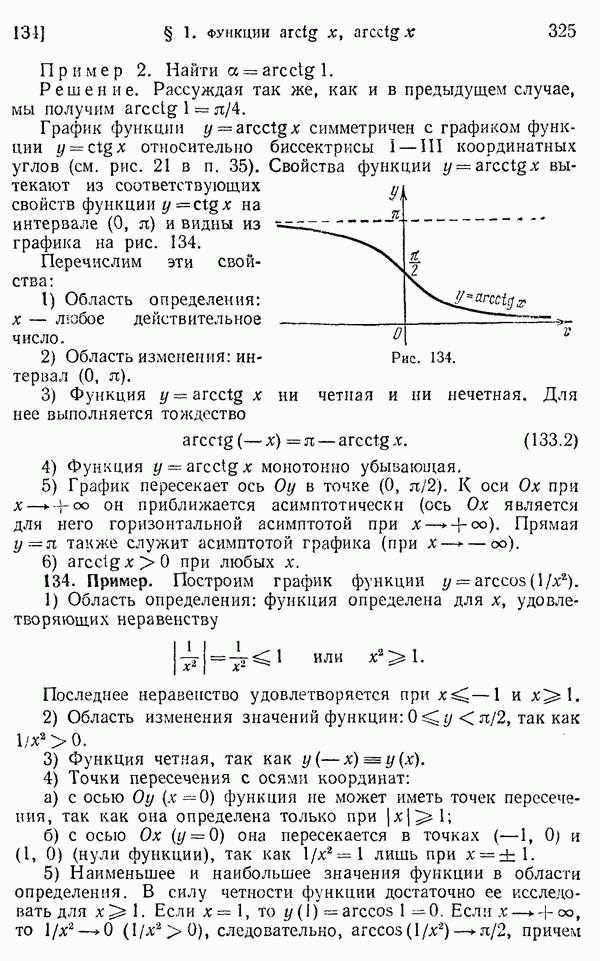
- 133. Функция y = arcctg x (арккотангенс).
- 134. Пример.
- § 2. Операции над обратными тригонометрическими функциями
- 135. Тригонометрические операции.
- 136. Операции сложения (вычитания).
- § 3. Обратные тригонометрические операции над тригонометрическими функциями
- 137. Функция у = arcsin (sin x).
- 138. Функция y = arctg (tg x).
- Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- 139. Уравнение sin х = а.
- 140. Уравнение cos х = a.
- 141. Уравнение tg x = a.
- 142. Уравнение ctg x = a.
- 143. Некоторые дополнения.
- § 2. Способ приведения к одной функции одного и того же аргумента
- 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
- 146. Способ разложения на множители.
- 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
- § 3. Некоторые частные приемы решения тригонометрических уравнений и систем
- 148. Введение вспомогательного аргумента.
- 149. Преобразование произведения в сумму или разность.
- 150. Переход к функциям удвоенного аргумента.
- 151. Решение уравнения типа…
- 152. Применение подстановок sinx ± соsx = y.
- § 4. Решение тригонометрических неравенств
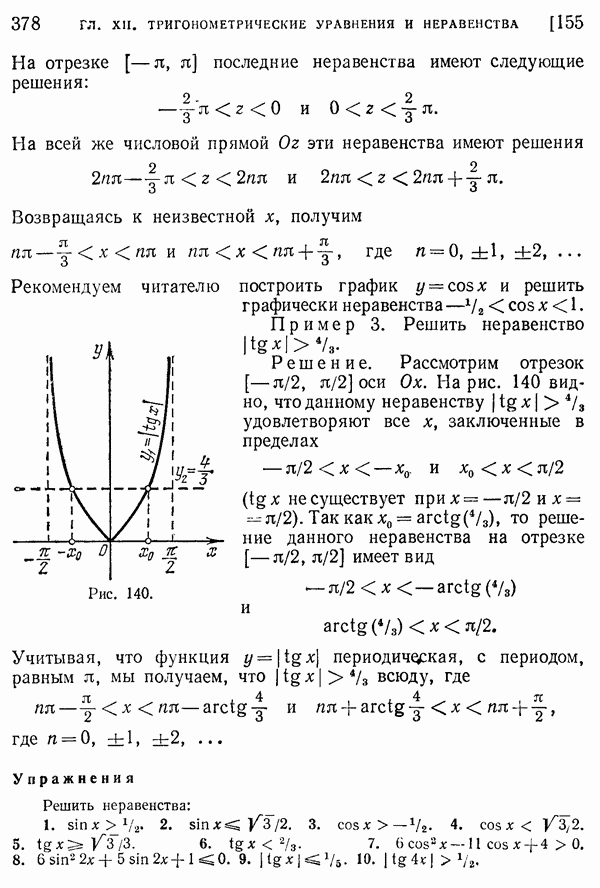
- 154. Простейшие тригонометрические неравенства.
- 155. Примеры тригонометрических неравенств, сводящихся к простейшим.
- Часть вторая. ГЕОМЕТРИЯ
- 156. Точка. Прямая. Луч. Отрезок.
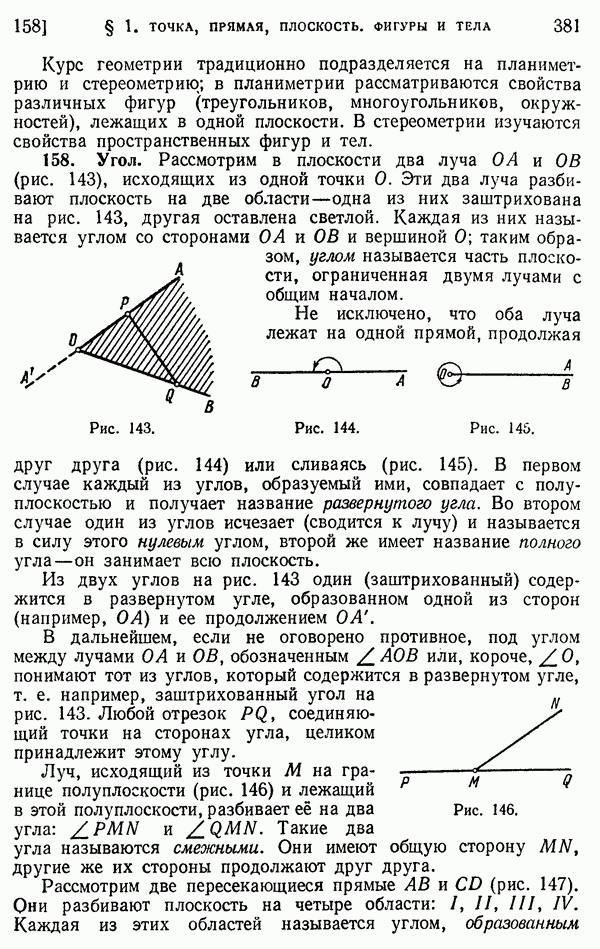
- 157. Плоскость. Фигуры и тела.
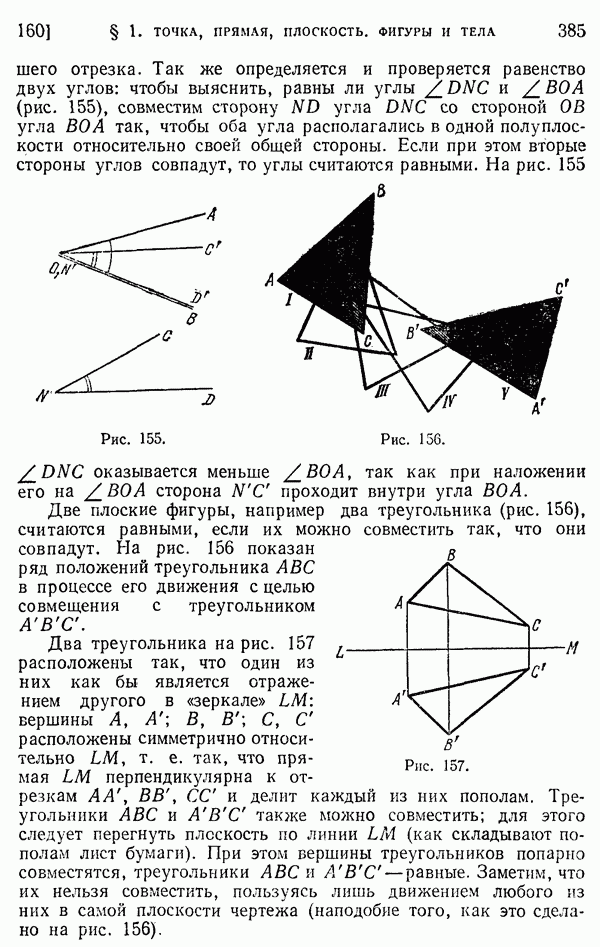
- 160. Равенство фигур. Движение.
- 161. Равенство тел.
- § 2. Измерение геометрических величин
- 162. Сложение отрезков. Длина отрезка.
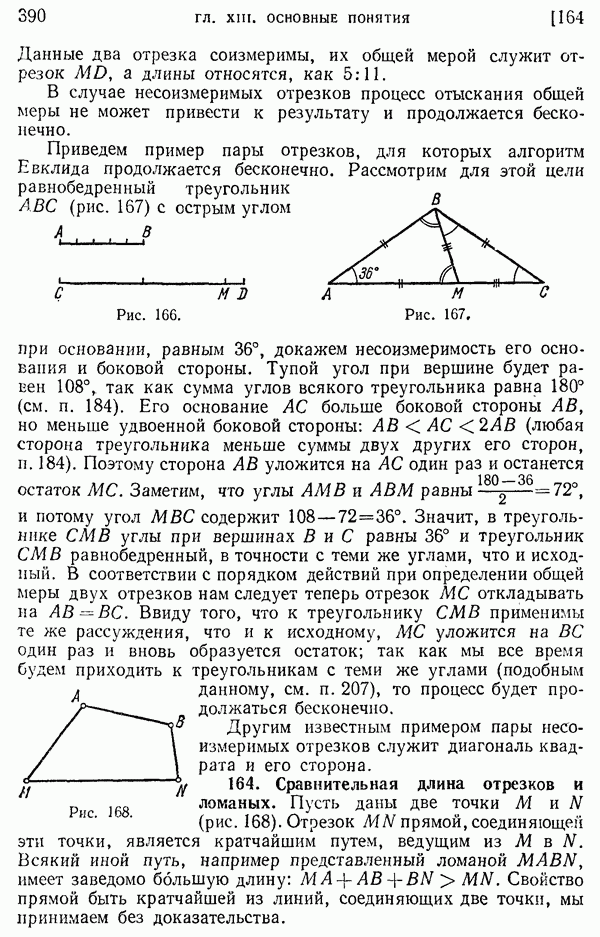
- 163. Общая мера двух отрезков.
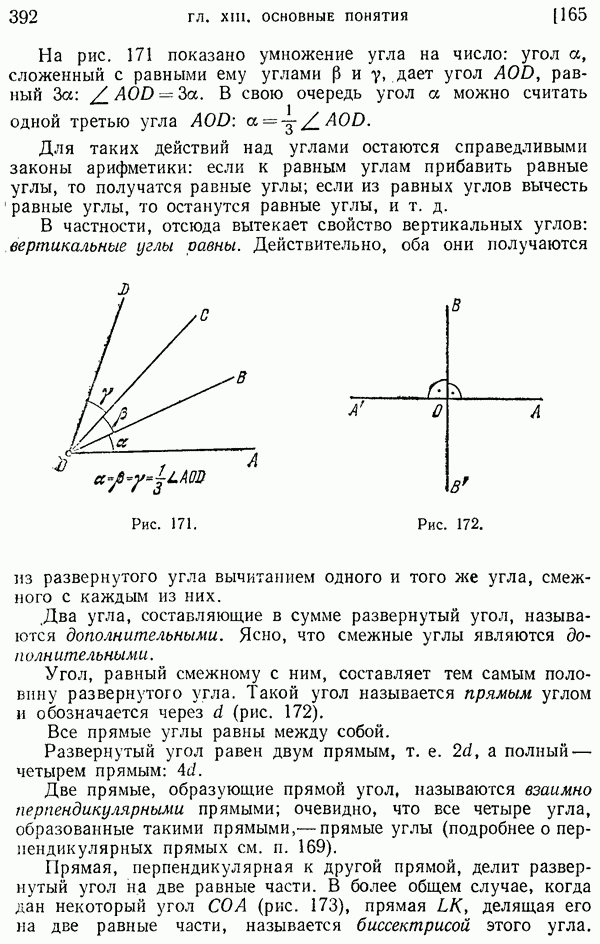
- 164. Сравнительная длина отрезков и ломаных.
- 165. Измерение углов.
- 166. Радианная мера угла.
- 167. Измерение площадей.
- 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
- Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
- 169. Перпендикуляр и наклонные.
- 170. Свойство перпендикуляра, проведенного к отрезку в его середине.
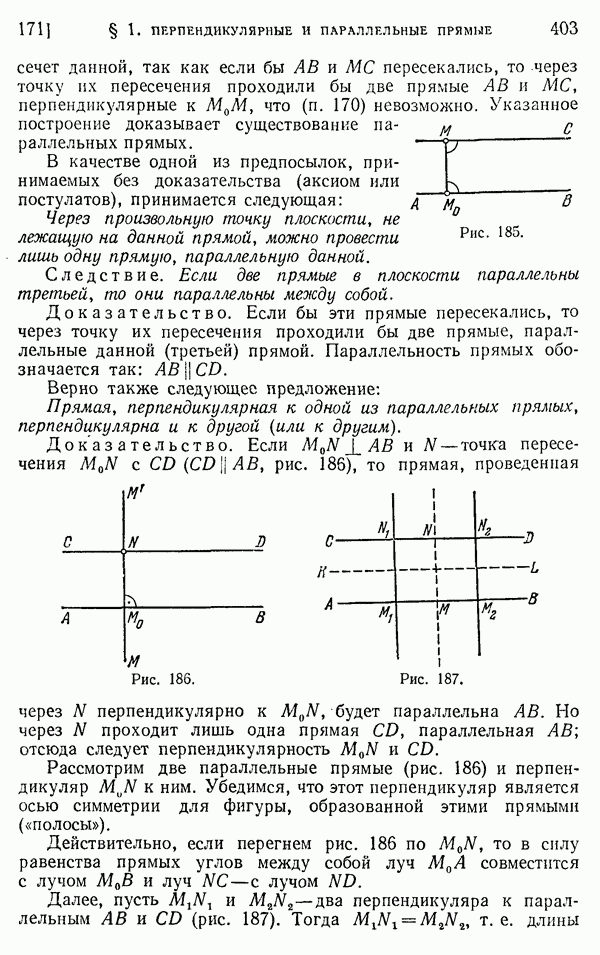
- 171. Параллельные прямые.
- 172. Углы, образованные двумя параллельными прямыми и секущей.
- 173. Углы с параллельными или перпендикулярными сторонами.
- § 2. Геометрические места точек. Окружность
- 174. Геометрическое место точек.
- 175. Свойство биссектрисы угла.
- 176. Окружность.
- 177. Взаимное расположение прямой и окружности. Касательная и секущая.
- 178. Хорда и диаметр. Сектор и сегмент.
- 179. Взаимное расположение двух окружностей.
- § 3. Основные задачи на построение
- 181. Деление отрезка пополам. Построение перпендикуляров.
- 182. Построение углов.
- 183. Другие задачи на построение.
- Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
- 184. Стороны и углы треугольника.
- 185. Биссектрисы треугольника. Вписанная окружность.
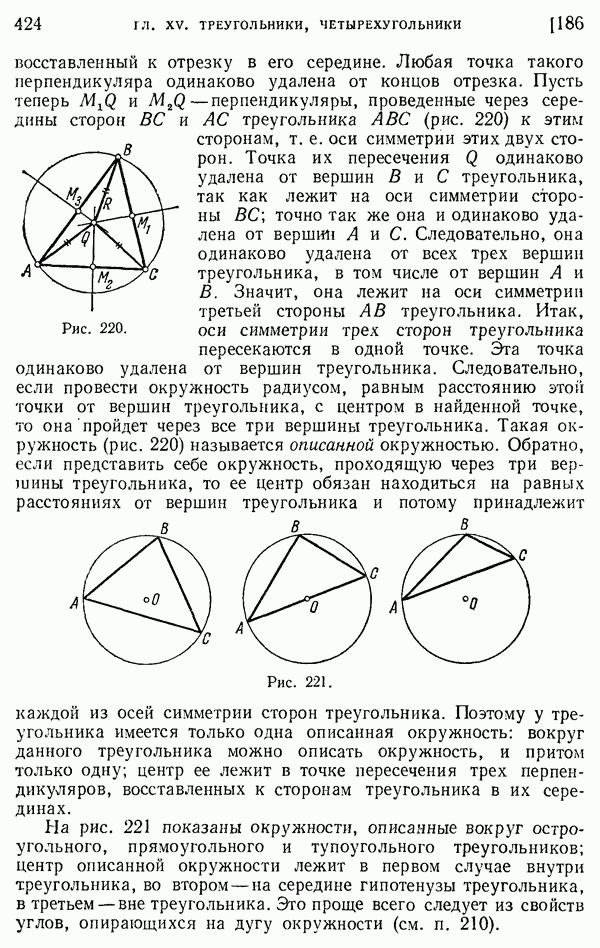
- 186. Оси симметрии сторон треугольника. Описанная окружность.
- 187. Медианы и выcоты треугольника.
- 188. Равенство треугольников.
- 189. Построение треугольников.
- 190. Равнобедренные треугольники.
- 191. Прямоугольные треугольники.
- § 2. Параллелограммы
- 192. Четырехугольники.
- 193. Параллелограмм и его свойства.
- 194. Прямоугольник.
- § 3. Трапеция
- 196. Трапеция.
- 197. Средняя линия треугольника.
- 198. Средняя линия трапеции.
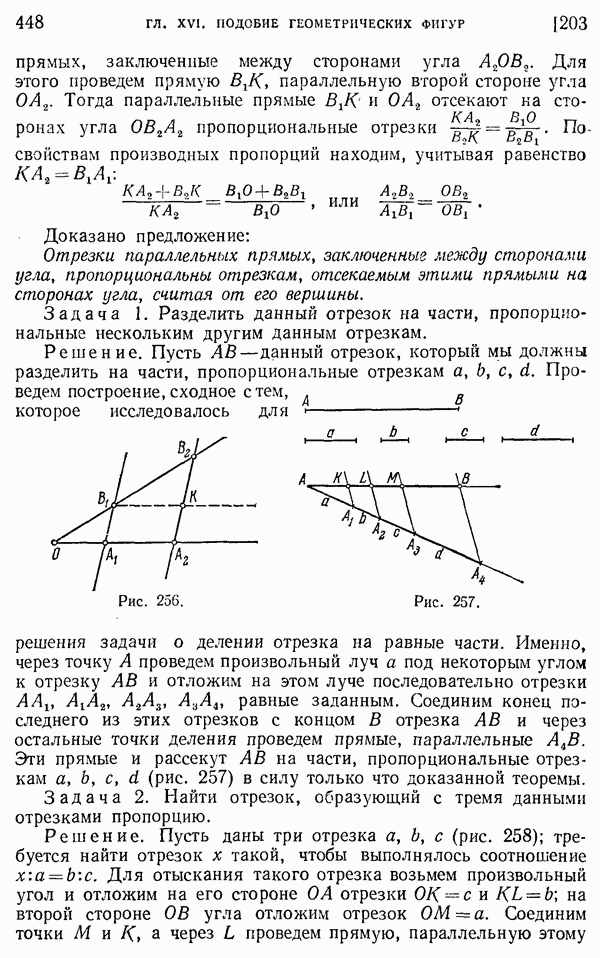
- 199. Деление отрезка на равные части.
- § 4. Площади треугольников и четырехугольников
- 200. Площадь параллелограмма.
- 201. Площадь треугольника.
- 202. Площадь трапеции.
- Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
- 203. Пропорциональные отрезки.
- 204. Свойства биссектрис внутреннего и внешнего углов треугольника.
- § 2. Подобное преобразование фигур (гомотетия)
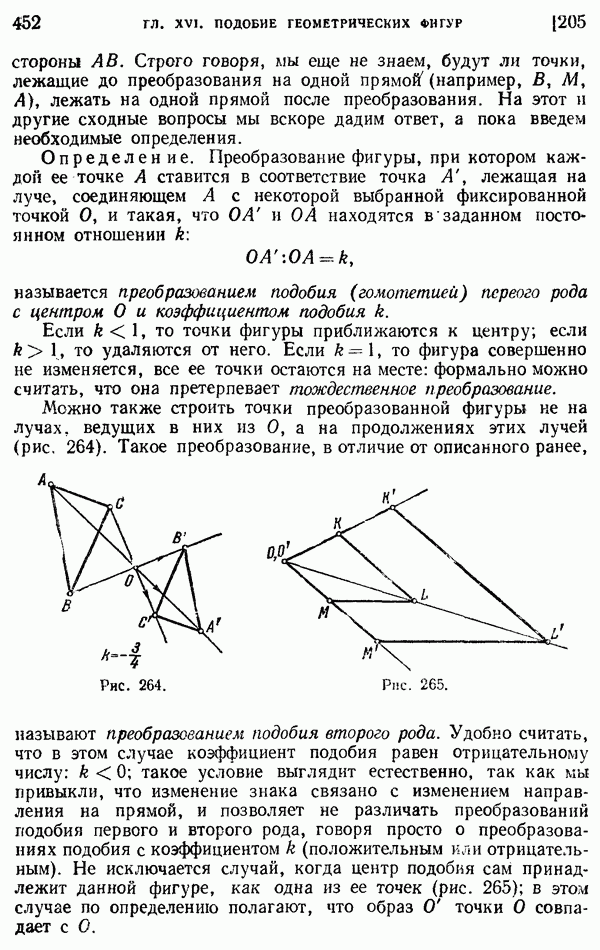
- 205. Определение гомотетичных фигур.
- 206. Свойства преобразования подобия.
- § 3. Общее подобное соответствие фигур
- 207. Подобные фигуры.
- 208. Периметры и площади подобных треугольников.
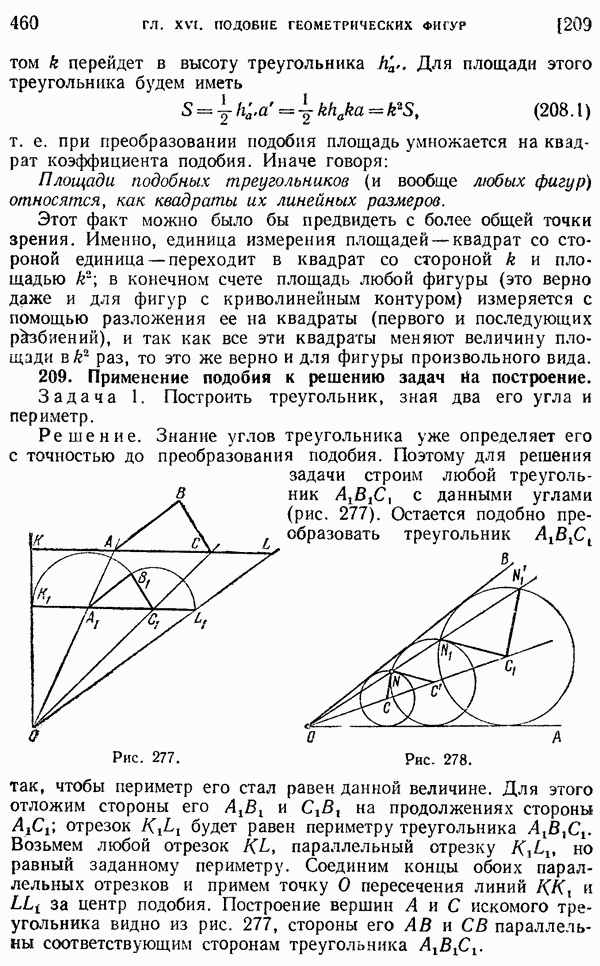
- 209. Применение подобия к решению задач на построение.
- Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
- 210. Углы с вершиной на окружности.
- 211. Углы с вершиной внутри и вне круга.
- 212. Угол, под которым виден данный отрезок.
- 213. Четырехугольники, вписанные в окружность.
- 214. Пропорциональные отрезки в круге.
- 215. Задачи на построение.
- § 2. Метрические соотношения в треугольнике
- 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора.
- 218. Теорема синусов. Формула Герона.
- 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
- 218. Теорема синусов. Формула Герона.
- 219. Радиусы вписанной и описанной окружностей.
- § 3. Решение треугольников
- 220. Таблицы функций.
- 221. Решение треугольников. Сводка основных формул.
- 222. Решение прямоугольных треугольников.
- 223. Решение косоугольных треугольников.
- Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
- 224. Выпуклые многоугольники.
- 225. Правильные многоугольники.
- 226. Соотношения между стороной, радиусом и апофемой.
- 227. Периметр и площадь правильного n-угольника.
- 228. Удвоение числа сторон правильного многоугольника.
- § 2. Длина окружности. Площадь круга и его частей
- 229. Длина окружности.
- 230. Площадь круга и его частей.
- Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- 231. Взаимное расположение двух прямых в пространстве.
- 232. Взаимное расположение прямой линии и плоскости.
- 233. Взаимное расположение двух плоскостей.
- 234. Свойства параллельных прямых и плоскостей.
- 235. Построения в стереометрии.
- § 2. Перпендикулярность прямых и плоскостей
- 236. Перпендикуляр к плоскости.
- 237. Перпендикуляр и наклонные.
- 238. Угол между прямой и плоскостью.
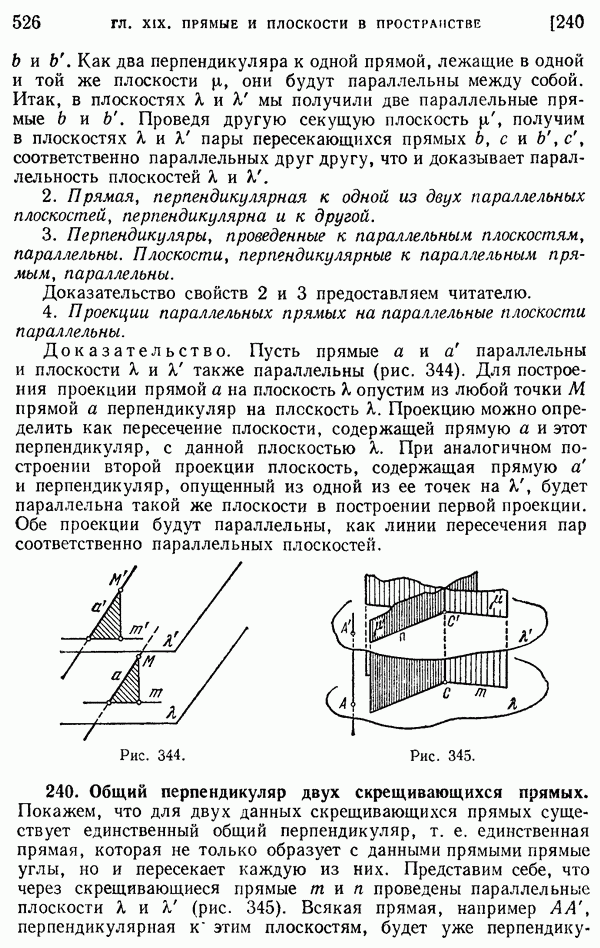
- 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
- 240. Общий перпендикуляр двух скрещивающихся прямых.
- § 3. Двугранные и многогранные углы
- 241. Двугранный угол.
- 242. Взаимно перпендикулярные плоскости.
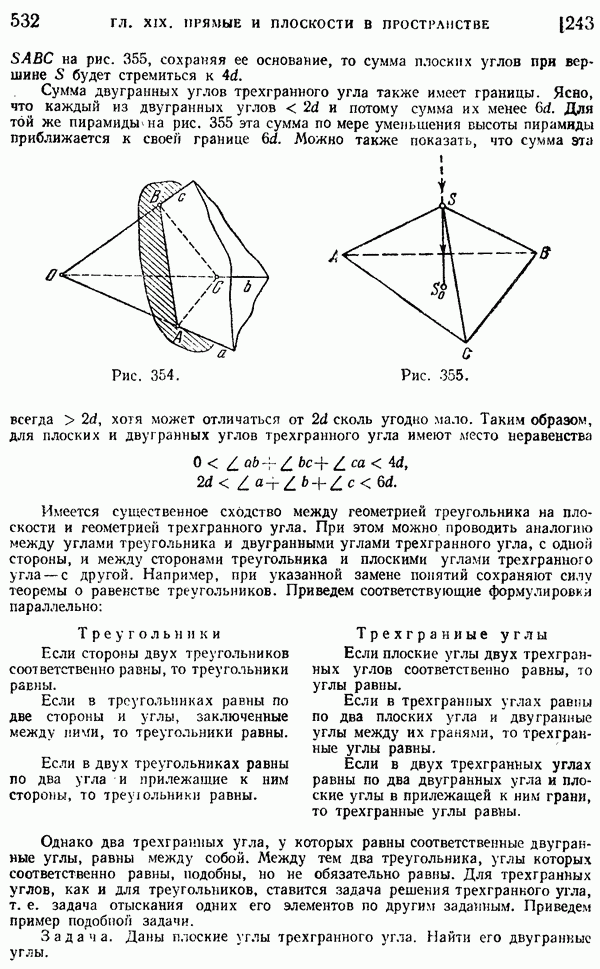
- 243. Трехгранные углы.
- 244. Многогранные углы.
- § 4. Многогранники
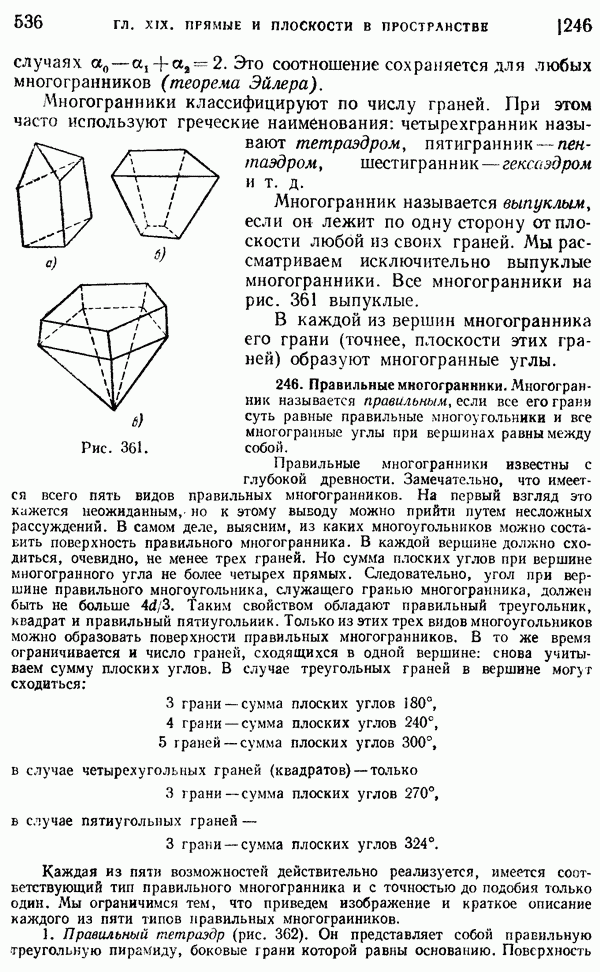
- 245. Многогранники.
- 246. Правильные многогранники.
- Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
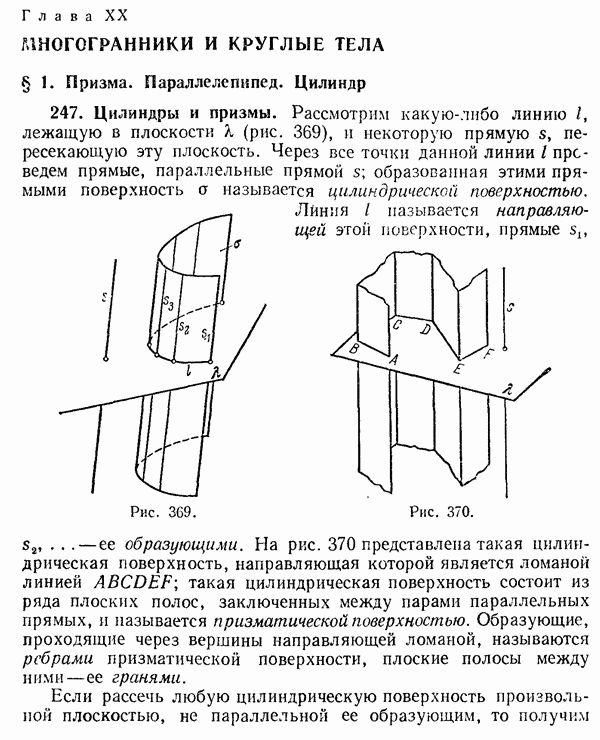
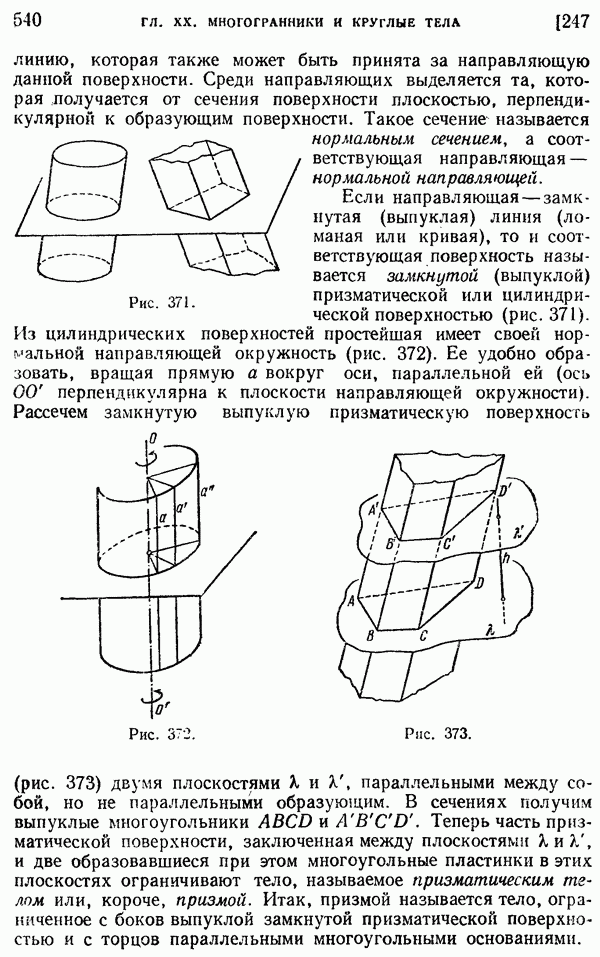
- 247. Цилиндры и призмы.
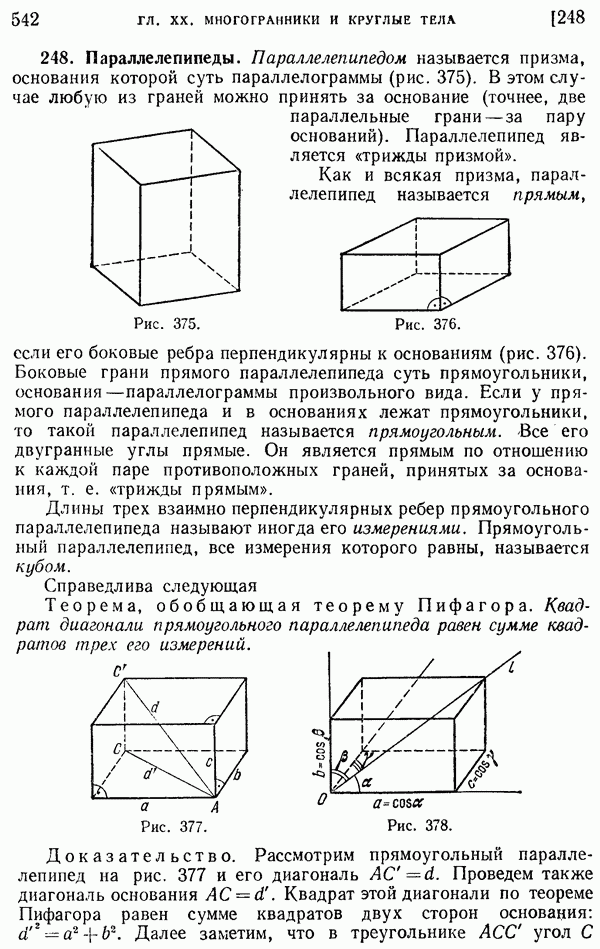
- 248. Параллелепипеды.
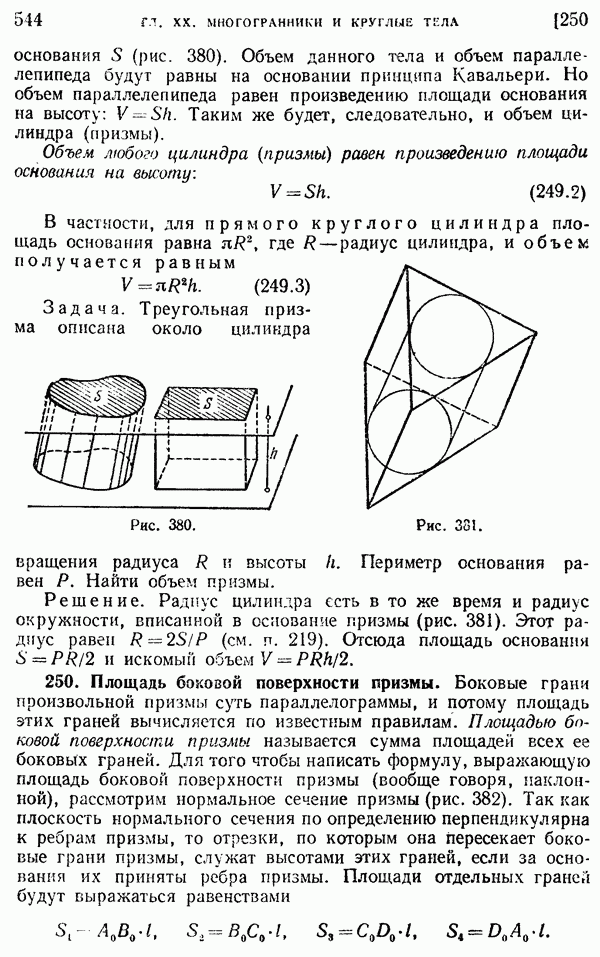
- 249. Объемы призм и цилиндров.
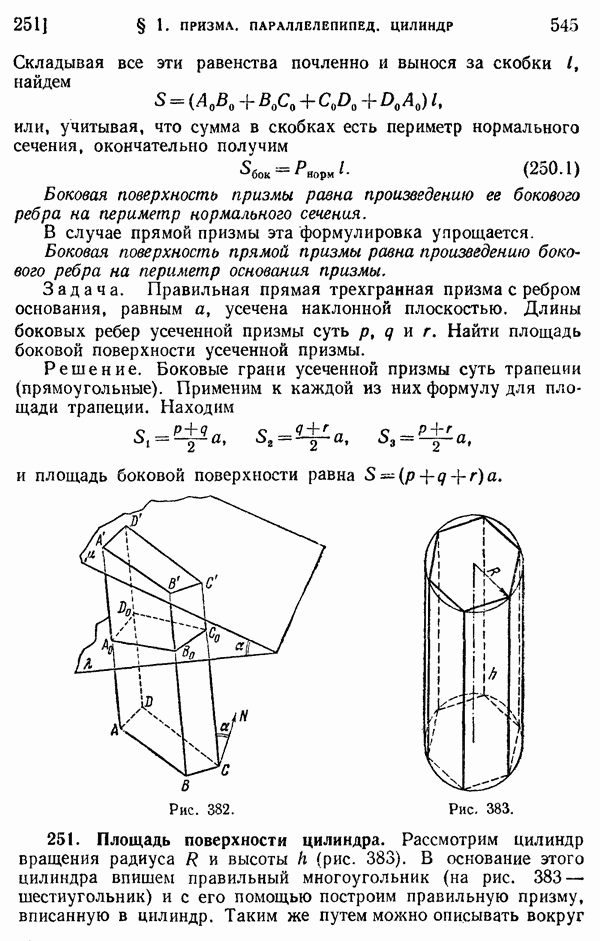
- 250. Площадь боковой поверхности призмы.
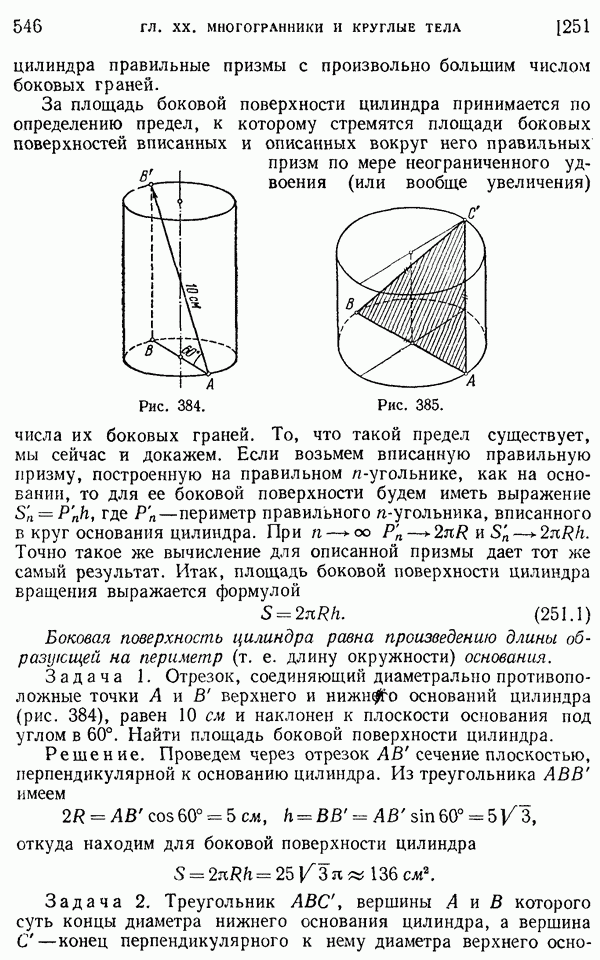
- 251. Площадь поверхности цилиндра.
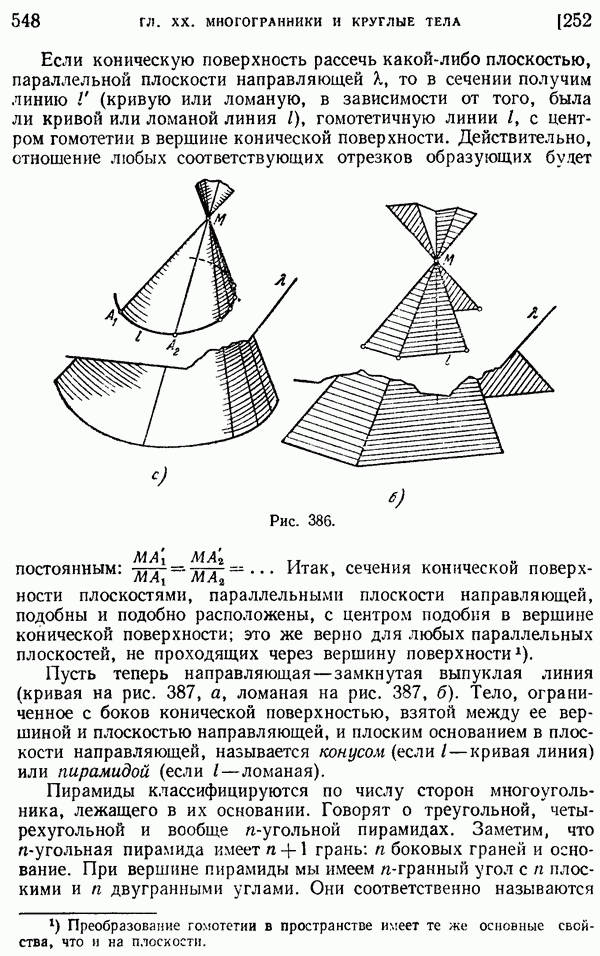
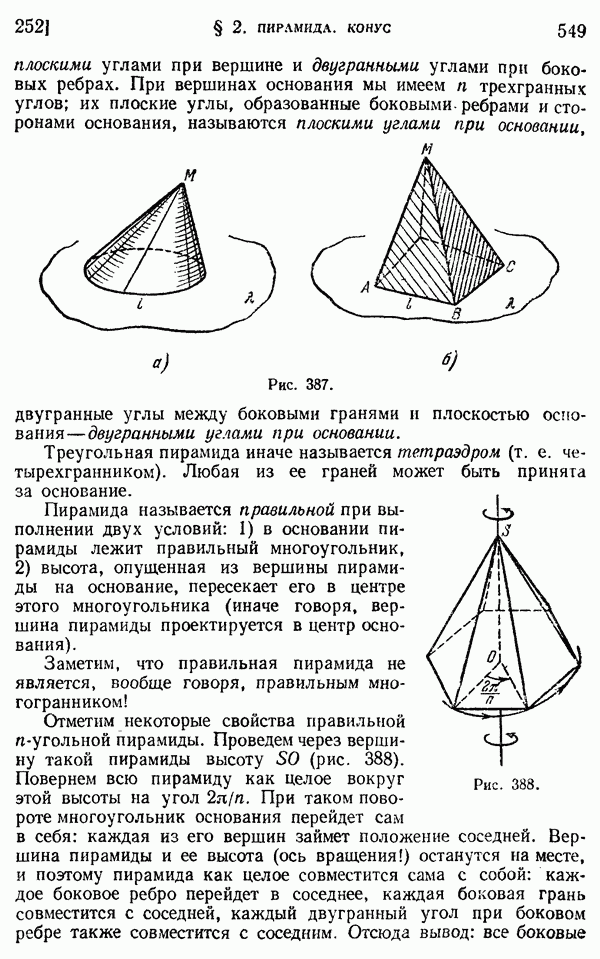
- § 2. Пирамида. Конус
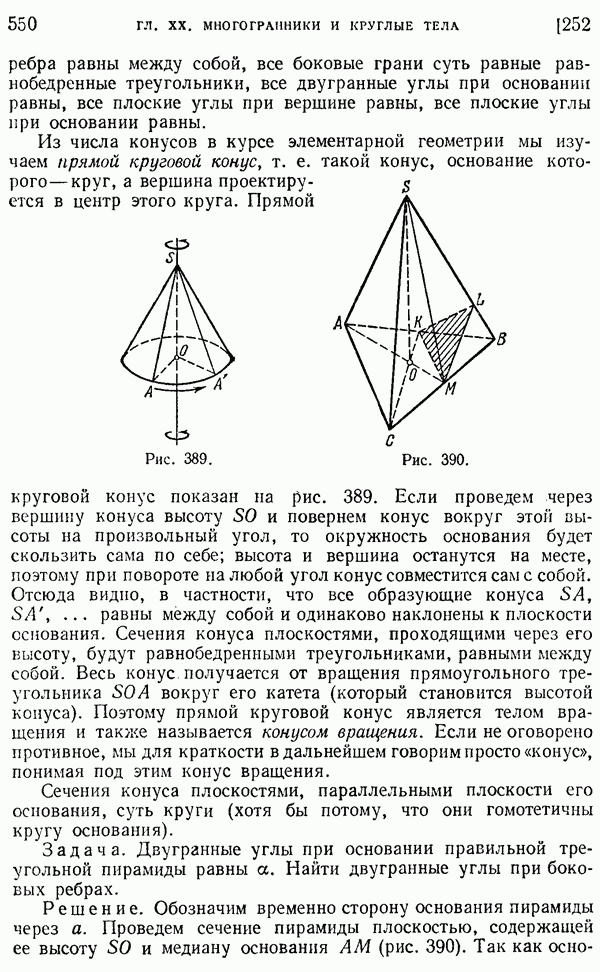
- 252. Свойства пирамиды и конуса.
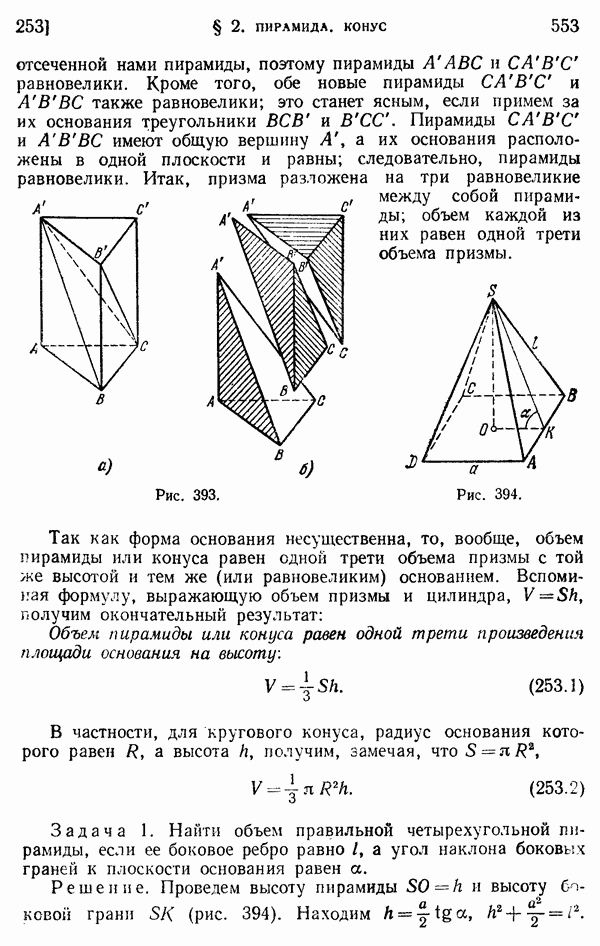
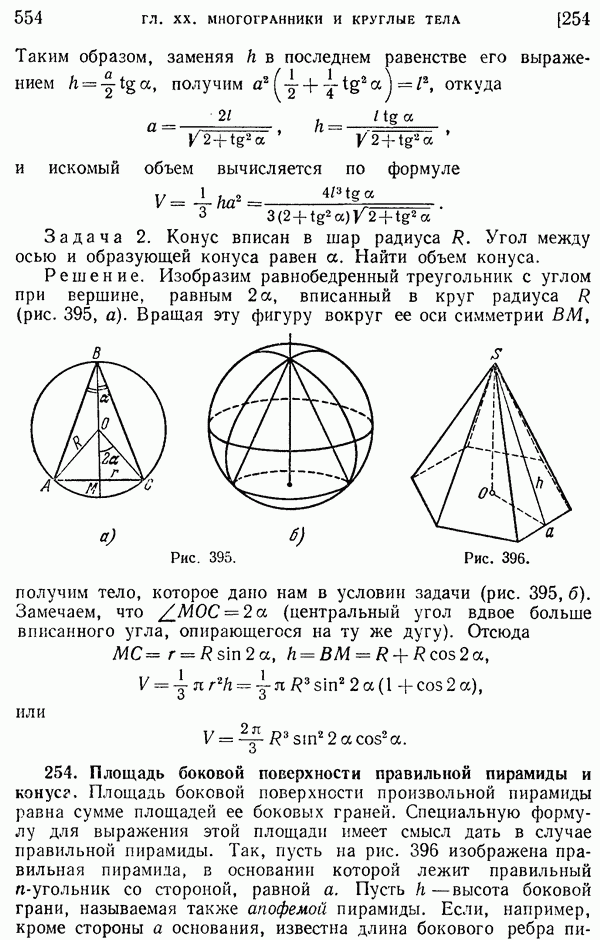
- 253. Объем пирамиды и конуса.
- 254. Площадь боковой поверхности правильной пирамиды и конуса.
- 255. Усеченный конус и усеченная пирамида.
- § 3. Шаровая поверхность. Шар
- 256. Шар и шаровая поверхность.
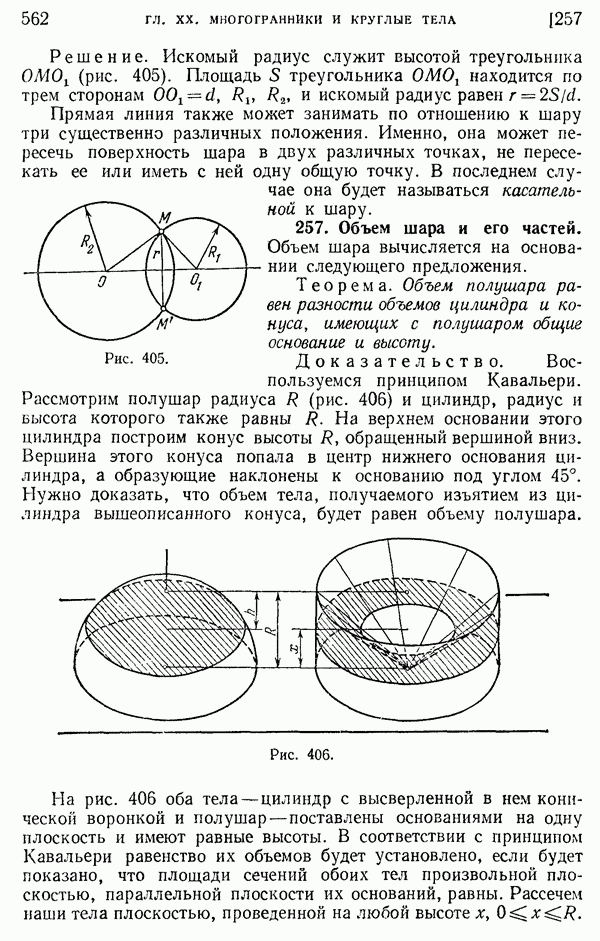
- 257. Объем шара и его частей.
- 258. Площадь поверхности шара и ее частей.
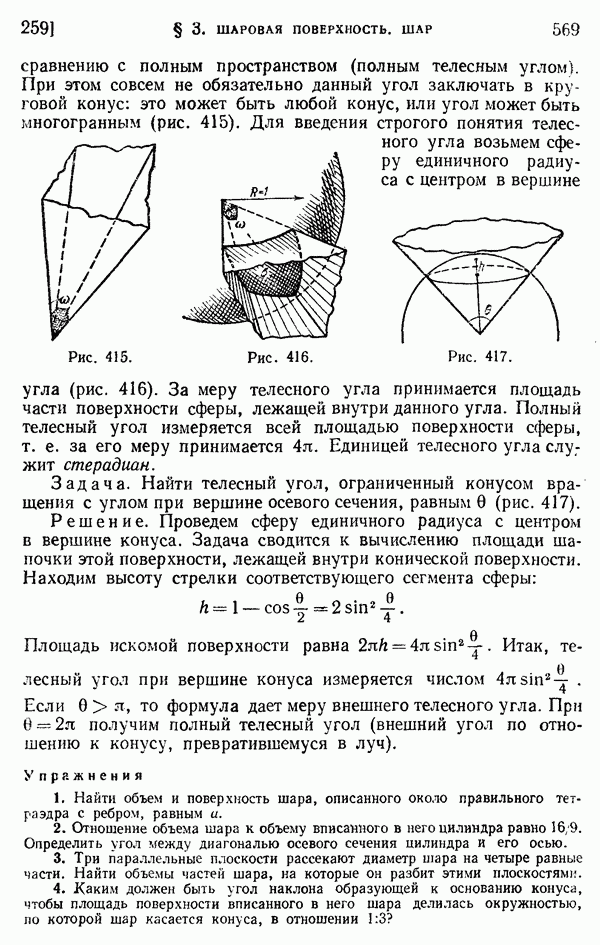
- 259. Понятие телесного угла.
- Ответы к упражнениям
- Приложения