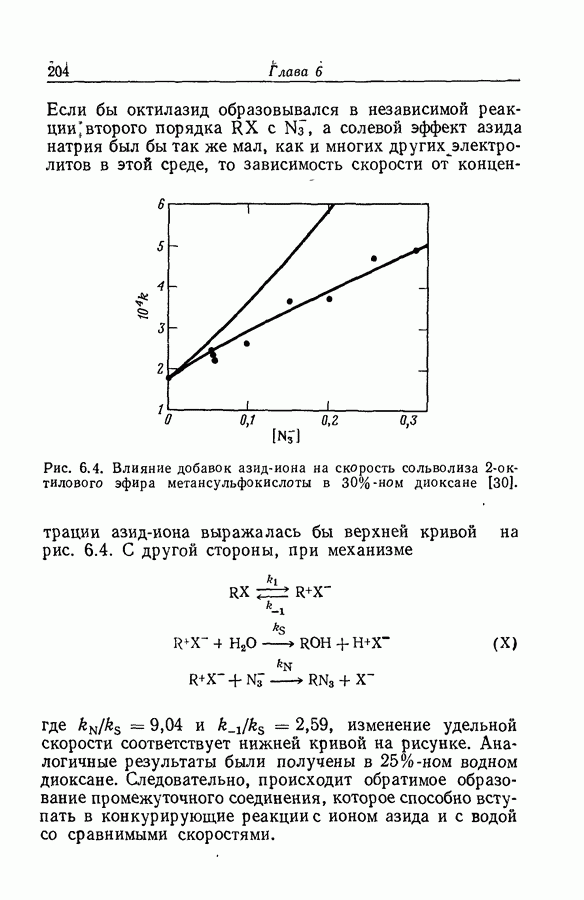
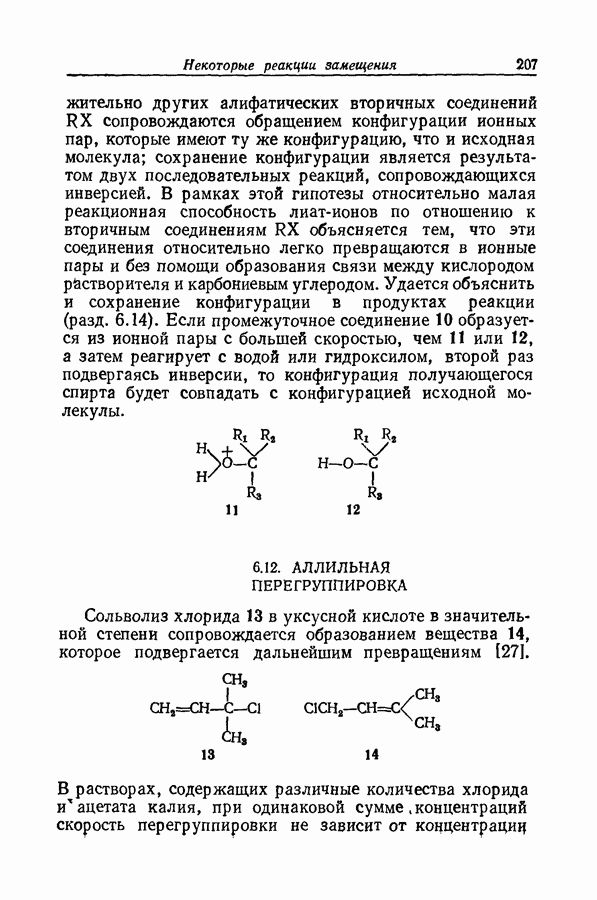
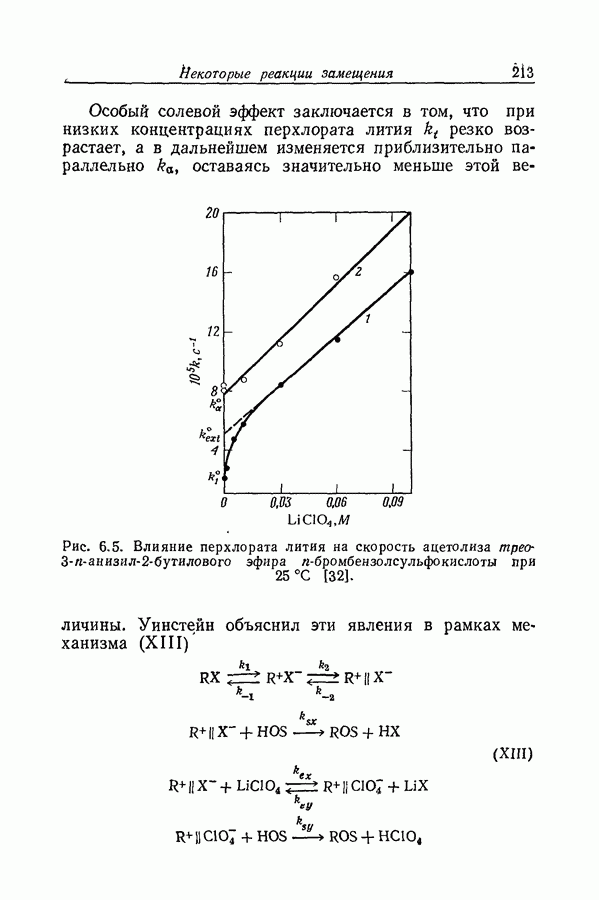
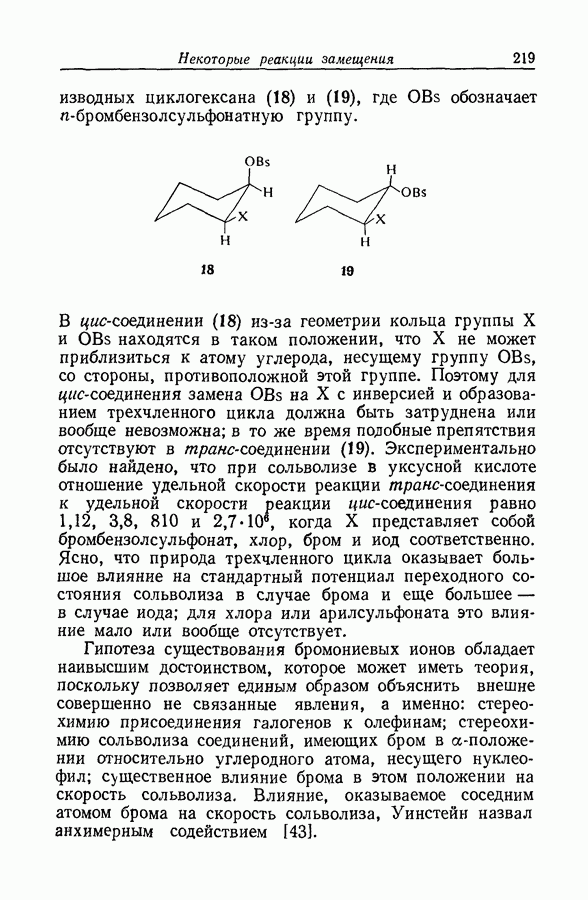
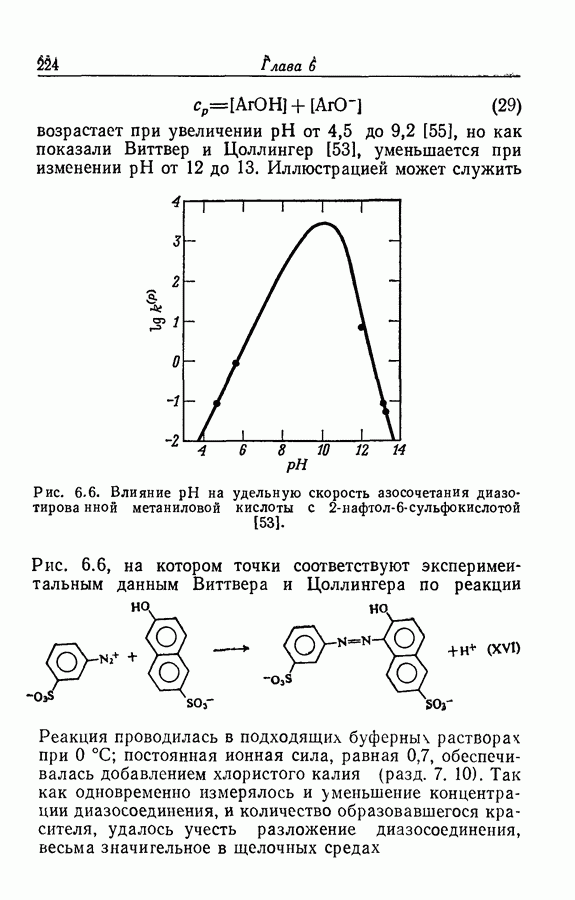
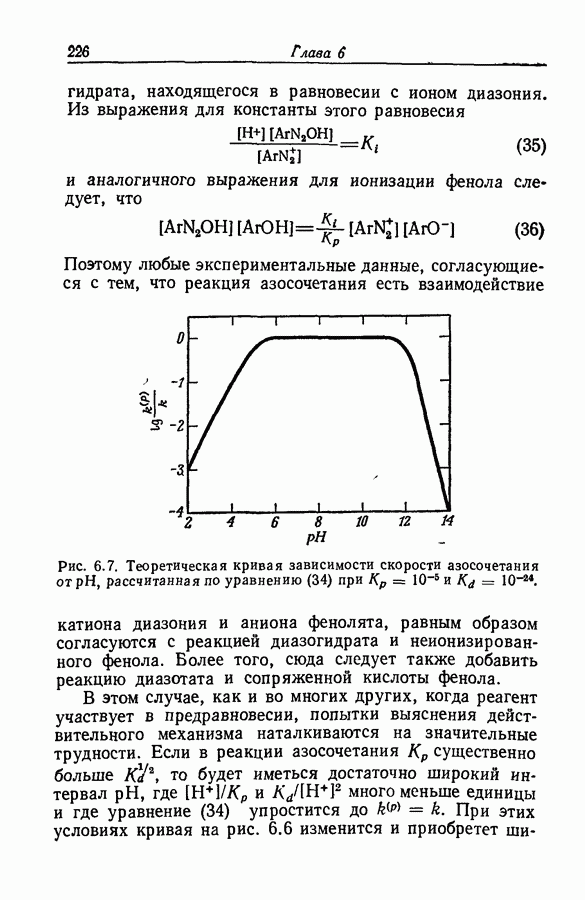
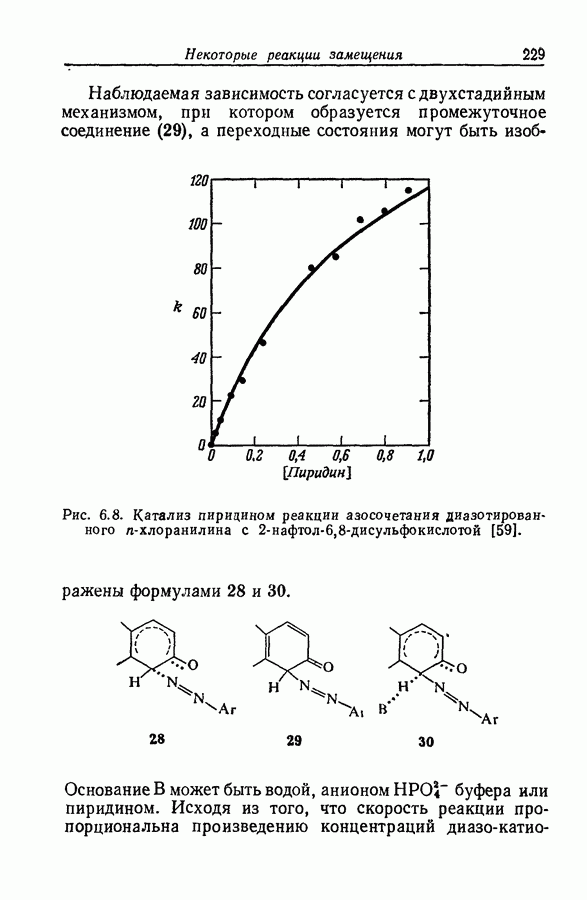
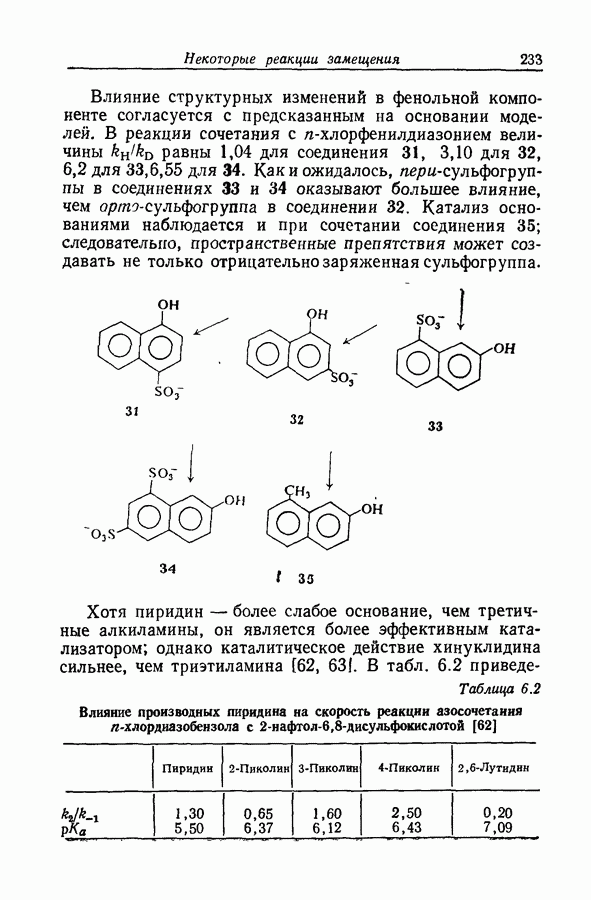
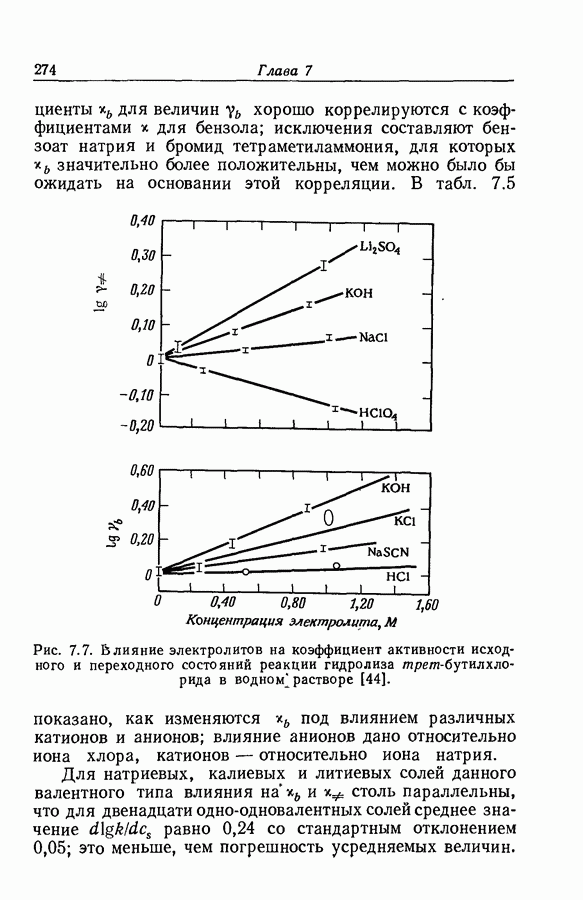
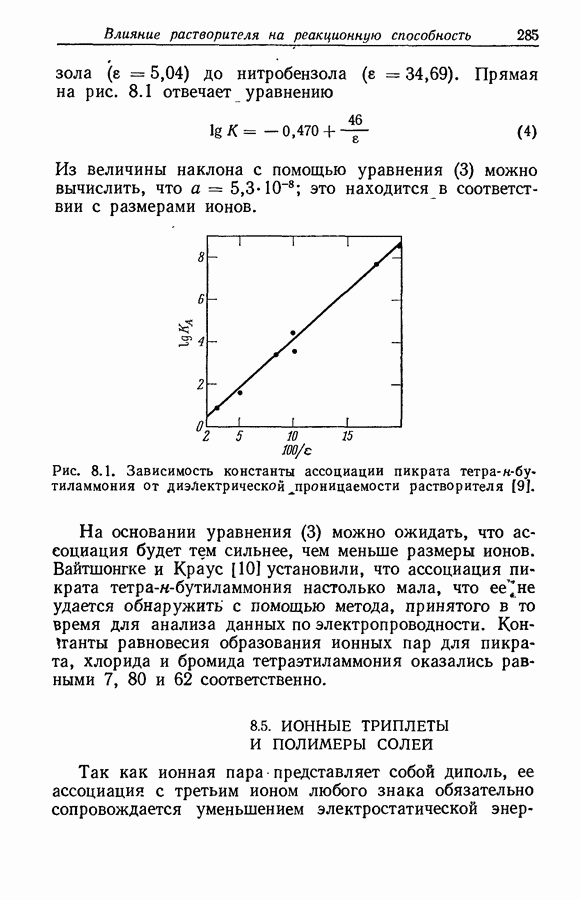
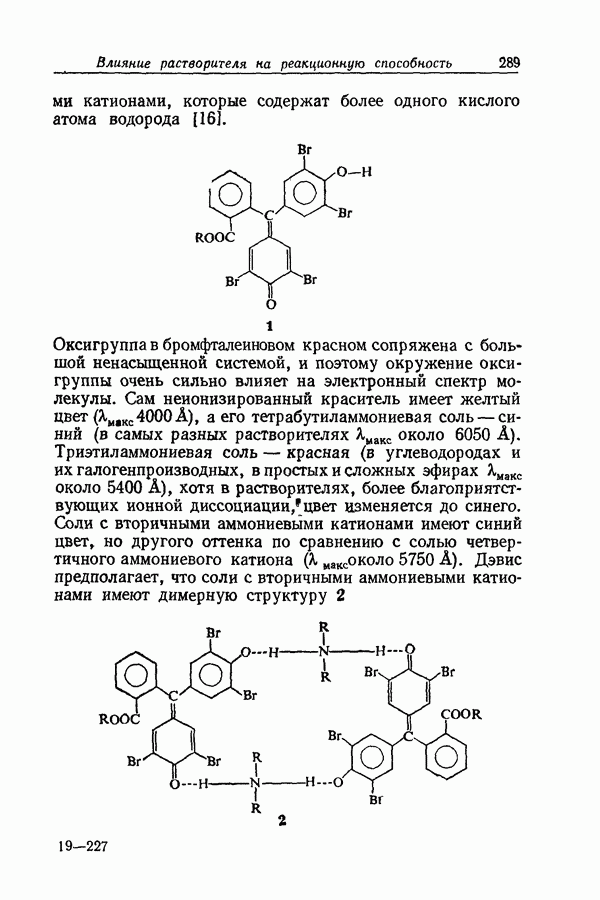
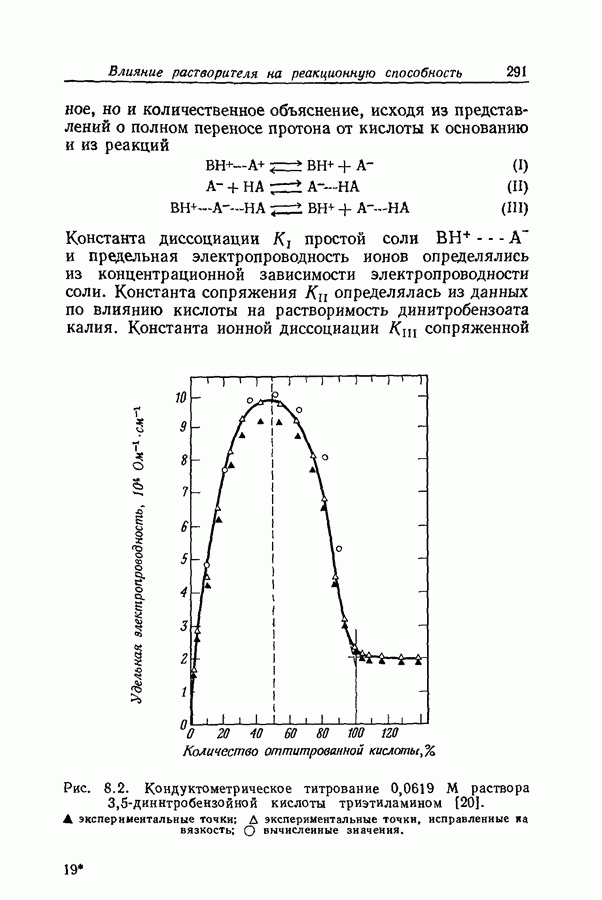
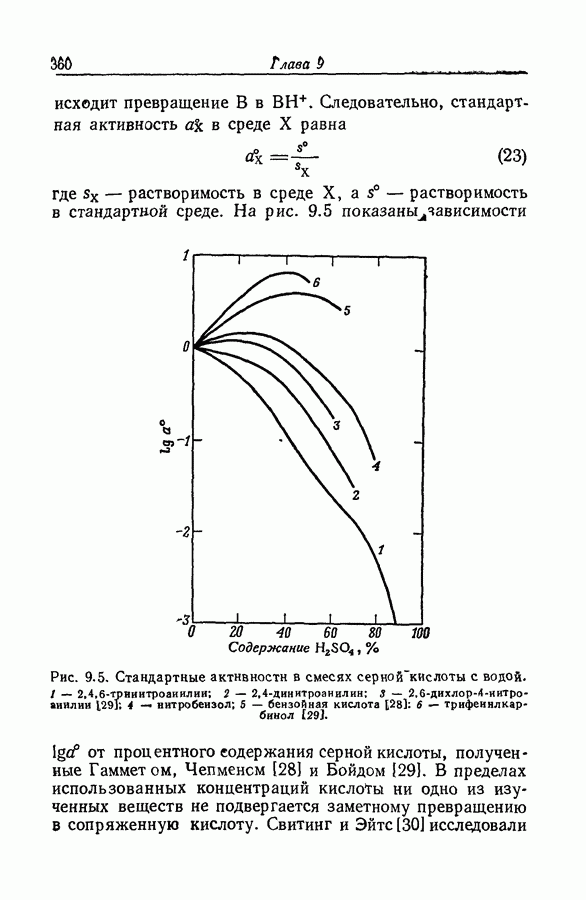
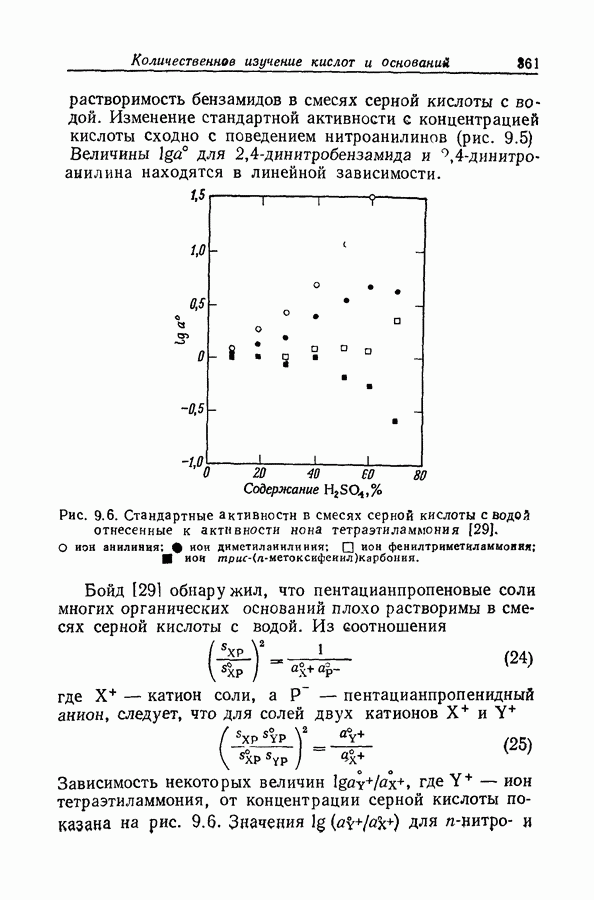
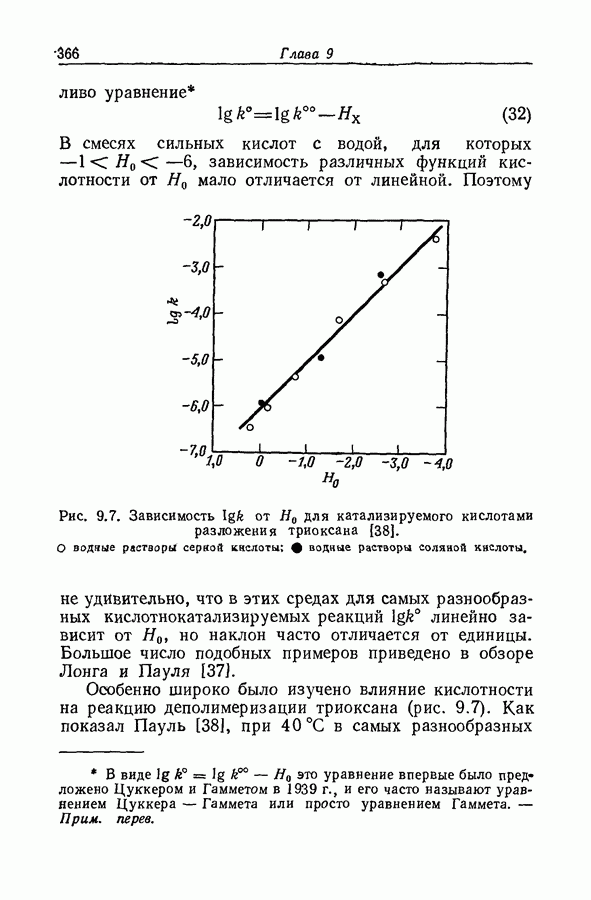
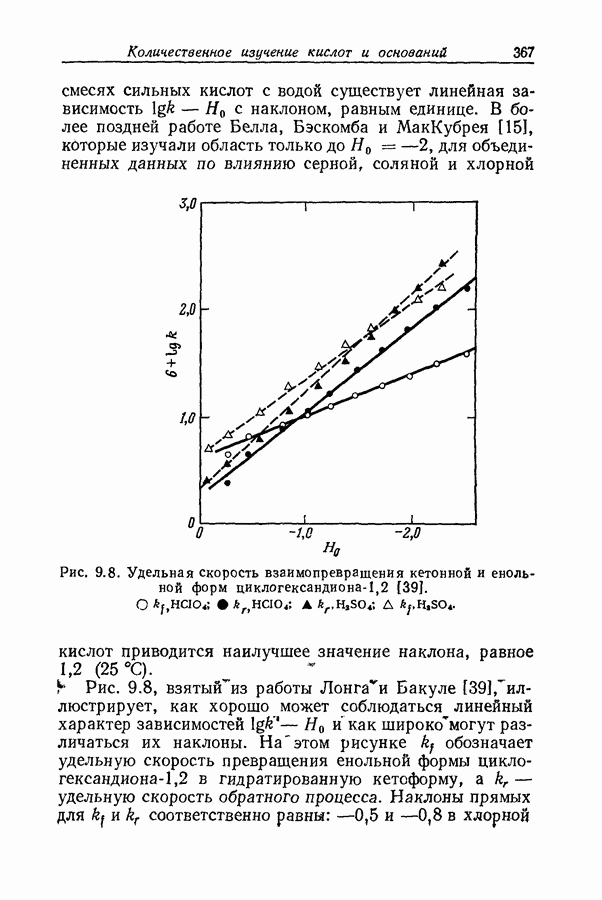
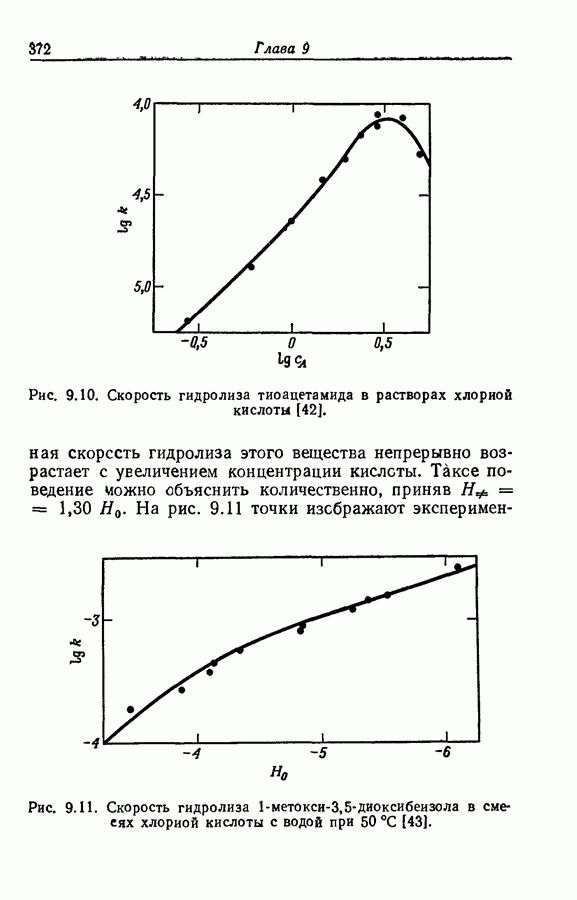
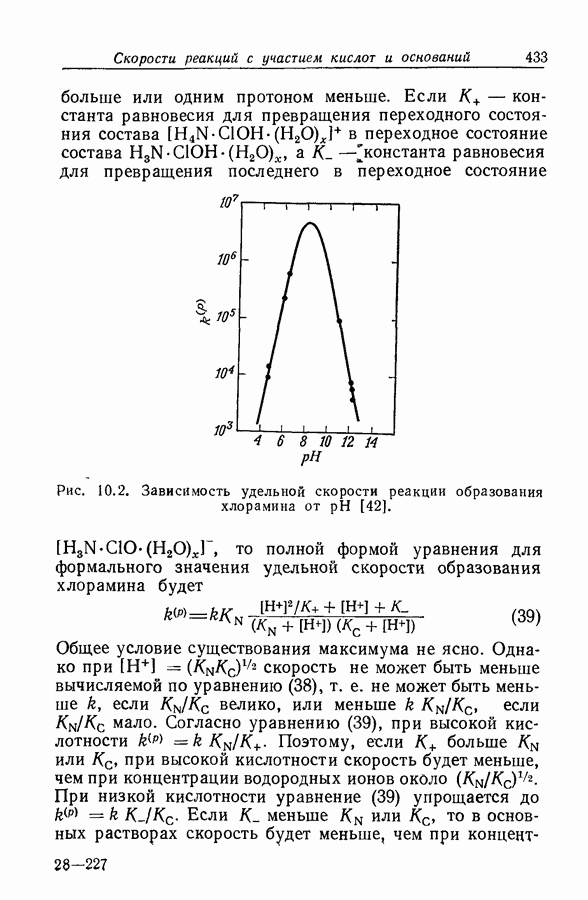
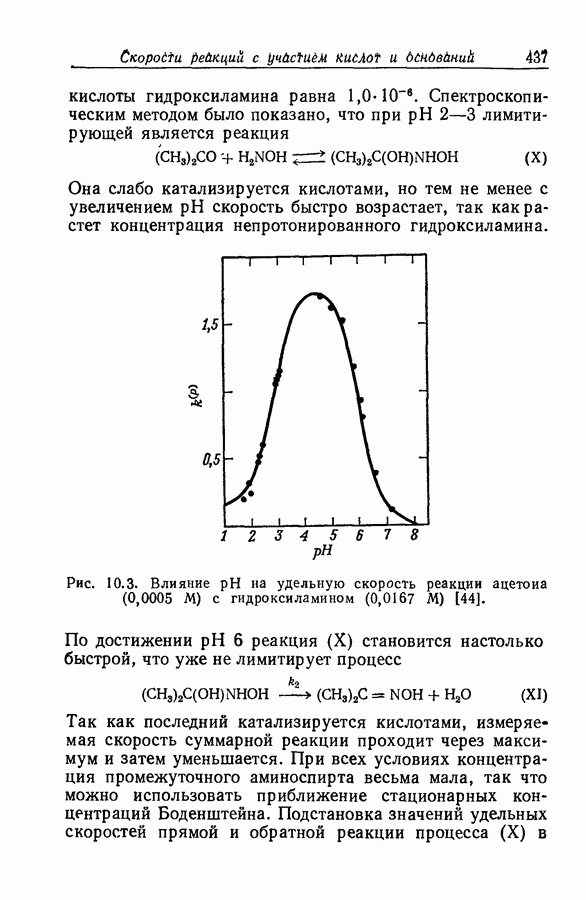
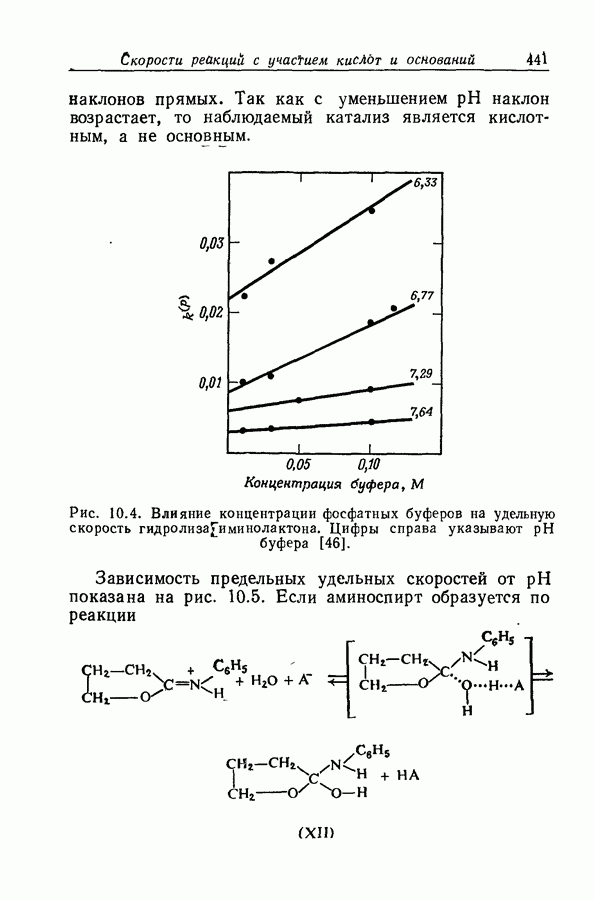
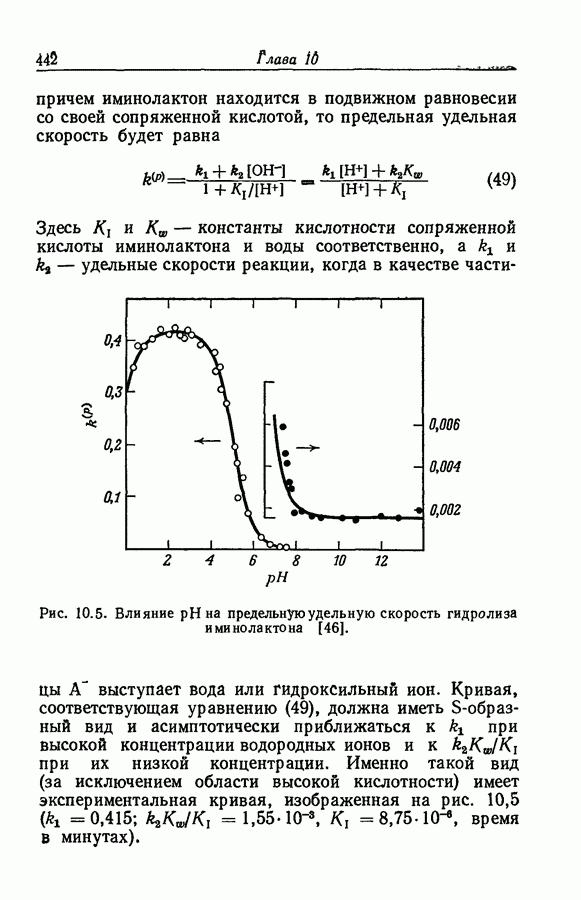
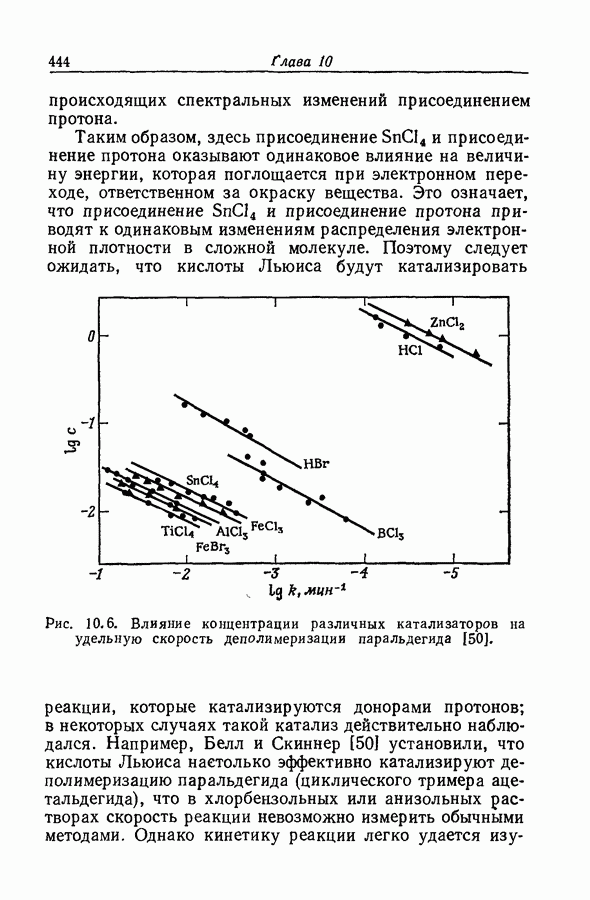
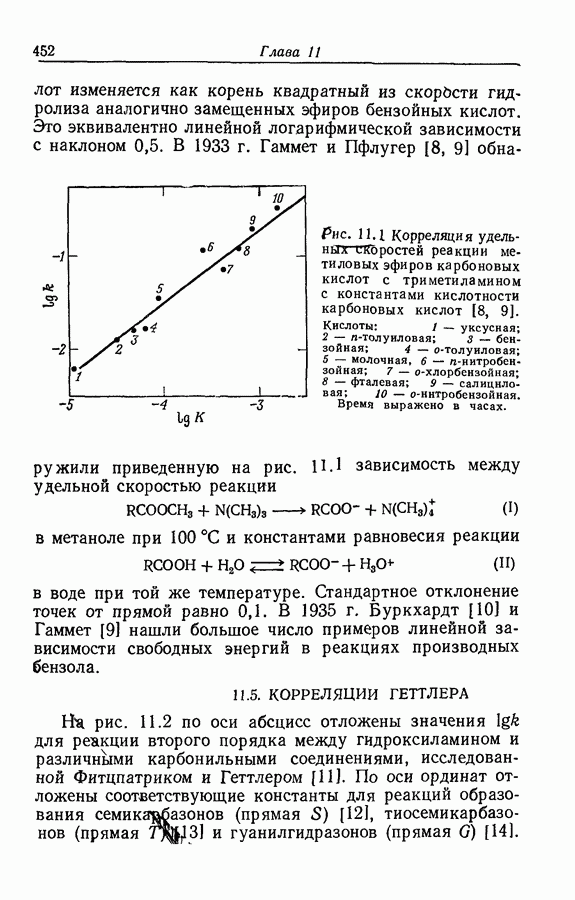
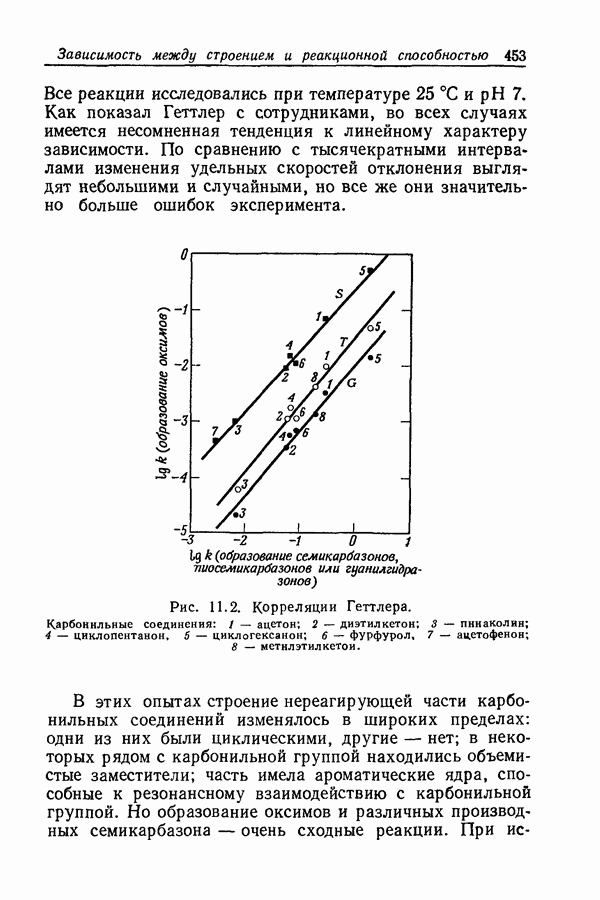
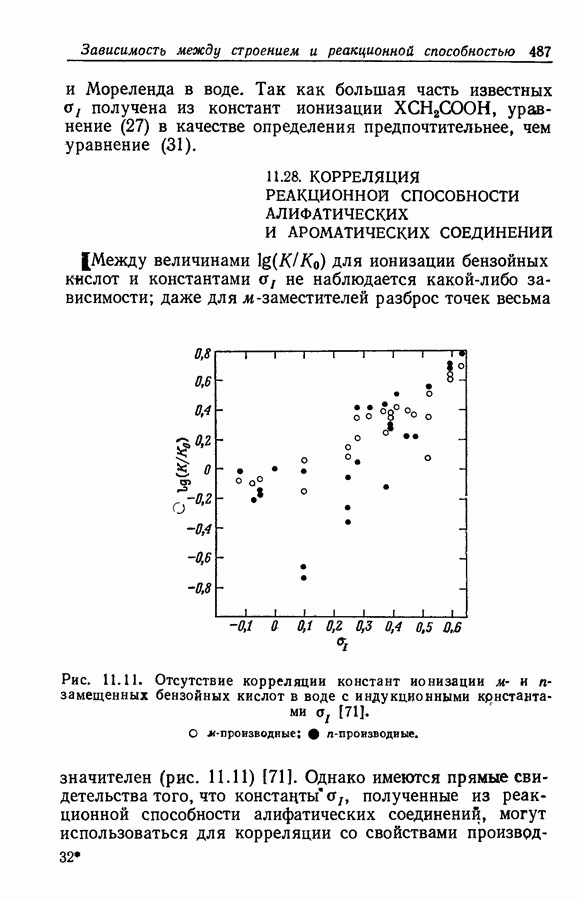
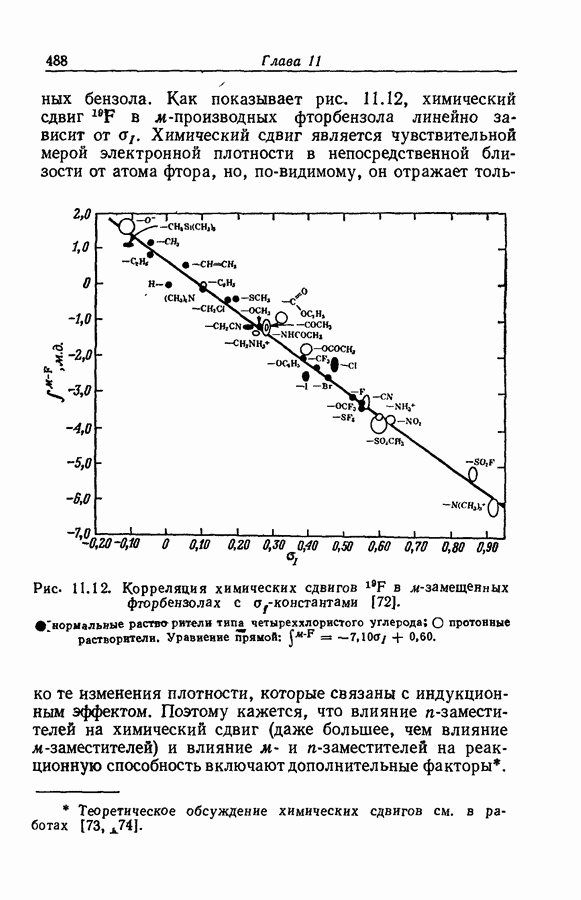
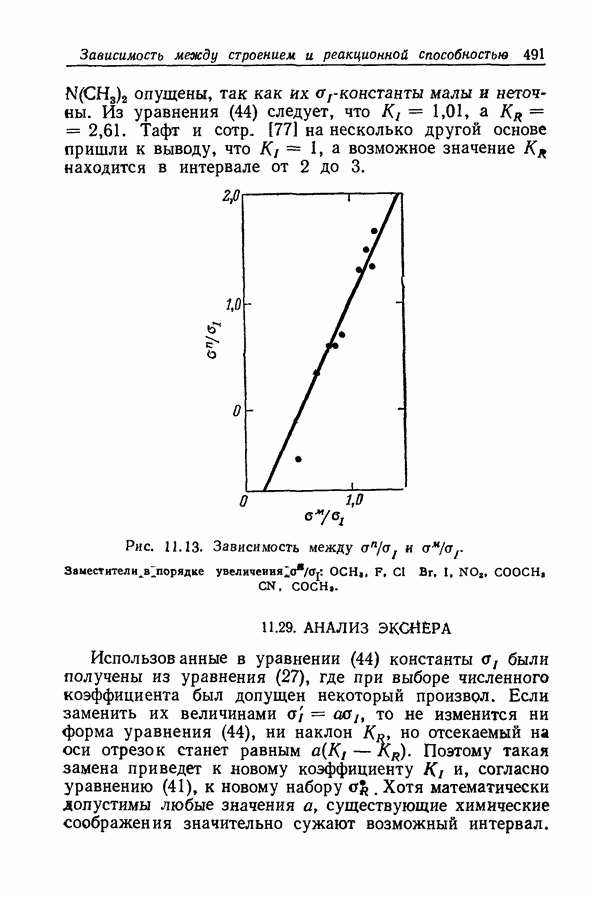
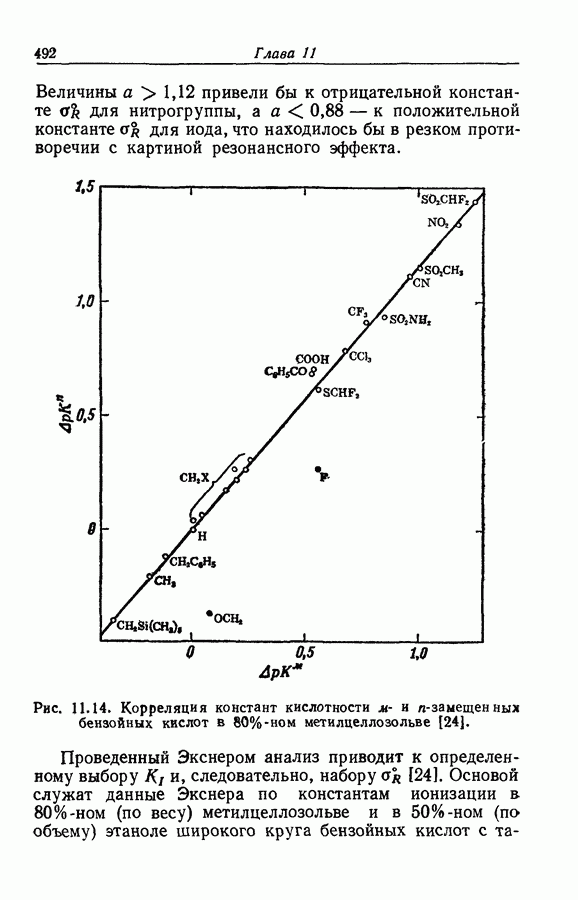
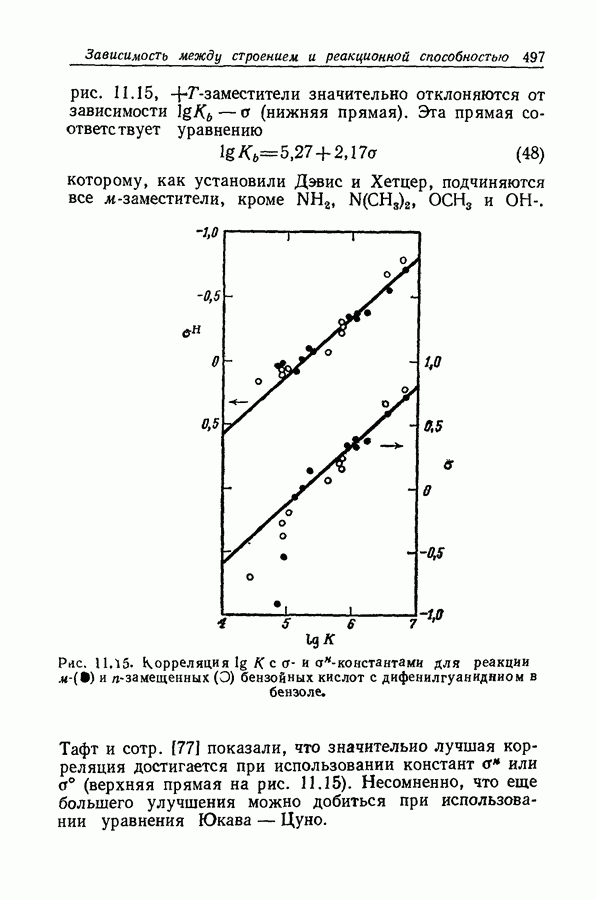
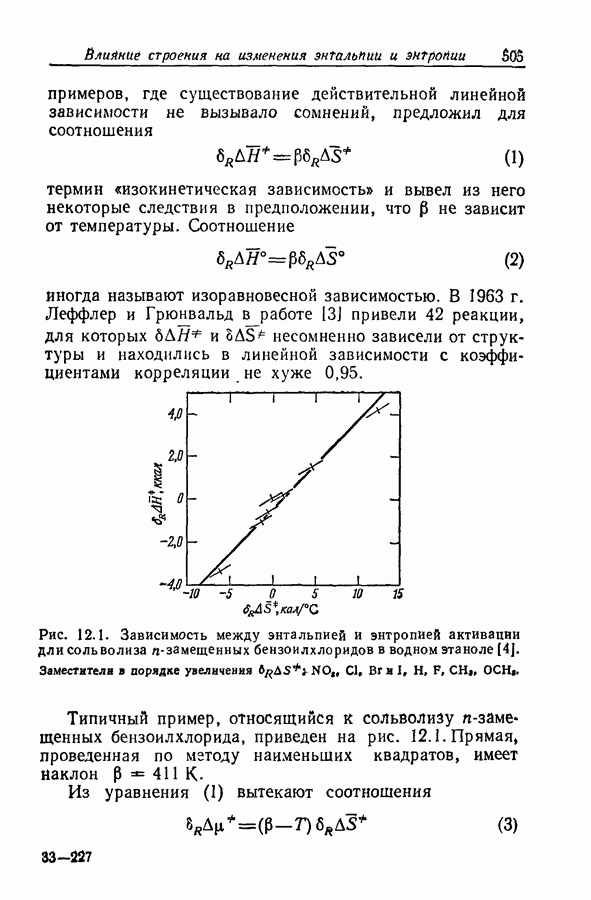
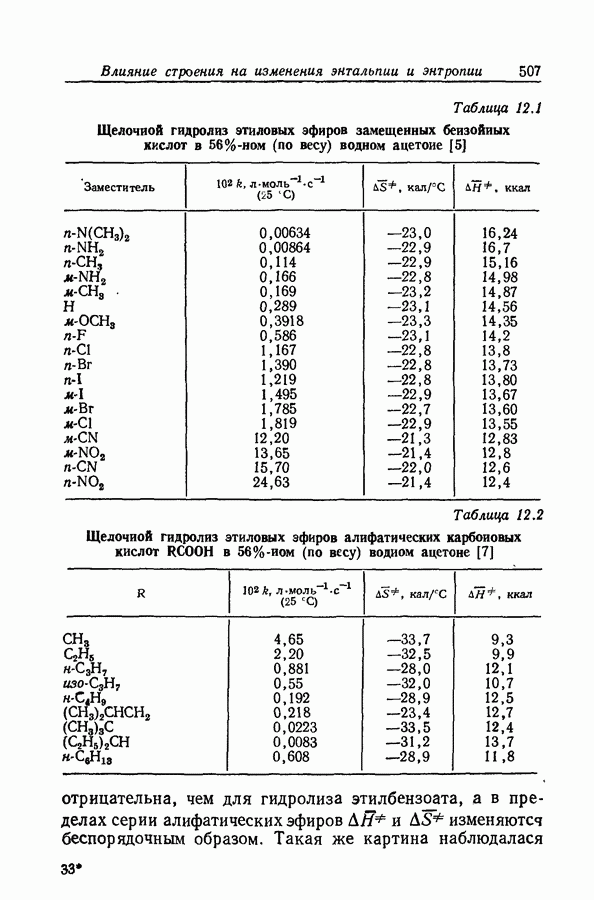
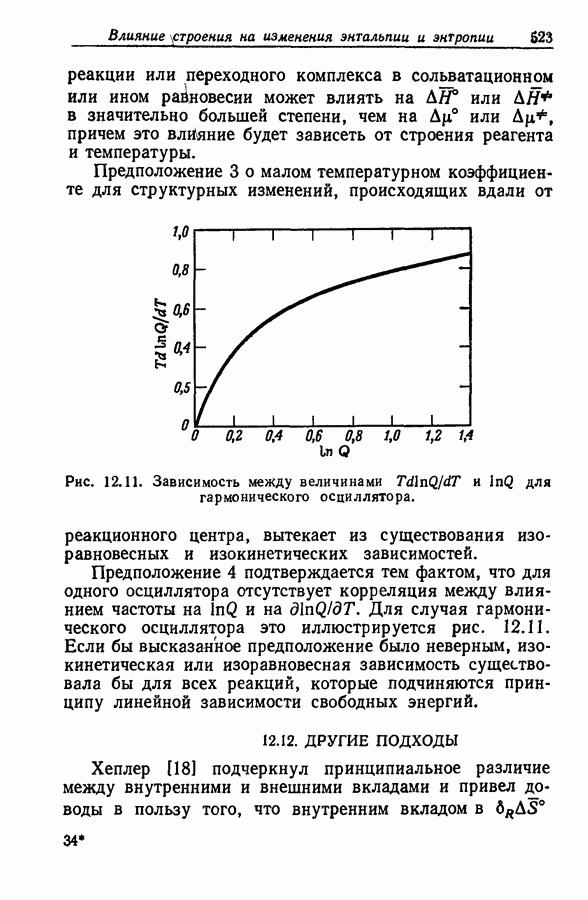
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
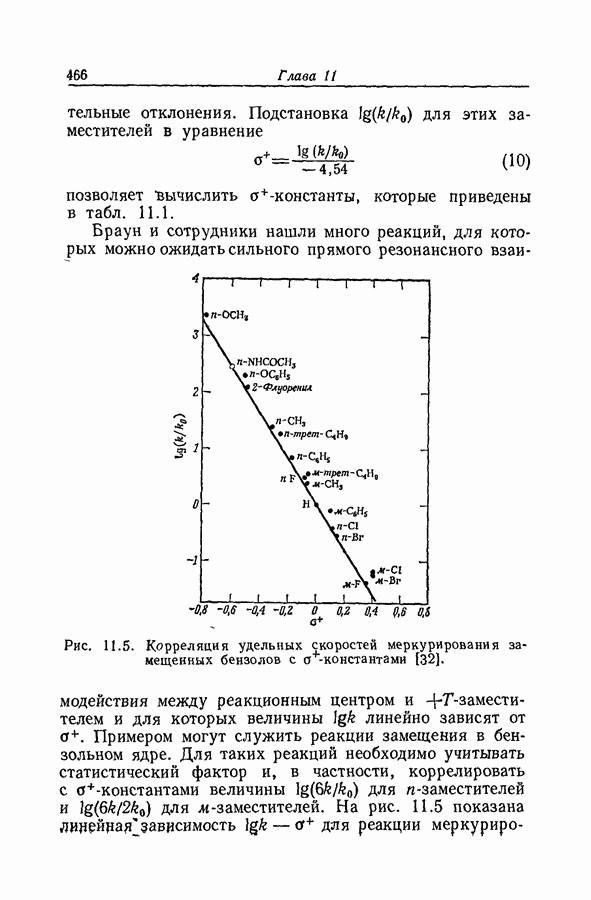
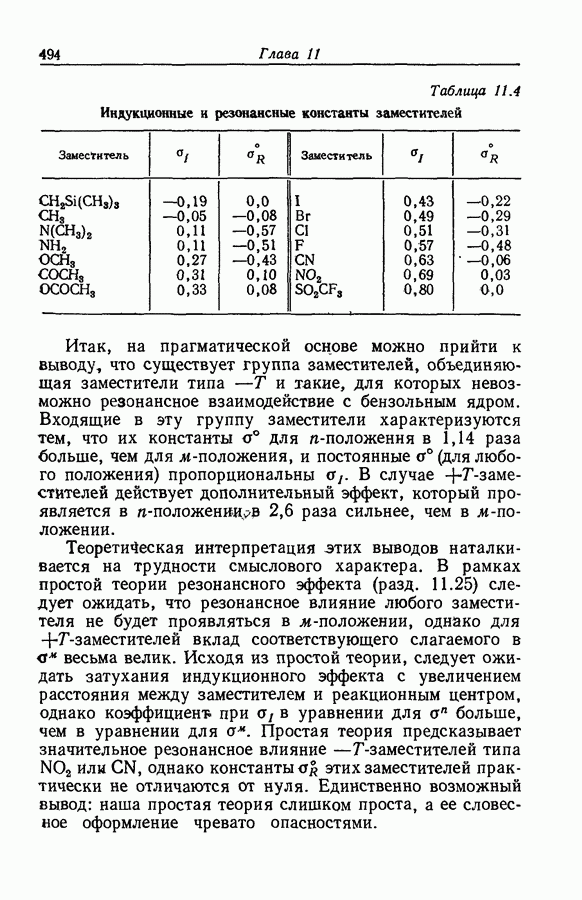
9.20. НАЛОЖЕНИЕ ЭФФЕКТОВ СРЕДЫ ПРИ СПЕКТРОФОТОМЕТРИЧЕСКОМ ОПРЕДЕЛЕНИИ ОСНОВНОСТИ
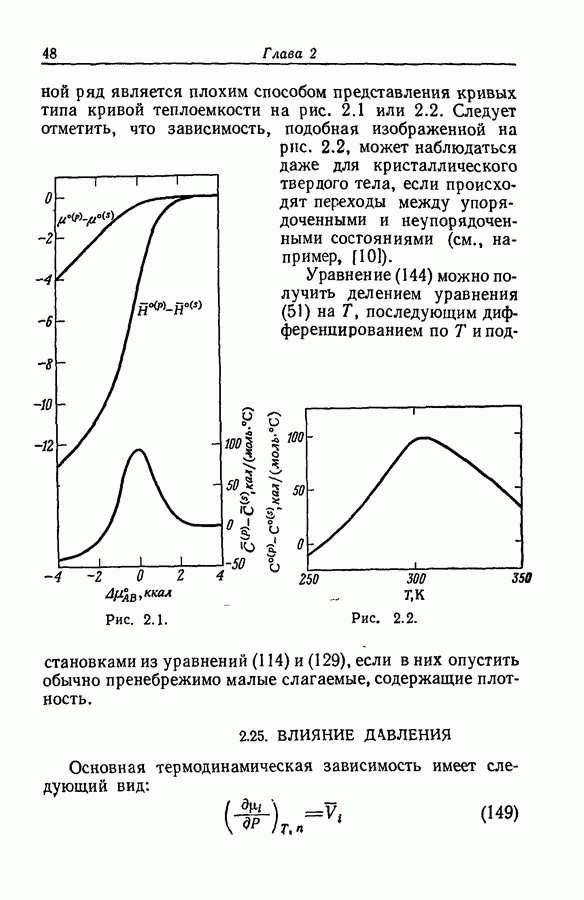
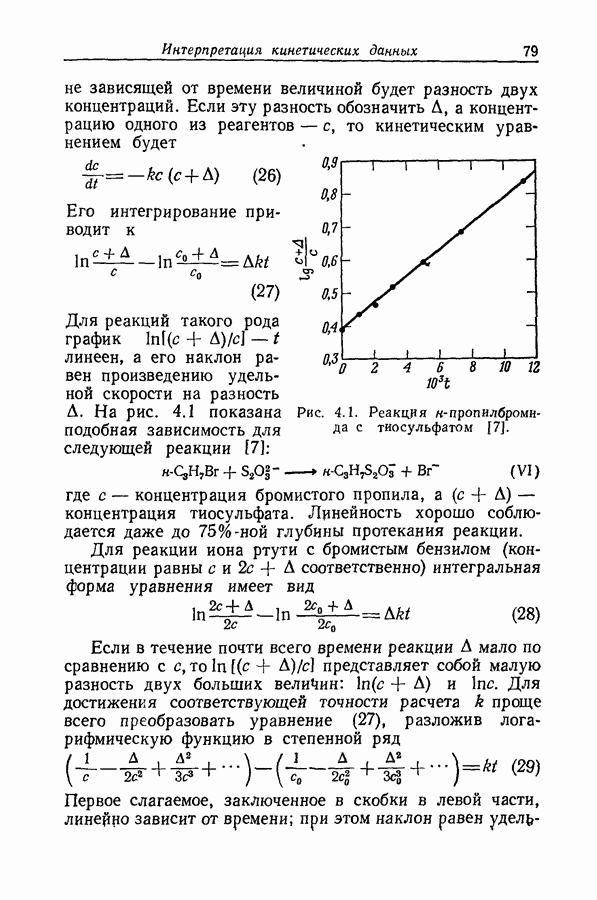
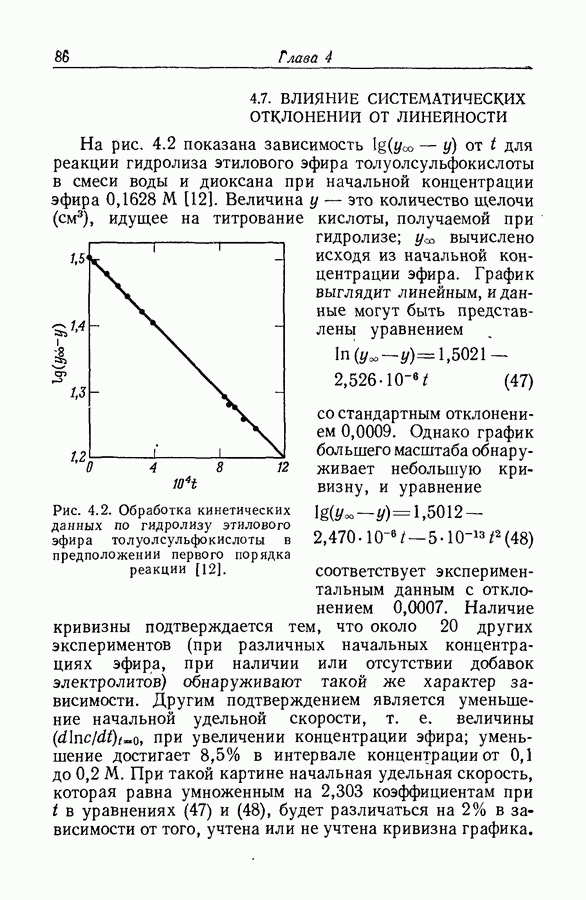
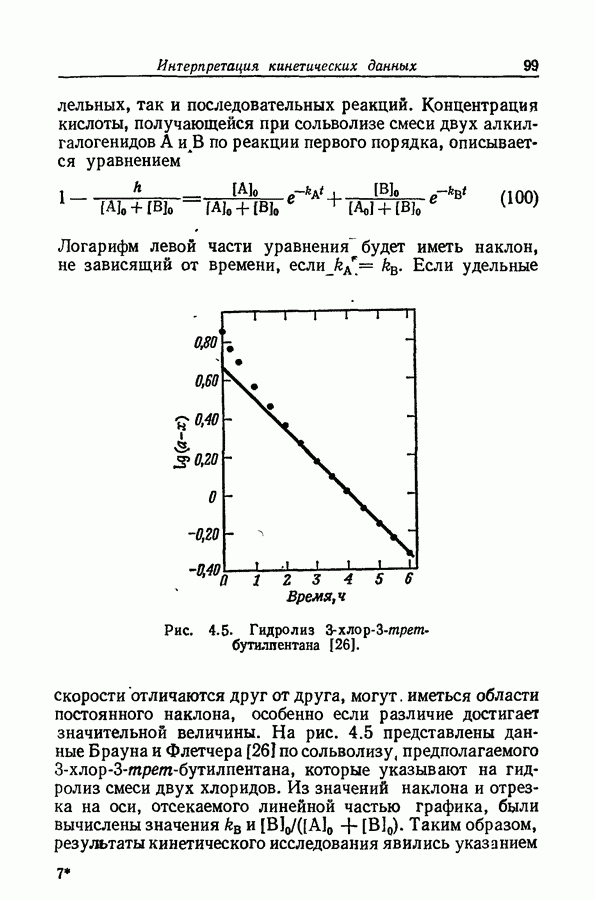
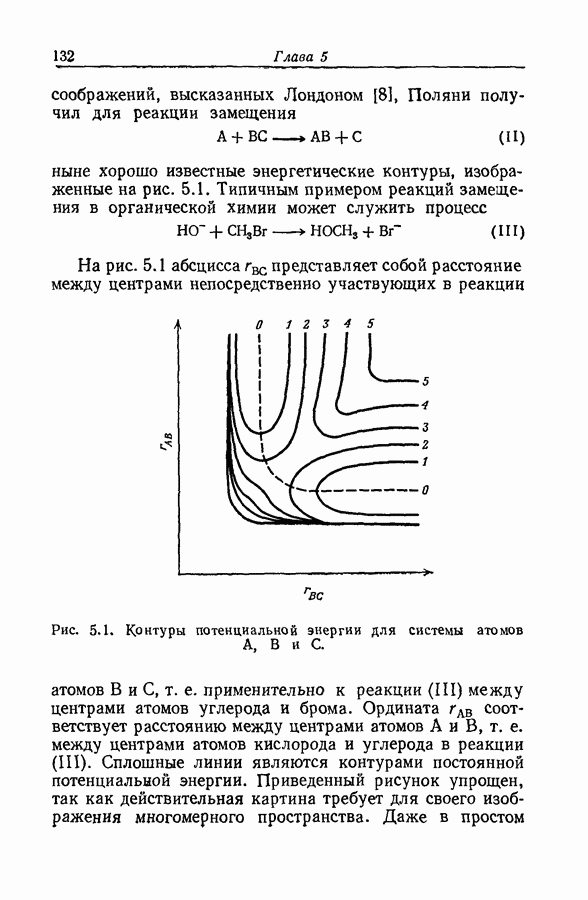
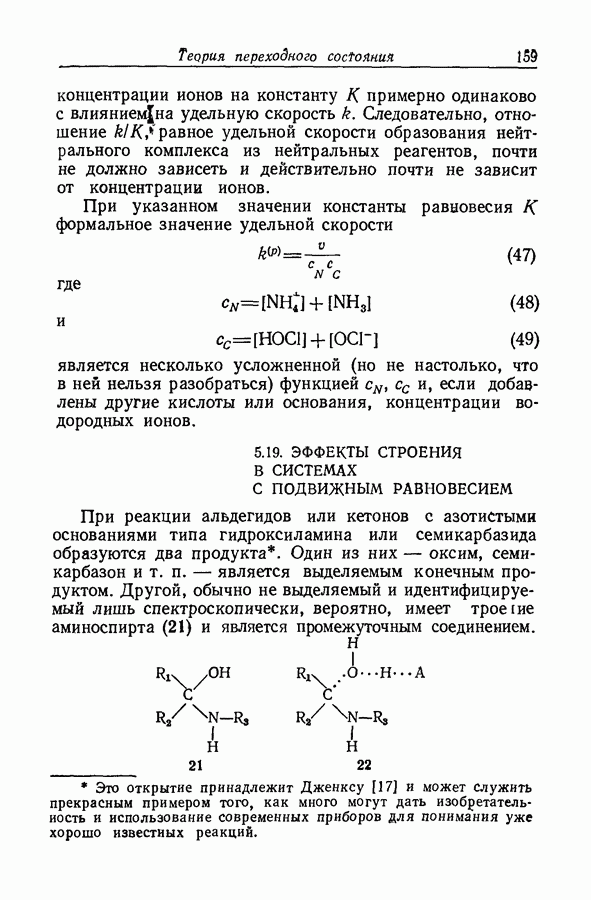
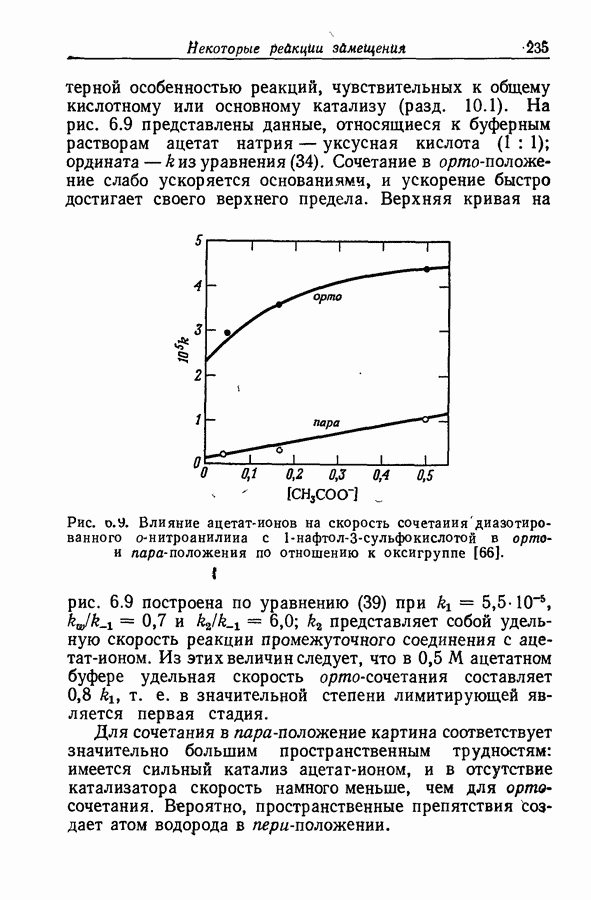
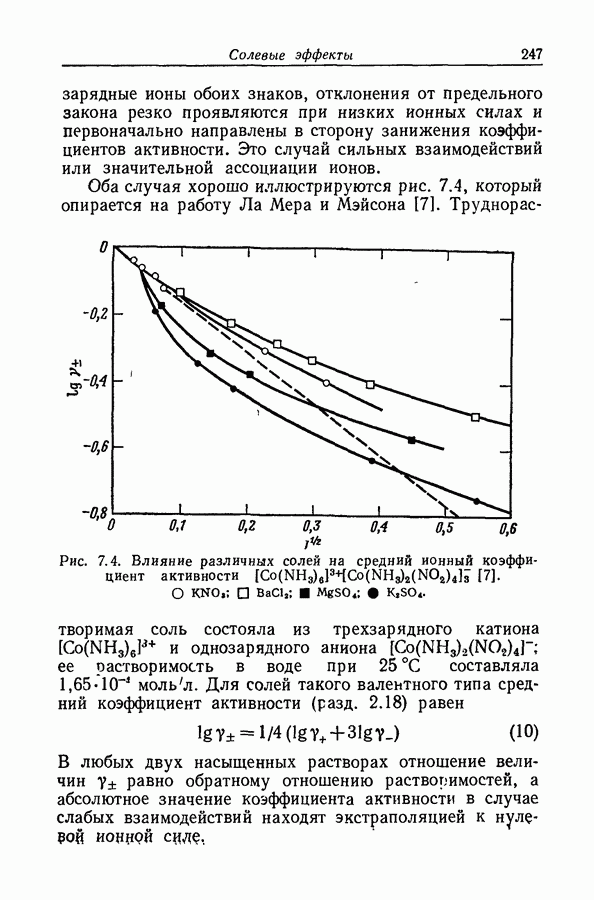
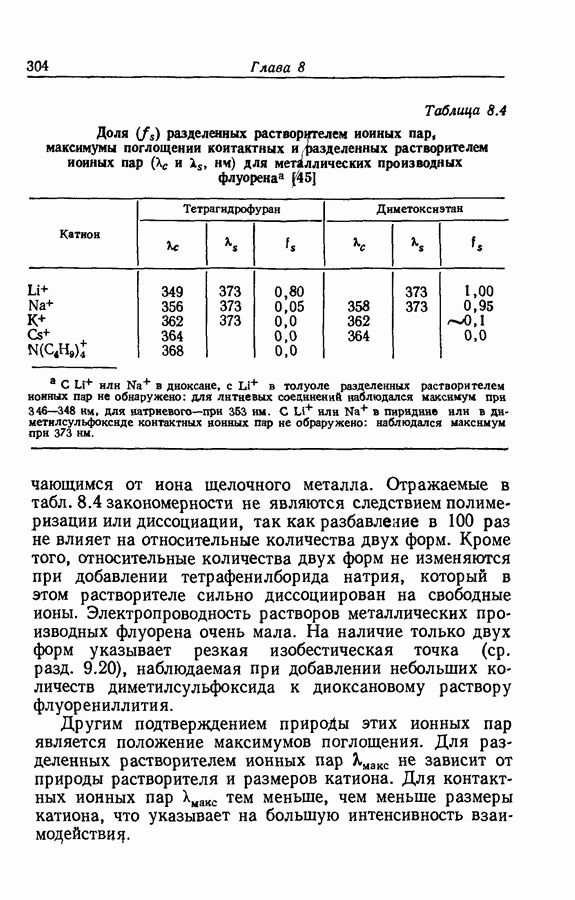
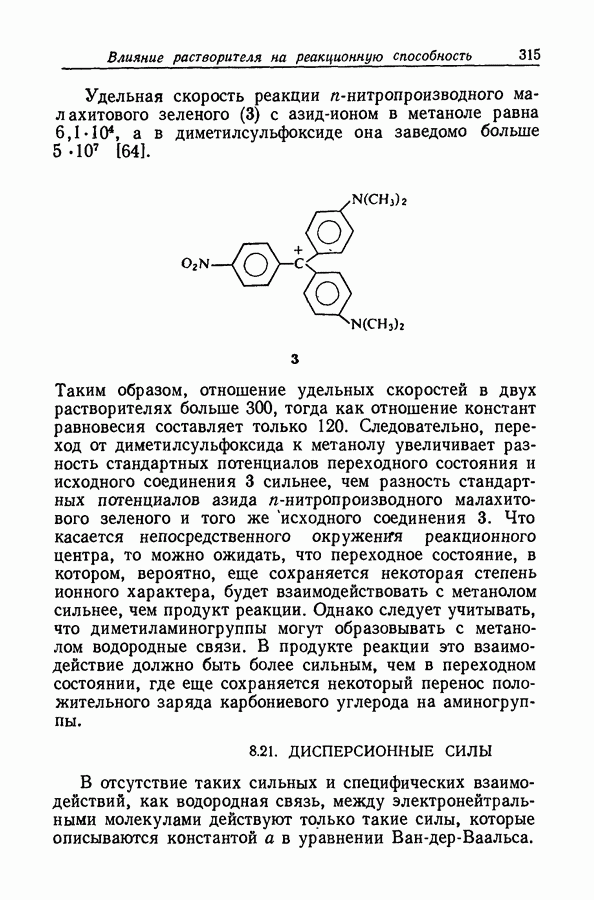
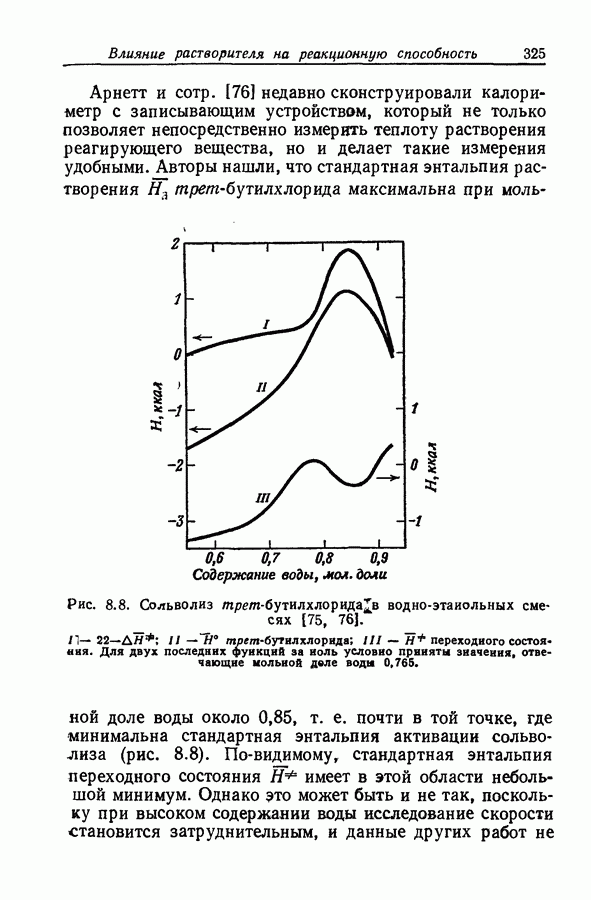
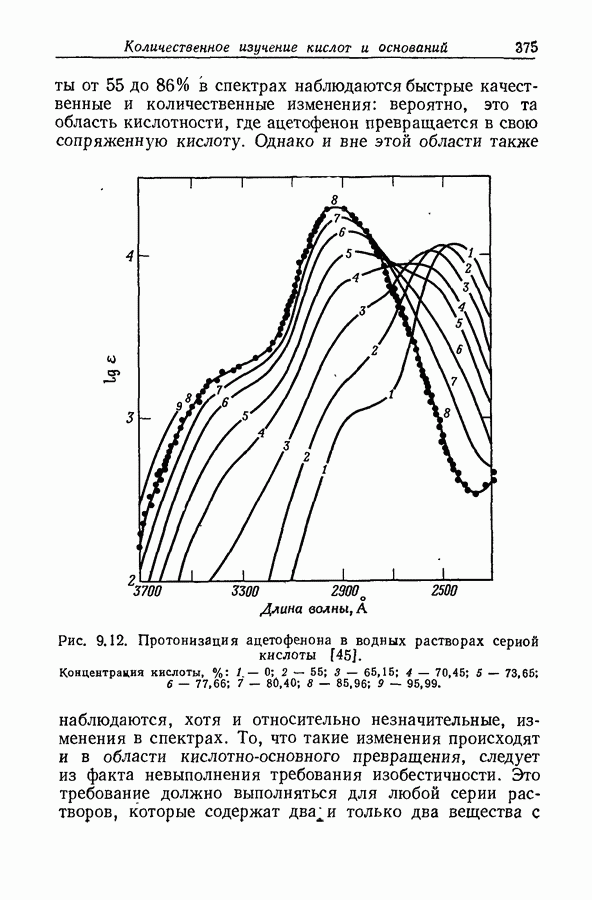
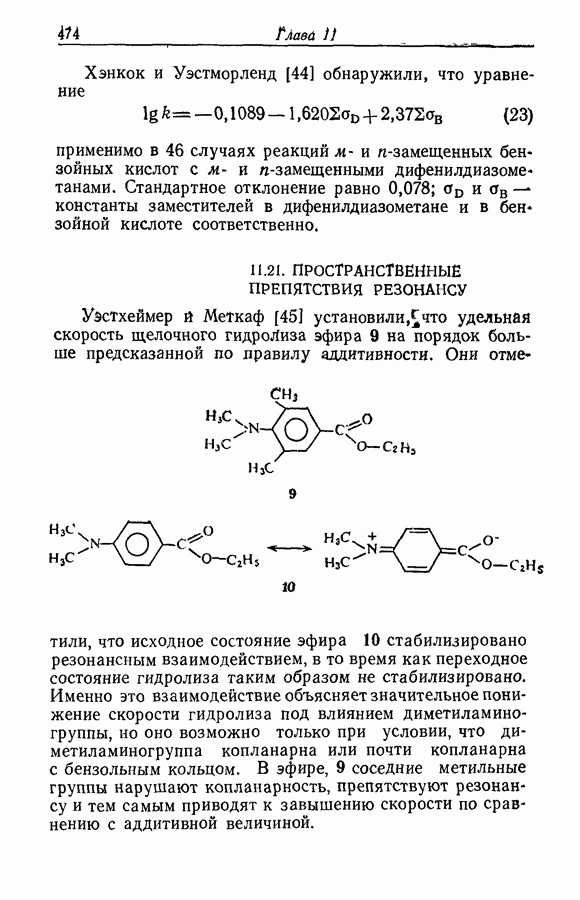
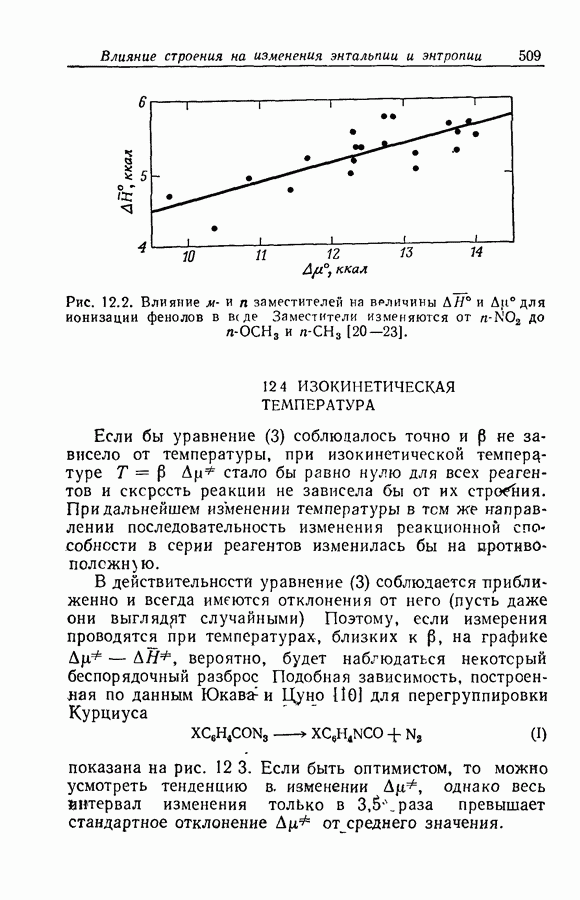
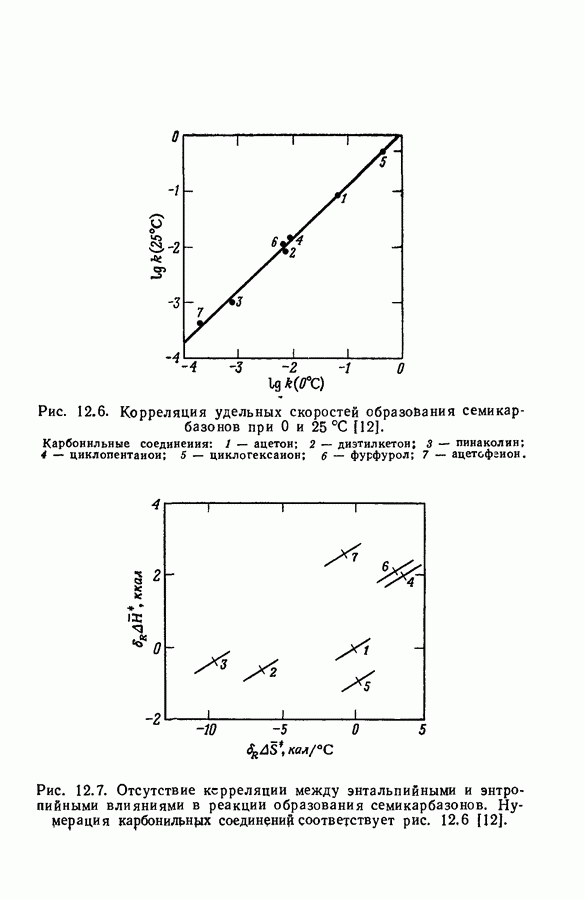
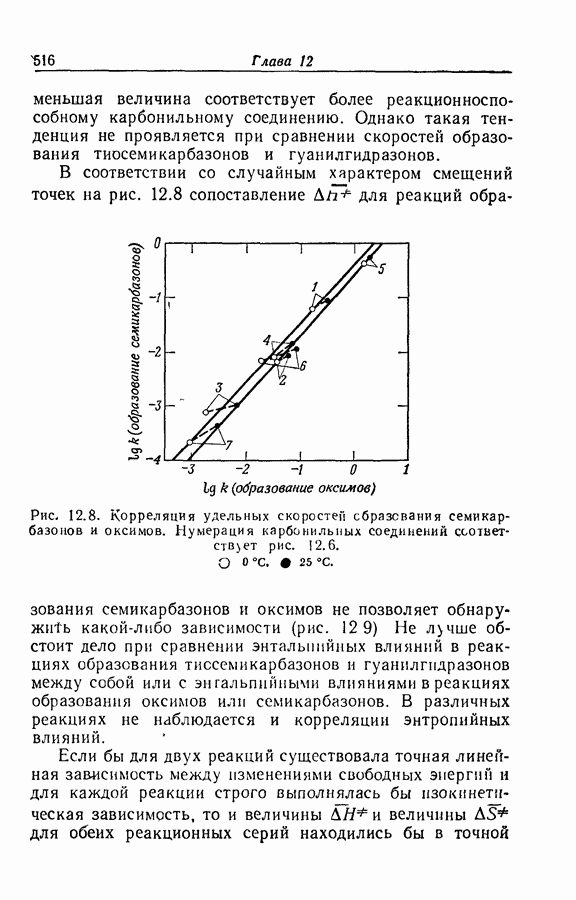
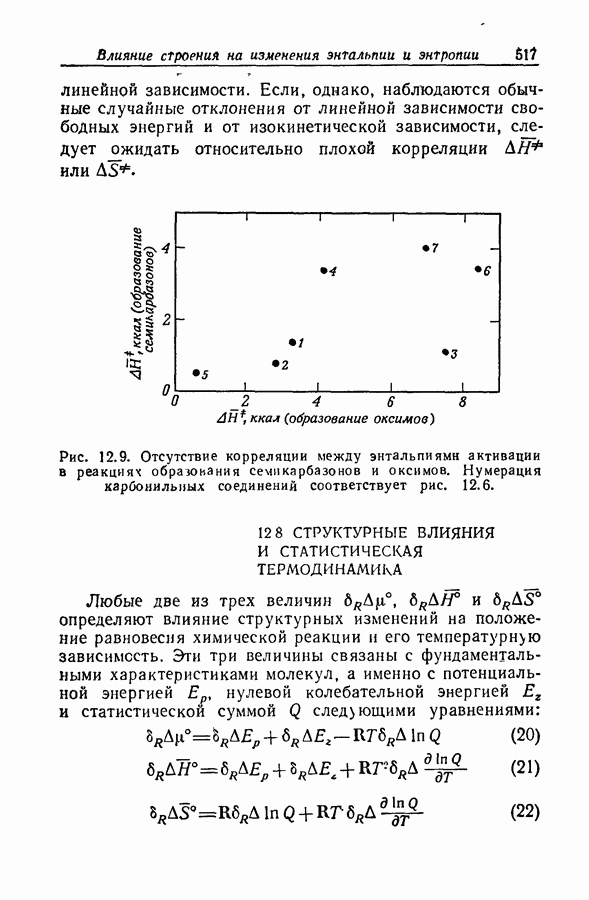
Задача определения силы основания осложняется тем обстоятельством, что при изменении среды спектр растворенного вещества часто изменяется даже в отсутствие заметной химической реакции. Это явление иллюстрируется рис. 9.12, на котором изображены спектры поглощения ацетофенона в растворах серной кислоты различной концентрации. При увеличении концентрации
кислоты от 55 до 86% в спектрах наблюдаются быстрые качественные и количественные изменения: вероятно, это та область кислотности, где ацетофенон превращается в свою сопряженную кислоту. Однако и вне этой области также наблюдаются, хотя и относительно незначительные, изменения в спектрах.

Рис. 9.12. Протонизация ацетофенона в водных растворах серной кислоты [45]. Концентрация кислоты, 
То, что такие изменения происходят и в области кислотно-основного превращения, следует из факта невыполнения требования изобестичности. Это требование должно выполняться для любой серии растворов, которые содержат дваи только два вещества с
неизменяющимися спектрами [45]. В такой серии точка пересечения спектральных кривых, соответствующих любым двум растворам, должна быть общей точкой для спектральных кривых всех растворов. Вследствие сдвига нельзя считать, что коэффициент экстинкции  основной формы ацетофенона в интервале его кислотно-основного равновесия равен коэффициенту экстинкции в воде или в разбавленной кислоте. По аналогичным соображениям коэффициент экстинкции в
основной формы ацетофенона в интервале его кислотно-основного равновесия равен коэффициенту экстинкции в воде или в разбавленной кислоте. По аналогичным соображениям коэффициент экстинкции в  -или
-или  -ной серной кислоте не может быть принят равным коэффициенту экстинкции сопряженной кислоты ацетофенона в области протонирозания.
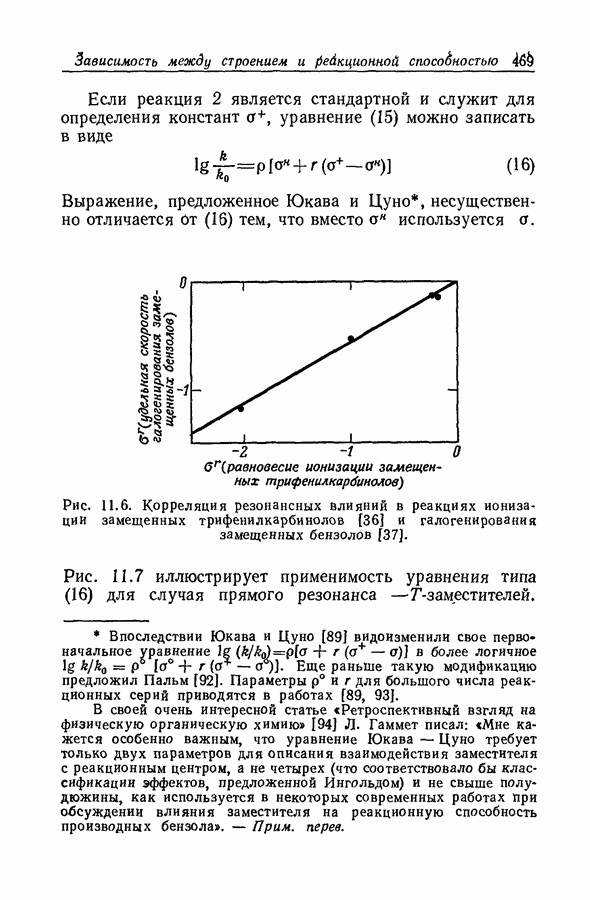
-ной серной кислоте не может быть принят равным коэффициенту экстинкции сопряженной кислоты ацетофенона в области протонирозания.
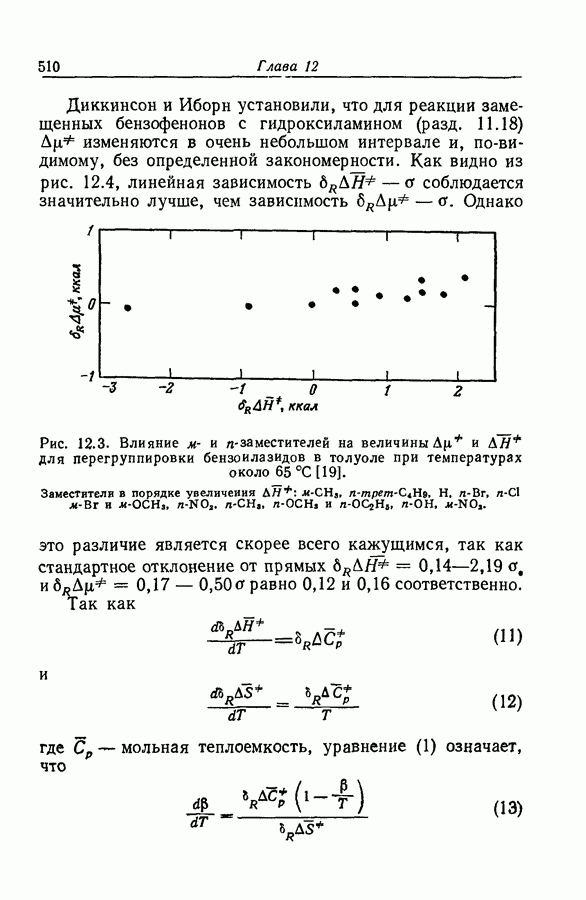
Если, однако, в сравнительно узкой области, где протонирование в основном уже заканчивается,  изменяются не очень резко, то в уравнении
изменяются не очень резко, то в уравнении

можно использовать их средние значения. При более ранних обсуждениях этой проблемы предполагалось, что для всех оснований  в настоящее время известно, что это не так. Но инструментальное определение левой части уравнения (48) для каждого данного основания возможно лишь в относительно небольшом интервале кислотности, где зависимость между различными функциями кислотности с хорошим приближением можно представить как линейную. Поэтому уравнение (48) следует заменить на
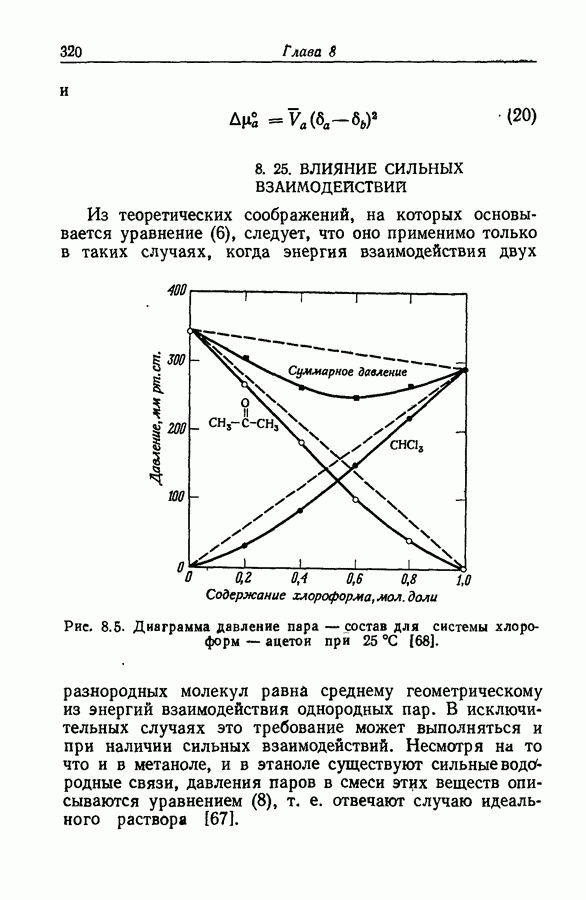
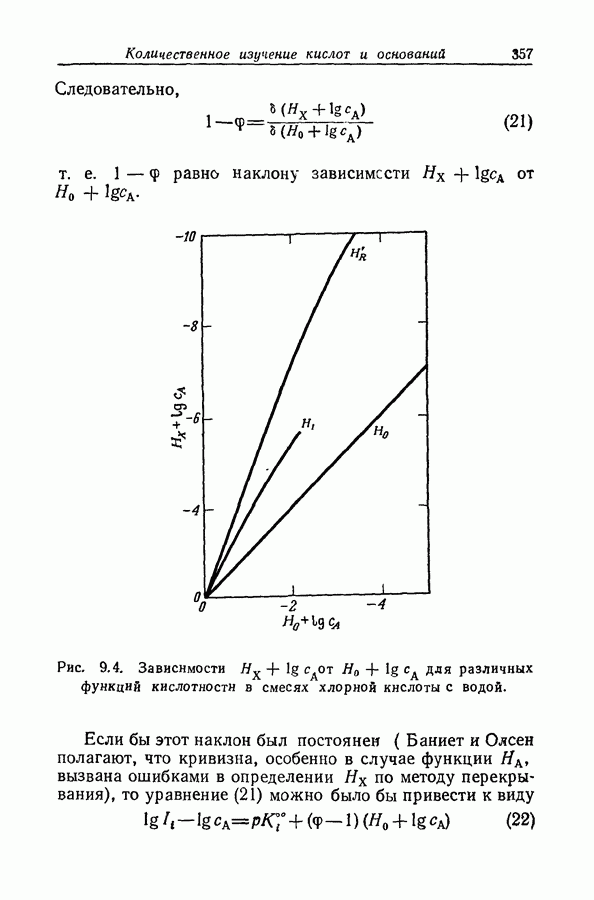
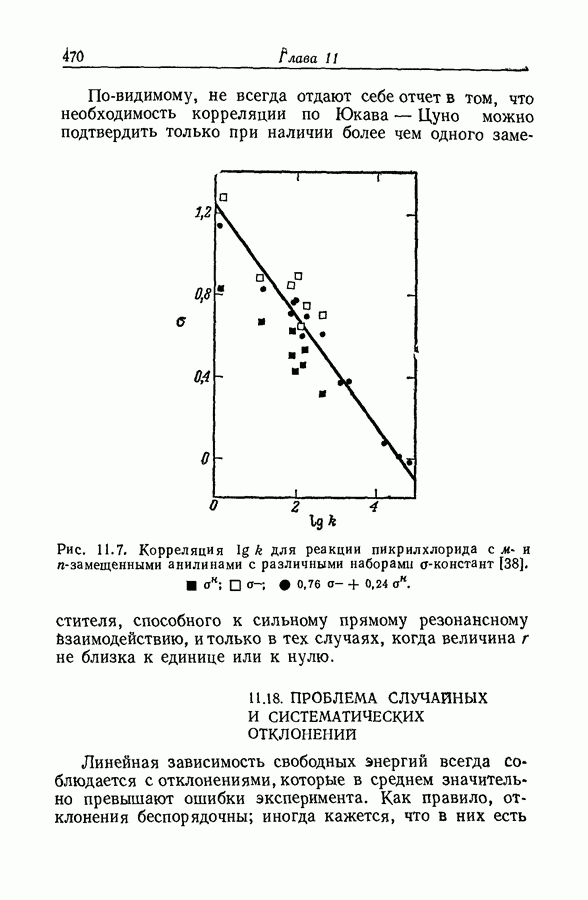
в настоящее время известно, что это не так. Но инструментальное определение левой части уравнения (48) для каждого данного основания возможно лишь в относительно небольшом интервале кислотности, где зависимость между различными функциями кислотности с хорошим приближением можно представить как линейную. Поэтому уравнение (48) следует заменить на

где  не зависят от концентрации кислоты. Если протонирование происходит при низких концентрациях кислоты, при которых наблюдаются существенные отклонения от линейных зависимостей между различными функциями кислотности, то следует использовать уравнение
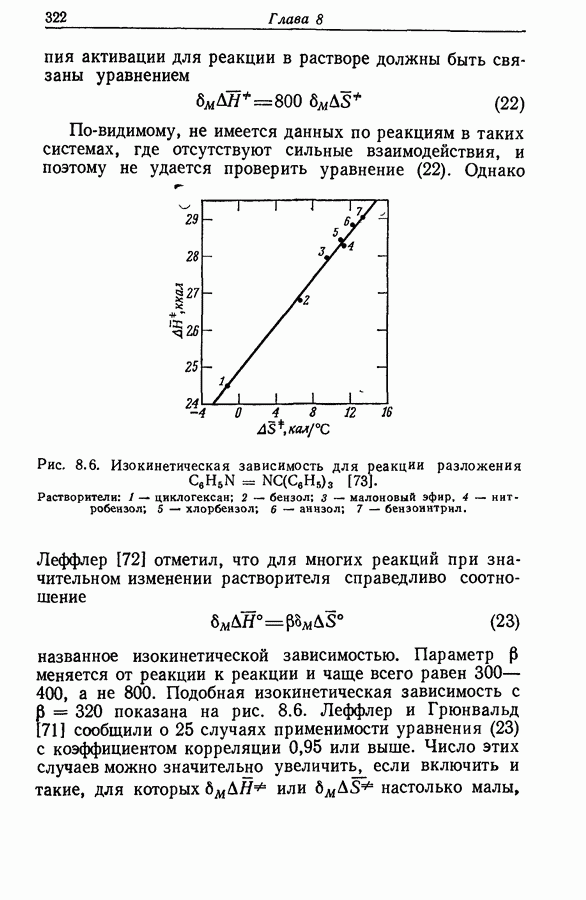
не зависят от концентрации кислоты. Если протонирование происходит при низких концентрациях кислоты, при которых наблюдаются существенные отклонения от линейных зависимостей между различными функциями кислотности, то следует использовать уравнение

(разд. 9.10). Каждое из уравнений содержит четыре регулируемых параметра и, хотя интервал допустимых изменений  ограничен, постоянство этих двух
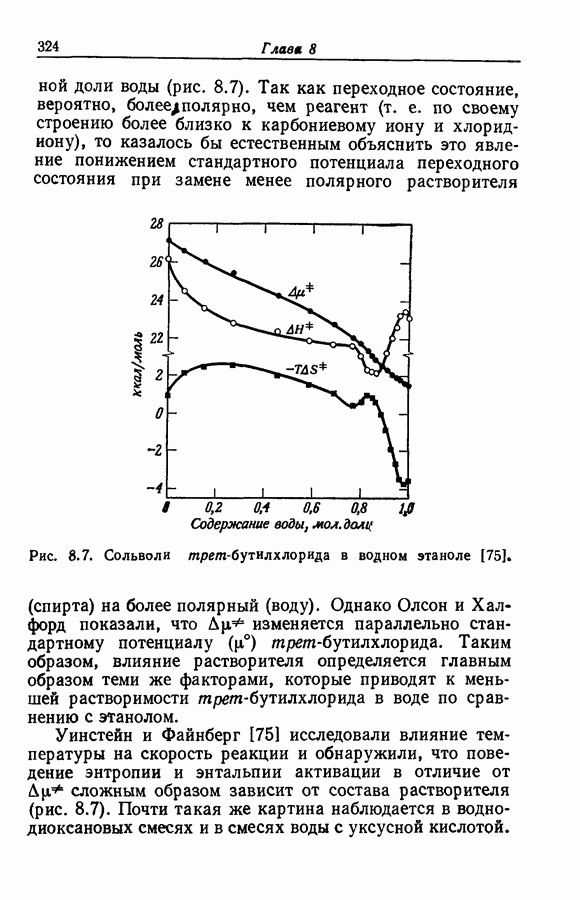
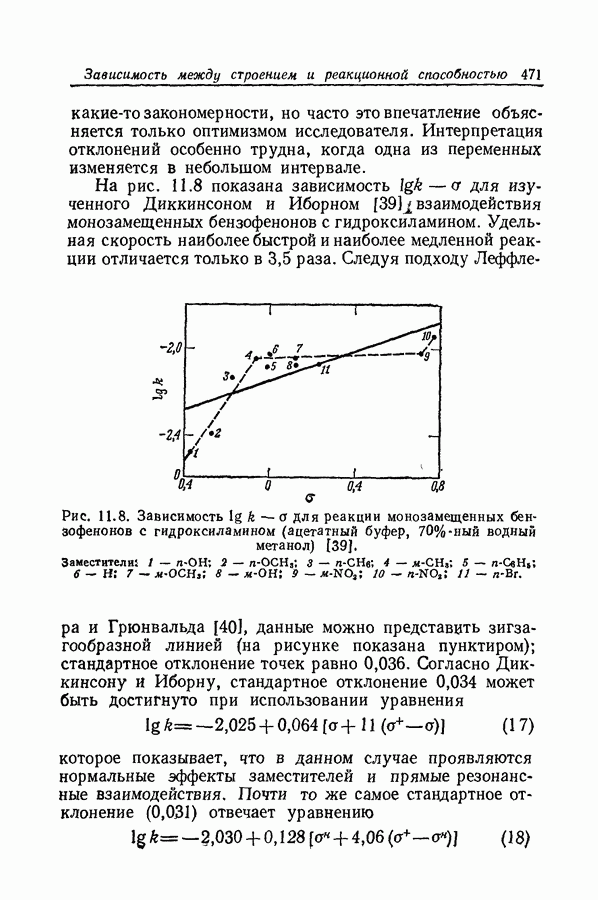
ограничен, постоянство этих двух
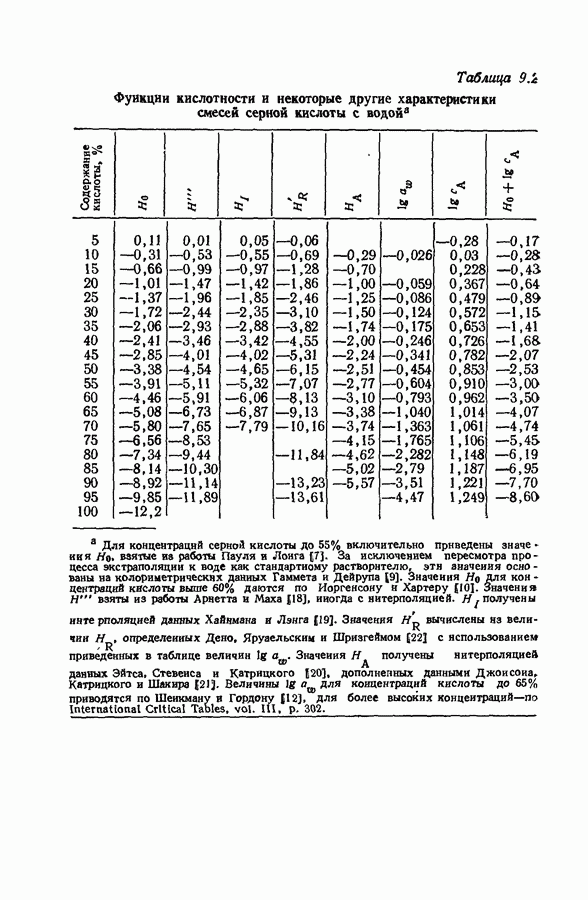
Таблица 9.3. Коэффициенты экстиикции ацетофзнона в смесях серной кислоты с водой [45]

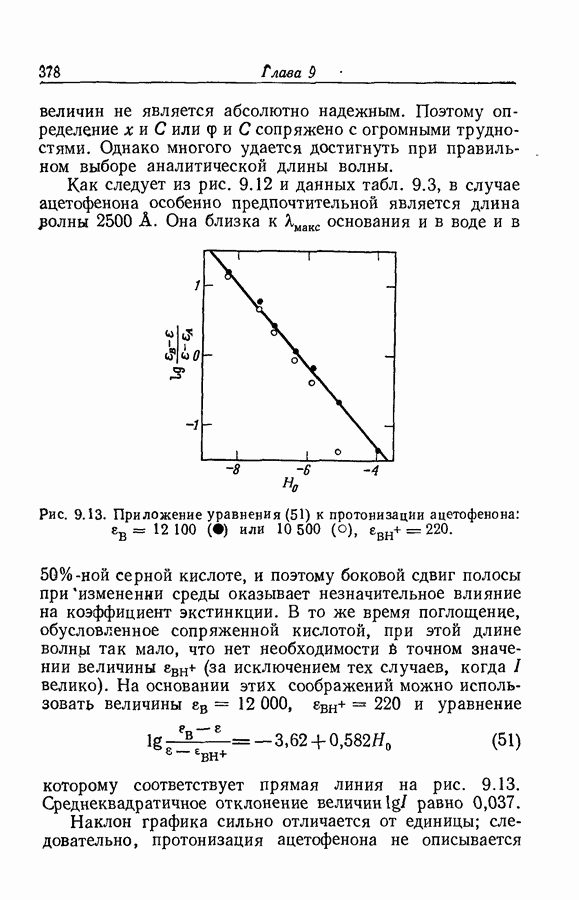
величин не является абсолютно надежным. Поэтому определение х и С или  и С сопряжено с огромными трудностями. Однако многого удается достигнуть при правильном выборе аналитической длины волны.
и С сопряжено с огромными трудностями. Однако многого удается достигнуть при правильном выборе аналитической длины волны.
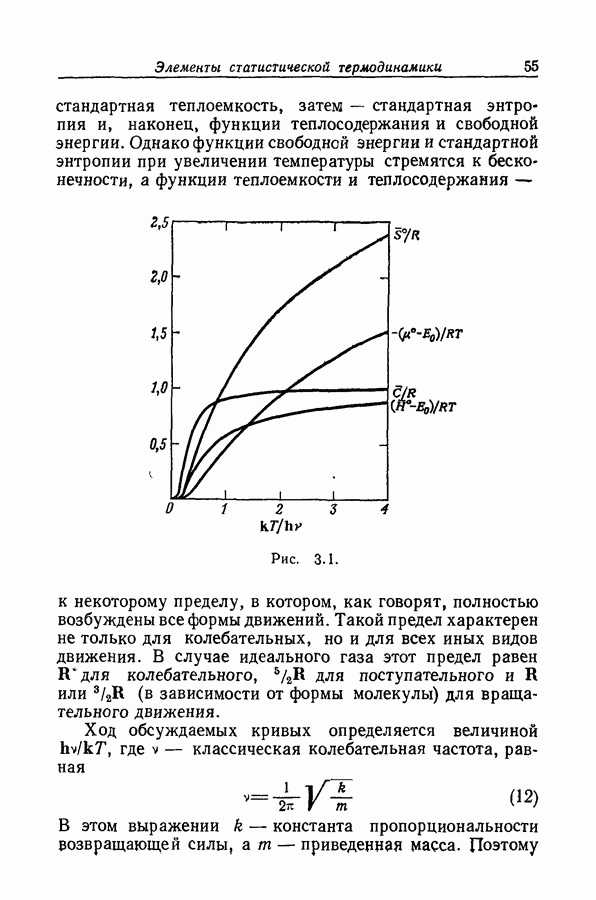
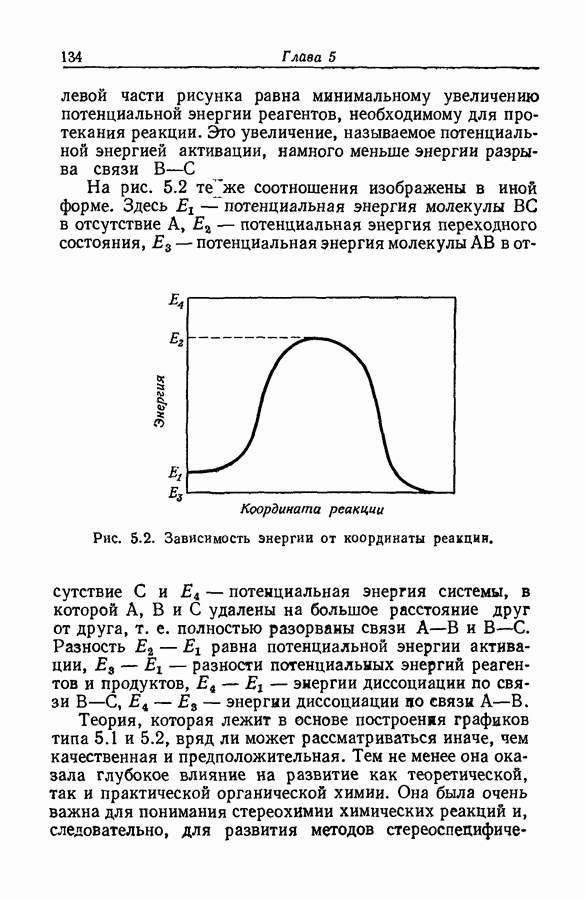
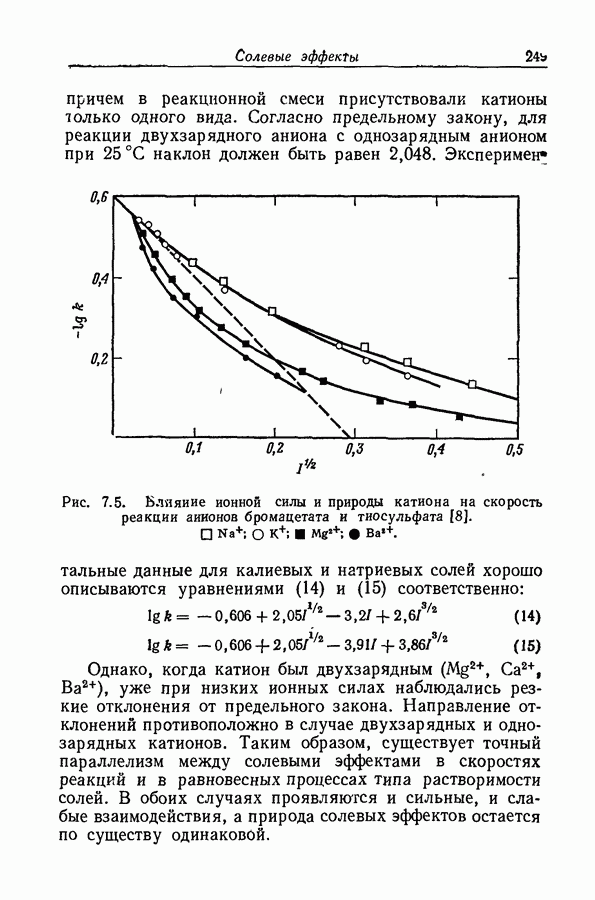
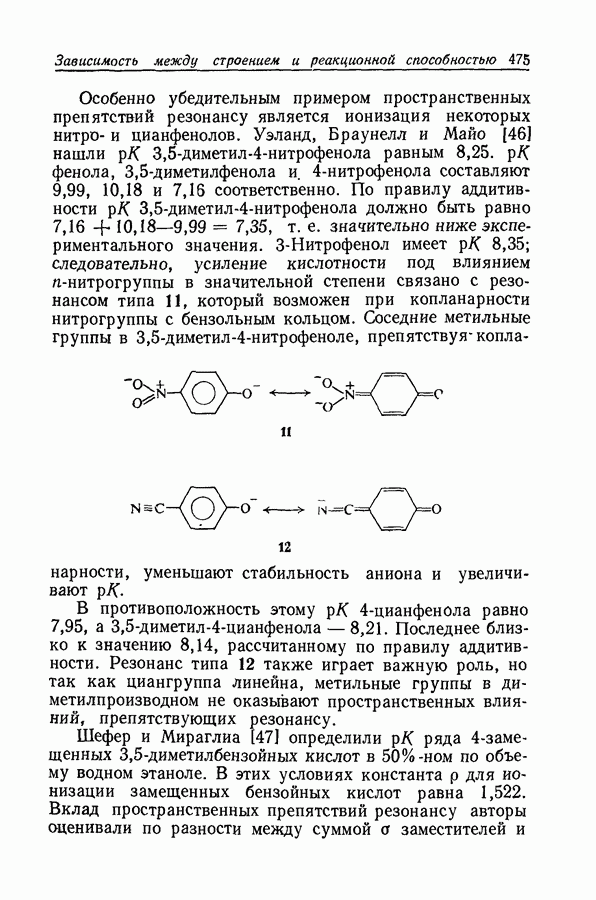
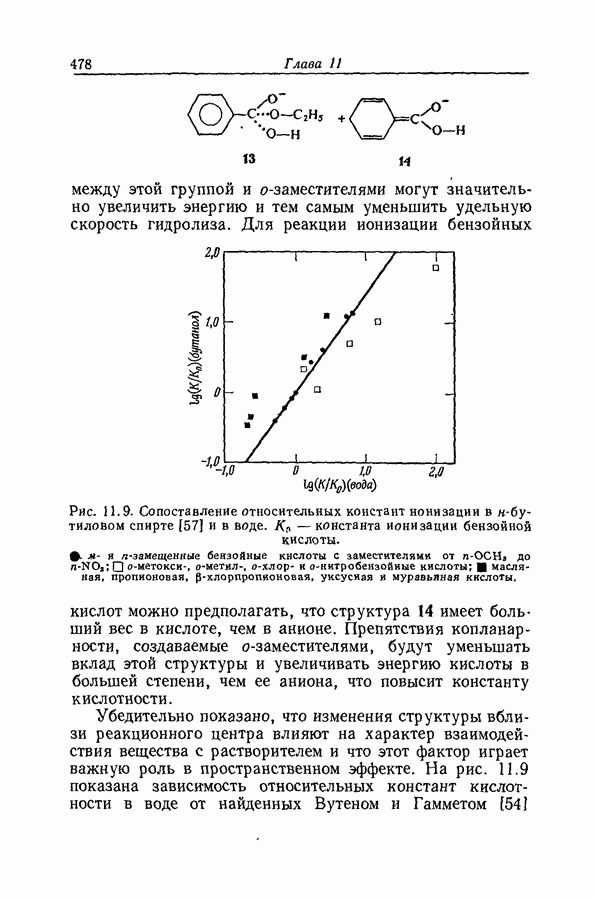
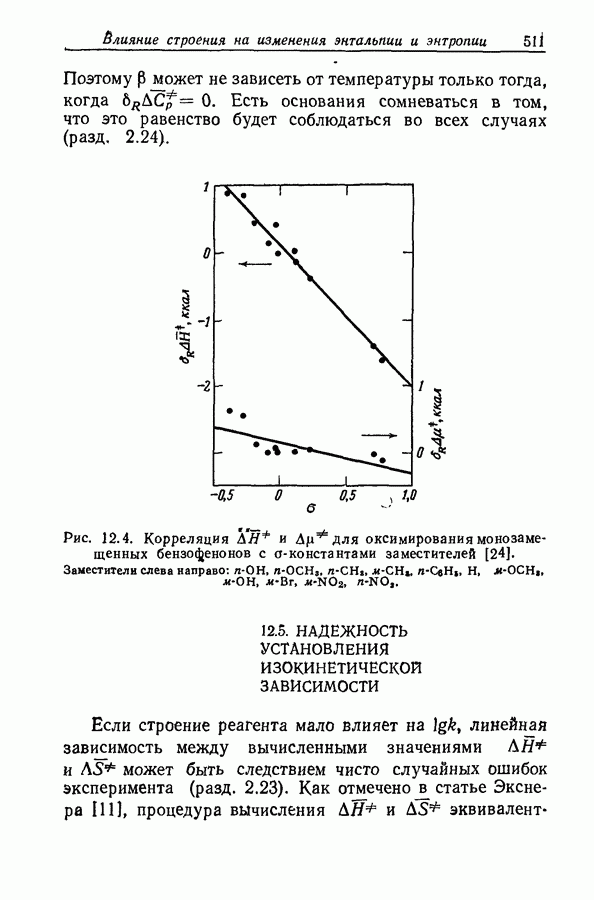
Как следует из рис. 9.12 и данных табл. 9.3, в случае ацетофенона особенно предпочтительной является длина олны 2500 А.

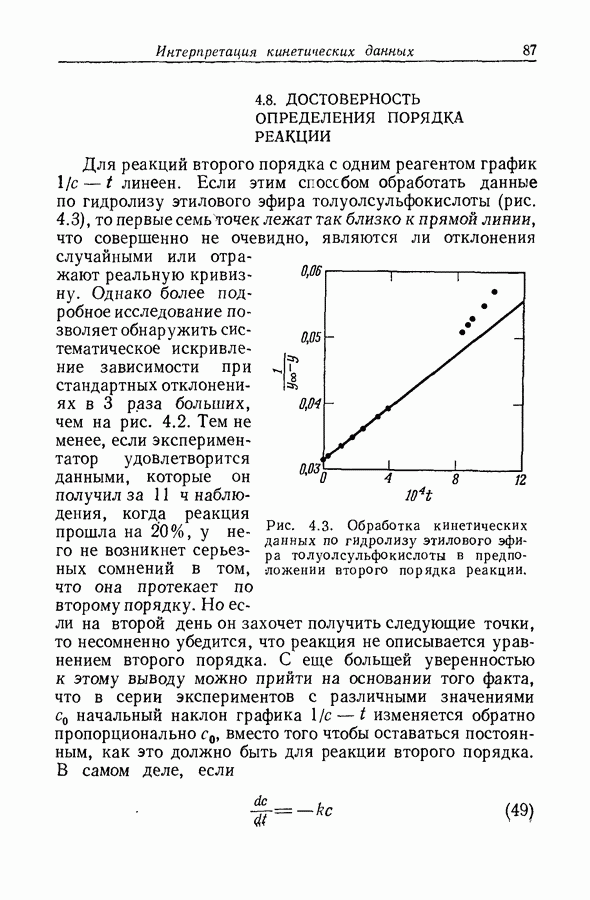
Рис. 9.13. Приложение уравнения (51) к протонизации ацетофенона:  или
или  .
.
Она близка к  основания и в воде и в 50%-ной серной кислоте, и поэтому боковой сдвиг полосы приизменении среды оказывает незначительное влияние на коэффициент экстинкции. В то же время поглощение, обусловленное сопряженной кислотой, при этой длине волны так мало, что нет необходимости в точном значении величины
основания и в воде и в 50%-ной серной кислоте, и поэтому боковой сдвиг полосы приизменении среды оказывает незначительное влияние на коэффициент экстинкции. В то же время поглощение, обусловленное сопряженной кислотой, при этой длине волны так мало, что нет необходимости в точном значении величины  (за исключением тех случаев, когда I велико). На основании этих соображений можно использовать величины
(за исключением тех случаев, когда I велико). На основании этих соображений можно использовать величины  и уравнение
и уравнение

которому соответствует прямая линия на рис. 9.13. Среднеквадратичное отклонение величин  равно 0,037.
равно 0,037.
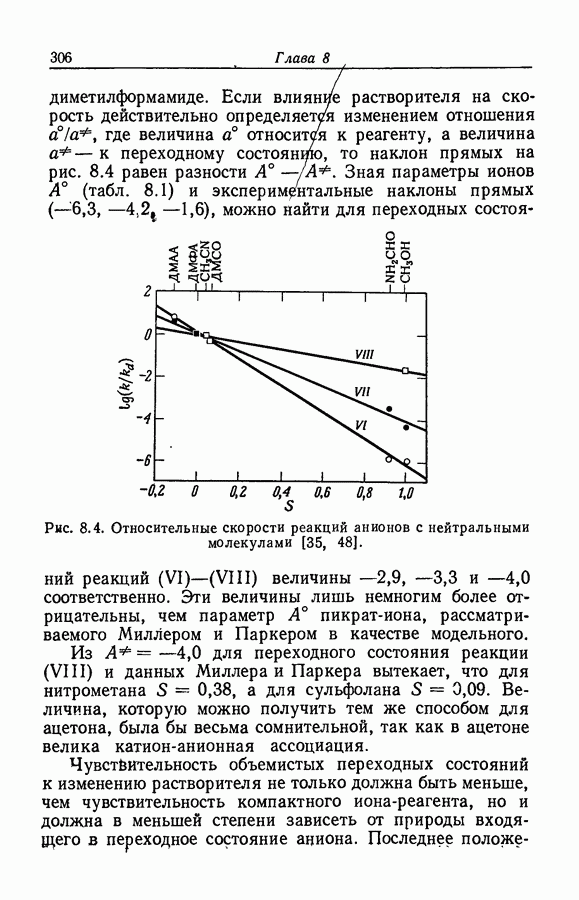
Наклон графика сильно отличается от единицы; следовательно, протонизация ацетофенона не описывается
функцией кислотности  . Если используемое значение
. Если используемое значение  понизить до неправдоподобной величины 10 500, то наклон в области полупревращения возрастет только до 0,7 и график приобретет заметную кривизну.
понизить до неправдоподобной величины 10 500, то наклон в области полупревращения возрастет только до 0,7 и график приобретет заметную кривизну.
Если опираться на функцию  и считать
и считать  , то экспериментальные данные могут быть представлены уравнением
, то экспериментальные данные могут быть представлены уравнением

со среднеквадратичным отклонением 0,021. Отсюда вытекает, что  ацетофенона составляет около —4.
ацетофенона составляет около —4.
Однако Флексер, Гаммет и Дингуэлл [45], использовавшие те же экспериментальные данные, не обнаружили несогласованности с функцией  (впрочем, другой они тогда и не знали) и пришли к выводу, что
(впрочем, другой они тогда и не знали) и пришли к выводу, что  ацетофенона несколько более отрицательно, чем —6. Стюарт и Эйтс [46], опираясь на новые данные, получили ту же величину. В работе Флексера уравнение (48) было преобразовано к виду
ацетофенона несколько более отрицательно, чем —6. Стюарт и Эйтс [46], опираясь на новые данные, получили ту же величину. В работе Флексера уравнение (48) было преобразовано к виду

Значение  определялось из спектров при высокой концентрации кислоты. Левая часть уравнения (53) линейно зависит от
определялось из спектров при высокой концентрации кислоты. Левая часть уравнения (53) линейно зависит от  и поэтому
и поэтому  равно отрезку, отсекаемому прямой на оси ординат. Удается получать удовлетворительные линейные зависимости, положение которых лишь незначительно зависит от выбора
равно отрезку, отсекаемому прямой на оси ординат. Удается получать удовлетворительные линейные зависимости, положение которых лишь незначительно зависит от выбора  Если учесть различие между нулевыми точками использованной шкалы
Если учесть различие между нулевыми точками использованной шкалы  и шкалы
и шкалы  Пауля и Лонга [7], то из данных при 2500 А следует, что
Пауля и Лонга [7], то из данных при 2500 А следует, что  . Среднее значение, полученное аналогичным образом из данных по нескольким длинам волн, равно —6,15. Эти величины, которые опираются на значения
. Среднее значение, полученное аналогичным образом из данных по нескольким длинам волн, равно —6,15. Эти величины, которые опираются на значения  по Паулю и Лонгу, нельзя непосредственно сравнивать с полученными из уравнения (51), так как оно основывается на значениях
по Паулю и Лонгу, нельзя непосредственно сравнивать с полученными из уравнения (51), так как оно основывается на значениях  по Йоргенсону и Хартеру. При использовании значений
по Йоргенсону и Хартеру. При использовании значений  по Паулю и Лонгу уравнение (51) преобразуется в
по Паулю и Лонгу уравнение (51) преобразуется в

Среднеквадратичное отклонение равно 0,037; точке полупротонизации соответствует 
Метод Флексера, Гаммета и Дингуэлла оказывается удивительно эффективным средством нахождения точки полупротонизации данного основания при использовании любой функции кислотности. Если в уравнении (53)  заменить на
заменить на  то также получится хорошая линейная зависимость, однако
то также получится хорошая линейная зависимость, однако  станет равным —4,1. Это находится в разумном соответствии с уравнением (52). Таким образом, метод удобен для тех, кто игнорирует или предпочитает не замечать, что используемая им функция кислотности в действительности неприменима.
станет равным —4,1. Это находится в разумном соответствии с уравнением (52). Таким образом, метод удобен для тех, кто игнорирует или предпочитает не замечать, что используемая им функция кислотности в действительности неприменима.
Стюарт и Эйтс, используя  по Паулю и Лонгу, также получили для ацетбфенона
по Паулю и Лонгу, также получили для ацетбфенона  . Обработка экспериментальных данных проводилась по методике, предложенной Дэвис и Гейсманом [47]. Предполагалось, что величины
. Обработка экспериментальных данных проводилась по методике, предложенной Дэвис и Гейсманом [47]. Предполагалось, что величины  не зависят от спектральных сдвигов, вызываемых изменением среды (индексы 1 и 2 обозначают две различные длины волны). Это допущение справедливо только тогда, когда и
не зависят от спектральных сдвигов, вызываемых изменением среды (индексы 1 и 2 обозначают две различные длины волны). Это допущение справедливо только тогда, когда и  линейно зависят от длины волны, что в общем случае сомнительно. Тем не менее эта методика часто приводит к таким значениям
линейно зависят от длины волны, что в общем случае сомнительно. Тем не менее эта методика часто приводит к таким значениям  в точке полупротонизации, которые согласуются с полученными иными способами.
в точке полупротонизации, которые согласуются с полученными иными способами.
Поэтому нахождение  в точке полупротонизации
в точке полупротонизации  не вызывает значительных трудностей даже при наличии спектральных сдвигов, обусловленных влиянием среды. Гораздо сложнее найти соответствующую данному случаю функцию кислотности и тем самым величину
не вызывает значительных трудностей даже при наличии спектральных сдвигов, обусловленных влиянием среды. Гораздо сложнее найти соответствующую данному случаю функцию кислотности и тем самым величину  Однако следует признать, что протонизация очень сходных веществ (например, ряда замещенных ацетофенонов, исследованных Стюартом и Элтсом), вероятнее всего, описывается одной и той же функцией кислотности. Так как функции кислотности приблизительно линейно связаны с
Однако следует признать, что протонизация очень сходных веществ (например, ряда замещенных ацетофенонов, исследованных Стюартом и Элтсом), вероятнее всего, описывается одной и той же функцией кислотности. Так как функции кислотности приблизительно линейно связаны с  то в серии сходных соединений величины
то в серии сходных соединений величины  будут линейно зависеть от
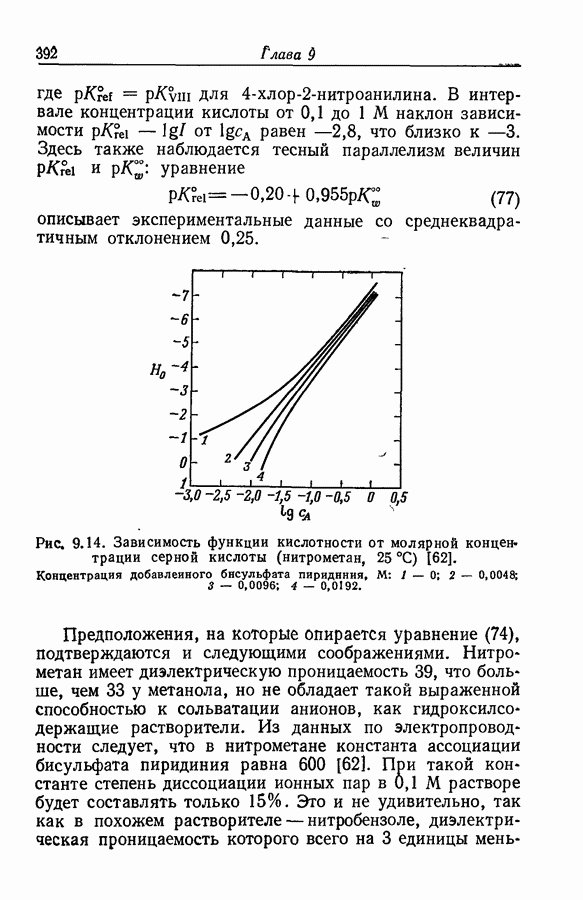
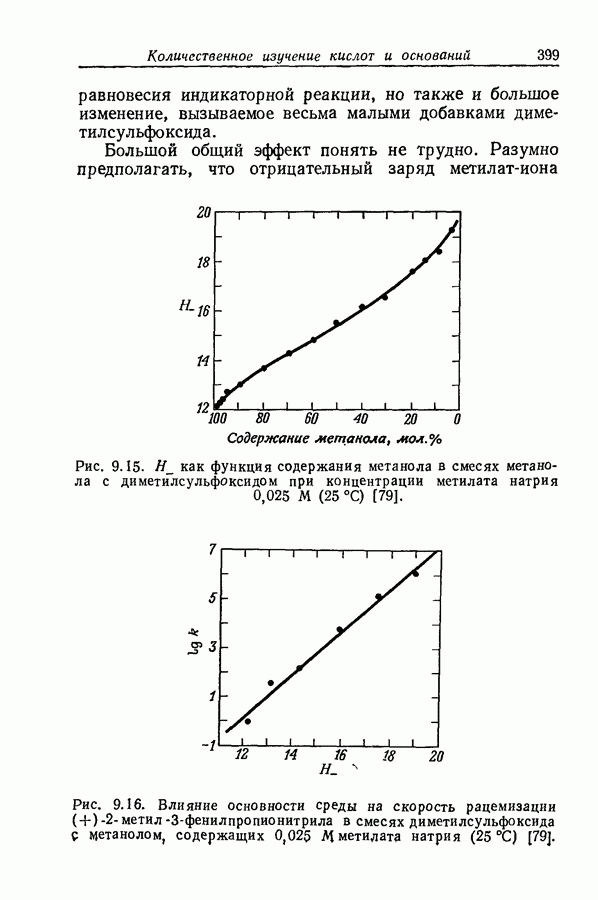
будут линейно зависеть от  в точке полупротонизации. Поэтому остаются справедливыми те выводы, к которым пришли Стюарт и Эйтс на основании линейной зависимости между
в точке полупротонизации. Поэтому остаются справедливыми те выводы, к которым пришли Стюарт и Эйтс на основании линейной зависимости между  и константами заместителей.
и константами заместителей.
К счастью, определение индикаторных отношений  на которых строится функция кислотности, может быть
на которых строится функция кислотности, может быть
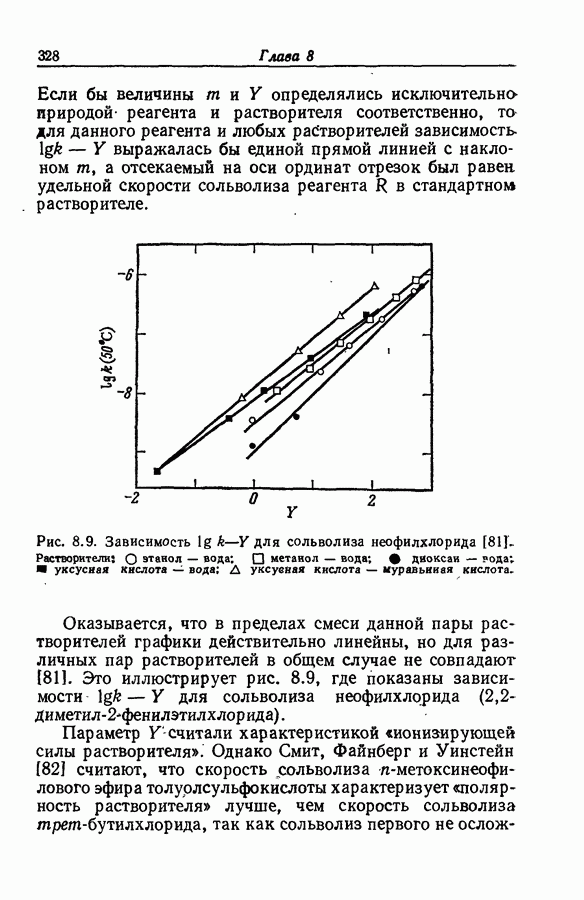
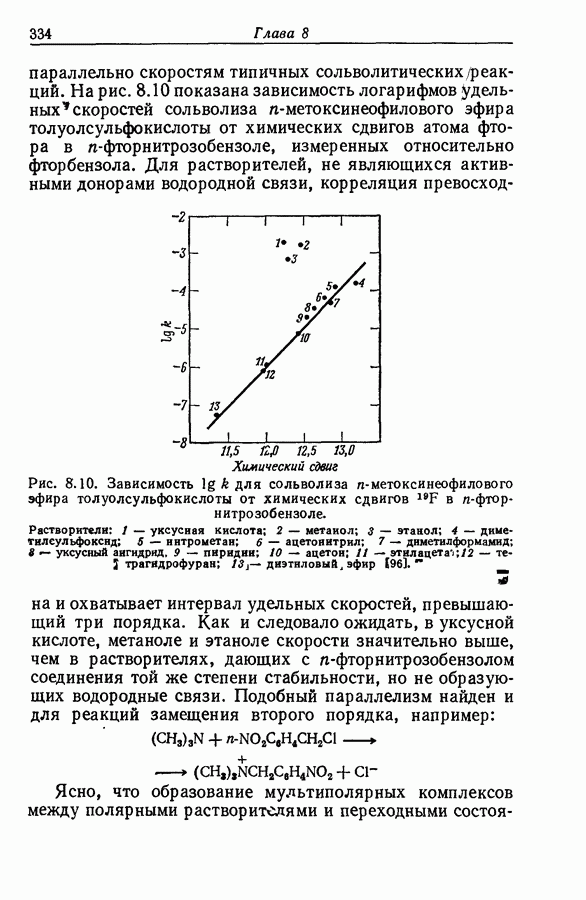
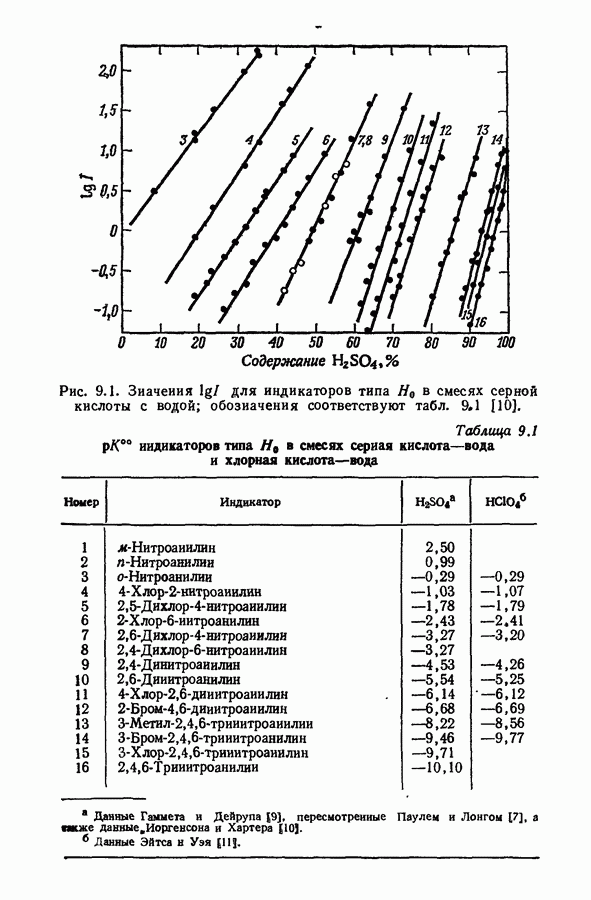
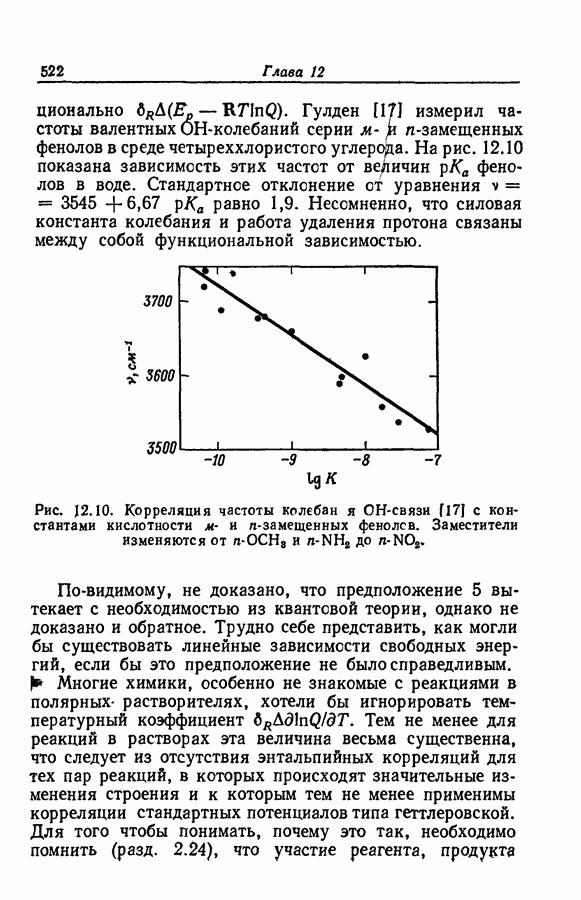
проведено или проверено в таких условиях, когда эффекты среды незначительны. Для измерений выбираются такие длины волн, при которых одна форма индикатора поглощает сильно, а другая — слабо, причем выбранная длина волны находится вблизи Ямакс сильно поглощающей формы. Далее, эффекты среды вне области протонирования обычно сводятся к небольшим боковым сдвигам. В ранней работе [9] использовалась визуальная колориметрия, но позднее данные этой работы были либо проверены спектрофотометрическим методом [8], либо заменены более новыми [10].
Если данные по средней области индикаторного равновесия можно описать с помощью функции кислотности  то в пределах этой области изменение отношения
то в пределах этой области изменение отношения  соответствует функции
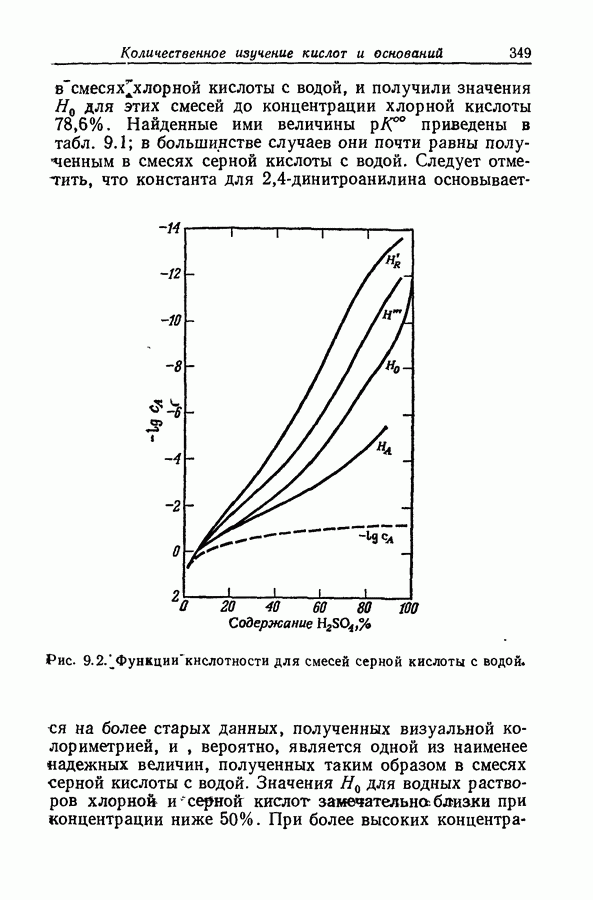
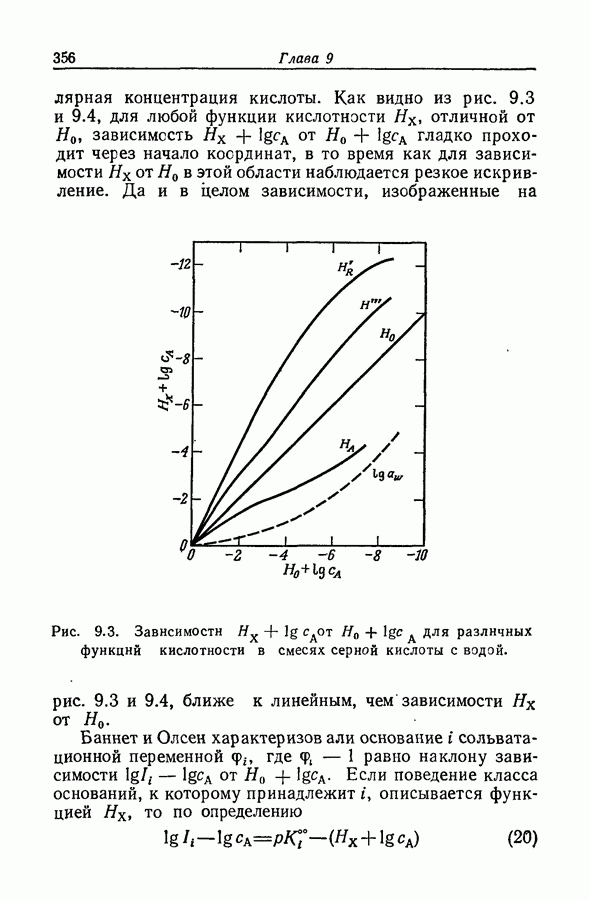
соответствует функции  Согласованность графиков на рис. 9.2-9.4 убедительно показывает, что такое поведение существует и за пределами средней области. Это не опровергается кажущейся несогласованностью с данными по низким и высоким степеням превращения индикатора, так как в этих случаях возрастает погрешность определения
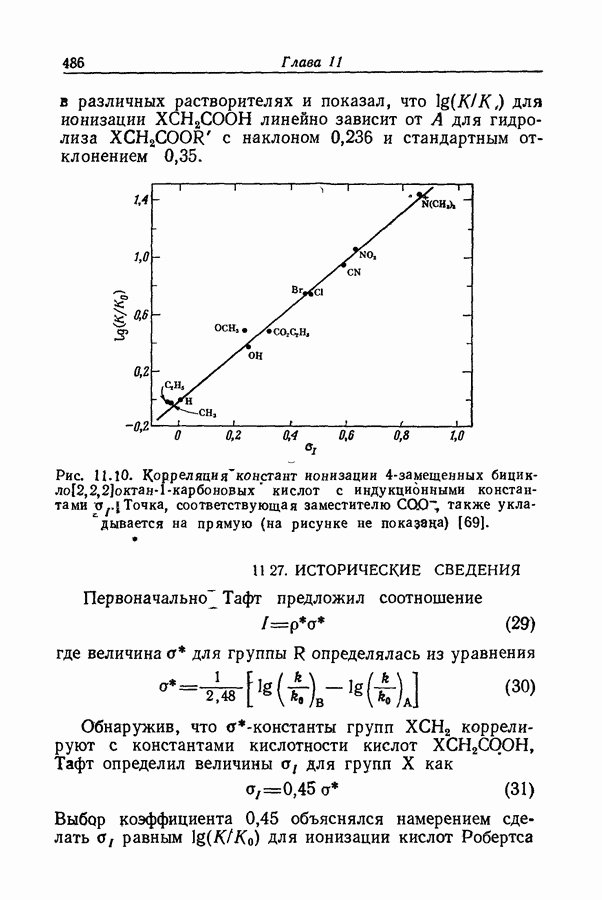
Согласованность графиков на рис. 9.2-9.4 убедительно показывает, что такое поведение существует и за пределами средней области. Это не опровергается кажущейся несогласованностью с данными по низким и высоким степеням превращения индикатора, так как в этих случаях возрастает погрешность определения  вызванная неточностью величин
вызванная неточностью величин 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ТЕРМОДИНАМИКА РЕАКЦИИ В РАСТВОРАХ
- 2.2. ИЗМЕНЕНИЕ ЭНЕРГИИ ГИББСА В ПРОЦЕССЕ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.3. УСЛОВИЕ РАВНОВЕСИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.4. ПРИБЛИЖЕНИЕ РАЗБАВЛЕННОГО РАСТВОРА
- 2.5. СТАНДАРТНЫЙ ПОТЕНЦИАЛ
- 2.6. ЗАКОН РАВНОВЕСИЯ В ПРИБЛИЖЕНИИ РАЗБАВЛЕННОГО РАСТВОРА
- 2.7. КОЭФФИЦИЕНТ АКТИВНОСТИ
- 2.8. ТОЧНЫЙ ЗАКОН РАВНОВЕСИЯ
- 2.9. ЗНАК ПРОИЗВОДНОЙ …
- 2.10. АКТИВНОСТЬ И СТАНДАРТНАЯ АКТИВНОСТЬ
- 2.11. КОНСТАНТЫ РАВНОВЕСИЯ В РАЗЛИЧНЫХ СРЕДАХ
- 2.12. ЧИСЛО И ВЫБОР КОМПОНЕНТОВ
- 2.13. ФОРМАЛЬНЫЕ И ИСТИННЫЕ ЗНАЧЕНИЯ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.14. ФУНКЦИЯ q°
- 2.15. УРАВНЕНИЕ ГИББСА—ДЮГЕМА
- 2.16. МОЛЕКУЛЯРНЫЕ ВЕСА В РАСТВОРЕ
- 2.17. УРАВНЕНИЕ ГИББСА—ДЮГЕМА ДЛЯ МНОГОКОМПОНЕНТНЫХ СИСТЕМ
- 2.18. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 2.19. ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.20. МОЛЬНАЯ ЭНТАЛЬПИЯ И МОЛЬНАЯ ЭНТРОПИЯ КАК ФУНКЦИИ КОНЦЕНТРАЦИИ
- 2.21. ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ
- 2.22. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЭНТАЛЬПИИ И СТАНДАРТНОЙ ЭНТРОПИИ РЕАКЦИИ
- 2.23. ПРОБЛЕМА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ …
- 2.24. ФОРМАЛЬНЫЕ ЗНАЧЕНИЯ СТАНДАРТНОЙ ЭНТАЛЬПИИ, ЭНТРОПИИ И ТЕПЛОЕМКОСТИ
- 3. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
- 3.2. СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА ИДЕАЛЬНОГО ГАЗА
- 3.3. ПРИРОДА СТАТИСТИЧЕСКИХ СУММ
- 3.4. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ПРОСТОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
- 3.5. ТИПИЧНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
- 3.6. РАСЧЕТ СТАТИСТИЧЕСКИХ СУММ
- 3.7. СТАТИСТИЧЕСКАЯ МЕХАНИКА И ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗОВОЙ ФАЗЕ
- 3.8. ИЗМЕНЕНИЕ ЭНТАЛЬПИИ И ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 3.9. СТАТИСТИЧЕСКАЯ МЕХАНИКА РАЗБАВЛЕННОГО РАСТВОРА
- 3.10. ПРАВИЛО БАРКЛЕЯ—БАТЛЕРА
- 3.11. НЕКОТОРЫЕ ОСОБЕННОСТИ ВОДНЫХ РАСТВОРОВ
- 3.12. ИЗМЕНЕНИЯ СТАНДАРТНОЙ ЭНТРОПИИ ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 3.13. СВЯЗЬ СО СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 3.14. СТАТИСТИЧЕСКАЯ СУММА q°
- 4. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ ДАННЫХ
- 4.2. СИСТЕМАТИКА И ТЕРМИНОЛОГИЯ
- 4.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИИ
- 4.4. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ КИНЕТИКИ
- 4.5. ЛИНЕЙНЫЕ ФОРМЫ УРАВНЕНИЙ ДЛЯ КИНЕТИЧЕСКИ ПРОСТЫХ НЕОБРАТИМЫХ РЕАКЦИИ
- 4.6. ПРОБЛЕМА ТОЧНОСТИ
- 4.7. ВЛИЯНИЕ СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ ОТ ЛИНЕЙНОСТИ
- 4.8. ДОСТОВЕРНОСТЬ ОПРЕДЕЛЕНИЯ ПОРЯДКА РЕАКЦИИ
- 4.9. ПРОТОЧНЫЕ РЕАКТОРЫ С ПЕРЕМЕШИВАНИЕМ
- 4.10. КИНЕТИЧЕСКИ ПРОСТЫЕ ОБРАТИМЫЕ РЕАКЦИИ
- 4.11. КИНЕТИЧЕСКИ СЛОЖНЫЕ РЕАКЦИИ
- 4.12. ЭКСПЕРИМЕНТАЛЬНОЕ РАСПОЗНАВАНИЕ СИСТЕМ, ВКЛЮЧАЮЩИХ РЕАКЦИИ ТОЛЬКО ПЕРВОГО ПОРЯДКА
- 4.13. ИНТЕГРАЛЬНЫЕ ФОРМЫ УРАВНЕНИИ ДЛЯ СИСТЕМ РЕАКЦИИ ПЕРВОГО ПОРЯДКА
- 4.14. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ УРАВНЕНИЙ, СОДЕРЖАЩИХ ДВА ЭКСПОНЕНЦИАЛЬНЫХ ЧЛЕНА
- 4.15. МЕТОД БОДЕНШТЕИНА (МЕТОД СТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ)
- 4.16. ПРОБЛЕМА ТОЧНОСТИ УРАВНЕНИИ С БОЛЬШИМ ЧИСЛОМ ПАРАМЕТРОВ
- 4.17. УРАВНЕНИЕ МИХАЭЛИСА-МЕНТЕН
- 4.18. СИСТЕМЫ С ПРЕДРАВНОВЕСИЕМ
- 4.19. ВЛИЯНИЕ АССОЦИАТИВНОГО РАВНОВЕСИЯ
- 4.20. РАСПОЗНАВАНИЕ СЛОЖНОСТИ РЕАКЦИИ
- 4.21. ИСПОЛЬЗОВАНИЕ ПРОТОЧНОГО РЕАКТОРА С ПЕРЕМЕШИВАНИЕМ ДЛЯ ИЗУЧЕНИЯ МНОГОСТАДИЙНЫХ РЕАКЦИЙ
- 4.22. ПРОТОЧНЫЙ ТРУБЧАТЫЙ РЕАКТОР
- 4.23. ИЗУЧЕНИЕ ОТНОСИТЕЛЬНОЙ РЕАКЦИОННОЙ СПОСОБНОСТИ МЕТОДОМ КОНКУРИРУЮЩИХ РЕАКЦИЙ
- 4.24. ОЧЕНЬ БЫСТРЫЕ РЕАКЦИИ, ЛИМИТИРУЕМЫЕ ДИФФУЗИЕЙ
- 4.25. СПРАВЕДЛИВОСТЬ ЗАКОНА ДЕЙСТВИЯ МАСС ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 4.26. ПРИНЦИП НЕЗАВИСИМОГО ПРОТЕКАНИЯ РЕАКЦИЙ
- 4.27. КАТАЛИТИЧЕСКИЕ РЕАКЦИИ И РЕАКЦИИ НУЛЕВОГО ПОРЯДКА
- 4.28. «МРАЧНЫЕ ВРЕМЕНА» И «ВОЗРОЖДЕНИЕ»
- 5. ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.2. ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СИСТЕМЫ В ХОДЕ РЕАКЦИИ
- 5.3. КООРДИНАТА РЕАКЦИИ
- 5.4. ДЕТАЛЬНАЯ ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.5. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.6. ОБОСНОВАННОСТЬ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.7. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА ДРУГИЕ ТИПЫ РЕАКЦИЙ
- 5.8. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА НЕИДЕАЛЬНЫЕ РАСТВОРЫ
- 5.9. СОСТАВ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.10. ЛИМИТИРУЮЩЕЕ ПЕРЕХОДНОЕ СОСТОЯНИЕ ИЛИ ЛИМИТИРУЮЩИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.11. ПАРАЛЛЕЛЬНЫЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.12. ОБЯЗАТЕЛЬНО ЛИ ОБРАЗОВАНИЕ ПРОМЕЖУТОЧНЫХ СОЕДИНЕНИЙ?
- 5.13. ПРОДВИЖЕНИЕ ОТ РЕАГЕНТОВ К ПЕРЕХОДНОМУ СОСТОЯНИЮ
- 5.14. ВОПРОСЫ ПО ПОВОДУ МЕХАНИЗМА, ИМЕЮЩИЕ И НЕ ИМЕЮЩИЕ СМЫСЛА
- 5.15. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ
- 5.16. ПРИНЦИП КЕРТИНА
- 5.17. РЕАКЦИЯ СТИЛЬБЕНА С БРОМОМ В МЕТАНОЛЕ
- 5.18. ПРОБЛЕМА МЕХАНИЗМА РЕАКЦИИ С УЧАСТИЕМ ИОНОВ
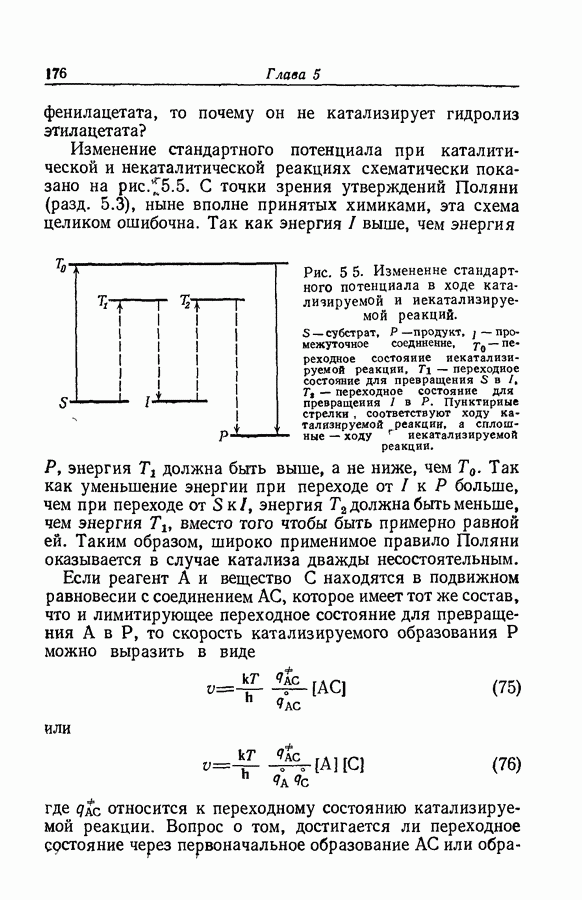
- 5.19. ЭФФЕКТЫ СТРОЕНИЯ В СИСТЕМАХ С ПОДВИЖНЫМ РАВНОВЕСИЕМ
- 5.20. ПРОБЛЕМА СТЕХИОМЕТРИЧЕСКОГО ВКЛЮЧЕНИЯ РАСТВОРИТЕЛЯ В ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 5.21. ЭНТРОПИЯ АКТИВАЦИИ
- 5.22. СТРУКТУРНЫЕ ИЗОТОПНЫЕ ЭФФЕКТЫ
- 5.23. ИЗОТОПНЫЕ ЭФФЕКТЫ РАСТВОРИТЕЛЕЙ
- 5.24. ВЛИЯНИЕ ДАВЛЕНИЯ НА СКОРОСТЬ РЕАКЦИЙ
- 5.25. СИСТЕМЫ С ПОДВИЖНЫМИ РАВНОВЕСИЯМИ В ИСХОДНЫХ И КОНЕЧНЫХ ВЕЩЕСТВАХ
- 5.26. КАТАЛИЗ
- 5.27. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ В СЛУЧАЕ КАТАЛИТИЧЕСКОГО ПРОЦЕССА
- 5.28. ФЕРМЕНТАТИВНЫЙ И ГЕТЕРОГЕННЫЙ КАТАЛИЗ
- 5.29. МИКРОСКОПИЧЕСКАЯ ОБРАТИМОСТЬ ИЛИ ДЕТАЛЬНОЕ РАВНОВЕСИЕ
- 6. НЕКОТОРЫЕ РЕАКЦИИ ЗАМЕЩЕНИЯ
- 6.1 НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ ВТОРОГО ПОРЯДКА У НАСЫЩЕННОГО АТОМА УГЛЕРОДА
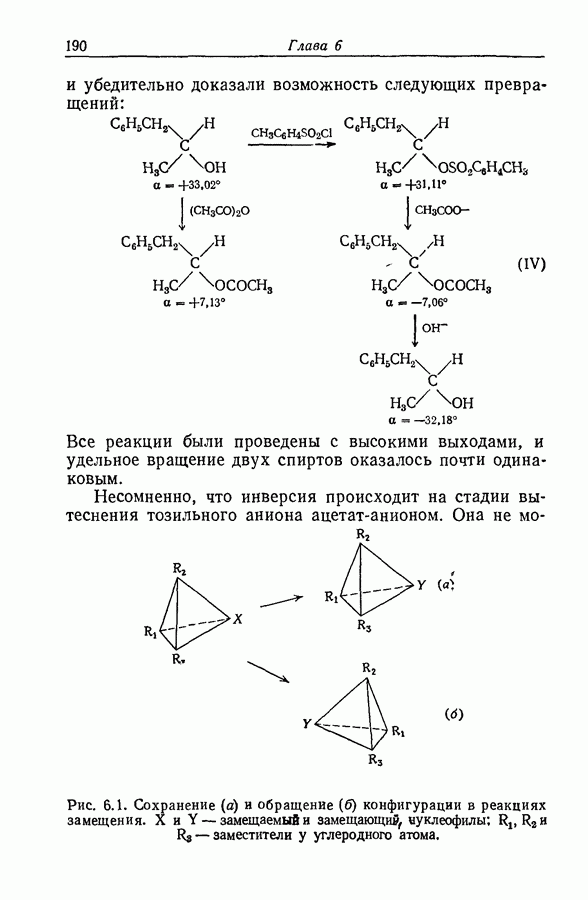
- 6.2. РАЦЕМИЗАЦИЯ И ИЗОТОПНЫЙ ОБМЕН
- 6.3. РЕАКЦИИ СОЛЬВОЛИЗА
- 6.4. КАРБОНИЕВО-ИОННЫЙ МЕХАНИЗМ
- 6.5. СОЛЕВЫЕ ЭФФЕКТЫ В СИЛЬНО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
- 6.6. РОЛЬ РАСТВОРИТЕЛЯ
- 6.7. ВОПРОСЫ ТЕРМИНОЛОГИИ
- 6.8. ОГРАНИЧЕННОСТЬ ПРЕДСТАВЛЕНИИ ОБ ОБРАЗОВАНИИ СВОБОДНЫХ ИОНОВ КАРБОНИЯ
- 6.9. ГИПОТЕЗА ИОННЫХ ПАР
- 6.10. ВЛИЯНИЕ ДОБАВОК АЗИДОВ
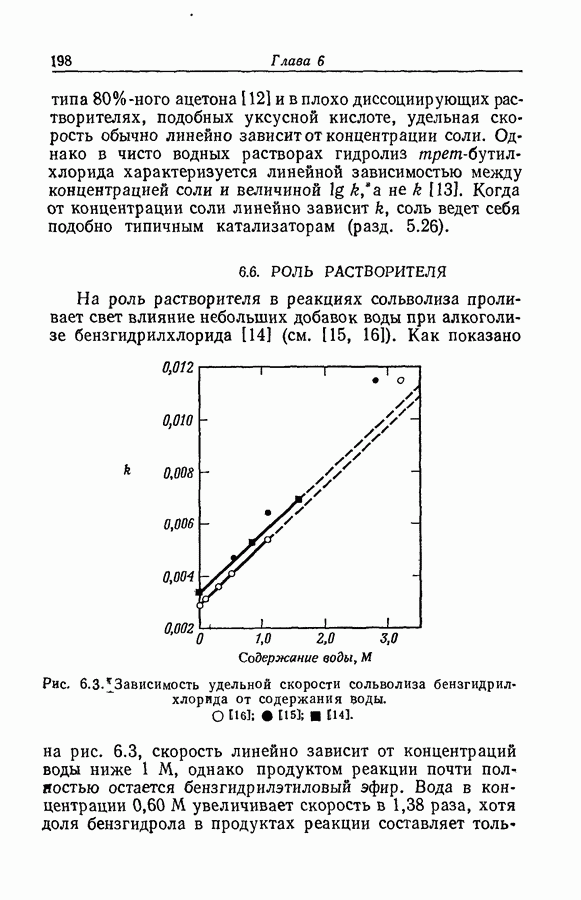
- 6.11. УЧАСТИЕ БЕЗГИДРОКСИЛЬНЫХ РАСТВОРИТЕЛЕЙ В ОБРАЗОВАНИИ ПЕРЕХОДНОГО КОМПЛЕКСА
- 6.12. АЛЛИЛЬНАЯ ПЕРЕГРУППИРОВКА
- 6.13. СОЛЬВОЛИЗ, СОПРОВОЖДАЮЩИЙСЯ РАЦЕМИЗАЦИЕЙ РЕАГЕНТА
- 6.14. ДОПОЛНИТЕЛЬНЫЕ ДАННЫЕ О ВЛИЯНИИ ДОБАВОК АЗИДОВ
- 6.15. ОСОБЫЙ СОЛЕВОЙ ЭФФЕКТ
- 6.16. ДВОЙНОЕ ОБРАЩЕНИЕ КОНФИГУРАЦИИ
- 6.17. БРОМОНИЕВЫЕ ИОНЫ КАК ПРОМЕЖУТОЧНЫЕ СОЕДИНЕНИЯ
- 6.18. ПРОБЛЕМА ФЕНОНИЕВОГО ИОНА
- 6.19. ПЕРЕГРУППИРОВКИ
- 6.20. ЭЛЕКТРОФИЛЬНОЕ АРОМАТИЧЕСКОЕ ЗАМЕЩЕНИЕ
- 6.21. РЕАКЦИЯ АЗОСОЧЕТАНИЯ
- 6.22. ВОЗМОЖНЫЕ ФОРМЫ РЕАГЕНТОВ
- 6.23. ПЕРЕХОДНОЕ СОСТОЯНИЕ РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.24. КАТАЛИТИЧЕСКОЕ ДЕЙСТВИЕ ПИРИДИНА
- 6.25. ИЗОТОПНЫЕ ЭФФЕКТЫ ВОДОРОДА В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.26. ПРОСТРАНСТВЕННЫЕ ВЛИЯНИЯ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.27. ЭНТРОПИЯ АЗОСОЧЕТАНИЯ
- 7. СОЛЕВЫЕ ЭФФЕКТЫ
- 7.1. УРАВНЕНИЕ БРЕНСТЕДА
- 7.2. ПРЕДЕЛЬНЫЙ ЗАКОН ДЕБАЯ — ХЮККЕЛЯ
- 7.3. СОЛЕВЫЕ ЭФФЕКТЫ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 7.4. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К НЕСИММЕТРИЧНЫМ ИОНАМ
- 7.5. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К МНОГОЗАРЯДНЫМ ИОНАМ
- 7.6. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИЙ СОЛЕЙ НА КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 7.7. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИИ СОЛЕЙ НА СКОРОСТЬ РЕАКЦИЙ МЕЖДУ ИОНАМИ
- 7.8. СОЛЕВЫЕ ЭФФЕКТЫ КАК ПОДТВЕРЖДЕНИЕ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 7.9. ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.10. ПОДАВЛЕНИЕ СОЛЕВЫХ ЭФФЕКТОВ, ПРИ ИЗУЧЕНИИ ПОРЯДКА РЕАКЦИЙ
- 7.11. ФИЗИЧЕСКИЙ СМЫСЛ ТЕОРИИ ДЕБАЯ — ХЮККЕЛЯ
- 7.12. МОДИФИКАЦИЯ ТЕОРИЙ ДЛЯ СЛУЧАЯ СЛАБЫХ ВЗАИМОДЕЙСТВИЙ
- 7.13. ПРИБЛИЖЕНИЕ БЬЕРРУМА
- 7.14. ИОННЫЕ ПАРЫ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 7.15. ОБРАЗОВАНИЕ ИОННЫХ ПАР И ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.16. О ПОНЯТИИ ИОННЫХ ПАР
- 7.17. О СЛАБОЙ АССОЦИАЦИИ ИОНОВ
- 7.18. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В ВОДНЫХ РАСТВОРАХ
- 7.19. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ВОДНЫХ РАСТВОРАХ
- 7.20. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ЖИДКОМ СЕРНИСТОМ АНГИДРИДЕ
- 7.21. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ СОЛЬВОЛИЗА В ВОДНЫХ РАСТВОРАХ
- 7.22. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В НЕВОДНЫХ РАСТВОРАХ
- 7.23. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 8. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ
- 8.3. ОБРАЗОВАНИЕ ИОННЫХ ПАР; СЛУЧАИ ИДЕАЛЬНОГО ЭЛЕКТРОСТАТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 8.4. АССОЦИАЦИЯ ИОНОВ В ЧЕТВЕРТИЧНЫХ АММОНИЕВЫХ СОЛЯХ
- 8.5. ИОННЫЕ ТРИПЛЕТЫ И ПОЛИМЕРЫ СОЛЕЙ
- 8.6. ВОДОРОДНАЯ СВЯЗЬ
- 8.7. ИОННЫЕ ПАРЫ С ВОДОРОДНОЙ СВЯЗЬЮ
- 8.8. ВЗАИМОДЕЙСТВИЕ АНИОНОВ С ДОНОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.9. ВЗАИМОДЕЙСТВИЕ КАТИОНОВ С АКЦЕПТОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.10. ДРУГИЕ ВИДЫ ВЗАИМОДЕЙСТВИИ ИОНОВ С НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
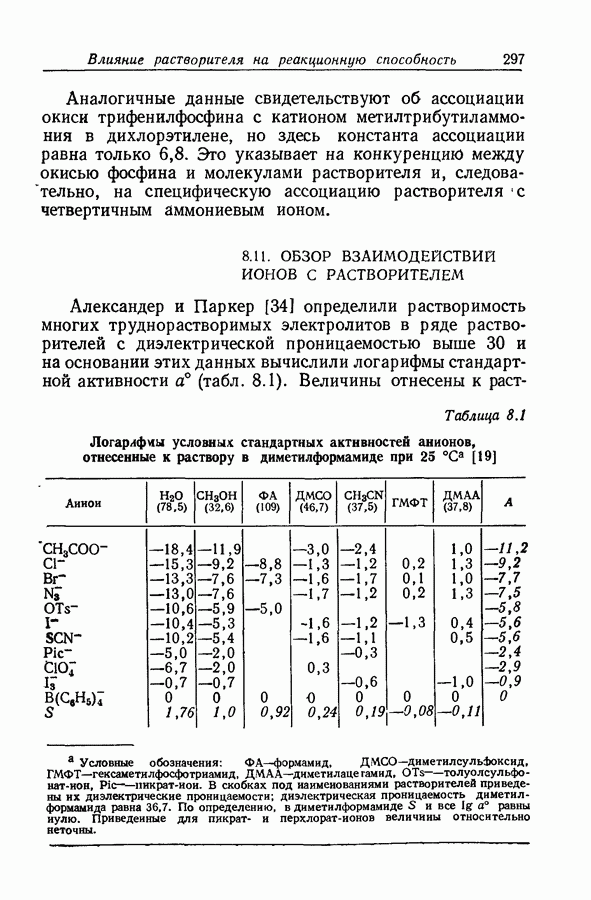
- 8.11. ОБЗОР ВЗАИМОДЕЙСТВИИ ИОНОВ С РАСТВОРИТЕЛЕМ
- 8.12. РОЛЬ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ
- 8.13. МЕТАЛЛООРГАНИЧЕСКИЕ СОЕДИНЕНИЯ ЭЛЕМЕНТОВ ПЕРВОЙ ГРУППЫ
- 8.14. ВЛИЯНИЕ СОЛЬВАТАЦИИ АНИОНА НА СКОРОСТЬ ВЗАИМОДЕЙСТВИЯ АНИОНА С НЕЙТРАЛЬНОЙ МОЛЕКУЛОЙ
- 8.15. ВЛИЯНИЕ СПЕЦИФИЧЕСКОЙ СОЛЬВАТАЦИИ КАТИОНОВ НА СКОРОСТИ РЕАКЦИЙ МЕЖДУ АНИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
- 8.16. ХЕЛАТНАЯ СОЛЬВАТАЦИЯ КАТИОНОВ
- 8.17. КИНЕТИКА РЕАКЦИЙ С УЧАСТИЕМ ИОННЫХ АГРЕГАТОВ
- 8.18. ИНЕРТНОСТЬ ТВЕРДЫХ РЕАГЕНТОВ
- 8.19. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ АМБИДЕНТНЫХ АНИОНОВ
- 8.20. ВЛИЯНИЕ ПРИРОДЫ РАСТВОРИТЕЛЯ НА РЕАКЦИИ КАТИОНОВ С АНИОНАМИ
- 8.21. ДИСПЕРСИОННЫЕ СИЛЫ
- 8.22. ПЛОТНОСТЬ КОГЕЗИОННОЙ ЭНЕРГИИ
- 8.23. РЕГУЛЯРНЫЕ И ИДЕАЛЬНЫЕ РАСТВОРЫ
- 8.24. ПЕРЕНОС РАСТВОРЕННОГО ВЕЩЕСТВА ИЗ ОДНОГО РЕГУЛЯРНОГО РАСТВОРА В ДРУГОЙ
- 8.25. ВЛИЯНИЕ СИЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
- 8.26. ИЗОКИНЕТИЧЕСКАЯ ЗАВИСИМОСТЬ ПРИ ИЗМЕНЕНИИ РАСТВОРИТЕЛЯ
- 8.27. СОЛЬВОЛИЗ В ВОДНО-СПИРТОВЫХ СМЕСЯХ
- 8.28. ИНЫЕ ВЛИЯНИЯ РАСТВОРИТЕЛЯ НА СКОРОСТЬ СОЛЬВОЛИЗА
- 8.29. КОМПЛЕКСЫ С ПЕРЕНОСОМ ЗАРЯДА
- 8.30. КОМПЛЕКСООБРАЗОВАНИЕ ЗА СЧЕТ МУЛЬТИПОЛЬНОГО ИЛИ ДИПОЛЬНОГО ВЗАИМОДЕЙСТВИЯ
- 9. КОЛИЧЕСТВЕННОЕ ИЗУЧЕНИЕ КИСЛОТ И ОСНОВАНИЙ
- 9.2. ЭЛЕКТРОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КИСЛОТНОСТИ В НЕВОДНЫХ РАСТВОРАХ
- 9.3. ИЗМЕРЕНИЕ КИСЛОТНОСТИ С ПОМОЩЬЮ ИНДИКАТОРОВ
- 9.4. ФУНКЦИЯ КИСЛОТНОСТИ Н0
- 9.5. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 9.6. ФУНКЦИИ КИСЛОТНОСТИ
- 9.7. ФУНКЦИИ КИСЛОТНОСТИ …
- 9.8. ДРУГИЕ ДАННЫЕ ПО ФУНКЦИЯМ КИСЛОТНОСТИ
- 9.9. ГИПОТЕЗА ТРЕХ ПЕРЕМЕННЫХ
- 9.10. СОЛЬВАТАЦИОННАЯ ПЕРЕМЕННАЯ «фи»
- 9.11. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ КИСЛОТНОСТИ
- 9.12. СТАНДАРТНЫЕ АКТИВНОСТИ В СМЕСЯХ СИЛЬНЫХ КИСЛОТ С ВОДОЙ
- 9.13. О ВЛИЯНИИ АКТИВНОСТИ ВОДЫ
- 9.14. ФУНКЦИИ КИСЛОТНОСТИ ДЛЯ ВЫСОКОКОНЦЕНТРИРОВАННЫХ РАСТВОРОВ КИСЛОТ
- 9.15. ФУНКЦИИ КИСЛОТНОСТИ И СКОРОСТИ КАТАЛИЗИРУЕМЫХ КИСЛОТАМИ РЕАКЦИЙ
- 9.16 НИТРОВАНИЕ АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ В СМЕСЯХ СЕРНОЙ КИСЛОТЫ С ВОДОЙ
- 9.17. СИСТЕМЫ, ОПИСЫВАЕМЫЕ ДВУМЯ ФУНКЦИЯМИ КИСЛОТНОСТИ
- 9.18. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ СИЛЫ ОСНОВАНИЯ
- 9.19. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН pK
- 9.20. НАЛОЖЕНИЕ ЭФФЕКТОВ СРЕДЫ ПРИ СПЕКТРОФОТОМЕТРИЧЕСКОМ ОПРЕДЕЛЕНИИ ОСНОВНОСТИ
- 9.21. МЕТОДЫ ВВЕДЕНИЯ ПОПРАВОК НА ЭФФЕКТЫ СРЕДЫ
- 9.22. ДРУГИЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ СИЛЫ СЛАБЫХ ОСНОВАНИЙ
- 9.23. ТЕМПЕРАТУРНЫЕ КОЭФФИЦИЕНТЫ
- 9.24. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ПЛОХО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
- 9.25. ПОВЕДЕНИЕ ИНДИКАТОРОВ В НИТРОМЕТАНЕ И СУЛЬФОЛАНЕ
- 9.26. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ДИМЕТИЛСУЛЬФОКСИДЕ
- 9.27. ФУНКЦИИ КИСЛОТНОСТИ И СИЛА ОСНОВАНИИ В ДРУГИХ ВЫСОКООСНОВНЫХ СРЕДАХ
- 9.28. СКОРОСТИ РЕАКЦИЙ В СИЛЬНООСНОВНЫХ СРЕДАХ
- 9.29. ОСНОВНОСТЬ АЛКОГОЛЯТОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ
- 10. СКОРОСТИ РЕАКЦИЙ С УЧАСТИЕМ КИСЛОТ И ОСНОВАНИЙ
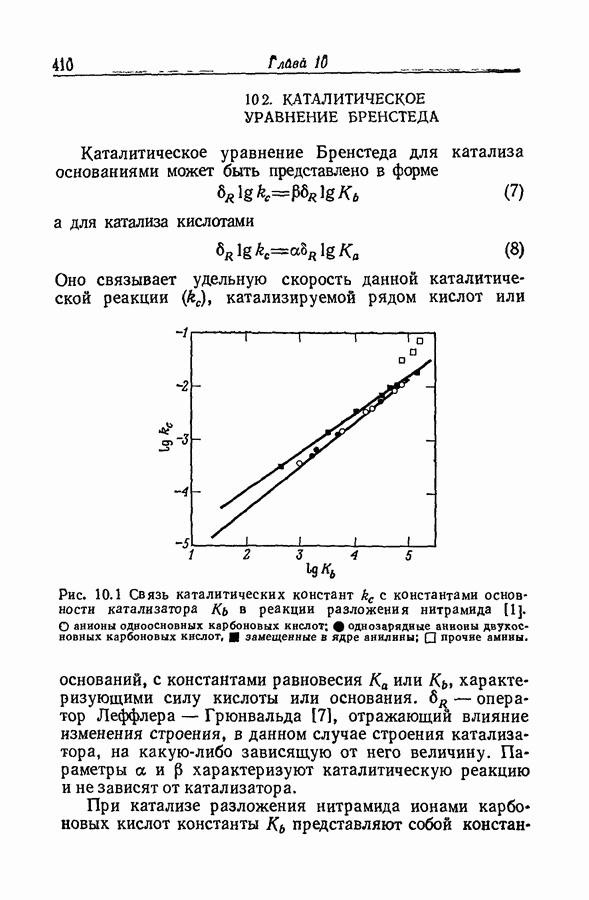
- 10.2. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА
- 10.3. СТАТИСТИЧЕСКИЕ ПОПРАВКИ
- 10.4. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 10.5. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА И ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 10.6. КАТАЛИЗ МОЛЕКУЛАМИ РАСТВОРИТЕЛЯ, ИОНАМИ ЛИОНИЯ И ЛИАТА
- 10.7. РАЗПОЗНАВАЕМОСТЬ ОБЩЕГО КИСЛОТНОГО И ОБЩЕГО ОСНОВНОГО КАТАЛИЗА
- 10.8. СКОРОСТИ РЕАКЦИЙ ПЕРЕНОСА ПРОТОНА
- 10.9. ТЕОРИЯ ЭЛЕКТРОННЫХ СМЕЩЕНИЙ
- 10.10. ГИДРАТАЦИЯ АЦЕТАЛЬДЕГИДА
- 10.11. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ ОСНОВАНИЯМИ
- 10.12. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ КИСЛОТАМИ
- 10.13. КАТАЛИЗ В РЕАКЦИИ ЕНОЛИЗАЦИИ
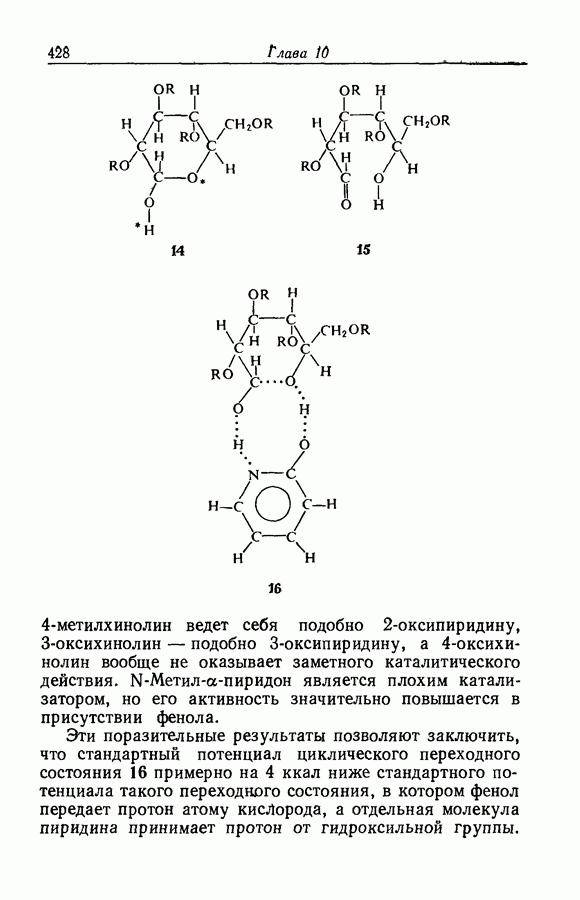
- 10.14. ЦИКЛИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 10.15. ГИДРОЛИЗ ЭФИРОВ
- 10.16. КРИВЫЕ ТИПА «КОЛОКОЛА» И «ПЕРЕВЕРНУТОГО КОЛОКОЛА»
- 10.17. ОБРАЗОВАНИЕ ОКСИМОВ И ДРУГИЕ ПОДОБНЫЕ РЕАКЦИИ
- 10.18. ГИДРОЛИЗ ФЕНИЛИМИНОЛАКТОНА
- 10.19. КАТАЛИЗ КИСЛОТАМИ ЛЬЮИСА
- 11. КОЛИЧЕСТВЕННЫЕ ЗАВИСИМОСТИ МЕЖДУ СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 11.2. ПРИНЦИП ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИЙ
- 11.4. ЛИНЕЙНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗМЕНЕНИЯМИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.5. КОРРЕЛЯЦИИ ГЕТТЛЕРА
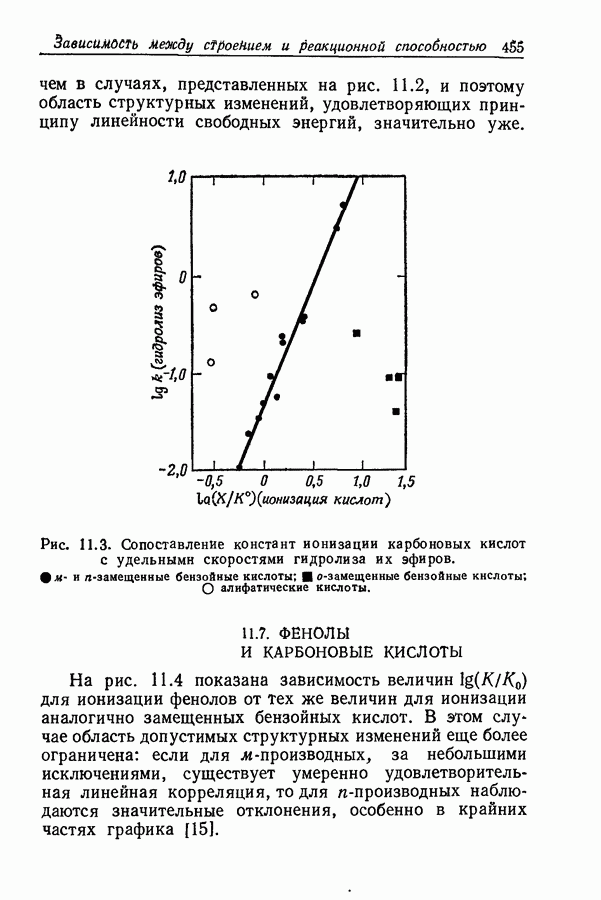
- 11.6. СИЛА КИСЛОТ И СКОРОСТЬ ГИДРОЛИЗА ИХ ЭФИРОВ
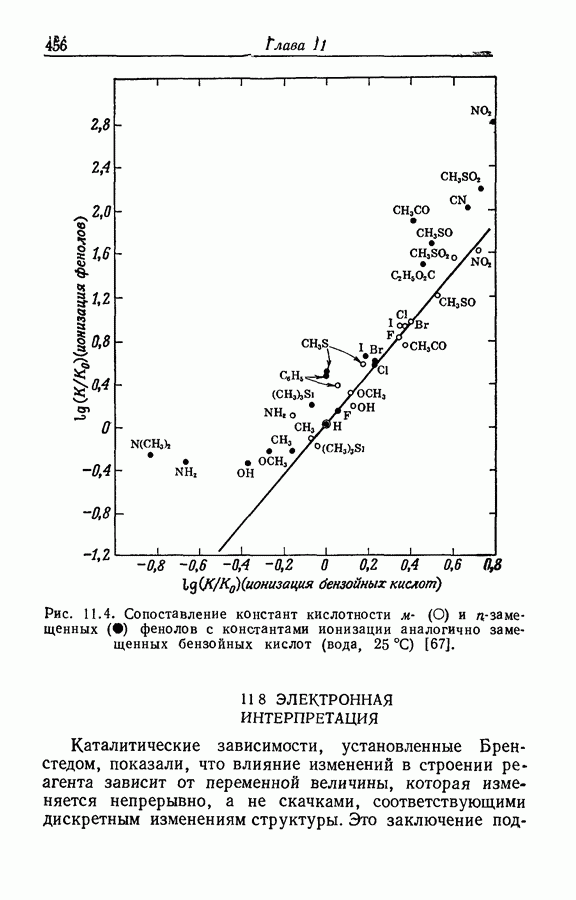
- 11.7. ФЕНОЛЫ И КАРБОНОВЫЕ КИСЛОТЫ
- 11.8 ЭЛЕКТРОННАЯ ИНТЕРПРЕТАЦИЯ
- 11.9. УРАВНЕНИЕ ГАММЕТА
- 11.10. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 11.11. ПРЯМЫЕ РЕЗОНАНСНЫЕ ВЗАИМОДЕИСТВИЯ
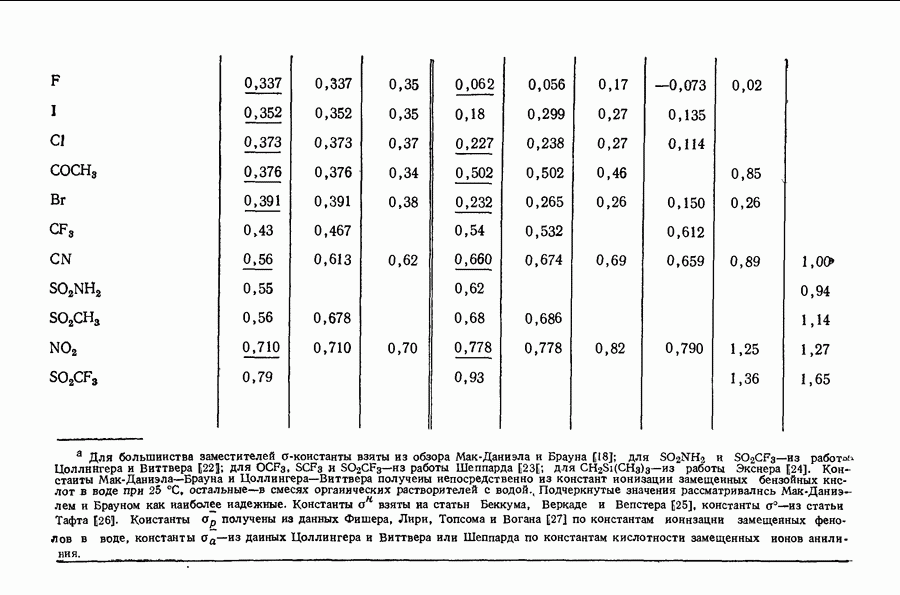
- 11.12. НОРМАЛЬНЫЕ КОНСТАНТЫ ЗАМЕСТИТЕЛЕЙ
- 11.13. «сигма»-КОНСТАНТЫ
- 11.14. «сигма+»-КОНСТАНТЫ
- 11.15. НЕДОСТАТОЧНОСТЬ ДВУХ ЗНАЧЕНИЙ «сигма»
- 11.16. ЗАКОНОМЕРНОСТИ ПРЯМОГО РЕЗОНАНСНОГО ВЗАИМОДЕИСТВИЯ
- 11.17. УРАВНЕНИЕ ЮКАВА—ЦУНО
- 11.18. ПРОБЛЕМА СЛУЧАЙНЫХ И СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ
- 11.19. ЗАТУХАНИЕ ЭЛЕКТРОННЫХ ВЛИЯНИЙ В БОКОВОЙ ЦЕПИ
- 11.20. СУММАРНОЕ ВЛИЯНИЕ НЕСКОЛЬКИХ ЗАМЕСТИТЕЛЕЙ
- 11.21. ПРОСТРАНСТВЕННЫЕ ПРЕПЯТСТВИЯ РЕЗОНАНСУ
- 11.22. ПРИРОДА ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.23. АДДИТИВНОСТЬ ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.24. ДАЛЬНЕЙШИЕ ОГРАНИЧЕНИЯ ПРИМЕНИМОСТИ ПРИНЦИПА ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИИ
- 11.25. ИНДУКЦИОННЫЙ И РЕЗОНАНСНЫЙ ЭФФЕКТЫ
- 11.26. УРАВНЕНИЕ ТАФТА
- 11.27. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 11.28. КОРРЕЛЯЦИЯ РЕАКЦИОННОЙ СПОСОБНОСТИ АЛИФАТИЧЕСКИХ И АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ
- 11.29. АНАЛИЗ ЭКСНЕРА
- 11.30. «ГИБКИЕ» И «ЖЕСТКИЕ» МОЛЕКУЛЫ
- 11.31. ВЛИЯНИЕ РАСТВОРИТЕЛЕЙ НА …
- 12. ВЛИЯНИЕ СТРОЕНИЯ НА ИЗМЕНЕНИЯ ЭНТАЛЬПИИ И ЭНТРОПИИ
- 12.2. ИЗОЭНТРОПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
- 12.3. ИЗОЭНТАЛЬПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
- 12.4. ИЗОКИНЕТИЧЕСКАЯ ТЕМПЕРАТУРА
- 12.5. НАДЕЖНОСТЬ УСТАНОВЛЕНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
- 12.6. ПРЕДЕЛЫ СУЩЕСТВОВАНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
- 12.7. НЕПОСТОЯНСТВО ЭНТАЛЬПИЙНЫХ И ЭНТРОПИЙНЫХ ВЛИЯНИЙ
- 12.8 СТРУКТУРНЫЕ ВЛИЯНИЯ И СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА
- 12.9. ПРЕДПОЛОЖЕНИЯ
- 12.10. СЛЕДСТВИЯ
- 12.11. ПОДТВЕРЖДЕНИЯ
- 12.12. ДРУГИЕ ПОДХОДЫ