| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
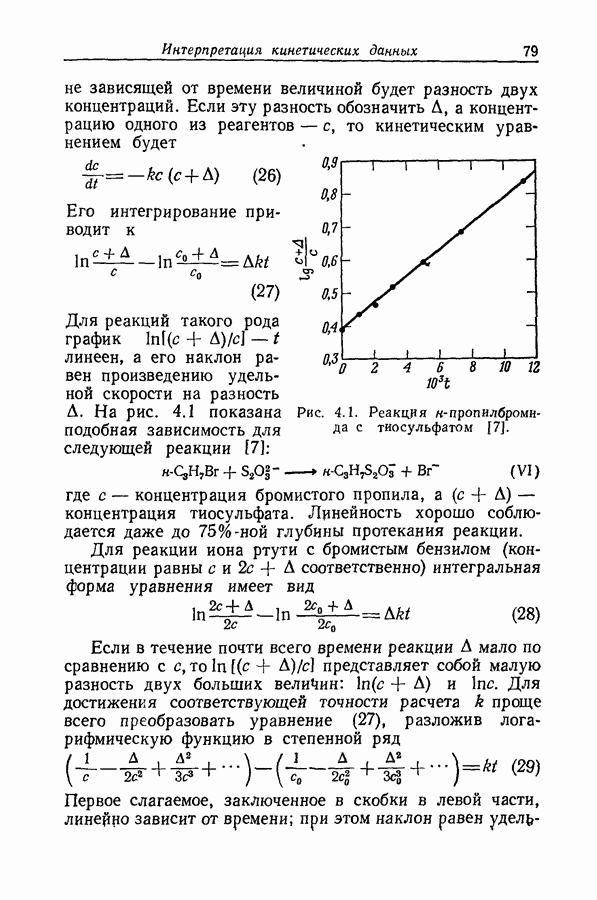
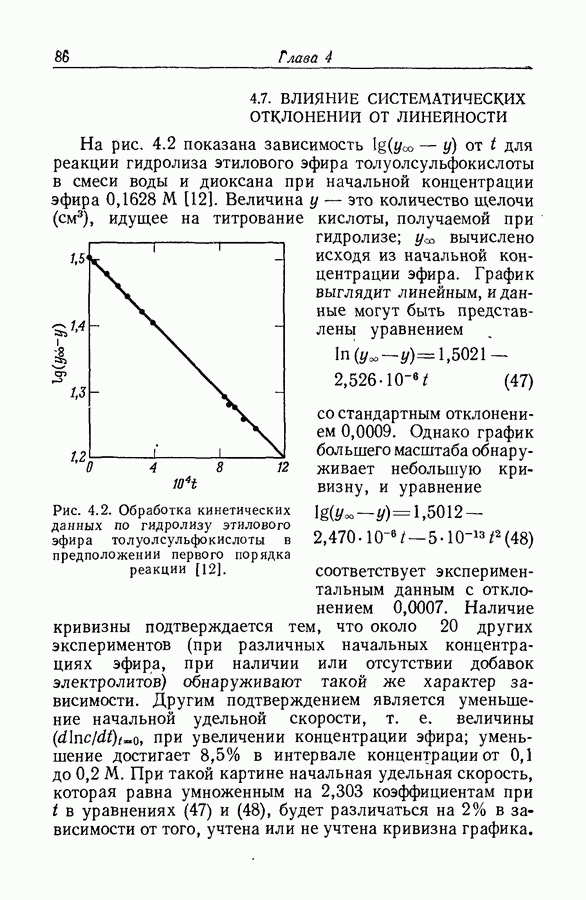
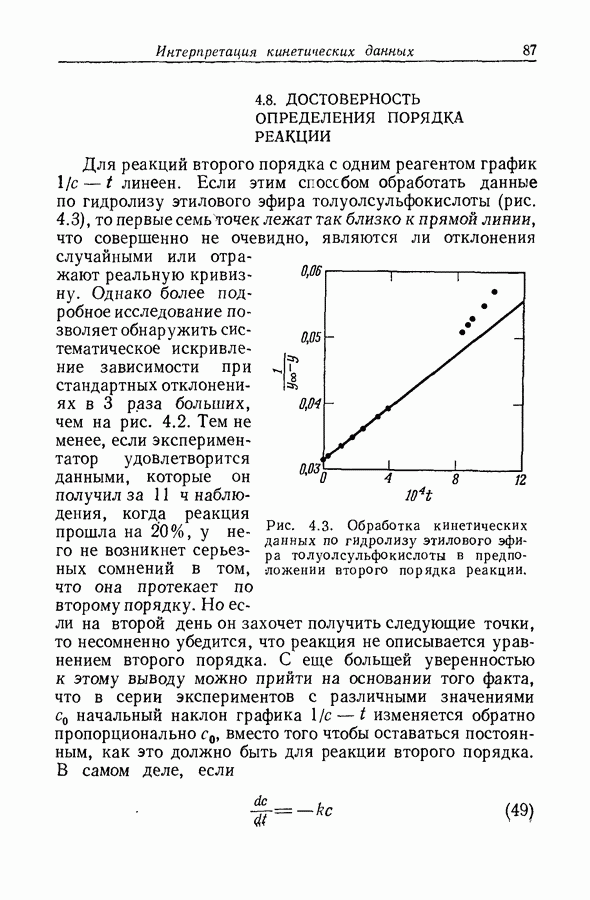
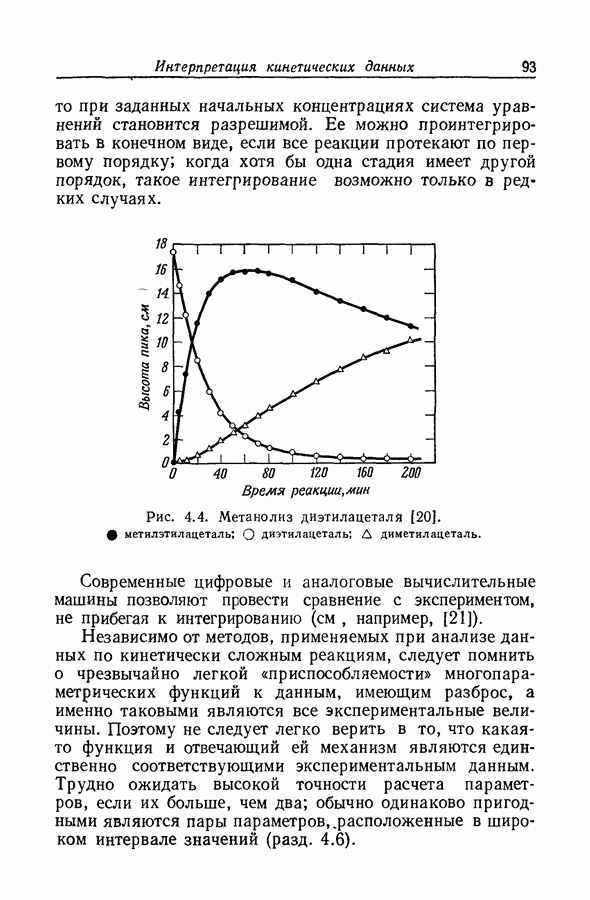
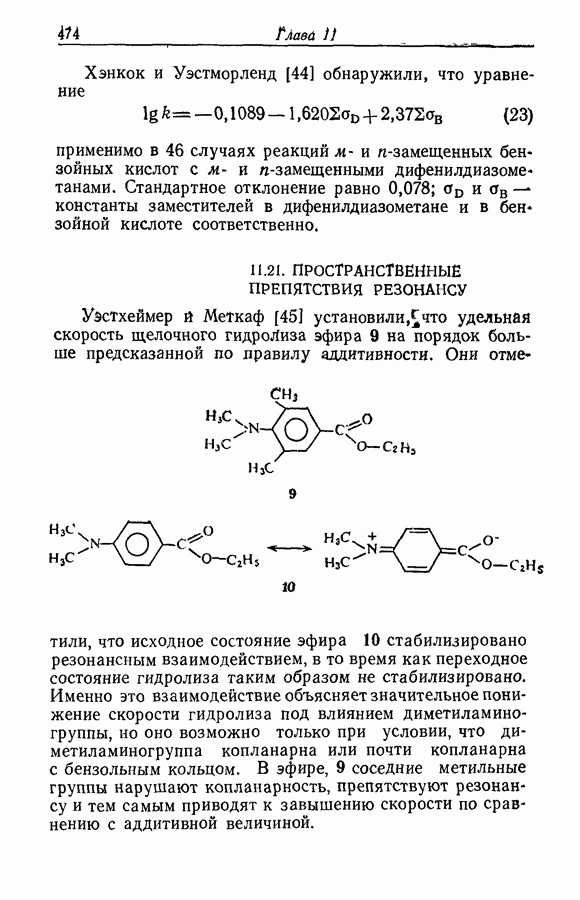
5.29. МИКРОСКОПИЧЕСКАЯ ОБРАТИМОСТЬ ИЛИ ДЕТАЛЬНОЕ РАВНОВЕСИЕ
Принцип микроскопической обратимости или детального равновесия легко выводится из теории переходного состояния, но его трудно вывести каким-либо другим путем. Согласно этому принципу, в системе реакций типа

где все  не зависят от концентраций
не зависят от концентраций  , но могут быть функциями других концентраций, независимыми являются только пять параметров, поскольку шестая величина
, но могут быть функциями других концентраций, независимыми являются только пять параметров, поскольку шестая величина  определяется зависимостью
определяется зависимостью

Любоешш все из отношений можно заменить константой равновесия  что это условие накладывается теорией переходного состояния, можно легко показать заменой
что это условие накладывается теорией переходного состояния, можно легко показать заменой  на
на  что приводит к тождеству
что приводит к тождеству

каждая сторона которого сокращается до  т. е. равна термодинамической константе равновесия для превращения
т. е. равна термодинамической константе равновесия для превращения  .
.
Принятие принципа микроскопической обратимости позволяет показать неосуществимость равновесий, которые Скрабель [59] называет циркуляционными. В крайнем случае циркуляционного равновесия можно было бы принять  тогда А превращалось бы в Р только прямым путем, а обратное превращение
тогда А превращалось бы в Р только прямым путем, а обратное превращение  протекало бы только кружным путем — через
протекало бы только кружным путем — через  Циркуляция в указанном смысле возможна, если равенство (94) выполняется неточно; когда левая часть уравнения больше правой, то циркуляция происходит по часовой стрелке, а когда левая часть меньше правой — против часовой стрелки.
Циркуляция в указанном смысле возможна, если равенство (94) выполняется неточно; когда левая часть уравнения больше правой, то циркуляция происходит по часовой стрелке, а когда левая часть меньше правой — против часовой стрелки.
Принцип детального равновесия может быть распространен на циклические превращения с участием большого числа веществ. Его использование помогает избежать опасных ловушек при интерпретации реакций, которые могут протекать как по каталитическому, так и по некаталитическому пути.
Например, Бруис и Бруно [60] предложили следующий механизм для катализируемого имидазолом гидролиза  -тиовалеролактона:
-тиовалеролактона:


Здесь  имидазол,
имидазол,  тиовалеролактон,
тиовалеролактон,  продукты реакции (тиовалериановая кислота и имидазол),
продукты реакции (тиовалериановая кислота и имидазол),  промежуточные соединения, к которым приложим метод стационарных концентраций Боденштейна. Для того чтобы зависимость скорости от кислотности соответствовала экспериментальной, необходимо было предположить,
промежуточные соединения, к которым приложим метод стационарных концентраций Боденштейна. Для того чтобы зависимость скорости от кислотности соответствовала экспериментальной, необходимо было предположить,  значительно меньше
значительно меньше  но
но  сравнимо с
сравнимо с  Как отметили Уэстхеймер и Бендер [61], такое допущение противоречит принципу микроскопической обратимости, поскольку допускает циркуляцию, при которой
Как отметили Уэстхеймер и Бендер [61], такое допущение противоречит принципу микроскопической обратимости, поскольку допускает циркуляцию, при которой  образуется без промежуточного
образуется без промежуточного  но снова образует
но снова образует  со сравнимой скоростью по обоим путям.
со сравнимой скоростью по обоим путям.
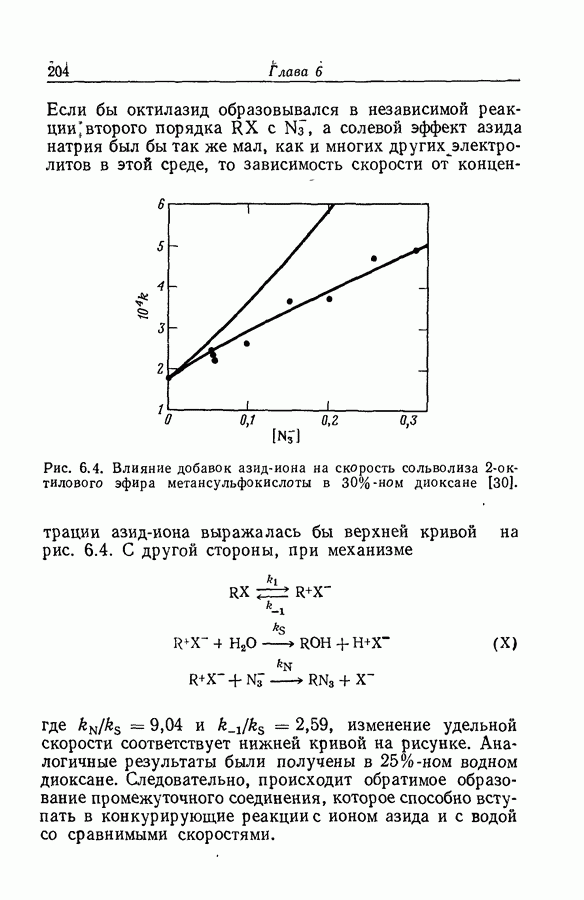
В системе реакций (X) имеются два пути, по которым Г может образовываться из  . Рассмотрение этих путей с точки зрения принципа микроскопической обратимости приводит к соотношению
. Рассмотрение этих путей с точки зрения принципа микроскопической обратимости приводит к соотношению

которое эквивалентно уравнению

а последнее несовместимо с допущением Бруисаи Бруно.
Принципу микроскопической обратимости посвящена обширная и часто противоречивая литература (см. обзор Скрабеля [59]), начало которой, по-видимому, положила книга Толмена [62].
Дэвидсон [63] рассматривает и иллюстрирует принцип микроскопической обратимости просто как «правдоподобное утверждение, опирающееся на предшествующее рассмотрение обратимости уравнений классической механики во времени». Онзагер [64] в своей классической статье по термодинамике необратимых процессов
рассматривает уравнения скорости реакций, входящих в систему (IX), а именно

Если система в целом находится в состоянии равновесия,  Исключая
Исключая  т. е. равновесную концентрацию X, получим
т. е. равновесную концентрацию X, получим

Однако здесь, согласно Онзагеру, химикам приходится накладывать очень интересное дополнительное ограничение, а именно при достигнутом равновесии каждая индивидуальная реакция должна быть сбалансированной. Это Означает, что переходы  должны происходить столь же часто, как и обратные переходы
должны происходить столь же часто, как и обратные переходы  и т. д., что эквивалентно соотношению
и т. д., что эквивалентно соотношению

Тогда уравнение (100) преобразуется в

или

что и эквивалентно уравнению (94).
ЛИТЕРАТУРА
(см. скан)
(см. скан)
(см. скан)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ТЕРМОДИНАМИКА РЕАКЦИИ В РАСТВОРАХ
- 2.2. ИЗМЕНЕНИЕ ЭНЕРГИИ ГИББСА В ПРОЦЕССЕ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.3. УСЛОВИЕ РАВНОВЕСИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.4. ПРИБЛИЖЕНИЕ РАЗБАВЛЕННОГО РАСТВОРА
- 2.5. СТАНДАРТНЫЙ ПОТЕНЦИАЛ
- 2.6. ЗАКОН РАВНОВЕСИЯ В ПРИБЛИЖЕНИИ РАЗБАВЛЕННОГО РАСТВОРА
- 2.7. КОЭФФИЦИЕНТ АКТИВНОСТИ
- 2.8. ТОЧНЫЙ ЗАКОН РАВНОВЕСИЯ
- 2.9. ЗНАК ПРОИЗВОДНОЙ …
- 2.10. АКТИВНОСТЬ И СТАНДАРТНАЯ АКТИВНОСТЬ
- 2.11. КОНСТАНТЫ РАВНОВЕСИЯ В РАЗЛИЧНЫХ СРЕДАХ
- 2.12. ЧИСЛО И ВЫБОР КОМПОНЕНТОВ
- 2.13. ФОРМАЛЬНЫЕ И ИСТИННЫЕ ЗНАЧЕНИЯ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.14. ФУНКЦИЯ q°
- 2.15. УРАВНЕНИЕ ГИББСА—ДЮГЕМА
- 2.16. МОЛЕКУЛЯРНЫЕ ВЕСА В РАСТВОРЕ
- 2.17. УРАВНЕНИЕ ГИББСА—ДЮГЕМА ДЛЯ МНОГОКОМПОНЕНТНЫХ СИСТЕМ
- 2.18. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 2.19. ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.20. МОЛЬНАЯ ЭНТАЛЬПИЯ И МОЛЬНАЯ ЭНТРОПИЯ КАК ФУНКЦИИ КОНЦЕНТРАЦИИ
- 2.21. ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ
- 2.22. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЭНТАЛЬПИИ И СТАНДАРТНОЙ ЭНТРОПИИ РЕАКЦИИ
- 2.23. ПРОБЛЕМА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ …
- 2.24. ФОРМАЛЬНЫЕ ЗНАЧЕНИЯ СТАНДАРТНОЙ ЭНТАЛЬПИИ, ЭНТРОПИИ И ТЕПЛОЕМКОСТИ
- 3. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
- 3.2. СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА ИДЕАЛЬНОГО ГАЗА
- 3.3. ПРИРОДА СТАТИСТИЧЕСКИХ СУММ
- 3.4. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ПРОСТОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
- 3.5. ТИПИЧНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
- 3.6. РАСЧЕТ СТАТИСТИЧЕСКИХ СУММ
- 3.7. СТАТИСТИЧЕСКАЯ МЕХАНИКА И ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗОВОЙ ФАЗЕ
- 3.8. ИЗМЕНЕНИЕ ЭНТАЛЬПИИ И ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 3.9. СТАТИСТИЧЕСКАЯ МЕХАНИКА РАЗБАВЛЕННОГО РАСТВОРА
- 3.10. ПРАВИЛО БАРКЛЕЯ—БАТЛЕРА
- 3.11. НЕКОТОРЫЕ ОСОБЕННОСТИ ВОДНЫХ РАСТВОРОВ
- 3.12. ИЗМЕНЕНИЯ СТАНДАРТНОЙ ЭНТРОПИИ ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 3.13. СВЯЗЬ СО СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 3.14. СТАТИСТИЧЕСКАЯ СУММА q°
- 4. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ ДАННЫХ
- 4.2. СИСТЕМАТИКА И ТЕРМИНОЛОГИЯ
- 4.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИИ
- 4.4. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ КИНЕТИКИ
- 4.5. ЛИНЕЙНЫЕ ФОРМЫ УРАВНЕНИЙ ДЛЯ КИНЕТИЧЕСКИ ПРОСТЫХ НЕОБРАТИМЫХ РЕАКЦИИ
- 4.6. ПРОБЛЕМА ТОЧНОСТИ
- 4.7. ВЛИЯНИЕ СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ ОТ ЛИНЕЙНОСТИ
- 4.8. ДОСТОВЕРНОСТЬ ОПРЕДЕЛЕНИЯ ПОРЯДКА РЕАКЦИИ
- 4.9. ПРОТОЧНЫЕ РЕАКТОРЫ С ПЕРЕМЕШИВАНИЕМ
- 4.10. КИНЕТИЧЕСКИ ПРОСТЫЕ ОБРАТИМЫЕ РЕАКЦИИ
- 4.11. КИНЕТИЧЕСКИ СЛОЖНЫЕ РЕАКЦИИ
- 4.12. ЭКСПЕРИМЕНТАЛЬНОЕ РАСПОЗНАВАНИЕ СИСТЕМ, ВКЛЮЧАЮЩИХ РЕАКЦИИ ТОЛЬКО ПЕРВОГО ПОРЯДКА
- 4.13. ИНТЕГРАЛЬНЫЕ ФОРМЫ УРАВНЕНИИ ДЛЯ СИСТЕМ РЕАКЦИИ ПЕРВОГО ПОРЯДКА
- 4.14. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ УРАВНЕНИЙ, СОДЕРЖАЩИХ ДВА ЭКСПОНЕНЦИАЛЬНЫХ ЧЛЕНА
- 4.15. МЕТОД БОДЕНШТЕИНА (МЕТОД СТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ)
- 4.16. ПРОБЛЕМА ТОЧНОСТИ УРАВНЕНИИ С БОЛЬШИМ ЧИСЛОМ ПАРАМЕТРОВ
- 4.17. УРАВНЕНИЕ МИХАЭЛИСА-МЕНТЕН
- 4.18. СИСТЕМЫ С ПРЕДРАВНОВЕСИЕМ
- 4.19. ВЛИЯНИЕ АССОЦИАТИВНОГО РАВНОВЕСИЯ
- 4.20. РАСПОЗНАВАНИЕ СЛОЖНОСТИ РЕАКЦИИ
- 4.21. ИСПОЛЬЗОВАНИЕ ПРОТОЧНОГО РЕАКТОРА С ПЕРЕМЕШИВАНИЕМ ДЛЯ ИЗУЧЕНИЯ МНОГОСТАДИЙНЫХ РЕАКЦИЙ
- 4.22. ПРОТОЧНЫЙ ТРУБЧАТЫЙ РЕАКТОР
- 4.23. ИЗУЧЕНИЕ ОТНОСИТЕЛЬНОЙ РЕАКЦИОННОЙ СПОСОБНОСТИ МЕТОДОМ КОНКУРИРУЮЩИХ РЕАКЦИЙ
- 4.24. ОЧЕНЬ БЫСТРЫЕ РЕАКЦИИ, ЛИМИТИРУЕМЫЕ ДИФФУЗИЕЙ
- 4.25. СПРАВЕДЛИВОСТЬ ЗАКОНА ДЕЙСТВИЯ МАСС ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 4.26. ПРИНЦИП НЕЗАВИСИМОГО ПРОТЕКАНИЯ РЕАКЦИЙ
- 4.27. КАТАЛИТИЧЕСКИЕ РЕАКЦИИ И РЕАКЦИИ НУЛЕВОГО ПОРЯДКА
- 4.28. «МРАЧНЫЕ ВРЕМЕНА» И «ВОЗРОЖДЕНИЕ»
- 5. ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.2. ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СИСТЕМЫ В ХОДЕ РЕАКЦИИ
- 5.3. КООРДИНАТА РЕАКЦИИ
- 5.4. ДЕТАЛЬНАЯ ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.5. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.6. ОБОСНОВАННОСТЬ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.7. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА ДРУГИЕ ТИПЫ РЕАКЦИЙ
- 5.8. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА НЕИДЕАЛЬНЫЕ РАСТВОРЫ
- 5.9. СОСТАВ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.10. ЛИМИТИРУЮЩЕЕ ПЕРЕХОДНОЕ СОСТОЯНИЕ ИЛИ ЛИМИТИРУЮЩИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.11. ПАРАЛЛЕЛЬНЫЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.12. ОБЯЗАТЕЛЬНО ЛИ ОБРАЗОВАНИЕ ПРОМЕЖУТОЧНЫХ СОЕДИНЕНИЙ?
- 5.13. ПРОДВИЖЕНИЕ ОТ РЕАГЕНТОВ К ПЕРЕХОДНОМУ СОСТОЯНИЮ
- 5.14. ВОПРОСЫ ПО ПОВОДУ МЕХАНИЗМА, ИМЕЮЩИЕ И НЕ ИМЕЮЩИЕ СМЫСЛА
- 5.15. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ
- 5.16. ПРИНЦИП КЕРТИНА
- 5.17. РЕАКЦИЯ СТИЛЬБЕНА С БРОМОМ В МЕТАНОЛЕ
- 5.18. ПРОБЛЕМА МЕХАНИЗМА РЕАКЦИИ С УЧАСТИЕМ ИОНОВ
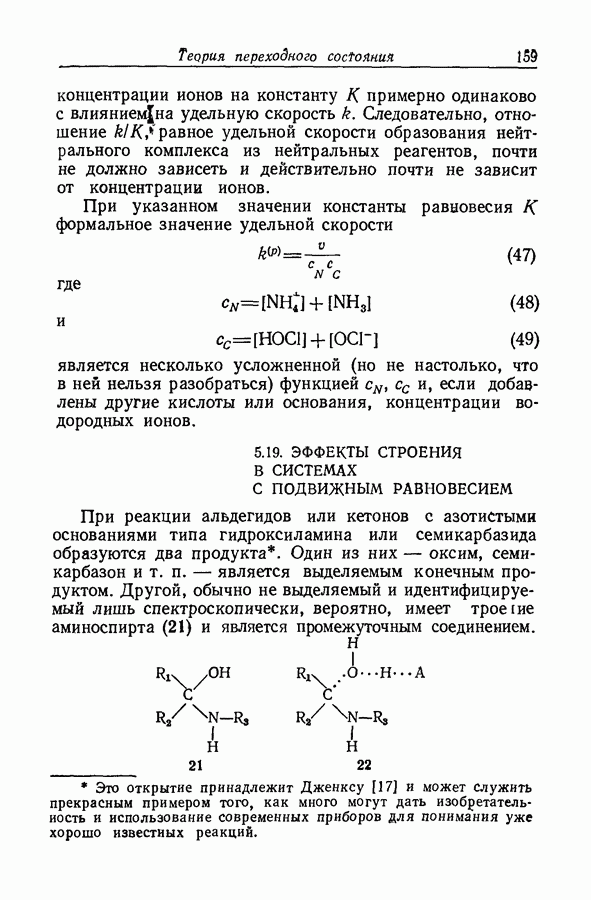
- 5.19. ЭФФЕКТЫ СТРОЕНИЯ В СИСТЕМАХ С ПОДВИЖНЫМ РАВНОВЕСИЕМ
- 5.20. ПРОБЛЕМА СТЕХИОМЕТРИЧЕСКОГО ВКЛЮЧЕНИЯ РАСТВОРИТЕЛЯ В ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 5.21. ЭНТРОПИЯ АКТИВАЦИИ
- 5.22. СТРУКТУРНЫЕ ИЗОТОПНЫЕ ЭФФЕКТЫ
- 5.23. ИЗОТОПНЫЕ ЭФФЕКТЫ РАСТВОРИТЕЛЕЙ
- 5.24. ВЛИЯНИЕ ДАВЛЕНИЯ НА СКОРОСТЬ РЕАКЦИЙ
- 5.25. СИСТЕМЫ С ПОДВИЖНЫМИ РАВНОВЕСИЯМИ В ИСХОДНЫХ И КОНЕЧНЫХ ВЕЩЕСТВАХ
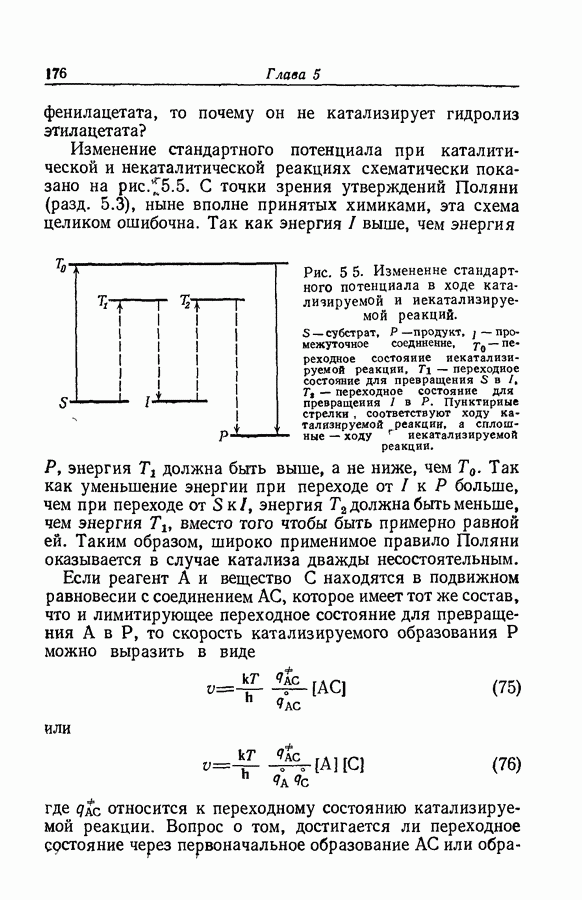
- 5.26. КАТАЛИЗ
- 5.27. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ В СЛУЧАЕ КАТАЛИТИЧЕСКОГО ПРОЦЕССА
- 5.28. ФЕРМЕНТАТИВНЫЙ И ГЕТЕРОГЕННЫЙ КАТАЛИЗ
- 5.29. МИКРОСКОПИЧЕСКАЯ ОБРАТИМОСТЬ ИЛИ ДЕТАЛЬНОЕ РАВНОВЕСИЕ
- 6. НЕКОТОРЫЕ РЕАКЦИИ ЗАМЕЩЕНИЯ
- 6.1 НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ ВТОРОГО ПОРЯДКА У НАСЫЩЕННОГО АТОМА УГЛЕРОДА
- 6.2. РАЦЕМИЗАЦИЯ И ИЗОТОПНЫЙ ОБМЕН
- 6.3. РЕАКЦИИ СОЛЬВОЛИЗА
- 6.4. КАРБОНИЕВО-ИОННЫЙ МЕХАНИЗМ
- 6.5. СОЛЕВЫЕ ЭФФЕКТЫ В СИЛЬНО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
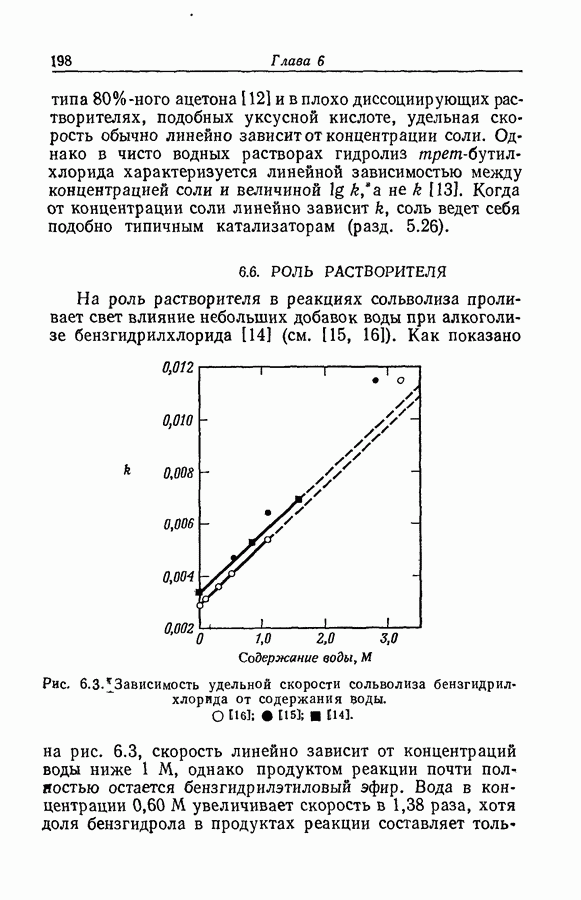
- 6.6. РОЛЬ РАСТВОРИТЕЛЯ
- 6.7. ВОПРОСЫ ТЕРМИНОЛОГИИ
- 6.8. ОГРАНИЧЕННОСТЬ ПРЕДСТАВЛЕНИИ ОБ ОБРАЗОВАНИИ СВОБОДНЫХ ИОНОВ КАРБОНИЯ
- 6.9. ГИПОТЕЗА ИОННЫХ ПАР
- 6.10. ВЛИЯНИЕ ДОБАВОК АЗИДОВ
- 6.11. УЧАСТИЕ БЕЗГИДРОКСИЛЬНЫХ РАСТВОРИТЕЛЕЙ В ОБРАЗОВАНИИ ПЕРЕХОДНОГО КОМПЛЕКСА
- 6.12. АЛЛИЛЬНАЯ ПЕРЕГРУППИРОВКА
- 6.13. СОЛЬВОЛИЗ, СОПРОВОЖДАЮЩИЙСЯ РАЦЕМИЗАЦИЕЙ РЕАГЕНТА
- 6.14. ДОПОЛНИТЕЛЬНЫЕ ДАННЫЕ О ВЛИЯНИИ ДОБАВОК АЗИДОВ
- 6.15. ОСОБЫЙ СОЛЕВОЙ ЭФФЕКТ
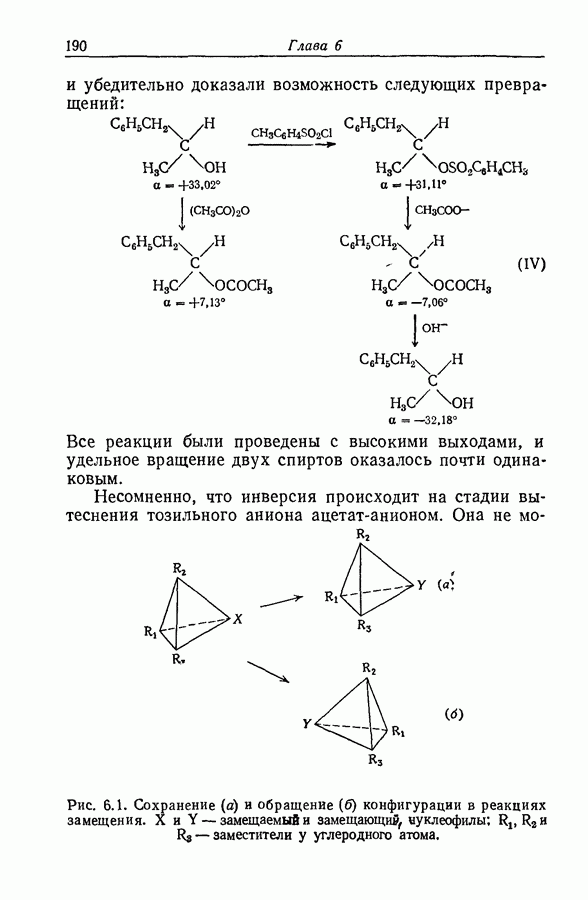
- 6.16. ДВОЙНОЕ ОБРАЩЕНИЕ КОНФИГУРАЦИИ
- 6.17. БРОМОНИЕВЫЕ ИОНЫ КАК ПРОМЕЖУТОЧНЫЕ СОЕДИНЕНИЯ
- 6.18. ПРОБЛЕМА ФЕНОНИЕВОГО ИОНА
- 6.19. ПЕРЕГРУППИРОВКИ
- 6.20. ЭЛЕКТРОФИЛЬНОЕ АРОМАТИЧЕСКОЕ ЗАМЕЩЕНИЕ
- 6.21. РЕАКЦИЯ АЗОСОЧЕТАНИЯ
- 6.22. ВОЗМОЖНЫЕ ФОРМЫ РЕАГЕНТОВ
- 6.23. ПЕРЕХОДНОЕ СОСТОЯНИЕ РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.24. КАТАЛИТИЧЕСКОЕ ДЕЙСТВИЕ ПИРИДИНА
- 6.25. ИЗОТОПНЫЕ ЭФФЕКТЫ ВОДОРОДА В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.26. ПРОСТРАНСТВЕННЫЕ ВЛИЯНИЯ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.27. ЭНТРОПИЯ АЗОСОЧЕТАНИЯ
- 7. СОЛЕВЫЕ ЭФФЕКТЫ
- 7.1. УРАВНЕНИЕ БРЕНСТЕДА
- 7.2. ПРЕДЕЛЬНЫЙ ЗАКОН ДЕБАЯ — ХЮККЕЛЯ
- 7.3. СОЛЕВЫЕ ЭФФЕКТЫ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 7.4. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К НЕСИММЕТРИЧНЫМ ИОНАМ
- 7.5. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К МНОГОЗАРЯДНЫМ ИОНАМ
- 7.6. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИЙ СОЛЕЙ НА КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 7.7. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИИ СОЛЕЙ НА СКОРОСТЬ РЕАКЦИЙ МЕЖДУ ИОНАМИ
- 7.8. СОЛЕВЫЕ ЭФФЕКТЫ КАК ПОДТВЕРЖДЕНИЕ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 7.9. ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.10. ПОДАВЛЕНИЕ СОЛЕВЫХ ЭФФЕКТОВ, ПРИ ИЗУЧЕНИИ ПОРЯДКА РЕАКЦИЙ
- 7.11. ФИЗИЧЕСКИЙ СМЫСЛ ТЕОРИИ ДЕБАЯ — ХЮККЕЛЯ
- 7.12. МОДИФИКАЦИЯ ТЕОРИЙ ДЛЯ СЛУЧАЯ СЛАБЫХ ВЗАИМОДЕЙСТВИЙ
- 7.13. ПРИБЛИЖЕНИЕ БЬЕРРУМА
- 7.14. ИОННЫЕ ПАРЫ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 7.15. ОБРАЗОВАНИЕ ИОННЫХ ПАР И ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.16. О ПОНЯТИИ ИОННЫХ ПАР
- 7.17. О СЛАБОЙ АССОЦИАЦИИ ИОНОВ
- 7.18. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В ВОДНЫХ РАСТВОРАХ
- 7.19. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ВОДНЫХ РАСТВОРАХ
- 7.20. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ЖИДКОМ СЕРНИСТОМ АНГИДРИДЕ
- 7.21. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ СОЛЬВОЛИЗА В ВОДНЫХ РАСТВОРАХ
- 7.22. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В НЕВОДНЫХ РАСТВОРАХ
- 7.23. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 8. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ
- 8.3. ОБРАЗОВАНИЕ ИОННЫХ ПАР; СЛУЧАИ ИДЕАЛЬНОГО ЭЛЕКТРОСТАТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 8.4. АССОЦИАЦИЯ ИОНОВ В ЧЕТВЕРТИЧНЫХ АММОНИЕВЫХ СОЛЯХ
- 8.5. ИОННЫЕ ТРИПЛЕТЫ И ПОЛИМЕРЫ СОЛЕЙ
- 8.6. ВОДОРОДНАЯ СВЯЗЬ
- 8.7. ИОННЫЕ ПАРЫ С ВОДОРОДНОЙ СВЯЗЬЮ
- 8.8. ВЗАИМОДЕЙСТВИЕ АНИОНОВ С ДОНОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.9. ВЗАИМОДЕЙСТВИЕ КАТИОНОВ С АКЦЕПТОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.10. ДРУГИЕ ВИДЫ ВЗАИМОДЕЙСТВИИ ИОНОВ С НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
- 8.11. ОБЗОР ВЗАИМОДЕЙСТВИИ ИОНОВ С РАСТВОРИТЕЛЕМ
- 8.12. РОЛЬ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ
- 8.13. МЕТАЛЛООРГАНИЧЕСКИЕ СОЕДИНЕНИЯ ЭЛЕМЕНТОВ ПЕРВОЙ ГРУППЫ
- 8.14. ВЛИЯНИЕ СОЛЬВАТАЦИИ АНИОНА НА СКОРОСТЬ ВЗАИМОДЕЙСТВИЯ АНИОНА С НЕЙТРАЛЬНОЙ МОЛЕКУЛОЙ
- 8.15. ВЛИЯНИЕ СПЕЦИФИЧЕСКОЙ СОЛЬВАТАЦИИ КАТИОНОВ НА СКОРОСТИ РЕАКЦИЙ МЕЖДУ АНИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
- 8.16. ХЕЛАТНАЯ СОЛЬВАТАЦИЯ КАТИОНОВ
- 8.17. КИНЕТИКА РЕАКЦИЙ С УЧАСТИЕМ ИОННЫХ АГРЕГАТОВ
- 8.18. ИНЕРТНОСТЬ ТВЕРДЫХ РЕАГЕНТОВ
- 8.19. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ АМБИДЕНТНЫХ АНИОНОВ
- 8.20. ВЛИЯНИЕ ПРИРОДЫ РАСТВОРИТЕЛЯ НА РЕАКЦИИ КАТИОНОВ С АНИОНАМИ
- 8.21. ДИСПЕРСИОННЫЕ СИЛЫ
- 8.22. ПЛОТНОСТЬ КОГЕЗИОННОЙ ЭНЕРГИИ
- 8.23. РЕГУЛЯРНЫЕ И ИДЕАЛЬНЫЕ РАСТВОРЫ
- 8.24. ПЕРЕНОС РАСТВОРЕННОГО ВЕЩЕСТВА ИЗ ОДНОГО РЕГУЛЯРНОГО РАСТВОРА В ДРУГОЙ
- 8.25. ВЛИЯНИЕ СИЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
- 8.26. ИЗОКИНЕТИЧЕСКАЯ ЗАВИСИМОСТЬ ПРИ ИЗМЕНЕНИИ РАСТВОРИТЕЛЯ
- 8.27. СОЛЬВОЛИЗ В ВОДНО-СПИРТОВЫХ СМЕСЯХ
- 8.28. ИНЫЕ ВЛИЯНИЯ РАСТВОРИТЕЛЯ НА СКОРОСТЬ СОЛЬВОЛИЗА
- 8.29. КОМПЛЕКСЫ С ПЕРЕНОСОМ ЗАРЯДА
- 8.30. КОМПЛЕКСООБРАЗОВАНИЕ ЗА СЧЕТ МУЛЬТИПОЛЬНОГО ИЛИ ДИПОЛЬНОГО ВЗАИМОДЕЙСТВИЯ
- 9. КОЛИЧЕСТВЕННОЕ ИЗУЧЕНИЕ КИСЛОТ И ОСНОВАНИЙ
- 9.2. ЭЛЕКТРОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КИСЛОТНОСТИ В НЕВОДНЫХ РАСТВОРАХ
- 9.3. ИЗМЕРЕНИЕ КИСЛОТНОСТИ С ПОМОЩЬЮ ИНДИКАТОРОВ
- 9.4. ФУНКЦИЯ КИСЛОТНОСТИ Н0
- 9.5. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 9.6. ФУНКЦИИ КИСЛОТНОСТИ
- 9.7. ФУНКЦИИ КИСЛОТНОСТИ …
- 9.8. ДРУГИЕ ДАННЫЕ ПО ФУНКЦИЯМ КИСЛОТНОСТИ
- 9.9. ГИПОТЕЗА ТРЕХ ПЕРЕМЕННЫХ
- 9.10. СОЛЬВАТАЦИОННАЯ ПЕРЕМЕННАЯ «фи»
- 9.11. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ КИСЛОТНОСТИ
- 9.12. СТАНДАРТНЫЕ АКТИВНОСТИ В СМЕСЯХ СИЛЬНЫХ КИСЛОТ С ВОДОЙ
- 9.13. О ВЛИЯНИИ АКТИВНОСТИ ВОДЫ
- 9.14. ФУНКЦИИ КИСЛОТНОСТИ ДЛЯ ВЫСОКОКОНЦЕНТРИРОВАННЫХ РАСТВОРОВ КИСЛОТ
- 9.15. ФУНКЦИИ КИСЛОТНОСТИ И СКОРОСТИ КАТАЛИЗИРУЕМЫХ КИСЛОТАМИ РЕАКЦИЙ
- 9.16 НИТРОВАНИЕ АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ В СМЕСЯХ СЕРНОЙ КИСЛОТЫ С ВОДОЙ
- 9.17. СИСТЕМЫ, ОПИСЫВАЕМЫЕ ДВУМЯ ФУНКЦИЯМИ КИСЛОТНОСТИ
- 9.18. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ СИЛЫ ОСНОВАНИЯ
- 9.19. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН pK
- 9.20. НАЛОЖЕНИЕ ЭФФЕКТОВ СРЕДЫ ПРИ СПЕКТРОФОТОМЕТРИЧЕСКОМ ОПРЕДЕЛЕНИИ ОСНОВНОСТИ
- 9.21. МЕТОДЫ ВВЕДЕНИЯ ПОПРАВОК НА ЭФФЕКТЫ СРЕДЫ
- 9.22. ДРУГИЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ СИЛЫ СЛАБЫХ ОСНОВАНИЙ
- 9.23. ТЕМПЕРАТУРНЫЕ КОЭФФИЦИЕНТЫ
- 9.24. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ПЛОХО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
- 9.25. ПОВЕДЕНИЕ ИНДИКАТОРОВ В НИТРОМЕТАНЕ И СУЛЬФОЛАНЕ
- 9.26. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ДИМЕТИЛСУЛЬФОКСИДЕ
- 9.27. ФУНКЦИИ КИСЛОТНОСТИ И СИЛА ОСНОВАНИИ В ДРУГИХ ВЫСОКООСНОВНЫХ СРЕДАХ
- 9.28. СКОРОСТИ РЕАКЦИЙ В СИЛЬНООСНОВНЫХ СРЕДАХ
- 9.29. ОСНОВНОСТЬ АЛКОГОЛЯТОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ
- 10. СКОРОСТИ РЕАКЦИЙ С УЧАСТИЕМ КИСЛОТ И ОСНОВАНИЙ
- 10.2. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА
- 10.3. СТАТИСТИЧЕСКИЕ ПОПРАВКИ
- 10.4. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 10.5. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА И ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 10.6. КАТАЛИЗ МОЛЕКУЛАМИ РАСТВОРИТЕЛЯ, ИОНАМИ ЛИОНИЯ И ЛИАТА
- 10.7. РАЗПОЗНАВАЕМОСТЬ ОБЩЕГО КИСЛОТНОГО И ОБЩЕГО ОСНОВНОГО КАТАЛИЗА
- 10.8. СКОРОСТИ РЕАКЦИЙ ПЕРЕНОСА ПРОТОНА
- 10.9. ТЕОРИЯ ЭЛЕКТРОННЫХ СМЕЩЕНИЙ
- 10.10. ГИДРАТАЦИЯ АЦЕТАЛЬДЕГИДА
- 10.11. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ ОСНОВАНИЯМИ
- 10.12. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ КИСЛОТАМИ
- 10.13. КАТАЛИЗ В РЕАКЦИИ ЕНОЛИЗАЦИИ
- 10.14. ЦИКЛИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 10.15. ГИДРОЛИЗ ЭФИРОВ
- 10.16. КРИВЫЕ ТИПА «КОЛОКОЛА» И «ПЕРЕВЕРНУТОГО КОЛОКОЛА»
- 10.17. ОБРАЗОВАНИЕ ОКСИМОВ И ДРУГИЕ ПОДОБНЫЕ РЕАКЦИИ
- 10.18. ГИДРОЛИЗ ФЕНИЛИМИНОЛАКТОНА
- 10.19. КАТАЛИЗ КИСЛОТАМИ ЛЬЮИСА
- 11. КОЛИЧЕСТВЕННЫЕ ЗАВИСИМОСТИ МЕЖДУ СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 11.2. ПРИНЦИП ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИЙ
- 11.4. ЛИНЕЙНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗМЕНЕНИЯМИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.5. КОРРЕЛЯЦИИ ГЕТТЛЕРА
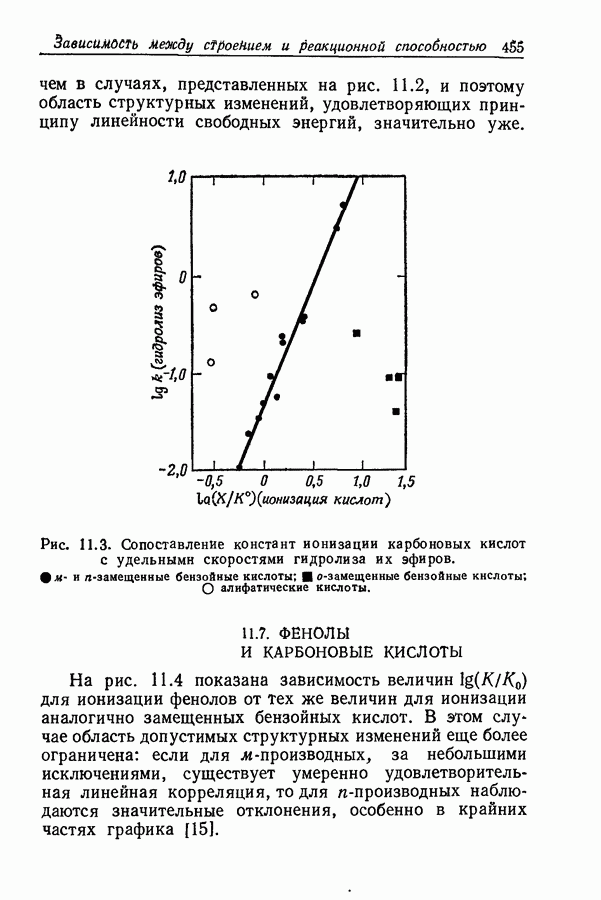
- 11.6. СИЛА КИСЛОТ И СКОРОСТЬ ГИДРОЛИЗА ИХ ЭФИРОВ
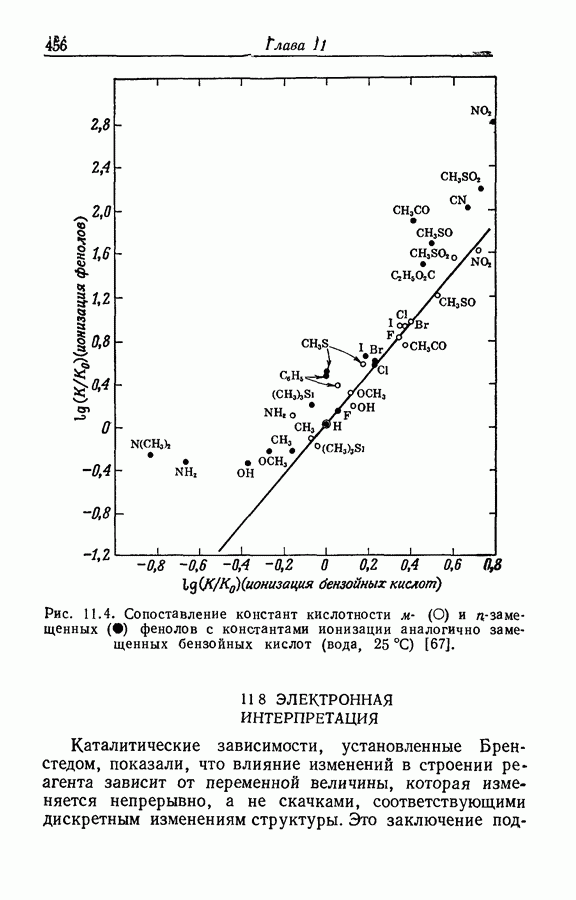
- 11.7. ФЕНОЛЫ И КАРБОНОВЫЕ КИСЛОТЫ
- 11.8 ЭЛЕКТРОННАЯ ИНТЕРПРЕТАЦИЯ
- 11.9. УРАВНЕНИЕ ГАММЕТА
- 11.10. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 11.11. ПРЯМЫЕ РЕЗОНАНСНЫЕ ВЗАИМОДЕИСТВИЯ
- 11.12. НОРМАЛЬНЫЕ КОНСТАНТЫ ЗАМЕСТИТЕЛЕЙ
- 11.13. «сигма»-КОНСТАНТЫ
- 11.14. «сигма+»-КОНСТАНТЫ
- 11.15. НЕДОСТАТОЧНОСТЬ ДВУХ ЗНАЧЕНИЙ «сигма»
- 11.16. ЗАКОНОМЕРНОСТИ ПРЯМОГО РЕЗОНАНСНОГО ВЗАИМОДЕИСТВИЯ
- 11.17. УРАВНЕНИЕ ЮКАВА—ЦУНО
- 11.18. ПРОБЛЕМА СЛУЧАЙНЫХ И СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ
- 11.19. ЗАТУХАНИЕ ЭЛЕКТРОННЫХ ВЛИЯНИЙ В БОКОВОЙ ЦЕПИ
- 11.20. СУММАРНОЕ ВЛИЯНИЕ НЕСКОЛЬКИХ ЗАМЕСТИТЕЛЕЙ
- 11.21. ПРОСТРАНСТВЕННЫЕ ПРЕПЯТСТВИЯ РЕЗОНАНСУ
- 11.22. ПРИРОДА ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.23. АДДИТИВНОСТЬ ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.24. ДАЛЬНЕЙШИЕ ОГРАНИЧЕНИЯ ПРИМЕНИМОСТИ ПРИНЦИПА ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИИ
- 11.25. ИНДУКЦИОННЫЙ И РЕЗОНАНСНЫЙ ЭФФЕКТЫ
- 11.26. УРАВНЕНИЕ ТАФТА
- 11.27. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 11.28. КОРРЕЛЯЦИЯ РЕАКЦИОННОЙ СПОСОБНОСТИ АЛИФАТИЧЕСКИХ И АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ
- 11.29. АНАЛИЗ ЭКСНЕРА
- 11.30. «ГИБКИЕ» И «ЖЕСТКИЕ» МОЛЕКУЛЫ
- 11.31. ВЛИЯНИЕ РАСТВОРИТЕЛЕЙ НА …
- 12. ВЛИЯНИЕ СТРОЕНИЯ НА ИЗМЕНЕНИЯ ЭНТАЛЬПИИ И ЭНТРОПИИ
- 12.2. ИЗОЭНТРОПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
- 12.3. ИЗОЭНТАЛЬПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
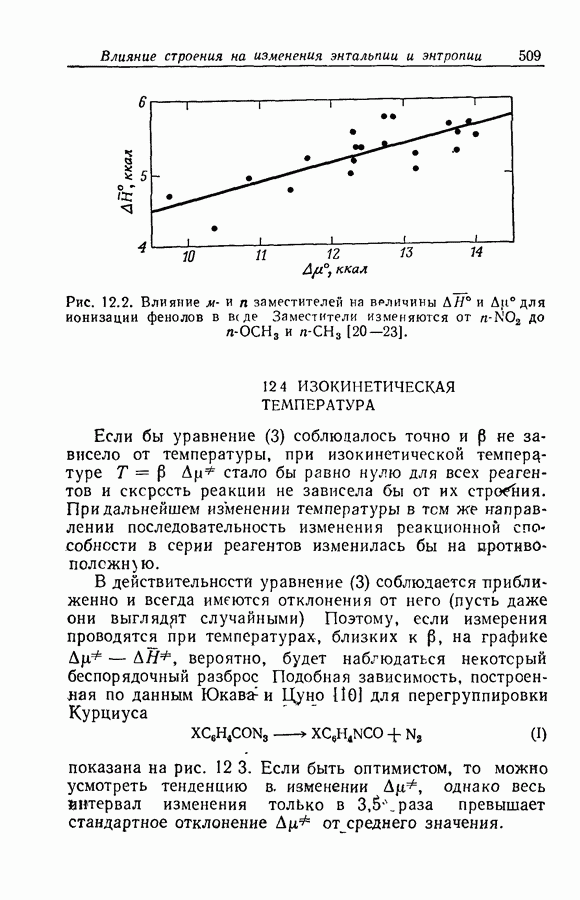
- 12.4. ИЗОКИНЕТИЧЕСКАЯ ТЕМПЕРАТУРА
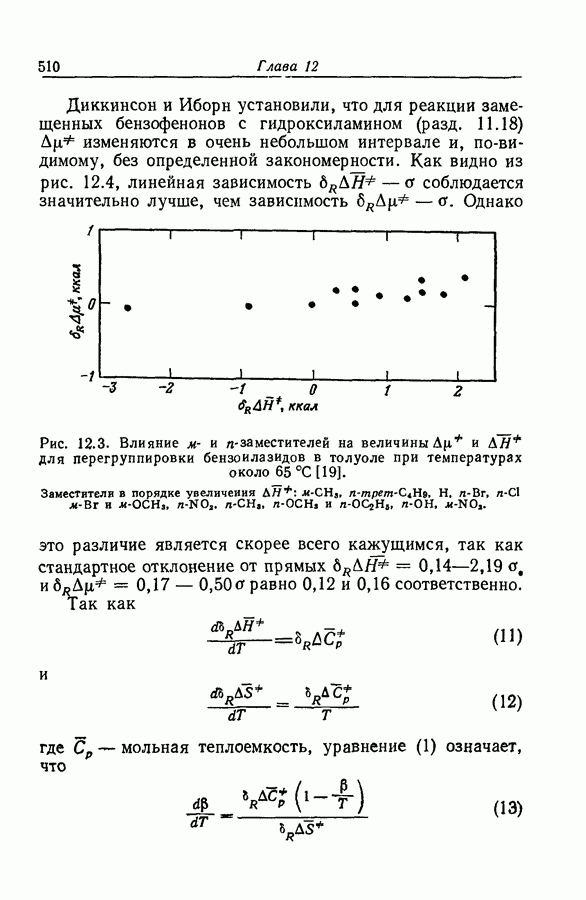
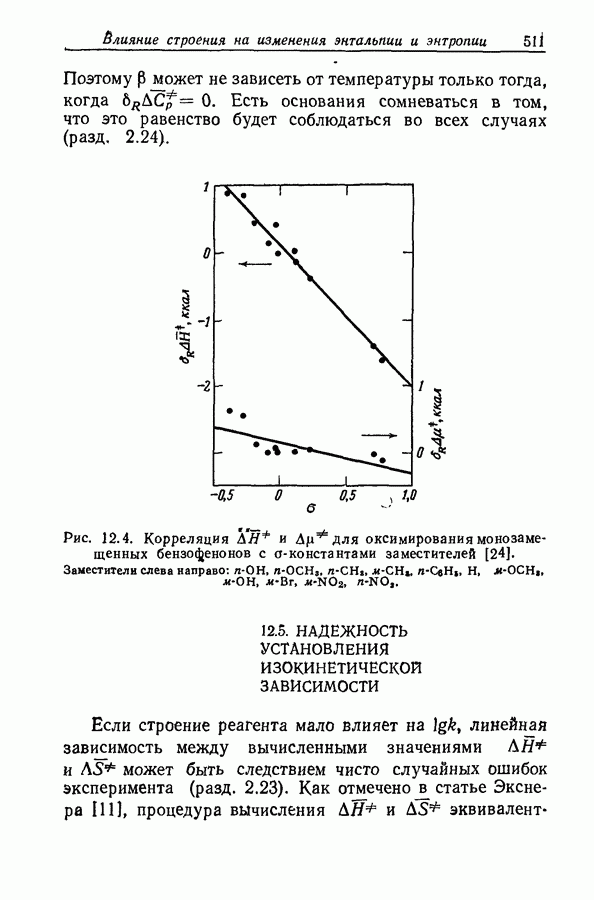
- 12.5. НАДЕЖНОСТЬ УСТАНОВЛЕНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
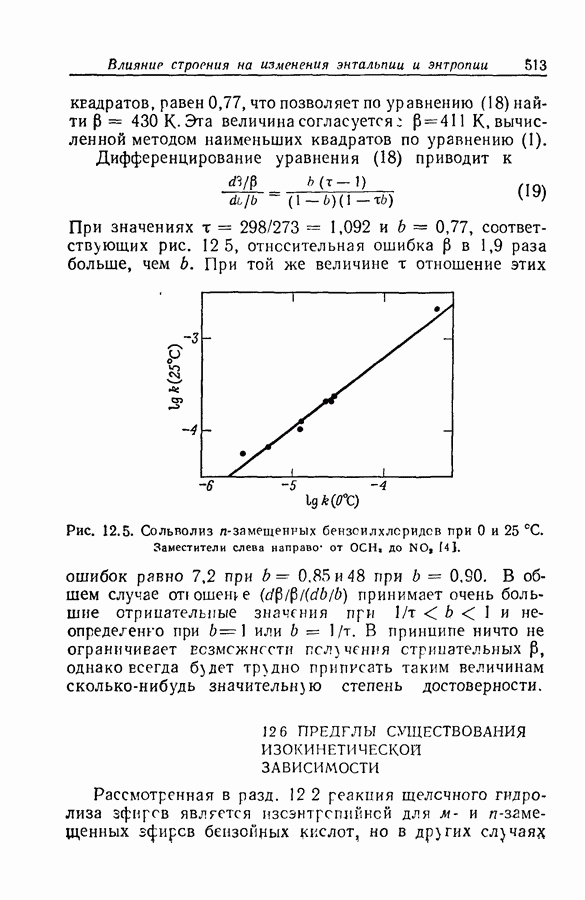
- 12.6. ПРЕДЕЛЫ СУЩЕСТВОВАНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
- 12.7. НЕПОСТОЯНСТВО ЭНТАЛЬПИЙНЫХ И ЭНТРОПИЙНЫХ ВЛИЯНИЙ
- 12.8 СТРУКТУРНЫЕ ВЛИЯНИЯ И СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА
- 12.9. ПРЕДПОЛОЖЕНИЯ
- 12.10. СЛЕДСТВИЯ
- 12.11. ПОДТВЕРЖДЕНИЯ
- 12.12. ДРУГИЕ ПОДХОДЫ