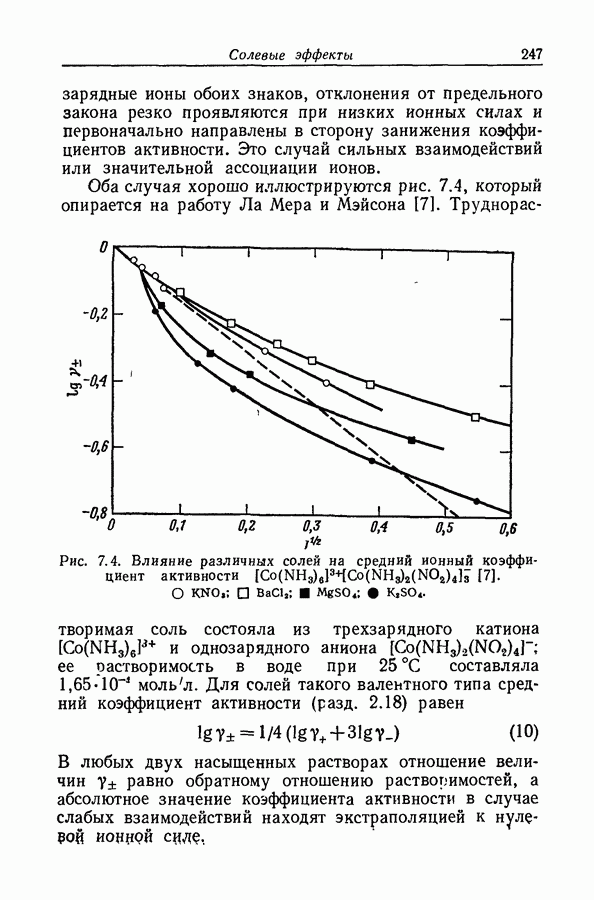
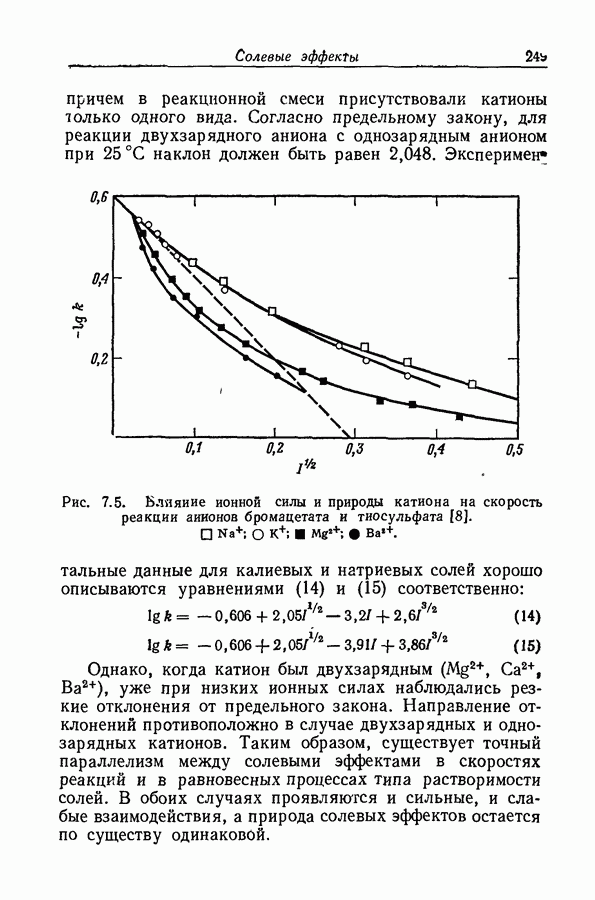
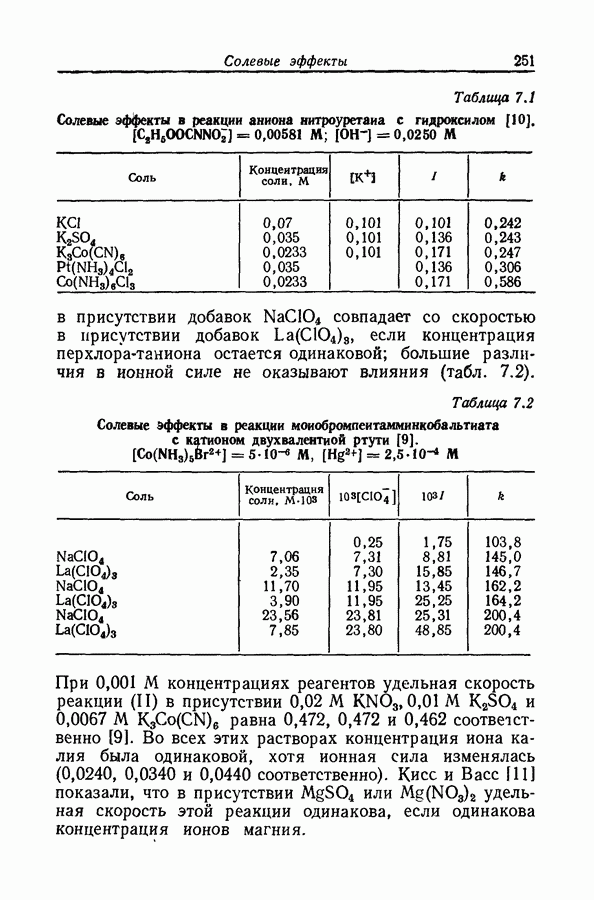
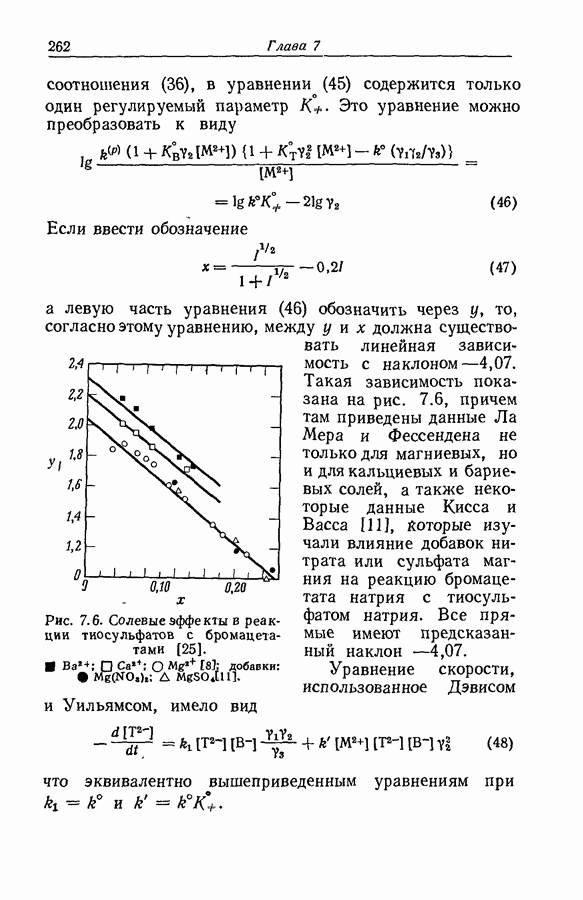
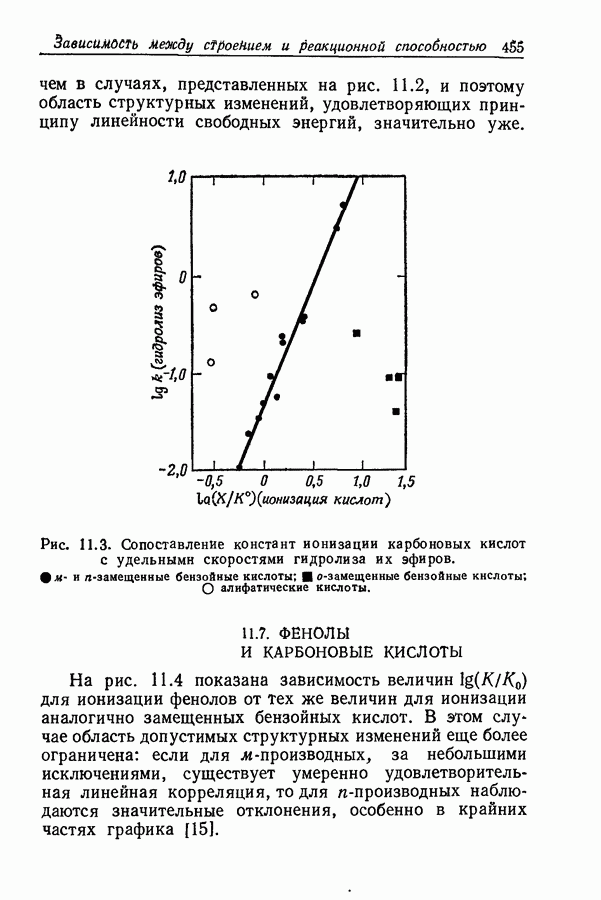
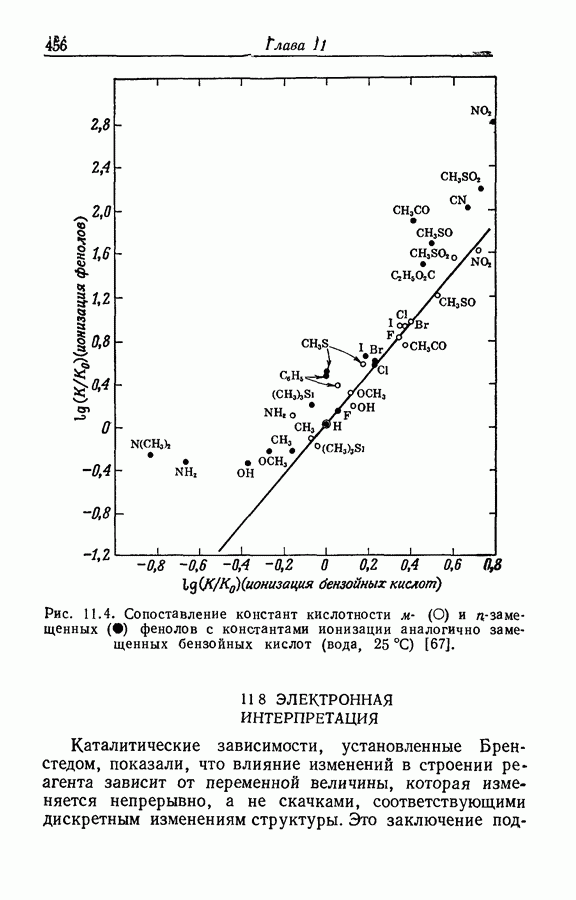
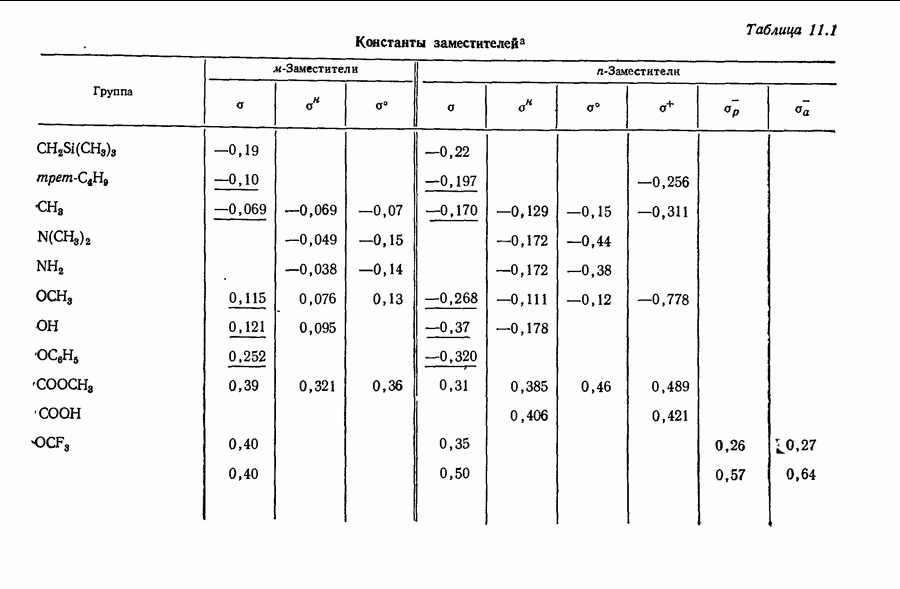
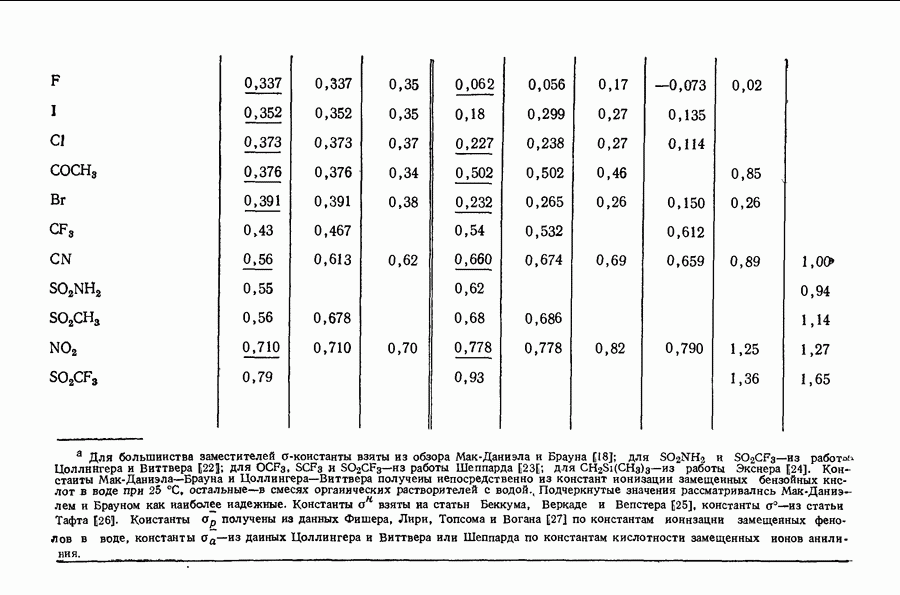
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
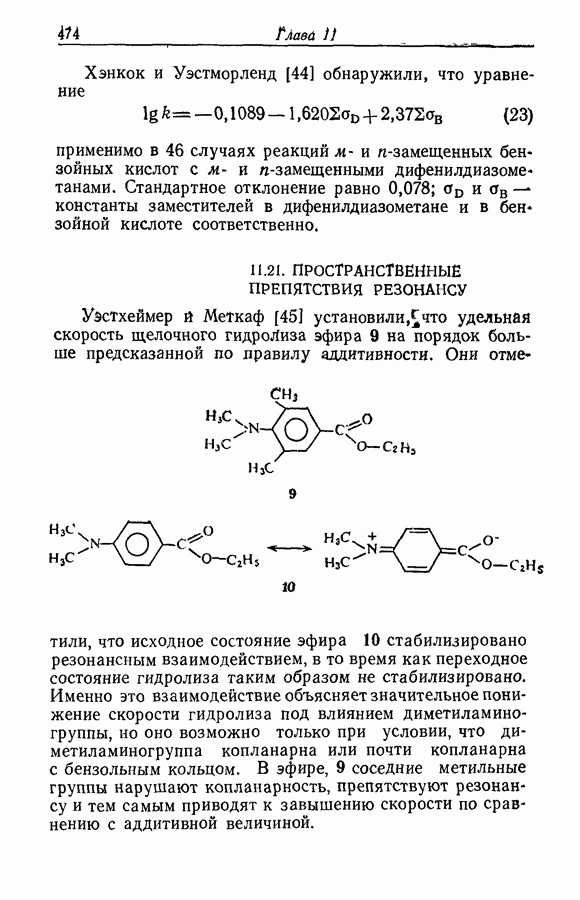
9.23. ТЕМПЕРАТУРНЫЕ КОЭФФИЦИЕНТЫ
Температурный коэффициент величины  равен (разд. 2.20)
равен (разд. 2.20)

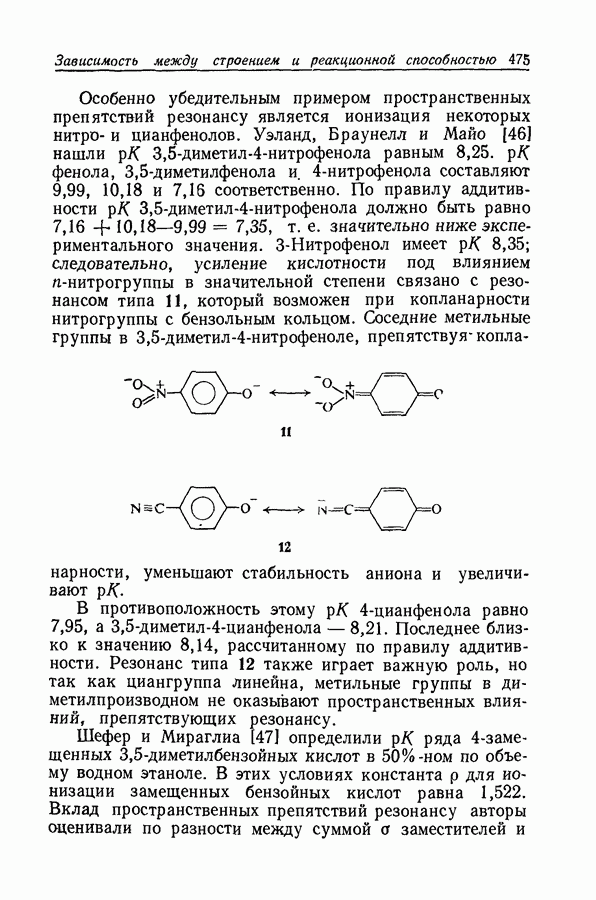
Если стандартным растворителем является вода, то член, содержащий  при 300 К вносит
при 300 К вносит  только 36 кал/моль, что намного меньше экспериментальной ошибки любых известных данных; для типичных органических растворителей его влияние в несколько раз больше.
только 36 кал/моль, что намного меньше экспериментальной ошибки любых известных данных; для типичных органических растворителей его влияние в несколько раз больше.
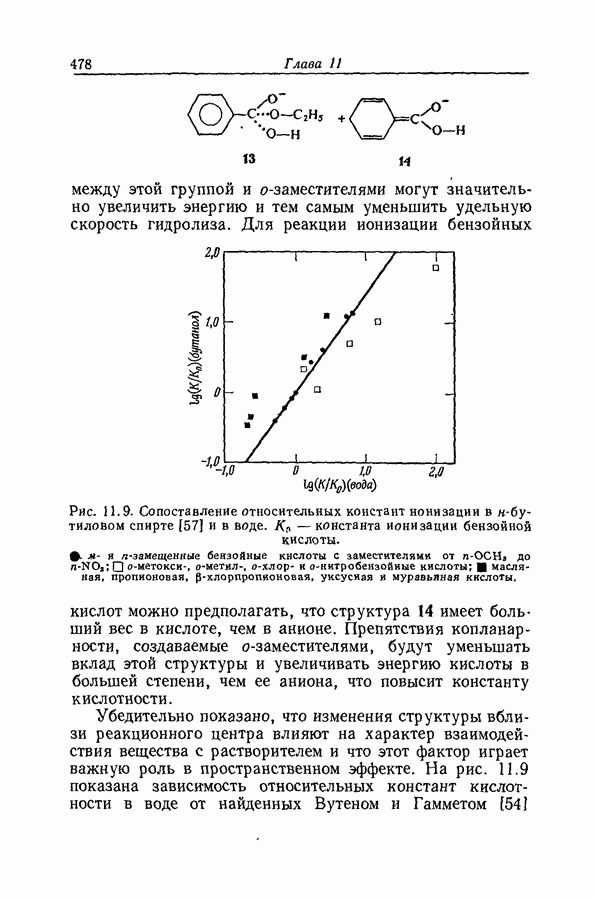
 равно изменению стандартной энтальпии реакции
равно изменению стандартной энтальпии реакции

в стандартном растворителе 
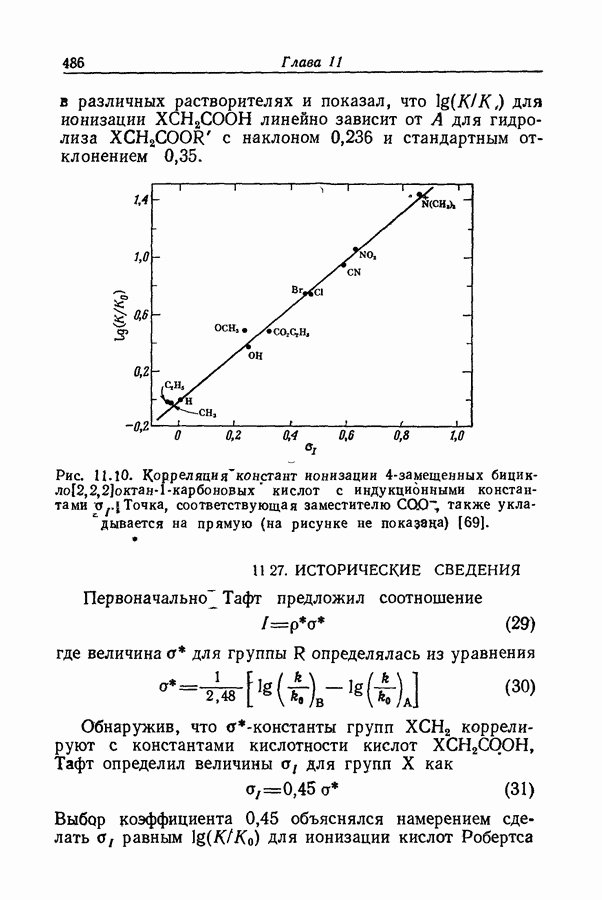
В любой среде, отличной от стандартного растворителя, предельное значение изменения мольной энтальпии для превращения  в В будет равно
в В будет равно

Здесь  мольная энтальпия всех форм сольватированного протона в исследуемой среде,
мольная энтальпия всех форм сольватированного протона в исследуемой среде,  мольная энтальпия сольватированного протона в стандартном растворителе; пределом являются нулевые концентрации
мольная энтальпия сольватированного протона в стандартном растворителе; пределом являются нулевые концентрации  Это уравнение непосредственно вытекает из соотношения
Это уравнение непосредственно вытекает из соотношения

Так как для двух оснований a и b, описываемых одной и той же функцией кислотности, отношение  имеет одинаковое значение, то для них и только для них
имеет одинаковое значение, то для них и только для них

Температурный коэффициент функции кислотности равен

Числитель в правой части уравнения (68) представляет собой разность между изменениями мольной энтальпии для превращения  в В в исследуемой и стандартной средах. Он также равен рассчитанному на 1 моль изменению стандартной энтальпии для процесса переноса эквивалентных бесконечно малых количеств
в В в исследуемой и стандартной средах. Он также равен рассчитанному на 1 моль изменению стандартной энтальпии для процесса переноса эквивалентных бесконечно малых количеств  из стандартной среды в исследуемую и переноса эквивалентного количества
из стандартной среды в исследуемую и переноса эквивалентного количества  в обратном направлении.
в обратном направлении.
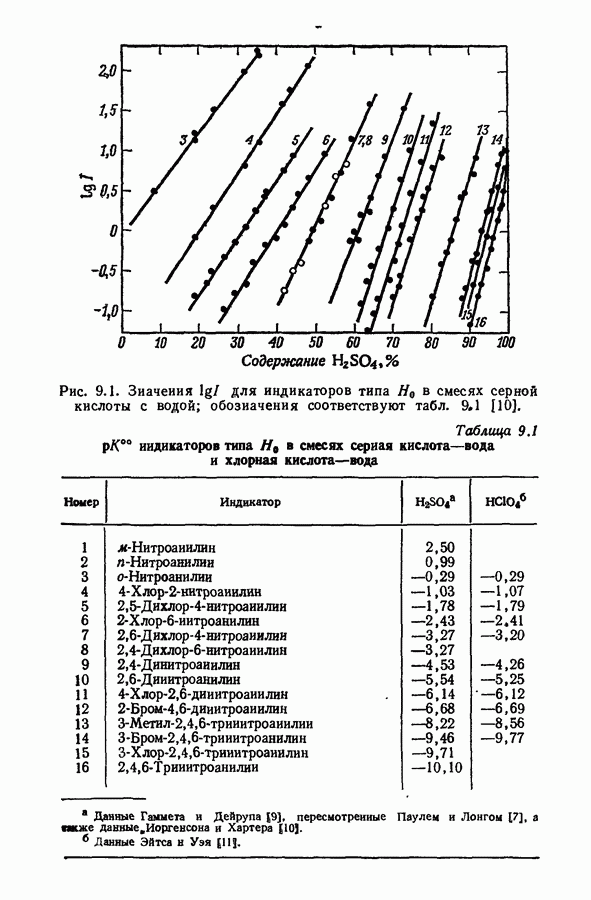
Гельбштейн, Щеглова и Тёмкин [55] исследовали влияние температуры на индикаторное отношение I оснований типа  в смесях серной кислоты с водой (табл. 9.4).
в смесях серной кислоты с водой (табл. 9.4).
Таблица 9.4. Термодинамические характеристики индикаторов типа  при
при 

Величины  для
для  -нитроанилина были получены экстраполяцией данных по разбавленным солянокислым растворам при каждой из исследованных температур, а именно при 20, 40, 60 и 80 °С. Для остальных индикаторов
-нитроанилина были получены экстраполяцией данных по разбавленным солянокислым растворам при каждой из исследованных температур, а именно при 20, 40, 60 и 80 °С. Для остальных индикаторов  при каждой температуре определялись методом перекрывания. В действительности не наблюдается настоящего перекрывания между
при каждой температуре определялись методом перекрывания. В действительности не наблюдается настоящего перекрывания между  -динитроанилином и 6-бром-2,4-динитроанилином, между 6-бром-2,4-динитроанилином и 2,4,6-тринитроанилином. Так как для последних двух индикаторов пришлось воспользоваться
-динитроанилином и 6-бром-2,4-динитроанилином, между 6-бром-2,4-динитроанилином и 2,4,6-тринитроанилином. Так как для последних двух индикаторов пришлось воспользоваться
неко торой экстраполяцией, данные по ним менее надежны, чем для остальных соединений. В каждом случае  линейно зависит от
линейно зависит от  в пределах ошибок эксперимента. Величины
в пределах ошибок эксперимента. Величины  при температуре
при температуре  приведены в табл. 9.4.
приведены в табл. 9.4.
Значения  изменяются параллельно и между ними существует линейная зависимость
изменяются параллельно и между ними существует линейная зависимость

Стандартное отклонение равно 400, если рассматривать все индикаторы, и 160, если опустить два последних. Конечно, должна существовать подобная линейная зависимость между  а также между
а также между 
В той степени, в какой ко всем этим основаниям приложима одна и та же функция кислотности, уравнение (69) должно выполняться во всех водных растворах кислот. В частности, оно должно выполняться и в  -ной серной кислоте, в растворе которой Арнетт и Бёрк [56] с помощью калориметрического метода определили
-ной серной кислоте, в растворе которой Арнетт и Бёрк [56] с помощью калориметрического метода определили  для процесса переноса ряда первичных анилинов из раствора в тетрахлорэтане в кислый раствор. Их измерения показали, что существует превосходная линейная зависимость между
для процесса переноса ряда первичных анилинов из раствора в тетрахлорэтане в кислый раствор. Их измерения показали, что существует превосходная линейная зависимость между  и величинами
и величинами  вычисленными для превращения сопряженной кислоты в основание в водном растворе. Эта зависимость, судя по приведенному в статье Арнетта и Бёрка рисунку, имеет вид
вычисленными для превращения сопряженной кислоты в основание в водном растворе. Эта зависимость, судя по приведенному в статье Арнетта и Бёрка рисунку, имеет вид

где  оператор Леффлера — Грюнвальда, отвечающий влиянию растворителя. Так как
оператор Леффлера — Грюнвальда, отвечающий влиянию растворителя. Так как

и

где  мольные энтальпии в кислом растворе, а
мольные энтальпии в кислом растворе, а  мольная энтальпия основания в инертном растворителе, то уравнения (69) и (70) приводят к
мольная энтальпия основания в инертном растворителе, то уравнения (69) и (70) приводят к

Таким образом, теплота не сопровождающегося протонированием переноса незаряженного основания из инертного растворителя в кислый раствор линейно связана с  и, следовательно, с теплотой кислотно-основного превращения. Это не удивительно, если иметь в виду образование водородных связей между основанием и сильнокислыми компонентами концентрированной серной кислоты.
и, следовательно, с теплотой кислотно-основного превращения. Это не удивительно, если иметь в виду образование водородных связей между основанием и сильнокислыми компонентами концентрированной серной кислоты.
Как отметили Арнетт и Бёрк, простота найденных зависимостей является сильным аргументом в пользу правильности использованных значений  и, следовательно, Справедливости допущения перекрывания.
и, следовательно, Справедливости допущения перекрывания.
Приводимые Гельбштейном и др. величины  не обнаруживают резкой зависимости от концентрации кислоты. Производная
не обнаруживают резкой зависимости от концентрации кислоты. Производная  имеет минимальное значение, равное —0,0025, при 8%-ной концентрации серной кислоты. Для
имеет минимальное значение, равное —0,0025, при 8%-ной концентрации серной кислоты. Для  -ной кислоты
-ной кислоты  , для
, для  -ной кислоты
-ной кислоты  Затем наблюдается постепенное возрастание до значения 0,013, соответствующего
Затем наблюдается постепенное возрастание до значения 0,013, соответствующего  -ной серной кислоте. Поэтому разность энтальпий в уравнении (68) изменяется от —1200 до 6000 кал/моль.
-ной серной кислоте. Поэтому разность энтальпий в уравнении (68) изменяется от —1200 до 6000 кал/моль.
Арнетт и Башик [57] определили температурный коэффициент индикаторного отношения для серии индикаторов  в смесях серной кислоты с водой. С увеличением
в смесях серной кислоты с водой. С увеличением  значения
значения  уменьшаются, но зависимости, по-видимому, не являются линейными. Для
уменьшаются, но зависимости, по-видимому, не являются линейными. Для  -тринитротрифенилкарбинола
-тринитротрифенилкарбинола  достигает заметной величины
достигает заметной величины  но для динитропроизводного
но для динитропроизводного  равно уже
равно уже  а для 4,4-диметокситрифенил-карбинола составляет
а для 4,4-диметокситрифенил-карбинола составляет  Такая величина энтропийных изменений должна отражать не только взаимодействие молекулы растворенного вещества с большим числом молекул растворителя, но также такое взаимодействие, степень которого сильно зависит от температуры, среды и структуры. Экспериментально обнаружено, что производная
Такая величина энтропийных изменений должна отражать не только взаимодействие молекулы растворенного вещества с большим числом молекул растворителя, но также такое взаимодействие, степень которого сильно зависит от температуры, среды и структуры. Экспериментально обнаружено, что производная  по-видимому, не зависит от температуры в пределах исследованного интервала в
по-видимому, не зависит от температуры в пределах исследованного интервала в  такое поведение может быть обманчивым.
такое поведение может быть обманчивым.
При изменении температуры или концентрации кислоты величины  (1/77) изменяются каждый раз
(1/77) изменяются каждый раз
по своему. По мере увеличения концентрации кислоты выше 65% они неизменно становятся более положительными. В 80%-ной кислоте  что соответствует разности энтальпий в уравнении (68), равной —13,5 ккал.
что соответствует разности энтальпий в уравнении (68), равной —13,5 ккал.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. ВВЕДЕНИЕ
- 2. ТЕРМОДИНАМИКА РЕАКЦИИ В РАСТВОРАХ
- 2.2. ИЗМЕНЕНИЕ ЭНЕРГИИ ГИББСА В ПРОЦЕССЕ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.3. УСЛОВИЕ РАВНОВЕСИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2.4. ПРИБЛИЖЕНИЕ РАЗБАВЛЕННОГО РАСТВОРА
- 2.5. СТАНДАРТНЫЙ ПОТЕНЦИАЛ
- 2.6. ЗАКОН РАВНОВЕСИЯ В ПРИБЛИЖЕНИИ РАЗБАВЛЕННОГО РАСТВОРА
- 2.7. КОЭФФИЦИЕНТ АКТИВНОСТИ
- 2.8. ТОЧНЫЙ ЗАКОН РАВНОВЕСИЯ
- 2.9. ЗНАК ПРОИЗВОДНОЙ …
- 2.10. АКТИВНОСТЬ И СТАНДАРТНАЯ АКТИВНОСТЬ
- 2.11. КОНСТАНТЫ РАВНОВЕСИЯ В РАЗЛИЧНЫХ СРЕДАХ
- 2.12. ЧИСЛО И ВЫБОР КОМПОНЕНТОВ
- 2.13. ФОРМАЛЬНЫЕ И ИСТИННЫЕ ЗНАЧЕНИЯ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.14. ФУНКЦИЯ q°
- 2.15. УРАВНЕНИЕ ГИББСА—ДЮГЕМА
- 2.16. МОЛЕКУЛЯРНЫЕ ВЕСА В РАСТВОРЕ
- 2.17. УРАВНЕНИЕ ГИББСА—ДЮГЕМА ДЛЯ МНОГОКОМПОНЕНТНЫХ СИСТЕМ
- 2.18. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 2.19. ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ ХИМИЧЕСКОГО ПОТЕНЦИАЛА
- 2.20. МОЛЬНАЯ ЭНТАЛЬПИЯ И МОЛЬНАЯ ЭНТРОПИЯ КАК ФУНКЦИИ КОНЦЕНТРАЦИИ
- 2.21. ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ
- 2.22. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЭНТАЛЬПИИ И СТАНДАРТНОЙ ЭНТРОПИИ РЕАКЦИИ
- 2.23. ПРОБЛЕМА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ …
- 2.24. ФОРМАЛЬНЫЕ ЗНАЧЕНИЯ СТАНДАРТНОЙ ЭНТАЛЬПИИ, ЭНТРОПИИ И ТЕПЛОЕМКОСТИ
- 3. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
- 3.2. СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА ИДЕАЛЬНОГО ГАЗА
- 3.3. ПРИРОДА СТАТИСТИЧЕСКИХ СУММ
- 3.4. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ ПРОСТОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
- 3.5. ТИПИЧНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
- 3.6. РАСЧЕТ СТАТИСТИЧЕСКИХ СУММ
- 3.7. СТАТИСТИЧЕСКАЯ МЕХАНИКА И ХИМИЧЕСКОЕ РАВНОВЕСИЕ В ГАЗОВОЙ ФАЗЕ
- 3.8. ИЗМЕНЕНИЕ ЭНТАЛЬПИИ И ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
- 3.9. СТАТИСТИЧЕСКАЯ МЕХАНИКА РАЗБАВЛЕННОГО РАСТВОРА
- 3.10. ПРАВИЛО БАРКЛЕЯ—БАТЛЕРА
- 3.11. НЕКОТОРЫЕ ОСОБЕННОСТИ ВОДНЫХ РАСТВОРОВ
- 3.12. ИЗМЕНЕНИЯ СТАНДАРТНОЙ ЭНТРОПИИ ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 3.13. СВЯЗЬ СО СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 3.14. СТАТИСТИЧЕСКАЯ СУММА q°
- 4. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ ДАННЫХ
- 4.2. СИСТЕМАТИКА И ТЕРМИНОЛОГИЯ
- 4.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИИ
- 4.4. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ КИНЕТИКИ
- 4.5. ЛИНЕЙНЫЕ ФОРМЫ УРАВНЕНИЙ ДЛЯ КИНЕТИЧЕСКИ ПРОСТЫХ НЕОБРАТИМЫХ РЕАКЦИИ
- 4.6. ПРОБЛЕМА ТОЧНОСТИ
- 4.7. ВЛИЯНИЕ СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ ОТ ЛИНЕЙНОСТИ
- 4.8. ДОСТОВЕРНОСТЬ ОПРЕДЕЛЕНИЯ ПОРЯДКА РЕАКЦИИ
- 4.9. ПРОТОЧНЫЕ РЕАКТОРЫ С ПЕРЕМЕШИВАНИЕМ
- 4.10. КИНЕТИЧЕСКИ ПРОСТЫЕ ОБРАТИМЫЕ РЕАКЦИИ
- 4.11. КИНЕТИЧЕСКИ СЛОЖНЫЕ РЕАКЦИИ
- 4.12. ЭКСПЕРИМЕНТАЛЬНОЕ РАСПОЗНАВАНИЕ СИСТЕМ, ВКЛЮЧАЮЩИХ РЕАКЦИИ ТОЛЬКО ПЕРВОГО ПОРЯДКА
- 4.13. ИНТЕГРАЛЬНЫЕ ФОРМЫ УРАВНЕНИИ ДЛЯ СИСТЕМ РЕАКЦИИ ПЕРВОГО ПОРЯДКА
- 4.14. ИНТЕРПРЕТАЦИЯ КИНЕТИЧЕСКИХ УРАВНЕНИЙ, СОДЕРЖАЩИХ ДВА ЭКСПОНЕНЦИАЛЬНЫХ ЧЛЕНА
- 4.15. МЕТОД БОДЕНШТЕИНА (МЕТОД СТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ)
- 4.16. ПРОБЛЕМА ТОЧНОСТИ УРАВНЕНИИ С БОЛЬШИМ ЧИСЛОМ ПАРАМЕТРОВ
- 4.17. УРАВНЕНИЕ МИХАЭЛИСА-МЕНТЕН
- 4.18. СИСТЕМЫ С ПРЕДРАВНОВЕСИЕМ
- 4.19. ВЛИЯНИЕ АССОЦИАТИВНОГО РАВНОВЕСИЯ
- 4.20. РАСПОЗНАВАНИЕ СЛОЖНОСТИ РЕАКЦИИ
- 4.21. ИСПОЛЬЗОВАНИЕ ПРОТОЧНОГО РЕАКТОРА С ПЕРЕМЕШИВАНИЕМ ДЛЯ ИЗУЧЕНИЯ МНОГОСТАДИЙНЫХ РЕАКЦИЙ
- 4.22. ПРОТОЧНЫЙ ТРУБЧАТЫЙ РЕАКТОР
- 4.23. ИЗУЧЕНИЕ ОТНОСИТЕЛЬНОЙ РЕАКЦИОННОЙ СПОСОБНОСТИ МЕТОДОМ КОНКУРИРУЮЩИХ РЕАКЦИЙ
- 4.24. ОЧЕНЬ БЫСТРЫЕ РЕАКЦИИ, ЛИМИТИРУЕМЫЕ ДИФФУЗИЕЙ
- 4.25. СПРАВЕДЛИВОСТЬ ЗАКОНА ДЕЙСТВИЯ МАСС ДЛЯ РЕАКЦИИ В РАСТВОРАХ
- 4.26. ПРИНЦИП НЕЗАВИСИМОГО ПРОТЕКАНИЯ РЕАКЦИЙ
- 4.27. КАТАЛИТИЧЕСКИЕ РЕАКЦИИ И РЕАКЦИИ НУЛЕВОГО ПОРЯДКА
- 4.28. «МРАЧНЫЕ ВРЕМЕНА» И «ВОЗРОЖДЕНИЕ»
- 5. ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.2. ИЗМЕНЕНИЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ СИСТЕМЫ В ХОДЕ РЕАКЦИИ
- 5.3. КООРДИНАТА РЕАКЦИИ
- 5.4. ДЕТАЛЬНАЯ ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.5. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.6. ОБОСНОВАННОСТЬ ДЕТАЛЬНОЙ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.7. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА ДРУГИЕ ТИПЫ РЕАКЦИЙ
- 5.8. РАСПРОСТРАНЕНИЕ ТЕОРИИ НА НЕИДЕАЛЬНЫЕ РАСТВОРЫ
- 5.9. СОСТАВ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 5.10. ЛИМИТИРУЮЩЕЕ ПЕРЕХОДНОЕ СОСТОЯНИЕ ИЛИ ЛИМИТИРУЮЩИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.11. ПАРАЛЛЕЛЬНЫЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 5.12. ОБЯЗАТЕЛЬНО ЛИ ОБРАЗОВАНИЕ ПРОМЕЖУТОЧНЫХ СОЕДИНЕНИЙ?
- 5.13. ПРОДВИЖЕНИЕ ОТ РЕАГЕНТОВ К ПЕРЕХОДНОМУ СОСТОЯНИЮ
- 5.14. ВОПРОСЫ ПО ПОВОДУ МЕХАНИЗМА, ИМЕЮЩИЕ И НЕ ИМЕЮЩИЕ СМЫСЛА
- 5.15. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ
- 5.16. ПРИНЦИП КЕРТИНА
- 5.17. РЕАКЦИЯ СТИЛЬБЕНА С БРОМОМ В МЕТАНОЛЕ
- 5.18. ПРОБЛЕМА МЕХАНИЗМА РЕАКЦИИ С УЧАСТИЕМ ИОНОВ
- 5.19. ЭФФЕКТЫ СТРОЕНИЯ В СИСТЕМАХ С ПОДВИЖНЫМ РАВНОВЕСИЕМ
- 5.20. ПРОБЛЕМА СТЕХИОМЕТРИЧЕСКОГО ВКЛЮЧЕНИЯ РАСТВОРИТЕЛЯ В ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 5.21. ЭНТРОПИЯ АКТИВАЦИИ
- 5.22. СТРУКТУРНЫЕ ИЗОТОПНЫЕ ЭФФЕКТЫ
- 5.23. ИЗОТОПНЫЕ ЭФФЕКТЫ РАСТВОРИТЕЛЕЙ
- 5.24. ВЛИЯНИЕ ДАВЛЕНИЯ НА СКОРОСТЬ РЕАКЦИЙ
- 5.25. СИСТЕМЫ С ПОДВИЖНЫМИ РАВНОВЕСИЯМИ В ИСХОДНЫХ И КОНЕЧНЫХ ВЕЩЕСТВАХ
- 5.26. КАТАЛИЗ
- 5.27. ПРОДВИЖЕНИЕ ОТ ПЕРЕХОДНОГО СОСТОЯНИЯ К ПРОДУКТАМ РЕАКЦИИ В СЛУЧАЕ КАТАЛИТИЧЕСКОГО ПРОЦЕССА
- 5.28. ФЕРМЕНТАТИВНЫЙ И ГЕТЕРОГЕННЫЙ КАТАЛИЗ
- 5.29. МИКРОСКОПИЧЕСКАЯ ОБРАТИМОСТЬ ИЛИ ДЕТАЛЬНОЕ РАВНОВЕСИЕ
- 6. НЕКОТОРЫЕ РЕАКЦИИ ЗАМЕЩЕНИЯ
- 6.1 НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ ВТОРОГО ПОРЯДКА У НАСЫЩЕННОГО АТОМА УГЛЕРОДА
- 6.2. РАЦЕМИЗАЦИЯ И ИЗОТОПНЫЙ ОБМЕН
- 6.3. РЕАКЦИИ СОЛЬВОЛИЗА
- 6.4. КАРБОНИЕВО-ИОННЫЙ МЕХАНИЗМ
- 6.5. СОЛЕВЫЕ ЭФФЕКТЫ В СИЛЬНО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
- 6.6. РОЛЬ РАСТВОРИТЕЛЯ
- 6.7. ВОПРОСЫ ТЕРМИНОЛОГИИ
- 6.8. ОГРАНИЧЕННОСТЬ ПРЕДСТАВЛЕНИИ ОБ ОБРАЗОВАНИИ СВОБОДНЫХ ИОНОВ КАРБОНИЯ
- 6.9. ГИПОТЕЗА ИОННЫХ ПАР
- 6.10. ВЛИЯНИЕ ДОБАВОК АЗИДОВ
- 6.11. УЧАСТИЕ БЕЗГИДРОКСИЛЬНЫХ РАСТВОРИТЕЛЕЙ В ОБРАЗОВАНИИ ПЕРЕХОДНОГО КОМПЛЕКСА
- 6.12. АЛЛИЛЬНАЯ ПЕРЕГРУППИРОВКА
- 6.13. СОЛЬВОЛИЗ, СОПРОВОЖДАЮЩИЙСЯ РАЦЕМИЗАЦИЕЙ РЕАГЕНТА
- 6.14. ДОПОЛНИТЕЛЬНЫЕ ДАННЫЕ О ВЛИЯНИИ ДОБАВОК АЗИДОВ
- 6.15. ОСОБЫЙ СОЛЕВОЙ ЭФФЕКТ
- 6.16. ДВОЙНОЕ ОБРАЩЕНИЕ КОНФИГУРАЦИИ
- 6.17. БРОМОНИЕВЫЕ ИОНЫ КАК ПРОМЕЖУТОЧНЫЕ СОЕДИНЕНИЯ
- 6.18. ПРОБЛЕМА ФЕНОНИЕВОГО ИОНА
- 6.19. ПЕРЕГРУППИРОВКИ
- 6.20. ЭЛЕКТРОФИЛЬНОЕ АРОМАТИЧЕСКОЕ ЗАМЕЩЕНИЕ
- 6.21. РЕАКЦИЯ АЗОСОЧЕТАНИЯ
- 6.22. ВОЗМОЖНЫЕ ФОРМЫ РЕАГЕНТОВ
- 6.23. ПЕРЕХОДНОЕ СОСТОЯНИЕ РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.24. КАТАЛИТИЧЕСКОЕ ДЕЙСТВИЕ ПИРИДИНА
- 6.25. ИЗОТОПНЫЕ ЭФФЕКТЫ ВОДОРОДА В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.26. ПРОСТРАНСТВЕННЫЕ ВЛИЯНИЯ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 6.27. ЭНТРОПИЯ АЗОСОЧЕТАНИЯ
- 7. СОЛЕВЫЕ ЭФФЕКТЫ
- 7.1. УРАВНЕНИЕ БРЕНСТЕДА
- 7.2. ПРЕДЕЛЬНЫЙ ЗАКОН ДЕБАЯ — ХЮККЕЛЯ
- 7.3. СОЛЕВЫЕ ЭФФЕКТЫ В РЕАКЦИИ АЗОСОЧЕТАНИЯ
- 7.4. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К НЕСИММЕТРИЧНЫМ ИОНАМ
- 7.5. ПРИМЕНИМОСТЬ ПРЕДЕЛЬНОГО ЗАКОНА К МНОГОЗАРЯДНЫМ ИОНАМ
- 7.6. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИЙ СОЛЕЙ НА КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 7.7. ВЛИЯНИЕ УМЕРЕННЫХ КОНЦЕНТРАЦИИ СОЛЕЙ НА СКОРОСТЬ РЕАКЦИЙ МЕЖДУ ИОНАМИ
- 7.8. СОЛЕВЫЕ ЭФФЕКТЫ КАК ПОДТВЕРЖДЕНИЕ ТЕОРИИ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 7.9. ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.10. ПОДАВЛЕНИЕ СОЛЕВЫХ ЭФФЕКТОВ, ПРИ ИЗУЧЕНИИ ПОРЯДКА РЕАКЦИЙ
- 7.11. ФИЗИЧЕСКИЙ СМЫСЛ ТЕОРИИ ДЕБАЯ — ХЮККЕЛЯ
- 7.12. МОДИФИКАЦИЯ ТЕОРИЙ ДЛЯ СЛУЧАЯ СЛАБЫХ ВЗАИМОДЕЙСТВИЙ
- 7.13. ПРИБЛИЖЕНИЕ БЬЕРРУМА
- 7.14. ИОННЫЕ ПАРЫ В ХИМИЧЕСКИХ РЕАКЦИЯХ
- 7.15. ОБРАЗОВАНИЕ ИОННЫХ ПАР И ПРАВИЛО ОЛСОНА — СИМОНСОНА
- 7.16. О ПОНЯТИИ ИОННЫХ ПАР
- 7.17. О СЛАБОЙ АССОЦИАЦИИ ИОНОВ
- 7.18. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В ВОДНЫХ РАСТВОРАХ
- 7.19. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ВОДНЫХ РАСТВОРАХ
- 7.20. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ МЕЖДУ ИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ В ЖИДКОМ СЕРНИСТОМ АНГИДРИДЕ
- 7.21. ВЛИЯНИЕ СОЛЕЙ НА РЕАКЦИИ СОЛЬВОЛИЗА В ВОДНЫХ РАСТВОРАХ
- 7.22. ВЛИЯНИЕ СОЛЕЙ НА НЕЭЛЕКТРОЛИТЫ В НЕВОДНЫХ РАСТВОРАХ
- 7.23. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 8. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ
- 8.3. ОБРАЗОВАНИЕ ИОННЫХ ПАР; СЛУЧАИ ИДЕАЛЬНОГО ЭЛЕКТРОСТАТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 8.4. АССОЦИАЦИЯ ИОНОВ В ЧЕТВЕРТИЧНЫХ АММОНИЕВЫХ СОЛЯХ
- 8.5. ИОННЫЕ ТРИПЛЕТЫ И ПОЛИМЕРЫ СОЛЕЙ
- 8.6. ВОДОРОДНАЯ СВЯЗЬ
- 8.7. ИОННЫЕ ПАРЫ С ВОДОРОДНОЙ СВЯЗЬЮ
- 8.8. ВЗАИМОДЕЙСТВИЕ АНИОНОВ С ДОНОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.9. ВЗАИМОДЕЙСТВИЕ КАТИОНОВ С АКЦЕПТОРАМИ ВОДОРОДНОЙ СВЯЗИ
- 8.10. ДРУГИЕ ВИДЫ ВЗАИМОДЕЙСТВИИ ИОНОВ С НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
- 8.11. ОБЗОР ВЗАИМОДЕЙСТВИИ ИОНОВ С РАСТВОРИТЕЛЕМ
- 8.12. РОЛЬ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ
- 8.13. МЕТАЛЛООРГАНИЧЕСКИЕ СОЕДИНЕНИЯ ЭЛЕМЕНТОВ ПЕРВОЙ ГРУППЫ
- 8.14. ВЛИЯНИЕ СОЛЬВАТАЦИИ АНИОНА НА СКОРОСТЬ ВЗАИМОДЕЙСТВИЯ АНИОНА С НЕЙТРАЛЬНОЙ МОЛЕКУЛОЙ
- 8.15. ВЛИЯНИЕ СПЕЦИФИЧЕСКОЙ СОЛЬВАТАЦИИ КАТИОНОВ НА СКОРОСТИ РЕАКЦИЙ МЕЖДУ АНИОНАМИ И НЕЙТРАЛЬНЫМИ МОЛЕКУЛАМИ
- 8.16. ХЕЛАТНАЯ СОЛЬВАТАЦИЯ КАТИОНОВ
- 8.17. КИНЕТИКА РЕАКЦИЙ С УЧАСТИЕМ ИОННЫХ АГРЕГАТОВ
- 8.18. ИНЕРТНОСТЬ ТВЕРДЫХ РЕАГЕНТОВ
- 8.19. ВЛИЯНИЕ РАСТВОРИТЕЛЯ НА РЕАКЦИОННУЮ СПОСОБНОСТЬ АМБИДЕНТНЫХ АНИОНОВ
- 8.20. ВЛИЯНИЕ ПРИРОДЫ РАСТВОРИТЕЛЯ НА РЕАКЦИИ КАТИОНОВ С АНИОНАМИ
- 8.21. ДИСПЕРСИОННЫЕ СИЛЫ
- 8.22. ПЛОТНОСТЬ КОГЕЗИОННОЙ ЭНЕРГИИ
- 8.23. РЕГУЛЯРНЫЕ И ИДЕАЛЬНЫЕ РАСТВОРЫ
- 8.24. ПЕРЕНОС РАСТВОРЕННОГО ВЕЩЕСТВА ИЗ ОДНОГО РЕГУЛЯРНОГО РАСТВОРА В ДРУГОЙ
- 8.25. ВЛИЯНИЕ СИЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
- 8.26. ИЗОКИНЕТИЧЕСКАЯ ЗАВИСИМОСТЬ ПРИ ИЗМЕНЕНИИ РАСТВОРИТЕЛЯ
- 8.27. СОЛЬВОЛИЗ В ВОДНО-СПИРТОВЫХ СМЕСЯХ
- 8.28. ИНЫЕ ВЛИЯНИЯ РАСТВОРИТЕЛЯ НА СКОРОСТЬ СОЛЬВОЛИЗА
- 8.29. КОМПЛЕКСЫ С ПЕРЕНОСОМ ЗАРЯДА
- 8.30. КОМПЛЕКСООБРАЗОВАНИЕ ЗА СЧЕТ МУЛЬТИПОЛЬНОГО ИЛИ ДИПОЛЬНОГО ВЗАИМОДЕЙСТВИЯ
- 9. КОЛИЧЕСТВЕННОЕ ИЗУЧЕНИЕ КИСЛОТ И ОСНОВАНИЙ
- 9.2. ЭЛЕКТРОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КИСЛОТНОСТИ В НЕВОДНЫХ РАСТВОРАХ
- 9.3. ИЗМЕРЕНИЕ КИСЛОТНОСТИ С ПОМОЩЬЮ ИНДИКАТОРОВ
- 9.4. ФУНКЦИЯ КИСЛОТНОСТИ Н0
- 9.5. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 9.6. ФУНКЦИИ КИСЛОТНОСТИ
- 9.7. ФУНКЦИИ КИСЛОТНОСТИ …
- 9.8. ДРУГИЕ ДАННЫЕ ПО ФУНКЦИЯМ КИСЛОТНОСТИ
- 9.9. ГИПОТЕЗА ТРЕХ ПЕРЕМЕННЫХ
- 9.10. СОЛЬВАТАЦИОННАЯ ПЕРЕМЕННАЯ «фи»
- 9.11. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ КИСЛОТНОСТИ
- 9.12. СТАНДАРТНЫЕ АКТИВНОСТИ В СМЕСЯХ СИЛЬНЫХ КИСЛОТ С ВОДОЙ
- 9.13. О ВЛИЯНИИ АКТИВНОСТИ ВОДЫ
- 9.14. ФУНКЦИИ КИСЛОТНОСТИ ДЛЯ ВЫСОКОКОНЦЕНТРИРОВАННЫХ РАСТВОРОВ КИСЛОТ
- 9.15. ФУНКЦИИ КИСЛОТНОСТИ И СКОРОСТИ КАТАЛИЗИРУЕМЫХ КИСЛОТАМИ РЕАКЦИЙ
- 9.16 НИТРОВАНИЕ АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ В СМЕСЯХ СЕРНОЙ КИСЛОТЫ С ВОДОЙ
- 9.17. СИСТЕМЫ, ОПИСЫВАЕМЫЕ ДВУМЯ ФУНКЦИЯМИ КИСЛОТНОСТИ
- 9.18. НЕОПРЕДЕЛЕННОСТЬ ПОНЯТИЯ СИЛЫ ОСНОВАНИЯ
- 9.19. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН pK
- 9.20. НАЛОЖЕНИЕ ЭФФЕКТОВ СРЕДЫ ПРИ СПЕКТРОФОТОМЕТРИЧЕСКОМ ОПРЕДЕЛЕНИИ ОСНОВНОСТИ
- 9.21. МЕТОДЫ ВВЕДЕНИЯ ПОПРАВОК НА ЭФФЕКТЫ СРЕДЫ
- 9.22. ДРУГИЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ СИЛЫ СЛАБЫХ ОСНОВАНИЙ
- 9.23. ТЕМПЕРАТУРНЫЕ КОЭФФИЦИЕНТЫ
- 9.24. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ПЛОХО ДИССОЦИИРУЮЩИХ РАСТВОРИТЕЛЯХ
- 9.25. ПОВЕДЕНИЕ ИНДИКАТОРОВ В НИТРОМЕТАНЕ И СУЛЬФОЛАНЕ
- 9.26. КИСЛОТНО-ОСНОВНЫЕ РЕАКЦИИ В ДИМЕТИЛСУЛЬФОКСИДЕ
- 9.27. ФУНКЦИИ КИСЛОТНОСТИ И СИЛА ОСНОВАНИИ В ДРУГИХ ВЫСОКООСНОВНЫХ СРЕДАХ
- 9.28. СКОРОСТИ РЕАКЦИЙ В СИЛЬНООСНОВНЫХ СРЕДАХ
- 9.29. ОСНОВНОСТЬ АЛКОГОЛЯТОВ ЩЕЛОЧНЫХ МЕТАЛЛОВ
- 10. СКОРОСТИ РЕАКЦИЙ С УЧАСТИЕМ КИСЛОТ И ОСНОВАНИЙ
- 10.2. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА
- 10.3. СТАТИСТИЧЕСКИЕ ПОПРАВКИ
- 10.4. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 10.5. КАТАЛИТИЧЕСКОЕ УРАВНЕНИЕ БРЕНСТЕДА И ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ
- 10.6. КАТАЛИЗ МОЛЕКУЛАМИ РАСТВОРИТЕЛЯ, ИОНАМИ ЛИОНИЯ И ЛИАТА
- 10.7. РАЗПОЗНАВАЕМОСТЬ ОБЩЕГО КИСЛОТНОГО И ОБЩЕГО ОСНОВНОГО КАТАЛИЗА
- 10.8. СКОРОСТИ РЕАКЦИЙ ПЕРЕНОСА ПРОТОНА
- 10.9. ТЕОРИЯ ЭЛЕКТРОННЫХ СМЕЩЕНИЙ
- 10.10. ГИДРАТАЦИЯ АЦЕТАЛЬДЕГИДА
- 10.11. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ ОСНОВАНИЯМИ
- 10.12. МЕХАНИЗМ ГИДРАТАЦИИ, КАТАЛИЗИРУЕМОЙ КИСЛОТАМИ
- 10.13. КАТАЛИЗ В РЕАКЦИИ ЕНОЛИЗАЦИИ
- 10.14. ЦИКЛИЧЕСКИЕ ПЕРЕХОДНЫЕ СОСТОЯНИЯ
- 10.15. ГИДРОЛИЗ ЭФИРОВ
- 10.16. КРИВЫЕ ТИПА «КОЛОКОЛА» И «ПЕРЕВЕРНУТОГО КОЛОКОЛА»
- 10.17. ОБРАЗОВАНИЕ ОКСИМОВ И ДРУГИЕ ПОДОБНЫЕ РЕАКЦИИ
- 10.18. ГИДРОЛИЗ ФЕНИЛИМИНОЛАКТОНА
- 10.19. КАТАЛИЗ КИСЛОТАМИ ЛЬЮИСА
- 11. КОЛИЧЕСТВЕННЫЕ ЗАВИСИМОСТИ МЕЖДУ СТРОЕНИЕМ И РЕАКЦИОННОЙ СПОСОБНОСТЬЮ
- 11.2. ПРИНЦИП ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.3. ЗАВИСИМОСТЬ МЕЖДУ КОНСТАНТАМИ СКОРОСТЕЙ И РАВНОВЕСИЙ
- 11.4. ЛИНЕЙНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗМЕНЕНИЯМИ СВОБОДНЫХ ЭНЕРГИЙ
- 11.5. КОРРЕЛЯЦИИ ГЕТТЛЕРА
- 11.6. СИЛА КИСЛОТ И СКОРОСТЬ ГИДРОЛИЗА ИХ ЭФИРОВ
- 11.7. ФЕНОЛЫ И КАРБОНОВЫЕ КИСЛОТЫ
- 11.8 ЭЛЕКТРОННАЯ ИНТЕРПРЕТАЦИЯ
- 11.9. УРАВНЕНИЕ ГАММЕТА
- 11.10. ПРОСТРАНСТВЕННЫЕ ЭФФЕКТЫ
- 11.11. ПРЯМЫЕ РЕЗОНАНСНЫЕ ВЗАИМОДЕИСТВИЯ
- 11.12. НОРМАЛЬНЫЕ КОНСТАНТЫ ЗАМЕСТИТЕЛЕЙ
- 11.13. «сигма»-КОНСТАНТЫ
- 11.14. «сигма+»-КОНСТАНТЫ
- 11.15. НЕДОСТАТОЧНОСТЬ ДВУХ ЗНАЧЕНИЙ «сигма»
- 11.16. ЗАКОНОМЕРНОСТИ ПРЯМОГО РЕЗОНАНСНОГО ВЗАИМОДЕИСТВИЯ
- 11.17. УРАВНЕНИЕ ЮКАВА—ЦУНО
- 11.18. ПРОБЛЕМА СЛУЧАЙНЫХ И СИСТЕМАТИЧЕСКИХ ОТКЛОНЕНИЙ
- 11.19. ЗАТУХАНИЕ ЭЛЕКТРОННЫХ ВЛИЯНИЙ В БОКОВОЙ ЦЕПИ
- 11.20. СУММАРНОЕ ВЛИЯНИЕ НЕСКОЛЬКИХ ЗАМЕСТИТЕЛЕЙ
- 11.21. ПРОСТРАНСТВЕННЫЕ ПРЕПЯТСТВИЯ РЕЗОНАНСУ
- 11.22. ПРИРОДА ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.23. АДДИТИВНОСТЬ ПРОСТРАНСТВЕННЫХ ЭФФЕКТОВ
- 11.24. ДАЛЬНЕЙШИЕ ОГРАНИЧЕНИЯ ПРИМЕНИМОСТИ ПРИНЦИПА ЛИНЕЙНОЙ ЗАВИСИМОСТИ СВОБОДНЫХ ЭНЕРГИИ
- 11.25. ИНДУКЦИОННЫЙ И РЕЗОНАНСНЫЙ ЭФФЕКТЫ
- 11.26. УРАВНЕНИЕ ТАФТА
- 11.27. ИСТОРИЧЕСКИЕ СВЕДЕНИЯ
- 11.28. КОРРЕЛЯЦИЯ РЕАКЦИОННОЙ СПОСОБНОСТИ АЛИФАТИЧЕСКИХ И АРОМАТИЧЕСКИХ СОЕДИНЕНИЙ
- 11.29. АНАЛИЗ ЭКСНЕРА
- 11.30. «ГИБКИЕ» И «ЖЕСТКИЕ» МОЛЕКУЛЫ
- 11.31. ВЛИЯНИЕ РАСТВОРИТЕЛЕЙ НА …
- 12. ВЛИЯНИЕ СТРОЕНИЯ НА ИЗМЕНЕНИЯ ЭНТАЛЬПИИ И ЭНТРОПИИ
- 12.2. ИЗОЭНТРОПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
- 12.3. ИЗОЭНТАЛЬПИЙНЫЕ РЕАКЦИОННЫЕ СЕРИИ
- 12.4. ИЗОКИНЕТИЧЕСКАЯ ТЕМПЕРАТУРА
- 12.5. НАДЕЖНОСТЬ УСТАНОВЛЕНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
- 12.6. ПРЕДЕЛЫ СУЩЕСТВОВАНИЯ ИЗОКИНЕТИЧЕСКОЙ ЗАВИСИМОСТИ
- 12.7. НЕПОСТОЯНСТВО ЭНТАЛЬПИЙНЫХ И ЭНТРОПИЙНЫХ ВЛИЯНИЙ
- 12.8 СТРУКТУРНЫЕ ВЛИЯНИЯ И СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА
- 12.9. ПРЕДПОЛОЖЕНИЯ
- 12.10. СЛЕДСТВИЯ
- 12.11. ПОДТВЕРЖДЕНИЯ
- 12.12. ДРУГИЕ ПОДХОДЫ