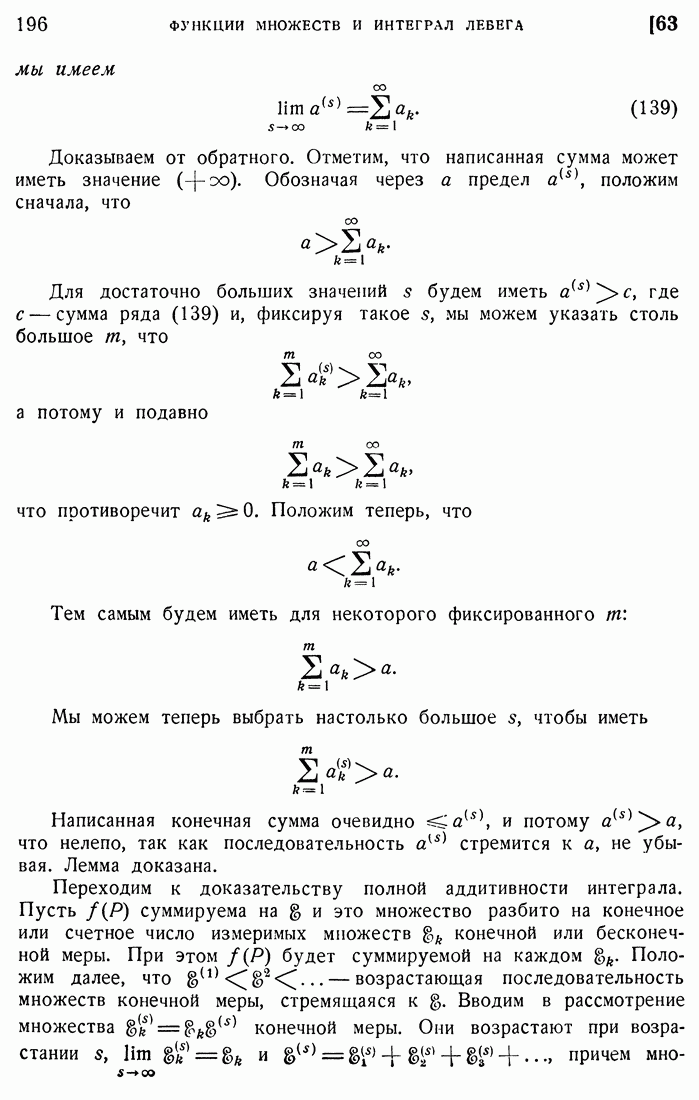
9. Интегрирующая функция ограниченной вариации.

Если непрерывная функция на ограниченной вариации, то, пользуясь представлением в виде разности двух возрастающих функций, можем написать

Суммы, стоящие справа, имеют определенный предел при беспредельном измельчании промежутков, и, следовательно, то же можно утверждать и относительно суммы, стоящей слева, т. е. непрерывная функция интегрируема по функции ограниченной вариации. Предельный переход в формуле (54) дает:

Укажем на те изменения, которые надо внести в формулировку свойств интеграла Стилтьеса, если есть функция ограниченной вариации.

Мы имеем

если . Предельный переход дает

Эта формула заменяет формулу (21) из [4]. Напомним еще формулу [2]

Если ограниченной вариации, то и их линейная комбинация есть также функция ограниченной вариации.

Рассмотрим интеграл Стилтьеса с переменным верхним пределом для того случая, когда непрерывна и ограниченной вариации:

Покажем, что функция есть функция ограниченной вариации. Составим для сумму :

Применяя формулу (56), получим

откуда и следует наше утверждение. В тех точках, где непрерывна, и функция непрерывна, и из неравенства

непосредственно вытекает, что в этих точках и непрерывна. Докажем еще следующее утверждение: если непрерывны на ограниченной вариации, то имеет место формула

Достаточно доказать эту формулу для случая возрастающей . Составим для интеграла, стоящего в левой части формулы (59), сумму :

или, согласно теореме о среднем [4]:

Точки и принадлежат одному и тому же промежутку, и, рассуждая совершенно так же, как это мы делали для формулы (9) из [2], убедимся, что сумма, стоящая в правой части, формулы (60), в пределе дает интеграл, стоящий в правой части (59), и этим самым эта последняя формула доказана.