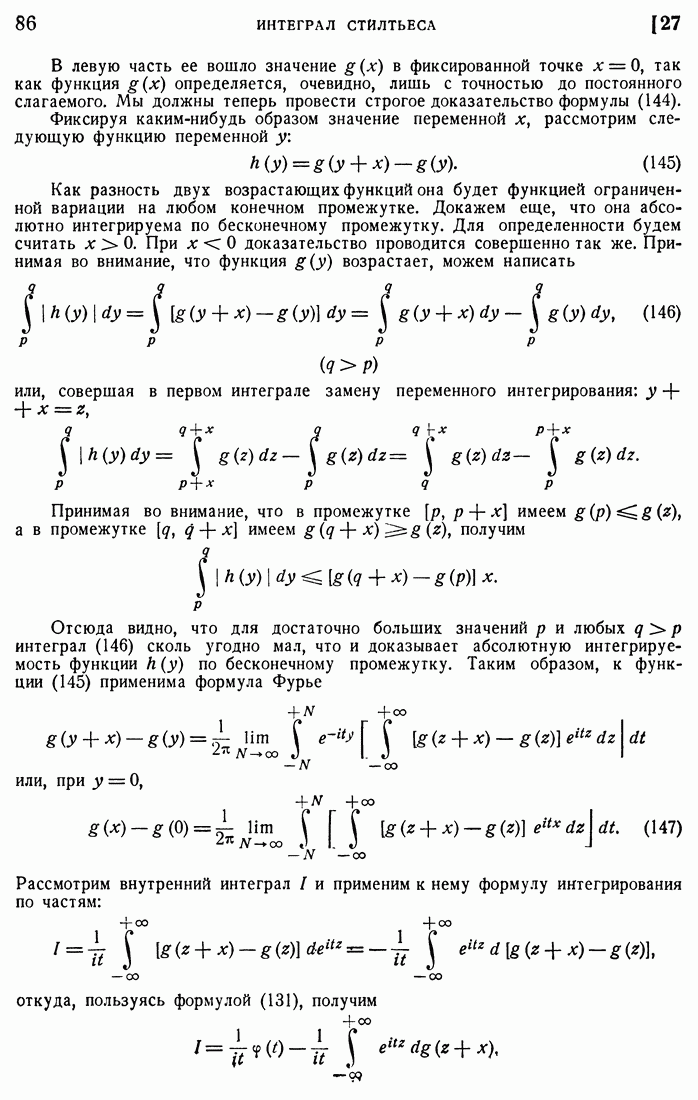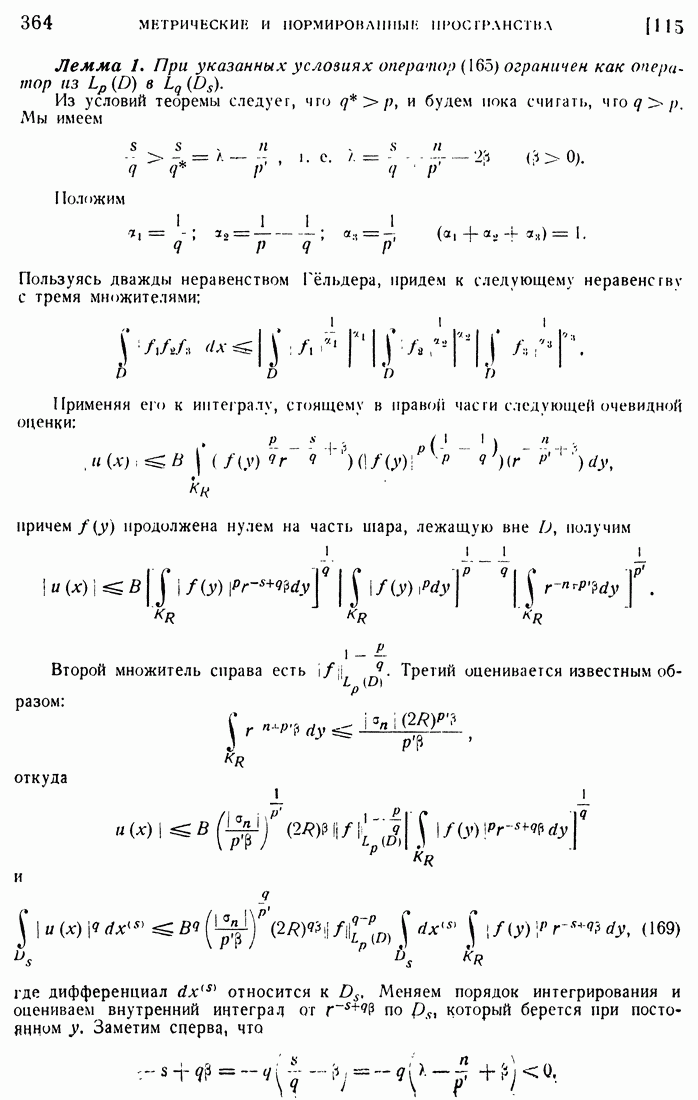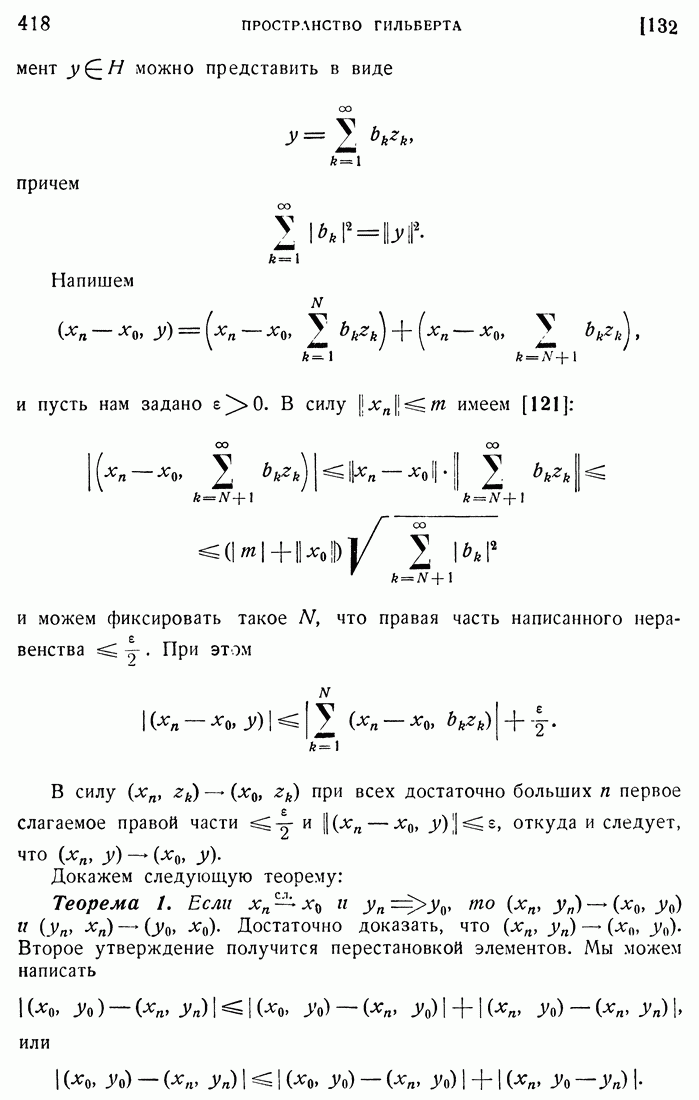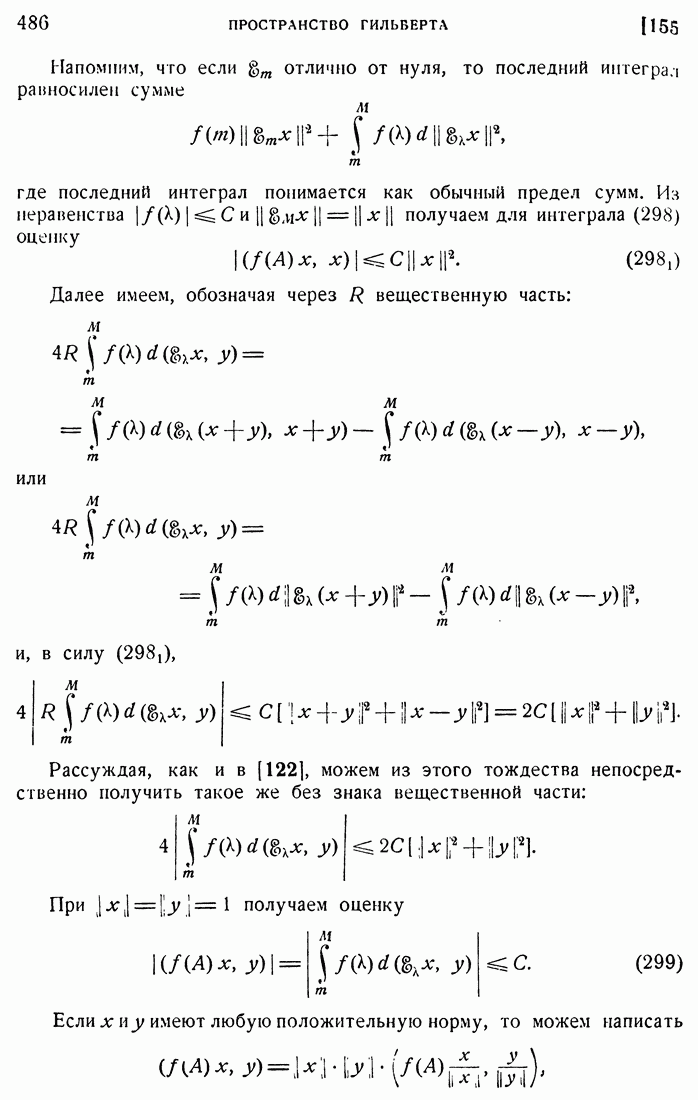| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
98. Линейные функционалы.
Рассмотрим вещественное пространство X типа В (элементы X умножаются лишь на вещественные числа). Функционалом в X называется оператор, область значений которого находится в пространстве вещественных чисел. Последнее есть вещественное пространство типа В при обычном определении сложения вещественных чисел и их умножения на вещественное число. Норма — абсолютное значение вещественного числа [87].
Все сказанное в [97] об операторах справедливо и для функционалов. Ограниченность функционала определяется неравенством

где  абсолютное значение вещественного числа
абсолютное значение вещественного числа  норма
норма  . Линейный функционал — частный случай линейного оператора. При этом
. Линейный функционал — частный случай линейного оператора. При этом  совпадает со всем X.
совпадает со всем X.
Теорема 1. Если на некотором линеале U задан дистрибутивный ограниченный функционал  то его можно распространить на все X так, что
то его можно распространить на все X так, что  будет в X линейным функционалом с той же нормой, что и в
будет в X линейным функционалом с той же нормой, что и в 
По условию, кроме дистрибутивности  имеем
имеем

где  норма
норма  в U. При доказательстве будем считать, что пространство X сепарабельно, что упростит рассуждения. Но теорема верна и для несепарабельных пространств.
в U. При доказательстве будем считать, что пространство X сепарабельно, что упростит рассуждения. Но теорема верна и для несепарабельных пространств.
В силу сепарабельности, существует счетное множество элементов, плотное в X. Оставим в этом счетном множестве лишь элементы, не принадлежащие U. Если таких элементов не будет, то U повсюду плотно в X, и мы можем продолжить  по непрерывности на всем
по непрерывности на всем  противном случае оставшиеся элементы счетного множества можно также пронумеровать:
противном случае оставшиеся элементы счетного множества можно также пронумеровать:  .
.
Рассмотрим множество  элементов
элементов  вида:
вида:  где у — любой элемент U и t — любое вещественное число. Нетрудно видеть, что
где у — любой элемент U и t — любое вещественное число. Нетрудно видеть, что  есть, как и
есть, как и  линеал. Покажем, что представление
линеал. Покажем, что представление  в указанном виде единственно. Нели
в указанном виде единственно. Нели  имеет два различных представления:
имеет два различных представления:

то в этих представлениях  ибо если
ибо если  то и
то и  Покажем, что неравенство
Покажем, что неравенство  приведет нас к нелепости. Из (52) имеем
приведет нас к нелепости. Из (52) имеем  откуда следует, что
откуда следует, что  а это противоречит сказанному выше. Возьмем теперь два любых элемента
а это противоречит сказанному выше. Возьмем теперь два любых элемента  из U и установим одно неравенство. Имеем
из U и установим одно неравенство. Имеем

Отметим, что если слева стоит отрицательное число, то неравенство тривиально. Принимая во внимание, что  получим, в силу
получим, в силу 
Взяв точную нижнюю границу множества чисел, стоящих справа, и точную верхнюю границу для левой части, когда  независимо пробегают все U, получим
независимо пробегают все U, получим

причем правая часть, очевидно, конечна, а, следовательно, и левая. Таким образом, существует вещественное число  удовлетворяющее неравенству
удовлетворяющее неравенству

Распространим теперь  на
на  . Пусть
. Пусть  любой элемент
любой элемент  Положим
Положим

где а — фиксированное вещественное число, удовлетворяющее неравенству (54). Если  то
то  совпадает с
совпадает с  т. е. формула (55) определяет на
т. е. формула (55) определяет на  функционал, совпадающий с прежним на U. Поэтому мы сохранили для расширенного функционала прежнее обозначение. Дистрибутивность
функционал, совпадающий с прежним на U. Поэтому мы сохранили для расширенного функционала прежнее обозначение. Дистрибутивность  непосредственно следует из (55), дистрибутивности
непосредственно следует из (55), дистрибутивности  на U и формул
на U и формул

Покажем наконец, что норма  не больше, чем
не больше, чем  и (понизиться она не может). Будем считать
и (понизиться она не может). Будем считать  Принимая во внимание, что
Принимая во внимание, что  причем
причем  получим
получим

Но из (54) следует

и заменяя в (56) а меньшим числом, стоящим в правой части этого неравенства, получим 

Переходим к случаю  . Из (54) следует
. Из (54) следует

и, заменяя в (56) в разности  а число а большим, получим
а число а большим, получим

Умножая обе части этого неравенства на отрицательное t и принимая во внимание (56), получим  Если
Если  то
то  и написанное неравенство очевидно. Таким образом, при всяком
и написанное неравенство очевидно. Таким образом, при всяком  имеем
имеем  Меняя в этом неравенстве
Меняя в этом неравенстве  на
на  и принимая во внимание, что
и принимая во внимание, что  получим
получим  Эти два неравенства приводят нас окончательно к неравенству
Эти два неравенства приводят нас окончательно к неравенству

из которого и следует, что при указанном распространении  из U на U! норма остается прежней.
из U на U! норма остается прежней.
Переходим теперь к дальнейшему распространению. Если элемент из указанной выше последовательности принадлежит  то отбрасываем его. Если же нет, то распространяем
то отбрасываем его. Если же нет, то распространяем  как и выше, с линеала
как и выше, с линеала  на линеал
на линеал  состоящий из элементов
состоящий из элементов  где у — любой элемент и t — любое вещественное число. Продолжая так и дальше, удержим прежнее обозначение
где у — любой элемент и t — любое вещественное число. Продолжая так и дальше, удержим прежнее обозначение  для элементов, которые не отбрасывались при указанном выше построении (их может быть и конечное число). Таким путем мы продолжим
для элементов, которые не отбрасывались при указанном выше построении (их может быть и конечное число). Таким путем мы продолжим  на линеал V элементов, имеющих вид
на линеал V элементов, имеющих вид

где у — любой элемент U  — любое целое положительное (не большее числа элементов
— любое целое положительное (не большее числа элементов  если это число конечно) и
если это число конечно) и  любые вещественные числа. Этот линеал V плотен в В, и на нем функционал
любые вещественные числа. Этот линеал V плотен в В, и на нем функционал  дистрибутивен, ограничен и с нормой
дистрибутивен, ограничен и с нормой  Теперь остается продолжить
Теперь остается продолжить  на все X по непрерывности. Теорема доказана.
на все X по непрерывности. Теорема доказана.
Для случая комплексного пространства типа В доказательство теоремы 1 имеется, например, в работе Г. А. Сухомлинова (Матем. сб., 3, 1938 г.) и в книге Ф. Рисса и Б. Секефальви-Надя „Лекции по функциональному анализу".
Доказанная теорема не распространяется на операторы.
Теорема 2. Если  какой-либо фиксированный элемент X, отличный от нулевого, то существует линейный функционал
какой-либо фиксированный элемент X, отличный от нулевого, то существует линейный функционал  с нормой единица
с нормой единица  такой, что
такой, что 
Рассмотрим линеал U элементов вида  где t — любое вещественное число, и определим по U дистрибутивный функционал
где t — любое вещественное число, и определим по U дистрибутивный функционал  формулой
формулой  . При
. При  имеем
имеем  По теореме 1 мы можем распространить
По теореме 1 мы можем распространить  на все X с сохранением нормы, и теорема доказана. Из нее вытекает, между прочим, что во всяком пространстве типа В существуют функционалы с положительной нормой.
на все X с сохранением нормы, и теорема доказана. Из нее вытекает, между прочим, что во всяком пространстве типа В существуют функционалы с положительной нормой.
Отметим, что теорема справедлива и в том случае, когда  есть нулевой элемент. Достаточно взять какой-либо элемент
есть нулевой элемент. Достаточно взять какой-либо элемент  отличный от
отличный от  , и образовать по теореме линейный функционал
, и образовать по теореме линейный функционал  такой, что
такой, что  Для него
Для него 
Сопряженные пространства. Рассмотрим пространство X, элементы которого суть всевозможные линейные функционалы в пространстве X типа В. Функционалы в  т. е. вещественные числа, соответствующие элементам
т. е. вещественные числа, соответствующие элементам  обозначаются через
обозначаются через  . Как элементы X мы будем их обозначать одной буквой:
. Как элементы X мы будем их обозначать одной буквой:  . Пространство X есть линейное пространство. Сложение и умножение функционалов на число вводятся следующим естественным образом:
. Пространство X есть линейное пространство. Сложение и умножение функционалов на число вводятся следующим естественным образом:

причем выполнены все свойства из аксиомы А. Нулевой элемент  есть функционал аннулирования, т. е. такой, что
есть функционал аннулирования, т. е. такой, что  для любого
для любого  . Норма I элемента X принимается равной норме соответствующего функционала. Эта норма О, причем
. Норма I элемента X принимается равной норме соответствующего функционала. Эта норма О, причем  имеет место только для функционала аннулирования. Имеют место и два других свойства аксиомы С.
имеет место только для функционала аннулирования. Имеют место и два других свойства аксиомы С.
Второе вытекает из неравенств  а третье очевидно. Докажем, что X — полное пространство. Пусть имеется сходящаяся в себе последовательность элементов X:
а третье очевидно. Докажем, что X — полное пространство. Пусть имеется сходящаяся в себе последовательность элементов X:

Надо доказать, что существует такой элемент  что
что  при
при  Обозначим
Обозначим  Мы имеем
Мы имеем  в СИЛУ (58) существует такое
в СИЛУ (58) существует такое  что
что  при
при  Фиксируя
Фиксируя  получаем
получаем  при а среди конечного числа неотрицательных чисел
при а среди конечного числа неотрицательных чисел  имеется наибольшее. Таким образом, из (58) следует, что существует такое
имеется наибольшее. Таким образом, из (58) следует, что существует такое  что
что  при всех значках
при всех значках  . Мы имеем далее
. Мы имеем далее  и из (58) следует, что
и из (58) следует, что  при
при  и любом выборе
и любом выборе  . В силу признака Коши (для чисел) существует предел последовательности чисел
. В силу признака Коши (для чисел) существует предел последовательности чисел  Этот предел, который мы обозначим
Этот предел, который мы обозначим  есть некоторый функционал, определенный во всем X. Покажем, что он есть линейный функционал. Его дистрибутивность вытекает из равенств:
есть некоторый функционал, определенный во всем X. Покажем, что он есть линейный функционал. Его дистрибутивность вытекает из равенств:  , а ограниченность — из неравенства
, а ограниченность — из неравенства  , т. е.
, т. е.  путем предельного перехода при
путем предельного перехода при  . Таким образом,
. Таким образом,  есть линейный функционал в X, т. е.
есть линейный функционал в X, т. е.  Остается доказать, что
Остается доказать, что  При любом в 0, в силу (58), существует такое
При любом в 0, в силу (58), существует такое  что
что  при
при  Переходя к пределу при
Переходя к пределу при  получим
получим  при
при  т. е.
т. е.  , при
, при  что и дает
что и дает  Полнота А доказана. Т аким образом, пространство X есть пространство типа В. Оно называется сопряженным с X.
Полнота А доказана. Т аким образом, пространство X есть пространство типа В. Оно называется сопряженным с X.
Введем второе сопряженное пространство  элементы которого суть всевозможные линейные функционалы в X. Пространство X получается из X совершенно так же, как А из X, и А есть пространство типа В.
элементы которого суть всевозможные линейные функционалы в X. Пространство X получается из X совершенно так же, как А из X, и А есть пространство типа В.
Если мы фиксируем  то любому элементу
то любому элементу  будет соответствовать определенное вещественное число
будет соответствовать определенное вещественное число  при фиксированном
при фиксированном  и изменении I в X есть функционал в X. Обозначим его символом
и изменении I в X есть функционал в X. Обозначим его символом  Из
Из  следует
следует  дистрибутивный функционал в X.
дистрибутивный функционал в X.
Из неравенства

в силу  следует
следует

где  норма
норма  норма I в
норма I в  Из
Из  следует, что норма функционала
следует, что норма функционала  не больше
не больше  т. е. он ограничен в
т. е. он ограничен в  Итак,
Итак,  есть линейный функционал в X. Если
есть линейный функционал в X. Если  есть нулевой элемент X, то
есть нулевой элемент X, то  для любого
для любого  есть нулевой элемент А. Из (60) следует, что норма
есть нулевой элемент А. Из (60) следует, что норма  не больше
не больше  Но в силу теоремы 2 из [98] при любом
Но в силу теоремы 2 из [98] при любом  существует такой функционал
существует такой функционал  что
что  и
и
 . Для такого I обе части (60) равны
. Для такого I обе части (60) равны  и имеет место знак
и имеет место знак  откуда следует, что норма
откуда следует, что норма  равна
равна  Далее из
Далее из  следует, что
следует, что  и вообще
и вообще 
 . В частности,
. В частности,  откуда, в силу сказанного выше о норме, следует:
откуда, в силу сказанного выше о норме, следует:  а отсюда следует, что различным
а отсюда следует, что различным  соответствуют различные элементы
соответствуют различные элементы  пространства А.
пространства А.
Из предыдущего вытекает следующее важное утверждение:
Теорема. Всякому элементу  можно сопоставить элемент
можно сопоставить элемент  При этом соответствии: различным х соответствуют различные
При этом соответствии: различным х соответствуют различные  сложению и умножению на число в X соответствуют те же операции для соответствующих элементов в X, и нормы соответствующих элементов в X и
сложению и умножению на число в X соответствуют те же операции для соответствующих элементов в X, и нормы соответствующих элементов в X и  одинаковы.
одинаковы.
Это утверждение дает возможность отождествить  т. е. погрузить X в
т. е. погрузить X в  что записываем в виде
что записываем в виде  Иными словами, X изометрично части А.
Иными словами, X изометрично части А.
Мы увидим дальше, что в некоторых случаях X изометрично всему X, т. е.  Такое пространство X называется регулярным. Часто вместо
Такое пространство X называется регулярным. Часто вместо  пользуются обозначением
пользуются обозначением  или
или  :
:

и  называют внутренним произведением элемента
называют внутренним произведением элемента  на элемент
на элемент  . Элементы I их называют ортогональными, если
. Элементы I их называют ортогональными, если 
Неравенство (59) записывается в виде;

из сказанного выше следует:

где а и b — любые вещественные числа.
До сих пор мы рассматривали вещественные пространства типа В. Все сказанное выше сохраняется и для комплексных пространств типа В (умножение элементов  на любые комплексные числа). В этом случае и функционалы могут принимать любые комплексные значения. В дальнейшем через а мы, как и раньше, будем обозначать число комплексное, сопряженное с
на любые комплексные числа). В этом случае и функционалы могут принимать любые комплексные значения. В дальнейшем через а мы, как и раньше, будем обозначать число комплексное, сопряженное с  Отметим, что если
Отметим, что если  есть линейный функционал в В, то
есть линейный функционал в В, то  есть также ограниченный в
есть также ограниченный в  но не линейный функционал, ибо
но не линейный функционал, ибо  умножается на с при умножении
умножается на с при умножении  на комплексное число с. Сопряженное пространство X определяется не как множество всех
на комплексное число с. Сопряженное пространство X определяется не как множество всех  а как множество всех
а как множество всех 
Сложение элементов X и умножение на комплексное число есть
обычное сложение и умножение комплексных чисел. Норма  берется равной
берется равной  при этом
при этом  и число
и число  нельзя заменить меньшим. Пространство — X типа В. Внутренние произведения определяются формулами
нельзя заменить меньшим. Пространство — X типа В. Внутренние произведения определяются формулами

При этом для любых комплексных а и b

Пространство  имеет ту же связь с X, что и в случае вещественного пространства.
имеет ту же связь с X, что и в случае вещественного пространства.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ИНТЕГРАЛ СТИЛТЬЕСА
- 1. Множества и их мощность.
- 2. Интеграл Стилтьеса и его основные свойства.
- 3. Суммы Дарбу.
- 4. Интеграл Стилтьеса от непрерывной функции.
- 5. Несобственный интеграл Стилтьеса.
- 6. Функция скачков.
- 7. Физическая интерпретация.
- 8. Функции ограниченной вариации.
- 9. Интегрирующая функция ограниченной вариации.
- 10. Существование Интеграла Стилтьеса.
- 11. Предельный переход в интеграле Стилтьеса.
- 12. Теорема Хелли.
- 13. Принцип выбора.
- 14. Пространство непрерывных функций.
- 15. Общая форма функционалов в С.
- 16. Линейные операторы в С.
- 17. Функции промежутков.
- 18. Общий интеграл Стилтьеса.
- 19. Свойства (общего) интеграла Стилтьеса.
- 20. Существование общего интеграла Стилтьеса.
- 21. Функции промежутков на плоскости.
- 22. Переход к функции точки.
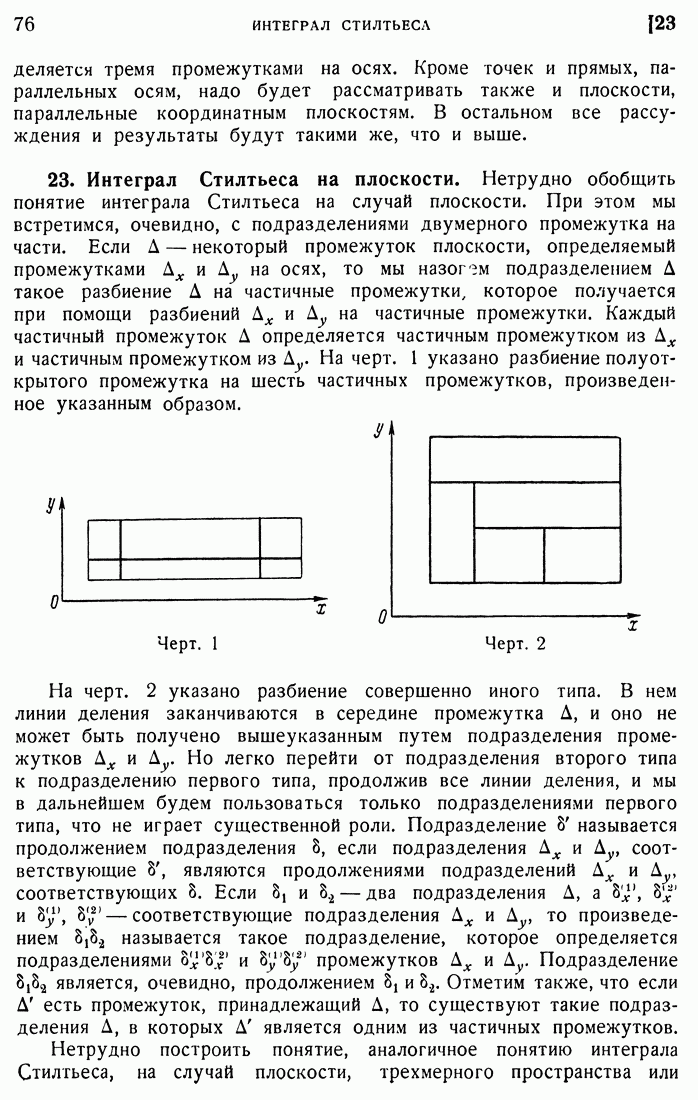
- 23. Интеграл Стилтьеса на плоскости.
- 24. Функция ограниченной вариации на плоскости.
- 25. Пространство непрерывных функций многих переменных.
- 26. Интеграл Фурье—Стилтьеса.
- 27. Формула обращения.
- 28. Теорема свертывания.
- ГЛАВА II. ФУНКЦИИ МНОЖЕСТВ И ИНТЕГРАЛ ЛЕБЕГА
- § 1. Функции множеств и теория измерения
- 31. Точечные множества.
- 32. Свойства замкнутых и открытых множеств.
- 33. Элементарная фигура.
- 34. Внешняя мера и ее свойства.
- 35. Измеримые множества.
- 36. Измеримые множества (продолжение).
- 37. Критерии измеримости.
- 38. Тело множеств.
- 39. Независимость от выбора осей.
- 40. Тело В.
- 41. Случай одного переменного.
- § 2. Измеримые функции
- 42. Определение измеримых функций.
- 43. Свойства измеримых функций.
- 44. Предел измеримых функций.
- 45. Свойство С.
- 46. Кусочно-постоянные функции.
- 47. Класс В.
- § 3. Интеграл Лебега
- 48. Интеграл от ограниченной функции.
- 49. Свойства интеграла.
- 50. Интеграл от неограниченной неотрицательной функции.
- 51. Свойства интеграла.
- 52. Функция любого знака.
- 53. Комплексные суммируемые функции.
- 54. Предельный переход под знаком интеграла.
- 55. Класс L2.
- 56. Сходимость в среднем.
- 57. Функциональное пространство Гильберта.
- 58. Ортогональные системы функций.
- 59. Пространство L2.
- 60. Линеалы в L2.
- 61. Примеры замкнутых систем.
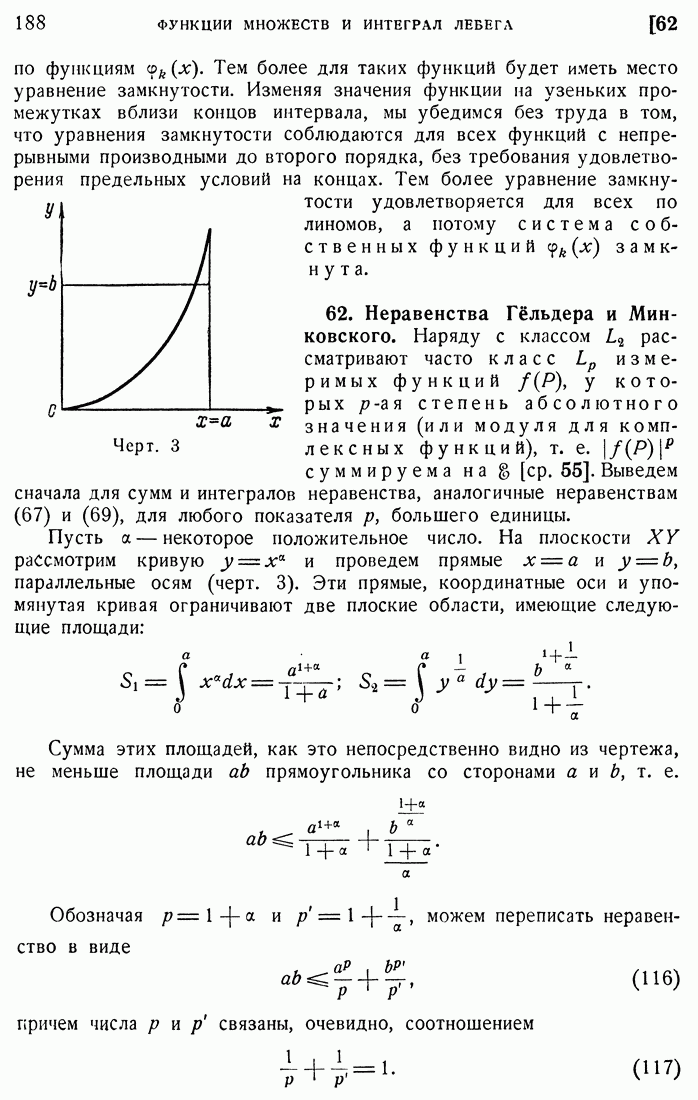
- 62. Неравенства Гёльдера и Минковского.
- 63. Интеграл по множеству бесконечной меры.
- 64. Класс L2 на множестве бесконечной меры.
- 65. Интегрирующая функция ограниченной вариации.
- 66. Приведение кратных интегралов.
- 67. Случай характеристической функции.
- 68. Теорема Фубини.
- 69. Перестановка порядка интегрирования.
- 70. Непрерывность в среднем.
- 71. Средние функции.
- ГЛАВА III. ФУНКЦИИ МНОЖЕСТВ. АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ, ОБОБЩЕНИЕ ПОНЯТИЯ ИНТЕГРАЛА
- 72. Аддитивные функции множеств.
- 73. Сингулярная функция.
- 74. Случай одного переменного.
- 75. Абсолютно непрерывные функции множеств.
- 76. Пример.
- 77. Абсолютно непрерывные функции многих переменных.
- 78. Вспомогательные предложения.
- 79. Вспомогательные предложения (продолжение).
- 80. Основная теорема.
- 81. Интеграл Хеллингера.
- 82. Случай одного переменного.
- 83. Свойства интеграла Хеллингера.
- ГЛАВА IV. МЕТРИЧЕСКИЕ И НОРМИРОВАННЫЕ ПРОСТРАНСТВА
- 84. Метрическое пространство.
- 85. Пополнение метрического пространства.
- 86. Операторы и функционалы. Принцип сжатых отображений.
- 87. Примеры.
- 88. Примеры применения принципа сжатых отображений.
- 89. Компактность.
- 90. Компактность в С.
- 91. Компактность в Lp.
- 92. Компактность в lр.
- 93. Функционалы на компактных в себе множествах.
- 94. Сепарабельность.
- 95. Линейные нормированные пространства.
- 96. Примеры нормированных пространств.
- 97. Операторы в нормированных пространствах.
- 98. Линейные функционалы.
- 100. Слабая сходимость функционалов.
- 101. Слабая сходимость элементов.
- 102. Линейные функционалы в …
- 103. Слабая сходимость в …
- 104. Пространство линейных операторов и сходимость последовательности операторов.
- 105. Сопряженные операторы.
- 106. Вполне непрерывные операторы.
- 107. Операторные уравнения.
- 108. Вполне непрерывные операторы в …
- 109. Обобщенные производные.
- 110. Обобщенные производные (продолжение).
- 111. Случай звездной области.
- 112. Пространства …
- 113. Свойства функций класса …
- 114. Теоремы вложения.
- 115. Интегральные операторы с полярным ядром.
- 116. Интегральные представления С. Л. Соболева.
- 117. Теоремы вложения.
- 118. Области более общего типа.
- 119. Пространство …
- ГЛАВА V. ПРОСТРАНСТВО ГИЛЬБЕРТА
- § 1. Теория ограниченных операторов
- 121. Ортогональность и ортогональные системы элементов.
- 122. Проекция.
- 123. Линейные функционалы.
- 124. Линейные операторы.
- 125. Билинейные и квадратичные функционалы.
- 126. Границы самосопряженного оператора.
- 127. Обратный оператор.
- 128. Спектр оператора.
- 129. Спектр самосопряженного оператора.
- 130. Резольвента.
- 131. Последовательности операторов.
- 132. Слабая сходимость.
- 133. Вполне непрерывные операторы.
- 134. Пространства Н и l2.
- 135. Линейные уравнения со вполне непрерывными операторами.
- 136. Вполне непрерывные самосопряженные операторы.
- 137. Унитарные операторы.
- 138. Абсолютная норма оператора.
- 139. Операции над подпространствами.
- 140. Операторы проектирования.
- 141. Разложение единицы. Интеграл Стилтьеса.
- 142. Спектральная функция самосопряженного оператора.
- 143. Непрерывные функции самосопряженного оператора.
- 144. Формула для резольвенты и характеристика регулярных значений «лямбда»
- 145. Собственные значения и собственные элементы.
- 146. Чисто точечный спектр.
- 147. Непрерывный простой спектр.
- 148. Инвариантные подпространства.
- 149. Общий случай непрерывного спектра.
- 150. Случай смешанного спектра.
- 151. Дифференциальные решения.
- 152. Операция умножения на независимую переменную.
- 153. Унитарная эквивалентность самосопряженных операторов.
- 154. Спектральное разложение унитарных операторов.
- 155. Функции самосопряженного оператора.
- 156. Коммутирующие операторы.
- 157. Возмущение спектра самосопряженного оператора.
- 158. Нормальные операторы.
- 159. Вспомогательные предложения.
- 160. Степенной ряд от оператора.
- 161. Спектральная функция. Теорема.
- § 2. Пространства и l2 и L2
- 162. Линейные операторы в l2.
- 163. Ограниченные операторы.
- 164. Унитарные матрицы и матрицы проектирования.
- 165. Самосопряженные матрицы.
- 166. Случай непрерывного спектра.
- 167. Матрицы Якоби.
- 168. Дифференциальные решения.
- 169. Примеры.
- 170. Слабая сходимость в l2.
- 171. Вполне непрерывные операторы в l2.
- 172. Интегральные операторы в L2.
- 173. Сопряженный оператор.
- 174. Вполне непрерывные операторы.
- 175. Спектральная функция.
- 176. Спектральная функция (продолжение).
- 177. Унитарные преобразования в L2.
- 178. Преобразования Фурье.
- 179. Преобразование Фурье и функции Эрмита.
- 180. Операция умножения.
- 181. Ядра, зависящие от разности.
- 182. Слабая сходимость.
- 183. Другие осуществления пространства H.
- § 2. Неограниченные операторы
- 184. Замкнутые операторы.
- 185. Сопряженный оператор.
- 186. График оператора.
- 187. Симметричные и самосопряженные операторы.
- 188. Примеры неограниченных операторов.
- 189. Спектр самосопряженного оператора.
- 190. Случай точечного спектра.
- 191. Инвариантные подпространства и приводимость оператора.
- 192. Разложение единицы. Интеграл Стилтьеса.
- 193. Непрерывные функции самосопряженного оператора.
- 194. Резольвента.
- 195. Собственные значения.
- 196. Случай смешанного спектра.
- 197. Функции самосопряженного оператора.
- 198. Малые возмущения спектра.
- 199. Оператор умножения.
- 200. Интегральные операторы.
- 201. Расширение замкнутого симметричного оператора.
- 202. Индексы дефекта.
- 203. Сопряженный оператор.
- 204. Максимальные операторы.
- 205. Расширение симметричных полуограниченных операторов.
- 206. Сравнение полуограниченных операторов.
- 207. Примеры на теорию расширений.
- 208. Спектр симметричного оператора.
- 209. Некоторые теоремы о расширениях и их спектрах.
- 210. Независимость индексов дефекта от «лямбда».
- 211. Об инвариантности непрерывной части ядра спектра при симметричных расширениях.
- 212. О спектрах самосопряженных расширений.
- 213. Примеры.
- 214. Бесконечные матрицы.
- 215. Матрицы Якоби.
- 216. Матрицы и операторы.
- 217. Унитарная эквивалентность С-матриц.
- 218. Существование спектральной функции.