| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
109. Обобщенные производные.
Мы введем сейчас новое понятие производной, которое часто применяется в современной математической физике. Пусть D — ограниченная область  -мерного эвклидова пространства
-мерного эвклидова пространства  точки которого
точки которого  определяются декартовыми координатами
определяются декартовыми координатами  Под областью будем всегда подразумевать открытое связное множество и будем считать, что границы областей, о которых мы будем говорить, имеют объемную меру нуль. Через b, как всегда, будем обозначать область D вместе с ее границей (замкнутая область). Будем говорить, что область
Под областью будем всегда подразумевать открытое связное множество и будем считать, что границы областей, о которых мы будем говорить, имеют объемную меру нуль. Через b, как всегда, будем обозначать область D вместе с ее границей (замкнутая область). Будем говорить, что область  лежит строго внутри D, если
лежит строго внутри D, если  и расстояние от D до границы D положительно. Это равносильно тому, что
и расстояние от D до границы D положительно. Это равносильно тому, что  Как и раньше, будем называть функцию финитной в
Как и раньше, будем называть функцию финитной в  если она равна нулю вне некоторой области
если она равна нулю вне некоторой области  лежащей строго внутри
лежащей строго внутри  может быть разной для разных функций). Положим, что функции
может быть разной для разных функций). Положим, что функции  имеют непрерывные производные до порядка l внутри D и функция
имеют непрерывные производные до порядка l внутри D и функция  финитна. Рассмотрим какую-либо производную порядка
финитна. Рассмотрим какую-либо производную порядка 

Применяя формулу интегрирования по частям, получим, принимая во внимание финитность 

Формула (123) может быть положена в основу более общего понятия производной.
Определение 1. Пусть функции  суммируемы по любой строго внутренней подобласти D области D и для любой финитной I раз непрерывно дифференцируемой функции
суммируемы по любой строго внутренней подобласти D области D и для любой финитной I раз непрерывно дифференцируемой функции  удовлетворяют соотношению
удовлетворяют соотношению

Тогда функция  называется обобщенной производной вида (122) функции
называется обобщенной производной вида (122) функции 
Убедимся, что у заданной функции  может существовать только одна обобщенная производная данного вида. Пусть
может существовать только одна обобщенная производная данного вида. Пусть  Две обобщенные производные. Для
Две обобщенные производные. Для  также справедливо равенство (124), Вычитая почленно, получим
также справедливо равенство (124), Вычитая почленно, получим

откуда, ввиду произвольности финитной функции  следует, что
следует, что  эквивалентные в D функции [71].
эквивалентные в D функции [71].
Если  имеет внутри D непрерывные производные до порядка
имеет внутри D непрерывные производные до порядка  то имеет место
то имеет место  . В дальнейшем мы сохраним обозначение (122) и для обобщенных производных. Отметим некоторые свойства обобщенной производной, непосредственно вытекающие из ее определения. Обобщенная производная
. В дальнейшем мы сохраним обозначение (122) и для обобщенных производных. Отметим некоторые свойства обобщенной производной, непосредственно вытекающие из ее определения. Обобщенная производная  не зависит от того, в каком порядке записано дифференцирование, ибо в формуле (124) можно произвольно переставлять порядок дифференцирования у функции
не зависит от того, в каком порядке записано дифференцирование, ибо в формуле (124) можно произвольно переставлять порядок дифференцирования у функции  имеющей непрерывные производные. Если
имеющей непрерывные производные. Если  имеют обобщенные производные вида
имеют обобщенные производные вида  , то
, то  имеет обобщенную производную
имеет обобщенную производную  того же вида
того же вида  постоянные). Если
постоянные). Если  есть обобщенная производная
есть обобщенная производная  в D, то она будет обобщенной производной того же вида и в любой области
в D, то она будет обобщенной производной того же вида и в любой области  принадлежащей
принадлежащей 
Если  имеет обобщенную производную
имеет обобщенную производную  имеет обобщенную производную
имеет обобщенную производную  имеет обобщенную
имеет обобщенную  производную
производную  Аналогично и для производных других видов. Далее, если
Аналогично и для производных других видов. Далее, если  имеет обобщенные производные
имеет обобщенные производные  производная от
производная от  по
по 
Ниже мы покажем также, что при некоторых дополнительных ограничениях справедлива обычная формула дифференцирования произведения:

Установим теперь связь между обобщенным дифференцированием и операцией усреднения. Пусть  какое-либо усредняющее ядро, зависящее от расстояния между точками
какое-либо усредняющее ядро, зависящее от расстояния между точками  средние функции, построенные для
средние функции, построенные для 

Предполагая, что  имеет в D обобщенную производную
имеет в D обобщенную производную  вида (122), вычислим соответствующую (очевидно, обычную) производную от средних функций [71]:
вида (122), вычислим соответствующую (очевидно, обычную) производную от средних функций [71]:

Будем считать точку  отстоящей от границы D на расстояние, большее чем h. Так как функция
отстоящей от границы D на расстояние, большее чем h. Так как функция  обращается в нуль вне шара радиуса h с центром в точке
обращается в нуль вне шара радиуса h с центром в точке  то ее можно взять в качестве финитной функции в формуле (124). Вместе с (128) это приводит к соотношению
то ее можно взять в качестве финитной функции в формуле (124). Вместе с (128) это приводит к соотношению

которое можно сформулировать так: средние функции от обобщен  производных совпадают с производными того же вида от средних функций во всех точках области D, расстояние которых до границы D больше радиуса усреднения.
производных совпадают с производными того же вида от средних функций во всех точках области D, расстояние которых до границы D больше радиуса усреднения.
На основании свойств средних функций  можем теперь утверждать, что при
можем теперь утверждать, что при  в L(D), где D — любая строго внутренняя подобласть области D. Более того, если дополнительно предположить, что
в L(D), где D — любая строго внутренняя подобласть области D. Более того, если дополнительно предположить, что  суммируема по любой строго внутренней подобласти D с какой-либо степенью 1, а обобщенная производная
суммируема по любой строго внутренней подобласти D с какой-либо степенью 1, а обобщенная производная  с какой-либо степенью
с какой-либо степенью  , то сходимость
, то сходимость  имеет место в
имеет место в  соответственно. Сделаем одно предостережение. Пусть функция
соответственно. Сделаем одно предостережение. Пусть функция  доопределена каким-либо образом на все
доопределена каким-либо образом на все  например, положена равной нулю вне D. Тогда функции
например, положена равной нулю вне D. Тогда функции  также определены во всем пространстве и при
также определены во всем пространстве и при  сходятся к
сходятся к  Однако функции
Однако функции  вообще говоря, не будут сходиться к
вообще говоря, не будут сходиться к  пространстве
пространстве  Это связано с тем, что так продолженная функция может не иметь соответствующей обобщенной производной во всем
Это связано с тем, что так продолженная функция может не иметь соответствующей обобщенной производной во всем 
Вернемся теперь к доказательству формулы (126) дифференцированию произведения. Докажем сначала одно простое утверждение. Пусть  в любой строго внутренней для D области D и
в любой строго внутренней для D области D и  ограниченная финитная в D функция. Тогда
ограниченная финитная в D функция. Тогда

Действительно, используя неравенство Гёльдера, найдем

Здесь  подобласть
подобласть  вне которой
вне которой  равна нулю. Правая часть последнего неравенства стремится к нулю при
равна нулю. Правая часть последнего неравенства стремится к нулю при  так как
так как  и сходящаяся в
и сходящаяся в  последовательность
последовательность  ограничена в
ограничена в  по норме.
по норме.
Установим теперь формулу (126) в предложении, что  для любой строго внутренней подобласти О. Используя предыдущее утверждение, имеем для любой непрерывно дифференцируемой финитной функции
для любой строго внутренней подобласти О. Используя предыдущее утверждение, имеем для любой непрерывно дифференцируемой финитной функции  равной нулю вне
равной нулю вне  :
:

и, следовательно,

При достаточно малом  можно применить в
можно применить в  формулу (129) и заменить
формулу (129) и заменить 
Применяя еще раз наше вспомогательное утверждение к правой части (130), получим:

Последнее равенство означает, что произведение  имеет в D обобщенную производную по
имеет в D обобщенную производную по  которая может быть вычислена по формуле (126).
которая может быть вычислена по формуле (126).
Заметим, что формула (126) справедлива и при  . В этом случае нужно только принять
. В этом случае нужно только принять  т. е. считать
т. е. считать  и ограниченными в любой подобласти
и ограниченными в любой подобласти  , Покажем теперь, что можно дать другое определение обобщен, ной производной и на основе формулы (129) установить его эквиват лентность первоначальному определению,
, Покажем теперь, что можно дать другое определение обобщен, ной производной и на основе формулы (129) установить его эквиват лентность первоначальному определению,
Определение 2, Функция  называется обобщенной
называется обобщенной  изводной вида (122) функции
изводной вида (122) функции  в
в  если существуем последа вательность I раз непрерывно дифференцируемых внутри Р функций
если существуем последа вательность I раз непрерывно дифференцируемых внутри Р функций  таких, что
таких, что  сходятся соответственно к
сходятся соответственно к  , где
, где  — любая строго внутренняя подобласть
— любая строго внутренняя подобласть 
Теорема  Определения 1 и 2 равносильны. Положим, что
Определения 1 и 2 равносильны. Положим, что  обобщенная производная от
обобщенная производная от  но второму определению, Имеет место формула (123), при замене
но второму определению, Имеет место формула (123), при замене  на
на  и, по скольку
и, по скольку  и в
и в  , мы можем при любом выборе финитной функции
, мы можем при любом выборе финитной функции  с указанными свойствами перейти к пределу под знаком интеграла
с указанными свойствами перейти к пределу под знаком интеграла  откуда и следует формула (124).
откуда и следует формула (124).
Положим теперь, что  обобщенная производная от
обобщенная производная от  в смысле первого определения. Тогда, в силу (129) и теоремы 4 из
в смысле первого определения. Тогда, в силу (129) и теоремы 4 из  требуемую вторым определением последовательность функций
требуемую вторым определением последовательность функций  дадут средние функции
дадут средние функции  при какой-либо последовательности
при какой-либо последовательности  стремящейся к нулю (при этом
стремящейся к нулю (при этом  ) считаем продолженной нулем вне D). Теорема 1 доказана. Из этой теоремы следует, что и в смысле второго определения обобщенная производная единственна, если она существует.
) считаем продолженной нулем вне D). Теорема 1 доказана. Из этой теоремы следует, что и в смысле второго определения обобщенная производная единственна, если она существует.
Докажем теперь теорему, которая показывает, что обобщенные производные выдерживают слабый предельный переход в 
Теорема 2. Пусть функции  определенные внутри
определенные внутри  слабо сходятся к некоторой функции
слабо сходятся к некоторой функции  где
где  любая область, лежащая строго внутри
любая область, лежащая строго внутри  имеют в D обобщенные производные
имеют в D обобщенные производные  вида (122) и нормы
вида (122) и нормы  ограничены некоторым числом
ограничены некоторым числом  , которое зависит от выбора
, которое зависит от выбора  . Тогда
. Тогда  имеет в D обобщенную производную вида (122), равную слабому пределу
имеет в D обобщенную производную вида (122), равную слабому пределу 
Доказательство. В силу слабой компактности ограниченных множеств в  при
при  из неравенства
из неравенства

вы 1 екает существование подпоследовательности  такой, что
такой, что  слабо сходятся в
слабо сходятся в  . Беря последовательность строго внутренних расширяющихся областей
. Беря последовательность строго внутренних расширяющихся областей  сходящихся к D, мы с помощью диагонального процесса построим подпоследовательность
сходящихся к D, мы с помощью диагонального процесса построим подпоследовательность  для которой производные
для которой производные  слабо сходятся в
слабо сходятся в  к некоторой функции
к некоторой функции  в любой строго внутренней подобласти
в любой строго внутренней подобласти  . Ясно, что
. Ясно, что  определена всюду в D и принадлежит
определена всюду в D и принадлежит  для любой строго внутренней области
для любой строго внутренней области 
Равенство (123) справедливо при замене  на
на  Переходя в нем к пределу при фиксированной функции
Переходя в нем к пределу при фиксированной функции  приходим ввиду финигносги
приходим ввиду финигносги  к равенству (124), (слабая сходимость), откуда следует, что
к равенству (124), (слабая сходимость), откуда следует, что  есть обобщенная производная
есть обобщенная производная  в D. Из сказанного выше вытекает, что любая слабо сходящаяся подпоследовательность
в D. Из сказанного выше вытекает, что любая слабо сходящаяся подпоследовательность  имеет один и тот же предел у(х) (единственность обобщенной производной), и отсюда легко заключить, что и вся последовательность
имеет один и тот же предел у(х) (единственность обобщенной производной), и отсюда легко заключить, что и вся последовательность  слабо сходится к
слабо сходится к 
Замечания. 1. Из доказанной теоремы следует, что если  и производные средних функций
и производные средних функций  имеют оценку (131), то в D существует обобщенная производная
имеют оценку (131), то в D существует обобщенная производная  Мы уже видели, что в этом случае
Мы уже видели, что в этом случае  и, следовательно, норма
и, следовательно, норма  удовлетворяет оценке (131).
удовлетворяет оценке (131).
2. В условиях теоремы 2 функции  могут принадлежать
могут принадлежать  соответственно и при
соответственно и при 
Теорема 2 сохраняет силу при  если вместо (131) предположить слабую компактность функций
если вместо (131) предположить слабую компактность функций  для всякой строго внутренней подобласти D области
для всякой строго внутренней подобласти D области 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ИНТЕГРАЛ СТИЛТЬЕСА
- 1. Множества и их мощность.
- 2. Интеграл Стилтьеса и его основные свойства.
- 3. Суммы Дарбу.
- 4. Интеграл Стилтьеса от непрерывной функции.
- 5. Несобственный интеграл Стилтьеса.
- 6. Функция скачков.
- 7. Физическая интерпретация.
- 8. Функции ограниченной вариации.
- 9. Интегрирующая функция ограниченной вариации.
- 10. Существование Интеграла Стилтьеса.
- 11. Предельный переход в интеграле Стилтьеса.
- 12. Теорема Хелли.
- 13. Принцип выбора.
- 14. Пространство непрерывных функций.
- 15. Общая форма функционалов в С.
- 16. Линейные операторы в С.
- 17. Функции промежутков.
- 18. Общий интеграл Стилтьеса.
- 19. Свойства (общего) интеграла Стилтьеса.
- 20. Существование общего интеграла Стилтьеса.
- 21. Функции промежутков на плоскости.
- 22. Переход к функции точки.
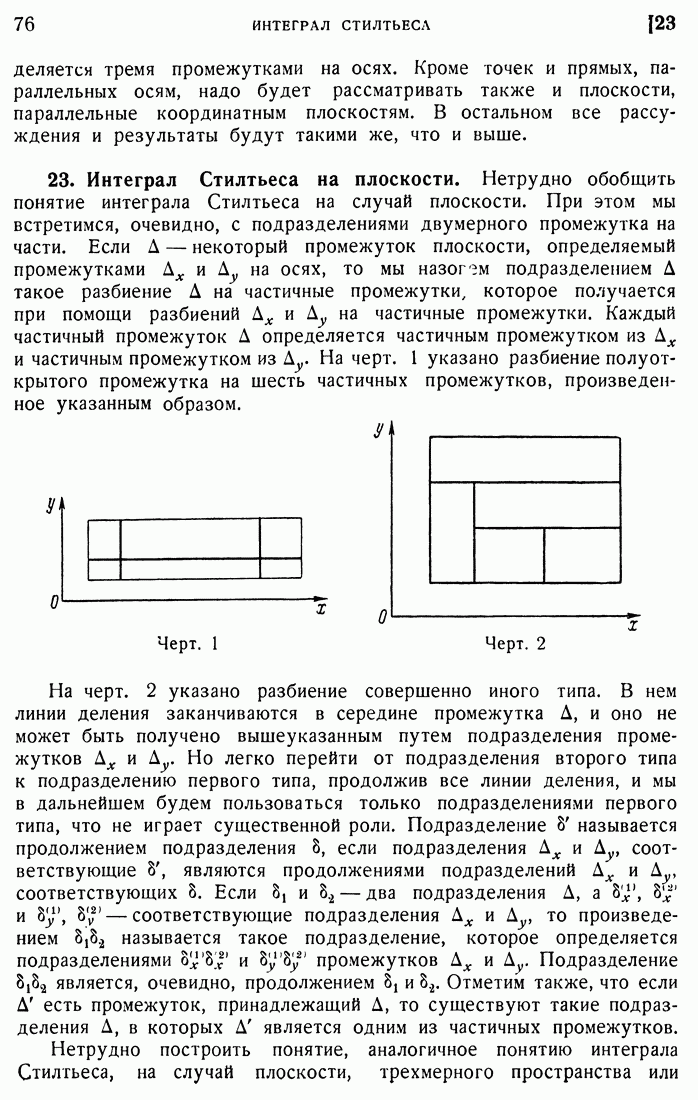
- 23. Интеграл Стилтьеса на плоскости.
- 24. Функция ограниченной вариации на плоскости.
- 25. Пространство непрерывных функций многих переменных.
- 26. Интеграл Фурье—Стилтьеса.
- 27. Формула обращения.
- 28. Теорема свертывания.
- ГЛАВА II. ФУНКЦИИ МНОЖЕСТВ И ИНТЕГРАЛ ЛЕБЕГА
- § 1. Функции множеств и теория измерения
- 31. Точечные множества.
- 32. Свойства замкнутых и открытых множеств.
- 33. Элементарная фигура.
- 34. Внешняя мера и ее свойства.
- 35. Измеримые множества.
- 36. Измеримые множества (продолжение).
- 37. Критерии измеримости.
- 38. Тело множеств.
- 39. Независимость от выбора осей.
- 40. Тело В.
- 41. Случай одного переменного.
- § 2. Измеримые функции
- 42. Определение измеримых функций.
- 43. Свойства измеримых функций.
- 44. Предел измеримых функций.
- 45. Свойство С.
- 46. Кусочно-постоянные функции.
- 47. Класс В.
- § 3. Интеграл Лебега
- 48. Интеграл от ограниченной функции.
- 49. Свойства интеграла.
- 50. Интеграл от неограниченной неотрицательной функции.
- 51. Свойства интеграла.
- 52. Функция любого знака.
- 53. Комплексные суммируемые функции.
- 54. Предельный переход под знаком интеграла.
- 55. Класс L2.
- 56. Сходимость в среднем.
- 57. Функциональное пространство Гильберта.
- 58. Ортогональные системы функций.
- 59. Пространство L2.
- 60. Линеалы в L2.
- 61. Примеры замкнутых систем.
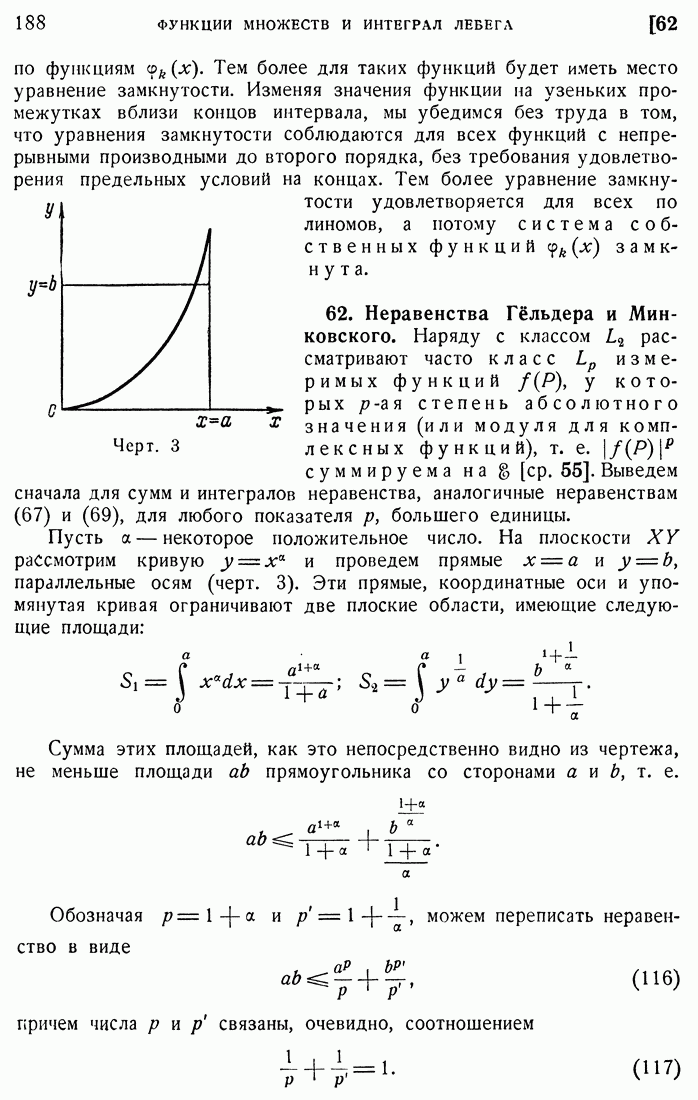
- 62. Неравенства Гёльдера и Минковского.
- 63. Интеграл по множеству бесконечной меры.
- 64. Класс L2 на множестве бесконечной меры.
- 65. Интегрирующая функция ограниченной вариации.
- 66. Приведение кратных интегралов.
- 67. Случай характеристической функции.
- 68. Теорема Фубини.
- 69. Перестановка порядка интегрирования.
- 70. Непрерывность в среднем.
- 71. Средние функции.
- ГЛАВА III. ФУНКЦИИ МНОЖЕСТВ. АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ, ОБОБЩЕНИЕ ПОНЯТИЯ ИНТЕГРАЛА
- 72. Аддитивные функции множеств.
- 73. Сингулярная функция.
- 74. Случай одного переменного.
- 75. Абсолютно непрерывные функции множеств.
- 76. Пример.
- 77. Абсолютно непрерывные функции многих переменных.
- 78. Вспомогательные предложения.
- 79. Вспомогательные предложения (продолжение).
- 80. Основная теорема.
- 81. Интеграл Хеллингера.
- 82. Случай одного переменного.
- 83. Свойства интеграла Хеллингера.
- ГЛАВА IV. МЕТРИЧЕСКИЕ И НОРМИРОВАННЫЕ ПРОСТРАНСТВА
- 84. Метрическое пространство.
- 85. Пополнение метрического пространства.
- 86. Операторы и функционалы. Принцип сжатых отображений.
- 87. Примеры.
- 88. Примеры применения принципа сжатых отображений.
- 89. Компактность.
- 90. Компактность в С.
- 91. Компактность в Lp.
- 92. Компактность в lр.
- 93. Функционалы на компактных в себе множествах.
- 94. Сепарабельность.
- 95. Линейные нормированные пространства.
- 96. Примеры нормированных пространств.
- 97. Операторы в нормированных пространствах.
- 98. Линейные функционалы.
- 100. Слабая сходимость функционалов.
- 101. Слабая сходимость элементов.
- 102. Линейные функционалы в …
- 103. Слабая сходимость в …
- 104. Пространство линейных операторов и сходимость последовательности операторов.
- 105. Сопряженные операторы.
- 106. Вполне непрерывные операторы.
- 107. Операторные уравнения.
- 108. Вполне непрерывные операторы в …
- 109. Обобщенные производные.
- 110. Обобщенные производные (продолжение).
- 111. Случай звездной области.
- 112. Пространства …
- 113. Свойства функций класса …
- 114. Теоремы вложения.
- 115. Интегральные операторы с полярным ядром.
- 116. Интегральные представления С. Л. Соболева.
- 117. Теоремы вложения.
- 118. Области более общего типа.
- 119. Пространство …
- ГЛАВА V. ПРОСТРАНСТВО ГИЛЬБЕРТА
- § 1. Теория ограниченных операторов
- 121. Ортогональность и ортогональные системы элементов.
- 122. Проекция.
- 123. Линейные функционалы.
- 124. Линейные операторы.
- 125. Билинейные и квадратичные функционалы.
- 126. Границы самосопряженного оператора.
- 127. Обратный оператор.
- 128. Спектр оператора.
- 129. Спектр самосопряженного оператора.
- 130. Резольвента.
- 131. Последовательности операторов.
- 132. Слабая сходимость.
- 133. Вполне непрерывные операторы.
- 134. Пространства Н и l2.
- 135. Линейные уравнения со вполне непрерывными операторами.
- 136. Вполне непрерывные самосопряженные операторы.
- 137. Унитарные операторы.
- 138. Абсолютная норма оператора.
- 139. Операции над подпространствами.
- 140. Операторы проектирования.
- 141. Разложение единицы. Интеграл Стилтьеса.
- 142. Спектральная функция самосопряженного оператора.
- 143. Непрерывные функции самосопряженного оператора.
- 144. Формула для резольвенты и характеристика регулярных значений «лямбда»
- 145. Собственные значения и собственные элементы.
- 146. Чисто точечный спектр.
- 147. Непрерывный простой спектр.
- 148. Инвариантные подпространства.
- 149. Общий случай непрерывного спектра.
- 150. Случай смешанного спектра.
- 151. Дифференциальные решения.
- 152. Операция умножения на независимую переменную.
- 153. Унитарная эквивалентность самосопряженных операторов.
- 154. Спектральное разложение унитарных операторов.
- 155. Функции самосопряженного оператора.
- 156. Коммутирующие операторы.
- 157. Возмущение спектра самосопряженного оператора.
- 158. Нормальные операторы.
- 159. Вспомогательные предложения.
- 160. Степенной ряд от оператора.
- 161. Спектральная функция. Теорема.
- § 2. Пространства и l2 и L2
- 162. Линейные операторы в l2.
- 163. Ограниченные операторы.
- 164. Унитарные матрицы и матрицы проектирования.
- 165. Самосопряженные матрицы.
- 166. Случай непрерывного спектра.
- 167. Матрицы Якоби.
- 168. Дифференциальные решения.
- 169. Примеры.
- 170. Слабая сходимость в l2.
- 171. Вполне непрерывные операторы в l2.
- 172. Интегральные операторы в L2.
- 173. Сопряженный оператор.
- 174. Вполне непрерывные операторы.
- 175. Спектральная функция.
- 176. Спектральная функция (продолжение).
- 177. Унитарные преобразования в L2.
- 178. Преобразования Фурье.
- 179. Преобразование Фурье и функции Эрмита.
- 180. Операция умножения.
- 181. Ядра, зависящие от разности.
- 182. Слабая сходимость.
- 183. Другие осуществления пространства H.
- § 2. Неограниченные операторы
- 184. Замкнутые операторы.
- 185. Сопряженный оператор.
- 186. График оператора.
- 187. Симметричные и самосопряженные операторы.
- 188. Примеры неограниченных операторов.
- 189. Спектр самосопряженного оператора.
- 190. Случай точечного спектра.
- 191. Инвариантные подпространства и приводимость оператора.
- 192. Разложение единицы. Интеграл Стилтьеса.
- 193. Непрерывные функции самосопряженного оператора.
- 194. Резольвента.
- 195. Собственные значения.
- 196. Случай смешанного спектра.
- 197. Функции самосопряженного оператора.
- 198. Малые возмущения спектра.
- 199. Оператор умножения.
- 200. Интегральные операторы.
- 201. Расширение замкнутого симметричного оператора.
- 202. Индексы дефекта.
- 203. Сопряженный оператор.
- 204. Максимальные операторы.
- 205. Расширение симметричных полуограниченных операторов.
- 206. Сравнение полуограниченных операторов.
- 207. Примеры на теорию расширений.
- 208. Спектр симметричного оператора.
- 209. Некоторые теоремы о расширениях и их спектрах.
- 210. Независимость индексов дефекта от «лямбда».
- 211. Об инвариантности непрерывной части ядра спектра при симметричных расширениях.
- 212. О спектрах самосопряженных расширений.
- 213. Примеры.
- 214. Бесконечные матрицы.
- 215. Матрицы Якоби.
- 216. Матрицы и операторы.
- 217. Унитарная эквивалентность С-матриц.
- 218. Существование спектральной функции.