| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
IV. Множители Лагранжа
176. Уравнения связей.
Пусть дана система, образованная  точками
точками

и подчиненная связям, выражаемым соотношениями между их координатами вида

Число  этих уравнений должно быть меньше числа
этих уравнений должно быть меньше числа  координат, ибо если бы оно равнялось
координат, ибо если бы оно равнялось  то все
то все  координат определялись бы этими уравнениями. Положим поэтому,
координат определялись бы этими уравнениями. Положим поэтому,

Такая система будет  лоно мной, так как при помощи равенств (1) можно выразить все координаты в функциях подходящим образом выбранных из них
лоно мной, так как при помощи равенств (1) можно выразить все координаты в функциях подходящим образом выбранных из них  координат. Система имеет, следовательно, к степеней свободы. В случае, когда
координат. Система имеет, следовательно, к степеней свободы. В случае, когда  система будет с полными связями, так как ее положение зависит только от одного параметра, например, от одной подходящим образом выбранной координаты.
система будет с полными связями, так как ее положение зависит только от одного параметра, например, от одной подходящим образом выбранной координаты.
Обозначим через  равнодействующую заданных сил, действующих на точку
равнодействующую заданных сил, действующих на точку  Тогда на основании принципа возможных скоростей имеем уравнение
Тогда на основании принципа возможных скоростей имеем уравнение

которое должно выполняться для всех перемещений  допускаемых связями.
допускаемых связями.
177. Множители Лагранжа.
Перемещения точек М связаны  соотношениями, которые получаются дифференцированием уравнений (1), а именно:
соотношениями, которые получаются дифференцированием уравнений (1), а именно:

Эти  соотношений между
соотношений между  вариациями координат показывают, что
вариациями координат показывают, что  из этих вариаций могут быть выбраны произвольно. Назовем эти вариации независимыми вариациями, а остальные, определяемые уравнениями (3), - зависимыми вариациями.
из этих вариаций могут быть выбраны произвольно. Назовем эти вариации независимыми вариациями, а остальные, определяемые уравнениями (3), - зависимыми вариациями.
Для нахождения условий равновесия применим метод множителей Лагранжа. Умножим уравнения (3) соответственно на неопределенные множители  и сложим их с уравнением (2); после этого определим множители таким образом, чтобы в полученной сумме обратить в нуль коэффициенты при
и сложим их с уравнением (2); после этого определим множители таким образом, чтобы в полученной сумме обратить в нуль коэффициенты при  зависимых вариациях; тогда коэффициенты при независимых вариациях должны также обратиться в нуль; в результате требуется определить X таким образом, чтобы обращались в нуль все коэффициенты, и мы получаем
зависимых вариациях; тогда коэффициенты при независимых вариациях должны также обратиться в нуль; в результате требуется определить X таким образом, чтобы обращались в нуль все коэффициенты, и мы получаем  совместных
совместных
уравнений:

Эти уравнения совместно с  уравнениями связей (1) составляют полную систему
уравнениями связей (1) составляют полную систему  уравнений, определяющих
уравнений, определяющих  координат и
координат и  вспомогательных неизвестных X.
вспомогательных неизвестных X.
Таковы общие уравнения равновесия.
Как только коэффициенты X будут известны, так сейчас же можно будет определить и реакции связей. В самом деле, мы видим, что уравнения равновесия не изменятся, если отбросить связь  и присоединить к заданным силам, действующим на точку
и присоединить к заданным силам, действующим на точку  силу
силу  с проекциями
с проекциями  эта сила является действием связи на точку
эта сила является действием связи на точку  т. е. тем, что мы называем реакцией связи. Мы непосредственно имеем величину этой силы; ее направление
т. е. тем, что мы называем реакцией связи. Мы непосредственно имеем величину этой силы; ее направление  нормально к поверхности, которая получится, если предположить, что в уравнении
нормально к поверхности, которая получится, если предположить, что в уравнении  всем координатам, кроме
всем координатам, кроме  приданы численные значения, соответствующие положению равновесия, а координаты уч, являются текущими.
приданы численные значения, соответствующие положению равновесия, а координаты уч, являются текущими.
Пример. Применим предыдущие рассуждения к равновесию веревочного многоугольника с  сторонами, концы которого закреплены в двух заданных точках. Здесь будет
сторонами, концы которого закреплены в двух заданных точках. Здесь будет  уравнений связи, а именно:
уравнений связи, а именно:

причем координаты  даны. Общие уравнения равновесия будут
даны. Общие уравнения равновесия будут

Они действительно совпадают с теми, которые получатся при помощи элементарных методов, если выразить, что сила  уравновешивается натяжениями двух нитей, оканчивающихся в точке
уравновешивается натяжениями двух нитей, оканчивающихся в точке  Так как коэффициенты при X в этих уравнениях равны направляющим косинусам сторон веревочного многоугольника, то эти X являются абсолютными значениями натяжений.
Так как коэффициенты при X в этих уравнениях равны направляющим косинусам сторон веревочного многоугольника, то эти X являются абсолютными значениями натяжений.
причем последние направлены вдоль сторон. Мы действительно видим, что они нормальны к поверхностям

где только  являются переменными, так как эти поверхности являются сферами с центрами в точках
являются переменными, так как эти поверхности являются сферами с центрами в точках 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
- ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
- II. Свободные векторы. Три координаты свободного вектора
- III. Скользящие векторы. Пять координат скользящего вектора
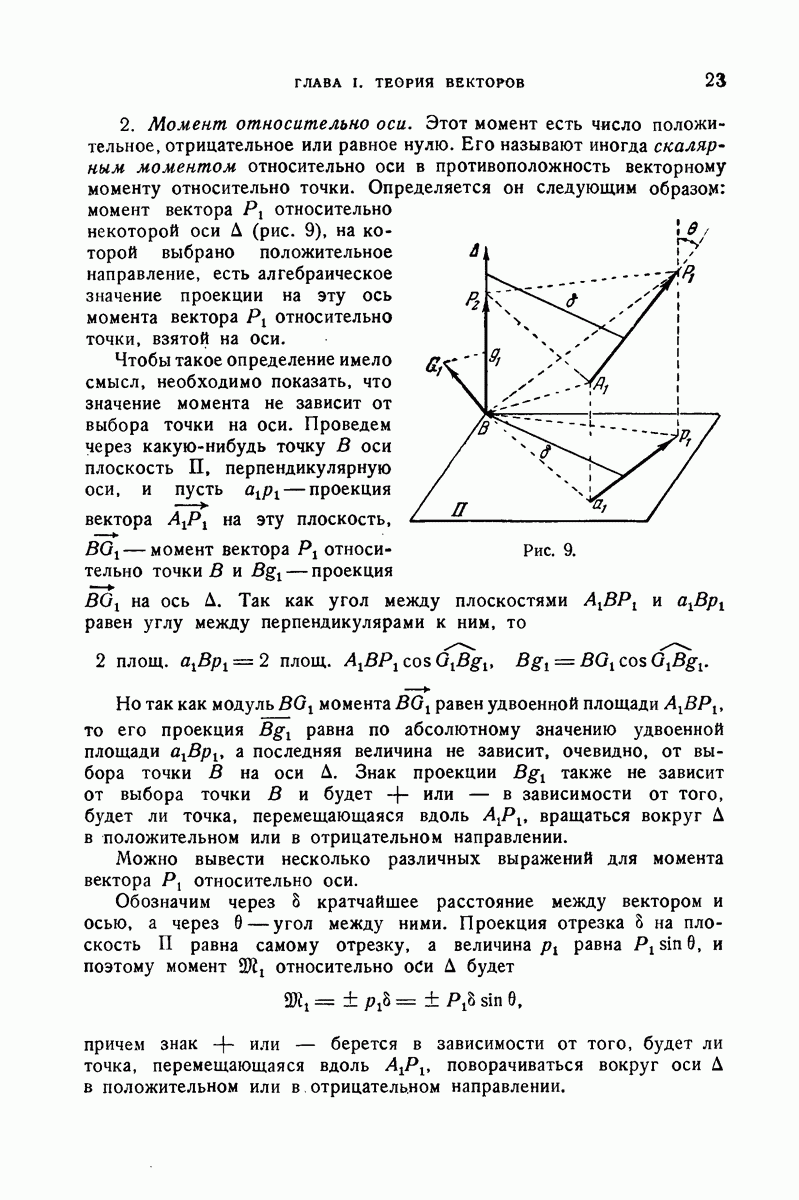
- 9. Теория моментов.
- 10. Аналитические выражения моментов вектора относительно осей координат.
- 11. Пять координат скользящего вектора.
- 12. Относительный момент двух векторов
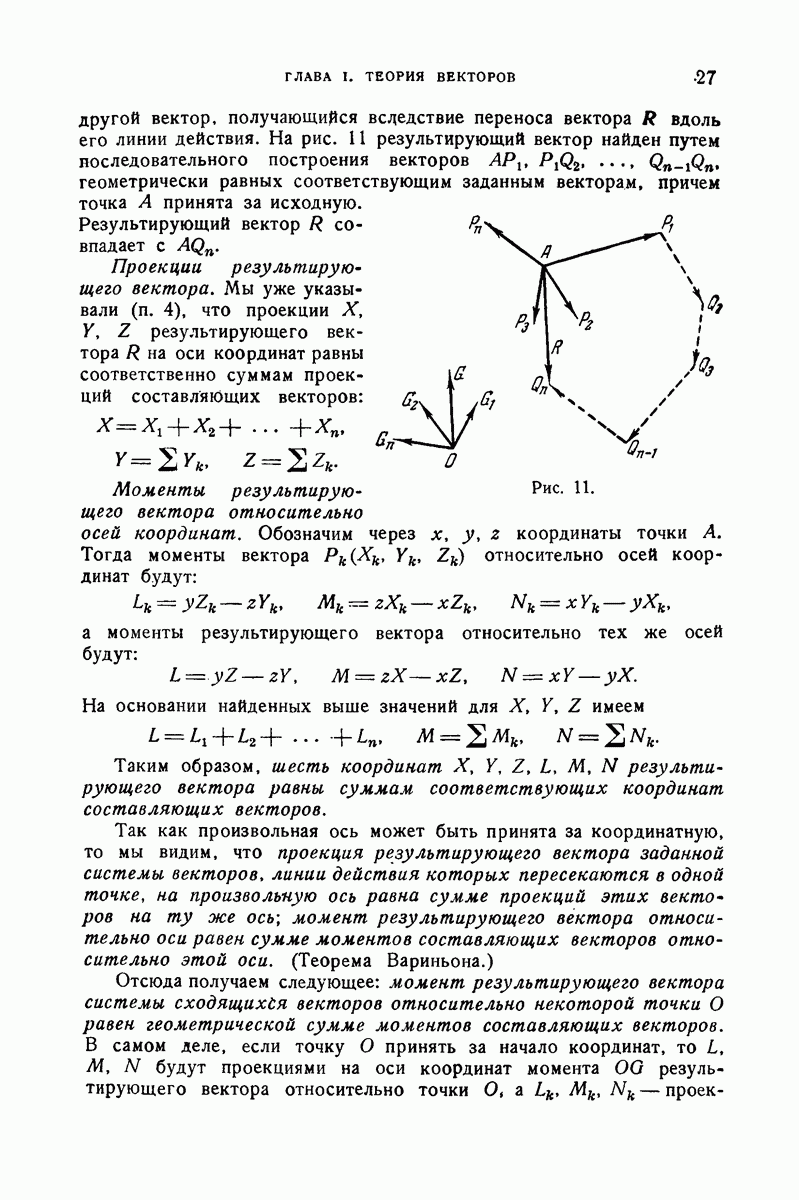
- 13. Скользящие векторы, сходящиеся в одной точке. Результирующий вектор.
- 14. Произвольная система векторов. Главный вектор и главный момент.
- 15. Изменение главного вектора и главного момента; инварианты; центральная ось.
- 16. Сумма моментов относительно произвольной оси. Прямые нулевого момента.
- IV. Эквивалентные системы скользящих векторов. Элементарные операции. Приведение системы скользящих векторов
- 19. Элементарные операции.
- 20. Приведение к двум векторам.
- 21. Геометрическое истолкование инварианта LX+MY+NZ.
- 22. Приведение двух эквивалентных систем друг к другу.
- 23. Пары.
- 24. Приведение к вектору и паре.
- 25. Винт.
- 26. Частные случаи приведения.
- 28. Взаимный момент системы скользящих векторов.
- 29. Приложение общих теорем к случаю параллельных скользящих векторов.
- V. Связанные векторы; шесть координат связанного вектора; центр параллельных связанных векторов. Векторные производные
- 31. Центр системы параллельных связанных векторов.
- 32. Моменты параллельных связанных векторов относительно плоскости.
- 33. Векторные производные.
- VI. Полярные векторы. Аксиальные векторы. Скалярные величины
- VII. Другие геометрические образы, которые могут быть использованы в механике
- ГЛАВА II. КИНЕМАТИКА
- I. Кинематика точки
- 37. Движение точки.
- 38. Прямолинейное равномерное движение; скорость.
- 39. Произвольное прямолинейное движение; скорость.
- 40. Вектор скорости в криволинейном движении.
- 41. Вектор ускорения.
- 42. Касательное и нормальное ускорения (Гюйгенс).
- II. Поступательное движение и вращение неизменяемой системы
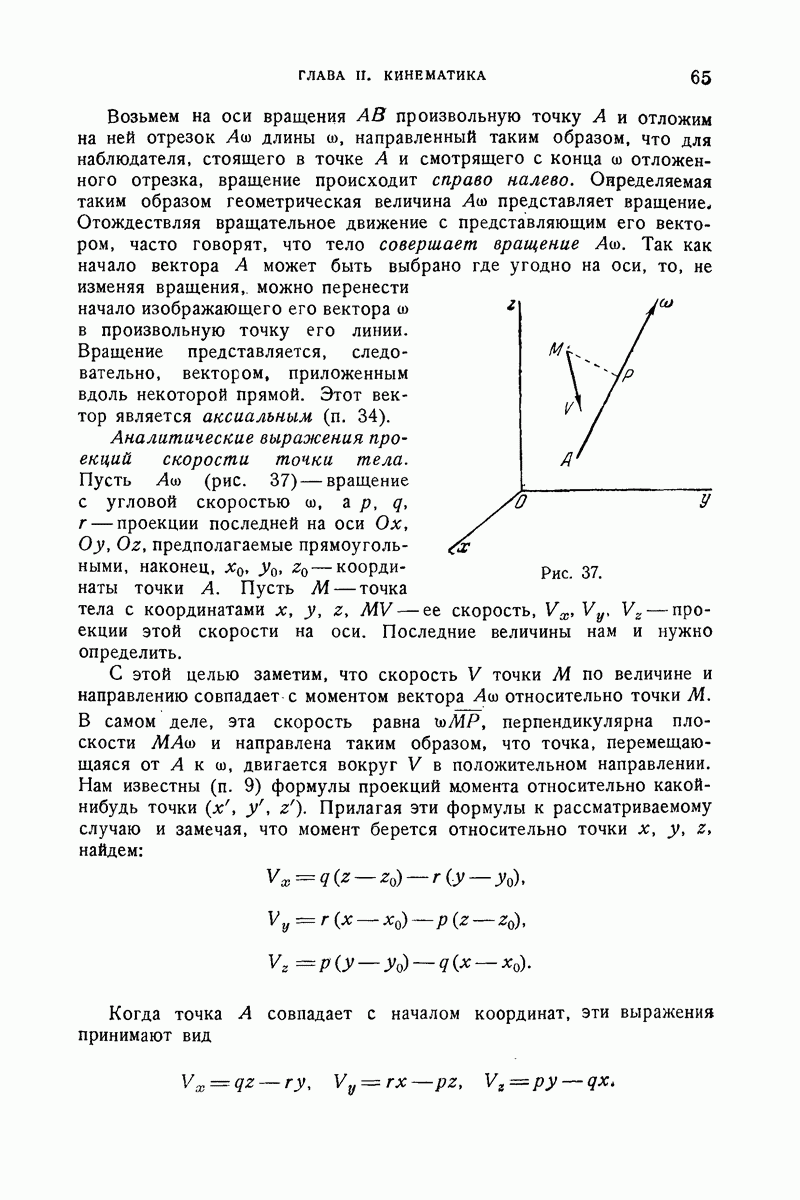
- 44. Вращение вокруг неподвижной оси. Угловая скорость. Геометрическое представление.
- III. Скорость в относительном движении. Сложение поступательных и вращательных движений. Скорости точек свободного тела
- 46. Сложение поступательных движений.
- 47. Совокупность двух вращений.
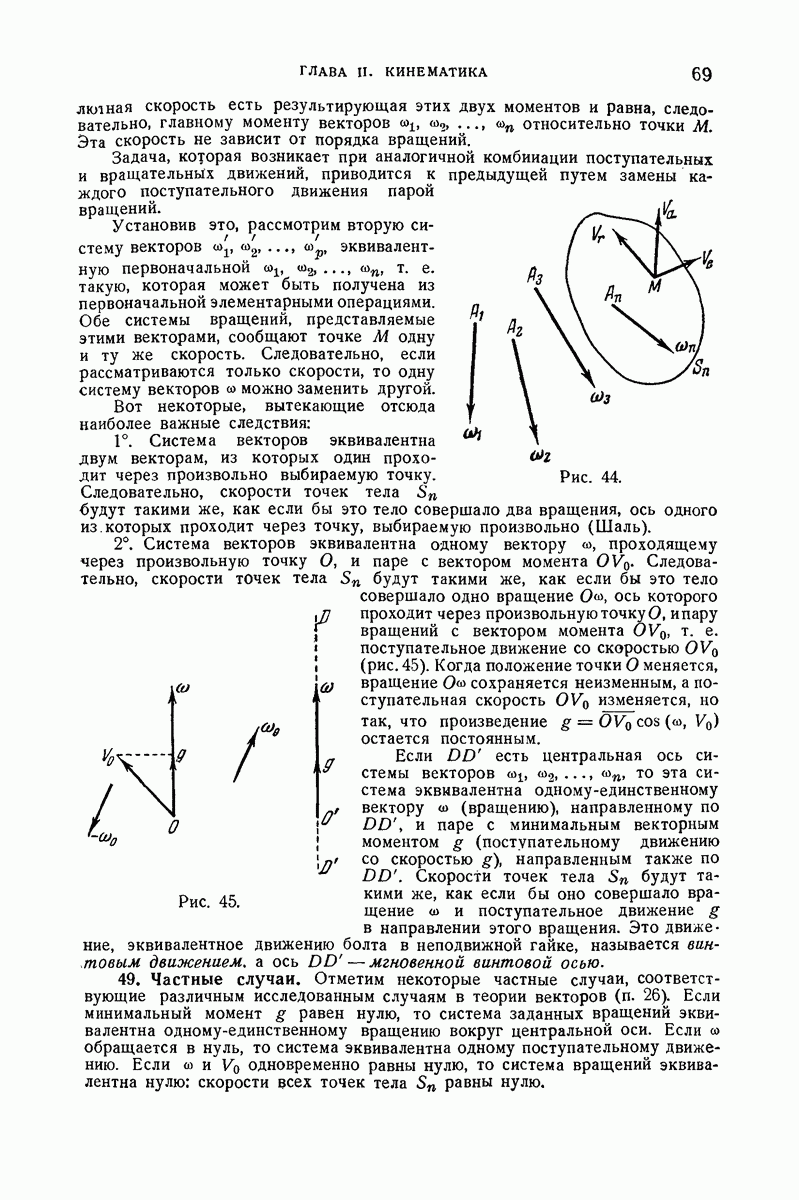
- 48. Произвольное число вращений.
- 49. Частные случаи.
- 50. Геометрические следствия.
- 51. Распределение скоростей в движущемся твердом теле.
- 52. Мгновенная винтовая ось. Касательное винтовое движение.
- 53. Величина скорости точки тела.
- 54. Непрерывное движение.
- 55. Твердое тело с неподвижной точкой.
- 56. Тело перемещается параллельно неподвижной плоскости.
- 57. Качение и верчение подвижной поверхности по неподвижной поверхности.
- IV. Ускорения. Теорема Кориолиса
- 59. Ускорение в относительном движении. Теорема Кориолиса.
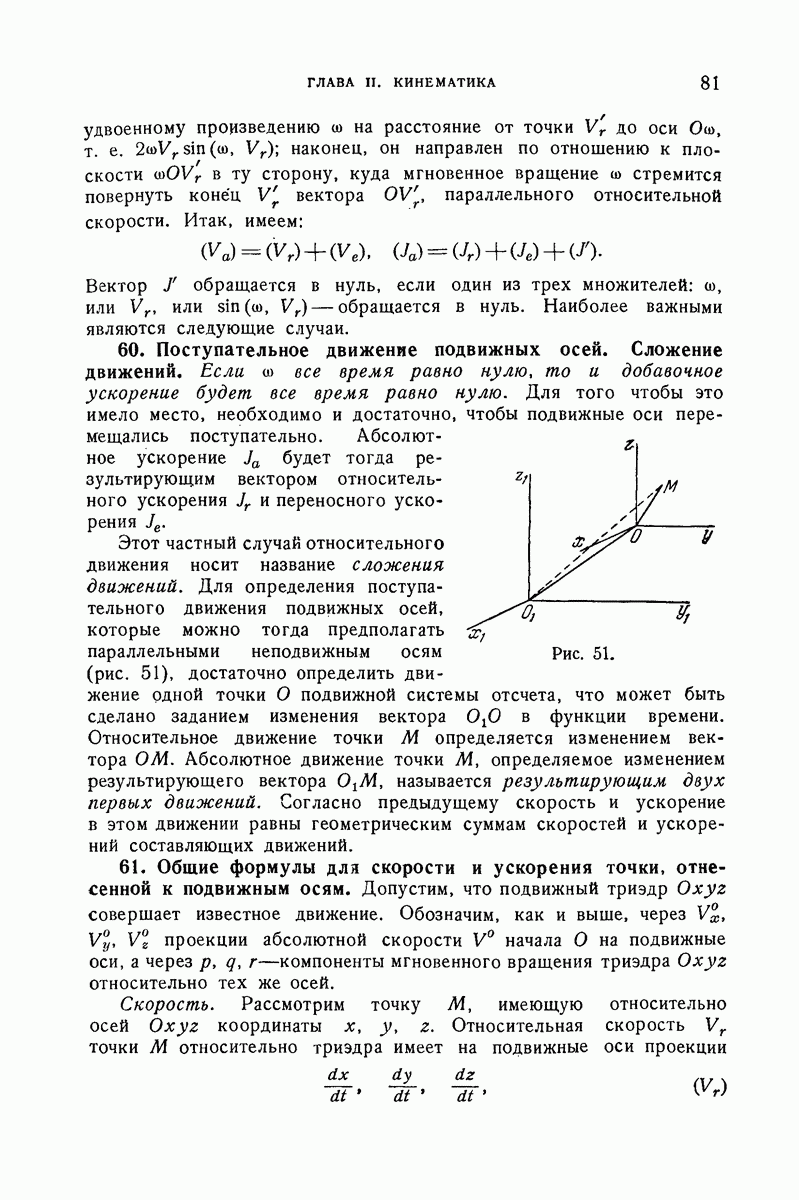
- 60. Поступательное движение подвижных осей. Сложение движений.
- 61. Общие формулы для скорости и ускорения точки, отнесенной к подвижным осям.
- ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ. МАССА И СИЛА
- II. Единицы массы и силы; однородность
- 73. Технические единицы. Килограмм-сила.
- 74. Абсолютные единицы. Дина.
- 75. Статическое измерение сил.
- 76. Однородность.
- ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ
- 78. Аналитическое выражение элементарной работы.
- 79. Полная работа. Единица работы.
- 80. Сила зависит от времени или скорости.
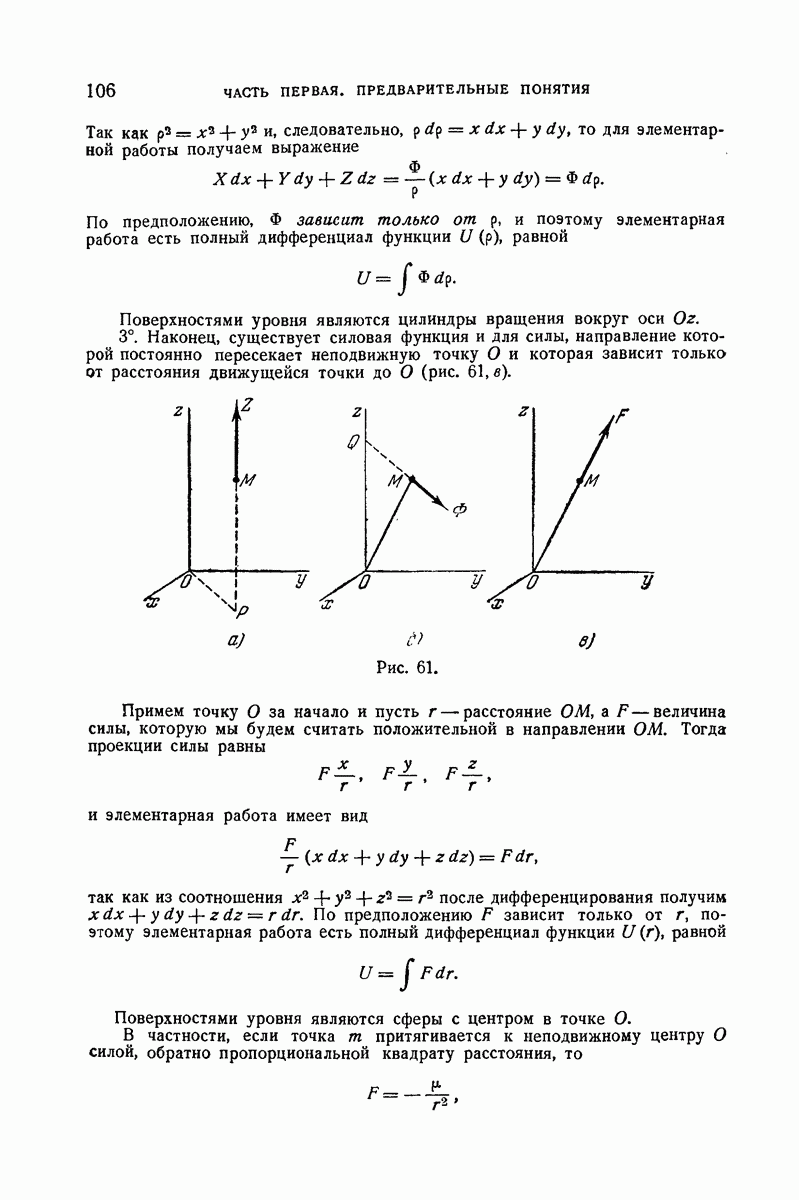
- 81. Сила зависит только от положения движущейся точки.
- 82. Частный случай, когда сила зависит только от начального и конечного положений. Силовая функция. Потенциальная энергия.
- 83. Поверхности уровня.
- 84. Примеры.
- 85. Замечание о поверхностях уровня.
- 86. Мощность.
- II. Система точек
- 88. Примеры.
- ЧАСТЬ ВТОРАЯ. СТАТИКА
- ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ
- 90. Пример. Притяжения, пропорциональные расстояниям.
- 91. Точка, движущаяся без трения по неподвижной поверхности.
- 92. Точка, движущаяся без трения по неподвижной кривой.
- II. Системы материальных точек
- 94. Силы внутренние и силы внешние. Шесть необходимых условий равновесия.
- 96. Разделение произвольной системы на части. Необходимые условия равновесия.
- ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
- I. Приведение сил, приложенных к твердому телу. Равновесие
- 97. Приведение сил, приложенных к твердому телу. Равновесие.
- 98. Эквивалентные системы сил.
- 99. Частные случаи приведения.
- 100. Другая форма условий равновесия.
- II. Приложения. Силы в плоскости. Параллельные силы. Центр тяжести
- 102. Примеры.
- 103. Параллельные силы.
- 104. Центр тяжести.
- 105. Координаты центра тяжести.
- III. Приложения. Произвольные силы в пространстве
- 107. Условия, при которых силы, находящиеся в равновесии, могут быть направлены по трем, четырем, пяти, шести прямым.
- IV. Твердое тело, подчиненное связям
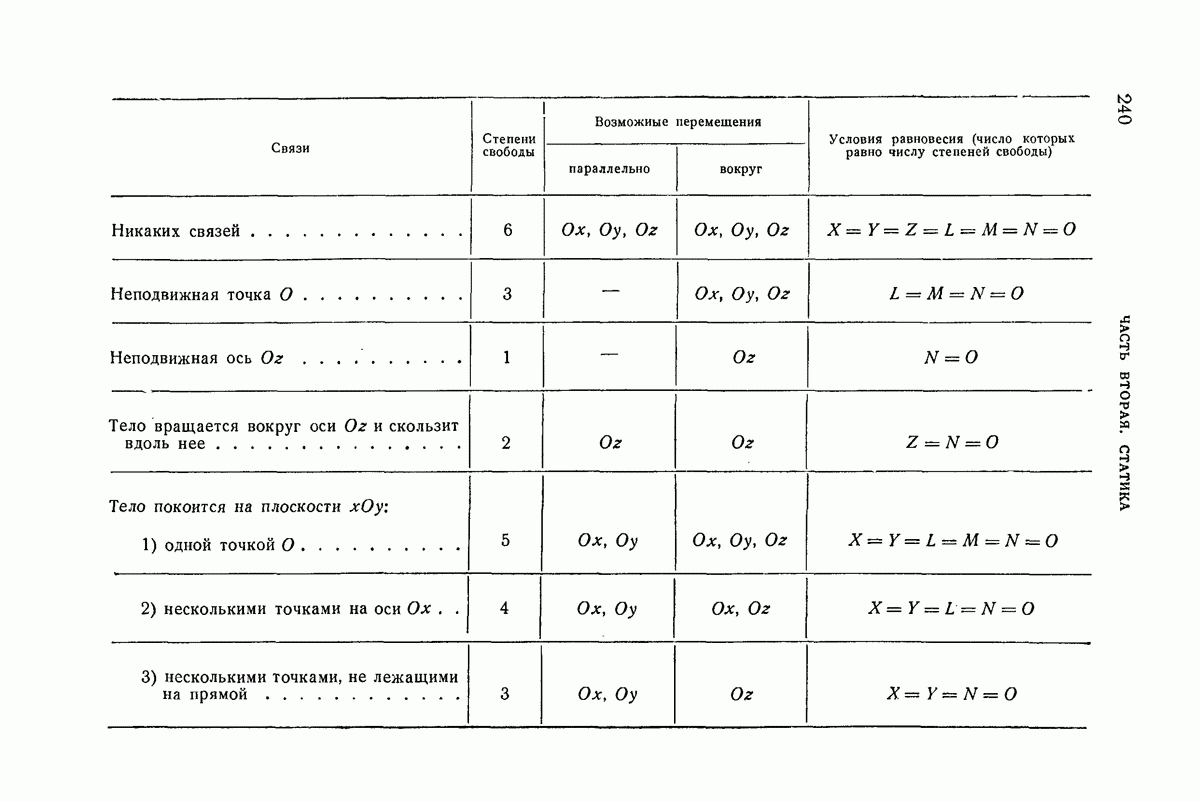
- 109. Тело с неподвижной точкой.
- 110. Тело, имеющее неподвижную ось.
- 111. Тело вращается вокруг оси и скользит вдоль нее.
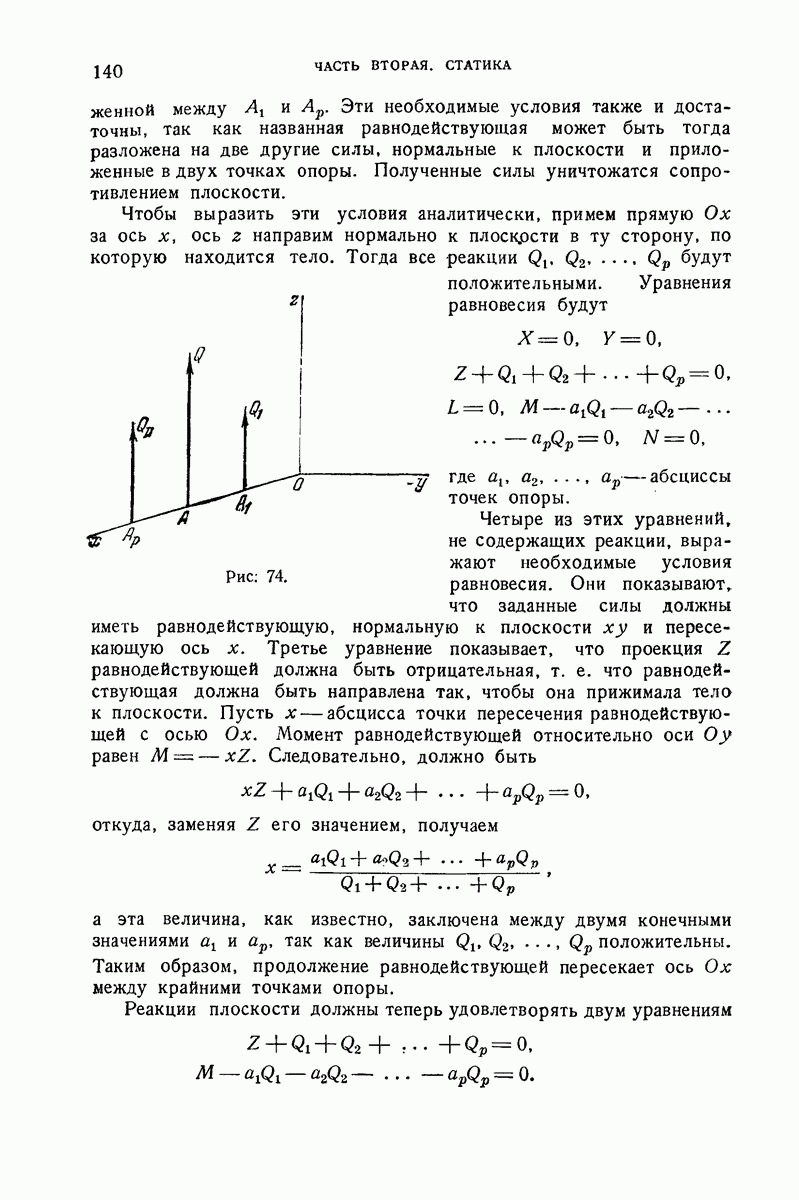
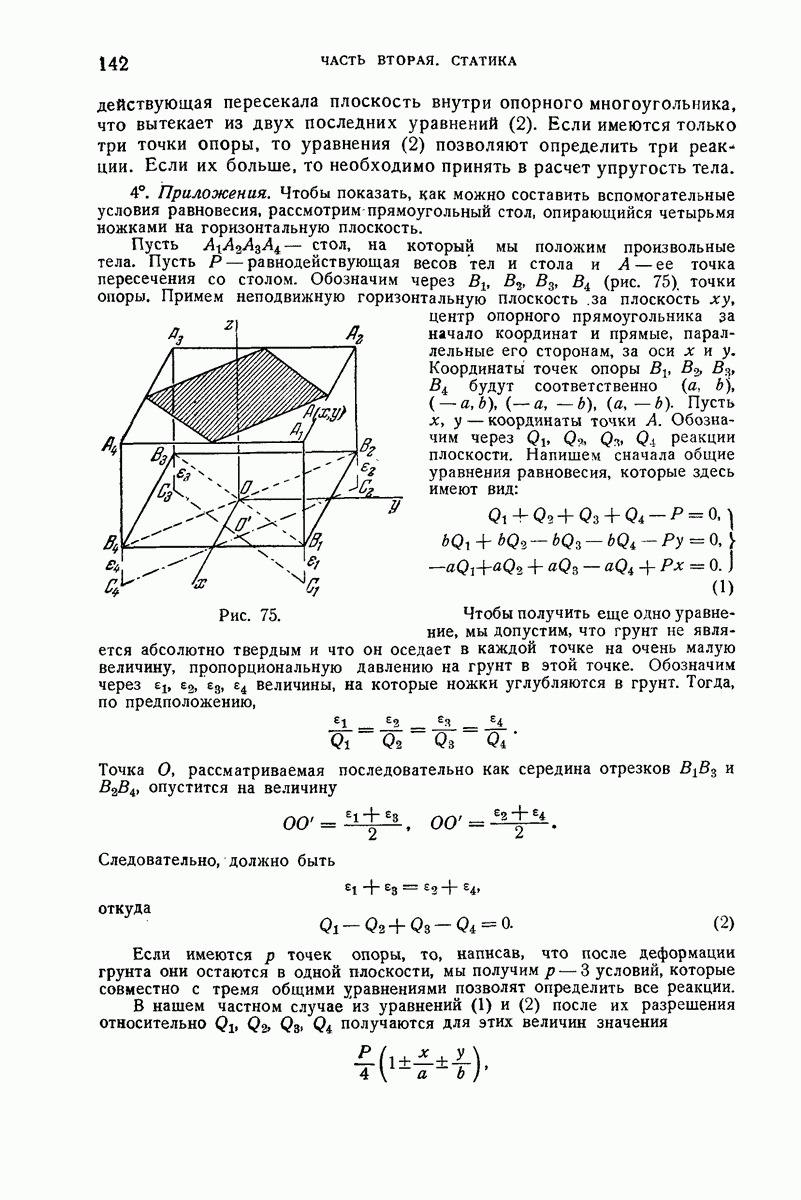
- 112. Тело, опирающееся на неподвижную плоскость.
- 113. Несколько твердых тел.
- V. Некоторые формулы для вычисления центра тяжести
- ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
- I. Веревочный многоугольник
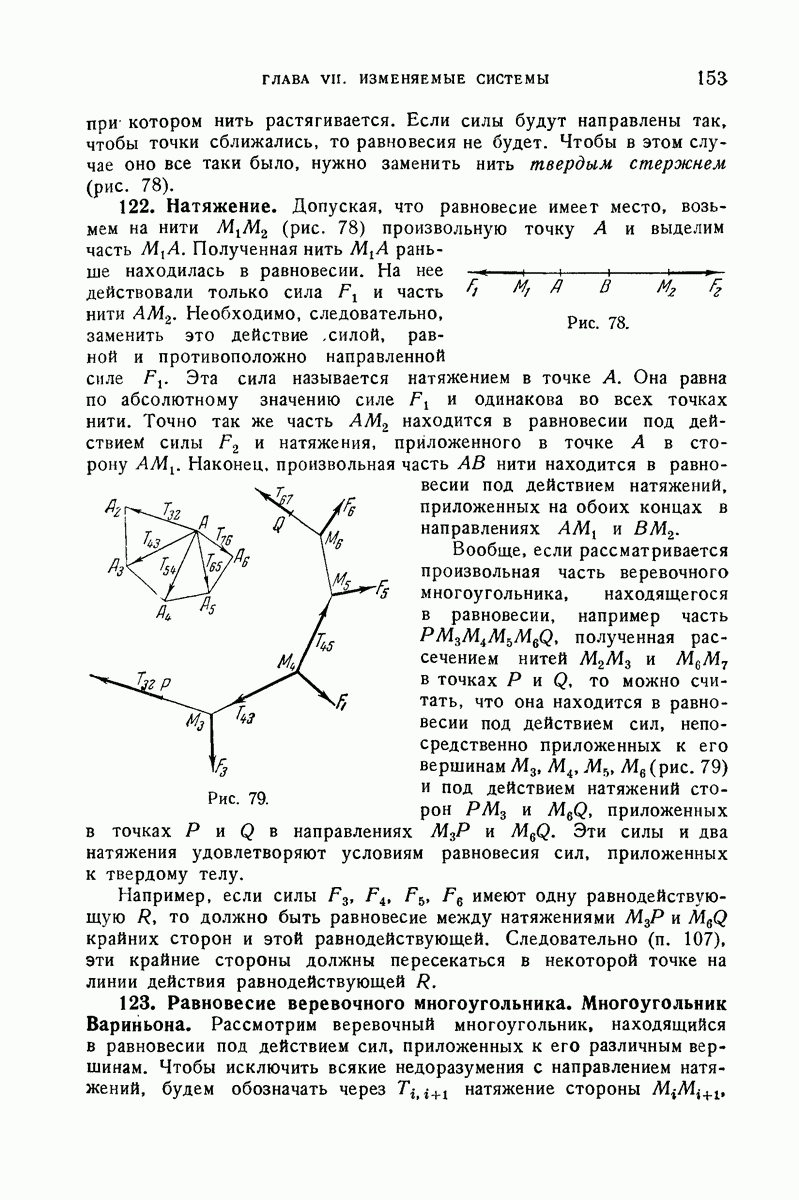
- 122. Натяжение.
- 123. Равновесие веревочного многоугольника. Многоугольник Вариньона.
- 124. Условия на концах.
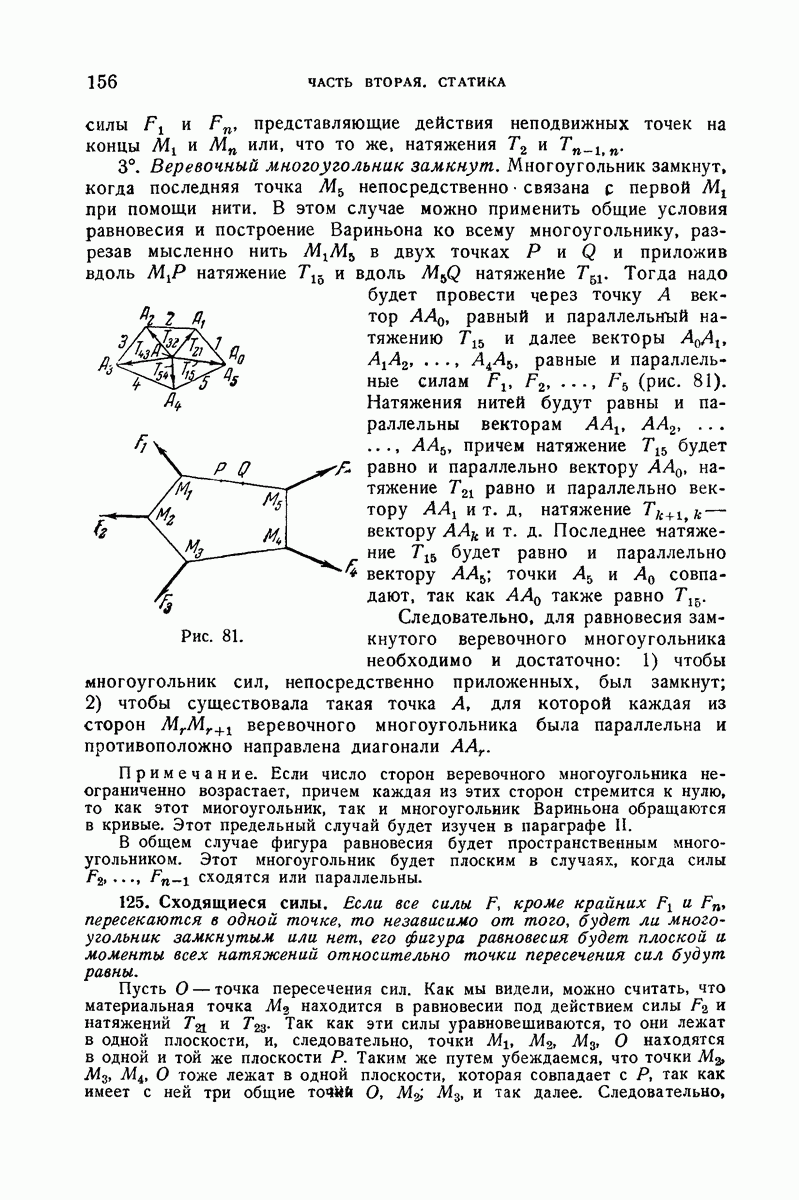
- 125. Сходящиеся силы.
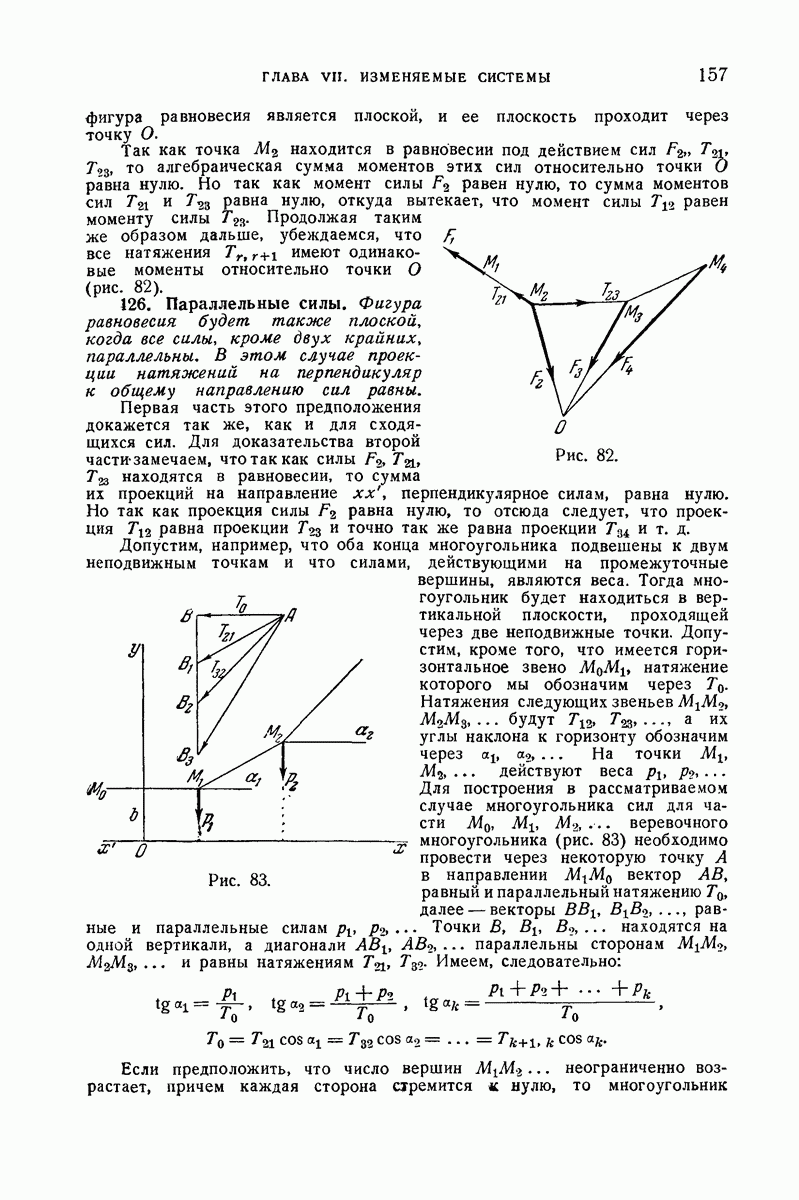
- 126. Параллельные силы.
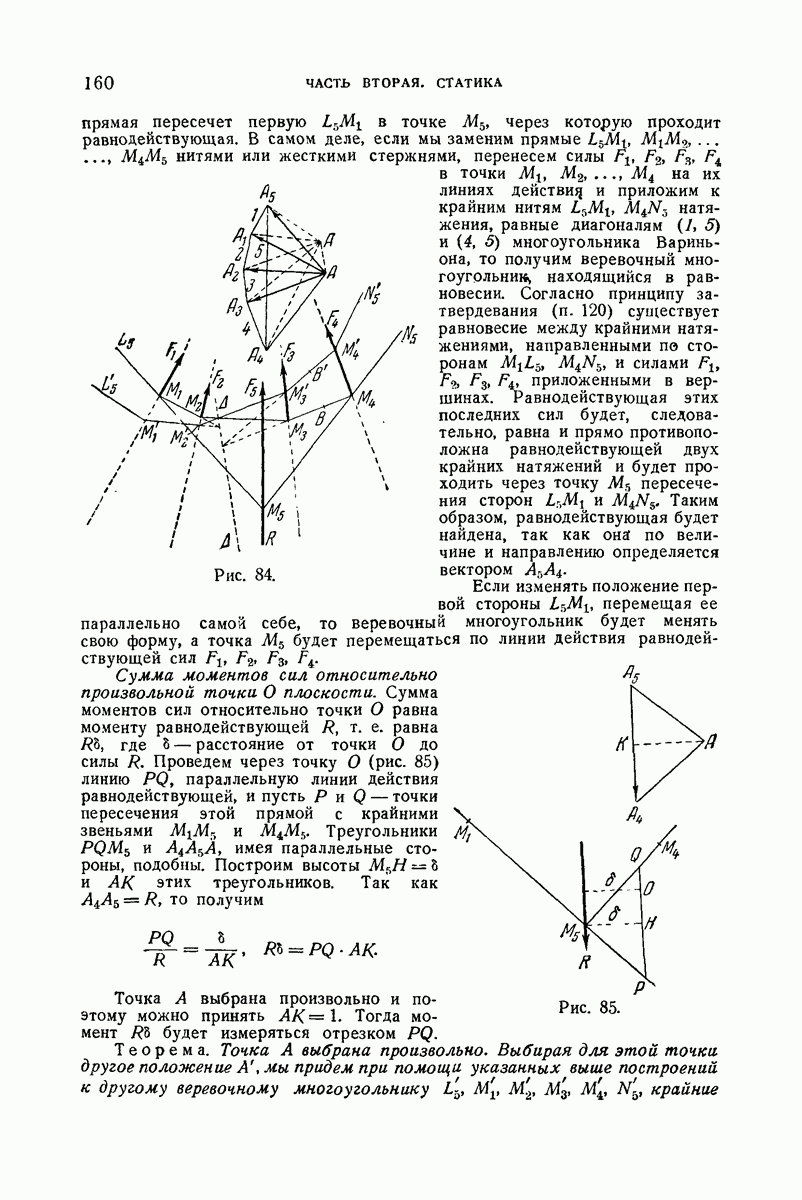
- 127. Графические приложения теории веревочных многоугольников.
- 128. Кольца, скользящие на нити.
- 129. Фермы.
- II. Равновесие нитей
- 131. Общие теоремы.
- 132. Общие интегралы.
- 133. Определение постоянных, условия на концах.
- 134. Случай, когда сила не зависит от длины дуги.
- 135. Замечание о натяжении.
- 136. Естественные уравнения равновесия нити.
- 137. Формула, определяющая натяжение, когда существует силовая функция.
- 138. Параллельные силы.
- 139. Цепная линия.
- 140. Определение постоянных.
- 141. Центральные силы.
- 142. Пример существования бесчисленного множества положений равновесия.
- 143. Равновесие нити на поверхности.
- 144. Примеры.
- 145. Естественные уравнения равновесия нити на поверхности.
- III. Исследование одного определенного интеграла
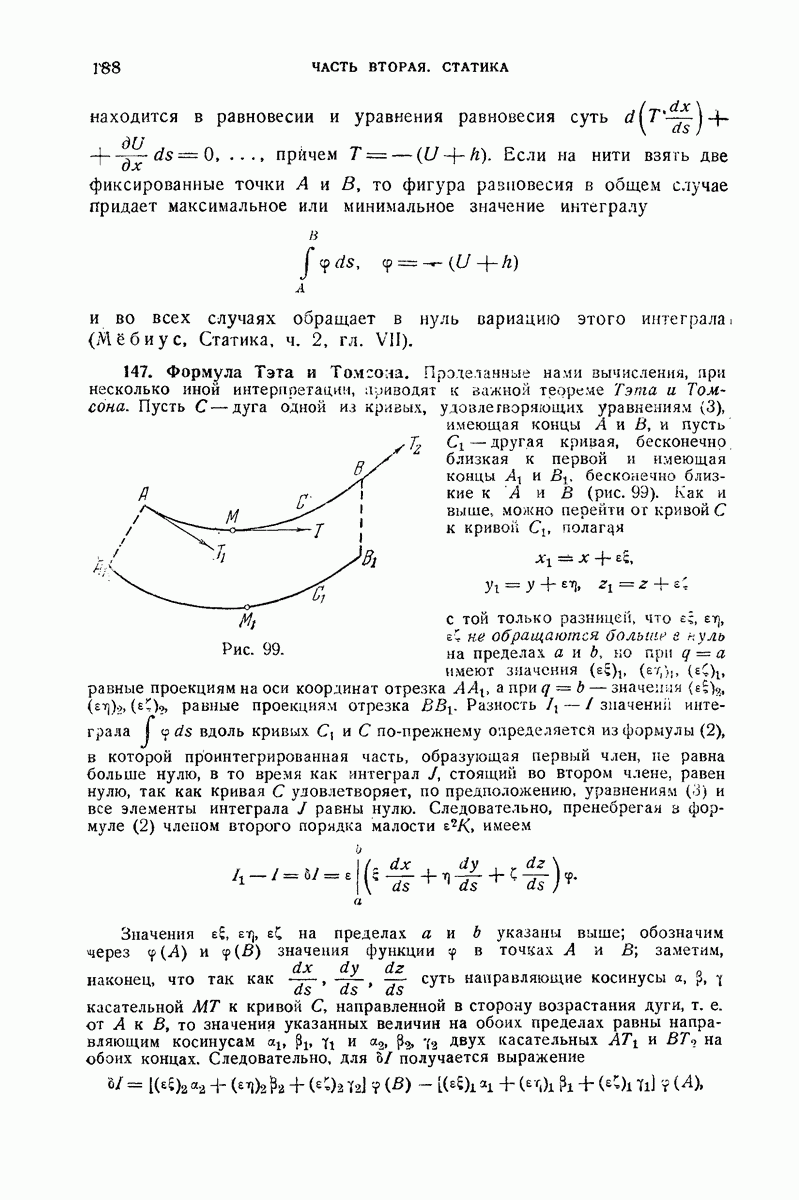
- 147. Формула Тэта и Томсона.
- 148. Примеры.
- 149. Та же задача на поверхности.
- 150. Рефракция.
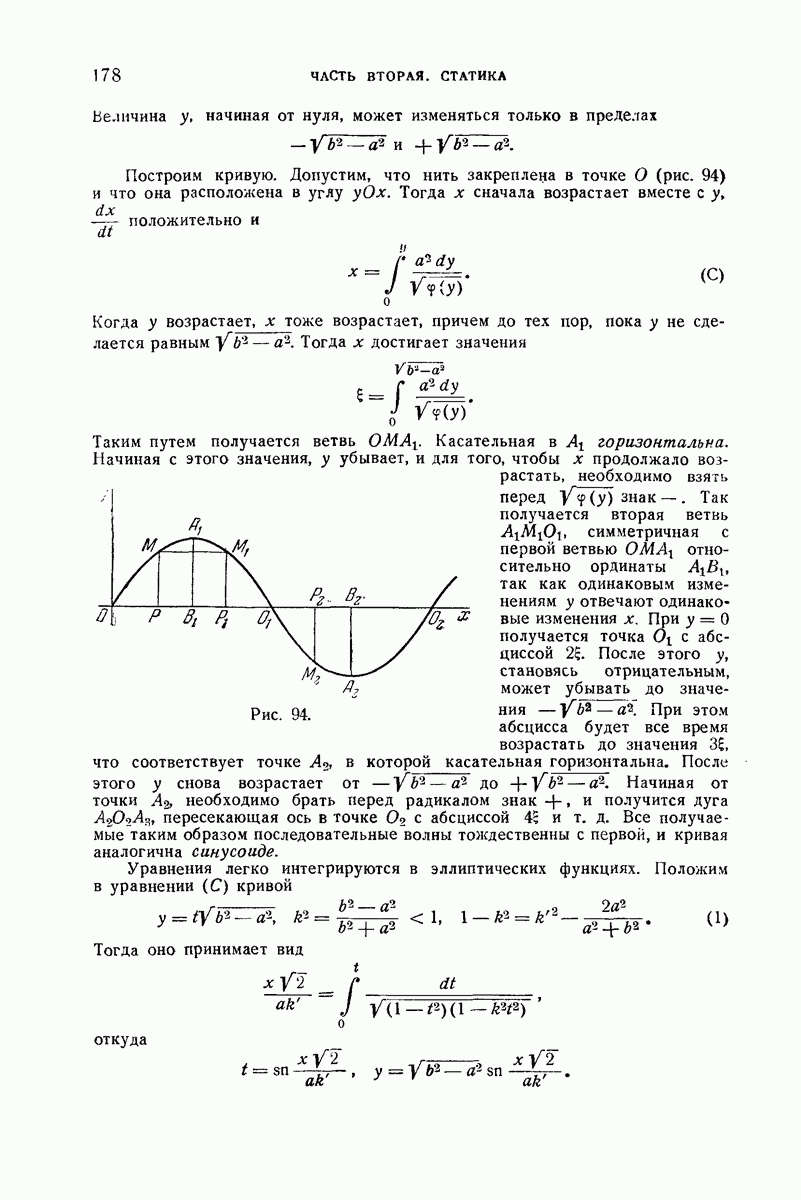
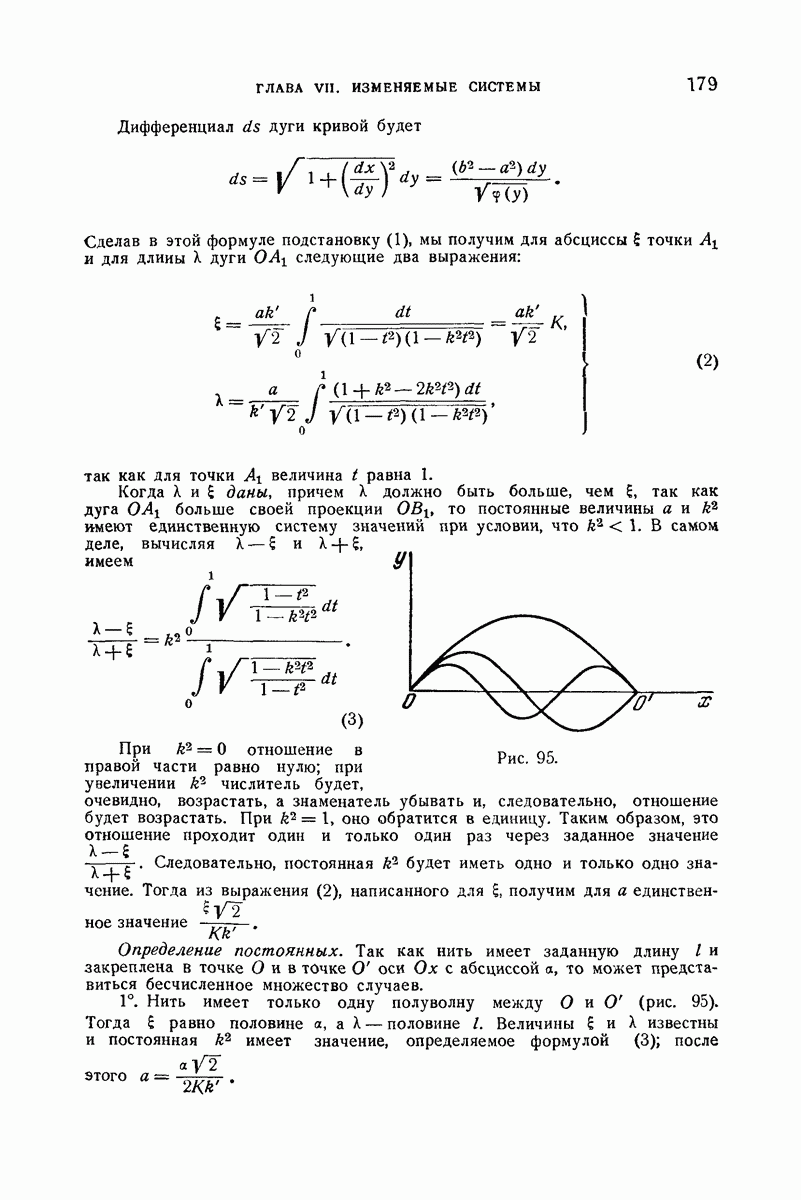
- IV. Плоские эластики
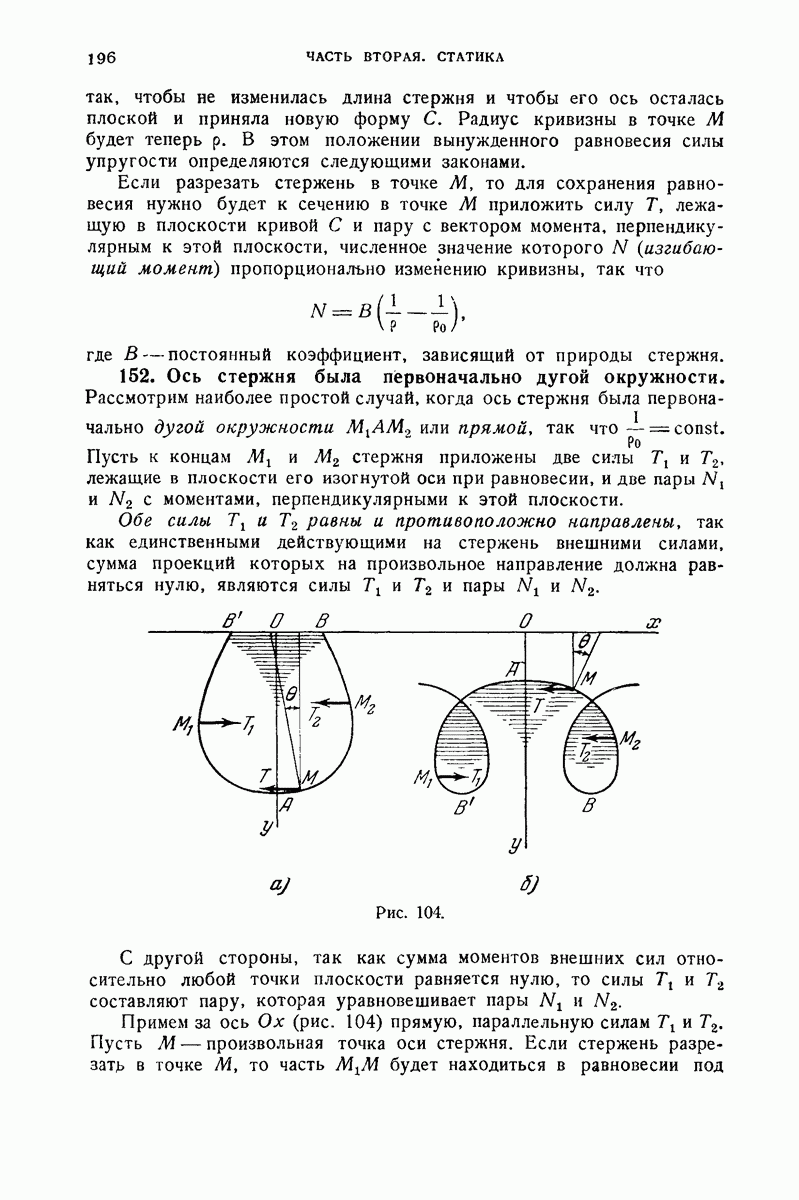
- 152. Ось стержня была первоначально дугой окружности.
- 153. Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами.
- 154. Стержень, изгибаемый действующим в одной плоскости постоянным нормальным давлением.
- ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
- I. Формулировка и доказательство принципа в случае связей, выражающихся равенствами
- 157. Формулировка принципа.
- 158. Свободная точка.
- 159. Точка на поверхности.
- 160. Точка на кривой.
- 161. Свободное твердое тело.
- 162. Лемма.
- 163. Сочетания предыдущих связей.
- 164. Общее определение идеальных связей.
- 165. Доказательство принципа.
- 166. Замечание о работе силы.
- 167. О связях, осуществляемых при помощи тел, не имеющих массы.
- II. Первые примеры. Системы с полными связями. Простые машины
- III. Общие условия равновесия, выводимые из принципа возможных скоростей
- 172. Голономные системы; координаты голономной системы.
- 173. Частный случай, когда выражение возможной работы есть полный дифференциал.
- 174. Приложения. Тяжелые системы.
- 175. Принцип Торричелли.
- IV. Множители Лагранжа
- 178. Случай неголономной системы.
- 179. Приложение принципа возможных скоростей к равновесию нитей.
- V. Общие теоремы, выводимые из принципа возможных скоростей
- VI Неудерживающие связи
- 187. Связи, выражаемые неравенствами в конечной форме.
- ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ
- 189. Трение скольжения.
- 190. Законы трения скольжения в состоянии покоя.
- 191. Равновесие тел с трением.
- 192. Тяжелое тело, опирающееся на плоскость в нескольких точках и находящееся под действием только одной силы F.
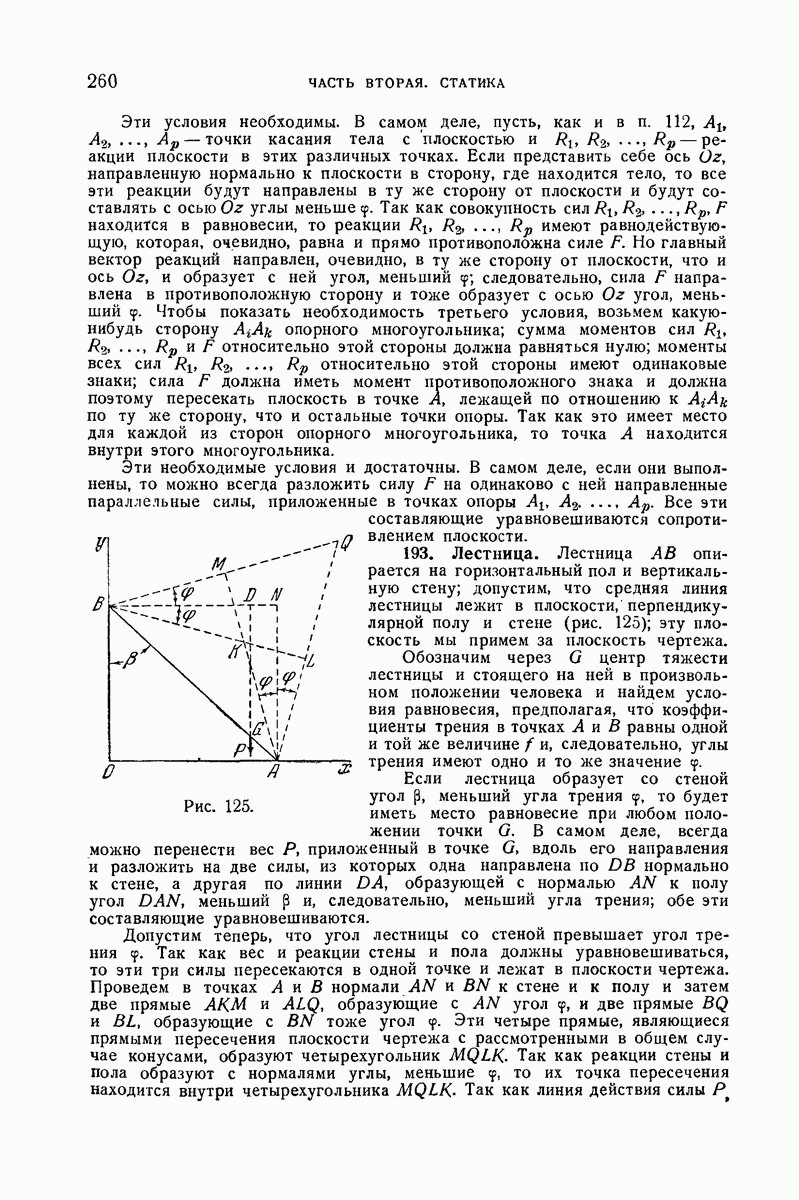
- 193. Лестница.
- 194. Веревка, навернутая на поперечное сечение цилиндра.
- 195. Трение скольжения при движении.
- 196. Трение качения в начале и во время движения.
- 197. Трение верчения.
- ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
- ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. ДВИЖЕНИЕ СНАРЯДОВ
- 199. Первые интегралы.
- 200. Естественные уравнения (Эйлер).
- 201. Количество движения.
- 202. Теорема о проекции количества движения.
- 203. Теорема о моменте количества движения. Закон площадей.
- 204. Геометрическая интерпретация двух предыдущих теорем.
- 205. Теорема кинетической энергии.
- 206. Примеры.
- 207. Замечание к интегралу кинетической энергии.
- 208. Устойчивость равновесия свободной материальной точки. Доказательство Лежен-Дирихле.
- II. Прямолинейное движение
- 210. Уравнение прямолинейного движения. Простые случаи интегрируемости.
- 211. Приложение к движениям, происходящим под действием силы зависящей только от положения.
- 212. Движения под действием силы, зависящей только от скорости.
- 213. Прямолинейное таутохронное движение.
- 214. Дан закон прямолинейного движения, найти силу.
- III. Криволинейное движение. Тяжелая точка в пустоте и в сопротивляющейся среде. Электрическая частица
- 217. Движение тяжелой точки в пустоте.
- 218. Определение параллельной силы по заданной траектории.
- 219. Криволинейное движение тяжелого тела в сопротивляющейся среде.
- 220. Движение легкого вращающегося шара в воздухе.
- 221. Движение наэлектризованной частицы в наложенных друг на друга электрическом и магнитном полях.
- ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ЭЛЛИПТИЧЕСКОЕ ДВИЖЕНИЕ ПЛАНЕТ
- 223. Сила есть функция только расстояния.
- 224. Сила вида …
- 225. Обратная задача. Определение центральной силы, когда задана траектория.
- II. Движение планет
- 228. Кометы.
- 229. Спутники.
- 230. Всемирное притяжение.
- 231. Двойные звезды.
- 232. Задача Бертрана.
- 233. Краткие указания по поводу некоторых других задач.
- III. Элементарные сведения из небесной механики
- 235. Задача двух тел.
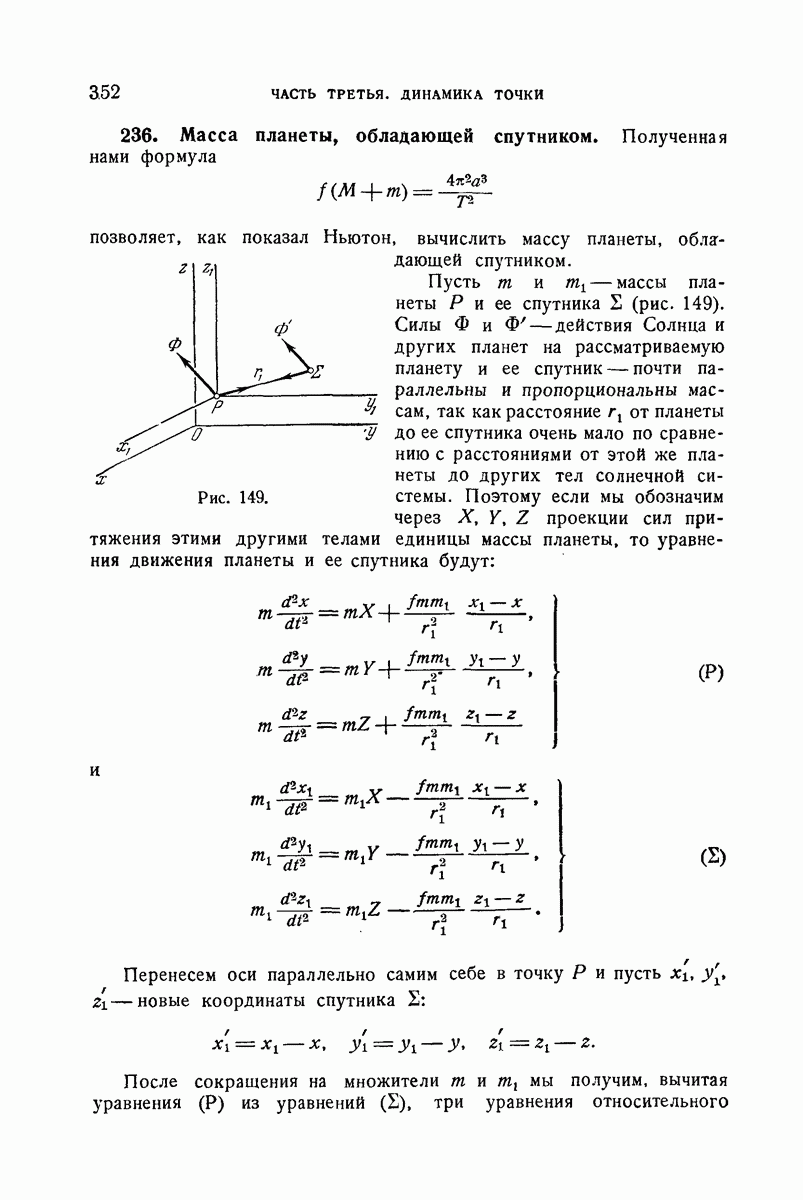
- 236. Масса планеты, обладающей спутником.
- 237. Определение времени в эллиптическом движении.
- 238. Геометрический метод.
- 239. Аналитические преобразования.
- 240. Элементы эллиптического движения.
- ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ КРИВОЙ
- 245. Устойчивость равновесия.
- 246. Движение тяжелой точки по неподвижной кривой.
- 247. Нормальная реакция. Естественные уравнения.
- 248. Математический маятник.
- 249. Движение математического маятника в сопротивляющейся среде.
- 250. Циклоидальный маятник.
- 251. Движение тяжелой точки по кривой, расположенной в вертикальной плоскости, при действии трения и сопротивления среды.
- 252. Таутохроны.
- 253. Приложения.
- 254. Брахистохрона для силы тяжести.
- 255. Брахистохроны в общем случае.
- 256. Приложение теорем Томсона и Тэта к брахистохронам.
- 257. Брахистохроны на заданной поверхности.
- II. Движение материальной точки на изменяемой кривой
- ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- II. Случай неподвижной поверхности
- 266. Вывод уравнения кинетической энергии из уравнений Лагранжа.
- 267. Устойчивость равновесия в случае существования силовой функции U.
- 268. Нормальная реакция.
- 269. Естественные уравнения и нормальная реакция.
- 270. Геодезические линии.
- 271. Применение уравнений Лагранжа.
- 272. Бесконечно малые колебания тяжелой точки около наинизшей точки поверхности.
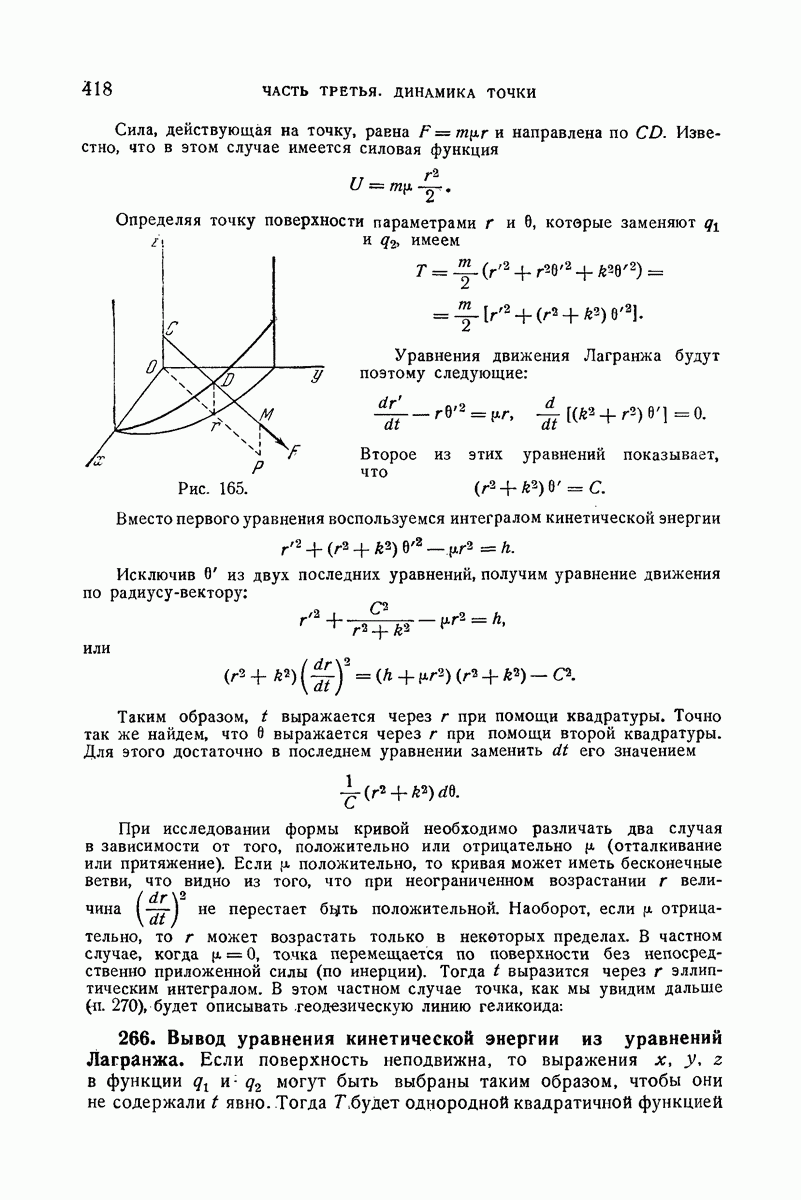
- III. Движение на поверхности вращения
- 274. Формула Клеро.
- 275. Упражнение. Геодезические линии поверхности, образованной вращением равносторонней гиперболы вокруг своей асимптоты.
- 276. Движение тяжелой точки на поверхности врадцения, ось которой Oz вертикальна.
- 277. Сферический маятник.
- 278. Вычисление нормальной реакции.
- 279. Интегрирование в эллиптических функциях.
- 280. Теорема Гринхилла.
- 281. Бесконечно малые колебания.
- ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
- 283. Интеграл кинетической энергии.
- 284. Приложение.
- 285. Сферические координаты.
- 286. Эллиптические координаты в пространстве.
- 287. Эллиптические координаты в плоскости ху.
- ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- 289. Замечание о силе инерции.
- 290. Принцип наименьшего действия.
- ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ. ПРИЛОЖЕНИЯ
- I. Канонические уравнения. Теорема Якоби
- II. Теорема Якоби
- 298. Частный случай, когда t не входит явно в коэффициенты уравнения Якоби.
- 299. Геометрическое свойство траекторий.
- 300. Декартовы координаты в пространстве.
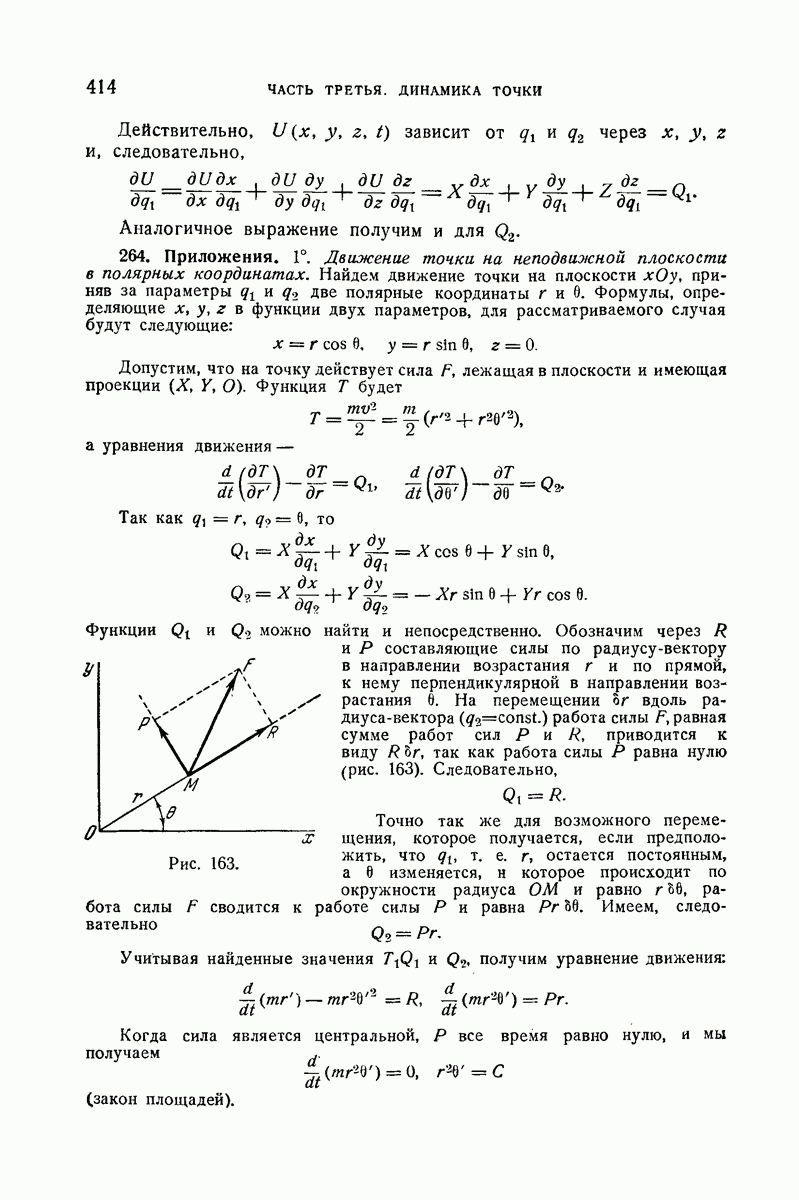
- III. Плоское движение. Движение по поверхности
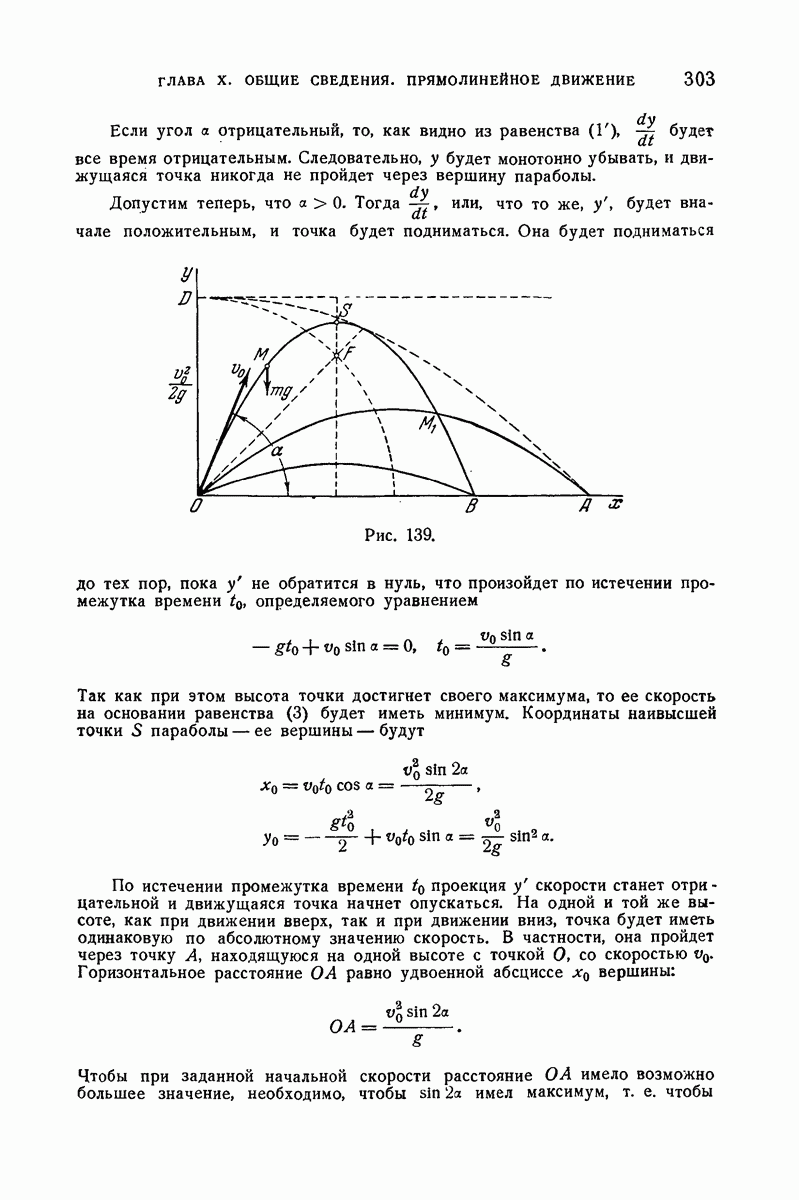
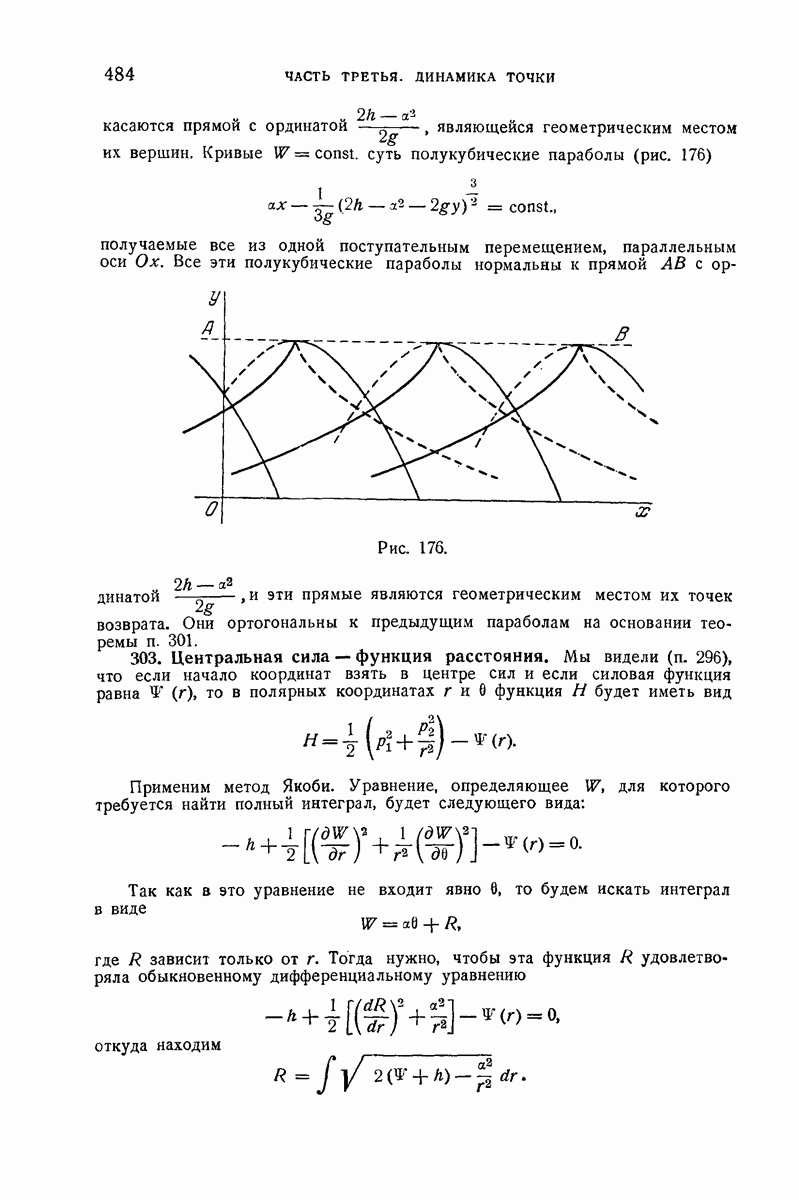
- 302. Параболическое движение тяжелой точки в пустоте.
- 303. Центральная сила — функция расстояния.
- 304. Уравнения движения планеты в форме Якоби.
- 305. Геодезические линии поверхностей Лиувилля. Приложение к эллипсоиду.
- IV. Движение в пространстве
- 306. Движение планеты в сферических координатах по Якоби
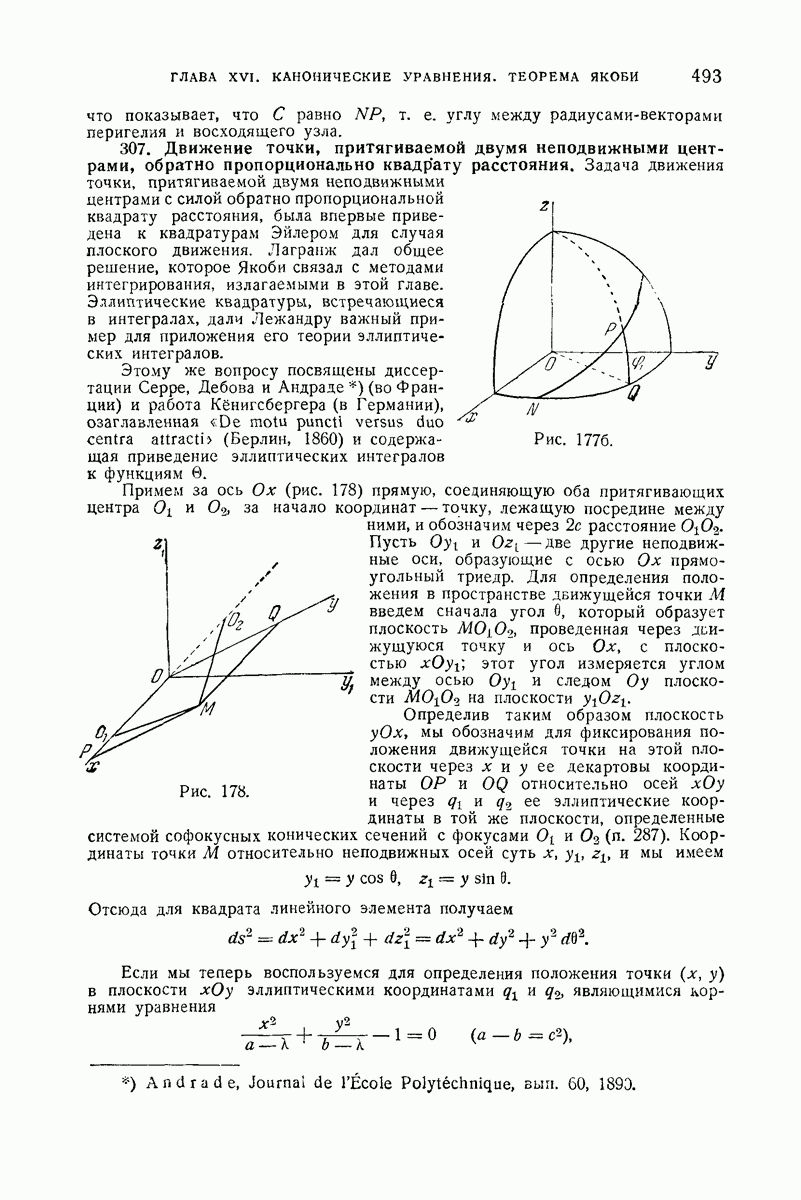
- 307. Движение точки, притягиваемой двумя неподвижными центрами, обратно пропорционально квадрату расстояния.
- 308. Эллиптические координаты в пространстве.
- V. Приложения к принципу наименьшего действия, к брахистохронам, к равновесию нитей
- 310. Точка на поверхности.
- 311. Параболическое движение.
- 312. Брахистохроны и фигуры равновесия нитей в случае силовой функции. Задача рефракции.