| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
153. Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами.
Наблюдения показывают, что первоначально, прямолинейный упругий стержень, к концам которого приложены две одинаковые и противоположно направленные силы Т, не изгибается до тех пор, пока значение Т не превысит некоторого предела; говорят, что тогда имеет место продольный изгиб. Когда Т меньше этого предела, единственно возможной фигурой равновесия является прямолинейная форма. Лишь при значениях Т превосходящих указанный предел, возможны изученные выше криволинейные фигуры равновесия. Найдем этот предел.
В рассматриваемом случае, так как ось стержня в естественном состоянии прямолинейна, то  и из формулы (1) для пары получаем
и из формулы (1) для пары получаем 

Эта пара обращается, следовательно, в нуль одновременно с кривизной. Но мы предположили, что к обоим концам  стержня приложены две силы Т, равные, противоположно направленные и не образующие пары, отсюда вытекает, что для обоих концов
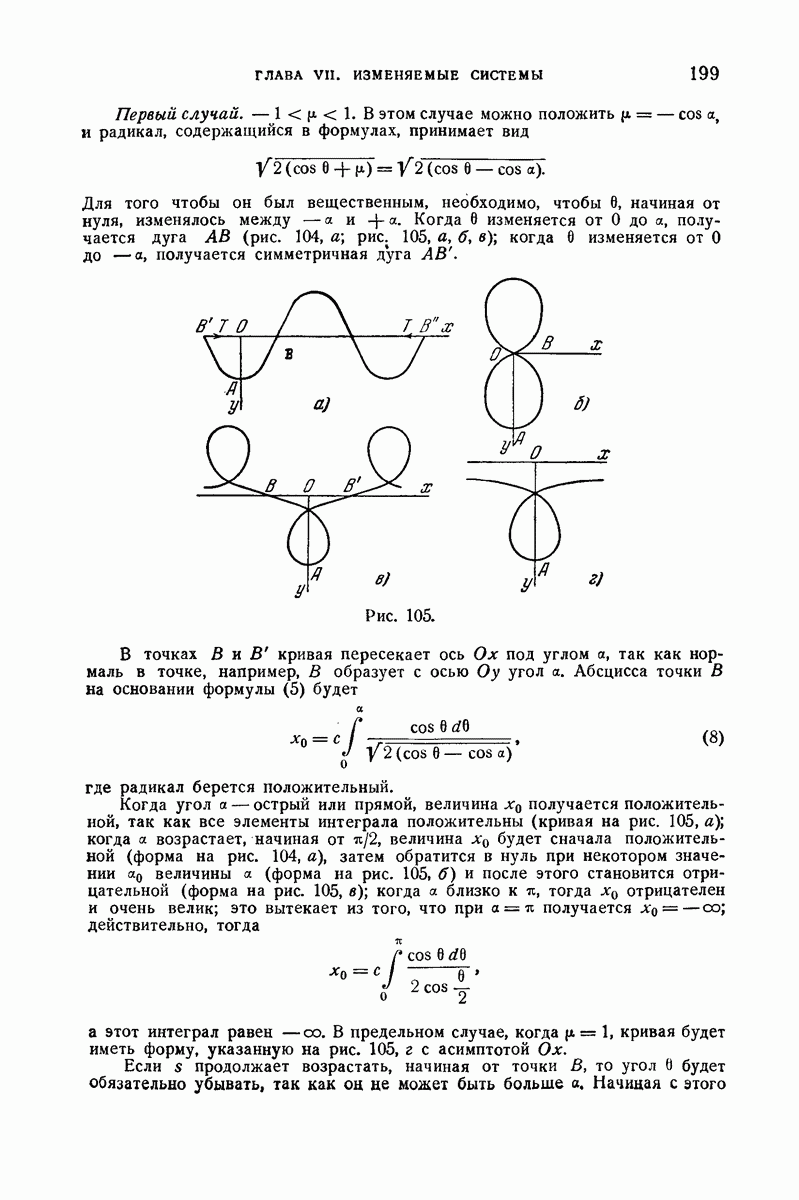
стержня приложены две силы Т, равные, противоположно направленные и не образующие пары, отсюда вытекает, что для обоих концов  следовательно, эти концы являются точками перегиба, как указано на рис. 105, а. Когда стержень очень мало отклоняется от первоначальной прямолинейной формы, величина а очень мала. Она равна нулю для прямолинейной формы. Допустим, что стержень может принять волнообразную фигуру равновесия, показанную на рис. 105, а, с
следовательно, эти концы являются точками перегиба, как указано на рис. 105, а. Когда стержень очень мало отклоняется от первоначальной прямолинейной формы, величина а очень мала. Она равна нулю для прямолинейной формы. Допустим, что стержень может принять волнообразную фигуру равновесия, показанную на рис. 105, а, с  волнами, и определим постоянную а, зная длину
волнами, и определим постоянную а, зная длину  стержня и сила Т на обоих концах В и
стержня и сила Т на обоих концах В и  Постоянная с будет тогда известна и равна
Постоянная с будет тогда известна и равна  Согласно выражению (4) для
Согласно выражению (4) для  дуга
дуга  имеет длину
имеет длину

Сделаем подстановку

тогда

Обозначим, для краткости,  и сделаем замену переменной
и сделаем замену переменной

Когда 0 изменяется от 0 до а, тогда и изменяется от 0 до 1 и мы имеем

где

Для всей длины  стержня, равной
стержня, равной  получаем
получаем

Это уравнение, в котором  неизвестно, определяет угол а. Для того чтобы фигура равновесия с
неизвестно, определяет угол а. Для того чтобы фигура равновесия с  волнами существовала, необходимо и достаточно, чтобы из этого уравнения получалось для
волнами существовала, необходимо и достаточно, чтобы из этого уравнения получалось для  значение, заключенное между 0 и 1. Но при
значение, заключенное между 0 и 1. Но при  имеем, согласно равенству (9),
имеем, согласно равенству (9),  при возрастании
при возрастании  интеграл К постоянно возрастает, так как возрастает подынтегральное выражение, и при
интеграл К постоянно возрастает, так как возрастает подынтегральное выражение, и при  интеграл К становится бесконечным. Таким образом, когда
интеграл К становится бесконечным. Таким образом, когда  изменяется от 0 до 1, интеграл К проходит один и только один раз через любое значение, больше чем
изменяется от 0 до 1, интеграл К проходит один и только один раз через любое значение, больше чем  Для того чтобы уравнение (10) имело для
Для того чтобы уравнение (10) имело для  решение, необходимо и достаточно, чтобы
решение, необходимо и достаточно, чтобы

Заменяя с его значением  находим
находим

Таким является условие существования фигуры равновесия с  волнами. Наименьшее значение нижнего предела для Т соответствует значению
волнами. Наименьшее значение нижнего предела для Т соответствует значению  Следовательно, для того чтобы существовала возможная фигура равновесия с одной волной, необходимо, чтобы
Следовательно, для того чтобы существовала возможная фигура равновесия с одной волной, необходимо, чтобы

Если давление Т меньше этого предела, то единственно возможной фигурой равновесия будет прямая линия.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
- ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
- II. Свободные векторы. Три координаты свободного вектора
- III. Скользящие векторы. Пять координат скользящего вектора
- 9. Теория моментов.
- 10. Аналитические выражения моментов вектора относительно осей координат.
- 11. Пять координат скользящего вектора.
- 12. Относительный момент двух векторов
- 13. Скользящие векторы, сходящиеся в одной точке. Результирующий вектор.
- 14. Произвольная система векторов. Главный вектор и главный момент.
- 15. Изменение главного вектора и главного момента; инварианты; центральная ось.
- 16. Сумма моментов относительно произвольной оси. Прямые нулевого момента.
- IV. Эквивалентные системы скользящих векторов. Элементарные операции. Приведение системы скользящих векторов
- 19. Элементарные операции.
- 20. Приведение к двум векторам.
- 21. Геометрическое истолкование инварианта LX+MY+NZ.
- 22. Приведение двух эквивалентных систем друг к другу.
- 23. Пары.
- 24. Приведение к вектору и паре.
- 25. Винт.
- 26. Частные случаи приведения.
- 28. Взаимный момент системы скользящих векторов.
- 29. Приложение общих теорем к случаю параллельных скользящих векторов.
- V. Связанные векторы; шесть координат связанного вектора; центр параллельных связанных векторов. Векторные производные
- 31. Центр системы параллельных связанных векторов.
- 32. Моменты параллельных связанных векторов относительно плоскости.
- 33. Векторные производные.
- VI. Полярные векторы. Аксиальные векторы. Скалярные величины
- VII. Другие геометрические образы, которые могут быть использованы в механике
- ГЛАВА II. КИНЕМАТИКА
- I. Кинематика точки
- 37. Движение точки.
- 38. Прямолинейное равномерное движение; скорость.
- 39. Произвольное прямолинейное движение; скорость.
- 40. Вектор скорости в криволинейном движении.
- 41. Вектор ускорения.
- 42. Касательное и нормальное ускорения (Гюйгенс).
- II. Поступательное движение и вращение неизменяемой системы
- 44. Вращение вокруг неподвижной оси. Угловая скорость. Геометрическое представление.
- III. Скорость в относительном движении. Сложение поступательных и вращательных движений. Скорости точек свободного тела
- 46. Сложение поступательных движений.
- 47. Совокупность двух вращений.
- 48. Произвольное число вращений.
- 49. Частные случаи.
- 50. Геометрические следствия.
- 51. Распределение скоростей в движущемся твердом теле.
- 52. Мгновенная винтовая ось. Касательное винтовое движение.
- 53. Величина скорости точки тела.
- 54. Непрерывное движение.
- 55. Твердое тело с неподвижной точкой.
- 56. Тело перемещается параллельно неподвижной плоскости.
- 57. Качение и верчение подвижной поверхности по неподвижной поверхности.
- IV. Ускорения. Теорема Кориолиса
- 59. Ускорение в относительном движении. Теорема Кориолиса.
- 60. Поступательное движение подвижных осей. Сложение движений.
- 61. Общие формулы для скорости и ускорения точки, отнесенной к подвижным осям.
- ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ. МАССА И СИЛА
- II. Единицы массы и силы; однородность
- 73. Технические единицы. Килограмм-сила.
- 74. Абсолютные единицы. Дина.
- 75. Статическое измерение сил.
- 76. Однородность.
- ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ
- 78. Аналитическое выражение элементарной работы.
- 79. Полная работа. Единица работы.
- 80. Сила зависит от времени или скорости.
- 81. Сила зависит только от положения движущейся точки.
- 82. Частный случай, когда сила зависит только от начального и конечного положений. Силовая функция. Потенциальная энергия.
- 83. Поверхности уровня.
- 84. Примеры.
- 85. Замечание о поверхностях уровня.
- 86. Мощность.
- II. Система точек
- 88. Примеры.
- ЧАСТЬ ВТОРАЯ. СТАТИКА
- ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ
- 90. Пример. Притяжения, пропорциональные расстояниям.
- 91. Точка, движущаяся без трения по неподвижной поверхности.
- 92. Точка, движущаяся без трения по неподвижной кривой.
- II. Системы материальных точек
- 94. Силы внутренние и силы внешние. Шесть необходимых условий равновесия.
- 96. Разделение произвольной системы на части. Необходимые условия равновесия.
- ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
- I. Приведение сил, приложенных к твердому телу. Равновесие
- 97. Приведение сил, приложенных к твердому телу. Равновесие.
- 98. Эквивалентные системы сил.
- 99. Частные случаи приведения.
- 100. Другая форма условий равновесия.
- II. Приложения. Силы в плоскости. Параллельные силы. Центр тяжести
- 102. Примеры.
- 103. Параллельные силы.
- 104. Центр тяжести.
- 105. Координаты центра тяжести.
- III. Приложения. Произвольные силы в пространстве
- 107. Условия, при которых силы, находящиеся в равновесии, могут быть направлены по трем, четырем, пяти, шести прямым.
- IV. Твердое тело, подчиненное связям
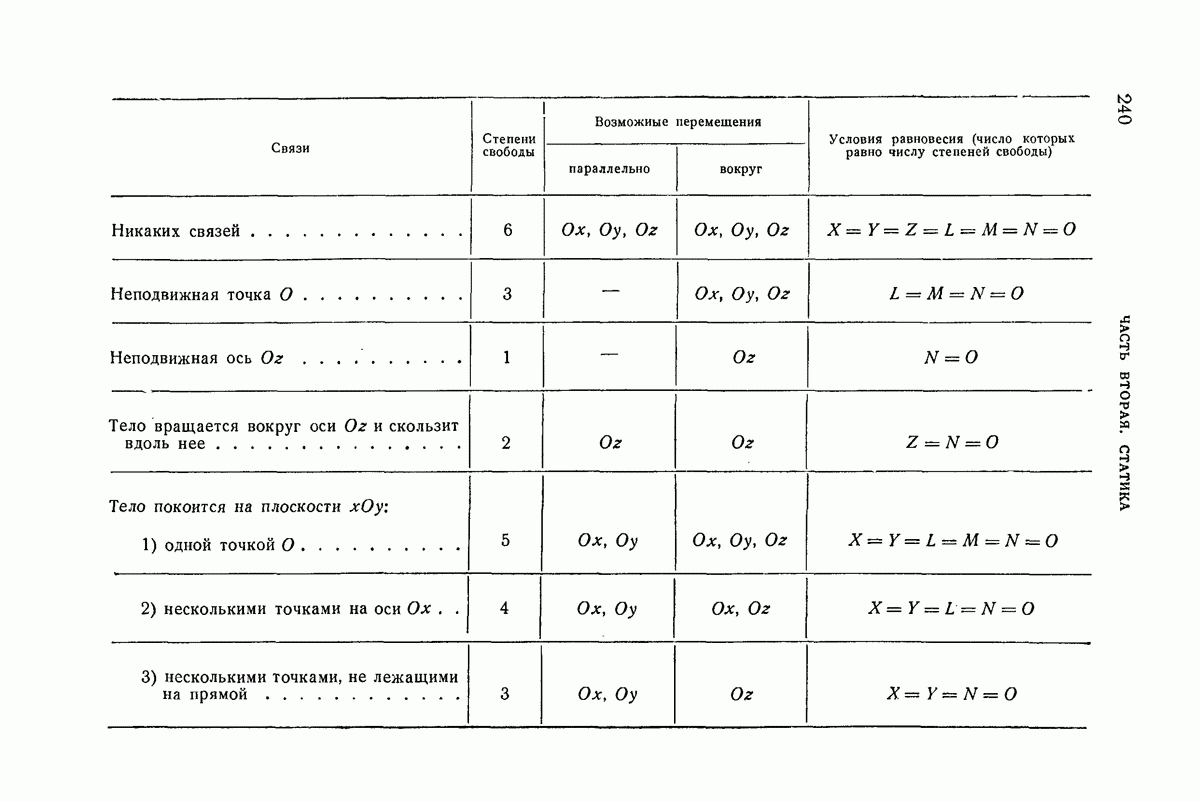
- 109. Тело с неподвижной точкой.
- 110. Тело, имеющее неподвижную ось.
- 111. Тело вращается вокруг оси и скользит вдоль нее.
- 112. Тело, опирающееся на неподвижную плоскость.
- 113. Несколько твердых тел.
- V. Некоторые формулы для вычисления центра тяжести
- ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
- I. Веревочный многоугольник
- 122. Натяжение.
- 123. Равновесие веревочного многоугольника. Многоугольник Вариньона.
- 124. Условия на концах.
- 125. Сходящиеся силы.
- 126. Параллельные силы.
- 127. Графические приложения теории веревочных многоугольников.
- 128. Кольца, скользящие на нити.
- 129. Фермы.
- II. Равновесие нитей
- 131. Общие теоремы.
- 132. Общие интегралы.
- 133. Определение постоянных, условия на концах.
- 134. Случай, когда сила не зависит от длины дуги.
- 135. Замечание о натяжении.
- 136. Естественные уравнения равновесия нити.
- 137. Формула, определяющая натяжение, когда существует силовая функция.
- 138. Параллельные силы.
- 139. Цепная линия.
- 140. Определение постоянных.
- 141. Центральные силы.
- 142. Пример существования бесчисленного множества положений равновесия.
- 143. Равновесие нити на поверхности.
- 144. Примеры.
- 145. Естественные уравнения равновесия нити на поверхности.
- III. Исследование одного определенного интеграла
- 147. Формула Тэта и Томсона.
- 148. Примеры.
- 149. Та же задача на поверхности.
- 150. Рефракция.
- IV. Плоские эластики
- 152. Ось стержня была первоначально дугой окружности.
- 153. Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами.
- 154. Стержень, изгибаемый действующим в одной плоскости постоянным нормальным давлением.
- ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
- I. Формулировка и доказательство принципа в случае связей, выражающихся равенствами
- 157. Формулировка принципа.
- 158. Свободная точка.
- 159. Точка на поверхности.
- 160. Точка на кривой.
- 161. Свободное твердое тело.
- 162. Лемма.
- 163. Сочетания предыдущих связей.
- 164. Общее определение идеальных связей.
- 165. Доказательство принципа.
- 166. Замечание о работе силы.
- 167. О связях, осуществляемых при помощи тел, не имеющих массы.
- II. Первые примеры. Системы с полными связями. Простые машины
- III. Общие условия равновесия, выводимые из принципа возможных скоростей
- 172. Голономные системы; координаты голономной системы.
- 173. Частный случай, когда выражение возможной работы есть полный дифференциал.
- 174. Приложения. Тяжелые системы.
- 175. Принцип Торричелли.
- IV. Множители Лагранжа
- 178. Случай неголономной системы.
- 179. Приложение принципа возможных скоростей к равновесию нитей.
- V. Общие теоремы, выводимые из принципа возможных скоростей
- VI Неудерживающие связи
- 187. Связи, выражаемые неравенствами в конечной форме.
- ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ
- 189. Трение скольжения.
- 190. Законы трения скольжения в состоянии покоя.
- 191. Равновесие тел с трением.
- 192. Тяжелое тело, опирающееся на плоскость в нескольких точках и находящееся под действием только одной силы F.
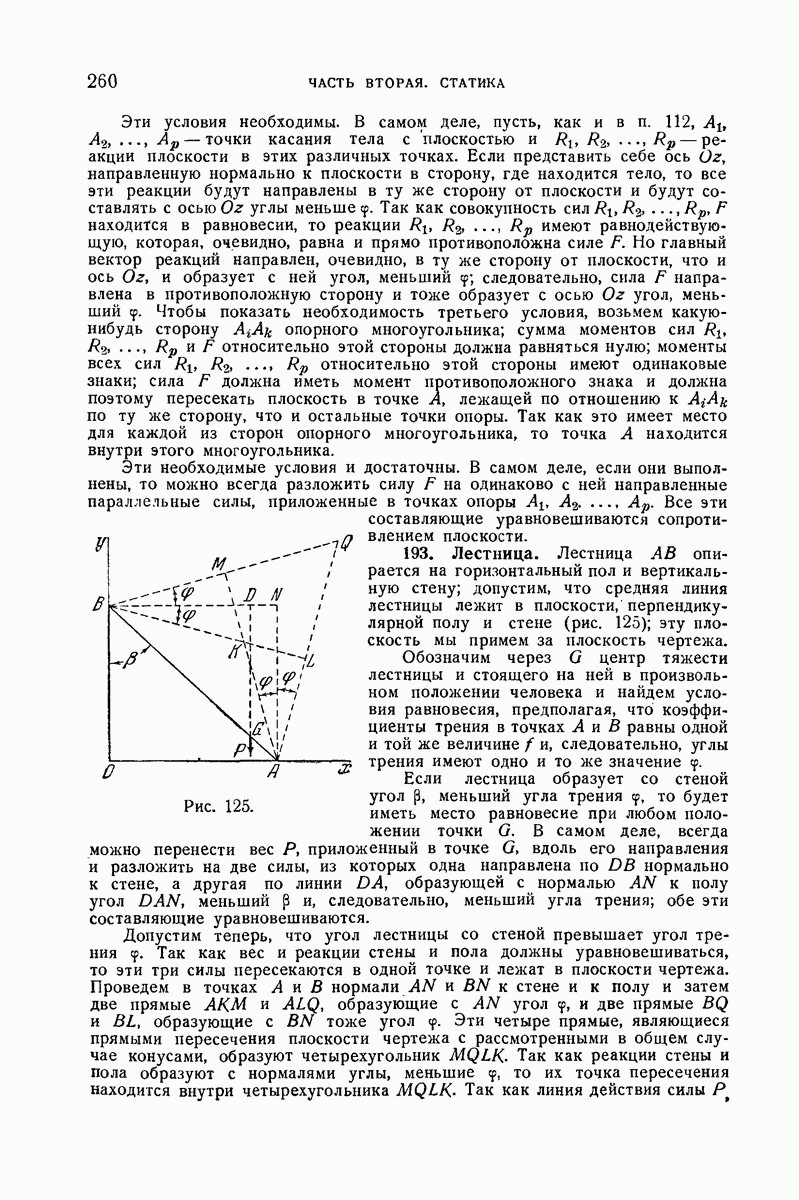
- 193. Лестница.
- 194. Веревка, навернутая на поперечное сечение цилиндра.
- 195. Трение скольжения при движении.
- 196. Трение качения в начале и во время движения.
- 197. Трение верчения.
- ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
- ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. ДВИЖЕНИЕ СНАРЯДОВ
- 199. Первые интегралы.
- 200. Естественные уравнения (Эйлер).
- 201. Количество движения.
- 202. Теорема о проекции количества движения.
- 203. Теорема о моменте количества движения. Закон площадей.
- 204. Геометрическая интерпретация двух предыдущих теорем.
- 205. Теорема кинетической энергии.
- 206. Примеры.
- 207. Замечание к интегралу кинетической энергии.
- 208. Устойчивость равновесия свободной материальной точки. Доказательство Лежен-Дирихле.
- II. Прямолинейное движение
- 210. Уравнение прямолинейного движения. Простые случаи интегрируемости.
- 211. Приложение к движениям, происходящим под действием силы зависящей только от положения.
- 212. Движения под действием силы, зависящей только от скорости.
- 213. Прямолинейное таутохронное движение.
- 214. Дан закон прямолинейного движения, найти силу.
- III. Криволинейное движение. Тяжелая точка в пустоте и в сопротивляющейся среде. Электрическая частица
- 217. Движение тяжелой точки в пустоте.
- 218. Определение параллельной силы по заданной траектории.
- 219. Криволинейное движение тяжелого тела в сопротивляющейся среде.
- 220. Движение легкого вращающегося шара в воздухе.
- 221. Движение наэлектризованной частицы в наложенных друг на друга электрическом и магнитном полях.
- ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ЭЛЛИПТИЧЕСКОЕ ДВИЖЕНИЕ ПЛАНЕТ
- 223. Сила есть функция только расстояния.
- 224. Сила вида …
- 225. Обратная задача. Определение центральной силы, когда задана траектория.
- II. Движение планет
- 228. Кометы.
- 229. Спутники.
- 230. Всемирное притяжение.
- 231. Двойные звезды.
- 232. Задача Бертрана.
- 233. Краткие указания по поводу некоторых других задач.
- III. Элементарные сведения из небесной механики
- 235. Задача двух тел.
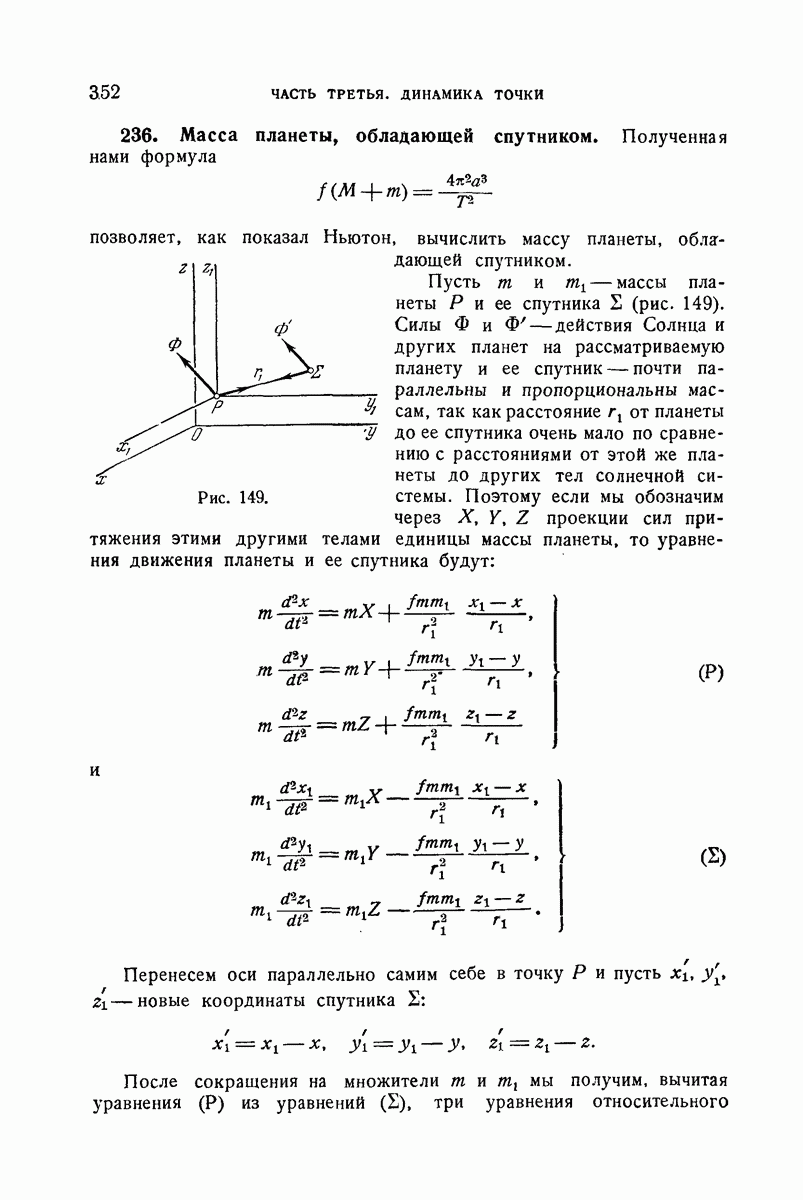
- 236. Масса планеты, обладающей спутником.
- 237. Определение времени в эллиптическом движении.
- 238. Геометрический метод.
- 239. Аналитические преобразования.
- 240. Элементы эллиптического движения.
- ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ КРИВОЙ
- 245. Устойчивость равновесия.
- 246. Движение тяжелой точки по неподвижной кривой.
- 247. Нормальная реакция. Естественные уравнения.
- 248. Математический маятник.
- 249. Движение математического маятника в сопротивляющейся среде.
- 250. Циклоидальный маятник.
- 251. Движение тяжелой точки по кривой, расположенной в вертикальной плоскости, при действии трения и сопротивления среды.
- 252. Таутохроны.
- 253. Приложения.
- 254. Брахистохрона для силы тяжести.
- 255. Брахистохроны в общем случае.
- 256. Приложение теорем Томсона и Тэта к брахистохронам.
- 257. Брахистохроны на заданной поверхности.
- II. Движение материальной точки на изменяемой кривой
- ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- II. Случай неподвижной поверхности
- 266. Вывод уравнения кинетической энергии из уравнений Лагранжа.
- 267. Устойчивость равновесия в случае существования силовой функции U.
- 268. Нормальная реакция.
- 269. Естественные уравнения и нормальная реакция.
- 270. Геодезические линии.
- 271. Применение уравнений Лагранжа.
- 272. Бесконечно малые колебания тяжелой точки около наинизшей точки поверхности.
- III. Движение на поверхности вращения
- 274. Формула Клеро.
- 275. Упражнение. Геодезические линии поверхности, образованной вращением равносторонней гиперболы вокруг своей асимптоты.
- 276. Движение тяжелой точки на поверхности врадцения, ось которой Oz вертикальна.
- 277. Сферический маятник.
- 278. Вычисление нормальной реакции.
- 279. Интегрирование в эллиптических функциях.
- 280. Теорема Гринхилла.
- 281. Бесконечно малые колебания.
- ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
- 283. Интеграл кинетической энергии.
- 284. Приложение.
- 285. Сферические координаты.
- 286. Эллиптические координаты в пространстве.
- 287. Эллиптические координаты в плоскости ху.
- ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- 289. Замечание о силе инерции.
- 290. Принцип наименьшего действия.
- ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ. ПРИЛОЖЕНИЯ
- I. Канонические уравнения. Теорема Якоби
- II. Теорема Якоби
- 298. Частный случай, когда t не входит явно в коэффициенты уравнения Якоби.
- 299. Геометрическое свойство траекторий.
- 300. Декартовы координаты в пространстве.
- III. Плоское движение. Движение по поверхности
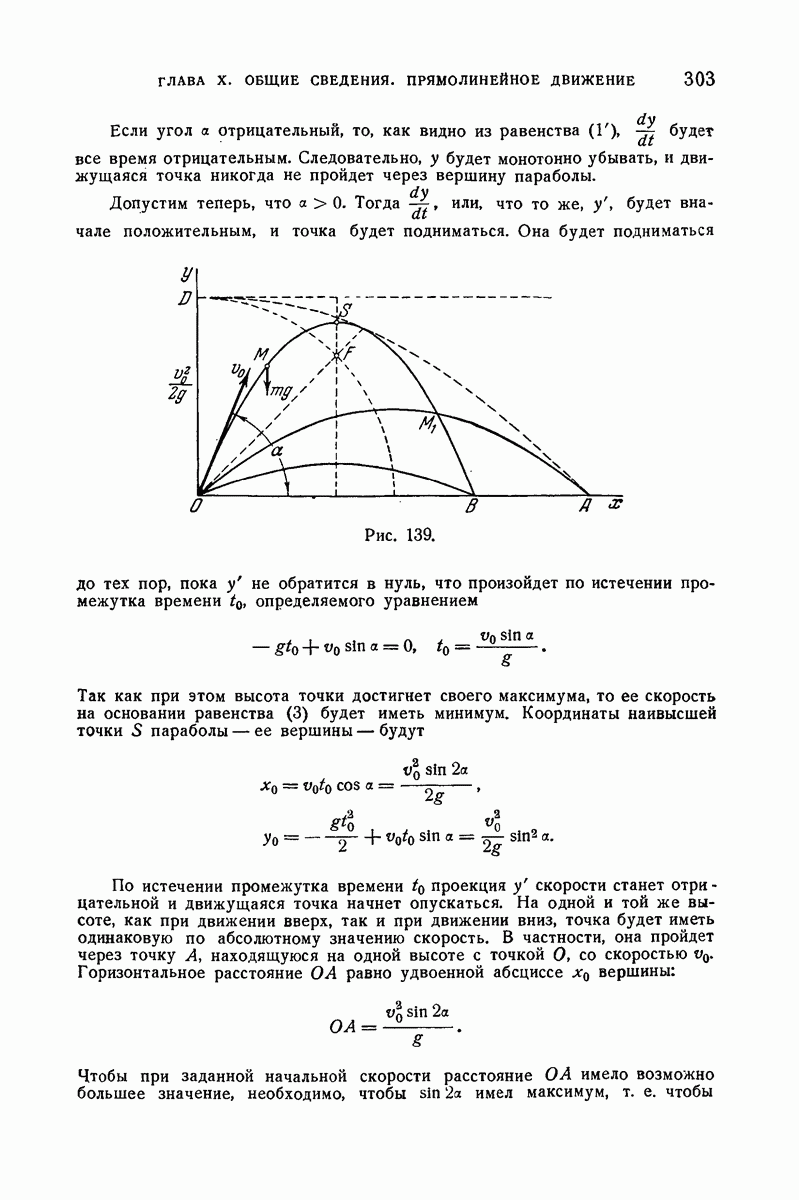
- 302. Параболическое движение тяжелой точки в пустоте.
- 303. Центральная сила — функция расстояния.
- 304. Уравнения движения планеты в форме Якоби.
- 305. Геодезические линии поверхностей Лиувилля. Приложение к эллипсоиду.
- IV. Движение в пространстве
- 306. Движение планеты в сферических координатах по Якоби
- 307. Движение точки, притягиваемой двумя неподвижными центрами, обратно пропорционально квадрату расстояния.
- 308. Эллиптические координаты в пространстве.
- V. Приложения к принципу наименьшего действия, к брахистохронам, к равновесию нитей
- 310. Точка на поверхности.
- 311. Параболическое движение.
- 312. Брахистохроны и фигуры равновесия нитей в случае силовой функции. Задача рефракции.