| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
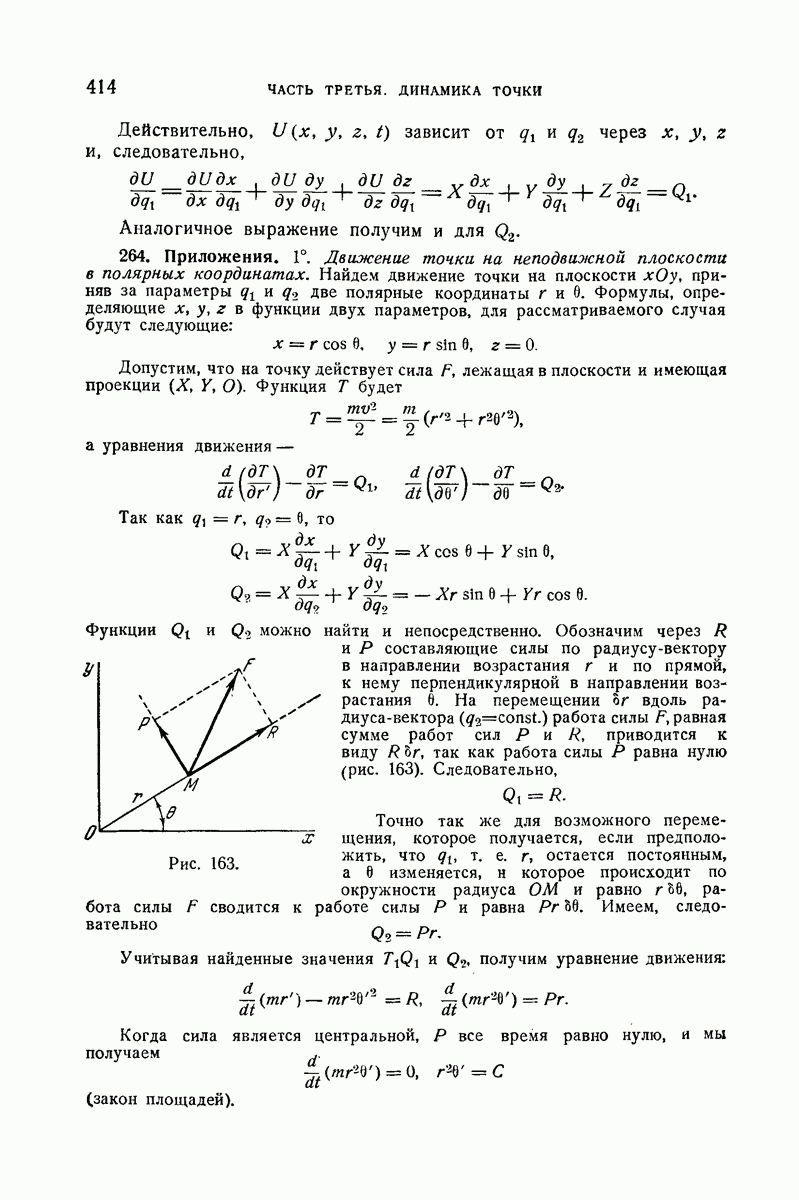
246. Движение тяжелой точки по неподвижной кривой.
Возьмем три прямоугольные оси, причем ось  направим вертикально верх. Проекции силы равны (рис. 155)
направим вертикально верх. Проекции силы равны (рис. 155)

элементарная работа силы тяжести есть  и уравнение
и уравнение
кинетической энергии будет

что можно написать в виде

где обозначено

Рассмотрим плоскость II, уравнение которой  . Расстояние
. Расстояние  от движущейся точки до этой плоскости равно
от движущейся точки до этой плоскости равно  так что скорость определяется формулой
так что скорость определяется формулой

Отсюда видно, что численное значение скорости будет такое, как при падении точки по вертикали из Р в М без начальной скорости.
Допустим, что рассматриваемая кривая замкнута. Могут представиться два случая в зависимости от того, будет ли плоскость П пересекать эту кривую или нет. Каково бы ни было начальное положение  точки, ей всегда можно сообщить такую достаточно большую начальную скорость
точки, ей всегда можно сообщить такую достаточно большую начальную скорость  чтобы плоскость П была расположена сколь угодно высоко, так как
чтобы плоскость П была расположена сколь угодно высоко, так как

Допустим, что  настолько велико, что плоскость П находится над кривой. Тогда скорость никогда не обратится в нуль и движущаяся точка будет бесконечное число раз оборачиваться по своей траектории. Движение будет периодическим, наибольшая скорость будет в наинизшей точке, а наименьшая — в наивысшей.
настолько велико, что плоскость П находится над кривой. Тогда скорость никогда не обратится в нуль и движущаяся точка будет бесконечное число раз оборачиваться по своей траектории. Движение будет периодическим, наибольшая скорость будет в наинизшей точке, а наименьшая — в наивысшей.
Допустим теперь, что плоскость П пересекает кривую. Пусть А и А — две последовательные точки пересечения. Допустим, что точка начинает движение из наинизшего положения  дуги
дуги  в сторону А. Легко видеть, что движущаяся точка подойдет к положению А сколь угодно близко; в самом деле, скорость между
в сторону А. Легко видеть, что движущаяся точка подойдет к положению А сколь угодно близко; в самом деле, скорость между  и В будет все время больше, чем
и В будет все время больше, чем  где
где  — расстояние от точки В до плоскости П, и точка обязательно придет в положение В за конечный промежуток времени. Если касательная в А не горизонтальна, то движущаяся точка достигнет этого положения. Действительно,
— расстояние от точки В до плоскости П, и точка обязательно придет в положение В за конечный промежуток времени. Если касательная в А не горизонтальна, то движущаяся точка достигнет этого положения. Действительно,

откуда

Будем отсчитывать дуги от положения  а время от начального момента. Так как
а время от начального момента. Так как  должно возрастать вместе с
должно возрастать вместе с  то в написанном уравнении нужно взять знак плюс, и мы получим
то в написанном уравнении нужно взять знак плюс, и мы получим

Если касательная в точке А не горизонтальна, то будет оставаться конечным при  и подынтегральное выражение будет обращаться в бесконечность порядка 1/2. Следовательно, этот интеграл остается конечным, когда
и подынтегральное выражение будет обращаться в бесконечность порядка 1/2. Следовательно, этот интеграл остается конечным, когда  стремится к а. Время Т, нужное для достижения точки А, будет тогда определяться формулой
стремится к а. Время Т, нужное для достижения точки А, будет тогда определяться формулой

После достижения положения А движущаяся точка будет возвращаться к  куда она придет со скоростью
куда она придет со скоростью  и дальше будет двигаться по дуге
и дальше будет двигаться по дуге  аналогичным образом в течение времени
аналогичным образом в течение времени  если касательная в точке А не горизонтальна. Движение будет, следовательно, колебанием между точками А и А, и продолжительность каждого простого колебания будет
если касательная в точке А не горизонтальна. Движение будет, следовательно, колебанием между точками А и А, и продолжительность каждого простого колебания будет
Можно указать два предела, между которыми должно заключаться Т; эти два предела будут тем ближе друг к другу, чем меньше дуга  Если положить
Если положить

то, как известно, будет

где  — радиус кривизны и у — косинус угла, который образует этот радиус кривизны с осью
— радиус кривизны и у — косинус угла, который образует этот радиус кривизны с осью  этот косинус положителен, так как угол острый. Пусть
этот косинус положителен, так как угол острый. Пусть  и К—пределы для
и К—пределы для  на рассматриваемой дуге; тогда между точками
на рассматриваемой дуге; тогда между точками  и А будет
и А будет

откуда, интегрируя, заключаем, что

так как эта функция, обращающаяся в нуль при  согласно предыдущему неравенству, монотонно убывает. Вследствие этого монотонно убывающей будет и первообразная функция
согласно предыдущему неравенству, монотонно убывает. Вследствие этого монотонно убывающей будет и первообразная функция  Написав,
Написав,
что она больше своего конечного значения, получим

где  — длина дуги
— длина дуги  Заменяя в выражении для Т величину
Заменяя в выражении для Т величину  правой частью этого неравенства, получим
правой частью этого неравенства, получим

Точно так же, исходя из неравенства  найдем
найдем

Если уменьшать начальную скорость таким образом, чтобы плоскость П приближалась к точке  то обе величины
то обе величины  будут одновременно стремиться к одному и тому же пределу, а именно, к значению
будут одновременно стремиться к одному и тому же пределу, а именно, к значению  в наинизшей точке, которое мы отметим индексом нуль. Поэтому, когда колебание будет иметь бесконечно малую амплитуду, продолжительность одного простого полуразмаха будет равна
в наинизшей точке, которое мы отметим индексом нуль. Поэтому, когда колебание будет иметь бесконечно малую амплитуду, продолжительность одного простого полуразмаха будет равна  а продолжительность простого размаха будет равна
а продолжительность простого размаха будет равна  если для части
если для части  траектории величина
траектории величина  имеет
имеет  тот же предел, что и для части
тот же предел, что и для части  . В частности, если траектория является окружностью радиуса
. В частности, если траектория является окружностью радиуса  в вертикальной плоскости, то получится известное выражение для продолжительности бесконечно малого размаха
в вертикальной плоскости, то получится известное выражение для продолжительности бесконечно малого размаха 
Вернемся теперь к колебаниям конечной амплитуды и рассмотрим случай, когда касательная в точке А горизонтальна. Вспомним формулу, определяющую время:

Когда  стремится к а, тогда
стремится к а, тогда  стремится к длине
стремится к длине  дуги
дуги  а стоящие под знаком интеграла выражения
а стоящие под знаком интеграла выражения  и неограниченно возрастают. Приняв
и неограниченно возрастают. Приняв  за независимую переменную, получим
за независимую переменную, получим

Пусть X — порядок малости величины  относительно
относительно  вблизи
вблизи  Тогда подынтегральное выражение будет обращаться в бесконечность порядка
Тогда подынтегральное выражение будет обращаться в бесконечность порядка  относительно
относительно  Если
Если  то интеграл, определяющий
то интеграл, определяющий  будет неограниченно возрастать; если, напротив,
будет неограниченно возрастать; если, напротив,  то интеграл останется конечным. Первый случай представится для обыкновенной точки, для которой
то интеграл останется конечным. Первый случай представится для обыкновенной точки, для которой  в этом можно убедиться, рассматривая
в этом можно убедиться, рассматривая  как функцию от
как функцию от  и разлагая ее по формуле Тэйлора вблизи
и разлагая ее по формуле Тэйлора вблизи  и замечая, что
и замечая, что  обращается, по предположению, в нуль при
обращается, по предположению, в нуль при  Второй случай может представиться для точки возврата, для которой в общем случае
Второй случай может представиться для точки возврата, для которой в общем случае  Если, следовательно, А является обыкновенной точкой с горизонтальной касательной, то движущаяся точка будет неограниченно приближаться к этому положению, никогда его не достигая. Если А является точкой возврата, то движущаяся точка может достигнуть точки возврата А со скоростью, равной нулю, после чего она остановится в этом положении равновесия. Такой пример мы найдем в упражнении 5.
Если, следовательно, А является обыкновенной точкой с горизонтальной касательной, то движущаяся точка будет неограниченно приближаться к этому положению, никогда его не достигая. Если А является точкой возврата, то движущаяся точка может достигнуть точки возврата А со скоростью, равной нулю, после чего она остановится в этом положении равновесия. Такой пример мы найдем в упражнении 5.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
- ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
- II. Свободные векторы. Три координаты свободного вектора
- III. Скользящие векторы. Пять координат скользящего вектора
- 9. Теория моментов.
- 10. Аналитические выражения моментов вектора относительно осей координат.
- 11. Пять координат скользящего вектора.
- 12. Относительный момент двух векторов
- 13. Скользящие векторы, сходящиеся в одной точке. Результирующий вектор.
- 14. Произвольная система векторов. Главный вектор и главный момент.
- 15. Изменение главного вектора и главного момента; инварианты; центральная ось.
- 16. Сумма моментов относительно произвольной оси. Прямые нулевого момента.
- IV. Эквивалентные системы скользящих векторов. Элементарные операции. Приведение системы скользящих векторов
- 19. Элементарные операции.
- 20. Приведение к двум векторам.
- 21. Геометрическое истолкование инварианта LX+MY+NZ.
- 22. Приведение двух эквивалентных систем друг к другу.
- 23. Пары.
- 24. Приведение к вектору и паре.
- 25. Винт.
- 26. Частные случаи приведения.
- 28. Взаимный момент системы скользящих векторов.
- 29. Приложение общих теорем к случаю параллельных скользящих векторов.
- V. Связанные векторы; шесть координат связанного вектора; центр параллельных связанных векторов. Векторные производные
- 31. Центр системы параллельных связанных векторов.
- 32. Моменты параллельных связанных векторов относительно плоскости.
- 33. Векторные производные.
- VI. Полярные векторы. Аксиальные векторы. Скалярные величины
- VII. Другие геометрические образы, которые могут быть использованы в механике
- ГЛАВА II. КИНЕМАТИКА
- I. Кинематика точки
- 37. Движение точки.
- 38. Прямолинейное равномерное движение; скорость.
- 39. Произвольное прямолинейное движение; скорость.
- 40. Вектор скорости в криволинейном движении.
- 41. Вектор ускорения.
- 42. Касательное и нормальное ускорения (Гюйгенс).
- II. Поступательное движение и вращение неизменяемой системы
- 44. Вращение вокруг неподвижной оси. Угловая скорость. Геометрическое представление.
- III. Скорость в относительном движении. Сложение поступательных и вращательных движений. Скорости точек свободного тела
- 46. Сложение поступательных движений.
- 47. Совокупность двух вращений.
- 48. Произвольное число вращений.
- 49. Частные случаи.
- 50. Геометрические следствия.
- 51. Распределение скоростей в движущемся твердом теле.
- 52. Мгновенная винтовая ось. Касательное винтовое движение.
- 53. Величина скорости точки тела.
- 54. Непрерывное движение.
- 55. Твердое тело с неподвижной точкой.
- 56. Тело перемещается параллельно неподвижной плоскости.
- 57. Качение и верчение подвижной поверхности по неподвижной поверхности.
- IV. Ускорения. Теорема Кориолиса
- 59. Ускорение в относительном движении. Теорема Кориолиса.
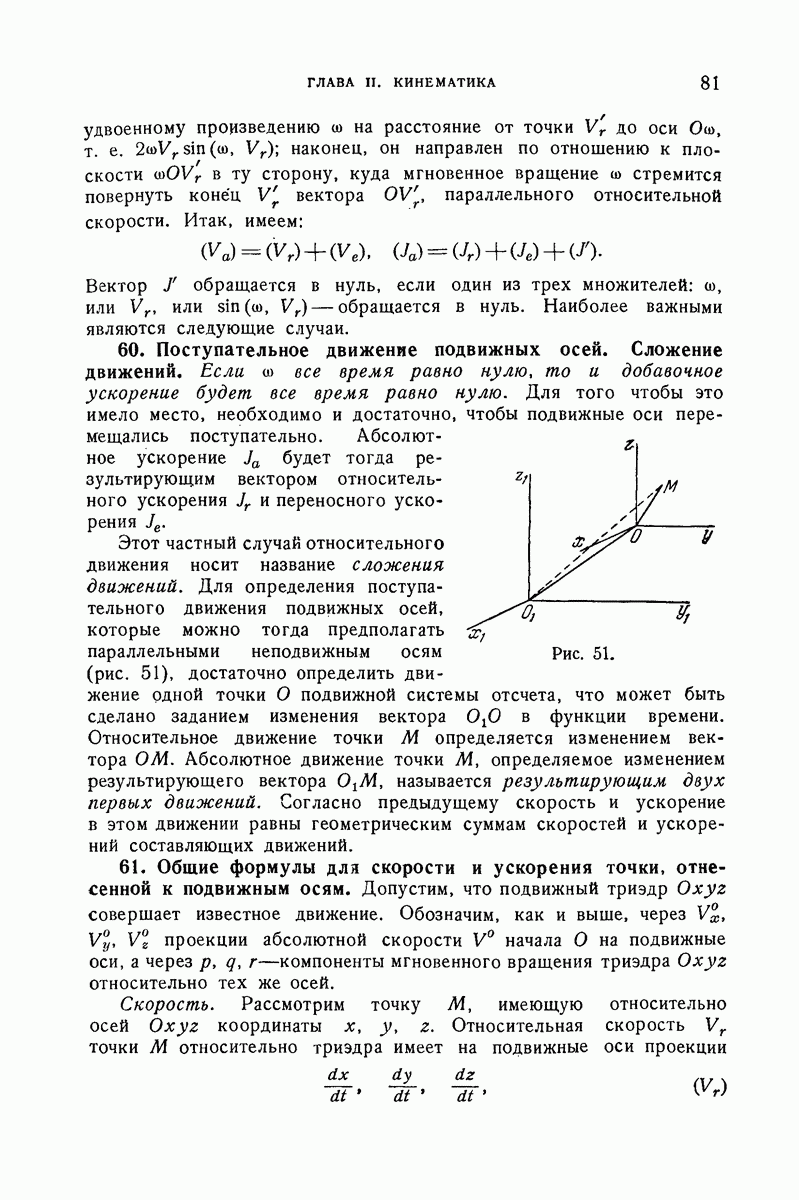
- 60. Поступательное движение подвижных осей. Сложение движений.
- 61. Общие формулы для скорости и ускорения точки, отнесенной к подвижным осям.
- ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ. МАССА И СИЛА
- II. Единицы массы и силы; однородность
- 73. Технические единицы. Килограмм-сила.
- 74. Абсолютные единицы. Дина.
- 75. Статическое измерение сил.
- 76. Однородность.
- ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ
- 78. Аналитическое выражение элементарной работы.
- 79. Полная работа. Единица работы.
- 80. Сила зависит от времени или скорости.
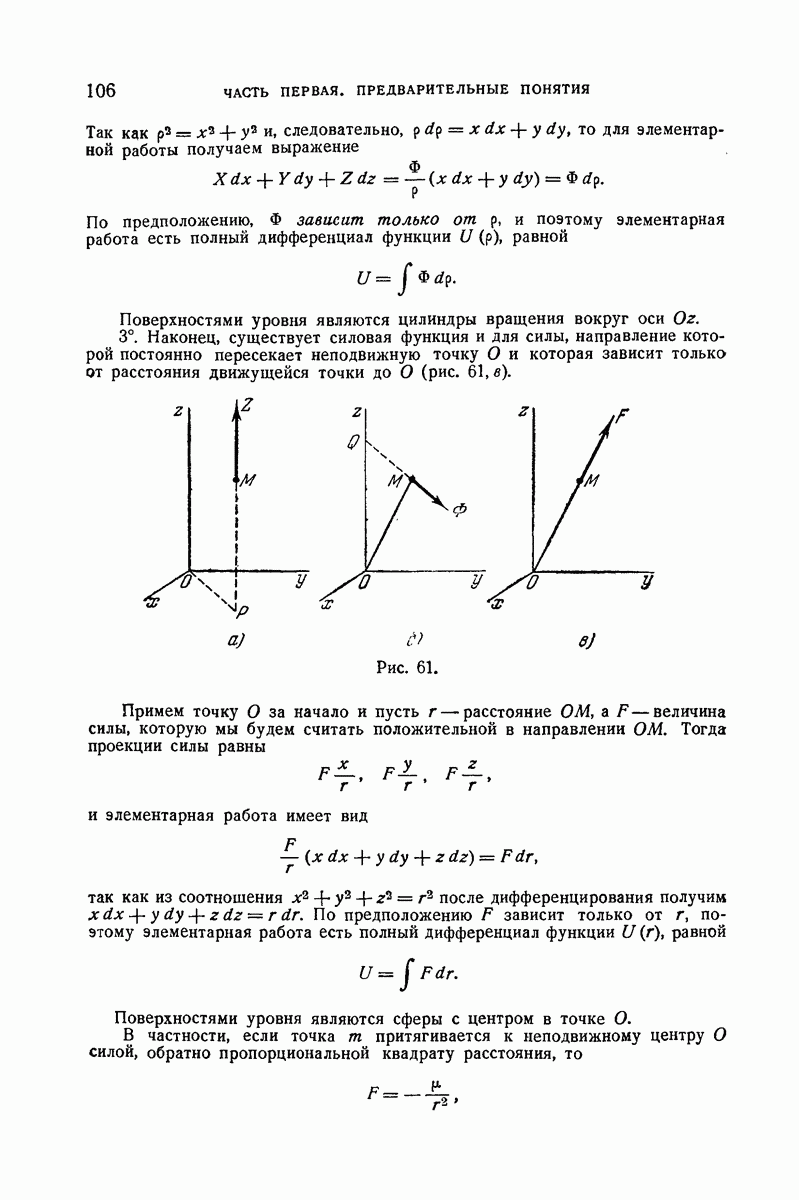
- 81. Сила зависит только от положения движущейся точки.
- 82. Частный случай, когда сила зависит только от начального и конечного положений. Силовая функция. Потенциальная энергия.
- 83. Поверхности уровня.
- 84. Примеры.
- 85. Замечание о поверхностях уровня.
- 86. Мощность.
- II. Система точек
- 88. Примеры.
- ЧАСТЬ ВТОРАЯ. СТАТИКА
- ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ
- 90. Пример. Притяжения, пропорциональные расстояниям.
- 91. Точка, движущаяся без трения по неподвижной поверхности.
- 92. Точка, движущаяся без трения по неподвижной кривой.
- II. Системы материальных точек
- 94. Силы внутренние и силы внешние. Шесть необходимых условий равновесия.
- 96. Разделение произвольной системы на части. Необходимые условия равновесия.
- ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
- I. Приведение сил, приложенных к твердому телу. Равновесие
- 97. Приведение сил, приложенных к твердому телу. Равновесие.
- 98. Эквивалентные системы сил.
- 99. Частные случаи приведения.
- 100. Другая форма условий равновесия.
- II. Приложения. Силы в плоскости. Параллельные силы. Центр тяжести
- 102. Примеры.
- 103. Параллельные силы.
- 104. Центр тяжести.
- 105. Координаты центра тяжести.
- III. Приложения. Произвольные силы в пространстве
- 107. Условия, при которых силы, находящиеся в равновесии, могут быть направлены по трем, четырем, пяти, шести прямым.
- IV. Твердое тело, подчиненное связям
- 109. Тело с неподвижной точкой.
- 110. Тело, имеющее неподвижную ось.
- 111. Тело вращается вокруг оси и скользит вдоль нее.
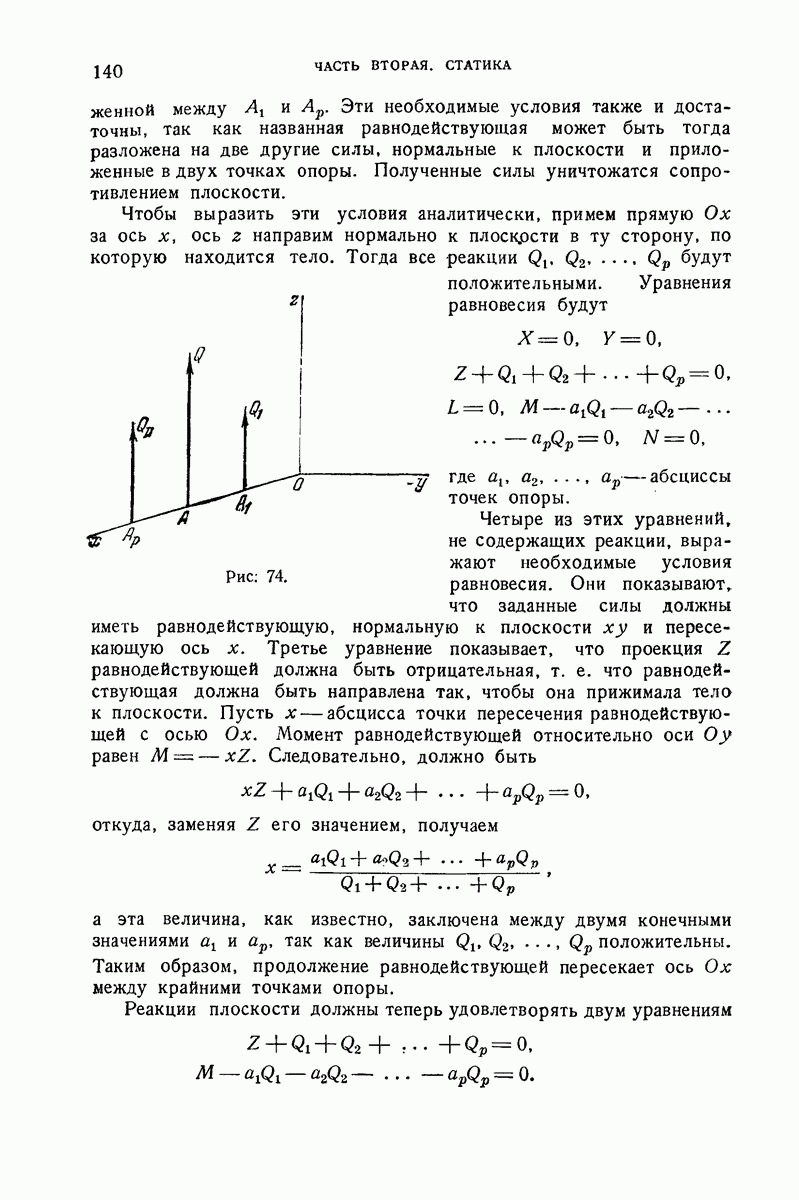
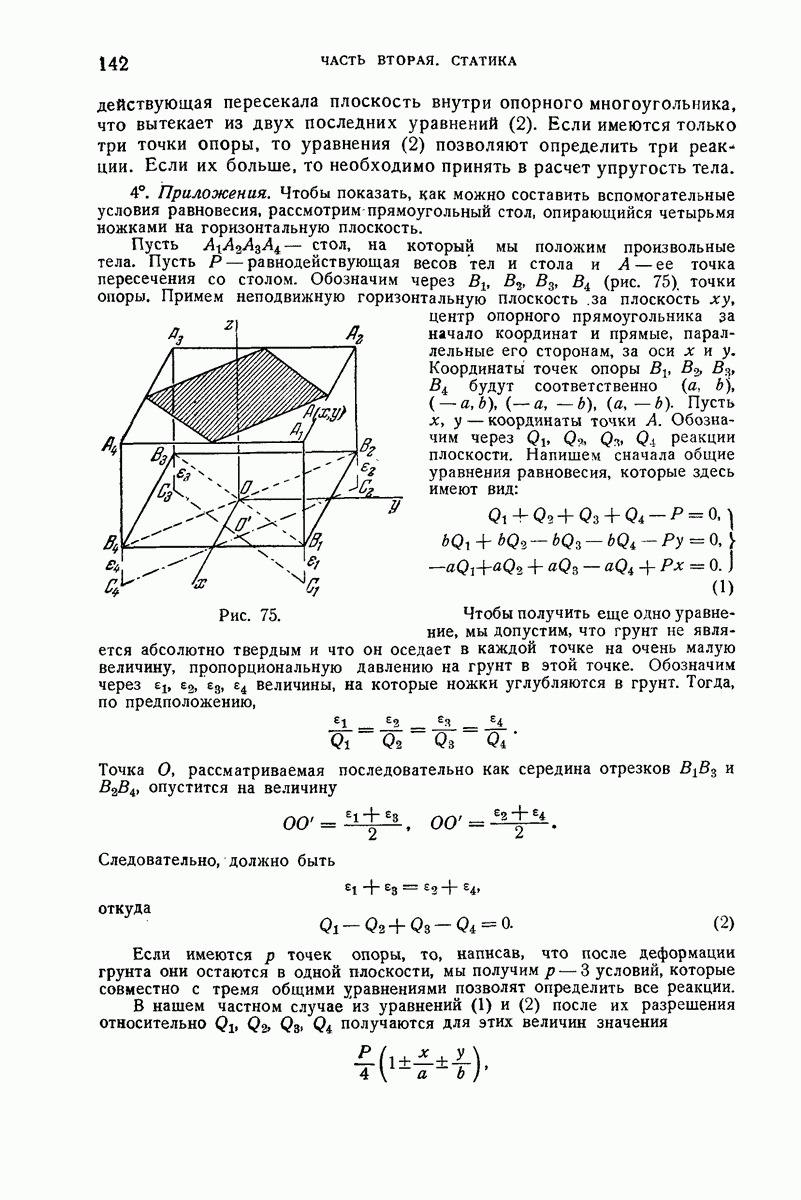
- 112. Тело, опирающееся на неподвижную плоскость.
- 113. Несколько твердых тел.
- V. Некоторые формулы для вычисления центра тяжести
- ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
- I. Веревочный многоугольник
- 122. Натяжение.
- 123. Равновесие веревочного многоугольника. Многоугольник Вариньона.
- 124. Условия на концах.
- 125. Сходящиеся силы.
- 126. Параллельные силы.
- 127. Графические приложения теории веревочных многоугольников.
- 128. Кольца, скользящие на нити.
- 129. Фермы.
- II. Равновесие нитей
- 131. Общие теоремы.
- 132. Общие интегралы.
- 133. Определение постоянных, условия на концах.
- 134. Случай, когда сила не зависит от длины дуги.
- 135. Замечание о натяжении.
- 136. Естественные уравнения равновесия нити.
- 137. Формула, определяющая натяжение, когда существует силовая функция.
- 138. Параллельные силы.
- 139. Цепная линия.
- 140. Определение постоянных.
- 141. Центральные силы.
- 142. Пример существования бесчисленного множества положений равновесия.
- 143. Равновесие нити на поверхности.
- 144. Примеры.
- 145. Естественные уравнения равновесия нити на поверхности.
- III. Исследование одного определенного интеграла
- 147. Формула Тэта и Томсона.
- 148. Примеры.
- 149. Та же задача на поверхности.
- 150. Рефракция.
- IV. Плоские эластики
- 152. Ось стержня была первоначально дугой окружности.
- 153. Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами.
- 154. Стержень, изгибаемый действующим в одной плоскости постоянным нормальным давлением.
- ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
- I. Формулировка и доказательство принципа в случае связей, выражающихся равенствами
- 157. Формулировка принципа.
- 158. Свободная точка.
- 159. Точка на поверхности.
- 160. Точка на кривой.
- 161. Свободное твердое тело.
- 162. Лемма.
- 163. Сочетания предыдущих связей.
- 164. Общее определение идеальных связей.
- 165. Доказательство принципа.
- 166. Замечание о работе силы.
- 167. О связях, осуществляемых при помощи тел, не имеющих массы.
- II. Первые примеры. Системы с полными связями. Простые машины
- III. Общие условия равновесия, выводимые из принципа возможных скоростей
- 172. Голономные системы; координаты голономной системы.
- 173. Частный случай, когда выражение возможной работы есть полный дифференциал.
- 174. Приложения. Тяжелые системы.
- 175. Принцип Торричелли.
- IV. Множители Лагранжа
- 178. Случай неголономной системы.
- 179. Приложение принципа возможных скоростей к равновесию нитей.
- V. Общие теоремы, выводимые из принципа возможных скоростей
- VI Неудерживающие связи
- 187. Связи, выражаемые неравенствами в конечной форме.
- ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ
- 189. Трение скольжения.
- 190. Законы трения скольжения в состоянии покоя.
- 191. Равновесие тел с трением.
- 192. Тяжелое тело, опирающееся на плоскость в нескольких точках и находящееся под действием только одной силы F.
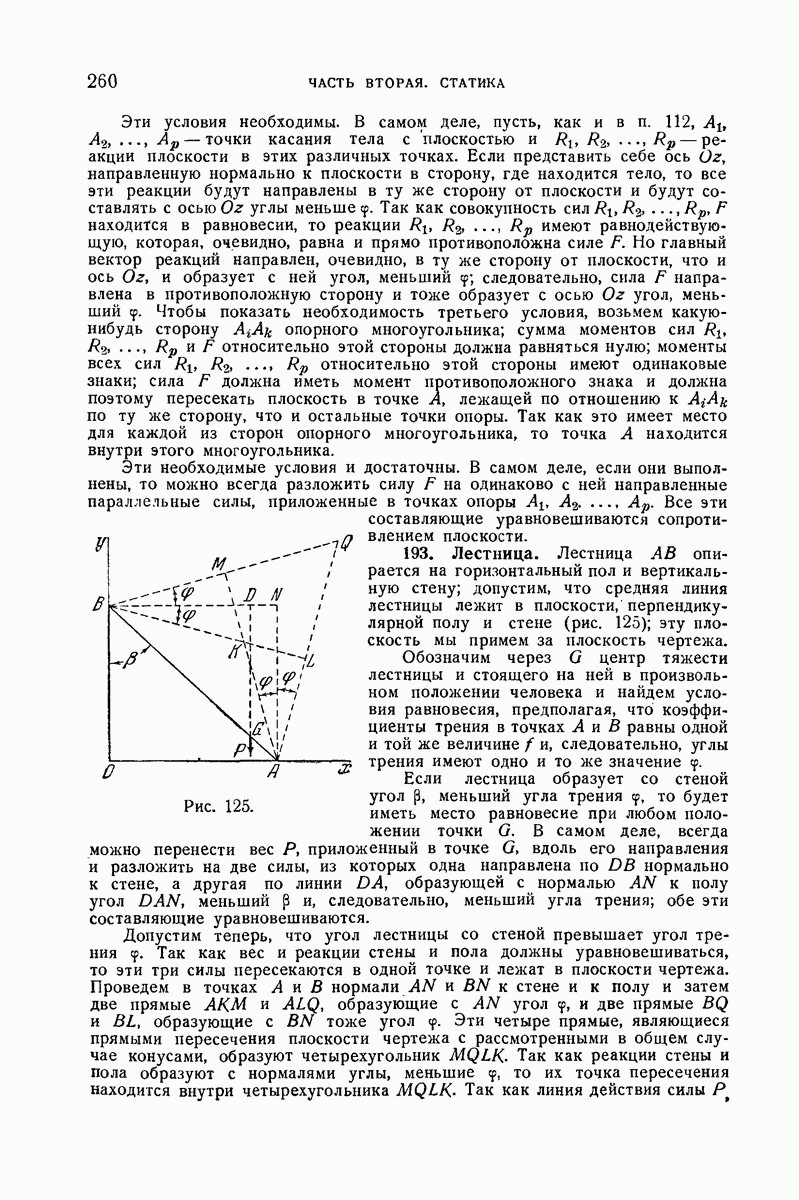
- 193. Лестница.
- 194. Веревка, навернутая на поперечное сечение цилиндра.
- 195. Трение скольжения при движении.
- 196. Трение качения в начале и во время движения.
- 197. Трение верчения.
- ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
- ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. ДВИЖЕНИЕ СНАРЯДОВ
- 199. Первые интегралы.
- 200. Естественные уравнения (Эйлер).
- 201. Количество движения.
- 202. Теорема о проекции количества движения.
- 203. Теорема о моменте количества движения. Закон площадей.
- 204. Геометрическая интерпретация двух предыдущих теорем.
- 205. Теорема кинетической энергии.
- 206. Примеры.
- 207. Замечание к интегралу кинетической энергии.
- 208. Устойчивость равновесия свободной материальной точки. Доказательство Лежен-Дирихле.
- II. Прямолинейное движение
- 210. Уравнение прямолинейного движения. Простые случаи интегрируемости.
- 211. Приложение к движениям, происходящим под действием силы зависящей только от положения.
- 212. Движения под действием силы, зависящей только от скорости.
- 213. Прямолинейное таутохронное движение.
- 214. Дан закон прямолинейного движения, найти силу.
- III. Криволинейное движение. Тяжелая точка в пустоте и в сопротивляющейся среде. Электрическая частица
- 217. Движение тяжелой точки в пустоте.
- 218. Определение параллельной силы по заданной траектории.
- 219. Криволинейное движение тяжелого тела в сопротивляющейся среде.
- 220. Движение легкого вращающегося шара в воздухе.
- 221. Движение наэлектризованной частицы в наложенных друг на друга электрическом и магнитном полях.
- ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ЭЛЛИПТИЧЕСКОЕ ДВИЖЕНИЕ ПЛАНЕТ
- 223. Сила есть функция только расстояния.
- 224. Сила вида …
- 225. Обратная задача. Определение центральной силы, когда задана траектория.
- II. Движение планет
- 228. Кометы.
- 229. Спутники.
- 230. Всемирное притяжение.
- 231. Двойные звезды.
- 232. Задача Бертрана.
- 233. Краткие указания по поводу некоторых других задач.
- III. Элементарные сведения из небесной механики
- 235. Задача двух тел.
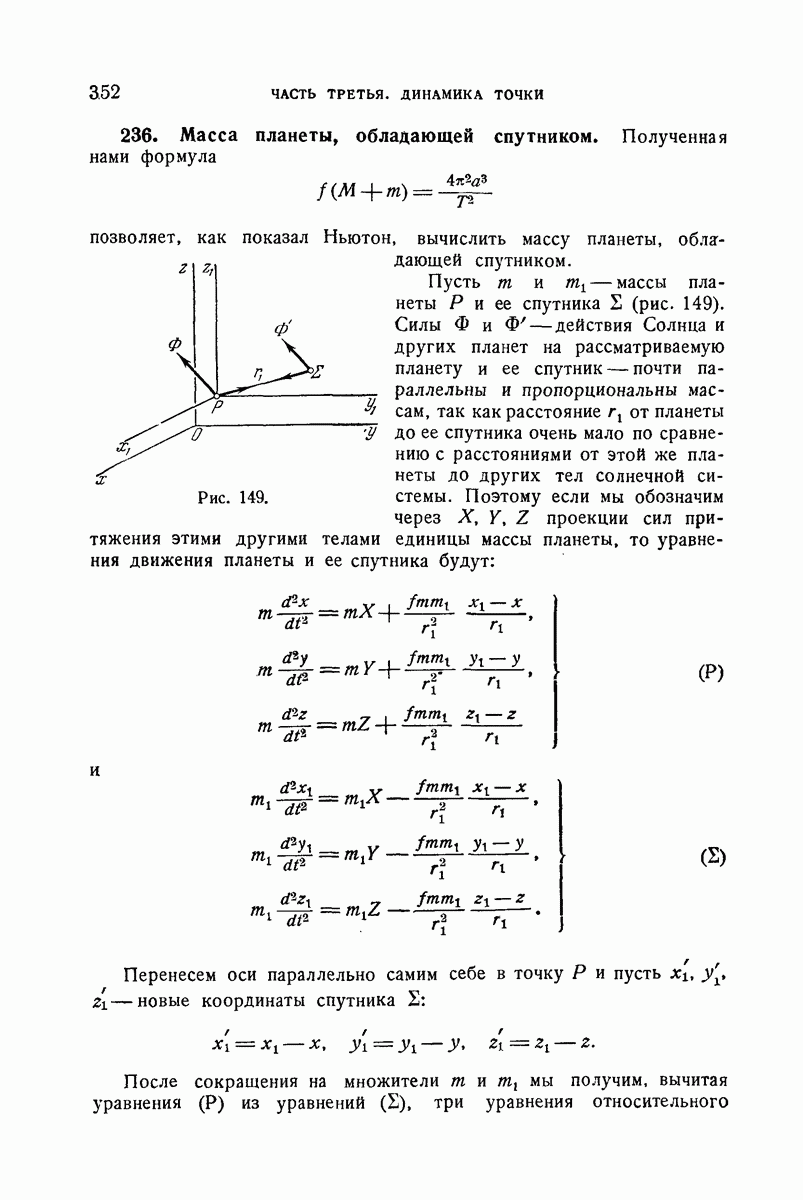
- 236. Масса планеты, обладающей спутником.
- 237. Определение времени в эллиптическом движении.
- 238. Геометрический метод.
- 239. Аналитические преобразования.
- 240. Элементы эллиптического движения.
- ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ КРИВОЙ
- 245. Устойчивость равновесия.
- 246. Движение тяжелой точки по неподвижной кривой.
- 247. Нормальная реакция. Естественные уравнения.
- 248. Математический маятник.
- 249. Движение математического маятника в сопротивляющейся среде.
- 250. Циклоидальный маятник.
- 251. Движение тяжелой точки по кривой, расположенной в вертикальной плоскости, при действии трения и сопротивления среды.
- 252. Таутохроны.
- 253. Приложения.
- 254. Брахистохрона для силы тяжести.
- 255. Брахистохроны в общем случае.
- 256. Приложение теорем Томсона и Тэта к брахистохронам.
- 257. Брахистохроны на заданной поверхности.
- II. Движение материальной точки на изменяемой кривой
- ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ ИЛИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
- II. Случай неподвижной поверхности
- 266. Вывод уравнения кинетической энергии из уравнений Лагранжа.
- 267. Устойчивость равновесия в случае существования силовой функции U.
- 268. Нормальная реакция.
- 269. Естественные уравнения и нормальная реакция.
- 270. Геодезические линии.
- 271. Применение уравнений Лагранжа.
- 272. Бесконечно малые колебания тяжелой точки около наинизшей точки поверхности.
- III. Движение на поверхности вращения
- 274. Формула Клеро.
- 275. Упражнение. Геодезические линии поверхности, образованной вращением равносторонней гиперболы вокруг своей асимптоты.
- 276. Движение тяжелой точки на поверхности врадцения, ось которой Oz вертикальна.
- 277. Сферический маятник.
- 278. Вычисление нормальной реакции.
- 279. Интегрирование в эллиптических функциях.
- 280. Теорема Гринхилла.
- 281. Бесконечно малые колебания.
- ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
- 283. Интеграл кинетической энергии.
- 284. Приложение.
- 285. Сферические координаты.
- 286. Эллиптические координаты в пространстве.
- 287. Эллиптические координаты в плоскости ху.
- ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- 289. Замечание о силе инерции.
- 290. Принцип наименьшего действия.
- ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ. ПРИЛОЖЕНИЯ
- I. Канонические уравнения. Теорема Якоби
- II. Теорема Якоби
- 298. Частный случай, когда t не входит явно в коэффициенты уравнения Якоби.
- 299. Геометрическое свойство траекторий.
- 300. Декартовы координаты в пространстве.
- III. Плоское движение. Движение по поверхности
- 302. Параболическое движение тяжелой точки в пустоте.
- 303. Центральная сила — функция расстояния.
- 304. Уравнения движения планеты в форме Якоби.
- 305. Геодезические линии поверхностей Лиувилля. Приложение к эллипсоиду.
- IV. Движение в пространстве
- 306. Движение планеты в сферических координатах по Якоби
- 307. Движение точки, притягиваемой двумя неподвижными центрами, обратно пропорционально квадрату расстояния.
- 308. Эллиптические координаты в пространстве.
- V. Приложения к принципу наименьшего действия, к брахистохронам, к равновесию нитей
- 310. Точка на поверхности.
- 311. Параболическое движение.
- 312. Брахистохроны и фигуры равновесия нитей в случае силовой функции. Задача рефракции.