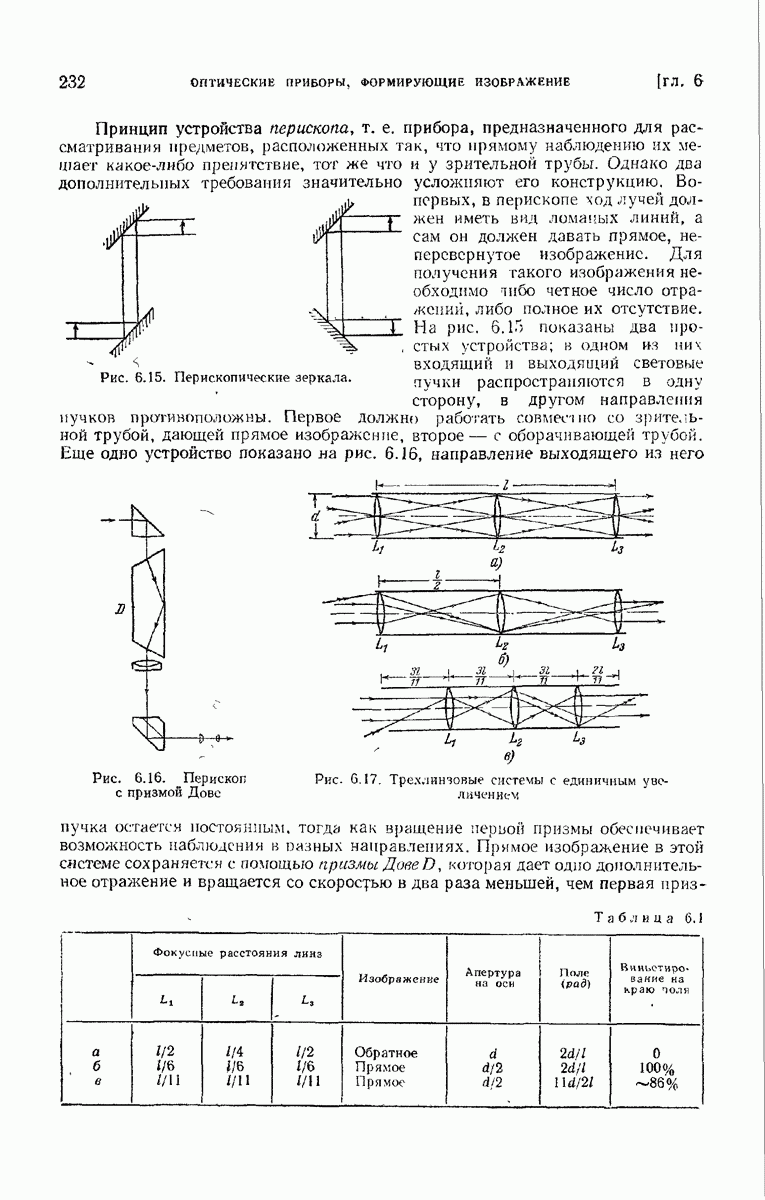
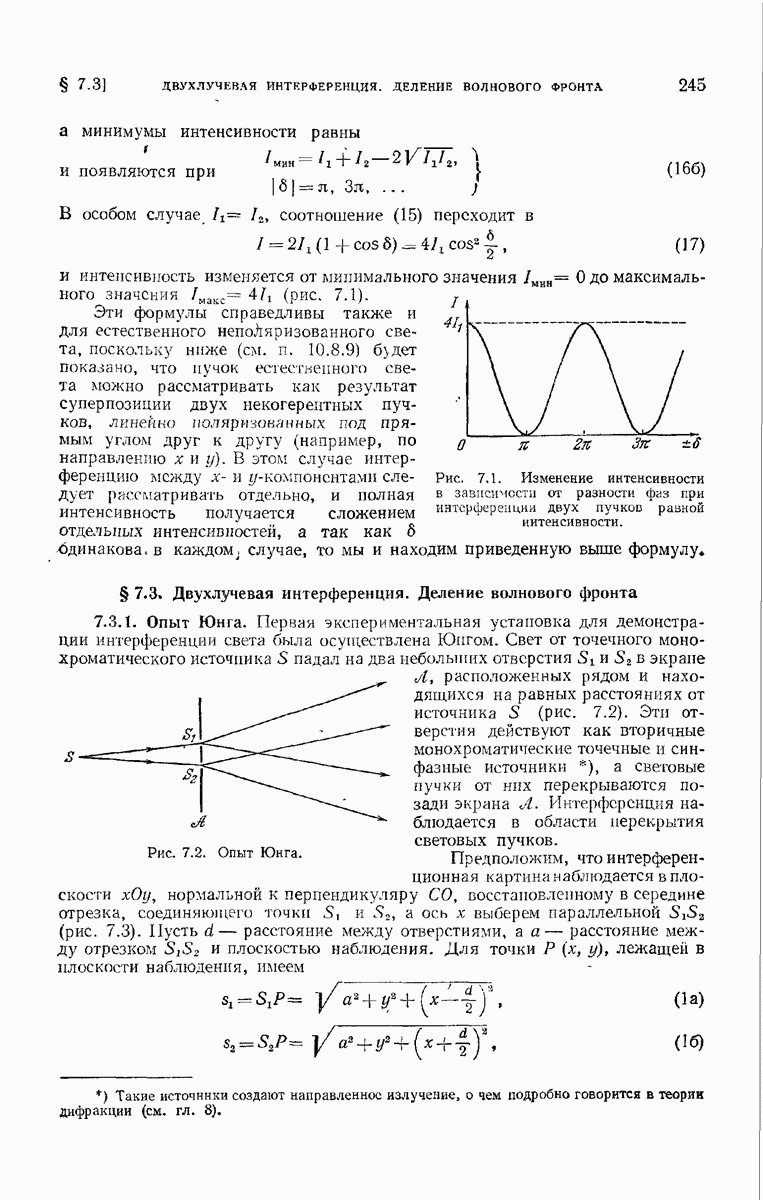
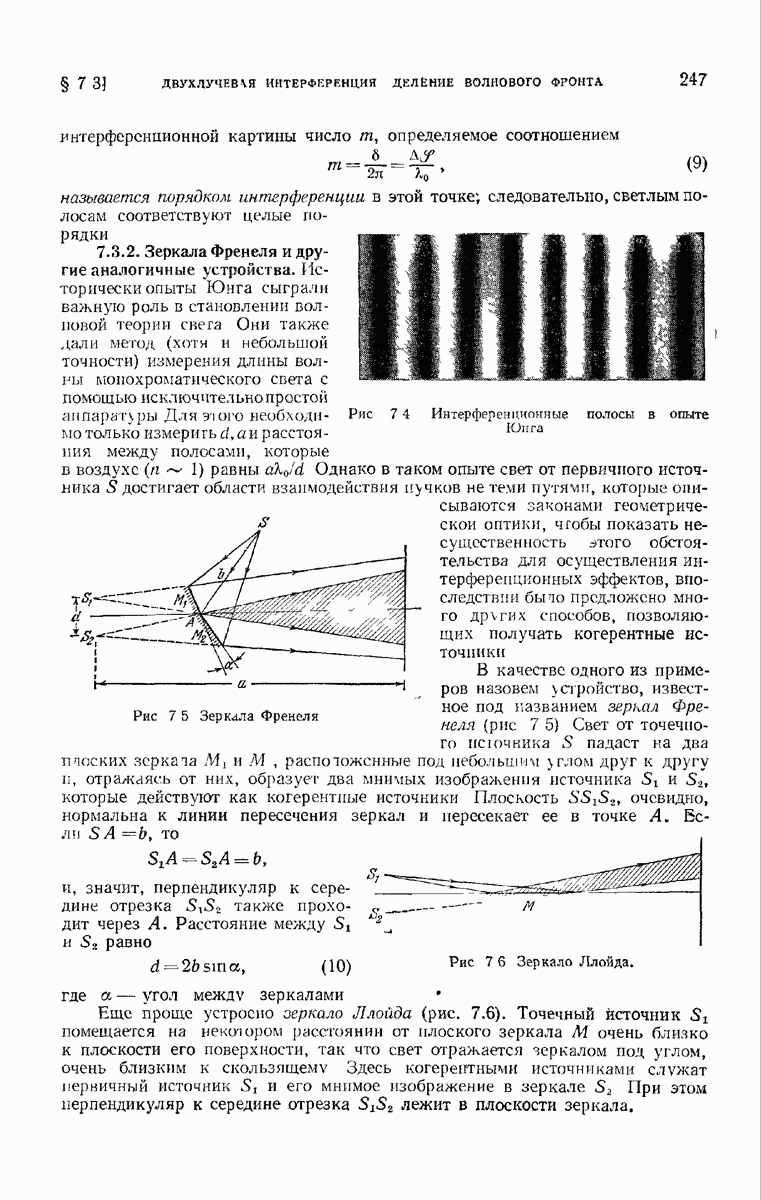
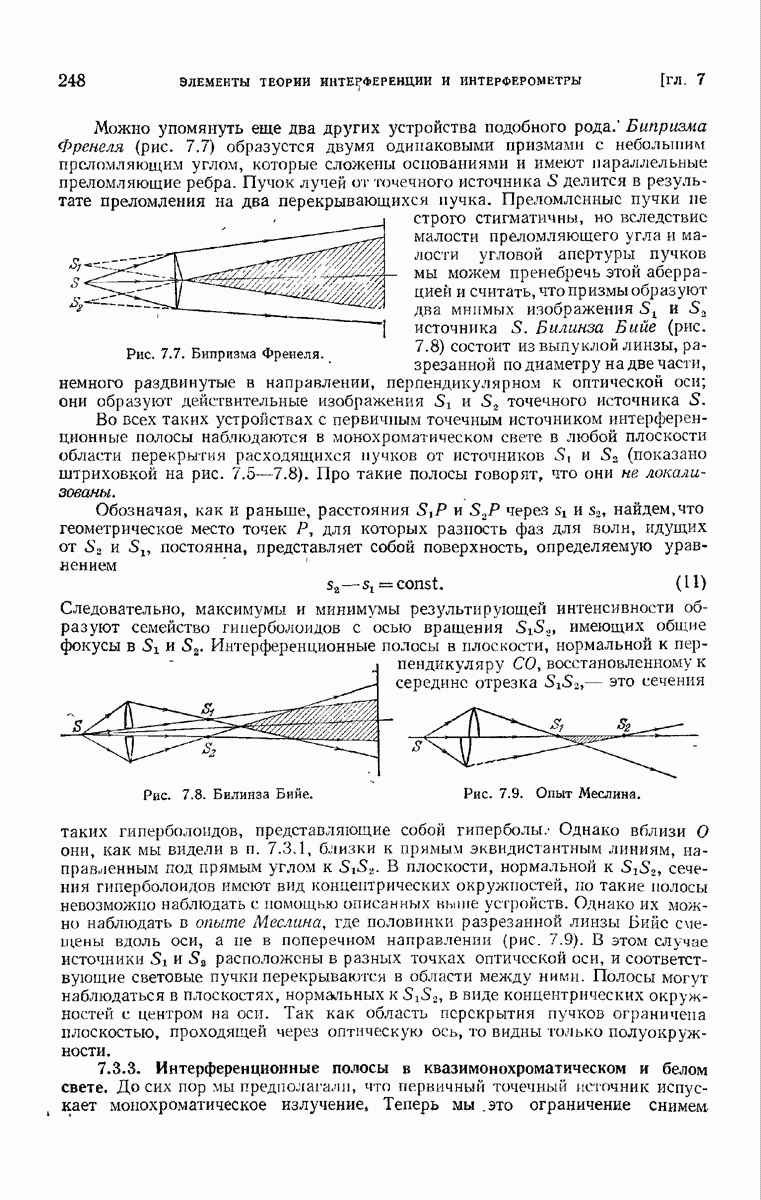
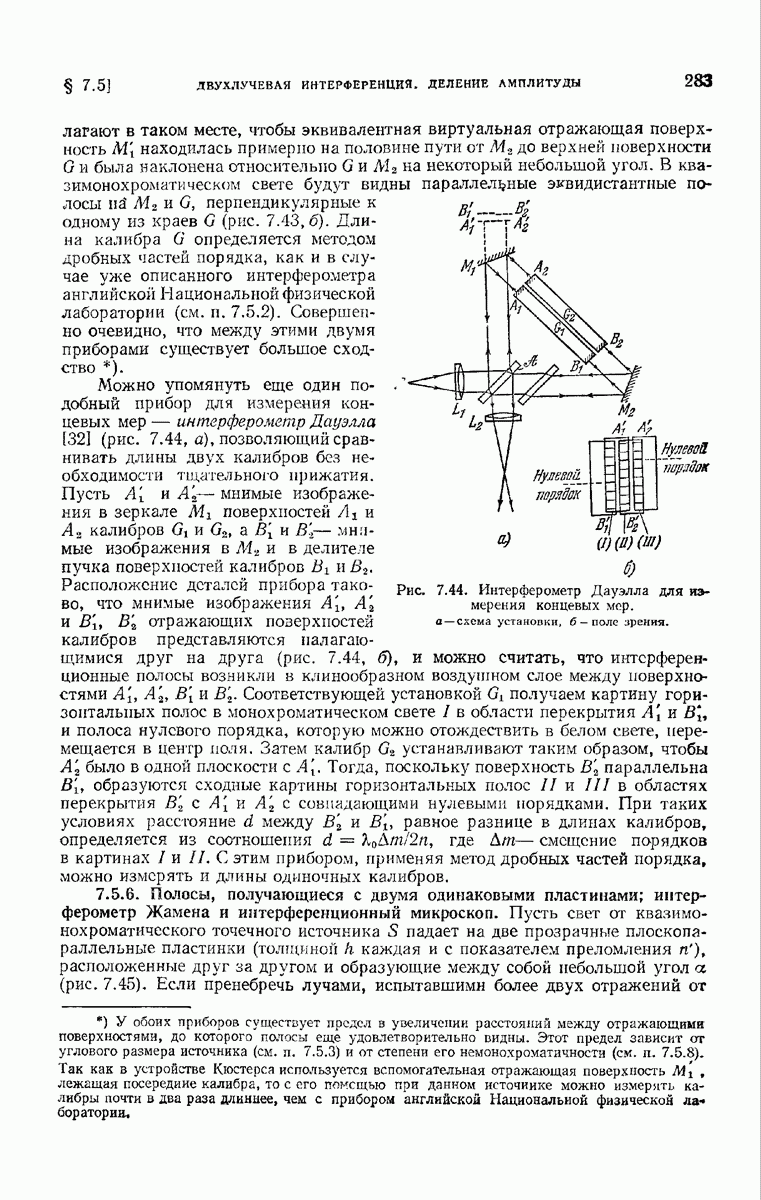
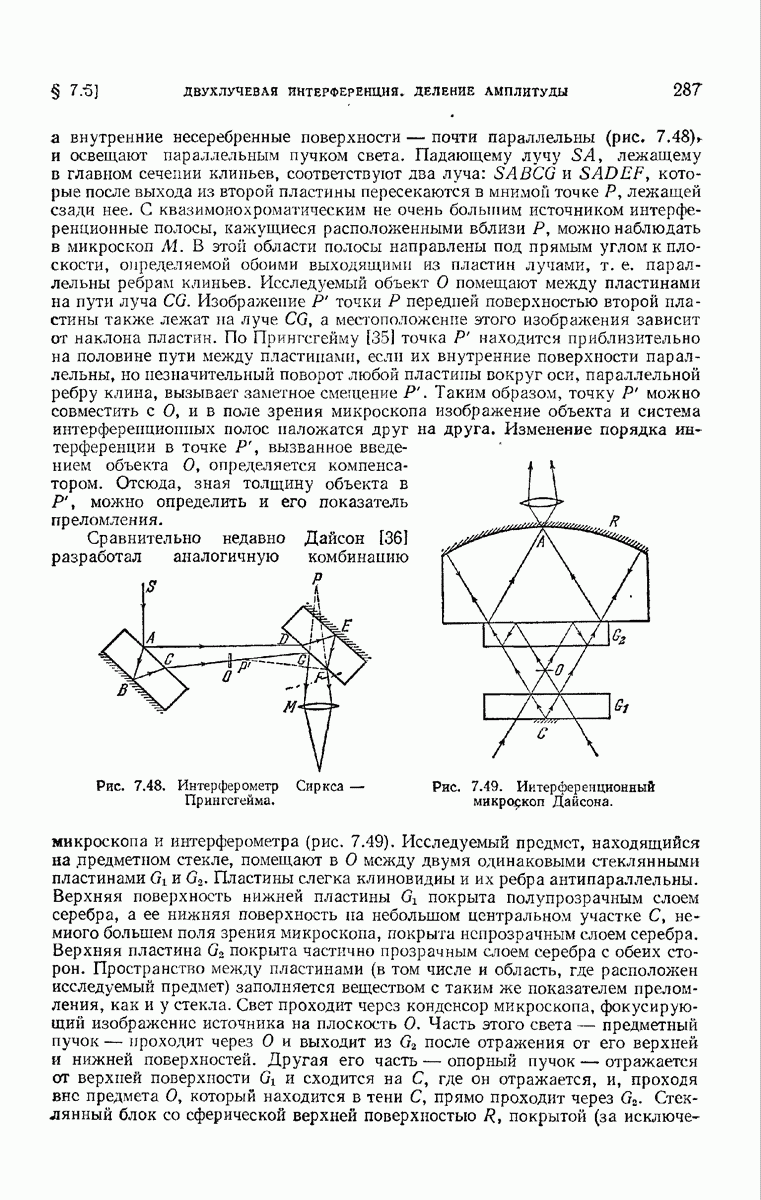
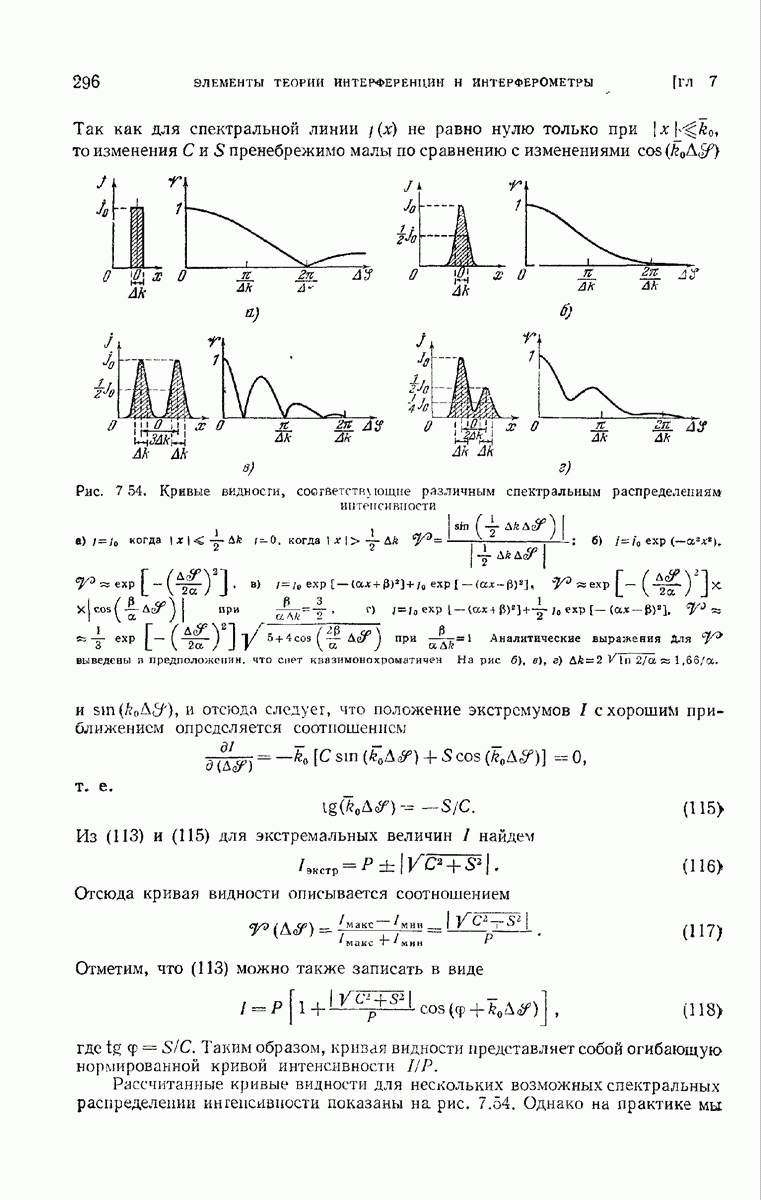
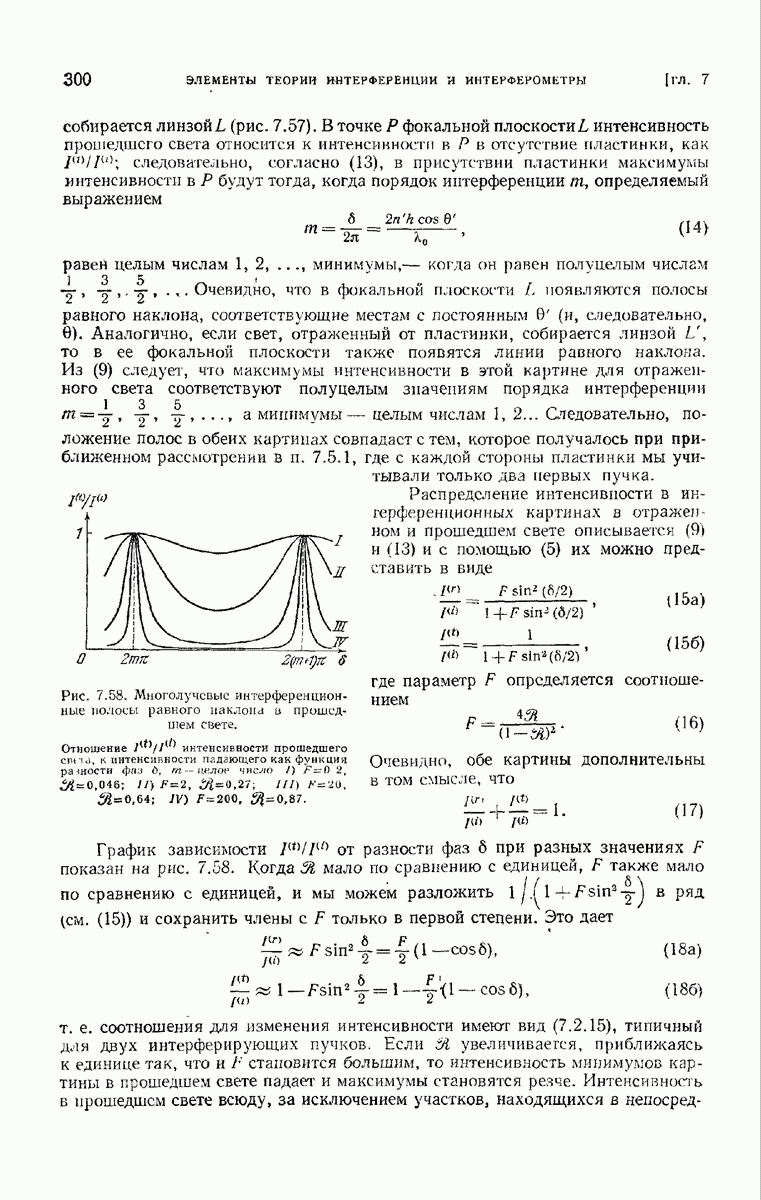
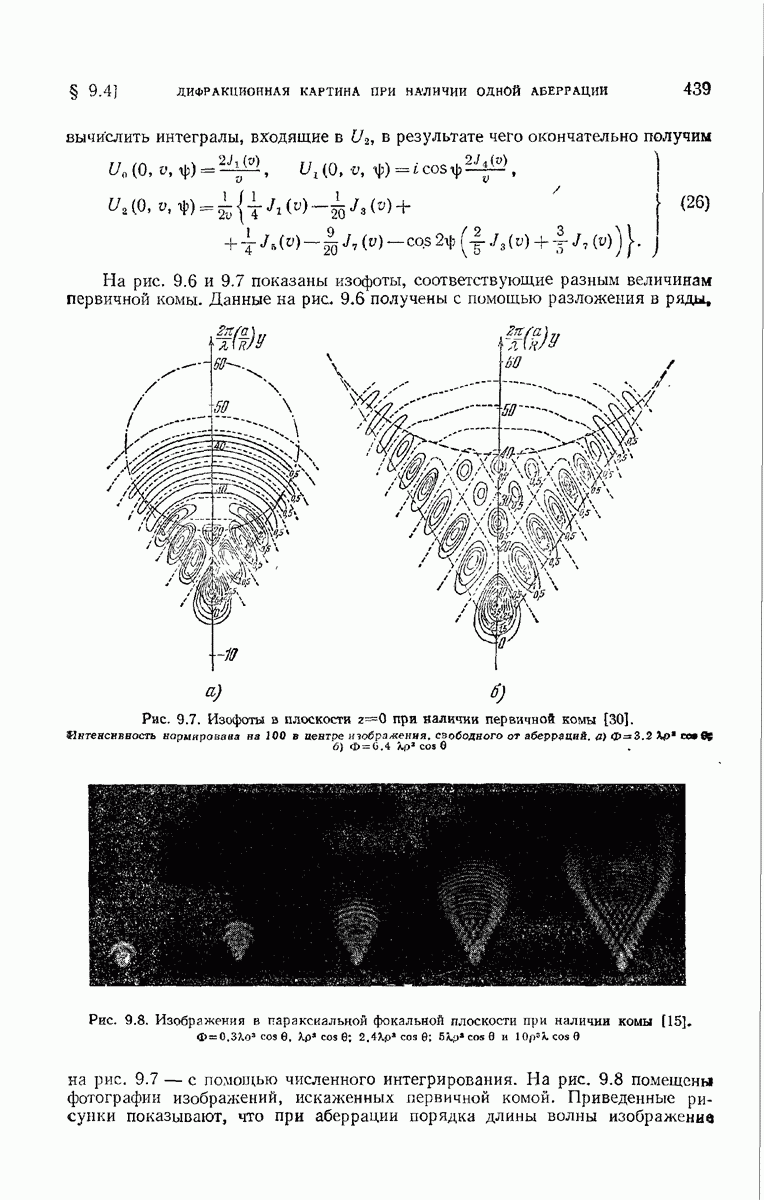
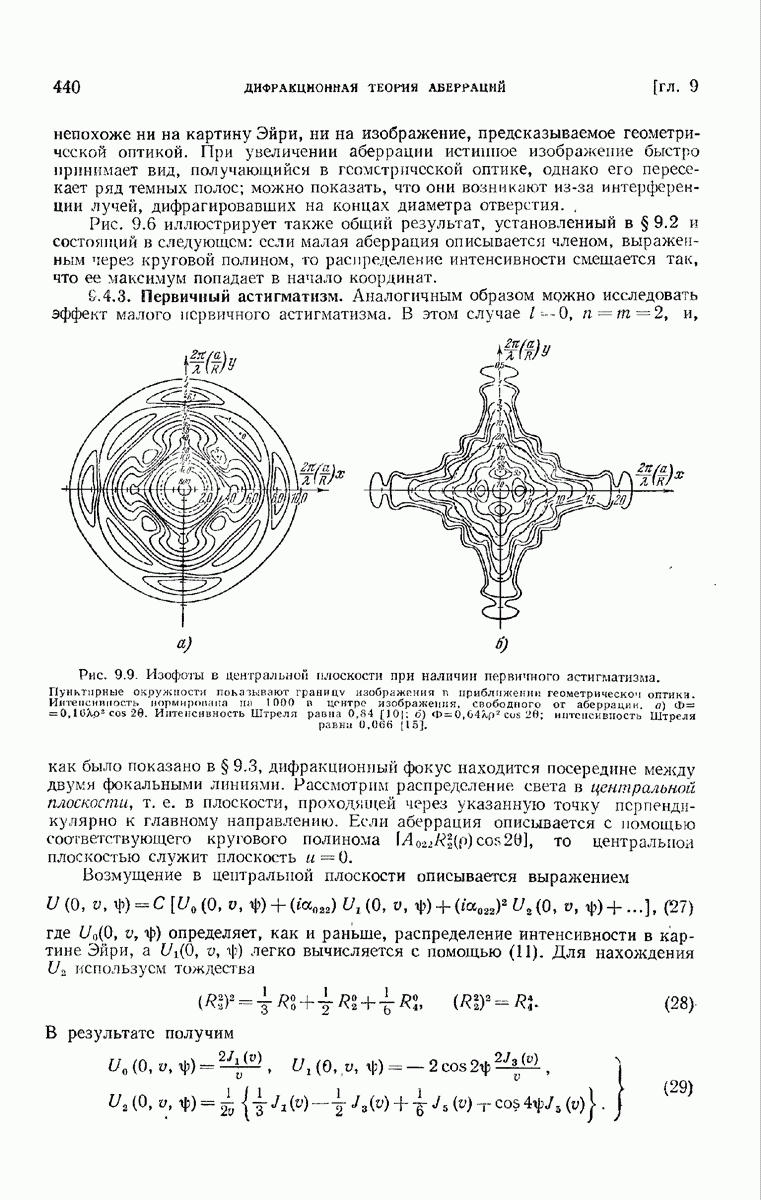
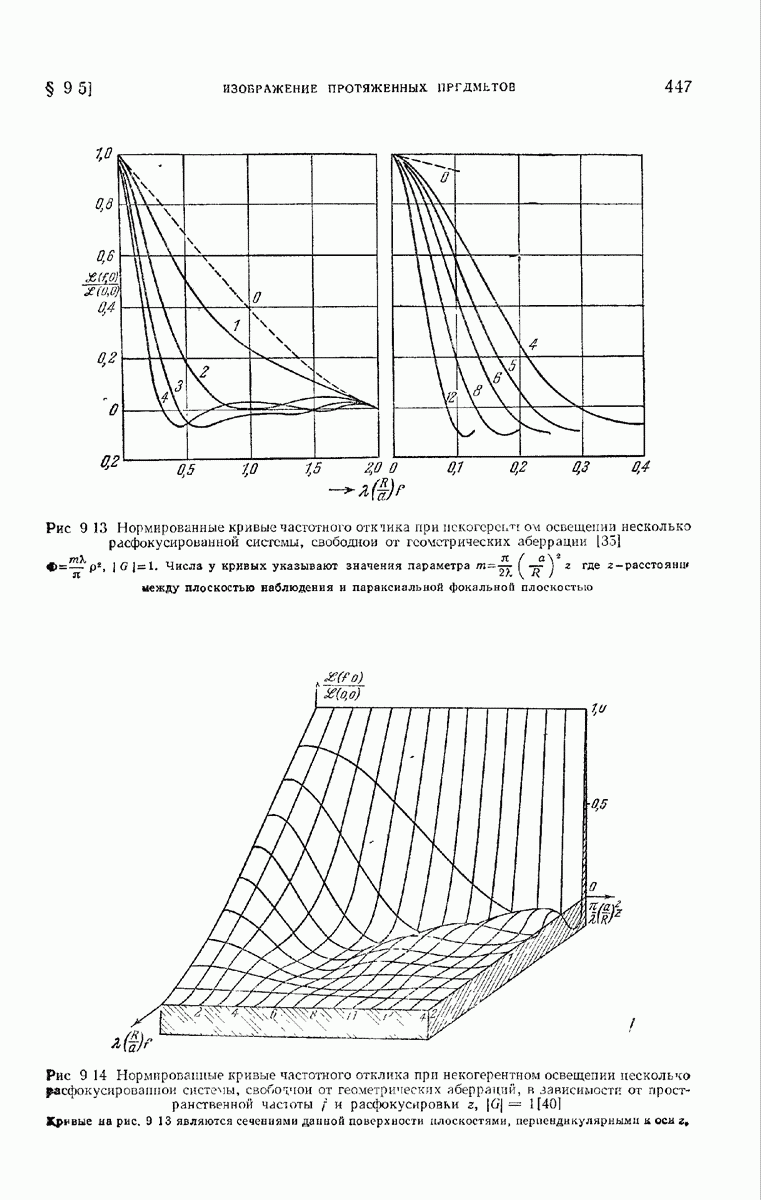
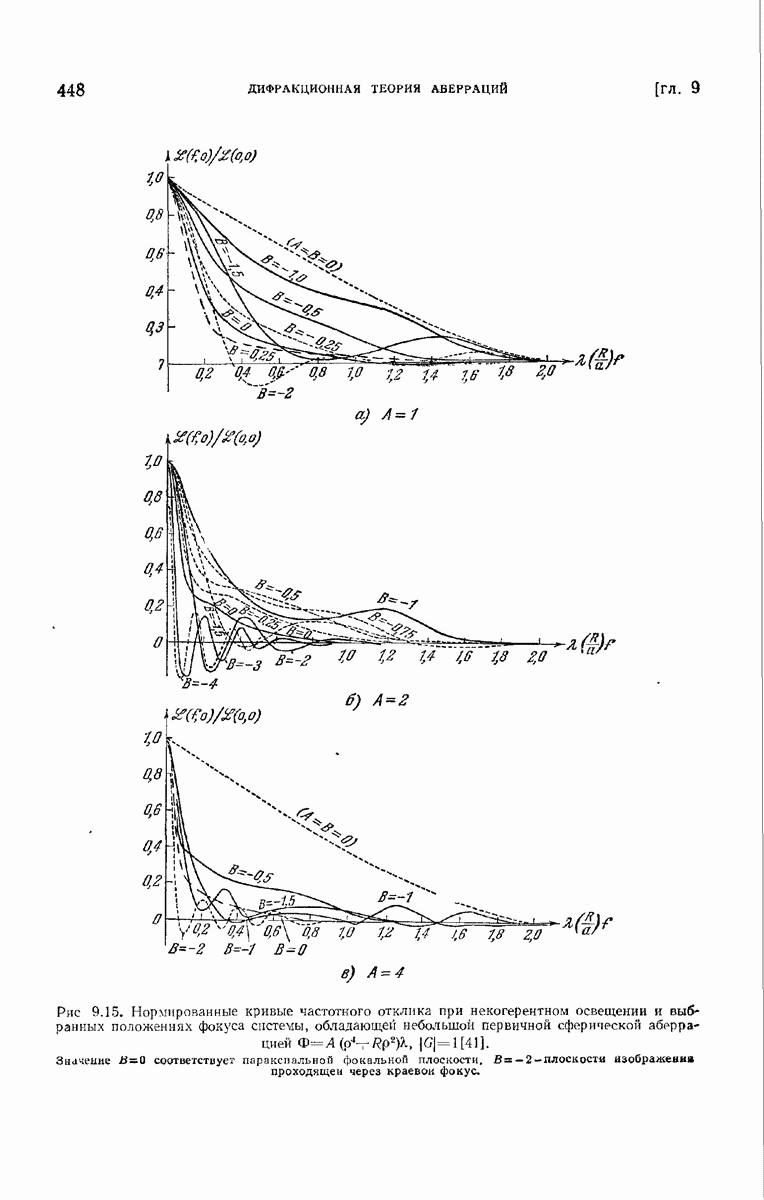
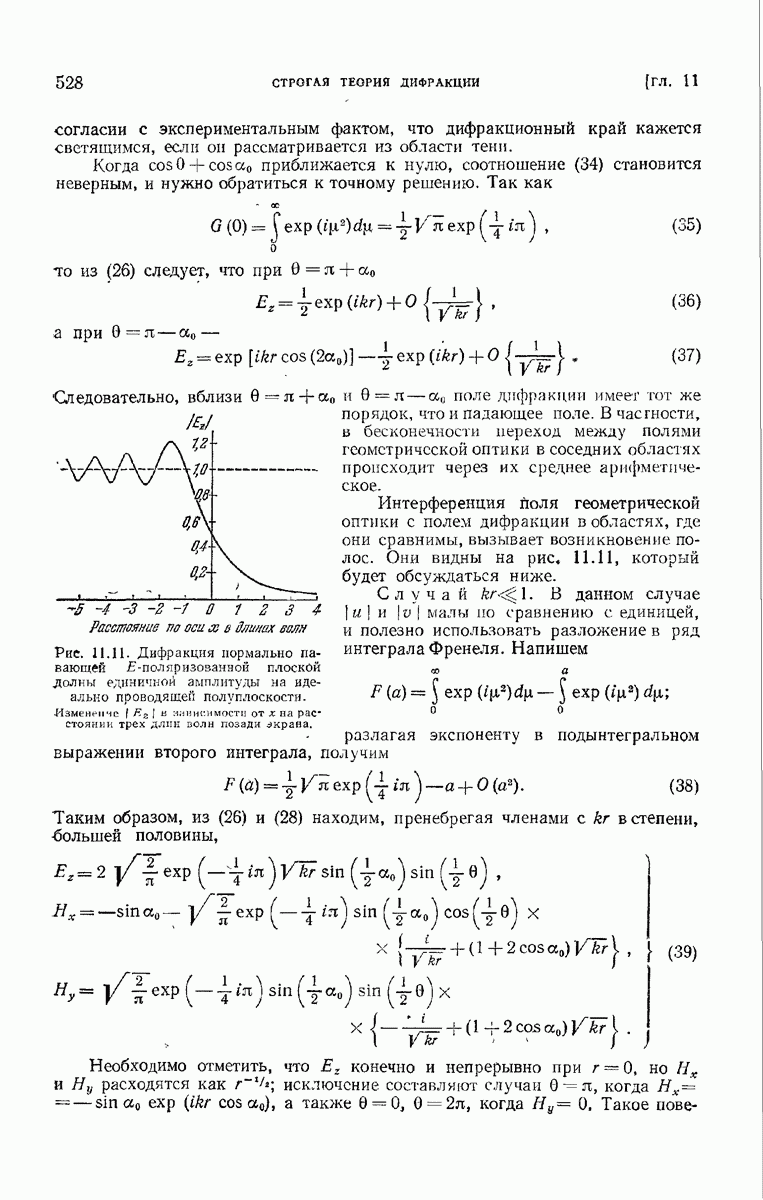
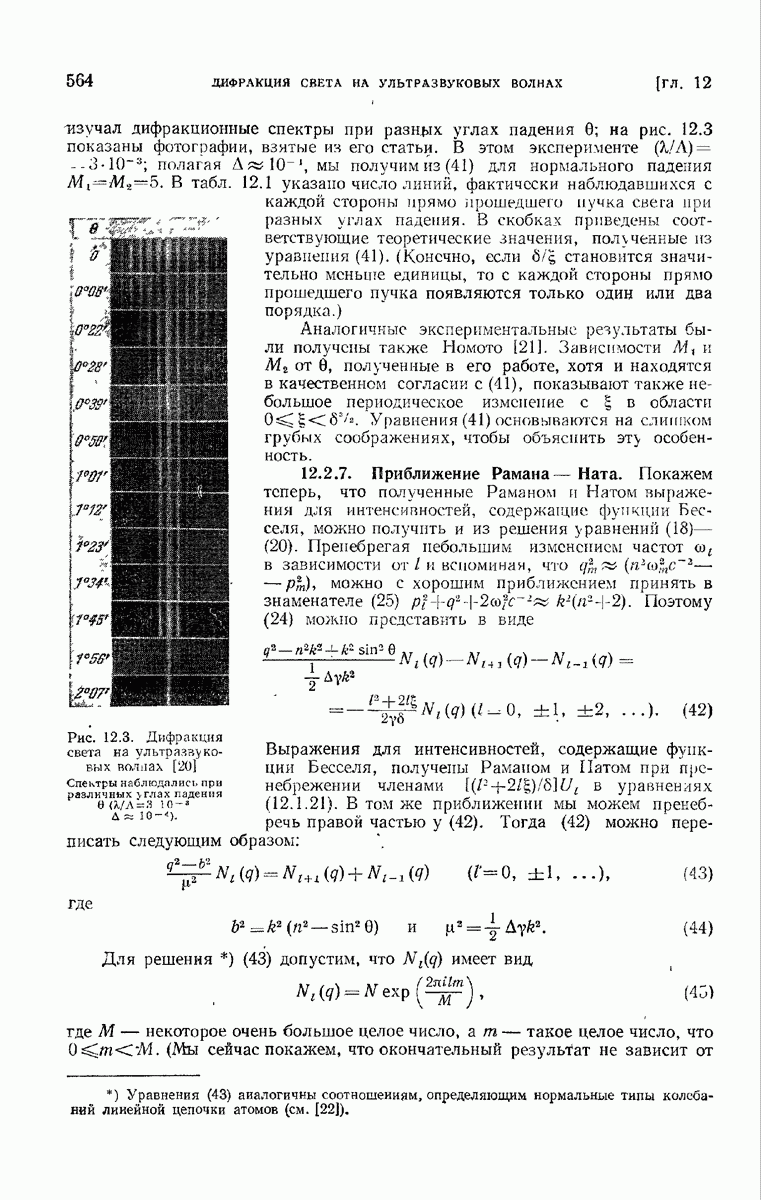
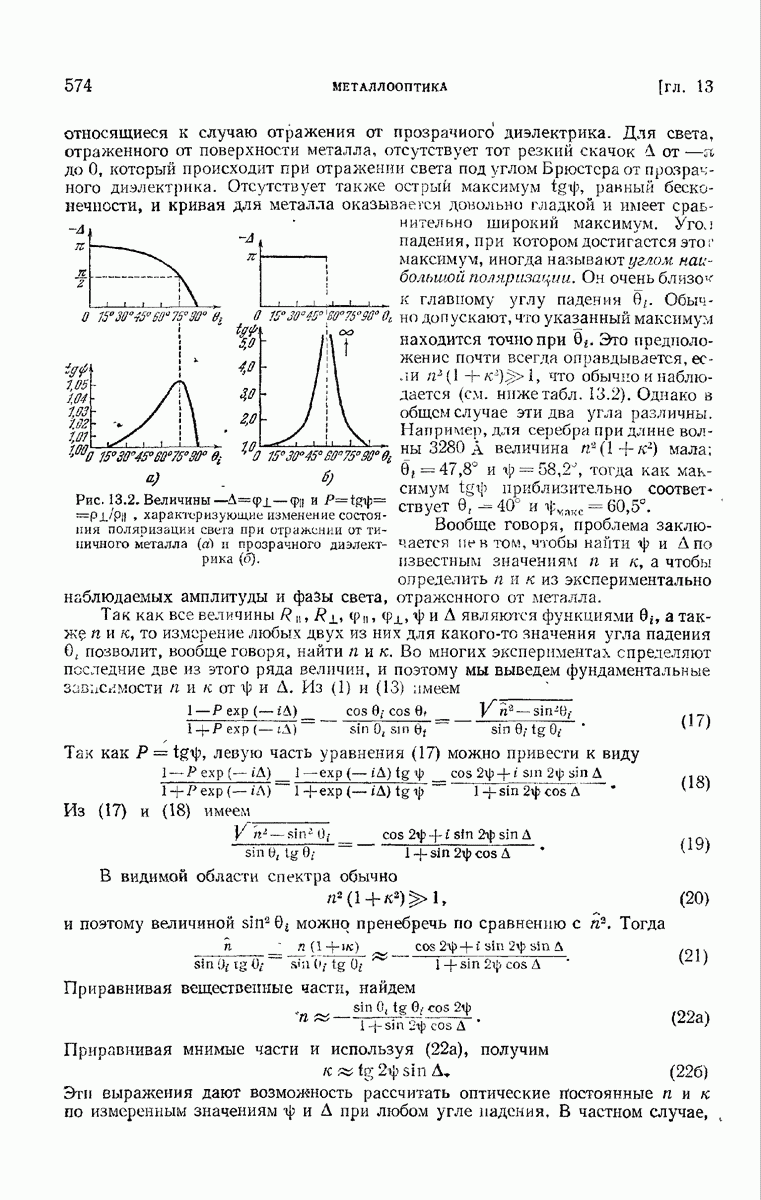
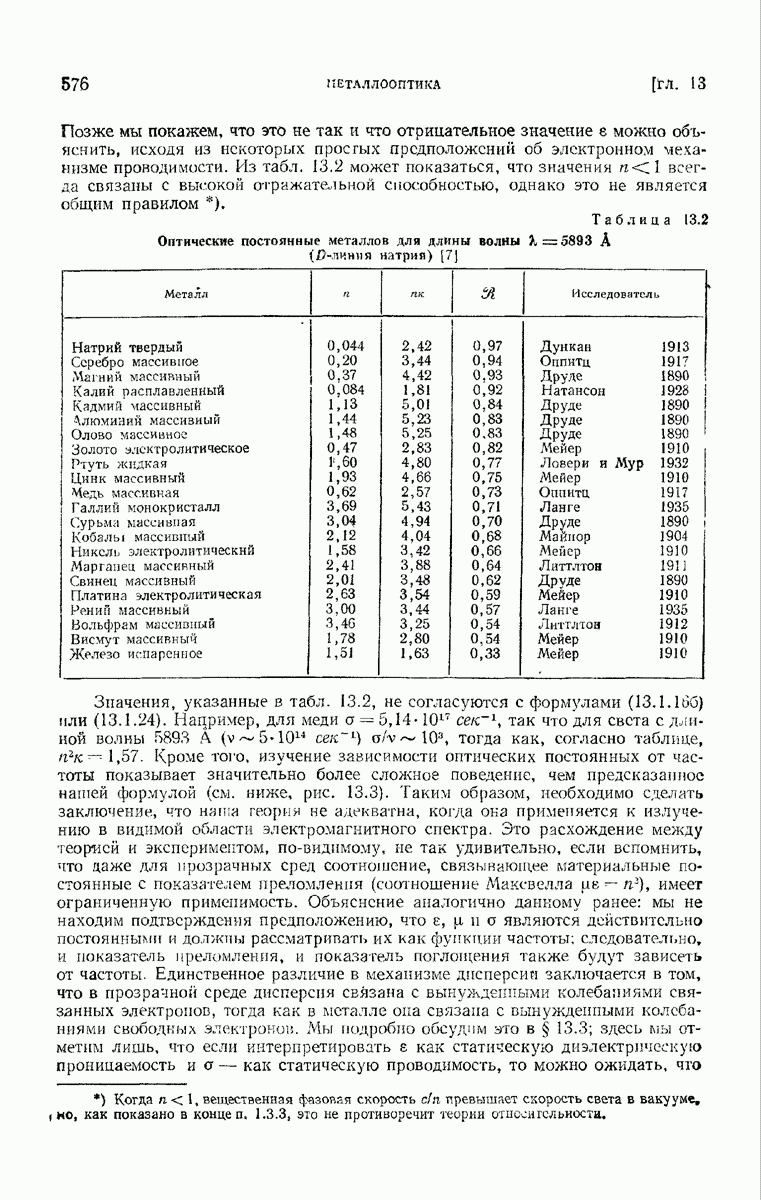
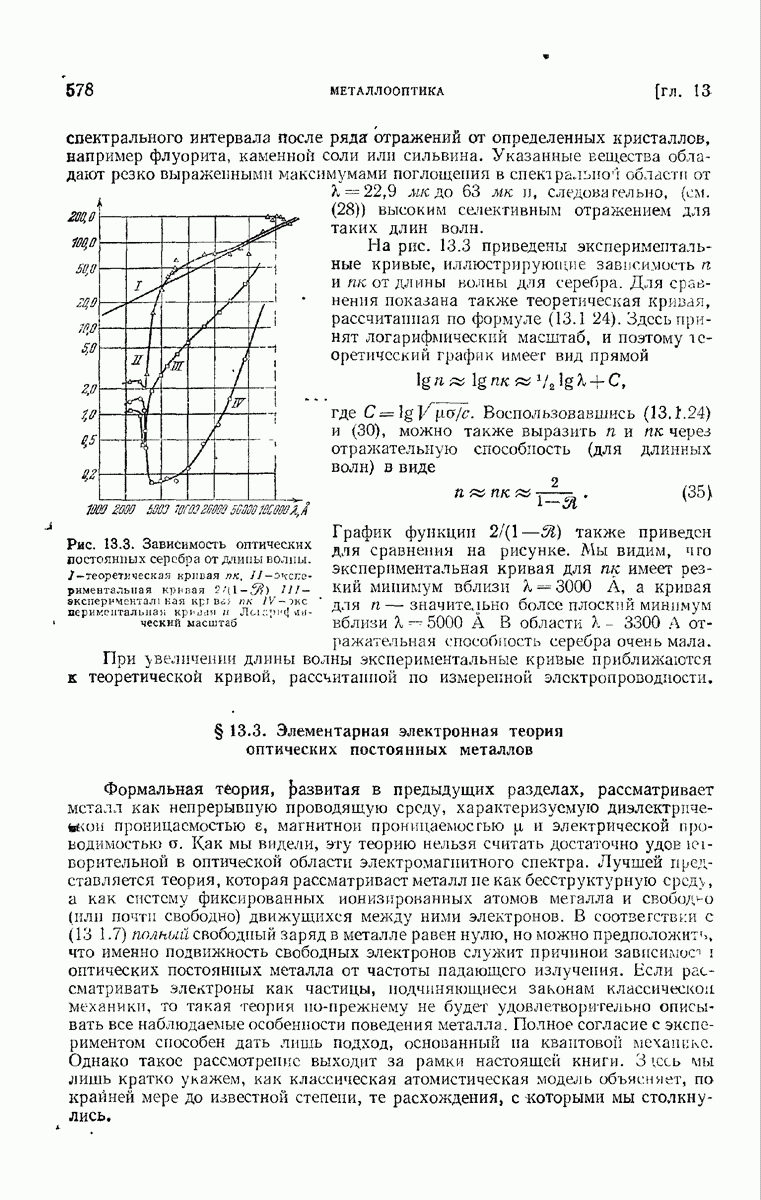
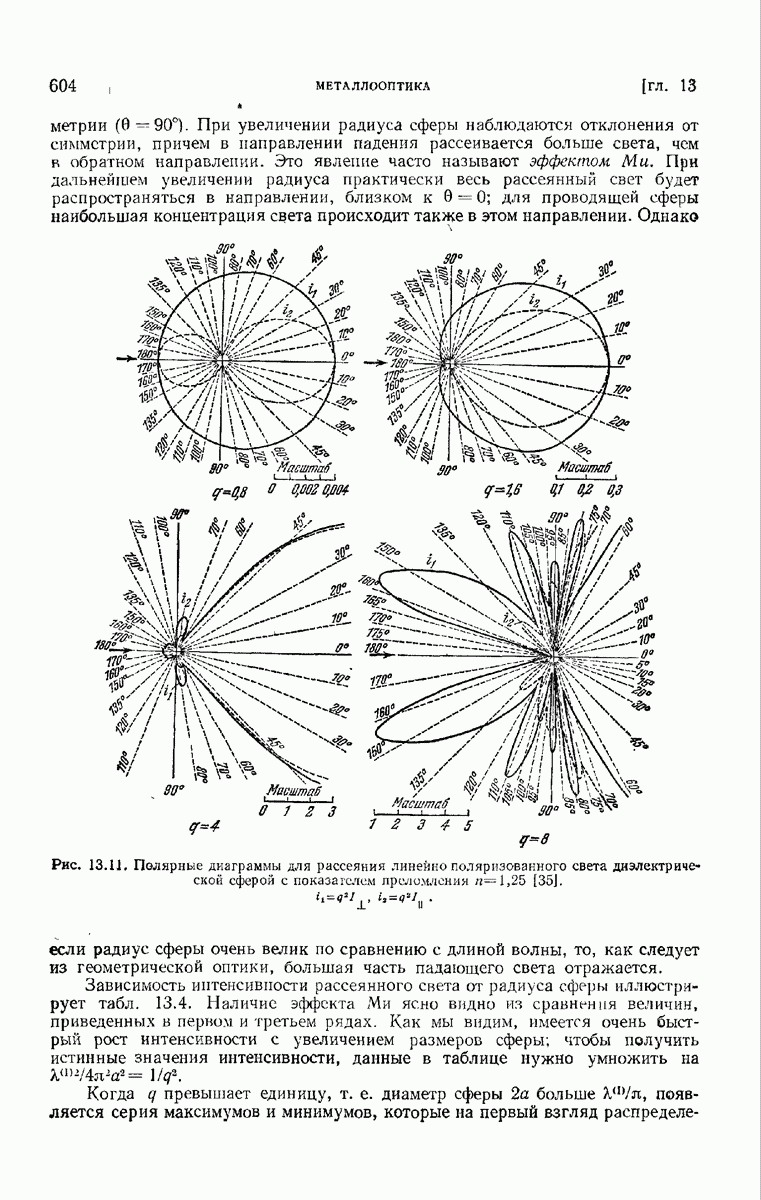
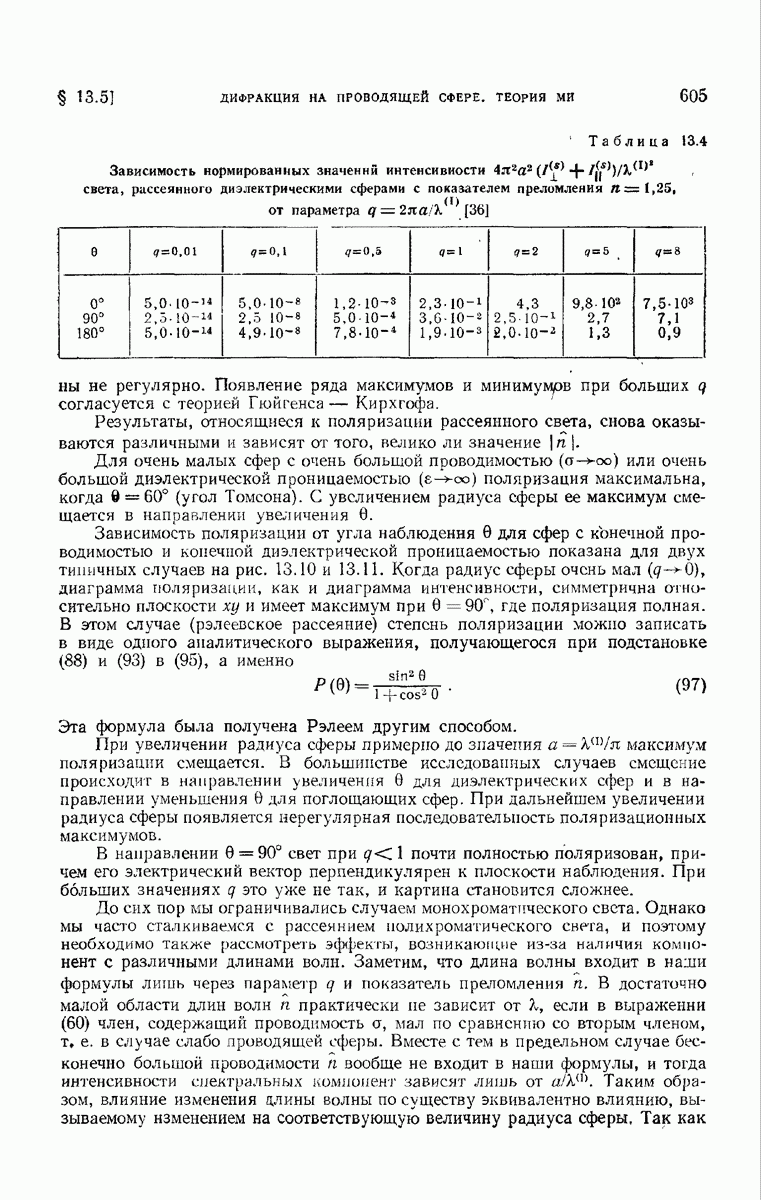
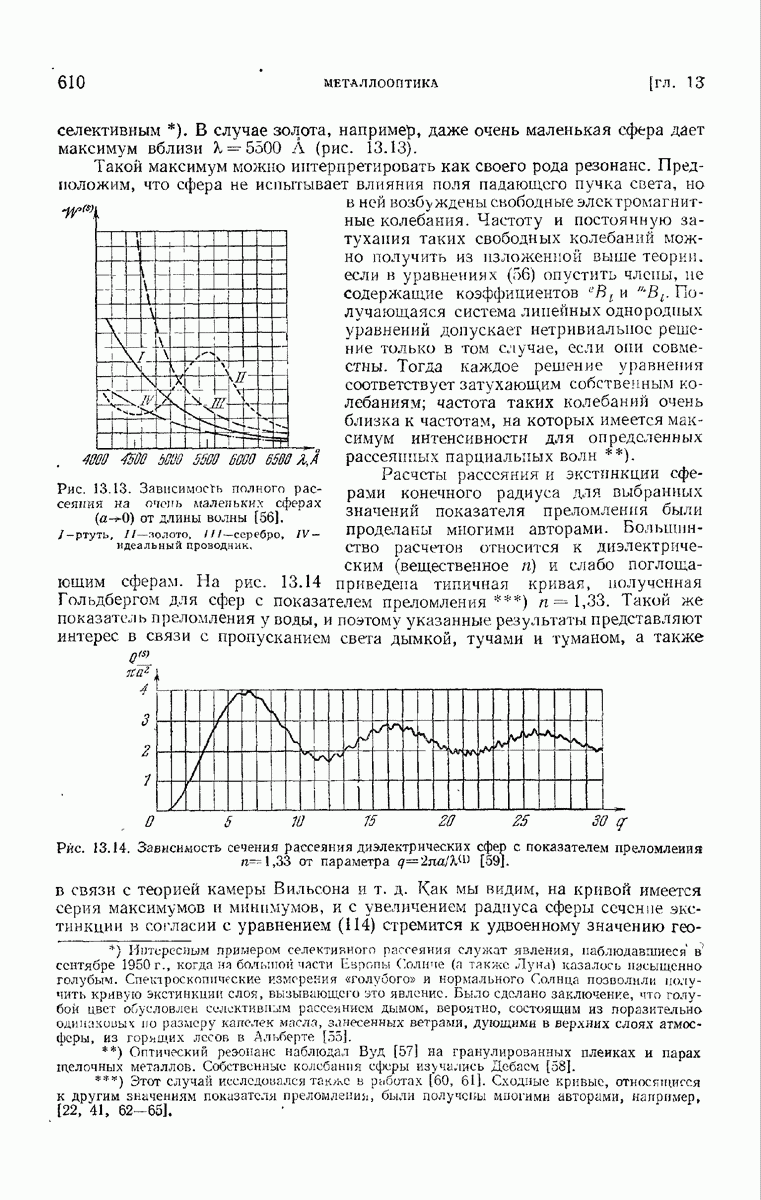
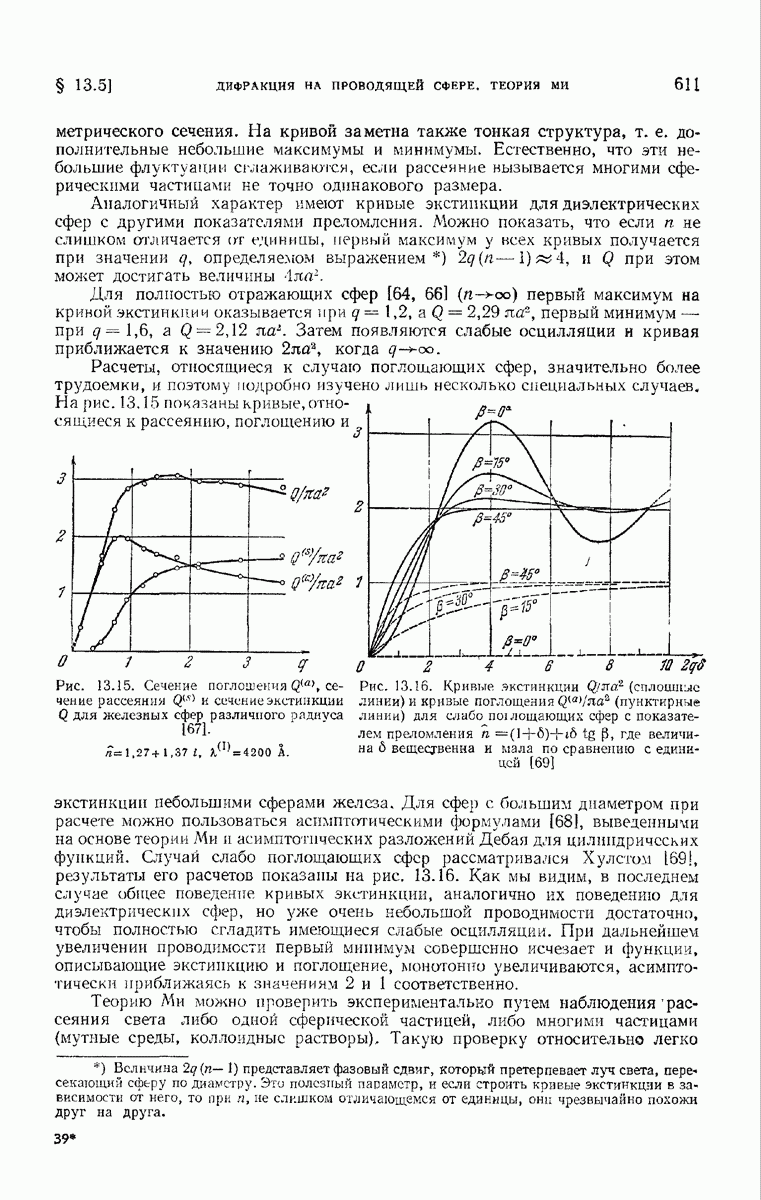
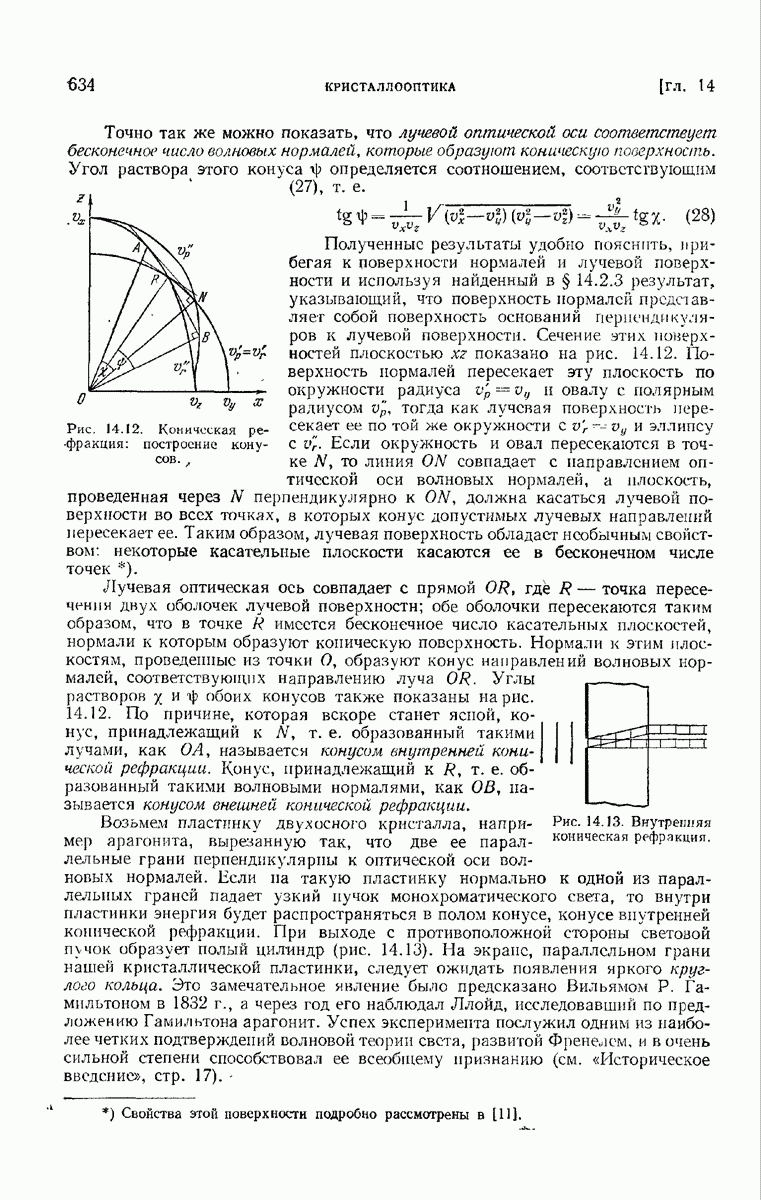
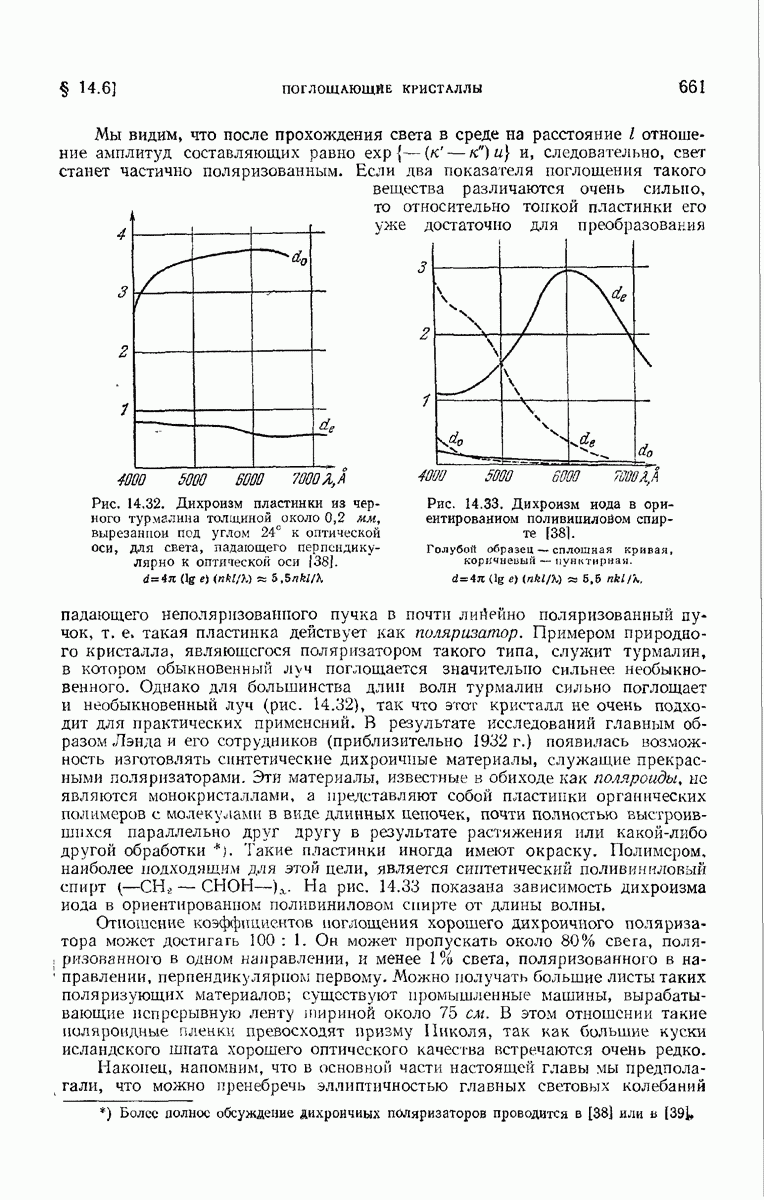
| << Предыдущий параграф | Следующий параграф >> |
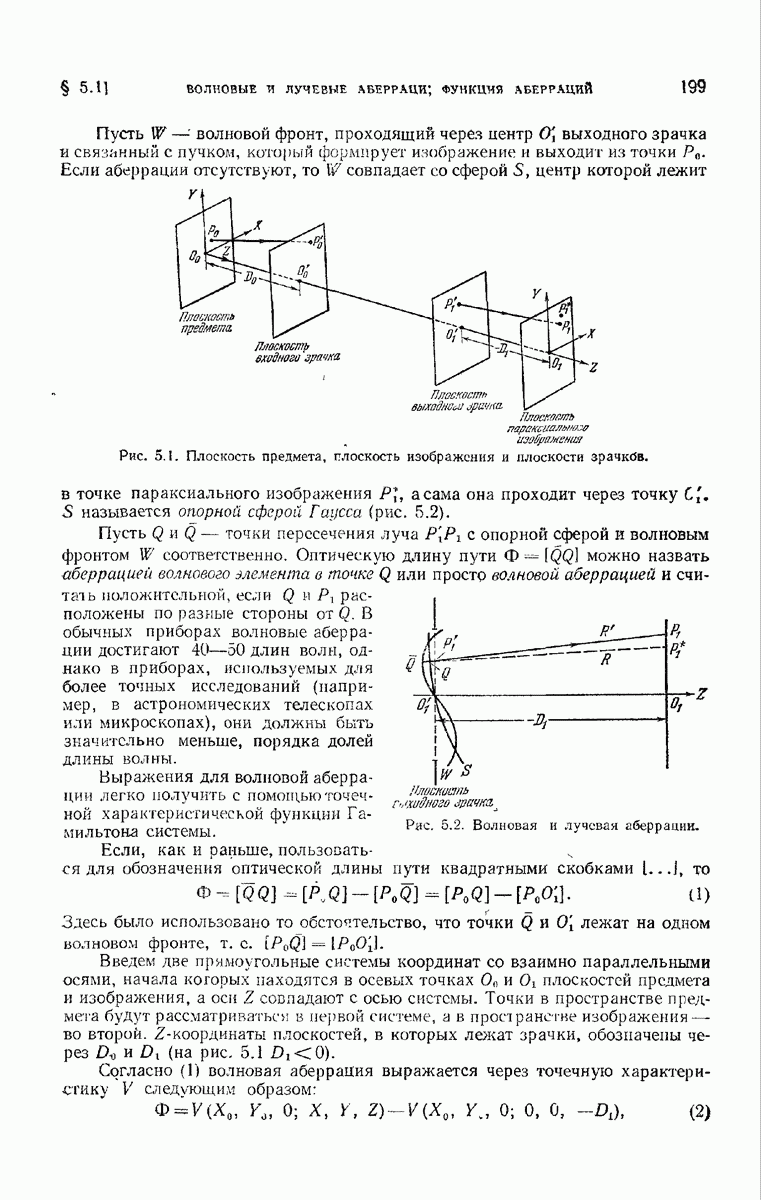
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8.6. Дифракция Фраунгофера в оптических приборах
8.6.1. Дифракционные решетки.
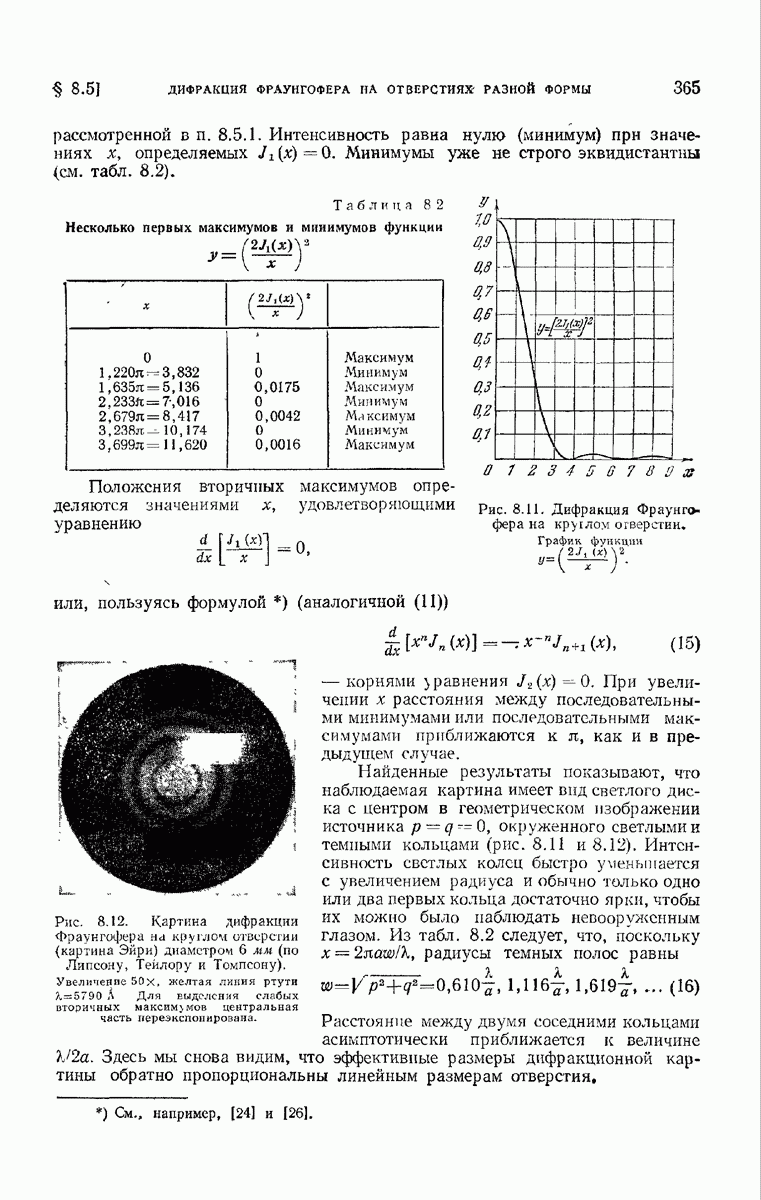
а) Принцип действия дифракционной решетки. Дифракционной решеткой можно назвать любое устройство, обеспечивающее периодическую модуляцию падающей волны по амплитуде или фазе, или одновременно по обоим этим параметрам. Любую данную решетку можно охарактеризовать ее функцией пропускания, определение которой мы сейчас дадим.

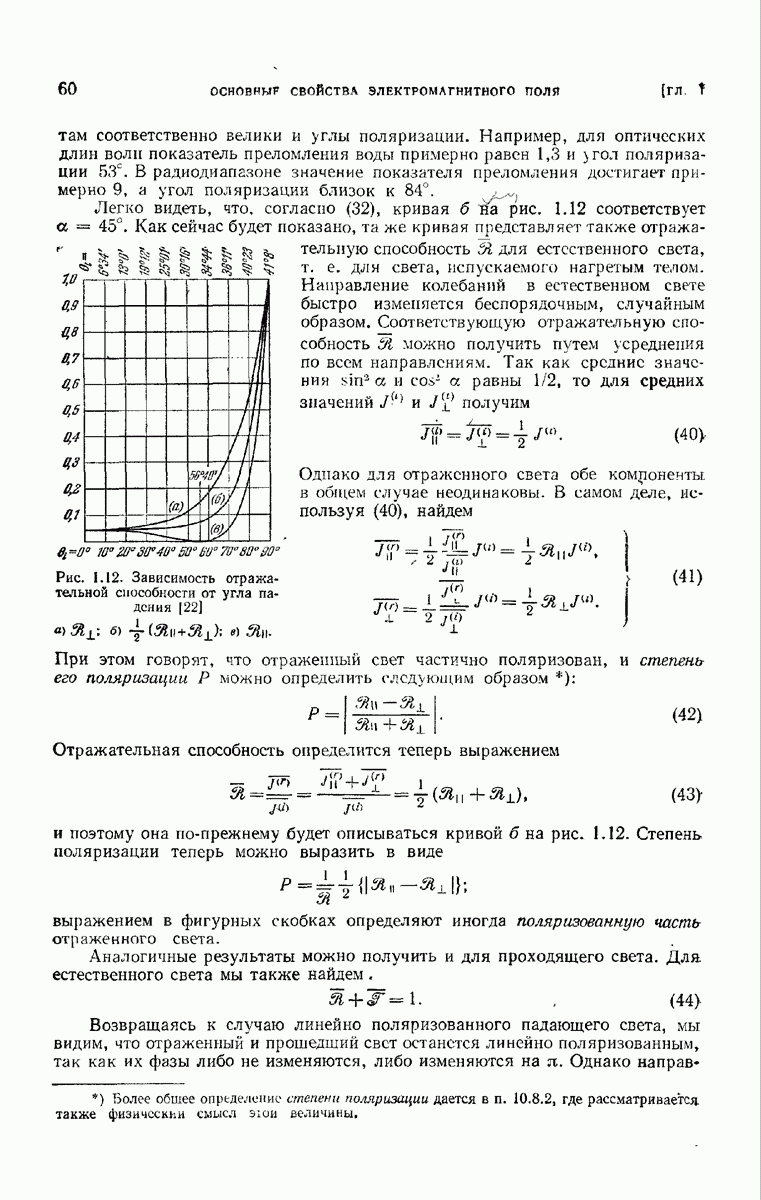
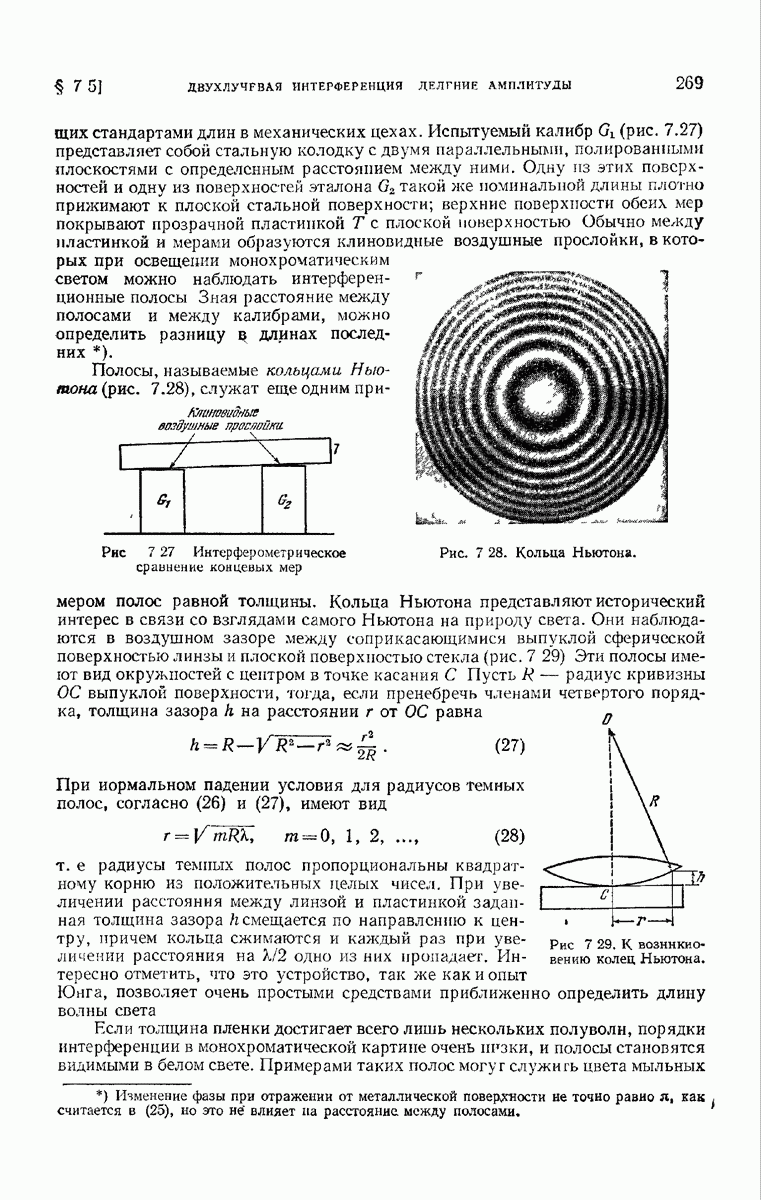
Рис. 8.16. К определению функции пропускания.
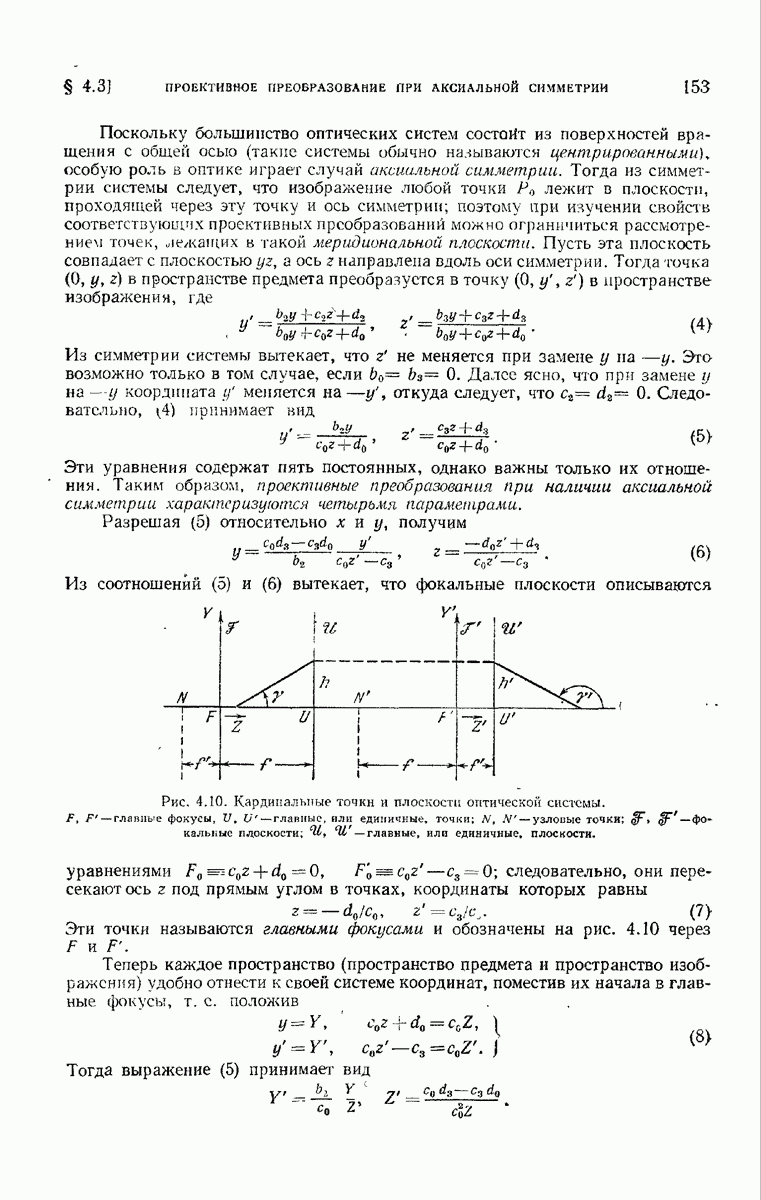
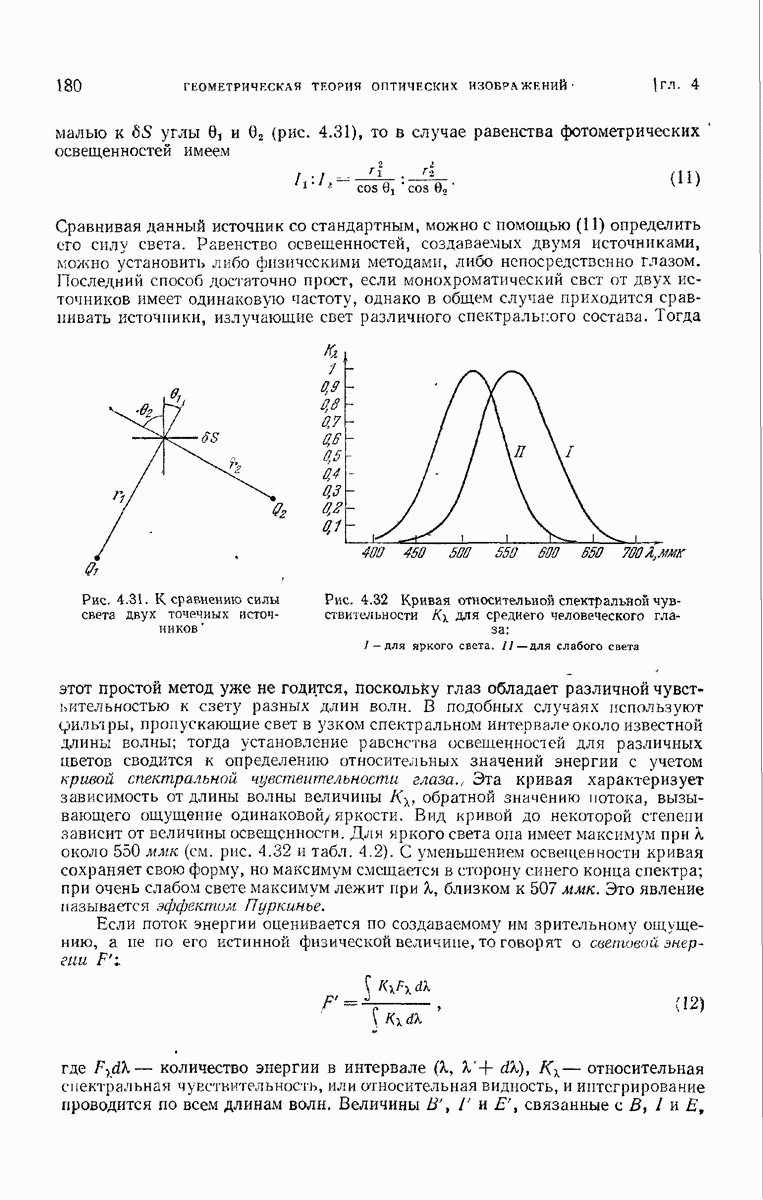
Пусть прозрачный или полупрозрачный предмет (не обязательно периодический) закрывает часть воображаемой координатной плоскости и освещается плоской монохроматической волной, направление падения которой определяется косинусами 10 и  . На рис. 8.16, иллюстрирующем это расположение, ось
. На рис. 8.16, иллюстрирующем это расположение, ось  перпендикулярна к плоскости рисунка. В отсутствие предмета возмущение в плоскости
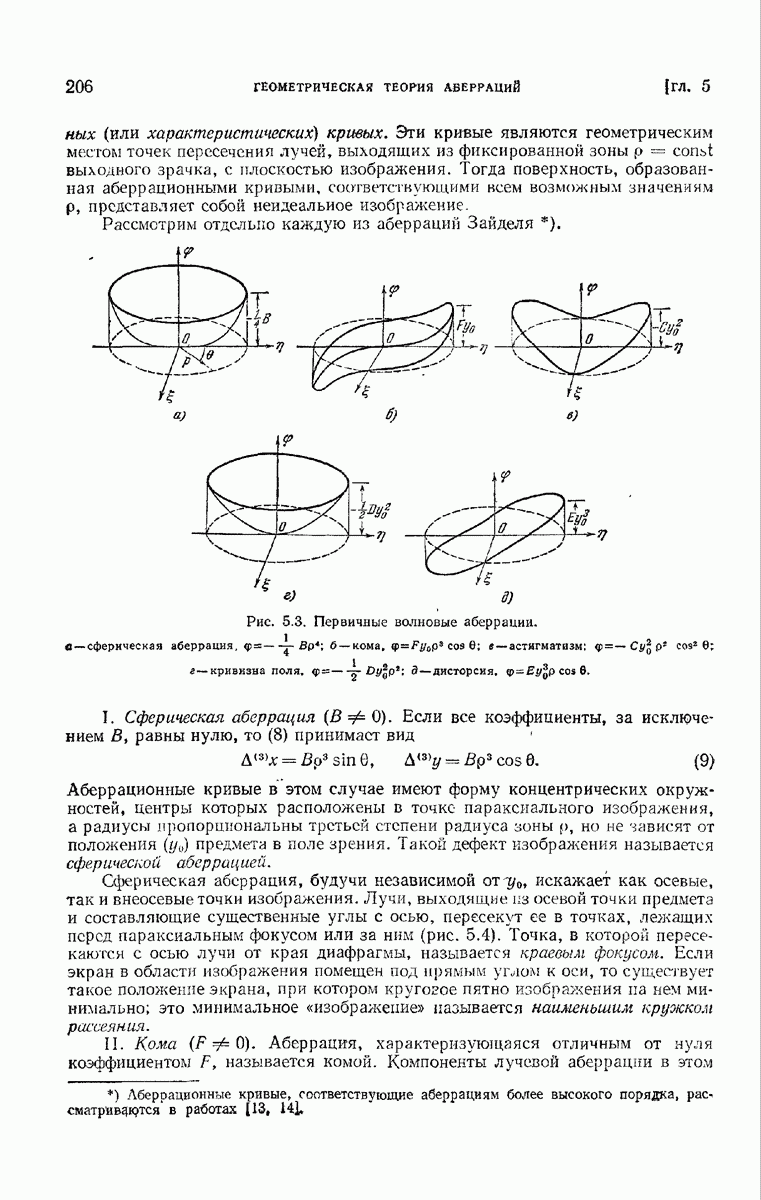
перпендикулярна к плоскости рисунка. В отсутствие предмета возмущение в плоскости  описывается функцией
описывается функцией  множитель
множитель  как обычно, здесь опущен. В присутствии предмета возмущение изменяется и описывается некоторой другой функцией, например
как обычно, здесь опущен. В присутствии предмета возмущение изменяется и описывается некоторой другой функцией, например  Тогда функция пропускания предмета определяется соотношением
Тогда функция пропускания предмета определяется соотношением

Вообще говоря, функция пропускания  зависит не только от
зависит не только от  но и от направления
но и от направления  освещения; кроме того, в общем случае функция
освещения; кроме того, в общем случае функция  комплексна, так как при прохождении сквозь предмет свет может менять и амплитуду, и фазу. В частности, когда предмет изменяет только амплитуду падающей волны, не изменяя ее фазу (т. е. если
комплексна, так как при прохождении сквозь предмет свет может менять и амплитуду, и фазу. В частности, когда предмет изменяет только амплитуду падающей волны, не изменяя ее фазу (т. е. если  мы говорим об амплитудном объекте,
мы говорим об амплитудном объекте,  же он изменяет фазу,
же он изменяет фазу,  не амплитуду (т. е.
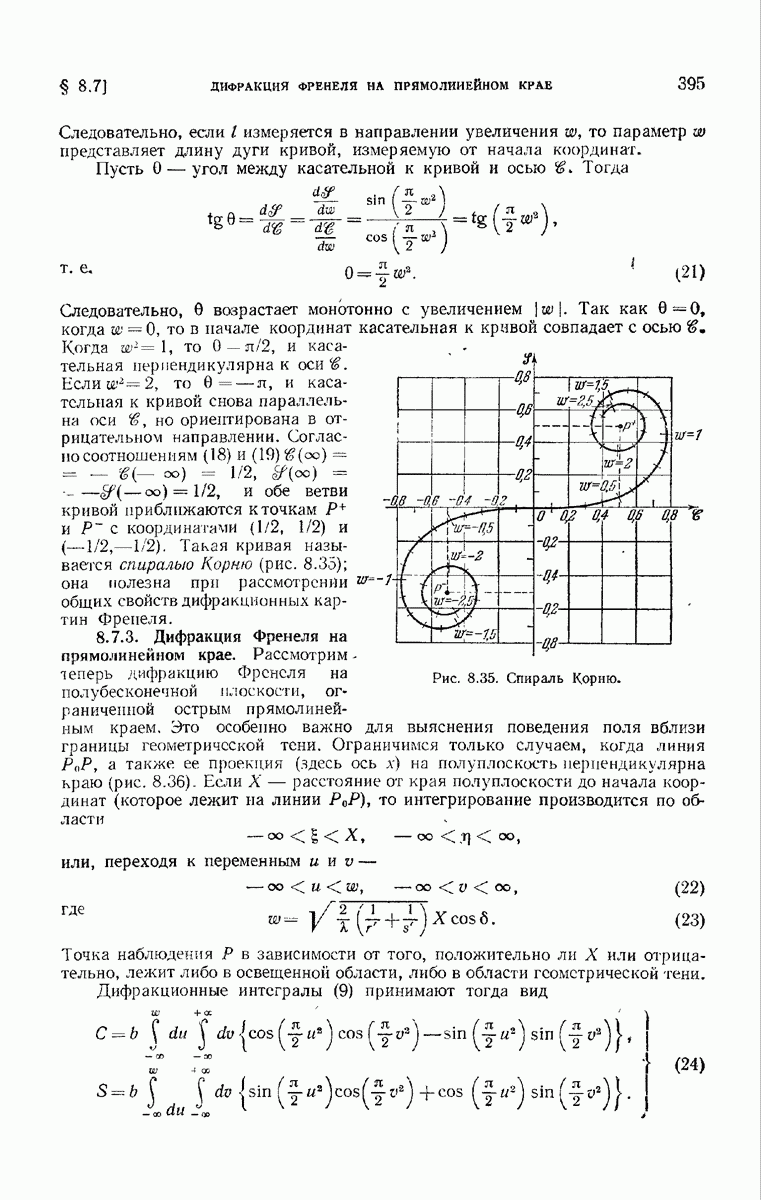
не амплитуду (т. е.  мы говорим о фазовом объекте.
мы говорим о фазовом объекте.
Если изучается свет, отраженный предметом, а не прошедший сквозь него, то рациональнее говорить о функции отражения, определяемой так же, как и функция пропускания, но тогда координатная плоскость помещается с той же стороны предмета, с которой падает свет.
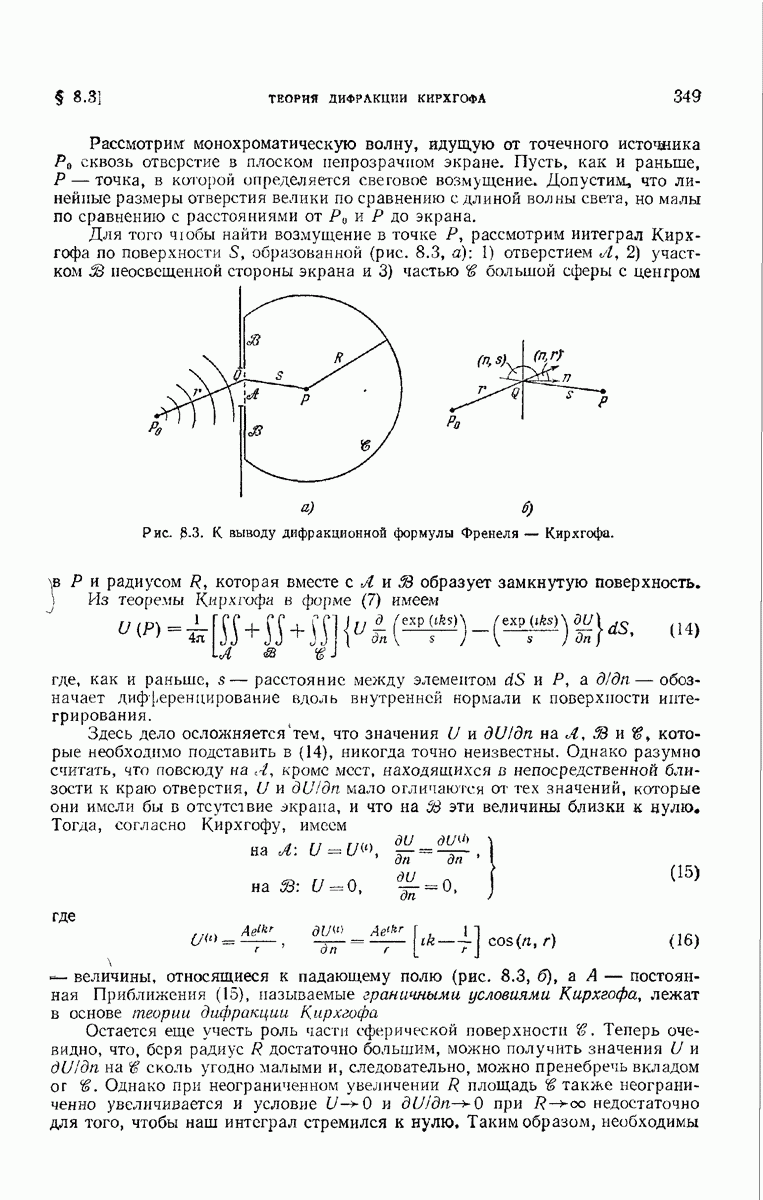
Отношение  практически равно единице для всех точек, находящихся вне геометрической тени (граница ее на рис. 8.16 обозначена точками А и В), отбрасываемой предметом. Закрывая область, лежащую за пределами тени, непрозрачным экраном, мы получим устройство, действующее как дифракционное отверстие
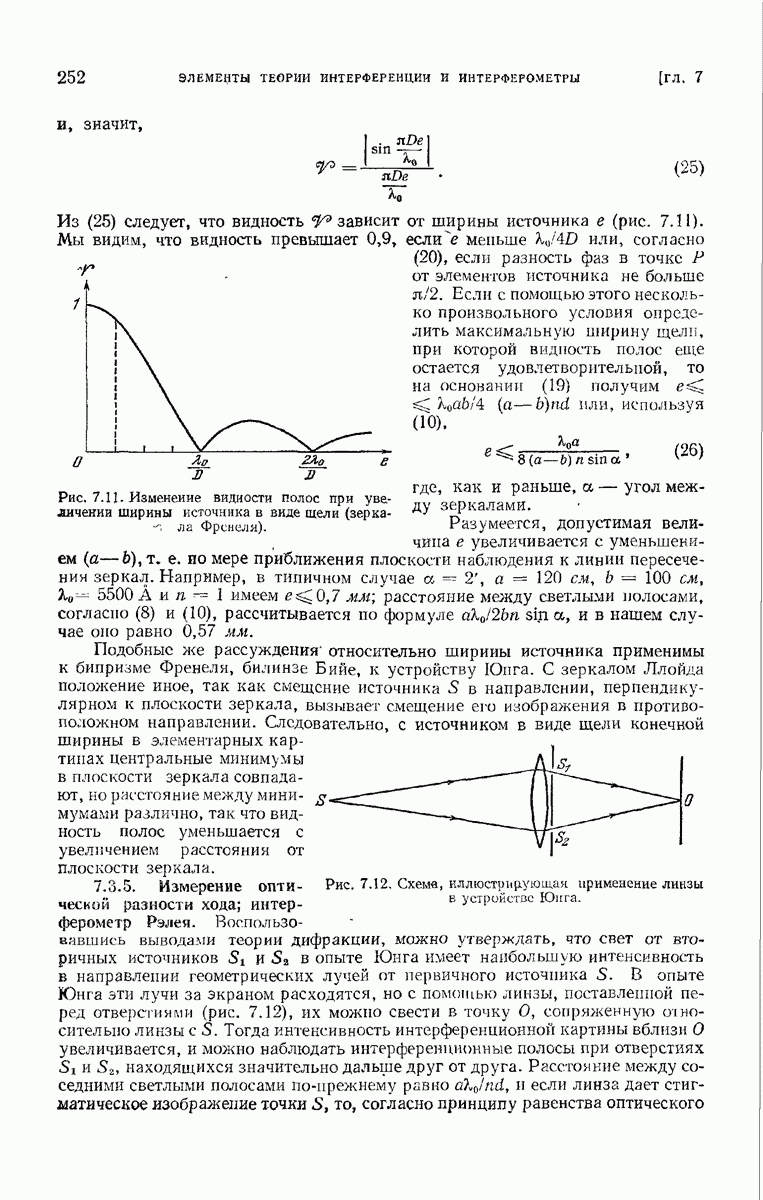
практически равно единице для всех точек, находящихся вне геометрической тени (граница ее на рис. 8.16 обозначена точками А и В), отбрасываемой предметом. Закрывая область, лежащую за пределами тени, непрозрачным экраном, мы получим устройство, действующее как дифракционное отверстие  с неоднородной функцией зрачка (см. (8.3.39)). Пусть линейные размеры 4, велики по сравнению с длиной волны, и пусть функция
с неоднородной функцией зрачка (см. (8.3.39)). Пусть линейные размеры 4, велики по сравнению с длиной волны, и пусть функция  остается в достаточной мере постоянной в областях, размеры которых сравнимы с длиной волны света; тогда дифракционная формула (8.3.23) остается справедливой при тех же условиях, что и раньше, если подынтегральное выражение дифракционного интеграла умножено на
остается в достаточной мере постоянной в областях, размеры которых сравнимы с длиной волны света; тогда дифракционная формула (8.3.23) остается справедливой при тех же условиях, что и раньше, если подынтегральное выражение дифракционного интеграла умножено на 
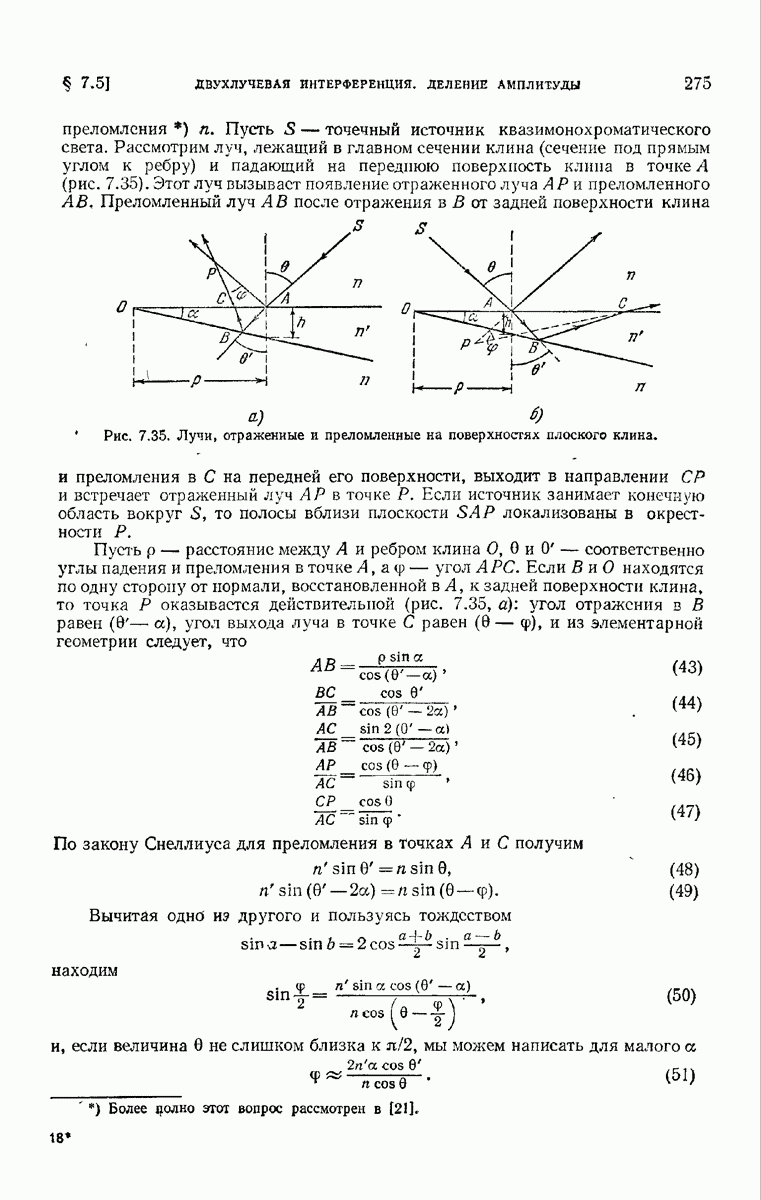
Рассмотрим одномерную решетку, состоящую из  параллельных штрихов произвольного профиля, нанесенных на одну из поверхностей плоскопараллельной стеклянной пластинки. Пусть плоскость
параллельных штрихов произвольного профиля, нанесенных на одну из поверхностей плоскопараллельной стеклянной пластинки. Пусть плоскость  совпадает с плоской поверхностью пластинки,
совпадает с плоской поверхностью пластинки,  — направление штрихов,
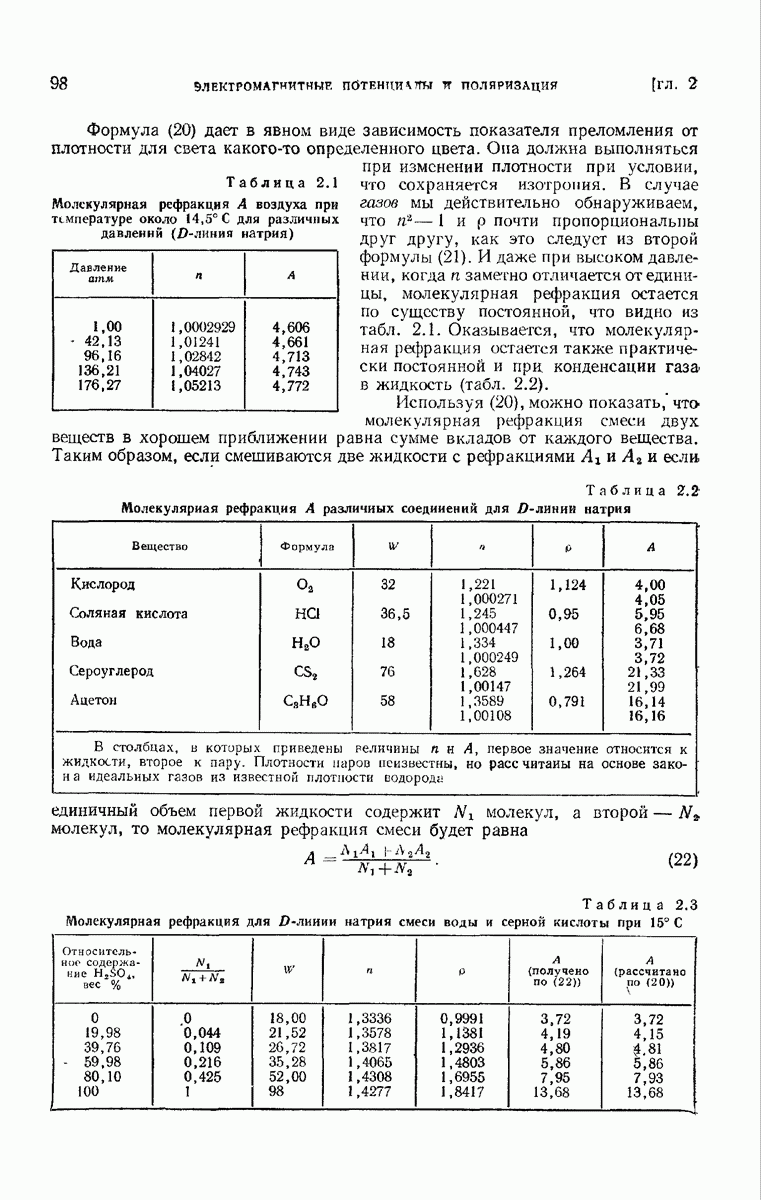
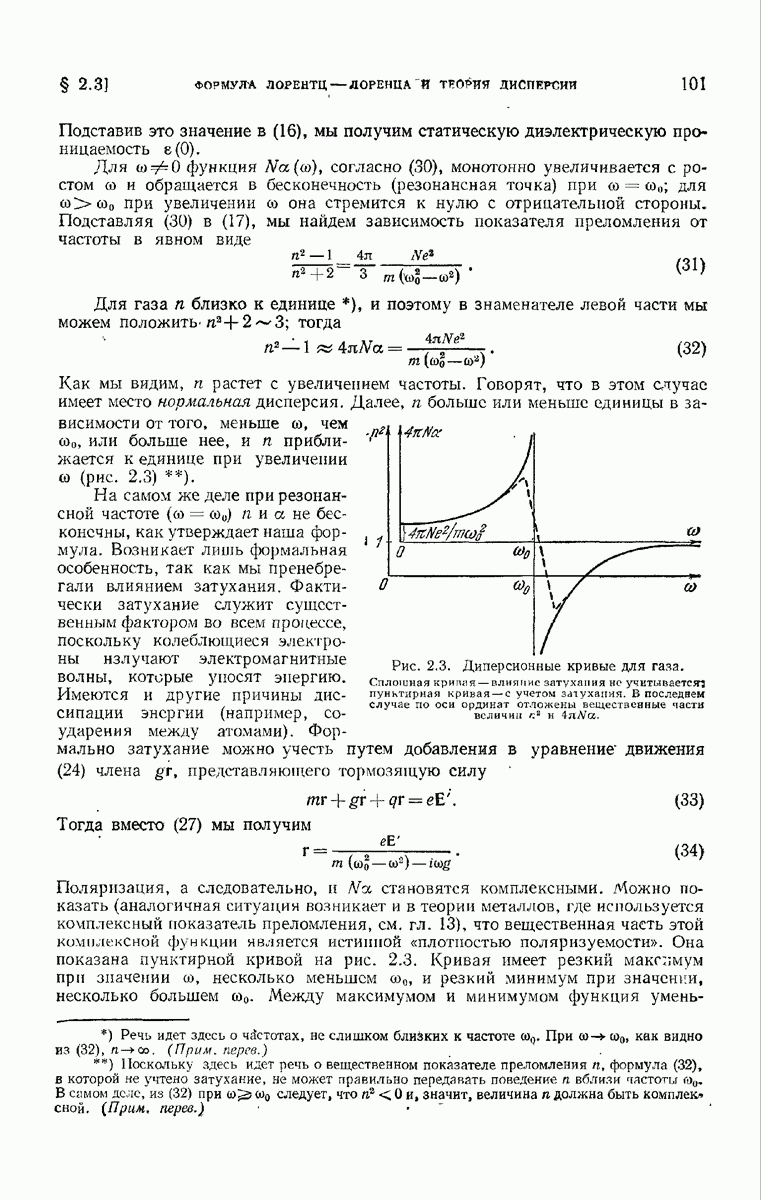
— направление штрихов,  период решетки в направлении
период решетки в направлении  (рис. 8.17).
(рис. 8.17).
Предположим, что направление падающей на решетку волны лежит в плоскости рисунка и образует угол  с осью
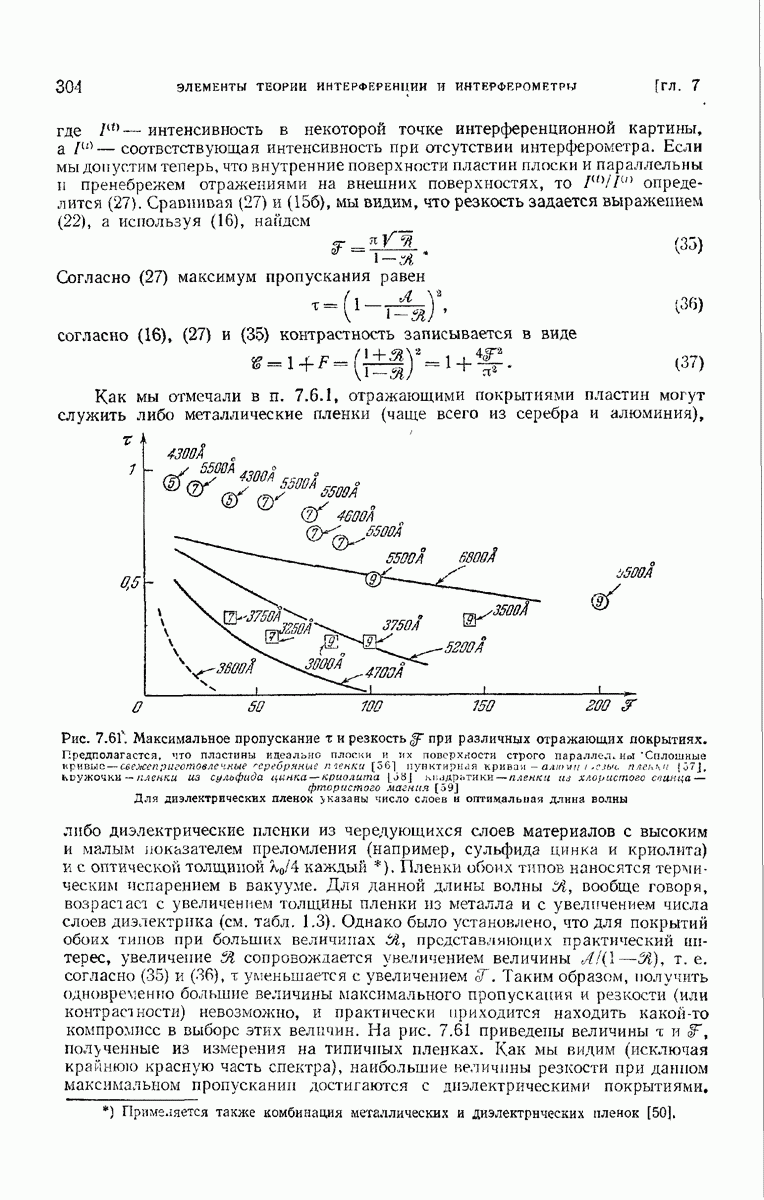
с осью  и пусть
и пусть  — угол между осью
— угол между осью  и линией, соединяющей очень удаленную точку наблюдения Р
и линией, соединяющей очень удаленную точку наблюдения Р
с решеткой. Как и раньше, положим  . В таком случае из (8.5.23) сразу же получаем выражение для комплексной амплитуды в Р, если подынтегральное выражение умножается на функцию пропускания
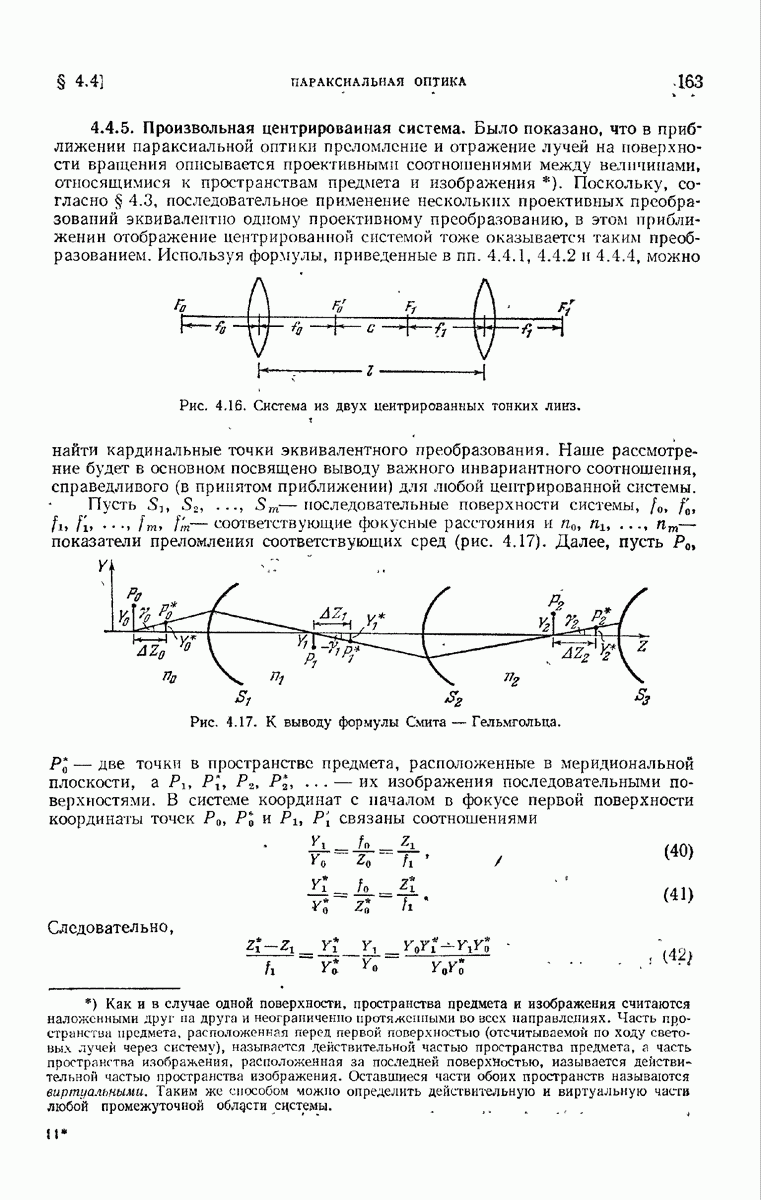
. В таком случае из (8.5.23) сразу же получаем выражение для комплексной амплитуды в Р, если подынтегральное выражение умножается на функцию пропускания  одного периодического элемента.
одного периодического элемента.

Рис. 8.17. К теории дифракционной решетки.
Полагая  и
и

находим

где

Следовательно,

где  Если ввести функцию
Если ввести функцию

то формула (5) для интенсивности примет вид

Прежде чем обсуждать содержание этой основной формулы, отметим, что, согласно (3), распределение интенсивности будет таким же, как и распределение, обусловленное системой вторичных когерентных источников; каждый из них характеризуется одной и той же амплитудной функцией  а их фазы отличаются на величину, кратную
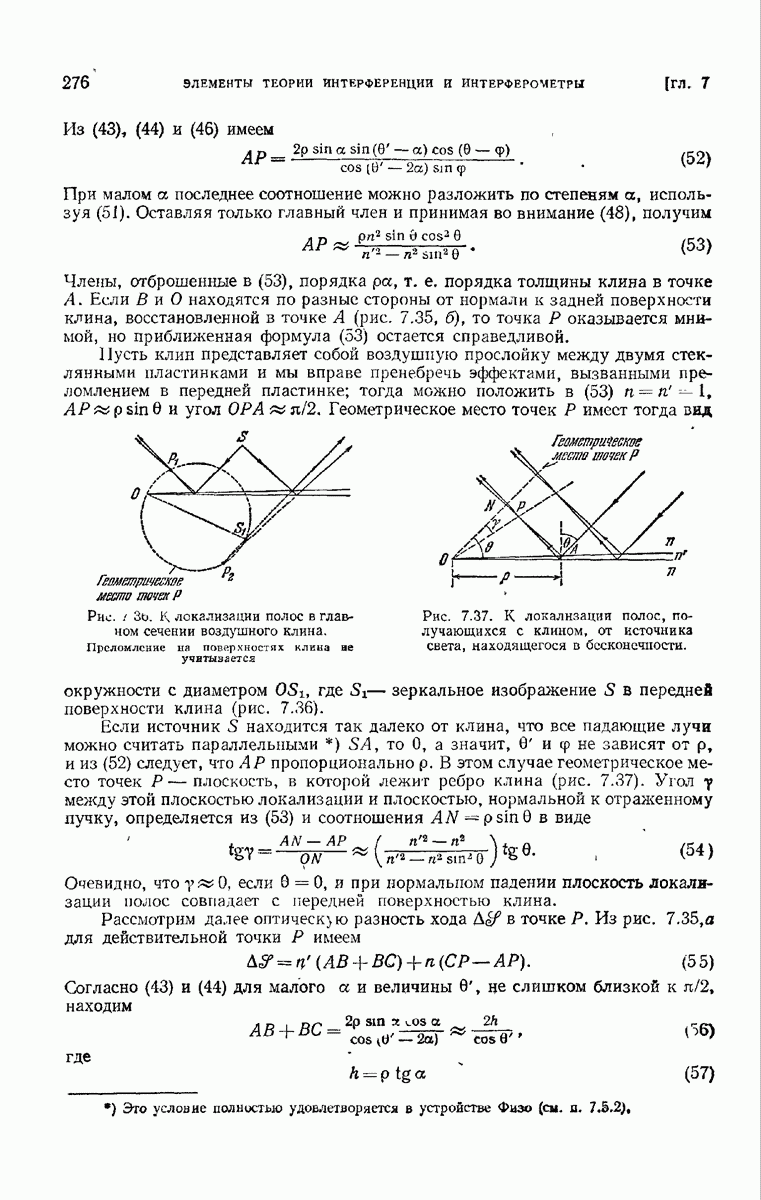
а их фазы отличаются на величину, кратную  Чтобы понять значение этой разности фаз, рассмотрим две соответствующие точки А и В в соседних штрихах решетки (рис. 8.18). Так как влияние решетки заключается в периодическом воздействии на падающую волну, то разность хода между световыми лучами, приходящими в А и В, такая же, как и в отсутствие решетки, т. е. равна
Чтобы понять значение этой разности фаз, рассмотрим две соответствующие точки А и В в соседних штрихах решетки (рис. 8.18). Так как влияние решетки заключается в периодическом воздействии на падающую волну, то разность хода между световыми лучами, приходящими в А и В, такая же, как и в отсутствие решетки, т. е. равна 

Рис. 8.18. К теории дифракционной решетки.
 . Здесь точка К — основание перпендикуляра, опушенного из В
. Здесь точка К — основание перпендикуляра, опушенного из В
на луч, падающий в А. Далее путь светового луча, выходящего из В в направлении 0, превышает путь луча, выходящего из  в том же направлении, на
в том же направлении, на  здесь
здесь  — основание перпендикуляра, опущенного из А на луч, дифрагировавший в В в направлении 0. Следовательно, полная разность хода между светом, приходящим в удаленную точку наблюдения от соответствующих точек двух соседних штрихов, равна
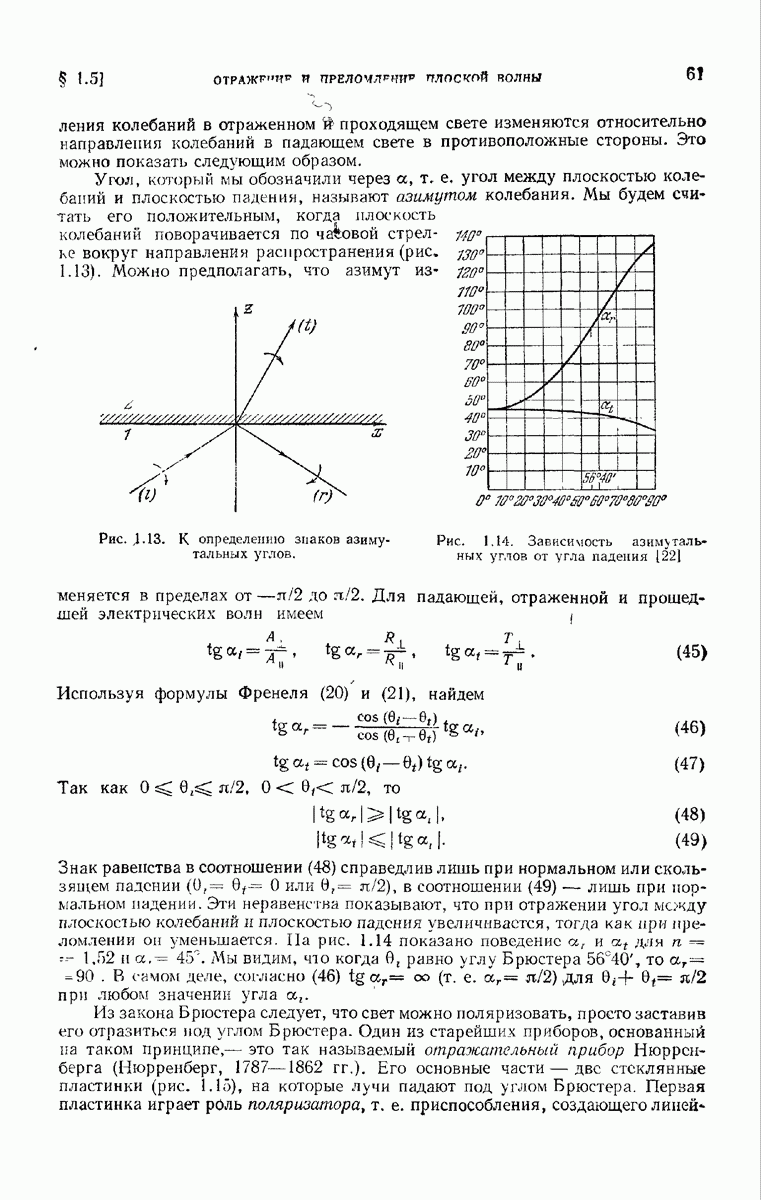
— основание перпендикуляра, опущенного из А на луч, дифрагировавший в В в направлении 0. Следовательно, полная разность хода между светом, приходящим в удаленную точку наблюдения от соответствующих точек двух соседних штрихов, равна

а соответствующая разность фаз равна 
Формула (5а) выражает  в виде произведения двух функций. Одна из них
в виде произведения двух функций. Одна из них  определяет действие одного периода решетки, другая Н отражает эффект интерференции света от различных периодов решетки. Функция
определяет действие одного периода решетки, другая Н отражает эффект интерференции света от различных периодов решетки. Функция  имеет максимумы величиной
имеет максимумы величиной  во всех точках, в которых исчезает знаменатель
во всех точках, в которых исчезает знаменатель  т. е. в тех точках, где х равно нулю или целому кратному
т. е. в тех точках, где х равно нулю или целому кратному  . Следовательно, функция
. Следовательно, функция  имеет максимумы величиной
имеет максимумы величиной  когда
когда


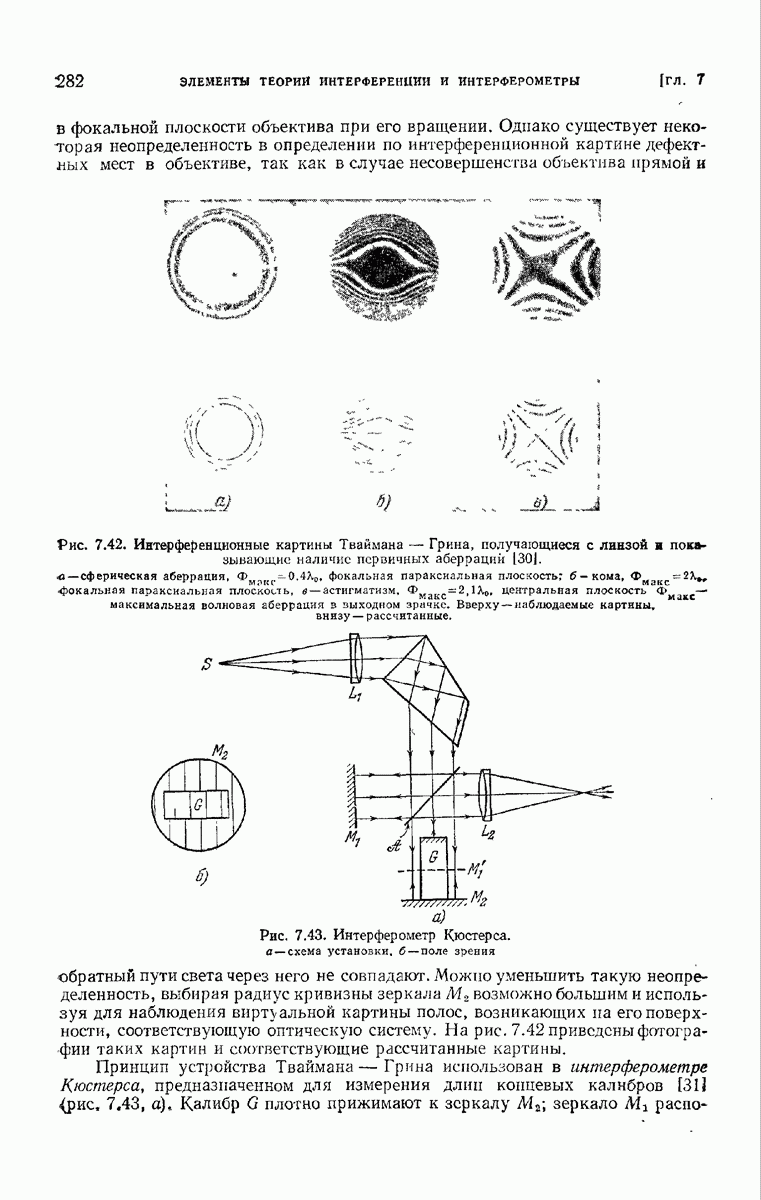
Рис. 8.19. Графики интерференционной функции и функции интенсивности, а) — нормированная интерференционная функция  - нормированная функция интенсивности в случае щели
- нормированная функция интенсивности в случае щели  нормированная функция интенсивности в случае решетки, состоящей из
нормированная функция интенсивности в случае решетки, состоящей из  одинаковых эквидистантных параллельные щелей
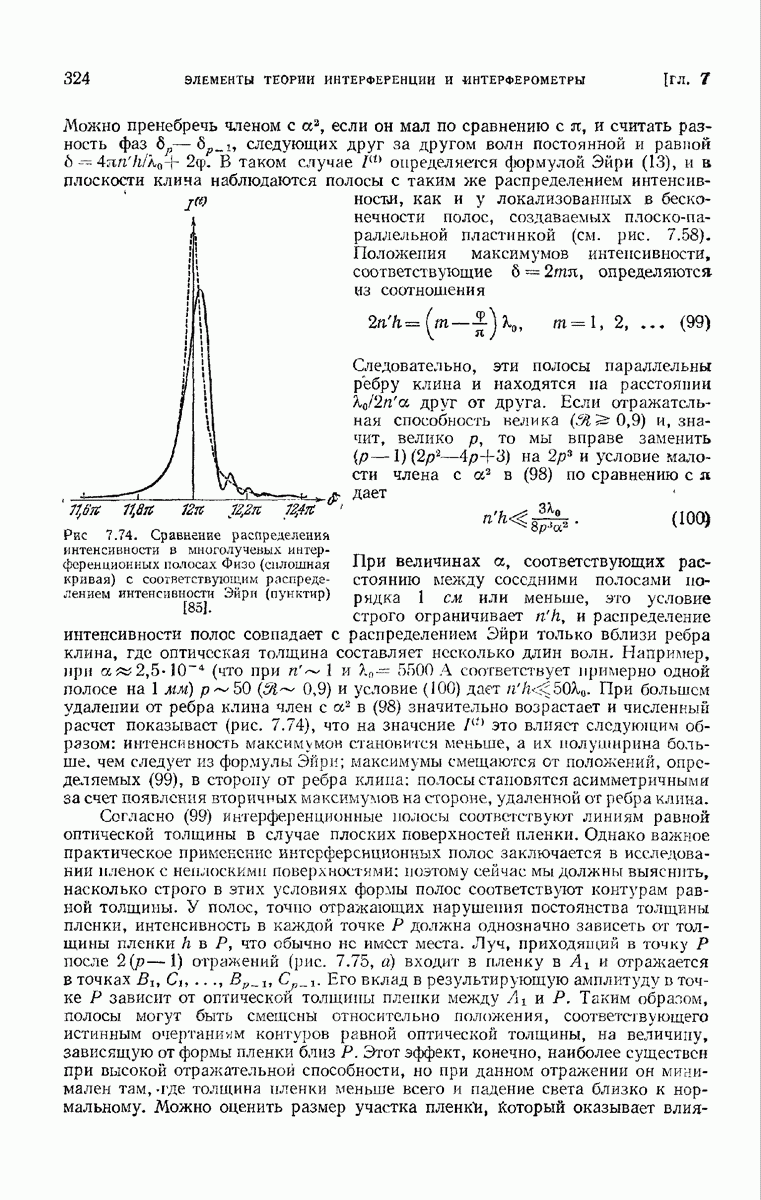
одинаковых эквидистантных параллельные щелей  Показана только область
Показана только область  нее кривые симметричны относительно вертикальной оси
нее кривые симметричны относительно вертикальной оси  .
.
Целое число  согласно (7), представляет собой разность хода (в длинах волн) между светом, дифрагирующим в направлении максимумов и распространяющимся от соответствующих точек
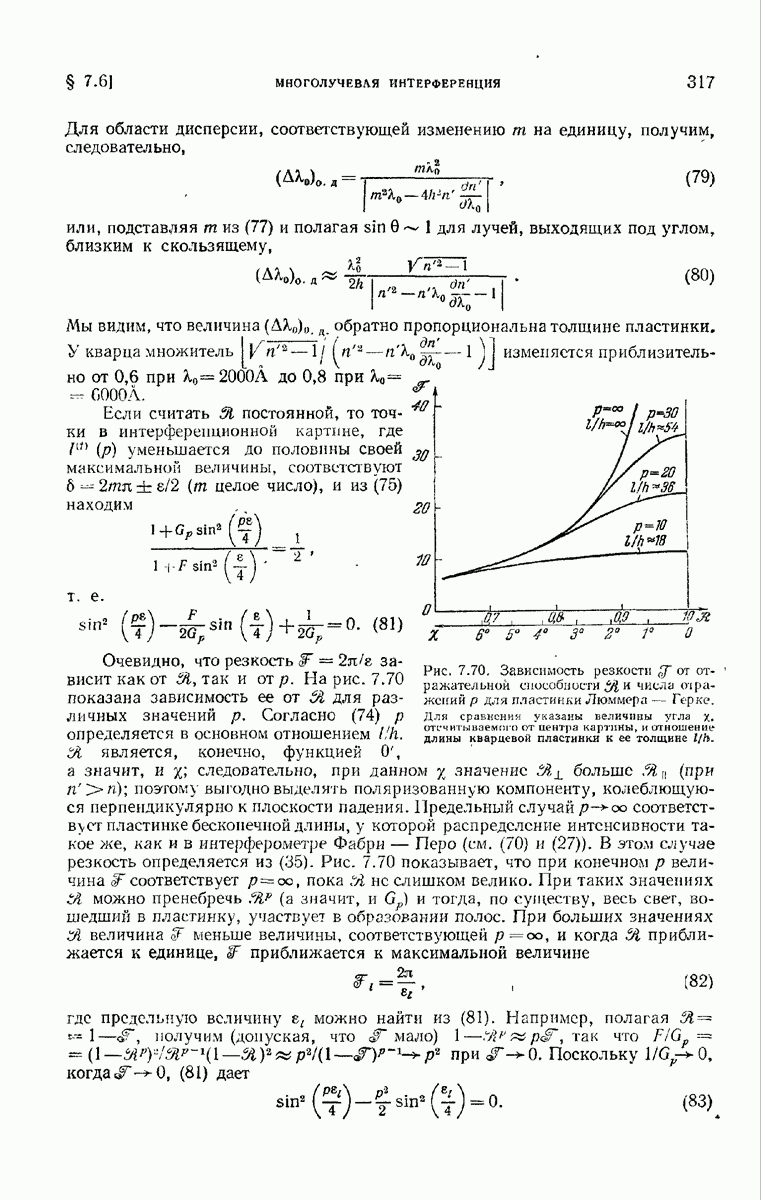
согласно (7), представляет собой разность хода (в длинах волн) между светом, дифрагирующим в направлении максимумов и распространяющимся от соответствующих точек  соседних штрихов. В согласии с нашим прежним определением (см. п. 7.3.1) назовем
соседних штрихов. В согласии с нашим прежним определением (см. п. 7.3.1) назовем  порядком интерференции. В промежутках между этими главными максимумами находятся слабые вторичные максимумы (рис. 8.19, а).
порядком интерференции. В промежутках между этими главными максимумами находятся слабые вторичные максимумы (рис. 8.19, а).
Когда N велико, первый вторичный максимум составляет лишь несколько процентов от главного максимума. Максимумы разделяются точками с нулевой интенсивностью при  т. е. расположены в направлениях, определяемых соотношениями
т. е. расположены в направлениях, определяемых соотношениями

случай, когда  равно целому числу, исключается.
равно целому числу, исключается.
Функция  зависит от формы штрихов. Предположим, что она имеет главный максимум в некотором направлении
зависит от формы штрихов. Предположим, что она имеет главный максимум в некотором направлении  и что с обеих сторон максимума она спадает медленно по сравнению с измеиением Н, В таком случае
и что с обеих сторон максимума она спадает медленно по сравнению с измеиением Н, В таком случае
 имеет общий вид интерференционной функции
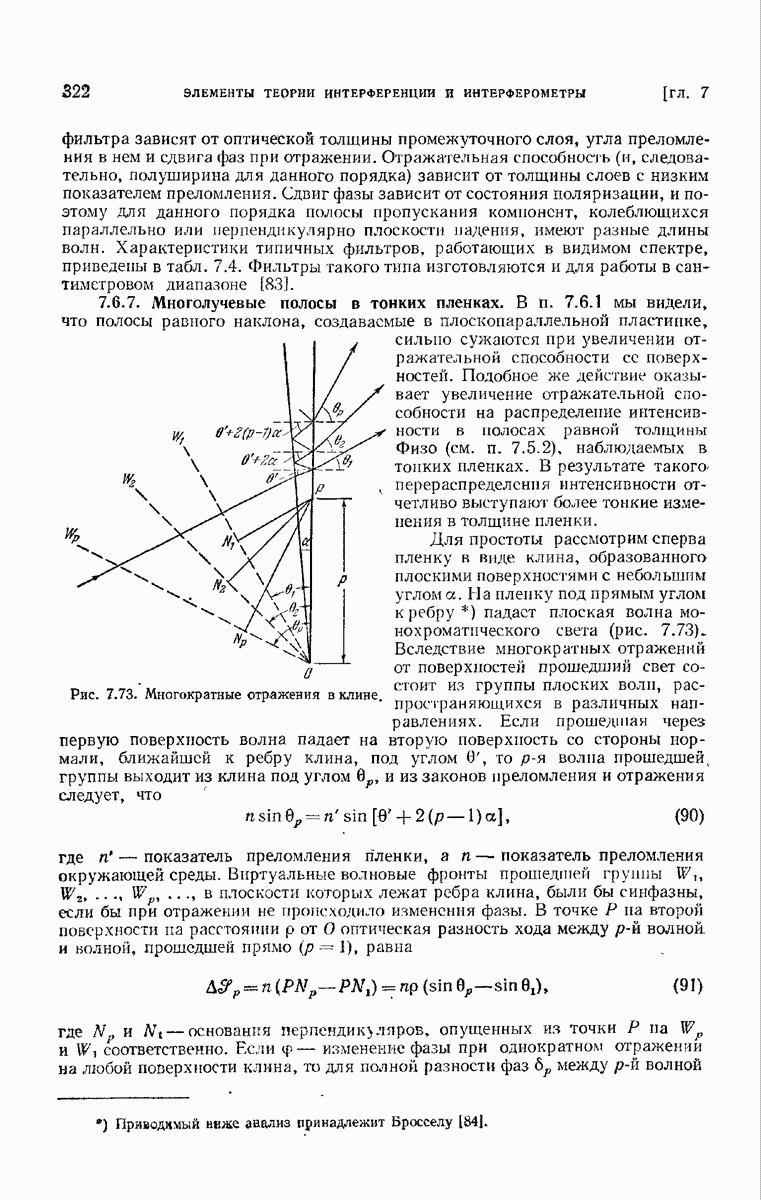
имеет общий вид интерференционной функции  , но «модулированной» функцией Рт. Следовательно,
, но «модулированной» функцией Рт. Следовательно,  также существуют достаточно острые максимумы в направлении, близком к
также существуют достаточно острые максимумы в направлении, близком к  Так как эти направления (исключая случай
Так как эти направления (исключая случай  зависят от длины волны, то очевидно, что решетка разлагает пучок немонохроматического света в спектры нескольких порядков.
зависят от длины волны, то очевидно, что решетка разлагает пучок немонохроматического света в спектры нескольких порядков.
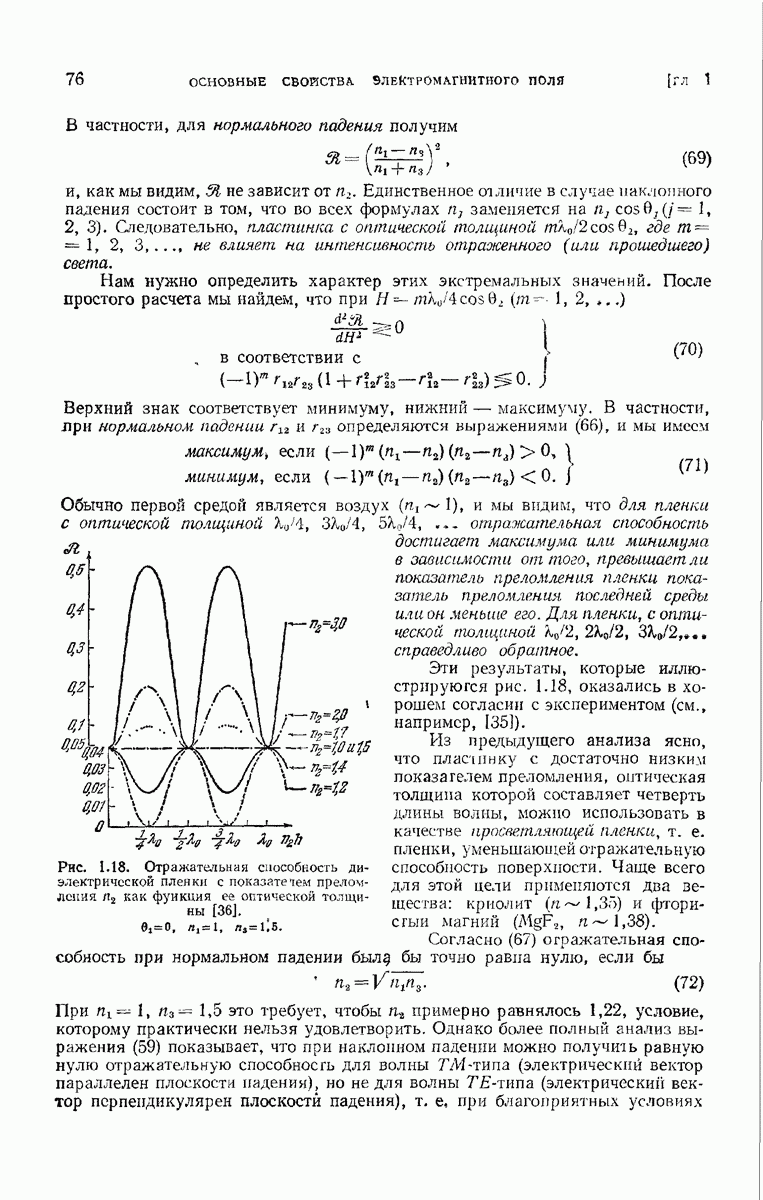
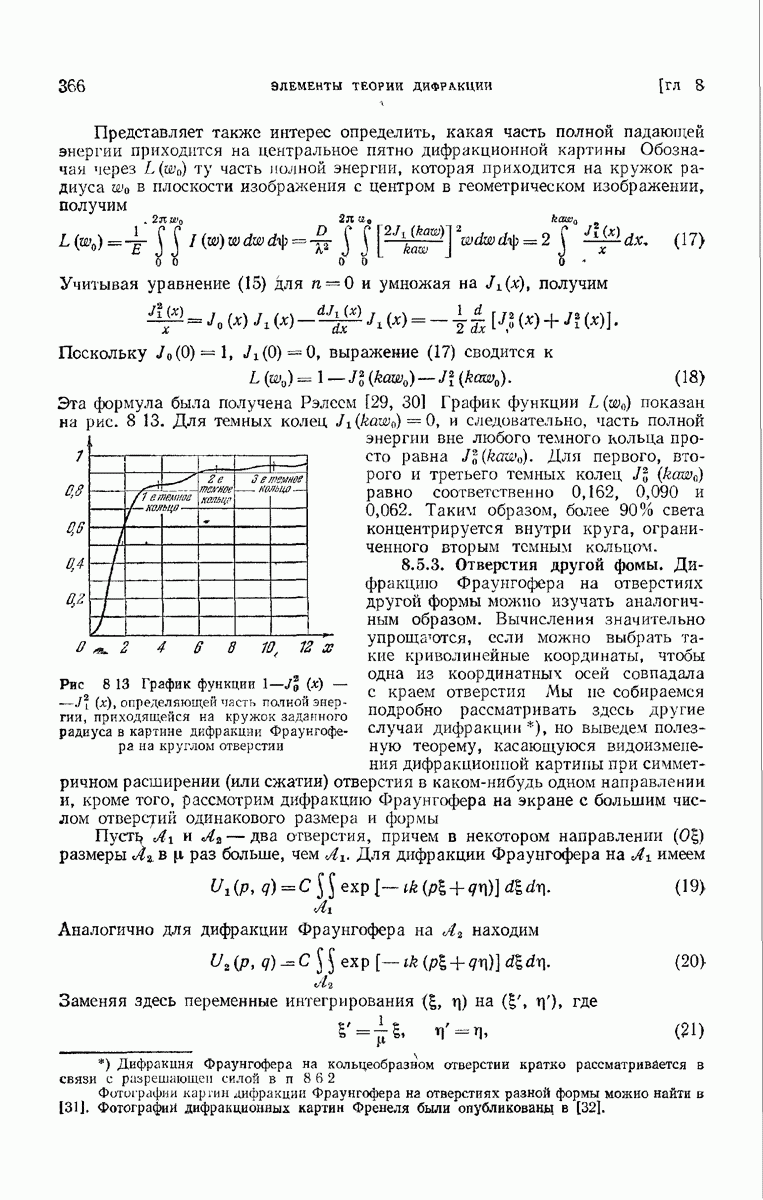
Для иллюстраций изложенного выше рассмотрим решетку, состоящую из ряда длинных эквидистантных щелей (рис. 8.20) шириной  и длиной
и длиной  в непрозрачном экране.
в непрозрачном экране.

Рис. 8.20. Простая линейная решетка.
Если решетка освещается очень удаленным линейным источником, расположенным параллельно щелям, то интенсивность  определяется выражением (8.5.4)
определяется выражением (8.5.4)  и мы получим
и мы получим

На рис. 8.19 приведены кривые, соответствующие обоим множителям в (10) и их произведению. Последний множитель в (10), представляющий действие одиночной щели, имеет главный максимум при  и минимумы при
и минимумы при 

разделенные слабыми вторичными максимумами. Если  т. е. если ширина каждой щели нала по сравнению с
т. е. если ширина каждой щели нала по сравнению с  то в дополнение к главному максимуму при
то в дополнение к главному максимуму при  функция
функция  имеет с обеих сторон от него ряд резких, но постепенно убывающих максимумов, расположенных в направлениях, определяемых (8).
имеет с обеих сторон от него ряд резких, но постепенно убывающих максимумов, расположенных в направлениях, определяемых (8).
Возвращаясь к общему случаю, мы видим, что при очень малой ширине каждого штриха — порядка длины волны (практически это часто бывает), выведенная в приближении Кирхгофа формула (4) не будет справедлива. В таких случаях для установлении детального распределения интенсивности требуется более тонкое исследование. Однако мы вправе ожидать, что основные качественные характеристики, указанные нашей элементарной теорией, а именно существование резких максимумов, положение которых по существу определяется интерференционной функцией Н, остаются правильными даже при очень  штрихах; конечно, при этом функция интенсивности для единичного периода должна мало изменяться в интервале порядка
штрихах; конечно, при этом функция интенсивности для единичного периода должна мало изменяться в интервале порядка 
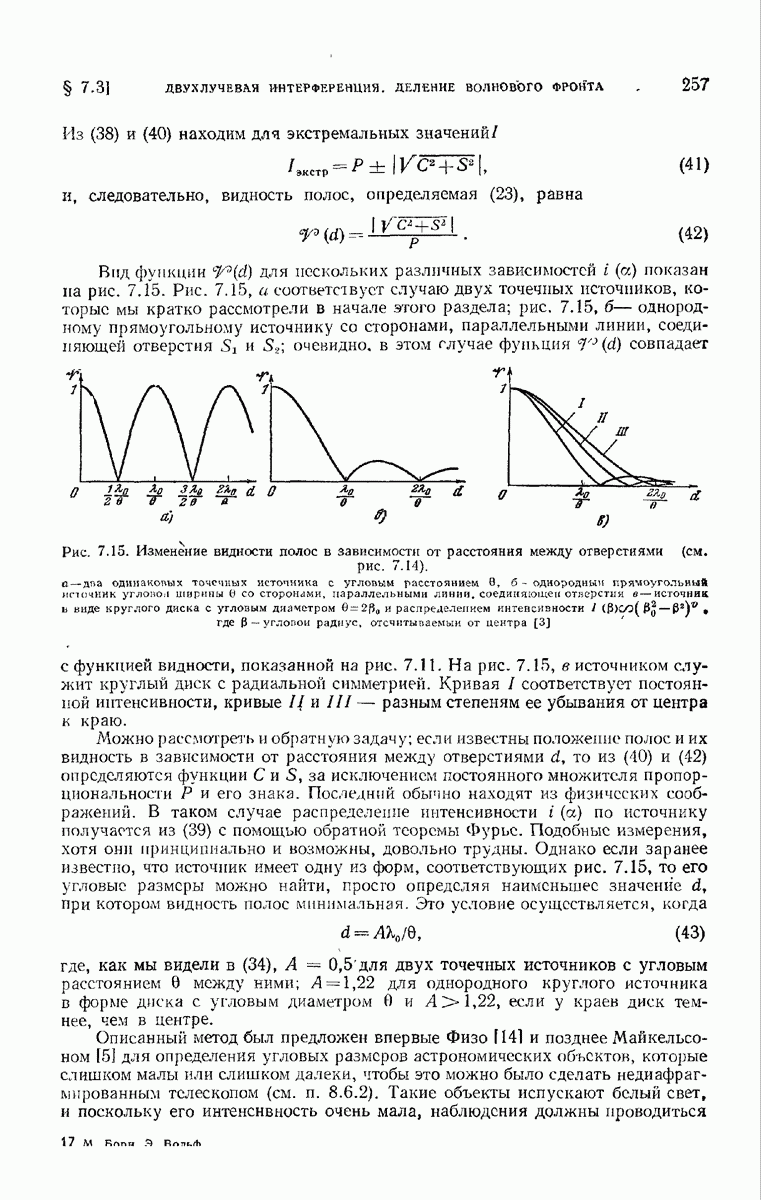
Выясним теперь, какова разрешающая сила дифракционной решетки. Расстояние между главным максимумом порядка  и соседним минимумом определяется, согласно (9), как
и соседним минимумом определяется, согласно (9), как 

Если длина ьолаы изменится на величину  максимум порядка
максимум порядка  сместится, согласно (8), на величину
сместится, согласно (8), на величину 

Предположим, что линии с длинами волн  начинают разрешаться, если максимум одной длины волны совпадает с минимумом другой (см. стр. 307); тогда для предела разрешения в порядке
начинают разрешаться, если максимум одной длины волны совпадает с минимумом другой (см. стр. 307); тогда для предела разрешения в порядке  получим
получим  т. е.
т. е.

Следовательно, разрешающая сила равна произведению номера порядка  на число штрихов
на число штрихов  Для порядка
Для порядка  согласно
согласно  и разрешающую силу можно записать в виде
и разрешающую силу можно записать в виде

В соответствии с (7) это означает, что разрешающая сила равна числу длин волн, укладывающихся в разность хода двух лучей, дифрагировавших от краев решетки (расстояние между ними составляет  в направлении 0. Следует отметить, что поскольку
в направлении 0. Следует отметить, что поскольку  не может превысить 2, разрешающая сила решетки шириной
не может превысить 2, разрешающая сила решетки шириной  не может быть больше
не может быть больше  .
.
Для иллюстрации формулы (14) определим число штрихов, которое должна иметь решетка, чтобы разрешить две линии, отстоящие друг от друга на  и лежащие в центре видимой области спектра. В этом случае
и лежащие в центре видимой области спектра. В этом случае  , и при наблюдении во втором порядке
, и при наблюдении во втором порядке  согласно (14), получим
согласно (14), получим  . Таким образом, решетка должна иметь по крайней мере 27 500 штрихов.
. Таким образом, решетка должна иметь по крайней мере 27 500 штрихов.
Для сравнения рассмотрим разрешающию силу призмы в положении наименьшего отклонения, освещаемую линейным источником, параллельным ребру А (щель спектрографа). Пучок параллельных лучей, падающий на призму, дифрагирует на прямоугольнике шириной  (см. рис. 4.28). Согласно (8.5.2) первый минимум интенсивности находится на угловом расстоянии (предполагается, что оно мало)
(см. рис. 4.28). Согласно (8.5.2) первый минимум интенсивности находится на угловом расстоянии (предполагается, что оно мало)

от геометрического изображения щели. Изменение угловой дисперсии, соответствующее изменению длины волны на величину  согласно (4.7.36), равно
согласно (4.7.36), равно

где  — наибольшая толщина стекла, сквозь которую проходит один из крайних лучей,
— наибольшая толщина стекла, сквозь которую проходит один из крайних лучей,  показатель преломления материала призмы. Па пределе разрешения
показатель преломления материала призмы. Па пределе разрешения  , и поэтому разрешающая сила определяется соотношением
, и поэтому разрешающая сила определяется соотношением

Последнее соотношение показывает, что при данном сорте стекла разрешающая сила призмы зависит только от наибольшей толщины стекла  которую луки проходят в призме; в частности, разрешающая сила не зависит от угла призмы. Например, пусть длина основания призмы равна 5 см и сделана она из тяжелого флинта с
которую луки проходят в призме; в частности, разрешающая сила не зависит от угла призмы. Например, пусть длина основания призмы равна 5 см и сделана она из тяжелого флинта с  на длине волны
на длине волны  . Если работает вся призма, то, согласно (17), в средней части видимой области спектра разрешаются линии, находящиеся на расстоянии, не меньшем
. Если работает вся призма, то, согласно (17), в средней части видимой области спектра разрешаются линии, находящиеся на расстоянии, не меньшем  где
где  Следовательно, у такой призмы довольно больших размеров разрешающая сила в десять раз меньше, чем у решетки с 27 500 штрихами, о которой мы говорили выше.
Следовательно, у такой призмы довольно больших размеров разрешающая сила в десять раз меньше, чем у решетки с 27 500 штрихами, о которой мы говорили выше.
До сих пор мы рассматривали только одномерную решетку, но наш анализ легко распространить на дву- и трехмерную периодические структуры, вызывающие дифракцию. Двумерные решетки (называемые пересекающимися) не нашли практического применения, хотя действие подобных решеток наблюдается часто, например при рассматривании яркого источника света скеозь тонкую ткань (хотя бы носовой платок). Теория же трехмерных решеток представляет огромный практический интерес, так как такие решетки образуются в кристаллах благодаря правильному расположению атомов. Постоянная этой
решетки (расстояние между соседними атомами) порядка  что совпадает по порядку величины с длиной волн рентгеновских лучей. Следовательно, при прохождении сквозь кристалл пучка рентгеновских лучей возникает дифракционная картина, и, анализируя ее, можно получить информацию относительно структуры кристалла (см., например, [35] или [36]). Дифракция рентгеновских лучей в кристаллах, предсказанная в 1912 г. Лауэ, наблюдалась впервые Фридрихом и Книппингом [37].
что совпадает по порядку величины с длиной волн рентгеновских лучей. Следовательно, при прохождении сквозь кристалл пучка рентгеновских лучей возникает дифракционная картина, и, анализируя ее, можно получить информацию относительно структуры кристалла (см., например, [35] или [36]). Дифракция рентгеновских лучей в кристаллах, предсказанная в 1912 г. Лауэ, наблюдалась впервые Фридрихом и Книппингом [37].
Другим примером решеткоподобной структуры служат ультразвуковые волны в жидкости. Они представляют собой упругие волны, создаваемые пьезоэлектрическим генератором, и отличаются от обычных звуковых волн только значительно более высокой частотой, лежащей существенно выше верхнего предела слышимости. Такие волны вызывают периодические разряжения и сжатия жидкости, действующие на проходящий свет, как решетка. Теория этого явления излагается в гл. 12. В заключение настоящего параграфа рассмотрим одномерные решетки, которые применяются в спектроскопии.
б) Типы дифракционных решеток. Принцип действия дифракционной решетки был открыт в 1785 г. Риттенхаузом ([39], см. также [40]), но тогда его открытие не привлекло внимания, и решетка была изобретена вновь в 1819 г. Фраунгофером [41]. Первые решечки, изготовленные Франугофером, были выполнены из очень тонкой проволоки, навитой на два параллельных винта. Изготовление таких проволочных решеток сравнительно несложно, и поэтому в некоторых случаях ими пользуются даже в наше время, особенно в длинноволновой (инфракрасной) области спектра. Позднее Фраунгофер с помощью специальной машины прочерчивал штрихи на золотой пленке, нанесенной на стеклянную пластинку, или же, пользуясь алмазным резцом, — параллельные штрихи на самой поверхности стекла.
Значительных успехов в технике изготовления решеток достиг Роуланд [42], который создал несколько превосходных гравировальных машин и, кроме того, изобрел так называемую вогнутую решетку (см. стр. 378, 379). При помощи машины Роуланда можно было наносить штрихи длиной более 10 см на решетку шириной 15 см. Первая машина Роуланда позволяла прочерчивать около 560 штрихов на 1 мм, что обеспечивало разрешающую силу решетки, превышающую  Позднее Майкельсон изготовлял решетки значительно шире 15 см с разрешающей силой, примерно равной 400 000.
Позднее Майкельсон изготовлял решетки значительно шире 15 см с разрешающей силой, примерно равной 400 000.
Большинство первых решеток гравировались на зеркальном металле или стекле, позднее появились решетки со штрихами, нанесенными на напыленный слой алюминия. Алюминий обладает хорошей отражательной способностью в ультрафиолете и, кроме того, вследствие своей мягкости не вызывает быстрого износа чертящего острия (алмаза).
У идеальной решетки штрихи должны быть строго параллельны и ими  одинаковую форму. Однако на практике оба эти требования обычно не выполняются. Совершенно нерегулярные ошибки приводят к затуманиванию картины и не так серьезны, как систематические ошибки, например в периоде решетки. Последние приводят к появлению в спектре паразитных линий, называемых духами. Очень часто такие духи с большим трудом можно отличить от настоящих линий.
одинаковую форму. Однако на практике оба эти требования обычно не выполняются. Совершенно нерегулярные ошибки приводят к затуманиванию картины и не так серьезны, как систематические ошибки, например в периоде решетки. Последние приводят к появлению в спектре паразитных линий, называемых духами. Очень часто такие духи с большим трудом можно отличить от настоящих линий.
Высокая разрешающая сила — не единственное серьезное требование, предъявляемое практической спектроскопией. В тех случаях, когда энергии недостаточно (с чем приходится сталкиваться, например, при изучении спектров слабых звезд и туманностей или при работе в инфракрасной области спектра) существенно, чтобы как можно больше света дифрагировало в определенном направлении. Кроме того, при точных измерениях длин волн применяемая
решетка должна обладать большой, дисперсией. Согласно (8) угловая дисперсия (при постоянном угле падения света) равна

следовательно, для получения большой дисперсии расстояние  должно быть малым или наблюдения должны вестись в высоких порядках (большое
должно быть малым или наблюдения должны вестись в высоких порядках (большое  При работе с решетками, имеющими вид последовательности непрозрачных и прозрачных (или отражающих) полосок, только малая часть падающего света попадает в какой-нибудь один порядок. Это недостаток устраняется у современных решеток тем, что наносимым штрихам придают определенную форму Специальная решетка, форма штрихов которой показана на рис. 8.21, позволяет направить большую часть света в один или два порядка, лежащие по одну сторону от дентрального изображения. Решетки такого типа с довольно грубыми штрихами называются эшелетами, так как они занимают промежуточное положение между решетками более старых типов и так называемыми эшелонами, которые будут описаны ниже. Эшелеты были впервые изготовлены Вудом 143) на медных пластинках. В качестве резца он пользовался естественной гранью специально отобранного кристалла карборунда. Позднее такие решетки гравировались алмазным острием, которому шлифовкой придавалась нужная форма. Эти решетки имели от 80 до 120 штрихов на 1 мм; при работе с видимым светом они посылают большую его часть в спектры 15-го или 30-го порядка. Эшелеты представляют значительную ценность для инфракрасной спектроскопии.
При работе с решетками, имеющими вид последовательности непрозрачных и прозрачных (или отражающих) полосок, только малая часть падающего света попадает в какой-нибудь один порядок. Это недостаток устраняется у современных решеток тем, что наносимым штрихам придают определенную форму Специальная решетка, форма штрихов которой показана на рис. 8.21, позволяет направить большую часть света в один или два порядка, лежащие по одну сторону от дентрального изображения. Решетки такого типа с довольно грубыми штрихами называются эшелетами, так как они занимают промежуточное положение между решетками более старых типов и так называемыми эшелонами, которые будут описаны ниже. Эшелеты были впервые изготовлены Вудом 143) на медных пластинках. В качестве резца он пользовался естественной гранью специально отобранного кристалла карборунда. Позднее такие решетки гравировались алмазным острием, которому шлифовкой придавалась нужная форма. Эти решетки имели от 80 до 120 штрихов на 1 мм; при работе с видимым светом они посылают большую его часть в спектры 15-го или 30-го порядка. Эшелеты представляют значительную ценность для инфракрасной спектроскопии.

Рис. 8.21. Отражательная решетка с задан ной формой штрихов.
Сравнительно недавно были разработаны методы нанесения штрихов заданного профиля на решетки со значительно меньшим расстоянием между штрихами [44]. Такие «блестящие» решетки, как их называют, со штрихами, похожими по форме на штрихи эшелета, образуют наиболее интенсивные спектры в очень низких порядках (обычно в первом или во втором).
По-видимому, разрешающая сила решеток описанных типов достигает примерно 400 000 и ограничивается практическими трудностями изготовления. В некоторых случаях (например, при изучении эффекта Зеемана и дифракционной картины сверхтонкой или изотопической структуры) необходима разрешающая сила, превосходящая эту величину. Такую высокую разрешающую силу имеют предложенные Гаррисоном [45] решетки, называемые эшелями. Эти решетки с широкими и неглубокими штрихами рассчитывают для работы при углах падения света, больших 45°, причем направление падения должно быть нормальным к узкой стороне ступеньки. При работе с эшелями используются сравнительно высокие порядки  Эшель длиной 25 см с 4 штрихами на 1 мм, рассчитанная для работы в
Эшель длиной 25 см с 4 штрихами на 1 мм, рассчитанная для работы в  порядке, имеет разрешающую силу в 1000000.
порядке, имеет разрешающую силу в 1000000.
Изготовление решеток хорошего качества представляет значительные трудности, и поэтому часто используются реплики. Они изготовляются путем отливки матрицы с оригинальной гравированной решетки.
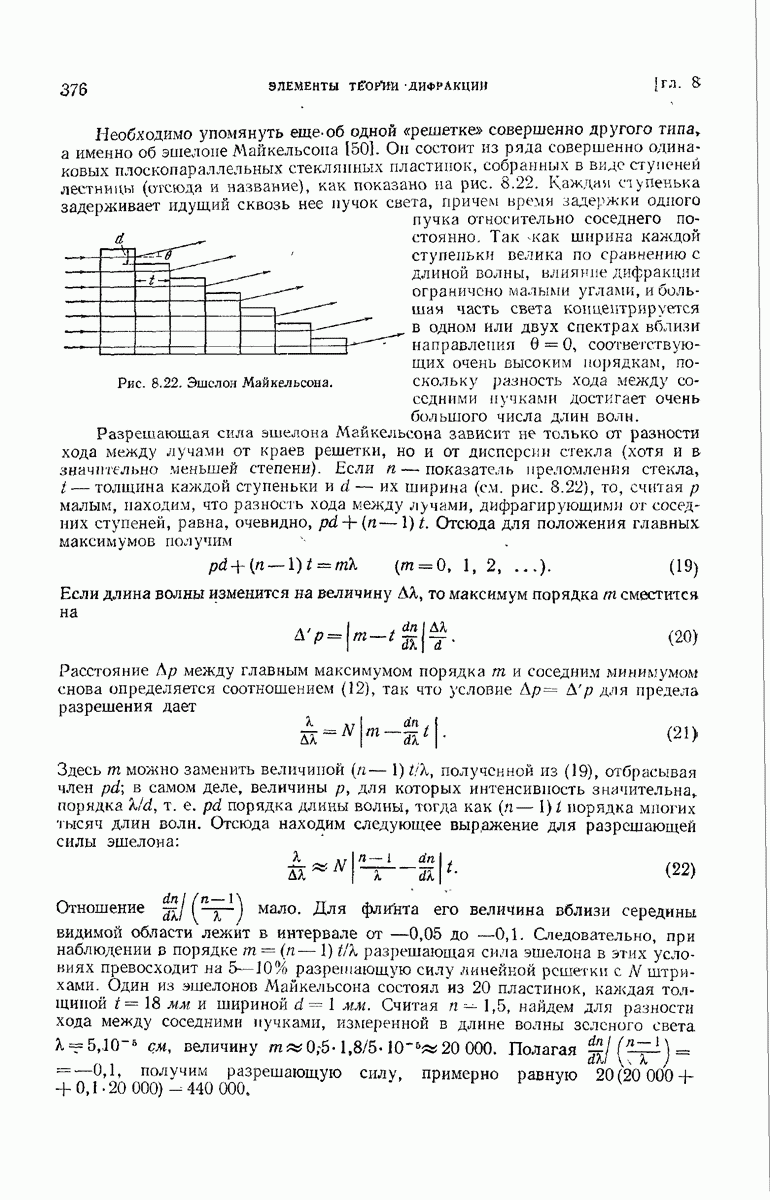
Необходимо упомянуть еще об одной «решетке» совершенно другого типа, а именно об эшелоне Майкельсона [50]. Он состоит из ряда совершенно одинаковых плоскопараллельных стеклянных пластинок, собранных в виде ступеней лестницы (отсюда и название), как показано на рис. 8.22. Каждая ступенька задерживает идущий сквозь нее пучок света, причем время задержки одного пучка относительно соседнего постоянно, Так как ширина каждой ступеньки велика по сравнению с. длиной волны, влияние дифракции ограничено малыми углами, и большая часть света концентрируется  в одном или двух спектрах вблизи направления
в одном или двух спектрах вблизи направления  соответствующих очень высоким порядкам, поскольку разность хода между соседними пучками достигает очень большого числа длин волн.
соответствующих очень высоким порядкам, поскольку разность хода между соседними пучками достигает очень большого числа длин волн.

Рис. 8.22. Эшелон Майкельсона.
Разрешающая сила эшелона Майкельсона зависит не только от разности хода между лучами от краев решетки, но и от дисперсии стекла (хотя и в значительно меньшей степени). Если  — показатель преломления стекла,
— показатель преломления стекла,  — толщина каждой ступеньки и
— толщина каждой ступеньки и  — их ширина (см. рис. 8.22), то, считая
— их ширина (см. рис. 8.22), то, считая  малым, находим, что разность хода между лучами, дифрагирующими от соседних ступеней, равна, очевидно,
малым, находим, что разность хода между лучами, дифрагирующими от соседних ступеней, равна, очевидно,  Отсюда для положения главных максимумов получим
Отсюда для положения главных максимумов получим

Если длина волны изменится на величину  то максимум порядка
то максимум порядка  сместится на
сместится на

Расстояние  между главным максимумом порядка
между главным максимумом порядка  и соседним минимумом снова определяется соотношением (12), так что условие
и соседним минимумом снова определяется соотношением (12), так что условие  для предела разрешения дает
для предела разрешения дает

Здесь  можно заменить величиной
можно заменить величиной  полученной из (19), отбрасывая член
полученной из (19), отбрасывая член  в самом деле, величины
в самом деле, величины  для которых интенсивность значительна, порядка
для которых интенсивность значительна, порядка  порядка длины волны, тогда как
порядка длины волны, тогда как  порядка многих тысяч длин волн. Отсюда находим следующее выражение для разрешающей силы эшелона:
порядка многих тысяч длин волн. Отсюда находим следующее выражение для разрешающей силы эшелона:

Отношение  мало. Для флинта его величина вблизи середины видимой области лежит в интервале от —0,05 до
мало. Для флинта его величина вблизи середины видимой области лежит в интервале от —0,05 до  Следовательно, при наблюдении в порядке
Следовательно, при наблюдении в порядке  разрешающая сила эшелона в этих условиях превосходит на 5—10% разрешающую силу линейной решетки с
разрешающая сила эшелона в этих условиях превосходит на 5—10% разрешающую силу линейной решетки с  штрихами. Один из эшелонов Майкельсона состоял из 20 пластинок, каждая толщиной
штрихами. Один из эшелонов Майкельсона состоял из 20 пластинок, каждая толщиной  мм и шириной
мм и шириной  мм. Считая
мм. Считая  найдем для разности хода между соседними пучками, измеренной в длине волны зеленого света
найдем для разности хода между соседними пучками, измеренной в длине волны зеленого света  см, величину
см, величину  . Полагая
. Полагая  , получим разрешающую силу, примерно равную
, получим разрешающую силу, примерно равную  ,
,
Более важное значение имеет отражательный эшелон. У него каждая ступенька покрывается высоко отражающим металлическим слоем и спектры наблюдаются в отраженном свете. Разрешающая сила отражательного эшелона превосходит разрешающую силу пропускающего эшелона таких же размеров в 3—4 раза, так как каждая ступенька вносит запаздывание между соседними пучками на величину  вместо
вместо  Так же, как и у эшели, у отражательного эшелона разрешающая сила может превышать миллион. Другое преимущество отражательного эшелона перед пропускающим состоит в том, что его можно использовать в ультрафиолетовой области спектра, где стекло непрозрачно. Майксльсон отчетливо представлял преимущества, которые имеет отражательный эшелон перед пропускающим, но технические трудности долго препятствовали изготовлению хороших приборов такого типа. Только спустя почти тридцать лет эти трудности были успешно преодолены Вильямсом [51]. Серьезные трудности представляет точная сборка эшелона, состоящего из большого числа пластинок одинаковой толщины.
Так же, как и у эшели, у отражательного эшелона разрешающая сила может превышать миллион. Другое преимущество отражательного эшелона перед пропускающим состоит в том, что его можно использовать в ультрафиолетовой области спектра, где стекло непрозрачно. Майксльсон отчетливо представлял преимущества, которые имеет отражательный эшелон перед пропускающим, но технические трудности долго препятствовали изготовлению хороших приборов такого типа. Только спустя почти тридцать лет эти трудности были успешно преодолены Вильямсом [51]. Серьезные трудности представляет точная сборка эшелона, состоящего из большого числа пластинок одинаковой толщины.
Поэтому число ступени; в эшелонах лрактически не превышает 40.

Рис. 8.23. Перекрывании спектров разных порядков, полученных с решеткой.
Наконец надо сделать несколько замечаний относительно перекрывания спектров, принадлежащих разным порядкам. Ограничимся рассмотрением видимого спектра, т. е. области длин волн от  до
до  Мы видим, что спектр первого порядка не налагается на спектр второго порядка, так как спектр первого порядка занимает участок от
Мы видим, что спектр первого порядка не налагается на спектр второго порядка, так как спектр первого порядка занимает участок от  до
до  тогда как спектр второго порядка начинается при
тогда как спектр второго порядка начинается при  Вместе с тем спектр второго порядка занимает область от
Вместе с тем спектр второго порядка занимает область от  до
до  а спектр третьего порядка начинается уже при
а спектр третьего порядка начинается уже при  так что оба они частично покрываются. При увеличении порядка соседние спектры перекрываются все больше и больше (рис. 8.23). Если линии с длинами волн X и
так что оба они частично покрываются. При увеличении порядка соседние спектры перекрываются все больше и больше (рис. 8.23). Если линии с длинами волн X и  налагаются в двух соседних порядках
налагаются в двух соседних порядках  то
то

Таким образом, свободная область дисперсии обратно пропорциональна порядку спектра.
Перекрывание порядков в свое время применялось для сравнения длин волн в методе совпадений (см. стр, 313). Позднее для этой цели начали пользоваться простой интерполяцией между длинами волн эталонных линий, которые определялись интерферометрически.
В заключение подведем итог главным отличительным чертам решеток различных типов. Напомним, что, согласно (14), высокая разрешающая сила достигается либо с большим числом периодов и относительно малыми порядками, либо с умеренным числом периодов и высокими порядками. Обычно с гравированными решетками работают в очень низких порядках  , тогда как эшелоны используются в высоких порядках
, тогда как эшелоны используются в высоких порядках  . В промежутках находятся эшелеты (отот 15 до 30) и эшели
. В промежутках находятся эшелеты (отот 15 до 30) и эшели  . Для практических целей следует помнить, что угловая дисперсия прямо пропорциональна порядку спектра и обратно пропорциональна периоду, а свободная область дисперсии обратно пропорциональна порядку.
. Для практических целей следует помнить, что угловая дисперсия прямо пропорциональна порядку спектра и обратно пропорциональна периоду, а свободная область дисперсии обратно пропорциональна порядку.
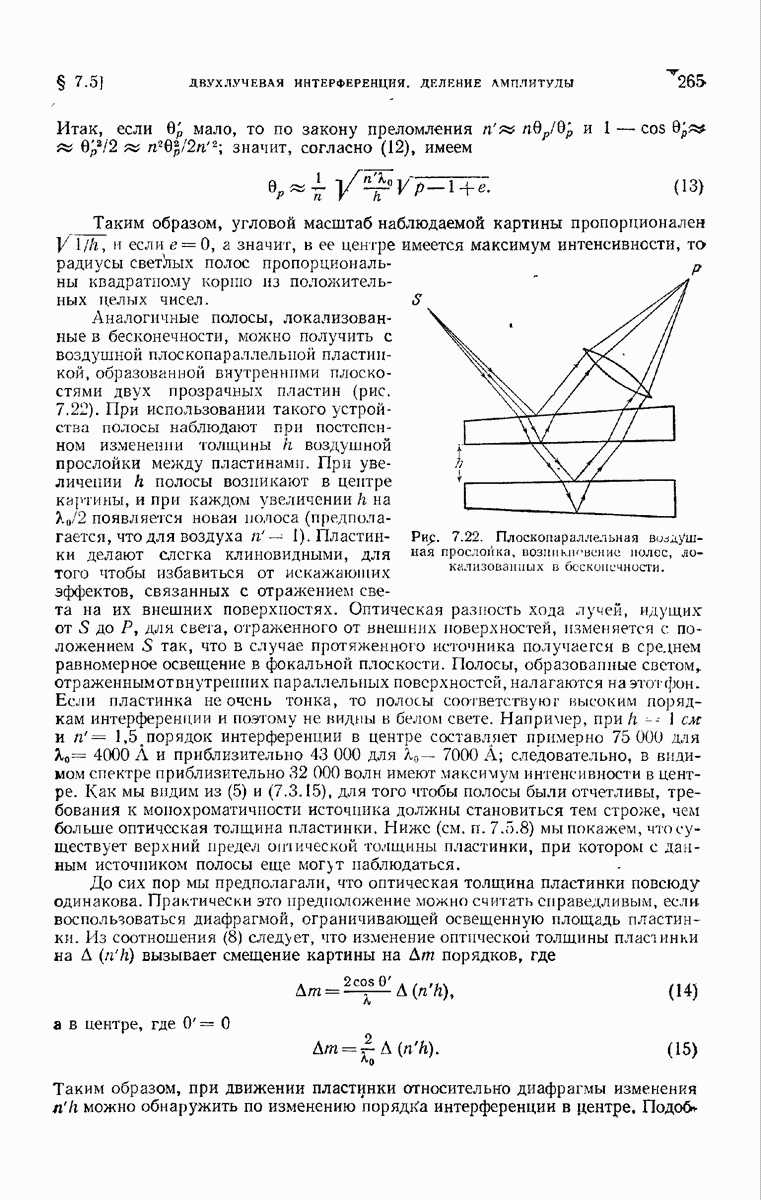
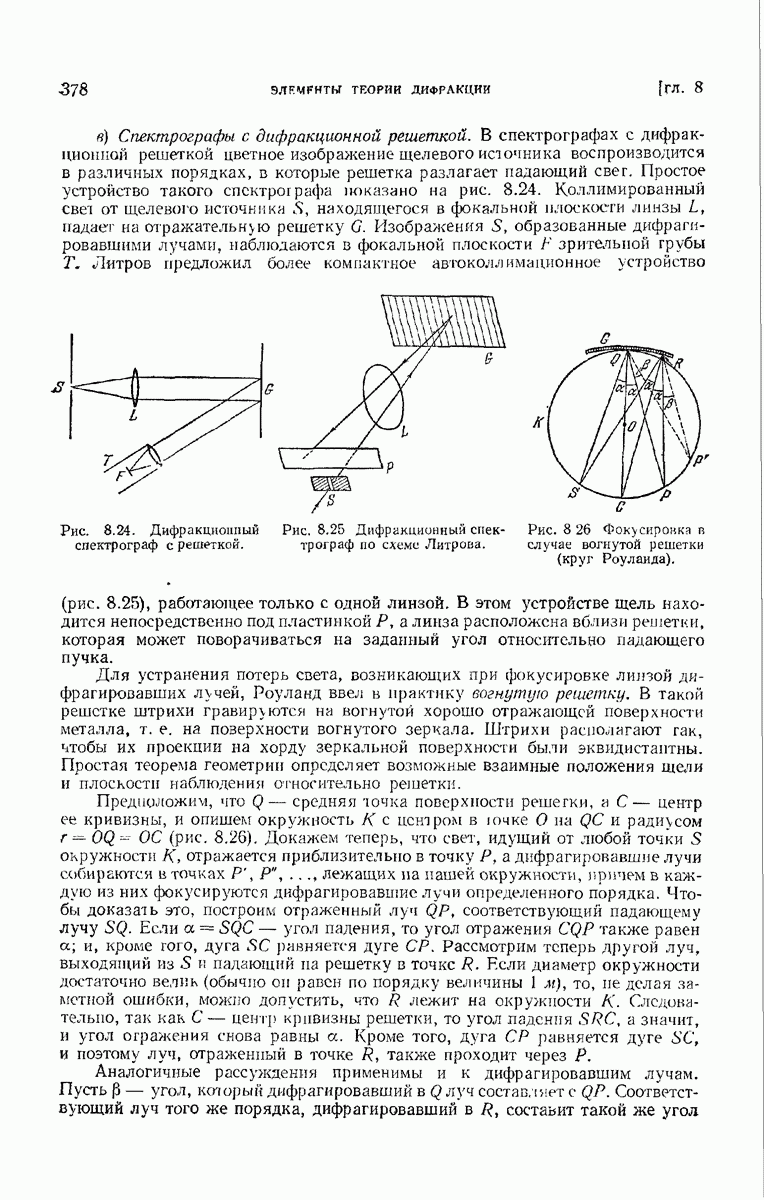
в) Спектрографы с дифракционной решеткой. В спектрографах с дифракционной решеткой цветное изображение щелевого источника воспроизводится в различных порядках, в которые решетка разлагает падающий свег. Простое устройство такого спектрографа показано на рис. 8.24. Коллимированный свет от щелевого источника  , находящегося в фокальной плоскости линзы
, находящегося в фокальной плоскости линзы  падает на отражательною решетку
падает на отражательною решетку  Изображения
Изображения  образованные дифрагировавшими лучами, наблюдаются в фокальной плоскости
образованные дифрагировавшими лучами, наблюдаются в фокальной плоскости  зрительной грубы Т. Литров предложил более компактное автоколлимационное устройство (рис. 8.25), работающее только с одной линзой.
зрительной грубы Т. Литров предложил более компактное автоколлимационное устройство (рис. 8.25), работающее только с одной линзой.

Рис. 8.24. Дифракционный спектрограф с решеткой.

Рис. 8.25 Дифракционный спектрограф по схеме Лнтропа.

Рис. 8 26 Фокусировка  случае вогнутой решетки (круг Роулаида).
случае вогнутой решетки (круг Роулаида).
В этом устройстве щель находится непосредственно под пластинкой Р, а линза расположена вблизи решетки, которая может поворачиваться на заданный угол относительно падающего пучка.
Для устранения потерь света, возникающих при фокусировке линзой дифрагировавших лучей, Роуланд ввел в практику вогнутую решетку. В такой решетке штрихи гравируются на вогнутой хорошо отражающей поверхности металла, т. е. на поверхности вогнутого зеркала. Штрихи располагают гак, чтобы их проекции на хорду зеркальной поверхности были эквидистантны. Простая теорема геометрии определяет возможные взаимные положения щели и плоскости наблюдения относительно решетки.
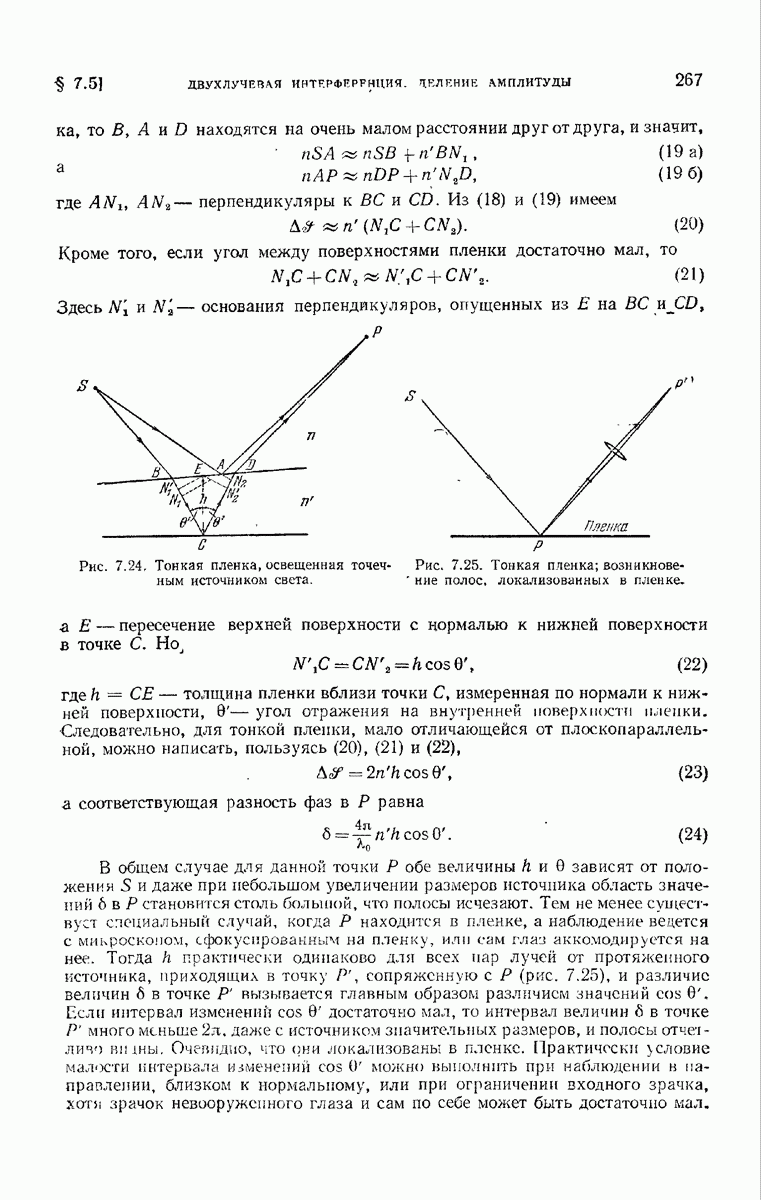
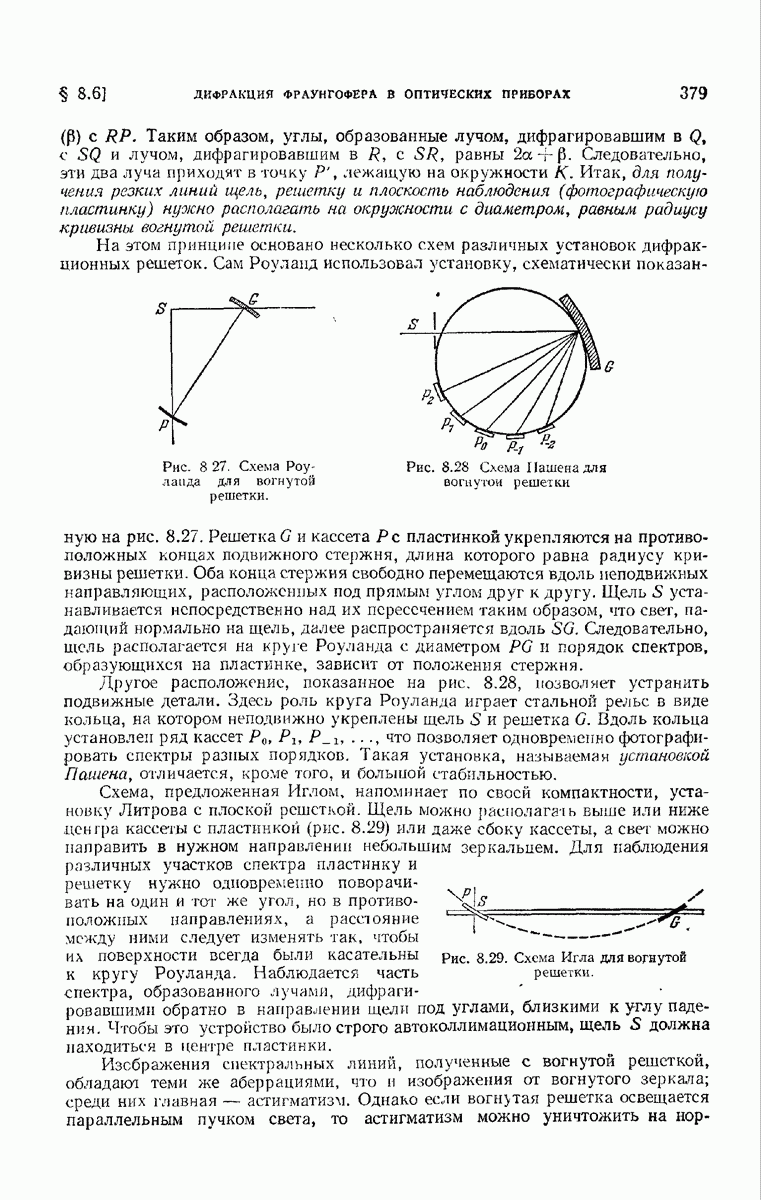
Предположим, что  средняя точка поверхности решетки, а С — центр ее кривизны, и опишем окружность К с центром в ючке О на
средняя точка поверхности решетки, а С — центр ее кривизны, и опишем окружность К с центром в ючке О на  и радиусом
и радиусом  (рис. 8.26). Докажем теперь, что свет, идущий от любой точки 5 окружности К, отражается приблизительно в точку Р, а дифрагировавшие лучи собираются в точках
(рис. 8.26). Докажем теперь, что свет, идущий от любой точки 5 окружности К, отражается приблизительно в точку Р, а дифрагировавшие лучи собираются в точках  лежащих на нашей окружности, причем в каждую из них фокусируются дифрагировавшие лучи определенного порядка. Чтобы доказать это, построим отраженный луч
лежащих на нашей окружности, причем в каждую из них фокусируются дифрагировавшие лучи определенного порядка. Чтобы доказать это, построим отраженный луч  соответствующий падающему лучу
соответствующий падающему лучу  Если
Если  — угол падения, то угол отражения
— угол падения, то угол отражения  также равен
также равен  и, кроме того, дуга
и, кроме того, дуга  равняется дуге
равняется дуге  Рассмотрим теперь другой луч, выходящий из
Рассмотрим теперь другой луч, выходящий из  и падающий на решетку в точке
и падающий на решетку в точке  Если диаметр окружности достаточно велик (обычно
Если диаметр окружности достаточно велик (обычно  равен по порядку величины
равен по порядку величины  то, не делая заметной ошибки, можно допустить, что
то, не делая заметной ошибки, можно допустить, что  лежит на окружности К. Следовательно, так как
лежит на окружности К. Следовательно, так как  центр кривизны решетки, то угол падения
центр кривизны решетки, то угол падения  а значит, и угол отражения снова равны а. Кроме того, дуга
а значит, и угол отражения снова равны а. Кроме того, дуга  равняется дуге
равняется дуге  и поэтому луч, отраженный в точке
и поэтому луч, отраженный в точке  также проходит через Р.
также проходит через Р.
Аналогичные рассуждения применимы и к дифрагировавшим лучам. Пусть  — угол, который дифрагировавший в
— угол, который дифрагировавший в  луч составляет с
луч составляет с  Соответствующий луч того же порядка, дифрагировавший в
Соответствующий луч того же порядка, дифрагировавший в  составит такой же угол
составит такой же угол
(Р) с  Таким образом, углы, образованные лучом, дифрагировавшим в
Таким образом, углы, образованные лучом, дифрагировавшим в  с
с  и лучом, дифрагировавшим в
и лучом, дифрагировавшим в  с
с  равны
равны  Следовательно, эти два луча приходят в точку
Следовательно, эти два луча приходят в точку  лежащую на окружности К. Итак, для получения резких линий щель, решетку и плоскость наблюдения (фотографическую пластинку) нужно располагать на окружности с диаметром, равным радиусу кривизны вогнутой решетки.
лежащую на окружности К. Итак, для получения резких линий щель, решетку и плоскость наблюдения (фотографическую пластинку) нужно располагать на окружности с диаметром, равным радиусу кривизны вогнутой решетки.
На этом принципе основано несколько схем различных установок дифракционных решеток. Сам Роуланд использовал установку, схематически показанную на рис. 8.27.

Рис. 8 27. Схема Роуланда для вогнутой решетки.

Рис. 8.28 Схема Пашенадля вогнутой решетки
Решетка  и кассета
и кассета  пластинкой укрепляются на противоположных концах подвижного стержня, длина которого равна радиусу кривизны решетки. Оба конца стержня свободно перемещаются вдоль неподвижных направляющих, расположенных под прямым углом друг к другу. Щель
пластинкой укрепляются на противоположных концах подвижного стержня, длина которого равна радиусу кривизны решетки. Оба конца стержня свободно перемещаются вдоль неподвижных направляющих, расположенных под прямым углом друг к другу. Щель  устанавливается непосредственно над их пересечением таким образом, что свет, падающий нормально на щель, далее распространяется вдоль
устанавливается непосредственно над их пересечением таким образом, что свет, падающий нормально на щель, далее распространяется вдоль  Следовательно, щель располагается на круге Роуланда с диаметром
Следовательно, щель располагается на круге Роуланда с диаметром  и порядок спектров, образующихся на пластинке, зависит от положения стержня.
и порядок спектров, образующихся на пластинке, зависит от положения стержня.
Другое расположение, показанное на рис. 8.28, позволяет устранить подвижные детали. Здесь роль круга Роуланда играет стальной рельс в виде кольца, на котором неподвижно укреплены щель  и решетка С. Вдоль кольца установлен ряд кассет
и решетка С. Вдоль кольца установлен ряд кассет  , что позволяет одновременно фотографировать спектры разных порядков. Такая установка, называемая установкой Пашена, отличается, кроме того, и большой стабильностью.
, что позволяет одновременно фотографировать спектры разных порядков. Такая установка, называемая установкой Пашена, отличается, кроме того, и большой стабильностью.
Схема, предложенная Иглом, напоминает по своей компактности, установку Литрова с плоской решеткой. Щель можно располагать выше или ниже центра кассеты с пластинкой (рис. 8.29) или даже сбоку кассеты, а свет можно направить в нужном направлении небольшим зеркальцем. Для наблюдения различных участков спектра пластинку и решетку нужно одновременно поворачивать на один и  же угол, но в противоположных направлениях, а расстояние между ними следует изменять так, чтобы их поверхности всегда были касательны к кругу Роуланда. Наблюдается часть спектра, образованного лучами, дифрагировавшими обратно в направлении щели под углами, близкими к углу падения. Чтобы это устройство было строго автоколлимационным, щель
же угол, но в противоположных направлениях, а расстояние между ними следует изменять так, чтобы их поверхности всегда были касательны к кругу Роуланда. Наблюдается часть спектра, образованного лучами, дифрагировавшими обратно в направлении щели под углами, близкими к углу падения. Чтобы это устройство было строго автоколлимационным, щель  должна находиться в центре пластинки.
должна находиться в центре пластинки.

Рис. 8.29. Схема Игла для вогнутой решетки.
Изображения спектральных линий, полученные с вогнутой решеткой, обладают теми же аберрациями, что и изображения от вогнутого зеркала; среди них главная — астигматизм. Однако если вогнутая решетка освещается параллельным пучком света, то астигматизм можно уничтожить на
нормали к решетке и свести к очень малой величине по всему полезному спектру.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 1.1. Электромагнитное поле
- 1.1.2. Материальные уравнения.
- 1.1.3. Граничные условия на поверхностях раздела.
- 1.1.4. Закон сохранения энергии для электромагнитного поля.
- § 1.2. Волновое уравнение и скорость света
- § 1.3. Скалярные волны
- 1.3.2. Сферические волны.
- 1.3.3. Гармонические волны. Фазовая скорость.
- 1.3.4. Волновые пакеты. Групповая скорость.
- § 1.4. Векторные волны
- 1.4.2. Гармоническая электромагнитная плоская волна.
- 1.4.3. Гармонические векторные волны произвольной формы.
- § 1.5. Отражение и преломление плоской волны
- 1.5.2. Формулы Френеля.
- 1.5.3. Отражательная и пропускательная способности; поляризация при отражении и преломлении.
- 1.5.4. Полное внутреннее отражение.
- § 1.6. Распространение волн в слоистой среде. Теория диэлектрических пленок
- 1.6.2. Характеристическая матрица для слоистой среды.
- 1.6.3. Коэффициенты отражения и пропускания.
- 1.6.4. Однородная диэлектрическая пленка.
- 1.6.5. Периодические слоистые среды.
- ГЛАВА 2. ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ И ПОЛЯРИЗАЦИЯ
- § 2.1. Электродинамические потенциалы в вакууме
- 2.1.2. Запаздывающие потенциалы.
- § 2.2. Поляризация и намагничение
- 2.2.2. Векторы Герца.
- 2.2.3. Поле линейного электрического диполя.
- § 2.3. Формула Лорентц — Лоренца и элементарная теория дисперсии
- 2.3.2. Эффективное поле.
- 2.3.3. Средняя поляризуемость. Формула Лорентц — Лоренца.
- 2.3.4. Элементарная теория дисперсии.
- § 2.4. Описание распространения электромагнитных волн с помощью интегральных уравнений
- 2.4.2. Теорема погашения Эвальда — Озеена и строгий вывод формулы Лорентц — Лоренца.
- 2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда — Озеена.
- ГЛАВА 3. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 3.1.2. Световые лучи и закон интенсивности в геометрической оптике.
- 3.1.3. Распространение векторных амплитуд.
- 3.1.4. Обобщения геометрической оптики и пределы ее применимости.
- § 3.2. Общие свойства лучей
- 3.2.2. Законы преломления и отражения.
- 3.2.3. Конгруэнции лучей и фокальные свойства.
- § 3.3. Другие основные теоремы геометрической оптики
- 3.3.2. Принцип Ферма
- 3.3.3. Теорема Малюса и Дюпина и некоторые другие связанные с ней теоремы.
- ГЛАВА 4. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ
- 4.1.2. Смешанная характеристика.
- 4.1.3. Угловая характеристика.
- 4.1.4. Приближенное выражение для угловой характеристики преломляющей поверхности вращения.
- 4.1.5. Приближенное выражение для угловой характеристики отражающей поверхности вращения.
- § 4.2. Идеальное отображение
- 4.2.2. «Рыбий глаз» Максвелла.
- 4.2.3. Стигматическое отображение поверхностей.
- § 4.3. Проективное преобразование (коллинеация) при наличии аксиальной симметрии
- 4.3.2. Телескопическое отображение.
- 4.3.3. Классификация проективных преобразований.
- 4.3.4. Комбинация проективных преобразований.
- § 4.4. Параксиальная оптика
- 4.4.2. Отражающая поверхность вращения.
- 4.4.3. Толстая линза.
- 4.4.4. Тонкая лииза.
- 4.4.5. Произвольная центрированная система.
- § 4.5. Стигматическое отображение пучками с большой угловой апертурой
- § 4.6. Астигматические пучки лучей
- 4.6.2. Преломление тонкого пучка.
- § 4.7. Хроматическая аберрация. Дисперсия призмы
- 4.7.2. Дисперсия призмы.
- § 4.8. Фотометрия. Апертуры оптических систем
- 4.8.2. Диафрагмы и зрачки.
- 4.8.3. Яркость и освещенность изображений.
- § 4.9. Метод построения хода лучей
- 4.9.2. Параксиальные лучи.
- 4.9.3. Косые лучи.
- § 4.10. Оптические системы с несферическими поверхностями
- 4.10.2. Получение апланатизма.
- ГЛАВА 5. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 5.2. Эйконал Шварншильда
- § 5.3. Первичные аберрации (аберрации Зайделя)
- § 5.4. Теорема сложения для случая первичных аберраций
- § 5.5. Коэффициенты первичных аберраций произвольной центрированной системы линз
- 5.5.2. Формулы Зайделя, выраженные через параметры одного параксиального луча.
- 5.5.3. Теорема Петцваля.
- § 5.6. Пример: первичные аберрации тонкой линзы
- § 5.7. Хроматическая аберрация произвольной центрированной системы линз
- ГЛАВА 6. ОПТИЧЕСКИЕ ПРИБОРЫ, ФОРМИРУЮЩИЕ ИЗОБРАЖЕНИЕ
- § 6.2. Фотографический аппарат
- § 6.3. Линзовый телескоп
- § 6.4. Зеркальный телескоп
- § 6.5. Осветители
- § 6.6. Микроскоп
- ГЛАВА 7. ЭЛЕМЕНТЫ ТЕОРИИ ИНТЕРФЕРЕНЦИИ И ИНТЕРФЕРОМЕТРЫ
- § 7.2. Интерференция двух монохроматических волн
- § 7.3. Двухлучевая интерференция. Деление волнового фронта
- 7.3.2. Зеркала Френеля и другие аналогичные устройства.
- 7.3.3. Интерференционные полосы в квазимонохроматическом и белом свете.
- 7.3.4. Источник в виде щели; видность полос.
- 7.3.5. Измерение оптической разности хода; интерферометр Рэлея.
- 7.3.6. Измерение угловых размеров источников; звездный интерферометр Майкельсона.
- § 7.4. Стоячие волны
- § 7.5. Двухлучевая интерференция. Деление амплитуды
- 7.5.2. Интерференция в тонких пленках; интерферометр Физо.
- 7.5.3. Локализация полос.
- 7.5.4. Интерферометр Майкельсона.
- 7.5.5. Интерферометр Тваймана — Грина и другие аналогичные приборы.
- 7.5.6. Полосы, получающиеся с двумя одинаковыми пластинами; интерферометр Жамена и интерференционный микроскоп.
- 7.5.7. Интерферометр Маха—Цендера; интерферометр Бейтса со смещенным волновым фронтом.
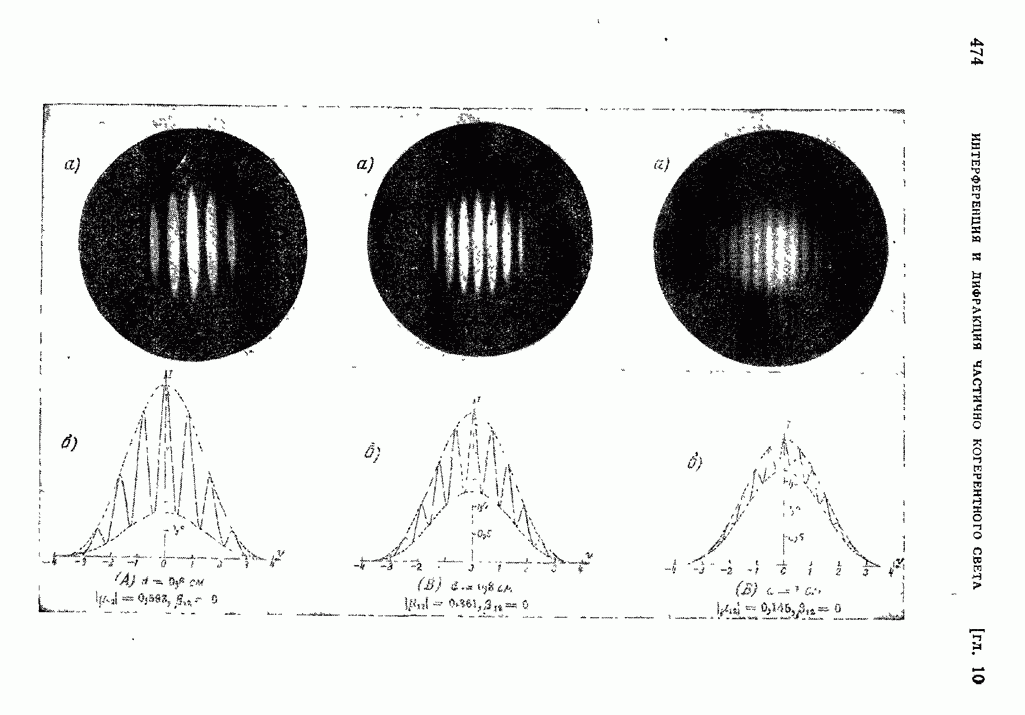
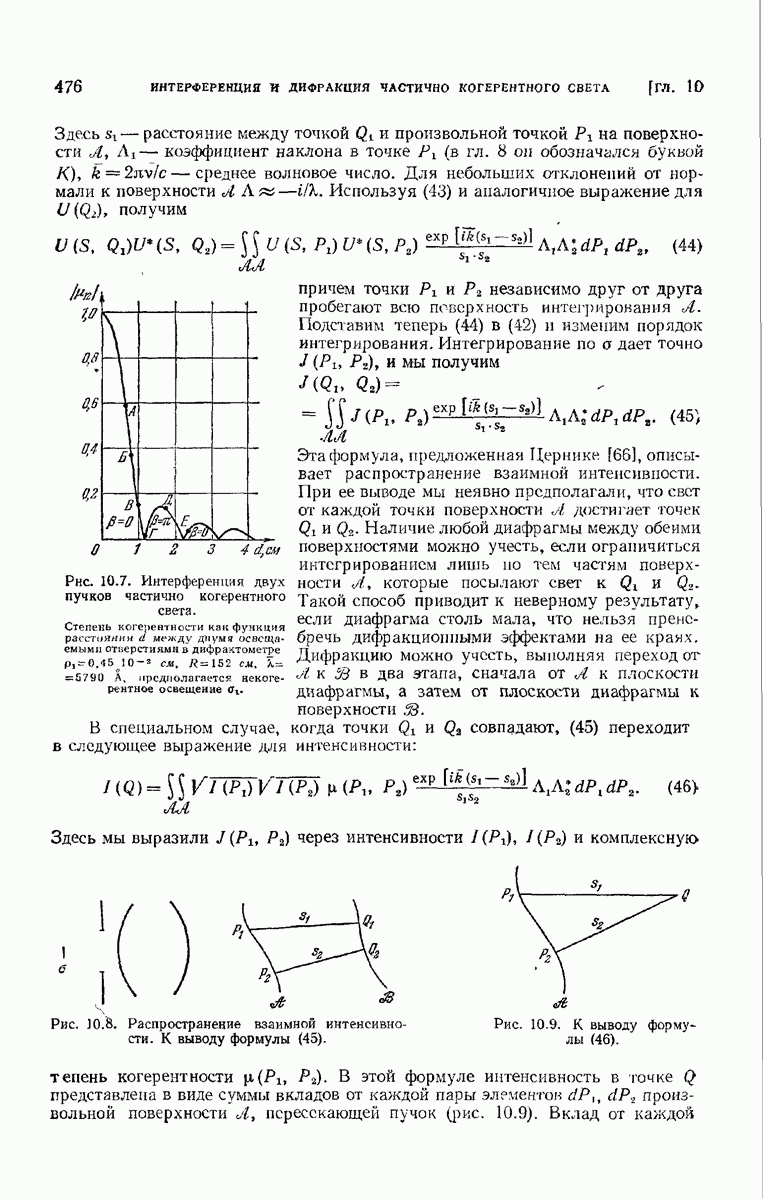
- 7.5.8. Длина когерентности; применение двухлучевой интерференции к изучению тонкой структуры спектральных линий.
- § 7.6. Многолучевая интерференция
- 7.6.2. Интерферометр Фабри — Перо.
- 7.6.3. Применение интерферометра Фабри — Перо для изучения тонкой структуры спектральных линий.
- 7.6.4. Применение интерферометра Фабри — Перо для сравнения длин волн.
- 7.6.5. Интерферометр Люммера — Герке.
- 7.6.6. Интерференционные фильтры.
- 7.6.7. Многолучевые полосы в тонких пленках.
- 7.6.8. Многолучевые полосы, получающиеся с двумя плоскопараллельными пластинками.
- § 7.7. Сравнение длин волн с эталонным метром
- ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ДИФРАКЦИИ
- § 8.2. Принцип Гюйгенса — Френеля
- § 8.3. Теория дифракции Кирхгофа
- 8.3.2. Теория дифракции Кирхгофа.
- 8.3.3. Дифракция Фраунгофера и Френеля.
- § 8.4. Переход к скалярной теории
- 8.4.2. Полное поле изображения.
- § 8.5. Дифракция Фраунгофера на отверстиях разной формы
- 8.5.2. Круглое отверстие.
- 8.5.3. Отверстия другой фомы.
- § 8.6. Дифракция Фраунгофера в оптических приборах
- 8.6.2. Разрешающая сила систем, образующих изображение.
- 8.6.3. Образование изображения в микроскопе.
- § 8.7. Дифракция Френеля на прямолинейном крае
- 8.7.2. Интегралы Френеля.
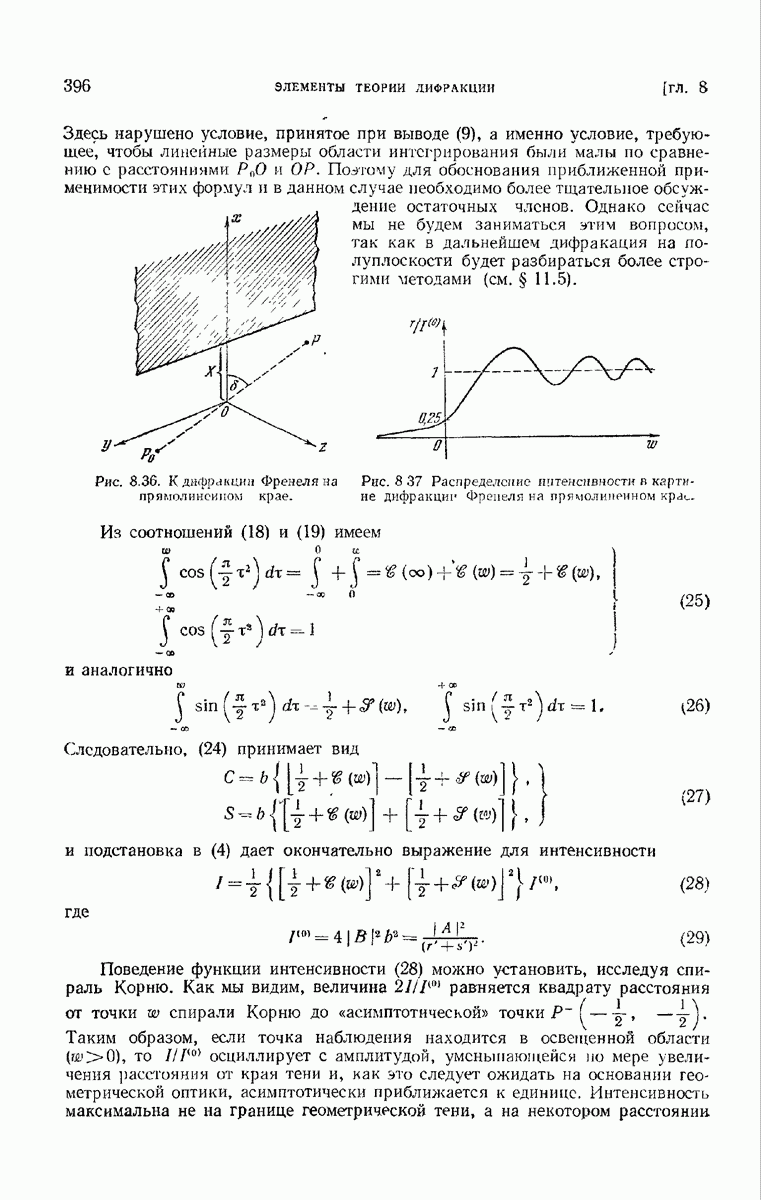
- 8.7.3. Дифракция Френеля на прямолинейном крае.
- § 8.8. Трехмерное распределение света вблизи фокуса
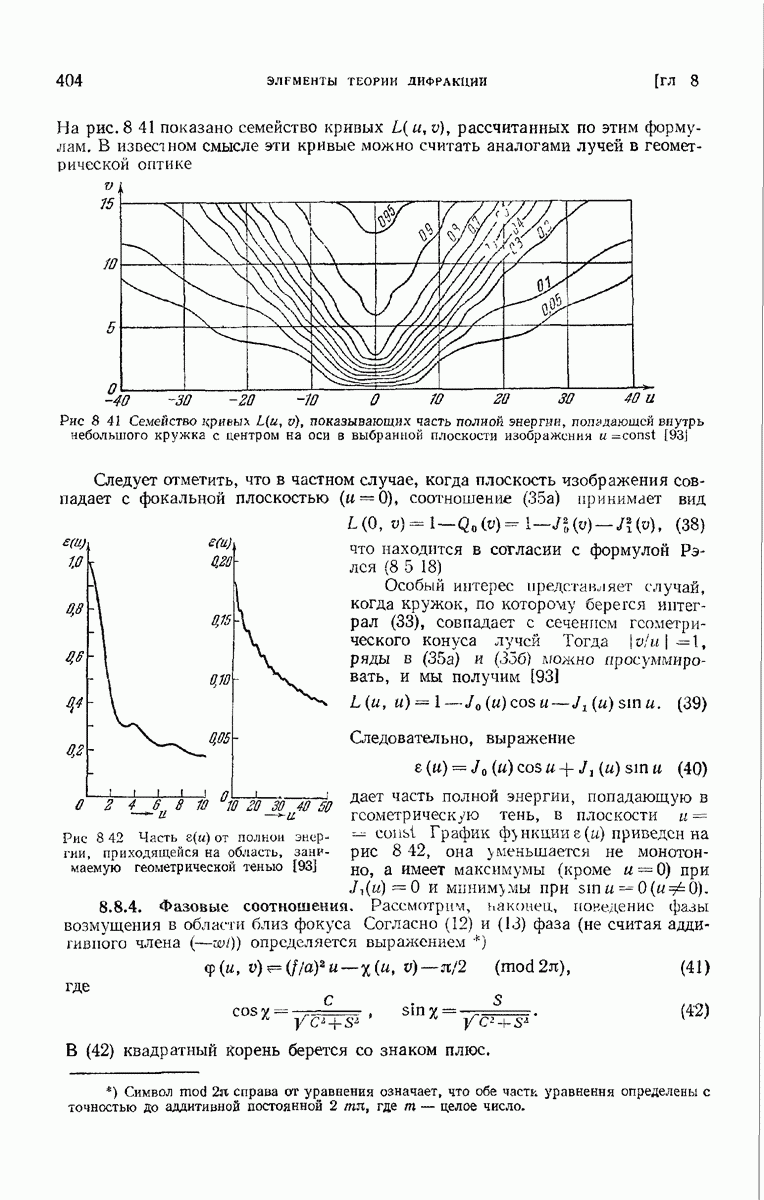
- 8.8.2. Распределение интенсивности.
- 8.8.3. Суммарная интенсивность.
- 8.8.4. Фазовые соотношения.
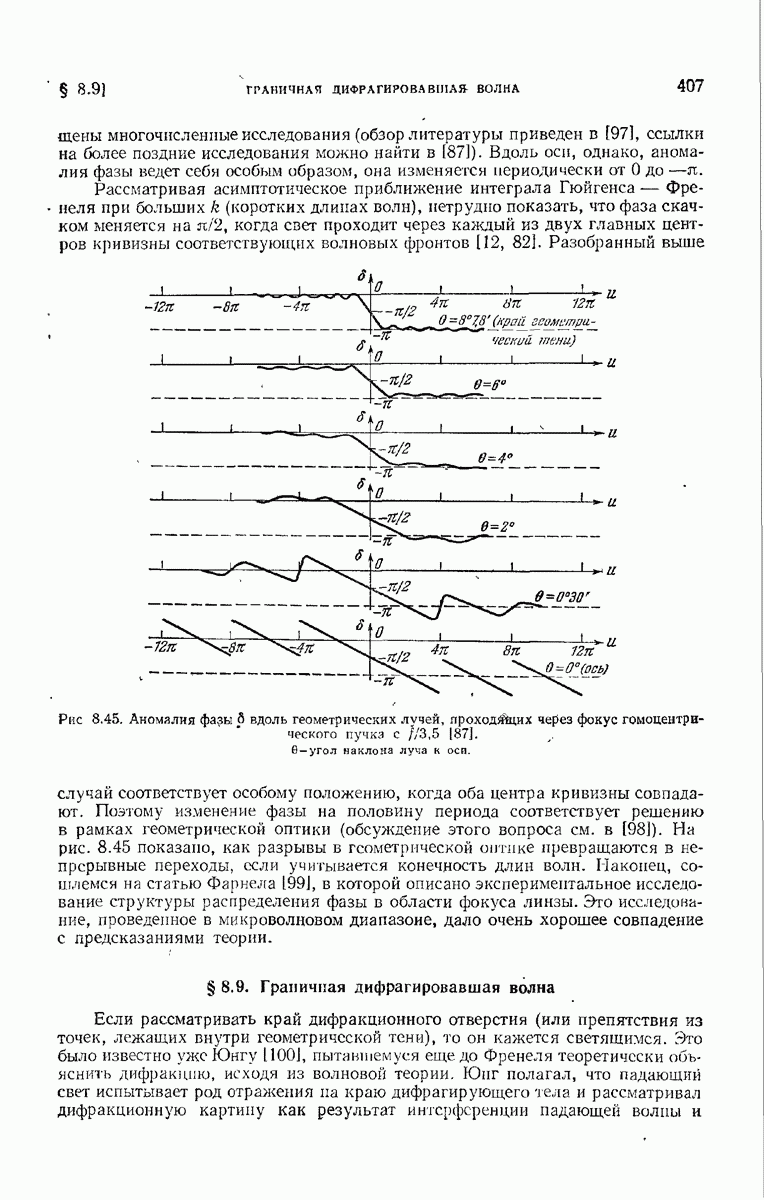
- § 8.9. Граничная дифрагировавшая волна
- § 8.10. Метод Габора получения изображения восстановлением волновых фронтов
- 8.10.2. Восстановление.
- ГЛАВА 9. ДИФРАКЦИОННАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 9.1. Дифракционный интеграл при наличии аберраций
- 9.1.2. Теорема смещения. Изменение опорной сферы.
- 9.1.3. Соотношение между интенсивностью и средней деформацией волновых фронтов.
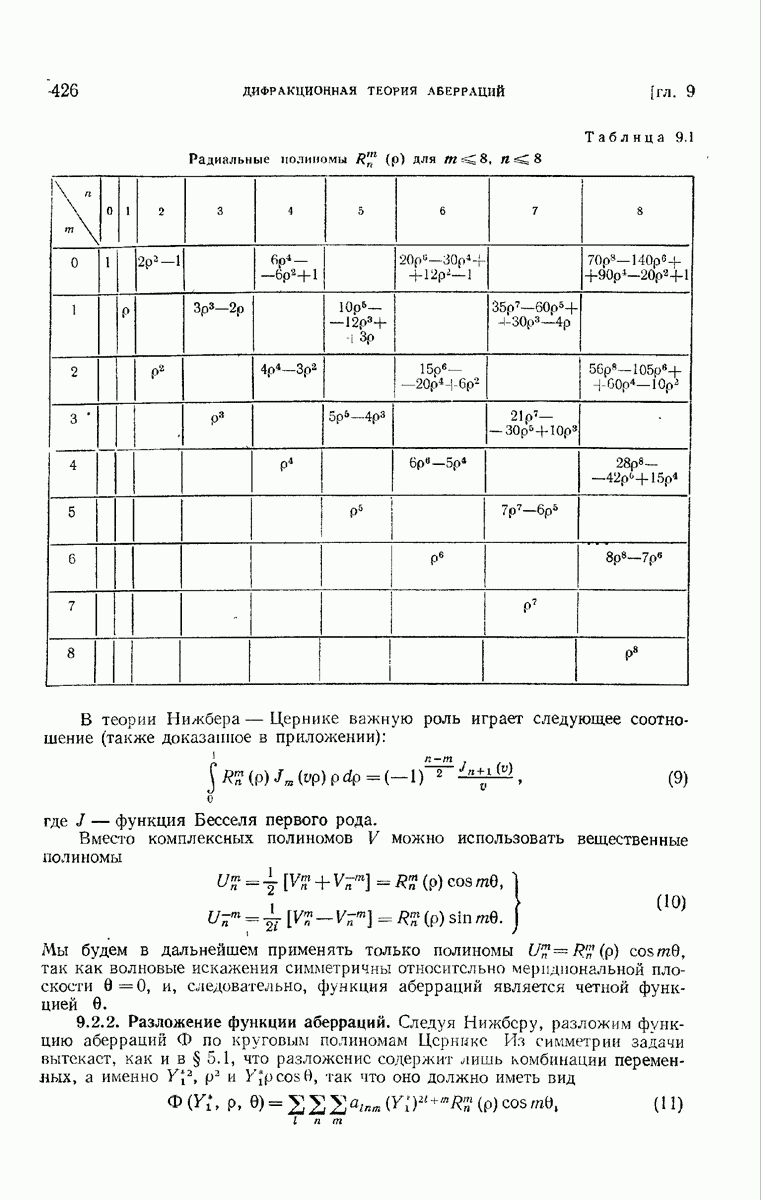
- § 9.2. Разложение функции аберрации
- 9.2.2. Разложение функции аберраций.
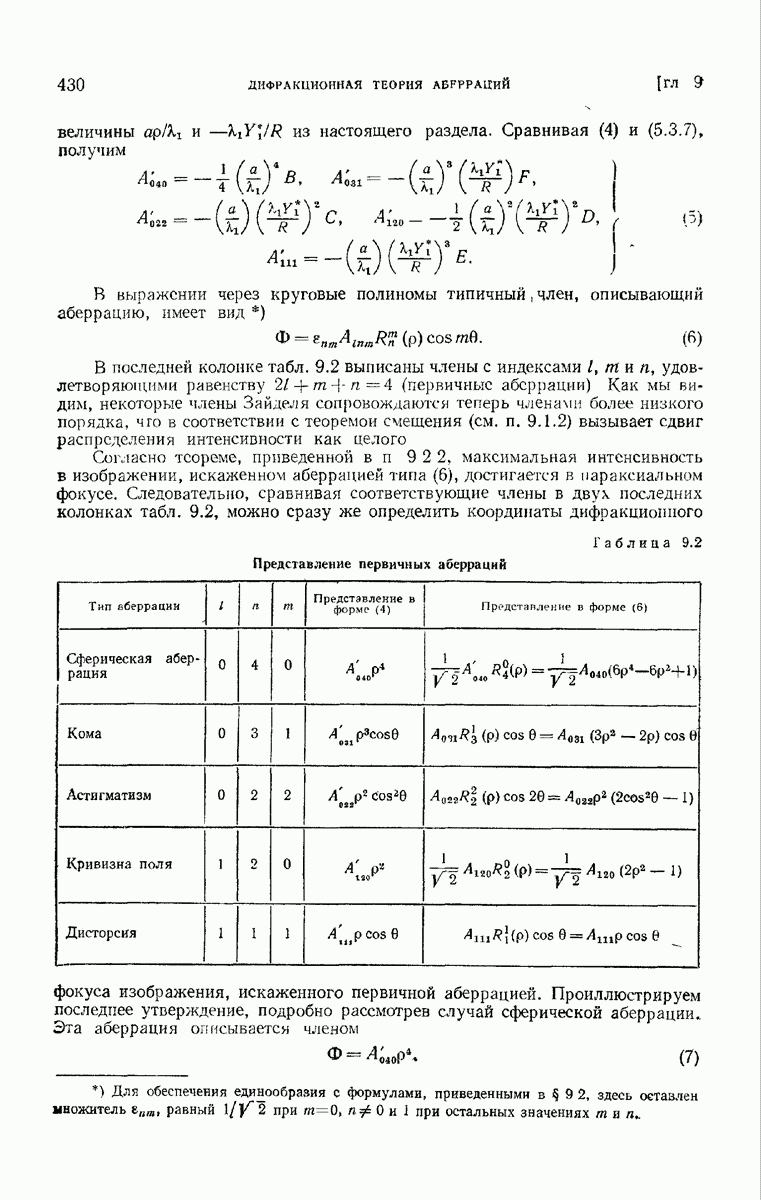
- § 9.3. Допустимые величины первичных аберраций
- § 9.4. Дифракционная картина, получающаяся при наличии одной аберрации
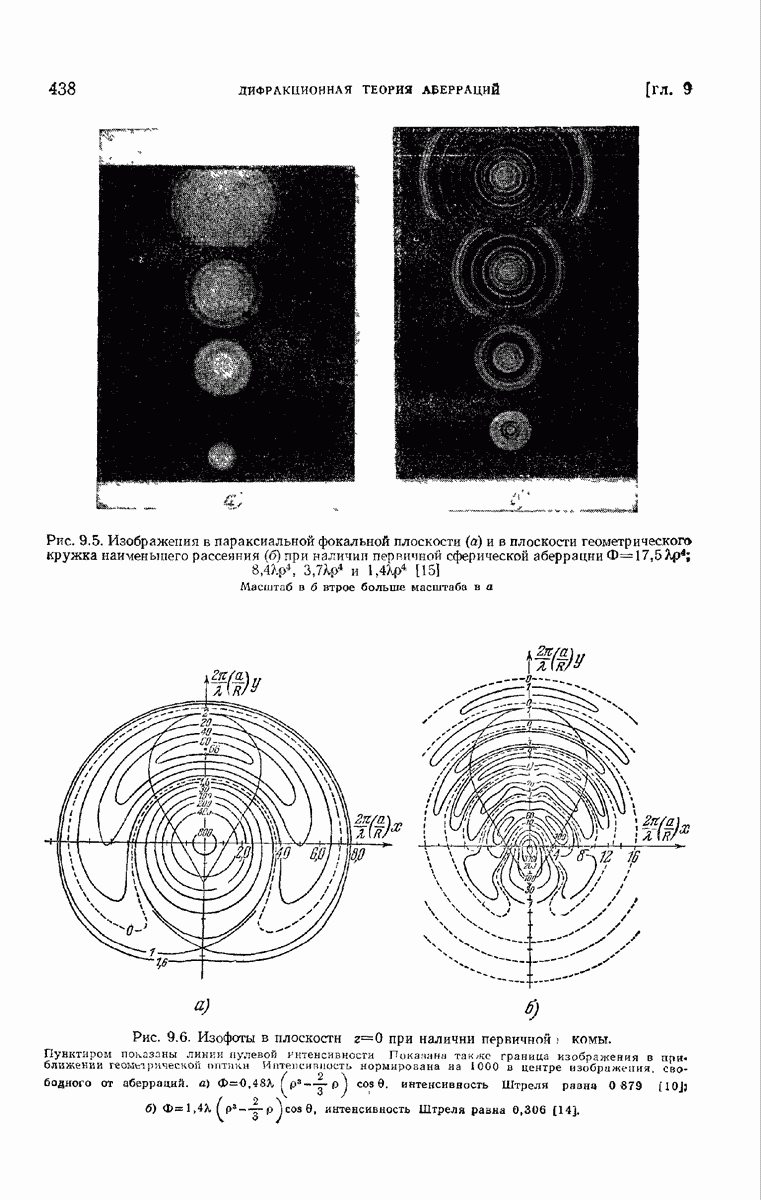
- 9.4.1. Первичная сферическая аберрация.
- 9.4.2. Первичная кома.
- 9.4.3. Первичный астигматизм.
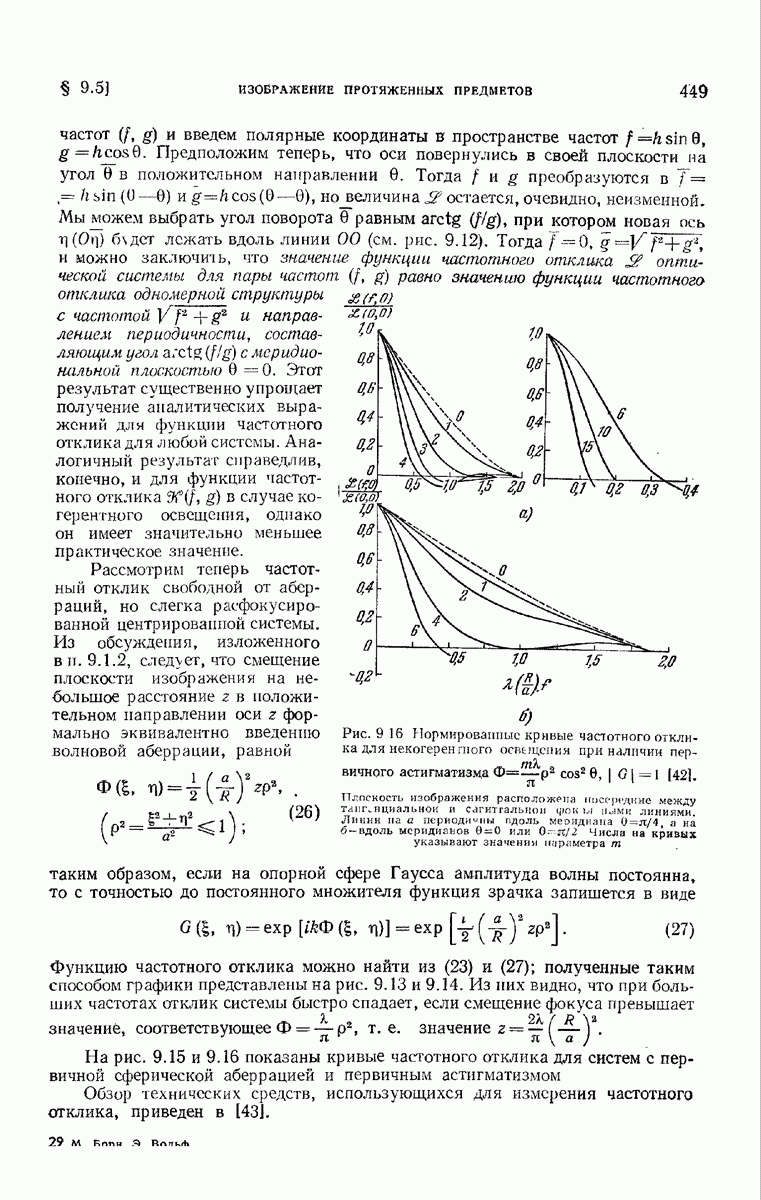
- § 9.5. Изображение протяженных предметов
- 9.5.2. Некогерентное освещение.
- ГЛАВА 10. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
- § 10.2. Комплексное представление вещественных полихроматических полей
- § 10.3. Корреляционные функции световых пучков
- 10.3.2. Спектральное представление взаимной когерентности.
- § 10.4. Интерференция и дифракция квазимонохроматического света
- 10.4.2. Расчет взаимной интенсивности и степени когерентности для света от протяженного некогерентного квазимонохроматического источника.
- 10.4.3. Пример.
- 10.4.4. Распространение взаимной интенсивности.
- § 10.5. Некоторые приложения
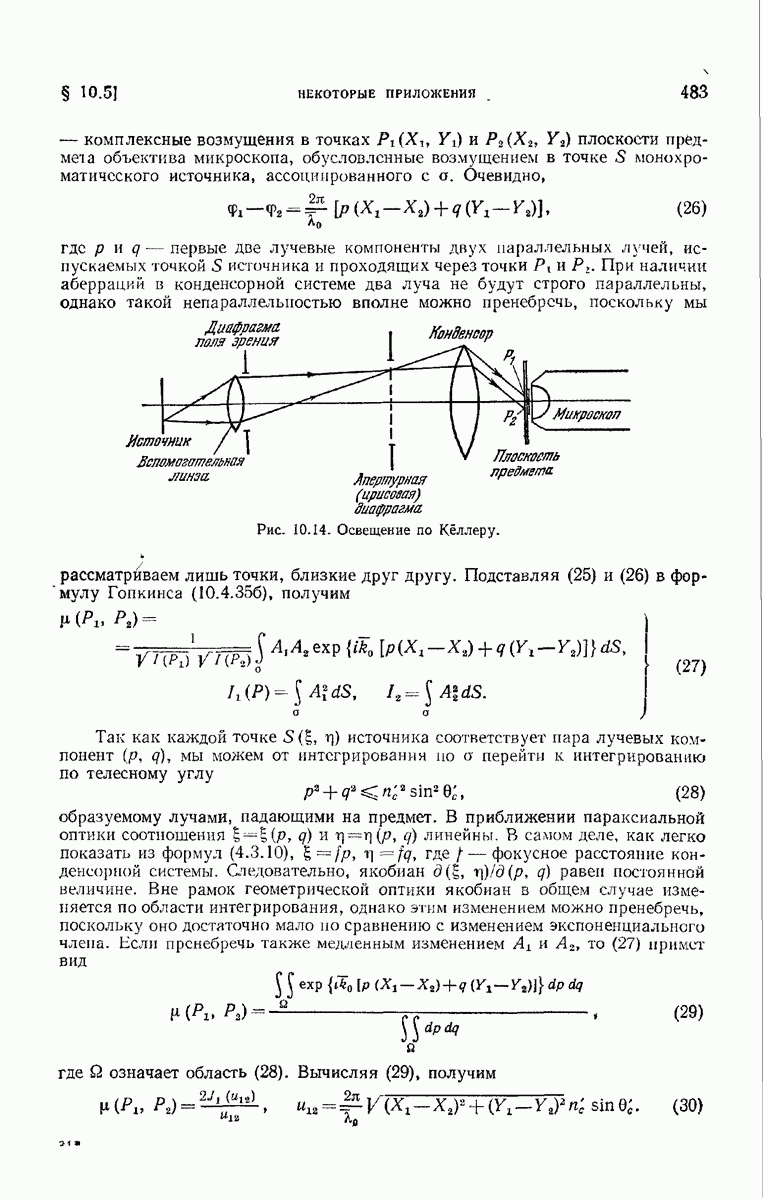
- 10.5.1. Степень когерентности в изображении протяженного некогерентного квазимонохроматического источника.
- 10.5.2. Влияние конденсора на разрешающую силу микроскопа.
- 10.5.3. Получение изображения при частично когерентном квазимонохроматическом освещении
- § 10.6. Некоторые теоремы, касающиеся взаимной когерентности
- 10.6.2. Распространение взаимной когерентности.
- § 10.7. Строгая теория частичной когерентности
- 10.7.2. Строгая формулировка закона распространения взаимной когерентности.
- 10.7.3. Время когерентности и эффективная ширина спектра.
- § 10.8. Поляризация квазимонохроматического света
- 10.8.2. Некоторые эквивалентные представления. Степень поляризации световой волны.
- 10.8.3. Параметры Стокса квазимонохроматичаской плоской волны.
- ГЛАВА 11. СТРОГАЯ ТЕОРИЯ ДИФРАКЦИИ
- § 11.2. Граничные условия и поверхностные токи
- § 11.3. Дифракция на плоском экране; электромагнитная форма принципа Бабине
- § 11.4. Двумерная дифракция на плоском экране
- 11.4.2. Угловой спектр плоских волн.
- 11.4.3. Формулировка задачи через дуальные интегральные уравнения.
- § 11.5. Двумерная дифракция плоской волны на полуплоскости
- 11.5.2. Выражение решения через интегралы Френеля.
- 11.5.3. Характер решения.
- 11.5.4. Решение для Н-поляризации.
- 11.5.5. Некоторые численные расчеты.
- 11.5.6. Сравнение с приближенной теорией и с экспериментальными результатами.
- § 11.6. Трехмерная дифракция плоской волны на полуплоскости
- § 11.7. Дифракция волн, испускаемых локализованным источником, на полуплоскости
- 11.7.2. Диполь.
- § 11.8. Другие задачи
- 11.8.1. Две параллельные полуплоскости.
- 11.8.2. Бесконечный набор параллельных полуплоскостей, расположенных ступеньками.
- 11.8.3. Полоса.
- 11.8.4. Другие задачи.
- § 11.9. Единственность решения
- ГЛАВА 12. ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКОВЫХ ВОЛНАХ
- 12.1.2. Краткое изложение теорий, основанных на уравнениях Максвелла.
- § 12.2. Рассмотрение дифракции света на ультразвуковых волнах методом интегральных уравнений
- 12.2.1. Интегральное уравнение для случая Е-поляризации.
- 12.2.2. Пробное решение интегрального уравнения.
- 12.2.3. Выражения для амплитуд световых волн в дифрагировавших и отраженных спектрах.
- 12.2.5. Выражения для интенсивностей линий в спектрах первого и второго порядков в некоторых специальных случаях
- 12.2.6. Некоторые качественные результаты.
- 12.2.7. Приближение Рамана—Ната.
- ГЛАВА 13. МЕТАЛЛООПТИКА
- § 13.2. Преломление и отражение на поверхности металла
- § 13.3. Элементарная электронная теория оптических постоянных металлов
- § 13.4. Распространение волн в слоистой проводящей среде. Теория металлических пленок
- 13.4.2. Прозрачная пленка на поглощающей подложке.
- § 13.5. Дифракция на проводящей сфере. Теория Ми
- 13.5.1. Математическое решение проблемы
- 13.5.2. Некоторые следствия из формул Ми.
- 13.5.3. Полное рассеяние и затухание
- ГЛАВА 14. КРИСТАЛЛООПТИКА
- § 14.1. Тензор диэлектрической проницаемости анизотропной среды
- § 14.2. Структура монохроматической плоской волны в анизотропной среде
- 14.2.2. Формулы Френеля для распространения света в кристаллах.
- 14.2.3. Геометрические построения для определения скоростей распространения и направлений колебаний.
- § 14.3. Оптические свойства одноосных и двухосных кристаллов
- 14.3.2. Распространение света в одноосных кристаллах.
- 14.3.3. Распространение света в двухосных кристаллах.
- 14.3.4. Преломление в кристаллах
- § 14.4. Измерения в кристаллооптике
- 14.4.2. Компенсаторы.
- 14.4.3. Интерференция в кристаллических пластинках.
- 14.4.4. Интерференционные картины, получающиеся с пластинками одноосных кристаллов.
- 14.4.5. Интерференционные картины, получающиеся с пластинками двухосных кристаллов.
- 14.4.6. Определение положения оптических осей и главных показателей преломления кристаллической среды.
- § 14.5. Искусственная анизотропия
- 14.5.2. Двойное лучепреломление формы.
- § 14.6. Поглощающие кристаллы
- 14.6.2. Интерференционные картины, получающиеся с пластинками поглощающих кристаллов.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ 1. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 2. Интеграл Гильберта и уравнение Гамильтона—Якоби.
- 3. Поле экстремалей.
- 4. Нахождение всех экстремалей из решения уравнения Гамильтона — Якоби.
- 5. Канонические уравнения Гамильтона.
- 6. Частный случай, когда независимая переменная не входит явно в подынтегральное выражение.
- 7. Разрывы.
- 8. Условия Вейерштрасса и Лежандра (достаточные условия экстремума).
- 9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
- 10. Критерий Якоби для минимума.
- 11. Пример I. Оптика.
- 12. Пример II. Механика материальных точек.
- ПРИЛОЖЕНИЕ 2. ОБЫЧНАЯ ОПТИКА, ЭЛЕКТРОННАЯ ОПТИКА И ВОЛНОВАЯ МЕХАНИКА
- 2. Аналогия Гамильтона в вариационной форме.
- 3. Волновая механика свободных электронов.
- 4. Применение оптических принципов в электронной оптике.
- ПРИЛОЖЕНИЕ 3. МЕТОД АСИМПТОТИЧЕСКИХ ОЦЕНОК ИНТЕГРАЛОВ
- 2. Метод стационарной фазы.
- 3. Двойные интегралы.
- ПРИЛОЖЕНИЕ 4. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
- ПРИЛОЖЕНИЕ 5. МАТЕМАТИЧЕСКАЯ ЛЕММА, ИСПОЛЬЗУЕМАЯ ПРИ СТРОГОМ ВЫВОДЕ ЗАКОНА ЛОРЕНТЦ — ЛОРЕНЦА
- ПРИЛОЖЕНИЕ 6. РАСПРОСТРАНЕНИЕ РАЗРЫВОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПРИЛОЖЕНИЕ 7. КРУГОВЫЕ ПОЛИНОМЫ ЦЕРНИКЕ
- ПРИЛОЖЕНИЕ 8. ДОКАЗАТЕЛЬСТВО ОДНОГО НЕРАВЕНСТВА, ПРИВЕДЕННОГО В П. 10.7.3
- ПРИЛОЖЕНИЕ 9. ВЫЧИСЛЕНИЕ ДВУХ ИНТЕГРАЛОВ, ИСПОЛЬЗУЕМЫХ В П. 12.2.2