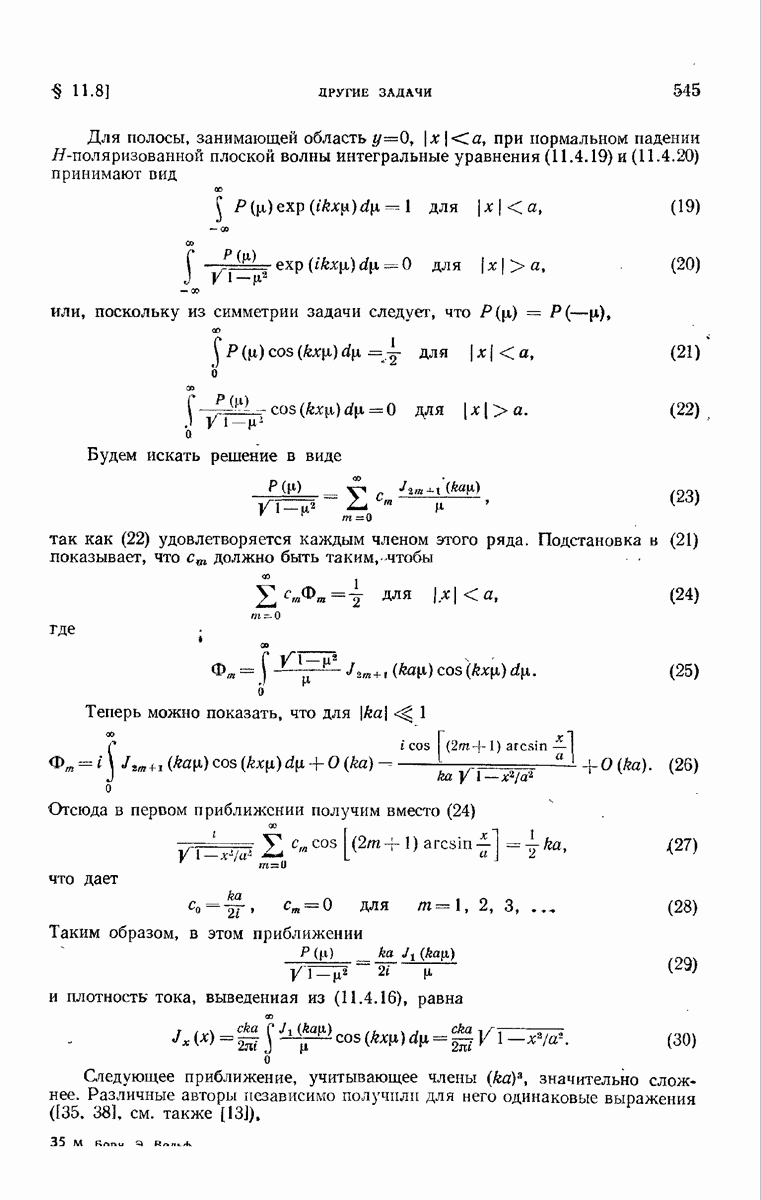| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
С помощью  -функции легко определить минимум вариационного интеграла (1) относительно всех кривых с одной общей концевой точкой
-функции легко определить минимум вариационного интеграла (1) относительно всех кривых с одной общей концевой точкой  а другими, связанными с заданной поверхностью
а другими, связанными с заданной поверхностью 

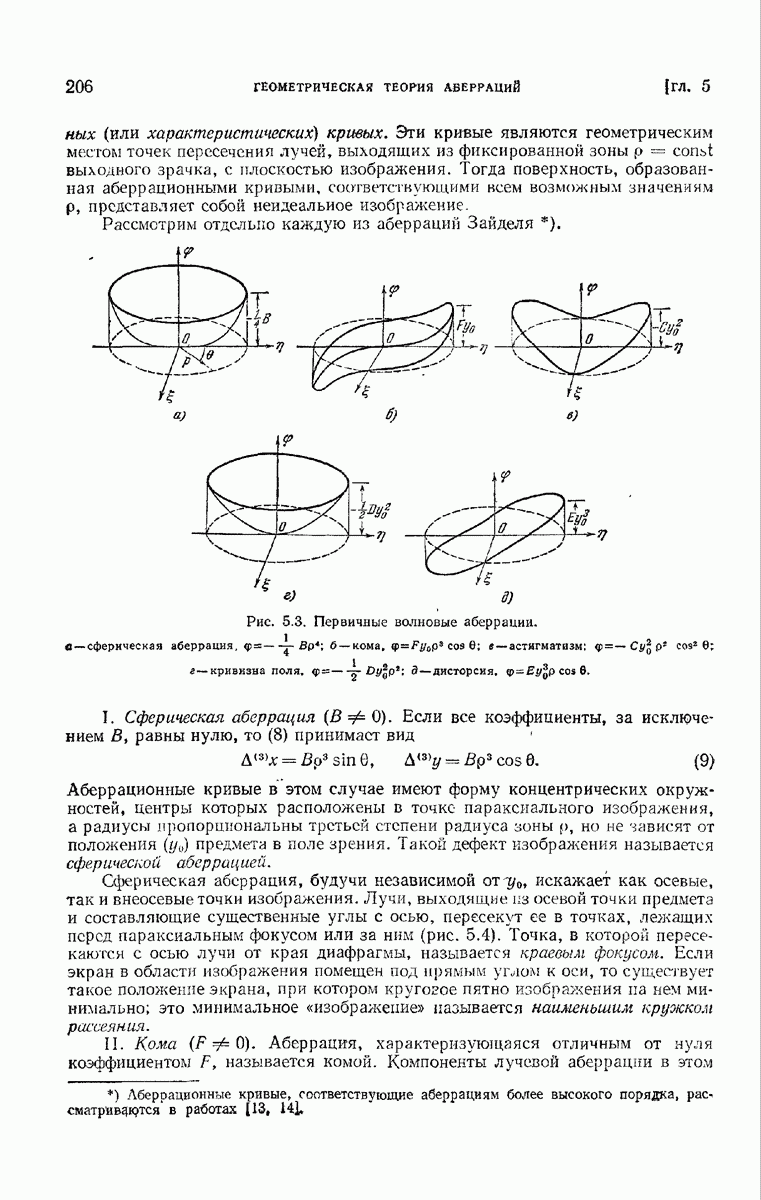
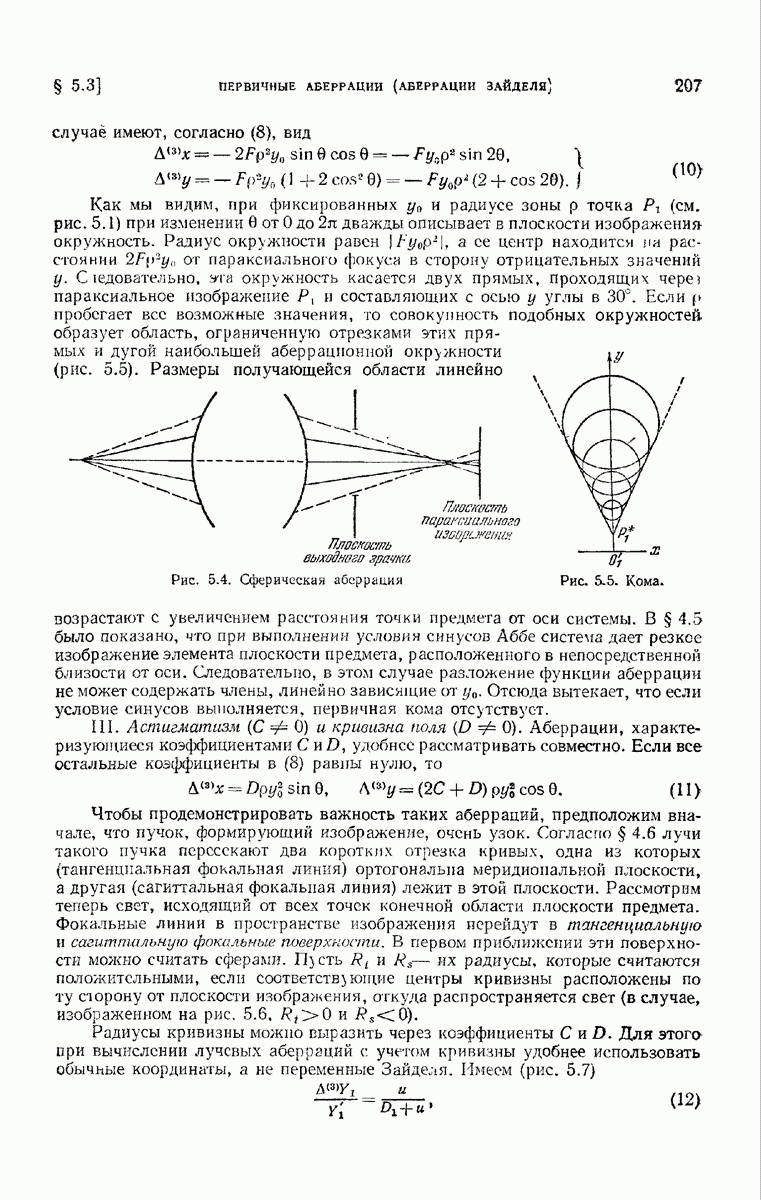
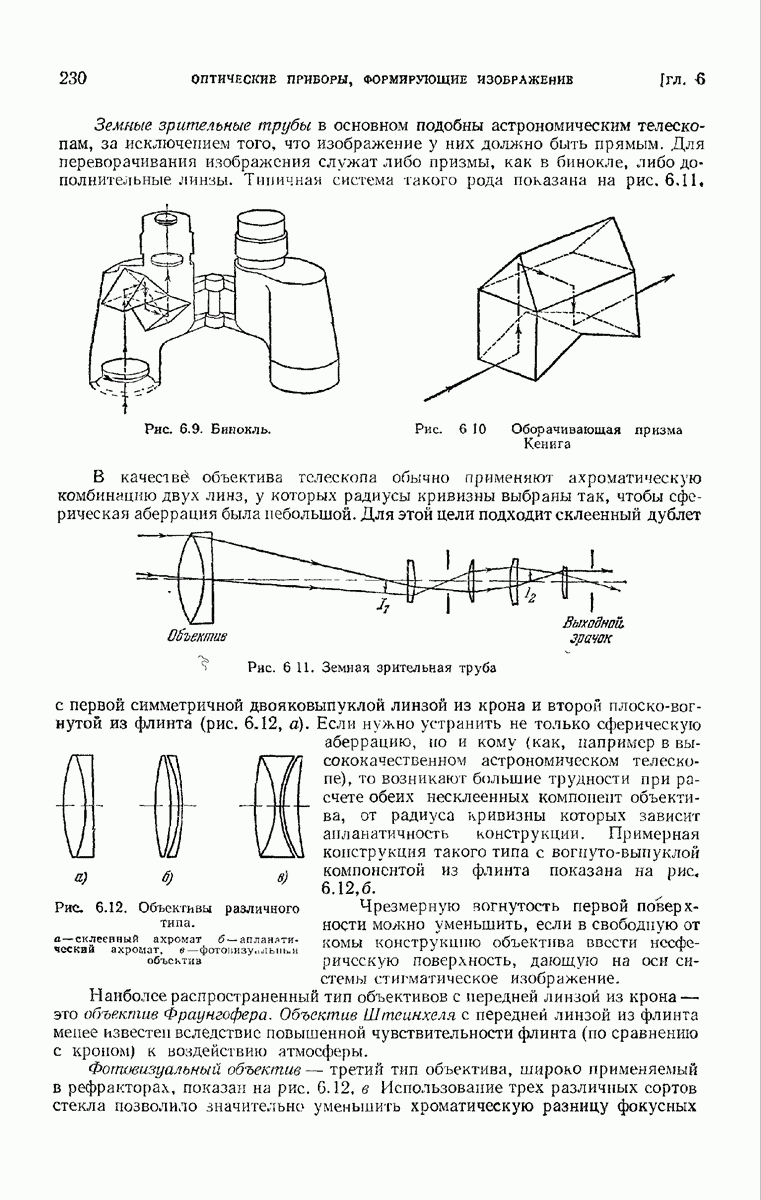
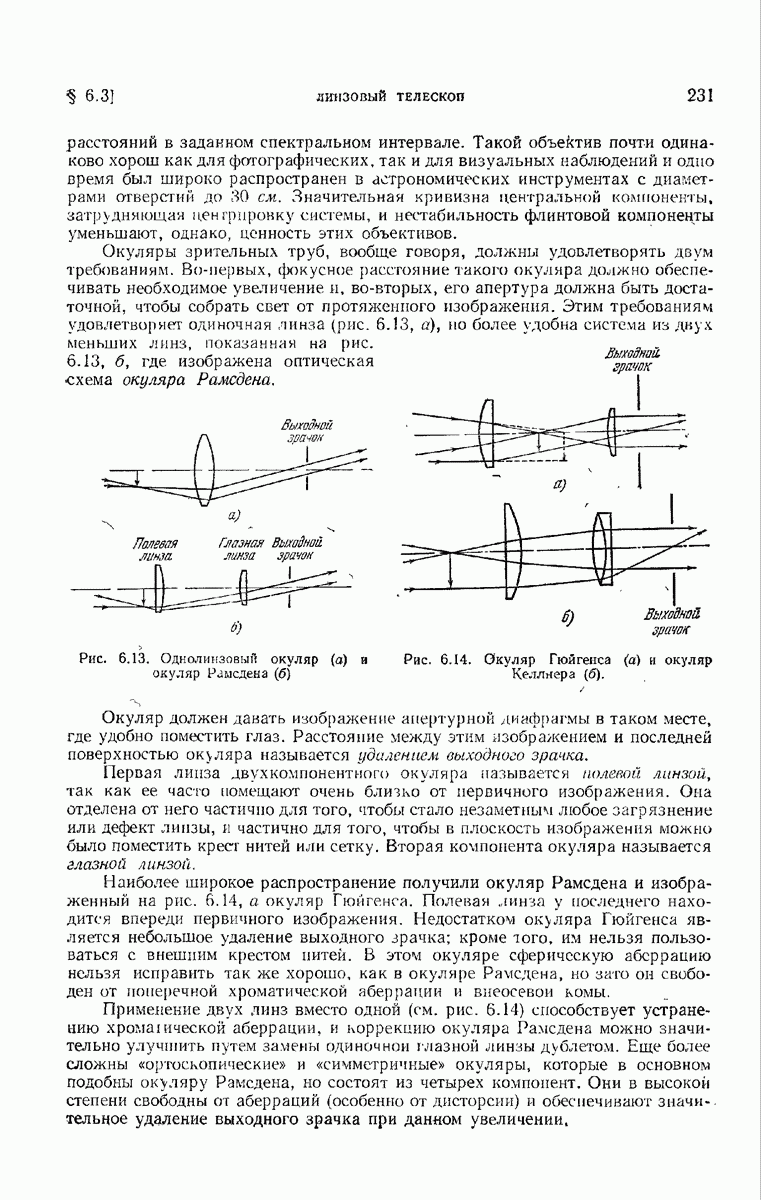
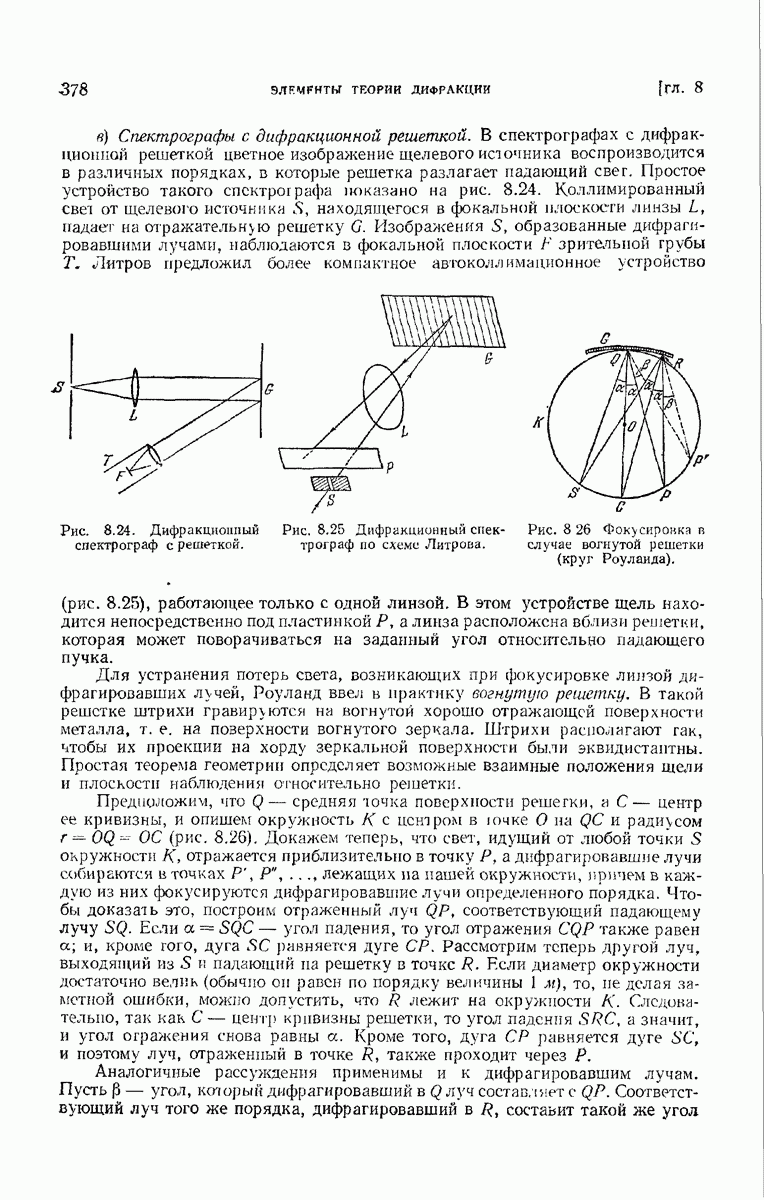
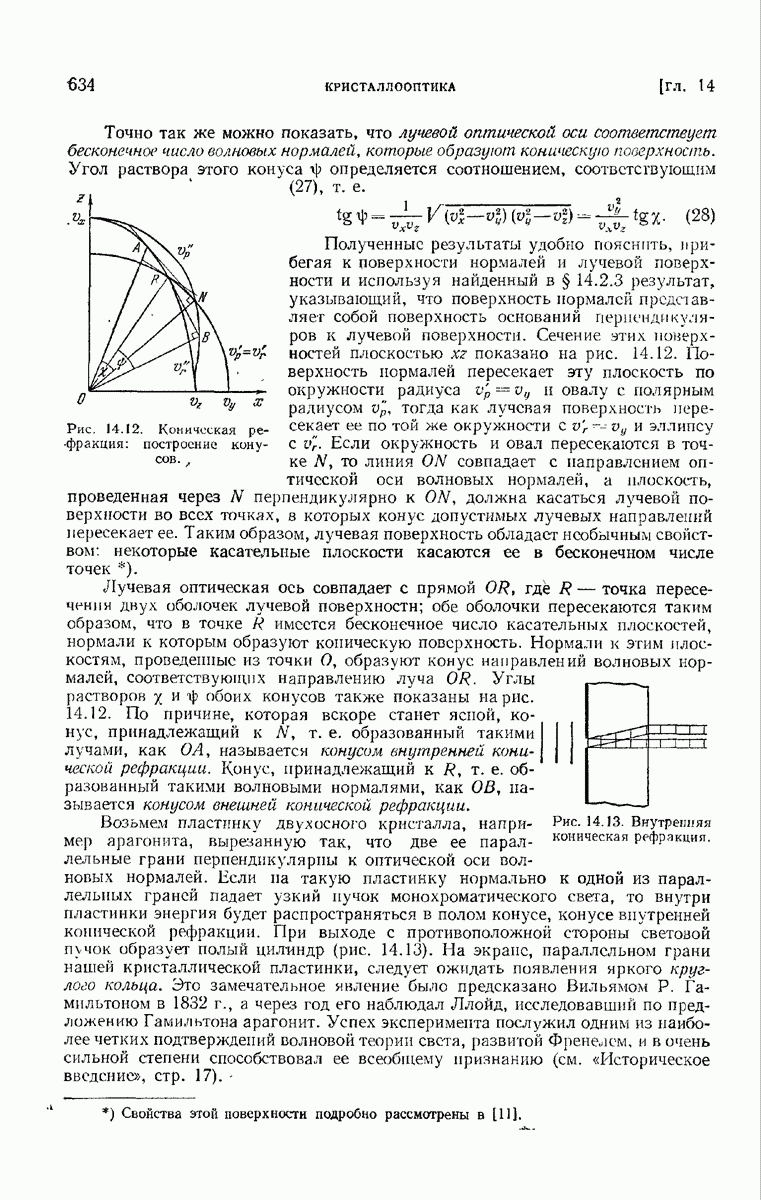
Рис. 7. К определению минимума вариационного интеграла для всех кривых, один конец которых фиксирован, а другой связан с поверхностью.
Кривая, очевидно, должна совпадать с одной из экстремалей двухпараметрического  семейства, проходящей через точку
семейства, проходящей через точку  и нужно лишь узнать, с какой из них. Среди всех
и нужно лишь узнать, с какой из них. Среди всех  экстремалей имеется только одна которая ортогональна поверхности
экстремалей имеется только одна которая ортогональна поверхности  и легко показать, что именно она служит решением данной задачи. Для этого обозначим через
и легко показать, что именно она служит решением данной задачи. Для этого обозначим через  точку пересечения такой экстремали с поверхностью
точку пересечения такой экстремали с поверхностью  и окружим ее полем всех экстремалей, перпендикулярных к поверхности. Пусть
и окружим ее полем всех экстремалей, перпендикулярных к поверхности. Пусть  — любая экстремаль, проходящая через
— любая экстремаль, проходящая через  - точка ее пересечения с поверхностью (рис. 7). Тогда интеграл Гильберта
- точка ее пересечения с поверхностью (рис. 7). Тогда интеграл Гильберта  обращается в нуль. Следовательно, интеграл
обращается в нуль. Следовательно, интеграл  вдоль пути
вдоль пути  равен вариационному интегралу
равен вариационному интегралу  Разность
Разность  можно выразить точно таким же образом, как и выше, через (
можно выразить точно таким же образом, как и выше, через ( -функцию; тогда, если условие (58) выполняется, она положительна для всех
-функцию; тогда, если условие (58) выполняется, она положительна для всех  отличных от
отличных от 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 1.1. Электромагнитное поле
- 1.1.2. Материальные уравнения.
- 1.1.3. Граничные условия на поверхностях раздела.
- 1.1.4. Закон сохранения энергии для электромагнитного поля.
- § 1.2. Волновое уравнение и скорость света
- § 1.3. Скалярные волны
- 1.3.2. Сферические волны.
- 1.3.3. Гармонические волны. Фазовая скорость.
- 1.3.4. Волновые пакеты. Групповая скорость.
- § 1.4. Векторные волны
- 1.4.2. Гармоническая электромагнитная плоская волна.
- 1.4.3. Гармонические векторные волны произвольной формы.
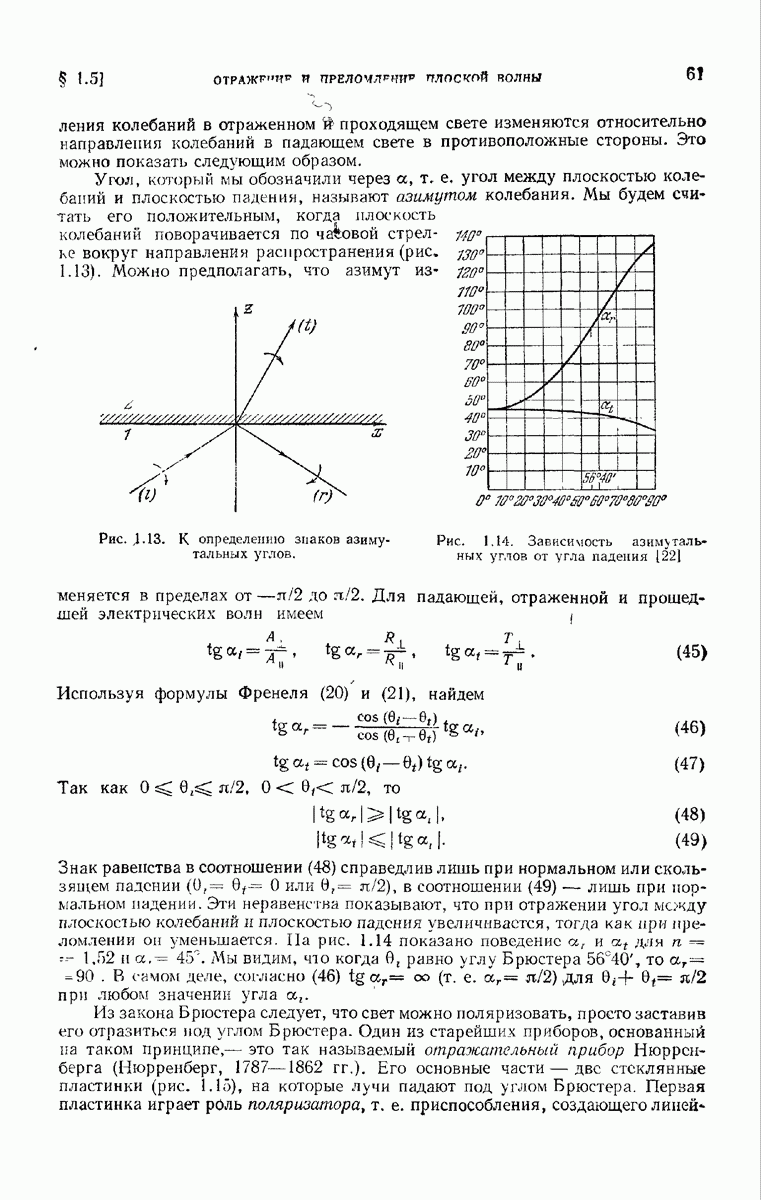
- § 1.5. Отражение и преломление плоской волны
- 1.5.2. Формулы Френеля.
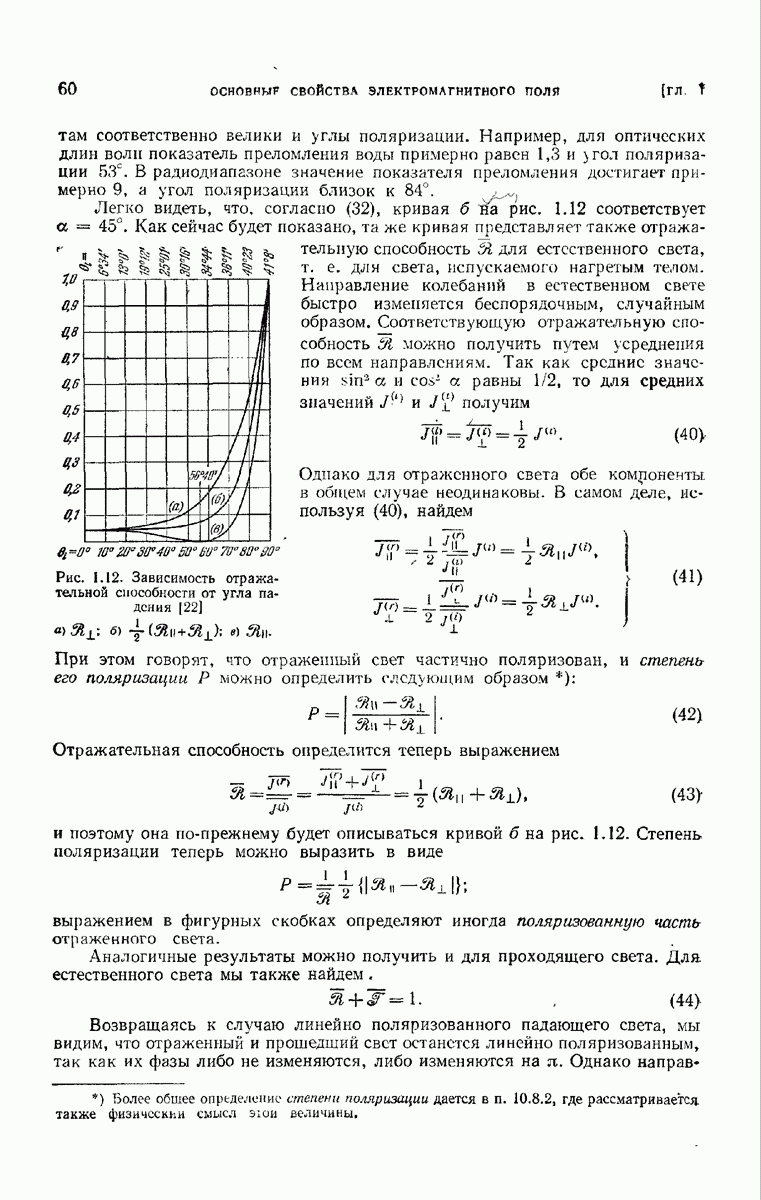
- 1.5.3. Отражательная и пропускательная способности; поляризация при отражении и преломлении.
- 1.5.4. Полное внутреннее отражение.
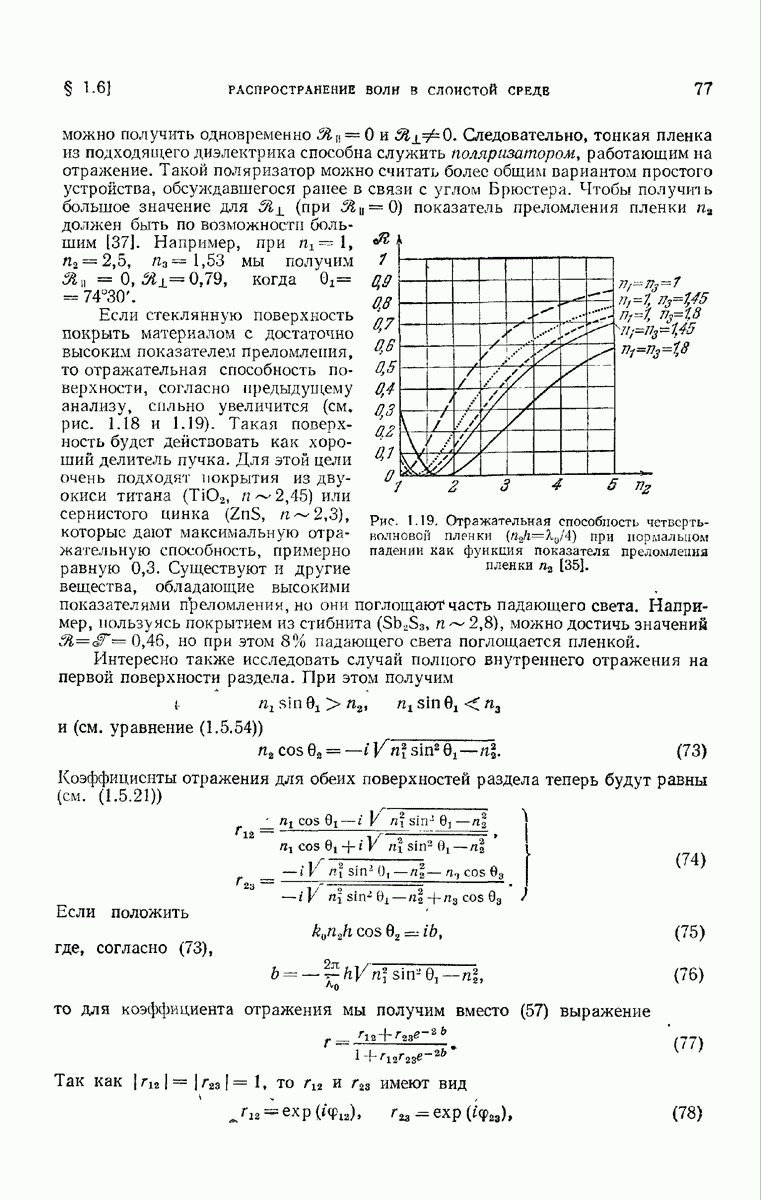
- § 1.6. Распространение волн в слоистой среде. Теория диэлектрических пленок
- 1.6.2. Характеристическая матрица для слоистой среды.
- 1.6.3. Коэффициенты отражения и пропускания.
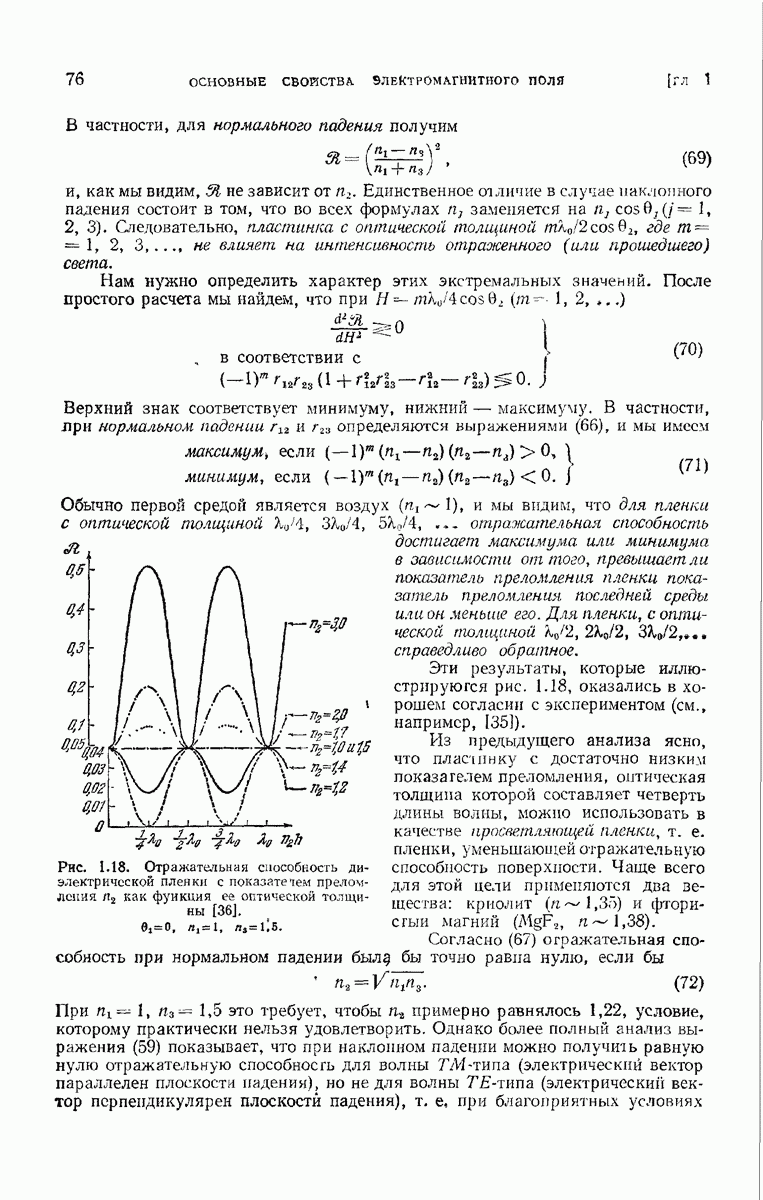
- 1.6.4. Однородная диэлектрическая пленка.
- 1.6.5. Периодические слоистые среды.
- ГЛАВА 2. ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ И ПОЛЯРИЗАЦИЯ
- § 2.1. Электродинамические потенциалы в вакууме
- 2.1.2. Запаздывающие потенциалы.
- § 2.2. Поляризация и намагничение
- 2.2.2. Векторы Герца.
- 2.2.3. Поле линейного электрического диполя.
- § 2.3. Формула Лорентц — Лоренца и элементарная теория дисперсии
- 2.3.2. Эффективное поле.
- 2.3.3. Средняя поляризуемость. Формула Лорентц — Лоренца.
- 2.3.4. Элементарная теория дисперсии.
- § 2.4. Описание распространения электромагнитных волн с помощью интегральных уравнений
- 2.4.2. Теорема погашения Эвальда — Озеена и строгий вывод формулы Лорентц — Лоренца.
- 2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда — Озеена.
- ГЛАВА 3. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 3.1.2. Световые лучи и закон интенсивности в геометрической оптике.
- 3.1.3. Распространение векторных амплитуд.
- 3.1.4. Обобщения геометрической оптики и пределы ее применимости.
- § 3.2. Общие свойства лучей
- 3.2.2. Законы преломления и отражения.
- 3.2.3. Конгруэнции лучей и фокальные свойства.
- § 3.3. Другие основные теоремы геометрической оптики
- 3.3.2. Принцип Ферма
- 3.3.3. Теорема Малюса и Дюпина и некоторые другие связанные с ней теоремы.
- ГЛАВА 4. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ
- 4.1.2. Смешанная характеристика.
- 4.1.3. Угловая характеристика.
- 4.1.4. Приближенное выражение для угловой характеристики преломляющей поверхности вращения.
- 4.1.5. Приближенное выражение для угловой характеристики отражающей поверхности вращения.
- § 4.2. Идеальное отображение
- 4.2.2. «Рыбий глаз» Максвелла.
- 4.2.3. Стигматическое отображение поверхностей.
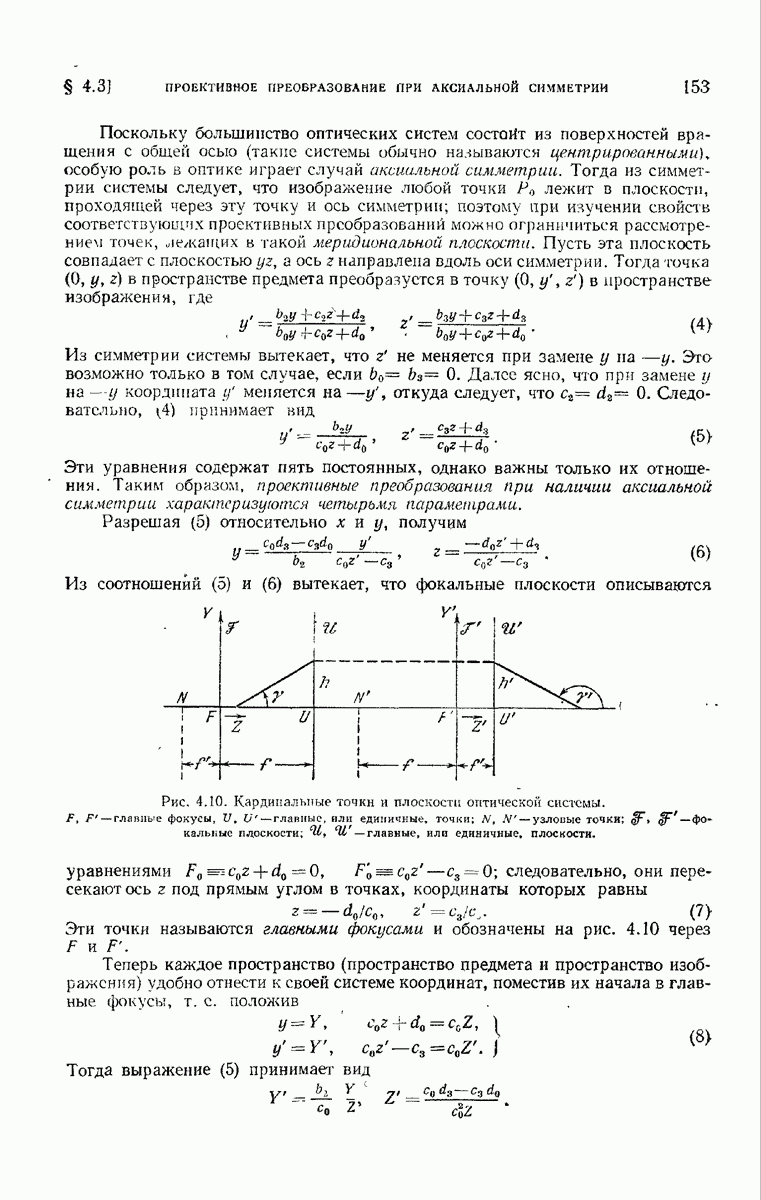
- § 4.3. Проективное преобразование (коллинеация) при наличии аксиальной симметрии
- 4.3.2. Телескопическое отображение.
- 4.3.3. Классификация проективных преобразований.
- 4.3.4. Комбинация проективных преобразований.
- § 4.4. Параксиальная оптика
- 4.4.2. Отражающая поверхность вращения.
- 4.4.3. Толстая линза.
- 4.4.4. Тонкая лииза.
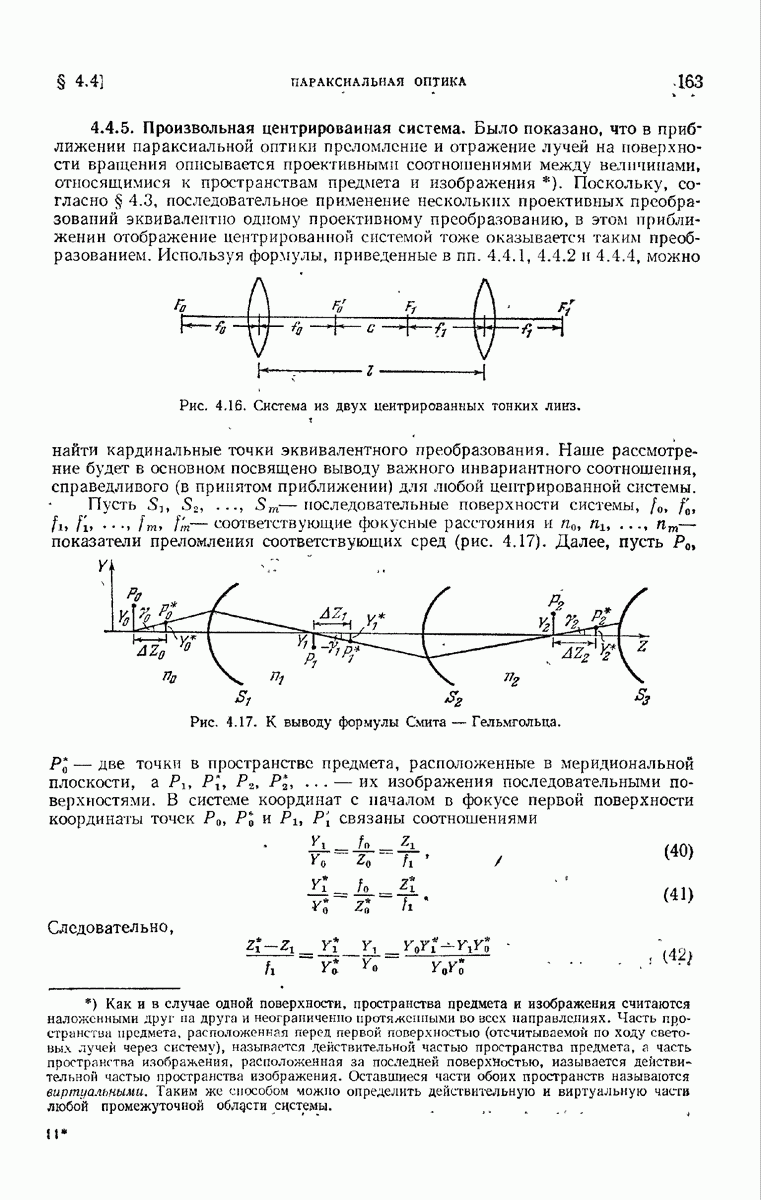
- 4.4.5. Произвольная центрированная система.
- § 4.5. Стигматическое отображение пучками с большой угловой апертурой
- § 4.6. Астигматические пучки лучей
- 4.6.2. Преломление тонкого пучка.
- § 4.7. Хроматическая аберрация. Дисперсия призмы
- 4.7.2. Дисперсия призмы.
- § 4.8. Фотометрия. Апертуры оптических систем
- 4.8.2. Диафрагмы и зрачки.
- 4.8.3. Яркость и освещенность изображений.
- § 4.9. Метод построения хода лучей
- 4.9.2. Параксиальные лучи.
- 4.9.3. Косые лучи.
- § 4.10. Оптические системы с несферическими поверхностями
- 4.10.2. Получение апланатизма.
- ГЛАВА 5. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 5.2. Эйконал Шварншильда
- § 5.3. Первичные аберрации (аберрации Зайделя)
- § 5.4. Теорема сложения для случая первичных аберраций
- § 5.5. Коэффициенты первичных аберраций произвольной центрированной системы линз
- 5.5.2. Формулы Зайделя, выраженные через параметры одного параксиального луча.
- 5.5.3. Теорема Петцваля.
- § 5.6. Пример: первичные аберрации тонкой линзы
- § 5.7. Хроматическая аберрация произвольной центрированной системы линз
- ГЛАВА 6. ОПТИЧЕСКИЕ ПРИБОРЫ, ФОРМИРУЮЩИЕ ИЗОБРАЖЕНИЕ
- § 6.2. Фотографический аппарат
- § 6.3. Линзовый телескоп
- § 6.4. Зеркальный телескоп
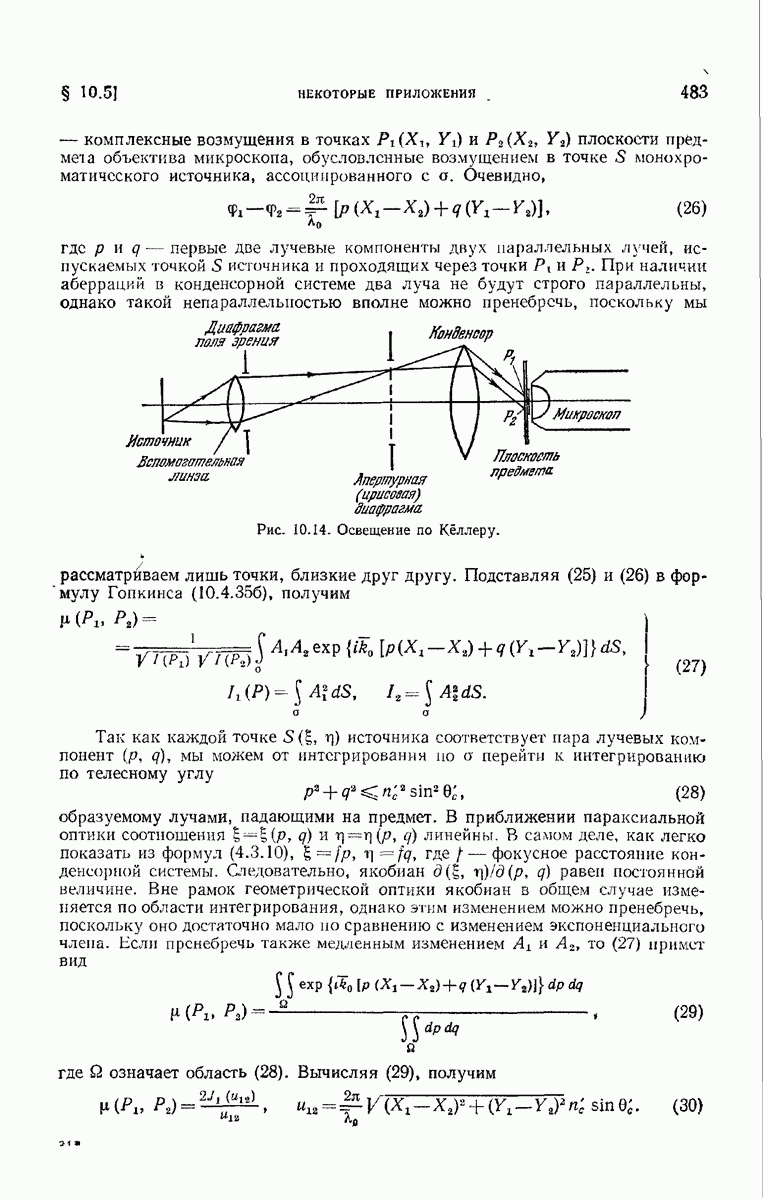
- § 6.5. Осветители
- § 6.6. Микроскоп
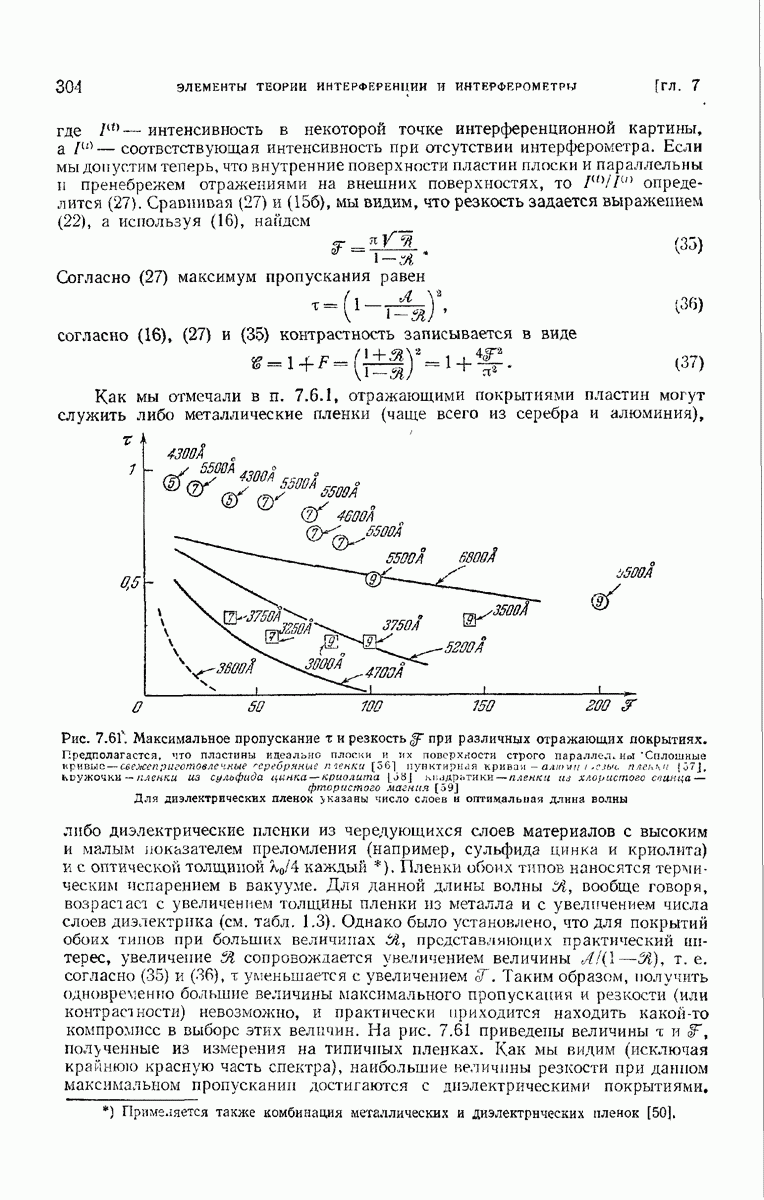
- ГЛАВА 7. ЭЛЕМЕНТЫ ТЕОРИИ ИНТЕРФЕРЕНЦИИ И ИНТЕРФЕРОМЕТРЫ
- § 7.2. Интерференция двух монохроматических волн
- § 7.3. Двухлучевая интерференция. Деление волнового фронта
- 7.3.2. Зеркала Френеля и другие аналогичные устройства.
- 7.3.3. Интерференционные полосы в квазимонохроматическом и белом свете.
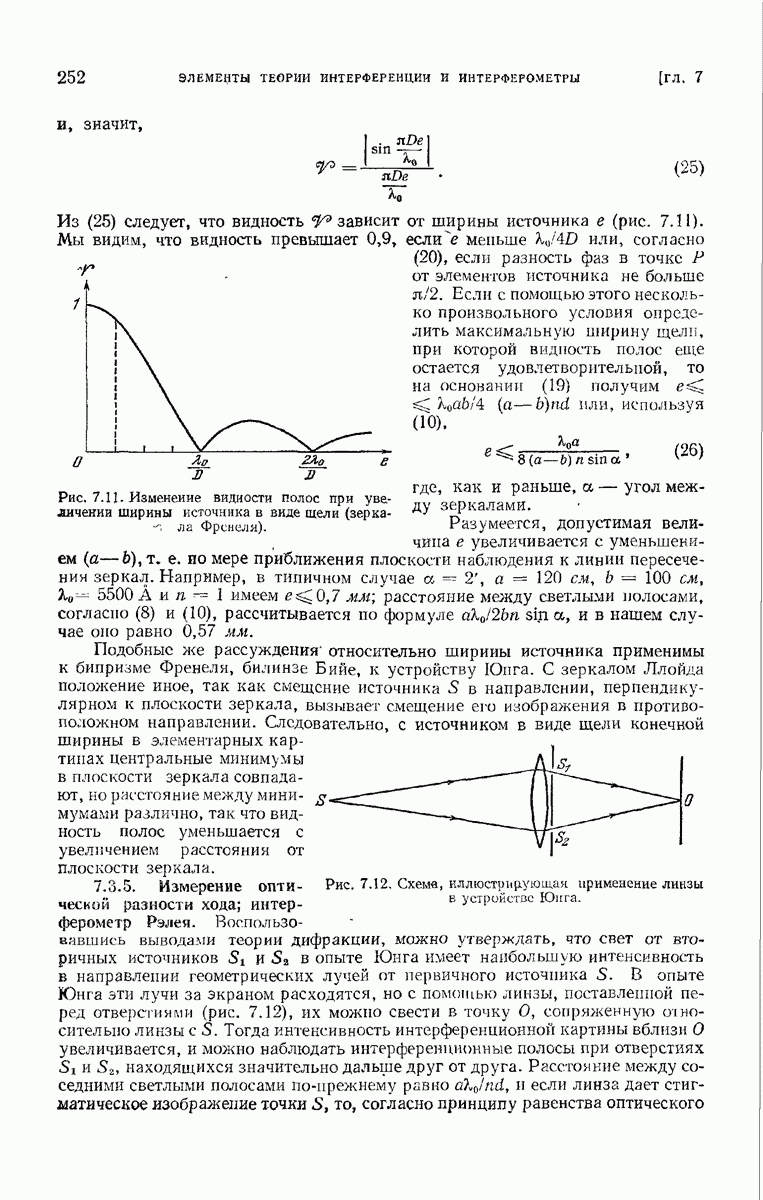
- 7.3.4. Источник в виде щели; видность полос.
- 7.3.5. Измерение оптической разности хода; интерферометр Рэлея.
- 7.3.6. Измерение угловых размеров источников; звездный интерферометр Майкельсона.
- § 7.4. Стоячие волны
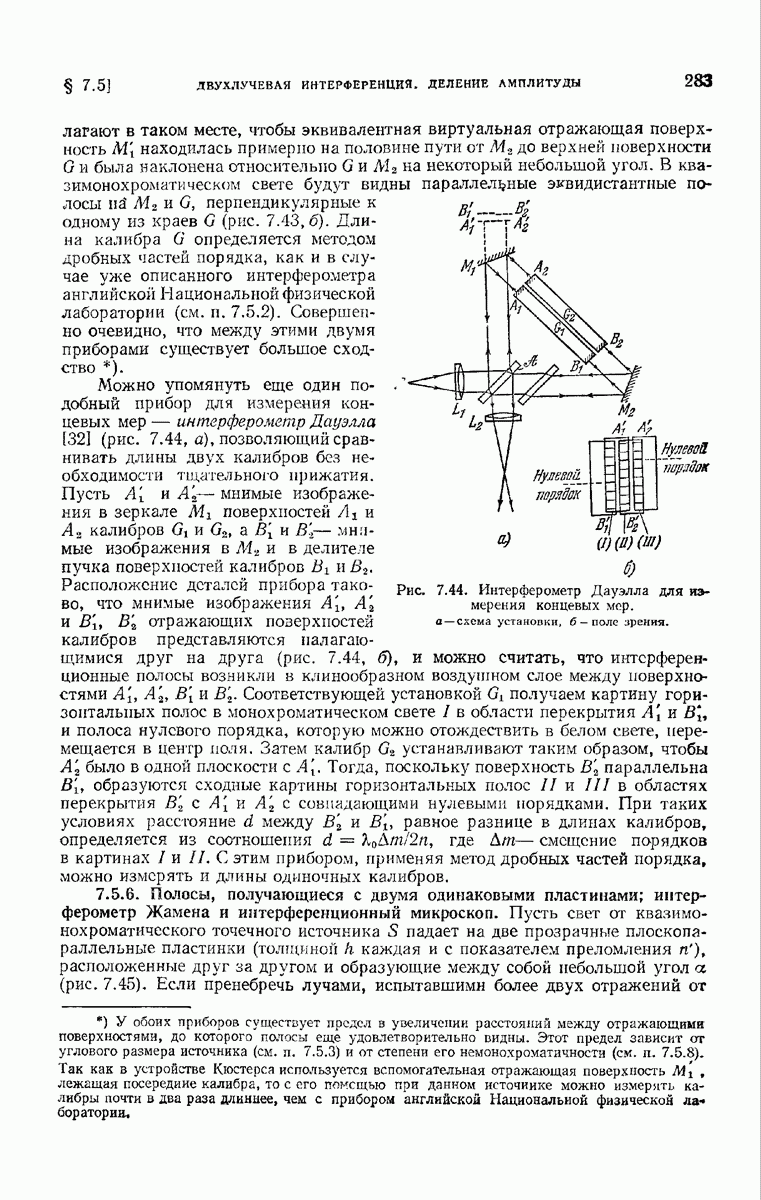
- § 7.5. Двухлучевая интерференция. Деление амплитуды
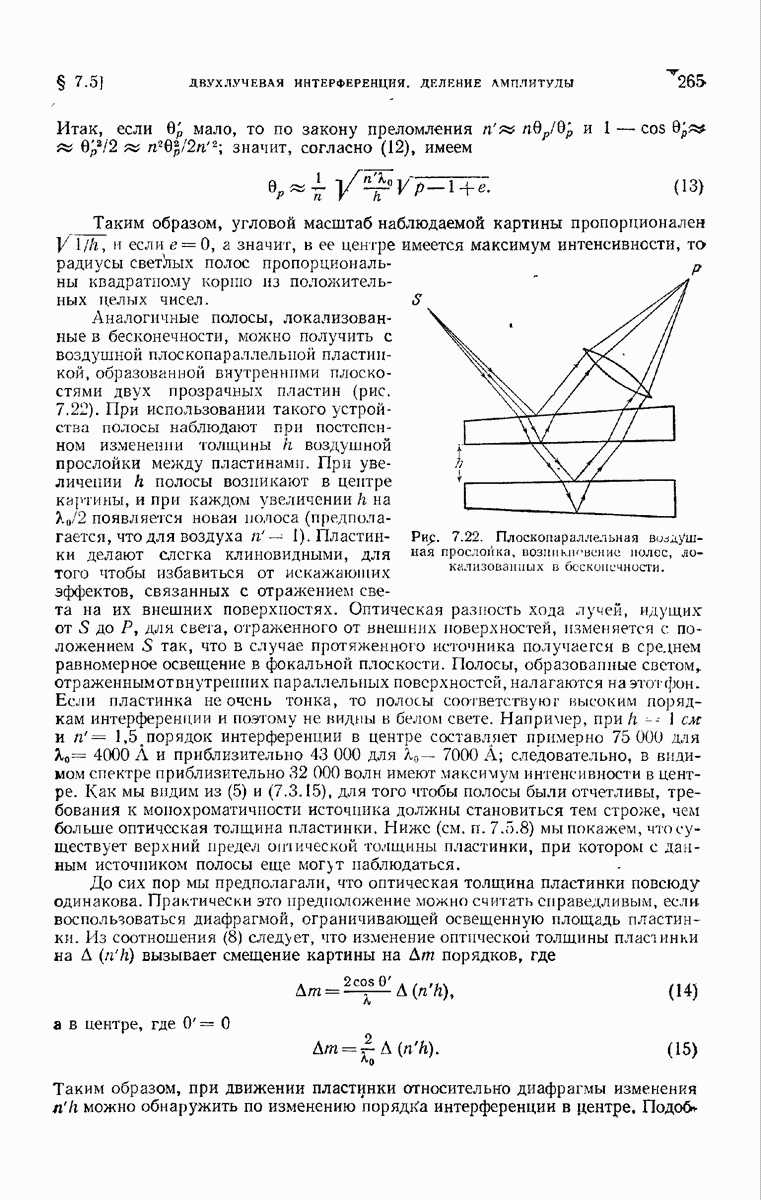
- 7.5.2. Интерференция в тонких пленках; интерферометр Физо.
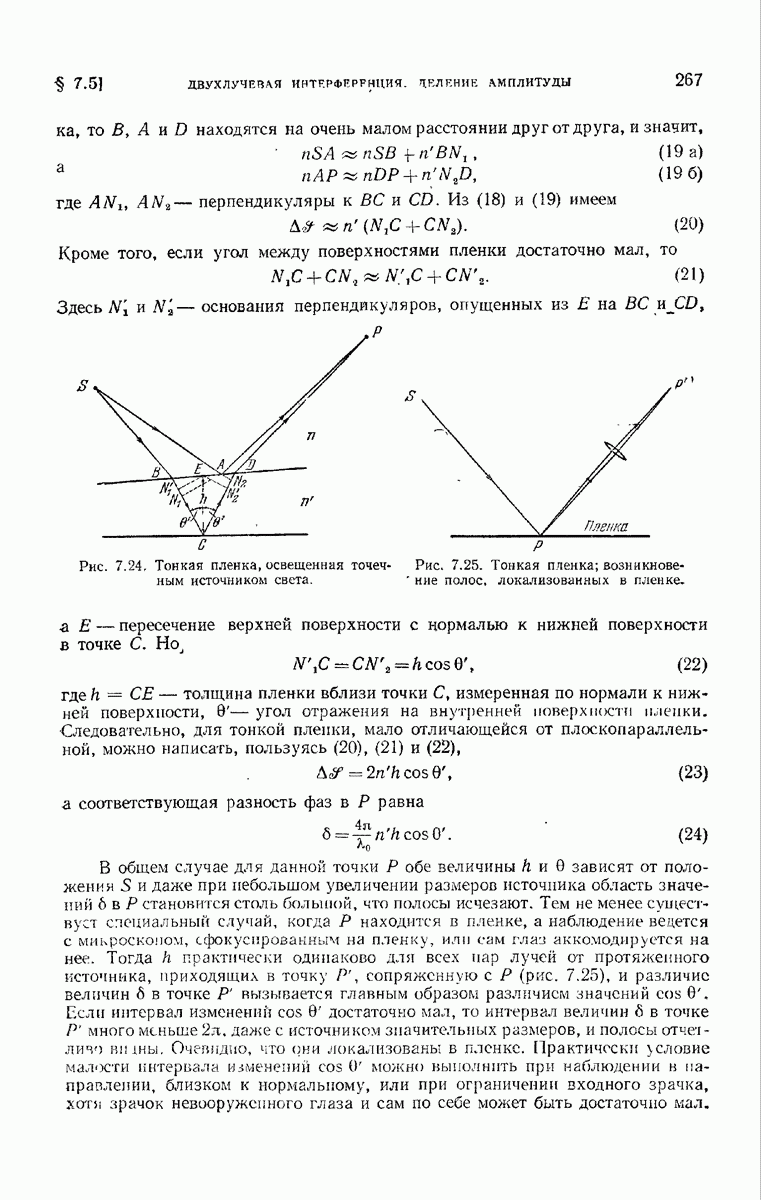
- 7.5.3. Локализация полос.
- 7.5.4. Интерферометр Майкельсона.
- 7.5.5. Интерферометр Тваймана — Грина и другие аналогичные приборы.
- 7.5.6. Полосы, получающиеся с двумя одинаковыми пластинами; интерферометр Жамена и интерференционный микроскоп.
- 7.5.7. Интерферометр Маха—Цендера; интерферометр Бейтса со смещенным волновым фронтом.
- 7.5.8. Длина когерентности; применение двухлучевой интерференции к изучению тонкой структуры спектральных линий.
- § 7.6. Многолучевая интерференция
- 7.6.2. Интерферометр Фабри — Перо.
- 7.6.3. Применение интерферометра Фабри — Перо для изучения тонкой структуры спектральных линий.
- 7.6.4. Применение интерферометра Фабри — Перо для сравнения длин волн.
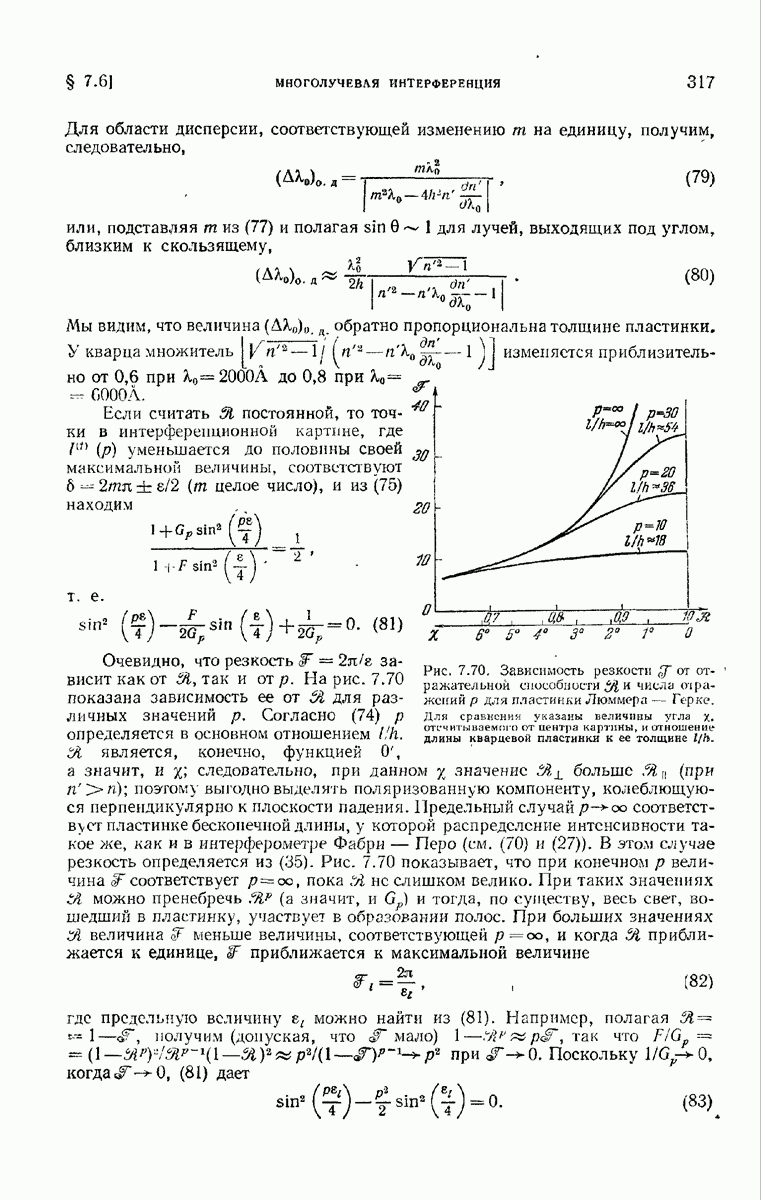
- 7.6.5. Интерферометр Люммера — Герке.
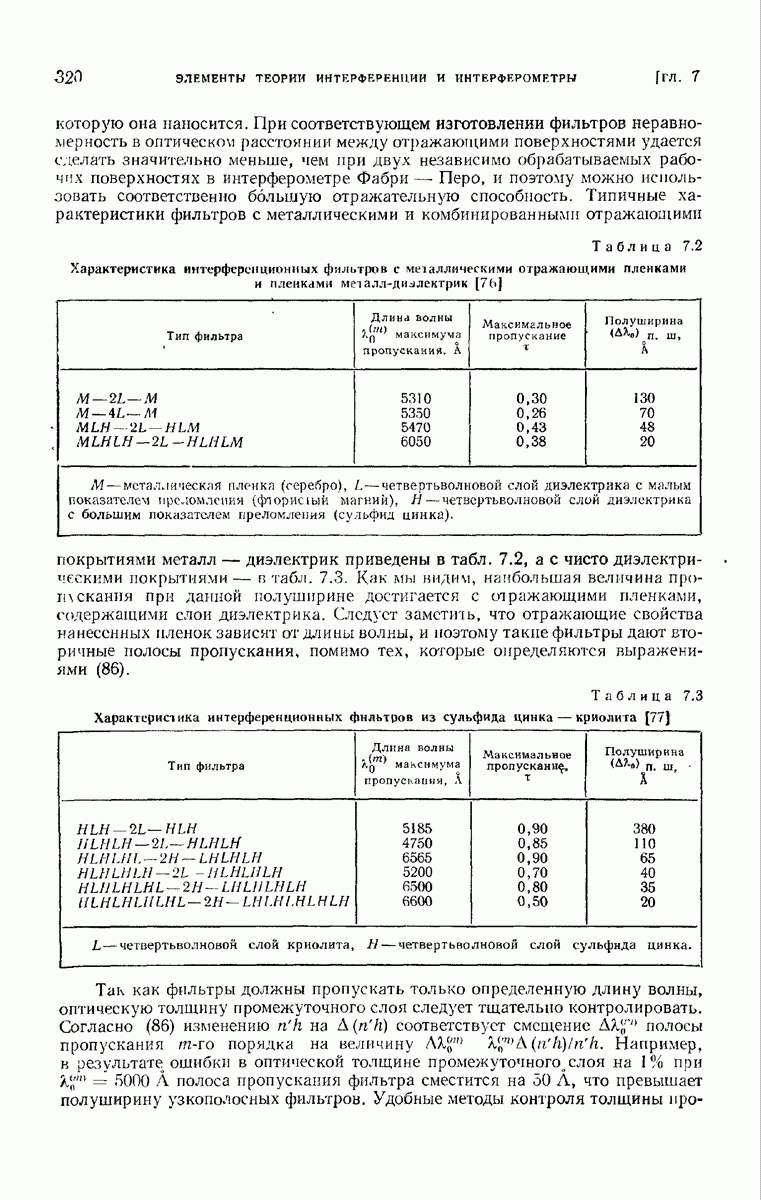
- 7.6.6. Интерференционные фильтры.
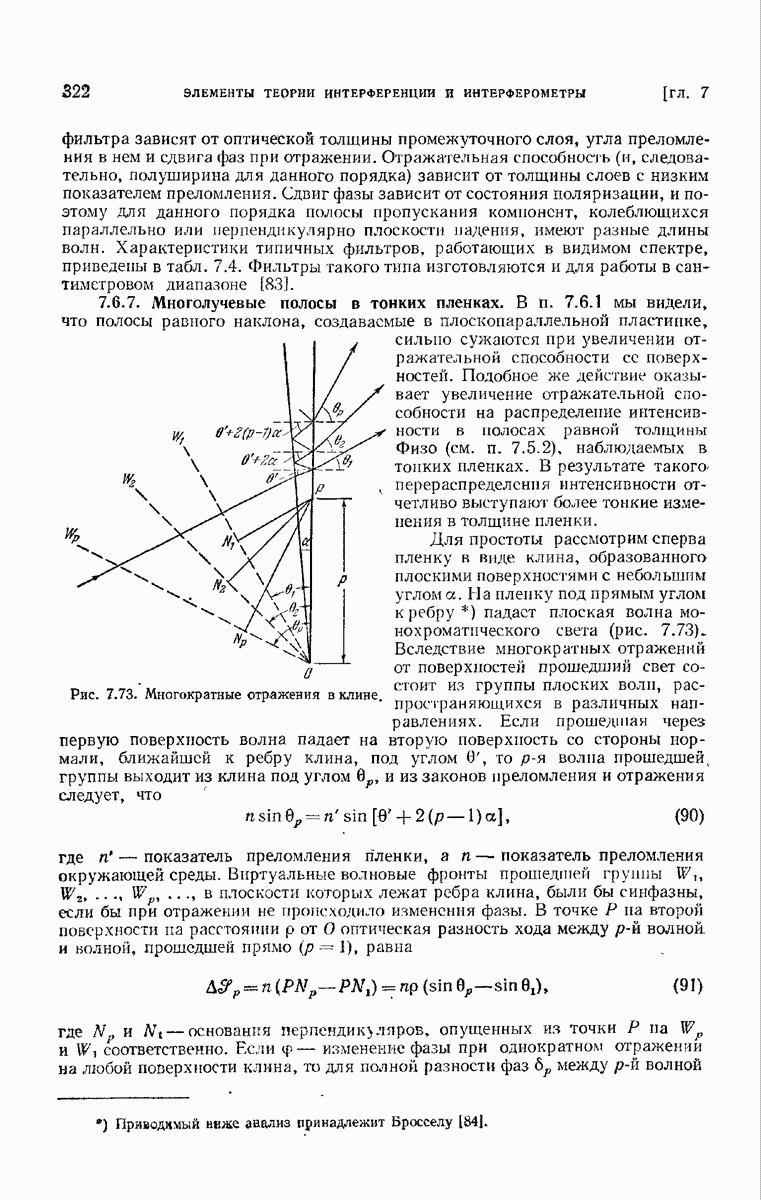
- 7.6.7. Многолучевые полосы в тонких пленках.
- 7.6.8. Многолучевые полосы, получающиеся с двумя плоскопараллельными пластинками.
- § 7.7. Сравнение длин волн с эталонным метром
- ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ДИФРАКЦИИ
- § 8.2. Принцип Гюйгенса — Френеля
- § 8.3. Теория дифракции Кирхгофа
- 8.3.2. Теория дифракции Кирхгофа.
- 8.3.3. Дифракция Фраунгофера и Френеля.
- § 8.4. Переход к скалярной теории
- 8.4.2. Полное поле изображения.
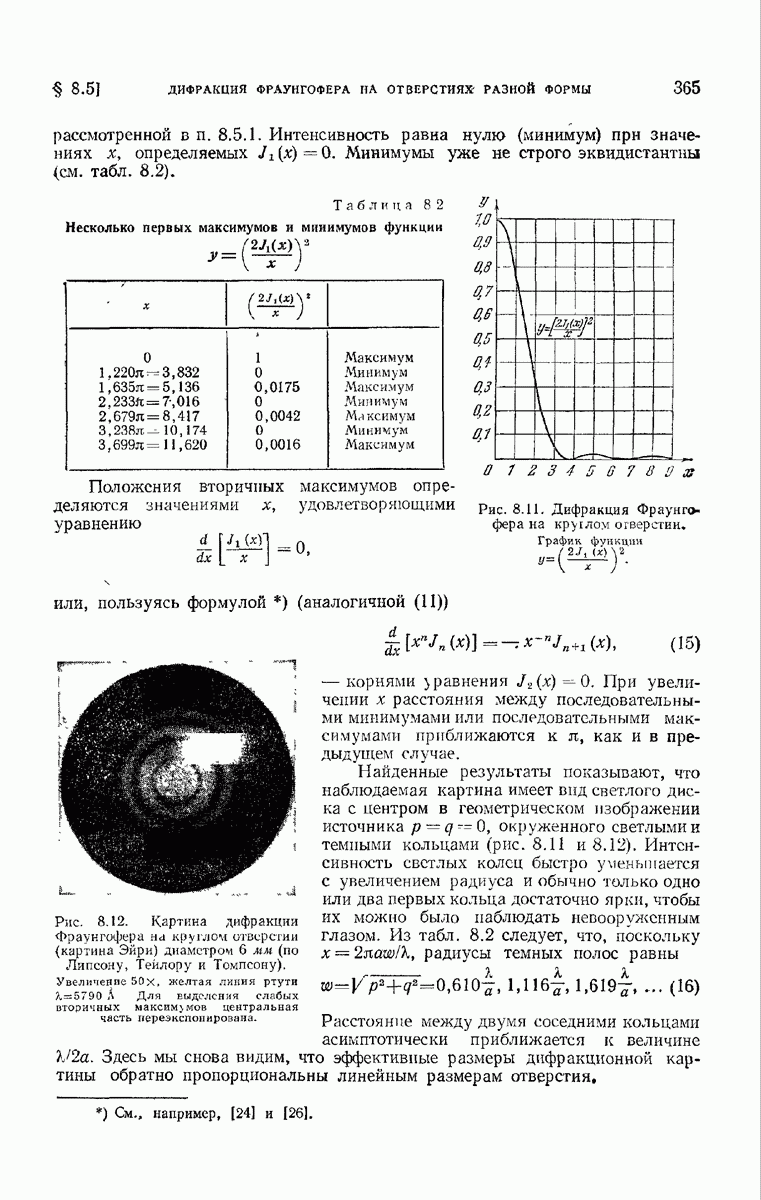
- § 8.5. Дифракция Фраунгофера на отверстиях разной формы
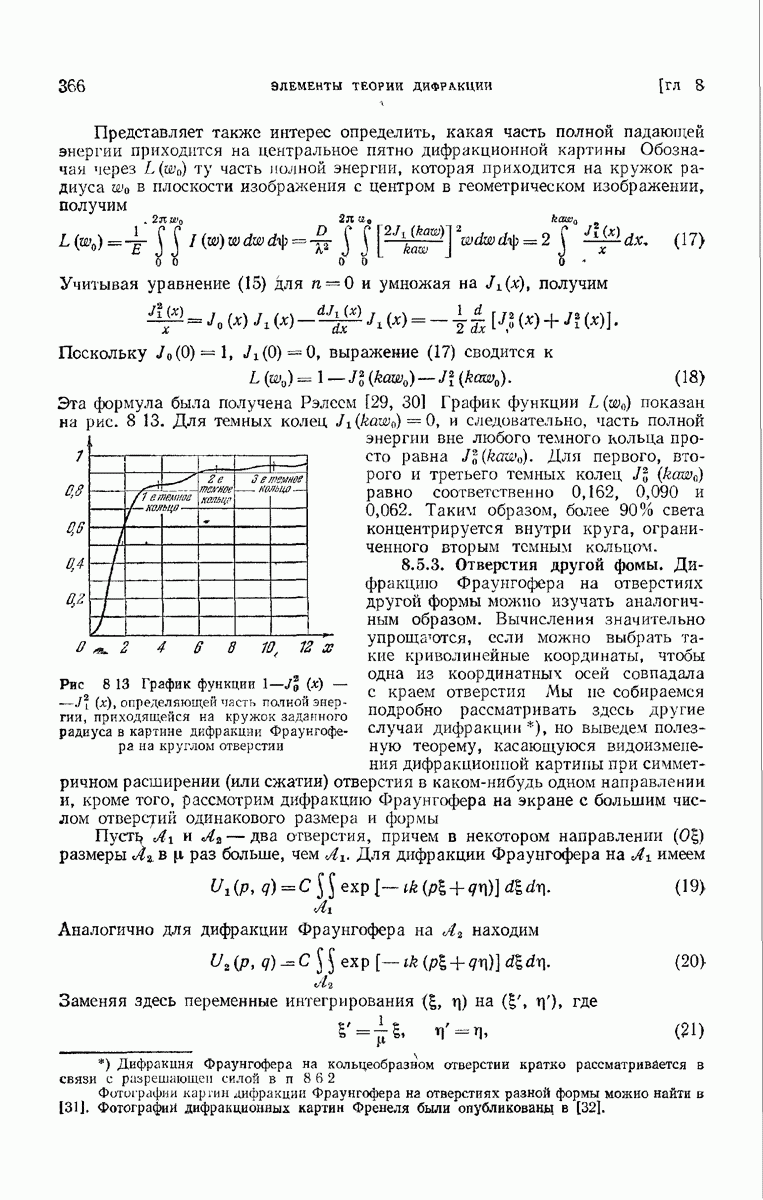
- 8.5.2. Круглое отверстие.
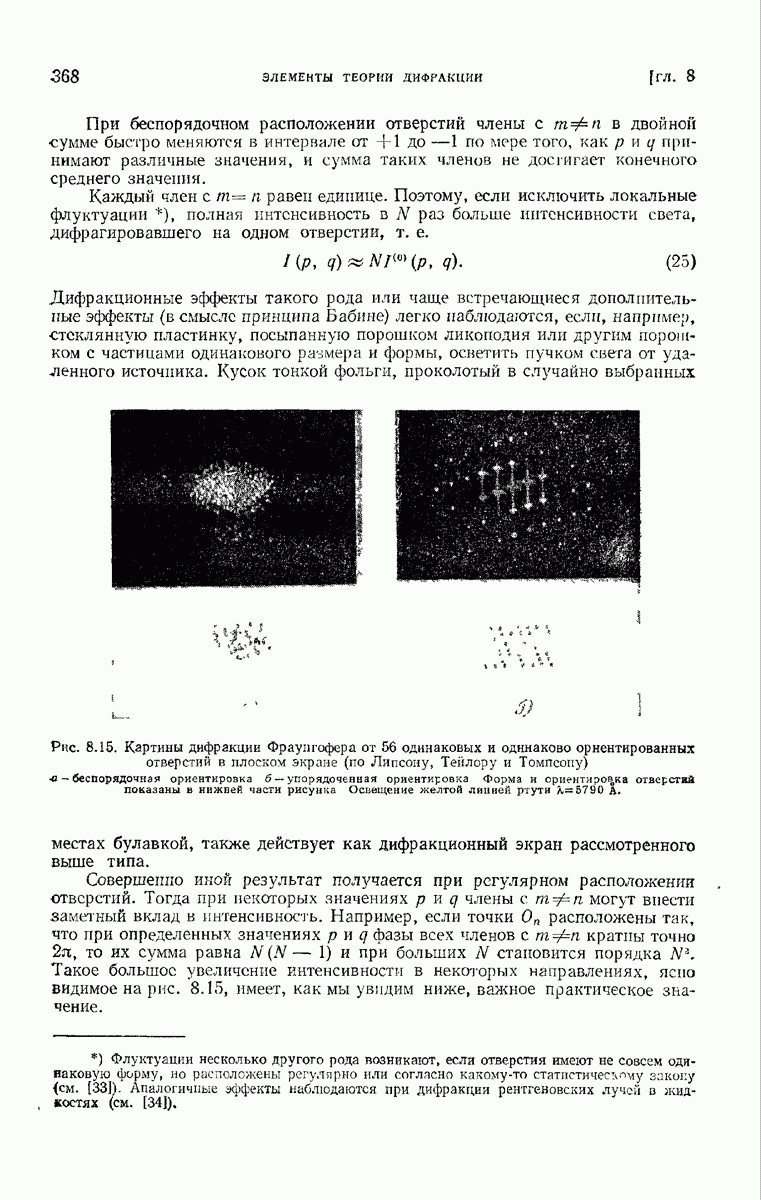
- 8.5.3. Отверстия другой фомы.
- § 8.6. Дифракция Фраунгофера в оптических приборах
- 8.6.2. Разрешающая сила систем, образующих изображение.
- 8.6.3. Образование изображения в микроскопе.
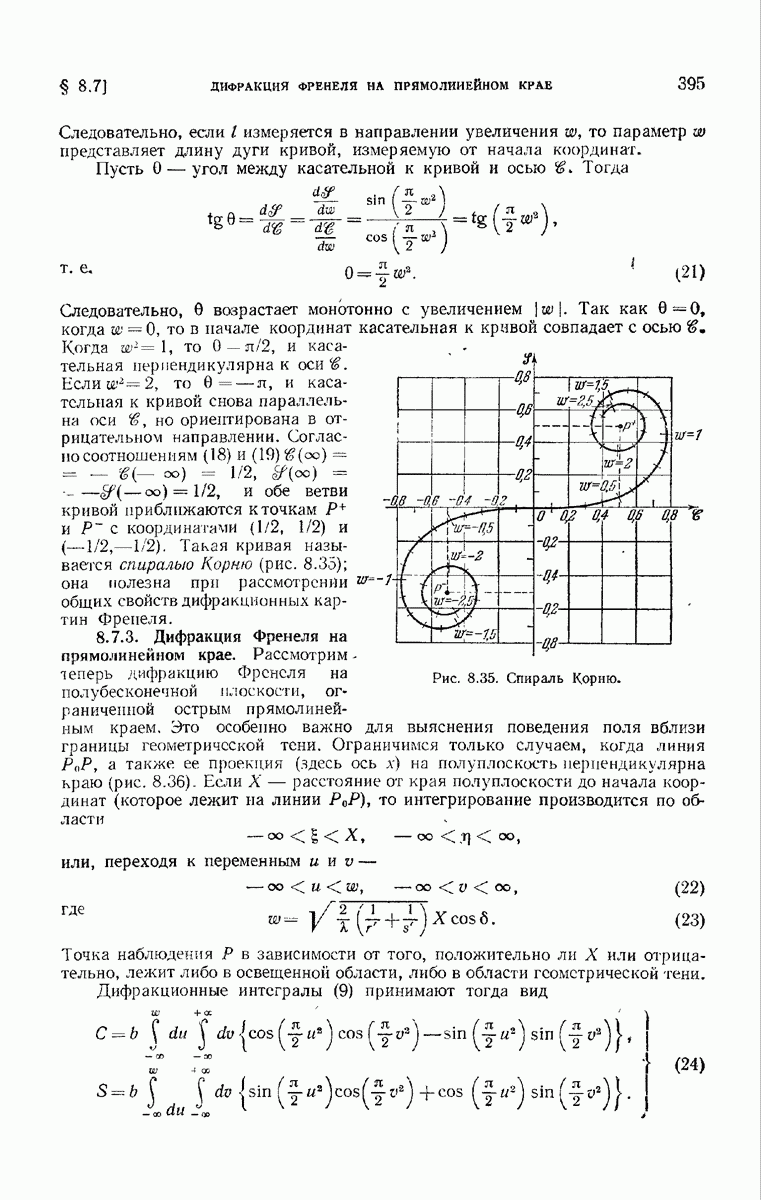
- § 8.7. Дифракция Френеля на прямолинейном крае
- 8.7.2. Интегралы Френеля.
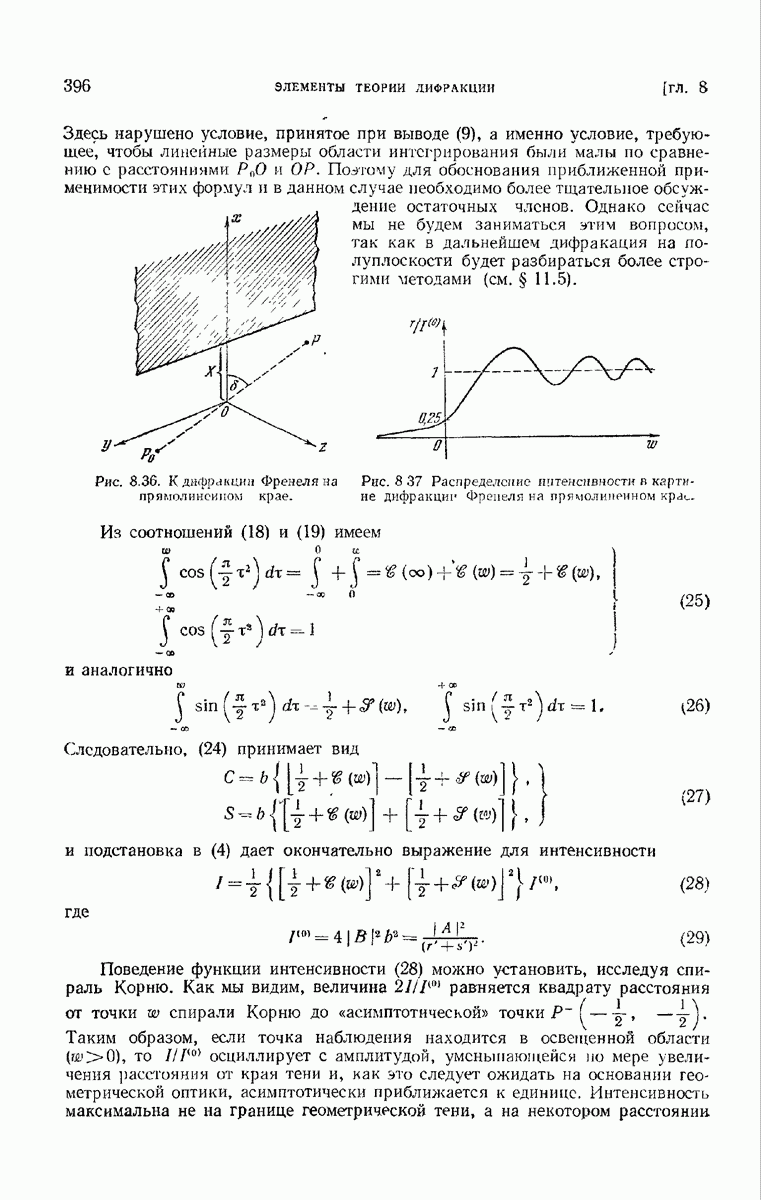
- 8.7.3. Дифракция Френеля на прямолинейном крае.
- § 8.8. Трехмерное распределение света вблизи фокуса
- 8.8.2. Распределение интенсивности.
- 8.8.3. Суммарная интенсивность.
- 8.8.4. Фазовые соотношения.
- § 8.9. Граничная дифрагировавшая волна
- § 8.10. Метод Габора получения изображения восстановлением волновых фронтов
- 8.10.2. Восстановление.
- ГЛАВА 9. ДИФРАКЦИОННАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 9.1. Дифракционный интеграл при наличии аберраций
- 9.1.2. Теорема смещения. Изменение опорной сферы.
- 9.1.3. Соотношение между интенсивностью и средней деформацией волновых фронтов.
- § 9.2. Разложение функции аберрации
- 9.2.2. Разложение функции аберраций.
- § 9.3. Допустимые величины первичных аберраций
- § 9.4. Дифракционная картина, получающаяся при наличии одной аберрации
- 9.4.1. Первичная сферическая аберрация.
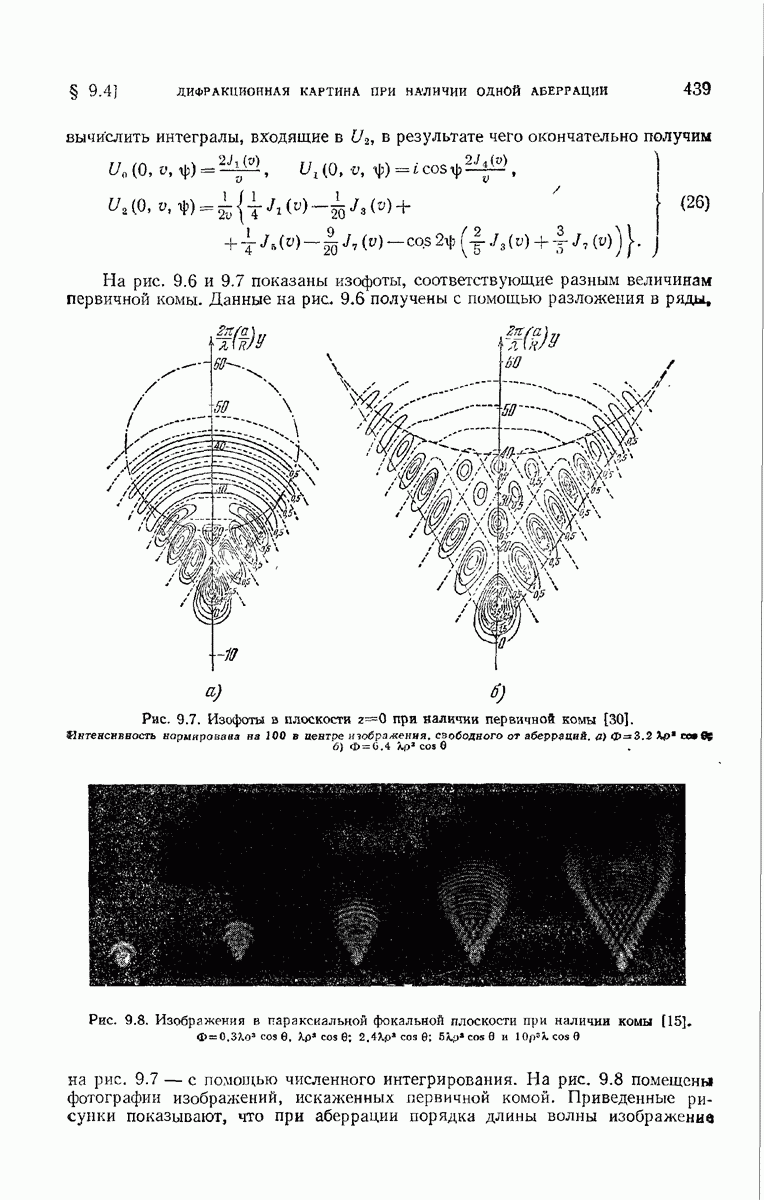
- 9.4.2. Первичная кома.
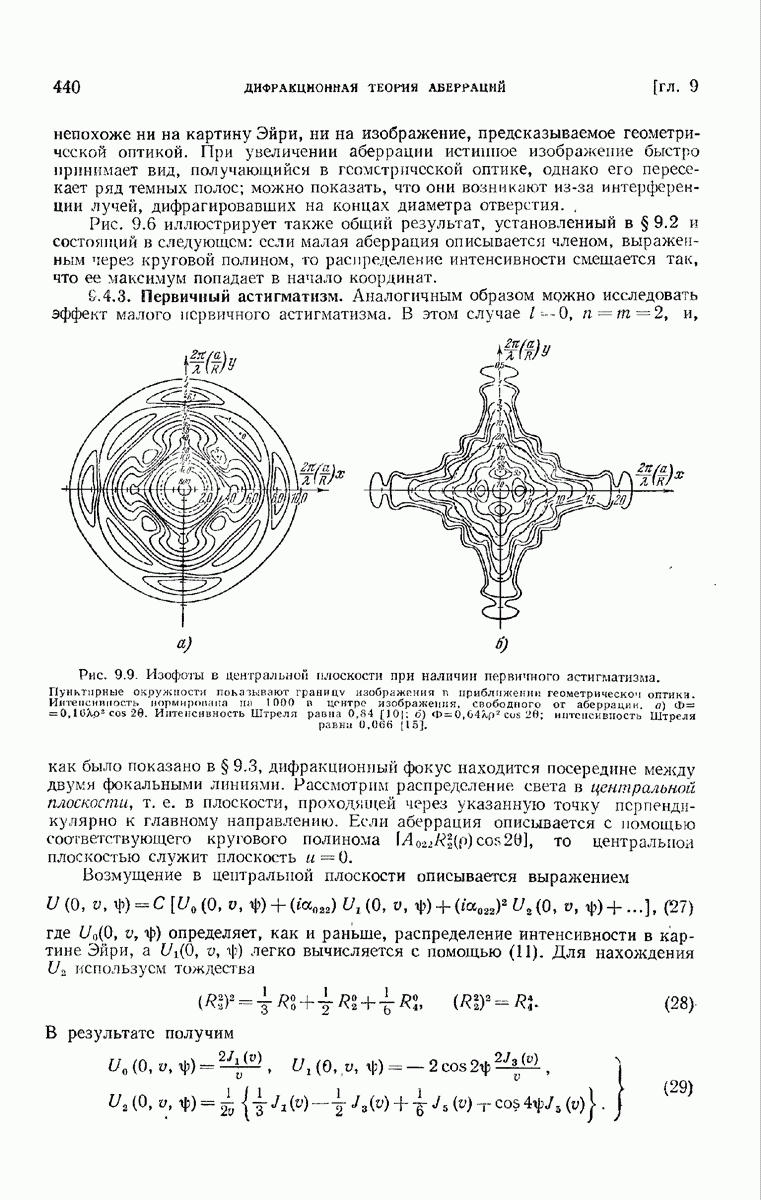
- 9.4.3. Первичный астигматизм.
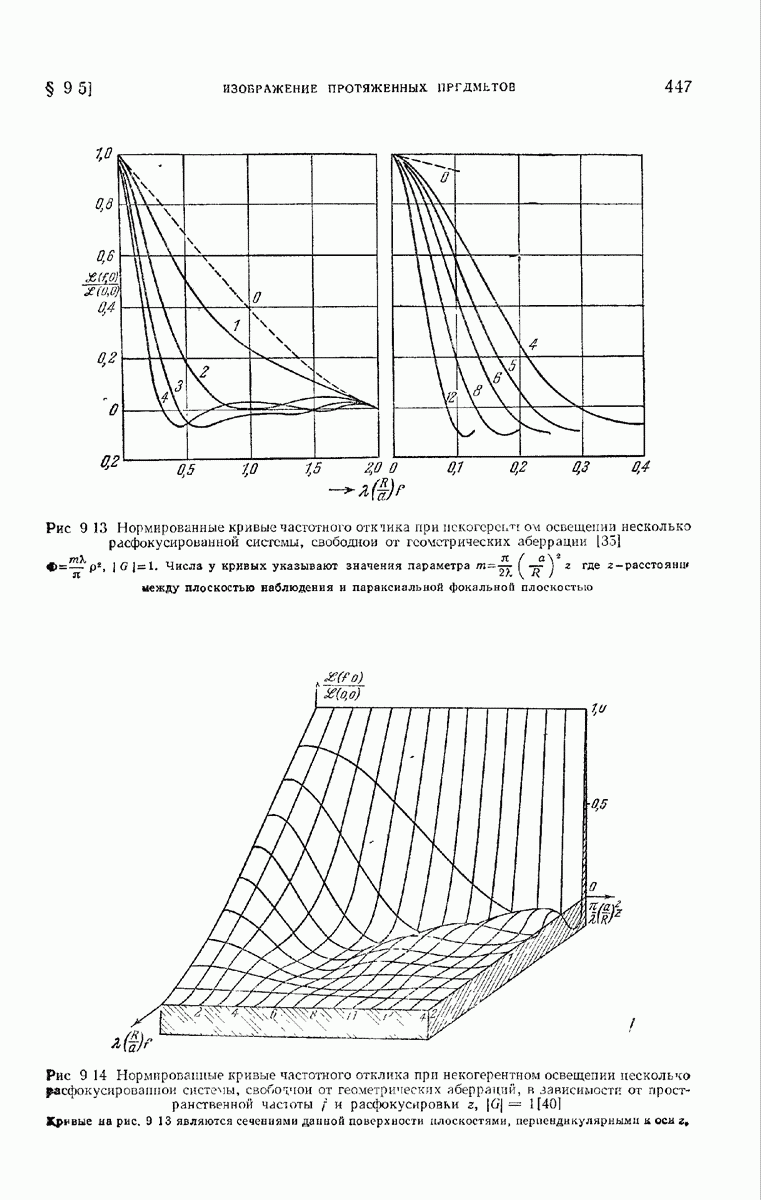
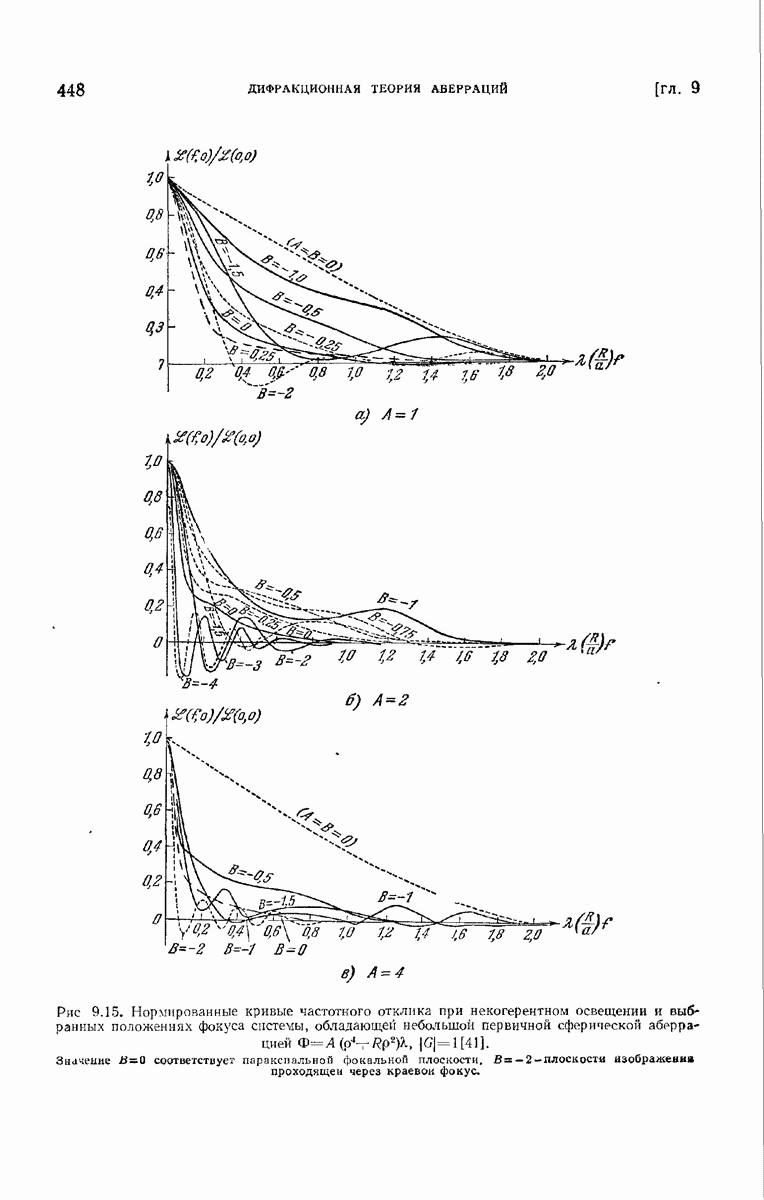
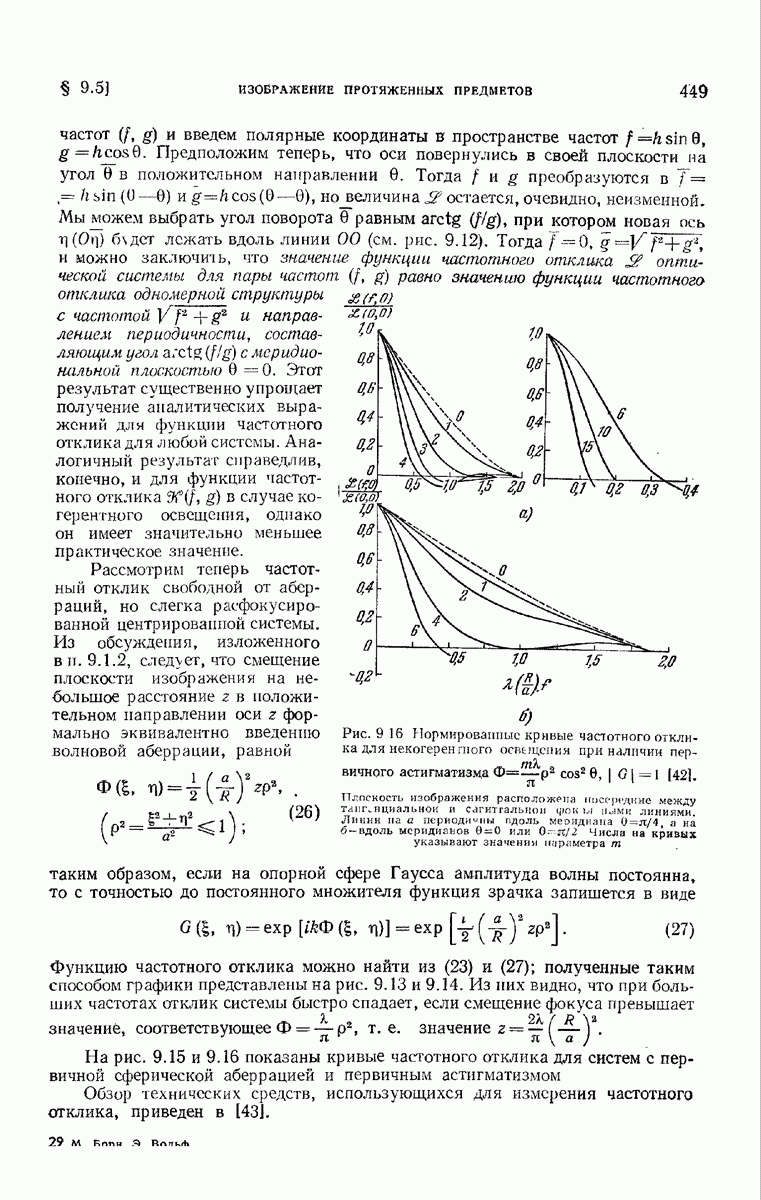
- § 9.5. Изображение протяженных предметов
- 9.5.2. Некогерентное освещение.
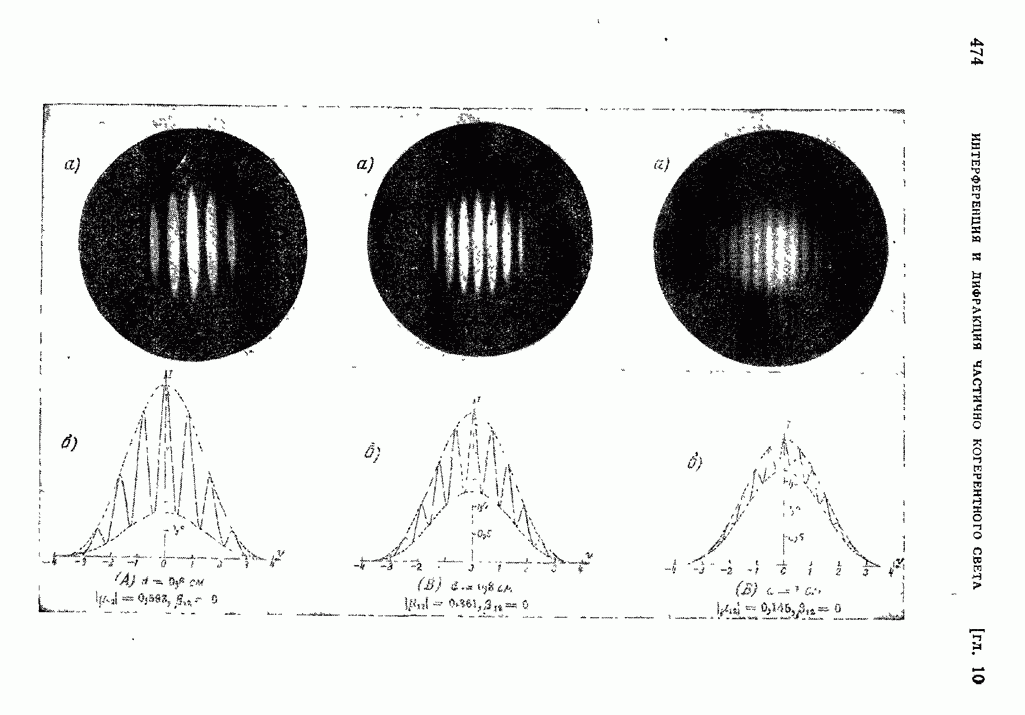
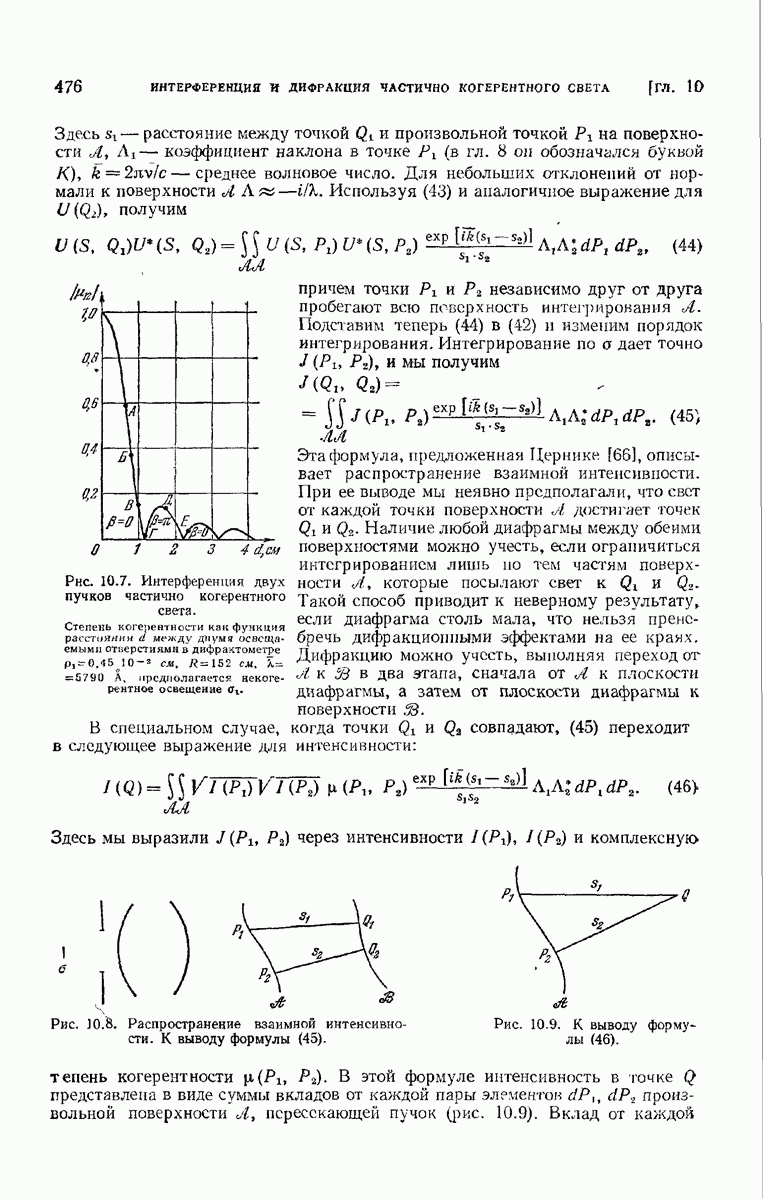
- ГЛАВА 10. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
- § 10.2. Комплексное представление вещественных полихроматических полей
- § 10.3. Корреляционные функции световых пучков
- 10.3.2. Спектральное представление взаимной когерентности.
- § 10.4. Интерференция и дифракция квазимонохроматического света
- 10.4.2. Расчет взаимной интенсивности и степени когерентности для света от протяженного некогерентного квазимонохроматического источника.
- 10.4.3. Пример.
- 10.4.4. Распространение взаимной интенсивности.
- § 10.5. Некоторые приложения
- 10.5.1. Степень когерентности в изображении протяженного некогерентного квазимонохроматического источника.
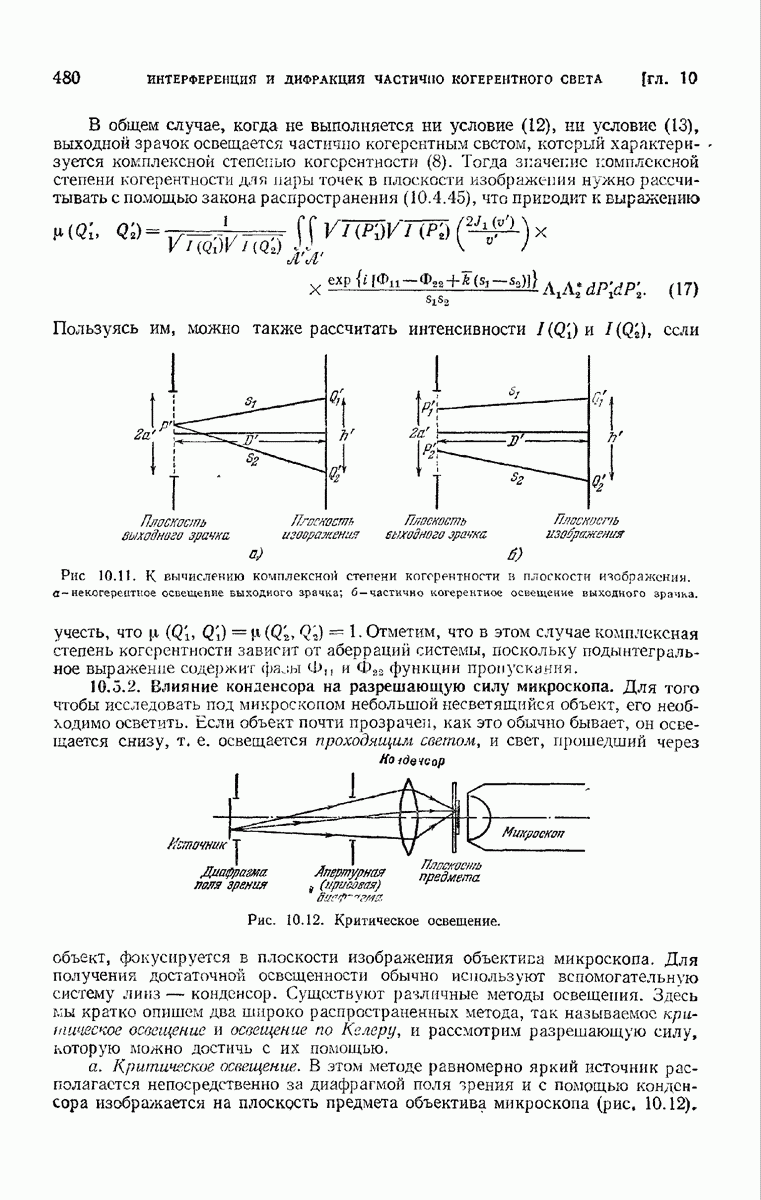
- 10.5.2. Влияние конденсора на разрешающую силу микроскопа.
- 10.5.3. Получение изображения при частично когерентном квазимонохроматическом освещении
- § 10.6. Некоторые теоремы, касающиеся взаимной когерентности
- 10.6.2. Распространение взаимной когерентности.
- § 10.7. Строгая теория частичной когерентности
- 10.7.2. Строгая формулировка закона распространения взаимной когерентности.
- 10.7.3. Время когерентности и эффективная ширина спектра.
- § 10.8. Поляризация квазимонохроматического света
- 10.8.2. Некоторые эквивалентные представления. Степень поляризации световой волны.
- 10.8.3. Параметры Стокса квазимонохроматичаской плоской волны.
- ГЛАВА 11. СТРОГАЯ ТЕОРИЯ ДИФРАКЦИИ
- § 11.2. Граничные условия и поверхностные токи
- § 11.3. Дифракция на плоском экране; электромагнитная форма принципа Бабине
- § 11.4. Двумерная дифракция на плоском экране
- 11.4.2. Угловой спектр плоских волн.
- 11.4.3. Формулировка задачи через дуальные интегральные уравнения.
- § 11.5. Двумерная дифракция плоской волны на полуплоскости
- 11.5.2. Выражение решения через интегралы Френеля.
- 11.5.3. Характер решения.
- 11.5.4. Решение для Н-поляризации.
- 11.5.5. Некоторые численные расчеты.
- 11.5.6. Сравнение с приближенной теорией и с экспериментальными результатами.
- § 11.6. Трехмерная дифракция плоской волны на полуплоскости
- § 11.7. Дифракция волн, испускаемых локализованным источником, на полуплоскости
- 11.7.2. Диполь.
- § 11.8. Другие задачи
- 11.8.1. Две параллельные полуплоскости.
- 11.8.2. Бесконечный набор параллельных полуплоскостей, расположенных ступеньками.
- 11.8.3. Полоса.
- 11.8.4. Другие задачи.
- § 11.9. Единственность решения
- ГЛАВА 12. ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКОВЫХ ВОЛНАХ
- 12.1.2. Краткое изложение теорий, основанных на уравнениях Максвелла.
- § 12.2. Рассмотрение дифракции света на ультразвуковых волнах методом интегральных уравнений
- 12.2.1. Интегральное уравнение для случая Е-поляризации.
- 12.2.2. Пробное решение интегрального уравнения.
- 12.2.3. Выражения для амплитуд световых волн в дифрагировавших и отраженных спектрах.
- 12.2.5. Выражения для интенсивностей линий в спектрах первого и второго порядков в некоторых специальных случаях
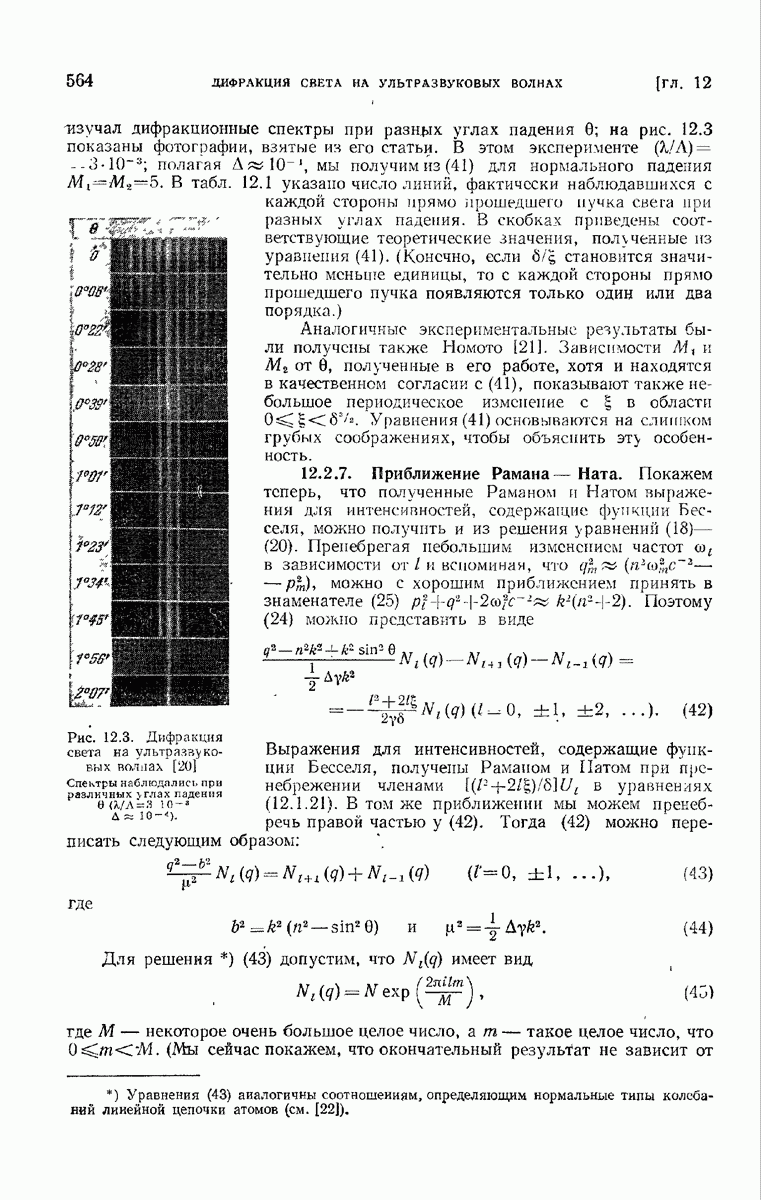
- 12.2.6. Некоторые качественные результаты.
- 12.2.7. Приближение Рамана—Ната.
- ГЛАВА 13. МЕТАЛЛООПТИКА
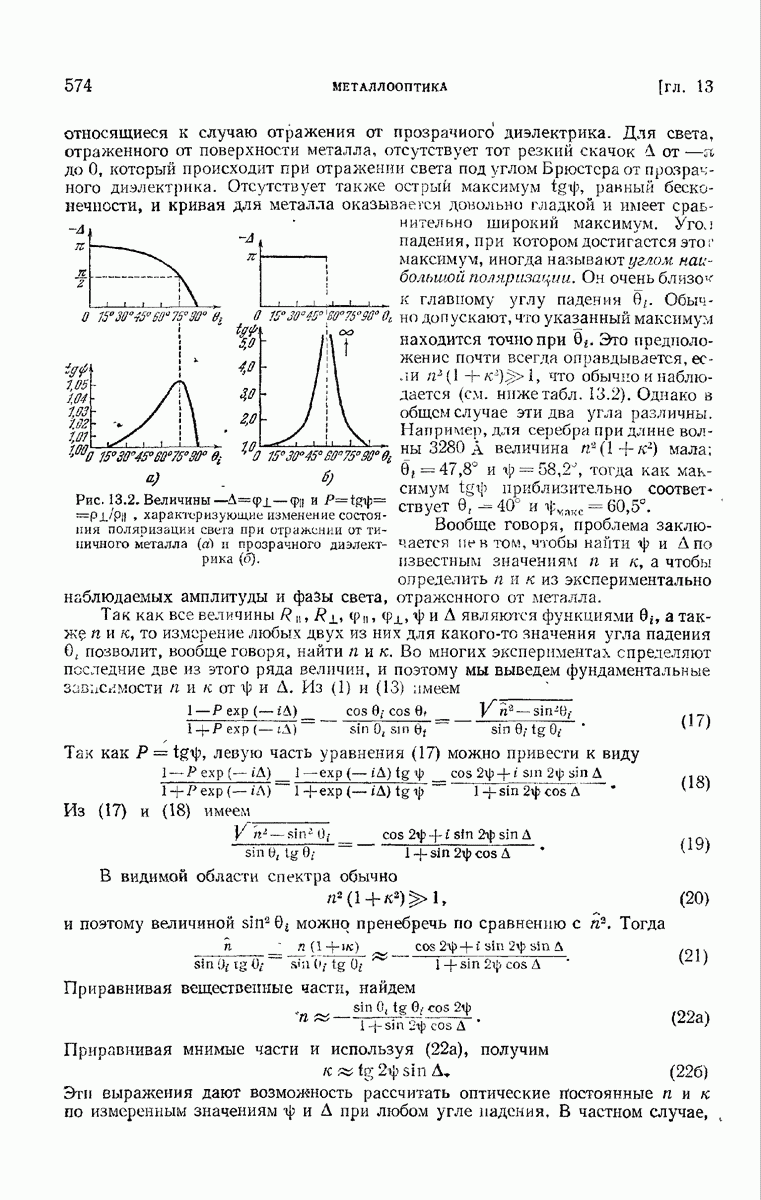
- § 13.2. Преломление и отражение на поверхности металла
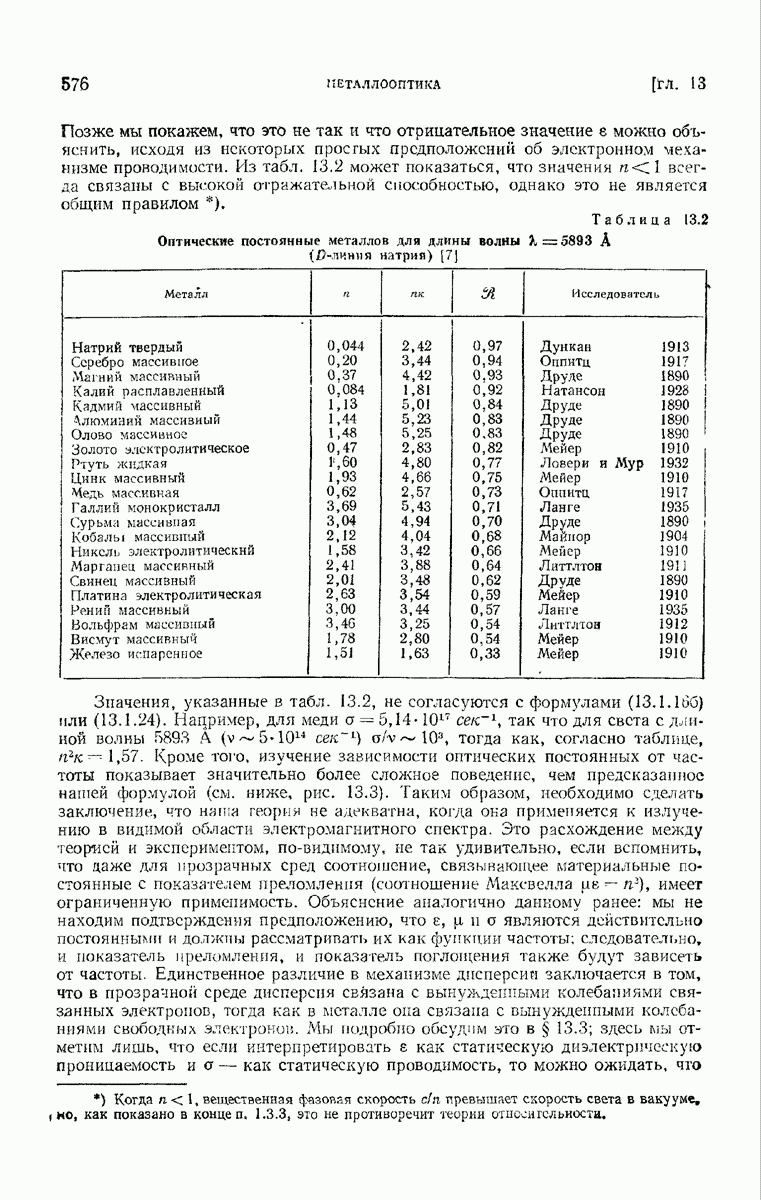
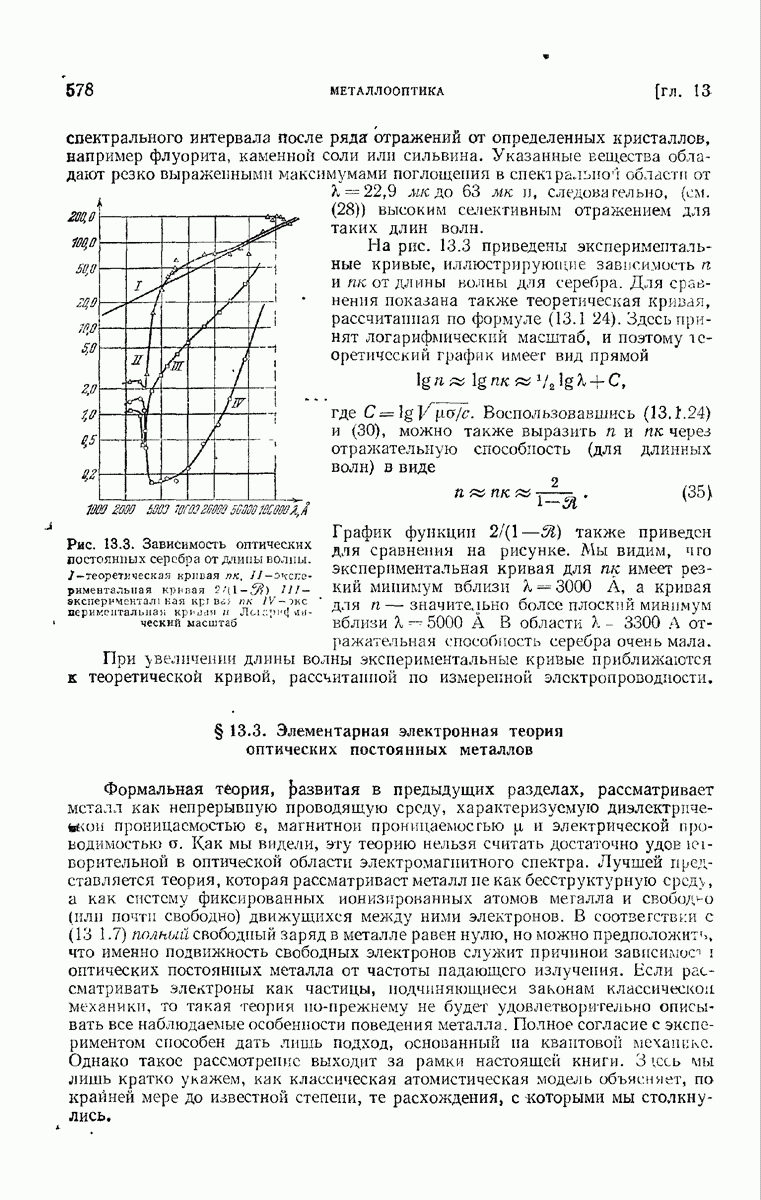
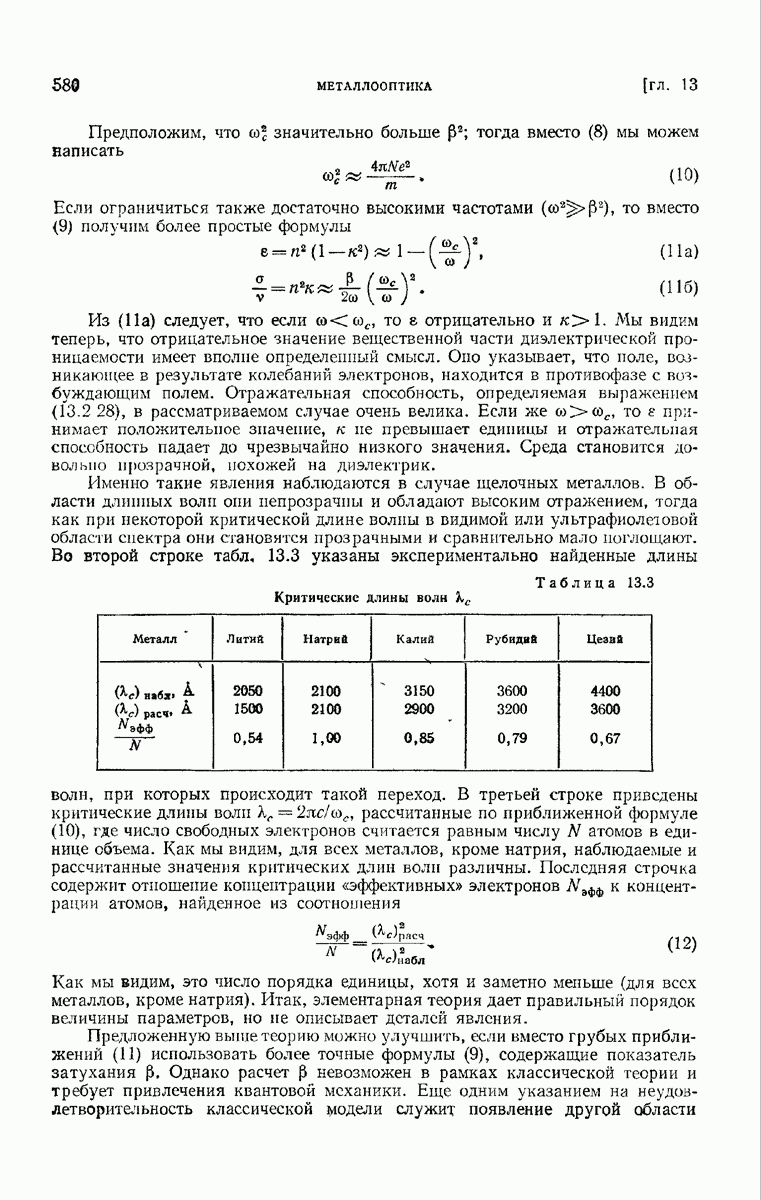
- § 13.3. Элементарная электронная теория оптических постоянных металлов
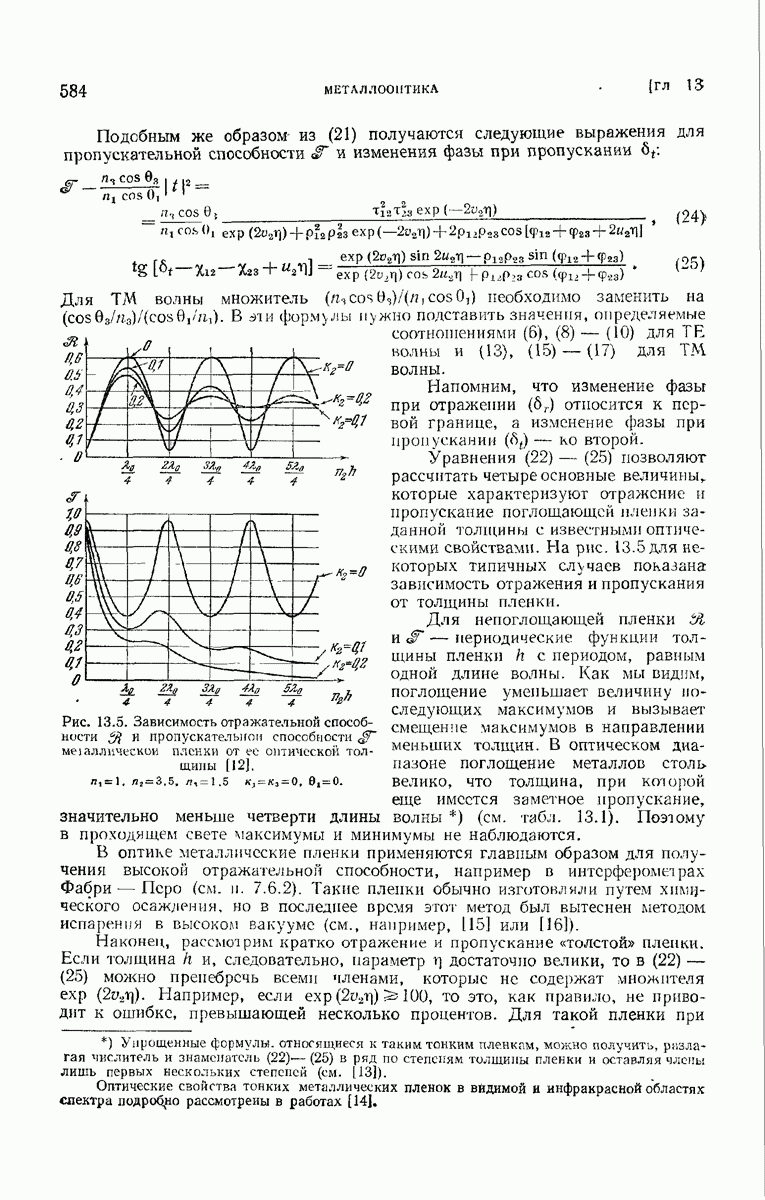
- § 13.4. Распространение волн в слоистой проводящей среде. Теория металлических пленок
- 13.4.2. Прозрачная пленка на поглощающей подложке.
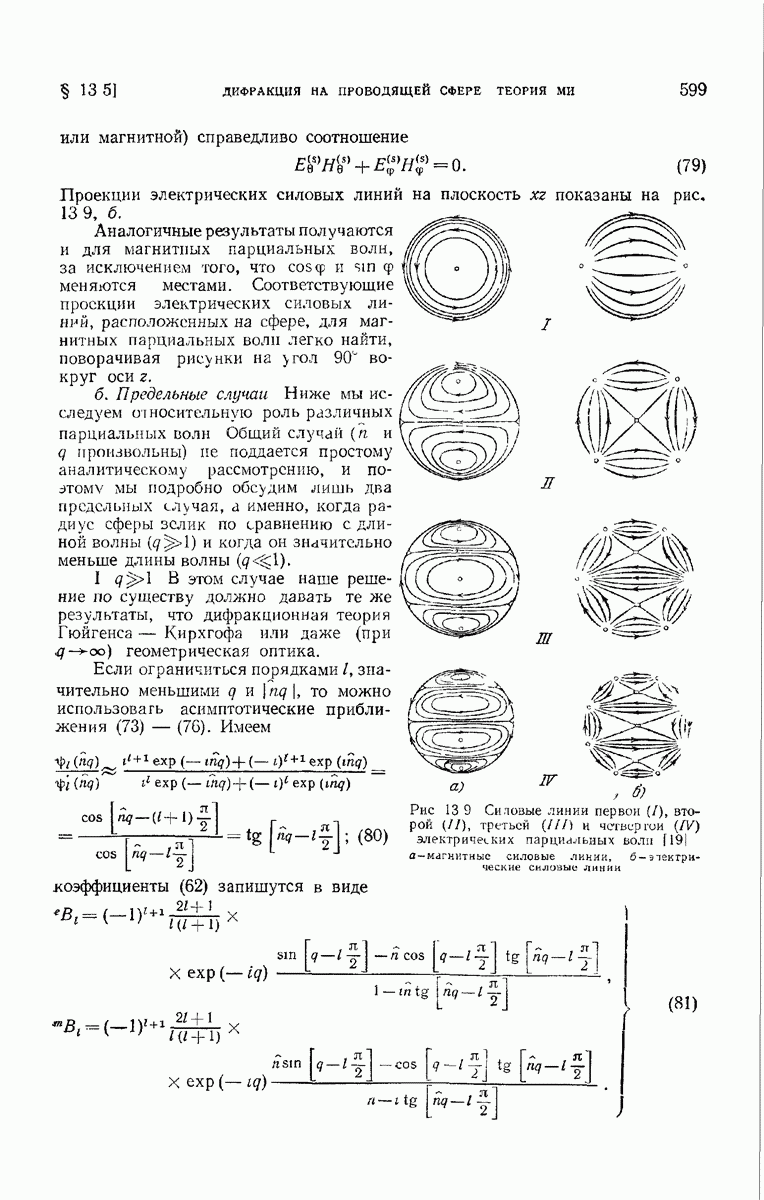
- § 13.5. Дифракция на проводящей сфере. Теория Ми
- 13.5.1. Математическое решение проблемы
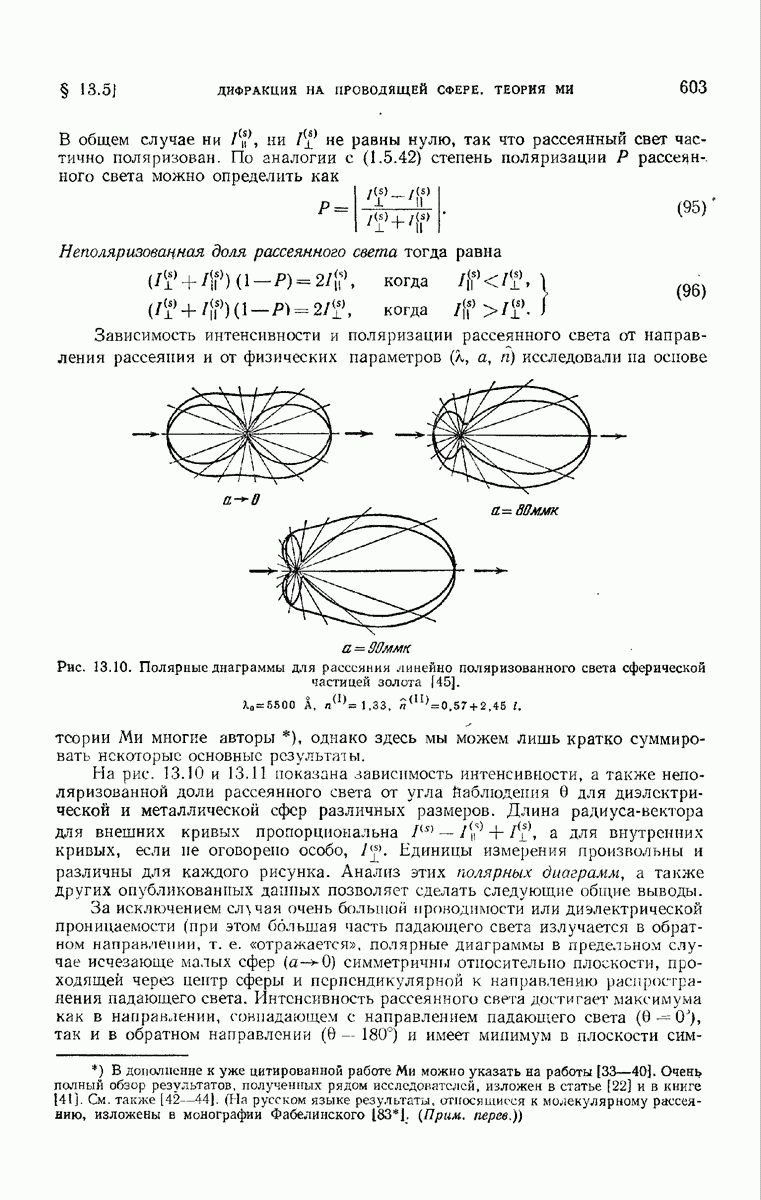
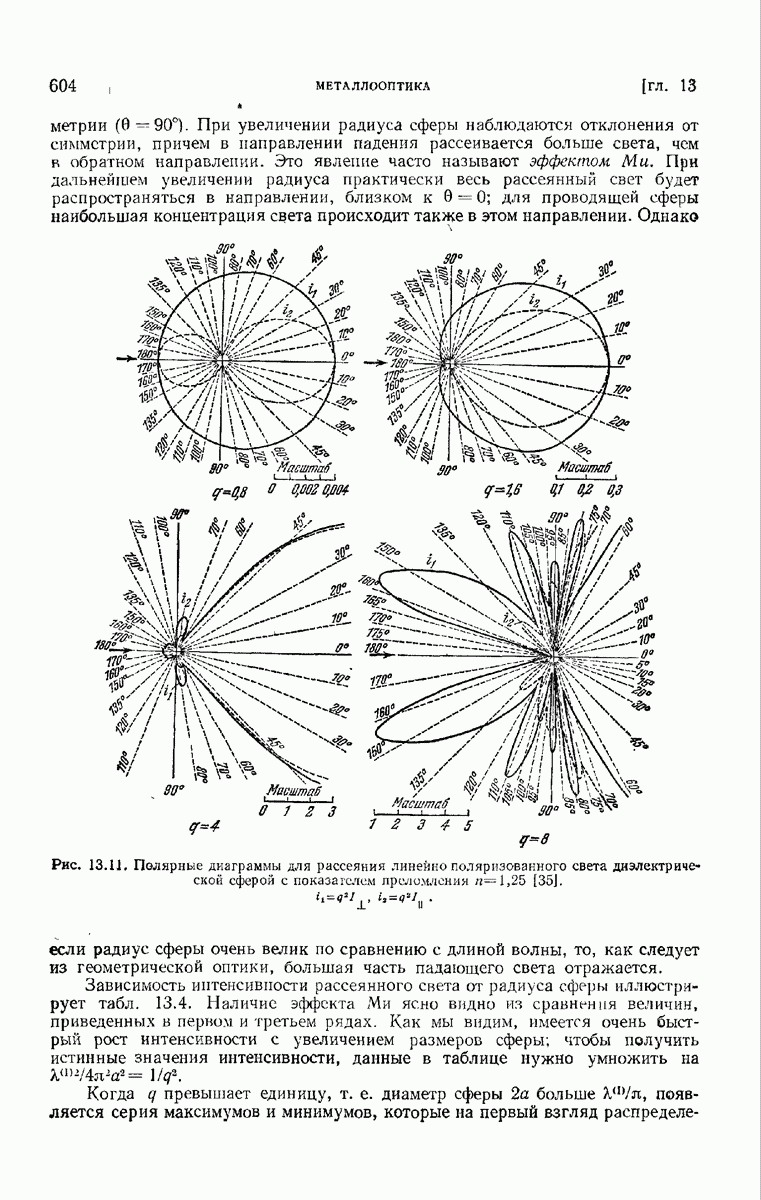
- 13.5.2. Некоторые следствия из формул Ми.
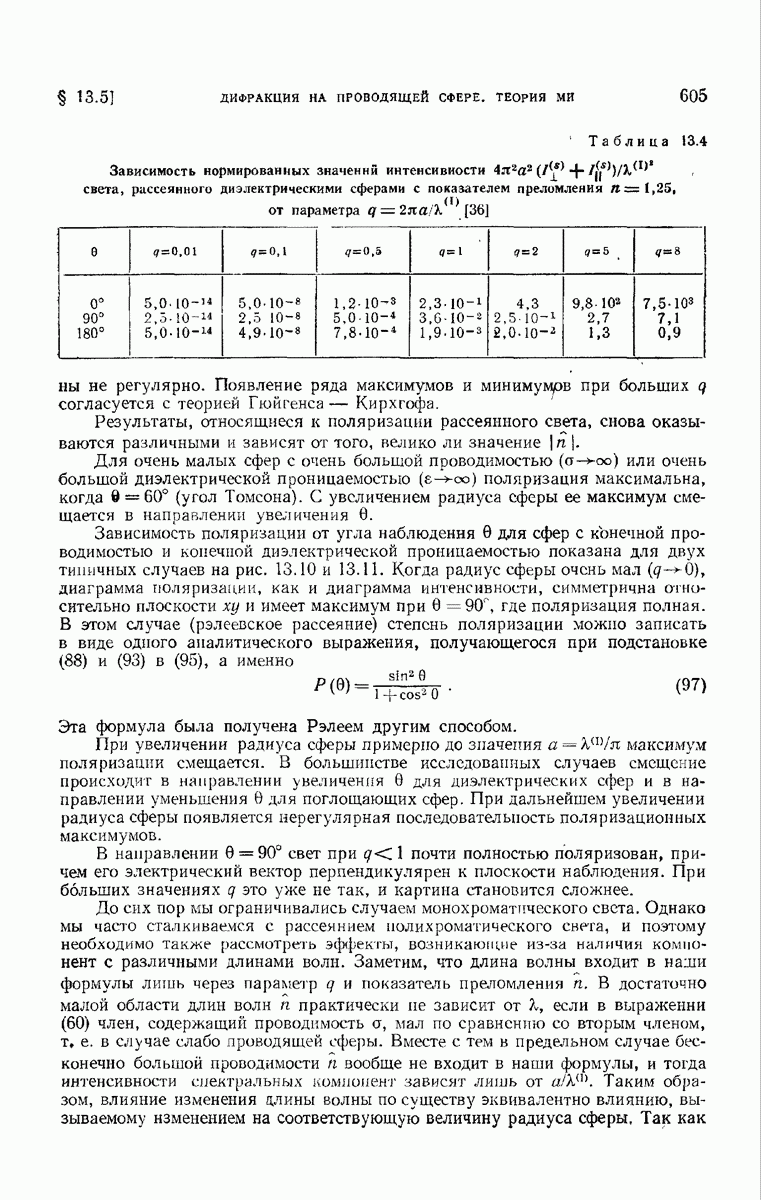
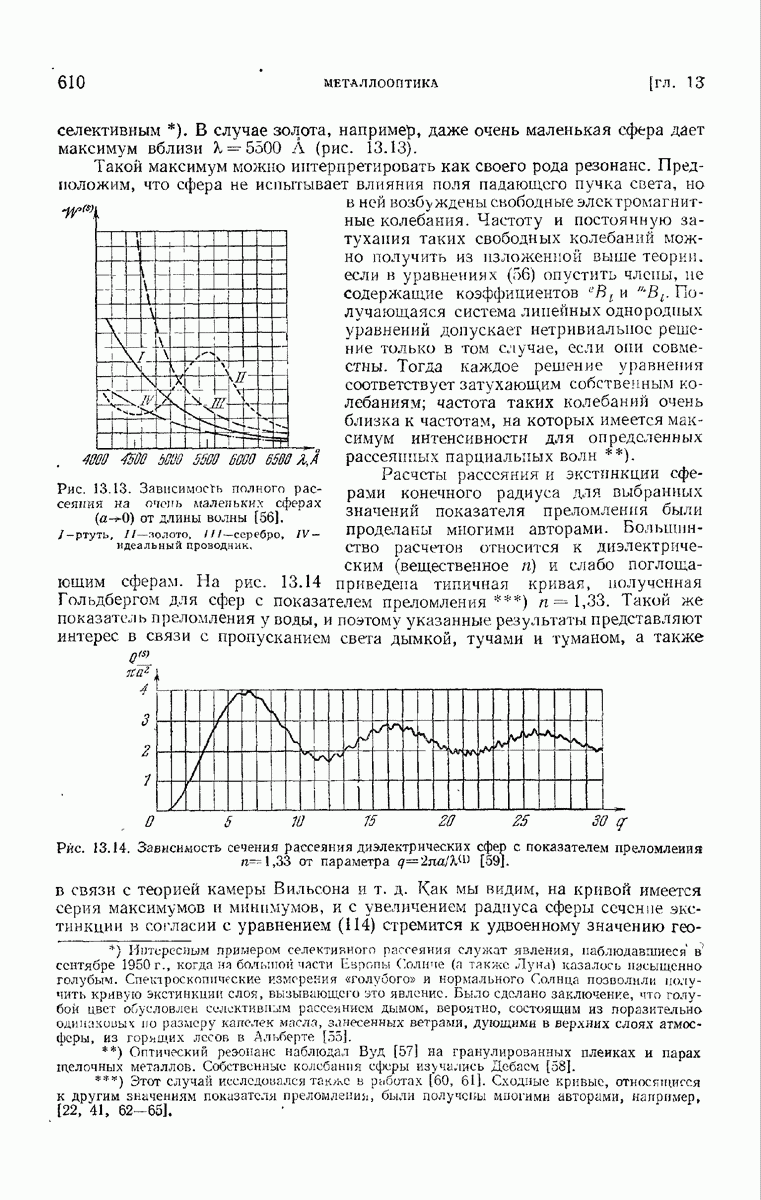
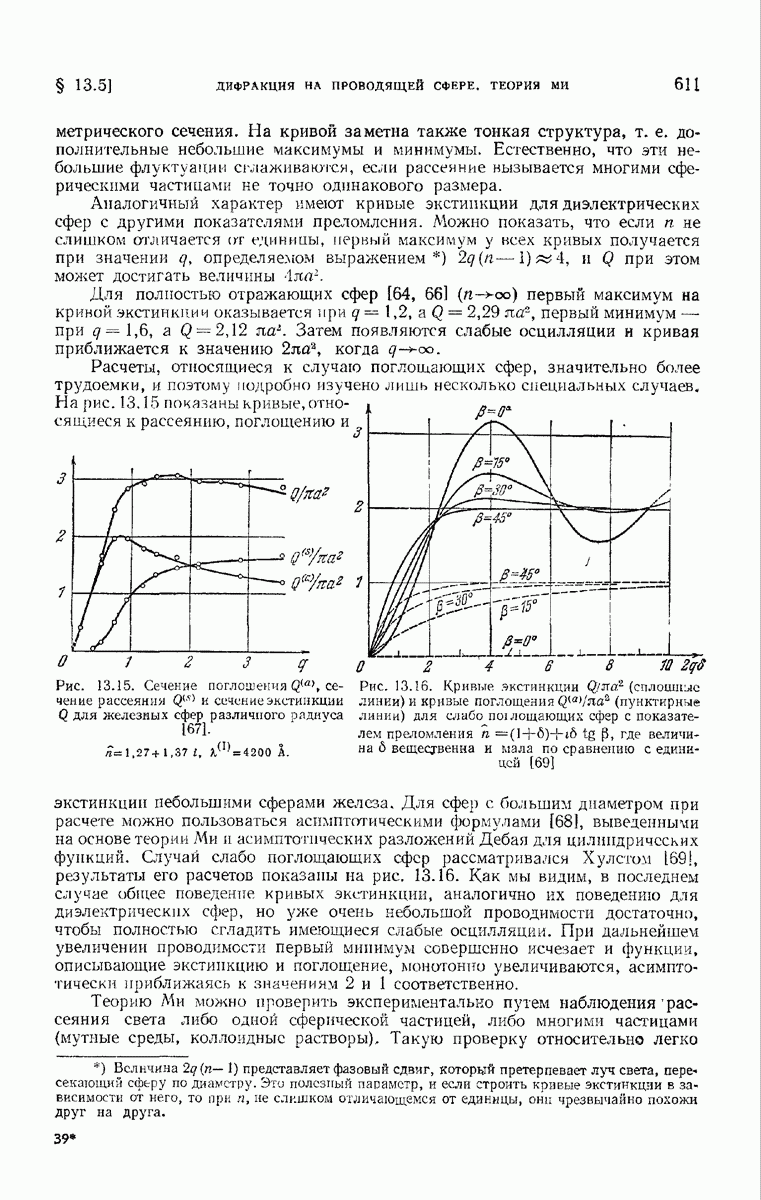
- 13.5.3. Полное рассеяние и затухание
- ГЛАВА 14. КРИСТАЛЛООПТИКА
- § 14.1. Тензор диэлектрической проницаемости анизотропной среды
- § 14.2. Структура монохроматической плоской волны в анизотропной среде
- 14.2.2. Формулы Френеля для распространения света в кристаллах.
- 14.2.3. Геометрические построения для определения скоростей распространения и направлений колебаний.
- § 14.3. Оптические свойства одноосных и двухосных кристаллов
- 14.3.2. Распространение света в одноосных кристаллах.
- 14.3.3. Распространение света в двухосных кристаллах.
- 14.3.4. Преломление в кристаллах
- § 14.4. Измерения в кристаллооптике
- 14.4.2. Компенсаторы.
- 14.4.3. Интерференция в кристаллических пластинках.
- 14.4.4. Интерференционные картины, получающиеся с пластинками одноосных кристаллов.
- 14.4.5. Интерференционные картины, получающиеся с пластинками двухосных кристаллов.
- 14.4.6. Определение положения оптических осей и главных показателей преломления кристаллической среды.
- § 14.5. Искусственная анизотропия
- 14.5.2. Двойное лучепреломление формы.
- § 14.6. Поглощающие кристаллы
- 14.6.2. Интерференционные картины, получающиеся с пластинками поглощающих кристаллов.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ 1. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 2. Интеграл Гильберта и уравнение Гамильтона—Якоби.
- 3. Поле экстремалей.
- 4. Нахождение всех экстремалей из решения уравнения Гамильтона — Якоби.
- 5. Канонические уравнения Гамильтона.
- 6. Частный случай, когда независимая переменная не входит явно в подынтегральное выражение.
- 7. Разрывы.
- 8. Условия Вейерштрасса и Лежандра (достаточные условия экстремума).
- 9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
- 10. Критерий Якоби для минимума.
- 11. Пример I. Оптика.
- 12. Пример II. Механика материальных точек.
- ПРИЛОЖЕНИЕ 2. ОБЫЧНАЯ ОПТИКА, ЭЛЕКТРОННАЯ ОПТИКА И ВОЛНОВАЯ МЕХАНИКА
- 2. Аналогия Гамильтона в вариационной форме.
- 3. Волновая механика свободных электронов.
- 4. Применение оптических принципов в электронной оптике.
- ПРИЛОЖЕНИЕ 3. МЕТОД АСИМПТОТИЧЕСКИХ ОЦЕНОК ИНТЕГРАЛОВ
- 2. Метод стационарной фазы.
- 3. Двойные интегралы.
- ПРИЛОЖЕНИЕ 4. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
- ПРИЛОЖЕНИЕ 5. МАТЕМАТИЧЕСКАЯ ЛЕММА, ИСПОЛЬЗУЕМАЯ ПРИ СТРОГОМ ВЫВОДЕ ЗАКОНА ЛОРЕНТЦ — ЛОРЕНЦА
- ПРИЛОЖЕНИЕ 6. РАСПРОСТРАНЕНИЕ РАЗРЫВОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПРИЛОЖЕНИЕ 7. КРУГОВЫЕ ПОЛИНОМЫ ЦЕРНИКЕ
- ПРИЛОЖЕНИЕ 8. ДОКАЗАТЕЛЬСТВО ОДНОГО НЕРАВЕНСТВА, ПРИВЕДЕННОГО В П. 10.7.3
- ПРИЛОЖЕНИЕ 9. ВЫЧИСЛЕНИЕ ДВУХ ИНТЕГРАЛОВ, ИСПОЛЬЗУЕМЫХ В П. 12.2.2