| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5.2. Эйконал Шварншильда
При исследовании геометрических аберраций Шварцшильд использовал метод, сходный с методом, применяемым в небесной механике при расчетах элементов орбит. В таких расчетах вводятся переменные, остающиеся постоянными при невозыущенном движении, а небольшие их изменения при действительном движении определяются с помощью функции возмущения. По аналогии
с этим методом Шварцшильд в своих работах (ссылки на них уже приводились) ввел некоторые переменные, которые в приближении параксиальной оптики остаются постоянными вдоль каждого луча, проходящего через оптическую систему. Затем, введя некоторую функцию возмущения, названную им эйконалом Зайделя, он исследовал изменения этих переменных, возникающие при учете членов четвертого порядка в разложении характеристической функции. Эти переменные были названы Шварцшильдом переменными Зайделя, поскольку они связаны с теми величинами, которые ранее использовал Зайдель.
Функция аберраций Ф, определенная выше, тесно связана в приближении теории Зайделя с возмущенным эйконалом Шварцшильда; используя метод Шварцшильда, можно получить выражения для коэффициентов стертого порядка в разложении функции аберраций для произвольной центрированной системы. Это будет подробно проведено в § 5.5. Здесь мы определим переменные Зайделя и исследуем связь между нашей функцией аберраций и возмущенной функцией Шварцшильда.
Введем такие новые единицы длины в плоскостях предмета и параксиального изображения соответственно  чтобы
чтобы

где  — поперечное гауссово увеличение. Точки на плоскости предмета будем определять координатами
— поперечное гауссово увеличение. Точки на плоскости предмета будем определять координатами  а на плоскости изображения координатами
а на плоскости изображения координатами  и для которых
и для которых

где  — обычные координаты точек.
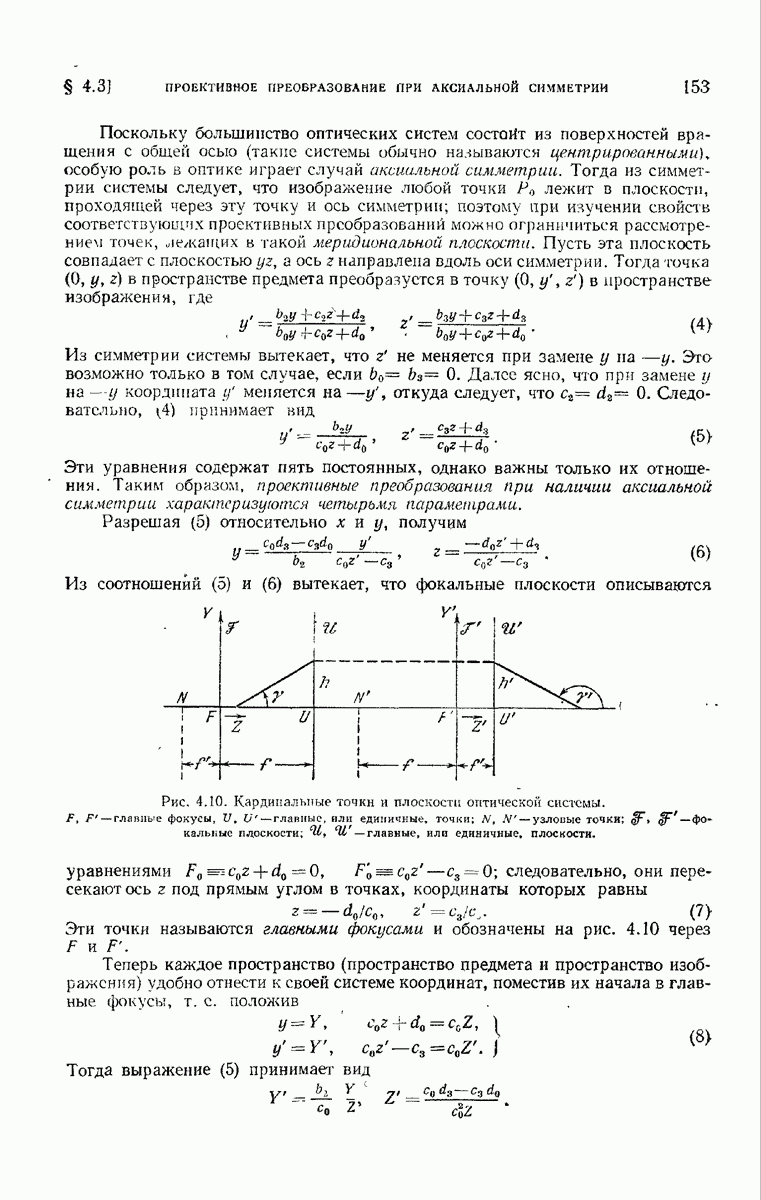
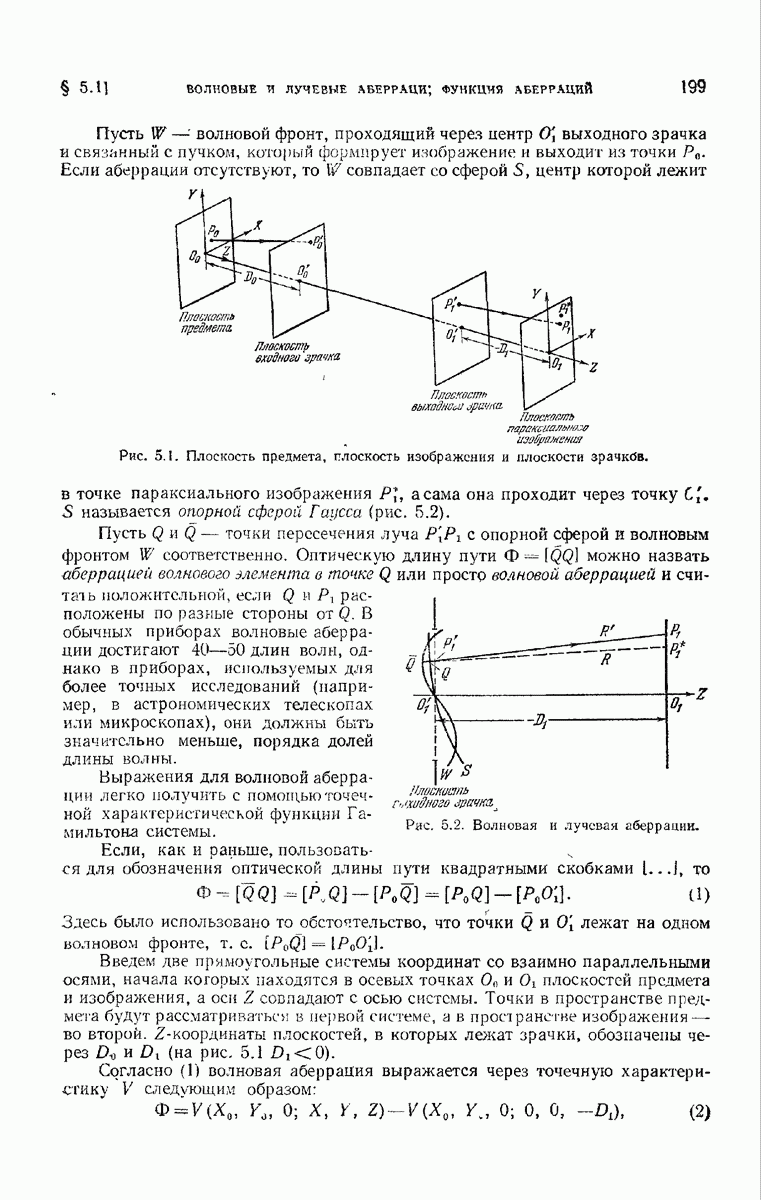
— обычные координаты точек.  (см. рис. 5.1) и С — постоянная, которую мы определим позже. В приближении параксиальной оптики
(см. рис. 5.1) и С — постоянная, которую мы определим позже. В приближении параксиальной оптики 
Координаты  точек пересечения луча, исходящего из
точек пересечения луча, исходящего из  с входным зрачком связаны с лучевыми компонентами следующими соотношениями:
с входным зрачком связаны с лучевыми компонентами следующими соотношениями:

Соотношения для точек пересечения луча с выходным зрачком имеют совершенно аналогичный вид. Квадратные корни в знаменателях можно в приближении параксиальной оптики заменить соответственно на  в результате чего мы получим линейные соотношения между координатами вида
в результате чего мы получим линейные соотношения между координатами вида

Теперь введем такие новые единицы длины I, и в плоскостях входного и выходного зрачков, чтобы

где  поперечное увеличение входной зрачок
поперечное увеличение входной зрачок  выходной зрачок. Вместо
выходной зрачок. Вместо
 используем следующие переменные:
используем следующие переменные:

В приближении параксиальной оптики 
Для упрощения дальнейших вычислений, удобно выбрать С в виде

Другое выражение для С, часто используемое при изучении изображений с помощью теории дифракции, имеет вид

Здесь  — волновое число для света в вакууме, а
— волновое число для света в вакууме, а  — угловые апертуры системы, или углы, под которыми видны входной и выходной зрачки соответственно из осевых точек предмета и изображения. При таком значении С имеем
— угловые апертуры системы, или углы, под которыми видны входной и выходной зрачки соответственно из осевых точек предмета и изображения. При таком значении С имеем

Равенство двух правых частей в выражении (7) следует из формулы Смита—Гельмгольца (1.4.48).
Величины, определенные соотношениями (2) и (6), являются переменными Зайделя. Нам потребуются и обратные соотношения, которые связывают старые переменные с переменными Зайделя. Решая (2) и (6), получим

Выразим теперь функцию аберраций через переменные Зайделя. Отметим сначала, что аргументы X и  можно заменить в функции Ф на
можно заменить в функции Ф на  не изменяя членов
не изменяя членов  в уравнениях (5.1.166) и (5.1.176). Обозначив функцию аберраций, выраженную через переменные Зайделя, через
в уравнениях (5.1.166) и (5.1.176). Обозначив функцию аберраций, выраженную через переменные Зайделя, через  имеем
имеем

Тогда

и, учитывая (1), (2), (7) и (5.1.4),

С помощью уравнений (11) находим вместо (5.1.166) и (5.1.176) соотношения

Ранее указывалось, что в приближении теории Зайделя  тесно связана с функцией возмущенны, введенной Шваршиильдом и названной им эйконалом Зайделя. Эта функция определяется соотношением
тесно связана с функцией возмущенны, введенной Шваршиильдом и названной им эйконалом Зайделя. Эта функция определяется соотношением

где  — угловая характеристика, отнесенная к системам с
— угловая характеристика, отнесенная к системам с
началами координат в  . Рассмотрим теперь небольшие вариации координат. Согласно уравнению (4.1.27) и условию
. Рассмотрим теперь небольшие вариации координат. Согласно уравнению (4.1.27) и условию  получим, что соответствующее изменение Т равно
получим, что соответствующее изменение Т равно

или, выразив его через переменные Зайделя, —

Используя последнее соотношение, находим из (13), что при малых изменениях переменных изменение  имеет вид
имеет вид

т. е.  является функцией
является функцией  и поэтому получим строго
и поэтому получим строго

Следовательно, зная  можно простым дифференцированием найти величины лучевых аберраций как в плоскости изображения, так и в плоскости выходного зрачка.
можно простым дифференцированием найти величины лучевых аберраций как в плоскости изображения, так и в плоскости выходного зрачка.
Сравнивая (17) и (12), видим, что в приближении теории Зайделя величина  не зависит от и
не зависит от и  , т. е.
, т. е.

где  — некоторая функция от
— некоторая функция от  Из определения
Из определения  следует, что
следует, что  следовательно,
следовательно,  и
и

В области применимости теории Зайделя члены в (12), учитывающие погрешность, можно отбросить Однако если оставляются члены более высокого порядка чем четвертый, то соотношения для компонент лучевой аберрации, выраженные через функцию аберраций  принимают более сложный вид. Вместе с тем простые соотношения (17), выражающие компоненты лучевой аберрации через возмущенный эйконал, оказываются точными; однако возмущенный эйконал, по-видимому, не имеет простого физического смысла.
принимают более сложный вид. Вместе с тем простые соотношения (17), выражающие компоненты лучевой аберрации через возмущенный эйконал, оказываются точными; однако возмущенный эйконал, по-видимому, не имеет простого физического смысла.
Определение членов более высокого порядка чем четвертый сопряжено, за исключением простейших случаев, с очень трудоемкими математическими выкладками. Поэтому обычно алгебраический анализ проводится в рамках теории Зайделя, которая затем в случае необходимости уточняется с помощью метода построения хода лучей.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 1.1. Электромагнитное поле
- 1.1.2. Материальные уравнения.
- 1.1.3. Граничные условия на поверхностях раздела.
- 1.1.4. Закон сохранения энергии для электромагнитного поля.
- § 1.2. Волновое уравнение и скорость света
- § 1.3. Скалярные волны
- 1.3.2. Сферические волны.
- 1.3.3. Гармонические волны. Фазовая скорость.
- 1.3.4. Волновые пакеты. Групповая скорость.
- § 1.4. Векторные волны
- 1.4.2. Гармоническая электромагнитная плоская волна.
- 1.4.3. Гармонические векторные волны произвольной формы.
- § 1.5. Отражение и преломление плоской волны
- 1.5.2. Формулы Френеля.
- 1.5.3. Отражательная и пропускательная способности; поляризация при отражении и преломлении.
- 1.5.4. Полное внутреннее отражение.
- § 1.6. Распространение волн в слоистой среде. Теория диэлектрических пленок
- 1.6.2. Характеристическая матрица для слоистой среды.
- 1.6.3. Коэффициенты отражения и пропускания.
- 1.6.4. Однородная диэлектрическая пленка.
- 1.6.5. Периодические слоистые среды.
- ГЛАВА 2. ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ И ПОЛЯРИЗАЦИЯ
- § 2.1. Электродинамические потенциалы в вакууме
- 2.1.2. Запаздывающие потенциалы.
- § 2.2. Поляризация и намагничение
- 2.2.2. Векторы Герца.
- 2.2.3. Поле линейного электрического диполя.
- § 2.3. Формула Лорентц — Лоренца и элементарная теория дисперсии
- 2.3.2. Эффективное поле.
- 2.3.3. Средняя поляризуемость. Формула Лорентц — Лоренца.
- 2.3.4. Элементарная теория дисперсии.
- § 2.4. Описание распространения электромагнитных волн с помощью интегральных уравнений
- 2.4.2. Теорема погашения Эвальда — Озеена и строгий вывод формулы Лорентц — Лоренца.
- 2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда — Озеена.
- ГЛАВА 3. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 3.1.2. Световые лучи и закон интенсивности в геометрической оптике.
- 3.1.3. Распространение векторных амплитуд.
- 3.1.4. Обобщения геометрической оптики и пределы ее применимости.
- § 3.2. Общие свойства лучей
- 3.2.2. Законы преломления и отражения.
- 3.2.3. Конгруэнции лучей и фокальные свойства.
- § 3.3. Другие основные теоремы геометрической оптики
- 3.3.2. Принцип Ферма
- 3.3.3. Теорема Малюса и Дюпина и некоторые другие связанные с ней теоремы.
- ГЛАВА 4. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ
- 4.1.2. Смешанная характеристика.
- 4.1.3. Угловая характеристика.
- 4.1.4. Приближенное выражение для угловой характеристики преломляющей поверхности вращения.
- 4.1.5. Приближенное выражение для угловой характеристики отражающей поверхности вращения.
- § 4.2. Идеальное отображение
- 4.2.2. «Рыбий глаз» Максвелла.
- 4.2.3. Стигматическое отображение поверхностей.
- § 4.3. Проективное преобразование (коллинеация) при наличии аксиальной симметрии
- 4.3.2. Телескопическое отображение.
- 4.3.3. Классификация проективных преобразований.
- 4.3.4. Комбинация проективных преобразований.
- § 4.4. Параксиальная оптика
- 4.4.2. Отражающая поверхность вращения.
- 4.4.3. Толстая линза.
- 4.4.4. Тонкая лииза.
- 4.4.5. Произвольная центрированная система.
- § 4.5. Стигматическое отображение пучками с большой угловой апертурой
- § 4.6. Астигматические пучки лучей
- 4.6.2. Преломление тонкого пучка.
- § 4.7. Хроматическая аберрация. Дисперсия призмы
- 4.7.2. Дисперсия призмы.
- § 4.8. Фотометрия. Апертуры оптических систем
- 4.8.2. Диафрагмы и зрачки.
- 4.8.3. Яркость и освещенность изображений.
- § 4.9. Метод построения хода лучей
- 4.9.2. Параксиальные лучи.
- 4.9.3. Косые лучи.
- § 4.10. Оптические системы с несферическими поверхностями
- 4.10.2. Получение апланатизма.
- ГЛАВА 5. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 5.2. Эйконал Шварншильда
- § 5.3. Первичные аберрации (аберрации Зайделя)
- § 5.4. Теорема сложения для случая первичных аберраций
- § 5.5. Коэффициенты первичных аберраций произвольной центрированной системы линз
- 5.5.2. Формулы Зайделя, выраженные через параметры одного параксиального луча.
- 5.5.3. Теорема Петцваля.
- § 5.6. Пример: первичные аберрации тонкой линзы
- § 5.7. Хроматическая аберрация произвольной центрированной системы линз
- ГЛАВА 6. ОПТИЧЕСКИЕ ПРИБОРЫ, ФОРМИРУЮЩИЕ ИЗОБРАЖЕНИЕ
- § 6.2. Фотографический аппарат
- § 6.3. Линзовый телескоп
- § 6.4. Зеркальный телескоп
- § 6.5. Осветители
- § 6.6. Микроскоп
- ГЛАВА 7. ЭЛЕМЕНТЫ ТЕОРИИ ИНТЕРФЕРЕНЦИИ И ИНТЕРФЕРОМЕТРЫ
- § 7.2. Интерференция двух монохроматических волн
- § 7.3. Двухлучевая интерференция. Деление волнового фронта
- 7.3.2. Зеркала Френеля и другие аналогичные устройства.
- 7.3.3. Интерференционные полосы в квазимонохроматическом и белом свете.
- 7.3.4. Источник в виде щели; видность полос.
- 7.3.5. Измерение оптической разности хода; интерферометр Рэлея.
- 7.3.6. Измерение угловых размеров источников; звездный интерферометр Майкельсона.
- § 7.4. Стоячие волны
- § 7.5. Двухлучевая интерференция. Деление амплитуды
- 7.5.2. Интерференция в тонких пленках; интерферометр Физо.
- 7.5.3. Локализация полос.
- 7.5.4. Интерферометр Майкельсона.
- 7.5.5. Интерферометр Тваймана — Грина и другие аналогичные приборы.
- 7.5.6. Полосы, получающиеся с двумя одинаковыми пластинами; интерферометр Жамена и интерференционный микроскоп.
- 7.5.7. Интерферометр Маха—Цендера; интерферометр Бейтса со смещенным волновым фронтом.
- 7.5.8. Длина когерентности; применение двухлучевой интерференции к изучению тонкой структуры спектральных линий.
- § 7.6. Многолучевая интерференция
- 7.6.2. Интерферометр Фабри — Перо.
- 7.6.3. Применение интерферометра Фабри — Перо для изучения тонкой структуры спектральных линий.
- 7.6.4. Применение интерферометра Фабри — Перо для сравнения длин волн.
- 7.6.5. Интерферометр Люммера — Герке.
- 7.6.6. Интерференционные фильтры.
- 7.6.7. Многолучевые полосы в тонких пленках.
- 7.6.8. Многолучевые полосы, получающиеся с двумя плоскопараллельными пластинками.
- § 7.7. Сравнение длин волн с эталонным метром
- ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ДИФРАКЦИИ
- § 8.2. Принцип Гюйгенса — Френеля
- § 8.3. Теория дифракции Кирхгофа
- 8.3.2. Теория дифракции Кирхгофа.
- 8.3.3. Дифракция Фраунгофера и Френеля.
- § 8.4. Переход к скалярной теории
- 8.4.2. Полное поле изображения.
- § 8.5. Дифракция Фраунгофера на отверстиях разной формы
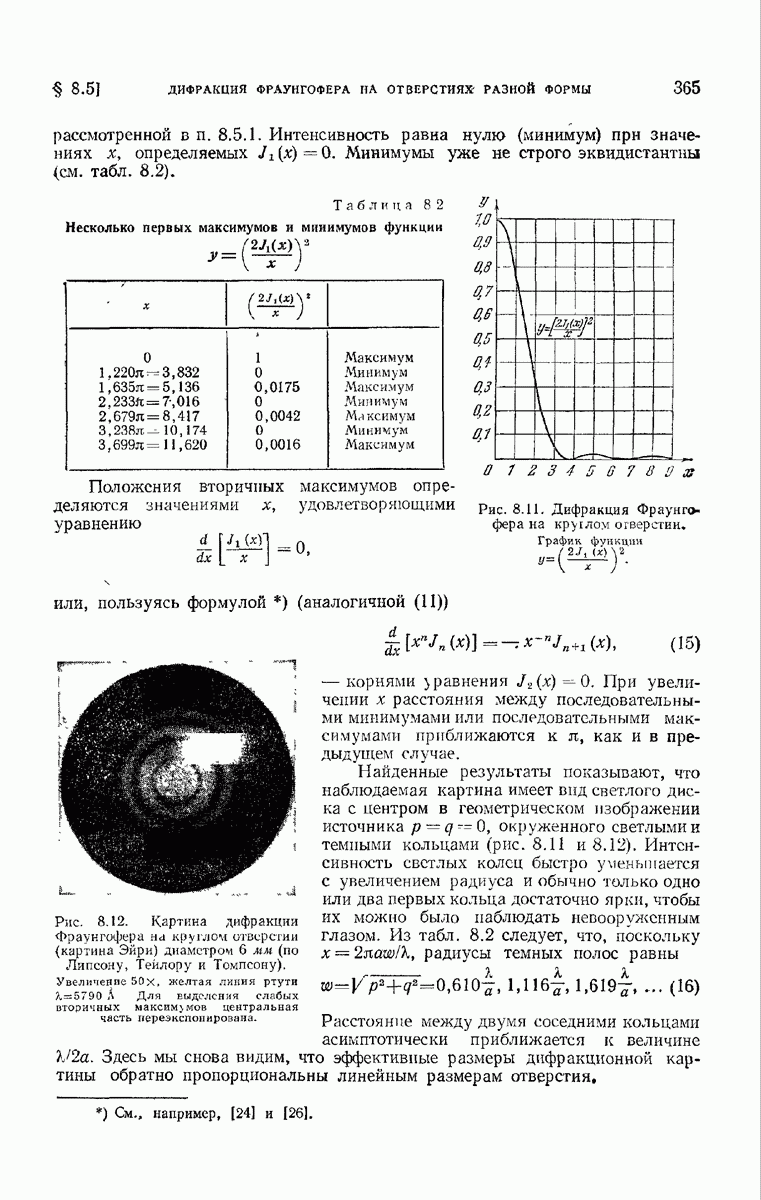
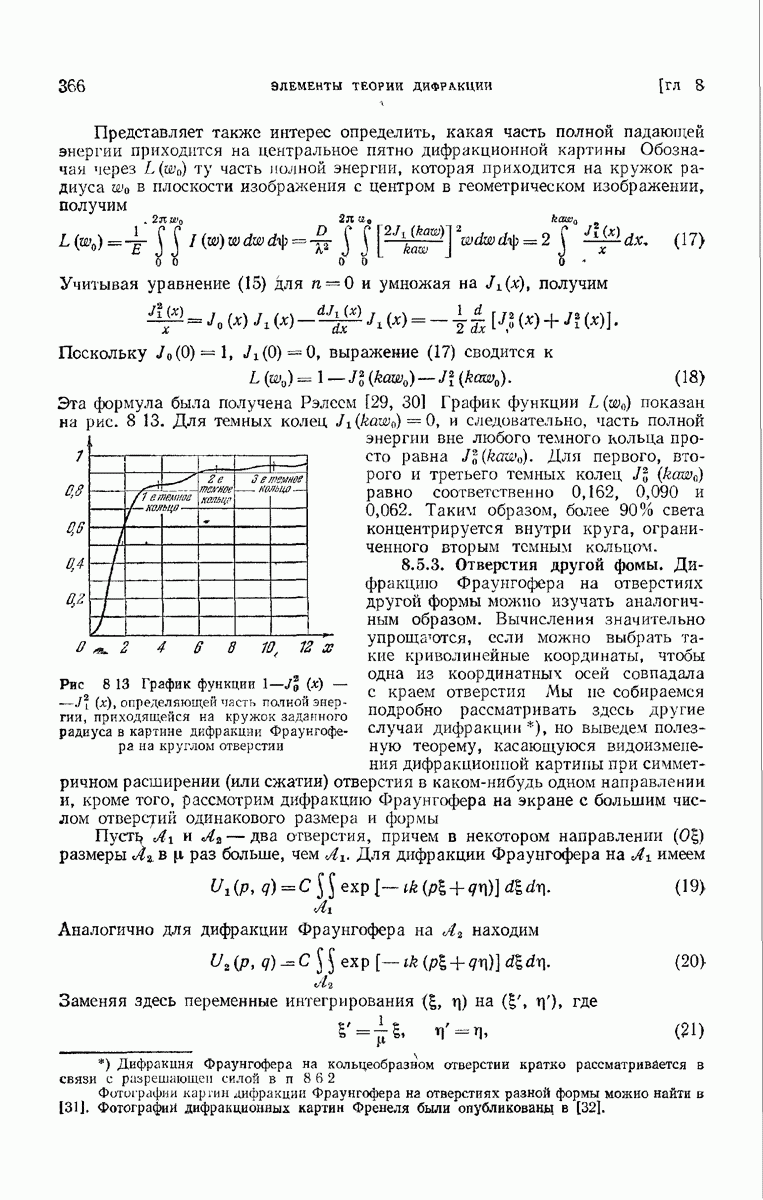
- 8.5.2. Круглое отверстие.
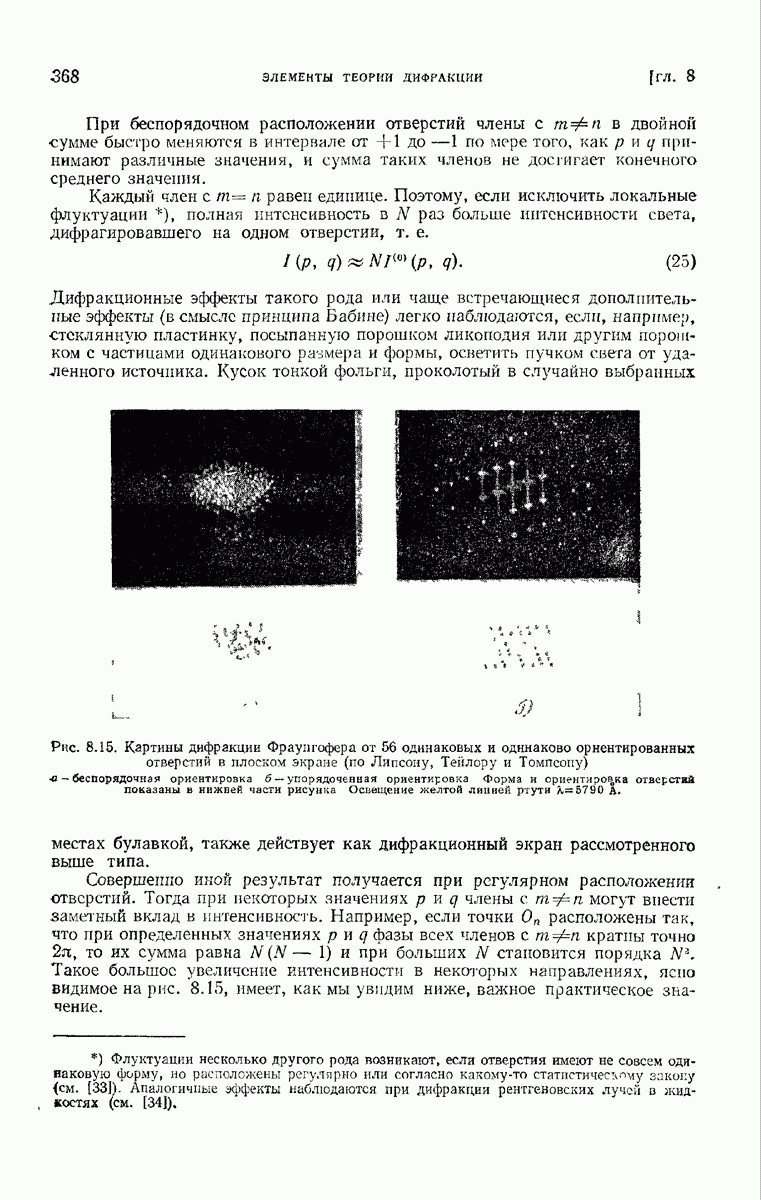
- 8.5.3. Отверстия другой фомы.
- § 8.6. Дифракция Фраунгофера в оптических приборах
- 8.6.2. Разрешающая сила систем, образующих изображение.
- 8.6.3. Образование изображения в микроскопе.
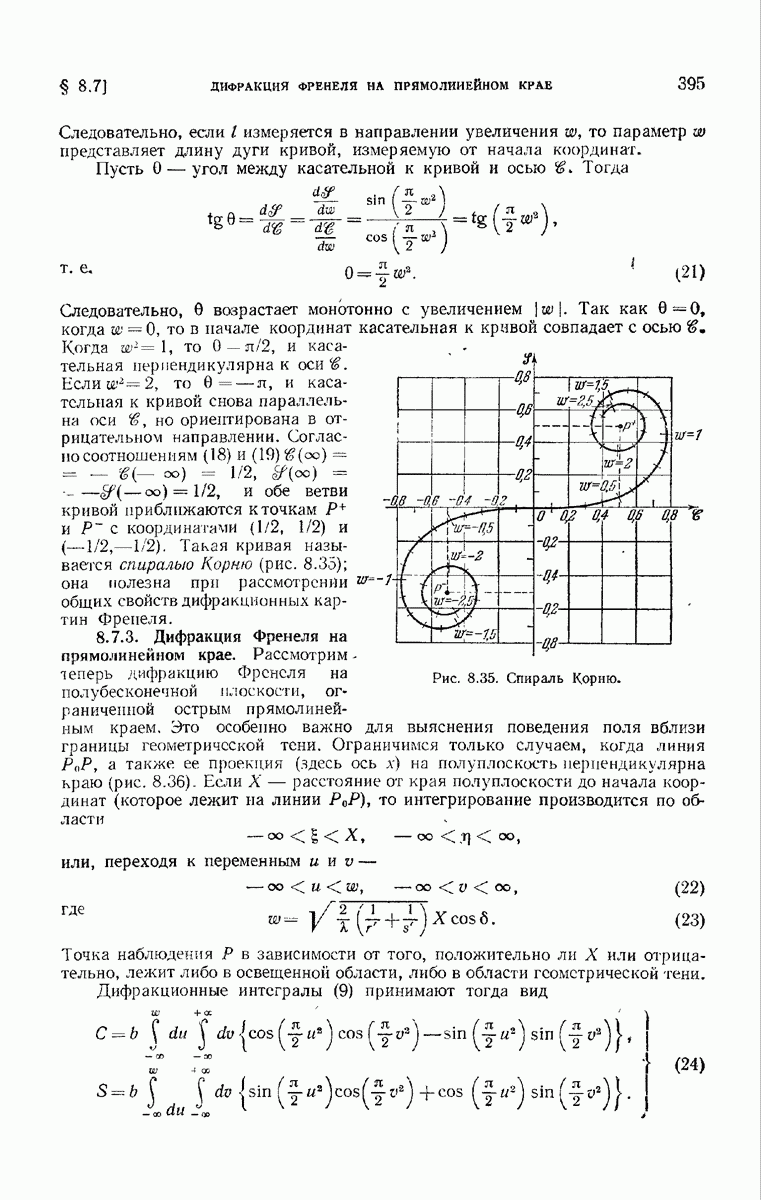
- § 8.7. Дифракция Френеля на прямолинейном крае
- 8.7.2. Интегралы Френеля.
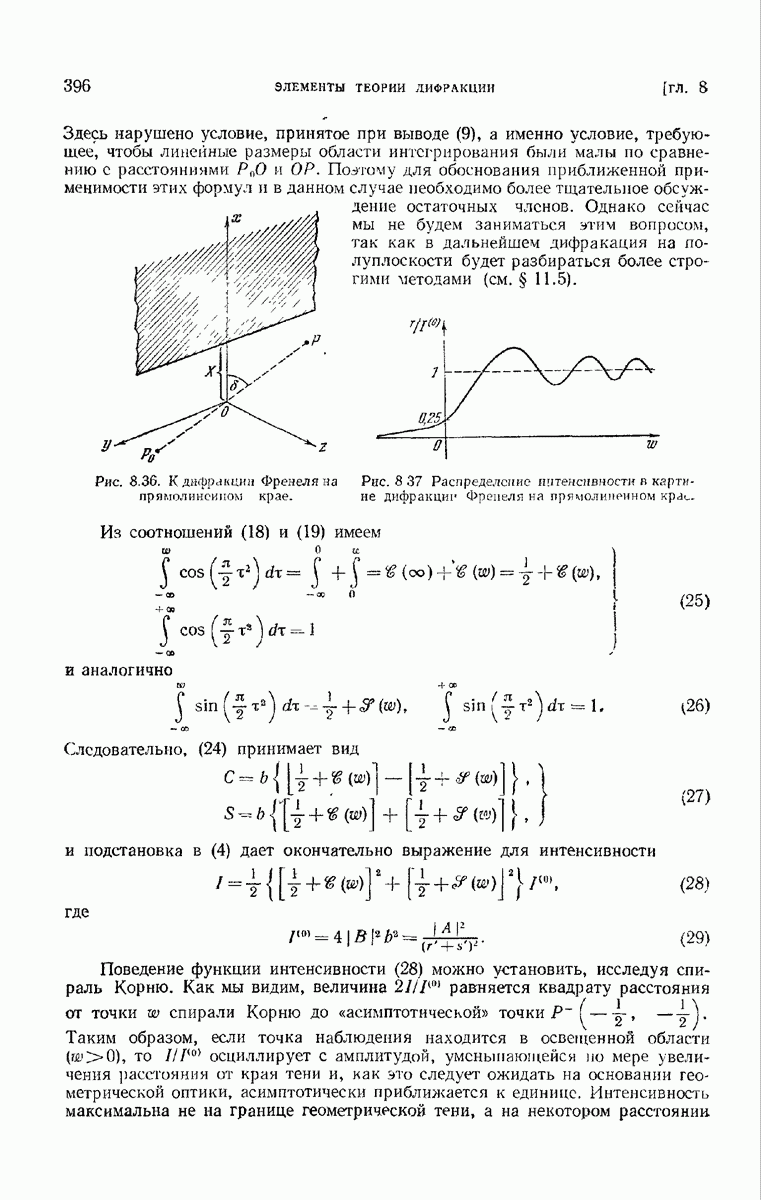
- 8.7.3. Дифракция Френеля на прямолинейном крае.
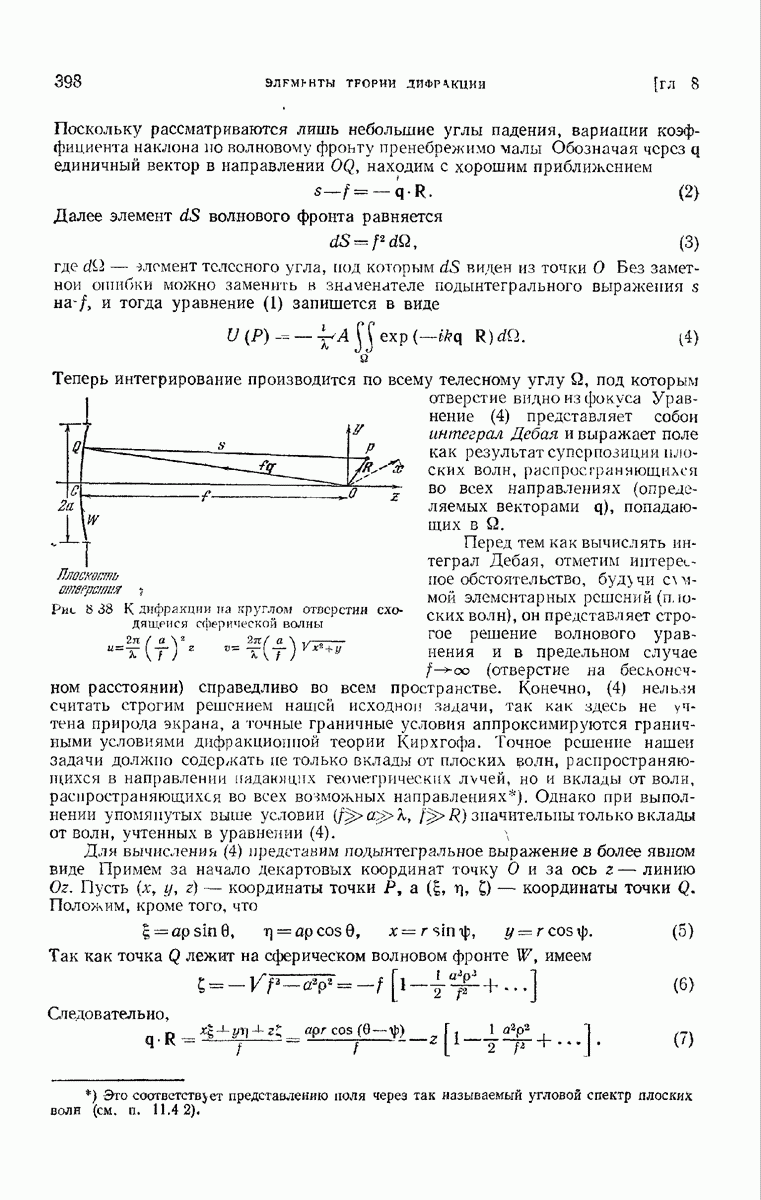
- § 8.8. Трехмерное распределение света вблизи фокуса
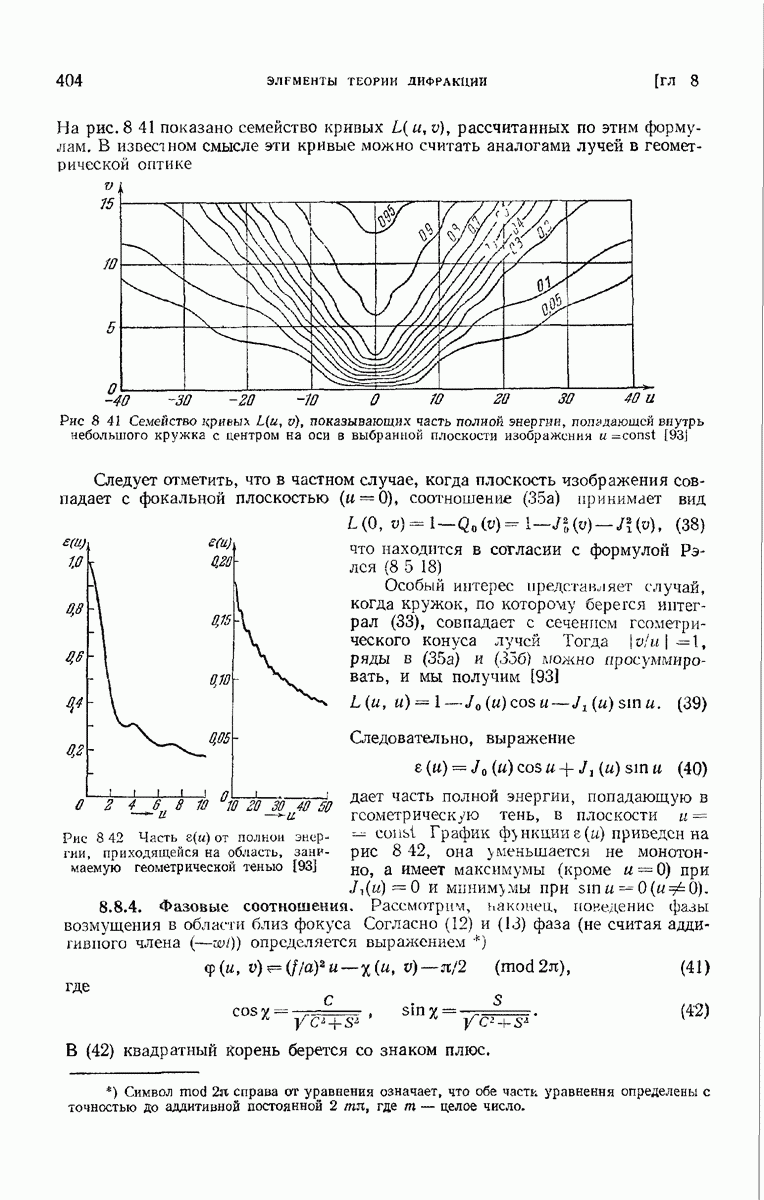
- 8.8.2. Распределение интенсивности.
- 8.8.3. Суммарная интенсивность.
- 8.8.4. Фазовые соотношения.
- § 8.9. Граничная дифрагировавшая волна
- § 8.10. Метод Габора получения изображения восстановлением волновых фронтов
- 8.10.2. Восстановление.
- ГЛАВА 9. ДИФРАКЦИОННАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 9.1. Дифракционный интеграл при наличии аберраций
- 9.1.2. Теорема смещения. Изменение опорной сферы.
- 9.1.3. Соотношение между интенсивностью и средней деформацией волновых фронтов.
- § 9.2. Разложение функции аберрации
- 9.2.2. Разложение функции аберраций.
- § 9.3. Допустимые величины первичных аберраций
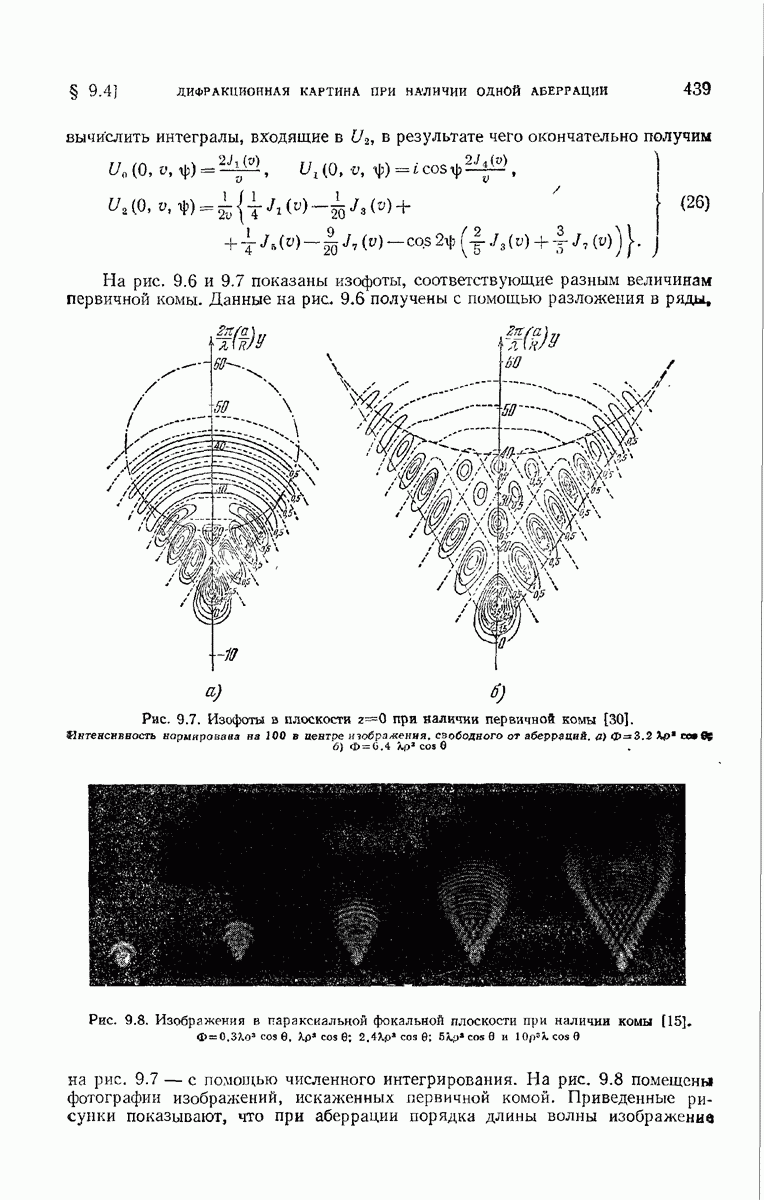
- § 9.4. Дифракционная картина, получающаяся при наличии одной аберрации
- 9.4.1. Первичная сферическая аберрация.
- 9.4.2. Первичная кома.
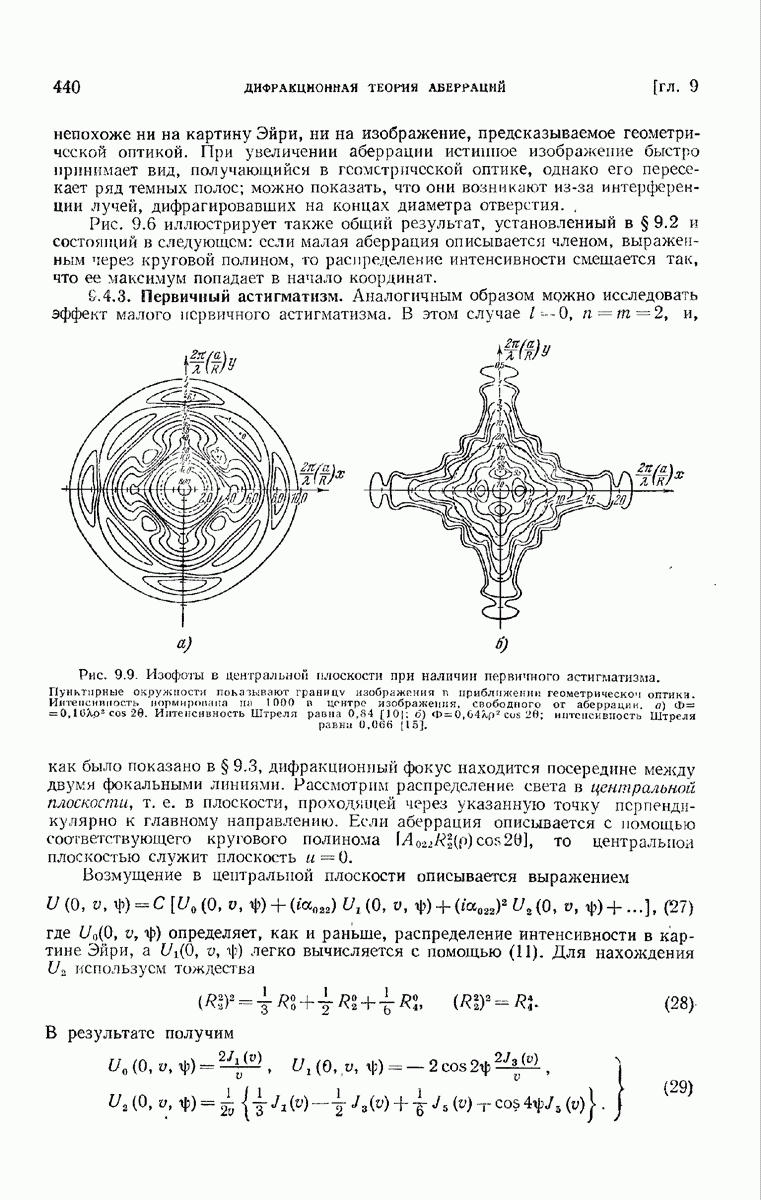
- 9.4.3. Первичный астигматизм.
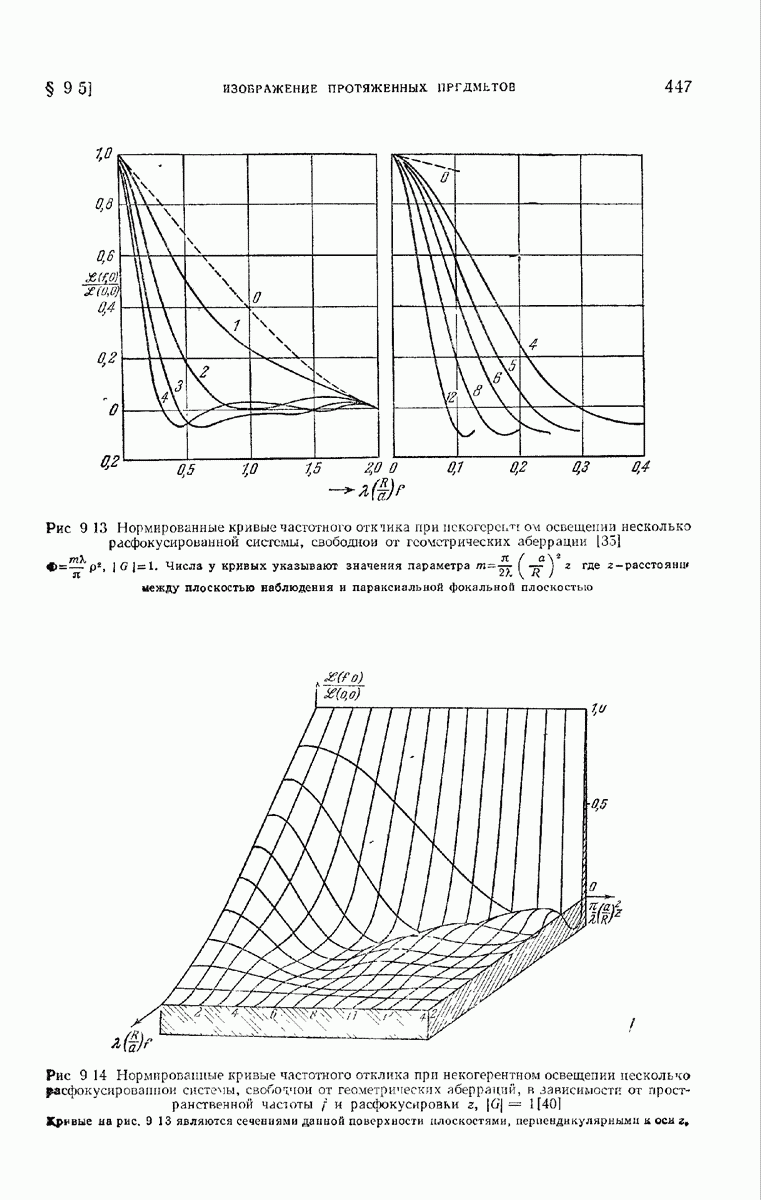
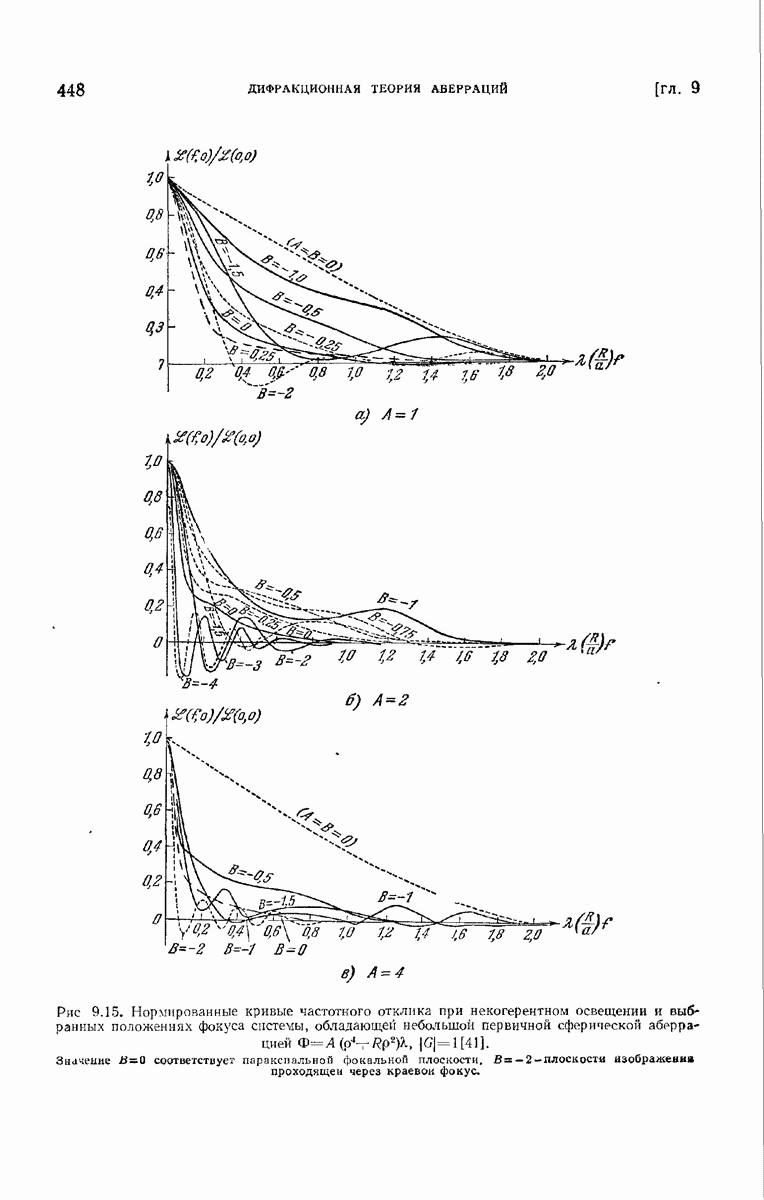
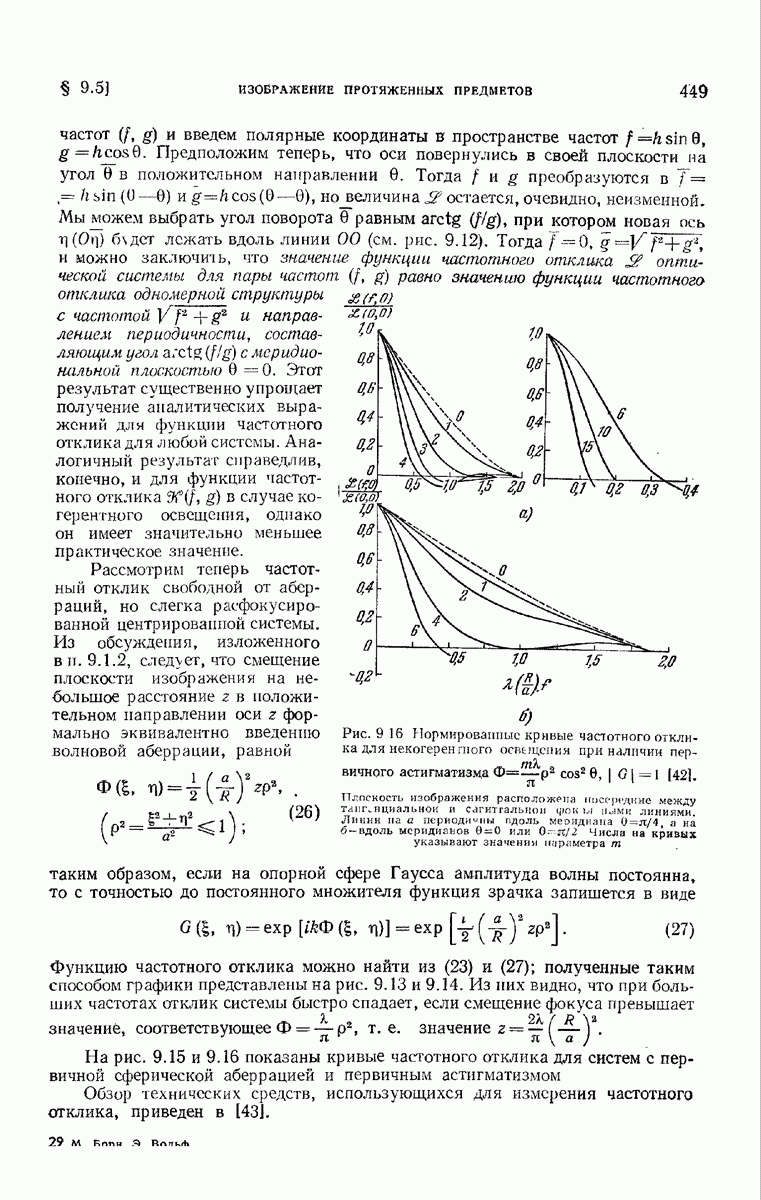
- § 9.5. Изображение протяженных предметов
- 9.5.2. Некогерентное освещение.
- ГЛАВА 10. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
- § 10.2. Комплексное представление вещественных полихроматических полей
- § 10.3. Корреляционные функции световых пучков
- 10.3.2. Спектральное представление взаимной когерентности.
- § 10.4. Интерференция и дифракция квазимонохроматического света
- 10.4.2. Расчет взаимной интенсивности и степени когерентности для света от протяженного некогерентного квазимонохроматического источника.
- 10.4.3. Пример.
- 10.4.4. Распространение взаимной интенсивности.
- § 10.5. Некоторые приложения
- 10.5.1. Степень когерентности в изображении протяженного некогерентного квазимонохроматического источника.
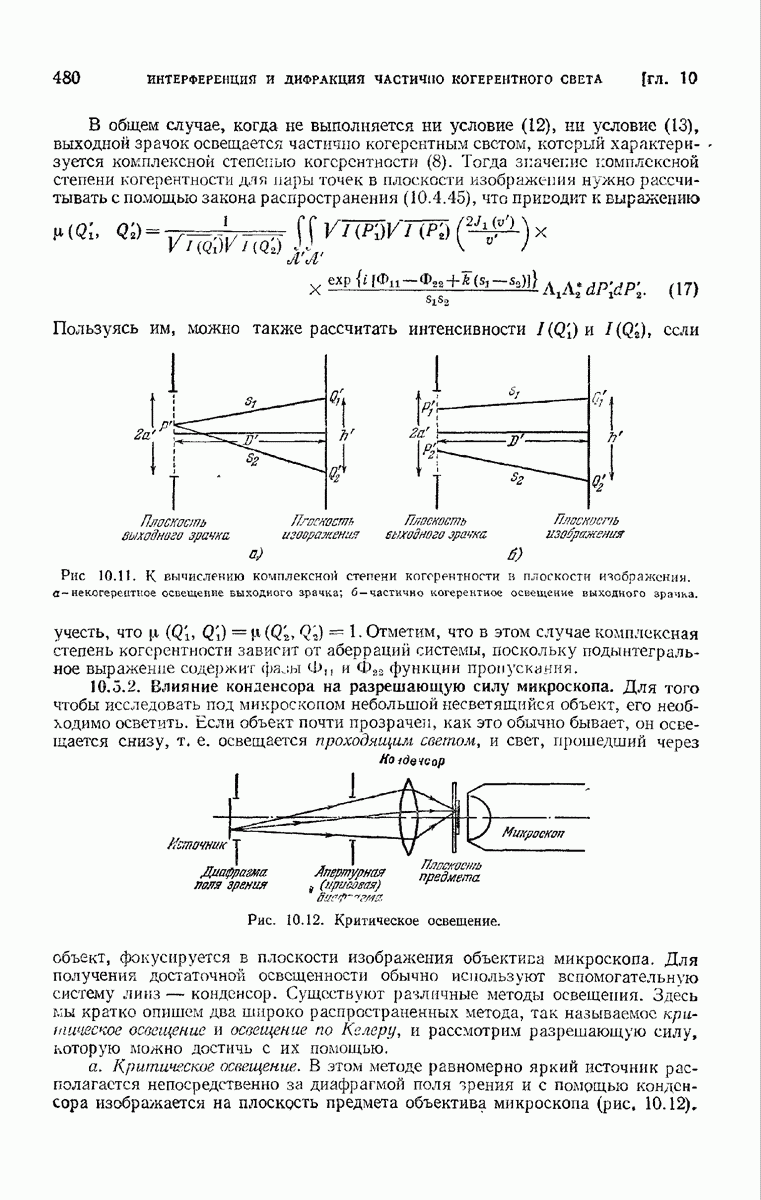
- 10.5.2. Влияние конденсора на разрешающую силу микроскопа.
- 10.5.3. Получение изображения при частично когерентном квазимонохроматическом освещении
- § 10.6. Некоторые теоремы, касающиеся взаимной когерентности
- 10.6.2. Распространение взаимной когерентности.
- § 10.7. Строгая теория частичной когерентности
- 10.7.2. Строгая формулировка закона распространения взаимной когерентности.
- 10.7.3. Время когерентности и эффективная ширина спектра.
- § 10.8. Поляризация квазимонохроматического света
- 10.8.2. Некоторые эквивалентные представления. Степень поляризации световой волны.
- 10.8.3. Параметры Стокса квазимонохроматичаской плоской волны.
- ГЛАВА 11. СТРОГАЯ ТЕОРИЯ ДИФРАКЦИИ
- § 11.2. Граничные условия и поверхностные токи
- § 11.3. Дифракция на плоском экране; электромагнитная форма принципа Бабине
- § 11.4. Двумерная дифракция на плоском экране
- 11.4.2. Угловой спектр плоских волн.
- 11.4.3. Формулировка задачи через дуальные интегральные уравнения.
- § 11.5. Двумерная дифракция плоской волны на полуплоскости
- 11.5.2. Выражение решения через интегралы Френеля.
- 11.5.3. Характер решения.
- 11.5.4. Решение для Н-поляризации.
- 11.5.5. Некоторые численные расчеты.
- 11.5.6. Сравнение с приближенной теорией и с экспериментальными результатами.
- § 11.6. Трехмерная дифракция плоской волны на полуплоскости
- § 11.7. Дифракция волн, испускаемых локализованным источником, на полуплоскости
- 11.7.2. Диполь.
- § 11.8. Другие задачи
- 11.8.1. Две параллельные полуплоскости.
- 11.8.2. Бесконечный набор параллельных полуплоскостей, расположенных ступеньками.
- 11.8.3. Полоса.
- 11.8.4. Другие задачи.
- § 11.9. Единственность решения
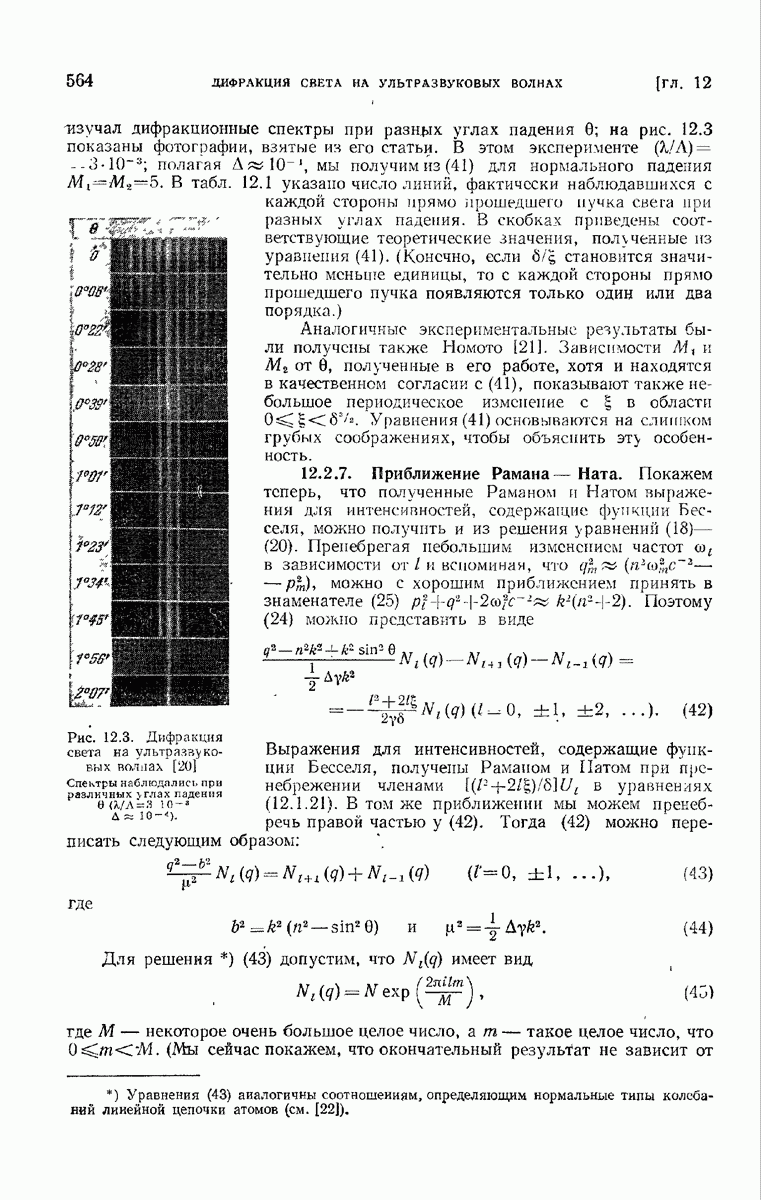
- ГЛАВА 12. ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКОВЫХ ВОЛНАХ
- 12.1.2. Краткое изложение теорий, основанных на уравнениях Максвелла.
- § 12.2. Рассмотрение дифракции света на ультразвуковых волнах методом интегральных уравнений
- 12.2.1. Интегральное уравнение для случая Е-поляризации.
- 12.2.2. Пробное решение интегрального уравнения.
- 12.2.3. Выражения для амплитуд световых волн в дифрагировавших и отраженных спектрах.
- 12.2.5. Выражения для интенсивностей линий в спектрах первого и второго порядков в некоторых специальных случаях
- 12.2.6. Некоторые качественные результаты.
- 12.2.7. Приближение Рамана—Ната.
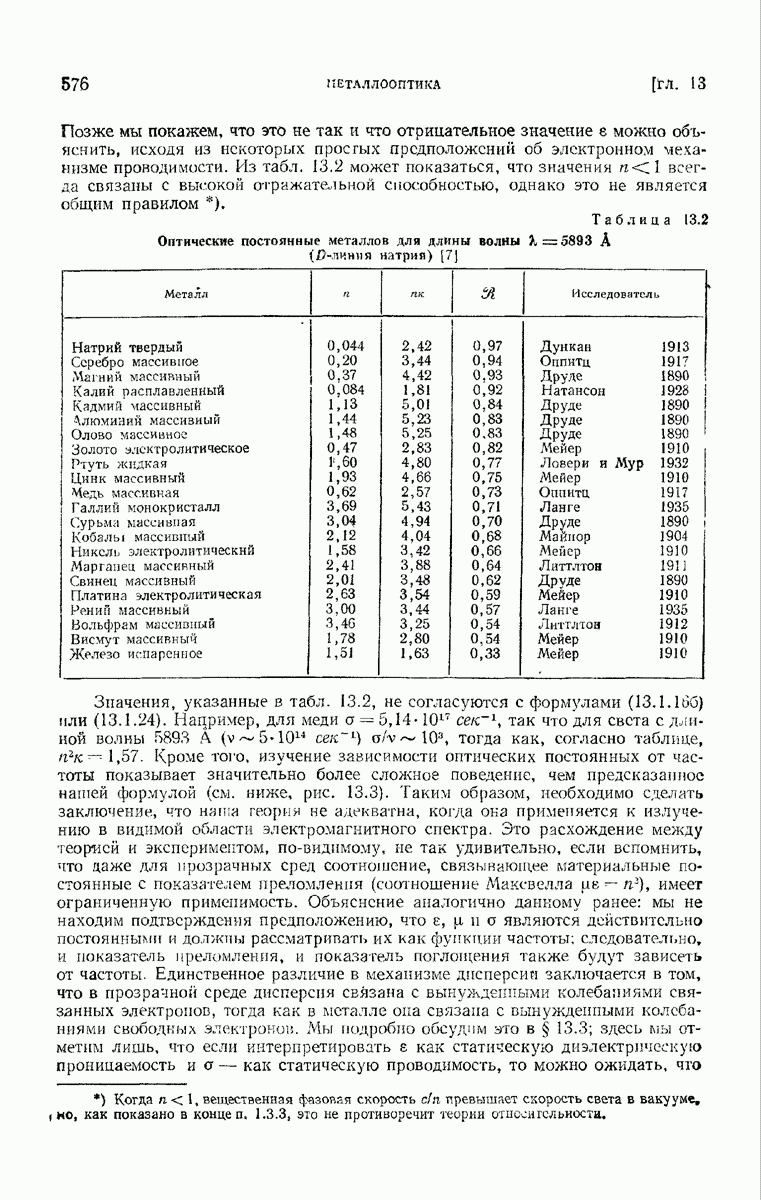
- ГЛАВА 13. МЕТАЛЛООПТИКА
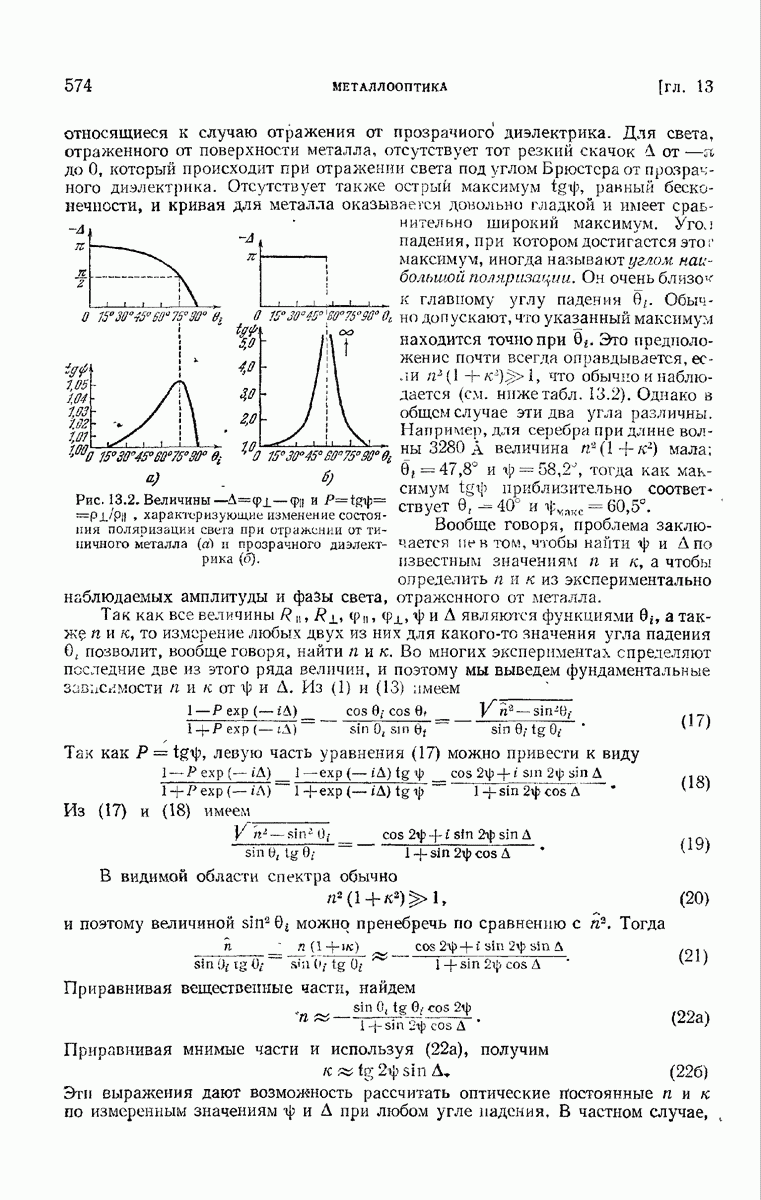
- § 13.2. Преломление и отражение на поверхности металла
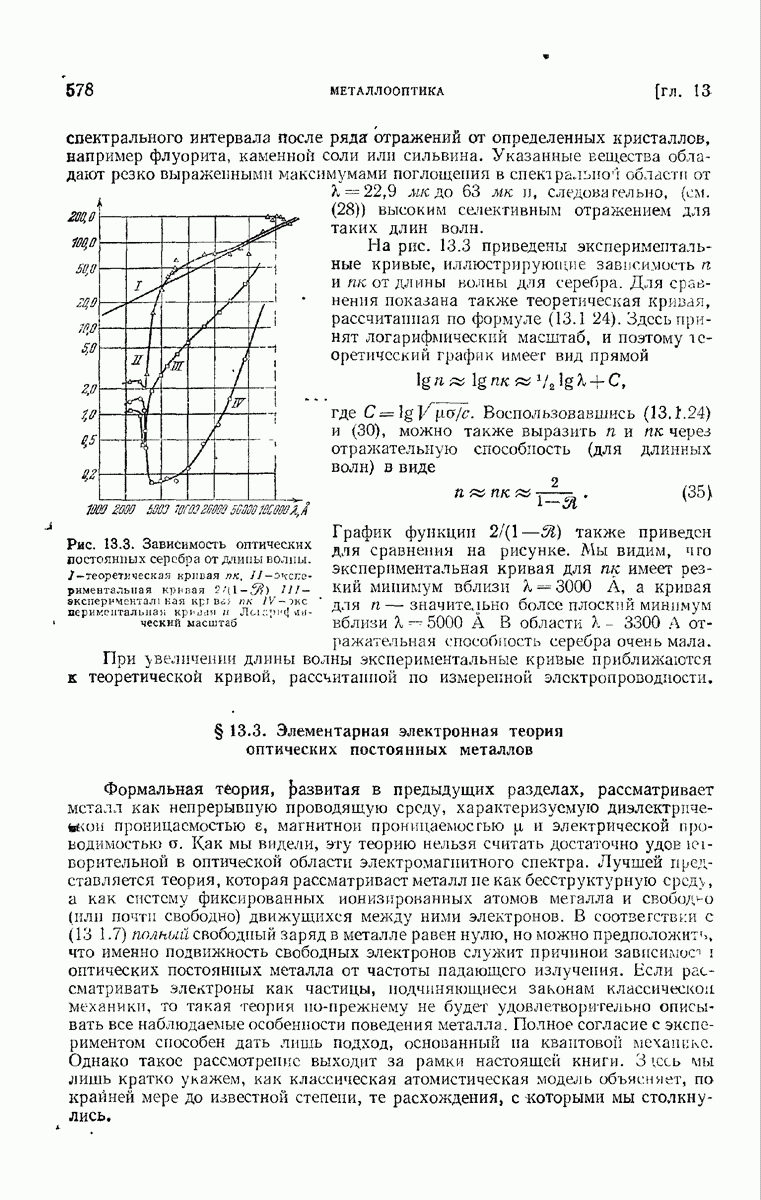
- § 13.3. Элементарная электронная теория оптических постоянных металлов
- § 13.4. Распространение волн в слоистой проводящей среде. Теория металлических пленок
- 13.4.2. Прозрачная пленка на поглощающей подложке.
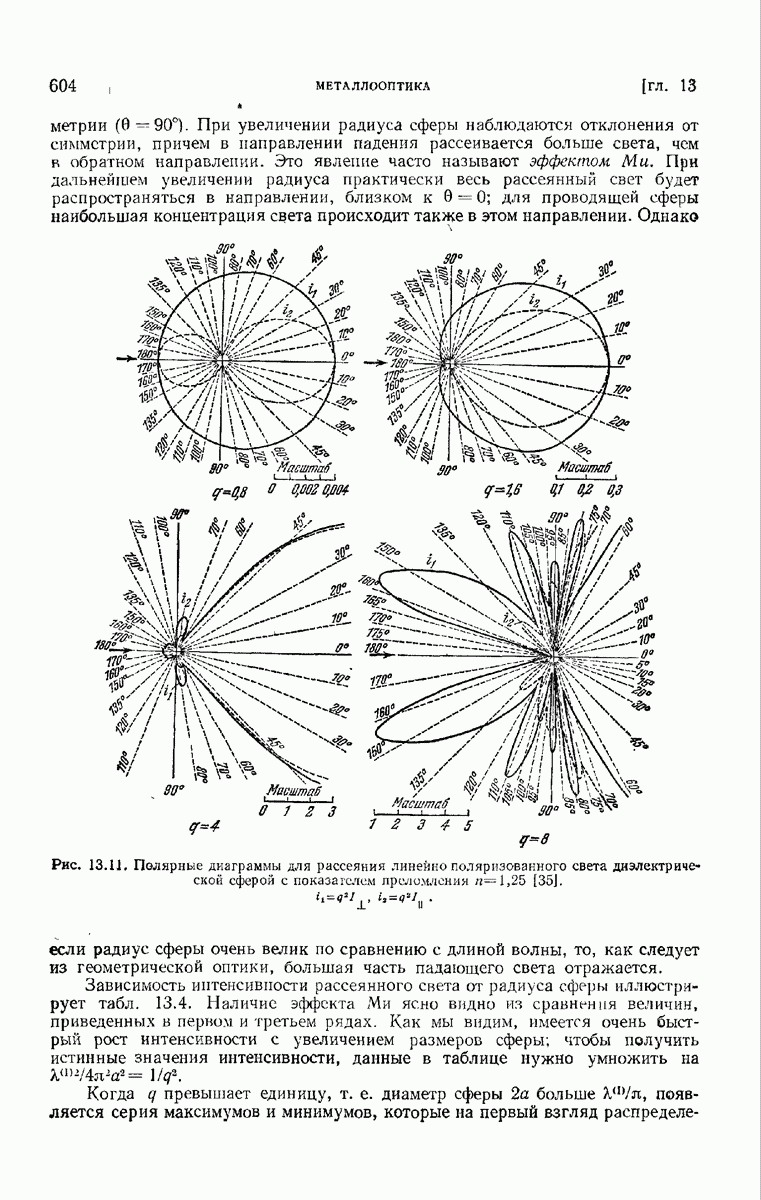
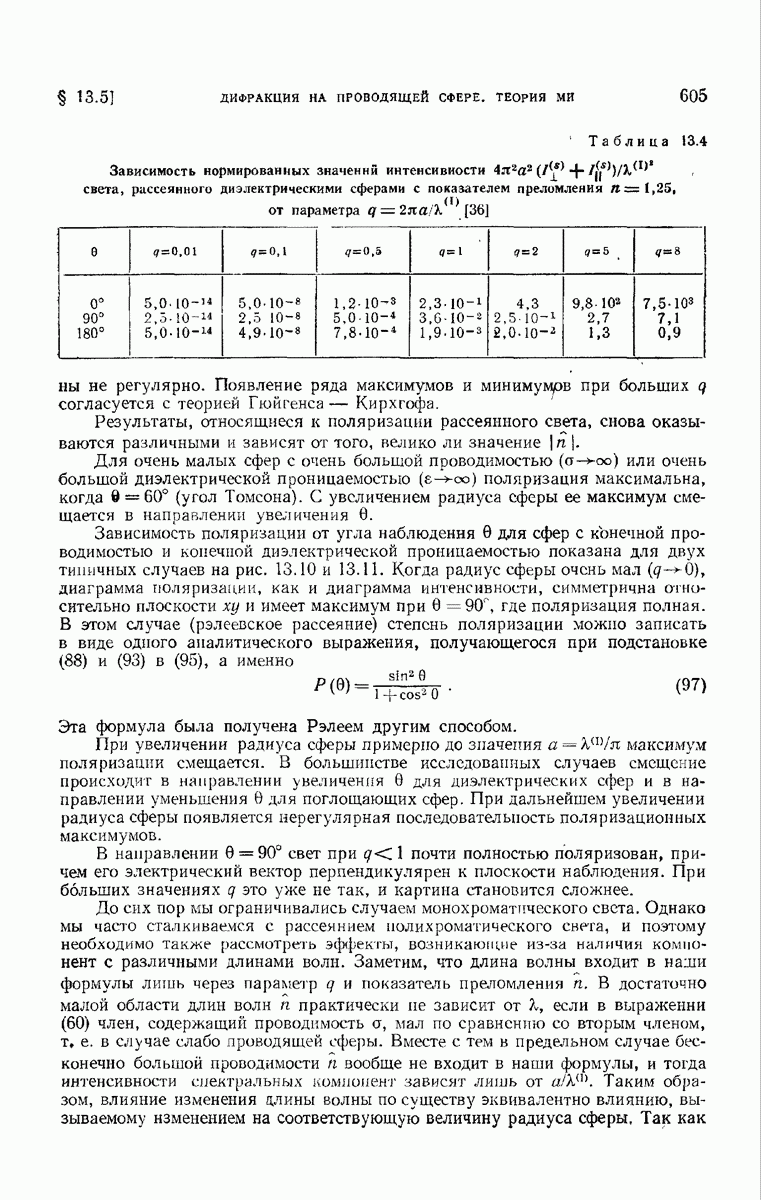
- § 13.5. Дифракция на проводящей сфере. Теория Ми
- 13.5.1. Математическое решение проблемы
- 13.5.2. Некоторые следствия из формул Ми.
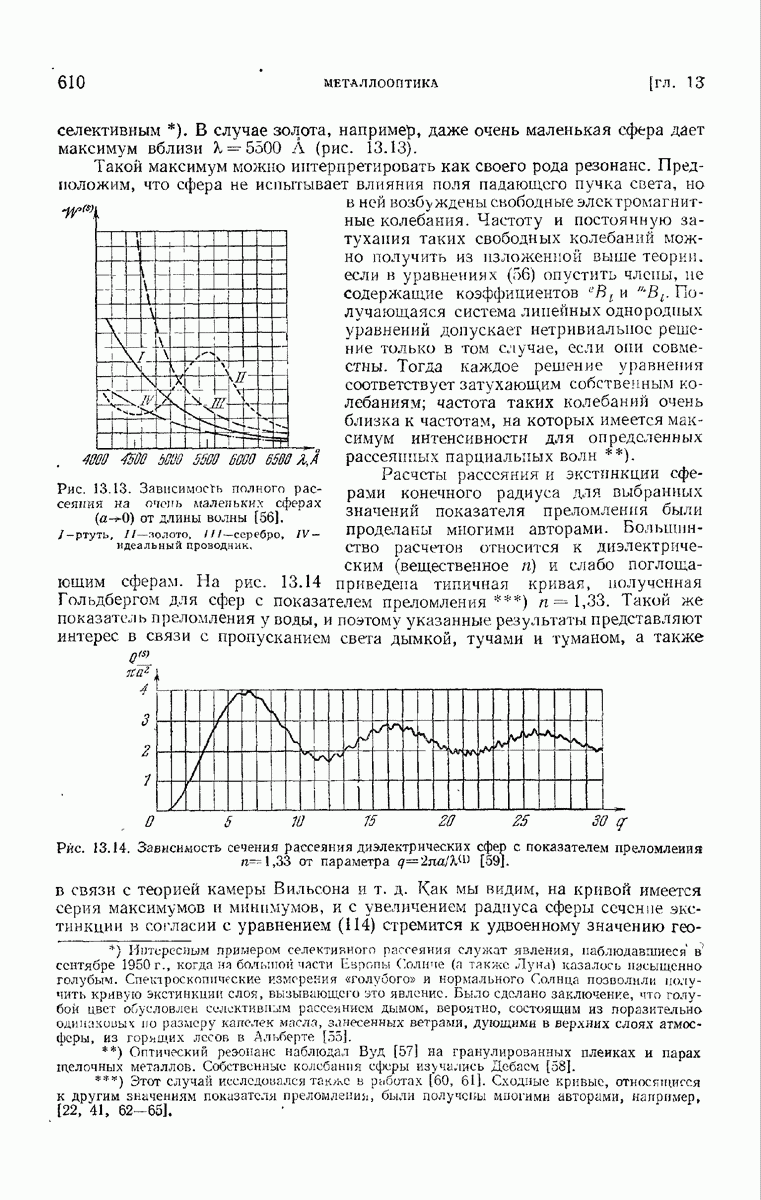
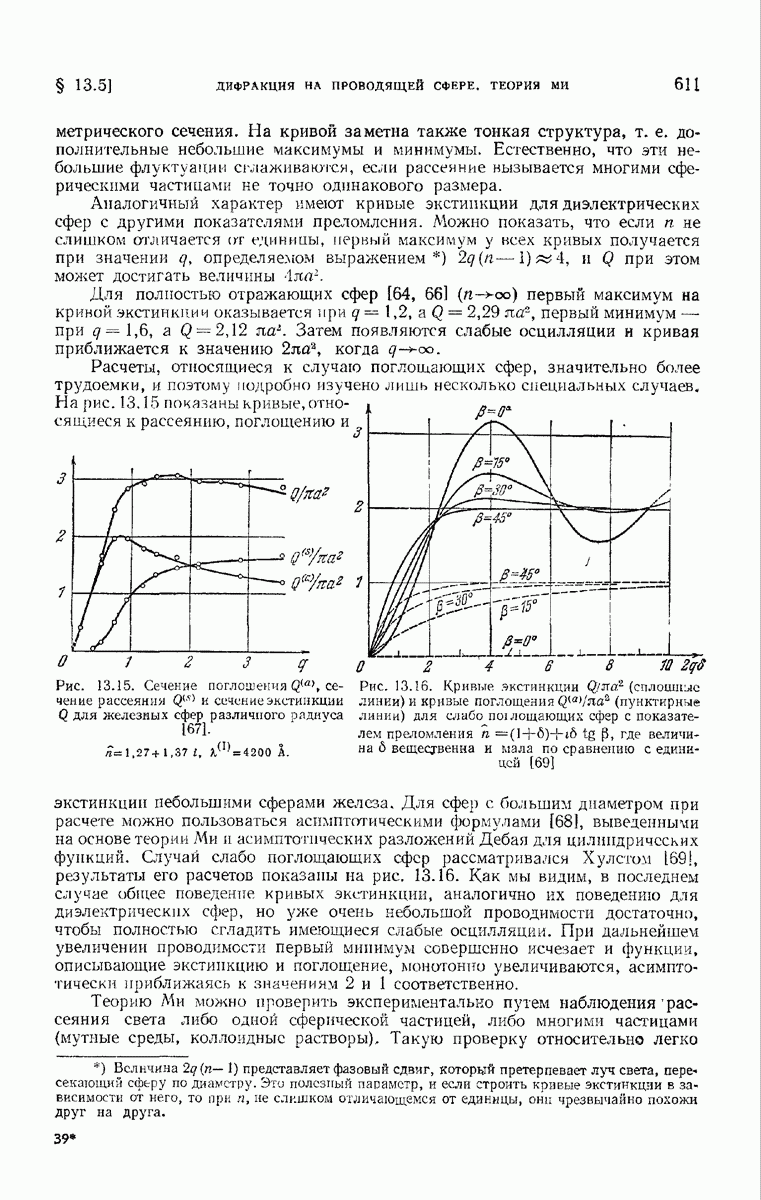
- 13.5.3. Полное рассеяние и затухание
- ГЛАВА 14. КРИСТАЛЛООПТИКА
- § 14.1. Тензор диэлектрической проницаемости анизотропной среды
- § 14.2. Структура монохроматической плоской волны в анизотропной среде
- 14.2.2. Формулы Френеля для распространения света в кристаллах.
- 14.2.3. Геометрические построения для определения скоростей распространения и направлений колебаний.
- § 14.3. Оптические свойства одноосных и двухосных кристаллов
- 14.3.2. Распространение света в одноосных кристаллах.
- 14.3.3. Распространение света в двухосных кристаллах.
- 14.3.4. Преломление в кристаллах
- § 14.4. Измерения в кристаллооптике
- 14.4.2. Компенсаторы.
- 14.4.3. Интерференция в кристаллических пластинках.
- 14.4.4. Интерференционные картины, получающиеся с пластинками одноосных кристаллов.
- 14.4.5. Интерференционные картины, получающиеся с пластинками двухосных кристаллов.
- 14.4.6. Определение положения оптических осей и главных показателей преломления кристаллической среды.
- § 14.5. Искусственная анизотропия
- 14.5.2. Двойное лучепреломление формы.
- § 14.6. Поглощающие кристаллы
- 14.6.2. Интерференционные картины, получающиеся с пластинками поглощающих кристаллов.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ 1. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 2. Интеграл Гильберта и уравнение Гамильтона—Якоби.
- 3. Поле экстремалей.
- 4. Нахождение всех экстремалей из решения уравнения Гамильтона — Якоби.
- 5. Канонические уравнения Гамильтона.
- 6. Частный случай, когда независимая переменная не входит явно в подынтегральное выражение.
- 7. Разрывы.
- 8. Условия Вейерштрасса и Лежандра (достаточные условия экстремума).
- 9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
- 10. Критерий Якоби для минимума.
- 11. Пример I. Оптика.
- 12. Пример II. Механика материальных точек.
- ПРИЛОЖЕНИЕ 2. ОБЫЧНАЯ ОПТИКА, ЭЛЕКТРОННАЯ ОПТИКА И ВОЛНОВАЯ МЕХАНИКА
- 2. Аналогия Гамильтона в вариационной форме.
- 3. Волновая механика свободных электронов.
- 4. Применение оптических принципов в электронной оптике.
- ПРИЛОЖЕНИЕ 3. МЕТОД АСИМПТОТИЧЕСКИХ ОЦЕНОК ИНТЕГРАЛОВ
- 2. Метод стационарной фазы.
- 3. Двойные интегралы.
- ПРИЛОЖЕНИЕ 4. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
- ПРИЛОЖЕНИЕ 5. МАТЕМАТИЧЕСКАЯ ЛЕММА, ИСПОЛЬЗУЕМАЯ ПРИ СТРОГОМ ВЫВОДЕ ЗАКОНА ЛОРЕНТЦ — ЛОРЕНЦА
- ПРИЛОЖЕНИЕ 6. РАСПРОСТРАНЕНИЕ РАЗРЫВОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПРИЛОЖЕНИЕ 7. КРУГОВЫЕ ПОЛИНОМЫ ЦЕРНИКЕ
- ПРИЛОЖЕНИЕ 8. ДОКАЗАТЕЛЬСТВО ОДНОГО НЕРАВЕНСТВА, ПРИВЕДЕННОГО В П. 10.7.3
- ПРИЛОЖЕНИЕ 9. ВЫЧИСЛЕНИЕ ДВУХ ИНТЕГРАЛОВ, ИСПОЛЬЗУЕМЫХ В П. 12.2.2