| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.5.3. Полное рассеяние и затухание
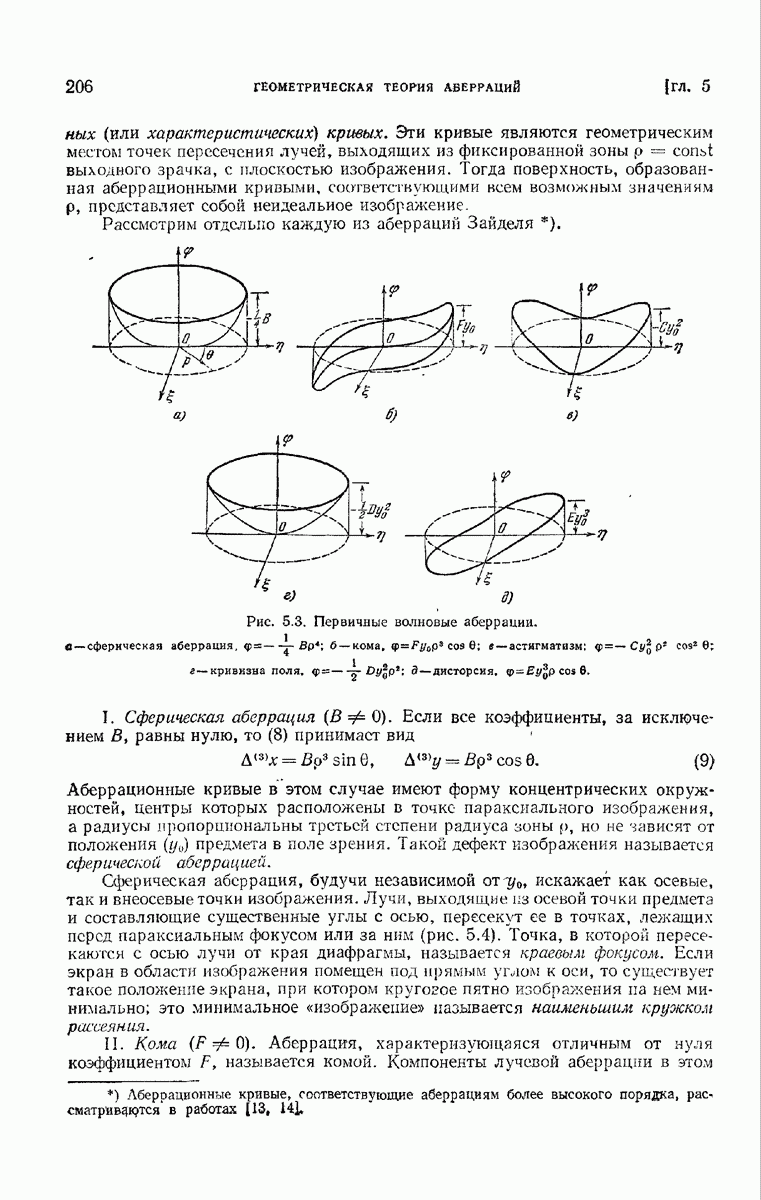
а. Некоторые общие соображения Представляет значительный практический интерес определить полное количество света, которое рассеивается или поглощается сферой. Его можно найги, вычисляя вектор Пойнтинга и интегрируя его по всем направлениям. С помощью соотношений ортогональности, которые существуют между присоединенными функциями Лежандра, интегралы можно выразить через коэффициенты  . Эти расчеты довольно длинны; полностью они выполнены в работе Ми [45].
. Эти расчеты довольно длинны; полностью они выполнены в работе Ми [45].
Полную потерю энергии падающей волной, т. е. сумму рассеянной и поглощенной энергии, можно определить другим способом из некоторых общих соображений, применимых к телу совершенно произвольной формы. Расчеты показывают существование тесной связи между потерей энергии и амплитудой рассеянной волны в первоначальном направлении  Из этого результата (который мы сейчас получим) и из формулы Ми для рассеянной волны легко найти полную потерю энергии на рассеяние и поглощение сферой
Из этого результата (который мы сейчас получим) и из формулы Ми для рассеянной волны легко найти полную потерю энергии на рассеяние и поглощение сферой
Рассмотрим плоскую монохроматическую волну, падающую на небольшое тело произвольной формы, находящееся в диэлектрической среде. Поле в любой точке среды, окружающей тело, вновь можно представить в виде суммы падающего и рассеянного полей, т. е.

Как обычно, мы опустим временной множитель  Усредненный по времени поток энергии определяется средним значением вектора Пойнтинга. На основании (98) и формулы (1.4 56) это среднее значение равно
Усредненный по времени поток энергии определяется средним значением вектора Пойнтинга. На основании (98) и формулы (1.4 56) это среднее значение равно

где

Рассмотрим усредненный поток энергии, выходящий через поверхность сферы большого радиуса  с центром в некоторой точке области, занятой телом. Полный поток в единицу времени равен интегралу от радиальной компоненты
с центром в некоторой точке области, занятой телом. Полный поток в единицу времени равен интегралу от радиальной компоненты  величины
величины  взятому по сфере Очевидно, что для диэлектрического тела он равен нулю Однако для проводящего тела, поглощающего часть падающей энергии, суммарный поток через поверхность сферы совпадает по величине со скоростью, с которой происходит поглощение. Пусть — скорость поглощения энергии телом. Тогда из (99) имеем
взятому по сфере Очевидно, что для диэлектрического тела он равен нулю Однако для проводящего тела, поглощающего часть падающей энергии, суммарный поток через поверхность сферы совпадает по величине со скоростью, с которой происходит поглощение. Пусть — скорость поглощения энергии телом. Тогда из (99) имеем

где  и
и  — интегралы от радиальных компонент
— интегралы от радиальных компонент  взятые по поверхности сферы. Поскольку предполагается, что среда, окружающая тело, является непроводящей,
взятые по поверхности сферы. Поскольку предполагается, что среда, окружающая тело, является непроводящей,  , следовательно,
, следовательно,

где  поверхность сферы и
поверхность сферы и  единичный вектор внешней нормали. Таким образом, выражение, стоящее в правой части (102), представляет скорость потери энергии на тепло и на рассеяние.
единичный вектор внешней нормали. Таким образом, выражение, стоящее в правой части (102), представляет скорость потери энергии на тепло и на рассеяние.
Введем единичный вектор  направление которого совпадает с направлением распространения падающей волны. Тогда
направление которого совпадает с направлением распространения падающей волны. Тогда

Предположим, что эта волна линейно поляризована, и поэтому  и
и  можно считать вещественными постоянными векторами. На больших расстояниях от тела рассеянную волну можно считать сферической, т. е.
можно считать вещественными постоянными векторами. На больших расстояниях от тела рассеянную волну можно считать сферической, т. е.

Векторы а  характеризуют силу излучения, рассеянного в направлении
характеризуют силу излучения, рассеянного в направлении  Так как и падающая, и рассеянная волны подчиняются уравнениям Максвелла, получим (см. уравнения (1.4.4) и (1.4.5))
Так как и падающая, и рассеянная волны подчиняются уравнениям Максвелла, получим (см. уравнения (1.4.4) и (1.4.5))

где  — диэлектрическая проницаемость внешней среды, которая предполагается немагнитной
— диэлектрическая проницаемость внешней среды, которая предполагается немагнитной  Из этих соотношений следует, что на поверхности
Из этих соотношений следует, что на поверхности  сферы большого радиуса
сферы большого радиуса

Подставим найденные выражения в (102). Для вычисления полученного интеграла воспользуемся леммой  которая утверждает, что для произвольной функции
которая утверждает, что для произвольной функции  при больших
при больших  можно написать
можно написать

Тогда мы получим 

а соотношение (102) примет вид

где  означает, что берется мнимая часть.
означает, что берется мнимая часть.
Из соотношения (109) следует, что в случае падения линейно поляризованного света скорость Оисеипации энергии пропорциональна проекции на направление электрического вектора падающей волны амплитуды волны, рассеянной в первоначальном направлении 
Величина  равная отношению скорости диссипации энергии
равная отношению скорости диссипации энергии  к количеству энергии, падающей в единицу времени на единичную площадку в сечении тела
к количеству энергии, падающей в единицу времени на единичную площадку в сечении тела  называется сечением акстинкции тела. Из
называется сечением акстинкции тела. Из  и (105) следует, что
и (105) следует, что  так что, согласно (109), найдем
так что, согласно (109), найдем

Эта формула получена Ван Xулстом [48].

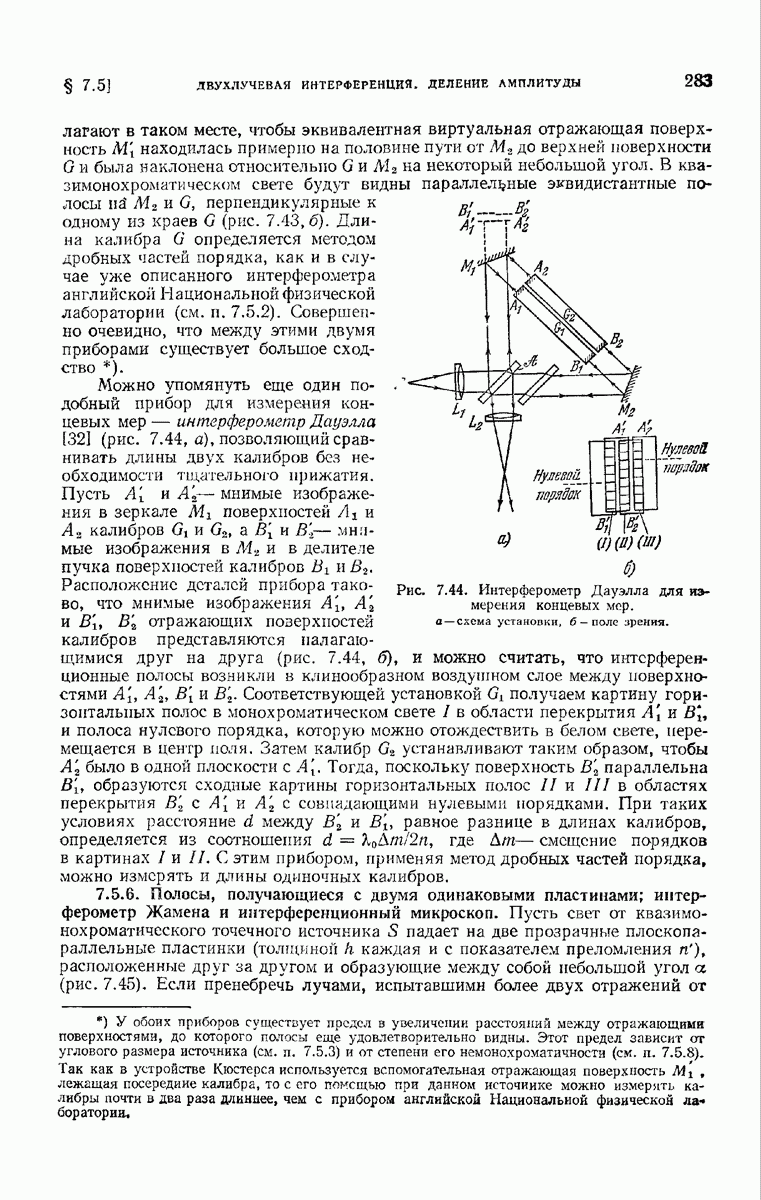
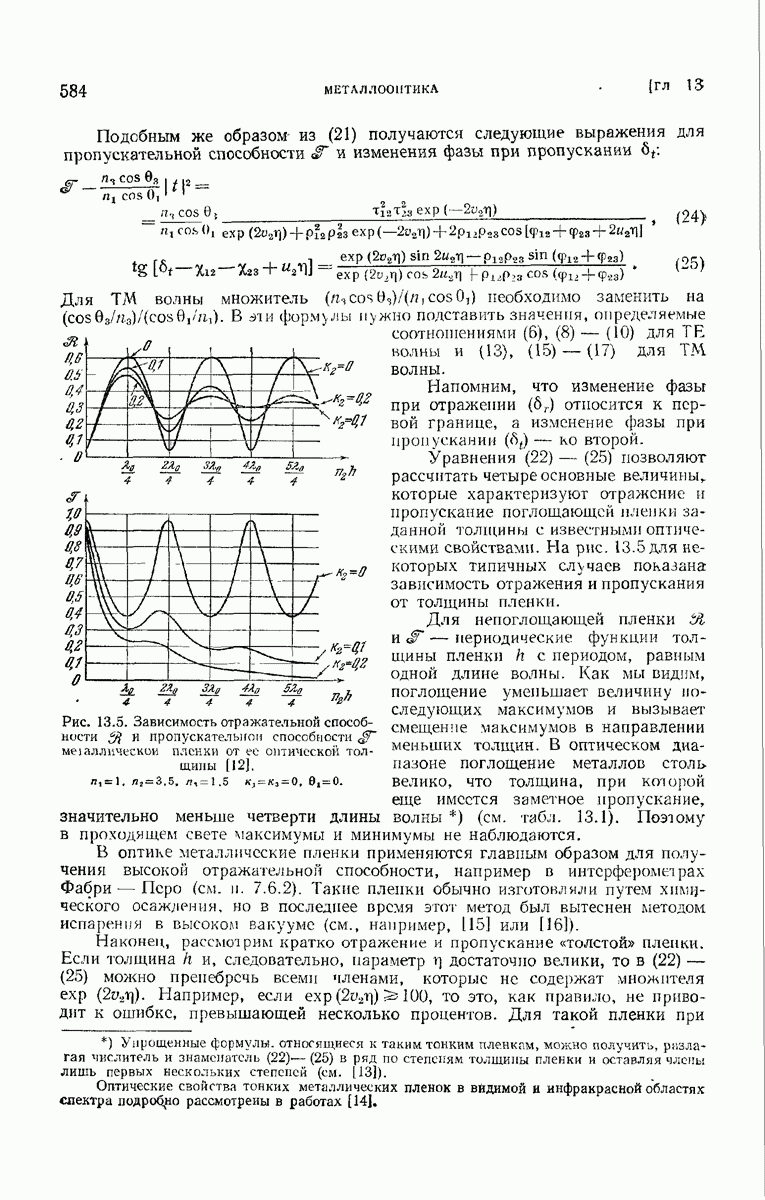
Рис. 13.12. К выводу соотношения {114) для сечения экстинкции при большом препятствии
Аналогичным образом можно определить сечение рассеяния  и сечение поглощения
и сечение поглощения  тела, а именно
тела, а именно

Очевидно, что  Для непоглощающего тела
Для непоглощающего тела  и сечение экстинкции совпадает с сечением рассеяния.
и сечение экстинкции совпадает с сечением рассеяния.
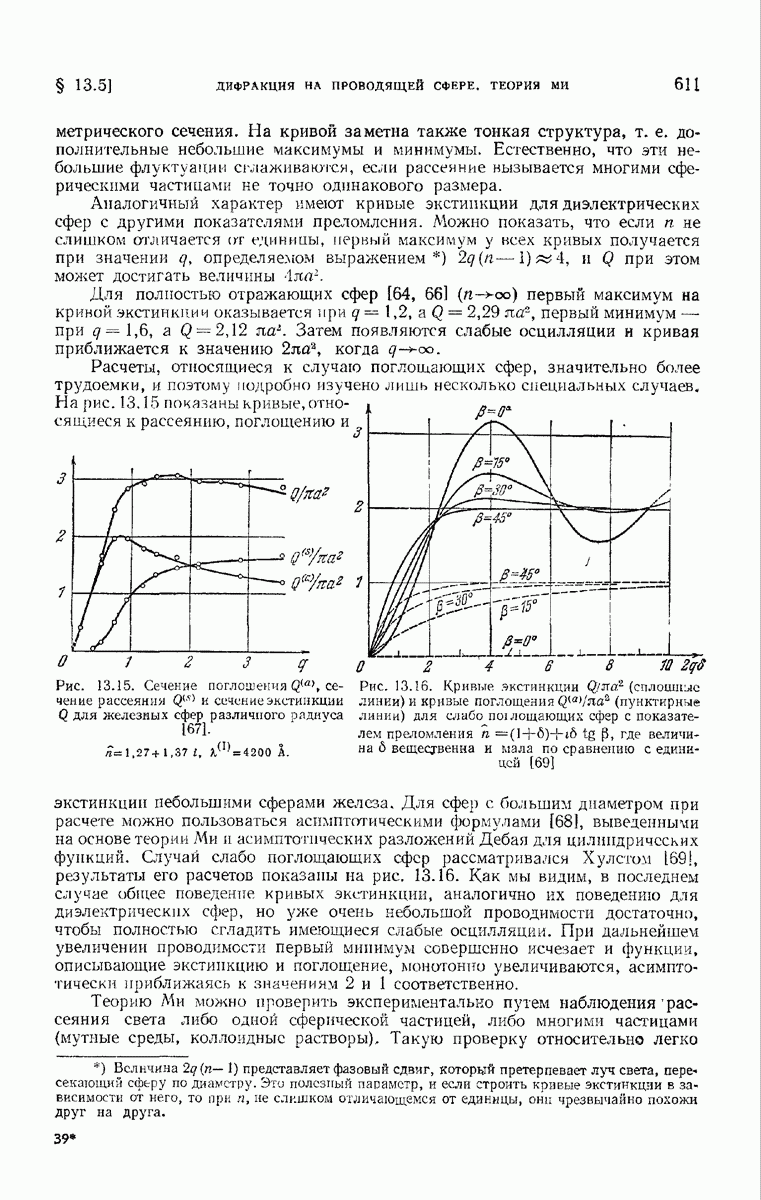
Прежде чем применить соотношение (110) к сферическому телу, найдем величину  для тела, которое практически не пропускает падающего света. Предположим также, что его линейные рачмеры велики по сравнению с длиной волны. В этом случае применима теория Гюйгенса—Кирхгофа, и основной вклад в рассеяние в направлении падения света обусловлен дифракцией Фраунгофера. Пусть на тело падает линейно поляризованная волна с плоским волновым фронтом, причем
для тела, которое практически не пропускает падающего света. Предположим также, что его линейные рачмеры велики по сравнению с длиной волны. В этом случае применима теория Гюйгенса—Кирхгофа, и основной вклад в рассеяние в направлении падения света обусловлен дифракцией Фраунгофера. Пусть на тело падает линейно поляризованная волна с плоским волновым фронтом, причем  — часть этого фронта, не закрываемая препятствием,
— часть этого фронта, не закрываемая препятствием,  его часть, занятая препятствием (рис. 13.12). Рассмотрим рассеянное поле
его часть, занятая препятствием (рис. 13.12). Рассмотрим рассеянное поле  в точке Р, находящейся на большом расстоянии от тела. Согласно принципу Гюйгенса — Френеля и принципу Бабине (8.3.21) имеем для малого угла дифракции
в точке Р, находящейся на большом расстоянии от тела. Согласно принципу Гюйгенса — Френеля и принципу Бабине (8.3.21) имеем для малого угла дифракции

Если точка Р находится очень далеко от препятствия в направлении распространения падающей волны, то  можно считать постоянным, и (112) дает
можно считать постоянным, и (112) дает

здесь  — геометрическое поперечное сечение тела (площадь А). Следовательно,
— геометрическое поперечное сечение тела (площадь А). Следовательно,  данном случае вектор а в (104) как функция
данном случае вектор а в (104) как функция  определяется выражением
определяется выражением  и из (110) находим, что
и из (110) находим, что

Таким образом, сечение экстинкции большого непрозрачного тела равно удвоенному значению его геоиетрического поперечного сечения. На первый взгляд полученный результат кажется несколько парадоксальным, так как можно было бы ожидать, что для тела большего размера должно было бы быть справедливым приближение геометрической оптики, а в этом приближении сечение экстинкции равно  Объяснение этого кажущегося противоречия заключается в том, что независимо от размеров тела и расстояния до точки, в которой рассматривается поле, всегда имеется хотя бы узкая область — вблизи края геометрической тени, — где приближение геометрической оптики несправедливо.
Объяснение этого кажущегося противоречия заключается в том, что независимо от размеров тела и расстояния до точки, в которой рассматривается поле, всегда имеется хотя бы узкая область — вблизи края геометрической тени, — где приближение геометрической оптики несправедливо.
Помимо света, задерживаемого телом с поперечным сечением  (потери на отражение и поглощение), возникает дополнительный вклад в экстннкцию, обусловленный соседством с краем тени, и очевидно, что этот вклад также равен
(потери на отражение и поглощение), возникает дополнительный вклад в экстннкцию, обусловленный соседством с краем тени, и очевидно, что этот вклад также равен  Для экспериментальной проверки соотношения (114) необходимо собрать свет с достаточно широкой площадки, расположенной достаточно далеко от тела.
Для экспериментальной проверки соотношения (114) необходимо собрать свет с достаточно широкой площадки, расположенной достаточно далеко от тела.
Применим теперь общую формулу (110) к сферическому телу. На основании (58) проекция амплитуды рассеянной волны на направление электрического вектора падающей волны  при рассеянии вперед
при рассеянии вперед  определяется выражением
определяется выражением

Оба члена, содержащих присоединенные полиномы Лежандра, легко найти из выражения [23]

здесь  зависят лишь
зависят лишь  . Из последнего выражения и из его производной находим
. Из последнего выражения и из его производной находим

Подставляя (117) в (115) и используя для  и асимптотические приближения (74) и (76), получим
и асимптотические приближения (74) и (76), получим

Вспоминая, что амплитуда падающего поля считается равной единице  находим искомую величину
находим искомую величину  разделив найденное выражение на
разделив найденное выражение на  Подставляя ее в (110) и используя тождество
Подставляя ее в (110) и используя тождество  справедливое для любого комплексного числа
справедливое для любого комплексного числа  мы окончательно получим следующие выражения для сечения экстинкции сферы.
мы окончательно получим следующие выражения для сечения экстинкции сферы.

здесь коэффициенты  определяются выражениями (62).
определяются выражениями (62).
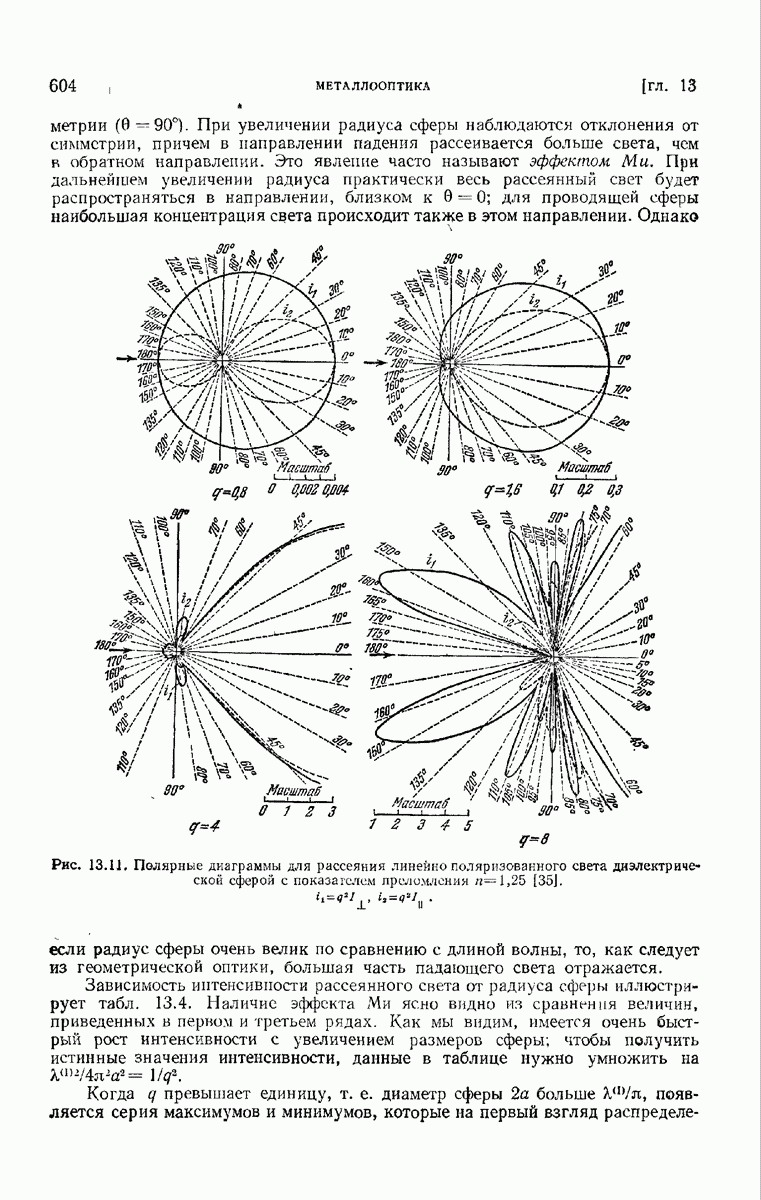
б. Результаты расчетов. Суммируем теперь основные результаты расчетов полного рассеяния, полного поглощения и экстинкции для сферы.  мы показали, что при диаметре сферы, значительно меньшем длины волны (рэлеевское рассеяние), необходимо учитывать лишь первую электрическую парциальную волну. В этом случае амплитуда рассеянной волны пропорциональна
мы показали, что при диаметре сферы, значительно меньшем длины волны (рэлеевское рассеяние), необходимо учитывать лишь первую электрическую парциальную волну. В этом случае амплитуда рассеянной волны пропорциональна  так что полное рассеяние обратно пропорционально четвертой степени длины волны. Если учитывать также члены более высокого порядка, которые зависят от радиуса сферы и материальных постоянных, то полное рассеяние станет очень сложной функцией длины волны и будет
так что полное рассеяние обратно пропорционально четвертой степени длины волны. Если учитывать также члены более высокого порядка, которые зависят от радиуса сферы и материальных постоянных, то полное рассеяние станет очень сложной функцией длины волны и будет
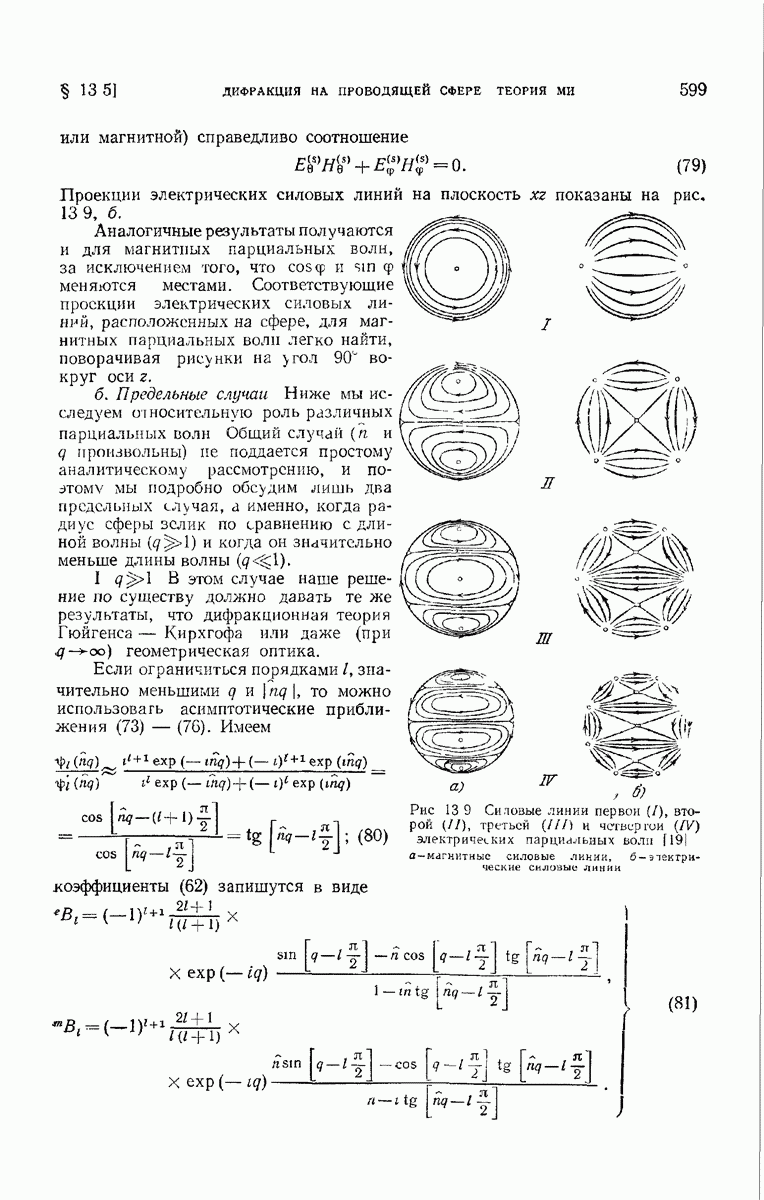
селективным  . В случае золота, например, даже очень маленькая сфера дает максимум вблизи
. В случае золота, например, даже очень маленькая сфера дает максимум вблизи  (рис. 13.13).
(рис. 13.13).
Такой максимум можно интерпретировать как своего рода резонанс. Предположим, что сфера не испытывает влияния поля падающего пучка света, но в ней возбуждены свободные электромагнитные колебания. Частоту и постоянную затухания таких свободных колебаний можно получить из изложенной выше теории, если в уравнениях (56) опустить члены, не содержащие коэффициентов  Получающаяся система линейных однородных уравнений допускает нетривиальное решение только в том случае, если они совместны. Тогда каждое решение уравнения соответствует затухающим собственным колебаниям; частота таких колебаний очень близка к частотам, на которых имеется максимум интенсивности для определенных рассеянных парциальных волн
Получающаяся система линейных однородных уравнений допускает нетривиальное решение только в том случае, если они совместны. Тогда каждое решение уравнения соответствует затухающим собственным колебаниям; частота таких колебаний очень близка к частотам, на которых имеется максимум интенсивности для определенных рассеянных парциальных волн 
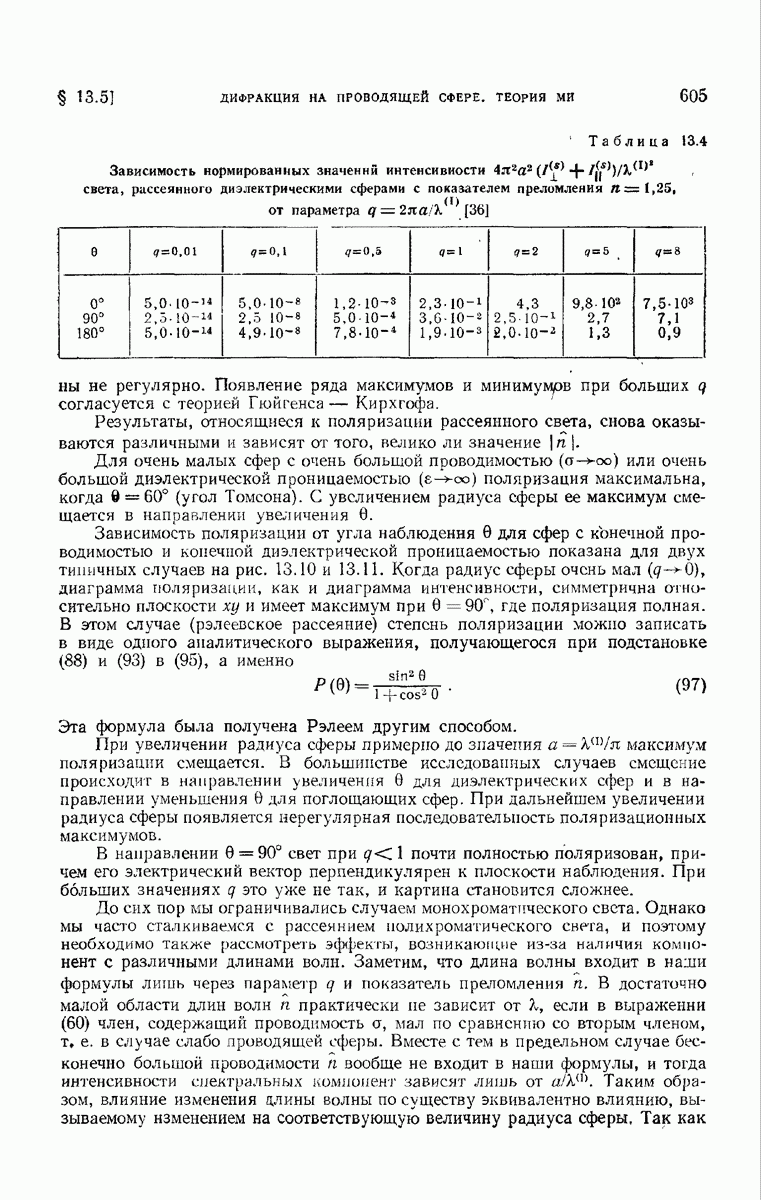
Расчеты рассеяния и экстинкции сферами конечного радиуса для выбранных значений показателя преломления были проделаны многими авторами. Большинство расчетов относится к диэлектрическим (вещественное  и слабо поглощающим сферам. На рис. 13.14 приведена типичная кривая, полученная Гольдбергом для сфер с показателем преломления и
и слабо поглощающим сферам. На рис. 13.14 приведена типичная кривая, полученная Гольдбергом для сфер с показателем преломления и  Такой же показатель преломления у воды, и поэтому указанные результаты представляют интерес в связи с пропусканием света дымкой, тучами и туманом, а также в связи с теорией камеры Вильсона и т. д.
Такой же показатель преломления у воды, и поэтому указанные результаты представляют интерес в связи с пропусканием света дымкой, тучами и туманом, а также в связи с теорией камеры Вильсона и т. д.

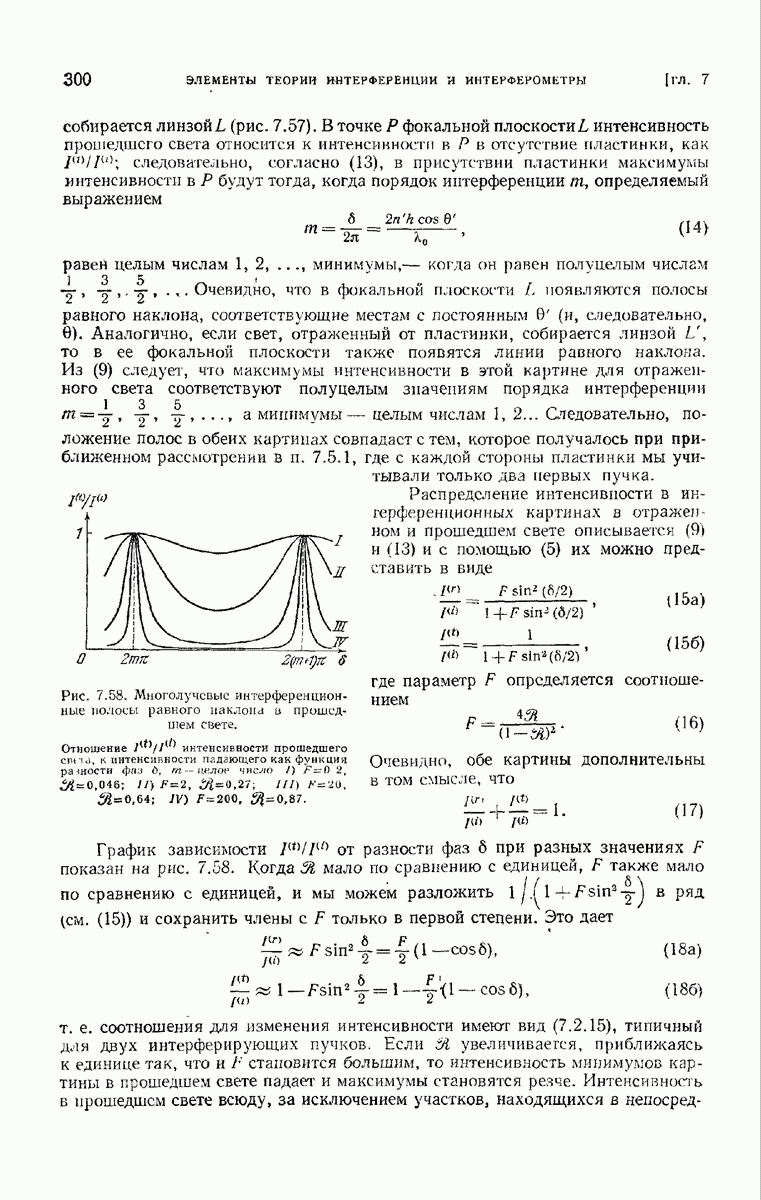
Рис. 13.13. Зависимость полного рассеяния на очень маленьких сферах  от длины волны [56]. I — ртуть, II - золото, III - серебро, IV — идеальный проводник.
от длины волны [56]. I — ртуть, II - золото, III - серебро, IV — идеальный проводник.

Рис. 13.14. Зависимость сечения рассеяния диэлектрических сфер с показателем преломления  от параметра
от параметра 
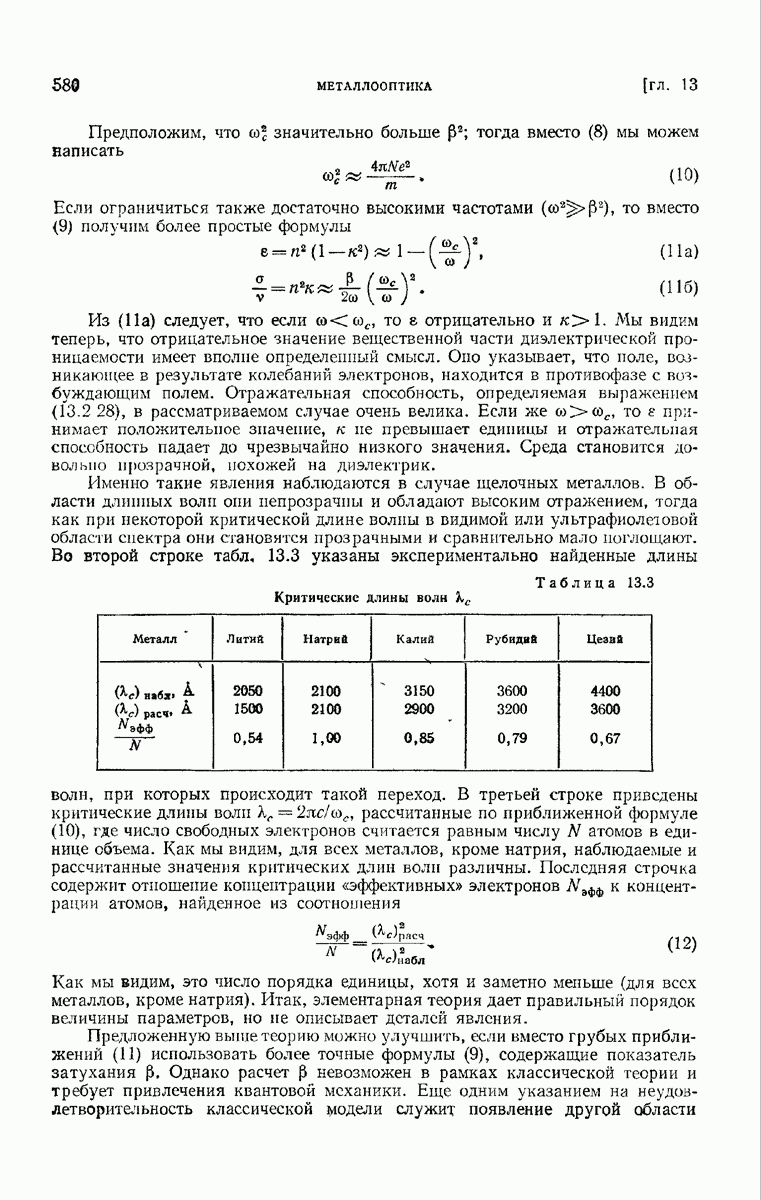
Как мы видим, на кривой имеется серия максимумов и минимумов, и с увеличением радиуса сферы сечение экстинкции в согласии с уравнением (114) стремится к удвоенному значению
геометрического сечения. На кривой заметна также тонкая структура, т. е. дополнительные небольшие максимумы и минимумы. Естественно, что эти небольшие флуктуации сглаживаются, если рассеяние нызывается многими сферическими частицами не точно одинакового размера.
Аналогичный характер имеют кривые экстиикции для диэлектрических сфер с другими показателями преломления. Можно показать, что если  не слишком отличается от единицы, первый максимум у всех кривых получается при значении
не слишком отличается от единицы, первый максимум у всех кривых получается при значении  определяемом выражением
определяемом выражением  и О при этом может достигать величины
и О при этом может достигать величины 
Для полностью отражающих сфер [64, 66]  первый максимум на криной экстинкиии оказывается при
первый максимум на криной экстинкиии оказывается при  первый минимум — при
первый минимум — при  Затем появляются слабые осцилляции и кривая приближается к значению
Затем появляются слабые осцилляции и кривая приближается к значению  когда
когда 
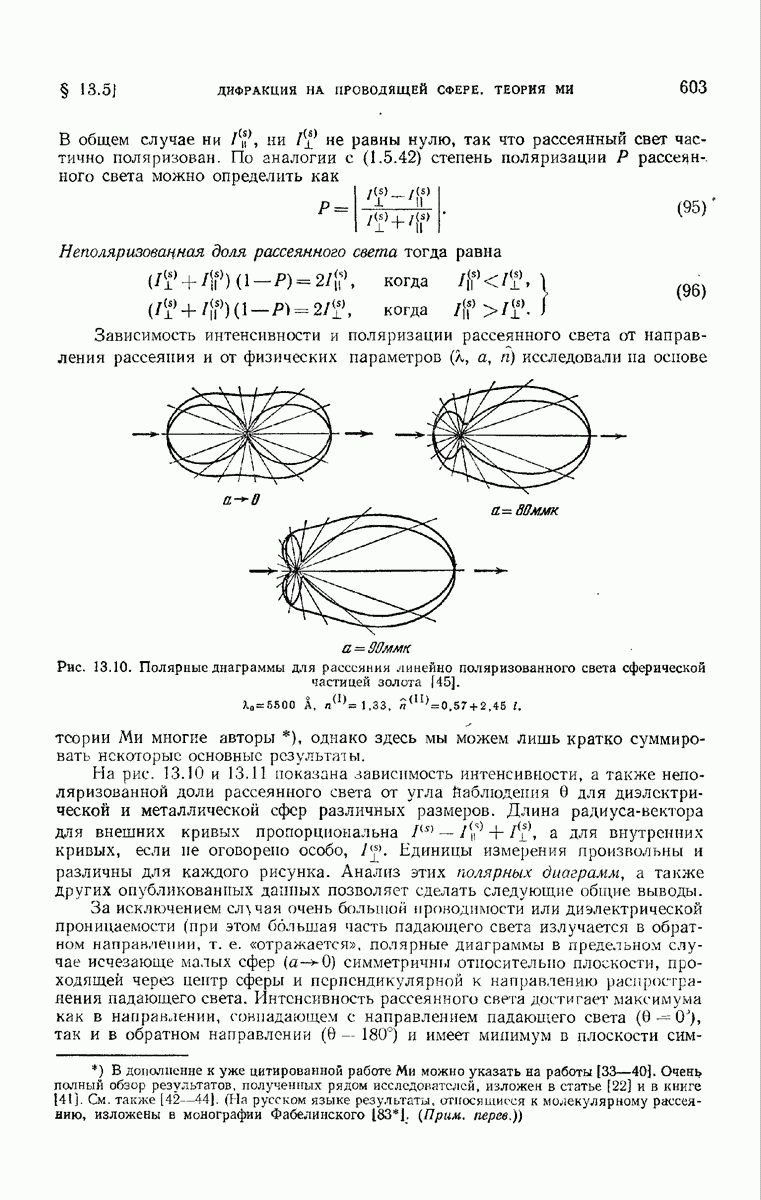
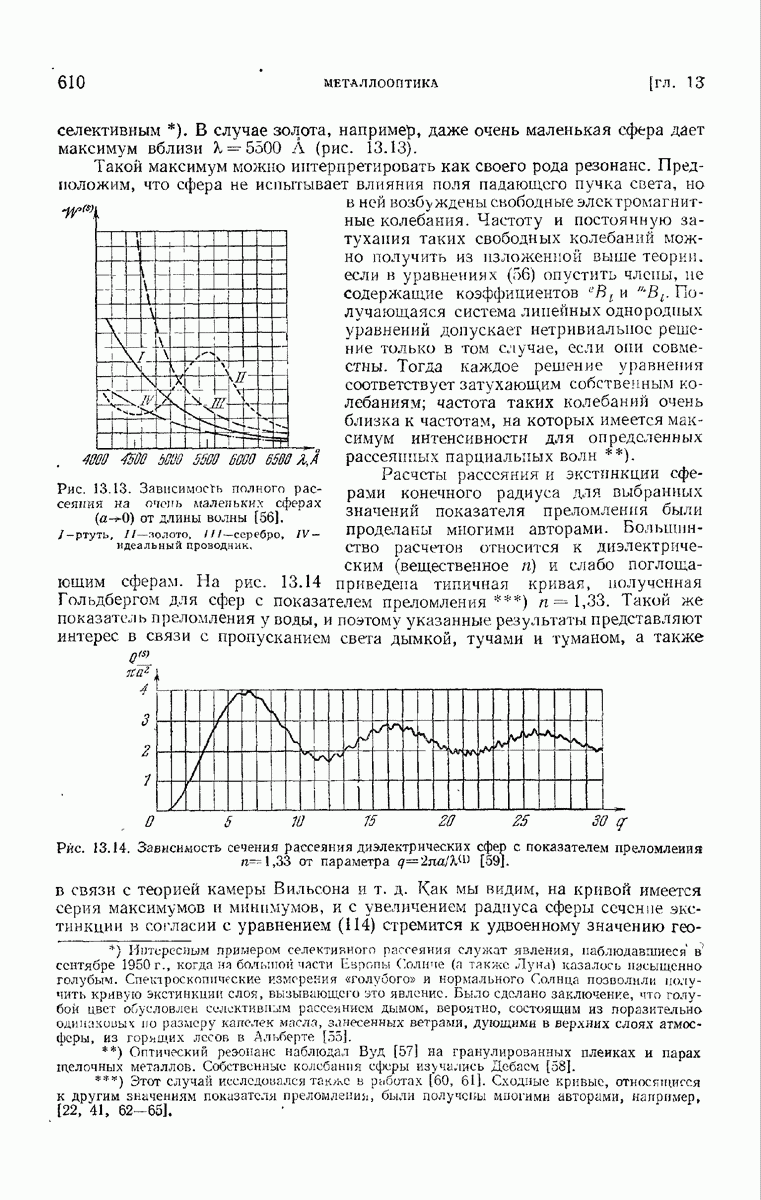
Расчеты, относящиеся к случаю поглощающих сфер, значительно более трудоемки, и поэтому подробно изучено лишь несколько специальных случаев. На рис. 13,15 показаны кривые, относящиеся к рассеянию, поглощению и экстинкции небольшими сферами железа.

Рис. 13.15. Сечение поглощения  сечение рассеяния
сечение рассеяния  и сечение экстиикции
и сечение экстиикции  для железных сфер различного радиуса [67].
для железных сфер различного радиуса [67]. 

Рис. 13.16. Кривые экстинкции  (сплошные линии) и кривые поглощения
(сплошные линии) и кривые поглощения  (пунктирные линии) для слабо пилощающих сфер с показателем преломления
(пунктирные линии) для слабо пилощающих сфер с показателем преломления  где величина
где величина  вещественна и мала по сравнению с единицей [69]
вещественна и мала по сравнению с единицей [69]
Для сфер с большим диаметром при расчете можно пользоваться асимптотическими формулами [68], выведенными на основе теории Ми и асимптотических разложений Дебая для цилиндрических функций. Случай слабо поглощающих сфер рассматривался Хулстом  результаты его расчетов показаны на рис. 13.16. Как мы видим, в последнем случае общее поведение кривых экстинкции, аналогично их поведению для диэлектрических сфер, но уже очень небольшой проводимости достаточно, чтобы полностью сгладить имеющиеся слабые осцилляции. При дальнейшем увеличении проводимости первый минимум совершенно исчезает и функции, описывающие экстипкцию и поглощение, монотонно увеличиваются, асимптотически приближаясь к значениям 2 и 1 соответственно.
результаты его расчетов показаны на рис. 13.16. Как мы видим, в последнем случае общее поведение кривых экстинкции, аналогично их поведению для диэлектрических сфер, но уже очень небольшой проводимости достаточно, чтобы полностью сгладить имеющиеся слабые осцилляции. При дальнейшем увеличении проводимости первый минимум совершенно исчезает и функции, описывающие экстипкцию и поглощение, монотонно увеличиваются, асимптотически приближаясь к значениям 2 и 1 соответственно.
Теорию Ми можно проверить экспериментально путем наблюдениярассеяния света либо одной сферической частицей, либо многими частицами (мутные среды, коллоидные растворы). Такую проверку относительно легко
провести для больших частиц, но она становится довольно трудной, когда диаметр каждой частицы порядка длины волны или меньше. Ла Меру с сотрудниками [62, 63, 701 удалось проверить теорию, измеряя угловое распределение рассеянного света, а также полное рассеяние от взвеси серных золей в воде (частицы диаметром от 3000 до 5000 А). Они использовали излучение с длинами волн в вакууме от 2850 до 10000 А и нашли прекрасное согласие с предсказаниями теории Ми. В некоторых случаях на кривой экстинкции наблюдались даже мелкие флуктуации (тонкая структура) (см. рис. 13.14).
Ряд авторов изучал рассеяние, света несферическими частицами, но в общем случае аналитический вид соответствующих волновых функций настолько сложен, что строгие решения имеют ограниченное практическое значение. Ганс [75] и другие исследователи рассматривали рассеяние электромагнитных волн эллипсоидами с размерами, малыми по сравнению с длиной волны; строгое решение для эллипсоида произвольного размера было получено в работе [761. Рассеяние длинными круглыми проводящими цилиндрами изучалось еще в 1905 г. Зейтцем [77] и Игнатовским [78], и полученные ими формулы подобны формулам Ми для сферы. Рассеяние длинными круглыми диэлектрическими цилиндрами и цилиндрами с высоким отражением исследовали Шеффер и Гроссманн [79] (см. также [80]).
ЛИТЕРАТУРА
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 1.1. Электромагнитное поле
- 1.1.2. Материальные уравнения.
- 1.1.3. Граничные условия на поверхностях раздела.
- 1.1.4. Закон сохранения энергии для электромагнитного поля.
- § 1.2. Волновое уравнение и скорость света
- § 1.3. Скалярные волны
- 1.3.2. Сферические волны.
- 1.3.3. Гармонические волны. Фазовая скорость.
- 1.3.4. Волновые пакеты. Групповая скорость.
- § 1.4. Векторные волны
- 1.4.2. Гармоническая электромагнитная плоская волна.
- 1.4.3. Гармонические векторные волны произвольной формы.
- § 1.5. Отражение и преломление плоской волны
- 1.5.2. Формулы Френеля.
- 1.5.3. Отражательная и пропускательная способности; поляризация при отражении и преломлении.
- 1.5.4. Полное внутреннее отражение.
- § 1.6. Распространение волн в слоистой среде. Теория диэлектрических пленок
- 1.6.2. Характеристическая матрица для слоистой среды.
- 1.6.3. Коэффициенты отражения и пропускания.
- 1.6.4. Однородная диэлектрическая пленка.
- 1.6.5. Периодические слоистые среды.
- ГЛАВА 2. ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ И ПОЛЯРИЗАЦИЯ
- § 2.1. Электродинамические потенциалы в вакууме
- 2.1.2. Запаздывающие потенциалы.
- § 2.2. Поляризация и намагничение
- 2.2.2. Векторы Герца.
- 2.2.3. Поле линейного электрического диполя.
- § 2.3. Формула Лорентц — Лоренца и элементарная теория дисперсии
- 2.3.2. Эффективное поле.
- 2.3.3. Средняя поляризуемость. Формула Лорентц — Лоренца.
- 2.3.4. Элементарная теория дисперсии.
- § 2.4. Описание распространения электромагнитных волн с помощью интегральных уравнений
- 2.4.2. Теорема погашения Эвальда — Озеена и строгий вывод формулы Лорентц — Лоренца.
- 2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда — Озеена.
- ГЛАВА 3. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 3.1.2. Световые лучи и закон интенсивности в геометрической оптике.
- 3.1.3. Распространение векторных амплитуд.
- 3.1.4. Обобщения геометрической оптики и пределы ее применимости.
- § 3.2. Общие свойства лучей
- 3.2.2. Законы преломления и отражения.
- 3.2.3. Конгруэнции лучей и фокальные свойства.
- § 3.3. Другие основные теоремы геометрической оптики
- 3.3.2. Принцип Ферма
- 3.3.3. Теорема Малюса и Дюпина и некоторые другие связанные с ней теоремы.
- ГЛАВА 4. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ
- 4.1.2. Смешанная характеристика.
- 4.1.3. Угловая характеристика.
- 4.1.4. Приближенное выражение для угловой характеристики преломляющей поверхности вращения.
- 4.1.5. Приближенное выражение для угловой характеристики отражающей поверхности вращения.
- § 4.2. Идеальное отображение
- 4.2.2. «Рыбий глаз» Максвелла.
- 4.2.3. Стигматическое отображение поверхностей.
- § 4.3. Проективное преобразование (коллинеация) при наличии аксиальной симметрии
- 4.3.2. Телескопическое отображение.
- 4.3.3. Классификация проективных преобразований.
- 4.3.4. Комбинация проективных преобразований.
- § 4.4. Параксиальная оптика
- 4.4.2. Отражающая поверхность вращения.
- 4.4.3. Толстая линза.
- 4.4.4. Тонкая лииза.
- 4.4.5. Произвольная центрированная система.
- § 4.5. Стигматическое отображение пучками с большой угловой апертурой
- § 4.6. Астигматические пучки лучей
- 4.6.2. Преломление тонкого пучка.
- § 4.7. Хроматическая аберрация. Дисперсия призмы
- 4.7.2. Дисперсия призмы.
- § 4.8. Фотометрия. Апертуры оптических систем
- 4.8.2. Диафрагмы и зрачки.
- 4.8.3. Яркость и освещенность изображений.
- § 4.9. Метод построения хода лучей
- 4.9.2. Параксиальные лучи.
- 4.9.3. Косые лучи.
- § 4.10. Оптические системы с несферическими поверхностями
- 4.10.2. Получение апланатизма.
- ГЛАВА 5. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 5.2. Эйконал Шварншильда
- § 5.3. Первичные аберрации (аберрации Зайделя)
- § 5.4. Теорема сложения для случая первичных аберраций
- § 5.5. Коэффициенты первичных аберраций произвольной центрированной системы линз
- 5.5.2. Формулы Зайделя, выраженные через параметры одного параксиального луча.
- 5.5.3. Теорема Петцваля.
- § 5.6. Пример: первичные аберрации тонкой линзы
- § 5.7. Хроматическая аберрация произвольной центрированной системы линз
- ГЛАВА 6. ОПТИЧЕСКИЕ ПРИБОРЫ, ФОРМИРУЮЩИЕ ИЗОБРАЖЕНИЕ
- § 6.2. Фотографический аппарат
- § 6.3. Линзовый телескоп
- § 6.4. Зеркальный телескоп
- § 6.5. Осветители
- § 6.6. Микроскоп
- ГЛАВА 7. ЭЛЕМЕНТЫ ТЕОРИИ ИНТЕРФЕРЕНЦИИ И ИНТЕРФЕРОМЕТРЫ
- § 7.2. Интерференция двух монохроматических волн
- § 7.3. Двухлучевая интерференция. Деление волнового фронта
- 7.3.2. Зеркала Френеля и другие аналогичные устройства.
- 7.3.3. Интерференционные полосы в квазимонохроматическом и белом свете.
- 7.3.4. Источник в виде щели; видность полос.
- 7.3.5. Измерение оптической разности хода; интерферометр Рэлея.
- 7.3.6. Измерение угловых размеров источников; звездный интерферометр Майкельсона.
- § 7.4. Стоячие волны
- § 7.5. Двухлучевая интерференция. Деление амплитуды
- 7.5.2. Интерференция в тонких пленках; интерферометр Физо.
- 7.5.3. Локализация полос.
- 7.5.4. Интерферометр Майкельсона.
- 7.5.5. Интерферометр Тваймана — Грина и другие аналогичные приборы.
- 7.5.6. Полосы, получающиеся с двумя одинаковыми пластинами; интерферометр Жамена и интерференционный микроскоп.
- 7.5.7. Интерферометр Маха—Цендера; интерферометр Бейтса со смещенным волновым фронтом.
- 7.5.8. Длина когерентности; применение двухлучевой интерференции к изучению тонкой структуры спектральных линий.
- § 7.6. Многолучевая интерференция
- 7.6.2. Интерферометр Фабри — Перо.
- 7.6.3. Применение интерферометра Фабри — Перо для изучения тонкой структуры спектральных линий.
- 7.6.4. Применение интерферометра Фабри — Перо для сравнения длин волн.
- 7.6.5. Интерферометр Люммера — Герке.
- 7.6.6. Интерференционные фильтры.
- 7.6.7. Многолучевые полосы в тонких пленках.
- 7.6.8. Многолучевые полосы, получающиеся с двумя плоскопараллельными пластинками.
- § 7.7. Сравнение длин волн с эталонным метром
- ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ДИФРАКЦИИ
- § 8.2. Принцип Гюйгенса — Френеля
- § 8.3. Теория дифракции Кирхгофа
- 8.3.2. Теория дифракции Кирхгофа.
- 8.3.3. Дифракция Фраунгофера и Френеля.
- § 8.4. Переход к скалярной теории
- 8.4.2. Полное поле изображения.
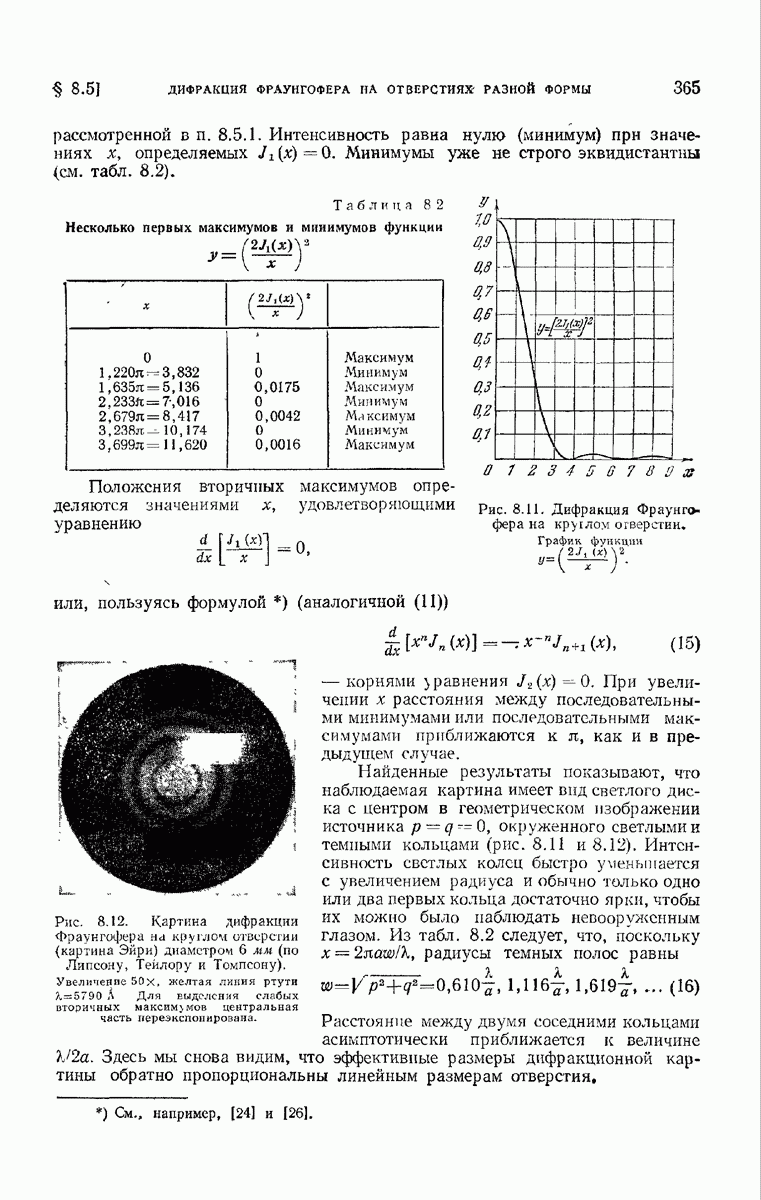
- § 8.5. Дифракция Фраунгофера на отверстиях разной формы
- 8.5.2. Круглое отверстие.
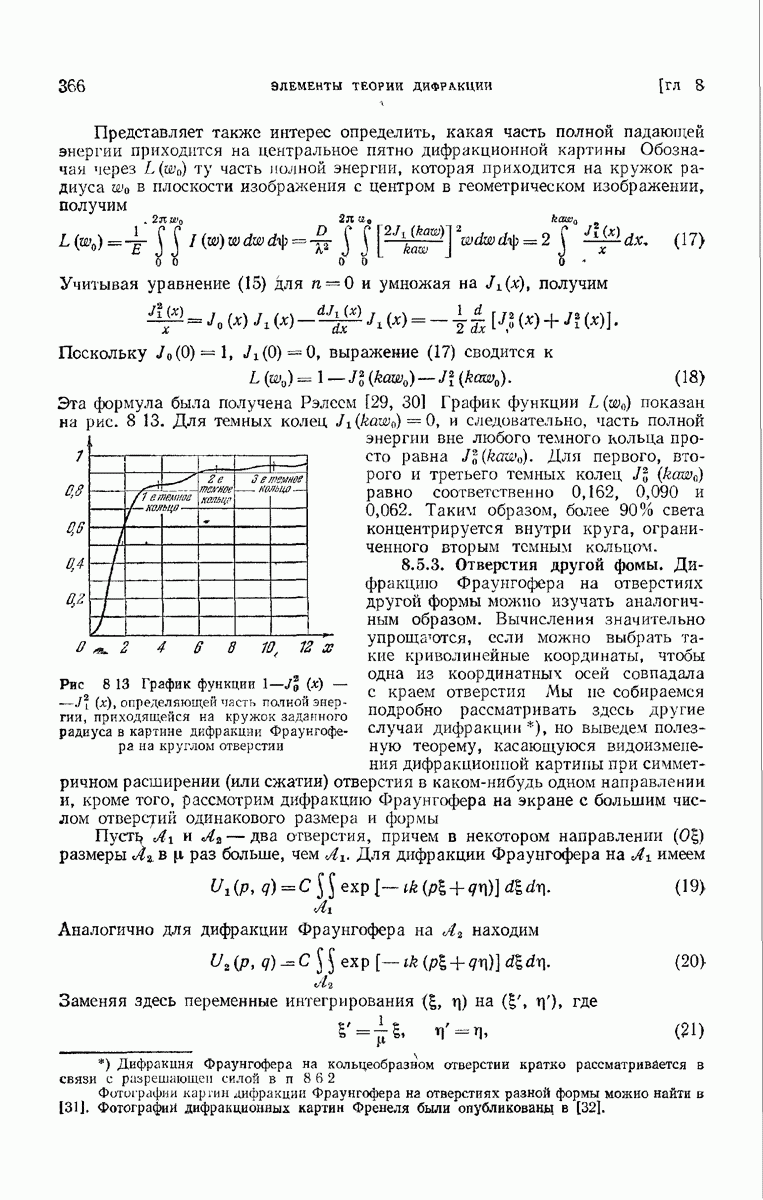
- 8.5.3. Отверстия другой фомы.
- § 8.6. Дифракция Фраунгофера в оптических приборах
- 8.6.2. Разрешающая сила систем, образующих изображение.
- 8.6.3. Образование изображения в микроскопе.
- § 8.7. Дифракция Френеля на прямолинейном крае
- 8.7.2. Интегралы Френеля.
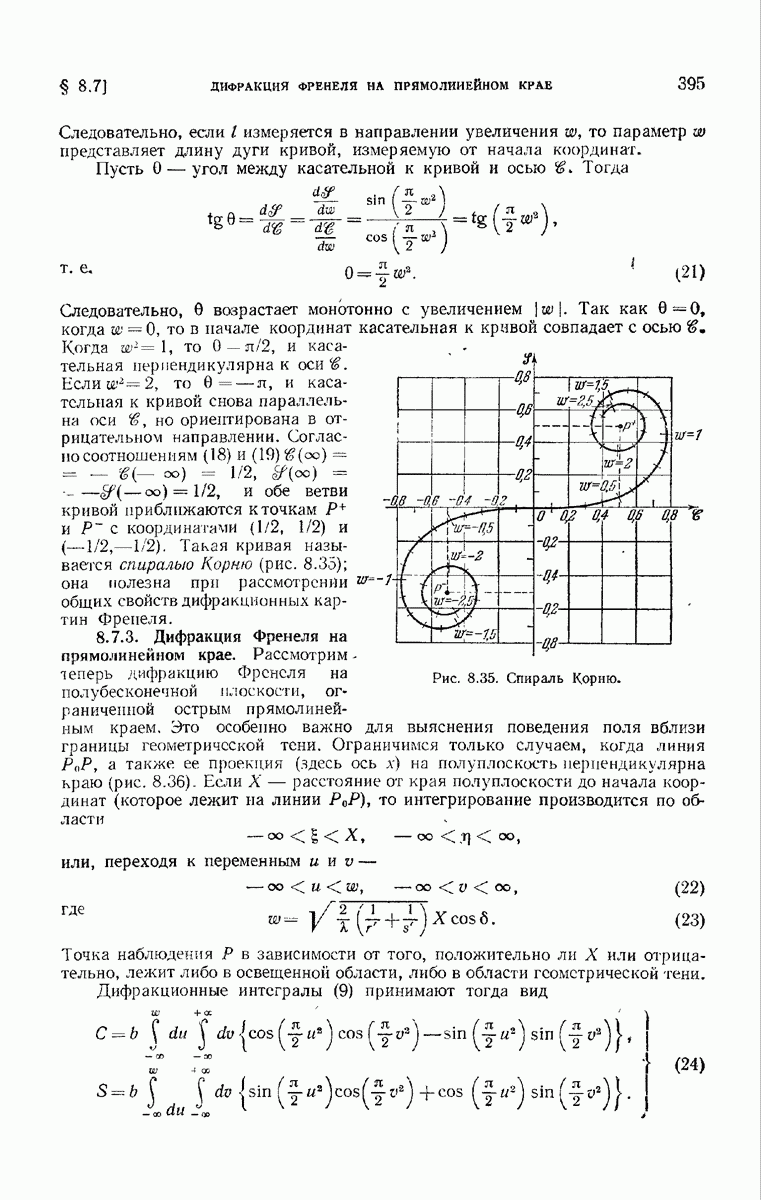
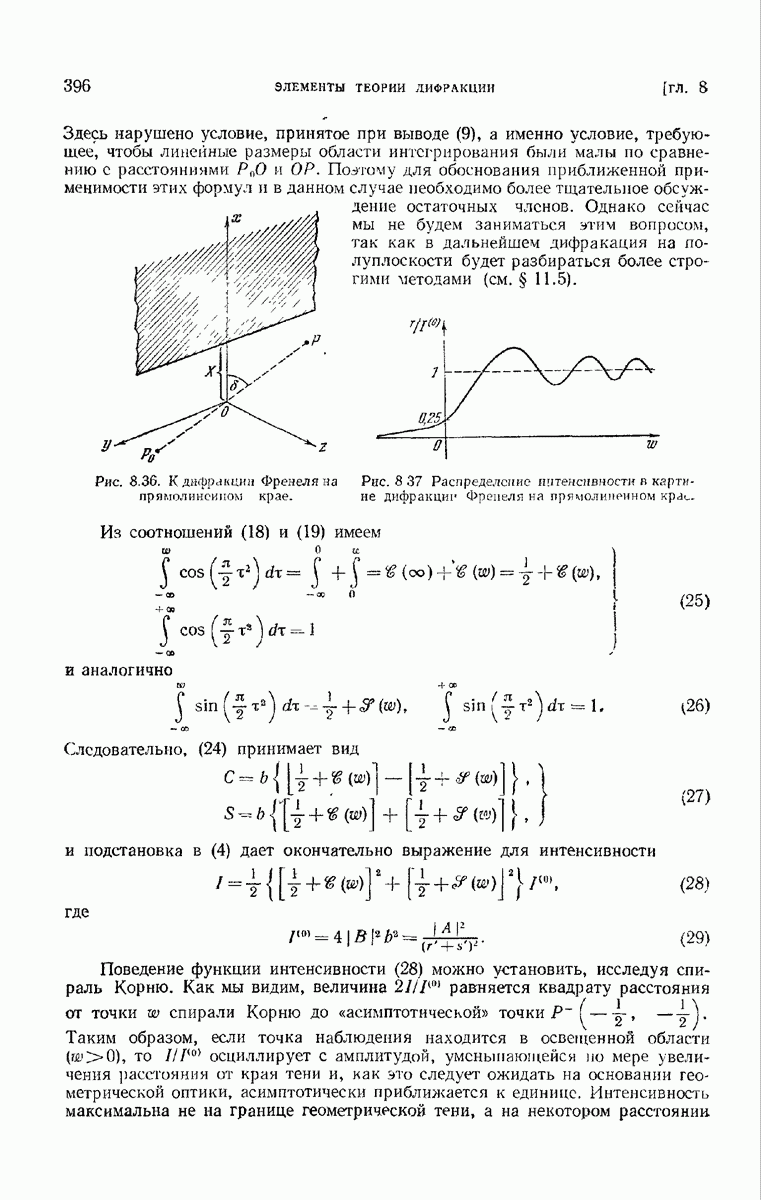
- 8.7.3. Дифракция Френеля на прямолинейном крае.
- § 8.8. Трехмерное распределение света вблизи фокуса
- 8.8.2. Распределение интенсивности.
- 8.8.3. Суммарная интенсивность.
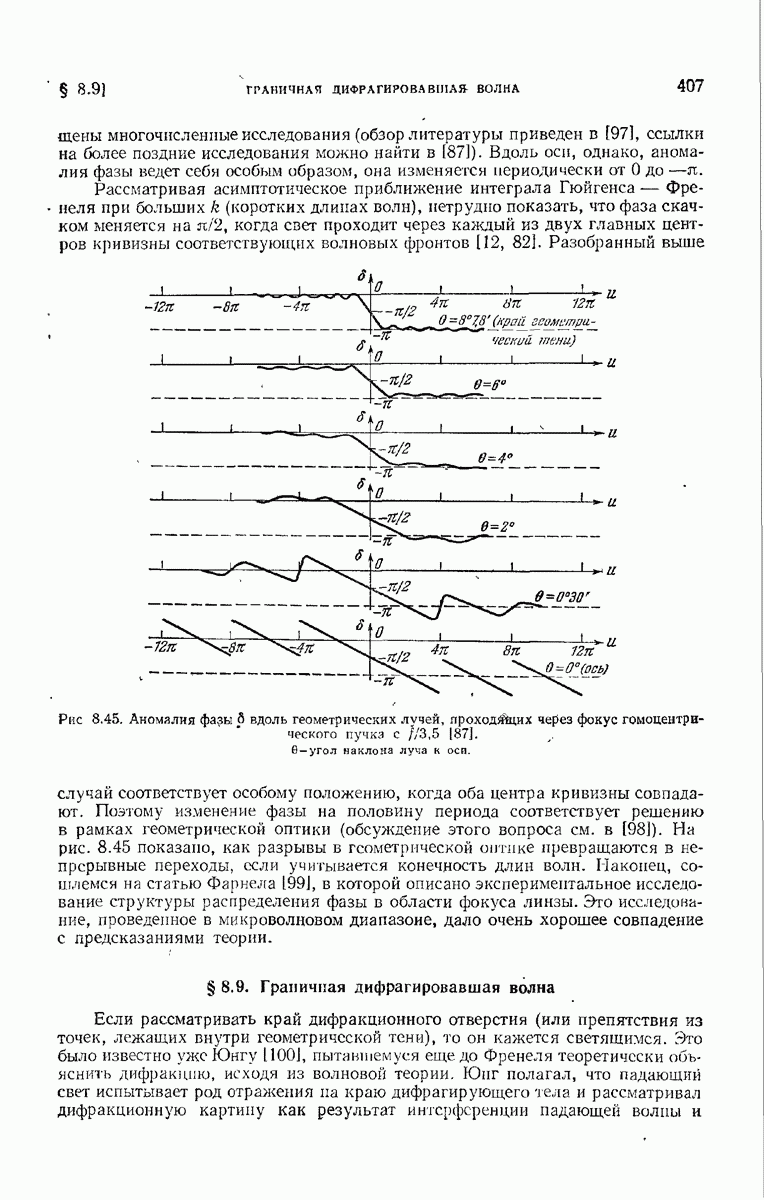
- 8.8.4. Фазовые соотношения.
- § 8.9. Граничная дифрагировавшая волна
- § 8.10. Метод Габора получения изображения восстановлением волновых фронтов
- 8.10.2. Восстановление.
- ГЛАВА 9. ДИФРАКЦИОННАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 9.1. Дифракционный интеграл при наличии аберраций
- 9.1.2. Теорема смещения. Изменение опорной сферы.
- 9.1.3. Соотношение между интенсивностью и средней деформацией волновых фронтов.
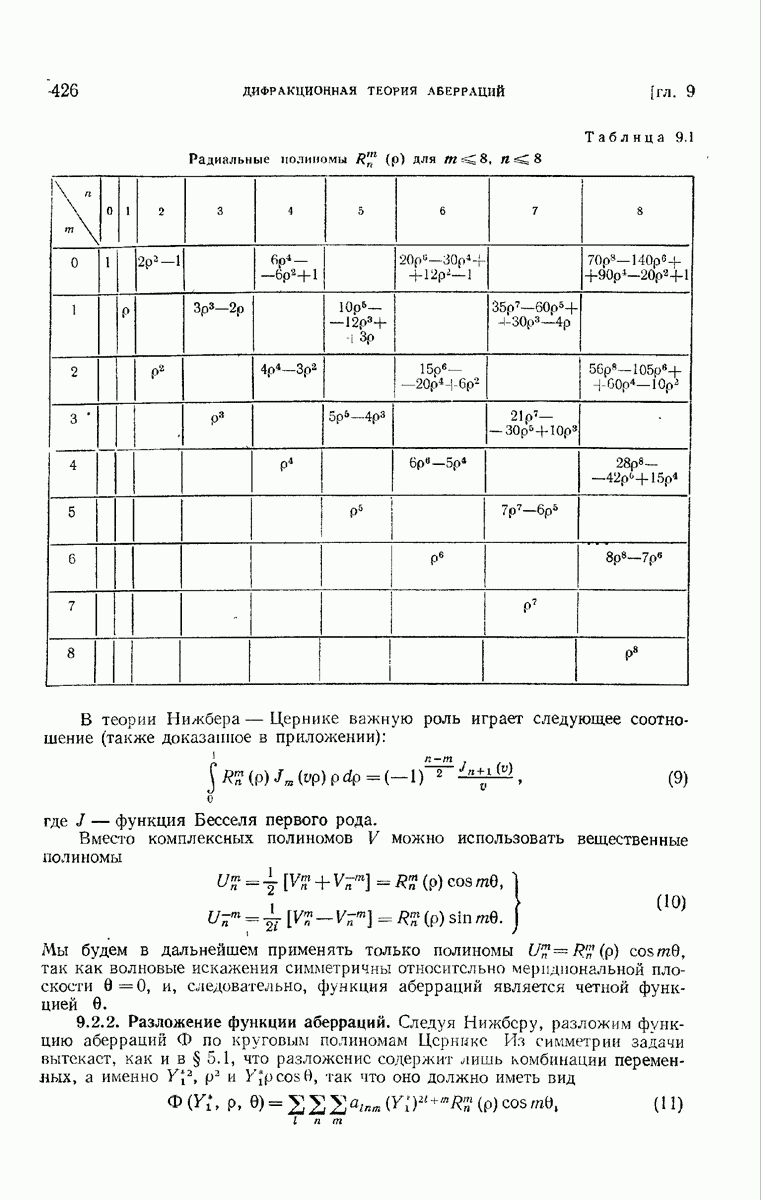
- § 9.2. Разложение функции аберрации
- 9.2.2. Разложение функции аберраций.
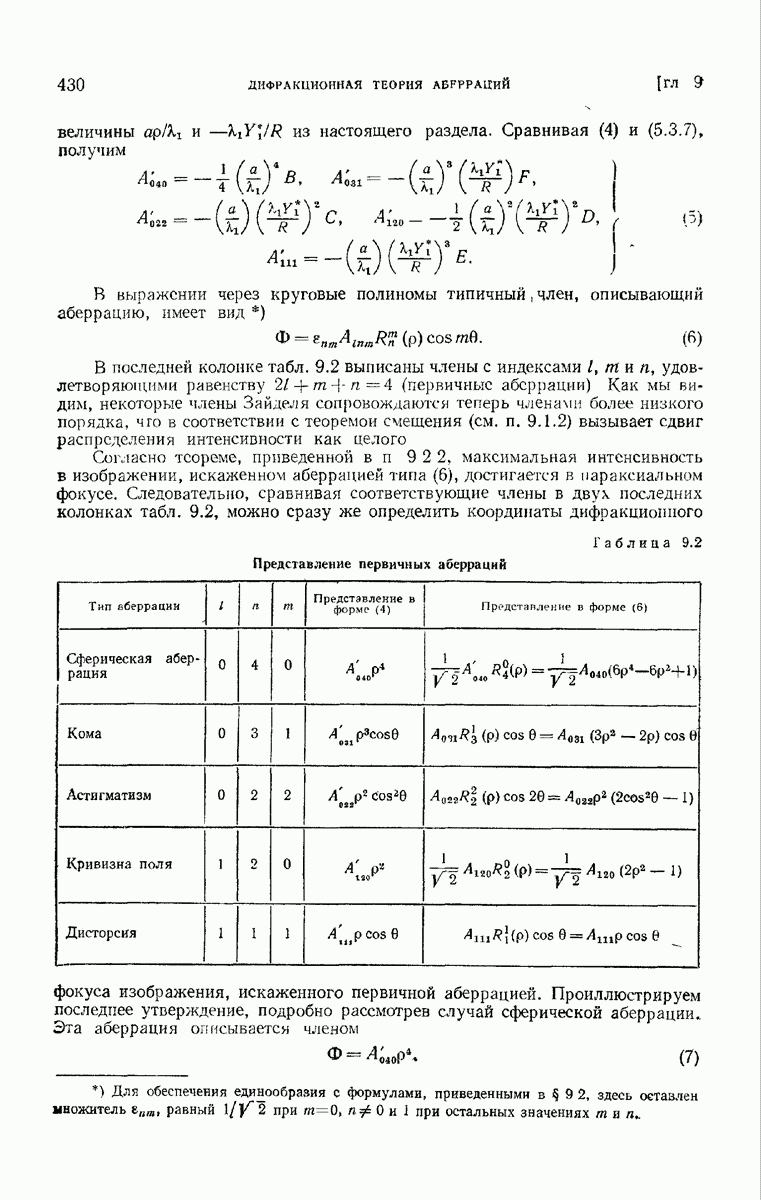
- § 9.3. Допустимые величины первичных аберраций
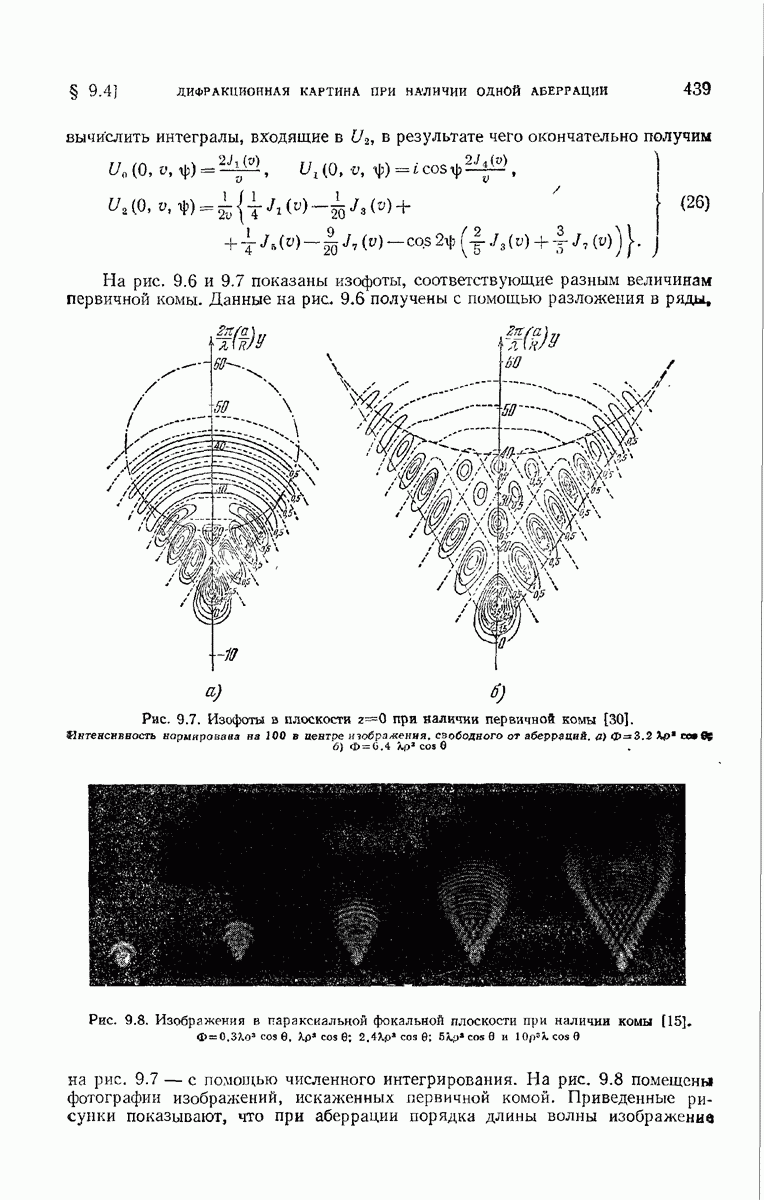
- § 9.4. Дифракционная картина, получающаяся при наличии одной аберрации
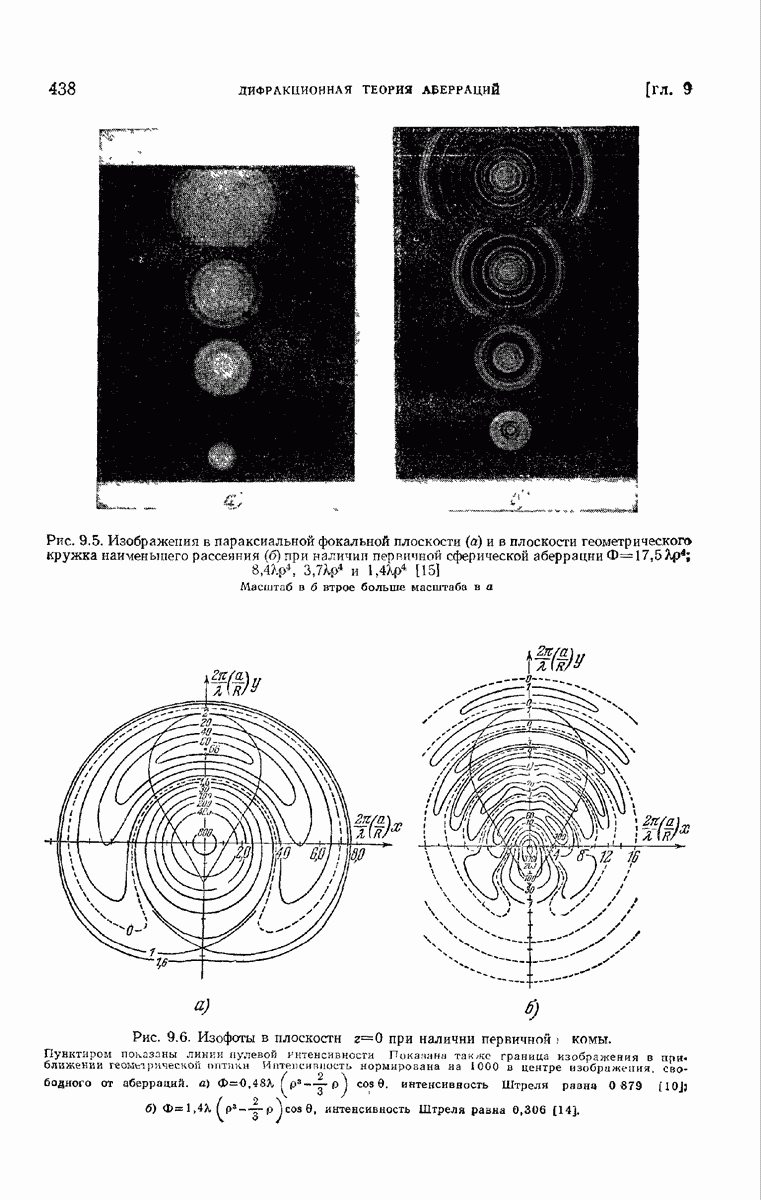
- 9.4.1. Первичная сферическая аберрация.
- 9.4.2. Первичная кома.
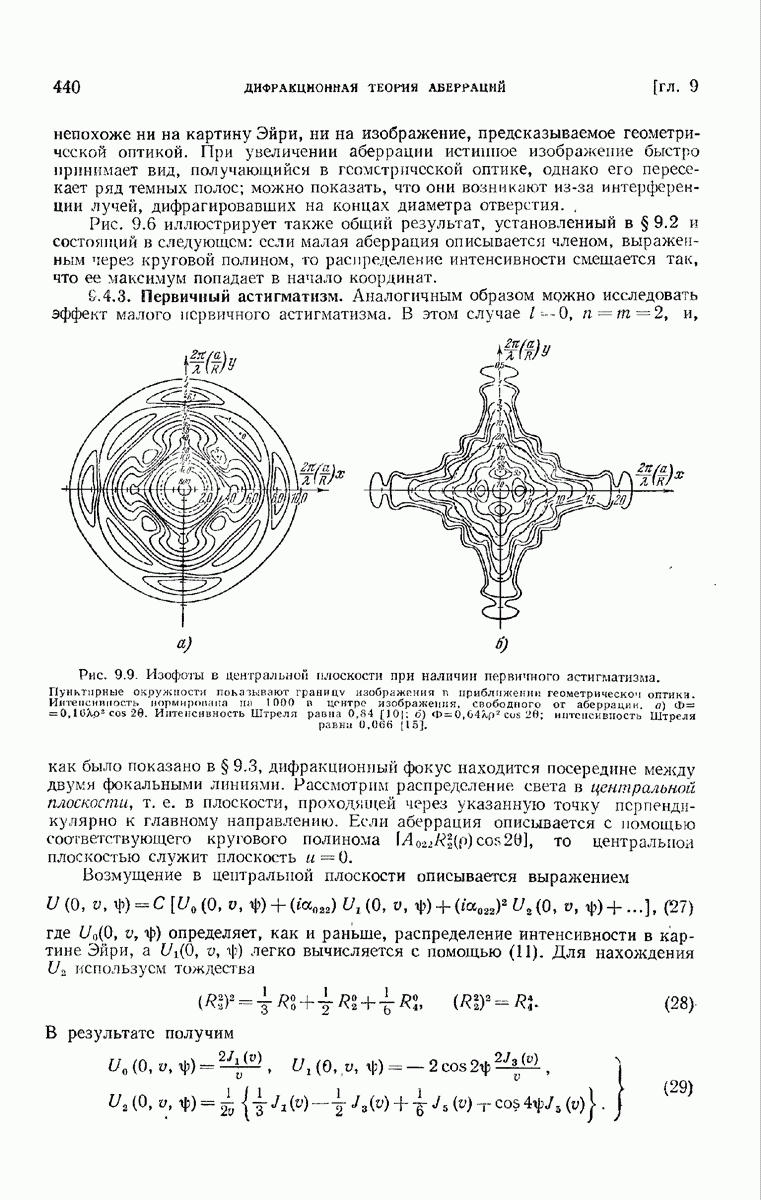
- 9.4.3. Первичный астигматизм.
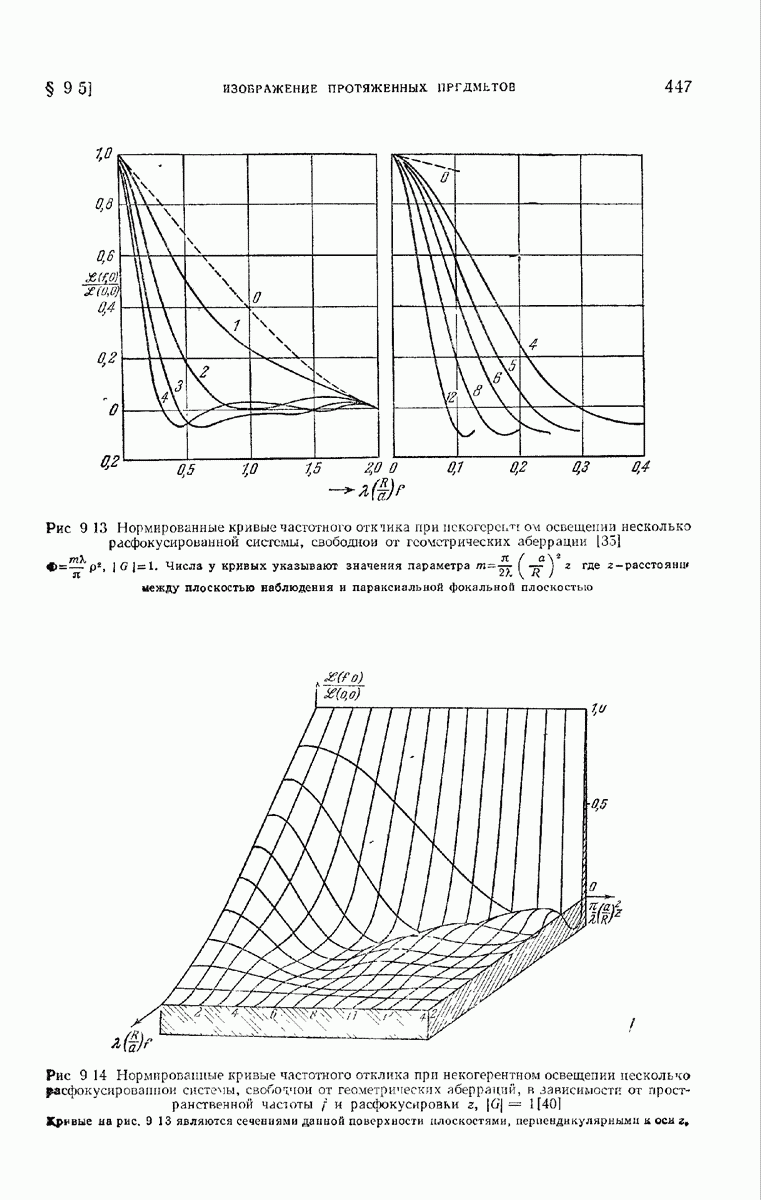
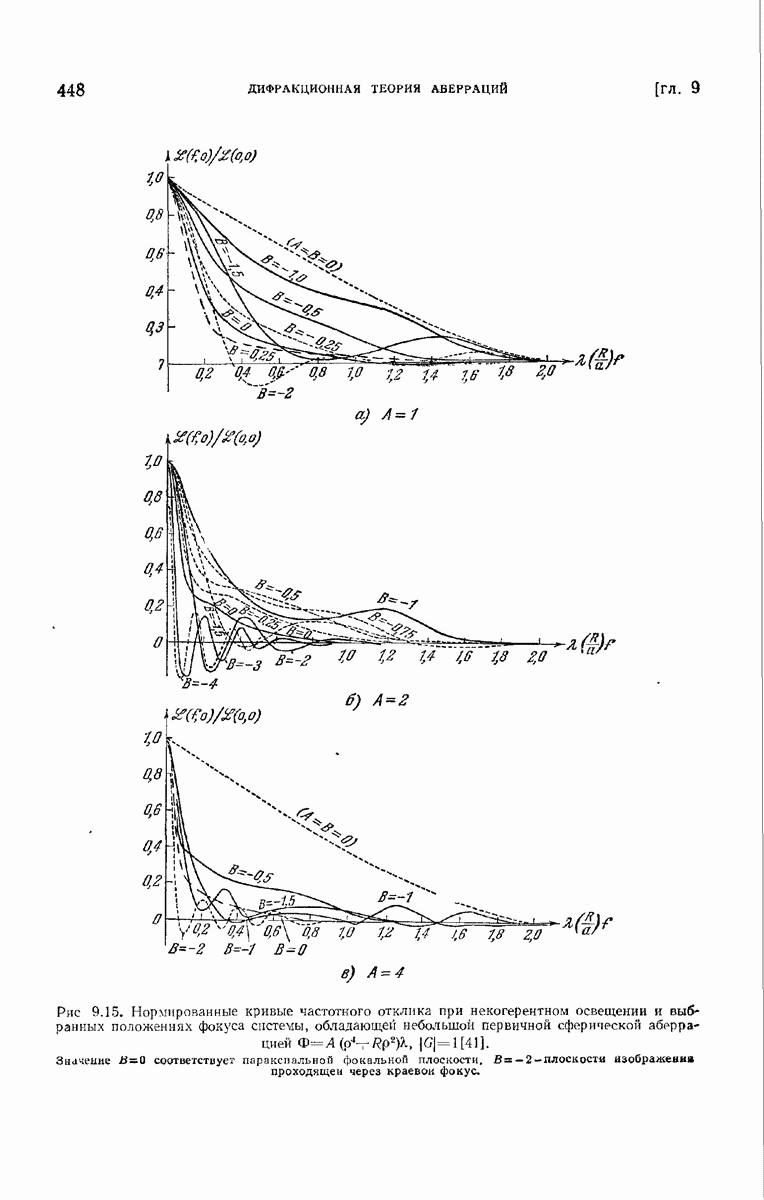
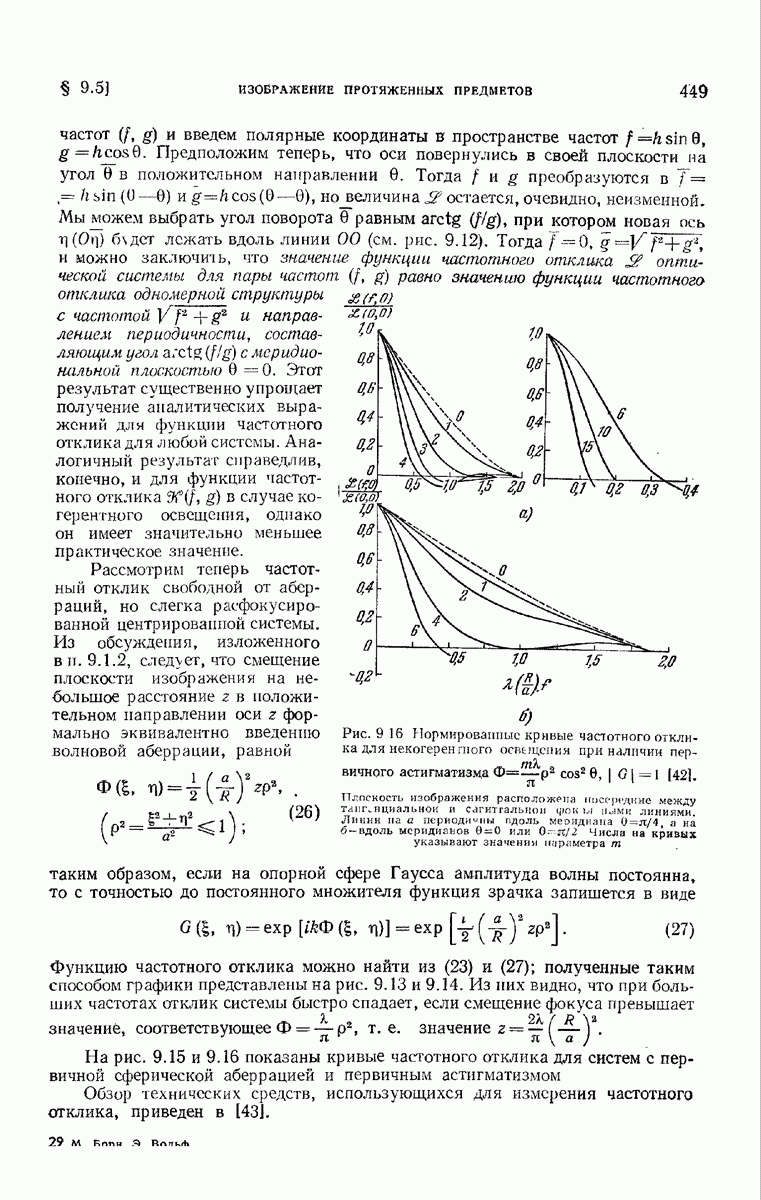
- § 9.5. Изображение протяженных предметов
- 9.5.2. Некогерентное освещение.
- ГЛАВА 10. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
- § 10.2. Комплексное представление вещественных полихроматических полей
- § 10.3. Корреляционные функции световых пучков
- 10.3.2. Спектральное представление взаимной когерентности.
- § 10.4. Интерференция и дифракция квазимонохроматического света
- 10.4.2. Расчет взаимной интенсивности и степени когерентности для света от протяженного некогерентного квазимонохроматического источника.
- 10.4.3. Пример.
- 10.4.4. Распространение взаимной интенсивности.
- § 10.5. Некоторые приложения
- 10.5.1. Степень когерентности в изображении протяженного некогерентного квазимонохроматического источника.
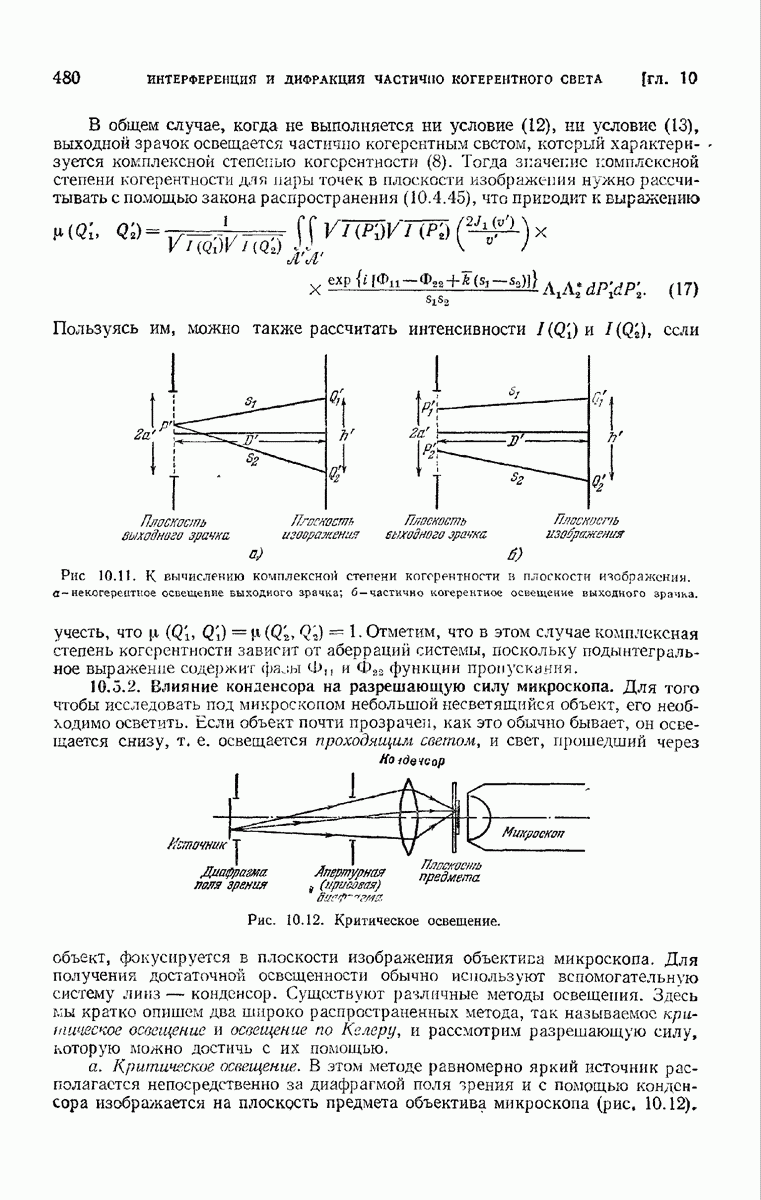
- 10.5.2. Влияние конденсора на разрешающую силу микроскопа.
- 10.5.3. Получение изображения при частично когерентном квазимонохроматическом освещении
- § 10.6. Некоторые теоремы, касающиеся взаимной когерентности
- 10.6.2. Распространение взаимной когерентности.
- § 10.7. Строгая теория частичной когерентности
- 10.7.2. Строгая формулировка закона распространения взаимной когерентности.
- 10.7.3. Время когерентности и эффективная ширина спектра.
- § 10.8. Поляризация квазимонохроматического света
- 10.8.2. Некоторые эквивалентные представления. Степень поляризации световой волны.
- 10.8.3. Параметры Стокса квазимонохроматичаской плоской волны.
- ГЛАВА 11. СТРОГАЯ ТЕОРИЯ ДИФРАКЦИИ
- § 11.2. Граничные условия и поверхностные токи
- § 11.3. Дифракция на плоском экране; электромагнитная форма принципа Бабине
- § 11.4. Двумерная дифракция на плоском экране
- 11.4.2. Угловой спектр плоских волн.
- 11.4.3. Формулировка задачи через дуальные интегральные уравнения.
- § 11.5. Двумерная дифракция плоской волны на полуплоскости
- 11.5.2. Выражение решения через интегралы Френеля.
- 11.5.3. Характер решения.
- 11.5.4. Решение для Н-поляризации.
- 11.5.5. Некоторые численные расчеты.
- 11.5.6. Сравнение с приближенной теорией и с экспериментальными результатами.
- § 11.6. Трехмерная дифракция плоской волны на полуплоскости
- § 11.7. Дифракция волн, испускаемых локализованным источником, на полуплоскости
- 11.7.2. Диполь.
- § 11.8. Другие задачи
- 11.8.1. Две параллельные полуплоскости.
- 11.8.2. Бесконечный набор параллельных полуплоскостей, расположенных ступеньками.
- 11.8.3. Полоса.
- 11.8.4. Другие задачи.
- § 11.9. Единственность решения
- ГЛАВА 12. ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКОВЫХ ВОЛНАХ
- 12.1.2. Краткое изложение теорий, основанных на уравнениях Максвелла.
- § 12.2. Рассмотрение дифракции света на ультразвуковых волнах методом интегральных уравнений
- 12.2.1. Интегральное уравнение для случая Е-поляризации.
- 12.2.2. Пробное решение интегрального уравнения.
- 12.2.3. Выражения для амплитуд световых волн в дифрагировавших и отраженных спектрах.
- 12.2.5. Выражения для интенсивностей линий в спектрах первого и второго порядков в некоторых специальных случаях
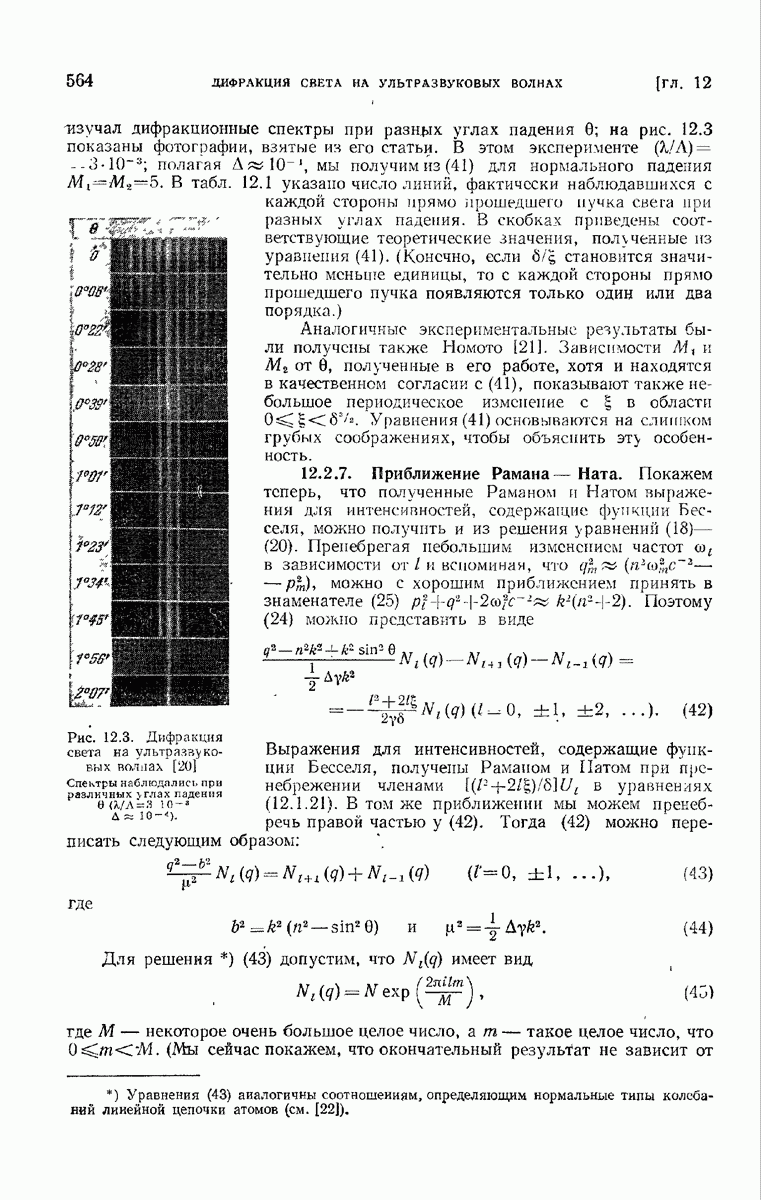
- 12.2.6. Некоторые качественные результаты.
- 12.2.7. Приближение Рамана—Ната.
- ГЛАВА 13. МЕТАЛЛООПТИКА
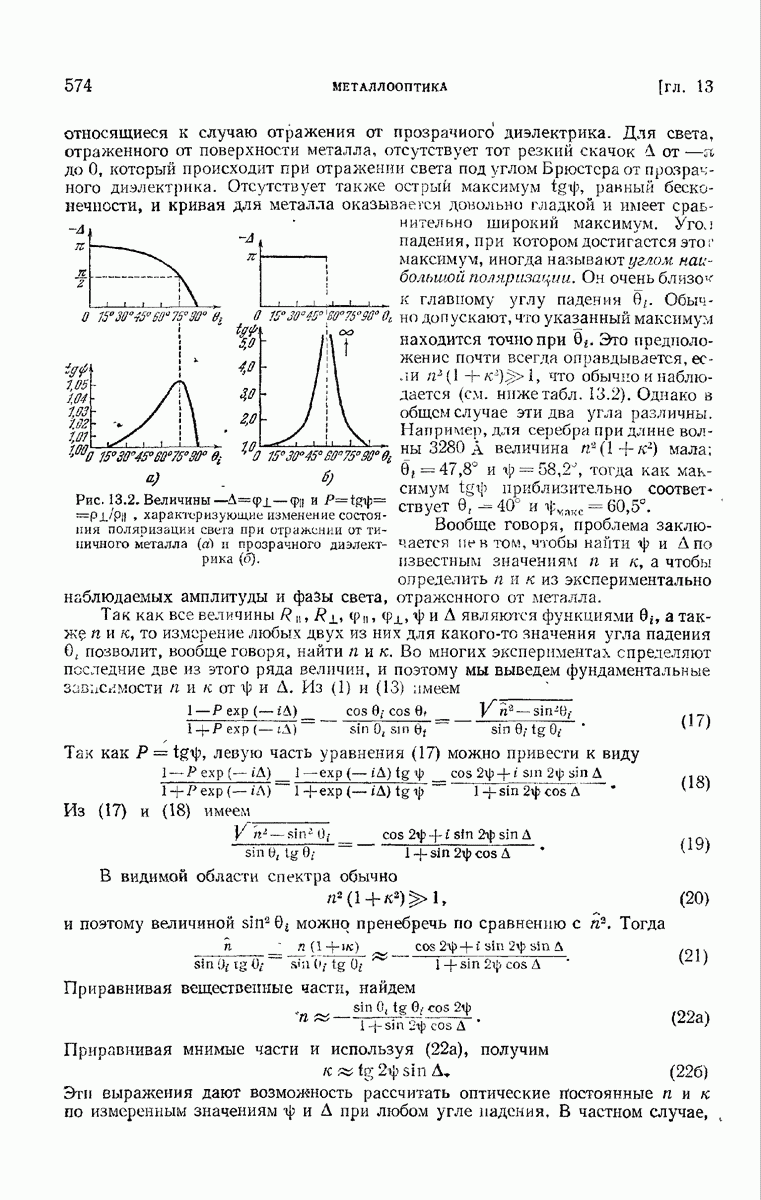
- § 13.2. Преломление и отражение на поверхности металла
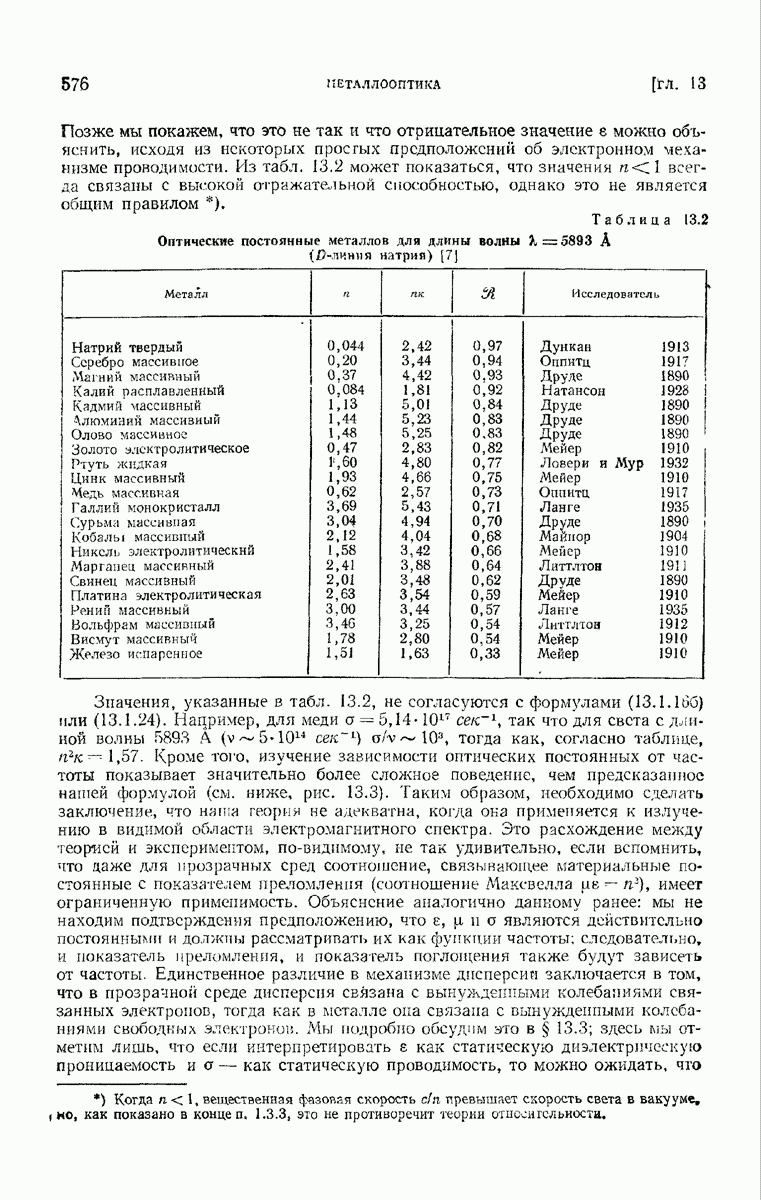
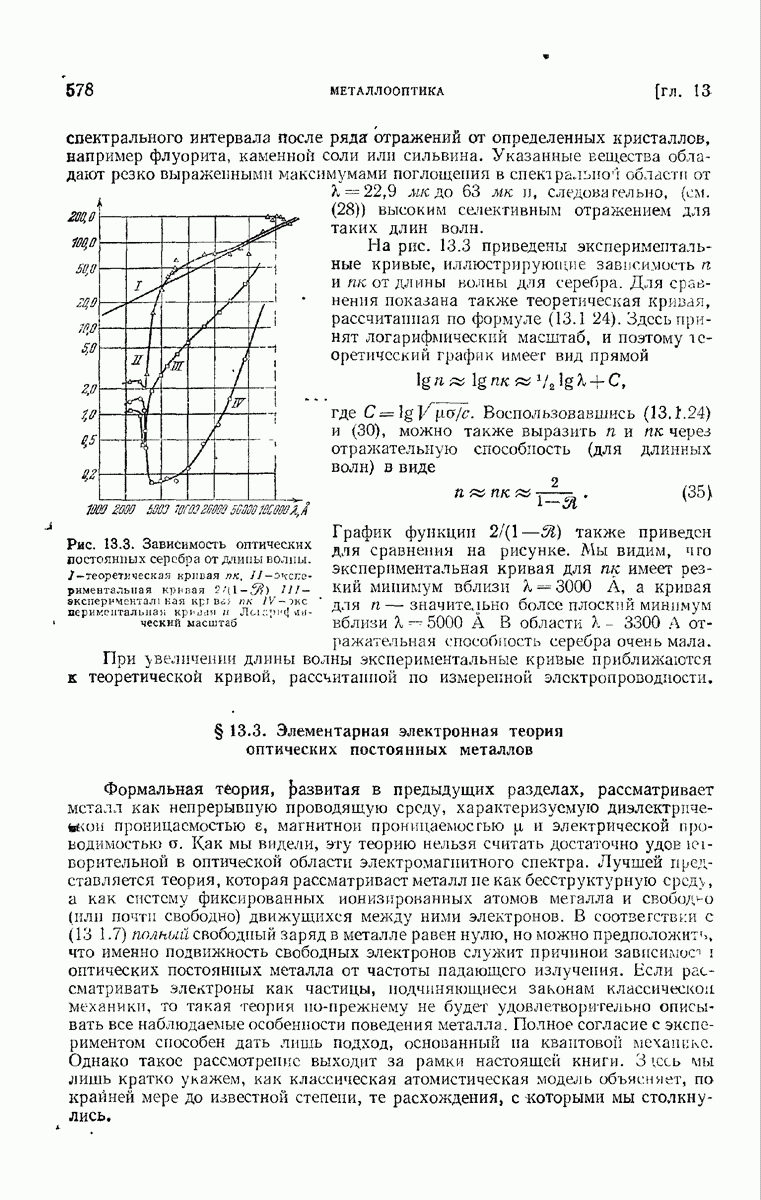
- § 13.3. Элементарная электронная теория оптических постоянных металлов
- § 13.4. Распространение волн в слоистой проводящей среде. Теория металлических пленок
- 13.4.2. Прозрачная пленка на поглощающей подложке.
- § 13.5. Дифракция на проводящей сфере. Теория Ми
- 13.5.1. Математическое решение проблемы
- 13.5.2. Некоторые следствия из формул Ми.
- 13.5.3. Полное рассеяние и затухание
- ГЛАВА 14. КРИСТАЛЛООПТИКА
- § 14.1. Тензор диэлектрической проницаемости анизотропной среды
- § 14.2. Структура монохроматической плоской волны в анизотропной среде
- 14.2.2. Формулы Френеля для распространения света в кристаллах.
- 14.2.3. Геометрические построения для определения скоростей распространения и направлений колебаний.
- § 14.3. Оптические свойства одноосных и двухосных кристаллов
- 14.3.2. Распространение света в одноосных кристаллах.
- 14.3.3. Распространение света в двухосных кристаллах.
- 14.3.4. Преломление в кристаллах
- § 14.4. Измерения в кристаллооптике
- 14.4.2. Компенсаторы.
- 14.4.3. Интерференция в кристаллических пластинках.
- 14.4.4. Интерференционные картины, получающиеся с пластинками одноосных кристаллов.
- 14.4.5. Интерференционные картины, получающиеся с пластинками двухосных кристаллов.
- 14.4.6. Определение положения оптических осей и главных показателей преломления кристаллической среды.
- § 14.5. Искусственная анизотропия
- 14.5.2. Двойное лучепреломление формы.
- § 14.6. Поглощающие кристаллы
- 14.6.2. Интерференционные картины, получающиеся с пластинками поглощающих кристаллов.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ 1. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 2. Интеграл Гильберта и уравнение Гамильтона—Якоби.
- 3. Поле экстремалей.
- 4. Нахождение всех экстремалей из решения уравнения Гамильтона — Якоби.
- 5. Канонические уравнения Гамильтона.
- 6. Частный случай, когда независимая переменная не входит явно в подынтегральное выражение.
- 7. Разрывы.
- 8. Условия Вейерштрасса и Лежандра (достаточные условия экстремума).
- 9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
- 10. Критерий Якоби для минимума.
- 11. Пример I. Оптика.
- 12. Пример II. Механика материальных точек.
- ПРИЛОЖЕНИЕ 2. ОБЫЧНАЯ ОПТИКА, ЭЛЕКТРОННАЯ ОПТИКА И ВОЛНОВАЯ МЕХАНИКА
- 2. Аналогия Гамильтона в вариационной форме.
- 3. Волновая механика свободных электронов.
- 4. Применение оптических принципов в электронной оптике.
- ПРИЛОЖЕНИЕ 3. МЕТОД АСИМПТОТИЧЕСКИХ ОЦЕНОК ИНТЕГРАЛОВ
- 2. Метод стационарной фазы.
- 3. Двойные интегралы.
- ПРИЛОЖЕНИЕ 4. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
- ПРИЛОЖЕНИЕ 5. МАТЕМАТИЧЕСКАЯ ЛЕММА, ИСПОЛЬЗУЕМАЯ ПРИ СТРОГОМ ВЫВОДЕ ЗАКОНА ЛОРЕНТЦ — ЛОРЕНЦА
- ПРИЛОЖЕНИЕ 6. РАСПРОСТРАНЕНИЕ РАЗРЫВОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПРИЛОЖЕНИЕ 7. КРУГОВЫЕ ПОЛИНОМЫ ЦЕРНИКЕ
- ПРИЛОЖЕНИЕ 8. ДОКАЗАТЕЛЬСТВО ОДНОГО НЕРАВЕНСТВА, ПРИВЕДЕННОГО В П. 10.7.3
- ПРИЛОЖЕНИЕ 9. ВЫЧИСЛЕНИЕ ДВУХ ИНТЕГРАЛОВ, ИСПОЛЬЗУЕМЫХ В П. 12.2.2