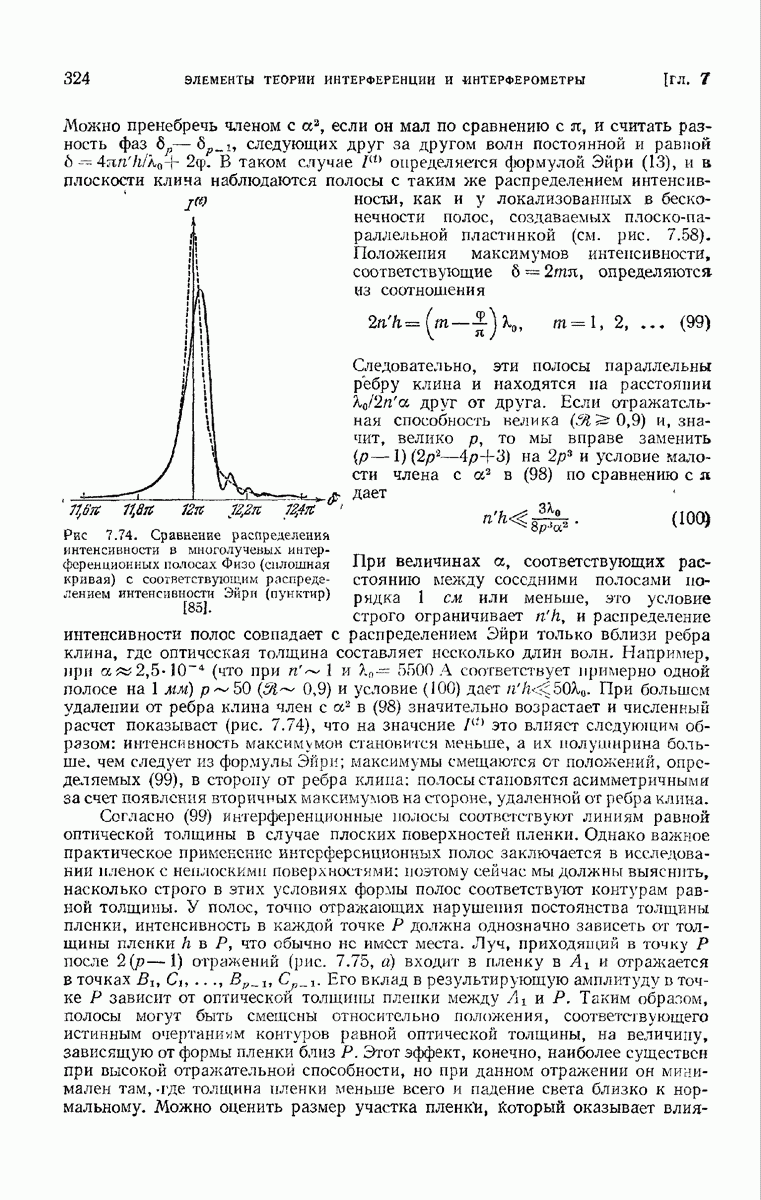
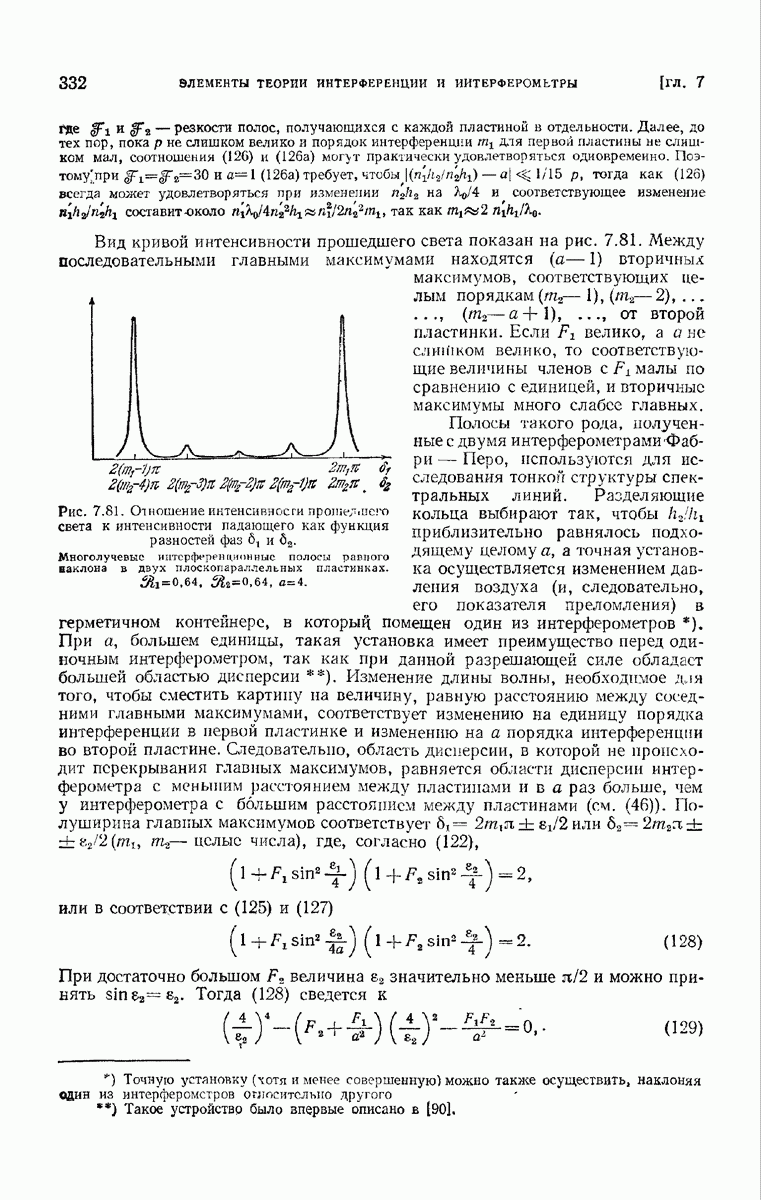
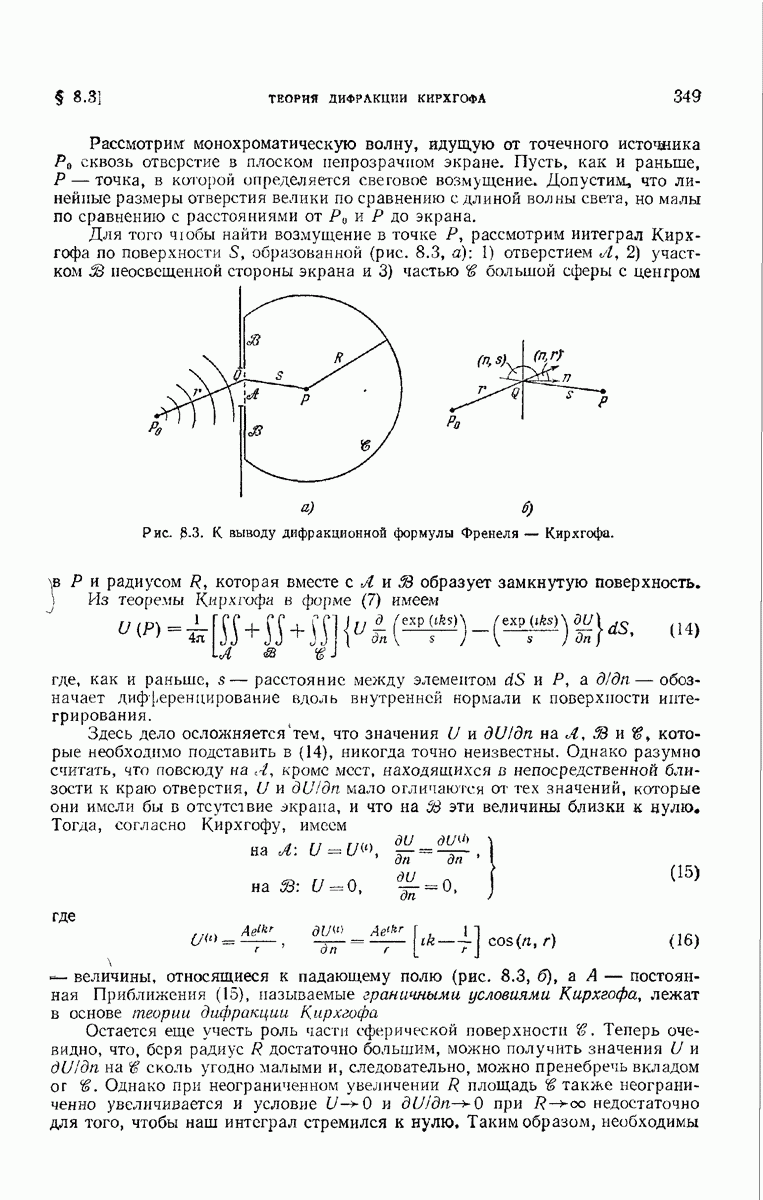
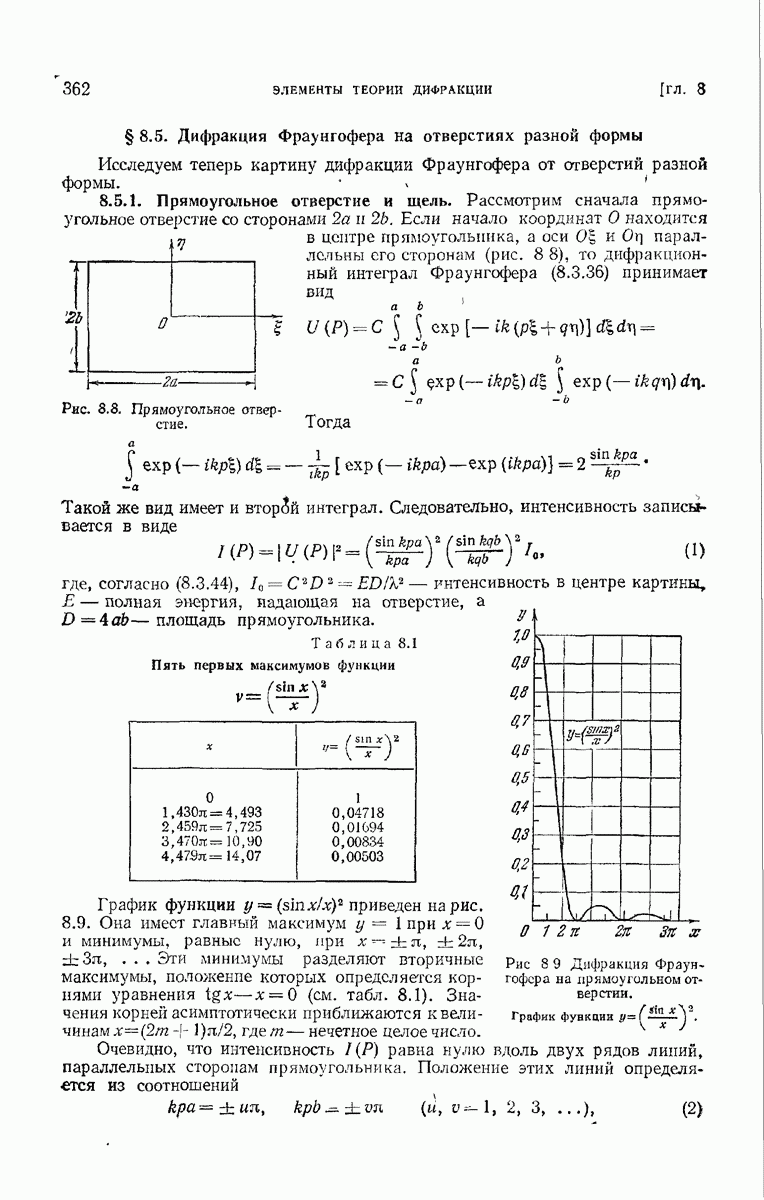
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
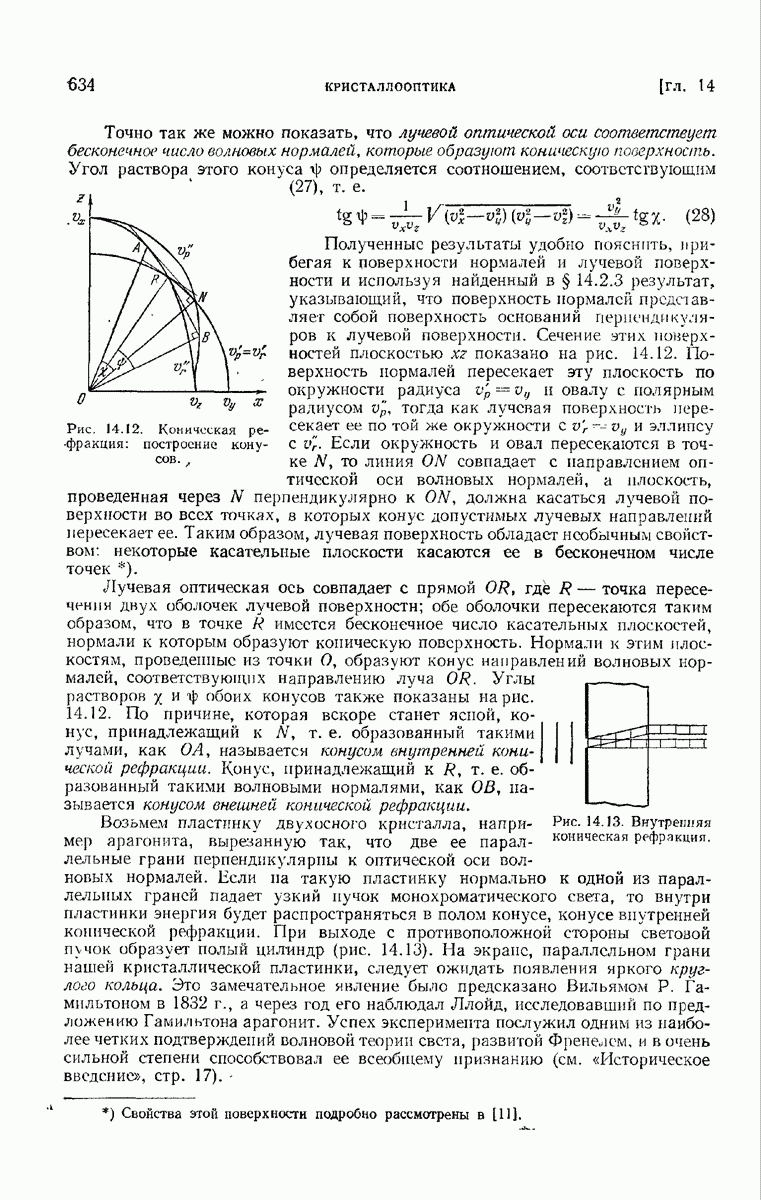
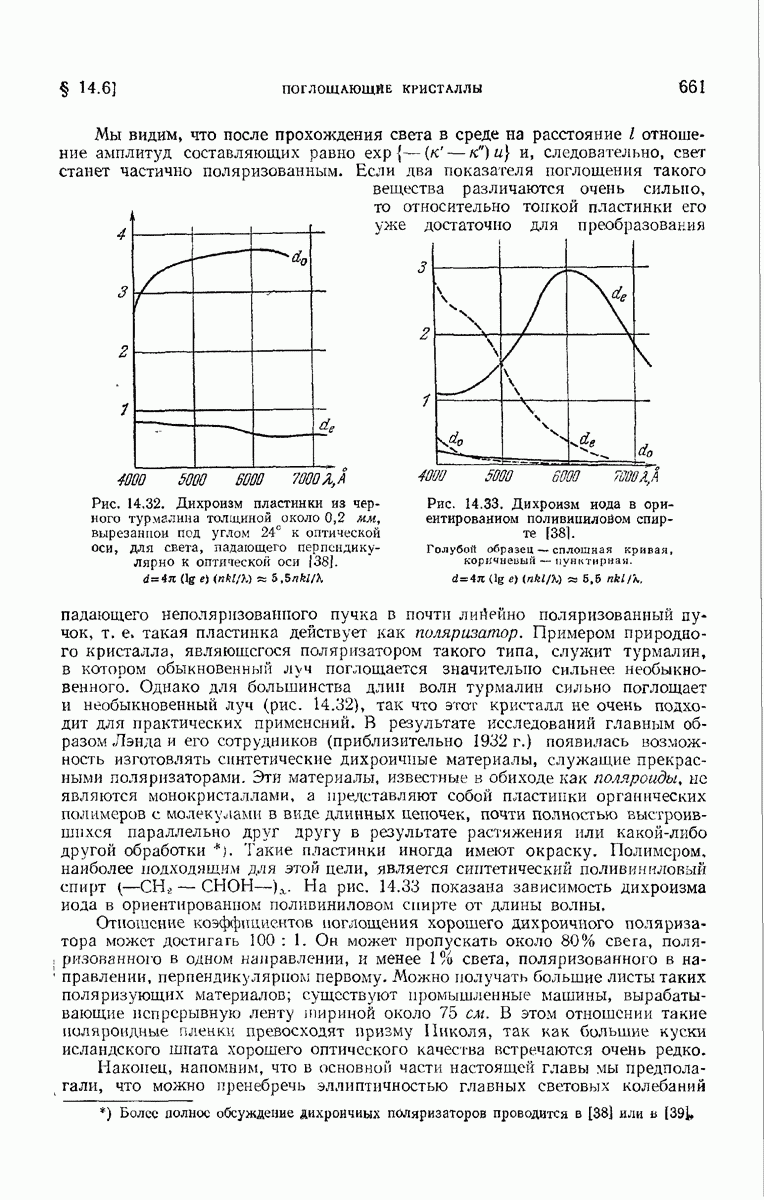
8.6.3. Образование изображения в микроскопе.
В нашем элементарном изложении теории разрешающей силы предполагалось, что свет от двух точек предмета некогерентсн. Это предположение справедливо, если оба объекта самосветящиеся, как, например, звезды, наблюдаемые в телескоп. Получающаяся интенсивность в любой точке плоскости изображения равна тогда сумме интенсивностей, обусловленных каждой точкой предмета.
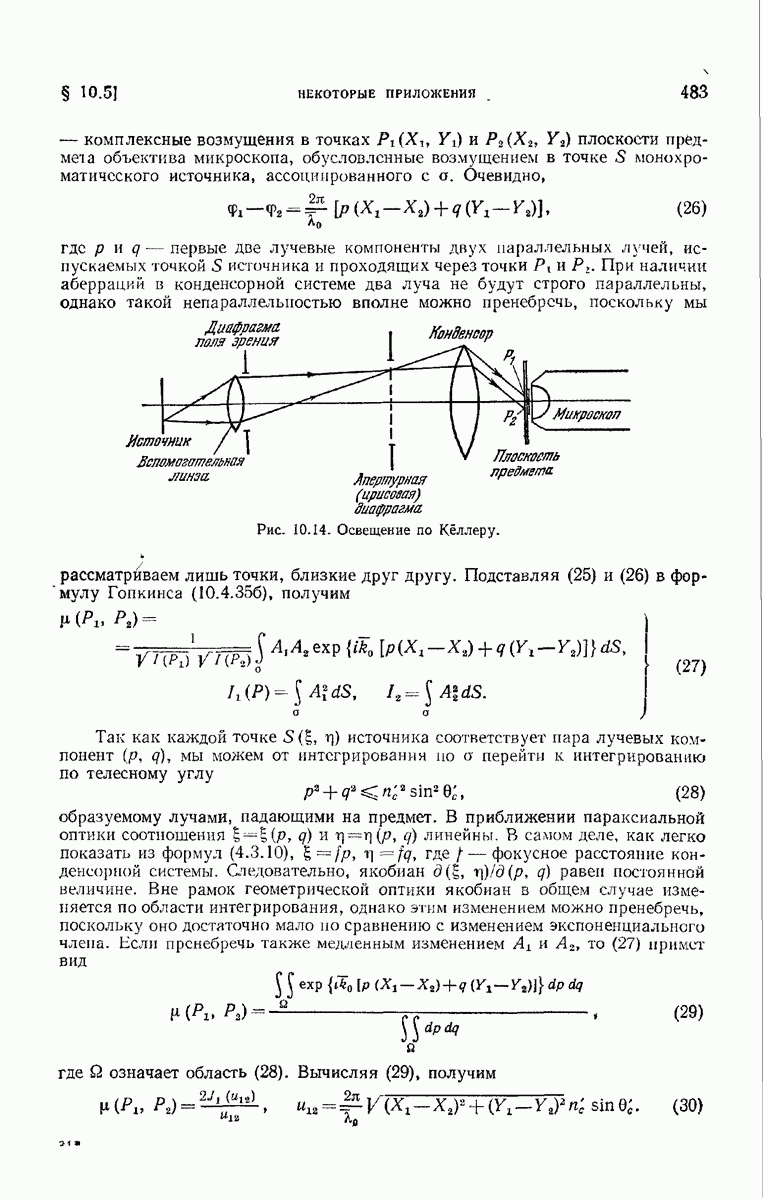
Как правило, при работе с микроскопом ситуация оказывается значительно сложнее. В большинстве случаев рассматриваемый предмет не является самосветящимся и, следовательно, должен освещаться с помощью вспомогательного устройства. Вследствие дифракции на отверстии осветительной системы (конденсора) каждый элемент источника создаст в предметной плоскости микроскопа дифракционную картину. Дифракционные картины с центрами в достаточно близких друг к другу точках частично перекрываются и, следовательно, в соседних точках плоскости предмета световые колебания в общем случае частично коррелированы. Часть этого света проходит сквозь предмет с изменением фазы или без него, тогда как оставшаяся его часть рассеивается, отражается или поглощается. Поэтому, вообще говоря, невозможно посредством одного наблюдения или, даже используя одно какое-то устройство, получить правильное увеличенное изображение всей микроструктуры объекта. По этой причине были разработаны различные методы наблюдения, пригодные для изучения определенных типов объектов или для выявления у них тех или иных характерных особенностей.
Изложим коротко теорию образования изображения в микроскопе, ограничиваясь двумя крайними случаями, а именно полностью некогерентным освещением и идеально когерентным освещением. Освещение частично когерентным светом рассматривается в п. 10.5.2.
а. Некогерентное освещения. Рассмотрим сначала самосветящийся объект, например накаленную пить электрической лампочки. Пусть Р — осевая точка объекта,  соседняя точка в плоскости предмета, находящаяся на расстоянии
соседняя точка в плоскости предмета, находящаяся на расстоянии  от Р, и пусть Р и
от Р, и пусть Р и  изображения этих точек (рис. 8.31). Далее пусть
изображения этих точек (рис. 8.31). Далее пусть  и
и  углы между крайними лучами осевых пучков и осью.
углы между крайними лучами осевых пучков и осью.

Рис. 8.31. К теории разрешающей силы микроскопа.
Если а— радиус площадки (предполагается, что она круглая), которую образует сходящийся в Р пучок лучей при пересечении с задней фокальной плоскостью  — расстояние от выходного зрачка до плоскости изображения, то, поскольку
— расстояние от выходного зрачка до плоскости изображения, то, поскольку  мало, можно написать
мало, можно написать

Далее, если  — расстояние от
— расстояние от  до Р, выраженное в «дифракционных единицах» (см. (8.3.35) и (8.5.7)), т. е. это синус угла, под которым из центра дифракционного отверстия видна прямая, соединяющая эти точки, то с хорошим приближением мыможем написать
до Р, выраженное в «дифракционных единицах» (см. (8.3.35) и (8.5.7)), т. е. это синус угла, под которым из центра дифракционного отверстия видна прямая, соединяющая эти точки, то с хорошим приближением мыможем написать

Пусть  — показатели преломления, а
— показатели преломления, а  — длины волн в пространстве предмета и в пространстве изображения, а
— длины волн в пространстве предмета и в пространстве изображения, а  — длина волны в вакууме. Тогда,
— длина волны в вакууме. Тогда,
согласно (8.5.16), первый минимум дифракционной картины от Р определяется величиной  и мы получим на пределе разрешения
и мы получим на пределе разрешения

Само собою разумеется, микроскоп рассчитывается так, чтобы он давал резкое изображение не только какой-либо осевой точки, но и соседних с ней точек, лежащих в плоскости предмета. Поэтому, согласно п. 4.5.1, должно удовлетворяться условие синусов

Так как угол  мал, можно заменить
мал, можно заменить  на
на  и, подставляя найденное отсюда значение
и, подставляя найденное отсюда значение  в (31), получим окончательно
в (31), получим окончательно

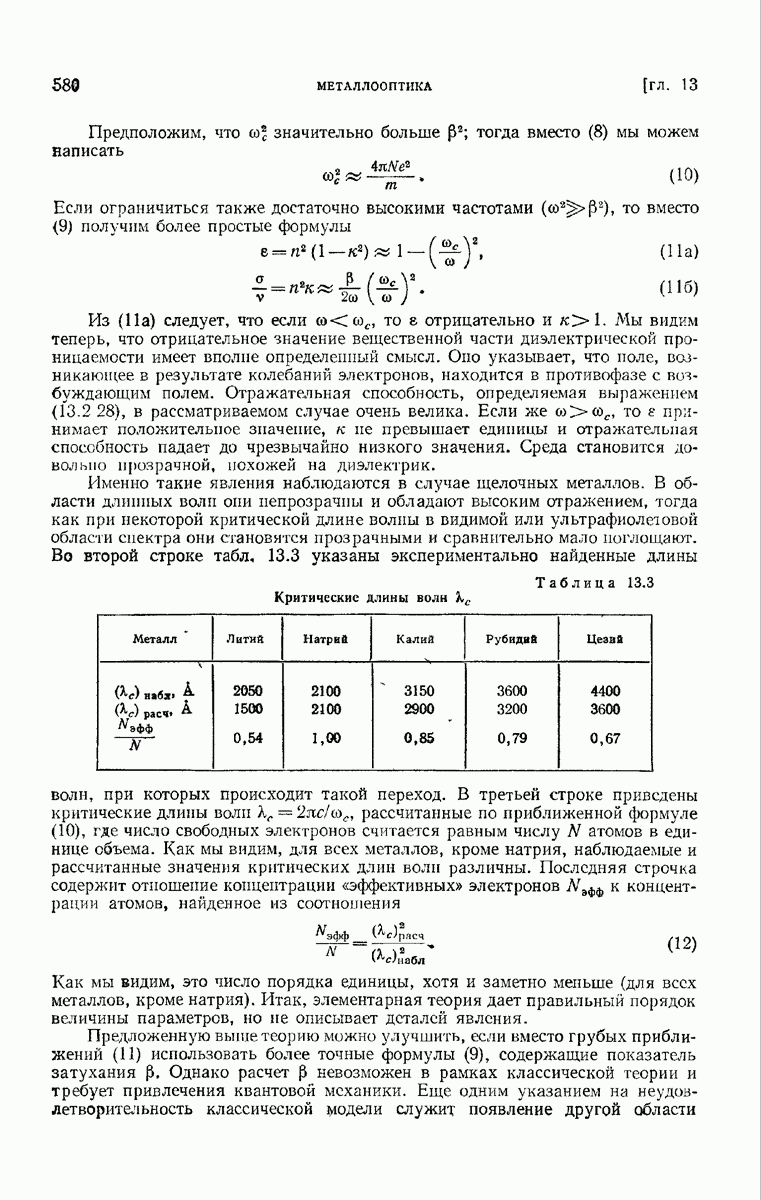
Эта формула дает расстояние между двумя точками объекта, которые при освещении некогерентным светом начинают разрешаться микроскопом с круглым отверстием объектива.
Величина  , входящая в (32), называется числовой апертурой (см. (4.8.13)). Она должна быть большой, если необходима большая разрешающая сила. Пути достижения большой числовой апертуры рассматривались в § 6.6.
, входящая в (32), называется числовой апертурой (см. (4.8.13)). Она должна быть большой, если необходима большая разрешающая сила. Пути достижения большой числовой апертуры рассматривались в § 6.6.
б. Когерентное освещение; теория Аббе. Ниже рассматривается другой крайний случай, а именно случай, когда свет, идущий от объекта, можно считать строго когерентным. Это положение приблизительно осуществляется при освещении тонкого предмета со сравнительно простой структурой свегом небольшого источника, проходящим через конденсор с малой апертурой (см. ниже, п. 10.5.2).
Первая удовлетворительная теория разрешения при когерентном освещении была сформулирована Аббе ([59, 60]); хорошее изложение теории Аббе дано в [611. Ему же принадлежат и прекрасные опыты, наглядно подтверждающие эту теорию. Согласно Аббе, предмет ведет себя как дифракционная решетка, и поэтому при определении комплексного возмущения в любых точках плоскости изображения должны учитываться не только все элементы отверстия объектива, но и все элементы самого предмета. Выражаясь матема тическим языком, можно сказать, что переход от предмета к изображению совершается с помощью двойного интегрирования: одного по предметной плоскости и другого по площади отверстия объектива. В теории Аббе в первую очередь рассматривается дифракция на предмете, а влияние апертуры учитывается во вторую очередь. Возможен также и обратный порядок, приводящий, естественно, к таким же результатам.
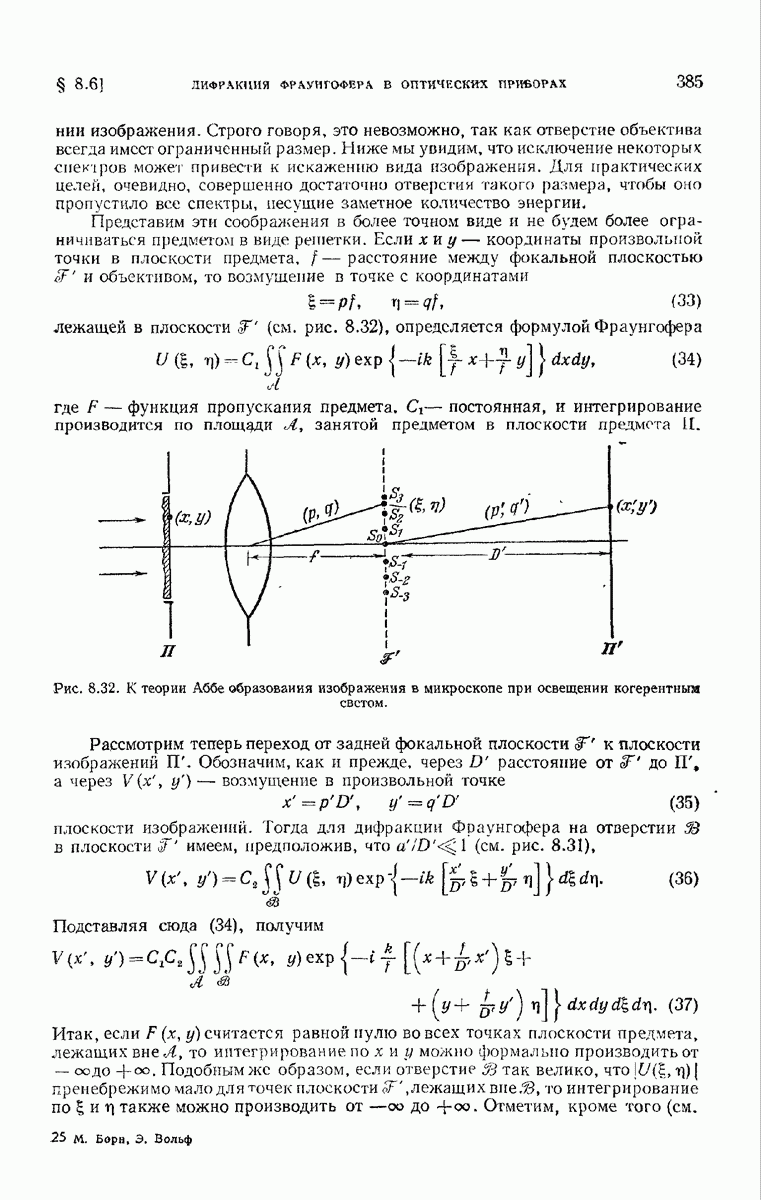
Для иллюстрации теории Аббе рассмотрим вначале образование изображения предмета в виде решетки, на который перпендикулярно его плоскости падает плоская волна (центральное освещение по Кёлеру). В результате дифракции волны на такой решетке (см. п. 8.6.1) на задней фокальной плоскости объектива возникает дифракционная картина Фраунгофера. На рис. 8.32 максимумы спектров последовательных порядков этой картины обозначены  . Каждую точку в фокальной плоскости можно рассматривать как центр вторичного когерентного возмущения, величина которого пропорциональна амплитуде в этой точке. Световые волны, идущие от таких вторичных источников, интерферируя между собой, образуют изображение предмета в плоскости изображения П объектива. Для получения точного изображения предмета необходимо, чтобы все спектры участвовали в
. Каждую точку в фокальной плоскости можно рассматривать как центр вторичного когерентного возмущения, величина которого пропорциональна амплитуде в этой точке. Световые волны, идущие от таких вторичных источников, интерферируя между собой, образуют изображение предмета в плоскости изображения П объектива. Для получения точного изображения предмета необходимо, чтобы все спектры участвовали в
формировании изображения. Строго говоря, это невозможно, так как отверстие объектива всегда имеет ограниченный размер. Ниже мы увидим, что исключение некоторых спектров может привести к искажению вида изображения. Для практических целей, очевидно, совершенно достаточно отверстия такого размера, чтобы оно пропустило все спектры, несущие заметное количество энергии.
Представим эти соображения в более точном виде и не будем более ограничиваться предметом в виде решетки. Если  — координаты произвольной точки в плоскости предмета,
— координаты произвольной точки в плоскости предмета,  — расстояние между фокальной плоскостью
— расстояние между фокальной плоскостью  и объективом, то возмущение в точке с координатами
и объективом, то возмущение в точке с координатами

лежащей в плоскости  (см. рис. 8.32), определяется формулой Фраунгофера
(см. рис. 8.32), определяется формулой Фраунгофера

где  — функция пропускания предмета.
— функция пропускания предмета.  постоянная, и интегрирование производится по площади
постоянная, и интегрирование производится по площади  , занятой предметом в плоскости предмета II.
, занятой предметом в плоскости предмета II.

Рис. 8.32. К теории Аббе образования изображения в микроскопе при освещении когерентным светом.
Рассмотрим теперь переход от задней фокальной плоскости  к плоскости изображений П. Обозначим, как и прежде, через
к плоскости изображений П. Обозначим, как и прежде, через  расстояние от
расстояние от  до
до  , а через
, а через  — возмущение в произвольной точке
— возмущение в произвольной точке

плоскости изображений. Тогда для дифракции Фраунгофера на отверстии 33 в плоскости  имеем, предположив, что
имеем, предположив, что  (см. рис. 8.31),
(см. рис. 8.31),

Подставляя сюда (34), получим

Итак, если  считается равной нулю во всех точках плоскости предмета, лежащих вне
считается равной нулю во всех точках плоскости предмета, лежащих вне  , то интегрирование по х и у можно формально производить от
, то интегрирование по х и у можно формально производить от  до
до  Подобным же образом, если отверстие
Подобным же образом, если отверстие  так велико, что
так велико, что  пренебрежимо мало для точек плоскости
пренебрежимо мало для точек плоскости  лежащих вне
лежащих вне  , то интегрирование по
, то интегрирование по  также можно производить от
также можно производить от  до
до  Отметим, кроме того (см.
Отметим, кроме того (см.
(4.3.10), где  соответствуют нашим
соответствуют нашим  и
и  что
что

где  увеличение П относительно
увеличение П относительно  , применяя интегральную теорему Фурье (см
, применяя интегральную теорему Фурье (см  например, [64]), получим
например, [64]), получим

где  — точка предмета, изображение которой находится в
— точка предмета, изображение которой находится в  , а
, а

— постоянная Следовательно, с принятой здесь точностью изображение будет полностью подобно предмету (но перевернуто), если апертура достаточно велика.
Нетрудно показать, что в изображении могут появляться совершенно искаженные детали, если исключены некоторые спектры, несущие заметную долю анергии Для этого рассмотрим предмет в виде решетки с периодом  состоящей из
состоящей из  эквидистантных конгруэнтных щелей шириной
эквидистантных конгруэнтных щелей шириной  разделенных непрозрачными промежутками. Для простоты предполагается, что диафрагма имеет прямоугольную форму, и две ее стороны параллельны щелям. Согласно (8.6.3) находим
разделенных непрозрачными промежутками. Для простоты предполагается, что диафрагма имеет прямоугольную форму, и две ее стороны параллельны щелям. Согласно (8.6.3) находим

где  заменено выражением, относящимся к дифракции на прямоугольном отверстии (см. п. 8.5.1). Если прямоугольное отверстие занимает в направлении
заменено выражением, относящимся к дифракции на прямоугольном отверстии (см. п. 8.5.1). Если прямоугольное отверстие занимает в направлении  область
область

то в соответствии с (6) и (40) возмущение в плоскости изображений равно

Положение главных максимумов интенсивности определяется корнями уравнения  , где
, где  — целое число. Между этими главными максимумами находятся слабые вторичные максимумы. При большом
— целое число. Между этими главными максимумами находятся слабые вторичные максимумы. При большом  главные максимумы очень остры и по сравнению с ними вторичные максимумы пренебрежимо малы. В таком случае с хорошим приближением можно заменить этот интеграл суммой интегралов, каждый из которых берется от средней точки
главные максимумы очень остры и по сравнению с ними вторичные максимумы пренебрежимо малы. В таком случае с хорошим приближением можно заменить этот интеграл суммой интегралов, каждый из которых берется от средней точки  интервала между соседними главными максимумами до средней точки
интервала между соседними главными максимумами до средней точки  следующего такого же интервала В каждом интервале мы можем заменить аргумент его значением в центре §
следующего такого же интервала В каждом интервале мы можем заменить аргумент его значением в центре § 

Здесь

а  интеграл
интеграл

который, не считая небольшого поправочного члена в высоких порядках, практически не зависит от т. Ряд (42) можно переписать в действительной форме» а именно

Предположим сперва, что длина а диафрагмы очень велика. Тогда суммирование формально можно распространить на весь бесконечный ряд  легко доказать, что при таких условиях изображение точно подобно предмету.
легко доказать, что при таких условиях изображение точно подобно предмету.

Рис. 8.33. Объект типа решетки.
Для этого разложим функцию пропускания  предмета типа решетки (рис. 8.33)
предмета типа решетки (рис. 8.33)

в ряд Фурье

Тогда

С точностью до постоянного множителя этот ряд не отличается от (45),
Предположим теперь, что длина а диафрагмы уменьшается. Если а так мале, что в образовании изображения участвует только спектр нулевого порядка, т. е. еэли  правильная дробь, то, согласно (45),
правильная дробь, то, согласно (45),  и плоскость изображений освещена равномерно. (Последний вывод, конечно, не совсем правилен, так как мы отбросили некоторые остаточные члены; на самом же деле наблюдается небольшое падение интенсивности в направлении края изображения.)
и плоскость изображений освещена равномерно. (Последний вывод, конечно, не совсем правилен, так как мы отбросили некоторые остаточные члены; на самом же деле наблюдается небольшое падение интенсивности в направлении края изображения.)
Если, кроме спектра нулевого порядка, сквозь диафрагмы проходят еще два спектра первого порядка  т. е. если
т. е. если  немного больше
немного больше
единицы, то из (45) находим

Теперь изображение имеет правильную периодичность  но значительно сглаженное распределение интенсивности. При увеличении диафрагмы изображение становится все более и более похожим на предмет.
но значительно сглаженное распределение интенсивности. При увеличении диафрагмы изображение становится все более и более похожим на предмет.
Совершенно искаженное изображение наблюдается в том случае, когда в его образовании спектры низших порядков совсем не участвуют. Если, например, исключены все порядки, кроме второго, то

и изображение имеет период  т. е. в таком «изображении» наблюдается вдвое больше линий, чем действительно есть у предмета.
т. е. в таком «изображении» наблюдается вдвое больше линий, чем действительно есть у предмета.
Определим теперь разрешающую силу микроскопа. Вернемся опять к рассмотрению рис. 8.31, но допустим, что свет, идущий из Р и  когерентен. В этом случае распределение интенсивности в плоскости изображений определяется в основном когерентной суперпозицией двух дифракционных картин Эйри с центром одной в Р, а другой в
когерентен. В этом случае распределение интенсивности в плоскости изображений определяется в основном когерентной суперпозицией двух дифракционных картин Эйри с центром одной в Р, а другой в  Комплексная амплитуда в точке, находящейся межцу Р и
Комплексная амплитуда в точке, находящейся межцу Р и  на расстоянии
на расстоянии  (измеренном в «дифракционных единицах») от
(измеренном в «дифракционных единицах») от  определяется соотношением
определяется соотношением

где  — расстояние между
— расстояние между  и
и  другие обозначения имеют такой же смысл, как и раньше. Следовательно, для интенсивности имеем
другие обозначения имеют такой же смысл, как и раньше. Следовательно, для интенсивности имеем

В случае некогерентного освещения  считались разрешенными, если главный максимум интенсивности одной картины совпадал с первым минимумом другой. Интенсивность в средней точке
считались разрешенными, если главный максимум интенсивности одной картины совпадал с первым минимумом другой. Интенсивность в средней точке  между двумя максимумами равняется тогда
между двумя максимумами равняется тогда  от интенсивности каждого максимума, т. с. кривая суммарной интенсивности спадаст на участке между двумя главными максимумами примерно на 26,5%. (Это соответствует 19% для отверстия в виде щели, см. рис, 7.62.) Если мы снова примем, что такое уменьшение интенсивности по существу определяет предел разрешения, то критическое расстояние
от интенсивности каждого максимума, т. с. кривая суммарной интенсивности спадаст на участке между двумя главными максимумами примерно на 26,5%. (Это соответствует 19% для отверстия в виде щели, см. рис, 7.62.) Если мы снова примем, что такое уменьшение интенсивности по существу определяет предел разрешения, то критическое расстояние  находится из соотношения
находится из соотношения

Первый корень этого трансцендентного уравнения равен  , следовательно, для критического расстояния, измеренного в обычных единицах, имеем
, следовательно, для критического расстояния, измеренного в обычных единицах, имеем

Для того чтобы перейти от  к соответствующему расстоянию
к соответствующему расстоянию  между точками предмета, используем условие синусов (допуская, что
между точками предмета, используем условие синусов (допуская, что  ) и получим окончательно, что предел разрешения при когерентном освещении равен
) и получим окончательно, что предел разрешения при когерентном освещении равен

Не считая несколько большего численного множителя (который всегда до известной степени произволен, так как он зависит от формы предмета и отверстия и от чувствительности приемника), мы получим то же выражение, что и в случае некогерентного освещения (см. уравнение (32)). Таким образом, разрешающая сила для света определенной длины волны по существу зависит только от числовой апертуры объектива.
в. Когерентное освещение; фазоконтрастный метод наблюдения Цернике. Мы определили фазовый объект как объект, который изменяет фазу, а не амплитуду падающего света. Объектом такого типа служит неоднородный по оптической толщине и вместе с тем совершенно не поглощающий света предмет. Такие объекты часто встречаются в биологии, кристаллографии и других областях науки. Из предыдущего очевидно, что обычные методы наблюдения дают мало информации о таких фазовых объектах. Комплексная амплитудная функция, определяющая возмущение в плоскости изображения, в этом случае подобна функции пропускания объекта. Поскольку глаз (или другой регистрирующий ирибор) способен отмечать только изменение интенсивности, можно делать выводы об изменении амплитуды, но не об изменениях фазы, вызванных объектом.
Для получения данных о фазовых объектах следует применять специальные методы наблюдения, например так называемый метод темного поля, где с помощью диафрагмы устраняется центральный порядок, пли метод свилей, в котором исключаются все спектры по одну сторону от цешрального порядка. Однако наиболее эффективным является метод, предложенный Цернике  впервые описанный им в 1935 г. и известный под названием метода фазового контраста. Его преимущество заключается в том, что распределение интенсивности в изображении прямо пропорционально изменению фазы, вносимому соответствующими точками объекта.
впервые описанный им в 1935 г. и известный под названием метода фазового контраста. Его преимущество заключается в том, что распределение интенсивности в изображении прямо пропорционально изменению фазы, вносимому соответствующими точками объекта.
Чтобы объяснить принцип метода фазового контраста, рассмотрим сначала прозрачный объект в виде одномерной фазовой решетки. Функция пропускания такого объекта по определению (см. стр. 369) имеет вид

где  — вещественная периодическая функция с периодом (например,
— вещественная периодическая функция с периодом (например,  равным периоду решетки. Предположим, что величина
равным периоду решетки. Предположим, что величина  мала по сравнению с единицей, и поэтому можно написать
мала по сравнению с единицей, и поэтому можно написать

Разлагая  в ряд Фурье
в ряд Фурье

и учитывая, что  имеет вид (56), а
имеет вид (56), а  - вещественная, но малая по сравнению с единицей величина, получим
- вещественная, но малая по сравнению с единицей величина, получим

Интенсивность спектров порядка  пропорциональна
пропорциональна 
В методе фазового контраста в заднюю фокальную плоскость  объектива помещают тонкую пластинку из прозрачного вещества, называемую фазовой пластинкой. Такая пластинка вызывает отставание или опережение фазы в нулевом порядке
объектива помещают тонкую пластинку из прозрачного вещества, называемую фазовой пластинкой. Такая пластинка вызывает отставание или опережение фазы в нулевом порядке  на рис. 8.32) относительно фазы в дифракционных спектрах
на рис. 8.32) относительно фазы в дифракционных спектрах
 на четверть периода. Это значит, что распределение комплексной амплитуды в фокальной плоскости будет отличаться от распределения, характеризующегося коэффициентами
на четверть периода. Это значит, что распределение комплексной амплитуды в фокальной плоскости будет отличаться от распределения, характеризующегося коэффициентами  и станет распределением, характеризующимся коэффициентами
и станет распределением, характеризующимся коэффициентами  где
где

Положительный или отрицательный знак берется в зависимости от того, получается ли отставание или опережение фазы в нулевом порядке. Теперь результирующее распределение света в плоскости изображений представляет не фазовую решетку (57), а фиктивную амплитудную решетку

Следовательно, пренебрегая  по сравнению с единицей, находим, что интенсивность в плоскости изображения пропорциональна
по сравнению с единицей, находим, что интенсивность в плоскости изображения пропорциональна

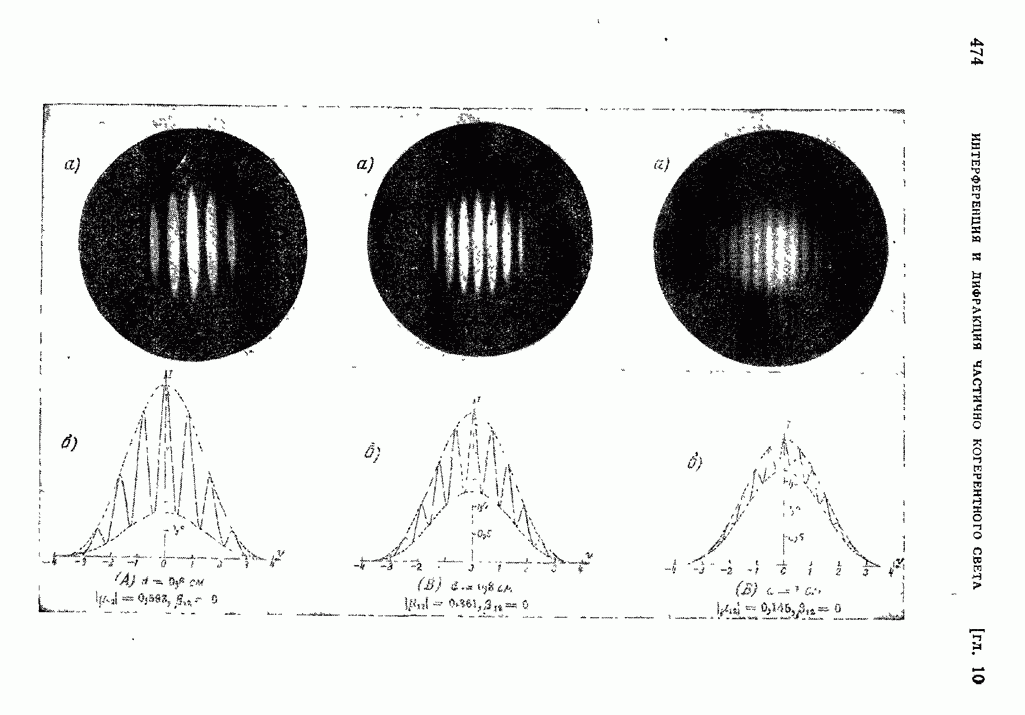
где, как и раньше,  увеличение. Отсюда следует, что в глучае наблюдения методом фазового контраста, изменение фазы, вносимое объектом, превращается в изменение интенсивности, а последняя в любой точке плоскости изображений прямо пропорциональна (с точностью до аддитивной постоянной) изменению фазы, вызванному соответствующим элементом объекта. При отставании фазы в нулевом порядке относительно фазы дифракционных спектров (верхний знак в (61)) области объекта с большей оптической толщиной кажутся ярче мест со средней освещенностью. Это светлый фазовый контраст. Если фаза в нулевом порядке опережает фазы дифракционных спектров, области больших оптических толщин кажутся темнее общего фона. Это так называемый темный фазовый контраст (рис. 1 и рис. 11 на вклейке).
увеличение. Отсюда следует, что в глучае наблюдения методом фазового контраста, изменение фазы, вносимое объектом, превращается в изменение интенсивности, а последняя в любой точке плоскости изображений прямо пропорциональна (с точностью до аддитивной постоянной) изменению фазы, вызванному соответствующим элементом объекта. При отставании фазы в нулевом порядке относительно фазы дифракционных спектров (верхний знак в (61)) области объекта с большей оптической толщиной кажутся ярче мест со средней освещенностью. Это светлый фазовый контраст. Если фаза в нулевом порядке опережает фазы дифракционных спектров, области больших оптических толщин кажутся темнее общего фона. Это так называемый темный фазовый контраст (рис. 1 и рис. 11 на вклейке).
Часто для получения хорошего разрешения отверстие осветительной системы делают кольцевым, а не круглым (см. п. 8.6.2). В таком случае роль спектра нулевого порядка на рис. 8.32 играет кольцевая область  сквозь которую проходит прямой (не дифрагированный) свет, причем фаза именно этого света должна отставать или опережать на четверть периода фазы дифракционных спектров.
сквозь которую проходит прямой (не дифрагированный) свет, причем фаза именно этого света должна отставать или опережать на четверть периода фазы дифракционных спектров.
Фазовую пластинку можно изготовить, нанося испарением тонкий слой соответствующего диэлектрика на стеклянную подложку. Если свет, прошедший сквозь пластинку, должен отставать по фазе на четверть периода, то толщина нанесенного на пластинку слоя  должна составлять
должна составлять  где
где  показатель преломления диэлектрика. Отставание по фазе на четверть периода нулевого порядка, конечно, эквивалентно опережению по фазе дифракционных спектров на три четверти периода и наоборот. Чувствительность метода фазового контраста можно увеличить, если применять слабо поглощающие покрытия вместо диэлектрических. К этому вопросу мы еще вернемся позднее.
показатель преломления диэлектрика. Отставание по фазе на четверть периода нулевого порядка, конечно, эквивалентно опережению по фазе дифракционных спектров на три четверти периода и наоборот. Чувствительность метода фазового контраста можно увеличить, если применять слабо поглощающие покрытия вместо диэлектрических. К этому вопросу мы еще вернемся позднее.
Остается показать, что применение метода фазового контраста не ограничивается только фазовыми объектами периодической структуры. Для этого разделим интеграл (34) на две части, а именно

где

 представляет распределение света в плоскости
представляет распределение света в плоскости  в отсутствие объекта, а
в отсутствие объекта, а  влияние дифракции. «Прямой свет»
влияние дифракции. «Прямой свет»  (соответствующий нулевому порядку
(соответствующий нулевому порядку  на рис. 8.32) концентрируется только в небольшой области
на рис. 8.32) концентрируется только в небольшой области  плоскости Т вблизи осевой точки
плоскости Т вблизи осевой точки  Вместе с тем в общем случае только очень небольшая часть дифрагировавшего света попадает в эту область; большая его часть окажется к других местах этой плоскости
Вместе с тем в общем случае только очень небольшая часть дифрагировавшего света попадает в эту область; большая его часть окажется к других местах этой плоскости 
Предположим, что область  , через которую проходит прямой свет, закрыта фазовой пластинкой. Действие последней описывается функцией пропускания
, через которую проходит прямой свет, закрыта фазовой пластинкой. Действие последней описывается функцией пропускания

Для пластинки, вызывающей только изменение фазы проходящего света,  для пластинки, еще и поглощающей свет,
для пластинки, еще и поглощающей свет,  Для света, прошедшего сквозь отверстие объектива, можно написать
Для света, прошедшего сквозь отверстие объектива, можно написать

поэтому, согласно (36), распределение комплексной амплитуды в изображении имеет вид

где

Так как отверстие  значительно превышает размеры участка
значительно превышает размеры участка  вне
вне  практически равно нулю, то, не вводя заметной ошибки, можно распространить область интегрирования в выражении для
практически равно нулю, то, не вводя заметной ошибки, можно распространить область интегрирования в выражении для  на всю плоскость
на всю плоскость  Кроме того, если допустить, что
Кроме того, если допустить, что  велико и пропускает все дифрагировавшие лучи, несущие заметную энергию, то у интеграла У, также можно написать бесконечные пределы. Наконец, если, как и раньше, функция пропускания
велико и пропускает все дифрагировавшие лучи, несущие заметную энергию, то у интеграла У, также можно написать бесконечные пределы. Наконец, если, как и раньше, функция пропускания  определена как нуль в точках плоскости предмета, лежащих вне области, занятой объектом, то интегралы (64) также можно взять с бесконечными пределами. Тогда, подставляя (64) в (68) и используя интегральную теорему Фурье и соотношение (38), получим
определена как нуль в точках плоскости предмета, лежащих вне области, занятой объектом, то интегралы (64) также можно взять с бесконечными пределами. Тогда, подставляя (64) в (68) и используя интегральную теорему Фурье и соотношение (38), получим

Из (67) и (69) следует, что интенсивность в плоскости изображений определяется выражением

При наличии фазового объекта имеем

и (70) сводится к

Так как мы предположили, что  мало, последнее соотношение можно переписать в виде
мало, последнее соотношение можно переписать в виде 

и если разность фаз, вносимая пластинкой, соответствует отставанию или опережению на четверть периода, то  и (73) сводится к
и (73) сводится к

Если пластинка не поглощает света  , мы снова получим выражение (62). В этом случае изменения интенсивности прямо пропорциональны изменению фаз, вносимому объектом. Для пластинки, поглощающей долю всего прямого света, равную
, мы снова получим выражение (62). В этом случае изменения интенсивности прямо пропорциональны изменению фаз, вносимому объектом. Для пластинки, поглощающей долю всего прямого света, равную  отношение второго члена к первому в (73) равно
отношение второго члена к первому в (73) равно  что указывает на увеличение контрастности изображения. Например, ослабление прямого света в девять раз повышает чувствительность этого метода в три раза.
что указывает на увеличение контрастности изображения. Например, ослабление прямого света в девять раз повышает чувствительность этого метода в три раза.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 1.1. Электромагнитное поле
- 1.1.2. Материальные уравнения.
- 1.1.3. Граничные условия на поверхностях раздела.
- 1.1.4. Закон сохранения энергии для электромагнитного поля.
- § 1.2. Волновое уравнение и скорость света
- § 1.3. Скалярные волны
- 1.3.2. Сферические волны.
- 1.3.3. Гармонические волны. Фазовая скорость.
- 1.3.4. Волновые пакеты. Групповая скорость.
- § 1.4. Векторные волны
- 1.4.2. Гармоническая электромагнитная плоская волна.
- 1.4.3. Гармонические векторные волны произвольной формы.
- § 1.5. Отражение и преломление плоской волны
- 1.5.2. Формулы Френеля.
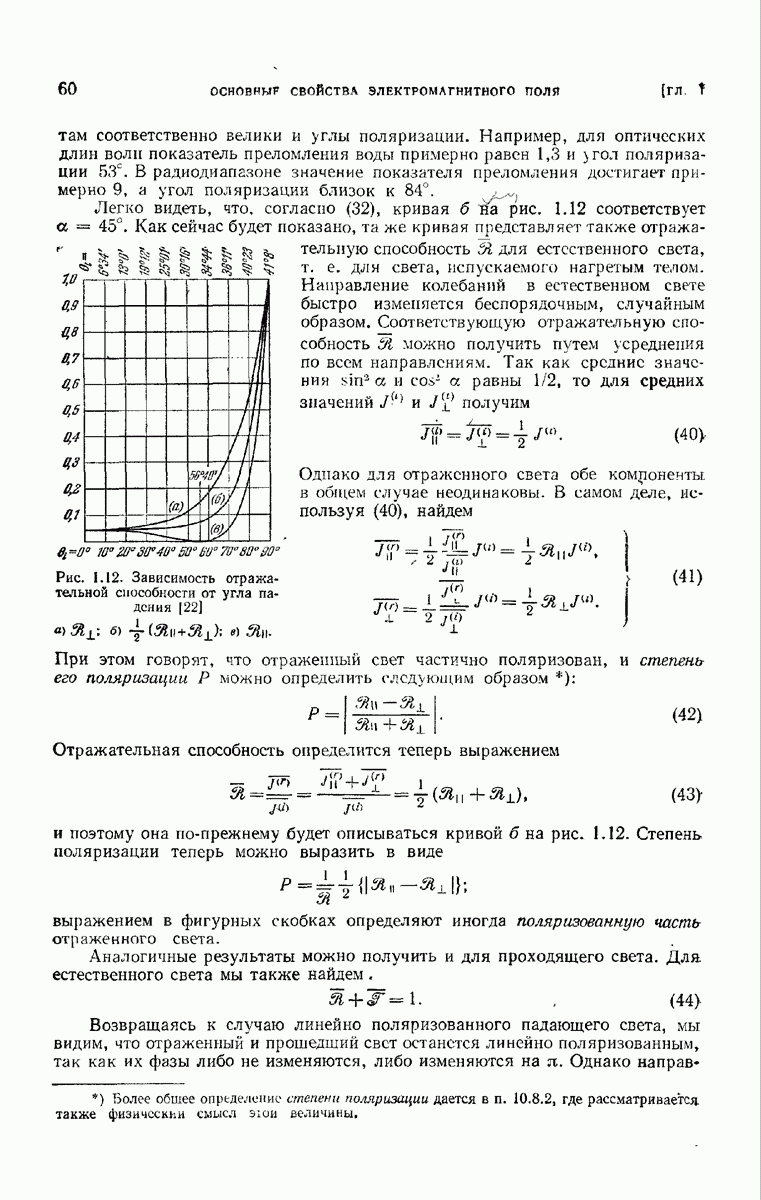
- 1.5.3. Отражательная и пропускательная способности; поляризация при отражении и преломлении.
- 1.5.4. Полное внутреннее отражение.
- § 1.6. Распространение волн в слоистой среде. Теория диэлектрических пленок
- 1.6.2. Характеристическая матрица для слоистой среды.
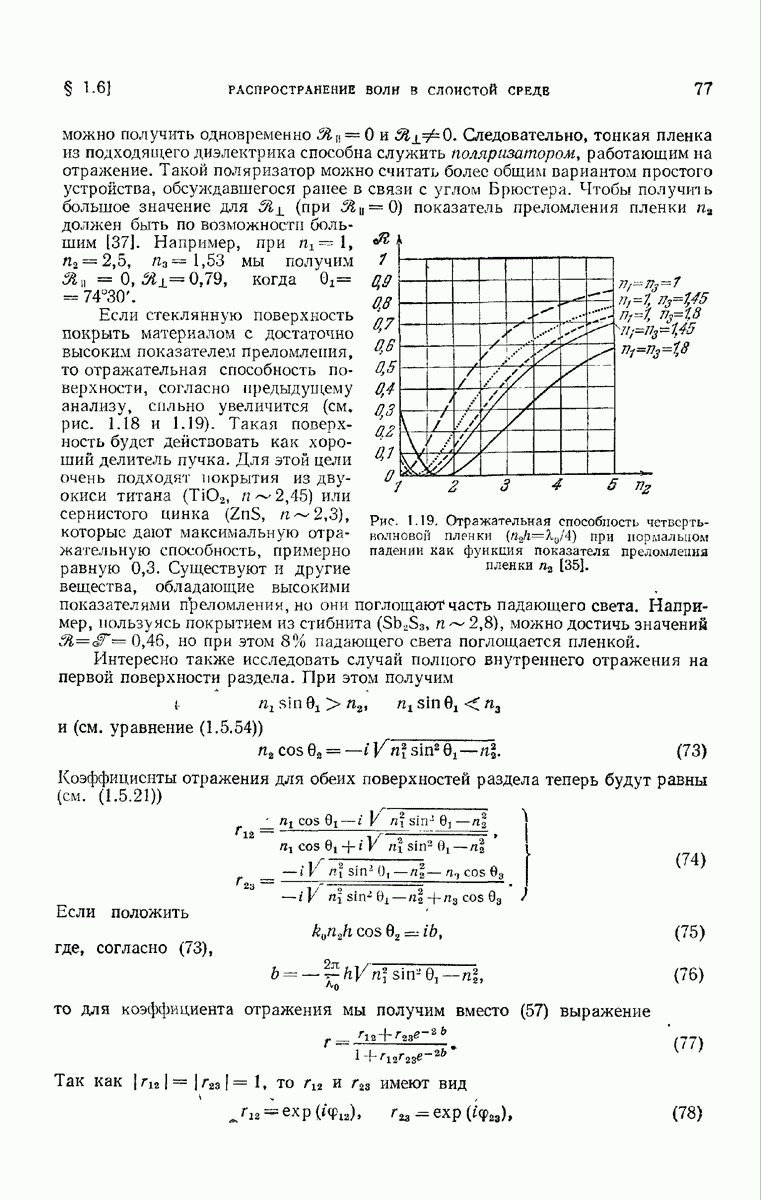
- 1.6.3. Коэффициенты отражения и пропускания.
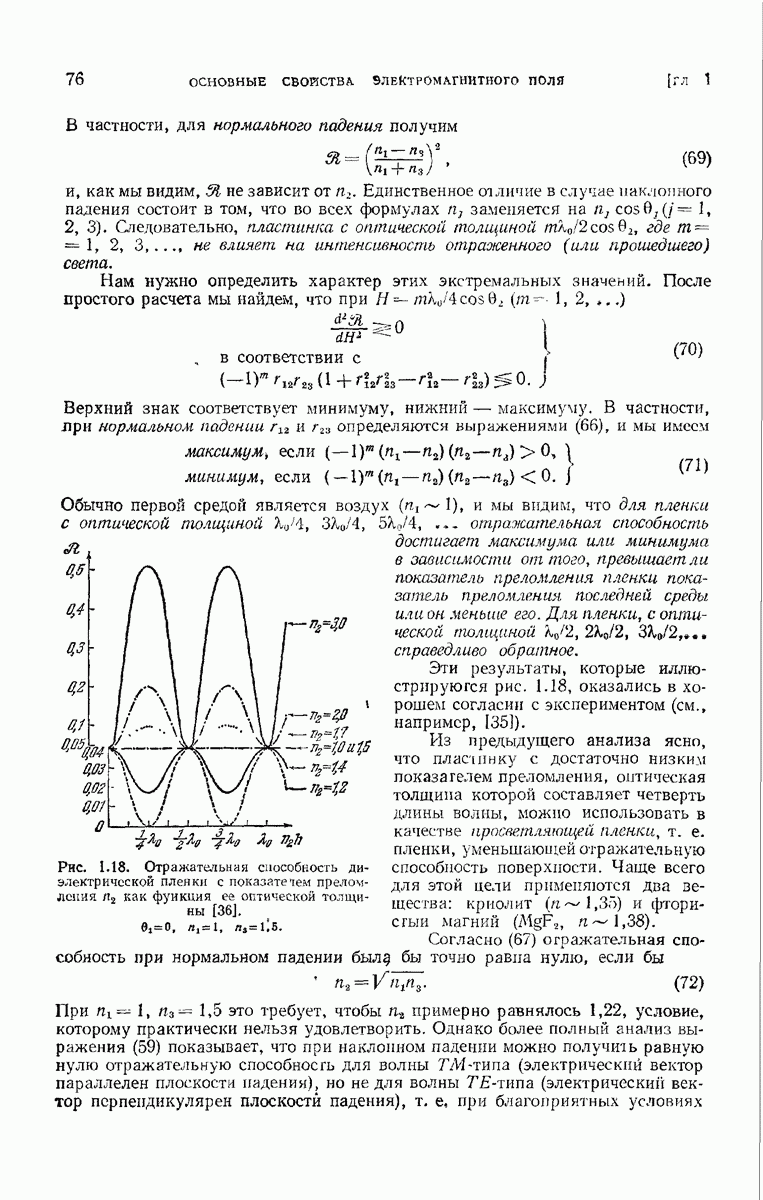
- 1.6.4. Однородная диэлектрическая пленка.
- 1.6.5. Периодические слоистые среды.
- ГЛАВА 2. ЭЛЕКТРОМАГНИТНЫЕ ПОТЕНЦИАЛЫ И ПОЛЯРИЗАЦИЯ
- § 2.1. Электродинамические потенциалы в вакууме
- 2.1.2. Запаздывающие потенциалы.
- § 2.2. Поляризация и намагничение
- 2.2.2. Векторы Герца.
- 2.2.3. Поле линейного электрического диполя.
- § 2.3. Формула Лорентц — Лоренца и элементарная теория дисперсии
- 2.3.2. Эффективное поле.
- 2.3.3. Средняя поляризуемость. Формула Лорентц — Лоренца.
- 2.3.4. Элементарная теория дисперсии.
- § 2.4. Описание распространения электромагнитных волн с помощью интегральных уравнений
- 2.4.2. Теорема погашения Эвальда — Озеена и строгий вывод формулы Лорентц — Лоренца.
- 2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда — Озеена.
- ГЛАВА 3. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 3.1.2. Световые лучи и закон интенсивности в геометрической оптике.
- 3.1.3. Распространение векторных амплитуд.
- 3.1.4. Обобщения геометрической оптики и пределы ее применимости.
- § 3.2. Общие свойства лучей
- 3.2.2. Законы преломления и отражения.
- 3.2.3. Конгруэнции лучей и фокальные свойства.
- § 3.3. Другие основные теоремы геометрической оптики
- 3.3.2. Принцип Ферма
- 3.3.3. Теорема Малюса и Дюпина и некоторые другие связанные с ней теоремы.
- ГЛАВА 4. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ОПТИЧЕСКИХ ИЗОБРАЖЕНИЙ
- 4.1.2. Смешанная характеристика.
- 4.1.3. Угловая характеристика.
- 4.1.4. Приближенное выражение для угловой характеристики преломляющей поверхности вращения.
- 4.1.5. Приближенное выражение для угловой характеристики отражающей поверхности вращения.
- § 4.2. Идеальное отображение
- 4.2.2. «Рыбий глаз» Максвелла.
- 4.2.3. Стигматическое отображение поверхностей.
- § 4.3. Проективное преобразование (коллинеация) при наличии аксиальной симметрии
- 4.3.2. Телескопическое отображение.
- 4.3.3. Классификация проективных преобразований.
- 4.3.4. Комбинация проективных преобразований.
- § 4.4. Параксиальная оптика
- 4.4.2. Отражающая поверхность вращения.
- 4.4.3. Толстая линза.
- 4.4.4. Тонкая лииза.
- 4.4.5. Произвольная центрированная система.
- § 4.5. Стигматическое отображение пучками с большой угловой апертурой
- § 4.6. Астигматические пучки лучей
- 4.6.2. Преломление тонкого пучка.
- § 4.7. Хроматическая аберрация. Дисперсия призмы
- 4.7.2. Дисперсия призмы.
- § 4.8. Фотометрия. Апертуры оптических систем
- 4.8.2. Диафрагмы и зрачки.
- 4.8.3. Яркость и освещенность изображений.
- § 4.9. Метод построения хода лучей
- 4.9.2. Параксиальные лучи.
- 4.9.3. Косые лучи.
- § 4.10. Оптические системы с несферическими поверхностями
- 4.10.2. Получение апланатизма.
- ГЛАВА 5. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 5.2. Эйконал Шварншильда
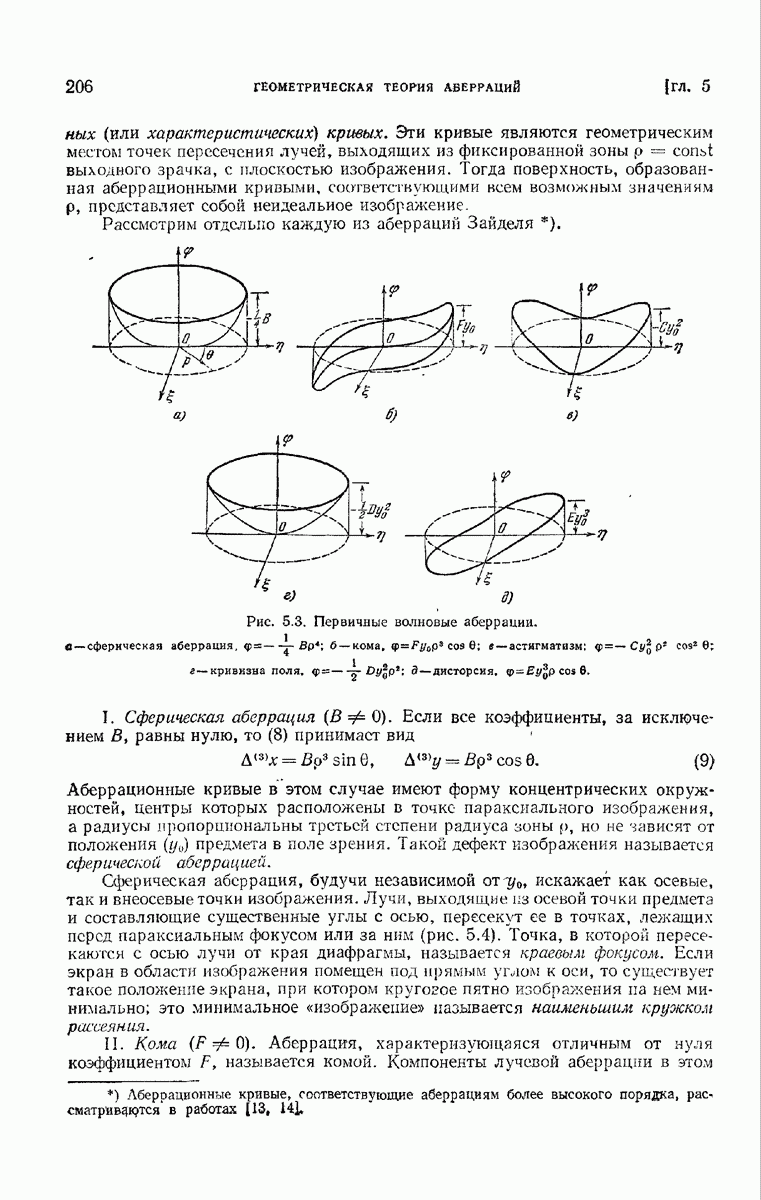
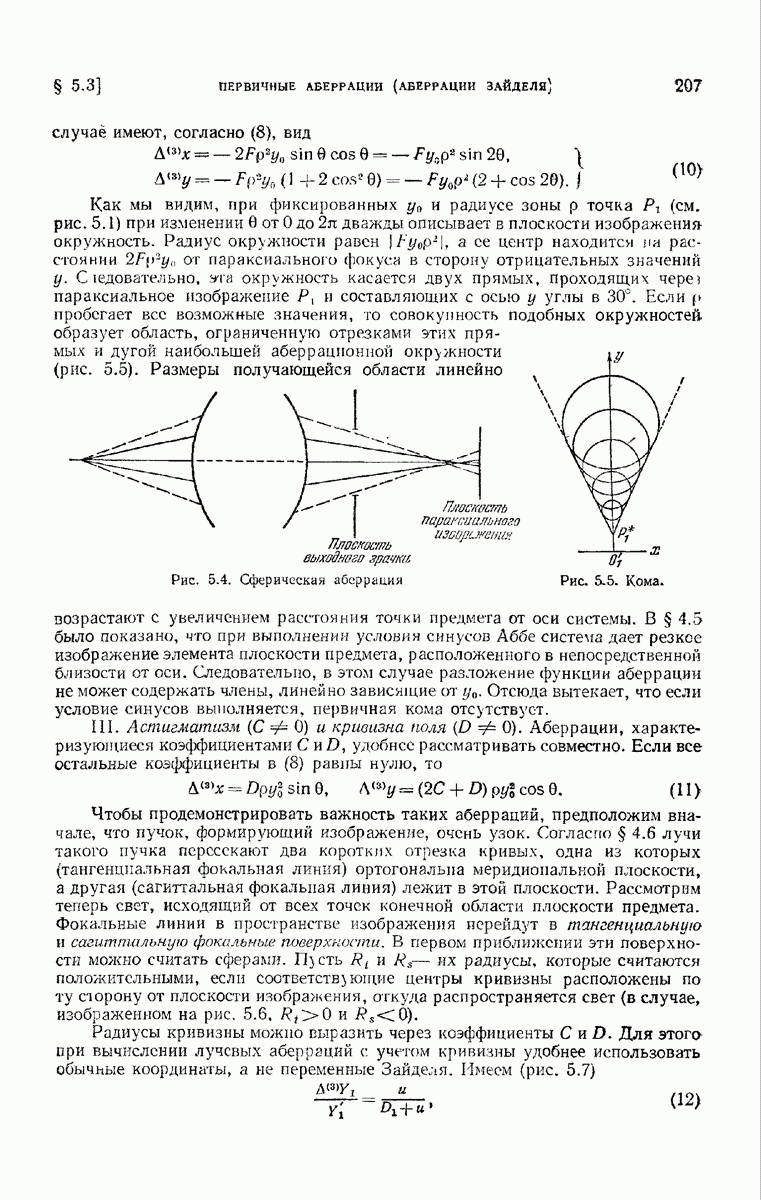
- § 5.3. Первичные аберрации (аберрации Зайделя)
- § 5.4. Теорема сложения для случая первичных аберраций
- § 5.5. Коэффициенты первичных аберраций произвольной центрированной системы линз
- 5.5.2. Формулы Зайделя, выраженные через параметры одного параксиального луча.
- 5.5.3. Теорема Петцваля.
- § 5.6. Пример: первичные аберрации тонкой линзы
- § 5.7. Хроматическая аберрация произвольной центрированной системы линз
- ГЛАВА 6. ОПТИЧЕСКИЕ ПРИБОРЫ, ФОРМИРУЮЩИЕ ИЗОБРАЖЕНИЕ
- § 6.2. Фотографический аппарат
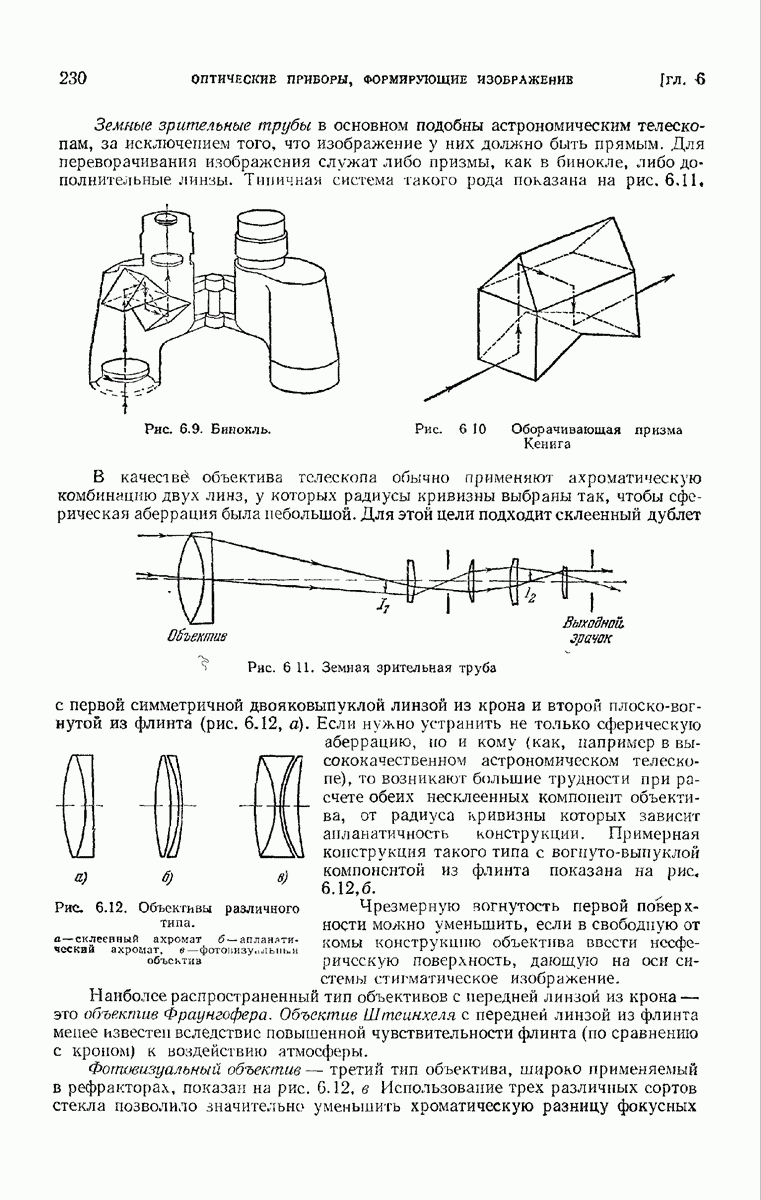
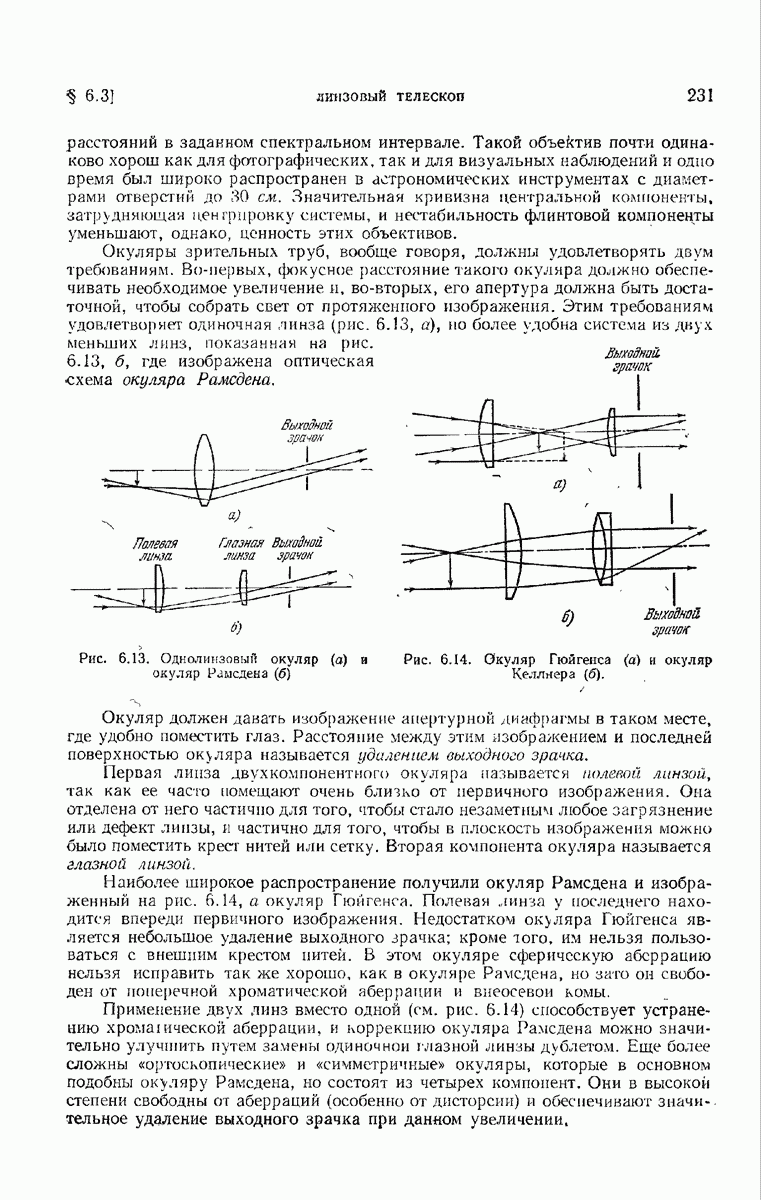
- § 6.3. Линзовый телескоп
- § 6.4. Зеркальный телескоп
- § 6.5. Осветители
- § 6.6. Микроскоп
- ГЛАВА 7. ЭЛЕМЕНТЫ ТЕОРИИ ИНТЕРФЕРЕНЦИИ И ИНТЕРФЕРОМЕТРЫ
- § 7.2. Интерференция двух монохроматических волн
- § 7.3. Двухлучевая интерференция. Деление волнового фронта
- 7.3.2. Зеркала Френеля и другие аналогичные устройства.
- 7.3.3. Интерференционные полосы в квазимонохроматическом и белом свете.
- 7.3.4. Источник в виде щели; видность полос.
- 7.3.5. Измерение оптической разности хода; интерферометр Рэлея.
- 7.3.6. Измерение угловых размеров источников; звездный интерферометр Майкельсона.
- § 7.4. Стоячие волны
- § 7.5. Двухлучевая интерференция. Деление амплитуды
- 7.5.2. Интерференция в тонких пленках; интерферометр Физо.
- 7.5.3. Локализация полос.
- 7.5.4. Интерферометр Майкельсона.
- 7.5.5. Интерферометр Тваймана — Грина и другие аналогичные приборы.
- 7.5.6. Полосы, получающиеся с двумя одинаковыми пластинами; интерферометр Жамена и интерференционный микроскоп.
- 7.5.7. Интерферометр Маха—Цендера; интерферометр Бейтса со смещенным волновым фронтом.
- 7.5.8. Длина когерентности; применение двухлучевой интерференции к изучению тонкой структуры спектральных линий.
- § 7.6. Многолучевая интерференция
- 7.6.2. Интерферометр Фабри — Перо.
- 7.6.3. Применение интерферометра Фабри — Перо для изучения тонкой структуры спектральных линий.
- 7.6.4. Применение интерферометра Фабри — Перо для сравнения длин волн.
- 7.6.5. Интерферометр Люммера — Герке.
- 7.6.6. Интерференционные фильтры.
- 7.6.7. Многолучевые полосы в тонких пленках.
- 7.6.8. Многолучевые полосы, получающиеся с двумя плоскопараллельными пластинками.
- § 7.7. Сравнение длин волн с эталонным метром
- ГЛАВА 8. ЭЛЕМЕНТЫ ТЕОРИИ ДИФРАКЦИИ
- § 8.2. Принцип Гюйгенса — Френеля
- § 8.3. Теория дифракции Кирхгофа
- 8.3.2. Теория дифракции Кирхгофа.
- 8.3.3. Дифракция Фраунгофера и Френеля.
- § 8.4. Переход к скалярной теории
- 8.4.2. Полное поле изображения.
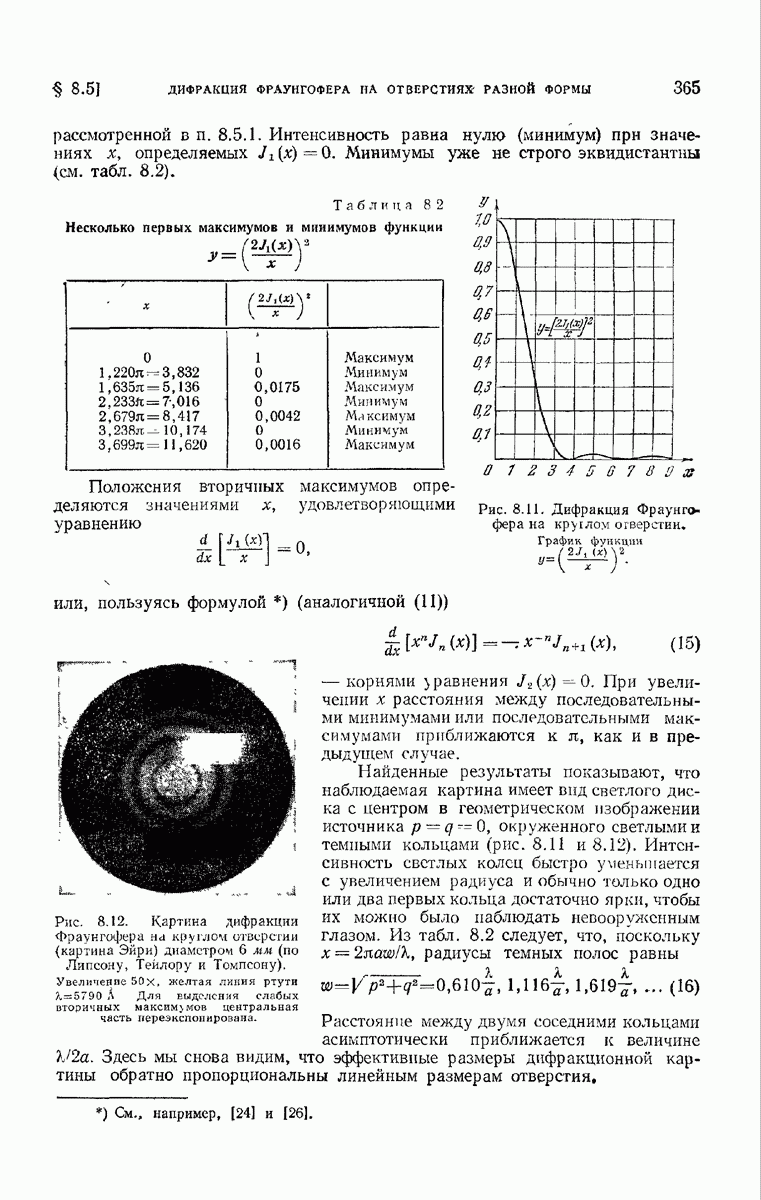
- § 8.5. Дифракция Фраунгофера на отверстиях разной формы
- 8.5.2. Круглое отверстие.
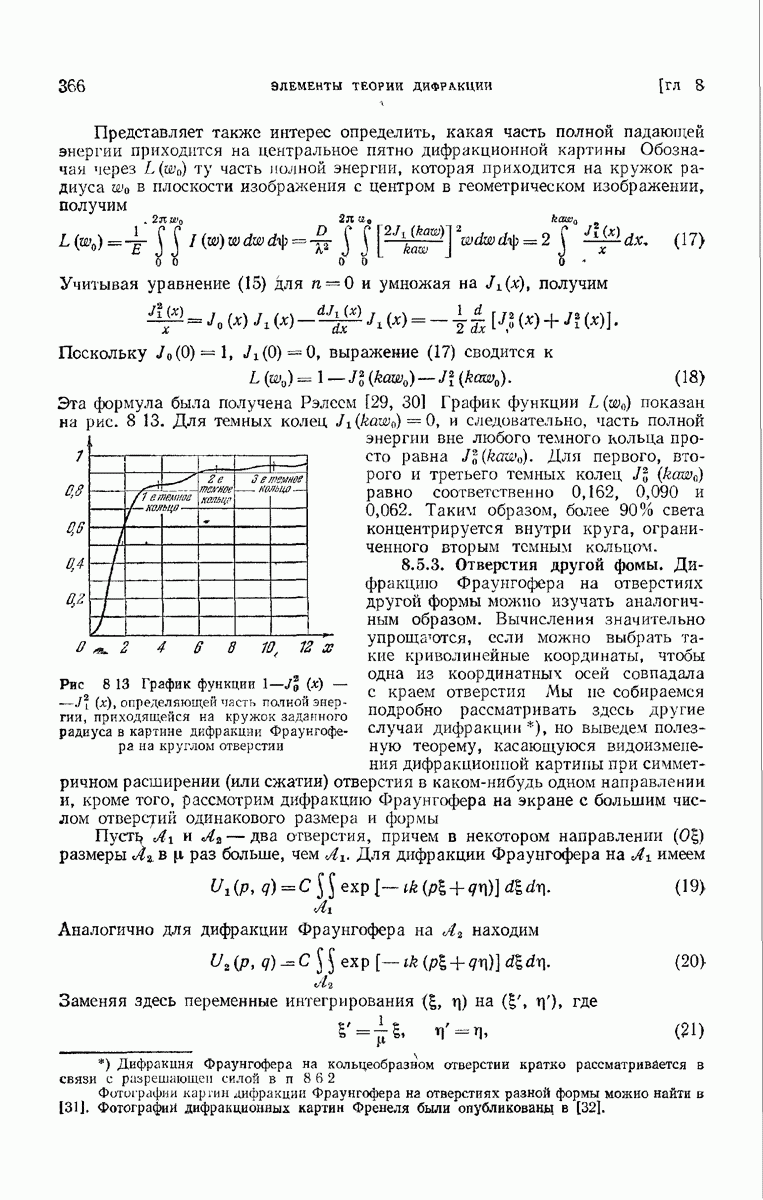
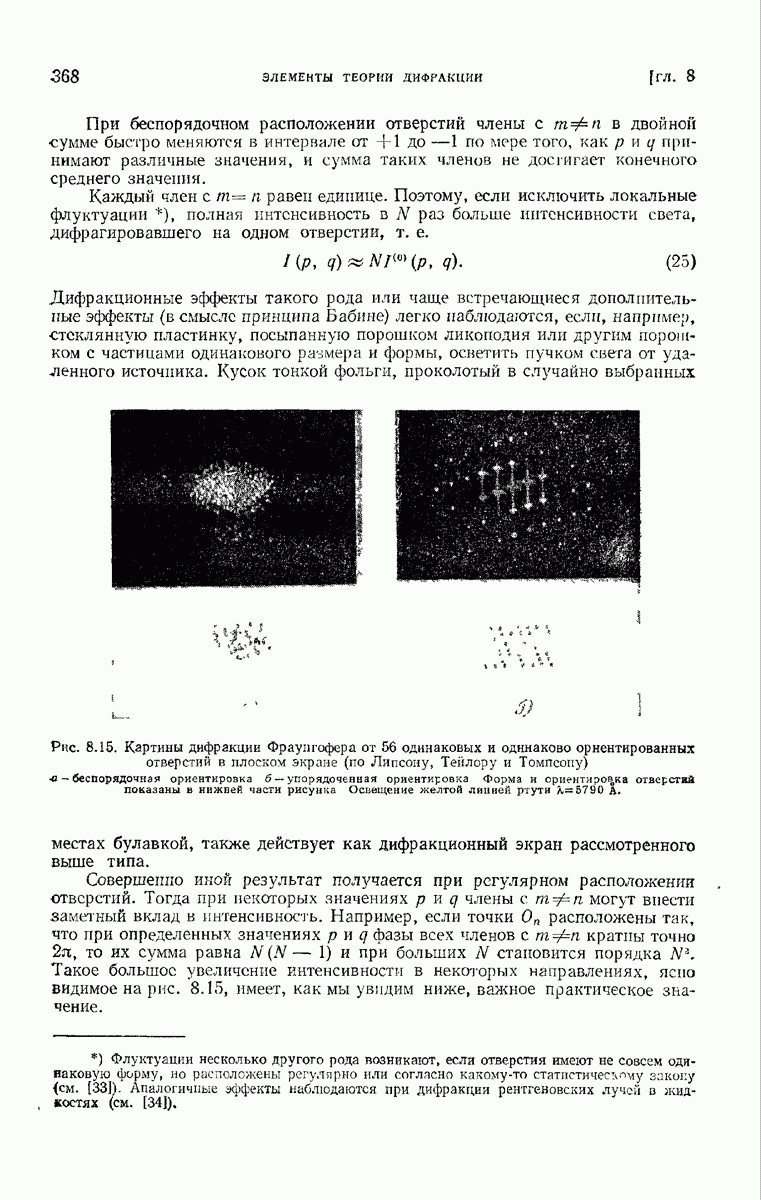
- 8.5.3. Отверстия другой фомы.
- § 8.6. Дифракция Фраунгофера в оптических приборах
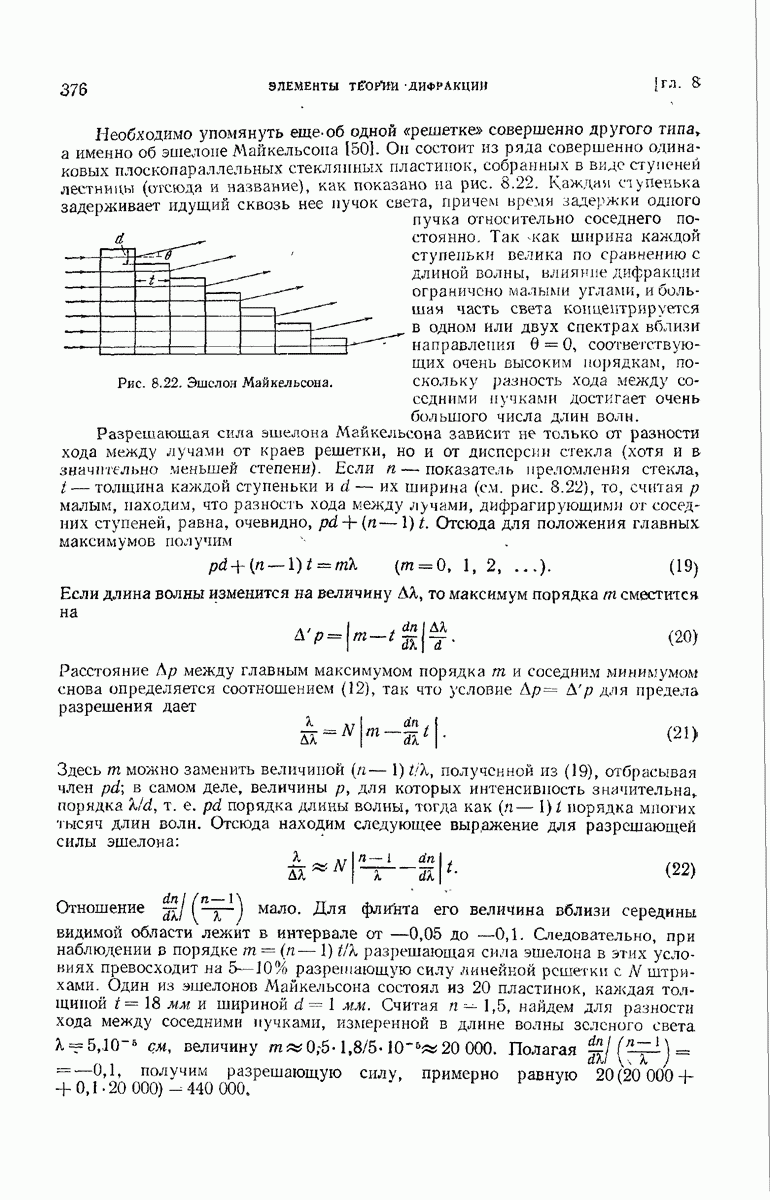
- 8.6.2. Разрешающая сила систем, образующих изображение.
- 8.6.3. Образование изображения в микроскопе.
- § 8.7. Дифракция Френеля на прямолинейном крае
- 8.7.2. Интегралы Френеля.
- 8.7.3. Дифракция Френеля на прямолинейном крае.
- § 8.8. Трехмерное распределение света вблизи фокуса
- 8.8.2. Распределение интенсивности.
- 8.8.3. Суммарная интенсивность.
- 8.8.4. Фазовые соотношения.
- § 8.9. Граничная дифрагировавшая волна
- § 8.10. Метод Габора получения изображения восстановлением волновых фронтов
- 8.10.2. Восстановление.
- ГЛАВА 9. ДИФРАКЦИОННАЯ ТЕОРИЯ АБЕРРАЦИЙ
- § 9.1. Дифракционный интеграл при наличии аберраций
- 9.1.2. Теорема смещения. Изменение опорной сферы.
- 9.1.3. Соотношение между интенсивностью и средней деформацией волновых фронтов.
- § 9.2. Разложение функции аберрации
- 9.2.2. Разложение функции аберраций.
- § 9.3. Допустимые величины первичных аберраций
- § 9.4. Дифракционная картина, получающаяся при наличии одной аберрации
- 9.4.1. Первичная сферическая аберрация.
- 9.4.2. Первичная кома.
- 9.4.3. Первичный астигматизм.
- § 9.5. Изображение протяженных предметов
- 9.5.2. Некогерентное освещение.
- ГЛАВА 10. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ЧАСТИЧНО КОГЕРЕНТНОГО СВЕТА
- § 10.2. Комплексное представление вещественных полихроматических полей
- § 10.3. Корреляционные функции световых пучков
- 10.3.2. Спектральное представление взаимной когерентности.
- § 10.4. Интерференция и дифракция квазимонохроматического света
- 10.4.2. Расчет взаимной интенсивности и степени когерентности для света от протяженного некогерентного квазимонохроматического источника.
- 10.4.3. Пример.
- 10.4.4. Распространение взаимной интенсивности.
- § 10.5. Некоторые приложения
- 10.5.1. Степень когерентности в изображении протяженного некогерентного квазимонохроматического источника.
- 10.5.2. Влияние конденсора на разрешающую силу микроскопа.
- 10.5.3. Получение изображения при частично когерентном квазимонохроматическом освещении
- § 10.6. Некоторые теоремы, касающиеся взаимной когерентности
- 10.6.2. Распространение взаимной когерентности.
- § 10.7. Строгая теория частичной когерентности
- 10.7.2. Строгая формулировка закона распространения взаимной когерентности.
- 10.7.3. Время когерентности и эффективная ширина спектра.
- § 10.8. Поляризация квазимонохроматического света
- 10.8.2. Некоторые эквивалентные представления. Степень поляризации световой волны.
- 10.8.3. Параметры Стокса квазимонохроматичаской плоской волны.
- ГЛАВА 11. СТРОГАЯ ТЕОРИЯ ДИФРАКЦИИ
- § 11.2. Граничные условия и поверхностные токи
- § 11.3. Дифракция на плоском экране; электромагнитная форма принципа Бабине
- § 11.4. Двумерная дифракция на плоском экране
- 11.4.2. Угловой спектр плоских волн.
- 11.4.3. Формулировка задачи через дуальные интегральные уравнения.
- § 11.5. Двумерная дифракция плоской волны на полуплоскости
- 11.5.2. Выражение решения через интегралы Френеля.
- 11.5.3. Характер решения.
- 11.5.4. Решение для Н-поляризации.
- 11.5.5. Некоторые численные расчеты.
- 11.5.6. Сравнение с приближенной теорией и с экспериментальными результатами.
- § 11.6. Трехмерная дифракция плоской волны на полуплоскости
- § 11.7. Дифракция волн, испускаемых локализованным источником, на полуплоскости
- 11.7.2. Диполь.
- § 11.8. Другие задачи
- 11.8.1. Две параллельные полуплоскости.
- 11.8.2. Бесконечный набор параллельных полуплоскостей, расположенных ступеньками.
- 11.8.3. Полоса.
- 11.8.4. Другие задачи.
- § 11.9. Единственность решения
- ГЛАВА 12. ДИФРАКЦИЯ СВЕТА НА УЛЬТРАЗВУКОВЫХ ВОЛНАХ
- 12.1.2. Краткое изложение теорий, основанных на уравнениях Максвелла.
- § 12.2. Рассмотрение дифракции света на ультразвуковых волнах методом интегральных уравнений
- 12.2.1. Интегральное уравнение для случая Е-поляризации.
- 12.2.2. Пробное решение интегрального уравнения.
- 12.2.3. Выражения для амплитуд световых волн в дифрагировавших и отраженных спектрах.
- 12.2.5. Выражения для интенсивностей линий в спектрах первого и второго порядков в некоторых специальных случаях
- 12.2.6. Некоторые качественные результаты.
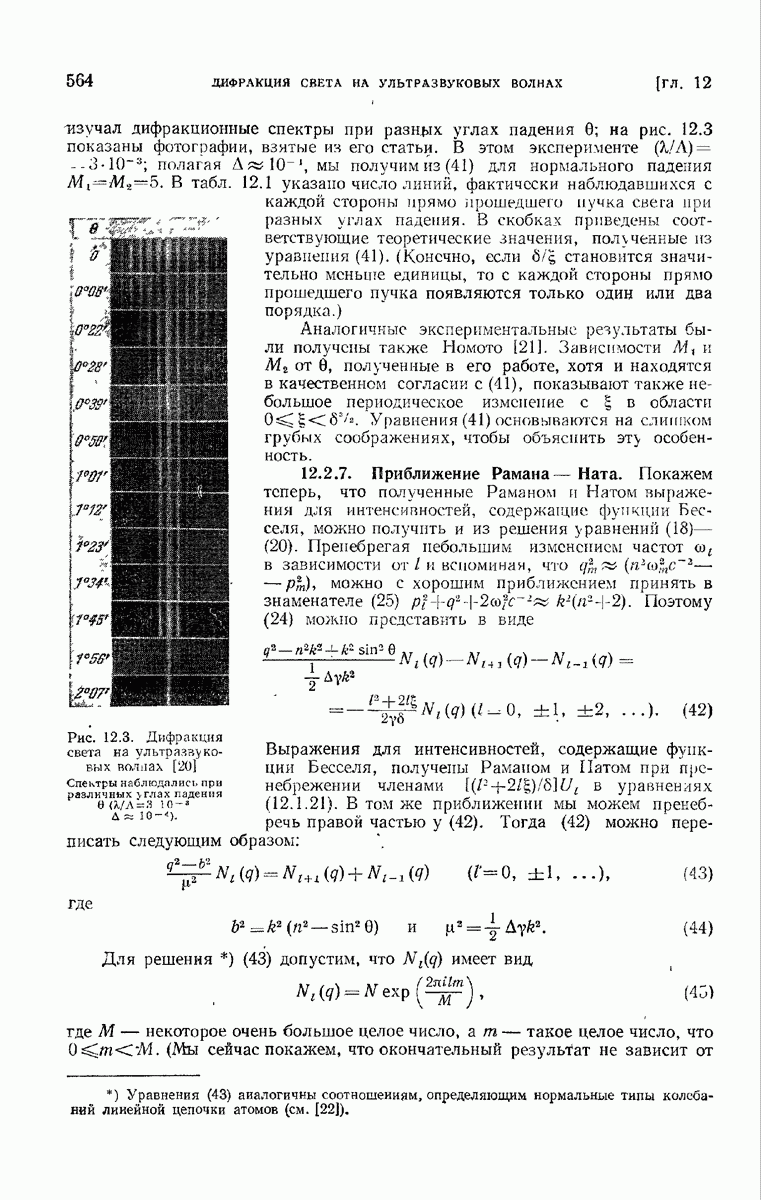
- 12.2.7. Приближение Рамана—Ната.
- ГЛАВА 13. МЕТАЛЛООПТИКА
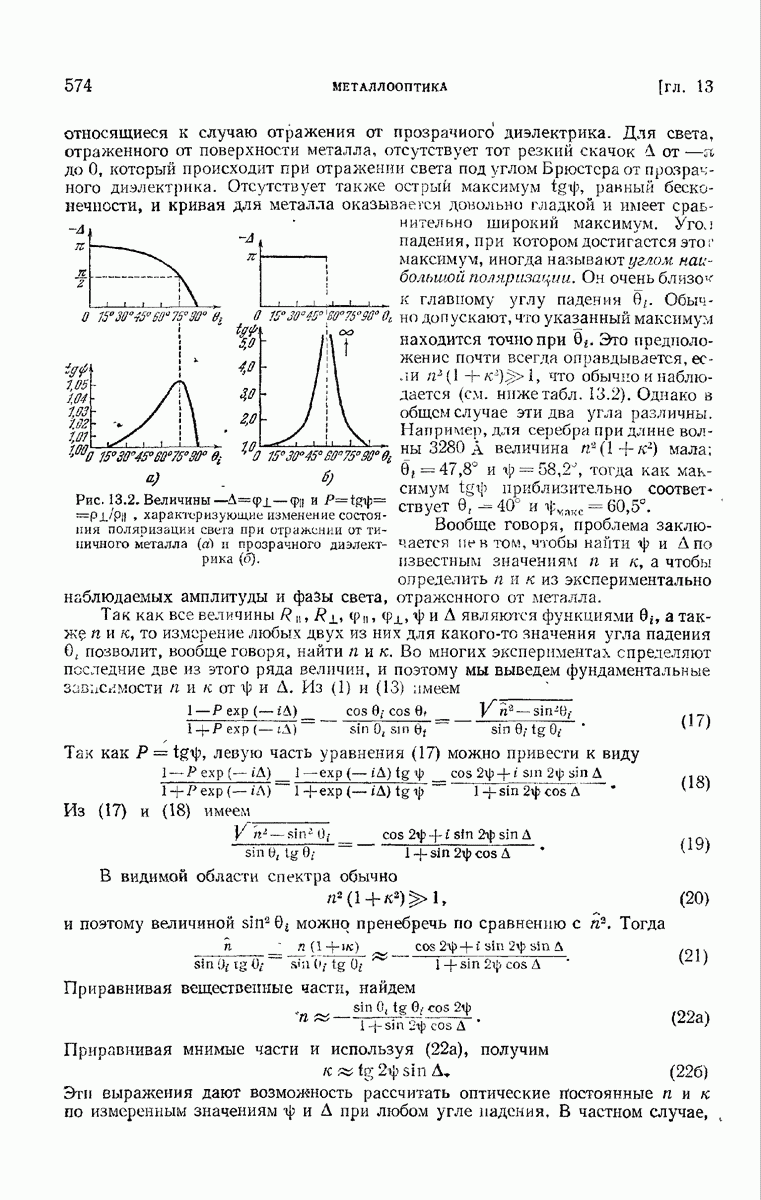
- § 13.2. Преломление и отражение на поверхности металла
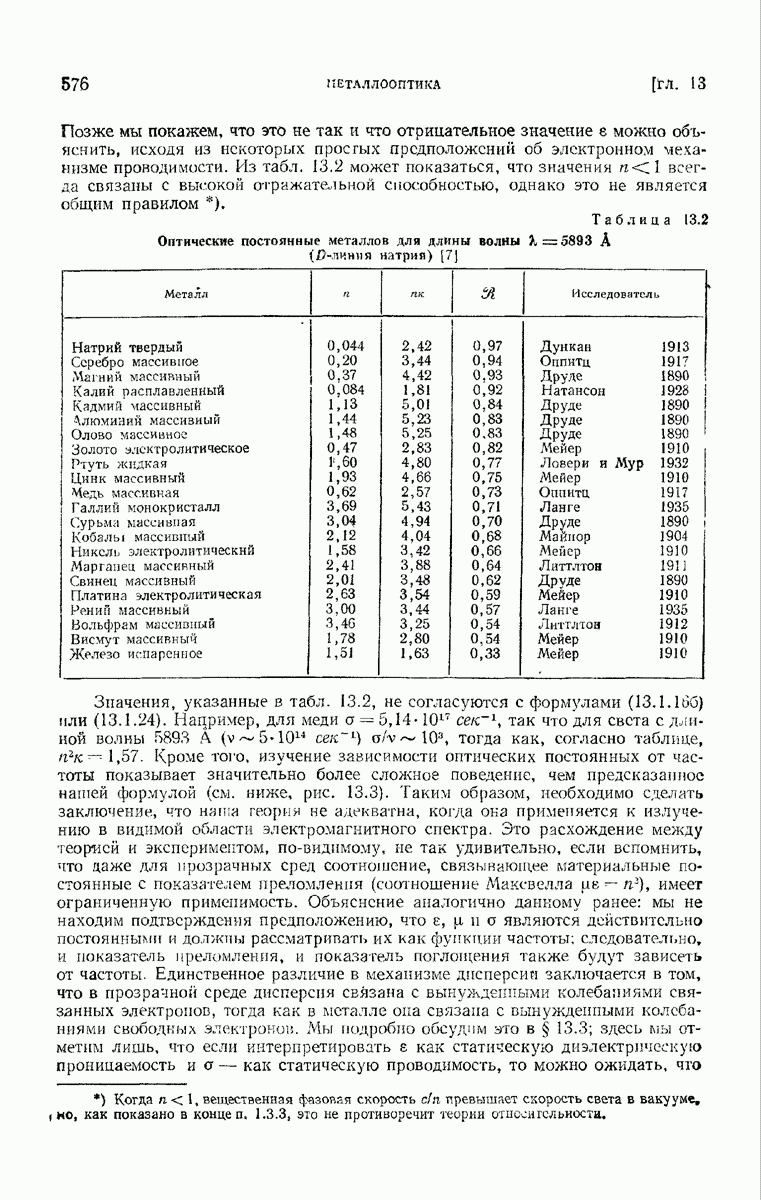
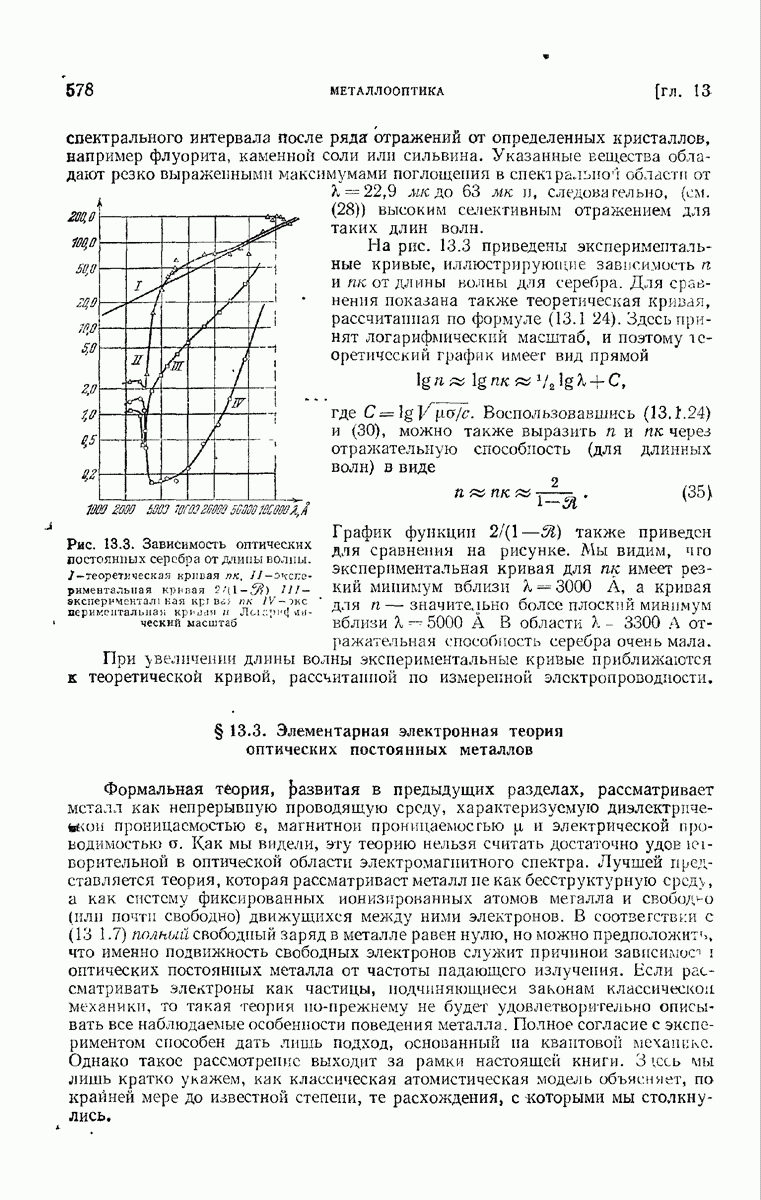
- § 13.3. Элементарная электронная теория оптических постоянных металлов
- § 13.4. Распространение волн в слоистой проводящей среде. Теория металлических пленок
- 13.4.2. Прозрачная пленка на поглощающей подложке.
- § 13.5. Дифракция на проводящей сфере. Теория Ми
- 13.5.1. Математическое решение проблемы
- 13.5.2. Некоторые следствия из формул Ми.
- 13.5.3. Полное рассеяние и затухание
- ГЛАВА 14. КРИСТАЛЛООПТИКА
- § 14.1. Тензор диэлектрической проницаемости анизотропной среды
- § 14.2. Структура монохроматической плоской волны в анизотропной среде
- 14.2.2. Формулы Френеля для распространения света в кристаллах.
- 14.2.3. Геометрические построения для определения скоростей распространения и направлений колебаний.
- § 14.3. Оптические свойства одноосных и двухосных кристаллов
- 14.3.2. Распространение света в одноосных кристаллах.
- 14.3.3. Распространение света в двухосных кристаллах.
- 14.3.4. Преломление в кристаллах
- § 14.4. Измерения в кристаллооптике
- 14.4.2. Компенсаторы.
- 14.4.3. Интерференция в кристаллических пластинках.
- 14.4.4. Интерференционные картины, получающиеся с пластинками одноосных кристаллов.
- 14.4.5. Интерференционные картины, получающиеся с пластинками двухосных кристаллов.
- 14.4.6. Определение положения оптических осей и главных показателей преломления кристаллической среды.
- § 14.5. Искусственная анизотропия
- 14.5.2. Двойное лучепреломление формы.
- § 14.6. Поглощающие кристаллы
- 14.6.2. Интерференционные картины, получающиеся с пластинками поглощающих кристаллов.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ 1. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 2. Интеграл Гильберта и уравнение Гамильтона—Якоби.
- 3. Поле экстремалей.
- 4. Нахождение всех экстремалей из решения уравнения Гамильтона — Якоби.
- 5. Канонические уравнения Гамильтона.
- 6. Частный случай, когда независимая переменная не входит явно в подынтегральное выражение.
- 7. Разрывы.
- 8. Условия Вейерштрасса и Лежандра (достаточные условия экстремума).
- 9. Минимум вариационного интеграла, когда один конец кривой связал с поверхностью.
- 10. Критерий Якоби для минимума.
- 11. Пример I. Оптика.
- 12. Пример II. Механика материальных точек.
- ПРИЛОЖЕНИЕ 2. ОБЫЧНАЯ ОПТИКА, ЭЛЕКТРОННАЯ ОПТИКА И ВОЛНОВАЯ МЕХАНИКА
- 2. Аналогия Гамильтона в вариационной форме.
- 3. Волновая механика свободных электронов.
- 4. Применение оптических принципов в электронной оптике.
- ПРИЛОЖЕНИЕ 3. МЕТОД АСИМПТОТИЧЕСКИХ ОЦЕНОК ИНТЕГРАЛОВ
- 2. Метод стационарной фазы.
- 3. Двойные интегралы.
- ПРИЛОЖЕНИЕ 4. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
- ПРИЛОЖЕНИЕ 5. МАТЕМАТИЧЕСКАЯ ЛЕММА, ИСПОЛЬЗУЕМАЯ ПРИ СТРОГОМ ВЫВОДЕ ЗАКОНА ЛОРЕНТЦ — ЛОРЕНЦА
- ПРИЛОЖЕНИЕ 6. РАСПРОСТРАНЕНИЕ РАЗРЫВОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ПРИЛОЖЕНИЕ 7. КРУГОВЫЕ ПОЛИНОМЫ ЦЕРНИКЕ
- ПРИЛОЖЕНИЕ 8. ДОКАЗАТЕЛЬСТВО ОДНОГО НЕРАВЕНСТВА, ПРИВЕДЕННОГО В П. 10.7.3
- ПРИЛОЖЕНИЕ 9. ВЫЧИСЛЕНИЕ ДВУХ ИНТЕГРАЛОВ, ИСПОЛЬЗУЕМЫХ В П. 12.2.2