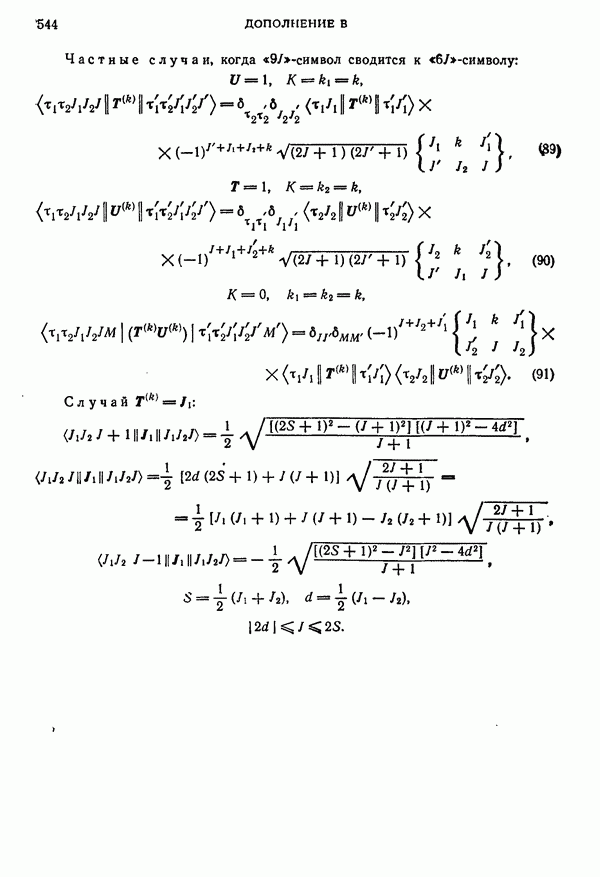| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 11. Вращение физической системы. Оператор вращения
При обсуждении свойств физической системы, связанных с вращениями, — все сказанное ниже справедливо для любого преобразования пространства — можно принять одну из двух точек зрения, которые следует четко различать. Согласно первой (иногда ее называют пассивной) производят вращение координатных осей, оставляя фиксированной каждую точку Р пространства и связанные с ней физические величины. Согласно второй (иногда ее называют активной) фиксированными остаются оси координат, а вращают физическую систему. Обе точки зрения эквивалентны. Поворот координатных осей или поворот физической системы в противоположном направлении приводят к одному и тому же результату. Далее, если не оговорено противное, мы будем придерживаться второй точки зрения (будем вращать физическую систему).
Определение «вращения физической системы» в квантовой механике требует большей осторожности, чем в классической, так как связь между динамическими переменными и динамическими состояниями значительно сложнее. Рассмотрим для простоты вначале случай одной частицы. Обозначим а — возможное динамическое состояние частицы и  соответствующую волновую функцию. Состояние, получаемое после вращения
соответствующую волновую функцию. Состояние, получаемое после вращения  , обозначим а и соответствующую а волновую функцию
, обозначим а и соответствующую а волновую функцию 

Когда мы говорим, что состояние а переходит при вращении  в состояние а, мы имеем в виду, что результаты любых наблюдений над системой в состоянии а могут быть получены посредством вращения
в состояние а, мы имеем в виду, что результаты любых наблюдений над системой в состоянии а могут быть получены посредством вращения  из результатов, которые дали бы те же
из результатов, которые дали бы те же
наблюдения, выполненные над системой в состоянии а. Рассмотрим, например, измерение координаты. Распределение вероятности для состояний а и а равно  соответственно. Согласно приведенному выше утверждению последнее получается из первого при вращении
соответственно. Согласно приведенному выше утверждению последнее получается из первого при вращении  , т. е. значение второй функции в данной точке
, т. е. значение второй функции в данной точке  равно значению первой функции в точке
равно значению первой функции в точке  которая переходит в
которая переходит в  при вращении
при вращении 

Аналогично, если  - волновые функции в импульсном пространстве, отвечающие
- волновые функции в импульсном пространстве, отвечающие  то имеем
то имеем

Ясно, что для того чтобы выполнялись все эти условия, достаточно равенства значений функции  в точке
в точке  и функции в точке
и функции в точке  т. е.
т. е.

Можно показать, что это равенство является и необходимым условием  . Следовательно, волновая функция определена однозначно.
. Следовательно, волновая функция определена однозначно.
Соотношение (47) устанавливает взаимно однозначное соответствие между  . Ясно, что это соответствие — линейное, т. е. существует оператор
. Ясно, что это соответствие — линейное, т. е. существует оператор  такой, что
такой, что

Оператор  — унитарный, так как нормы
— унитарный, так как нормы  равны,
равны,

(последний интеграл получается заменой переменной  с учетом того факта, что при вращении сохраняется элемент объема
с учетом того факта, что при вращении сохраняется элемент объема 
Все эти рассуждения без труда обобщаются на систему N частиц; при вращении  волновая функция
волновая функция  переходит в
переходит в

Как и выше, оператор вращения  — линейный и унитарный.
— линейный и унитарный.
В общем случае, с каждым вращением  физической системы связан унитарный оператор
физической системы связан унитарный оператор  действие
действие  на вектор
на вектор  , представляющий динамическое состояние системы до вращения, дает вектор
, представляющий динамическое состояние системы до вращения, дает вектор  , представляющий ее динамическое состояние после вращения,
, представляющий ее динамическое состояние после вращения,

Используя закон преобразования (50) и определение оператора плотности, легко получить закон его преобразования. Пусть  — оператор плотности, представляющий некоторое (чистое или смешанное) состояние системы, а
— оператор плотности, представляющий некоторое (чистое или смешанное) состояние системы, а  оператор плотности, представляющий состояние, получившееся в результате вращения
оператор плотности, представляющий состояние, получившееся в результате вращения  . Тогда имеем
. Тогда имеем

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ III. СИММЕТРИИ И ИНВАРИАНТНОСТЬ
- Раздел I. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ МОМЕНТА ИМПУЛЬСА
- § 2. Определение момента импульса
- § 3. Основные алгебраические соотношения
- § 4. Спектр операторов
- § 5. Собственные векторы операторов. Построение инвариантных пространств
- § 6. Стандартное представление …
- § 7. Заключение
- Раздел II. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА И СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 8. Спектр операторов l^2 и lz
- § 9. Определение и построение сферических функций
- Раздел III. МОМЕНТ ИМПУЛЬСА И ВРАЩЕНИЯ
- § 10. Определение вращений. Углы Эйлера
- § 11. Вращение физической системы. Оператор вращения
- § 12. Вращение наблюдаемых
- § 13. Момент импульса и инфинитезимальные вращения
- § 14. Построение оператора …
- § 15. Вращение на угол 2pi и полуцелый момент импульса
- § 16. Неприводимые инвариантные подпространства. Матрицы вращений
- § 17. Инвариантность относительно вращений и сохранение момента импульса
- Раздел IV. СПИН
- § 18. Гипотеза спина электрона
- § 19. Спин 1/2 и матрицы Паули
- § 20. Наблюдаемые и волновые функции частицы спина 1/2. Спинорные поля
- § 21. Векторные поля и частицы спина 1
- § 22. Зависящие от спина взаимодействия в атомах
- § 23. Зависящие от спина нуклол-нуклонные взаимодействия
- Раздел V. СЛОЖЕНИЕ МОМЕНТОВ ИМПУЛЬСА
- § 25. Теорема сложения двух моментов импульса
- § 26. Приложения и примеры
- § 27. Собственные векторы полного момента импульса. Коэффициенты Клебша—Гордана
- § 28. Приложение: система двух нуклонов
- § 29. Сложение трех и более моментов импульса. Коэффициенты Рака. «3sj»-символы
- Раздел VI. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 31. Неприводимые тензорные операторы. Определение
- § 32. Представление неприводимых тензорных операторов. Теорема Вигнера — Эккарта
- § 33. Приложения
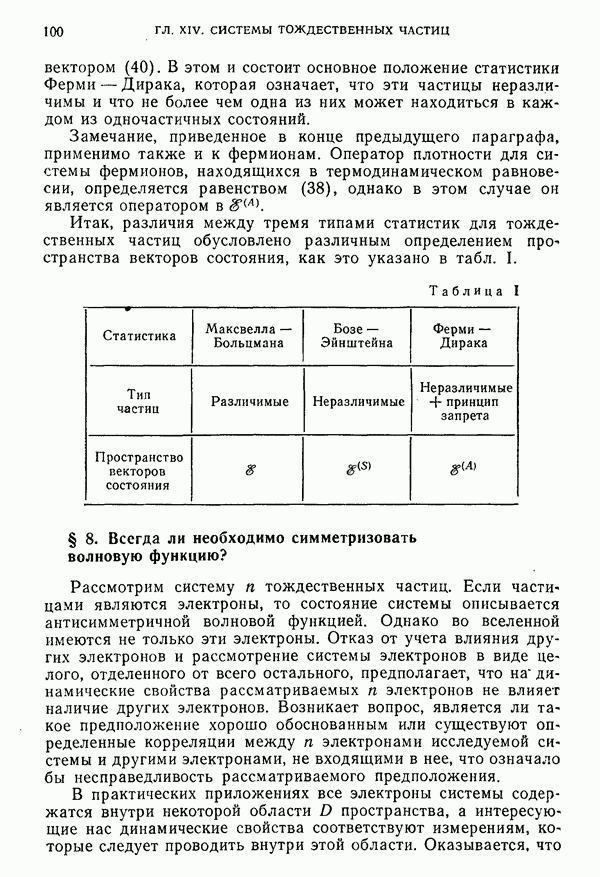
- ГЛАВА XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ. ПРИНЦИП ЗАПРЕТА ПАУЛИ
- Раздел I. ПОСТУЛАТ СИММЕТРИЗАЦИИ
- § 2. Подобные частицы и симметрическое представление
- § 3. Операторы перестановки
- § 4. Алгебра операторов перестановки. Симметризаторы и антисимметризаторы
- § 5. Тождественные частицы и постулат симметризации
- § 6. Бозоны и статистика Бозе—Эйнштейна
- § 7. Фермионы и статистика Ферми — Дирака. Принцип запрета
- § 8. Всегда ли необходимо симметризовать волновую функцию?
- Раздел II. ПРИЛОЖЕНИЯ
- § 9. Столкновение двух тождественных бесспиновых частиц
- § 10. Столкновение протонов
- § 11. Статистика атомных ядер
- § 12. Сложные атомы. Приближение центрального поля
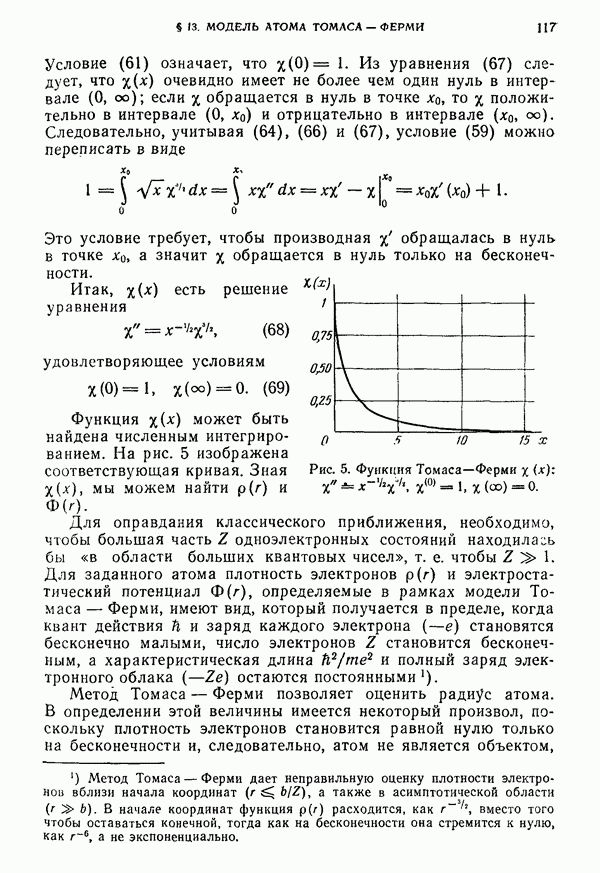
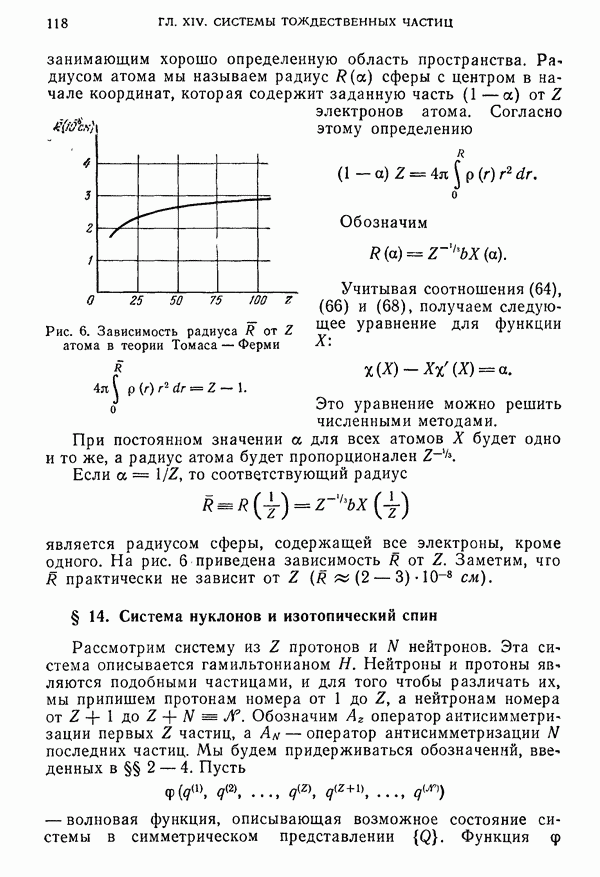
- § 13. Модель атома Томаса—Ферми
- § 14. Система нуклонов и изотопический спин
- § 15. Использование изотопического спина. Зарядовая независимость
- ГЛАВА XV. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
- Раздел I. ДОПОЛНИТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ. АНТИЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 3. Антилинейные операторы в гильбертовом пространстве
- § 4. Антиунитарные преобразования
- § 5. Антилинейные операторы и представления
- Раздел II. ПРЕОБРАЗОВАНИЯ И ГРУППЫ ПРЕОБРАЗОВАНИЙ
- § 6. Преобразования динамических переменных и динамических состояний системы
- § 7. Группы преобразований
- § 8. Группы операторов преобразований
- § 9. Непрерывные группы и инфинитезимальные преобразования. Трансляции. Вращения
- § 10. Конечные группы. Отражения
- Раздел III. ИНВАРИАНТНОСТЬ УРАВНЕНИИ ДВИЖЕНИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 12. Свойства инвариантности гамильтониана и законы сохранения
- § 13. Свойства инвариантности и эволюция динамических состояний
- § 14. Симметрии эффектов Штарка и Зеемана
- Раздел IV. ОБРАЩЕНИЕ ВРЕМЕНИ И ПРИНЦИП МИКРООБРАТИМОСТИ
- § 15. Сдвиги во времени и сохранение энергии
- § 16. Обращение времени в классической и квантовой механиках
- § 17. Обращение времени. Частица нулевого спина
- § 18. Общее определение обращения времени
- § 19. Обращение времени и комплексное сопряжение
- § 20. Принцип микрообратимости
- § 21. Следствие: вырождение Крамерса
- § 22. Вещественный гамильтониан, инвариантный относительно вращений
- ЧАСТЬ IV. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- ГЛАВА XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
- Раздел I. ВОЗМУЩЕНИЕ НЕВЫРОЖДЕННОГО УРОВНЯ
- § 2. Разложение по степеням возмущения
- § 3. Возмущение первого порядка
- § 4. Основное состояние атома гелия
- § 5. Кулоновская энергия атомных ядер
- § 6. Поправки высших порядков
- § 7. Эффект Штарка для жесткого ротатора
- Раздел II. ВОЗМУЩЕНИЕ ВЫРОЖДЕННОГО УРОВНЯ
- § 9. Атомные уровни без учета спин-орбитального взаимодействия
- § 10. Спин-орбитальное взаимодействие. LS- и jj-связь
- § 11. Атом с LS-связью. Расщепление за счет спии-орбитального взаимодействия
- § 12. Эффект Зеемана и эффект Пашена—Бака
- § 13. Симметрия Н и устранение вырождения
- § 14. Квазивырождение
- Раздел III. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ РАЗЛОЖЕНИЙ ПО ТЕОРИИ ВОЗМУЩЕНИЙ ВО ВСЕХ ПОРЯДКАХ
- § 15. Гамильтониан Н и его резольвента G(z)
- § 16. Разложение G(z), в ряд по степеням
- § 17. Вычисление собственных значений и собственных функций
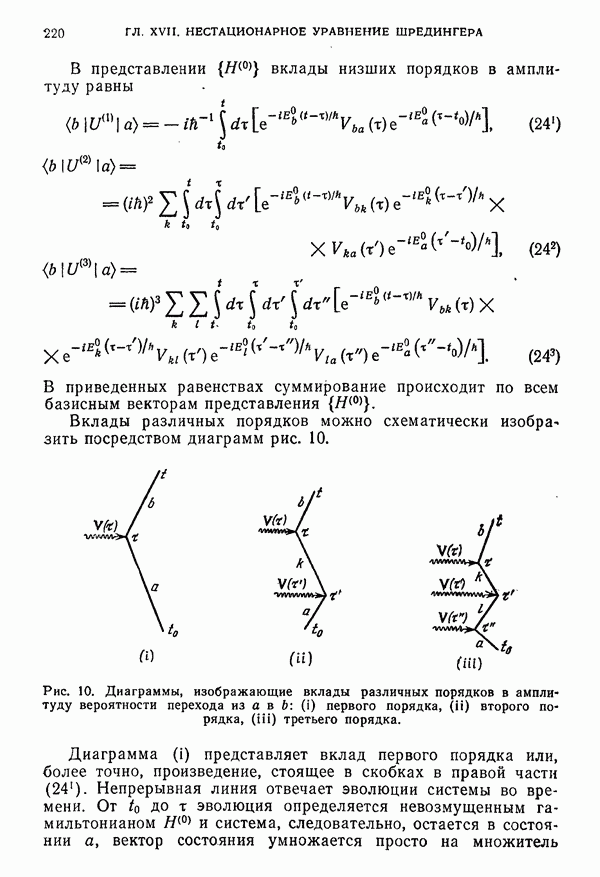
- ГЛАВА XVII. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- Раздел I. НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Определение и вычисление по теории возмущений вероятностей переходов
- § 3. Полуклассическая теория кулоновского возбуждения ядер
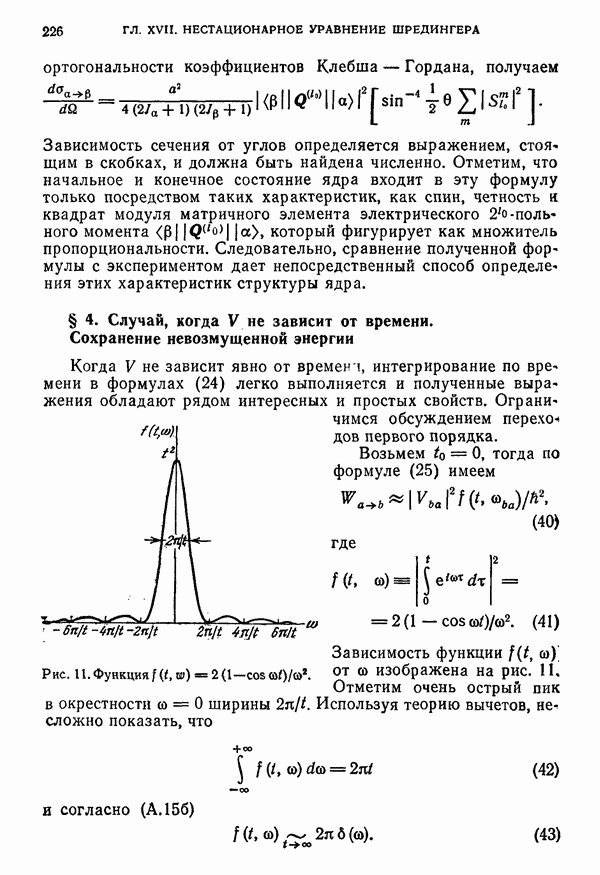
- § 4. Случай, когда V не зависит от времени. Сохранение невозмущенной энергии
- § 5. Приложение к вычислению сечений в борновском приближении
- § 6. Периодическое возмущение. Резонансы
- Раздел II. МГНОВЕННОЕ И АДИАБАТИЧЕСКОЕ ИЗМЕНЕНИЯ ГАМИЛЬТОНИАНА
- § 8. Быстрый переход и мгновенное приближение
- § 9. Мгновенное обращение магнитного поля
- § 10. Адиабатический переход. Общие положения. Тривиальный случай
- § 11. «Представление вращающихся осей»
- § 12. Доказательство адиабатической теоремы
- § 13. Адиабатическое приближение
- § 14. Адиабатическое обращение магнитного поля
- ГЛАВА XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
- § 1. Вариационный метод Ритца
- Раздел I. ВАРИАЦИОННЫЙ МЕТОД ДЛЯ СВЯЗАННЫХ СОСТОЯНИЙ
- § 2. Вариационная форма задачи на собственные значения
- § 3. Вариационное вычисление дискретных уровней
- § 4. Простой пример: атом водорода
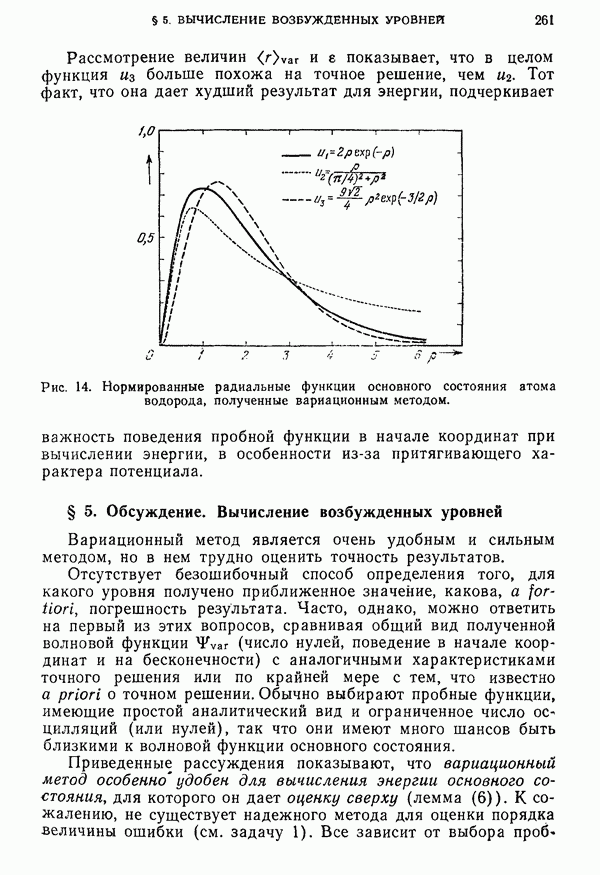
- § 5. Обсуждение. Вычисление возбужденных уровней
- § 6. Основное состояние атома гелия
- Раздел II. АТОМЫ ХАРТРИ И ФОКА—ДИРАКА
- § 7. Метод самосогласованного поля
- § 8. Вычисление Е[Ф]
- § 9. Уравнения Фока — Дирака
- § 10. Обсуждение результатов
- § 11. Уравнения Хартри
- § 12. Общие понятия. Разделение движения ядер и электронов
- § 13. Движение электронов в поле фиксированных ядер
- § 14. Адиабатическое приближение
- § 15. Гамильтониан ядер в адиабатическим приближении
- § 16. Метод Борна — Оппенгеймера
- § 17. Основные представления о двухатомных молекулах
- ГЛАВА XIX. ТЕОРИЯ РАССЕЯНИЯ
- Раздел I. СВОБОДНАЯ ФУНКЦИЯ ГРИНА И ПРИБЛИЖЕНИЕ БОРНА
- § 2. Интегральные представления амплитуды рассеяния
- § 3. Сечение рассеяния и T-матрица. Микрообратимость
- § 4. Борновское приближение
- § 5. Интегральное уравнение теории рассеяния
- § 6. Борновское разложение
- § 7. Критерий применимости борновского приближения
- § 8. Упругое рассеяние электронов на атоме
- § 9. Центральный потенциал. Вычисление сдвигов фаз
- § 10. Функция Грина как оператор. Связь с резольвентой оператора
- Раздел II. ОБОБЩЕНИЕ НА ИСКАЖЕННЫЕ ВОЛНЫ
- § 11. Обобщенное борновское приближение
- § 12. Обобщение борновского разложения
- § 13. Функция Грина искаженных волн
- § 14. Приложения. Определение и формальные свойства Т-матрицы
- § 15. Замечание о потенциалах 1/r
- Раздел III. СЛОЖНЫЕ СТОЛКНОВЕНИЯ И БОРНОВСКОЕ ПРИБЛИЖЕНИЕ
- § 17. Каналы
- § 18. Вычисление сечений. T-матрицы
- § 19. Интегральные представления амплитуды перехода
- § 20. Борновское приближение и его обобщения
- § 21. Рассеяние быстрых электронов атомом
- § 22. Кулоновское возбуждение ядер
- § 23. Функции Грина и интегральные уравнения для стационарных решений рассеяния
- § 24. Рассеяние частицы на двух центрах
- § 25. Простое рассеяние. Интерференция
- § 26. Многократное рассеяние
- Раздел IV. ВЫЧИСЛЕНИЕ АМПЛИТУД ПЕРЕХОДА ВАРИАЦИОННЫМ МЕТОДОМ
- § 27. Стационарные выражения сдвигов фаз. Обсуждение
- § 28. Вариационные вычисления сдвига фаз. Обсуждение
- § 29. Распространение метода на сложные столкновения
- Раздел V. ОБЩИЕ СВОЙСТВА МАТРИЦЫ ПЕРЕХОДА
- § 30. Сохранение потока. S-матрица
- § 31. Соотношение Бора—Пайерлса—Плачека (оптическая теорема)
- § 32. Микрообратимость
- § 33. Свойства инвариантности T-матрицы
- ЧАСТЬ V. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ КВАНТОВОЙ МЕХАНИКИ
- § 1. Релятивистская квантовая механика
- § 2. Обозначения и различные определения
- § 3. Группа Лоренца
- § 4. Классическая релятивистская динамика
- Раздел II. УРАВНЕНИЯ КЛЕЙНА — ГОРДОНА И ДИРАКА
- § 5. Уравнение Клейна—Гордона
- § 6. Уравнение Дирака
- § 7. Построение пространства. Представление Дирака
- § 8. Ковариантная форма уравнения Дирака
- § 9. Сопряженное уравнение. Определение тока
- Раздел III. СВОЙСТВА ИНВАРИАНТНОСТИ УРАВНЕНИЯ ДИРАКА
- § 10. Свойства матриц Дирака
- § 11. Инвариантность уравнения Дирака при ортохронных преобразованиях системы координат
- § 12. Преобразования собственной группы
- § 13. Пространственное отражение и ортохронная группа
- § 14. Построение ковариантных величин
- § 15. Другая формулировка свойств инвариантности: преобразование состояний
- § 16. Условие инвариантности уравнения движения
- § 17. Операторы преобразования. Импульс, момент импульса, четность
- § 18. Законы сохранения и интегралы движения
- § 19. Обращение времени и зарядовое сопряжение
- § 20. Калибровочная инвариантность
- Раздел IV. ИНТЕРПРЕТАЦИЯ ОПЕРАТОРОВ И ПРОСТЫЕ РЕШЕНИЯ
- § 21. Уравнение Дирака и принцип соответствия
- § 22. Динамические переменные частицы Дирака
- § 23. Свободный электрон. Плоские волны
- § 24. Построение плоских волн посредством преобразования Лоренца
- § 25. Центральный потенциал
- § 26. Свободные сферические волны
- § 27. Атом водорода
- Раздел V. НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛ УРАВНЕНИЯ ДИРАКА
- § 29. Теория Паули как нерелятивистский предел теории Дирака
- § 30. Приложение: сверхтонкая структура и диполь-дипольная связь
- § 31. Поправки высших порядков и преобразование Фолди — Вотхойзена
- § 32. ФВ-преобразование для свободной частицы
- § 33. ФВ-преобразование для частицы во внешнем поле
- § 34. Электрон в центральном электростатистическом потенциале
- § 35. Обсуждения и выводы
- Раздел VI. РЕШЕНИЯ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ И ТЕОРИЯ ПОЗИТРОНОВ
- § 36. Свойства зарядово-сопряженных решений
- § 37. Особое поведение решений с отрицательной энергией
- § 38. Изменение интерпретации состояний с отрицательной энергией. Теория дырок и позитронов
- § 39. Трудности теории дырок
- ГЛАВА XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
- Раздел I. КВАНТОВАНИЕ ВЕЩЕСТВЕННОГО СКАЛЯРНОГО ПОЛЯ
- § 2. Классические свободные поля. Нормальные колебания
- § 3. Квантование свободного поля
- § 4. Лагранжиан поля. Импульс, сопряженный к Ф(r)
- § 5. Комплексные базисные функции
- § 6. Плоские волны. Определение импульса
- § 7. Сферические волны. Определение момента импульса
- § 8. Пространственное отражение и обращение времени
- Раздел II. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ
- § 9. Взаимодействие с системой частиц
- § 10. Слабая связь и рассмотрение по теории возмущений
- § 11. Сдвиги уровней
- § 12. Излучение квантов
- § 13. Квантовая теория распадающихся состояний. Ширина линии
- § 14. Упругое рассеяние. Дисперсионная формула
- § 15. Резонансное рассеяние. Образование метастабильного состояния
- § 16. Поглощение кванта (фотоэлектрический эффект). Радиационный захват
- Раздел III. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
- § 17. Уравнения классической теории Максвелла — Лоренца
- § 18. Инвариантность и законы сохранения классической теории
- § 19. Собственная энергия и классический радиус электрона
- § 20. Электромагнитный потенциал. Выбор калибровки
- § 21. Продольная и поперечная часть векторного поля
- § 22. Исключение продольного поля
- § 23. Энергия, импульс, момент импульса
- § 24. Гамильтониан свободного электромагнитного поля
- § 25. Гамильтониан излучения, взаимодействующего с частицами
- Раздел IV. КВАНТОВАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 26. Квантование свободного поля излучения. Фотоны
- § 27. Плоские волны. Импульс излучения
- § 28. Поляризация
- § 29. Разложение по мультиполям. Фотоны с определенным моментом импульса и четностью
- § 30. Взаимодействие с атомной системой
- § 31. Излучение фотона атомом. Дипольное излучение
- § 32. Комптоновское рассеяние при низких энергиях. Формула Томсона
- ДОПОЛНЕНИЕ В. КОЭФФИЦИЕНТЫ ВЕКТОРНОГО СЛОЖЕНИЯ И МАТРИЦЫ ВРАЩЕНИЯ
- § 1. Момент импульса. Основные обозначения и принятые соглашения
- Раздел I. КОЭФФИЦИЕНТЫ КЛЕБША — ГОРДАНА (К. — Г.) И «3j»-СИМВОЛЫ
- § 3. Основные свойства коэффициентов К. — Г.
- § 4. Методы вычисления
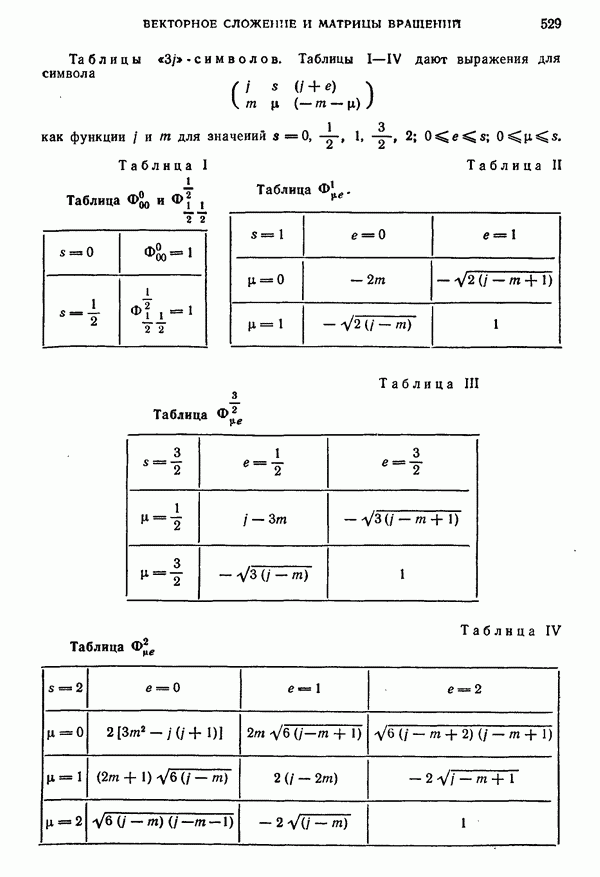
- § 5. Специальные значения и таблицы
- Раздел II. КОЭФФИЦИЕНТЫ РАКА И «6j»-СИМВОЛЫ
- § 6. Определение и основные обозначения
- § 7. Основные свойства «6j»-символов
- § 8. Формула Рака, таблицы
- Раздел III. «9j»-СИМВОЛЫ
- Раздел IV. МАТРИЦЫ ВРАЩЕНИЯ
- § 11. Основные свойства матриц R^J
- § 12. Вычисление матричных элементов
- § 13. Целые значения J (J=l) и преобразование сферических функций при вращениях
- Раздел V. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 15. Тензорное произведение неприводимых тензорных операторов
- ДОПОЛНЕНИЕ Г. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- Раздел I. ОСНОВНЫЕ ПОНЯТИЯ
- § 3. Классы сопряженных элементов
- § 4. Подгруппы
- § 5. Изоморфизм, гомоморфизм
- Раздел II. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ
- § 7. Операции над пространствами представлений. Приводимость
- § 8. Основные теоремы
- § 9. Приложения к квантовой механике
- Раздел III. КОНЕЧНЫЕ ГРУППЫ
- § 10. Основные понятия
- § 11. Представления
- § 12. Неприводимые компоненты представления
- § 13. Построение неприводимых инвариантных подпространств
- Раздел IV. ПЕРЕСТАНОВКИ
- § 14. Основные понятия. Циклы. Классы
- § 15. Разбиения
- § 16. «Симметризаторы» Юнга. Построение неприводимых представлений
- § 17. Основные свойства неприводимых представлений группы
- § 18. Система n фермионов спина 1/2